Najpierw sprawdzamy czy zadanie jest zbilansowane. Suma zdolności produkcyjnych wynosi

3·900=2700 ton, a suma zapotrzebowań to 500+600+700+800=2600 ton. Liczby te są różne,
więc zadanie jest niezbilansowane. Dodajemy więc piątego odbiorcę – niewykorzystane moce

produkcyjne (NM). Musi do niego trafić 100 ton (bo o tyle zdolności produkcyjne są większe od
zapotrzebowań). Tworzymy macierz kosztów. Dla odbiorców S1-S4 koszty to koszt

wyprodukowania + koszt transportu, dla niewykorzystanych mocy koszt to 0 (bo nic nie
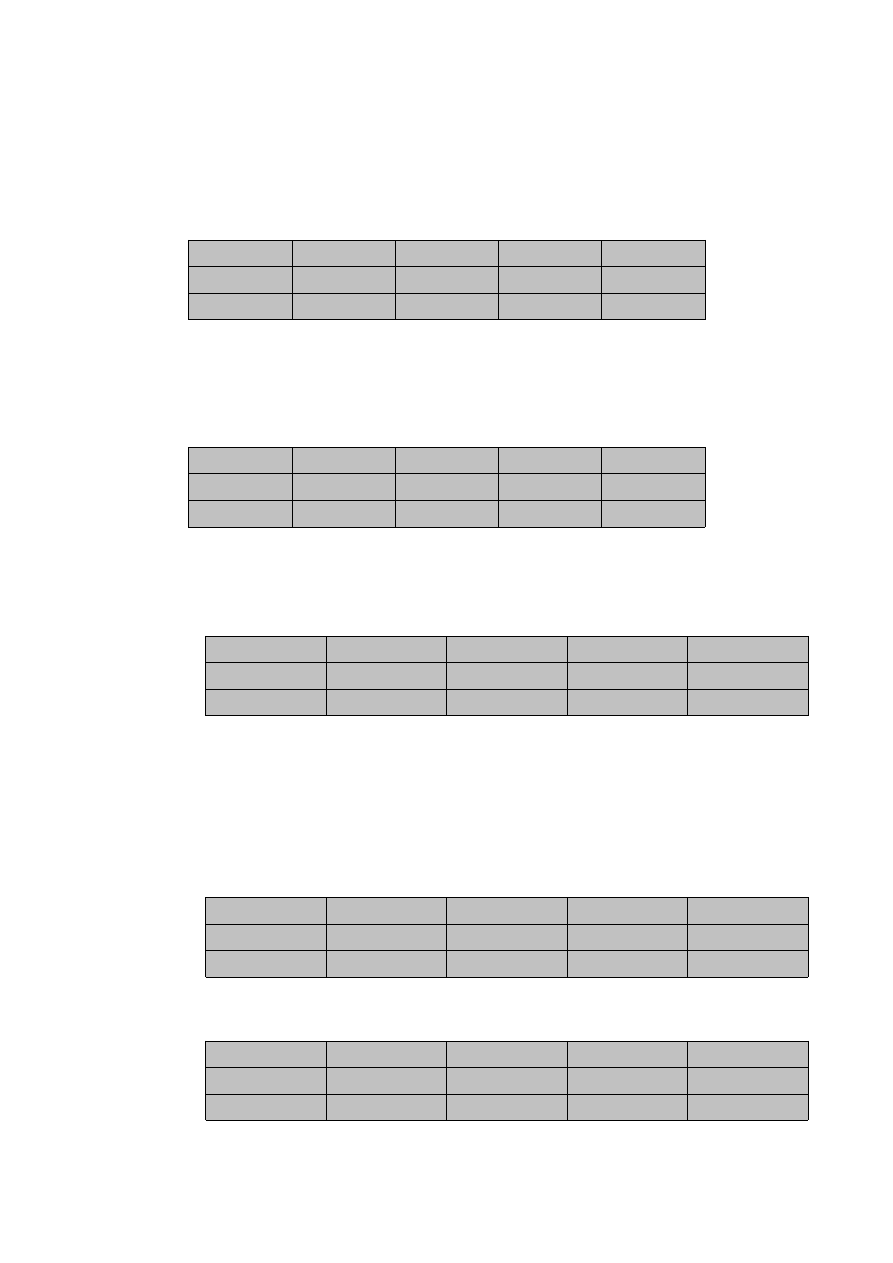
produkujemy). Czyli macierz kosztów wygląda tak:

S1

S2

S3

S4

NM

Produkcja

C1

113

113

111

110

0

900

C2

108

104

102

103

0

900

C3

114

117

116

114

0

900

Zapotrz.

500

600

700

800

100

Zaczynamy od wyznaczenia jakiegoś rozwiązania startowego. Może być ono zupełnie dowolne,

ale im lepsze będzie tym mniej liczenia potem, więc staramy się jak najbardziej korzystać z
tych komórek, w których są małe koszty (tutaj będą to koszty 0, 102, 103, 104...) A więc

może to wyglądać np. tak:

S1

S2

S3

S4

NM

Produkcja

C1

300

600

900

C2

700

200

900

C3

500

300

100

900

Zapotrz.

500

600

700

800

100

Sprawdzamy czy to odgadnięte rozwiązanie jest optymalne. W tym celu tworzymy sobie tabelę
z tzw. potencjałami. Zaczynamy od nadania potencjału 0 któremuś (np. pierwszemu)

wierszowi:

0

Potencjał komórki, to suma potencjałów wiersza i kolumny, w której ona leży minus jej koszt

(czyli liczba z pierwszej tabelki). Chcemy tak nadać potencjały wierszom i kolumnom, aby
komórki, w których mamy w naszym odgadniętym rozwiązaniu jakieś liczby miały potencjały

równe zero.

Np. chcemy mieć potencjał 0 w komórce odpowiadającej za C1-S2 (druga komórka w

pierwszym rzędzie), więc potencjał drugiej kolumny musi być równy 113. Wtedy bowiem
potencjał komórki to 0+113-113=0 (potencjał wiersza+potencjał kolumny-koszt komórki):

113

0

0+113-113=0

Kolejna komórka do wyzerowania potencjału to C1-S4. Potencjał czwartej kolumny musi być
więc równy 110:

113

110

0

0+113-113=0

0+110-110=0

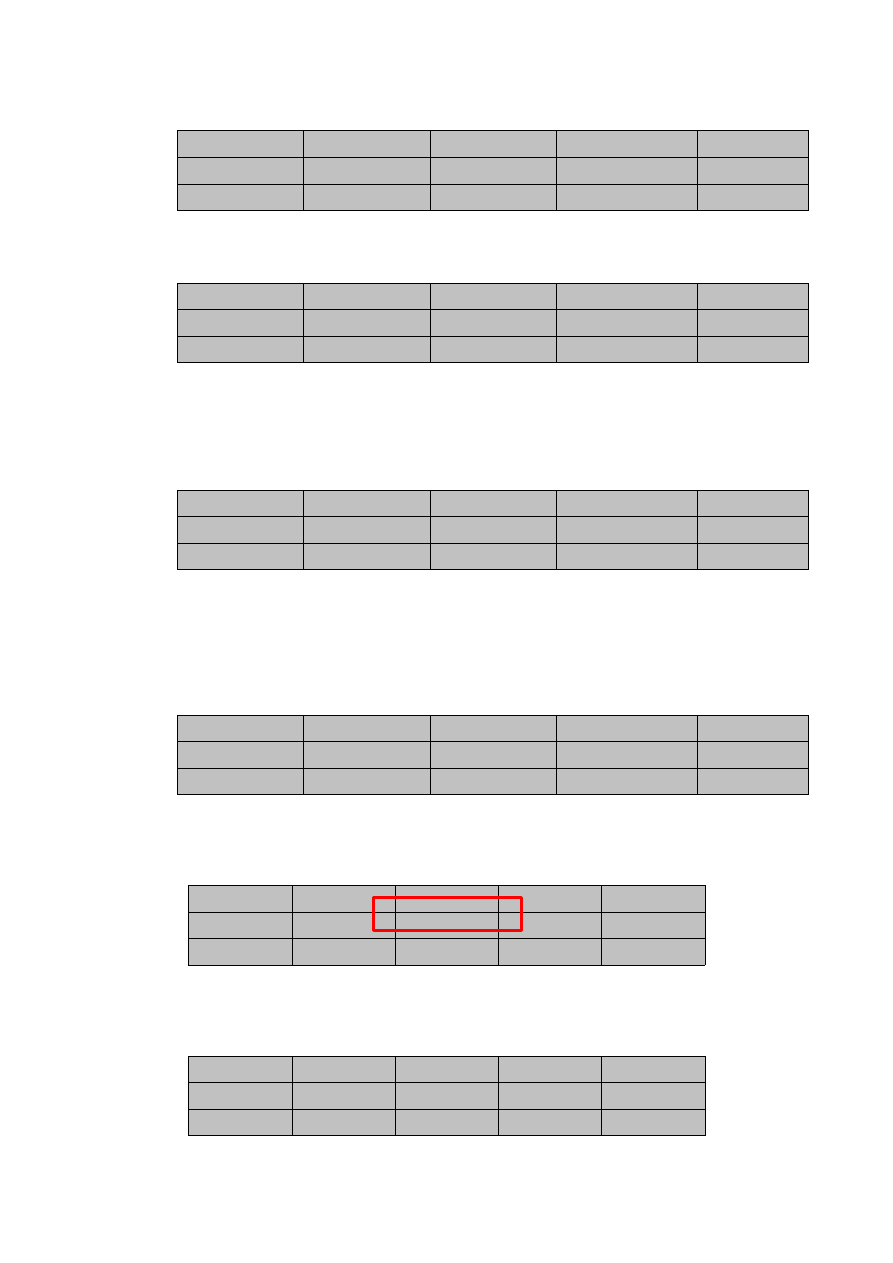
Teraz np. komórka C2-S4. Potencjał drugiego wiersza musi być równy -17:

113

110

0

0+113-113=0

0+110-110=0

-7

-7+110-103=0

I tak dalej, aż wyzerujemy wszystkie potencjały w komórkach, w których mamy jakieś liczby w
naszym odgadniętym rozwiązaniu:

110

113

109

110

-4

0

0

0

-7

0

0

4

0

0

0

Doliczamy teraz potencjały do pozostałych komórek, cały czas stosując wzór

potencjał=potencjał wiersza + potencjał komórki – koszt komórki

i mamy ostateczną tabelkę z potencjałami:

110

113

109

110

-4

0

-3

0

-2

0

-4

-7

-5

2

0

0

-11

4

0

0

-3

0

0

Rozwiązanie jest optymalne, jeśli w tabelce z potencjałami nie ma liczb dodatnich. U nas jest

taka liczba, więc nasze zgadnięte rozwiązanie można poprawić.

Aby poprawić rozwiązanie bierzemy komórkę z największą liczbą w tabeli z potencjałami (czyli

komórkę C2-S2, bo tam jest 2) i znajdujemy cykl zawierający tą komórkę oraz same zera.
Przez cykl rozumiemy łamaną zamkniętą (np. prostokąt). Tutaj taki cykl łatwo znaleźć:

110

113

109

110

-4

0

-3

0

-2

0

-4

-7

-5

2

0

0

-11

4

0

0

-3

0

0

Taki sam cykl rysujemy sobie na naszym zgadniętym rozwiązaniu i oznaczamy kolejne
wierzchołki tego cyklu na zmianę plusami i minusami (zaczynając od + w komórce, którą nam

wskazały potencjały czyli w C2-S2:

S1

S2

S3

S4

NM

Produkcja

C1

300 -

600 +

900

C2

+

700

200 -

900

C3

500

300

100

900

Zapotrz.

500

600

700

800

100

Bierzemy teraz najmniejszą liczbę w komórkach z minusami (czyli 200) i dodajemy ją do
komórek z plusami, a odejmujemy od komórek z minusami i to jest nasze nowe rozwiązanie:

S1

S2

S3

S4

NM

Produkcja

C1

100

800

900

C2

200

700

900

C3

500

300

100

900

Zapotrz.

500

600

700

800

100

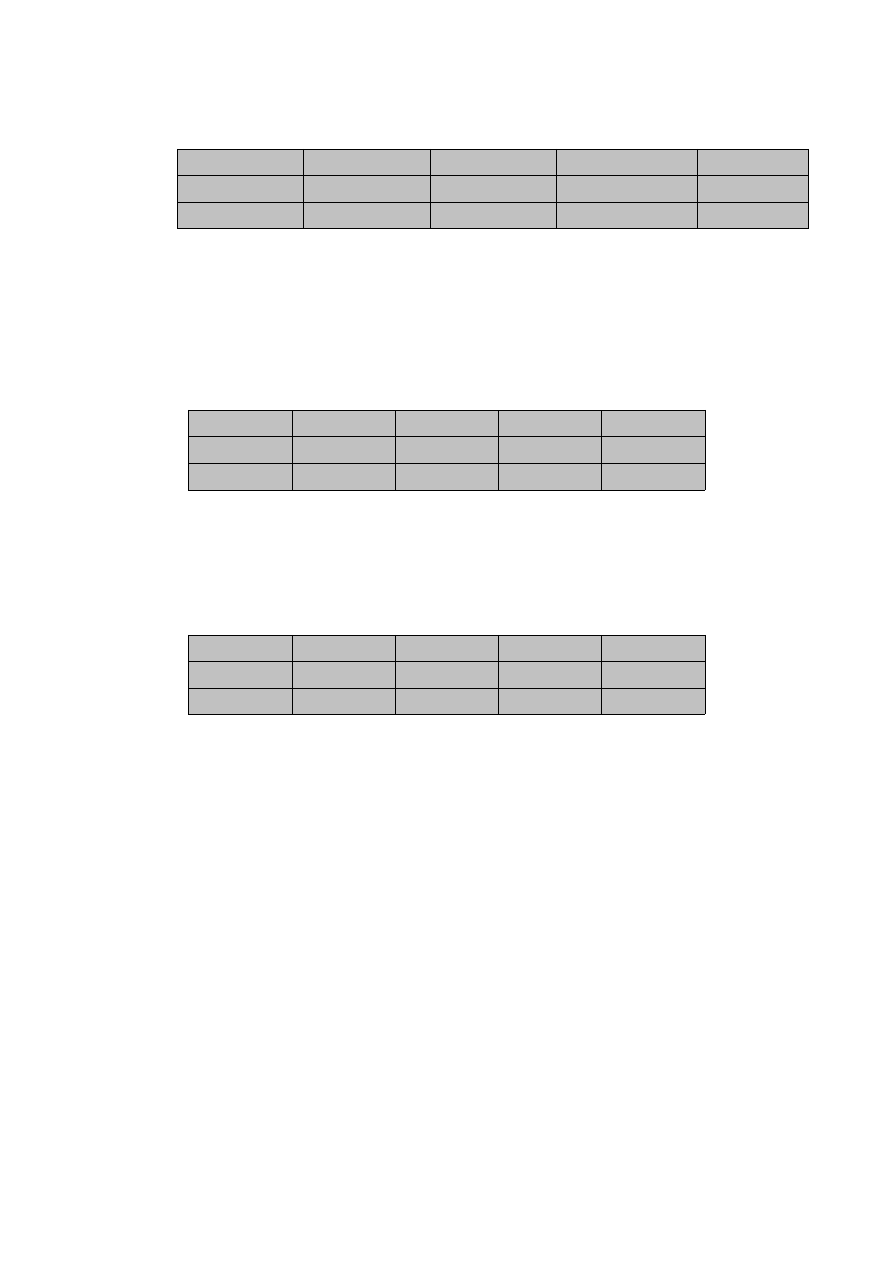
I znów musimy, za pomocą potencjałów sprawdzić, czy jest ono optymalne, a więc budujemy

tabelkę z potencjałami, zupełnie identycznie, jak do rozwiązania odgadniętego. Wychodzi taka:

110

113

111

110

-4

0

-3

0

0

0

-4

-9

-7

0

0

-2

-13

4

0

0

-1

0

0

Jak widać, tu już nie ma liczb dodatnich, a więc rozwiązanie jest optymalne.

Możemy wyliczyć jego koszt mnożąc liczby z tabelki z rozwiązaniem przez liczby z tabeli
kosztów (pierwsza tabela w tym rozwiązaniu):

K=100·113+800·110+200·104+700·102+500·114+300·117+100·0=283600.

Jeśli za kryterium przyjmiemy tylko koszty transportu, to macierz kosztów jest taka jak w
zadaniu (bo nie dodajemy kosztów produkcji) :

S1

S2

S3

S4

NM

Produkcja

C1

8

8

6

5

0

900

C2

8

4

2

3

0

900

C3

4

7

6

4

0

900

Zapotrz.

500

600

700

800

100

Nasze rozwiązanie optymalne dla zadania z kosztami produkcji ma koszt

K=100·8+800·5+200·4+700·2+500·4+300·7+100·0=11100.

Popatrzmy np. na takie rozwiązanie:

S1

S2

S3

S4

NM

Produkcja

C1

800

100

900

C2

200

700

900

C3

500

400

900

Zapotrz.

500

600

700

800

100

Koszt takiego rozwiązania wynosi: K=11000 (wyliczony, tak jak wyżej, mnożąc liczby z
powyższej tabelki przez liczby z tabeli kosztów), a więc jest niższy niż koszt rozwiązania

optymalnego z uwzględnieniem kosztów produkcji. Stąd wniosek, że jeśli nie bierzemy pod
uwagę kosztów produkcji, to rozwiązanie optymalne można jeszcze poprawić. A więc

rozwiązanie optymalne bez kosztów produkcji jest inne niż z tymi kosztami. (Zadanie nie każe
wyliczać rozwiązania optymalnego bez kosztów produkcji, więc tego nie robimy).