1

Wymagania stawiane układom

automatyki

2

W zastosowaniach praktycznych układom

automatyki stawiane są wymagania:

- zapewnienia odpowiedniego

zapasu

stabilności

,

- osiągnięcia właściwej

jakości regulacji

w

stanach przejściowych,

- nie przekroczenia dopuszczalnego

uchybu ustalonego

.

3

Do analizy

stabilności

liniowych układów automatyki

wykorzystuje się:

 kryterium analityczne Hurwitza,
 kryterium graficzne Nyquista.

Do oceny

jakości regulacji

w stanie przejściowym

stosuje się:

 parametry odpowiedzi skokowej,
 wskaźnik regulacji,
 kryteria całkowe.

Do określenia

uchybu ustalonego

regulacji służy

twierdzenie o wartości końcowej przekształcenia
Laplace’a.

4

Stabilność jest jednym z podstawowych pojęć teorii
sterowania, wyrażającym własność pozostawania
rozwiązań równań różniczkowych opisujących układ
dynamiczny w odpowiednio określonym obszarze
ograniczonym.
Układ sterowania jest

stabilny

, jeżeli po wytrąceniu ze

stanu równowagi sam wraca do stanu poprzedniego.

Pojęcie to odnosi się zarówno do zamkniętych jak i

otwartych liniowych układów sterowania.

O stabilności układu sterowania można wnioskować na

podstawie równania różniczkowego, opisującego

związek między wielkością wyjściową y(t) a wejściową
x(t).

ZAPAS STABILNOŚCI

5

Dokonując przekształcenia Laplace'a równania
różniczkowego można wyznaczyć transformatę
odpowiedzi układu Y(s) w postaci:

Wielomian M(s) w mianowniku transmitancji G(s)

określa właściwości dynamiczne tego układu i nazywa

się

wielomianem charakterystycznym.

)

s

(

X

)

s

(

M

)

s

(

L

)

s

(

X

s

a

s

b

)

s

(

X

)

s

(

G

)

s

(

Y

l

n

0

l

l

k

m

0

k

k















)

dt

x

d

b

(

)

dt

y

d

a

(

k

k

m

0

k

k

l

l

n

0

l

l











6

Rozwiązanie równania różniczkowego, stanowiące
odpowiedź układu sterowania, jest sumą składowej
wymuszonej y

w

(t) i składowej przejściowej y

p

(t):

y(t)= y

w

(t) + y

p

(t)

Składowa wymuszona jest określona przez parametry

układu oraz przebieg wymuszenia i nie musi być

brana pod uwagę przy badaniu stabilności układu.

O tym czy układ nadąża za zmianami wielkości

sterującej, decyduje przebieg składowej przejściowej,

zależny od właściwości dynamicznych układu.
Badanie

stabilności

układu sterowania można zatem

ograniczyć do analizy składowej przejściowej, która

jest rozwiązaniem jednorodnego równania

różniczkowego badanego układu.

7

Przebieg składowej przejściowej jest określony przez

równanie charakterystyczne

,

które otrzymuje się

poprzez przyrównanie wielomianu charakterystycznego
do zera:

M(s)=a

n

s

n

+ a

n-1

s

n-1

+ ... + a

1

s + a

o

= 0

Jeżeli pierwiastki równania charakterystycznego

s

i

są

jednokrotne, to składowa przejściowa wyraża się

kombinacją liniową funkcji wykładniczych:







n

0

i

t

s

i

p

i

e

c

)

t

(

y

Na przebieg składowej przejściowej i

stabilność

układu

sterowania ma wpływ położenie pierwiastków równania

charakterystycznego

s

i

na płaszczyźnie zmiennej

zespolonej.

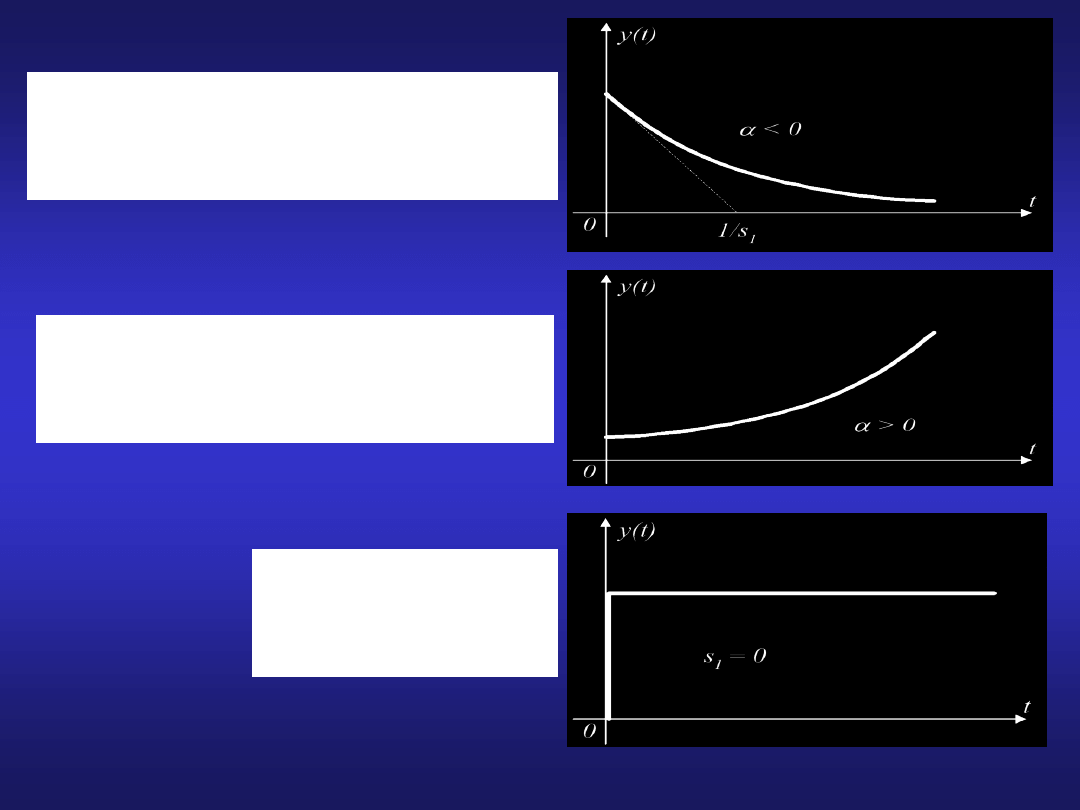
8

Pierwiastki rzeczywiste

















t

przy

e

c

)

t

(

y

s

t

1

p

1



















t

przy

0

e

c

)

t

(

y

s

t

1

p

1

1

t

0

1

p

1

c

e

c

)

t

(

y

0

s









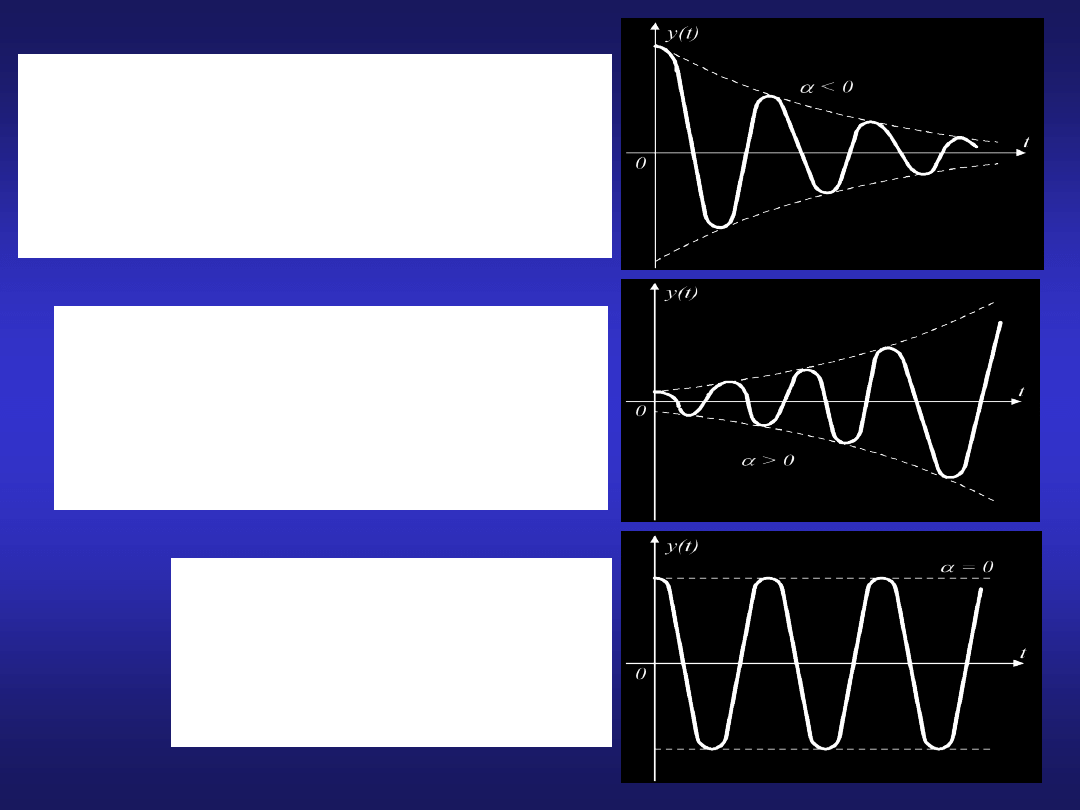
9

Pierwiastki zespolone

)

t

cos(

ce

e

c

e

c

)

t

(

y

j

s

t

t

)

j

(

2

t

)

j

(

1

p

2

,

1











































)

t

cos(

ce

e

c

e

c

)

t

(

y

j

s

t

t

)

j

(

2

t

)

j

(

1

p

2

,

1



































)

t

cos(

c

e

c

e

c

)

t

(

y

j

s

t

j

2

t

j

1

p

2

,

1

























10

Aby procesy przejściowe zanikały, czyli żeby badany

układ był

stabilny

, wszystkie pierwiastki rzeczywiste

muszą być ujemne, a zespolone mieć ujemną część

rzeczywistą.

Jeżeli chociażby jeden z pierwiastków równania

charakterystycznego ma dodatnią część rzeczywistą, to

układ sterowania jest

niestabilny

.

W przypadku, w którym istnieją pierwiastki

jednokrotne o części rzeczywistej równej zeru, układ

znajduje się na

granicy stabilności

.

Przy czym dla pierwiastków rzeczywistych odpowiedź
jest

aperiodyczna

, a dla pierwiastków zespolonych

odpowiedź układu ma charakter

oscylacyjny

.

Koniecznym i dostatecznym warunkiem stabilności

asymptotycznej (układ wraca do poprzedniego

stanu ustalonego) jest aby: Re(s

i

)<0

11

Liniowy układ sterowania jest stabilny jeżeli wszystkie

pierwiastki równania charakterystycznego mają część

rzeczywistą mniejszą od zera, czyli leżą w lewej

półpłaszczyźnie zmiennej zespolonej s.

Twierdzenia, pozwalające ocenić stabilność bez
obliczania pierwiastków równania
charakterystycznego układu (biegunów), nazywane są

kryteriami stabilności

.

Wyróżnia się:
• kryteria analityczne, np. Hurwitza lub Routha
• kryteria graficzne częstotliwościowe, np. Nyquista
• kryteria grafo-analityczne, np. Michajłowa.

12

Określa warunki, jakie powinny spełniać
współczynniki równania charakterystycznego, aby
pierwiastki tego równania miały ujemne części
rzeczywiste.

Kryterium Hurwitza

Układ automatyki jest stabilny tylko wówczas, gdy
współczynniki równania charakterystycznego
(a

n

, a

n-1

, ..., a

0

) układu zamkniętego:

a

n

s

n

+ a

n-1

s

n-1

+ ... + a

1

s + a

0

= 0

oraz podwyznaczniki W

1

, W

2

, ... ,W

n-1

wyznacznika

Hurwitza W

n

są większe od zera.

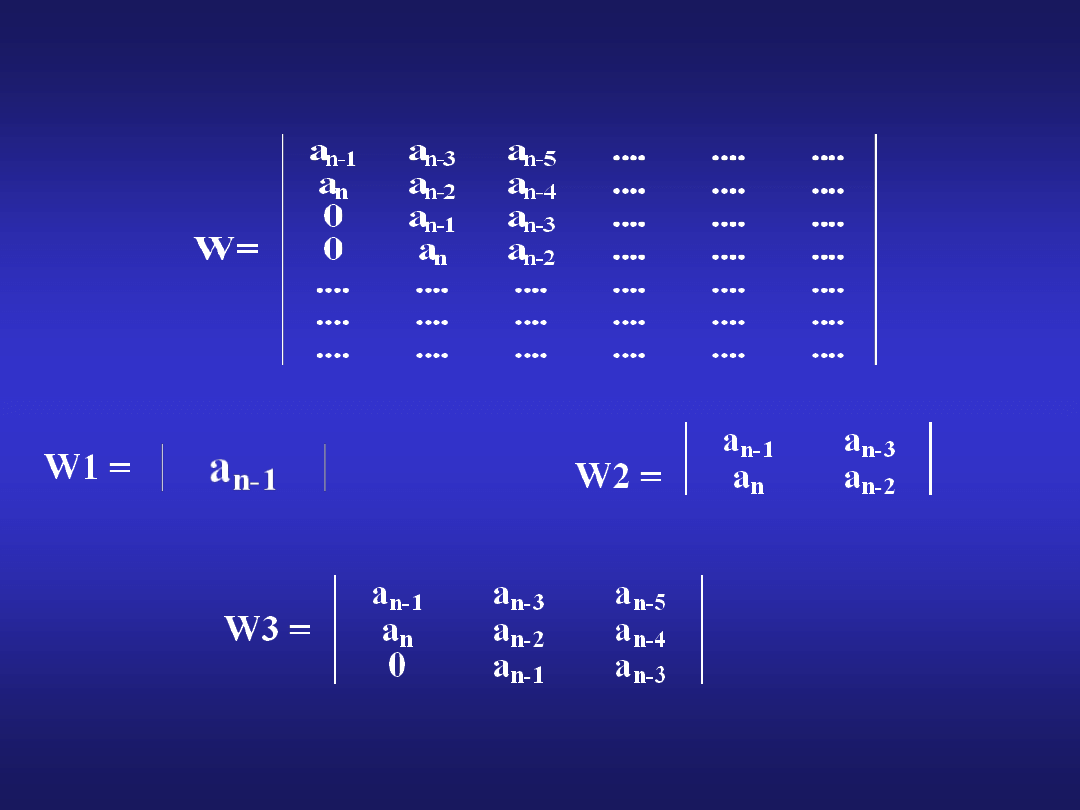
13

n

14

W przypadku, gdy układ jest

niestabilny

, kryterium

Hurwitza nie pozwala określić liczby pierwiastków
równania charakterystycznego leżących w prawej
półpłaszczyźnie zmiennej zespolonej s.

Kryterium Hurwitza nie pozwala określić

zapasu

stabilności

, ale umożliwia znalezienie wartości

parametrów układu automatyki przy których
będzie stabilny, np. wartości nastaw regulatora.

15

Przykład

Transmitancja układu otwartego ma postać:

Należy wyznaczyć graniczną wartość współczynnika
wzmocnienia k, taką aby układ zamknięty był stabilny
dla: T

1

= 5 sek, T

2

= 2 sek, T

3

= 1.4 sek

)

s

T

1

)(

s

T

1

)(

s

T

1

(

k

)

s

(

G

3

2

1

o









Transmitancja układu zamkniętego:

Równanie charakterystyczne układu:

T

1

T

2

T

3

s

3

+(T

1

T

2

+T

1

T

3

+T

2

T

3

)s

2

+(T

1

+T

2

+T

3

)s+1+k = 0

k

)

s

T

1

)(

s

T

1

)(

s

T

1

(

k

)

s

(

G

3

2

1

z











16

stąd k > -1, zaś w praktyce k > 0

Wyznacznik Hurwitza:

gdzie: a

3

= T

1

T

2

T

3

> 0 a

2

= T

1

T

2

+ T

1

T

3

+ T

2

T

3

> 0

a

1

= T

1

+ T

2

+ T

3

> 0 a

0

= 1+k > 0

W

1

= a

2

= 5 · 2 + 2 · 1.4 + 1.4 · 5= 19.8 > 0

W

2

= a

2

a

1

- a

0

a

3

= 19.8 · 8.4 - 14 ( 1 + k) > 0

K< 10.88

Układ zamknięty będzie stabilny dla:
0 < k < 10.88

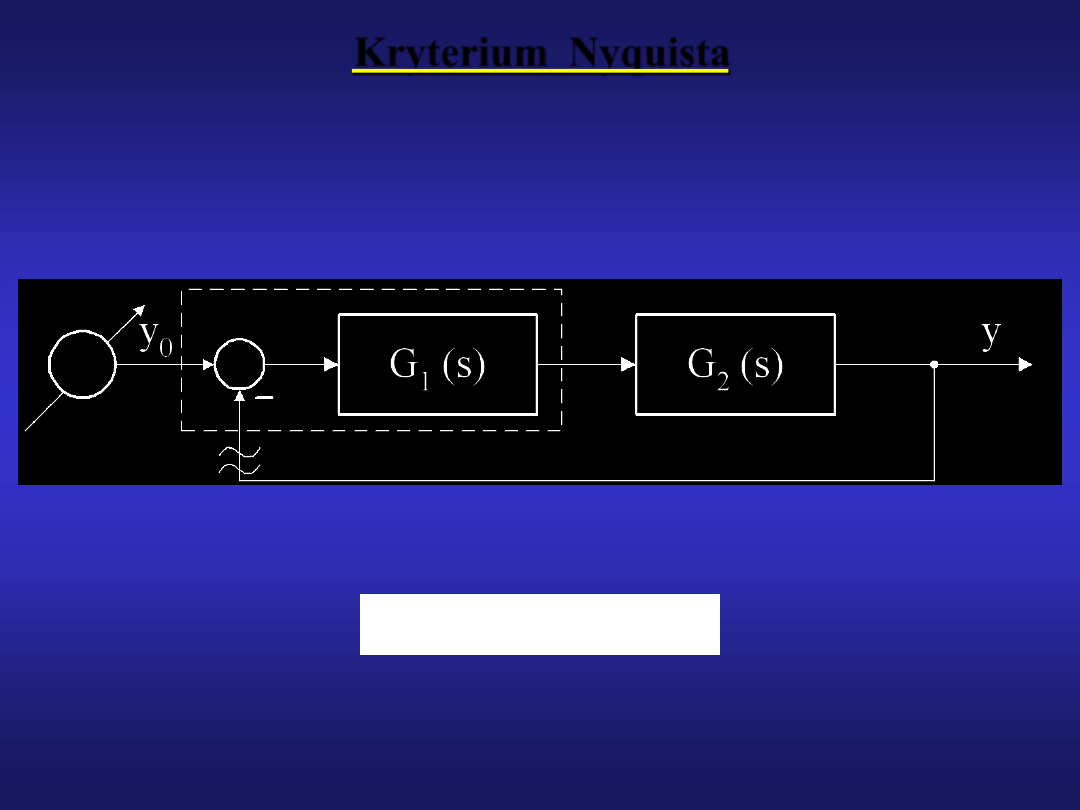
17

Kryterium Nyquista

Kryterium pozwala określić

stabilność

układu

zamkniętego na podstawie charakterystyki amplitudowo-
fazowej układu otwartego.

Transmitancja układu otwartego G

o

(s):

G

0

(s) = G

1

(s) G

2

(s)

18

Transmitancja układu zamkniętego:

Równanie charakterystyczne:

M(s)=1 + G

0

(s)=0

stąd

G

0

(s) = -1

Warunek graniczny stabilności:
- amplituda: |G

0

(s)| = 1

- faza: φ = -π
czyli przejście charakterystyki amplitudowo-fazowej

układu otwartego przez punkt (-1, j0)

)

s

(

G

1

)

s

(

G

)

s

(

G

o

o

z





19

Jeżeli układ otwarty jest stabilny, to układ zamknięty
jest również stabilny, jeżeli charakterystyka
amplitudowo-fazowa układu otwartego nie obejmuje

punktu (-1, j0).

Jeżeli układ otwarty jest niestabilny i ma k
pierwiastków na prawej półpłaszczyźnie, to układ
zamknięty jest stabilny, jeżeli charakterystyka
amplitudowo-fazowa układu otwartego obejmuje
punkt (-1, j0) k/2 razy.

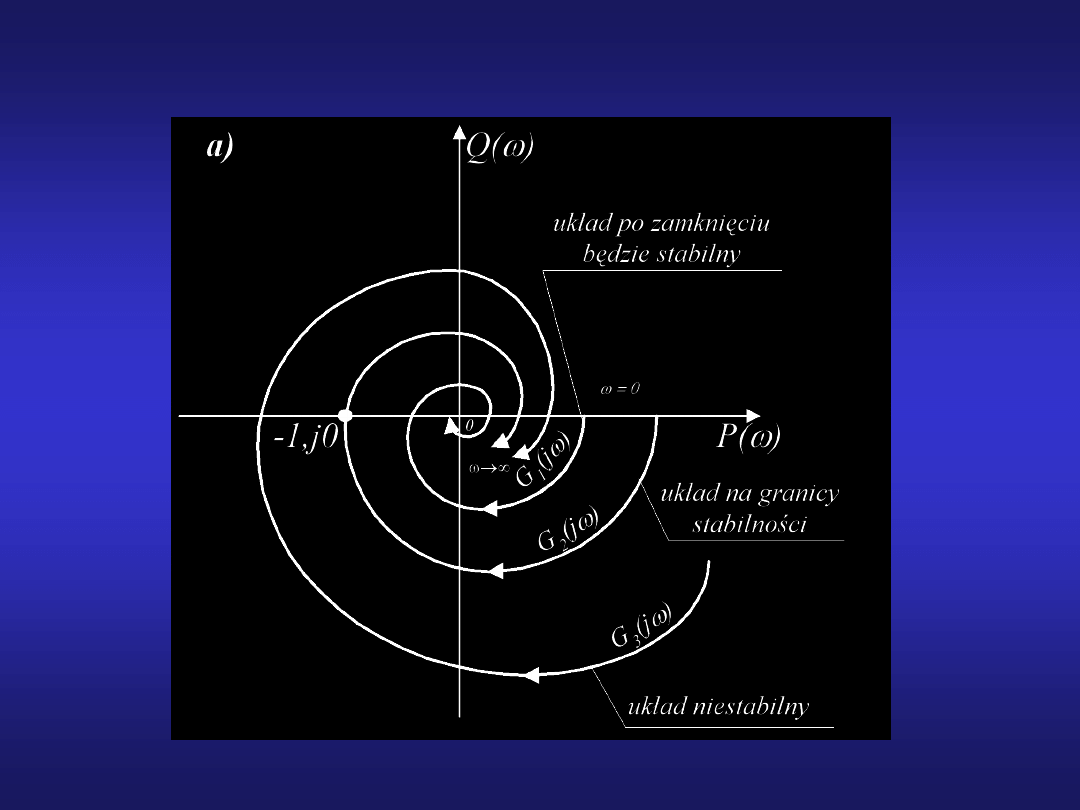
20

Kryterium Nyquista dla układów statycznych

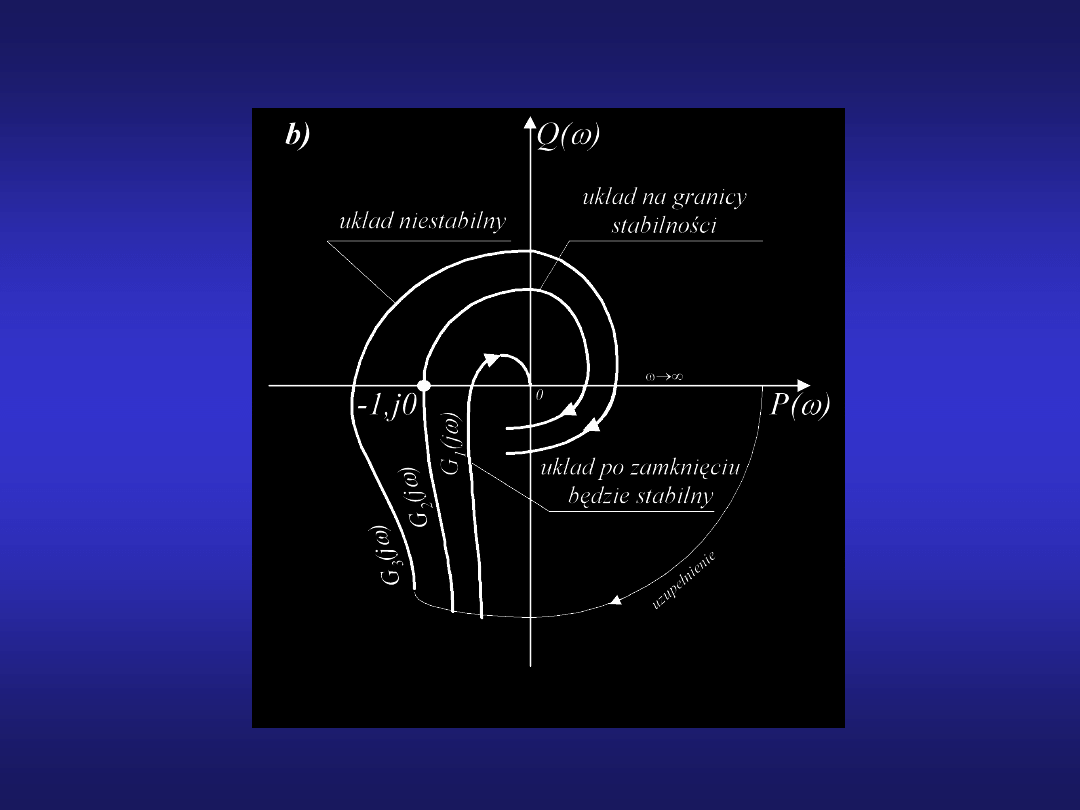
21

Kryterium Nyquista dla układów astatycznych I rzędu

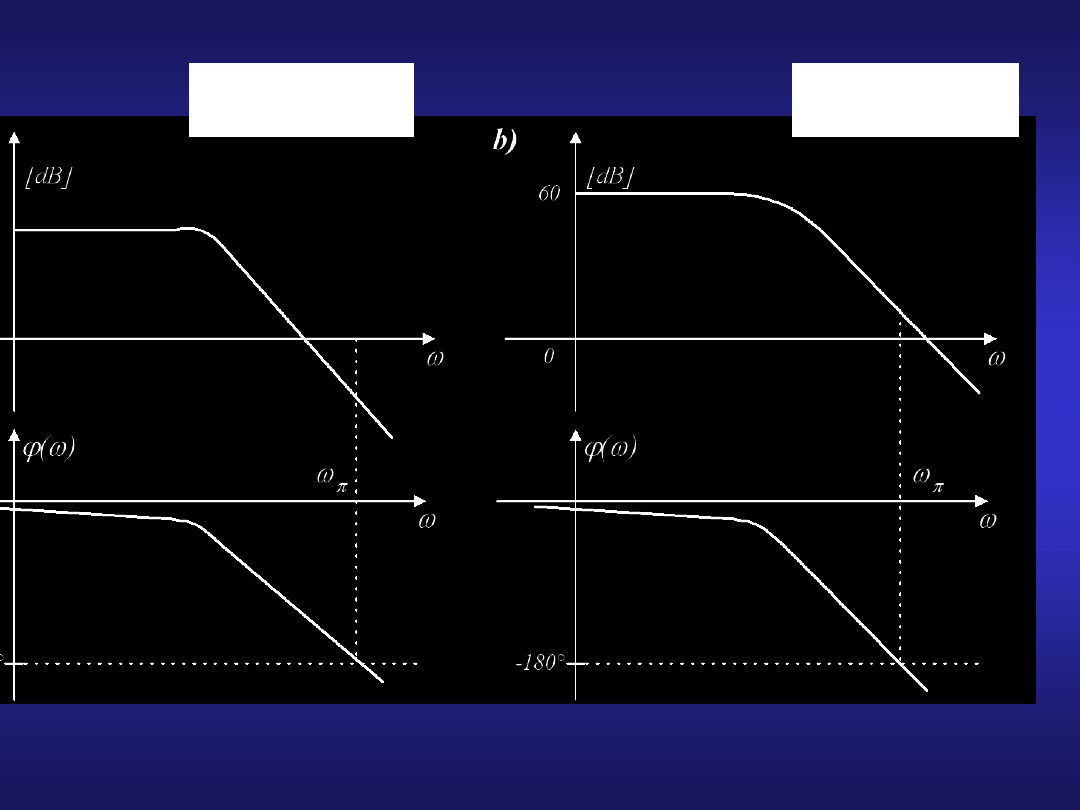
22

Logarytmiczne kryterium Nyquista

układ po zamknięciu

będzie stabilny

układ po zamknięciu

będzie niestabilny















0

A

lg

20

1

A















0

A

lg

20

1

A

20 lg |G(jω)|

20 lg |G(jω)|

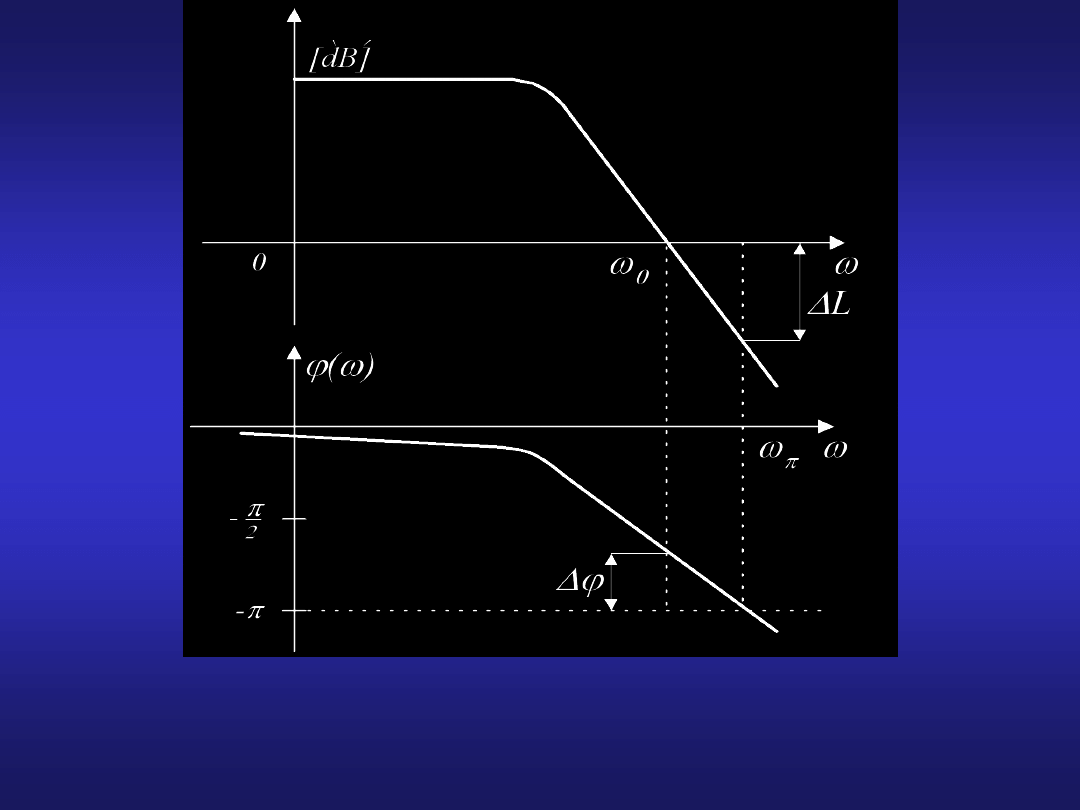
23

zapas
amplitudy

zapas fazy

W dobrze tłumionych układach, niepodatnych na samowzbudzenie

zapas amplitudy powinien wynosić od 6 do 12 dB, a zapas fazy od

30

0

do 60

0

.

20 lg |G(jω)|

24

JAKOŚĆ REGULACJI W STANACH

PRZEJŚCIOWYCH

Kryteria czasowe

Tworzą parametry odpowiedzi układu (uchybu regulacji e lub

wielkości regulowanej y) na skokowe zmiany wielkości zadanej

lub zakłóceń:

•

czasu regulacji

t

r

jako czasu po upływie którego uchyb regulacji

staje się mniejszy niż przyjęta wartość dopuszczalna



e,

najczęściej przyjmuje się t

r

 min oraz



e = (0.02

0.05) y

z

•przeregulowania

æ = e

2

/ e

1

· 100% = 10

30 % , najczęściej

przyjmuje się 20%

Czas regulacji określający szybkość działania układu, w praktyce
można ocenić w przybliżeniu jako: t

r

= (3

5) T

zast ob

25

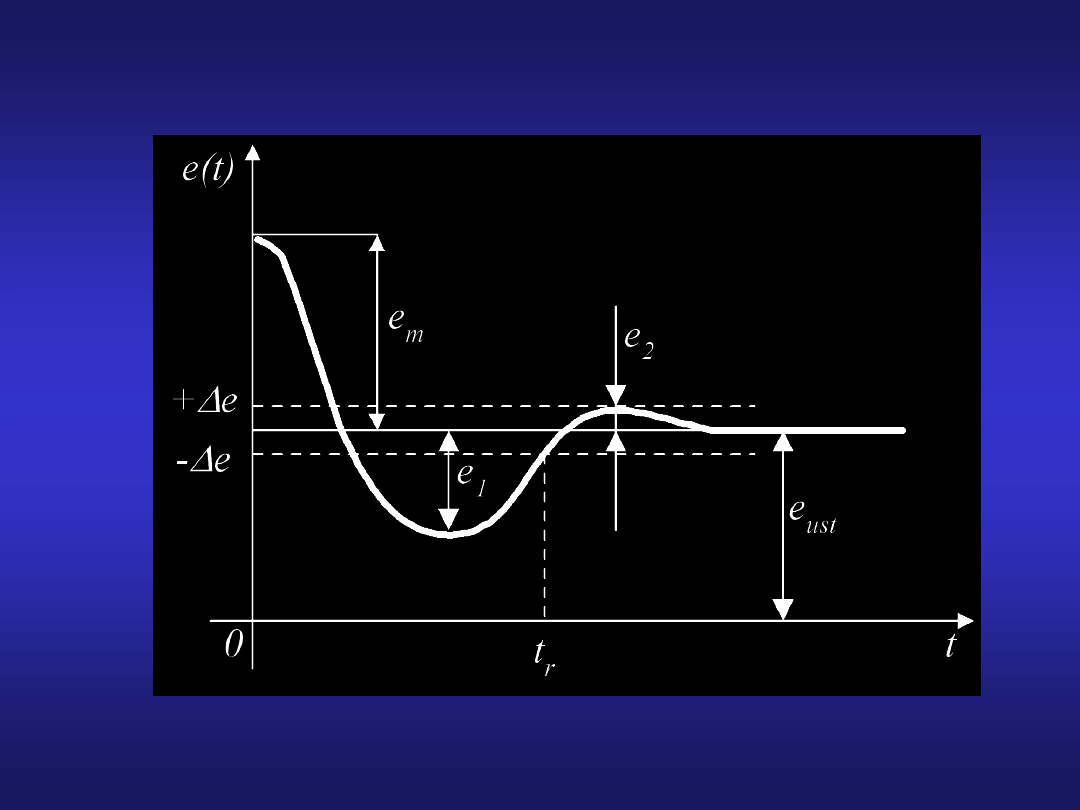
Oscylacyjny przebieg uchybu regulacji wywołany skokową zmianą

wartości zadanej

26

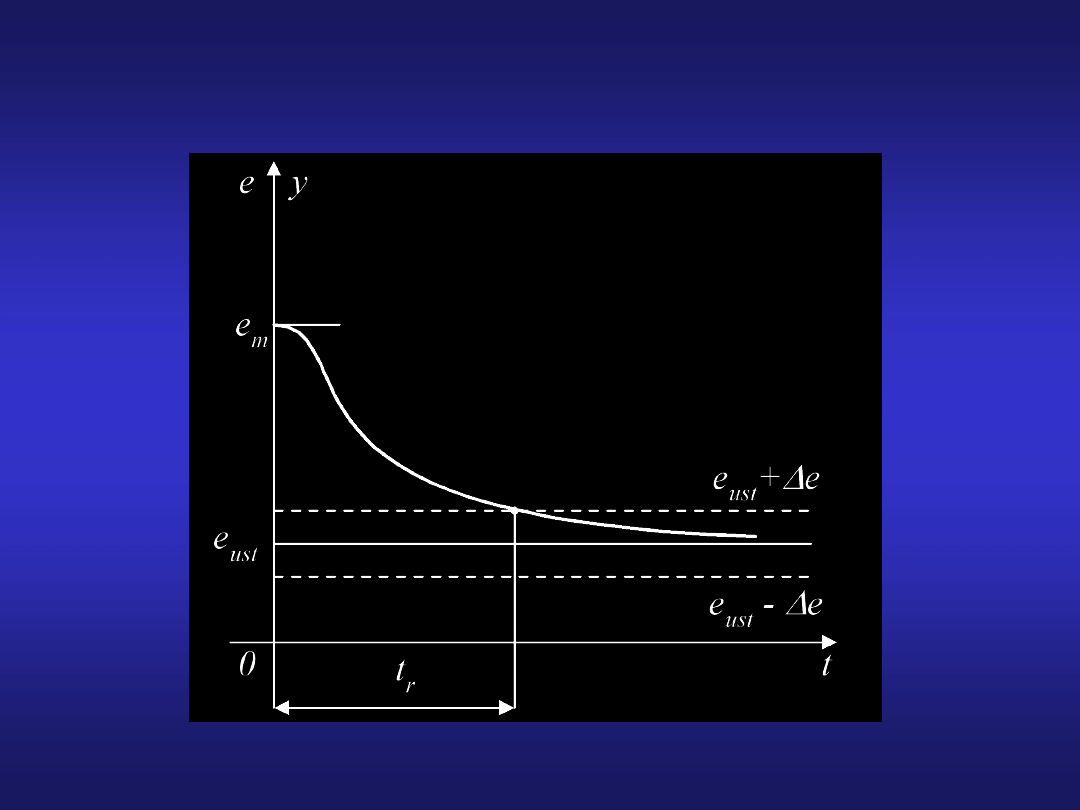
Aperiodyczny przebieg uchybu regulacji wywołany skokową zmianą

wartości zadanej

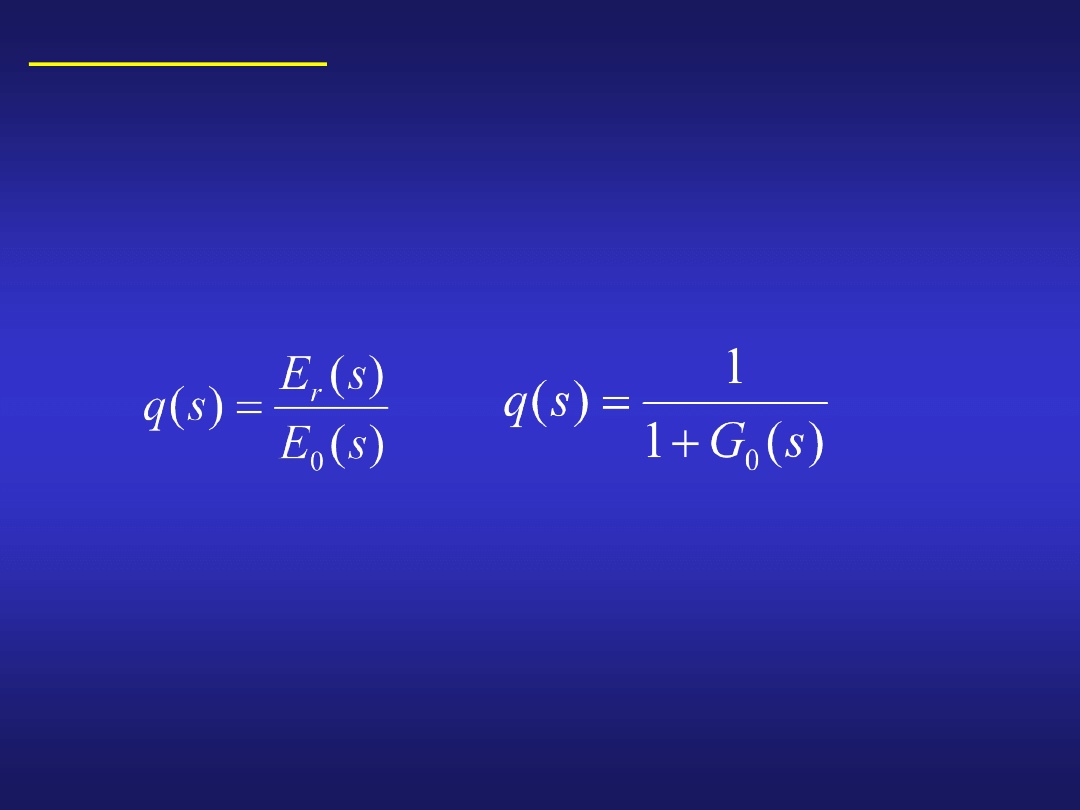
27

Wskaźnik regulacji

Za wskaźnik regulacji przyjmuje się stosunek
transformaty Laplace`a uchybu regulacji układu
zamkniętego E

r

(s) (z regulatorem) do transformaty

Laplace`a uchybu sterowania układu otwartego E

o

(s)

(bez regulatora):

Jeżeli rozpatrywać ten sam układ sterowania przed i po
zamknięciu pętli sprzężenia zwrotnego, to wskaźnik
regulacji pozwala ocenić, o ile zmienia się uchyb
sterowania w wyniku zastosowania ujemnego
sprzężenia zwrotnego.

28

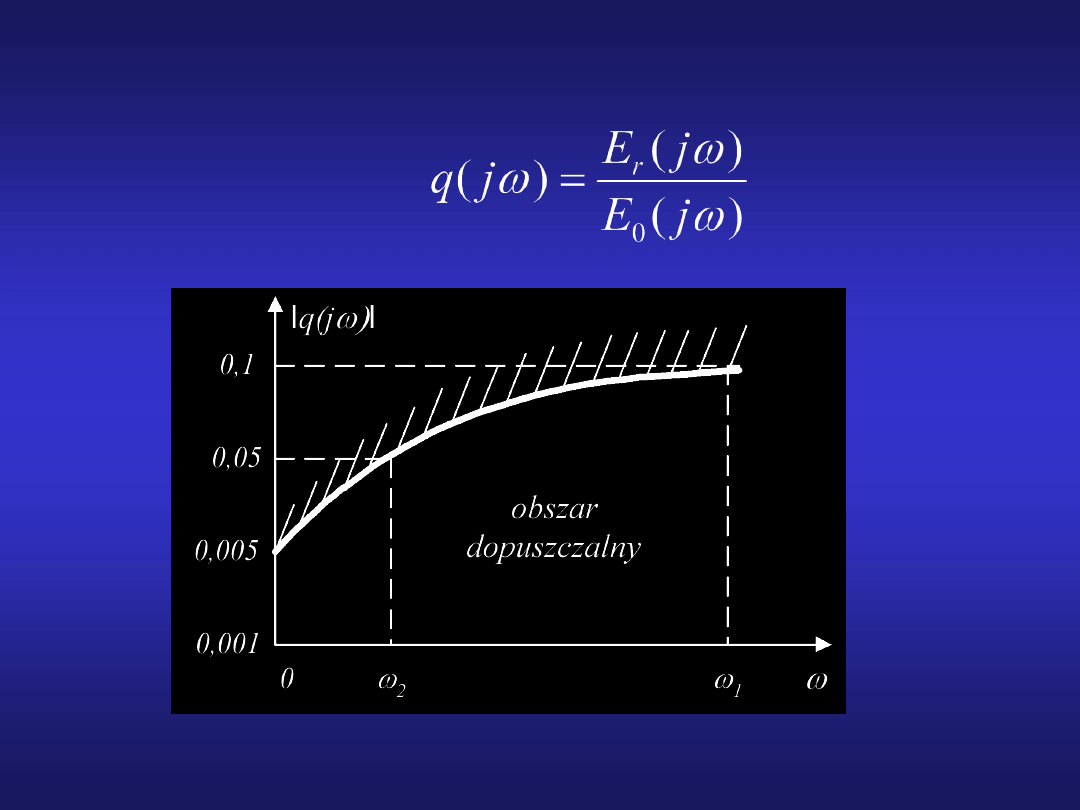
Wskaźnik regulacji najczęściej przedstawia się w
postaci widmowej:

29

Kryteria całkowe

Całkowe kryteria jakości pozwalają ocenić zarówno
jakość regulacji w stanie ustalonym (dokładność
statyczna), jak i w stanie nieustalonym (zapas
stabilności i szybkość działania układu).
Za całkowe kryteria jakości regulacji przyjmuje się
funkcjonały typu:

I

1

= e (t) dt  min IE- integral error

I

2

= e

2

(t) dt min ISE- integral squared

error

30

min

dt

)

t

(

e

t

I

0

2

3



 





min

dt

)

t

(

e

I

0

4









min

dt

)

t

(

e

t

I

0

5









ITSE - integral of time multiplied

by squared error

IAE - integral value of error

ITAE - integral of time multiplied

by absolute value of error

31

DOPUSZCZALNY UCHYB USTALONY

Za

miarę

dokładności

statycznej

regulacji

przyjmuje się wartość uchybu regulacji w stanie
ustalonym:

e(t) = y

o

(t) – y(t)

Wartość

tą

można

wyznaczyć

analitycznie

wykorzystując twierdzenia o wartości końcowej
rachunku operatorowego Laplace’a.

Oczywistym jest, że najbardziej pożądaną wartością
tego uchybu jest wartość zero.

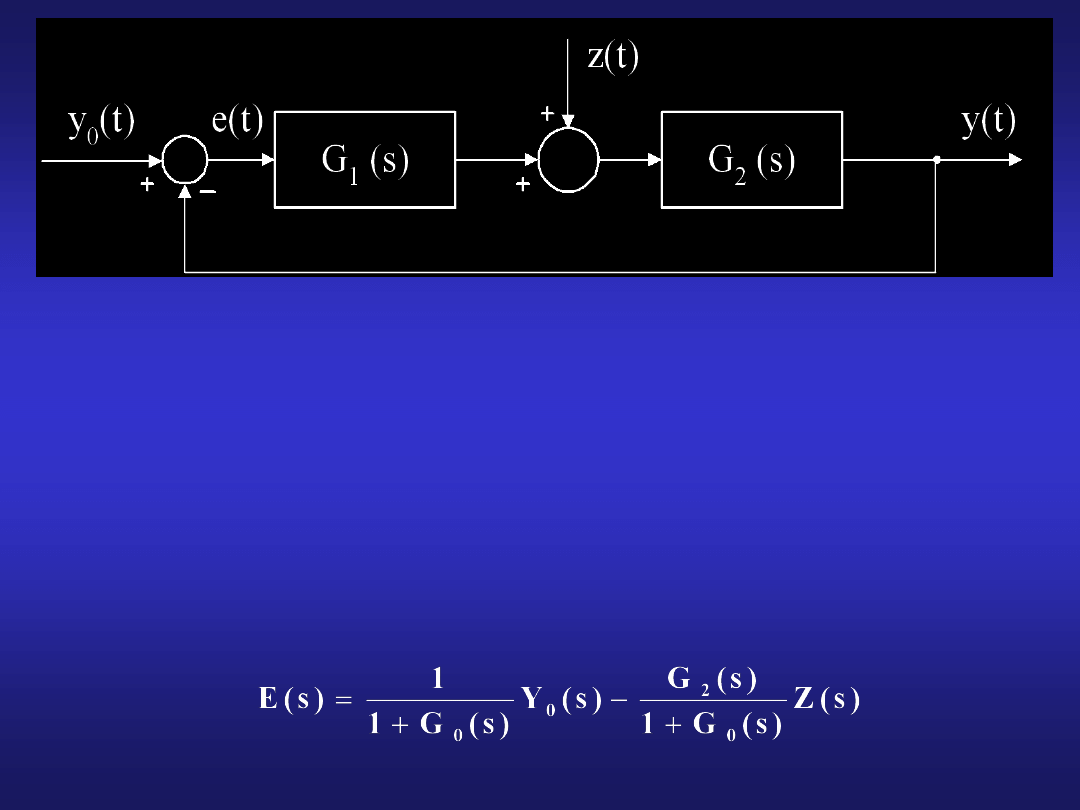
32

Transformata wielkości wyjściowej y(t) jest sumą

składowej wywołanej zmianą wymuszenia i składowej
spowodowanej działaniem zakłócenia:

Y(s) = G

1

(s) G

2

(s) E(s) + G

2

(s) Z(s)

nastepnie

E(s) = Y

o

(s) – Y(s)

E(s) = Y

0

(s) – G

1

(s) G

2

(s) E(s) – G

2

(s) Z(s)

G

o

(s) = G

1

(s) G

2

(s)

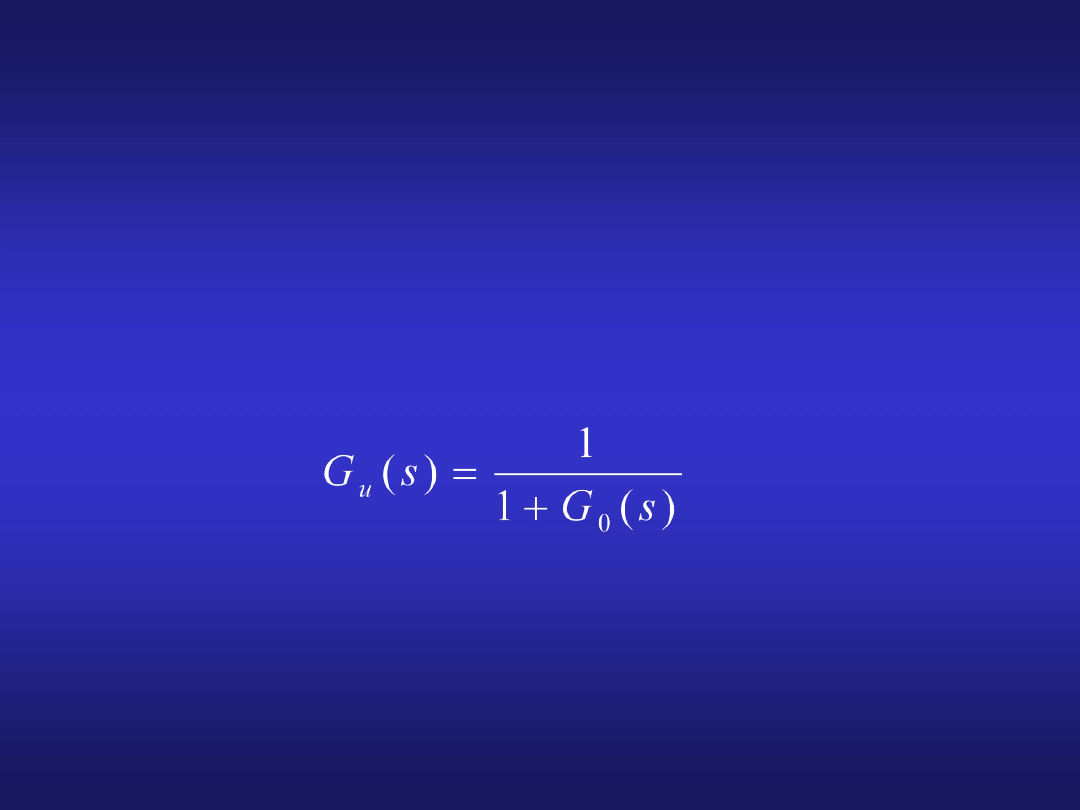
33

Biorąc pod uwagę, że zakłócenia są przypadkowe i nie
można przewidzieć, jaki będzie moduł i argument
transformaty Z(s), dlatego znak minus można zastąpić
znakiem plus:

E(s) = G

u

(s) Y

o

(s) + G

u

(s) G

2

(s) Z(s)

gdzie

nazywa się

transmitancją uchybową

układu zamkniętego.

34

Uchyb nadążania i zakłóceniowy

Na podstawie ostatniej zależności można wyrazić

składową transformaty uchybu wnoszoną przez

zmiany wielkości zadanej y

o

(t) jako

uchyb nadążania

za zmianami wartości zadanej:

E

y

(s) = G

u

(s) Y

o

(s)

a składową – wywołaną oddziaływaniem zakłóceń

można przedstawić w postaci

uchybu zakłóceniowego

:

E

z

(s) = G

u

(s) G

2

(s) Z(s)

Wartość tych składowych w stanie ustalonym
wyznacza się korzystając z twierdzenia o wartości

końcowej przekształcenia Laplace’a.

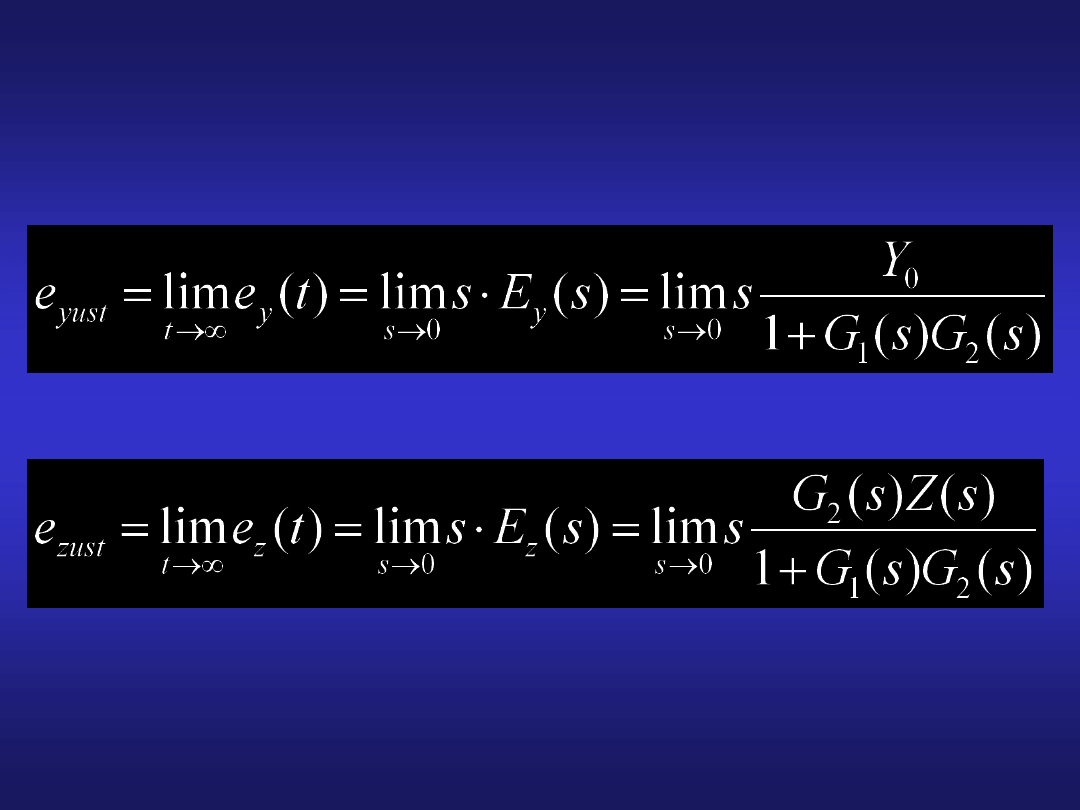
35

Wartości

składowych

uchybu

ustalonego

wyznacza się z następujących zależności: