1
Więźba dachowa rozporowa
Zaprojektować w domu jednorodzinnym dwukondygnacyjnym murowanym wiązar jętkowy
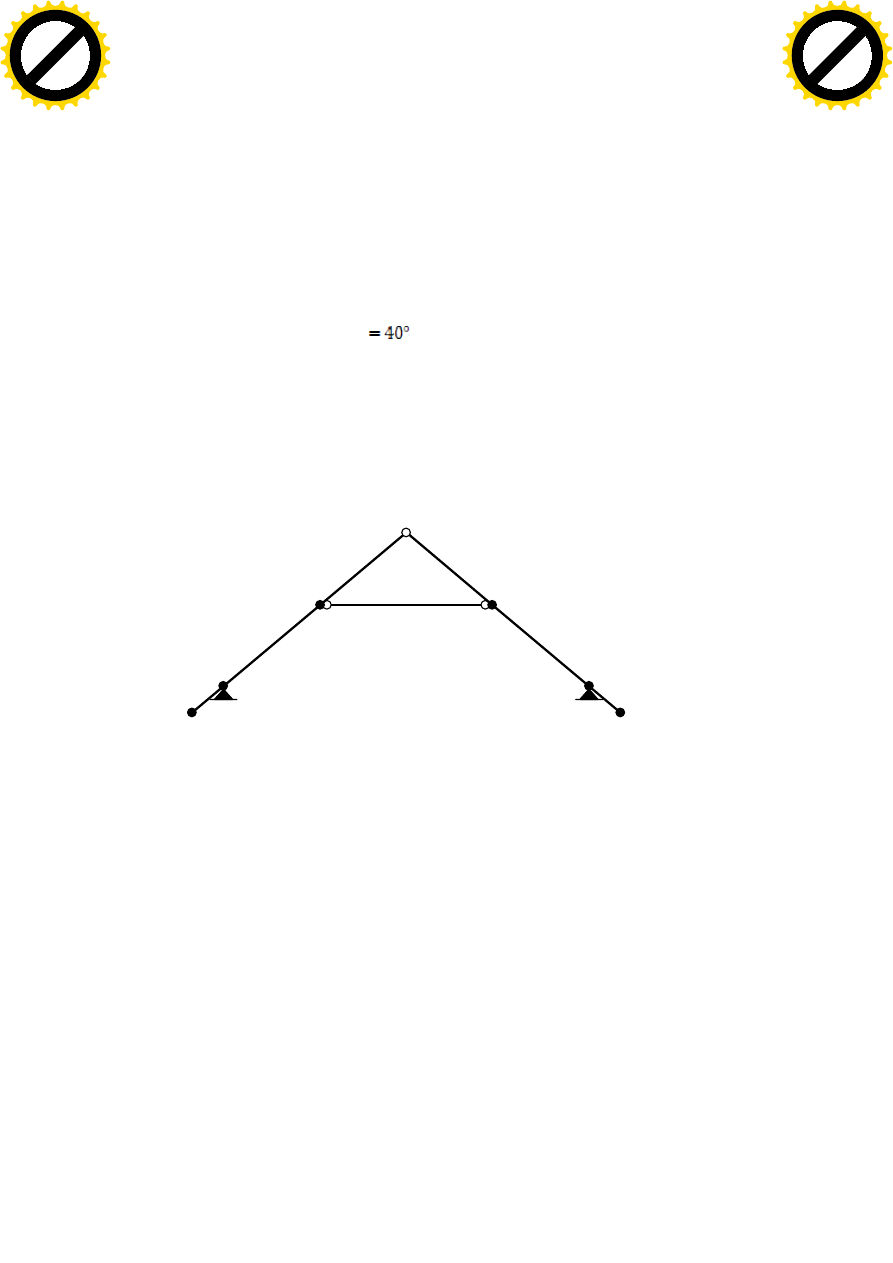
o rozpiętości obliczeniowej 6,24m, o geometrii przedstawionej na rysunku 1. Obliczenia należy
wykonać dla następujących elementów konstrukcyjnych: łata, krokiew, jętka, murłat oraz połączenia
krokwi z jętką i krokwi z murłatem.
Dane do projektowania:
Konstrukcja dachu
– jętkowa
Rozstaw krokwi
– 0,88m
Nachylenie połaci dachowej
Pokrycie dachu
− dachówka ceramiczna - dachówka zakładkowa drążona
H 14 – o szerokości pokrycia (rozstawie łat) 0,213m
Lokalizacja budynku
− Kraków
Obciążenie śniegiem
− strefa III
Obciążenie wiatrem
− strefa I
1
2
3
4
5
6
7
0,540
1,652
1,468
1,468
1,652
0,540
H=7,320
0,453
1,386
1,232
V=3,071
Rys. 1 Geometria projektowanego wiązara jętkowego
Dla drewna sosnowego wartość charakterystyczna ciężaru objętościowego wynosi
ρ
sosna
= 5,5 kN/m
3
. Więźba będzie wykonana z drewna odpowiadającego klasie sortowniczej KG, co
odpowiada klasie wytrzymałościowej C18 (dla tarcicy grubości < 38mm) i C22 (dla tarcicy grubości ≥
38mm).
2
1. OBLICZENIE ŁATY
Przyjęto do obliczeń łaty z drewna sosnowego o grubości 50mm i szerokości 75mm.
Pole przekroju poprzecznego wynosi A = 0,00375m
2
. Więźba będzie wykonana z drewna o klasie
wytrzymałościowej C22 (dla tarcicy grubości
)
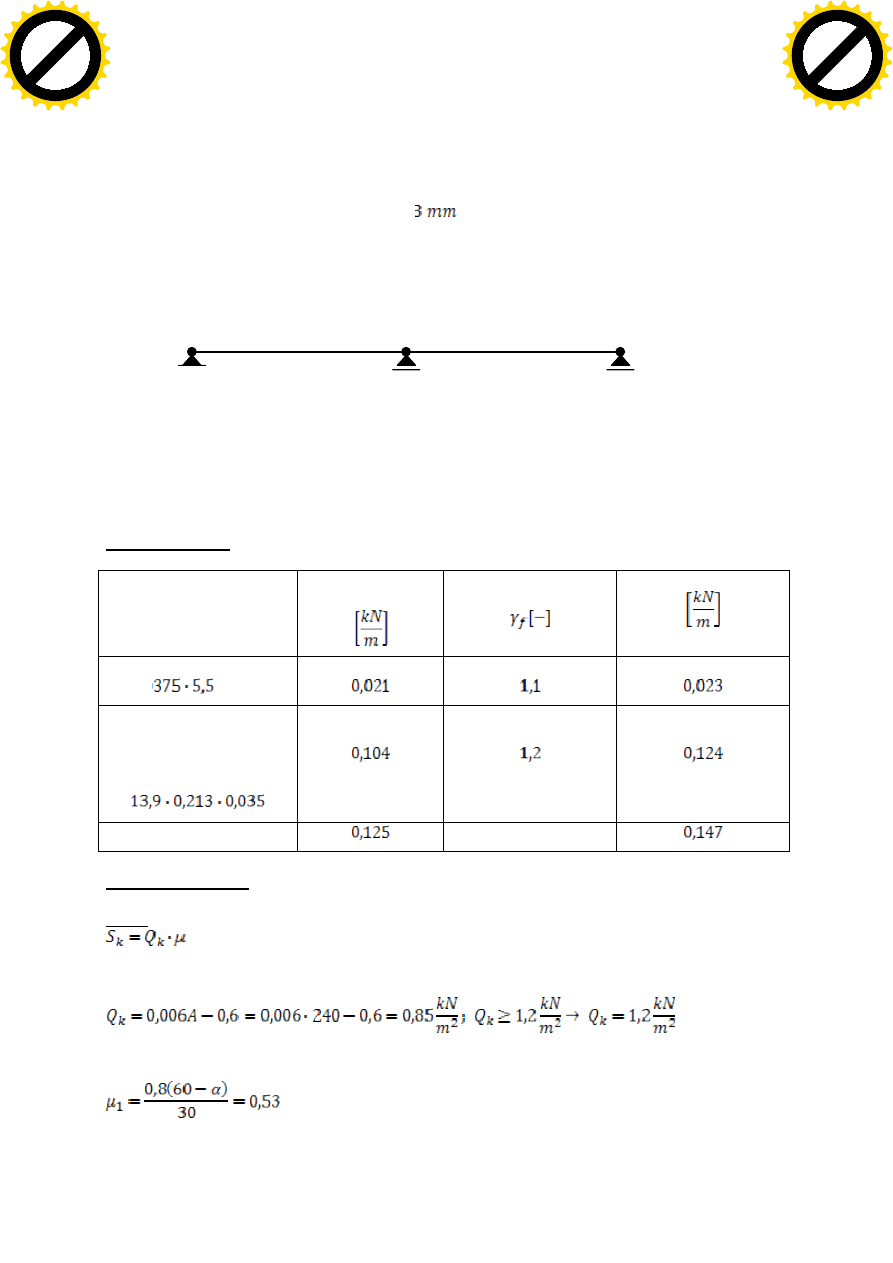
1.1. Schemat statyczny elementu konstrukcyjnego
1
2
3
0,880
0,880
H=1,760
Łata jest elementem wykonanym z drewna krótkiego, dlatego do obliczeń przyjmuje się schemat
statyczny w postaci belki dwuprzęsłowej, swobodnie podpartej.
1.2 Zestawienie obciążeń
Obciążenia stałe g
Obciążenie
Wartość
charakterystyczna
Współczynnik
obciążenia
Wartość obliczeniowa
Ciężar własny łaty
Ciężar pokrycia – waga
jednej dachówki 3,5 kg,
liczba – 13,9 szt./
(wg katalogu producenta)
Razem
Obciążenia zmienne:
Śnieg:
Obciążenie charakterystyczne śniegu w strefie III:
Współczynnik kształtu dachu:
l
eff
l
eff
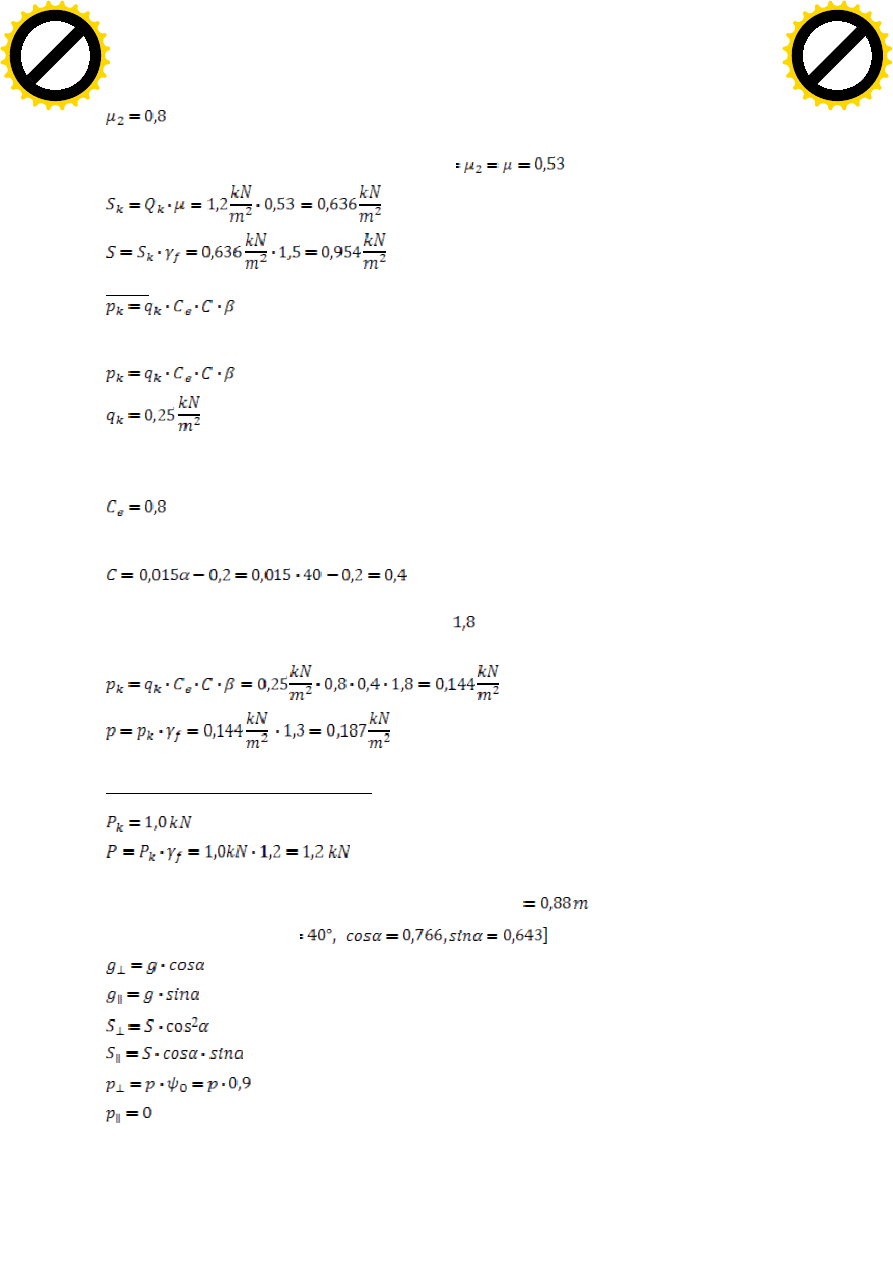
3
Do obliczeń pojedynczych elementów przyjmuje, że
Wiatr:
Obciążenie charakterystyczne wiatru w strefie I:
Współczynnik ekspozycji:
Przyjęto, że budynek ma ok. 10m, oraz znajduje się na terenie typu B
Współczynnik aerodynamiczny:
Przyjmuję współczynnik działania porywów wiatru
Obciążenie charakterystyczne skupione:
Przyjęto długość przęseł równą średniemu rozstawowi krokwi
Składowe obciążeń wynoszą
4
Obciążenie
Wartość
charakterystyczna
Współczynnik
obciążenia
Wartość
obliczeniowa
Wartości składowe prostopadłe
obciążenia
Wartości składowe równoległe
obciążenia
Charakterystyczna
Obliczeniowa
Charakterysty
czna
Obliczeniowa
g – ciężar
własny i
pokrycia
S – śnieg
0,636x0,213
p – wiatr
0,144x
x0,213x
x0,9
RAZEM
P [kN]
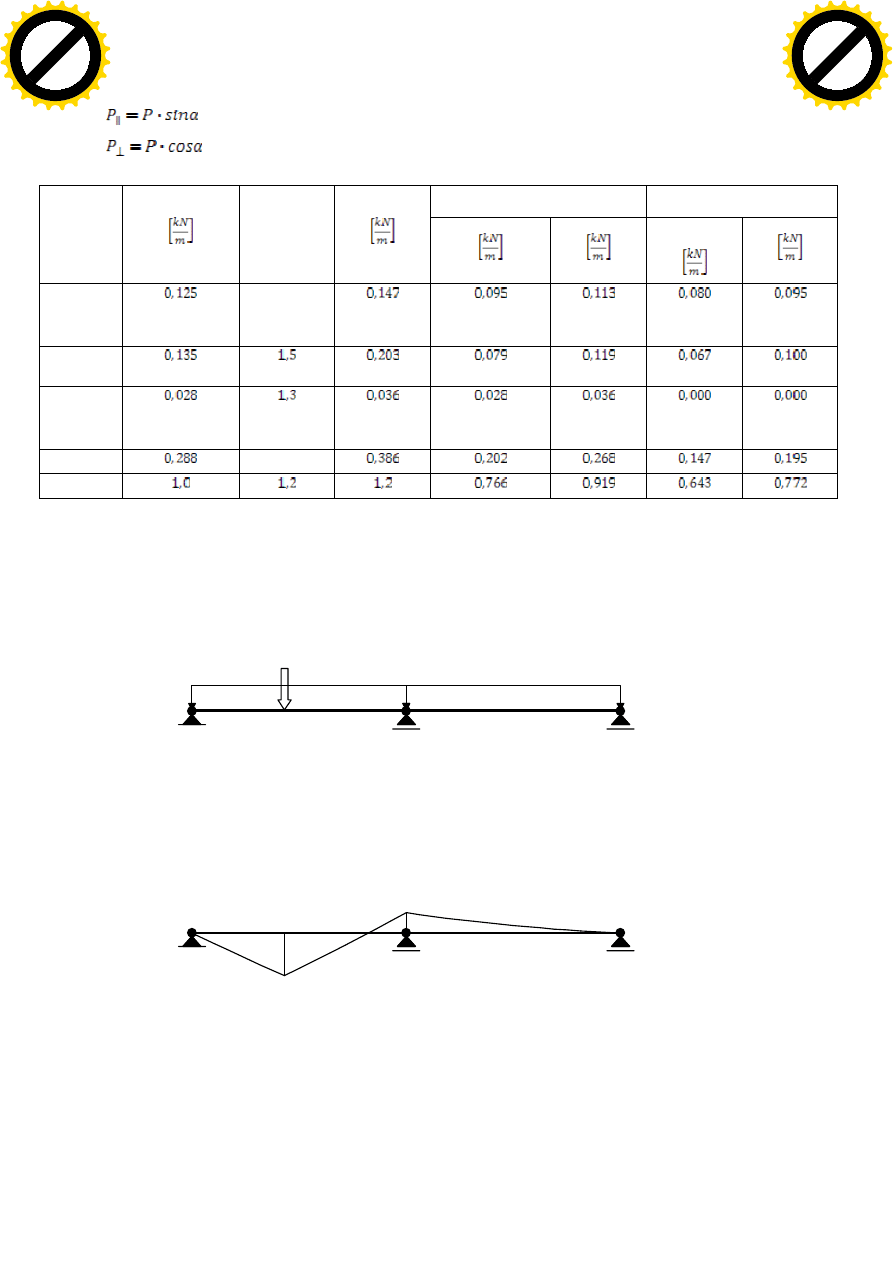
1.3 Wymiarowanie łaty
Wariant I – obciążenie ciężarem własnym i pokryciem oraz siłą skupioną
OBCIĄŻENIA PROSTOPADŁE:
1
2
0,919
0,113
0,113
0,113
0,113
MOMENTY OD OBCIĄŻEŃ PROSTOPADŁYCH:
1
2
0,174
0,174
-0,082
0,174
-0,082 -0,082
-0,082
OBCIĄŻENIA RÓWNOLEGŁE:

5
1
2
0,772
0,095
0,095
0,095
0,095
MOMENTY OD OBCIĄŻEŃ RÓWNOLEGŁYCH:
1
2
0,146
0,146
-0,069
0,146
-0,069 -0,069
-0,069
1.4 Sprawdzenie stanu granicznego nośności
Obliczenie wskaźników wytrzymałości łaty o wymiarach 50x75 mm:
Naprężenia obliczeniowe od zginania w stosunku do osi głównych
Wytrzymałość obliczeniowa na zginanie:
Dla drewna klasy C22 – wytrzymałość charakterystyczna na zginanie
Decydujące znaczenie na obciążenie chwilowe, stąd -
Częściowy współczynnik bezpieczeństwa -
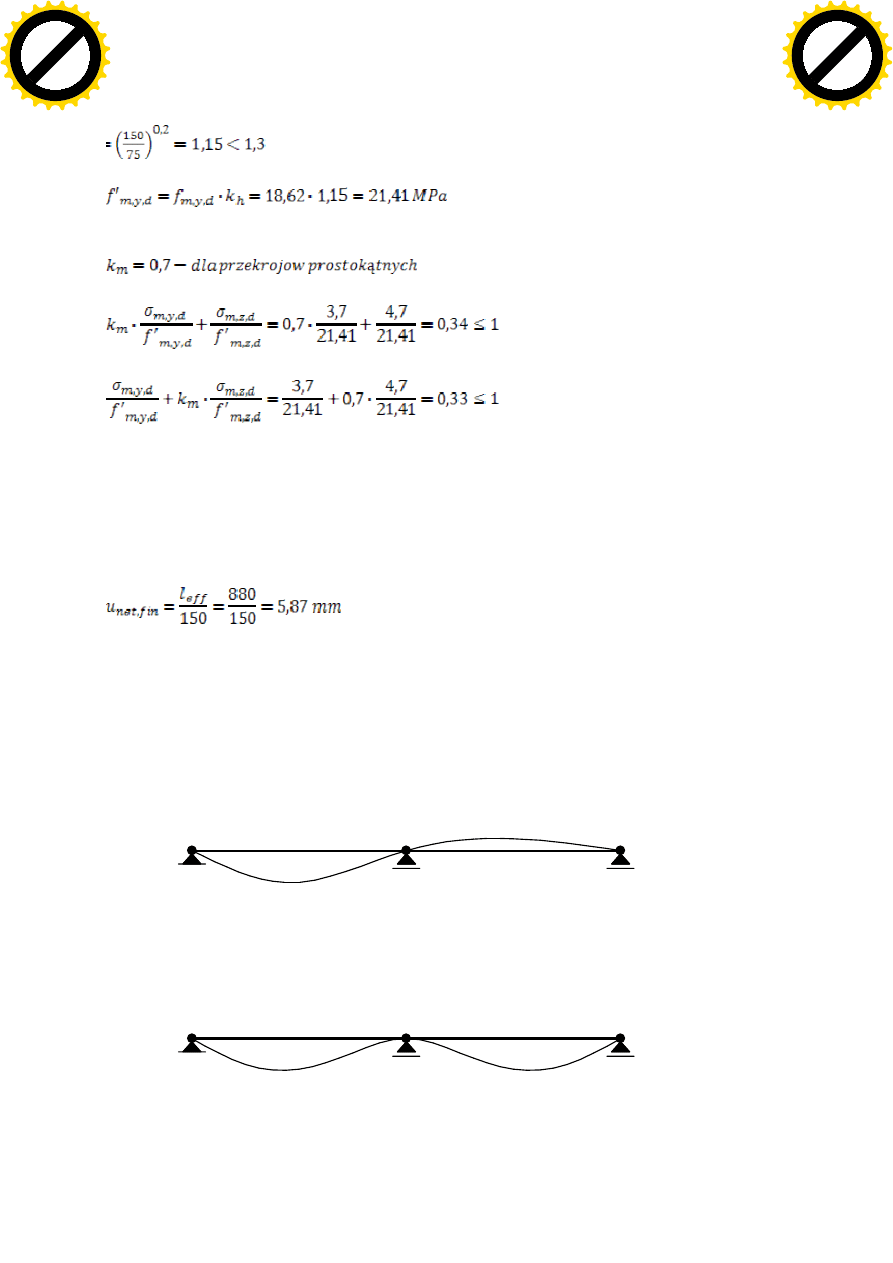
6
Przekrój ma wysokość mniejszą niż 150 mm, można zatem zastosować współczynnik:
zatem:
Sprawdzenie warunku stanu granicznego:
Warunek stanu granicznego nośności dla łaty został spełniony
1.5 Sprawdzanie stanu granicznego użytkowalności
Graniczna wartość ugięcia dla deskowania dachowego:
PRZEMIESZCZENIA OD SKŁADOWEJ PROSTOPADŁEJ SIŁY SKUPIONEJ:
1
2
PRZEMIESZCZENIA OD SKŁADOWEJ PROSTOPADŁEJ CIĘŻARU WŁASNEGO:
1
2
PRZEMIESZCZENIA OD SKŁADOWEJ RÓWNOLEGŁEJ SIŁY SKUPIONEJ:
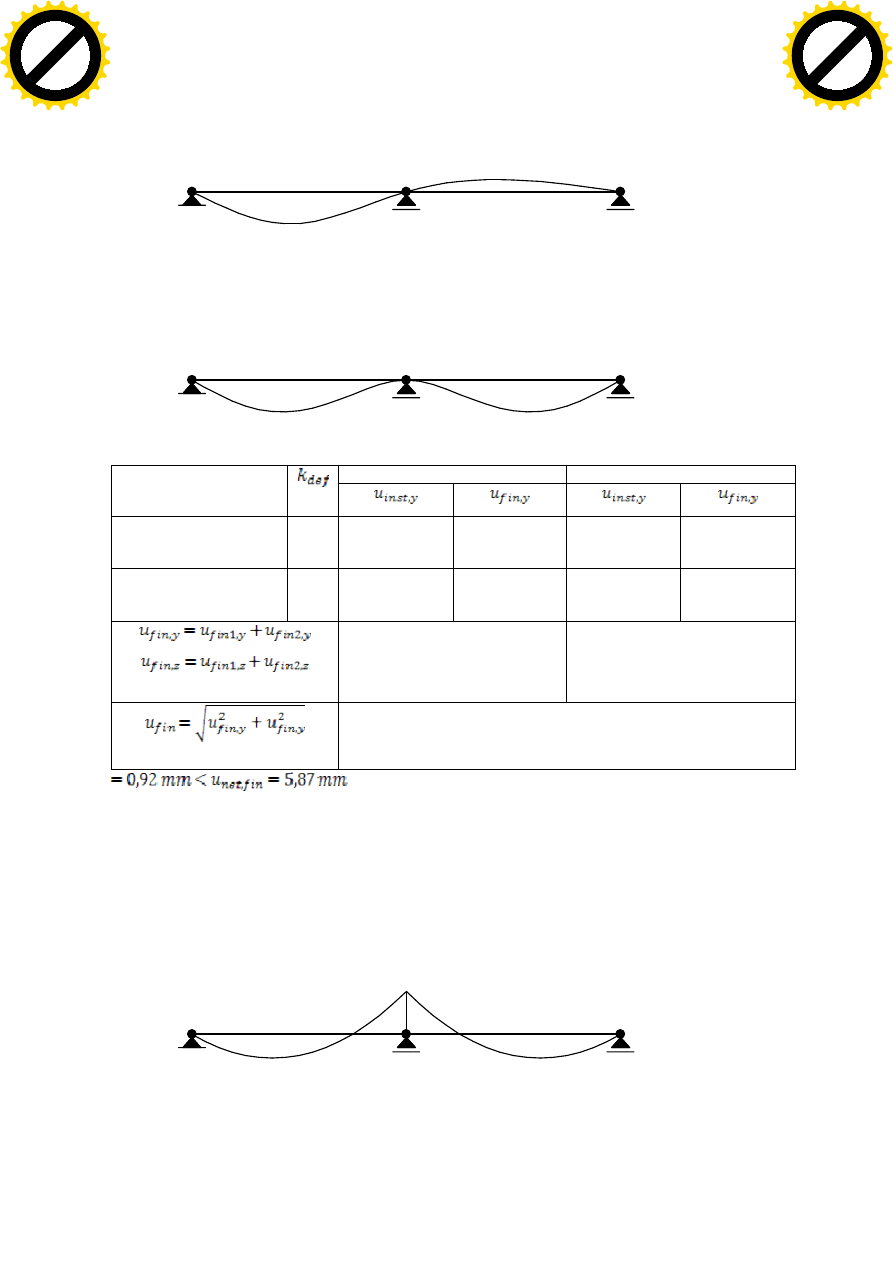
7
1
2
PRZEMIESZCZENIA OD SKŁADOWEJ RÓWNOLEGŁEJ CIĘŻARU WŁASNEGO:
1
2
Obciążenie
Składowe prostopadłe [mm]
Składowe równoległe [mm]
1. Ciężar własny (klasa
trwania obciążenia =
stałe)
0,8
0
0
0
0
2. Siła skupiona (klasa
trwania obciążenia =
obciążenia krótkotrwałe)
0
0,7
0,7
0,6
0,6
0,7
0,6
0,92
-
Warunek stanu granicznego użytkowalności został spełniony
Wariant II – obciążenie ciężarem własnym i pokryciem oraz śniegiem i wiatrem
MOMENTY OD OBCIĄŻEŃ PROSTOPADŁYCH:
1
2
-0,026
0,015
-0,026 -0,026
0,015
-0,026
MOMENTY OD OBCIĄŻEŃ RÓWNOLEGŁYCH:

8
1
2
-0,019
0,011
-0,019 -0,019
0,011
-0,019
Wniosek:
Maksymalne momenty zginające w wariancie II są znacznie mniejsze niż w wariancie I. Ponadto ze
względu na inną klasę trwania obciążenia decydującego. Nie ma więc potrzeby sprawdzania stanu
granicznego nośności i użytkowalności dla wariantu II.
Ostatecznie przyjęto łatę o wymiarach przekroju poprzecznego 50x75 mm.
2. OBLICZENIE KROKWI
Przyjęto, że wiązar dachowy będzie wykonany z bali grubości 80 mm. Wiązar jest elementem
zadaszenia nad balkonem, zatem zarówno na jętkach jak i na krokwiach nie występuje ocieplenie. Ze
względu na jego występowanie w innych częściach dachu, przyjęto wysokość bala dla krokwi i jętki
160 mm.
WĘZŁY WIĄZARA JĘTKOWEGO:
------------------------------------------------------------------
Nr: X [m]: Y [m]: Nr: X [m]: Y [m]:
------------------------------------------------------------------
1 0,540 0,453 5 3,660 3,071
2 6,780 0,453 6 0,000 0,000
3 2,192 1,839 7 7,320 0,000
4 5,128 1,839
------------------------------------------------------------------
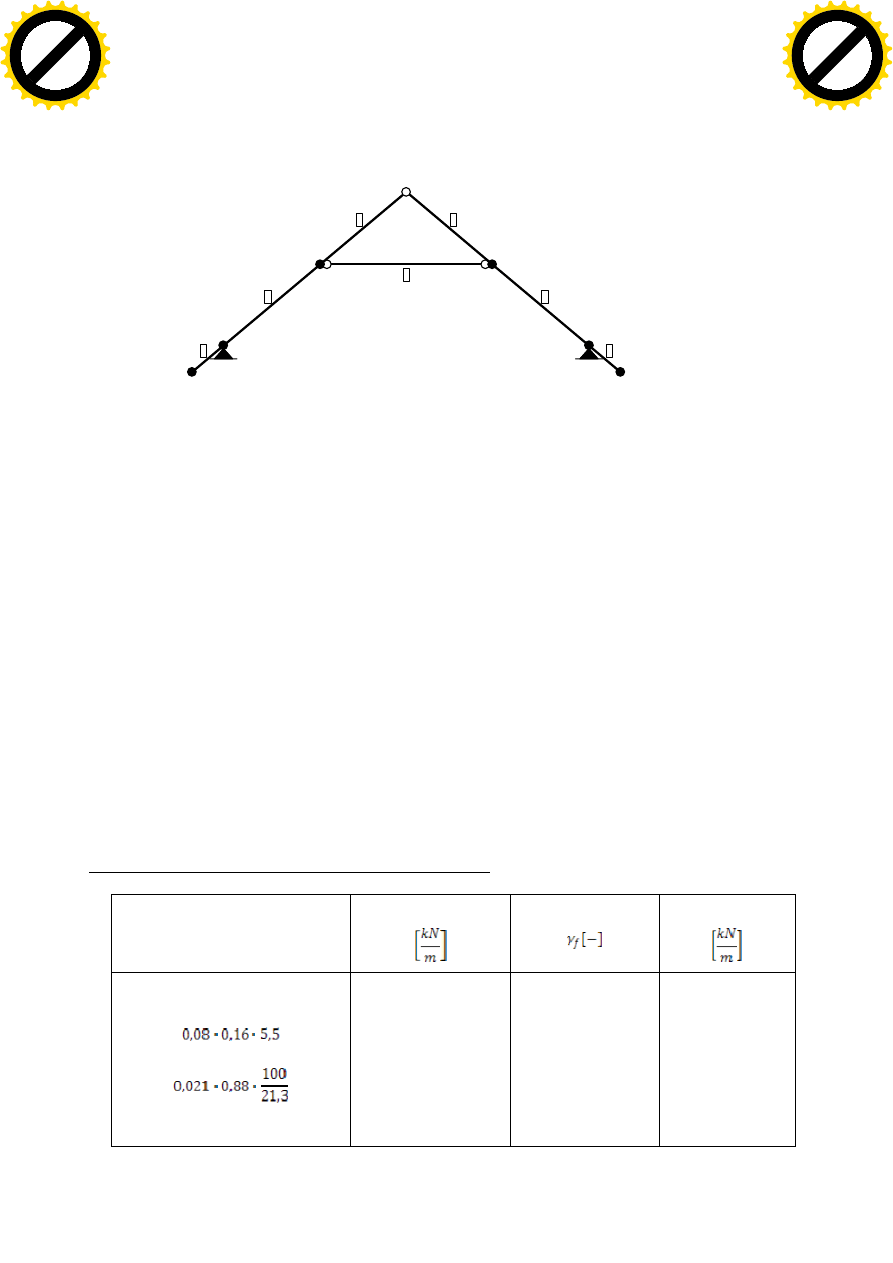
9
1
2
3
4
5
6
7
0,540
1,652
1,468
1,468
1,652
0,540
H=7,320
0,453
1,386
1,232
V=3,071
2
2
1
2
2
2
2
PRĘTY WIĄZARA JĘTKOWEGO:
Typy prętów: 00 - sztyw.-sztyw.; 01 - sztyw.-przegub;
10 - przegub-sztyw.; 11 - przegub-przegub
22 - cięgno
------------------------------------------------------------------
Pręt: Typ: A: B: Lx[m]: Ly[m]: L[m]: Red.EJ: Przekrój:
------------------------------------------------------------------
1 00 1 3 1,652 1,386 2,156 1,000 2
Krokiew 160x80
2 00 4 2 1,652 -1,386 2,156 1,000 2
Krokiew 160x80
3 11 4 3 -2,936 0,000 2,936 1,000 1
Jętka 160x80
4 01 3 5 1,468 1,232 1,916 1,000 2
Krokiew 160x80
5 10 5 4 1,468 -1,232 1,916 1,000 2
Krokiew 160x80
6 00 6 1 0,540 0,453 0,705 1,000 2
Krokiew 160x80
7 00 2 7 0,540 -0,453 0,705 1,000 2
Krokiew 160x80
------------------------------------------------------------------
ZESTAWIENIE OBCIĄŻEŃ DLA WIĄZARA JETKOWEGO:
Obciążenie
Wartość
charakterystyczna
Współczynnik
obciążenia
Wartość
obliczeniowa
A1. Ciężar własny dachu
z uwzględnieniem ciężaru krokwi g:
- ciężar krokwi
- ciężar łaty
- Ciężar dachówki
0,07
0,087
0,428
1,1
1,1
1,2
0,077
0,096
0,514

10
RAZEM:
0,585
0,687
B. Śnieg (w przeliczeniu na połać):
- połać lewa
-połać prawa
C. Wiatr
- połać nawietrzna
- połać nawietrzna
0,647
0,429
0,114
-0,114
1,5
1,5
1,3
1,3
0,971
0,644
0,148
-0,148
A2. Ciężar jętki
0,07
1,1
0,077
WYZNACZENIE SIL WEWNETRZNYCH:
OBCIĄŻENIA:
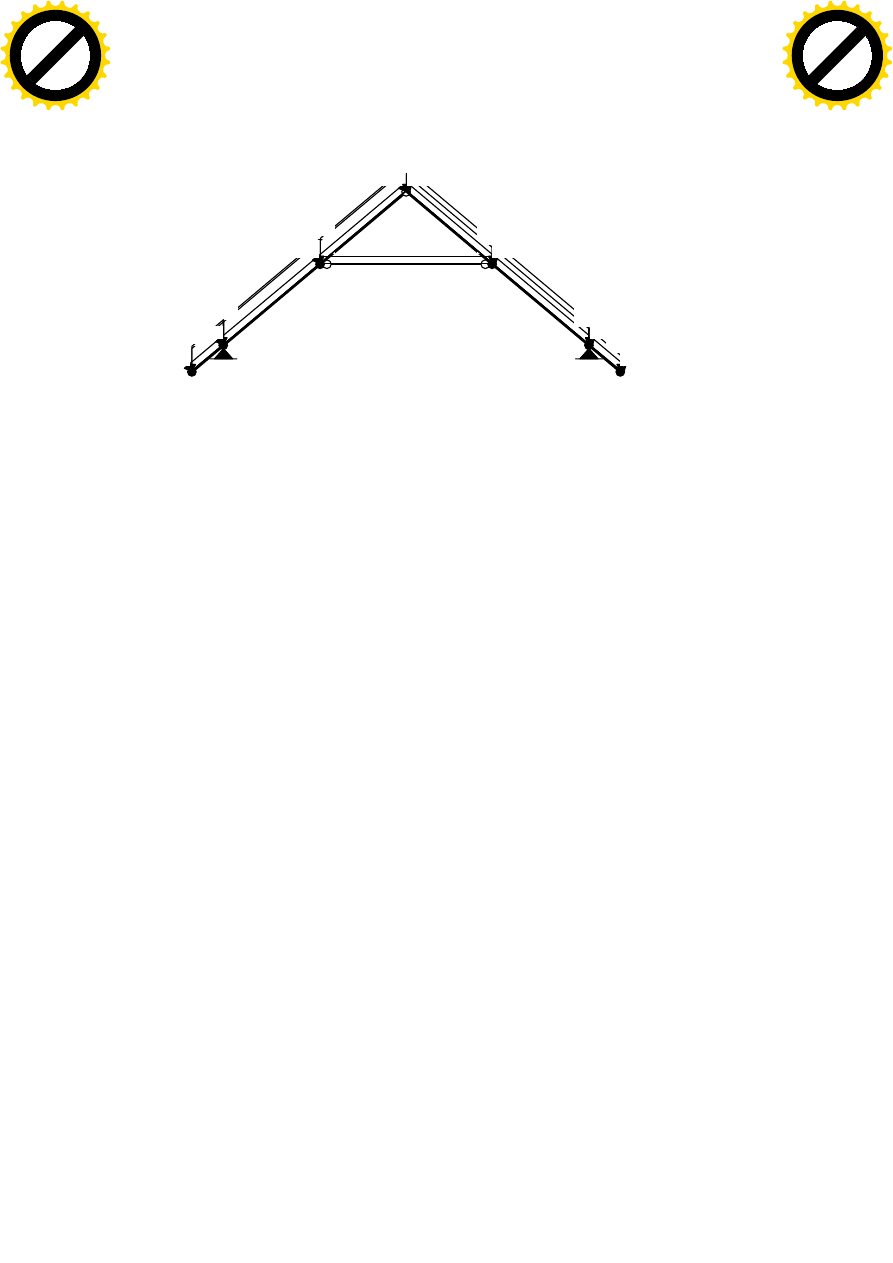
11
1
2
3
4
5
6
7
0,585
0,585
0,647
0,647
0,114
0,114
0,585
0,585
0,429
0,429
-0,114
-0,114
0,070
0,070
0,585
0,585
0,647
0,647
0,114
0,114
0,585
0,585
0,429
0,429
-0,114
-0,114
0,585
0,585
0,647
0,647
0,114
0,114
0,585
0,585
0,429
0,429
-0,114
-0,114
OBCIĄŻENIA: ([kN],[kNm],[kN/m])
------------------------------------------------------------------
Pręt: Rodzaj: Kąt: P1(Tg): P2(Td): a[m]: b[m]:
------------------------------------------------------------------
Grupa: A "Ciężar dachu" Stałe
gf= 1,20
1 Liniowe 0,0 0,585 0,585 0,00 2,16
2 Liniowe 0,0 0,585 0,585 0,00 2,16
3 Liniowe 0,0 0,070 0,070 0,00 2,94
4 Liniowe 0,0 0,585 0,585 0,00 1,92
5 Liniowe 0,0 0,585 0,585 0,00 1,92
6 Liniowe 0,0 0,585 0,585 0,00 0,70
7 Liniowe 0,0 0,585 0,585 0,00 0,70
Grupa: B "Śnieg S" Zmienne
gf= 1,50
1 Liniowe 0,0 0,647 0,647 0,00 2,16
2 Liniowe 0,0 0,429 0,429 0,00 2,16
4 Liniowe 0,0 0,647 0,647 0,00 1,92
5 Liniowe 0,0 0,429 0,429 0,00 1,92
6 Liniowe 0,0 0,647 0,647 0,00 0,70
7 Liniowe 0,0 0,429 0,429 0,00 0,70
Grupa: C "Wiatr p" Zmienne
gf= 1,30
1 Liniowe 40,0 0,114 0,114 0,00 2,16
2 Liniowe -40,0 -0,114 -0,114 0,00 2,16
4 Liniowe 40,0 0,114 0,114 0,00 1,92
5 Liniowe -40,0 -0,114 -0,114 0,00 1,92
6 Liniowe 40,0 0,114 0,114 0,00 0,70
7 Liniowe -40,0 -0,114 -0,114 0,00 0,70
------------------------------------------------------------------
MOMENTY:
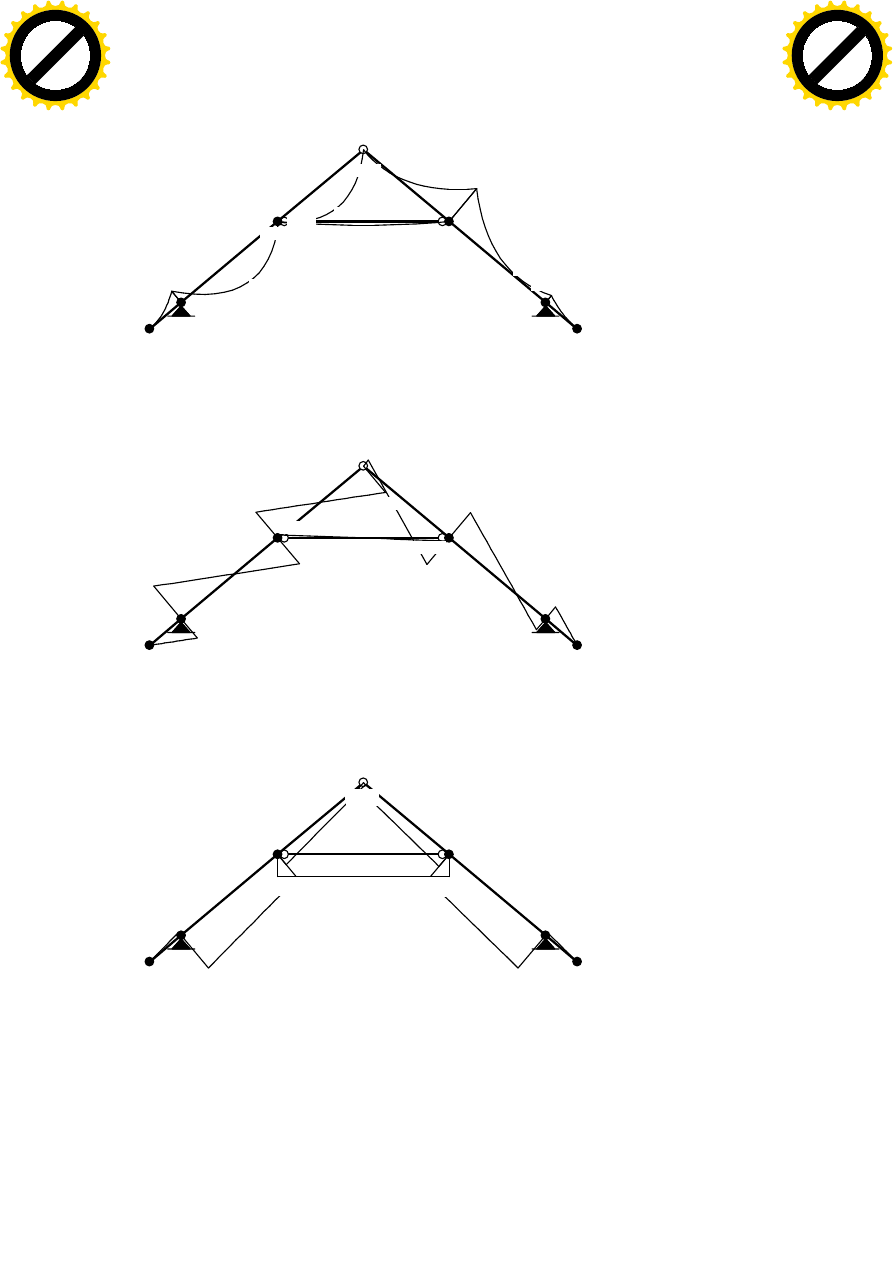
12
1
2
3
4
5
6
7
-0,355
0,029
0,679
-0,355
-1,037
-0,219
-0,034
-1,037
0,091
0,029
0,671
-1,037
0,053
-1,037
-0,355
-0,355
-0,219
-0,219
TNĄCE:
1
2
3
4
5
6
7
1,719
-1,363
1,719
-1,363
1,331
-0,572
1,331
-0,572
0,123
-0,123
0,123
-0,123
1,354
-1,385
1,354
-1,385
0,305
-1,387
0,305
-1,387
-1,008
-1,008
0,622
0,622
NORMALNE:
1
2
3
4
5
6
7
-8,363
-6,045
-6,045
-8,363
-6,549
-8,413
-6,549
-8,413
-4,376
-4,376
-4,376
-4,376
-2,614
-0,553
-0,553
-2,614
-1,460
-3,117
-1,460
-3,117
0,758
0,758
0,610
0,610
SIŁY PRZEKROJOWE:
T.I rzędu
Obciążenia obl.: ABC
------------------------------------------------------------------
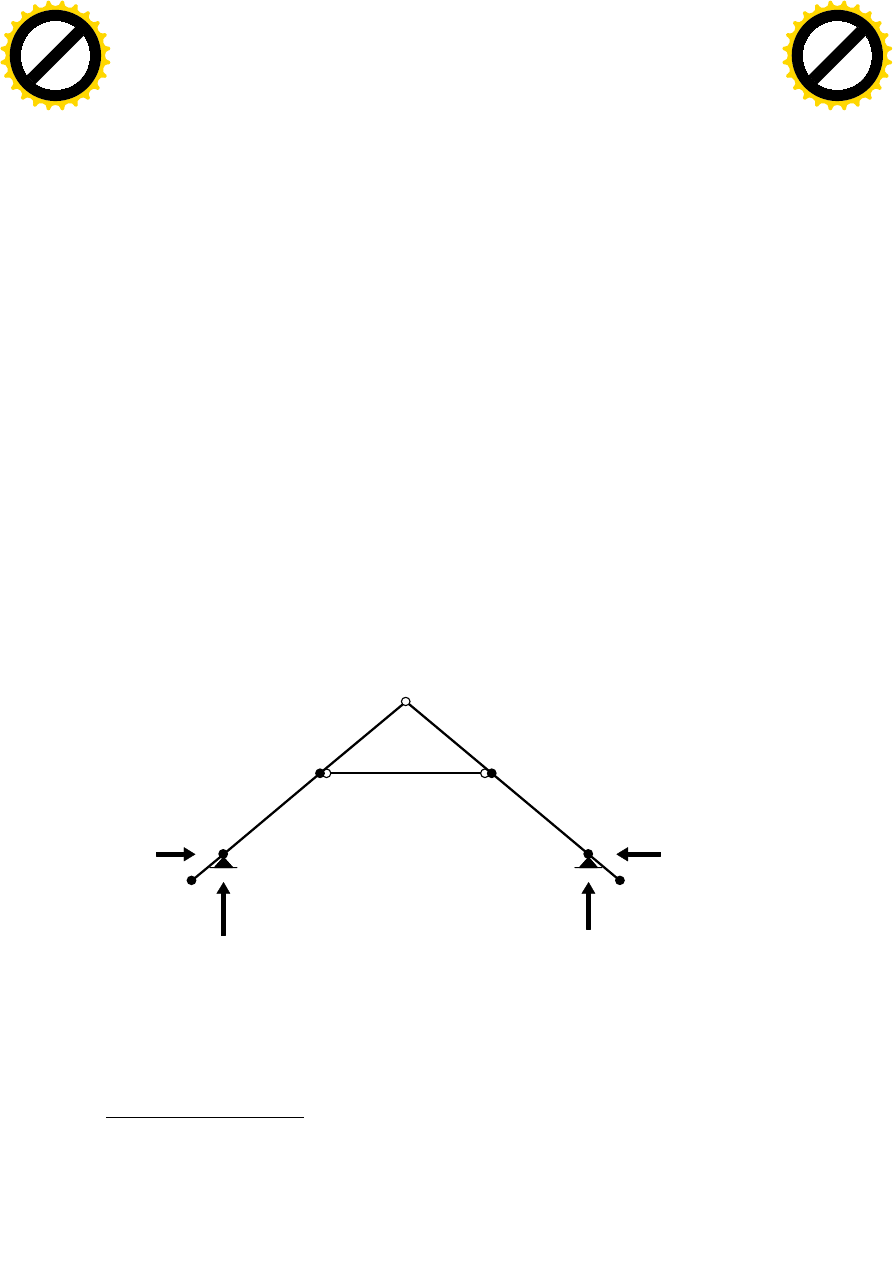
13
Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:
------------------------------------------------------------------
1 0,00 0,000 -0,355 1,719 -8,363
0,56 1,205
0,679* -0,002 -7,068
1,00 2,156 0,029 -1,363 -6,045
2 0,00 0,000 -1,037 1,331 -6,549
0,70 1,508
-0,034* 0,000 -7,853
1,00 2,156 -0,219 -0,572 -8,413
3 0,00 0,000 0,000 0,123 -4,376
0,50 1,457
0,091* 0,001 -4,376
1,00 2,936 0,000 -0,123 -4,376
4 0,00 0,000 0,029 1,354 -2,614
0,49 0,943
0,671* 0,006 -1,600
0,50 0,951
0,671* -0,005 -1,592
1,00 1,916 -0,000 -1,385 -0,553
5 0,00 0,000 0,000 0,305 -1,460
0,18 0,344
0,053* 0,001 -1,758
1,00 1,916 -1,037 -1,387 -3,117
6 0,00 0,000 0,000 0,000 -0,000
0,00 0,003
-0,000* -0,004 0,003
1,00 0,705 -0,355 -1,008 0,758
7 0,00 0,000 -0,219 0,622 0,610
1,00 0,702
-0,000* 0,002 0,002
1,00 0,705 -0,000 -0,000 -0,000
------------------------------------------------------------------
* = Wartości ekstremalne
REAKCJE PODPOROWE:
1
2
3
4
5
6
7
5,234
7,951
6,145
6,715
REAKCJE PODPOROWE:
T.I rzędu
Obciążenia obl.: ABC
------------------------------------------------------------------
Węzeł: H[kN]: V[kN]: Wypadkowa[kN]: M[kNm]:
------------------------------------------------------------------
1 5,234 7,951 9,520
2 -6,145 6,715 9,102
------------------------------------------------------------------
WYMIAROWANIE KROKWI:

14
Sprawdzanie stanu granicznego nośności
Maksymalny moment zginający i odpowiadająca mu siła podłużna wynoszą:
(ściskanie)
Przyjęto przekrój krokwi 80x160 mm, dla którego;
Naprężenia obliczeniowe ściskające w kierunku równoległym do włókien (bez uwzględnienia
wyboczenia), wynoszą:
Naprężenia obliczeniowe od zginania w stosunku do osi głównych wynoszą:
Występuje przypadek zginania z osiową siłą ściskającą.
Dla klasy drewna C22 wytrzymałość charakterystyczna na ściskanie wynosi
= 20,0MPa, a na
zginanie
22,0MPa. Częściowy współczynnik bezpieczeństwa -
Decydujące znaczenie na obciążenie stałe, stąd -
Wytrzymałość obliczeniowa wynosi:
Długość wyboczeniowa krokwi przy ściskaniu:
Stateczność giętno-skrętna, występująca przy zginaniu:
Dane:
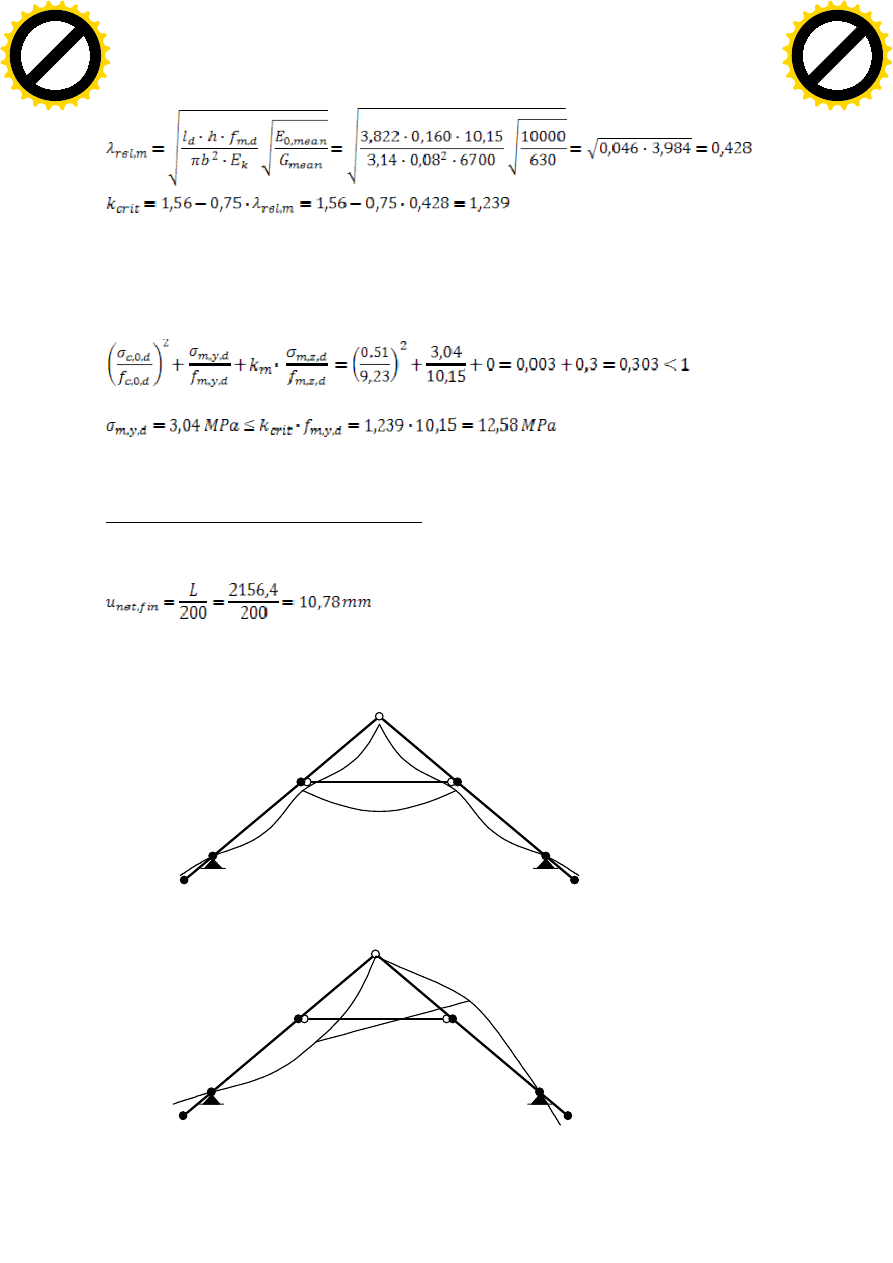
15
Sprawdzenie warunków stanu granicznego nośności:
Warunek stanu granicznego nośności dla krokwi jest spełniony.
Sprawdzanie stanu granicznego użytkowalności
Graniczne przemieszczenie dla krokwi:
PRZEMIESZCZENIA OD OBCIĄŻENIA CIĘŻAREM WŁASNYM:
1
2
3
4
5
6
7
PRZEMIESZCZENIA OD OBCIĄŻENIA ŚNIEGIEM:
1
2
3
4
5
6
7
PRZEMIESZCZENIA OD OBCIĄŻENIA WIATREM:
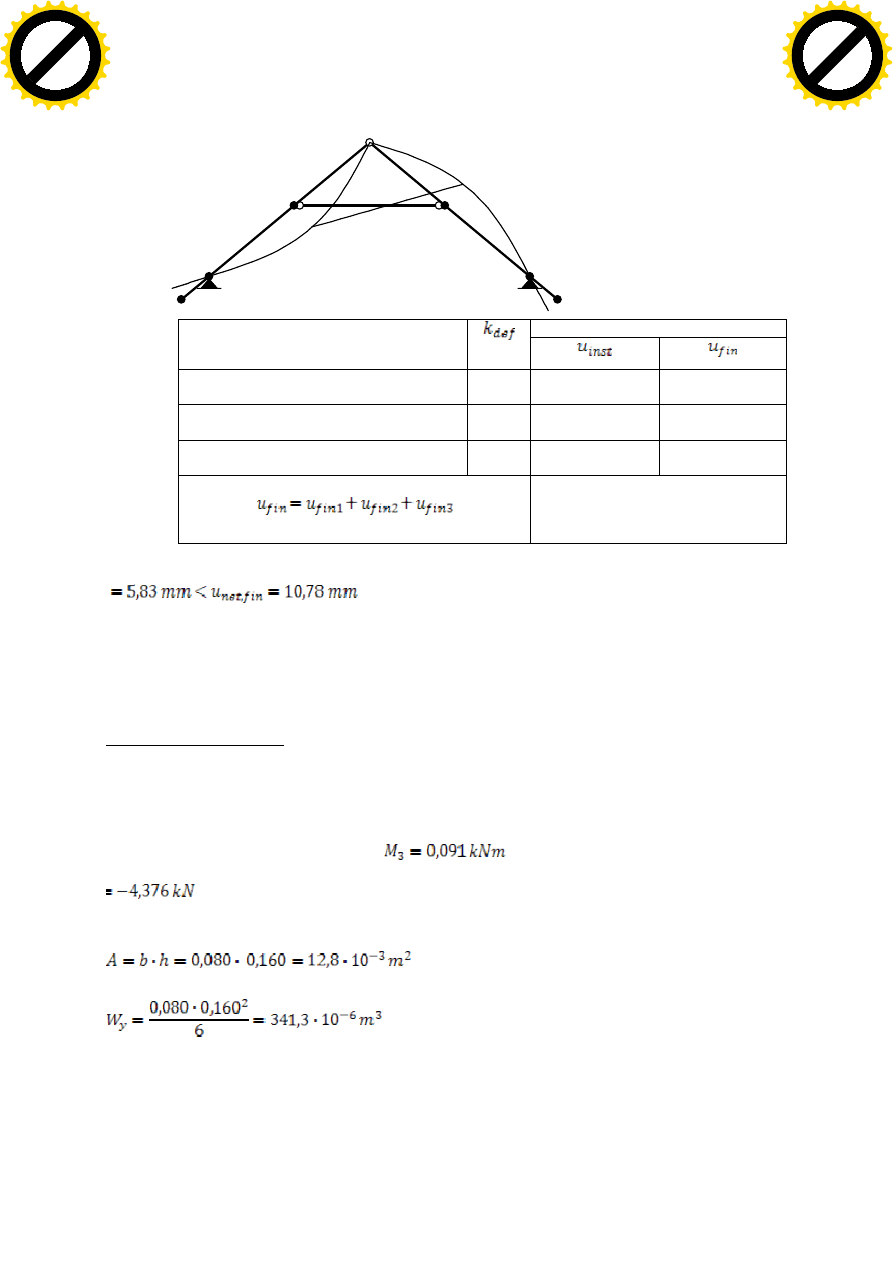
16
1
2
3
4
5
6
7
Obciążenie
Składowe prostopadłe [mm]
1. Ciężar własny (klasa trwania obciążenia
= stałe, klasa użytkowania =2)
0,8
0,5
0,9
2. Śnieg (klasa trwania obciążenia
= średniotrwałe, klasa użytkowania =2)
0,25
2,1
2,63
3. Siła skupiona (klasa trwania obciążenia
= krótkotrwałe, klasa użytkowania =2)
0
2,3
2,3
5,83
-
Warunek stanu granicznego użytkowalności dla krokwi został spełniony.
Ostatecznie przyjęto krokiew o wymiarach przekroju poprzecznego 80x160 mm
WYMIAROWANIE JĘTKI:
Sprawdzanie stanu granicznego nośności
Maksymalny moment zginający i odpowiadająca mu siła podłużna wynoszą:
(ściskanie)
Przyjęto przekrój jętki 80x160 mm, dla którego;
Naprężenia obliczeniowe ściskające w kierunku równoległym do włókien (bez uwzględnienia
wyboczenia), wynoszą:
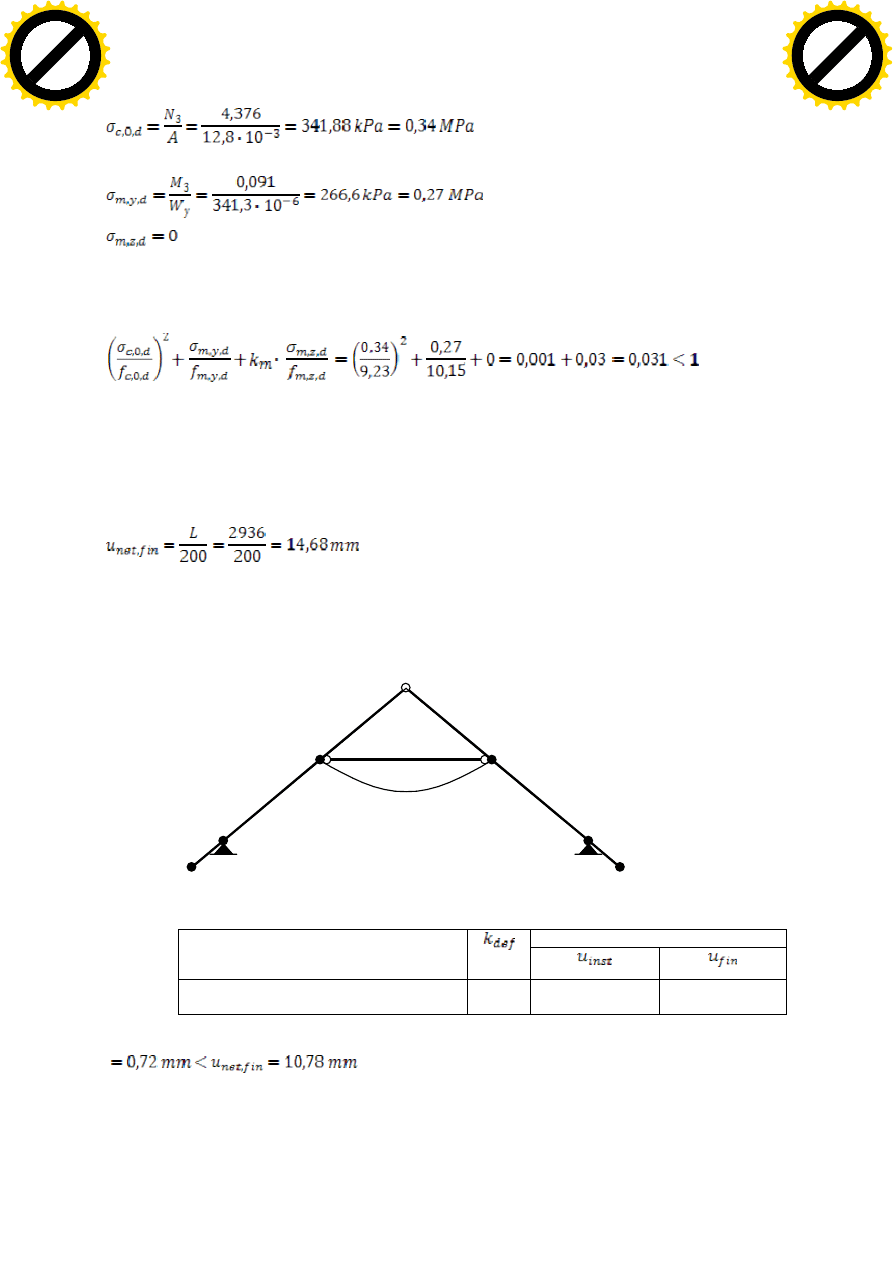
17
Naprężenia obliczeniowe od zginania w stosunku do osi głównych wynoszą:
Jętka wykonana identycznie jak krokiew, stąd wytrzymałość obliczeniowa drewna na ściskanie i
zginanie jest taka sama jak w przypadku krokwi.
Sprawdzenie warunku stanu granicznego nośności:
Warunek stanu granicznego nośności dla jętki został spełniony.
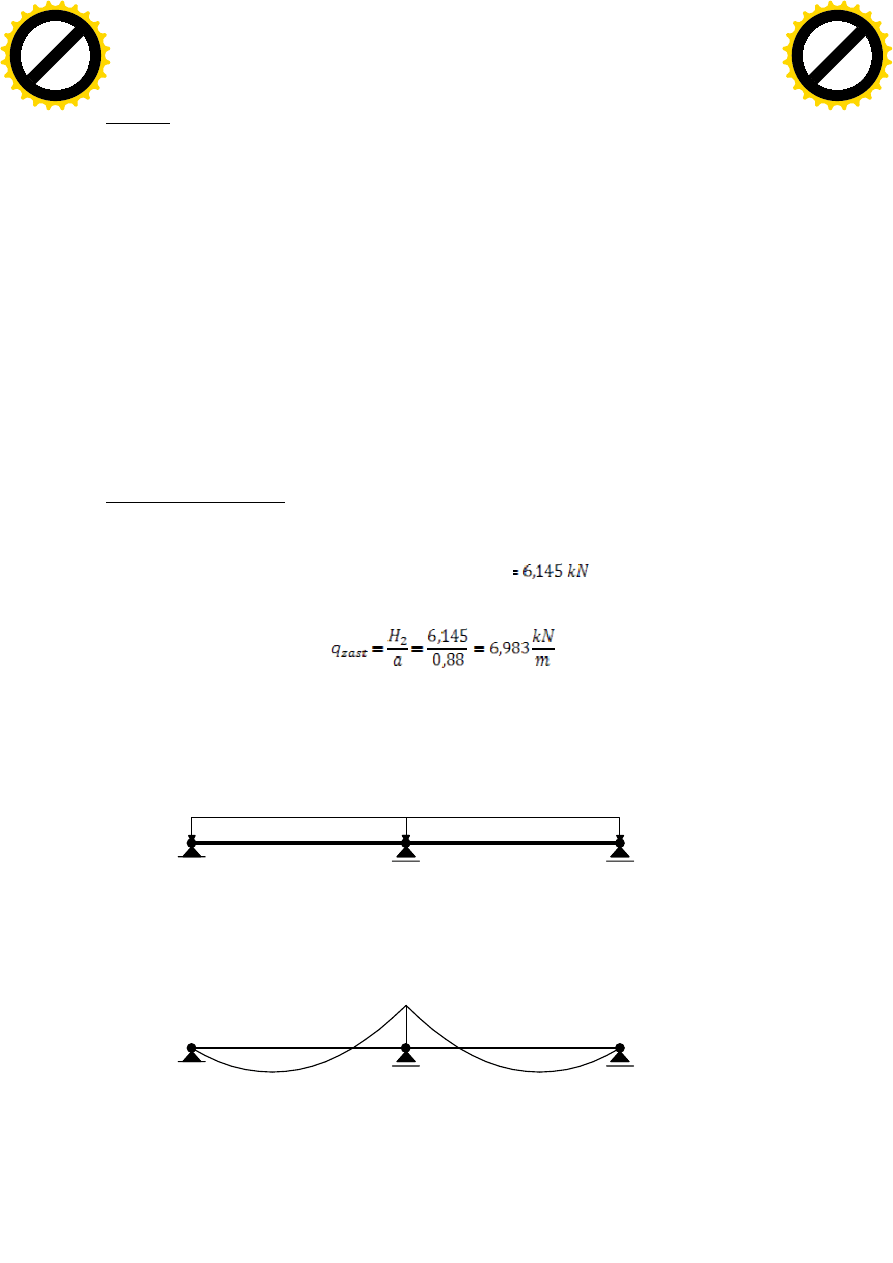
Sprawdzanie stanu granicznego użytkowalności
Graniczne przemieszczenie dla krokwi:
PRZEMIESZCZENIA OD OBCIĄŻENIA CIĘŻAREM WŁASNYM:
1
2
3
4
5
6
7
Obciążenie
Składowe prostopadłe [mm]
1. Ciężar własny (klasa trwania obciążenia
= stałe, klasa użytkowania =2)
0,8
0,4
0,72
Warunek stanu granicznego użytkowalności dla jętki został spełniony.
18
UWAGA:
Ze względów konstrukcyjnych nie zmniejszono wymiarów jętki oraz krokwi, pomimo dużego zapasu
ugięcia, gdyż jest to związane z wymaganą grubością wełny mineralnej ocieplającej strop między
jętkami wewnątrz budynku oraz polać dachową (między krokwiami).
OBLICZENIE MURŁATU:
Założono, że murłat mocowany jest do wieńca żelbetowego śrubami co 1,80 m. Jako schemat
statyczny murłatu przyjęto belkę dwuprzęsłową o długości 3,60 m. maksymalna wartość siły poziomej
(reakcji podporowej), jaka przypada na murłat, wynosi
. Ponieważ murłat leży
bezpośrednio na wieńcu, pominięto obciążenia pionowe. Jednakże występuje nierównomierny rozstaw
krokwi, zatem obliczono obciążenie równomierne zastępcze:
SCHEMAT STATYCZNY I OBCIĄŻENIA MURŁATU:
1
2
6,983
6,983
6,983
6,983
MOMENTY OD OBCIĄZENIA MURŁATU:
1
2
-2,828
1,591
-2,828 -2,828
1,591
-2,828
Sprawdzanie stanu granicznego nośności
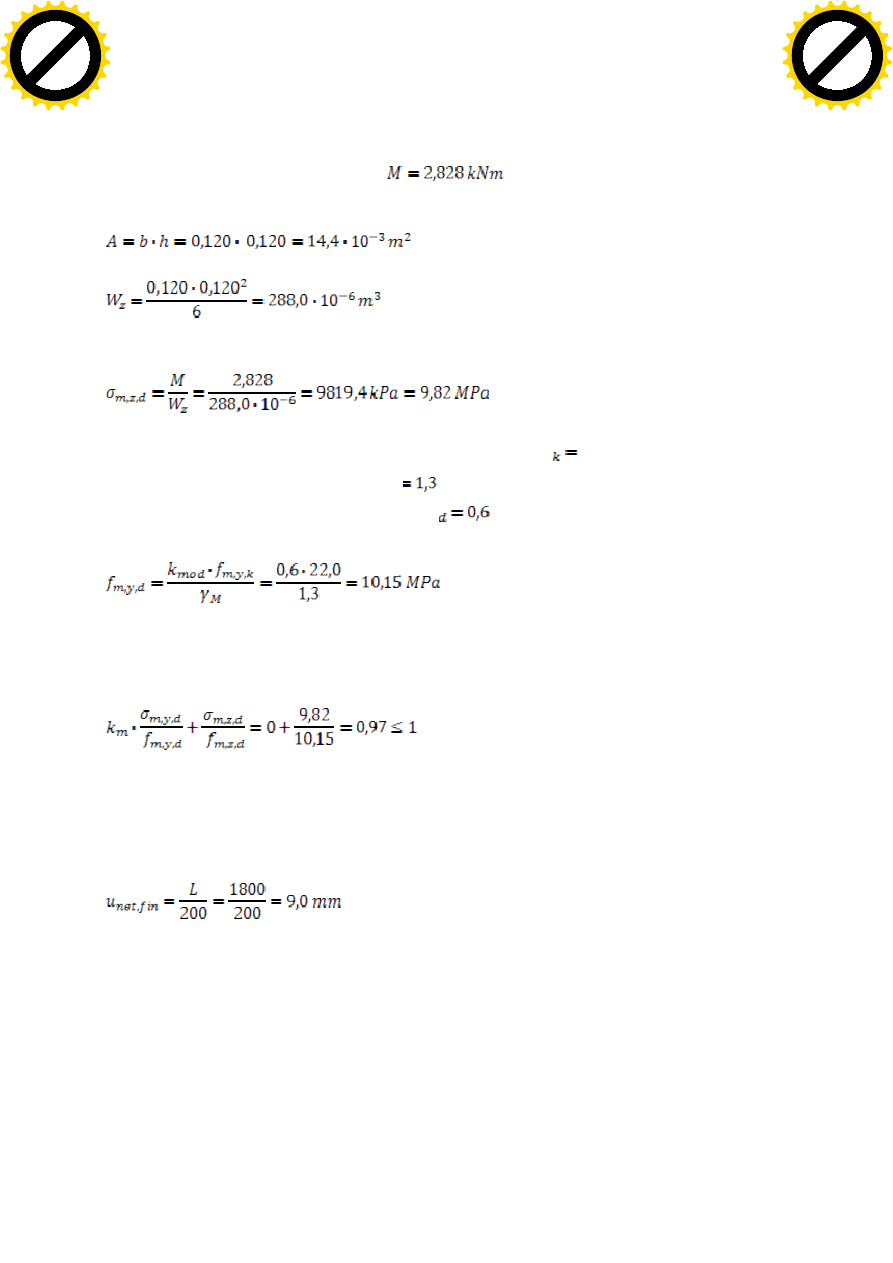
19
Maksymalny moment zginający przypadający na murłat wynosi:
Przyjęto przekrój murłatu 120x120 mm, dla którego;
Naprężenia obliczeniowe od zginania w stosunku do osi głównych wynoszą:
Dla klasy drewna C22 wytrzymałość charakterystyczna na zginanie
22,0MPa.
Częściowy współczynnik bezpieczeństwa -
Decydujące znaczenie na obciążenie stałe, stąd -
Wytrzymałość obliczeniowa wynosi:
Sprawdzanie warunku stanu granicznego nośności:
Sprawdzanie stanu granicznego użytkowalności:
Graniczne przemieszczenie dla murłatu:
PRZEMIESZCZENIA MURŁATU:
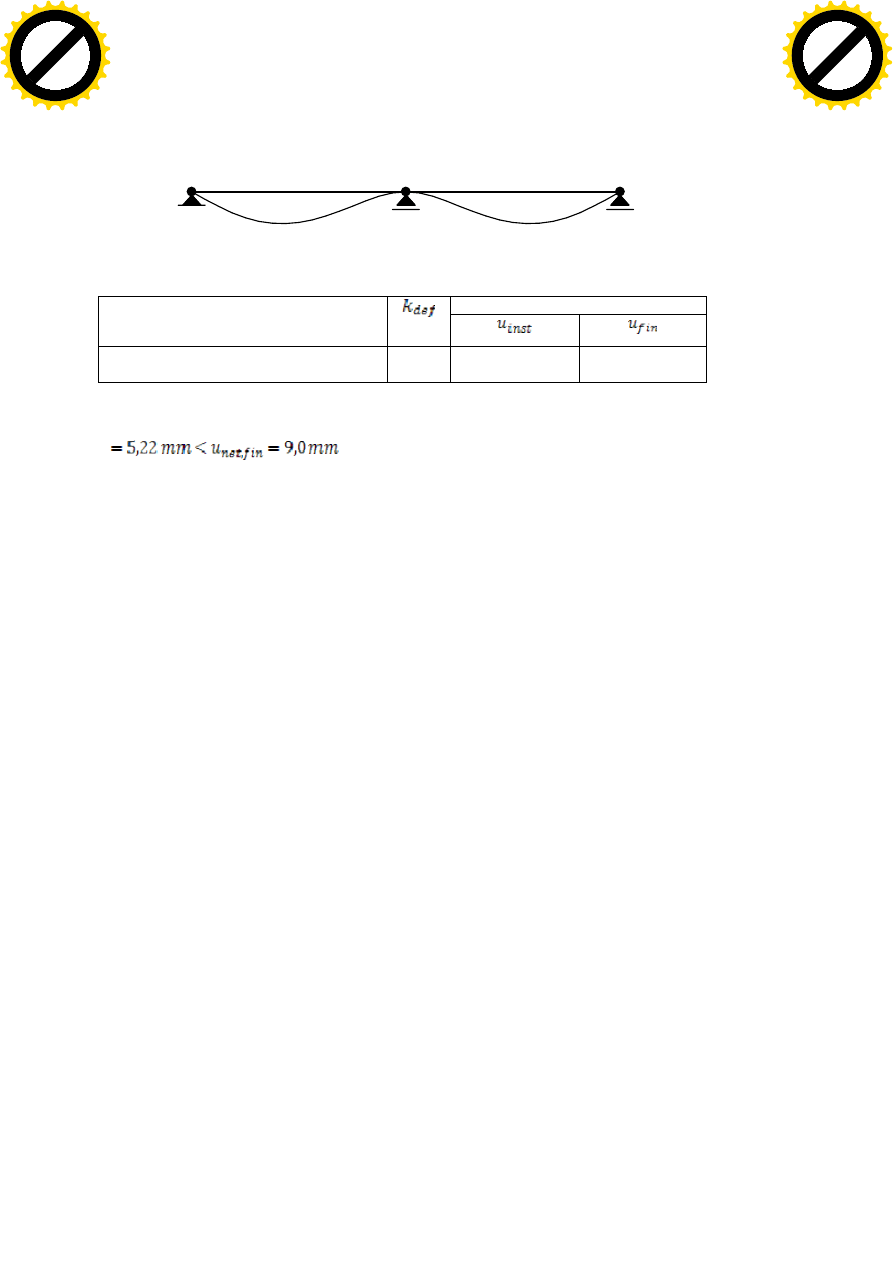
20
1
2
Obciążenie
Składowe prostopadłe [mm]
1. Ciężar własny (klasa trwania obciążenia
= stałe, klasa użytkowania =2)
0,8
2,9
5,22
Zatem:
Warunek stanu granicznego użytkowalności dla murłatu został spełniony.
Ostatecznie przyjęto murłat o wymiarach przekroju poprzecznego 120 x 120 mm.
Wyszukiwarka
Podobne podstrony:
Budownictwo Ogólne 2 - Projekt - przykład 2, Obliczenia - więźba dachowa, OBLICZENIA STATYCZNE WIĘŹB
Budownictwo Ogólne 2 Projekt przykład 4 Projekt Więźba?chowa rozporowa
POLITECHNIKA BIAŁOSTOCKA, NAUKA, Politechnika Bialostocka - budownictwo, Semestr III od Karola, Budo
budownictwo ogolne obliczenia więźby dachowej
strona tytułowa, Budownictwo, ROK II, Budownictwo Ogólne, Budownictwo - projekt, Misia, Budownictwo
Budownictwo ogólne projekt 1
Budownictwo ogólne projekt Model (09)
Budownictwo ogólne projekt Model (07)
Budownictwo ogólne projekt Model (02)
Budownictwo ogólne projekt Model (06)
Budownictwo ogólne projekt Model (08)
Budownictwo Ogólne 2 - Projekt - przykład 2, Pozycja obliczeniowa nr 4, Obliczenia ław fundamentowyc
Budownictwo Ogólne, Projekty, BO
projekt z budownictwa martyna, Prywatne, Budownictwo, Materiały, III semestr, od Beaty, Semestr 3, b
PROJEKT-OBLICZENIA, Energetyka AGH, semestr 3, III Semestr, BUDOWNICTWO OGÓLNE.J, projekt Mileny
Budownictwo ogólne projekt Model (04)
Budownictwo ogólne projekt Model (05)
droga komuno-przodek bs jhsjdheihd, NAUKA, Politechnika Bialostocka - budownictwo, Semestr III od Ka
więcej podobnych podstron