Rachunek prawdopodobieństwa i statystyka

Z

2

1. Wiadomo, że na pytanie nr 5 w pewnej ankiecie prawdziwą odpowiedź daje 80% mężczyzn i

90% kobiet. Na jednym z arkuszy nie zaznaczono płci respondenta. Wiedząc, że 60% arkuszy tej
ankiety wypełnili mężczyźni, a resztę kobiety, wyznaczyć prawdopodobieństwo, że odpowiedź na
pytanie nr 5 we wspomnianym arkuszu jest prawdziwa.

2. Jakie jest prawdopodobieństwo, że w losowo wybranej rodzinie z trojgiem dzieci są przynajmniej

dwie dziewczynki, jeśli wiadomo, że:

(a) Najstarszym dzieckiem jest chłopiec?

(b) W rodzinie jest przynajmniej jeden chłopiec?

3. Prawdopodobieństwo, że pacjent przeżyje pewną operację transplantacji jest równe 0, 55. Praw-

dopodobieństwo, że organizm pacjenta, który przeżył operację transplantacji odrzuci przeszcze-
piony narząd w ciągu miesiąca jest równe 0, 2. Jakie jest prawdopodobieństwo przeżycia obu tych
krytycznych etapów leczenia?

4. Są dwie urny. W pierwszej jest 5 kul białych i 5 czarnych, w drugiej 3 białe i 7 czarnych. Z pierwszej

urny wyjęto jedną kulę i przełożono do drugiej urny. Następnie z drugiej urny wylosowano jedną
kulę. Jakie jest prawdopodobieństwo zdarzenia, że z drugiej urny wylosowano białą kulę?

5. Test na obecność pewnego wirusa w organizmie człowieka daje poprawną odpowiedź w 90%

przypadków, gdy wirus jest rzeczywiście obecny, i w 70% przypadków, gdy wirus nie jest obecny.
W przypadku pewnego pacjenta wynik testu był:

(a) pozytywny (test wskazał obecność wirusa w organizmie pacjenta);

(b) negatywny.

Wiedząc, że na 100 osób w całej populacji wirusem zarażona jest jedna osoba, obliczyć prawdo-
podobieństwo, że pacjent jest zarażony.

6. Pan Olgierd może mieć i synów, i = 0, 1, . . . , 4, z prawdopodobieństwami równymi odpowiednio:

p

0

= 0.4, p

1

= p

2

= 0.2, p

3

= p

4

= 0.1. Każdy z tych synów może mieć i synów z tymi samymi

prawdopodobieństwami, niezależnie od ojca i braci. Obliczyć prawdopodobieństwo, że protopla-
sta rodu będzie miał 2 wnuków.

Uwaga. W poniższych zadaniach na każde z pytań należy odpowiedzieć tak (wpisując w kratce
obok T) lub nie (wpisując N).

7. Kwoka wysiaduje 3 jaja. Prawdopodobieństwo, że z jajka wykluje się kura jest takie samo, jak

prawdopodobieństwo, że wykluje się kogut i wynosi

1

2

. Wprowadźmy zdarzenia: A - z jaj wykluje

się co najwyżej jedna kura; B - z jaj wykluje się co najmniej jeden kogut i co najmniej jedna
kura; C - wszystkie wyklute z jaj pisklęta będą tej samej płci. Wtedy:

P (A) =

1

2

P (B) =

3

8

Zdarzenia A i B są niezależne

Zdarzenia A, B, C są niezależne parami

Zdarzenia A, B, C są niezależne

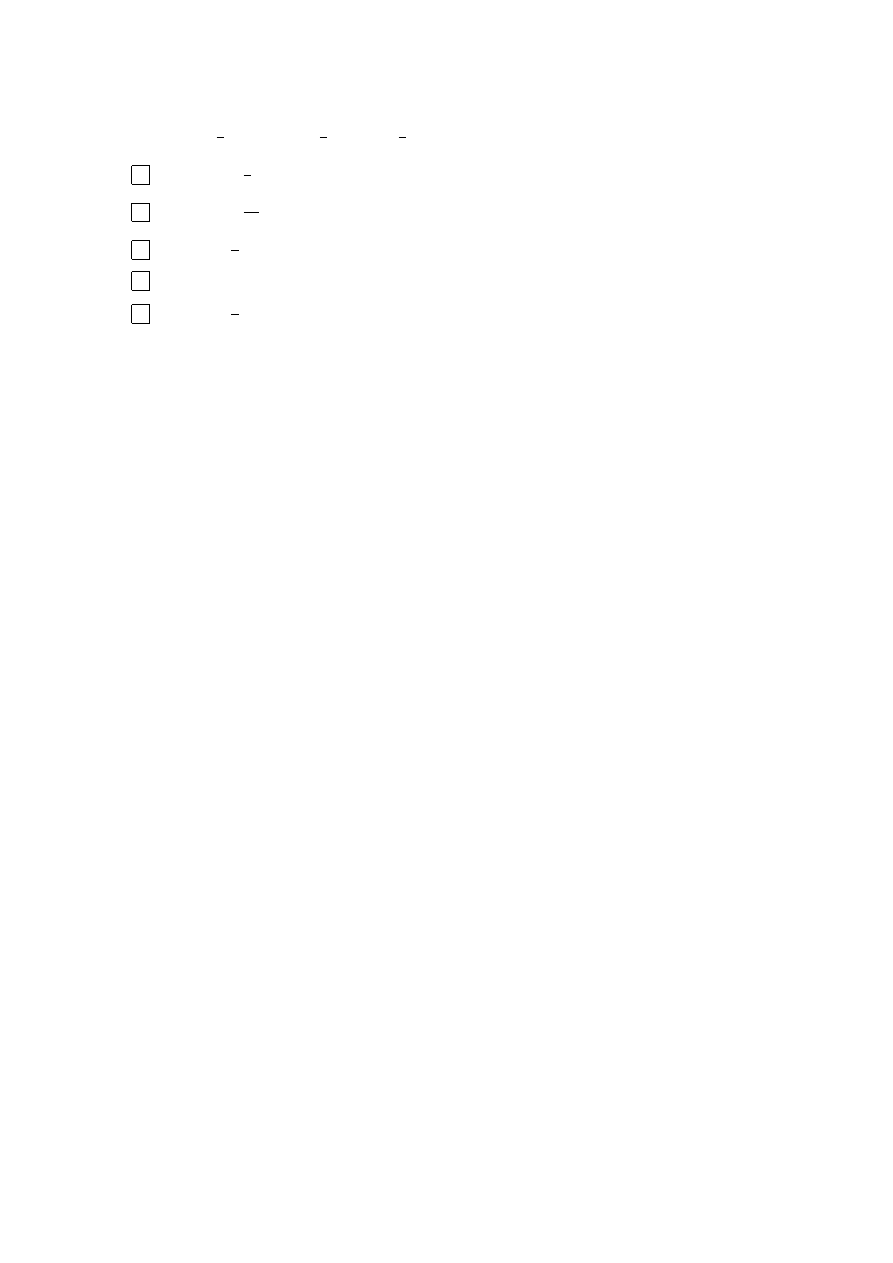
8. A i B są zdarzeniami z tej samej przestrzeni probabilistycznej. Wiadomo, że

P (A ∪ B) =

3

4

, P (A ∩ B) =

1

2

, P (A

0

) =

1

3

. Wtedy:

P (A ∩ B

0

) =

1

6

P (A ∪ B

0

) =

1

12

P (B

0

|A) =

3

5

A i B są zdarzeniami niezależnymi

P (A|B

0

) =

2

5