1

Katedra Biotechnologii w Ochronie Środowiska

Wydział Ochrony Środowiska i Rybactwa

UWM w Olsztynie

Przewodnik do ćwiczeń z

Genetyki

dla studentów II roku

kierunku Ochrona Środowiska

Sławomir Ciesielski
Dariusz Kaczmarczyk
Mirosław Łuczyński
Małgorzata Jankun
Paweł Woźnicki

www.genetics.wustl.edu/

Olsztyn 2013

2

Ć

wiczenia z przedmiotu Genetyka

•



Pa

ń

stwo studenci przychodz

ą

na zaj

ę

cia przygotowani teoretycznie oraz

wyposa

ż

eni w przybory do pisania, kalkulator oraz w przypadku

ć

wicze

ń

laboratoryjnych w białe fartuchy,

•



podczas ka

ż

dego

ć

wiczenia mo

ż

e si

ę

odby

ć

sprawdzian z

wiadomo

ś

ci dotycz

ą

cych poprzedniego i bie

żą

cego

ć

wiczenia,

•



zaliczenie

ć

wicze

ń

musi zako

ń

czy

ć

si

ę

przed letni

ą

sesj

ą

egzaminacyjn

ą

.

Kierownik przedmiotu:

dr hab. Sławomir Ciesielski

Katedra Biotechnologii w Ochronie

Ś

rodowiska ul. Słoneczna 45G

telefon: [phone]

e-mail: [e-mail]

Prowadz

ą

cy

ć

wiczenia:

dr in

ż

. Dariusz Kaczmarczyk

Katedra Biotechnologii w Ochronie

Ś

rodowiska ul. Słoneczna 45G

telefon : [phone]

e-mail:

[e-mail]

3

Szczegółowy program ćwiczeń

Ćwiczenie 1. Wprowadzenie: regulamin ćwiczeń i zasady zaliczania, plan ćwiczeń, literatura

do ćwiczeń z przedmiotu. Podstawy dziedziczenia: I i II prawo Mendla.

Ćwiczenie 2. Efekt plejotropowy genu. Geny letalne i subletalne na przykładzie dziedziczenia

kształtu płetw mieczyka Xiphophorus helleri - rozwiązywanie zadań, teoretyczne przykłady

krzyżówek pomiędzy osobnikami o różnych fenotypach.

Ćwiczenie 3. Chromosomy płci. Dziedziczenie cech sprzężonych z płcią – rozwiązywanie

zadań.

Ćwiczenie 4. Allele wielokrotne na przykładzie systemu grup krwi ABO u człowieka.

Czynnik Rh a konflikt serologiczny.

Ćwiczenie 5. Częstość występowania alleli i genotypów. Prawo Hardy-Weinberga.

Ćwiczenie 6. Efektywna liczebność populacji i współczynnik inbredu – rozwiązywanie zadań

rachunkowych.

Ćwiczenie 7. Genetyka muszki owocowej (Drosophila melanogaster). Wykorzystanie

programu komputerowego DrosophiLab (sala komputerowa).

Ćwiczenie 8. Geny autosomalne i sprzężone z płcią. Drosophila melanogaster jako obiekt

badań genetycznych (laboratorium).

Ćwiczenie 9. Modele doboru naturalnego w populacjach - symulacje komputerowe dotyczące

zmian frekwencji alleli w populacji pod wpływem doboru naturalnego (sala komputerowa).

Ćwiczenie 10. Analiza wyników hodowli muszki owocowej (ćwiczenie 8). Genotyp a

ś

rodowisko: wpływ zagęszczenia populacji na masę ciała Drosophila melanogaster -

zakładanie hodowli muszki owocowej (laboratorium).

Ćwiczenie 11. Zastosowania badań polimorfizmu sekwencji mikrosatelitarnych w genetyce –

przeprowadzenie rozdziału produktu PCR w żelu agarozowym.

Ćwiczenie 12. Dystans genetyczny. Analiza prążków uzyskanych w wyniku trawienia

restrykcyjnego (wykorzystanie wyników z poprzedniego ćwiczenia). (laboratorium).

Ćwiczenie 13. Kolokwium.

Ćwiczenie 14. Wpływ zagęszczenia populacji na masę ciała Drosophila melanogaster-

zamknięcie doświadczenia. Analiza wyników przy pomocy testu t-Studenta i wnioski

(laboratorium).

Ćwiczenie 15. Niepełna dominacja i addycja dwu loci genowych. Prawo Hardy'ego-

Weinberga dla dwuch loci genowych. Zaliczenie ćwiczeń.

Ćwiczenie 1

4

Ć

wiczenie 1. Podstawy dziedziczenia. Prawa Mendla

I prawo Mendla

Prawo czysto

ś

ci gamet: podczas tworzenia gamet u organizmów

diploidalnych allele oddzielaj

ą

si

ę

i w gametach wyst

ę

puj

ą

pojedynczo

Rodzice P AA x aa

Gamety G A a

Pokolenie 1. F1 Aa x Aa

Gamety G A, a A,a

Pokolenie 2. F2

Szachownica genetyczna (Punneta)

A a

A AA Aa

a Aa aa

I Prawo Mendla, dominacja pełna i kodominacja – zadania

Czarna barwa nasion u fasoli dominuje nad biał

ą

. Po skrzy

ż

owaniu ro

ś

lin o

czarnych nasionach z ro

ś

linami białonasiennymi otrzymano tylko czarne nasiona.

Jak

ą

barw

ę

nasion b

ę

dzie miało potomstwo ro

ś

lin otrzymanych w wyniku

krzy

ż

owania dwóch czarnonasiennych osobników F1?

Ż

ółta barwa nasion grochu dominuje nad barw

ą

zielon

ą

. Ro

ś

liny homozygotyczne

o

ż

ółtej barwie nasion skrzy

ż

owano z ro

ś

linami o nasionach zielonych, nast

ę

pnie

ro

ś

liny z pokolenia F1 powtórnie skrzy

ż

owano z:

a) zielononasienn

ą

form

ą

rodzicielsk

ą

b)

ż

ółtonasienn

ą

form

ą

rodzicielsk

ą

Prosz

ę

poda

ć

genotypy i fenotypy potomstwa uzyskane po krzy

ż

owaniu a i b.

Ćwiczenie 1

5

Skrzy

ż

owano ro

ś

lin

ę

lwiej paszczy o kwiatach czerwonych z ro

ś

lin

ą

o kwiatach

białych. W pokoleniu F1 wszystkie ro

ś

liny miały kwiaty ró

ż

owe. Jak b

ę

dzie wygl

ą

dało

pokolenie F2 (powstałe ze skrzy

ż

owania dwóch ro

ś

lin ró

ż

ni

ą

cych si

ę

z kwiatami z

pokolenia F1)?

Molinezja (Poecilia sphenops) wykazuje polimorfizm genetyczny pod

wzgl

ę

dem kształtu płetw. W locus L odpowiedzialnym za kształt płetw molinezji

znajduj

ą

si

ę

2 allele L i l. Niepełna dominacja L nad I sprawia,

ż

e 3 genotypom

odpowiadaj

ą

3 fenotypy przedstawione na rysunku:

fenotyp genotyp

A II
B LI
C LL

Skrzy

ż

owano molinezj

ę

o fenotypie A z osobnikiem o fenotypie C. W

pokoleniu F1 wszystkie ryby miały fenotyp B. Jakie b

ę

d

ą

proporcje fenotypów w

pokoleniu F2?

Normalne ubarwienie u karpia dominuje nad ubarwieniem bł

ę

kitnym.

Skrzy

ż

owano ryb

ę

normalnie ubarwion

ą

z bł

ę

kitn

ą

. W pokoleniu F1 wszystkie karpie

były normalnie ubarwione. Jakich fenotypów mo

ż

na spodziewa

ć

si

ę

w pokoleniu

F2? Jak sprawdzi

ć

, czy normalnie ubarwiony karp jest homozygot

ą

czy

heterozygot

ą

?

Skrzy

ż

owano pstr

ą

ga t

ę

czowego o ubarwieniu złocistym z osobnikiem o

ubarwieniu normalnym. W pokoleniu F1 otrzymano 100% ryb o ubarwieniu

po

ś

rednim (tzw palomino). Jakie b

ę

d

ą

proporcje fenotypów w pokoleniu F2?

Ćwiczenie 1

6

II prawo Mendla

Prawo niezale

ż

nego dziedziczenia cech: cechy warunkowane przez ró

ż

ne

pary genów dziedzicz

ą

si

ę

niezale

ż

nie i mog

ą

tworzy

ć

dowolne poł

ą

czenia u

osobników potomnych.

P AABB x aabb

G AB ab

F1 AaBb x AaBb

G AB, aB, ab, Ab AB, aB, ab, Ab

F2

AB aB ab Ab

AB AABB AaBB AaBb AABb

aB AaBB aaBB aaBb AaBb

ab AaBb aaBb aabb Aabb

Ab AABb AaBb Aabb AAbb

Zadania

Długa sier

ść

kotów perskich jest uwarunkowana genem recesywnym (p) w

stosunku do allelu krótkiej sier

ś

ci kotów syjamskich (P), za

ś

czarne umaszczenie

persów uwarunkowane jest allelem dominuj

ą

cym (B) w stosunku do genu

kawowego umaszczenia syjamczyków (b). Podaj mo

ż

liwe genotypy syjamczyków i

persów. Skrzy

ż

owano homozygotycznego persa z homozygotycznymsyjamczykiem.

Jak b

ę

dzie wygl

ą

dało pokolenie F1 i F2?

Br

ą

zowa barwa oczu człowieka (B), dominuje nad niebiesk

ą

(b),

prawor

ę

czno

ść

nad lewor

ę

czno

ś

ci

ą

. Br

ą

zowooki, prawor

ę

czny m

ęż

czyzna

po

ś

lubia niebieskook

ą

, prawor

ę

czn

ą

kobiet

ę

. Ich pierwsze dziecko jest

niebieskookie i lewor

ę

czne.

Je

ś

li urodz

ą

si

ę

inne dzieci, jakie cechy ( z wymienionych)

ujawni

ą

si

ę

? Wyja

ś

nij genotypy rodziców i dzieci.

Ć

wiczenie 1

7

Wiadomo

ś

ci wymagane na tym

ć

wiczeniu mo

ż

na odnale

źć

w

nast

ę

puj

ą

cych podr

ę

cznikach:

1. W. Gajewski. Genetyka ogólna i molekularna. PWN Warszawa, 1980, str. 125-

135

2. B. Rodkiewicz i G. Kerszman. Zarys genetyki. PWN Warszawa, 1987. str. 27- 40.

3. J. Maciejowski i J. Zi

ę

ba. Genetyka i ogólna hodowla zwierz

ą

t. Tom 1.PWN

Warszawa, 1972 str. 129-164.

4. B. Nowicki. Genetyka i metody doskonalenia zwierz

ą

t. PWR i L Warszawa,

1985. str. 30-40.

5. P.C. Winter, G.I. Hickey, H.L. Fletcher. Krótkie wykłady, genetyka. PWN

Warszawa, 2001. str. 139-149.

6. A. Sadakierska-Chudy, G. D

ą

browska, A. Goc. Genetyka ogólna. Wydawnictwo

Uniwersytetu Mikołaja Kopernika, Toru

ń

2004.

Ć

wiczenie 2

8

Ć

wiczenie 2. Efekt pleiotropowy genu. Geny letalne i

subletalne na przykładzie mieczyka (Xiphophorus helleri).

Mieczyk (Xiphophorus helleri) jest ryb

ą

akwariow

ą

pochodz

ą

c

ą

z tropikalnych

regionów Ameryki Południowej i

Ś

rodkowej oraz Meksyku. Ta niewielka,

jajo

ż

yworodna ryba wykazuje ogromny polimorfizm ubarwienia i pokroju ciała. Oprócz

form krótkopłetwych w akwariach spotykane s

ą

równie

ż

formy długopłetwe. Jedna z

tych form charakteryzuje si

ę

wydłu

ż

on

ą

płetw

ą

grzbietow

ą

(mieczyk

ż

aglopłetwy,

mieczyk Simpsona). Druga forma posiada wszystkie płetwy wydłu

ż

one, przy czym

charakterystyczne jest wydłu

ż

enie skrajnych promieni płetwy ogonowej oraz

pierwszych promieni płetwy grzbietowej (tzw. mieczyk lirogon lub widlak). Kształt

płetw mieczyka jest determinowany przez dwie pary alleli w dwu nie sprz

ęż

onych i

niezale

ż

nych loci genowych. Obie powy

ż

ej opisane mutacje maj

ą

charakter

dominuj

ą

cy i obni

ż

aj

ą

prze

ż

ywalno

ść

, odporno

ść

na choroby, tempo wzrostu i

płodno

ść

mieczyków w stanie heterozygotycznym (efekt subletalny). Zmutowane

dominuj

ą

ce allele w stanie homozygotycznym (w ka

ż

dym z dwu loci niezale

ż

nie)

uniemo

ż

liwiaj

ą

prze

ż

ycie organizmu ju

ż

w fazie embrionalnej (efekt letalny).

Zjawisko, w którym jeden locus genowy decyduje o kilku cechach (np. kształt

płetw i tempo wzrostu, barwa kwiatów-i barwa nasion, biała barwa sier

ś

ci,

czerwone oczy oraz nieostre widzenie) nazywamy pleiotropi

ą

lub efektem

pleiotropowym. Geny o charakterze letalnym i subletalnym zazwyczaj wykazuj

ą

siln

ą

pleiotropi

ę

w organizmie. Je

ż

eli pierwszy locus oznaczymy liter

ą

S (Simpson) a

drugi L (lirogon), to osobnik o fenotypie dzikim (krótkopłetwy) b

ę

dzie podwójn

ą

homozygot

ą

recesywn

ą

o genotypie ssll. Mieczyk Simpsona b

ę

dzie miał genotyp Ssll,

natomiast lirogon ssLl. Wszystkie mieczyki o genotypie SS lub LL b

ę

d

ą

zamierały w

trakcie rozwoju embrionalnego. Fenotyp podwójnej heterozygoty SsLI (mieczyk

welonowy) przedstawia si

ę

nast

ę

puj

ą

co: wszystkie płetwy silnie wydłu

ż

one, płetwa

grzbietowa w kształcie

ż

agla (jak u formy Simpson), płetwa ogonowa wydłu

ż

ona

równomiernie (tak skrajne jak i

ś

rodkowe promienie płetwy ogonowej wydłu

ż

one).

Zadanie

Badana populacja mieczyka składa si

ę

z 16 osobników krótkopłetwych, 14

ż

aglopłetwych, 4 lirogonów i 15 welonowych. Ryby te s

ą

potomstwem jednej pary:

samica lirogon x samiec

ż

aglopłetwy.

Ć

wiczenie 2

9

a) oblicz frekwencje alleli S i s oraz L i I,

b) Jaki b

ę

dzie rezultat krzy

ż

ówek mieczyka:

krótkopłetwy x welonowy,

welonowy x welonowy,

lirogon x lirogon,

krótkopłetwy x

ż

aglopłetwy

Ć

wiczenie 2

10

Ć

wiczenie 2

11

Ć

wiczenie 2. Chromosomy płci. Dziedziczenie cech sprz

ęż

onych z

płci

ą

.

Cechami sprz

ęż

onymi z płci

ą

nazywamy cechy zale

ż

ne od genów maj

ą

cych loci

w chromosomie płci X. Chromosom X ró

ż

ni si

ę

od wszystkich pozostałych

(autosomów) tym,

ż

e u jednej z płci nie ma swojego homologa. Innym chromosomem

płci wyst

ę

puj

ą

cym u ssaków jest chromosom Y. Ró

ż

ni si

ę

on od chromosomu X

kształtem, długo

ś

ci

ą

i, co najwa

ż

niejsze, z reguły nie zawiera loci odpowiadaj

ą

cych

tym, które spotykamy w chromosomie X.

Płe

ć

charakteryzuj

ą

ca si

ę

dwoma ró

ż

nymi chromosomami XY lub tylko jednym

X nazywamy płci

ą

heterogametyczn

ą

. Powstaj

ą

bowiem u niej dwojakiego rodzaju

gamety w równych ilo

ś

ciach: 50% z chromosomem X i 50% z Y.

Ple

ć

przeciwna do omówionej jest nazywana homogametyczn

ą

, ma dwa takie

same chromosomy płci (np. XX) i dlatego wszystkie wytwarzane przez ni

ą

gamety

zawieraj

ą

po jednym tym samym chromosomie płci (np. X).

U zwierz

ą

t płci heterogametycznej wszystkie cechy sprz

ęż

one z płci

ą

zale

żą

od

jednego tylko genu, a nie jak u płci homogametycznej od pary genów. Rozpatrzmy

tak

ą

cech

ę

na przykładzie hemofilii u psów. Hemofilia wywołana jest recesywnym

genem h. Dominuj

ą

cy gen tej pary H daje normaln

ą

krzepliwo

ść

krwi. Tak wi

ę

c,

wszystkie mo

ż

liwe fenotypy i genotypy spotykane u psów mo

ż

emy zapisa

ć

odpowiednimi symbolami w dwojaki sposób.

zdrowe nosiciele chore

samice HH Hh hh

samce H0 h0

U ssaków i wi

ę

kszo

ś

ci owadów samice s

ą

płci

ą

homogametyczn

ą

XX, a samce

heterogametyczn

ą

XY. Natomiast u ptaków i niektórych motyli samice maj

ą

tylko

jeden chromosom X a samce XX. Jak wynika z tych wyja

ś

nie

ń

gamety wytwarzane

przez zwierz

ę

ta płci heterogametycznej s

ą

dwojakiego rodzaju i od tego, która z nich

we

ź

mie udział w wytworzeniu (podczas procesu zapłodnienia) zygoty zale

ż

y płe

ć

zwierz

ę

cia. U ssaków, samce otrzymuj

ą

chromosom X wył

ą

cznie od swojej matki, u

ptaków jest odwrotnie - samice otrzymuj

ą

chromosom płci X.-tylko od ojca. a wraz z

nim geny koduj

ą

ce cechy sprz

ęż

one z płci

ą

.

Autosomalne cechy pozostaj

ą

ce pod wpływem płci cz

ę

sto s

ą

nazywane cechami

zwi

ą

zanymi z płci

ą

. Wynika to st

ą

d,

ż

e zwierz

ę

ta heterozygotyczne ze wzgl

ę

du na te

Ć

wiczenie 2

12

cechy maj

ą

mimo jednakowego genotypu ró

ż

ne fenotypy zale

ż

nie od płci. Na

przykład, je

ż

eli gen bezro

ż

no

ś

ci okre

ś

limy symbolem B. a rogato

ś

ci b - to u pewnych

ras owiec zwierz

ę

ta BB b

ę

d

ą

bezro

ż

ne niezale

ż

nie od płci, zwierz

ę

ta bb - rogate,

natomiast heterozygoty Bb samce b

ę

d

ą

rogate, a Bb samice - bezro

ż

ne. Tak wi

ę

c,

ten sam genotyp mo

ż

e dawa

ć

ró

ż

ne efekty fenotypowe zale

ż

nie od płci osobnika.

Ć

wiczenie 3

13

Ć

wiczenie 3. Geny autosomalne i sprz

ęż

one z płci

ą

– rozwi

ą

zywanie

zada

ń

Cechami sprz

ęż

onymi z płci

ą

nazywamy cechy zale

ż

ne od genów maj

ą

cych

loci w chromosomie płci X. Chromosom X ró

ż

ni si

ę

od wszystkich pozostałych

autosomów) tym,

ż

e u jednej z płci nie ma swojego homologa. Innym chromosomem

płci wyst

ę

puj

ą

cym u ssaków jest chromosom Y. Ró

ż

ni si

ę

on od chromosomu X

kształtem, długo

ś

ci

ą

i, co najwa

ż

niejsze, z reguły nie zawiera loci odpowiadaj

ą

cych

tym, które spotykamy w chromosomie X. Płe

ć

charakteryzuj

ą

ca si

ę

dwoma ró

ż

nymi

chromosomami XY lub tylko jednym Xnazywamy płci

ą

heterogametyczn

ą

. Powstaj

ą

bowiem u niej dwojakiego rodzaju gamety wrównych ilo

ś

ciach: 50% z chromosomem

X i 50% z Y.

Ple

ć

przeciwna do omówionej jest nazywana homogametyczn

ą

, ma dwa takie

same chromosomy płci (np. XX) i dlatego wszystkie wytwarzane przez ni

ą

gamety

zawieraj

ą

po jednym tym samym chromosomie płci (np. X).

U zwierz

ą

t płci heterogametycznej wszystkie cechy sprz

ęż

one z płci

ą

zale

żą

od jednego tylko genu, a nie jak u płci homogametycznej od pary genów. Rozpatrzmy

tak

ą

cech

ę

na przykładzie hemofilii u psów. Hemofilia wywołana jest recesywnym

genem h. Dominuj

ą

cy gen tej pary H daje normaln

ą

krzepliwo

ść

krwi. Tak wi

ę

c,

wszystkie mo

ż

liwe fenotypy i genotypy spotykane u psów mo

ż

emy zapisa

ć

odpowiednimi symbolami w dwojaki sposób.

zdrowe

nosiciele

chore

samice

HH

Hh

hh

samce

H0

h0

U ssaków i wi

ę

kszo

ś

ci owadów samice s

ą

płci

ą

homogametyczn

ą

XX, a

samce heterogametyczn

ą

XY. Natomiast u ptaków i niektórych motyli samice maj

ą

tylko jedenchromosom X a samce XX. Jak wynika z tych wyja

ś

nie

ń

gamety

wytwarzane przez zwierz

ę

tapłci heterogametycznej s

ą

dwojakiego rodzaju i od tego,

która z nich we

ź

mie udział w wytworzeniu (podczas procesu zapłodnienia) zygoty

zale

ż

y płe

ć

zwierz

ę

cia. U ssaków, samce otrzymuj

ą

chromosom X wył

ą

cznie od

swojej matki, u ptaków jest odwrotnie – samice otrzymuj

ą

chromosom płci X.-tylko od

ojca. a wraz z nim geny koduj

ą

ce cechy sprz

ęż

one z płci

ą

.

Ć

wiczenie 3

14

Autosomalne cechy pozostaj

ą

ce pod wpływem płci cz

ę

sto s

ą

nazywane

cechami zwi

ą

zanymi z płci

ą

. Wynika to st

ą

d,

ż

e zwierz

ę

ta heterozygotyczne ze

wzgl

ę

du na te cechy maj

ą

mimo jednakowego genotypu ró

ż

ne fenotypy zale

ż

nie od

płci. Na przykład, je

ż

eli gen bezro

ż

no

ś

ci okre

ś

limy symbolem B. a rogato

ś

ci b - to u

pewnych ras owiec zwierz

ę

ta BB b

ę

d

ą

bezro

ż

ne niezale

ż

nie od płci, zwierz

ę

ta bb -

rogate, natomiast heterozygoty Bb samce b

ę

d

ą

rogate, a Bb samice - bezro

ż

ne. Tak

wi

ę

c, ten sam genotyp mo

ż

e dawa

ć

ró

ż

ne efekty fenotypowe zale

ż

nie od płci

osobnika.

Ć

wiczenie 4

15

Ć

wiczenie 4. Allele wielokrotne na przykładzie sytemu grup krwi

ABO u człowieka. Czynnik RH a konflikt serologiczny.
Rozwi

ą

zywanie zada

ń

rachunkowych: obliczanie frekwencji alleli w

populacji na podstawie cz

ę

sto

ś

ci poszczególnych grup krwi.

A. Allele wielokrotne na przykładzie sytemu grup krwi ABO u człowieka.

Czynnik RH a konflikt serologiczny. Mechanizm dziedziczenia grup krwi u

człowieka

Dziedziczenie grup krwi w systemie ABO u człowieka zale

ż

y od

wyst

ę

powania kombinacji dwu z trzech alleli w jednym locus genowym. Dwa allele I

A

oraz I

B

s

ą

dominuj

ą

ce wobec trzeciego allelu i. Pomi

ę

dzy dominuj

ą

cymi allelami

IA i IB wyst

ę

puje zjawisko kodominacji (współdominacji). Polega to na

jednoczesnej ekspresji obu tych alleli w heterozygocie. Produktem ekspresji

allelu I

A

jest antygen A obecny w błonie komórkowej erytrocytu. Produktem

ekspresji allelu I

B

jest antygen B. Allel recesywny i jest odpowiedzialny

za brak antygenu w błonie komórkowej erytrocytu.

Osoby z grupa krwi A posiadaj

ą

antygen A w błonie komórkowej

erytrocytu, oraz przeciwciała (izoaglutyniny) anty-B, skierowane przeciw antygenowi

B. Osoby z grupa krwi B posiadaj

ą

antygen B oraz izoaglutyniny anty-A. Osoby z

grupa AB posiadaj

ą

oba antygeny w błonie erytrocytu i

ż

adnych izoaglutynin w

osoczu. Osoby z grupa krwi 0 posiadaj

ą

izoaglutyniny anty-A i anty-B w

osoczu, nie posiadaj

ą

natomiast

ż

adnych antygenów w błonie erytrocytu. Osoby z

grupa krwi A mog

ą

mie

ć

genotypy: I

A

I

A

oraz I

A

i osoby z grupa B: I

B

I

B

oraz I

B

i osoby z

grupa AB - tylko I

A

I

B

a osoby z grupa 0 tylko ii. W ten sposób sze

ść

ró

ż

nych

genotypów ( 3 homo- i 3 heterozygotyczne) daje w efekcie 4 fenotypy. Dzieje si

ę

tak

na skutek pełnej dominacji alleli IA oraz IB nad allelem i w odpowiednich

genotypach heterozygotycznych. W genotypie heterozygotycznym IAIB wyst

ę

puje

zjawisko kodominacji (jednoczesne wyst

ę

powanie obu antygenów w błonie

erytrocytu.

Wyst

ę

powanie czynnika Rh zale

ż

y od układu zale

ż

y pary alleli jednym locus

genowym. W tym locus wyst

ę

puj

ą

dwa allele: D oraz d. Wyst

ę

puje pełna dominacja

D nad d. Genotypy DD i Dd b

ę

d

ą

wiec miały wspólny fenotyp (Rh+), natomiast

homozygota recesywna dd b

ę

dzie miała fenotyp Rh-(brak czynnika Rh).

Wyst

ę

powanie konfliktu serologicznego wi

ąż

e si

ę

z odpowiedzi

ą

immunologiczn

ą

Ć

wiczenie 4

16

organizmu matki o fenotypie Rh- przeciwko krwinkom czerwonym dziecka o

fenotypie Rh+. W takiej sytuacji nast

ę

puje indukcja syntezy specyficznych

przeciwciał skierowanych przeciwko czynnikowi Rh w erytrocytach dziecka, gdy

ż

czynnik ten jest rozpoznawany w organizmie matki jako obcy antygen). W

trakcie ci

ąż

y wzrost koncentracji przeciwciał przeciwko czynnikowi RH we krwi matki

przebiega stopniowo, niemniej pierwsze dziecko rodzi si

ę

zwykle bez wi

ę

kszych

komplikacji. Poziom przeciwciał przeciw czynnikowi Rh we krwi matki o genotypie

dd po przebytej ci

ąż

y jest ju

ż

podwy

ż

szony (organizm nabył „odporno

ść

" na oby

antygen - czynnik Rh, podobnie jak to ma miejsce w przypadku wytwarzania si

ę

odporno

ść

naturalnej po przebytej chorobie). Przy kolejnej ci

ąż

y dojdzie do

szybkiego dalszego wzrostu koncentracji przeciwciał i w rezultacie nast

ą

pi

odpowiedz immunologiczna organizmu matki, polegaj

ą

ca na niszczeniu krwinek

dziecka posiadaj

ą

cego czynnik Rh w błonie erytrocytu (genotyp Dd).

Osoby z grup

ą

krwi Rh- stanowi

ą

15% całej populacji, natomiast osoby z

grup

ą

krwi Rh+ stanowi

ą

85% populacji.

Ć

wiczenie 5

17

Ć

wiczenie 5. Model Hardy’ego-Weinberga (H-W). Svmulowanie

losowego kojarzenia gamet w populacji panmiktvcznei.

Stosowanie testu

χ

2 (chi2) do okre

ś

lenia czy obserwacje

potwierdzaj

ą

prawo H-W.

Proces analizy zmienno

ś

ci genetycznej składa si

ę

:

- ze zbadania jednego lub wi

ę

cej typów markerów genetycznych,

- ilo

ś

ciowego wyra

ż

enia frekwencji fenotypów,

- wywnioskowania na tej podstawie frekwencji genotypów koduj

ą

cych zbadane

fenotypy. Nast

ę

pnie potrzebny jest okre

ś

lony model, który powi

ąż

e ze sob

ą

frekwencje genotypów z frekwencjami alleli i umo

ż

liwi wyciagni

ę

cie wniosków na

temat procesów, oddziałuj

ą

cych na badan

ą

populacj

ę

. U

ż

yteczno

ść

modelu polega

na tym, i

ż

pozwala on zidentyfikowa

ć

kluczowe obserwacje (lub eksperymenty)

które nale

ż

y poczyni

ć

, aby lepiej zrozumie

ć

stan obecny populacji oraz zaradzi

ć

ewentualnym kłopotom.

Najpowszechniej stosowanym modelem, wi

ążą

cym frekwencje genotypów z

frekwencjami alleli, jest model opracowany niezale

ż

nie przez G.H. Hardy'ego

(1908) oraz W. Weinberga (1908).

Model Hardy'ego-Weinberga opiera si

ę

na kilku wa

ż

nych zało

ż

eniach:

- liczebno

ść

populacji jest wielka i stała w kolejnych pokoleniach,

- kojarzenie si

ę

osobników jest losowe (populacja jest panmiktyczna, albo

bardzo dobrze wymieszana),

- organizmy s

ą

diploidalne,

- pokolenia nie zaz

ę

biaj

ą

si

ę

,

- rozród odbywa si

ę

drog

ą

płciow

ą

,

- wpływy mutacji, migracji i selekcji s

ą

zaniedbywalne.

W przypadku autosomalnych (tych, które nie s

ą

ulokowane na chromosomach płci)

loci genowych o dwóch allelach, model Hardy'ego-Weinberga przyjmuje posta

ć

:

(p + q)

2

= p

2

+ 2pq + q

2

= 1

Ć

wiczenie 5

18

gdzie p to frekwencja cz

ę

stszego allelu A podczas gdy q jest frekwencj

ą

rzadziej wyst

ę

puj

ą

cego allelu a, natomiast p +q = 1. Proporcje genotypów

b

ę

d

ą

odpowiadały rozwini

ę

ciu dwumianu (p + q)

2

.

AA Aa aa

p

2

2pq q

2

Model Hardy'ego-Weinberga zakłada,

ż

e je

ś

li zostan

ą

spełnione ww. zało

ż

enia, to

frekwencje alleli i genotypów w populacji nie b

ę

d

ą

si

ę

zmieniały z pokolenia na

pokolenie. Zgodnie z tym zało

ż

eniem, model mo

ż

e by

ć

stosowany do przewidywania

frekwencji genotypów na podstawie obecnej frekwencji alleli. Zastosowania modelu

Hardy'ego-Weinberga dostarczaj

ą

podstawy do oceny sił ewolucyjnych, wpływaj

ą

cych

na wachlarz genotypów w populacji. Je

ś

li stwierdzamy

ż

e obserwowane frekwencje

genotypów s

ą

inne ni

ż

frekwencje przewidywane przez model, mo

ż

na stawia

ć

hipotezy co do przyczyn tych odchyle

ń

. Id

ą

c dalej, mo

ż

na zaplanowa

ć

nowe

obserwacje lub eksperymenty, których celem b

ę

dzie wyja

ś

nienie procesów, które

spowodowały ró

ż

nice mi

ę

dzy obserwowanymi i przewidywanymi frekwencjami alleli w

populacji. Rozumowanie takie opiera si

ę

na przypuszczeniu, i

ż

w rezultacie

rozmaitych mechanizmów ekologicznych jedno lub wi

ę

cej zało

ż

e

ń

modelu nie jest

spełnione w przypadku obserwowanej populacji.

Jednym z zało

ż

e

ń

modelu Hardy'ego-Weinberga jest losowe kojarzenie si

ę

osobników w procesie rozrodu. To zało

ż

enie cz

ę

sto nie jest spełniane wskutek

najrozmaitszych zachowa

ń

rozrodczych. Wybiórcze krzy

ż

owanie si

ę

osobników to

wybór partnera rozrodczego na podstawie jego fenotypu. Dodatnie krzy

ż

owanie

wybiórcze wyst

ę

puje wtedy. gdy osobniki krzy

ż

uj

ą

si

ę

z podobnymi do siebie cz

ęś

ciej

ni

ż

gdyby było to wył

ą

cznie dziełem przypadku. Inbreeding to krzy

ż

owanie si

ę

ze sob

ą

osobników spokrewnionych, co stanowi szczególny przypadek pozytywnego

krzy

ż

owania si

ę

wybiórczego. Negatywne wybiórcze kojarzenie si

ę

wyst

ę

puje

wówczas, gdy cz

ęś

ciej ni

ż

wynikałoby to z przypadku osobniki krzy

ż

uj

ą

si

ę

z

partnerami niepodobnymi do siebie fenotypowo jak w przypadku "korzy

ś

ci rzadkich

samców" [rare-male advantage] Drosophila). Genetyczny podział populacji gatunku

jest równie

ż

odmian

ą

krzy

ż

owania wybiórczego, w którym na pul

ę

genow

ą

gatunku

składaj

ą

si

ę

pule genowe grupy subpopulacji (stad), których osobniki krzy

ż

uj

ą

si

ę

panmiktycznie w ramach subpopulacji (stad).

W niektórych przypadkach wpływ doboru naturalnego na frekwencje genotypów

Ć

wiczenie 5

19

nie jest zaniedbywalny. Dobrze znanym przykładem u człowieka jest korzystne

dostosowanie heterozygot w locus B-hemoglobiny, kiedy to genotyp +s (odporny na

malari

ę

, nie anemiczny) jest lepiej dostosowany ni

ż

++ (podatny na malari

ę

) i

genotyp ss (cierpi na anemi

ę

zwi

ą

zan

ą

z sierpowato

ś

ci

ą

erytrocytów).

Złamanie zało

ż

e

ń

prawa Hardy'ego-Weinberga mo

ż

e wynikn

ąć

z rozmaitych

innych mechanizmów ekologicznych. W rzeczywisto

ś

ci, model Hardy'ego-Weinberga

jest do

ść

odporny na niewielkie odst

ę

pstwa od jego zało

ż

e

ń

, co czyni go u

ż

ytecznym

w zastosowaniach praktycznych. Trzeba jednak zaznaczy

ć

, i

ż

je

ś

li obserwowane

frekwencje genotypowe spełniaj

ą

oczekiwania Hardy'ego-Weinberga, to nie musi to

koniecznie oznacza

ć

ż

e wszystkie zało

ż

enia modelu s

ą

spełnione.

Symulowanie losowego kojarzenia gamet w populacji panmiktvcznej.

Stosowanie testu

χ

2 (chi2) do okre

ś

lenia czy obserwacje potwierdzaj

ą

spodziewania H-W

Populacj

ę

okre

ś

lamy jako pamniktyczn

ą

, je

ż

eli kojarzenia nale

żą

cych do niej

osobników zachodz

ą

całkowicie losowo. Rozkład genotypów w populacji zale

ż

y od

wielu czynników. W najprostszym przypadku mo

ż

e on by

ć

losowy i bezpo

ś

rednio

wynika

ć

z frekwencji wyst

ę

puj

ą

cych w tej populacji alleli.

Załó

ż

my,

ż

e populacja spełnia nast

ę

puj

ą

ce warunki:

1. organizmy s

ą

diploidalne,

2. rozmna

ż

aj

ą

si

ę

płciowo,

3. pokolenia nie zachodz

ą

na siebie,

4. osobniki kojarz

ą

si

ę

losowo (populacja jest panmiktyczna),

5. populacja jest bardzo du

ż

a,

6. nie ma migracji,

7. nie ma mutacji,

8. dobór naturalny nie wpływa na badany locus.

Populacja b

ę

dzie spełniała te warunki tak

ż

e wtedy, gdy czynniki wymienione w

pkt. 6, 7 i 8 b

ę

d

ą

si

ę

równowa

ż

y

ć

. W takich warunkach proporcje genotypów, dla locus

o dwu allelach A i a, których frekwencje wynosz

ą

odpowiednio p i q, (przy czym p + q =

1), b

ę

d

ą

odpowiadały rozwini

ę

ciu dwumianu (p + q)2.

Ć

wiczenie 5

20

Powy

ż

sze stwierdzenie jest zwane prawem Hardy'ego i Weinberga. Prawo to

mówi,

ż

e je

ś

li zostan

ą

spełnione zało

ż

enia 1-8, to frekwencje alleli i genotypów w

populacji nie b

ę

d

ą

si

ę

zmieniały z pokolenia na pokolenie; dla dwu alleli frekwencje

genotypów b

ę

d

ą

odpowiadały rozwini

ę

ciu dwumianu (p + q)2.

Ka

ż

dy ze studentów losuje dwie. "gamety" z locus A i dwie z locus B, nast

ę

pnie

ka

ż

dy odczytuje swój "genotyp".

Jakie s

ą

liczebno

ś

ci poszczególnych genotypów w locus A a jakie w locus B?

Jakie s

ą

oczekiwane liczebno

ś

ci tych genotypów z równania Hardy'ego i

Weinberga?

Czy frekwencje obserwowane odpowiadaj

ą

oczekiwanym - sprawdzenie

za pomoc

ą

testu chi-kwadrat.

Test

χ

2 stosuje si

ę

do okre

ś

lania, czy obserwowane liczby osobników o danych

genotypach s

ą

takie same, jakich spodziewaliby

ś

my si

ę

na podstawie H-W (to

znaczy, czy spełniaj

ą

oczekiwania H-W, otrzymane warto

ś

ci z obu (obserwowane i

oczekiwane) kolumn podstawiamy do wzoru i obliczamy według modelu

∑

−

=

Exp

Exp

Obs

2

2

)

(

χ

gdzie: Obs to liczba obserwowanych osobników o okre

ś

lonym fenotypie

Exp to liczba oczekiwanych osobników o okre

ś

lonym fenotypie

suma (

Σ

) b

ę

dzie zawierała 3 składniki - odpowiednio dla trzech genotypów w

ka

ż

dym z badanych loci genowych (oddzielnie AA, Aa i aa oraz BB, Bb i bb).

Liczba stopni swobody, zwi

ą

zana z t

ą

wielko

ś

ci

ą

χ

2

, równa si

ę

liczbie klas

danych (w tym przykładzie trzy klasy, czyli liczby AA, Aa oraz aa) minus jeden, minus

liczba parametrów oszacowanych na podstawie danych (w tym przykładzie jeden

parametr, p, oszacowano na podstawie danych), czyli 3 - 1 - 1 = 1. Zauwa

ż

my,

ż

e

stopie

ń

swobody nie jest pomniejszany z powodu oszacowania na podstawie danych

wielko

ś

ci parametru q, gdy

ż

kiedy ju

ż

oszacowali

ś

my p. wówczas q mo

ż

na otrzyma

ć

z zale

ż

no

ś

ci q = 1 - p. Przy jednym stopniu swobody otrzymana wy

ż

ej warto

ść

χ

2

jest

wysoce istotna (P < 0,01).

Warto

ść

krytyczna statystyki

χ

2

na poziomie istotno

ś

ci a = 0,05 wynosi w tym

przypadku 3,84

Ć

wiczenie 5

21

Obliczanie frekwencji alleli w locus przy pełnej dominacji. Rozpatrujemy dwie

cechy:

1. barwa oczu: br

ą

zowe. piwne lub zielone - genotyp M lub Aa niebieskie lub szare

- genotyp aa

2. ucho: wolny koniec - genotyp BB lub Sb, przyro

ś

ni

ę

ty koniec - genotyp bb.

Ka

ż

dy ze studentów okre

ś

la genotyp s

ą

siada (na podstawie jego fenotypu)

jako Ax lub aa oraz Bx lub bb.(gdzie x oznacza dowolny allel z danego locus).

Zauwa

ż

my.

ż

e tylko homozygoty recesywne s

ą

wyró

ż

nialne (dotyczy to obu

badanych loci genowych). Obliczamy udział homozygot recesywnych (dla ka

ż

dej

cechy oddzielnie) w całej grupie studenckiej. Dodajemy równie

ż

w miar

ę

mo

ż

liwo

ś

ci wyniki z grup poprzednich, aby zwi

ę

kszy

ć

liczebno

ść

próby i

zminimalizowa

ć

bł

ą

d statystyczny. Przykładowo, je

ż

eli liczba homozygot w locus

A wynosiła 5 na 20 osób, to frekwencja homozygot recesywnych w próbie wynosi

5/20 czyli 0.25. Z równania Hardy'ego i Weinberga wiemy.

ż

e frekwencja

homozygot recesywnych w populacji wynosi q

2

, a zatem frekwencja allelu

recesywnego q =

√

q

2

= 0,5. Frekwencja allelu dominuj

ą

cego wynosi za

ś

p = 1-q = 0,5

Mamy ju

ż

frekwencje alleli A i a (p i q) oraz B i b (p

1

i q

1

). Mo

ż

emy teraz

obliczy

ć

, jaki procent w populacji stanowi

ą

heterozygoty - nosiciele cech

recesywnych. Obliczamy to ze wzoru:

liczba heterozygot Aa = 2pq

liczba heterozygot Bb = 2p1q1.

Ka

ż

dy ze studentów, szczególnie potencjalnych heterozygot w badanych loci

przypomni sobie jak wygl

ą

daj

ą

wspomniane cechy u jego rodziców i rodze

ń

stwa, a

nast

ę

pnie wyci

ą

gnie wnioski co do swojego genotypu w loci A i B.

Ć

wiczenie 6

22

Ć

wiczenie 6. Efektywna wielko

ść

populacji i współczynnik inbredu –

rozwi

ą

zywanie zada

ń

.

Efektywna wielko

ść

populacji:

f

m

f

m

e

N

N

N

N

N

+

=

*

4

gdzie: N

m

- liczba samców, N

f

- liczba samic

Współczynnik inbredu:

t

e

t

N

F

)

5

,

0

1

(

1

−

−

=

gdzie: F - współczynnik inbredu, t - liczba pokole

ń

, N

e

- efektywna wielko

ść

populacji

AA p

o

2

+P

o

q

o

F

t

Aa 2p

o

q

o

-2p

o

q

o

F

t

aa q

o

2

+P

o

q

o

F

t

Im wy

ż

sza warto

ść

współczynnika inbredu tym szybciej wzrasta nadwy

ż

ka

homozygot w populacji. Inbred nie ma wpływu na frekwencje alleli A i a, natomiast

ma znaczny wpływ na frekwencje poszczególnych genotypów AA, Aa, i aa.

Zadania

1) Oblicz efektywn

ą

wielko

ść

populacji, w której jest:

a) 150 samic i 50 samców,

b) 180 samic i 20 samców,

c) 280 samic i 20 samców,

d) 380 samic i 20 samców,

e) 170 samic i 30 samców.

2) Oblicz efektywn

ą

wielko

ść

populacji zło

ż

onej z 10 kur i 1 koguta.

3) Efektywna wielko

ść

pewnej populacji wynosi 20. Frekwencje alleli A i a wynosz

ą

odpowiednio 0,6 i 0,4.

Ć

wiczenie 6

23

4) Oblicz współczynnik inbredu oraz frekwencje genotypów w tej populacji w

dziesi

ą

tym pokoleniu. Oblicz to samo dla populacji licz

ą

cej 1000 samic i 1000

samców.

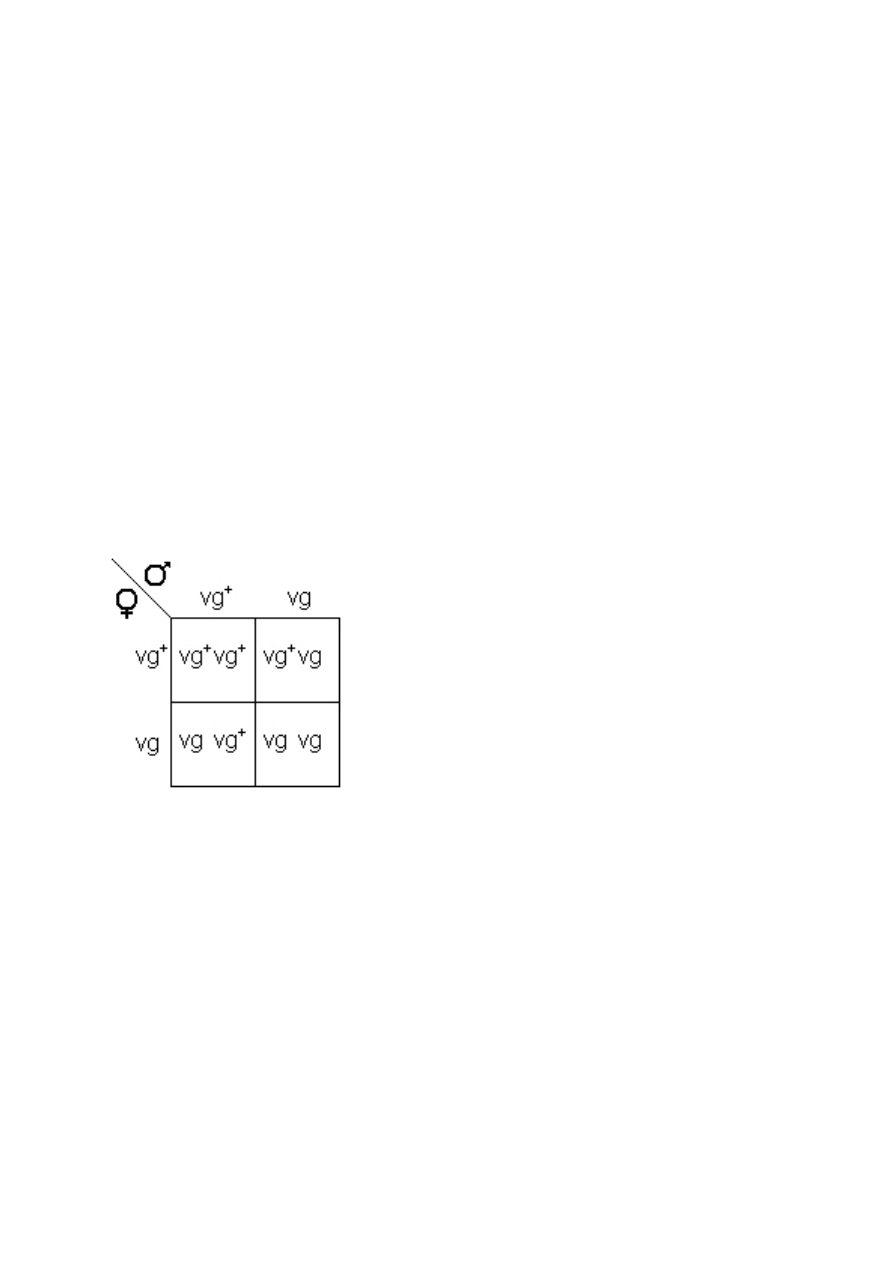
Ć

wiczenie 7

24

Ć

wiczenie 7. Genetyka muszki owocowej (Drosophila

melanogaster). Wykorzystanie programu komputerowego

drosophiLab.

DrosophiLab (autor programu: Hannes Jensen)

I Konstrukcja prostego eksperymentu

Przewodnik ten pozwala na przeprowadzenie prostego eksperymentu, w którym

analizowane b

ę

dzie dziedziczenie pojedynczego genu (vg – vestigial vings)

odpowiedzialnego za mutacj

ę

polegaj

ą

c

ą

na redukcji skrzydeł u D. melanogaster. Do

eksperymentu wybieramy rodziców, którzy s

ą

heterozygotami pod wzgl

ę

dem tego

genu. Jako,

ż

e rodzice nie wykazuj

ą

ż

adnej obecno

ś

ci tej mutacji mo

ż

emy si

ę

spodziewa

ć

, i

ż

25% pokolenia potomnego (F1) b

ę

dzie posiadało zredukowane

skrzydła (co ilustruje poni

ż

szy diagram)

Krok 1.

Uruchom program DrosophiLab i wybierz File> New Experiment. Wpisz nazw

ę

eksperymentu „mutacja vg” a nazw

ę

generacji zostaw bez zmian „P1”. Kliknij na ikon

ę

Male (samiec) i w oknie dialogowym wybierz vgmale.fly. Zrób te same czynno

ś

ci

wybieraj

ą

c samic

ę

(Female – vgfemale.fly).

Kliknij prawym przyciskiem myszy na białe pole opisane jako Counting jar (naczynie

do zliczania muszek) i wybierz Add jar (dodaj naczynie) wpisuj

ą

c jednocze

ś

nie nazw

ę

naczynia „forma dzika”. Dodaj jeszcze jedno naczynie i nazwij je jako „forma vg”.

Kliknij OK

ż

eby przej

ść

do drugiego kroku.

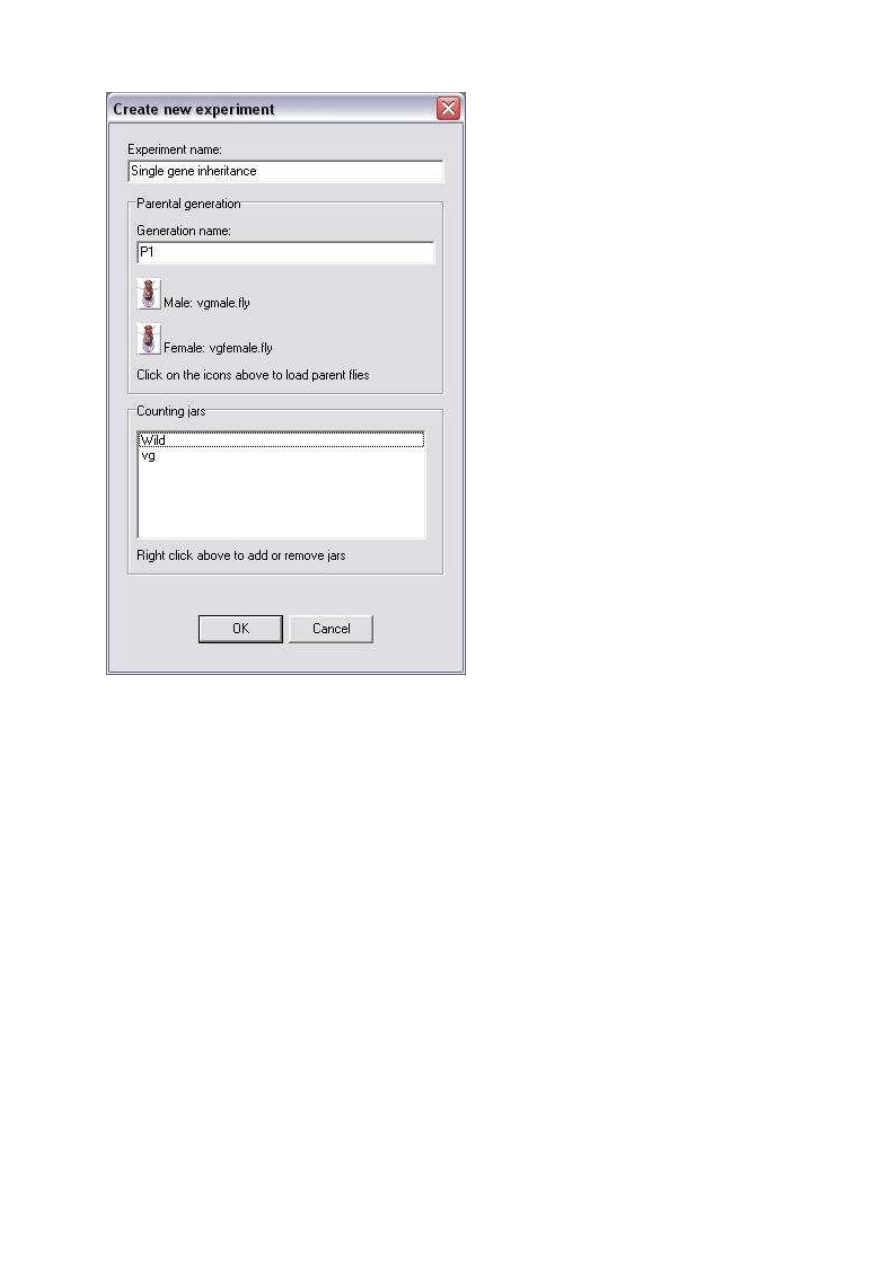
Ć

wiczenie 7

25

Krok 2.

Kolejny etap to rozpocz

ę

cie eksperymentu z wybranymi rodzicami. Osobniki te

ukazane s

ą

w formie małych ikon oznaczonych jako P1. Aby obejrze

ć

wybrane

muszki nale

ż

y przeci

ą

gn

ąć

je przy pomocy myszki na pole oznaczone Microscope.

Ogl

ą

dane osobniki mo

ż

na powi

ę

kszy

ć

poprzez przeci

ą

gni

ę

cie w dół suwaka

znajduj

ą

cego si

ę

po prawej stronie pola obserwacyjnego. Ponadto, ogl

ą

dane muszki

mo

ż

na obróci

ć

w dowolnym kierunku przytrzymuj

ą

c klawisz ctrl na klawiaturze. Aby

usun

ąć

muszk

ę

spod mikroskopu nale

ż

y klikn

ąć

Empty microscope. Nale

ż

y zwróci

ć

uwag

ę

, i

ż

obydwie muszki posiadaj

ą

normalne skrzydła. Aby zatwierdzi

ć

muszk

ę

jako rodzica klikn

ąć

na set as parent. Wybór muszki na rodzica jest potwierdzany

przez ró

ż

owe zabarwienie ikony muszki.

Z górnego paska dialogowego wybierz Experiment>New generation. Wprowad

ź

liczb

ę

potomstwa Number of offspring (tym razem niech to b

ę

dzie 20) i upewnij si

ę

,

ż

e poni

ż

ej zaznaczona jest opcja Icons (ikony). Inne mo

ż

liwo

ś

ci pokazania wyników

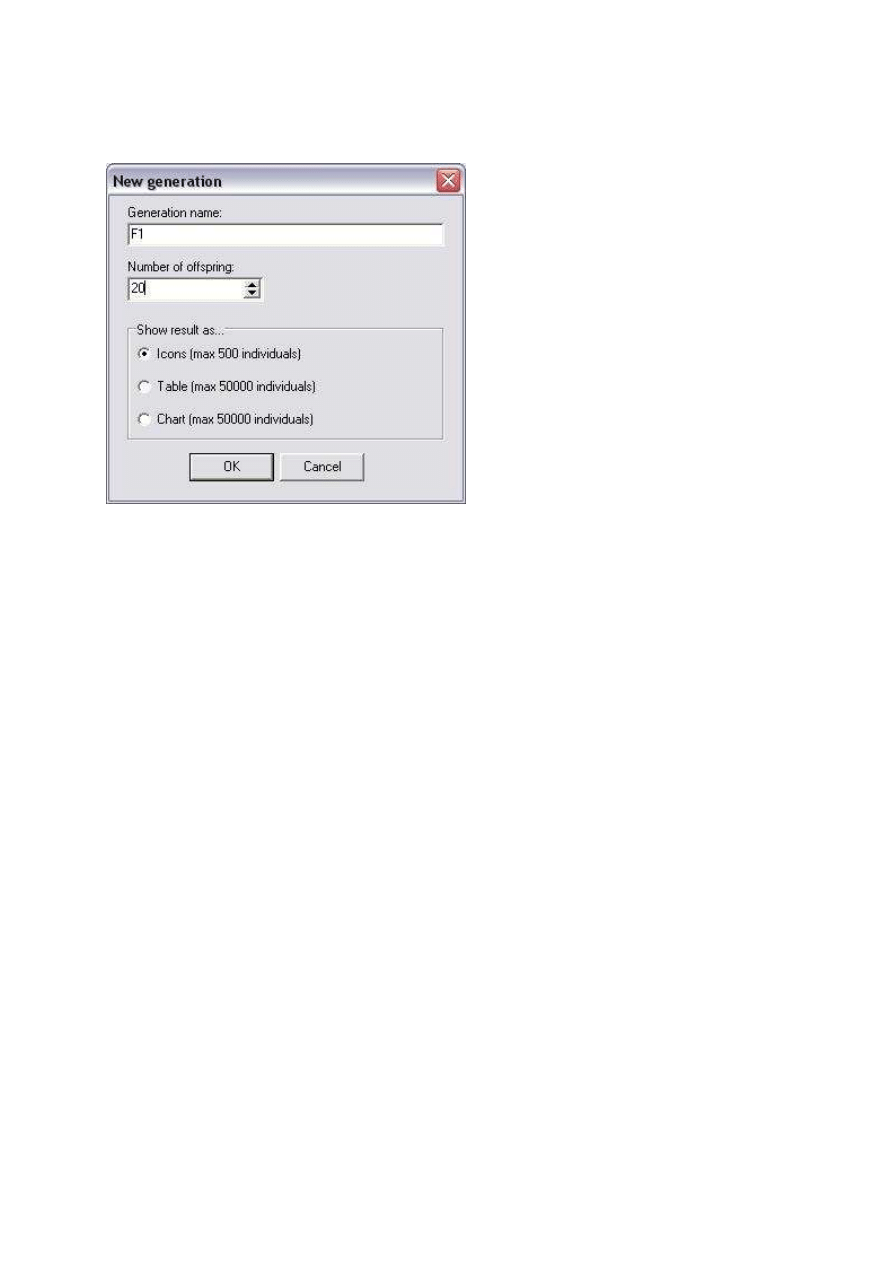
Ć

wiczenie 7

26

to Tabela (Table) lub wykres (Chart). Przejd

ź

do kolejnego kroku poprzez klikni

ę

cie

OK.

Krok 3.

Potomstwo wybranych rodziców (w formie małych ikon) powinno znajdowa

ć

si

ę

w

oknie oznaczonym jako F1.

Ka

ż

d

ą

potomn

ą

muszk

ę

przeci

ą

gnij przy pomocy myszki pod mikroskop i sprawd

ź

czy posiada ona normalne skrzydła czy te

ż

zredukowane. Muszki z normalnymi

skrzydłami bezpo

ś

rednio spod mikroskopu przeci

ą

gnij do naczynia „forma dzika”

natomiast muszki ze zredukowanymi skrzydłami przenie

ś

do naczynia „forma vg”.

Ile jest much z efektem mutacji vg a ile powinno by

ć

?

II Eksperyment. Dziedziczenie cech recesywnych.

Krok 1.

Utwórz muszki o podanym poni

ż

ej genotypie przy pomocy Edytora Chromosomów:

Tools>Chromosome Editor.

Samiec (zaznacz opcj

ę

Male!): (w+) (vg+/vg+), zapisz (File>Save) w katalogu Flies

(C:/Program Files\Drosohilab/Flies) jako dzikisamiec.fly .

Samica (zaznacz opcj

ę

Female!): (w/w) (vg/vg), zapisz jako bialookasamica.fly.

Krok 2.

Ć

wiczenie 7

27

Utwórz nowy eksperyment (File>New Experiment) i wybierz samca

(dzikisamiec.fly) i samic

ę

(bialookasamica.fly). Potwierd

ź

poprzez klikni

ę

cie

OK.

Krok 3.

Sprawd

ź

pod mikroskopem czy wybrałe

ś

odpowiednie osobniki, je

ś

li tak to zatwierd

ź

je jako rodziców. Kontynuuj prac

ę

Experiment>New generation, wpisz liczb

ę

osobników potomnych (100), zaznacz format wyniku jako ikony (opcja Icone) i kliknij

OK.

Krok 4.

Przeanalizuj wyniki, dodaj trzy naczynia do liczenia muszek (Experiment>Add

counting jar), i nazwij je kolejno: białe oczy, czerwone oczy, bez skrzydeł. Ile

osobników ma czerwone oczy (forma dzika), ile osobników ma białe oczy a ile

powstało osobników ze zredukowanymi skrzydłami?

Wyja

ś

nij otrzymane wyniki. Jakie genotypy i jakie fenotypy powinny posiada

ć

osobniki potomne?

Krok 5.

Powtórz krok 2 i 3, Z potomstwa otrzymanego w krok 4, wybierz po jednym

osobniku z czerwonymi oczami (forma dzika) oraz białymi oczami, wska

ż

je jako

osobniki rodzicielskie. Utwórz pokolenie F2 (Experiment>New Generation).

Wpisz liczb

ę

osobników potomnych (100), wyniki utwórz w formie tabeli (opcja

Table).

Jakich genotypów i jakich fenotypów mo

ż

emy si

ę

spodziewa

ć

? Jaki jest

empiryczny stosunek otrzymanych fenotypów?

Wykaz skrótów oznacz

ę

fenotypów u

ż

ywanych przez program DrosophiLab

w (white eyes) – białe oczy

rb (ruby eyes) – rubinowe oczy

t (tan body) –

ż

ółtobr

ą

zowe ciało

B (bar eyes) – ograniczona wielko

ść

oczu

al (aristaless antena) – urz

ę

sione czułki

Cy (curly wings) – podwini

ę

te skrzydła

Ć

wiczenie 7

28

b (black body) – czarne ciało

p (purple eyes) – purpurowe oczy

vg (vestigial vings) – zredukowane skrzydła

L (lobe eyes) – oczy ograniczone

c (curved wings) – zakrzywione skrzydła

jv (javelin bristles) – odstaj

ą

ce rz

ę

ski

se (sepia eyes) – oczy w kolorze sepii th (thread arista) – nitkowate czułki

cu (curly wings) – podwini

ę

te skrzydła, jednocze

ś

nie czarne ciało

sr (striped body) – pr

ąż

kowane ciało

ci (cubitus interruptus veins) – najwi

ę

ksze skrzydła poprzerywane, mniejsze w

zaniku

sv (shaven bristles) – rz

ę

ski krótkie lub w zaniku

Ć

wiczenie 8

29

Ć

wiczenie 8. Geny autosomalne i sprz

ęż

one z płci

ą

. Drosophila

melanogaster jako obiekt bada

ń

genetycznych

Przygotowanie hodowli

Do próbówki wsypa

ć

1 g IDM (Instant Drosophila Medium) (3,5-3,7ml obj

ę

to

ś

ci).

Doda

ć

5 ml wody destylowanej. UWAGA!

Ś

cianki próbówki musz

ą

pozosta

ć

suche.

Wszystkie naczynia musz

ą

by

ć

całkowicie suche. Oznakuj probówki swoimi

inicjałami, dat

ą

i zaznacz, jakie muchy tam hodujesz (gdzie Mel oznacza Drosophila

melanogaster - czyli muszka owocowa):

• Mel + (dzikie),

• Mel Vg (bezskrzydłe),

• Mel W (białookie),

• Mel W/Vg (białookie, bezskrzydle).

Je

ż

eli wykonujesz krzy

ż

ówki zaznacz w opisie płe

ć

poszczególnych u

ż

ytych

osobników.

Usypianie much przy u

ż

yciu anestetyku Fly Nap.

Preparat Fly Nap to nowoczesny anestetyk stosowany do usypiania much. W

przeciwie

ń

stwie wcze

ś

niej stosowanych

ś

rodków jak: CO2 , chloroform, jest on

nieszkodliwy dla owadów. Jego u

ż

ycie nie wpływa na prze

ż

ywalno

ść

larw, poczwarek

i osobników dorosłych. Muchy u

ś

pione preparatem Fly Nap pozostaj

ą

w stanie

narkozy przez okres 1-1,5 godziny. Jego prawidłowe zastosowanie uzale

ż

nione jest

jednak od przestrzegania poni

ż

szej instrukcji. Przy usypianiu much anestetykiem Fly

Nap mo

ż

na tak

ż

e skorzysta

ć

z rysunku zamieszczonego na s

ą

siedniej stronie.

1. Prosz

ę

przygotowa

ć

:

a. butelk

ę

z preparatem Fly Nap i dozownik do preparatu Fly Nap,

b. czarne pudełko na dozownik Fly Nap,

c. płytk

ę

szklan

ą

(szalka Petriego),

d. próbówki z rozrobion

ą

po

ż

ywk

ą

wraz z korkiem,

e. p

ę

dzelek.

2. Odkr

ę

ci

ć

butelk

ę

z preparatem Fly Nap i umocz ko

ń

cówk

ę

dozownika Fly Nap

w preparacie. Po umoczeniu ko

ń

cówki dozownika DOKŁADNIE ZAKR

Ę

CI

Ć

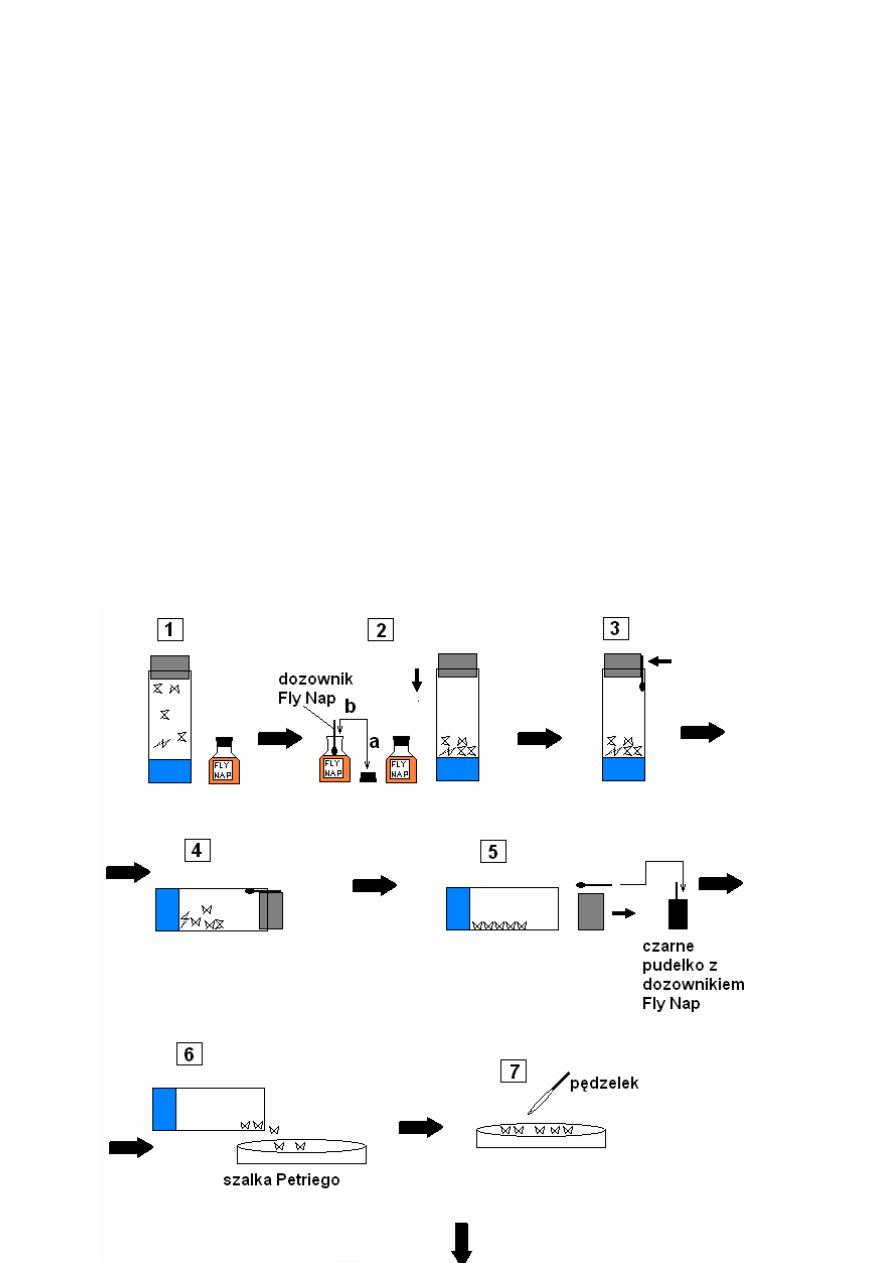
Ć

wiczenie 8

30

butelk

ę

!

3. Strz

ą

sn

ąć

delikatnie muchy na dno próbówki.

4. Odsun

ąć

cz

ęś

ciowo korek próbówki i umie

ść

dozownik poni

ż

ej korka (czynno

ść

t

ą

trzeba wykona

ć

szybko aby muchy nie uciekły z próbówki).

5. Uło

ż

y

ć

próbówk

ę

z dozownikiem na stole w pozycji horyzontalnej.

6. Pozostawi

ć

dozownik Fly Nap pod korkiem próbówki na czas 8-iu minut.

7. Gdy muchy przestan

ą

si

ę

rusza

ć

usun

ąć

jednocze

ś

nie korek i dozownik Fly Nap.

Nast

ę

pnie dozownik umie

ś

ci

ć

w czarnym pudełku.

8. Wysypa

ć

muchy na szalk

ę

Petriego.

9. Z po

ś

ród much znajduj

ą

cych si

ę

w szalce wybra

ć

interesuj

ą

ce nas osobniki.

Selekcj

ę

much dokonujemy przy u

ż

yciu p

ę

dzelka.

10. Przy u

ż

yciu p

ę

dzelka przenie

ść

wyselekcjonowane osobniki do nowej próbówki.

11. Zatka

ć

próbówk

ę

i pozostawi

ć

j

ą

w pozycji horyzontalnej.

Ć

wiczenie 8

31

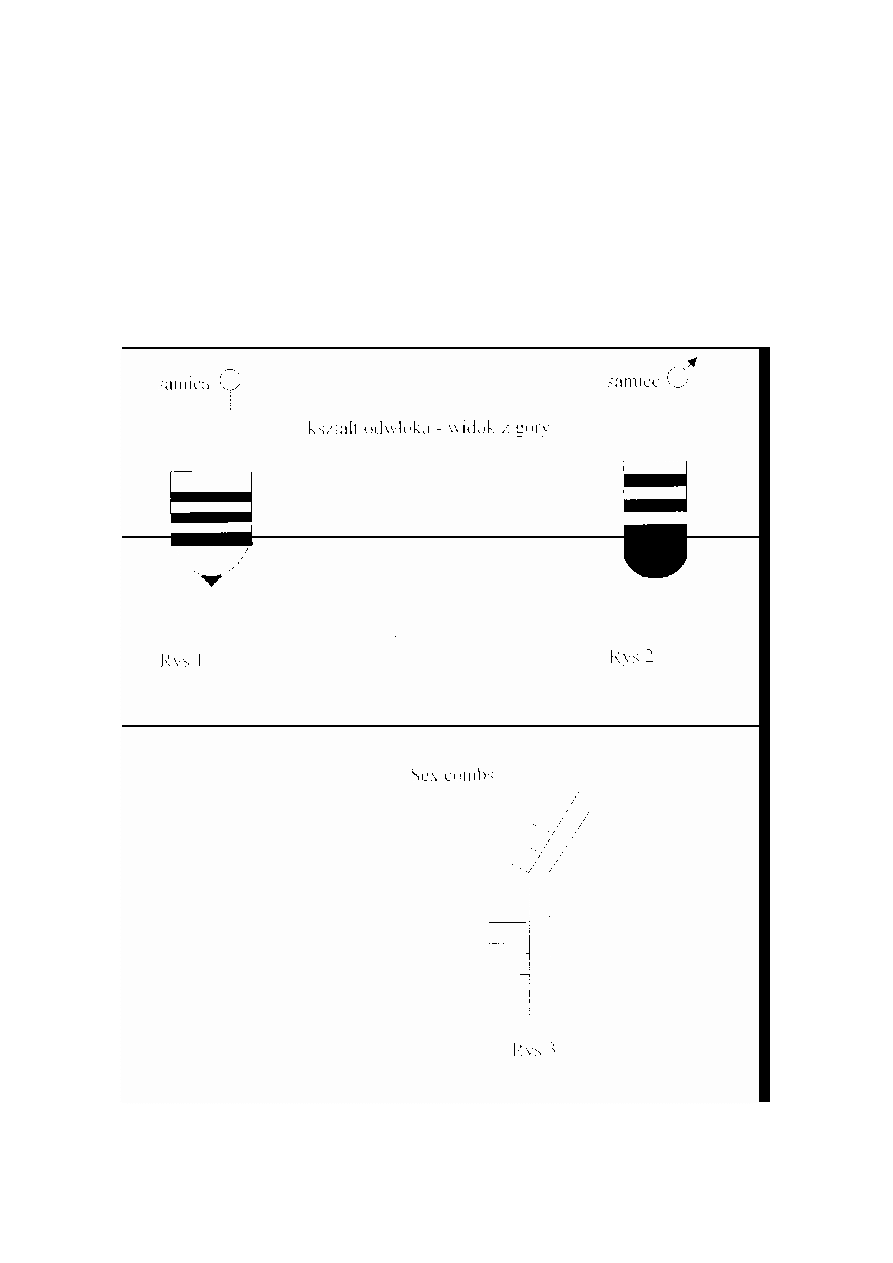
Odró

ż

nianie płci u Drosophila melcmogaster

1.

Samice s

ą

nieco wi

ę

ksze od samców.

2. Samice maja, pr

ąż

kowany odwłok, szeroki i zaostrzony na ko

ń

cu do składania jaj

(Rys. 1).

3. Koniec odwłoka samca jest okr

ą

gły i prawie czarny w porównaniu do pr

ąż

ków

samicy (Rys.2). U młodych muszek me wida

ć

tak wyra

ź

nej ró

ż

nicy.

4. U samców na pierwszej parze odnó

ż

y znajduj

ą

. si

ę

tzw. sex combs - szereg

g

ę

stych czarnych szczecinek (Rys.3).

Bierzemy pod uwag

ę

dwie cechy muszki owocowej wykazuj

ą

ce zmienno

ść

Ć

wiczenie 8

32

•



barwa oczu - biała (w) lub czerwona (+)

•



skrzydła - normalne (+) lub zredukowane (vg).

Nale

ż

y okre

ś

li

ć

, które z tych cech sa dominuj

ą

ce, a które recesywne oraz ktore

s

ą

autosomalne, a które sprz

ęż

one z płci

ą

. W tym celu ka

ż

da podgrupa wykona 2

ró

ż

ne krzy

ż

ówki miedzy osobnikami z ró

ż

nych linii hodowlanych muszki. Przy

analizowaniu wyników nale

ż

y uwzgl

ę

dni

ć

fakt, i

ż

niektóre samice mogły zosta

ć

zapłodnione ju

ż

w hodowli macierzystej, (je

ż

eli przebywały w niej dłu

ż

ej ni

ż

8

godzin od momentu opuszczenia poczwarki). Cz

ęść

potomstwa takiej samicy ( z

jaj zło

ż

onych najwcze

ś

niej) nie b

ę

dzie rezultatem zało

ż

onej przez nas krzy

ż

ówki.

Tej cz

ęś

ci potomstwa nie uwzgl

ę

dniamy w naszej analizie.

W ka

ż

dej podgrupie (połowa grupy) zakładane s

ą

dwie uzupełniaj

ą

ce si

ę

krzy

ż

ówki: bialooka bezskrzydła samica (Mel w/vg) z samcem o fenotypie

dzikim (Mel +) (czerwone oczy i normalne skrzydła) oraz krzy

ż

ówka odwrotna.

Trzecia hodowla b

ę

dzie zało

ż

ona wył

ą

cznie z muszek dzikich w liczbie: 3

samce i 3 samice.

Ć

wiczenie 9

33

Ć

wiczenie 9. Modele doboru naturalnego w populacjach -

symulacje komputerowe dotycz

ą

ce zmian frekwencji alleli w

populacji pod wpływem doboru naturalnego.

Współczynnik reprodukcji (R):

R = FxP, gdzie F oznacza liczb

ę

potomków przypadaj

ą

cych na jednego osobnika

rodzicielskiego a P to prawdopodobie

ń

stwo prze

ż

ycia potomka do wieku

reprodukcyjnego.

Warto

ść

przystosowawcza genotypu:

jest to stosunek współczynnika reprodukcji danego genotypu do współczynnika

reprodukcji najkorzystniejszego genoypu: W = R/Rmax.

Dobór przeciw homozygotom recesywnym:

(np. melanizm przemysłowy Biston betularia na obszarach

zanieczyszczonych). WAA = WAa = 1, Waa = 1-s

∆

q = -pq2s/1-sq2

p,q – frekwencje alleli A i a

∆

q – zmiana frekwencji allelu a

Dobór przeciw homozygotom dominuj

ą

cym i heterozygotom:

(np. forma nie-melanistyczna motyla Biston betularia na obszarach nie

zanieczyszczonych) WAA = WAa = 1-s, Waa = 1

∆

q = -pq2s/1-ps(1+q)

Dobór przeciw obu homozygotom:

(np. anemia sierpowata u człowieka na obszarach

malarycznych) WAa = 1, WAA = 1 – sAA, Waa = 1 - saa

Dobór przeciw heterozygotom:

WAa = 1, WAA = 1 + sAA, Waa = 1 + saa

∆

q = pq(qsaa-psAA)/1+p2sAA+q2saa

∆

q=0 – punkt równowagi

nietrwałej, przy niewielkim odchyleniu wyst

ę

puje tendencja do jego pogł

ę

bienia

(dodatnie sprz

ęż

enie zwrotne).

Dwa punkty równowagi trwałej: q=1, p=0 oraz q=0, p=1.

POPULUS

Celem

ć

wicze

ń

jest analiza wpływu naturalnej selekcji, dryfu genetycznego,

Ć

wiczenie 9

34

migracji, mutacji oraz ich kombinacji na cz

ę

sto

ść

wyst

ę

powania alleli w populacji.

W

ć

wiczeniu analizowana b

ę

dzie populacja myszy. Kolor sier

ś

ci myszy

kontrolowany jest przez jeden gen posiadaj

ą

cy dwa allele. W przypadku tej cechy

wyst

ę

puje nie pełna dominacja: homozygoty dominuj

ą

ce (AA) posiadaj

ą

sier

ść

koloru czarnego, heterozygoty (Aa) posiadaj

ą

sier

ść

koloru szarego a homozygoty

recesywne (aa) maj

ą

sier

ść

koloru białego. Zakłada si

ę

,

ż

e myszy

ż

yj

ą

na wyspie

bez drapie

ż

nika. Frekwencja obu alleli jest identyczna, chyba

ż

e podane jest

inaczej.

Symulacja I

Na bardzo du

żą

, odizolowana populacj

ę

myszy, swobodnie si

ę

krzy

ż

uj

ą

cych nie

działaj

ą

ż

adne czynniki mutagenne. Je

ś

li na wysp

ę

przedostanie si

ę

drapie

ż

nik (np.

mysz) bardziej zagro

ż

one s

ą

białe myszy. Celem symulacji jest okre

ś

lenie kierunku

ewolucji wobec działania powy

ż

szego czynnika selekcyjnego.

1. Uruchom program Populus i przejd

ź

do Model > Natural selections. Wybierz

Selection on Diallelic Autosomal Locus.

2. Zaznacz opcj

ę

genotypic frequencies vs. t.

3. Wybierz Fitness (przystosowanie) i okre

ś

l je dla ka

ż

dego genotypu:

AA przystosowanie 1.0

Aa przystosowanie 1.0

aa przystosowanie 0.7

4. Wybierz jedn

ą

pocz

ą

tkow

ą

frekwencj

ę

(One Initial Frequency) i wpisz 0.5. Ustaw

liczb

ę

generacji (Generations) na 130.

5. Naci

ś

nij View.

6. Odpowiedz na nast

ę

puj

ą

ce pytania:

a) Okre

ś

l linie dotycz

ą

ce poszczególnych genotypów. Jak nale

ż

y je

interpretowa

ć

?

b) Je

ś

li przystosowanie genotypów AA i Aa jest takie same dlaczego

frekwencja genotypu AA wzrasta a genotypu Aa obni

ż

a si

ę

?

c) Je

ś

li genotyp aa jest "zły" dlaczego nie zanikł zupełnie? Wró

ć

do Plot

Options i zaznacz "p vs. t". Pozwoli to zbada

ć

jak zmienia si

ę

frekwencja

allelu A (p) w czasie. Co mo

ż

na zaobserwowa

ć

?

Ć

wiczenie 9

35

d) Zmie

ń

pocz

ą

tkow

ą

frekwencj

ę

allelu A na 0.1 i zaznacz ponownie genotypic

frequencies vs. t (pozostaw reszt

ę

bez zmian). Przypuszczamy, i

ż

ilo

ść

białych myszy

(genotyp aa) przewy

ż

szała ilo

ść

ciemnych myszy na wyspie przed przybyciem

drapie

ż

nika. Dlaczego linia genotypu aa obni

ż

yła si

ę

tak szybko. Dlaczego

frekwencja genotypu Aa pocz

ą

tkowo wzrastała a potem si

ę

obni

ż

yła?

e) Jakie wnioski dotycz

ą

ce działania selekcji mo

ż

na wyci

ą

gn

ąć

na

podstawie przeprowadzonych symulacji.

Symulacja II

Symulacji poddana b

ę

dzie ta sama, du

ż

a, odizolowana, swobodnie krzy

ż

uj

ą

ca

si

ę

populacja myszy, w której nie wyst

ę

puj

ą

ż

adne mutacje wpływaj

ą

ce na kolor ich

sier

ś

ci. Najbardziej nara

ż

one na działanie drapie

ż

nika s

ą

osobniki białe, potem

czarne a na ko

ń

cu szare.

Wybierz opcj

ę

Selection on a Diallelic Autosomal Locus ustawiaj

ą

c reszt

ę

opcji jak

w poprzedniej symulacji (initial frequency 0.5) Przystosowanie (Fitness) ustaw w

nast

ę

puj

ą

cy sposób:

AA - 0.9

Aa - 1.0

aa - 0.7

Jakie s

ą

główne ró

ż

nice mi

ę

dzy wynikami tej a poprzedniej symulacji ?

Symulacja III

W niniejszej symulacji ta sama odizolowana populacja myszy, swobodnie

krzy

ż

uj

ą

ca si

ę

ma niewielk

ą

liczebno

ść

. Brakuje mutacji wpływaj

ą

cych na kolor

sier

ś

ci nie ma te

ż

ró

ż

nic w prze

ż

ywalno

ś

ci ró

ż

nych form barwnych.

1. Wybierz model Mendelian Genetics i Genetic Drift . Wybierz zakładk

ę

Monte

Carlo i ustaw opcj

ę

w nast

ę

puj

ą

cy sposób:

a) Runtime = 3N

generations b) Loci = 6

Ć

wiczenie 9

36

c) Initial frequency = 0.5

d) Population size = 500

2. Naci

ś

nij View. Linia ka

ż

dego koloru oznacza przypadkowo wybrany allel genomu

myszy. Allele te s

ą

niezale

ż

ne od siebie i nie wpływaj

ą

one na prze

ż

ywalno

ść

.

3. Przeprowad

ź

18 prób (Iterate): sze

ść

dla populacji 500 osobników, sze

ść

dla

populacji 50 osobników i sze

ść

dla populacji licz

ą

cej 5 osobników.

4. Dla ka

ż

dej próby zanotuj nast

ę

puj

ą

ce informacje:

a) Wielko

ść

populacji (Population size - N)

b) Liczb

ę

generacji do momentu osi

ą

gni

ę

cia frekwencji równej 1 lub zero przez

pierwszy z alleli (Fixation)

c) Kolor allelu który jako pierwszy osi

ą

gn

ą

ł frekwencj

ę

1 lub zero

d) W ilu przypadkach doszło najpierw do osi

ą

gni

ę

cia frekwencji 0 a w ilu

przypadkach frekwencji 1

5. Odpowiedz na nast

ę

puj

ą

ce pytania:

a) Czy we wszystkich próbach frekwencje alleli przebiegały w ten sam sposób?

Dlaczego tak, dlaczego nie?

b) Czy frekwencje poszczególnych alleli wygl

ą

dały tak samo w ró

ż

nych

próbach? Dlaczego tak, dlaczego nie?

c) Jak du

ż

e były ró

ż

nice w czasie osi

ą

gni

ę

cia przez pierwszy allel frekwencji 1 lub

zero?

d) Je

ś

li allele te nie s

ą

zwi

ą

zane z selekcj

ą

to dlaczego zmienia si

ę

ich

frekwencja?

e) Bardzo cz

ę

sto uwa

ż

a si

ę

dryft genetyczny zwi

ą

zany jest tylko z małymi

populacjami. Jednak

ż

e ma on równie

ż

wpływ na du

ż

e populacje ale wpływa

na nie w sposób mniej zauwa

ż

alny.

f) Symulacja ta pokazuje zmian

ę

frekwencji alleli w czasie. Czy mo

ż

na

powiedzie

ć

,

ż

e w taki sposób przebiega ewolucja?

g) Czy mo

ż

na przewidzie

ć

dla danej populacji kiedy dojdzie do utraty konkretnego

allelu?

Symulacja IV

Ć

wiczenie 9

37

Dryf genetyczny a selekcja.

W rzeczywisto

ś

ci dryf genetyczny i selekcja działaj

ą

zazwyczaj jednocze

ś

nie, s

ą

one

dwoma najwa

ż

niejszymi czynnikami ewolucyjnymi.

W omawianej populacji myszy wraz z przybyciem na wysp

ę

drapie

ż

nika selekcja

działa przeciwko białym myszom (aa), jednak

ż

e nie jest to cecha letalna - myszy

białych jest o 10% mniej ni

ż

ciemnych.

1. W opcji Mendelian Genetics zaznacz Drift and Selection. Wprowad

ź

dane:

a) N = 500, p = 0.1, Generations = 500

b) AA = 1.0 Aa = 1.0 aa = 0.9

2. Zanim sprawdzisz wynik rozwa

ż

: je

ś

li nie działa dryf genetyczny czy allel a

zostanie wyparty z populacji?

3. Naci

ś

nij View i zobacz co stanie si

ę

po 500 generacjach. Przeprowad

ź

5

symulacji obserwuj

ą

c za ka

ż

dym wyniki. Jaki jest wynik? Czy za ka

ż

dym razem

wyniki były takie same? Dlaczego warto

ść

allelu A osi

ą

gn

ę

ła 1?

4. Selekcja (obecno

ść

drapie

ż

nika) spowodowała

ż

e frekwencja allelu A wzrosła.

Jednak

ż

e jak wida

ć

było w symulacji pierwszej linia wzrostu frekwencji tego

allelu nie jest prosta. Wzrost jest bardzo niejednorodny - jest to wynikiem

działania dryfu genetycznego.

5. Teraz zmie

ń

wielko

ść

populacji na 50 i naci

ś

nij View. Co si

ę

dzieje w

mniejszej populacji?

6. Przeprowad

ź

5 symulacji. Czy otrzymane wyniki podobne s

ą

do tych, które były

uzyskane dla wi

ę

kszej populacji.

7. Gdy wielko

ść

populacji wynosiła 500 bez w

ą

tpienia mo

ż

na było zauwa

ż

y

ć

,

ż

e

frekwencja allelu A wzrastała do momentu przekroczenia warto

ś

ci 1.

Najprawdopodobniej sytuacja powtórzyła si

ę

, gdy wielko

ść

populacji wynosiła 50.

8. Czy populacja myszy na wyspie ewoluowała? Je

ś

li tak to jakie były

mechanizmy tej ewolucji?

9. Co otrzymane wyniki mog

ą

powiedzie

ć

o działaniu dryfu genetycznego i selekcji

w małej i du

ż

ej populacji?

Ć

wiczenie 10

38

Ć

wiczenie 10.

Analiza wyników hodowli muszki owocowej (

ć

wiczenie

8). Genotyp a

ś

rodowisko: wpływ zag

ę

szczenia populacji na mas

ę

ciała Drosophila melanogaster - zakładanie hodowli muszki

owocowej

A. Analiza wyników krzy

ż

ówek z

ć

wiczenia 8.

a) Geny autosomalne i sprz

ęż

one z płci

ą

. Analiza wyników do

ś

wiadczenia

1. Usypiamy muchy i rozdzielamy według płci.

2. Analizujemy fenotyp uzyskanych w pokoleniu F1 samców i samic.

3. Ustalamy, do której z rubryk tabeli z

ć

wiczenia 3 pasuj

ą

otrzymane wyniki.

4. Wyci

ą

gamy wnioski na temat mechanizmu dziedziczenia badanych dwu cech u

muszki owocowej.

B. Genotyp a

ś

rodowisko. Wpływ zag

ę

szczenia populacji na mas

ę

ciała muszki

owocowej (Drosophila melanogaster). Zało

ż

enie do

ś

wiadczenia

Ka

ż

da podgrupa zakłada 3 hodowle (ka

ż

da para po 1, o wy

ż

szym lub ni

ż

szym

zag

ę

szczeniu much)

• 2 samce + 2 samice (6 hodowli w całej grupie) (zag

ę

szczenie 1)

• 6 samców + 6 samic (6 hodowli w całej grupie) (zag

ę

szczenie 2)

Po 48h muchy rodzicielskie zostan

ą

usuni

ę

te z próbówek przez osob

ę

prowadz

ą

ca

ć

wiczenia. Wszystkie muchy potomne uzyskane po 2 tygodniach b

ę

d

ą

nale

ż

ały do

pokolenia F1.

Ć

wiczenie 11

39

Ć

wiczenie 11. Zastosowania bada

ń

polimorfizmu sekwencji

mikrosatelitarnych w genetyce – przeprowadzenie rozdziału

produktu PCR w

ż

elu agarozowym.

Przeprowadzony zostanie rozdział fragmentów DNA zawieraj

ą

cych mikrosatelity

OMM 1007, OMM 1008, OMM 1036 i OMM 1037, amplifikowane uprzednio technik

ą

PCR.

Rozdział produktu PCR zostanie przeprowadzony w

ż

elu agarozowym o st

ęż

eniu

1,5%.

WYKONANIE

Ć

WICZENIA

Przygotowane

ż

elu agarozowego. Uwaga wszystkie poni

ż

sze prace nale

ż

y

wykona

ć

w r

ę

kawiczkach lateksowych.

1. Wł

ą

cz wag

ę

elektroniczn

ą

wskazan

ą

prze prowadz

ą

cego

ć

wiczenia.

2. Umie

ść

kolb

ę

Erlenmeyer-a o pojemno

ś

ci 250 ml na wadze i wytaruj wag

ę

.

3. Za pomoc

ą

ły

ż

eczki wsyp do kolby 1,5g agarowy.

4. Za pomoc

ą

cylindra z napisem TBE odmierz 100 ml buforu 1X TBE i wlej do

kolby.

5. Umie

ść

magnes w kolbie.

6. Wł

ą

cz mieszadło elektromagnetyczne wskazane przez prowadz

ą

cego

ć

wiczenia, postaw kolb

ę

na mieszadle.

7. Ustaw cz

ę

stotliwo

ść

mieszania na 450 obr /min i mieszaj przez 1 minut

ę

.

8. Ustaw pokr

ę

tło pr

ę

dko

ś

ci mieszania na 0 i przenie

ś

kolb

ę

do kuchenki

mikrofalowej.

9. Zagotuj zawarto

ść

kolby. W momencie osi

ą

gni

ę

cia temperatury wrzenia

natychmiast wył

ą

cz kuchenk

ę

. Nie wolno dopu

ś

ci

ć

do wykipienia

zawarto

ś

ci kolby!

10. Załó

ż

r

ę

kawic

ę

kuchenn

ą

, wyci

ą

gnij kolb

ę

z mikrofalówki, postaw na stole pod

wyci

ą

giem, ustaw temperatur

ę

płyty mieszadła elektromagnetycznego na

150

o

C.

Ć

wiczenie 11

40

11. Prowadz

ą

cy doda do kolby 5

µ

l bromku etydyny.

Uwaga: bromek etydyny jest bardzo silnym mutagenem! Niebezpieczny jest

kontakt ze skór

ą

oraz wdychanie oparów.

12. Kolb

ę

trzeba przykry

ć

folia aluminiow

ą

(niebezpiecze

ń

stwo oparów bromku

etydyny!).

13. Ustaw kolb

ę

na mieszadle elektromagnetycznym, mieszaj 5 minut

cz

ę

stotliwo

ś

ci

ą

450 rpm w takcie mieszania przygotuj sanki do wylania

ż

elu

zgodnie ze wskazówkami prowadz

ą

cego.

14. Wył

ą

cz mieszadło elektromagnetyczne, pokr

ę

tło temperatury płyty ustaw na 0.

Przygotowanie rozdziału elektroforetycznego.

1. Je

ś

li w kolbie

ż

el zastygł, konieczne b

ę

dzie jego roztopienie. Zdejmij

aluminiow

ą

foli

ę

z szyjki kolby. Wstaw kolb

ę

do mikrofalówki i podgrzewaj j

ą

do momentu osi

ą

gni

ę

cia przez

ż

el temperatury wrzenia. Pami

ę

taj! Nie wolno

dopu

ś

ci

ć

do wykipienia zawarto

ś

ci kolby! W trakcie ogrzewania musisz

stale kontrolowa

ć

jej zawarto

ść

. B

ą

d

ź

gotowy do natychmiastowego

wył

ą

czenia mikrofalówki momencie zagotowania si

ę

ż

elu.

2. Prowadz

ą

cy

ć

wiczenia przygotuje sanki i wleje do nich odpowiedni

ą

obj

ę

to

ść

przygotowanego

ż

elu. Pami

ę

taj!

Ż

el agarozowym o st

ęż

eniu 1,5%

potrzebuje około 15 minut do zastygni

ę

cia.

Przygotowanie i naniesienie próbek do

ż

elu oraz przeprowadzenie elektroforezy

odcinków DNA zawieraj

ą

cych fragmenty mikrosatelitarne.

1. Prowadz

ą

cy

ć

wiczenia odmierzy za pomoc

ą

pipety automatycznej po 1

µ

l

buforu obci

ąż

aj

ą

cego dla ka

ż

dej przygotowywanej próbki. Nast

ę

pnie do

pierwszej kropli doda 0,3

µ

l wzorca masowego oraz 5

µ

l wody dejonizowanej.

2. Dodaj do pozostałych kropli buforu obci

ąż

aj

ą

cego 5

µ

l roztworu z próbek

przyniesionych przez prowadz

ą

cego. Zmie

ń

ko

ń

cówk

ę

pipety w momencie gdy

zako

ń

czysz sporz

ą

dzanie próbek pierwszego spo

ś

ród badanych fragmentów

mikrosatelitarnych.

3. Wstaw sanki do aparatu wskazanego przez prowadz

ą

cego. Nanie

ś

próbki do

studzienek w

ż

elu agarozowym.

Ć

wiczenie 11

41

4. Prowadz

ą

cy dobierze parametry napi

ę

cia i nat

ęż

ania pr

ą

du zasilaj

ą

cego aparat

do elektroforezy oraz czas trwania elektroforezy.

5. Aby rozpocz

ąć

elektroforez

ę

naci

ś

nij przycisk "run" na zasilaczu.

W trakcie trwania elektroforezy wysłuchaj uwa

ż

nie prezentacji prowadz

ą

cego

ć

wiczenia na temat zastosowania bada

ń

polimorfizmu sekwencji mikrosatelitarnych w

genetyce ryb.

Wizualizacja i interpretacja uzyskanych wyników.

1. Po zako

ń

czeniu elektroforezy prowadz

ą

cy przeniesie sanki z

ż

elem na

transiluminator, uruchomi komputer i program Kodak 1D Image Software. Przy

u

ż

yciu podł

ą

czonej do komputera kamery i drukarki wykona odbitk

ę

fotograficzn

ą

otrzymanego elektroforogramu.

2. Na postawie wzorca masowego i zostanie przeprowadzone szacowanie

długo

ś

ci zamplifikowanych fragmentów DNA.

3. Porównaj długo

ść

zamplifikowanych fragmentów i wyci

ą

gnij wnioski dotycz

ą

ce

ró

ż

nic długo

ś

ci analizowanych fragmentów.

Ć

wiczenie 12

42

Ć

wiczenie 12. Obliczanie dystansu genetycznego z zastosowaniem

modelu: wariancji

ś

rednich rozmiarów alleli (

δµ

2

) – zadania rachunkowe

Model wariancji kwadratów

ś

rednich rozmiarów alleli został opracowany przez roku

Goldstein i in. (1995) jest stosowany do oblicze

ń

dystansu genetycznego

istniej

ą

cego pomi

ę

dzy populacjami. Model ten umo

ż

liwia precyzyjne obliczenie

dystansu genetycznego istniej

ą

cego pomi

ę

dzy próbami o ró

ż

nej liczebno

ś

ci.

gdzie:

δ

- wariancja

µ

-

Ś

redni rozmiar alleli w badanym locus mierzony

liczb

ą

powtórze

ń

motywu podstawowego

x - populacja x, y – populacja y

Przykładowa frekwencja wyst

ę

powania alleli w locus mikrosatelitarnym w populacjach

X i Y

Frekwencja allelu

Rozmiar

allelu

(bp.)

Rozmiar

allelu (r.m.)

populacja X

populacja Y

98

49

0,24

0,06

102

51

0,08

0,14

106

53

0,32

0,01

110

55

0,14

0,32

114

57

0,18

0,20

118

59

0,04

0,12

126

63

0

0,15

Rozmiar ka

ż

dego allelu mno

ż

ymy przez jego frekwencj

ę

odpowiednio dla populacji X

i Y.

st

ą

d:

76

,

11

24

,

0

*

49

=

i

94

,

2

06

,

0

*

49

=

( )

2

2

)

(

y

r

j

x

µ

µ

δµ

−

=

∑

Ć

wiczenie 12

43

nast

ę

pnie podstawiaj

ą

c do wzoru

otrzymujemy:

czyli

Zadanie 1.

Na podstawie frekwencji alleli tabeli frekwencji alleli Oblicz dystans genetyczny

istniej

ą

cy pomi

ę

dzy nast

ę

puj

ą

cymi populacjami przy wykorzystaniu modelu wariancji

kwadratów

ś

rednich rozmiarów alleli.

A).

Frekwencja allelu

Rozmiar

allelu (bp.)

Rozmiar

allelu

(r.m.)

populacja X

populacja Z

98

49

0,24

0,23

102

51

0,08

0,10

106

53

0,32

0,36

110

55

0,14

0,14

114

57

0,18

0,16

118

59

0,04

0,01

2

2

))

45

,

9

08

,

7

4

,

11

6

,

17

53

,

0

14

,

7

94

,

2

(

)

36

,

2

26

,

10

7

,

7

96

,

16

08

,

4

76

,

11

((

)

(

+

+

+

+

+

+

−

+

+

+

+

+

=

δµ

( )

2

2

)

(

y

r

j

x

µ

µ

δµ

−

=

∑

12

,

9

2

=

δµ

Ć

wiczenie 12

44

B).

Frekwencja allelu

Rozmiar

allelu (bp.)

Rozmiar

allelu

(r.m.)

populacja Z

populacja Y

98

49

0,23

0,06

102

51

0,10

0,14

106

53

0,36

0,16

110

55

0,14

0,32

114

57

0,16

0,20

118

59

0,01

0

126

63

0

0,12

Zadanie 2.

Umie

ść

w odpowiednich miejscach dendrogramu populacje X, Y i Z. Uzasadnij swoj

ą

decyzj

ę

. Jak mo

ż

na zinterpretowa

ć

uzyskane wyniki?

Ć

wiczenie 12

45

Literatura

Goldstein D.B., Ruiz Linares A., Cavalli-Sforza L.L, Feldman M.W. 1995. An

evaluation of genetic distances for use with microsatellite loci. Genetics, 139:

463-471.

Ć

wiczenie 13

46

Ć

wiczenie 13. Kolokwium.

Na kolokwium obowi

ą

zuj

ą

wiadomo

ś

ci z

ć

wicze

ń

1 – 12.

]

Ć

wiczenie 15

47

Ć

wiczenie 14. Genotyp a

ś

rodowisko. Wpływ zag

ę

szczenia

populacji na mas

ę

ciała muszki owocowej

(Drosophilamelanogaster) - weryfikacja hipotezy przy pomocy testu

t-Studenta – wnioski.

PRZEPROWADZENIE

Ć

WICZENIA

Po 2 tygodniach w ka

ż

dej grupie do

ś

wiadczalnej oddzielnie:

-muchy usypiamy i rozdzielamy według płci,

-liczymy samce i samice,

-wa

ż

ymy oddzielnie samce i samice w ramach grupy do

ś

wiadczalnej,

-obliczmy

ś

rednia mas

ę

w próbie samców i samic dziel

ą

c całkowit

ą

mas

ę

próby

przez liczb

ę

much w próbie.

Je

ż

eli

ś

rednia masa muchy b

ę

dzie mniejsza ni

ż

0,5 mg lub wi

ę

ksza ni

ż

2 mg,

powtórzy

ć

wa

ż

enie.

Zanotowa

ć

uzyskane dane w zeszycie. Wszystkie obliczenia prowadzimy oddzielnie

dla samców i samic, poniewa

ż

ś

rednia masa samców jest o około 20% ni

ż

sza ni

ż

samic.

ZADANIE

Porównaj testem t-Studenta mas

ę

ciała samic z najmniejszego i najwi

ę

kszego

zag

ę

szczenia.

podgrupa

zag

ę

szczenie 2+2

zag

ę

szczenie 6+6

samce

samice

samce

samice

1

2

3

Ć

wiczenie 15

48

4

Warto

ść

statystyki t obliczon

ą

przez nas porównujemy z krytyczna warto

ś

ci

ą

z tabeli

,,poziom istotno

ś

ci dla testu dwustronnego dla poziomu istotno

ś

ci 0,05. Liczba stopni

swobody df=N

1

+N

2

-2, gdzie N

1

i N

2

to liczby powtórze

ń

, odpowiednio dla

zag

ę

szczenia 1 (2+2) i 2 (6+6)

X

1

, X

2

-

ś

rednie arytmetyczne

Sx - bł

ą

d standardowy

Bł

ą

d standardowy obliczamy ze wzoru:

2

2

1

1

N

S

N

S

S

x

+

=

gdzie S

1

i S

2

to wariancje, odpowiednio dla zag

ę

szczenia 1 (2+2) oraz 2 (6+6).

Aby obliczy

ć

Sx musimy mie

ć

najpierw S

1

i S

2

(wariancje). Obliczamy je ze wzoru:

1

/

)

(

2

2

−

−

=

∑

∑

N

N

X

X

S

Gdy obliczymy wariancj

ę

S

1

i S

2

, wstawiamy je do wzoru na bł

ą

d standardowy (N

1

i

N

2

s

ą

liczbami powtórze

ń

w ka

ż

dym zag

ę

szczeniu). Obliczamy ka

ż

d

ą

wariancj

ę

oddzielnie wstawiaj

ą

c dla S

1

odpowiednio X

1

i N

1

a dla S

2

- X

2

oraz N

2

. Gdy obliczymy

Sx, wstawiamy do wzoru na t i obliczamy warto

ść

statystyki t. Znajdujemy w tabeli

warto

ść

krytyczna.:

Liczba stopni swobody df = N

1

+ N

2

-2. Poziom istotno

ś

ci dla testu dwustronnego

α

= 0,05

Nast

ę

pnie mo

ż

emy zweryfikowa

ć

hipotez

ę

zerowa, która brzmi:

H

O

= ,,Brak jest istotnych ró

ż

nic pomi

ę

dzy

ś

rednimi masami ciała osobników

ż

yj

ą

cych w ró

ż

nych zag

ę

szczeniach".

Je

ż

eli obliczona przez nas warto

ść

statystyki t jest ni

ż

sza od warto

ś

ci krytycznej, to:

Nie ma podstaw do odrzucenia hipotezy zerowej.

x

S

X

X

t

2

1

−

=

Ć

wiczenie 15

49

Je

ż

eli obliczona warto

ść

t jest wy

ż

sza od krytycznej to:

Hipotez

ę

zerowa nale

ż

y odrzuci

ć

na rzecz hipotezy alternatywnej, która brzmi:

,,Wyst

ę

puj

ą

istotne ró

ż

nice pomi

ę

dzy

ś

rednimi masami ciała osobników

ż

yj

ą

cych w

ró

ż

nych zag

ę

szczeniach".

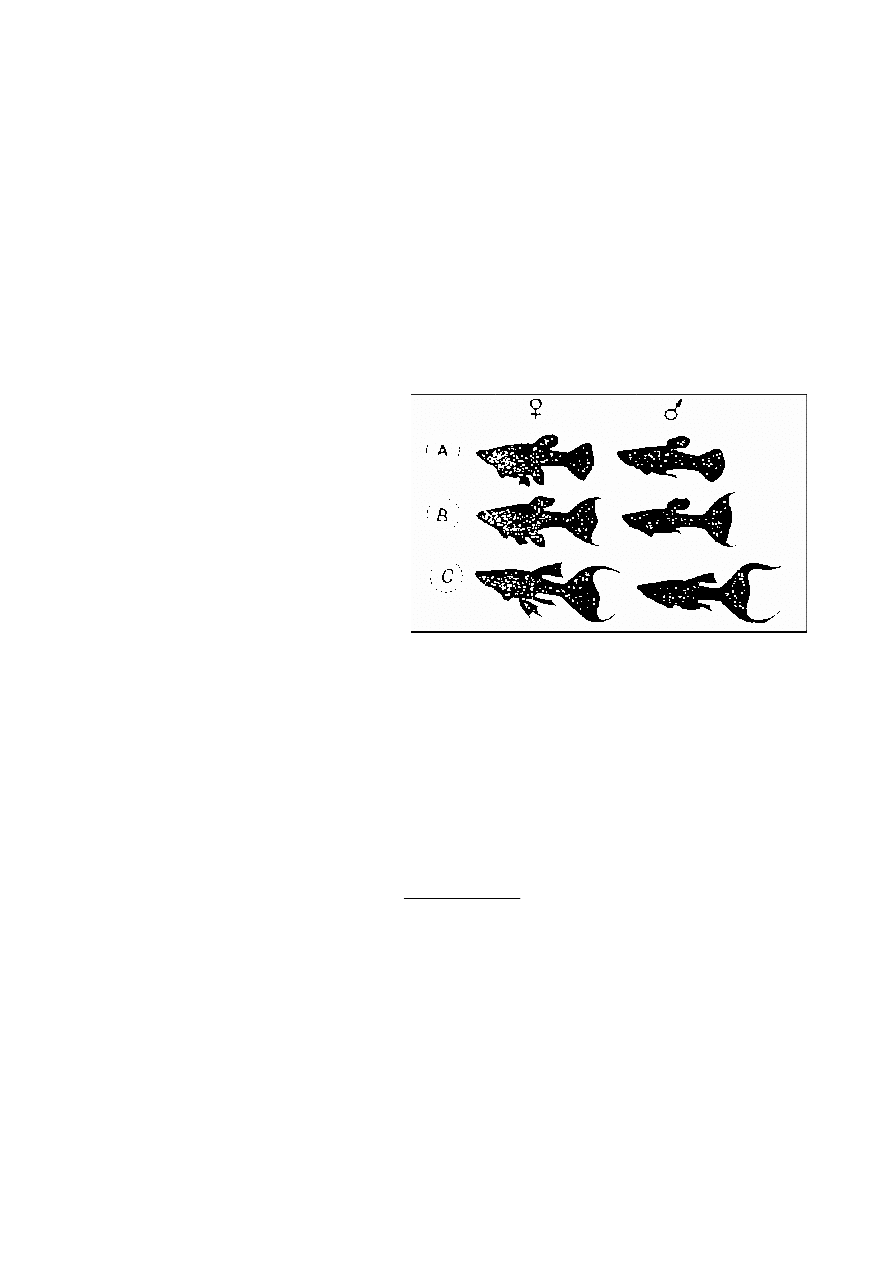
Ć

wiczenie 15

50

Ć

wiczenie 15. Niepełna dominacja i addycja dwu loci genowych.

Prawo Hardy'ego-Weinberga dla dwu loci genowych

Molinezja (Poecilia sphenops) wykazuje polimorfizm genetyczny pod wzgl

ę

dem

ubarwienia ciała oraz kształtu płetw. W locus L odpowiedzialnym za kształt płetw

molinezji znajduj

ą

si

ę

2 allele L i l.

Niepełna dominacja L nad 1 sprawia, ze 3 genotypom odpowiadaj

ą

3 fenotypy

przedstawione na rysunku:

fenotyp genotyp

A ll

B Ll

C LL

Frekwencje poszczególnych alleli (p i q) w populacji obliczamy korzystaj

ą

c z danych

do

ś

wiadczalnych (obserwowane cz

ę

sto

ś

ci fenotypów).

W przypadku cechy kształtu płetw:

N

n

n

p

lL

LL

2

2

+

=

P = f(L); q = r(l)

gdzie f to frekwencja allelu.

gdzie: n

LL

, n

Ll

to liczba osobników o odpowiednim genotypie i odpowiadaj

ą

cym mu

fenotypie, N to liczba badanych osobników.

Frekwencj

ę

allelu recesywnego (q) oblicza si

ę

z zale

ż

no

ś

ci p + q = 1

Równanie Hardy-Weinberga dla pary alleli w pojedynczym locus przyjmuje posta

ć

Ć

wiczenie 15

51

(p+q)2 =1, co po rozwini

ę

ciu daje: p2 + 2pq + q2 = 1

gdzie p = frekwencja allelu A natomiast q = frekwencja allelu a

Trzy wyra

ż

enia z lewej strony równania odpowiadaj

ą

oczekiwanym proporcjom

poszczególnych (3) fenotypów molinezji w badanej populacji (odpowiednio: p

2

homozygot LL, 2pq heterozygot i q

2

homozygot ll). Po pomno

ż

eniu ka

ż

dego z

tych wyra

ż

e

ń

przez N (liczba badanych osobników) otrzymamy odpowiednio

oczekiwane liczby osobników ka

ż

dego fenotypu wynikaj

ą

ce z równania Hardy-

Weinberga, ktore zapisujemy w prawej kolumnie. W lewej kolumnie zapisujemy

rzeczywiste (obserwowane) liczby osobników o okre

ś

lonych fenotypach.

Nast

ę

pnie otrzymane warto

ś

ci z obu kolumn podstawiamy do wzoru i obliczmy

według modelu

χ



2

(chi-kwadrat).

∑

−

=

Exp

Exp

Obs

2

2

)

(

χ

gdzie: Obs to liczba obserwowanych osobników o okre

ś

lonym fenotypie

Exp to liczba oczekiwanych osobników o okre

ś

lonym fenotypie

(w tym przypadku suma Z b

ę

dzie zawierała 3 składniki)

Warto

ść

krytyczna statystyki y1 na poziomie istotno

ś

ci a = 0,05 wynosi w tym

przypadku 3,84

(liczba stopni swobody: K - l - s = 3-1-1 = 1)

P + q= 1 stad p -zmienna niezale

ż

na: p + (1 - p) = 1, albo

q -zmienna niezale

ż

na: q + (1-q) = 1

Je

ż

eli obliczona warto

ść

statystyki przekroczy warto

ść

krytyczn

ą

(3,84) to istniej

ą

podstawy do odrzucenia hipotezy zerowej (ze populacja molinezji znajduje si

ę

w

równowadze Hardy- Weiberga) na rzecz hipotezy alternatywnej. W takim przypadku

nale

ż

y zastanowi

ć

si

ę

nad przyczynami takiej struktury genetycznej populacji. Jakie

czynniki mogły to wywoła

ć

?

Zadanie przykładowe

Za ubarwienie ciała odpowiadaj

ą

dwie pary alleli w dwu loci genowych. Fenotyp

ka

ż

dego osobnika jest sum

ą

oddziaływania alleli zlokalizowanych w locus M i N.

Takie współoddziaływanie dwóch lub wi

ę

cej loci genowych nazywamy addycj

ą

. W

ka

ż

dym z dwu loci (M i N) wyst

ę

puj

ą

u Poecilia sphenops po 2 allele, odpowiednio: M

Ć

wiczenie 15

52

i m oraz N i n. Dominuj

ą

ce allele M i N warunkuj

ą

melanistyczne (czarne) ubarwienie

ryb, natomiast allele recesywne m i n (allele dzikie) warunkuj

ą

srebrnoszare

ubarwienie ciała ryb. Fenotyp ka

ż

dego osobnika zale

ż

y od liczby alleli dominuj

ą

cych

(M i N) w obu loci genowych odpowiedzialnych za barw

ę

ciała (liczba ta mo

ż

e

wynosi

ć

0,1, 2, 3 lub 4). 9 mo

ż

liwych kombinacji genotypów daje w efekcie 5

fenotypów:

mmnn – fenotyp I

Mmnn – fenotyp II

mmNn

MMnn

MmNn – fenotyp III

mmNN

MMNn – fenotyp IV

MmNN

MMNN – fenotyp V

Ubarwienie ryb zmienia si

ę

tak

ż

e wraz z

wiekiem. Im ryby s

ą

starsze tym bardziej ujawnia si

ę

ubarwienie melanistyczne. U

bardzo młodych osobników fenotypy I II nie ró

ż

ni

ą

si

ę

od siebie -ryby s

ą

jednolicie

srebrzystoszare. U dojrzałych ryb w starszym wieku bardzo trudno odró

ż

ni

ć

fenotypy

IV i V - ryby te s

ą

jednolicie czarne. Najlepsze do analizowania zmienno

ś

ci

genetycznej ubarwienia s

ą

osobniki 2-4 centymetrowe. Ryby tej wielko

ś

ci daj

ą

si

ę

podzieli

ć

wyra

ź

nie na 5 ró

ż

nych fenotypów (w zale

ż

no

ś

ci od nat

ęż

enia ubarwienia

melanistycznego).

• Fenotyp I ryby jednolicie srebrzystoszare (niezale

ż

nie od wieku).

Fenotyp II ryby srebrzystoszare z mniej lub bardziej licznymi czarnymi plamami na

ciele (z wiekiem ich przybywa).

• Fenotyp III ryby o ciele czarnym z mniej lub bardziej licznymi rozja

ś

nieniami (z

wiekiem ich ubywa). T

ę

czówka oka i brzuch srebrzyste przez całe

ż

ycie.

• Fenotyp IV ryby prawie całkowicie czarne, prze

ś

wituj

ą

ce rozja

ś

nienia głownie w

Ć

wiczenie 15

53

t

ę

czówce oka i dolnej cz

ęś

ci pokryw skrzelowych (z wiekiem zanikaj

ą

ce i trudno

zauwa

ż

alne).

• Fenotyp V ryby całkowicie czarne (niezale

ż

nie od wieku).

W przypadku opisanej wy

ż

ej addycji 2 loci u molinezji przyjmujemy:

p - frekwencja alleli M i N (ł

ą

cznie)

q - frekwencja alleli m i n (ł

ą

cznie) w "podwójnym" locus MN

W przypadku cechy melanizmu frekwencja alleli M + N (p) wynosi zatem:

N

n

n

n

n

p

II

III

IV

V

25

,

0

5

,

0

75

,

0

+

+

+

=

gdzie n

i

to liczba osobników o fenotypie i w badanej populacji ryb.

N to liczba badanych osobników.

W tej sytuacji równanie Hardy-Weinberga przyjmuje posta

ć

:

[(P + q)

2

]

2

= 1 czyli (P + q)

4

= 1 gdzie: P = f(M + N) (frekwencja ł

ą

czna alleli M i

N)

q = f(m + n)

p + q = 1

po rozwini

ę

ciu otrzymujemy równanie:

p

4

+ 4p

3

q + 6p

2

q

2

+ 4pq

3

+ q

4

= 1

Pi

ęć

wyra

ż

e

ń

z lewej strony równania odpowiada oczekiwanym proporcjom

poszczególnych fenotypów molinezji w badanej populacji. Po pomno

ż

eniu ka

ż

dego z

tych wyra

ż

e

ń

przez N (liczba badanych osobników) otrzymamy odpowiednio

oczekiwane liczby osobników ka

ż

dego fenotypu wynikaj

ą

ce z równania Hardy-

Weinberga, które zapisujemy w prawej kolumnie. Po przeliczeniu ryb znajduj

ą

cych si

ę

w akwariach, w lewej kolumnie zapisujemy rzeczywiste (obserwowane) liczby

osobników o okre

ś

lonych fenotypach. Nast

ę

pnie otrzymane warto

ś

ci z obu kolumn

podstawiamy do wzoru i obliczmy według modelu

χ



2

∑

−

=

Exp

Exp

Obs

2

2

)

(

χ

Tablice

54

gdzie: Obs to liczba obserwowanych osobników o okre

ś

lonym fenotypie

Exp to liczba oczekiwanych osobników o okre

ś

lonym fenotypie (w tym

przypadku suma b

ę

dzie zawierała 5 składników).

Warto

ść

krytyczna statystyki

χ



2

na poziomie istotno

ś

ci a = 0,05 wynosi w tym

przypadku = 7,81 (liczba stopni swobody: K – l - s = 5 - 1 - 1 = 3)

p + q= 1 stad p -zmienna niezale

ż

na: p + (1 - p) = 1,

albo q -zmienna niezale

ż

na: q + (1 - q) = 1

Je

ż

eli obliczona warto

ść

statystyki

χ



2

przekroczy warto

ść

krytyczn

ą

(7,81) to

istniej

ą

podstawy do odrzucenia hipotezy zerowej (ze populacja molinezji znajduje si

ę

w równowadze Hardy-Weiberga) na rzecz hipotezy alternatywnej. W takim przypadku

nale

ż

y zastanowi

ć

si

ę

nad przyczynami takiej struktury genetycznej populacji. Jakie

czynniki mogły to wywoła

ć

?

Tablice

55

Zał

ą

cznik A

Tablica wartości t

Prawdopodobie

ń

stwo

Stopnie swobody

0.5

0.1

0.05

0.02

0.01

0.001

1

1,00

6,31

12,71

31,82

63,66

63,70

2

0,82

2,92

4,30

6,96

9,92

31,60

3

0,77

2,35

3,18

4,54

5,84

12,90

4

0,74

2,13

2,78

3,75

4,60

8,61

5

0,73

2,02

2,57

3,36

4,03

6,86

6

0,72

1,94

2,45

3,14

3,71

5,96

7

0,71

1,90

2,36

3,00

3,50

5,40

8

0,71

1,86

2,31

2,90

3,36

5,04

9

0,70

1,83

2,26

2,82

3,25

4,78

10

0,70

1,81

2,23

2,76

3,17

4,59

11

0,70

1,80

2,20

2,72

3,11

4,44

12

0,70

1,78

2,08

2,68

3,06

4,32

13

0,69

1,77

2,16

2,65

3,01

4,22

14

0,69

1,76

2,14

2,62

2,98

4,14

15

0,69

1,75

2,13

2,60

2,95

4,07

16

0,69

1,75

2,12

2,58

2,92

4,02

17

0,69

1,74

2,11

2,57

2,90

3,96

18

0,69

1,73

2,10

2,55

2,88

3,92

19

0,69

1,73

2,09

2,54

2,86

3,88

20

0,69

1,72

2,09

2,53

2,84

3,85

21

0,69

1,72

2,08

2,52

2,83

3,82

22

0,69

1,72

2,07

2,51

2,82

3,79

23

0,69

1,71

2,07

2,50

2,81

3,77

24

0,69

1,71

2,06

2,49

2,80

3,74

25

0,68

1,71

2,06

2,48

2,79

3,72

26

0,68

1,71

2,06

2,48

2,78

3,71

27

0,68

1,70

2,05

2,47

2,77

3,69

28

0,68

1,70

2,05

2,47

2,76

3,67

29

0,68

1,70

2,04

2,46

2,76

3,66

30

0,68

1,70

2,04

2,46

2,75

3,65

35

0,68

1,69

2,03

2,44

2,72

3,59

40

0,68

1,68

2,02

2,42

2,71

3,55

45

0,68

1,68

2,02

2,41

2,69

3,52

50

0,68

1,68

2,01

2,40

2,68

3,50

60

0,68

1,67

2,00

2,39

2,66

3,46

70

0,68

1,67

2,00

2,38

2,65

3,44

80

0,68

1,66

1,99

2,38

2,64

3,42

90

0,68

1,66

1,99

2,37

2,63

3,40

100

0,68

1,66

1,98

2,36

2,63

3,39

120

0,68

1,66

1,98

2,36

2,62

3,37

150

0,68

1,66

1,98

2,35

2,61

3,36

200

0,68

1,65

1,97

2,35

2,60

3,34

300

0,68

1,65

1,97

2,34

2,59

3,32

400

0,68

1,65

1,97

2,34

2,59

3,32

500

0,67

1,65

1,96

2,33

2,59

3,31

1000

0,67

1,65

1,96

2,33

2,58

3,30

Tablice

56

Zał

ą

cznik B

Tablica wartości chi-kwadrat (χ

2

)

Prawdopodobie

ń

stwo

Stopnie

swobody

0,99

0,95

0,5

0,25

0,1

0,05

0,025

0,01

0,005

1

-

-

0,45

1,32

2,71

3,84

5,02

6,63

7,88

2

0,02

0,10

1,39

2,77

4,61

5,99

7,38

9,21

10,60

3

0,11

0,35

2,37

4,11

6,25

7,81

9,35

11,34

12,84

4

0,30

0,71

3,36

5,39

7,78

9,49

11,14

13,28

14,86

5

0,55

1,15

4,35

6,63

9,24

11,07

12,83

15,09

16,75

6

0,87

1,64

5,35

7,84

10,64

12,59

14,45

16,81

18,55

7

1,24

2,17

6,35

9,04

12,02

14,07

16,01

18,48

20,28

8

1,65

2,73

7,34

10,22

13,36

15,51

17,53

20,09

21,96

9

2,09

3,33

8,34

11,39

14,68

16,92

19,02

21,67

23,59

10

2,56

3,94

9,34

12,55

15,99

18,31

20,48

23,21

25,19

11

3,05

4,57

10,34

13,70

17,28

19,68

21,92

24,72

26,76

12

3,57

5,23

11,34

14,85

18,55

21,03

23,34

26,22

28,30

13

4,11

5,89

12,34

15,98

19,81

22,36

24,74

27,69

29,82

14

4,66

6,57

13,34

17,12

21,06

23,68

26,12

29,14

31,32

15

5,23

7,26

14,34

18,25

22,31

25,00

27,49

30,58

32,80

16

5,81

7,96

15,34

19,37

23,54

26,30

28,85

32,00

34,27

17

6,41

8,67

16,34

20,49

24,77

27,59

30,19

33,41

35,72

18

7,01

9,39

17,34

21,60

25,99

28,87

31,53

34,81

37,16

19

7,63 10,12 18,34

22,72

27,20

30,14

32,85

36,19

38,58

20

8,26 10,85 19,34

23,83

28,41

31,41

34,17

37,57

40,00

21

8,90 11,59 20,34

24,93

29,62

32,67

35,48

38,93

41,40

22

9,54 12,34 21,34

26,04

30,81

33,92

36,78

40,29

42,80

23

10,20 13,09 22,34

27,14

32,01

35,17

38,08

41,64

44,18

24

10,86 13,85 23,34

28,24

33,20

36,42

39,36

42,98

45,56

25

11,52 14,61 24,34

29,34

34,38

37,65

40,65

44,31

46,93

26

12,20 15,38 25,34

30,43

35,56

38,89

41,92

45,64

48,29

27

12,88 16,15 26,34

31,53

36,74

40,11

43,19

46,96

49,64

28

13,56 16,93 27,34

32,62

37,92

41,34

44,46

48,28

50,99

29

14,26 17,71 28,34

33,71

39,09

42,56

45,72

49,59

52,34

30

14,95 18,49 29,34

34,80

40,26

43,77

46,98

50,89

53,67

40

22,16 26,51 39,34

45,62

51,80

55,76

59,34

63,69

66,77

50

29,71 34,76 49,33

56,33

63,17

67,50

71,42

76,15

79,49

60

37,48 43,19 59,33

66,98

74,40

79,08

83,30

88,38

91,95

70

45,44 51,74 69,33

77,58

85,53

90,53

95,02

100,42 104,22

80

53,54 60,39 79,33

88,13

96,58 101,88

106,63

112,33 116,32

90

61,75 69,13 89,33

98,64

107,56 113,14

118,14

124,12 128,30

100

70,06 77,93 99,33 109,14 118,50 124,34

129,56

135,81 140,17