PROFIL PRĘDKOŚCI W RURZE PROSTOOSIOWEJ

PROFIL PRĘDKOŚCI W RURZE PROSTOOSIOWEJ

1. Cel ćwiczenia.

Celem ćwiczenia jest doświadczalne wyznaczenie rozkładu

prędkości przepływu płynu w rurociągu przy różnych liczbach

Reynoldsa i porównanie kształtów otrzymanych profilów.

2. Podstawy teoretyczne.

Przepływ, w którym można wydzielić warstwy cieczy,

między którymi nie ma wymiany masy, a poszczególne cząsteczki

poruszają się po torach o kierunku wyznaczonym przez ściany

przewodu nazywać będziemy przepływem laminarnym

(lub uwarstwionym). Natomiast przepływ, w którym cząsteczki

oprócz ruchu głównego wzdłuż przewodu wykonują także ruchy

poboczne w kierunku poprzecznym nazywać będziemy

przepływem turbulentnym (lub burzliwym). Kształt profilów

prędkości przepływu płynu w rurociągu jest różny dla ruchu

laminarnego i turbulentnego:

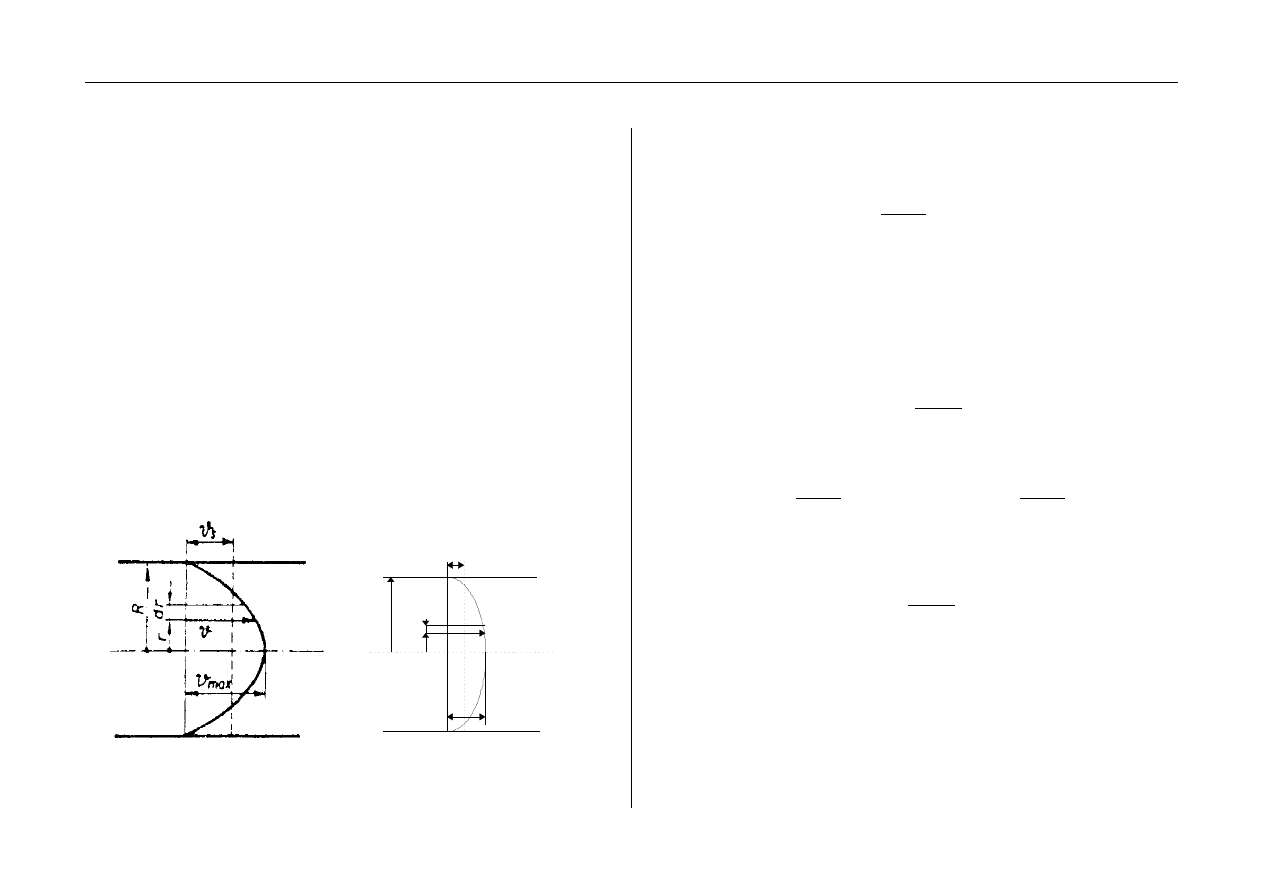
v

S

R dr

r v

v

max

Rys. 1. Profile prędkości: a) ruchu laminarnego, b) ruchu turbulentnego

W ruchu laminarnym rozkład prędkości

ν

przepływu płynu

lepkiego i nieściśliwego przez długą cylindryczną rurę o średnicy

D = 2R opisuje równanie Poiseuille’a:

)

r

R

(

l

4

p

2

2

−

⋅

⋅

⋅

=

η

∆

ν

(1)

gdzie :

∆

p - spadek ciśnienia na długości l,

η

- dynamiczny współczynnik lepkości.

Wzór (1) otrzymuje się w wyniku rozwiązania równań

Naviera-Stokesa dla płynu lepkiego nieściśliwego. Z powyższego

równania wynika, że rozkład prędkości jest paraboliczny,

a prędkość maksymalna występuje w osi rurociągu i wynosi:

2

max

R

l

4

p

⋅

⋅

⋅

=

η

∆

ν

(2)

Dzieląc natężenie przepływu Q wyrażone wzorem:

4

R

0

2

2

R

l

8

p

dr

r

2

)

r

R

(

l

4

p

Q

⋅

⋅

⋅

=

⋅

⋅

⋅

−

⋅

⋅

⋅

=

∫

η

∆

π

η

∆

(3)

przez przekrój rurociągu A =

π

R

2

otrzymuje się prędkość średnią

przepływu :

2

s

R

l

8

p

⋅

⋅

⋅

=

η

∆

ν

(4)

Ze wzorów (2) i (4) wynika, że prędkości v

max

i v

s

związane

są zależnością:

v

s

= 0.5 v

max

Doświadczenia wykazały dobrą zgodność wzorów (2) i (4)

z wynikami pomiarów. W praktyce występują najczęściej

przepływy turbulentne.

1

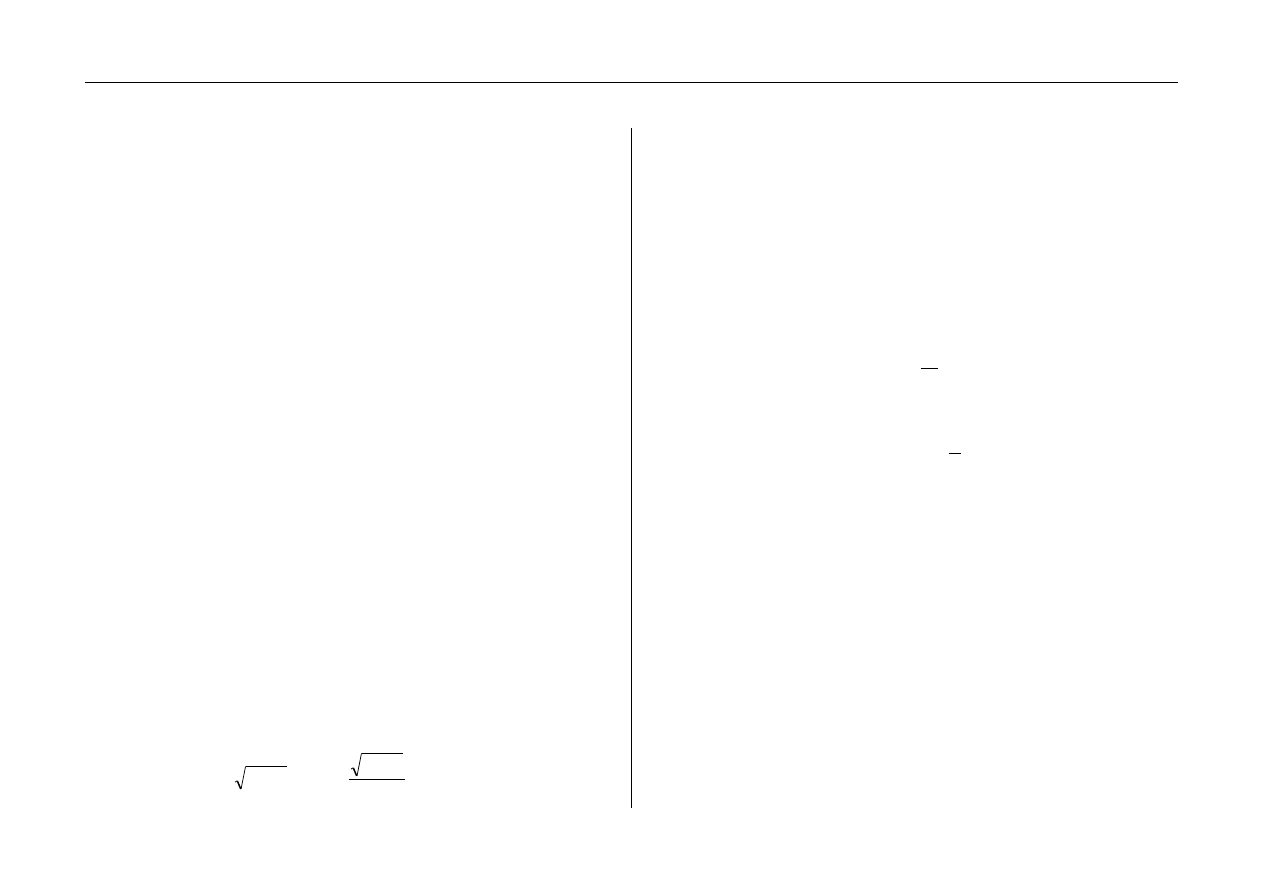
PROFIL PRĘDKOŚCI W RURZE PROSTOOSIOWEJ

Rozwiązania równań Naviera-Stokesa są rozwiązaniami

statecznymi. Wprowadzenie małego zaburzenia do rozwiązań

nie powoduje zwiększania się zaburzenia z upływem czasu,

ale jego wytłumianie. Rozwiązania takie są jednak stateczne tylko

dla niewielkich prędkości przepływu. Przy większych prędkościach

ruch traci stateczność i cząsteczki cieczy poruszają się ruchem

nieregularnym, mającym wybitne cechy ruchu nieustalonego.

Niezmienne w czasie mogą być w takim ruchu, zwanym

ruchem turbulentnym, tylko pewne wartości uśrednione,

charakteryzujące ruch. W celu uzyskania równań ruchu

turbulentnego są one uśredniane, w wyniku czego otrzymuje się

tzw. równania Reynoldsa. W przepływie turbulentnym w rurze

można wyróżnić dwa obszary. Zasadniczą część pola przekroju

przepływu obejmuje rdzeń turbulentny, w pobliżu ścianek

natomiast występuje cienka warstwa przepływu laminarnego,

zwana podwarstwą laminarną. Podwarstwa ta odgrywa ważną rolę

ze względu na występujący tu duży gradient prędkości, z czym

wiążą się naprężenia styczne. W rdzeniu turbulentnym wskutek

występowania ruchów pobocznych, wywołujących intensywną

wymianę pędu między poruszającymi się z różną prędkością

elementami płynu, pojawiają się tzw. naprężenia turbulentne.

Ich wartość jest wielokrotnie większa od naprężeń w podwarstwie,
zwanej laminarną. Można więc powiedzieć, że o naprężeniach

w podwarstwie laminarnej decydują naprężenia wywołane

lepkością, w rdzeniu turbulentnym natomiast naprężenia

turbulentne. Naprężenia laminarne można określić wychodząc

z hipotezy Newtona, skąd otrzyma się wzór na rozkład prędkości

w podwarstwie laminarnej. W rdzeniu turbulentnym można

otrzymać rozwiązanie określające rozkład prędkości ruchu

uśrednionego w czasie, dopiero po wprowadzeniu kilku hipotez

i uproszczeń. Przy czym rozwiązanie to uzyskuje się

z dokładnością do dwóch stałych, które trzeba wyznaczyć

doświadczalne. Wzór na rozkład prędkości w prosto osiowej rurze

jest następujący:

)

5

,

5

y

p

/

ln

5

,

2

(

p

/

0

0

+

⋅

⋅

=

υ

τ

τ

ν

(5)

gdzie :

τ

0

-

naprężenia styczne na ściance rury,

zależne od liczby Reynoldsa Re;

Re=v

s

.

d/

ν

-

liczba Reynoldsa,

v

s

-

średnia prędkość przepływu w rurze o

średnicy d;

y-

∈

[, d -

δ

] -

współrzędna;

δ

-

grubość warstwy laminarnej.

Ze wzoru (6) wynika, że rozkład (profil) prędkości

w rdzeniu ruchu turbulentnego jest inny niż w ruchu laminarnym

(wzór-1). W podwarstwie laminarnej rozkład prędkości jest

liniowy:

y

0

⋅

=

η

τ

ν

W przybliżeniu rozkład prędkości dla przepływu

turbulentnego można również wyrazić równaniem:

n

/

1

max

)

R

r

1

(

v

v

−

=

(6)

gdzie :

R-

promień rurociągu,

r-

współrzędna promieniowa,

n-

współczynnik zależny od liczby Reynoldsa.

Badania Nikuradsego wykazały dużą zgodność między

profilami otrzymanymi wg. wzoru (7) i profilami otrzymanymi

na podstawie pomiarów. Badania przepływów turbulentnych

najczęściej przeprowadza się metodami doświadczalnymi. Pomiaru

prędkości miejscowych dokonuje się zwykle poprzez pomiar

ciśnienia dynamicznego. Jeżeli w płynie poruszającym się

z prędkością v zostanie zanurzone ciało, to nastąpi spiętrzenie

przepływu oraz rozdział strug dookoła tego ciała.

W punkcie S (rys.2) znajdującym się w środku spiętrzenia,

zwanym punktem wejścia (stagnacji), prędkość przepływu v jest

równa zeru.

2

PROFIL PRĘDKOŚCI W RURZE PROSTOOSIOWEJ

Równanie Bernouliego dla „zatrzymanej” linii prądu, można

napisać w postaci:

g

p

g

p

g

2

2

⋅

=

⋅

+

∞

∞

ρ

ρ

ν

(7)

gdzie:

v

∞

, p

∞

-

prędkość i ciśnienie w przepływie

niezakłóconym,

p-

ciśnienie statyczne w punkcie stagnacji.

Rys. 2. Punkt stagnacji

Przekształcając wzór (8) otrzymamy :

2

+

p

=

p

2

∞

∞

⋅

ν

ρ

(8)

Ciśnienie p będące sumą ciśnienia statycznego p

∞

i ciśnienia

dynamicznego

2

v

2

⋅

ρ

nazywamy ciśnieniem całkowitym. Wynika

stąd, że ciśnienie w punkcie stagnacji jest równe ciśnieniu

całkowitemu. Jeśli zatem w punkcie stagnacji zostanie wykonany

niewielki otwór, to wewnątrz tego otworu będzie panowało

ciśnienie całkowite Wyznaczanie prędkości przepływu płynu

można zatem sprowadzić do pomiaru ciśnienia spiętrzenia oraz

ciśnienia statycznego. Warto zauważyć, że mierzona prędkość jest

prędkością miejscową a nie punktową, gdyż sonda ma daną

średnicę.

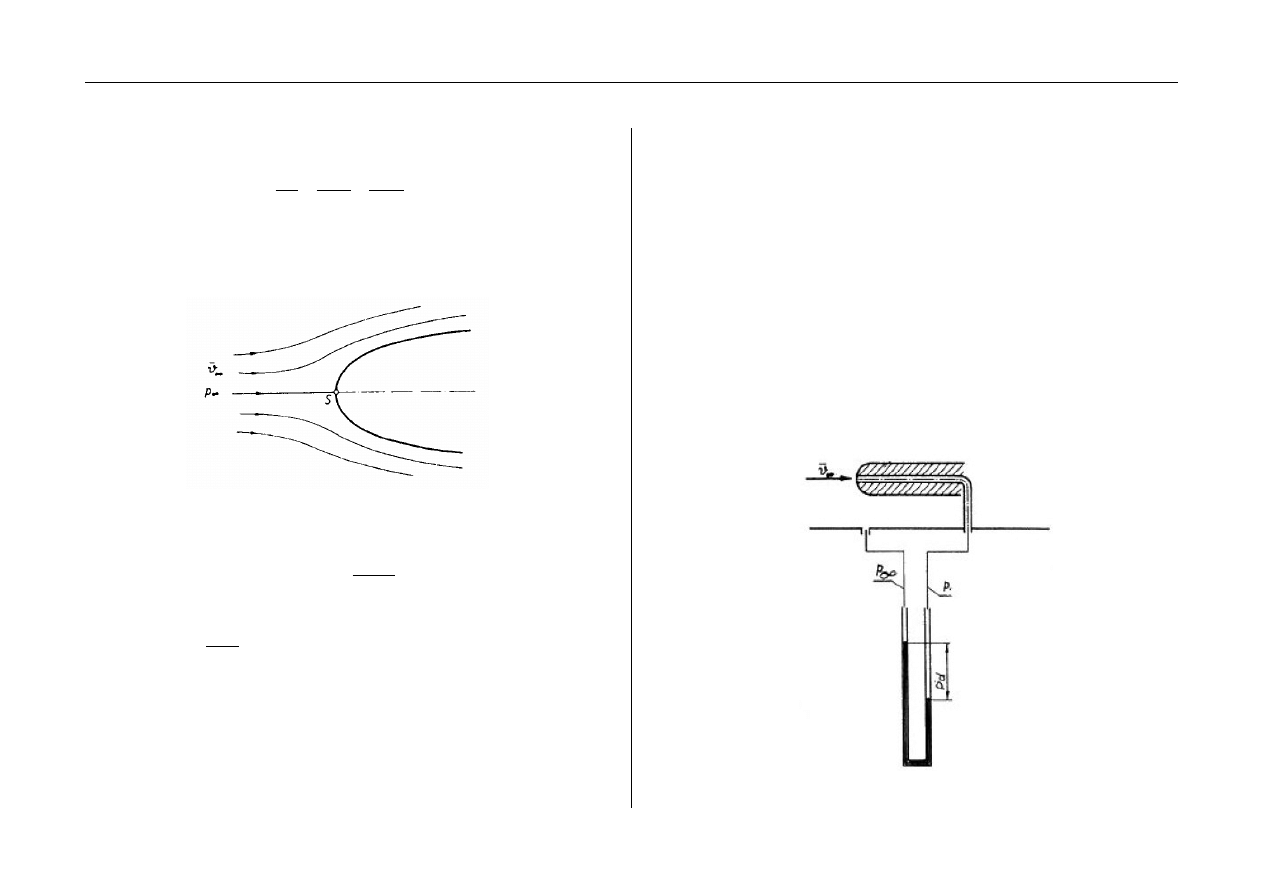
W omawianym ćwiczeniu do wyznaczania prędkości

zastosowano metodę pomiarową przedstawioną schematycznie

na rysunku (rys.3).

Polega ona na pomiarze ciśnienia całkowitego w punkcie

stagnacji oraz ciśnienia statycznego na ściance rurociągu.

Wymaga to jednak założenia, że ciśnienie statyczne w całym

przekroju jest jednakowe. Z tego względu do wyznaczania

prędkości miejscowej wygodniej jest posługiwać się rurką

Prandtla, umożliwiającą zarówno pomiar ciśnienia statycznego,

jak i całkowitego. Schemat tego przyrządu przedstawiono

na rysunku (rys.4).

Ciśnienie całkowite jest odbierane w punkcie stagnacji,

ciśnienie statyczne natomiast przez otworki znajdujące się

w bocznych ściankach, wykonane w takiej odległości od wlotu,

że ustala się w nich ciśnienie statyczne, panujące w przepływie

niezakłóconym.

Rys. 3. Rurka Pitota

3

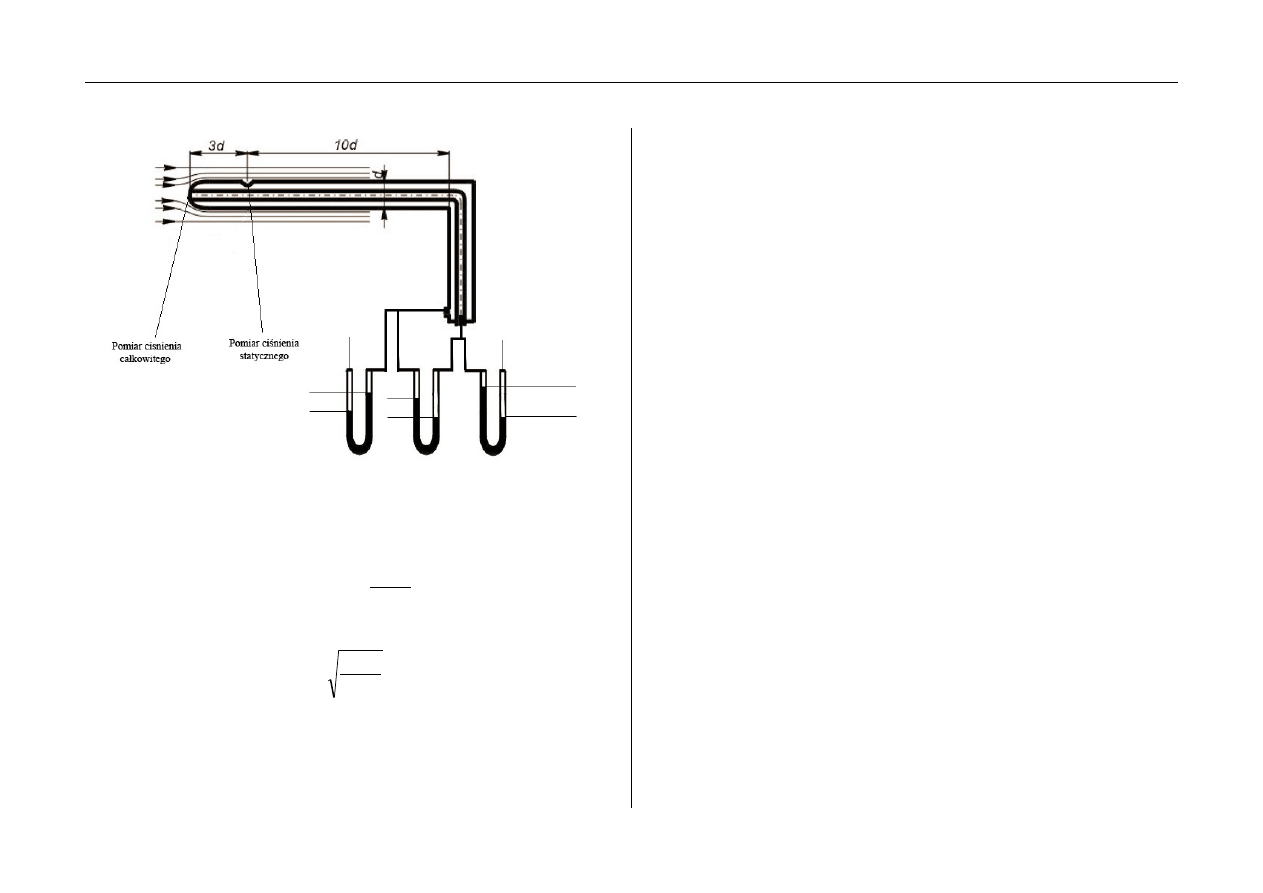
PROFIL PRĘDKOŚCI W RURZE PROSTOOSIOWEJ

Rys. 4. Rurka Prandtla

Wychylenie manometru różnicowego jest wywołane różnicą

ciśnienia całkowitego i statycznego, określa ciśnienie dynamiczne.

Wyrażając tą zależność otrzymamy:

2

=

p

-

p

=

p

2

s

c

d

ν

ρ ⋅

(9)

Prędkość przepływu obliczamy ze wzoru:

ρ

ν

d

p

2

=

⋅

(10)

Różnicę p

c

-p

s

określa się na podstawie wskazań manometru

różnicowego.

Rurkę Prandtla należy ustawić równolegle do osi rurociągu.

Istotną zaletą tego przyrządu jest mała wrażliwość na odchylenia

od kierunku strumienia.

3. Opis stanowiska pomiarowego.

Stanowisko składa się z następujących elementów:

 rurociągu R

u

z przezroczystego tworzywa,

 rurki Pitota P

t

,

 mikromanometru z rurką pochyłą M,
 termomertu rtęciowego T,
 psychrometru Assmanna PA
 manometru U

Rurociągiem R

u

przepływa powietrze o regulowanym

natężeniu przepływu Q tłoczone z układu zasilania. Rurka Pitota

służy do pomiaru ciśnienia całkowitego (rys.3). Ciśnienie

statyczne jest mierzone na ściance rurociągu. Przyjęto tu zgodne z

doświadczeniem i teorią założenie o stałości ciśnienia statycznego

w całym przekroju rury. Uchwyt rurki Pitota umożliwia jej

przesuwanie w kierunku pionowym oraz pomiar rzędnej położenia

osi tej rurki względem osi rury. Przełożenie mikromanometru

należy dobrać tak, aby uzyskać znaczne wychylenie słupków

cieczy manometrycznej.

4

PROFIL PRĘDKOŚCI W RURZE PROSTOOSIOWEJ

Rys. 5. Schemat stanowiska pomiarowego

4. Przebieg ćwiczenia.

Pomiary rozkładu prędkości należy wykonać dla trzech

różnych natężeń przepływu w rurociągu. Ciśnienie dynamiczne

mierzyć w dziewięciu punktach rozłożonych wzdłuż średnicy.

Pomiary należy przeprowadzić po ustaleniu się temperatury

powietrza w rurociągu. Odczyty wskazań przyrządów oraz wyniki

obliczeń należy zestawić w tablicy pomiarowej, w której powinny

się znajdować:

a) jednorazowo odczytane następujące wielkości:

 ciśnienie atmosferyczne [Pa],
 temperaturę termometru suchego i mokrego

[°C],

 średnicę wewnętrzną rurociągu [m],

b) zmieniając natężenie przepływu powietrza zapisać dla

każdego punktu pomiarowego:

 wysokość różnicy ciśnienia całkowitego i ciśnienia

statycznego (zapisać ponadto przełożenie

mikromanometru),

 współrzędną promieniową położenia rurki Pitota,
 temperaturę przepływającego czynnika.

c) Profil prędkości we współrzędnych bezwymiarowych (v/

v

max

,r/R) przedstawić graficznie.

Do obliczenia prędkości należy skorzystać z równania (11),

w którym:

pd- ciśnienie dynamiczne mierzone za pomocą sondy Pr

jako różnica ciśnienia całkowitego i statycznego,

ρ

- gęstość powietrza w miejscu pomiaru V

max

wyznaczona

dla zmierzonej temperatury, ciśnienia i wilgotności.

Gęstość czynnika którym jest powietrze wyznaczymy

w oparciu o równanie stanu gazu doskonałego:

mRT

pV

=

Wiedząc, że

ρ

= m/V otrzymujemy:

RT

p

=

ρ

(11)

gdzie:

p- ciśnienia atmosferyczne [Pa],

R- indywidualna stała gazowa dla powietrza [J/kg*K]

T- temperatura powietrza w układzie pomiarowym [K].

5

PROFIL PRĘDKOŚCI W RURZE PROSTOOSIOWEJ

Następnie należy obliczyć wilgotność bezwzględną x

zawartą w powietrzu z zależności:

nas

nas

p

p

p

622

.

0

x

ϕ

ϕ

−

=

(12)

gdzie:

ϕ

-

wilgotność względna,

p-

ciśnienie otoczenia [Pa],

p

nas

- ciśnienie nasycenia w danej temperaturze [Pa]

<temperatura w układzie pomiarowym>,

Wartość ciśnienia nasycenia w danej temperaturze należy

odczytać z ogólnie dostępnych tablic. Następnie posługując się

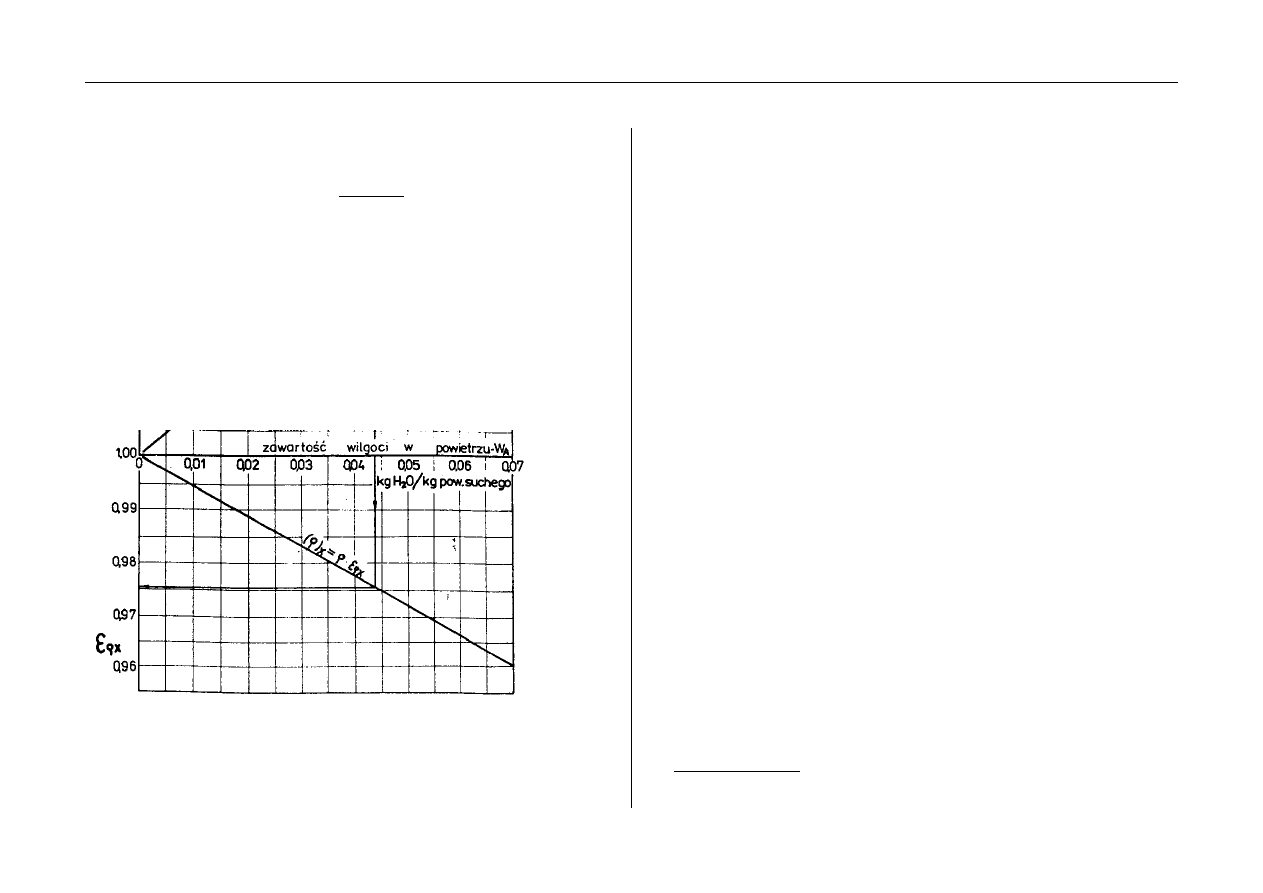
rysunkiem 6 należy odczytać poprawkę gęstości zależną od ilości

wilgoci zawartej w powietrzu suchym.

Rys. 6. Poprawka gęstości dla powietrza wilgotnego uzależniona od wilgotności

bezwzględnej

Następnie należy obliczyć gęstość powietrza wilgotnego

z zależności:

x

x

*

ρ

ε

ρ

ρ =

gdzie:

ρ

x

- gęstość powietrza wilgotnego [kg/m

3

],

ρ

- gęstość powietrza suchego [kg/m

3

],

ε

ρ

x

- odczytana poprawka.

Różnicę ciśnień p

d

obliczymy uwzględniając wysokość

wychylenia się słupa rtęci w manometrze z zależności:

g

*

*

h

p

m

d

ρ

=

1

(13)

gdzie:

h-

wysokość słupa cieczy w manometrze [m],

ρ

m

-

gęstość cieczy manometrycznej [kg/m

3

],

g - przyspieszenie ziemskie [m/s

2

]

Wykres powinien zawierać trzy profile prędkości otrzymane

w wyniku własnych pomiarów. Dla każdego profilu należy obliczyć

liczby Reynoldsa Re=v

s

d/

ν

. W końcowej części sprawozdania

należy umieścić wnioski dotyczące analizowanego zagadnienia.

Pomiar wilgotności powietrza psychrometrem Assmanna

Metoda psychrometryczna- pomiar wilgotności psychrometrem

Assmanna:

 zwilżyć tkaninę umieszczoną na zbiorniczku rtęci

termometru mokrego (niebieski)

 włączyć wentylator psychrometru
 obserwować wskazania termometrów
 w chwili ustabilizowania się temperatur na obu

termometrach dokonać odczytu.

1

UWAGA!!! W przypadku ciśnienia dynamicznego wyniki należy skorygować
o przełożenie mikromanometru

6

PROFIL PRĘDKOŚCI W RURZE PROSTOOSIOWEJ

a) Obliczanie wilgotności względnej

ϕ

1

. Wilgotność względną

powietrza można wyliczyć na podstawie zmierzonych

wartości temperatury powietrza mierzonej termometrem

suchym t

s

i termometrem mokrym t

m

.

(

)

[

]

ns

b

m

s

nm

ns

p

p

p

t

t

A

p

p

p

−

−

=

=

ϕ

(14)

gdzie:

p

p

–

ciśnienie cząstkowe pary wodnej w badanym

powietrzu

p

nm

– ciśnienie nasycenia pary wodnej w temperaturze t

m

termometru mokrego.

p

ns

–

ciśnienie nasycenia pary wodnej w temperaturze t

s

termometru suchego.

p

b

–

ciśnienie barometryczne w chwili pomiaru

A–

współczynnik psychrometryczny

5

10

w

75

,

6

65

A

−





















÷

=

(15)

gdzie:

w –

prędkość powietrza w pobliżu naczynia termometru

mokrego [m/s],

Dla psychrometru Assmanna w = 2,5 m/s, czyli A = 0,000677

b) Wyznaczenie wilgotności względnej powietrza

ϕ

2

korzystając

z tablic psychrometrycznych.

c) Wyznaczenie wilgotności względnej powietrza

ϕ

3

korzystając

z załączonego wykresu i – x

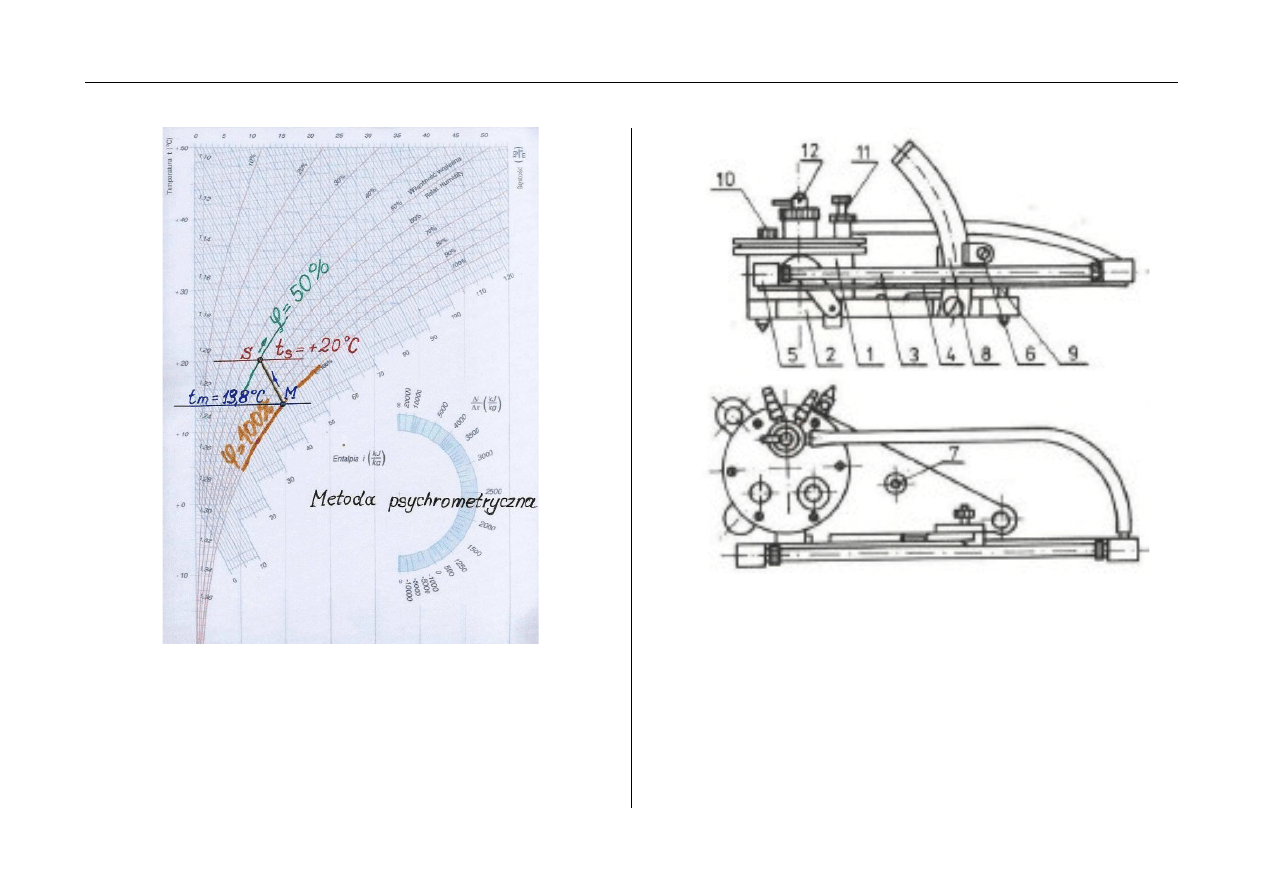
Opis metody:

 na wykresie i-x rysujemy izotermę temperatury odczytanej

na termometrze mokrym

t

m

(linia niebieska),

do

przecięcia z krzywą

ϕ

= 100%

, punkt przecięcia

M

 rysujemy izotermę temperatury odczytanej na

termometrze suchym

t

s

(linia czerwona).

 Z punktu M rysujemy ukośnie w lewo w górę linię po stałej

entalpii do przecięcia z linią

t

s

(punkt S).

 Przez punkt przecięcia S rysujemy krzywą

ϕ

S

= const

(wg

kierunku wyznaczonego przez najbliższe krzywe), na

rysunku przykładzie jest to linia

ϕ

= 50%

7

PROFIL PRĘDKOŚCI W RURZE PROSTOOSIOWEJ

Obsługa mikromanometru MPR-4

Rys. 7. Budowa mikromanometru MPR-4

1- zbiornik pomiarowy

2- poziomowana podstawie

3- szklana, wycechowana rurka pomiarowa

4- ruchome ramię mikromanometru

5- uchwyt rurki

6- blokada ramienia

7- poziomica

8- prowadnica do mocowania rurki pod odpowiednim kątem

9- śruby poziomujące

10- króciec do napełniania zbiornika mikromanometru cieczą

manometryczną

11- pokrętło do ustawiania poziomu zerowego cieczy manometrycznej

12- kurek rozdzielczy, zaopatrzony w dwa króćce, oznaczone (+) i (–), do

których doprowadza się wężyki impulsowe ciśnienia (możliwe są trzy

położenia: P - pomiar, Z - zamknięte, 0 -zerowanie manometru).

8

PROFIL PRĘDKOŚCI W RURZE PROSTOOSIOWEJ

Mikromanometr z pochyłą rurką służy do pomiaru

nadciśnienia, podciśnienia oraz różnicy ciśnień. Mikromanometr

mpR-4 jest manometrem hydrostatycznym, w którym mierzone

ciśnienie równoważone jest słupem cieczy manometrycznej.

a) przeprowadzenie pomiaru

 do otworu pomiarowego w przewodzie włożyć rurkę

spiętrzającą lub sondę prędkościową.

 następnie połączyć rurkę lub sondę

z mikromanometrem przewodami impulsowymi wg

zasady

•

końcówka „+” służy do pomiaru

nadciśnienia

•

końcówka „-„ służy do pomiaru

podciśnienia

•

przy pomiarze różnicy ciśnień wyższe

ciśnienie podłączamy do końcówki „+”,

niższe do końcówek „-„.

 rurkę pomiarową (3) ustawiamy na odpowiedni

stosunek przeniesienia i zabezpieczamy zatyczkę

 kurek (12) ustawić w położenie „Z” i na rurce

odczytujemy

wysokość

słupa

cieczy

manometrycznej

 przy pomiarach trwających przez dłuższy okres

czasu, należy kontrolować co pewien czas p-t

zerowy- przez ustawienie kurka w pozycji „0”

 po zakończonym pomiarze odłączyć od

mikromanometru przewody impulsowe

 wyjąć rurkę Prandtla lub sondę z przewodu
 zabezpieczyć miernik- umieścić w skrzynce

9

PROFIL PRĘDKOŚCI W RURZE PROSTO OSIOWEJ

KARTA POMIAROWA

Imię i nazwisko ..............................................................................................................................................................................

Imię i nazwisko ..............................................................................................................................................................................

Kierunek

...........................................................................................

Rok.....................................

Grupa.......................

Ćw..........

...............................

(nr)

(data)

Ciśnienie atmosferyczne [Pa]

..............................

Przełożenie mikromanometru [-]

..............................

Poziom początkowy cieczy mikromanometrycznej [mmH

2

O] ..............................

Średnica wew. rurociągu [mm]

..............................

Termometr „suchy” [

o

C]

..............................

Termometr „mokry” [

o

C]

..............................

10

Lp.

Promień

rury

Poziom cieczy manometrycznej

r

[mm]

h

1

[mm]

h

2

[mm]

h

3

[mm]

T =

0

C

T =

0

C

T =

0

C

1

2
3
4
5
6
7
8
9

PROFIL PRĘDKOŚCI W RURZE PROSTO OSIOWEJ

11