Grafy planarne - 1
Grafy izomorficzne
Dwa grafy G
1
i G
2
są izomorficzne, jeżeli istnieje wzajemnie
jednoznaczna odpowiedniość m-dzy wierzchołkami grafu G
1
i G
2
taka,
że liczba krawędzi łączących dane dwa wierzchołki grafu G
1
jest równa
liczbie krawędzi łączących odpowiadające im wierzchołki grafu G
2
.
Krótko: można znaleźć przyporządkowanie wierzchołków obu grafów,
dla którego macierze sąsiedztwa są jednakowe.
Przykład:
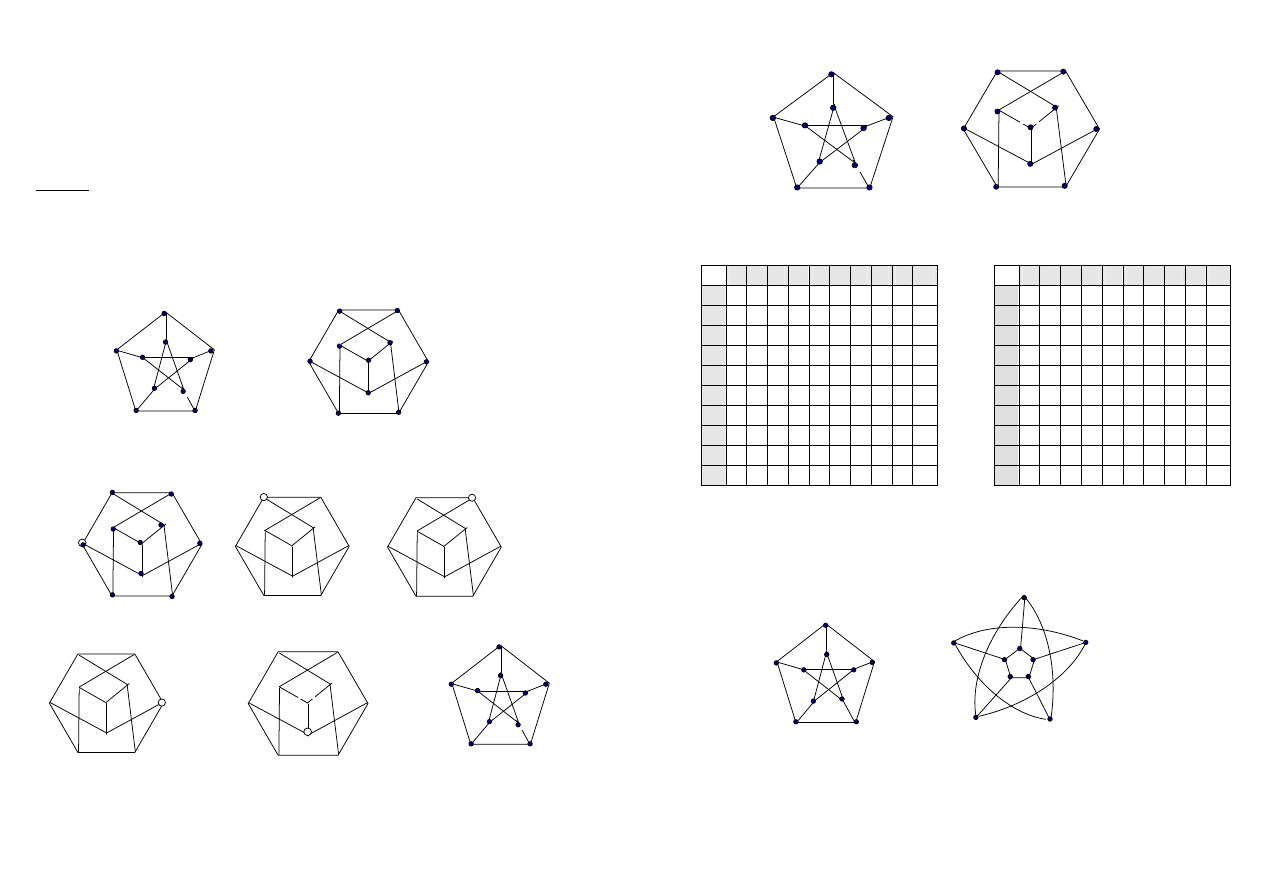
Grafy pokazane na poniższym rysunku są izomorficzne
Proces przyporządkowania wierzchołków
6
1
2
3
5
7
b)
6
c)
1
2
3
4
5
7
8
d)
1
2
3
4
5
6
7
8
9
1
2
5
6
a)
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
e)
1
2
3
4
5
6
7
8
9
10
Grafy planarne - 2
Macierze sąsiedztwa
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1
1
1 1
1
1
1 1
2 1
1
1
2 1
1
1
3
1
1
1
3
1
1
1
4
1
1
1
4
1
1
1
5 1
1
1
5 1
1
1
6 1
1 1
6 1
1 1
7
1
1 1
7
1
1 1
8
1
1
1
8
1
1
1
9
1
1 1
9
1
1 1
10
1
1 1
10
1
1 1
Inny graf izomorfizmiczny dla tego grafu
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
Grafy planarne - 3
Grafy planarne
Graf planarny to taki graf, który można narysować na płaszczyźnie bez
przecięć krawędzi, poza wierzchołkami z którymi sa one incydentne.
Płaski rysunek grafu planarnego nazywamy też grafem płaskim.
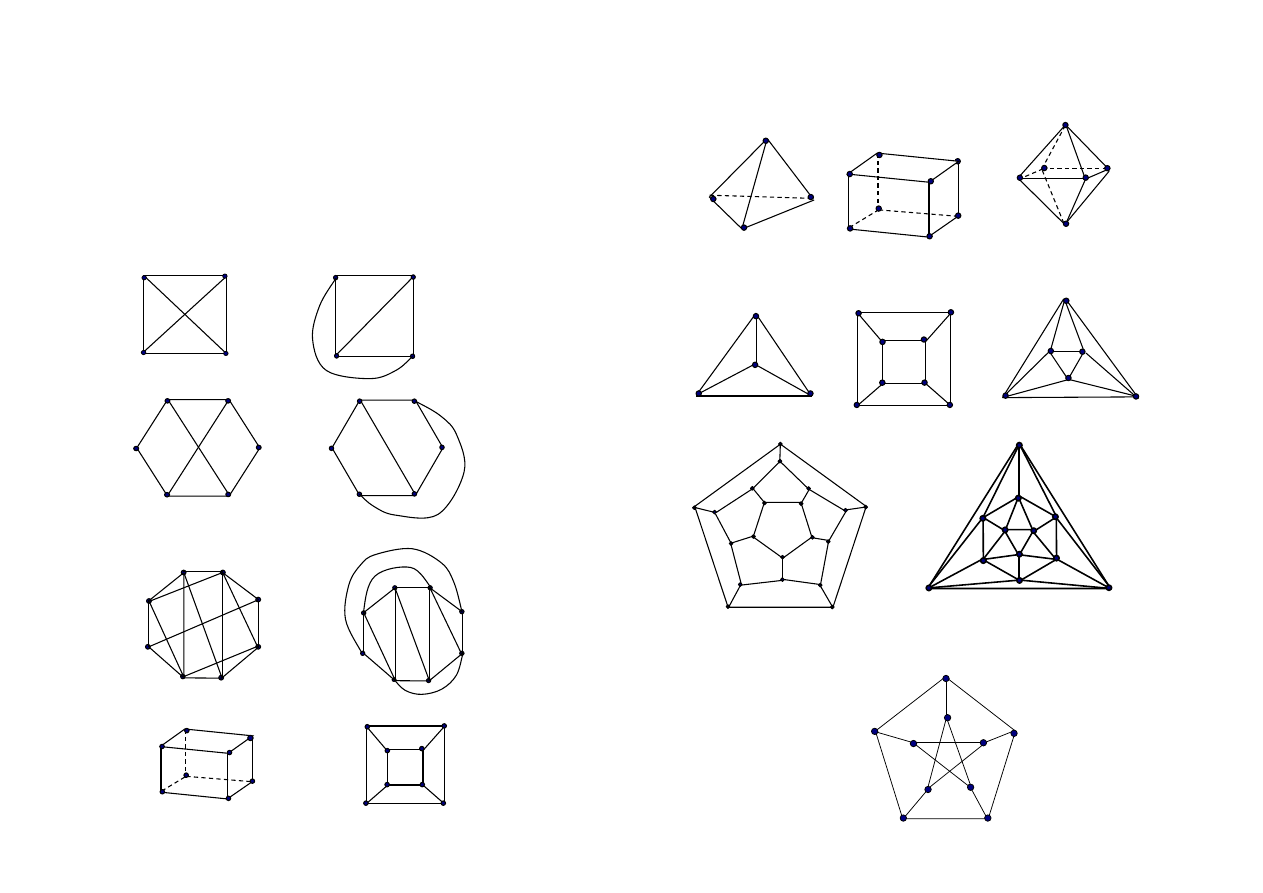
Przykłady
Grafy planarne - 4
Grafy planarne – przykłady grafów regularnych
Graf Petersena – nieplanarny
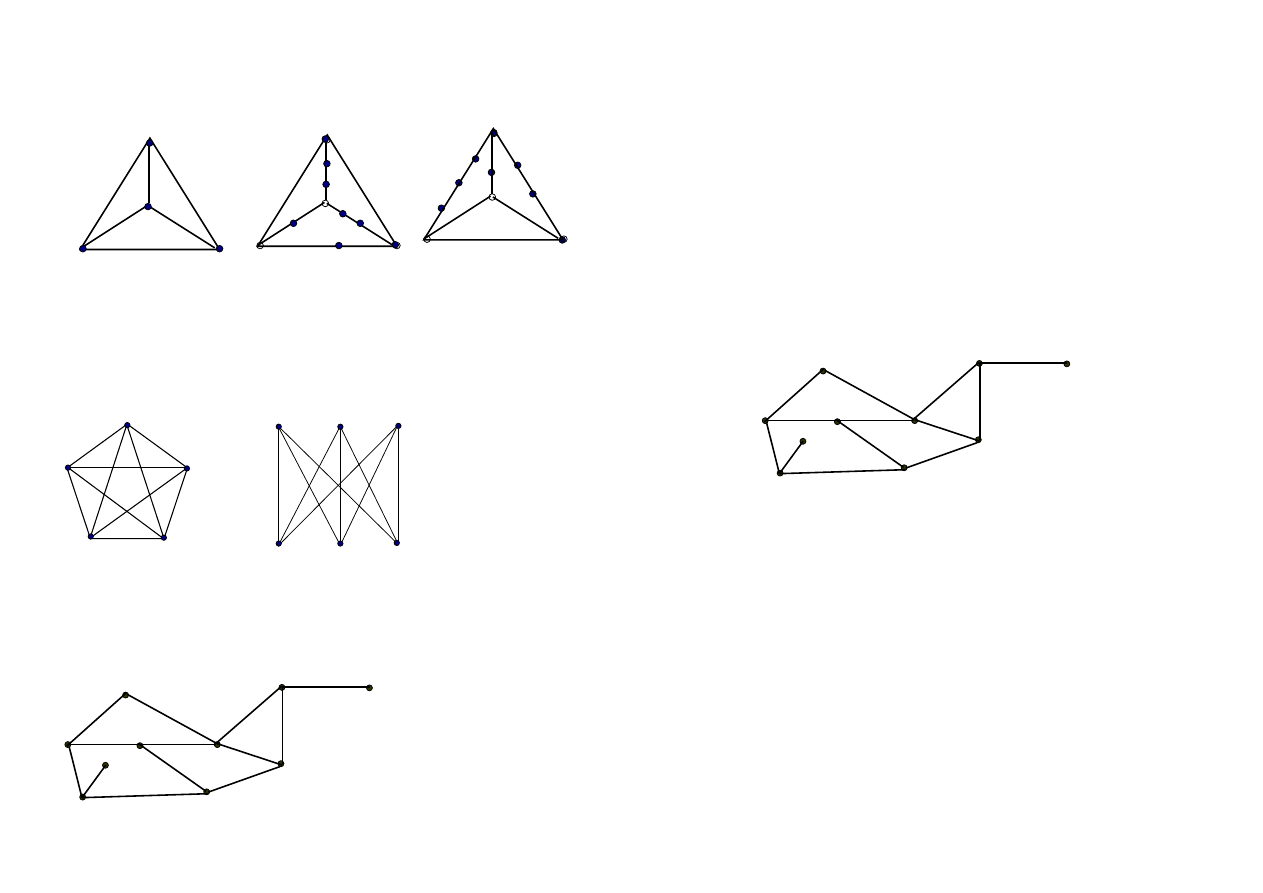
Grafy planarne - 5
Grafy homeomorficzne - gdy można je otrzymać z tego samego grafu
przez wstawienie nowych wierzchołków stopnia 2 wewntrz jego
krawędzi.
Twierdzenie (Kuratowski, 1930)
Graf jest planarny wtedy i tylko wtedy, gdy nie zawiera podgrafu
homeomorficznego z grafem K
5
lub K
3,3
.
bez dowodu.
Sciany w grafie planarnym
Graf K
5
Graf K
3,3
f
1
f
2
f
3
f
4
f
5
Ściany w grafie - f
5
ściana nieskończona (nieograniczona)
Grafy planarne - 6
Ściany – spójne obszary płaszczyzny, powstałe z podziału rysunkiem
grafu. Punkty grafu nie należą do ściany.
Twierdzenie (Euler, 1750)
Niech G będzie rysunkiem płaskim spójnego grafu płaskiego, w którym
n – liczba wierzchołków
m – liczba krawędzie
f – liczba ścian
Wtedy zachodzi równość
n − m + f = 2
Przykład
n = 10 m = 13 f = 5 n − m + f = 10 − 13 +5 = 2
Wykonać podobne sprawdzenie dla poprzednio podanych planarnych
regularnych
f
1
f
2
f
3
f
4
f
5
Wyszukiwarka
Podobne podstrony:
Grafy rodzaje
RODZAJE WYSIŁKU FIZYCZNEGO
rodzaje ooznaczen i ich ochrona
rodzaje struktur rynkowych 2
rodzaje diet
Rodzaje zanieczyszczeń środowiska
rodzaje wi za
Rodzaje fundamentów
Wykład 5 Rodzaje audytu wewnetrznegoSTUDENCIZAO
Rodzaje aberracji chromosomowych pop
Różne rodzaje grzejników
II wyklad Interakcje i rodzaje wiedzy
Rodzaje przedsiębiorstw2
Rodzaje cery
Rodzaje manipulacji
Narzędzia chirurgiczne i ich rodzaje
W 4 biomonitoring testy rodzaje
więcej podobnych podstron