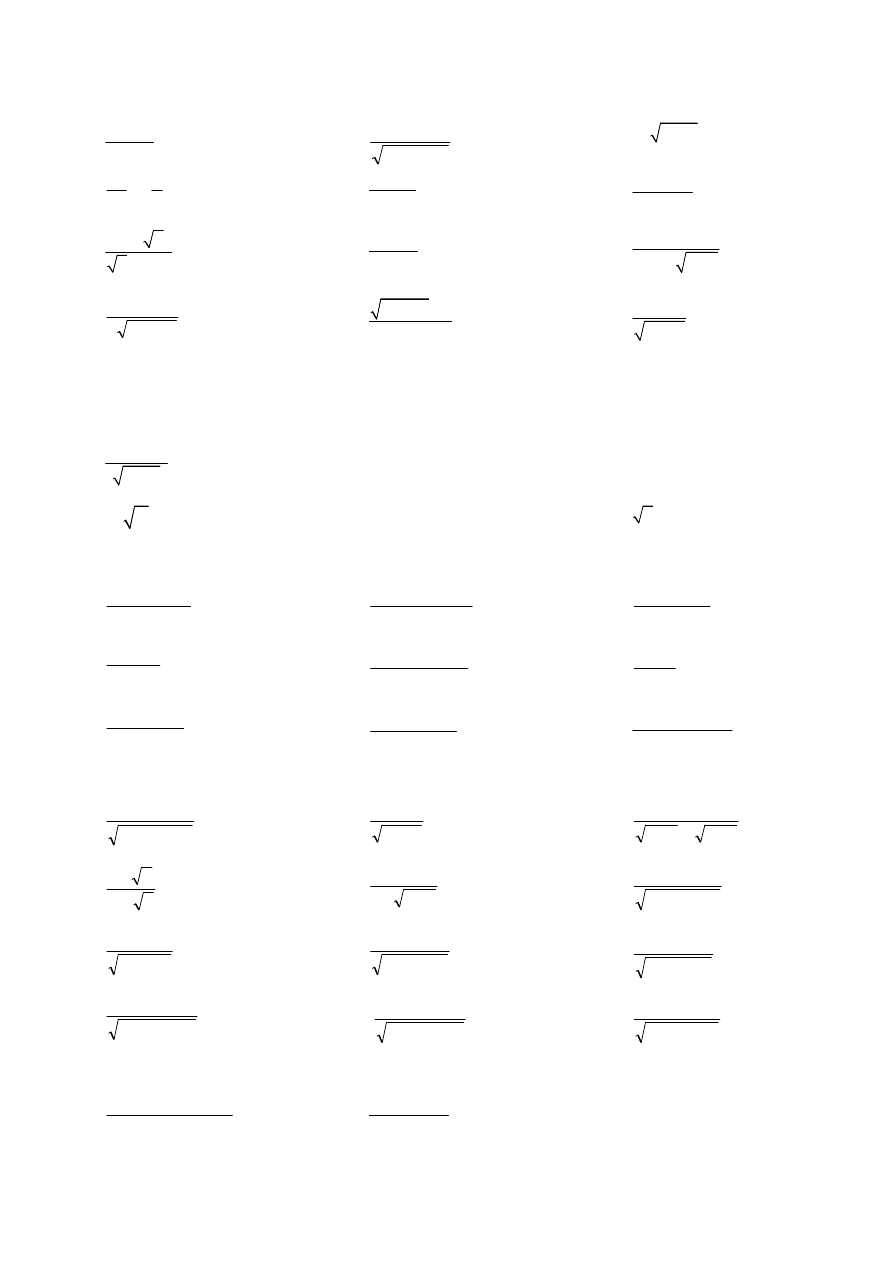
CAŁKA NIEOZNACZONA

Zad.1. Obliczyć podane całki (wykorzystując twierdzenie o całkowaniu przez podstawienie):

1.

7

dx

4

9

x

x

e

e

+

∫

2.

∫

+

3

3

sin

1

dx

3

cos

x

x

3.

2

3

4

1

dx

x

x

+

∫

4.

∫

dx

x

x

1

sin

1

2

5.

sin ln

dx

x

x

∫

6.

arctg

2

2

dx

1

x

e

x

−

+

∫

7.

(

)

arctg

dx

1

x

x

x

+

∫

8.

3

2

4

dx

cos

x

x

∫

9.

2

dx

sin

ctg

x

x

∫

10.

∫

+

x

x

dx

ln

3

11.

2

tg

5 dx

3cos

x

x

+

∫

12.

4

5

dx

2

x

x

+

∫

Zad.2. Obliczyć podane całki (wykorzystując twierdzenie o całkowaniu przez części):

13.

∫

dx

2

arctgx

x

14.

arcsin

dx

x

∫

15.

(

)

2

1 4 dx

x

x

x

+ −

∫

16.

2

arcsin

dx

1

x

x

x

−

∫

17.

2

cos dx

x

e

x

∫

18.

∫

xdx

x sin

2

19.

ln x dx

∫

20.

sin ln dx

x

∫

21.

ln dx

x

x

∫

Zad.3. Obliczyć całki funkcji wymiernych:

22.

∫

+

−

10

7

2

2

x

x

xdx

23.

∫

−

−

x

x

x

dx

3

7

6

2

3

24.

∫

+

+

+

dx

x

x

x

8

5

1

3

2

25.

(

)

∫

−

+

dx

x

x

3

2

3

4

26.

(

)

(

)

∫

+

−

+

+

dx

x

x

x

x

1

1

3

3

2

3

2

27.

∫

+

dx

x

x

1

2

4

28.

∫

+

−

−

dx

x

x

x

9

6

5

4

2

29.

(

)

∫

−

+

−

dx

x

x

x

x

2

3

2

3

2

4

2

30.

4

3

2

3

1

dx

x

x

x

x

x

− +

+

−

∫

Zad.4. Obliczyć całki funkcji niewymiernych:

31.

∫

−

−

dx

2

1

1

2

x

x

32.

∫

−

dx

1

5

1

7

x

33.

∫

+

+

+

dx

1

1

3

x

x

x

34.

∫

+

+

dx

1

4

x

x

x

35.

∫

+

+

dx

1

1

3

x

x

36.

∫

−

+

dx

1

2

1

2

x

x

37.

∫

−

+

dx

4

1

2

x

x

x

38.

∫

−

+

+

dx

1

3

2

2

x

x

x

39.

∫

−

+

dx

1

2

2

x

x

x

40.

∫

+

−

−

dx

7

4

5

2

x

x

x

41.

∫

+

−

dx

7

4

2

2

x

x

x

42.

∫

−

+

+

dx

1

5

5

3

3

2

x

x

x

Zad.5. Obliczyć całki funkcji trygonometrycznych:

43.

∫

+

−

dx

5

sin

4

cos

3

1

x

x

44.

1

dx

cos

sin

x

x

+

∫

45.

5

4

cos

sin

dx

x

x

∫

46.

5

cos

dx

x

∫

47.

cos 3 sin 4

dx

x

x

∫

48.

∫

xdx

xcos

sin

2

4