ZASTOSOWANIE CAŁEK PODWÓJNYCH W GEOMETRII

1. Pole obszaru regularnego
Jeśli funkcja f jest stale równa 1 w obszarze regularnym to

-pole obszaru D.

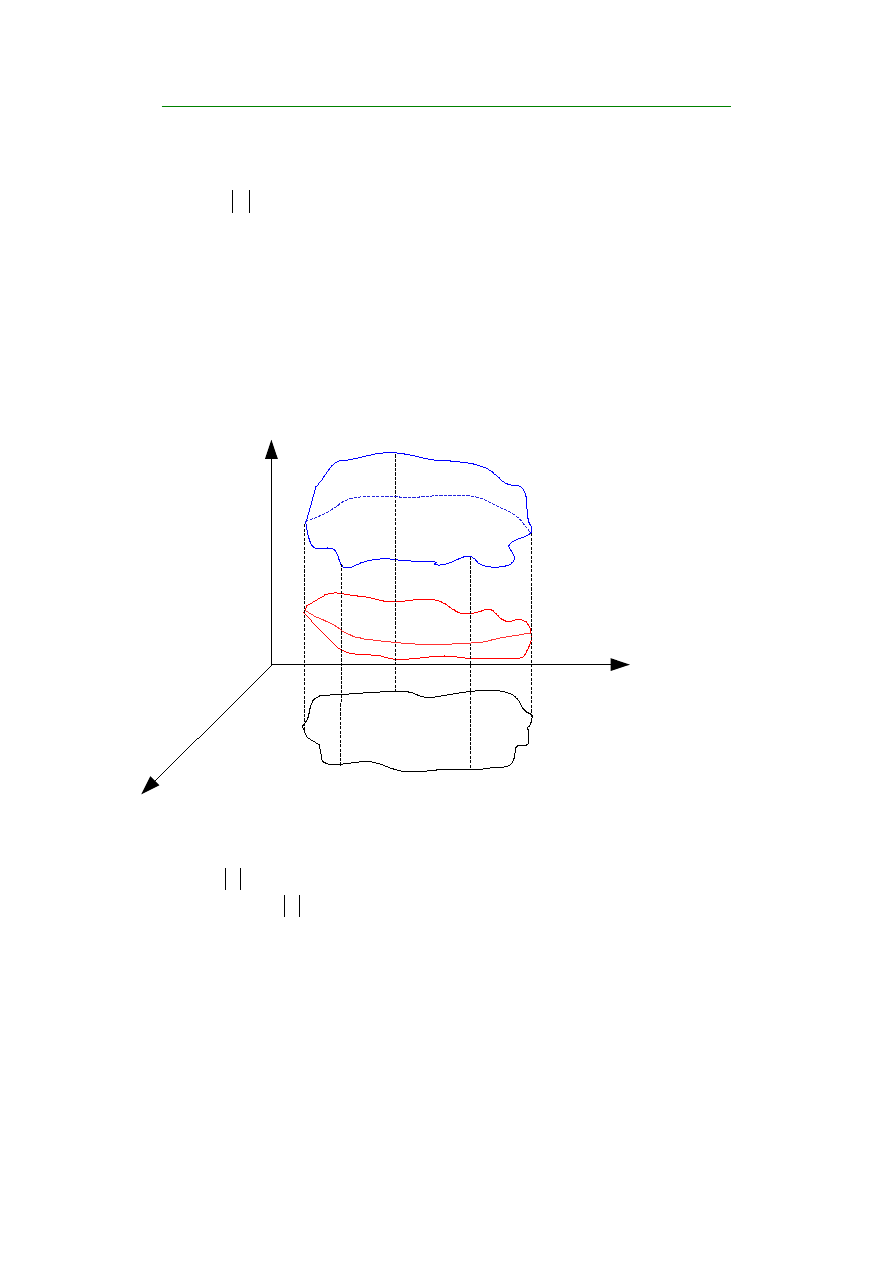
2. Objętość bryły

Niech D - obszar regularny
-funkcje ciagłe na obszarze D

Rozważmy bryłę ograniczoną wykresami funkcji:

3. Wtedy objętość tej bryły jest całką podwójną z różnicy funkcji f i g w obszarze D,

3. Pole płata powierzchniowego
Niech D – obszar regularny w

S -zbiór punktów wykresu funkcji f ,

zbiór ten nazywamy

płatem powierzchniowym.

1

y

x

z

D

z=f(x,y)

y=g(x,y)

V

,

2

R



D

.

oraz

g

f



   





.

,

,







D

dxdy

y

x

g

y

x

f

V

,

)

(

1

D

C

f







   





D

y

x

y

x

f

z

z

y

x

S







,

;

,

:

,

,

.

)

,

(

dla

D

y

x



)

,

(

)

,

(

y

x

g

z

y

x

f

z





D

dxdy

D





,

2

R



 

g

f

D

C

g

f

,

tzn

,

,



V

,

2

R

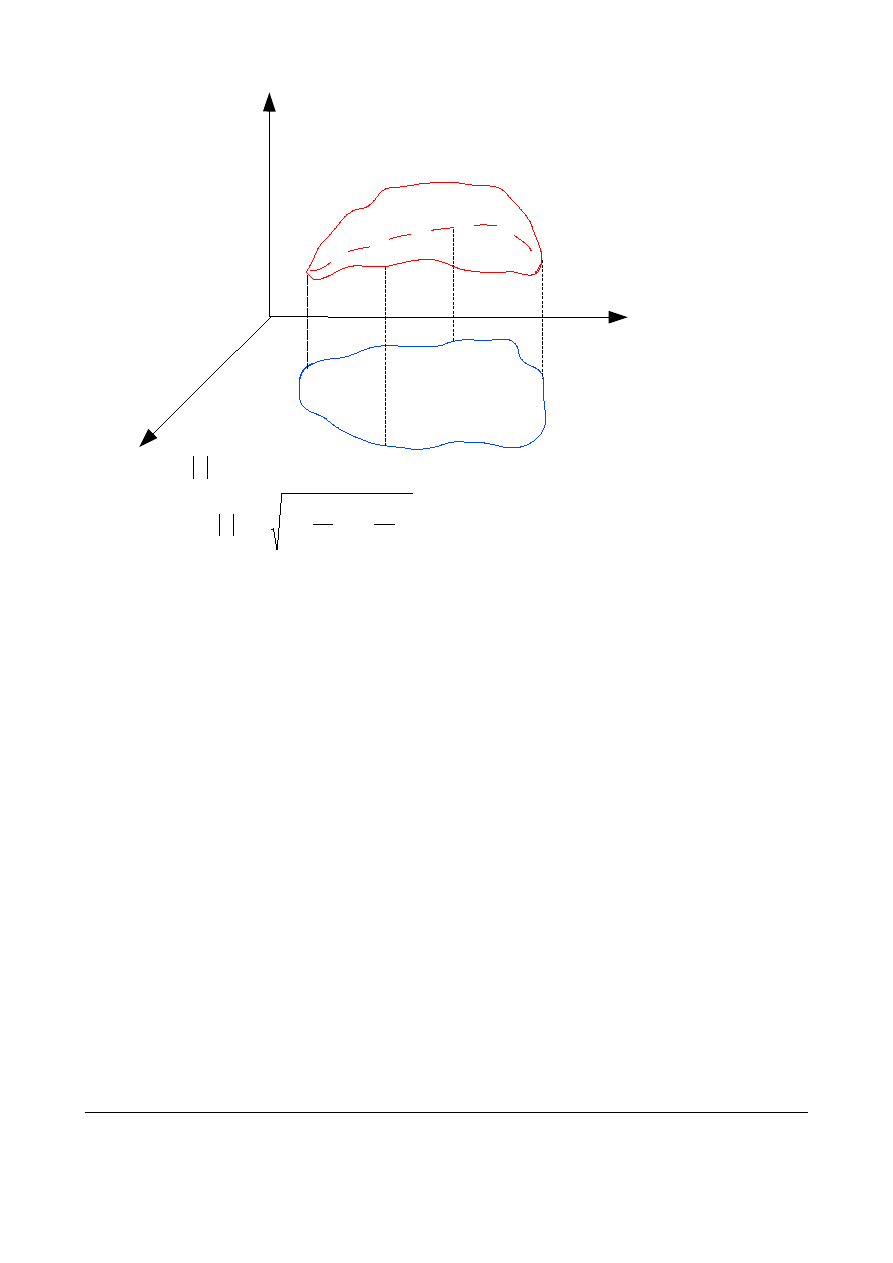
Wtedy pole płata powierzchniowego S wynosi

opracował Marcin Uszko

2

y

x

z

D

S

z=f(x,y)

S

.

1

2

2

dxdy

y

f

x

f

S

D







































