Automatyka i Robotyka –Analiza – Wykład 11 – dr Adam Ćmiel – cmiel@agh.edu.pl
1
Rozszerzenie znaczenia symbolu całki Riemanna
Z definicji całki Riemanna widać, że istotną rolę odgrywa uporządkowanie prostej R ( przy tworzeniu
podziału P). Jeżeli zmienimy uporządkowanie prostej , to sumy całkowe zmieniają znak, bo zmieniają
znak różnice x
k
-x
k-1
. Przyjmiemy więc dla a<b
∫
∫
−
=
b
a
df
a
b
dx
x
f
dx
x
f
)
(
)
(
.
Stąd w szczególności
0
)
(
=
∫
a
a
dx
x
f
.
Całkowanie a różniczkowanie
Tw
. Niech
f
∈ℜ[a,b] i niech
b
x
a
≤
≤
. Wówczas
a) funkcja
∫
=
x
a
dt
t
f
x
F
)
(
)
(
jest ciągła na [a,b].
b) jeśli f jest ciągła w punkcie x
0
∈[a,b] , to F jest różniczkowalna w punkcie
0
x
i F
’
(x
0
)=f(x
0
).
Dow
. a)
Niech x
∈[a,b]. Wybieramy dowolne h takie, że x+h∈[a,b]
∫
∫
∫
∫
∫
∫
+
+
+
=
−
+
=
−
=
−
+
h
x
x
x
a
h
x
x
x
a
x
a
h
x
a
dt
t
f
dt
t
f
dt
t
f
dt
t
f
dt
t
f
dt
t
f
x
F
h
x
F
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
(
∗)
⇒
∈
]
,
[ b
a
R
f
f jest ograniczona na [a,b]
M
t
f
b
a
t
M
≤
∀
∃
⇔
∈
)
(
]
,
[
(
∗∗)
Z (
∗) i (∗∗)
|
∫
+
+
≤
≤
−
+
}
,
max{
}
,
min{
|
|
|
)
(
|
|
)
(
)
(
h
x
x
h
x
x
h
M
dt
t
f
x
F
h
x
F
⇒ ciągłość
Dow
. b)
Niech x
0
∈[a,b] - punkt ciągłości funkcji f. Wybieramy dowolne h takie, że
x
0
+h
∈[a,b]. Wówczas
(
)
=
−
=
−
=
−
−
+
∫
∫
+
+
h
x
x
h
x
x
dt
x
f
t
f
h
x
f
dt
t
f
h
x
f
h
x
F
h
x
F
0
0
0
0
)
(
)
(
1
)
(
)
(
1
)
(
)
(
)
(
0
0
0
0
0
(
)
∫
∫
+
+
+
−
≤
−
=
}
,
max{
}
,
min{
0
0
0
0
0
0
0
0
)
(
)
(
1
)
(
)
(
1
h
x
x
h
x
x
h
x
x
dt
x
f
t
f
h
dt
x
f
t
f
h
f jest ciągła w punkcie
0
x
ε
δ
δ
ε
≤
−
⇒
≤
−
∀
∃
∀
⇒
∈
>
>
)
(
)
(
0
0
]
,
[
0
0
x
f
t
f
x
t
b
a
t
. Stąd
ε
ε
δ
=
≤
−
−
+
⇒
<
h
h
x
f
h
x
F
h
x
F
h
1
)
(
)
(
)
(
|
|
0
0
0
, co implikuje
)
(
)
(
)
(
lim
)
(
0
0
0
0
0
x
f
h
x
F
h
x
F
x
F
h
=
−
+
=
′
→
Wniosek.
Jeżeli f
∈C[a,b], to
∫
=
x
a
dt
t
f
x
F
)
(
)
(
jest funkcją pierwotną funkcji f na [a,b] i F(a)=0.
Tw
. (Newtona-Leibniza) Jeżeli f
∈ℜ[a,b] i istnieje funkcja F różniczkowalna na [a,b] taka, że
)
(
)
(
]
,
[
x
f
x
F
b
a
x
=
′
∀
∈
, to
)
(
)
(
)
(
a
F
b
F
dx
x
f
b
a
−
=
∫
.

Automatyka i Robotyka –Analiza – Wykład 11 – dr Adam Ćmiel – cmiel@agh.edu.pl
2
Dow
. Dla podziału
}
,...,
,
{
1
0
n
x
x
x
=
P
wybieramy punkty pośrednie
]
,
[
1
k
k
k
x
x
−
∈
ξ
tak, aby
)
)(
(
)
(
)
(
1
1
−
−
−
=
−
k
k
k
k
k
x
x
f
x
F
x
F
ξ
(z tw. Lagrange’a dla F wynika, że jest to możliwe).
Wówczas
)
(
)
(
))
(
)
(
(
)
)(
(
1
1
1
1
a
F
b
F
x
F
x
F
x
x
f
k
n
k
k
k
n
k
k
k
−
=
−
=
−
−
=
−
=
∑
∑
ξ
(wszystkie wyrazy sumy z wyjątkiem F(a) i F(b) ulegną redukcji).
Wobec założonej całkowalności f , jeżeli
0
→
P
d
, to
∫
∑
→
−
=
−
b
a
n
k
k
k
k
dx
x
f
x
x
f
)
(
)
)(
(
1
1
ξ
.
Stąd
)
(
)
(
)
(
a
F
b
F
dx
x
f
b
a
−
=
∫
.
Tw
. (całkowe o wartości średniej)
Jeżeli funkcja f jest ciągła na [a,b],
⇒
∃ c∈(a,b): )
)(
(
)
(
a
b
c
f
dx
x
f
b
a
−
=
∫
Dow
.
∫
=
x
a
dt
t
f
x
F
)
(
)
(
jest funkcją pierwotną funkcji f na [a,b]. Wobec tego
)
(x
F
- różniczkowalna
na [a,b], czyli również ciągła na [a,b], czyli F spełnia zał. tw. Lagrange’a , więc
∃c∈(a,b):
F(b)-F(a)=F
’
(c)(b-a)=f(c) (b-a).
Jeżeli f
∈ℜ[a,b] to liczbę
a
b
dx
x
f
b
a
−
∫
=
)
(
µ
nazywamy wartością średnią funkcji f na przedziale [a,b].
Jeżeli f jest ciągła, to
∃c∈(a,b) :
)
(c
f
=
µ
Tw
. (o
całkowaniu przez części dla całki oznaczonej)
Jeżeli
• f i g są różniczkowalne na [a,b],
•
g
f
′
′,
∈ℜ[a,b]
to
[
]
∫
∫
∫
′
−
−
=
′
−
=
′
b
a
b
a
b
a
b
a
dx
x
g
x
f
a
g
a
f
b
g
b
f
dx
x
g
x
f
x
g
x
f
dx
x
g
x
f
)
(
)
(
)}
(
)
(
)
(
)
(
{
)
(
)
(
)
(
)
(
)
(
)
(
Dowód
. Łatwo zauważyć, że funkcje f g’ i f ’g
∈ℜ[a,b]. Ze woru (fg)’= fg’ + f ’g i tw. Newtona –
Leibniza mamy
)
(
)
(
)
(
)
(
)
(
a
g
a
f
b
g
b
f
dx
g
f
g
f
b
a
−
=
′
+
′
∫
, stąd teza.
Tw
. (o
całkowaniu przez podstawienie całki oznaczonej)
a)
∫
∫
′
=
⇒
}
,
∈
=
=
)
=
∈
β
α
β
α
ϕ
ϕ
β
α
ϕ
β
β
ϕ
α
ϕ
ϕ
dt
t
t
f
dx
x
f
t
t
x
x
f
a
C
b
a
)
(
))
(
(
)
(
]
[
)
(
:
{
na
cg.
jest
(
,
)
(
1
]
,
[
b)
∫
∫
=
′
⇒
}
∈
=
=
=
∈
B
A
b
a
b
a
dy
y
g
dx
x
h
x
h
g
x
x
h
y
y
g
B
b
h
A
a
h
C
h
)
(
)
(
))
(
(
]
b
a,
[
)
(
:
{
na
cg.
jest
)
(
,
)
(
1
]
,
[
Dow.
(a).Niech F będzie funkcją pierwotną funkcji f na [a,b]. Wówczas
))
(
( t
F
ϕ
jest funkcją
pierwotną funkcji
)
(
))
(
(
t
t
f
ϕ
ϕ
′
na [
α
,
β
]. (z tw. o różniczkowaniu funkcji złożonej). Stąd
∫
∫
=
−
=
−
=
′
b
a
dx
x
f
a
F
b
F
F
F
dt
t
t
f
)
(
)
(
)
(
))
(
(
))
(
(
)
(
))
(
(
α
ϕ
β
ϕ
ϕ
ϕ
β
α
Automatyka i Robotyka –Analiza – Wykład 11 – dr Adam Ćmiel – cmiel@agh.edu.pl
3
Zastosowanie
całki Riemanna
Zastosowania geometryczne całek
I.
Pole trapezu krzywoliniowego
{
:
)
,
( y
x
b
x
a
≤
≤
)
(
)
(
2
1
x
f
y
x
f
≤
≤
,
2
1
f
f
≤
na [a,b],
2
1
, f
f
- ciągłe na [a,b]
(
)
∫
−
=
b
a
dx
x
f
x
f
P
)
(
)
(
1
2
II.
Długość łuku krzywej
Niech
(
)
3
)
(
),
(
),
(
)
(
]
[
:
R
t
z
t
y
t
x
t
r
t
r
∈
=
→
,
∈
r
r
β
α
będzie funkcją wektorową określoną na
]
[
β
α
,
.
W daną krzywą wpisujemy łamaną i bierzemy kres górny długości łamanych. Jeżeli będzie on
skończony, to krzywą nazywamy prostowalną.
Tw
. Jeżeli
1
]
,
[
β
α
C
r
∈
r
to krzywa
)
(
{
:
t
r
K
r
]}
,
[
β
α
∈
t
jest prostowalna (ma długość) i
(
) (
) (
)
∫
′
+
′
+
′
=
β
α
dt
t
z
t
y
t
x
l
2
2
2
)
(
)
(
)
(
Szkic dowodu
.
Długość łamanej=
∑
=
−
−
n
k
k
k
r
r
1
1
|
|
r
r
=
∑
=
−
−
−
−
+
−
+
−
n
k
k
k
k
k
k
k
t
z
t
z
t
y
t
y
t
x
t
x
1
2
1
2
1
2
1
))
(
)
(
(
))
(
)
(
(
))
(
)
(
(
=
={ 3 razy tw. Lagrange’a}=
)
(
)]
(
'
[
)]
(
'
[
)]
(
'
[
1
1
2
2
2
−
=
−
+
+
∑
k
k
n
k
k
k
k
t
t
z
y
x
ψ
η
ξ
={przejście graniczne}
⇒
teza.
Przypadek szczególny
: Jeżeli K={(x, f(x) : x
∈ [a,b] , f∈
1
]
,
[ b
a
C
, to
∫
+
=
b
a
dx
x
f
l
2
'
))
(
(
1
III.
Objętość bryły
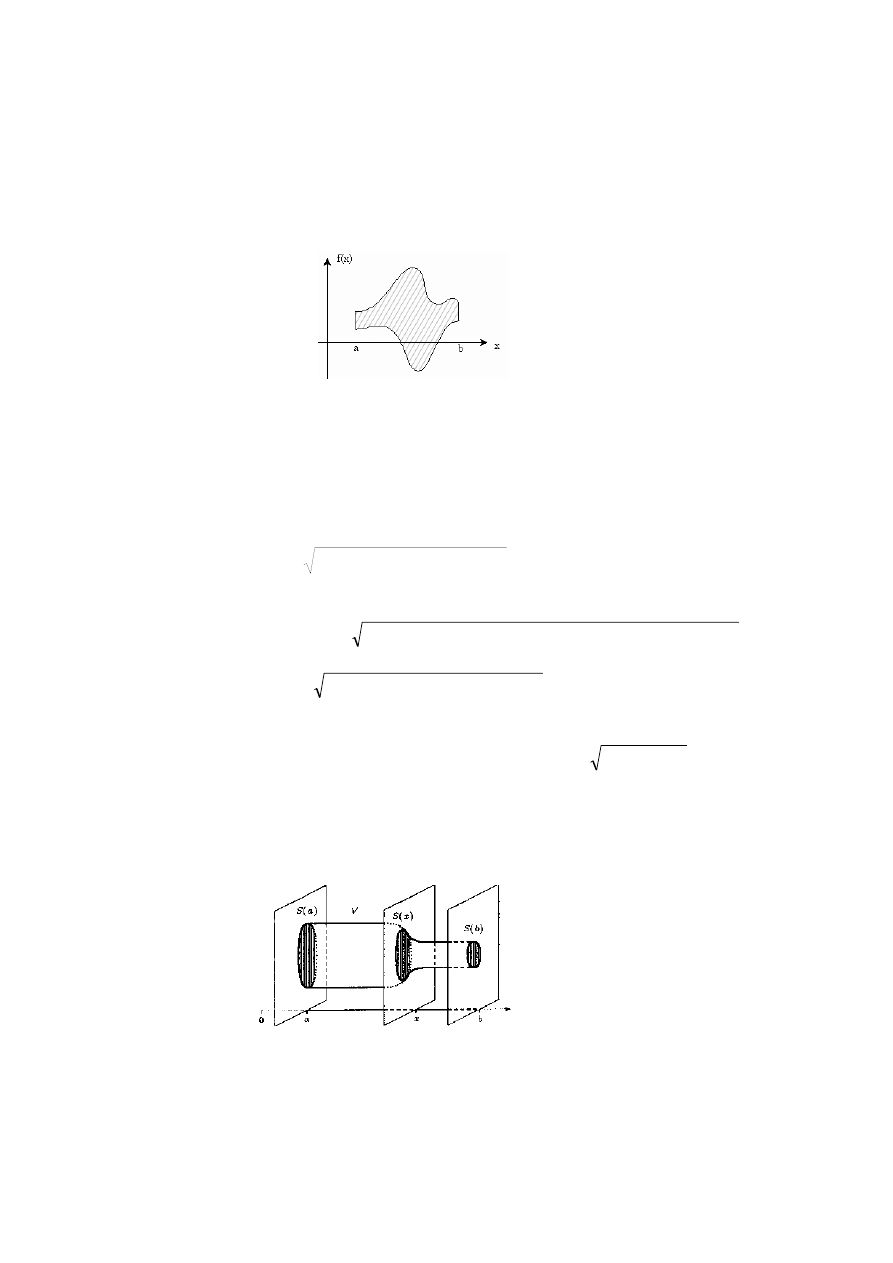
Niech S(x),
b
x
a
≤
≤
oznacza pole przekroju bryły V płaszczyzna prostopadłą do osi OX w
punkcie x i niech funkcja S(x) będzie ciągła na przedziale [a,b].
Wtedy
∫
=
b
a
dx
x
S
V
)
(
W szczególności dla bryły obrotowej:
∫
=
b
a
dx
x
f
V
)
(
2
π

Automatyka i Robotyka –Analiza – Wykład 11 – dr Adam Ćmiel – cmiel@agh.edu.pl
4
IV.
Pole powierzchni bryły obrotowej
Pole powierzchni bryły obrotowej aproksymujemy sumą pól powierzchni stożków ściętych
zakreślonych przez łamaną wpisaną w daną krzywą.
(
)
∫
′
+
=
b
a
dx
x
f
x
f
P
2
)
(
1
|
)
(
|
2
π
Zastosowania fizyczne całek
V. Droga przebyta w ruchu zmiennym
Niech punkt materialny porusza się po płaszczyźnie lub w przestrzeni ze zmienną prędkością
))
(
),
(
),
(
(
)
(
t
v
t
v
t
v
t
v
z
y
x
=
r
. Oznaczmy
)
(
)
(
)
(
|
)
(
|
)
(
2
2
2
t
v
t
v
t
v
t
v
t
v
z
y
x
+
+
=
= r
.
Droga przebyta przez punkt w przedziale czasowym [t
1
,t
2
] wyraża się wzorem
∫
=
2
1
)
(
t
t
dt
t
v
L
a przemieszczenie
]
)
(
,
)
(
,
)
(
[
)
(
2
1
2
1
2
1
2
1
∫
∫
∫
∫
=
=
t
t
t
t
z
t
t
y
x
t
t
dt
t
v
dt
t
v
dt
t
v
dt
t
v
r
r
r
VI. Praca wykonana przez zmienną siłę działającą wzdłuż prostej
Załóżmy, że równolegle do osi OX działa zmienna siła
|
)
(
|
)
(
x
F
x
F
r
=
.
Praca wykonana przez tę siłę od punktu x=a do punktu x=b wyraża się wzorem
∫
=
b
a
dx
x
F
W
)
(
.
VII. Masa odcinka materialnego
Załóżmy że odcinek [a,b] obdarzony jest masą o gęstości liniowej
ρ
(x) . Wówczas jego masa wyraża
się wzorem
∫
=
b
a
dx
x
m
)
(
ρ
.
Wyszukiwarka
Podobne podstrony:
5 5 Zastosowania całek oznaczonych (2)
zastosowania calek
zastosowanie calek wielokrotnych z podpowiedziami
Arkusz nr 9 (zastosowania calek Nieznany (2)
09Calki wielokrotne 5. Zastosowanie całek podwójnych w geometrii
AM23 w12 Zastosowania całek
EN w11 zastos naped
05 Zastosowanie całek podwójnych w geometrii
Zastosowania całek teo
Podstawy zastosowania gradientowego pola magnetycznego w rehabilitacji
zastosowanie całek potrójnych
7 - Zastosowania geometryczne całek, Analiza matematyczna
Pola magnetyczne niskiej częstotliwości – zastosowanie w praktyce
9 Zastosowanie norm żywienia i wyżywienia w pracy dietetyka
więcej podobnych podstron