ŚCISKANIE SŁUPÓW PROSTYCH

1

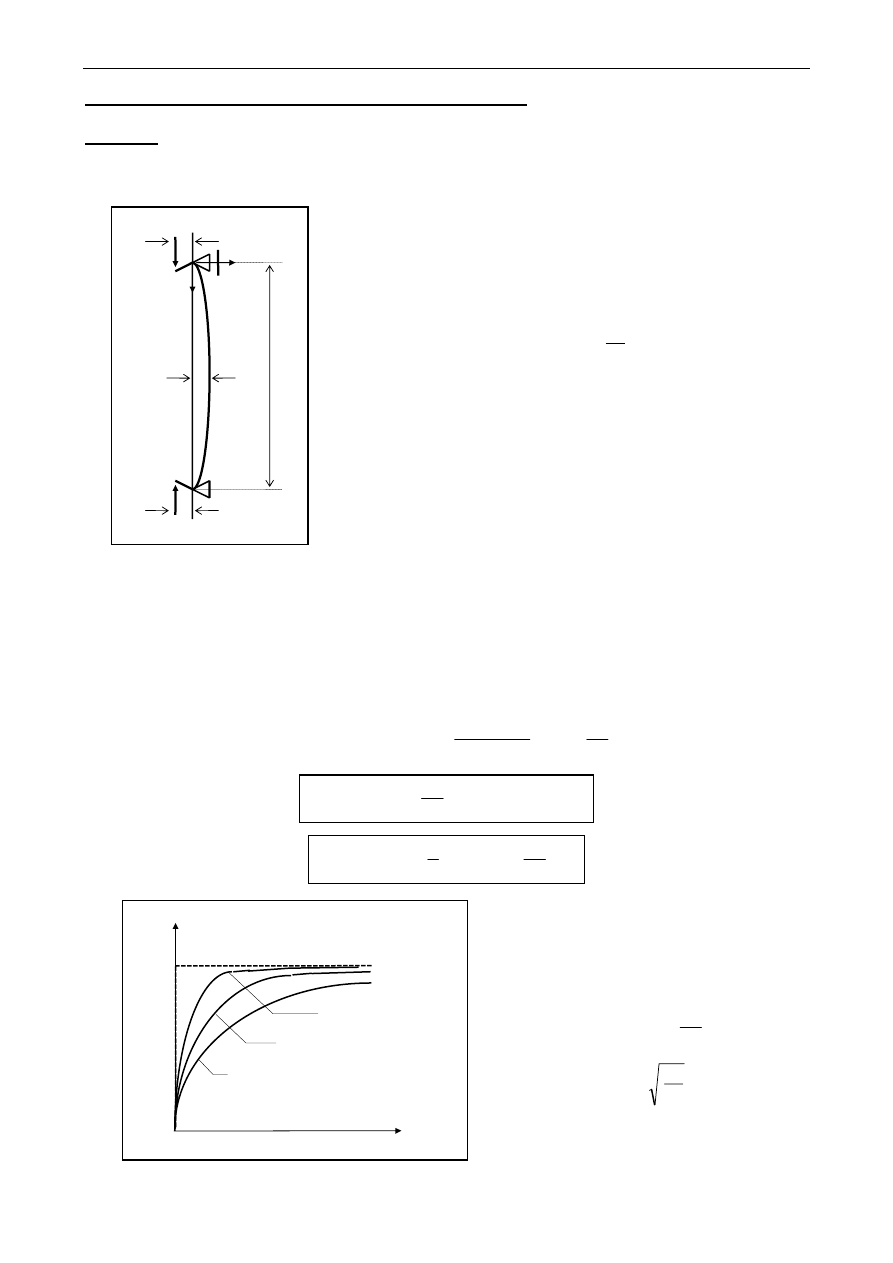
1. ANALIZA SŁUPA MIMOŚRODOWO ŚCISKANEGO

ZADANIE: przeanalizować zachowanie słupa wolnopodpartego mimośrodowo ściskanego siłą P
(obciążenie konserwatywne). Mimośród e mierzony jest od środka ciężkości przekroju do linii
działania siły P.

( )

( )

[

]

M x

P e w x

=

+

( )

( )

( )

[

]

E I w

x

M x

P e w x

′′

= −

= −

+

k

P

E I

def

2

=

( )

( )

′′

+

= −

w

x

k w x

k e

2

2

( )

( )

( )

w x

w

x

w

x

oRJ

sRN

=

+

( )

w

x

C

kx C

kx

oRJ

=

+

1

2

sin

cos

( )

w

x

e

sRN

= −

( )

w x

C

kx C

kx e

=

+

−

1

2

sin

cos

∗

warunki brzegowe dla wyznaczenia stałych całkowania C

1

i C

2

(

)

(

)

w x

w x L

=

=

=

=

0

0

0

;

C

e

C

e

k L

k L

e

k L

2

1

1

2

=

=

−

=

;

cos

sin

tan

( )

w x

e

k L

k x

k x

=

+

−









tan

sin

cos

2

1

w

w x

L

e

k L

max

sec

=

=









=

−









2

2

1

w

e

k L

max

sec

=

−









2

1

k

P

E I

=

e

e

P

P

L

w

x

M,w

e=0

e

3

e

2

e

1

e

3

> e

2

> e

1

w

max

P

P

kr

ŚCISKANIE SŁUPÓW PROSTYCH

2

∗

związek w

max

z siłą P jest nieliniowy, mimo że wykorzystano zlinearyzowane równanie linii

ugięcia (zlinearyzowany wzór na krzywiznę), jak również liniowy związek fizyczny (w oparciu o
niego otrzymano równanie linii ugięcia). Jest to wynikiem „sprzężenia” momentu zginającego z
ugięciami (moment zginający nie da się określić bez znajomości ugięć). Mówiąc inaczej - jest to
wynik odstępstwa od zasady zesztywnienia (mówi ona, że wpływ przemieszczeń na wielkości
sił przekrojowych jest pomijalny)

∗

ugięcie rośnie nieograniczenie, gdy siła zmierza do pewnej wartości, którą nazwano siłą

krytyczną P

kr

.

w

k L

max

cos

→ ∞ ⇔

→

2

0

k L

n

n

2

2

1 3 5

=

=

π

, , ....

P n

E I

L

=

2

2

2

π

P

E I

L

kr

= π

2

2

∗

jeżeli mimośród e=0, ugięcie w

max

wynosi:

dla skończonej i dodatniej wartości

k L

czyli

k L

w

sec

;

max

2

1

2

2

0

−









<

=

π

dla

kL

czyli P

P

w

kr

2

2

=

=

π

;

max

jest nieokreślone i może przyjmować dowolną wartość

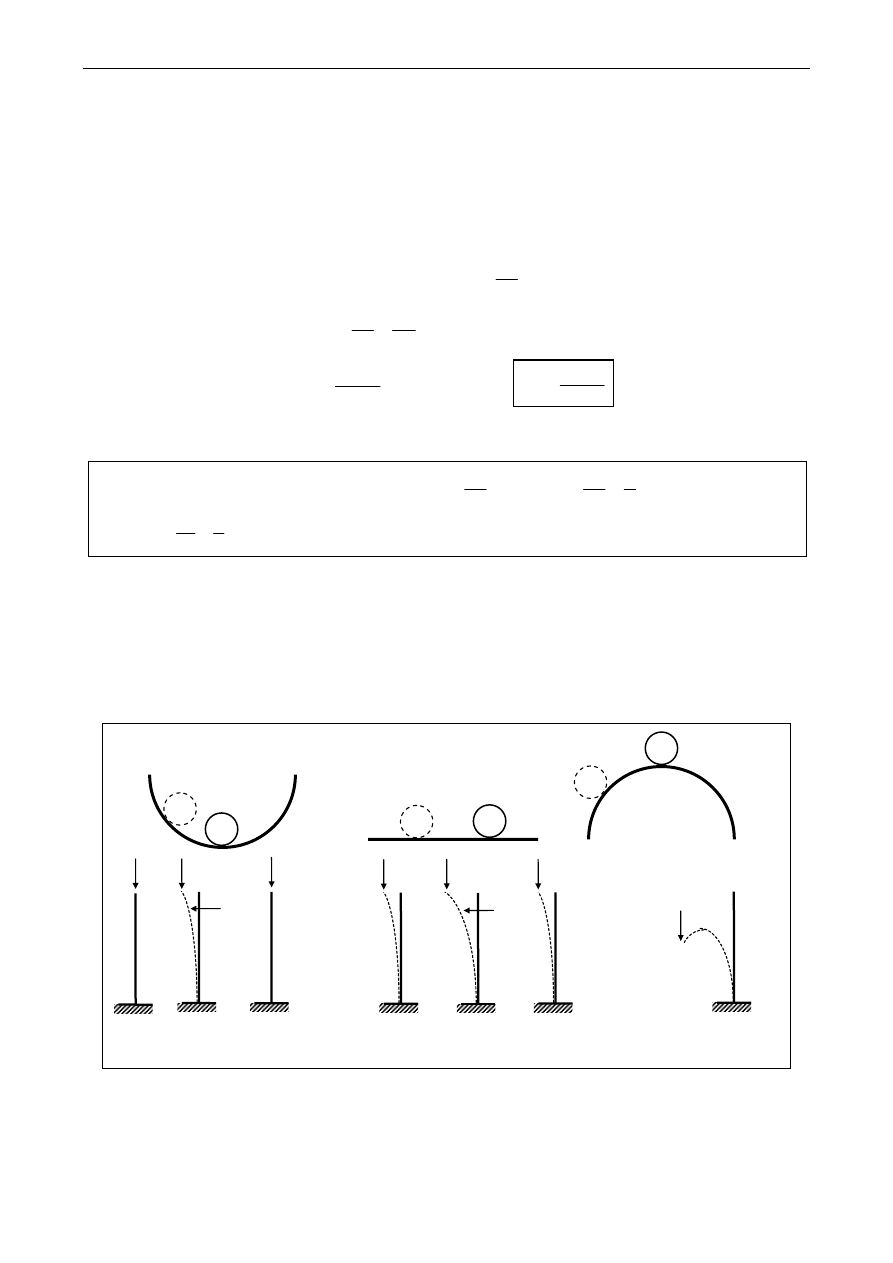
Tak długo, jak P<P

kr

pręt zachowuje się w sposób „stateczny”, tzn. znajduje się w stanie

początkowej równowagi prostoliniowej. Wówczas, gdy siła osiągnie wartość krytyczną P

kr

pręt

traci stateczność (ulega wyboczeniu),

a jego ugięcia mogą być dowolnie duże.

Wyboczenie

jest to zatem utrata przez ściskany pręt stanu równowagi statecznej na rzecz

równowagi obojętnej lub niestatecznej

.

P < P

kr

P > P

kr

równowaga

stateczna

P

≅

P

kr

równowaga

obojętna

równowaga

niestateczna

ŚCISKANIE SŁUPÓW PROSTYCH

3

1.1. Naprężenie w słupie z odstępstwem od zasady zesztywnienia

M

P e

k L

max

sec

=

2

σ

max

max

max

sec

= −

−

=

+





















P

A

M

I

z

P

A

A e

W

L

P

E I

1

2

( I człon opisuje osiowe ściskanie pręta, zaś drugi - zginanie słupa )

σ

max

sec

=

+





















<

P

A

A e

W

L

r

P

E A

R

1

2

∗

naprężenie maksymalne przy wykorzystaniu zasady zesztywnienia (postępowanie

analogiczne, jak w przypadku mimośrodowego rozciągania)

σ

max

max

max

max

= −

−

= −

−

=

+









<

P

A

M

I

z

P

A

P e

I

z

P

A

A e

W

R

1

∗

Przykład liczbowy

Obliczyć nośność pręta ściskanego P, wykonanego z dwuteownika 120, o długości L=5 m.

I

m

x

=

×

−

328 10

8

4

A

m

=

×

−

14 2 10

4

2

.

E

GPa

=

210

R

MPa

=

200

e

m

=

0 05

.

Rozwiązanie:

∗

bez zasady zesztywnienia (teoria II rzędu)

P

kN

II

=

912

.

∗

z zasadą

zesztywnienia

P

kN

I

=

123 5

.

∆

P = 26 %

2. SIŁA KRYTYCZNA DLA SŁUPA

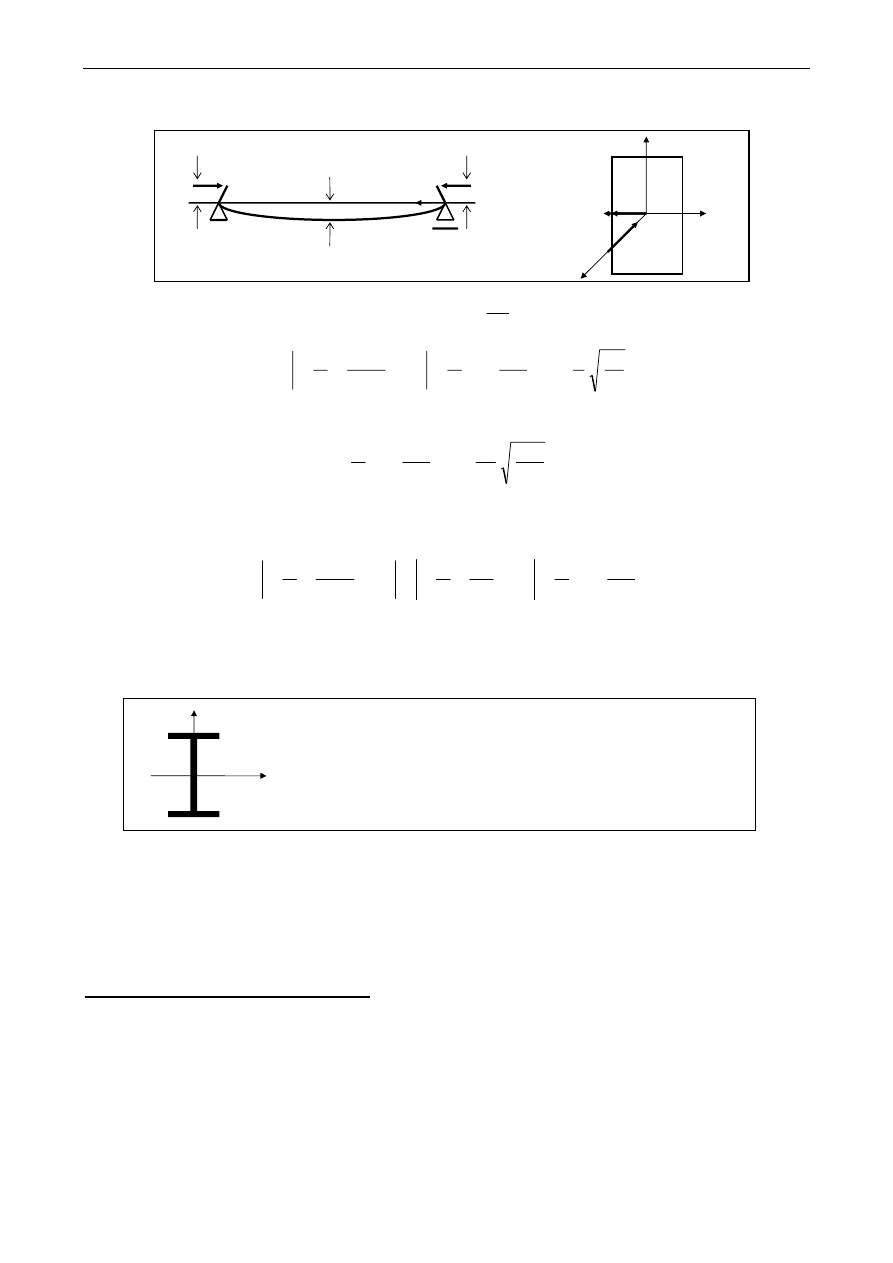
2.1. Zakres liniowo sprężysty

∗

analizowany jest tzw. słup idealny, tzn. idealnie prosty i obciążony centralnie przyłożoną siłą

ściskającą P

∗

materiał słupa jest liniowo sprężysty (materiał Hooke’a)

x

y

e

e

P

P

w

x

x

y

z

P

M

ŚCISKANIE SŁUPÓW PROSTYCH

4

∗

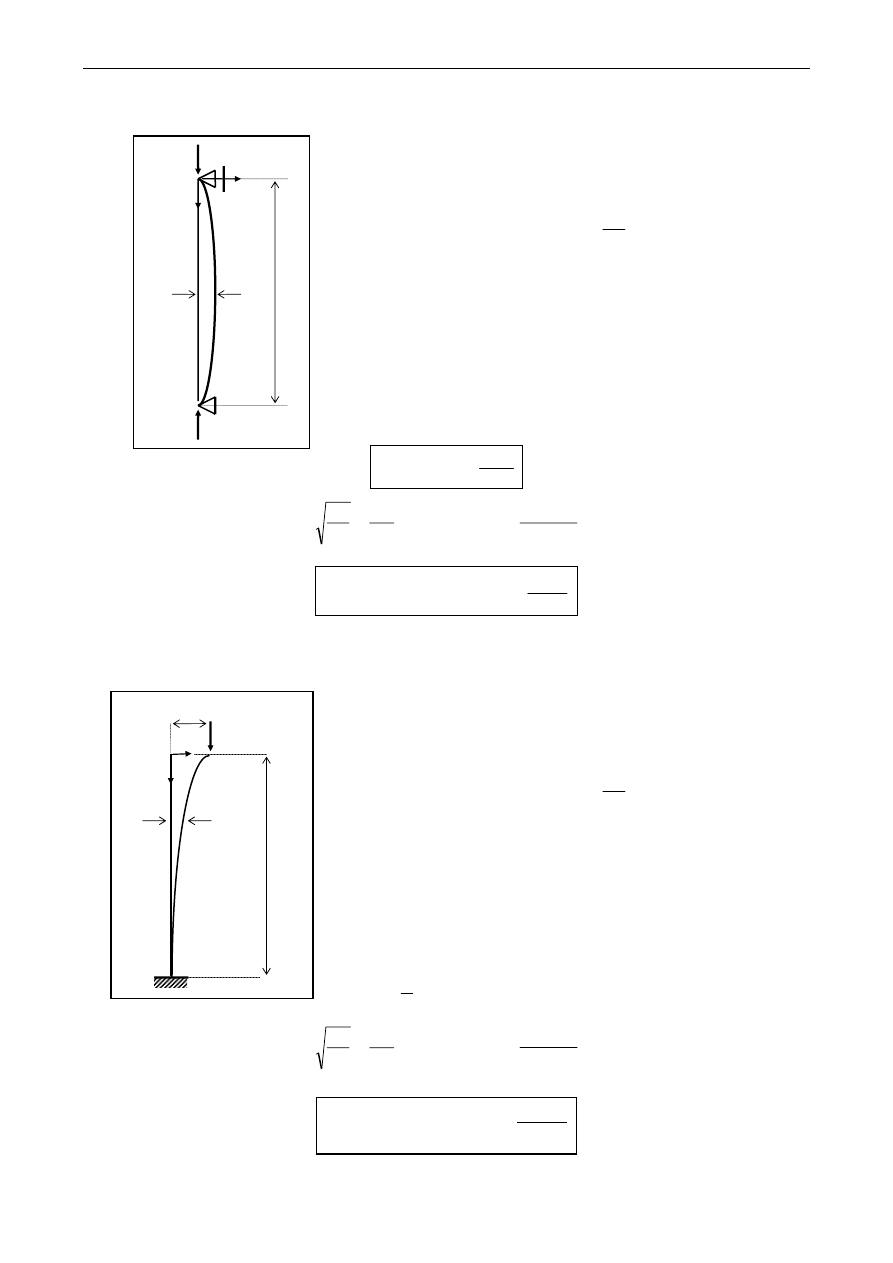
pręt swobodnie podparty

( )

( )

M x

P w x

kr

=

( )

( )

( )

E I w

x

M x

P w x

kr

′′

= −

= −

k

P

E I

def

kr

2

=

( )

( )

′′

+

=

w

x

k w x

2

0

( )

w x

A

kx B

kx

=

+

sin

cos

(

)

w x

B

=

=

⇒

=

0

0

0

(

)

w x L

A

k L

=

=

⇒

=

0

0

sin

k L n

n

=

=

π

;

, , .....

1 2 3

( )

w x

A

n x

L

=

sin

π

P

EI

n

L

P

n

EI

L

kr

kr

=

⇒

=

π

π

2

2

2

(

)

minP

P

n

P

EI

L

kr

kr

E

=

=

=

=

1

2

2

π

∗

pręt wspornikowy

( )

( )

[

]

M x

P

f w x

kr

= −

−

( )

( )

E I w

x

M x

′′

= −

k

P

E I

def

kr

2

=

( )

w x

A

kx B

kx f

=

+

+

sin

cos

(

)

w x

f

B

=

=

⇒

=

0

0

(

)

w x L

A

k L f

=

=

⇒

=

+

0

0

sin

(

)

′

=

=

⇒

=

w x L

k A

k L

0

0

cos

k L n

n

=

=

π

2

1 3 5

;

, , .....

( )

P

EI

n

L

P

n

EI

L

kr

kr

=

⇒

=

π

π

2

2

2

2

2

(

)

( )

minP

P

n

P

EI

L

kr

kr

E

=

=

=

=

1

2

2

2

π

P

kr

L

w

x

M,w

f

P

P

L

w

x

M,w

ŚCISKANIE SŁUPÓW PROSTYCH

5

∗

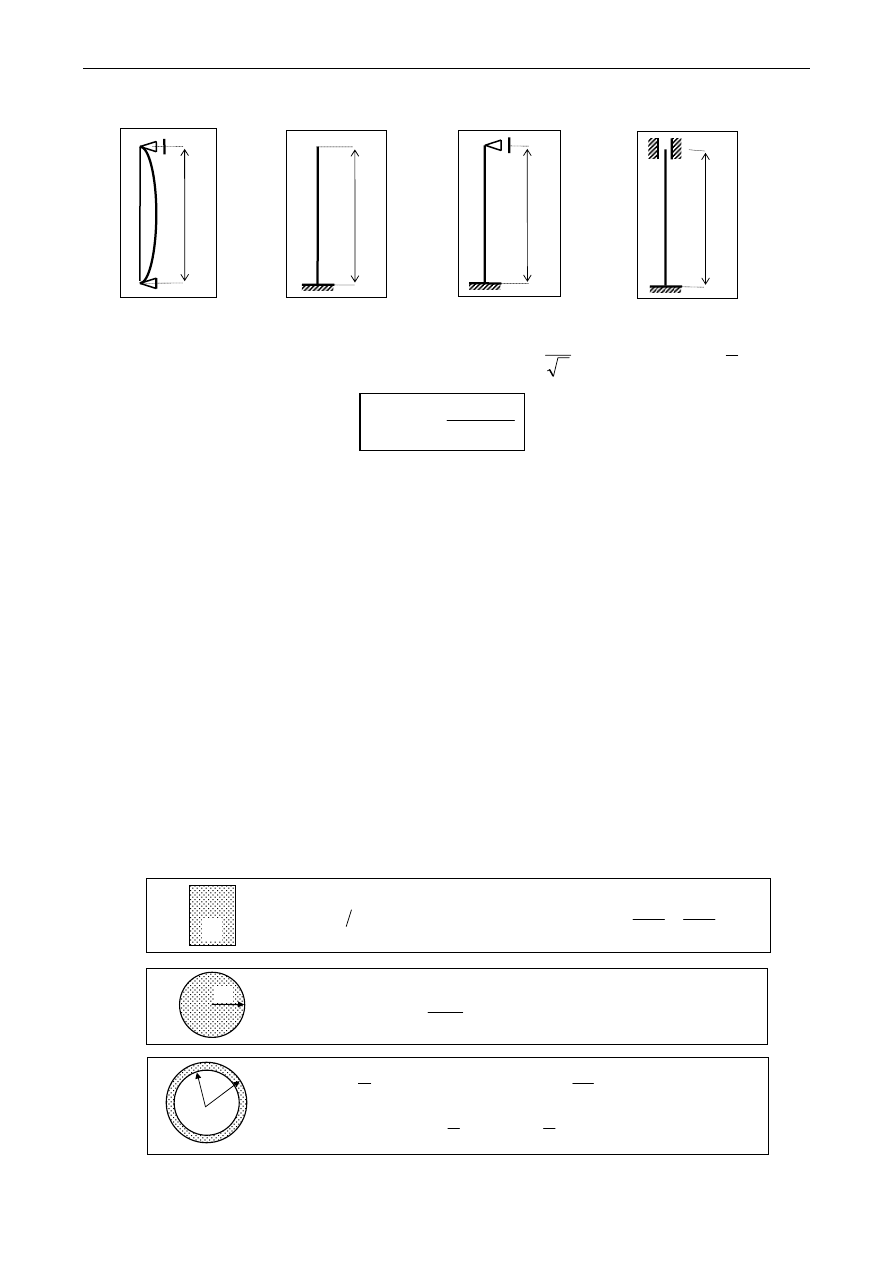
ogólna postać siły krytycznej (siły Eulera 1707-1783)

długości wyboczeniowe L

w

L

w

= L

L

w

= 2 L

L

L

w

≅

1

2

L

L

w

=

1

2

P

P

E I

L

kr

E

w

=

=

π

2

2

min

∗

podstawowe zasady kształtowania słupów

¬

siła krytyczna, jako obciążenie powodujące wyboczenie słupa (z reguły wyboczenie oznacza

utratę przez konstrukcję zdolności do prawidłowej pracy), powinna być jak największa

¬

siła krytyczna jest proporcjonalna do sztywności giętnej słupa E I

min

i odwrotnie proporcjonalna

do długości wyboczeniowej L

w

- tak więc zwiększenie siły P

kr

może nastąpić jedynie w

drodze odpowiedniego ukształtowania przekroju poprzecznego lub/i schematu
statycznego

słupa. Nie zwiększa siły krytycznej zastosowanie materiału o bardzo wysokiej

wytrzymałości !

¬

w przypadku słupów przez odpowiednie ukształtowanie przekroju rozumie się taki dobór

jego geometrii, który z określonej ilości materiału pozwala uzyskać przekrój o
maksymalnej sztywności

, czyli maksymalnym momencie bezwładności. Można to osiągnąć

poprzez rozmieszczenie materiału tak daleko od środka ciężkości przekroju, jak to tylko
możliwe.

Przykład.

Pole przekroju słupa ma wynosić A=50 cm

2

. Porównać siły krytyczne dla słupa o przekroju

prostokątnym, kołowym i rurowym.

h b k

k

=

>

;

1 ; A k b

=

2

; I

h b

A

k

min

=

=

3

2

12

12

A

R

I

R

=

=

π

π

2

4

4

;

; R

cm

=

3 989

.

; I

cm

=

198 944

4

.

(

)

(

)

k

R

r

A

R

r

r

R

r

r k

=

=

−

=

−







=

−

;

π

π

π

2

2

2

2

2

2

2

1

1

(

)

(

)

I

R

r

r

k

=

−

=

−

π

π

4

4

1

4

4

4

4

R

b

h

R

r

L

L

L

L

ŚCISKANIE SŁUPÓW PROSTYCH

6

¬

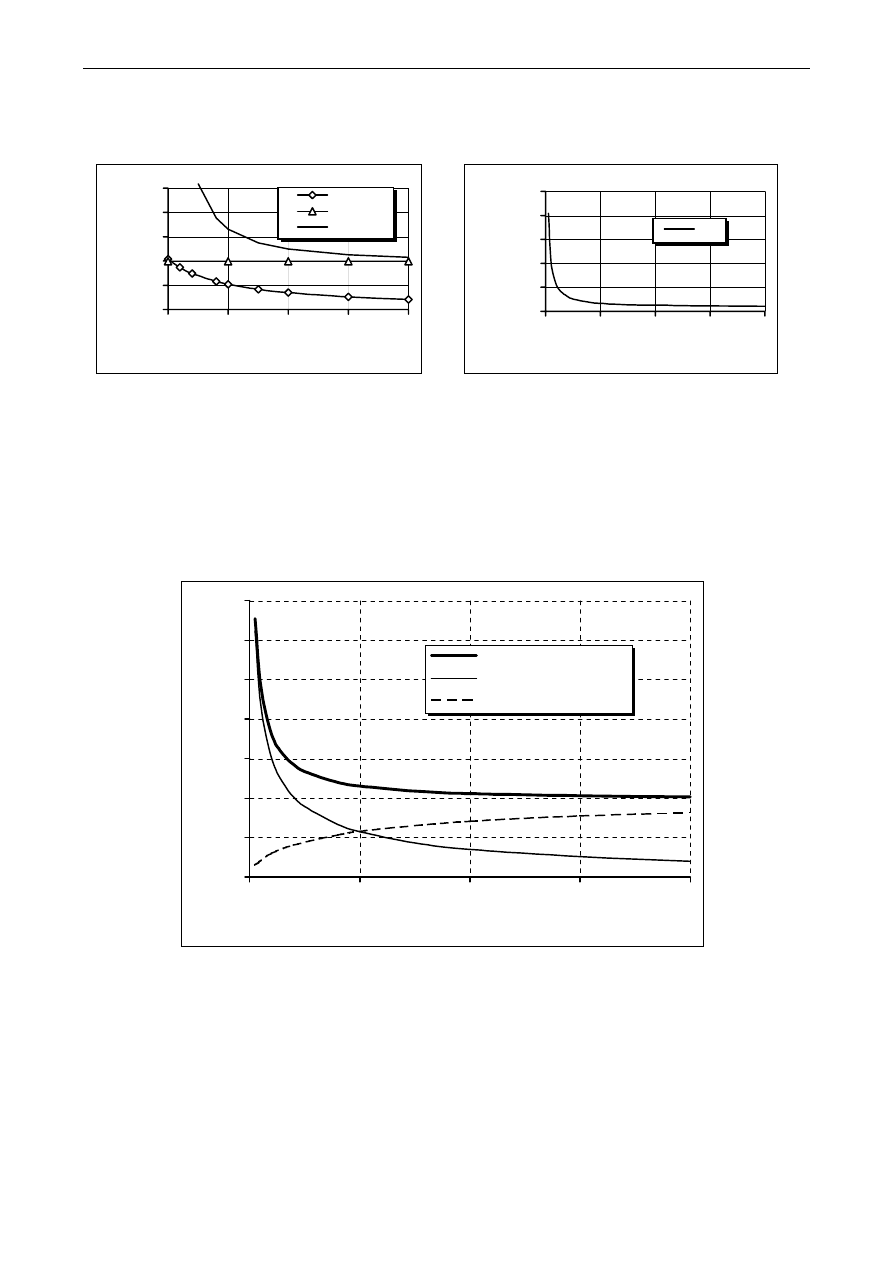
z wykresów widać, że przekrój rury jest zdecydowanie bardziej ekonomiczny niż przekrój

lity

o tym samym polu

0

100

200

300

400

500

1

2

3

4

5

współczynnik wymiarów k

mom. bezw

ładn. [cm

4

]

prostokąt
koło
rura

0

1000

2000

3000

4000

5000

1

2

3

4

5

stosunek średnic k

mom. bezw

ładn. [cm

4

]

rura

¬

czym stosunek promieni ścianki zewn. i wewn. jest mniejszy (a zatem „cieńsza” jest

ścianka rury) tym korzyści płynące z zastosowania przekroju rurowego są większe. Niestety,
jeżeli grubość jest zbyt mała

ścianka rury sama staje się niestateczna i może dojść do

lokalnego wyboczenia

w postaci „pofałdowania” powierzchni rury. Zamiast globalnego

wyboczenia słupa mamy wówczas tzw. lokalną utratę stateczności (zapobiega się jej przez
stosowanie użebrowania).

0

2

4

6

8

10

12

14

1

2

3

4

5

stosunek średnic k = R/r

promienie R, r i grubo

ść

[cm]

promień zewnętrzny R
promień wewnętrzny r
grubość ścianki

ŚCISKANIE SŁUPÓW PROSTYCH

7

3. NAPRĘŻENIE NORMALNE W SŁUPIE

∗

średnie naprężenie ściskające

2

w

2

min

2

2

w

min

2

kr

E

kr

L

i

E

L

A

I

E

A

P

π

=

π

=

=

σ

=

σ

min

w

.

def

smukłość

i

L

=

λ

⇒

σ

π

λ

E

E

=

2

2

∗

zakres liniowo sprężystej ( LS )pracy materiału

σ

λ λ

π

E

H

gr

H

R

E

R

<

⇒

>

=

∗

zakres pozaliniowo sprężystej pracy materiału

R

R

H

E

e

gr

<

<

⇒

<

σ

λ λ

R

R

H

E

e

gr

<

<

⇒

<

σ

λ λ

warunki „brzegowe”

λ

σ

λ λ

σ

=

⇒

=

=

⇒

=

0

R

R

e

gr

H

;

aproksymacja liniowa T-J

σ

λ

σ

π

λ

kr

T J

kr

T J

e

e

H

H

a b

R

R

R

R

E

−

−

= −

⇒

=

−

−

aproksymacja paraboliczna J-O

σ

λ

σ

π

λ

kr

J O

kr

J O

e

e

H

H

A B

R

R

R R

E

−

−

= −

⇒

=

−

−

2

2

2

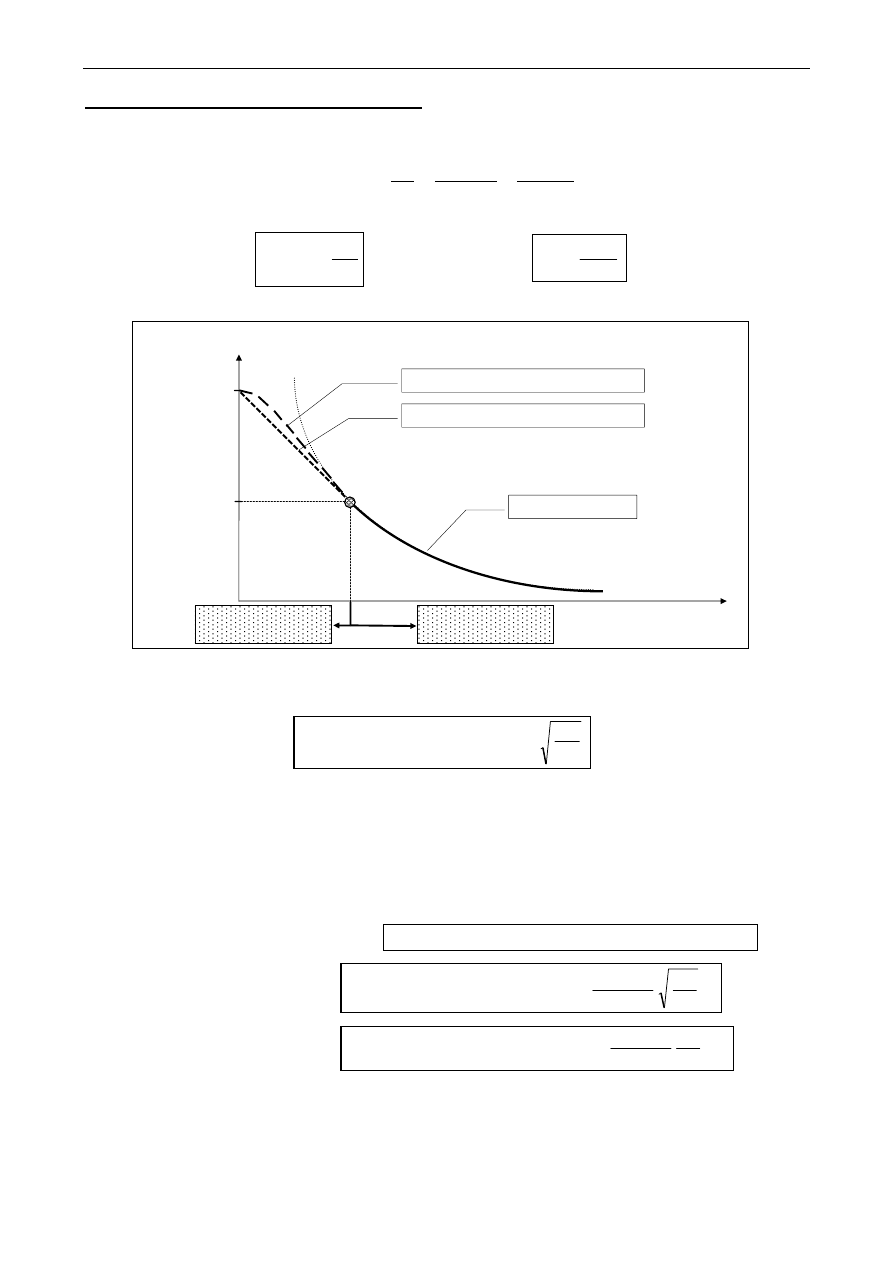
krzywa Eulera

aproks. Johnsona-Ostenfelda

aproks. Tetmajera-Jasińskiego

smukłość

λ

λ

gr

R

H

naprężenie krytyczne

σ

E

wyboczenie poza

zakresem LS

wyboczenie w

zakresie LS

R

e

ŚCISKANIE SŁUPÓW PROSTYCH

8

4. PROJEKTOWANIE PRĘTÓW ŚCISKANYCH

z

warunek projektowania

kr

A

P

σ

≤

=

σ

z

W przypadku dopuszczenia do wyboczenia w zakresie pozaliniowo sprężystym przyjmuje
się, że zamiast granicy plastyczności R

e

należy wziąć wytrzymałość obliczeniową na

rozciąganie R

o

.













λ

<

λ

<

λ

π

−

−

π

=

λ

>

λ

λ

π

=

σ

gr

H

H

o

o

H

gr

2

2

kr

0

dla

E

R

R

R

R

R

E

dla

E

z

założenie

( )

o

kr

R

λ

ϕ

=

σ

( )

o

kr

R

σ

=

λ

ϕ

współczynnik wyboczeniowy

Normy uwzględniają we współczynniku wyboczeniowym takie czynniki jak losowość
charakterystyk materiałowych, losowość obciążenia i odstępstwa od prostoliniowości pręta
ściskanego (tzw. imperfekcje)

( )













λ

<

λ

<

λ

π

−

−

π

=

λ

>

λ

λ

π

=

λ

ϕ

gr

H

o

H

o

H

gr

o

2

2

0

dla

E

R

R

R

R

1

R

E

dla

R

E

4.1. Algorytm obliczeń

1. warunek

wytrzymałościowy

A

R

A

P

o

⇒

≤

2. przyjąć przekrój

A

3

A

×

≅

′

3. obliczyć smukłość pręta

min

w

i

L

=

λ

oraz tzw. smukłość porównawczą

o

p

R

E

15

.

1

π

=

λ

4. z tablic wziąć wartość wsp. wyboczeniowego

ϕ

dla określonego stosunku

p

λ

λ

5. sprawdzić warunek projektowania

( )

o

kr

R

A

P

≤

λ

ϕ

⇒

σ

≤

σ

6. jeżeli warunek projektowania jest spełniony, to proces projektowania jest zakończony. W

przeciwnym wypadku należy zwiększyć przekrój A’ i wrócić do punktu 3.