SPRAWOZDANIE

1. Cel

ć

wiczenia.

Identyfikacja modelu

ż

urawia na

ś

ciennego poprzez pomiar sił obci

ąż

aj

ą

cych

urz

ą

dzenie podczas podnoszenia ładunku oraz teoretyczne oszacowanie jego

działania.

2. Przebieg

ć

wiczenia

Podczas

ć

wiczenia wyznaczyli

ś

my pr

ę

dko

ść

podnoszenie

ż

urawia mierz

ą

c czas,

w którym ładunek przebył jeden metr.

S

1 m

⋅

:=

t

12 s

⋅

:=

vp

S

t

5

m

min

⋅

=

:=

Nast

ę

pnie za pomoc

ą

siłomierza podł

ą

czonego do komputera PC wykonali

ś

my

pomiar przebiegu siły działaj

ą

cej na

ż

uraw podczas podnoszenia. Wyniki pomiaru

przedstawia wykres F(t).

3. Obliczenia

W pierwszym kroku wyznaczamy mas

ę

ładunku z cz

ęś

ci wykresu F(t), gdzie

ładunek ju

ż

si

ę

wyrównowa

ż

ył, mi

ę

dzy 6 a 9,5 sekund

ą

. Siła była mierzona w

kilogramach siły [kG], wi

ę

c jej

ś

rednia arytmetyczna b

ę

dzie równa co do warto

ś

ci

masie w kilogramach [kg].

m

173.6 kg

⋅

:=

Nast

ę

pnie tworzymy wykres siły pochodz

ą

cej od mechanizmu nap

ę

dowego P(t)

odejmuj

ą

c od zmierzonej siły ci

ęż

ar ł

ą

dunku czyli 173,6 kG. Z tego wykresu

mo

ż

emy w prosty sposób wyznaczy

ć

okres drga

ń

licz

ą

c

ś

redni

ą

arytmetyczn

ą

z

21 okresów.

21T

3 s

⋅

:=

21

T

3

21

s

⋅

0.143 s

⋅

=

:=

Obliczamy cz

ę

stotliwo

ść

drga

ń

.

ω

2 π

⋅

T

43.982

1

s

=

:=

f

1

T

7 Hz

⋅

=

:=

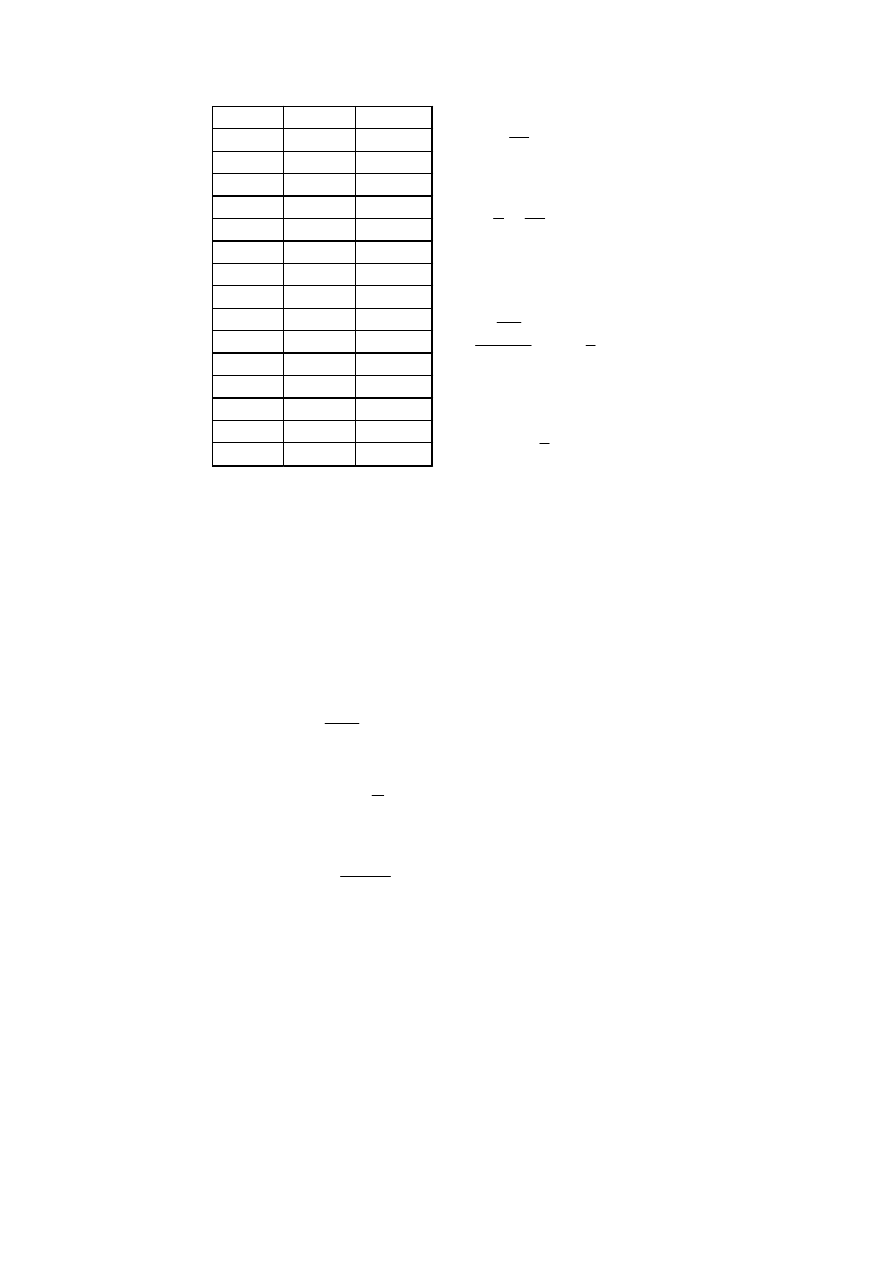
Wyznaczamy logarytmiczny dekrement tłumienia.

n

Xn

h

1

457 1,4593693

2

371 0,4479971

3

348 1,4225977

4

284 0,7814798

5

254 -0,581466

6

276 1,9130533

7

210 -0,132079

8

214 1,2501315

9

179 0,8735354

10

158 -0,951314

11

181 0,9071498

12

159 0,1333374

13

156 2,0137745

14

117 -0,235316

15

121

δ

=

ln

Xn
Xn

=

h T

⋅

h

=

1

T

ln

Xn
Xn

np.

ln

457

371













T

1.459

1

s

=

hśr

=0,664

1

s

Dziel

ą

c warto

ś

ci siły przez mas

ę

otrzymujemy wykres przyspieszenia a(t).

Poprzez jego scałkowanie numeryczne metod

ą

trapezów otrzymujemy wykres

pr

ę

dko

ś

ci v(t).

Całkuj

ą

c ponownie otrzymujemy wykres przemieszczenia x(t).

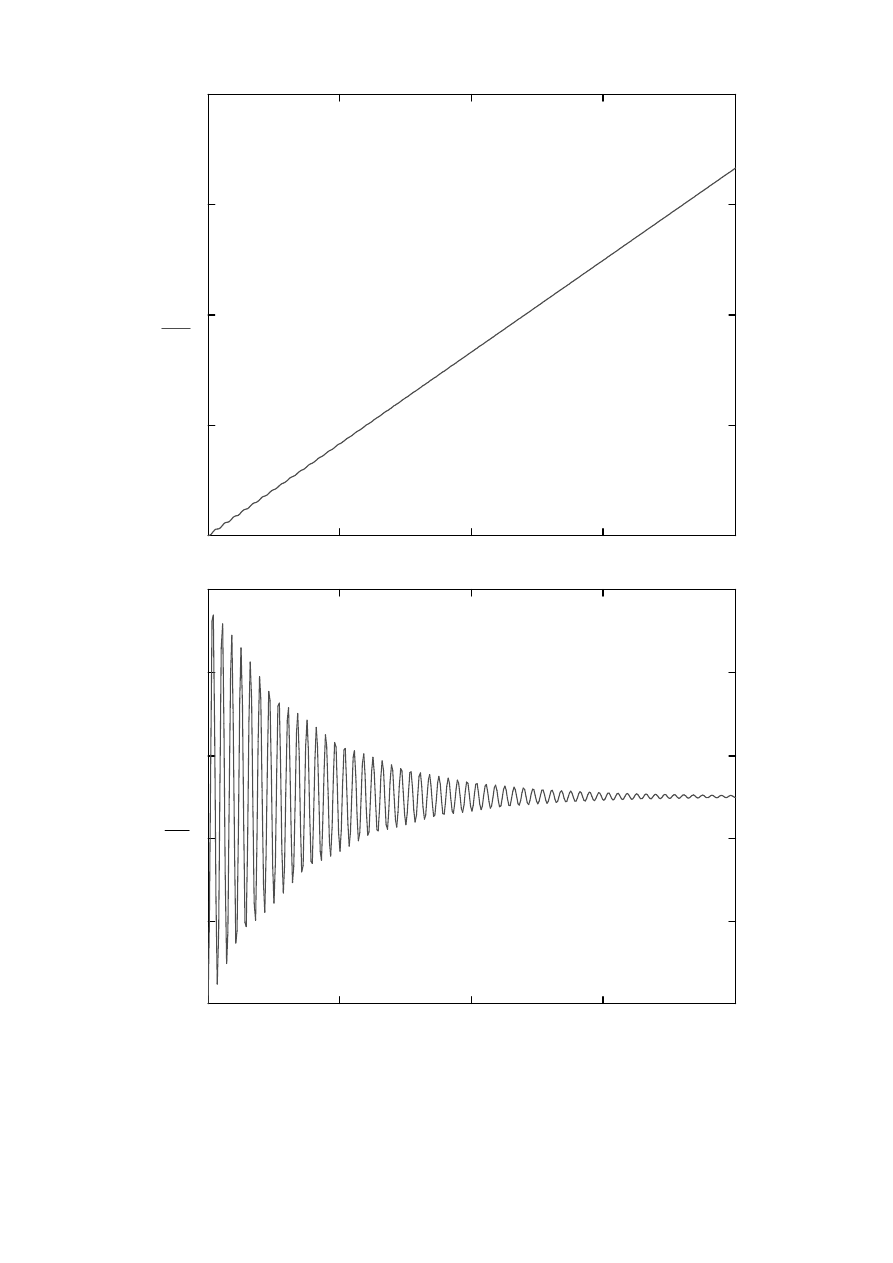
Wykresy przewidywane otrzymamy z poni

ż

szych równa

ń

podstawiaj

ą

c do nich wcze

ś

niej obliczone

warto

ś

ci pr

ę

dko

ś

ci podnoszenia, cz

ę

stotliwo

ś

ci drga

ń

oraz współczynnika tłumienia.

x t

( )

vp t

e

h

−

t

⋅

ω

sin ω t

⋅

(

)

⋅

−













⋅

:=

v t

( )

vp 1 e

h

−

t

⋅

h

ω

sin ω t

⋅

(

)

⋅

cos ω t

⋅

(

)

−













⋅

+













⋅

:=

a t

( )

vp e

h

−

t

⋅

⋅

ω

2

h

2

−

ω

sin ω t

⋅

(

)

⋅

2 h

⋅

cos ω t

⋅

(

)

⋅

+













⋅

:=

0

2

4

6

8

0

20

40

60

80

x t

( )

t

WYKRESY PRZEWIDYWANE

[cm]

0

2

4

6

8

0

2

4

6

8

10

v t

( )

t

[

m

min

]

0

2

4

6

8

4

−

2

−

0

2

4

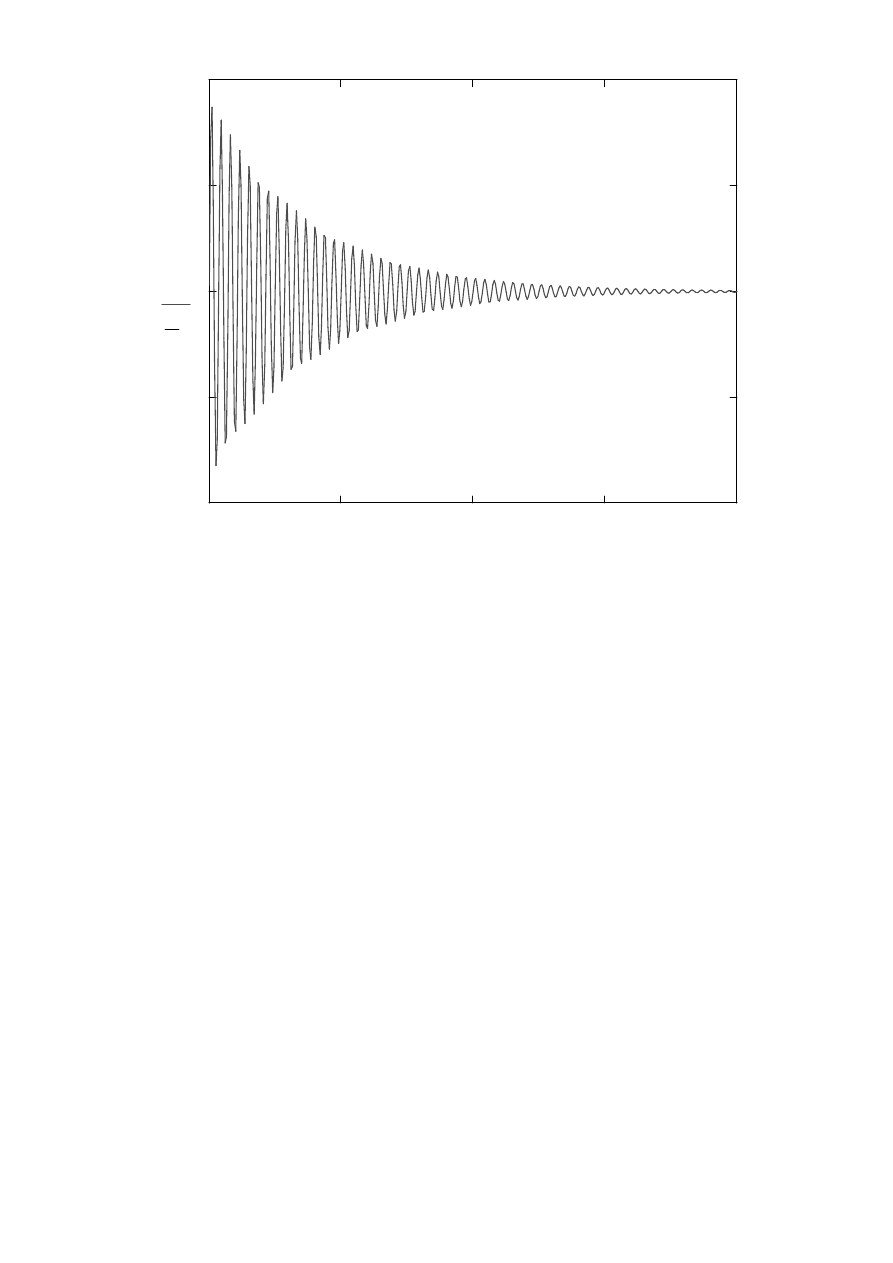
a t

( )

t

[

m

s

2

]

WNIOSKI:

Wykresy rzeczywiste i przewidywane s

ą

zbli

ż

one jednak w rzeczywisto

ś

ci osi

ą

gamy

mniejsze przyspieszenia, pr

ę

dko

ś

ci oraz przemieszczenia. Powodem tego mo

ż

e by

ć

uproszczenie modelu dynamicznego

ż

urawia. Masa obci

ąż

enia została wyznaczona

na podstawie wykresu pomiarowego i jej niedokładne wyznaczenie niesie za sob

ą

niedokładno

ść

kolejnych wykresów rzeczywistych.