
WYKŁAD Z ANALIZY MATEMATYCZNEJ
I
dr. Elżbieta Kotlicka
Centrum Nauczania Matematyki i Fizyki
Łódź 2006


Spis treści
4
Własności ciągów liczbowych o wyrazach rzeczywistych: monotoniczność,
4
Twierdzenia o ciągach zbieżnych i rozbieżnych.
6
Zbieżność pewnych ciągów specjalnych.
8
Zbiory ograniczone na prostej. Kresy górny i dolny.
9
11
11
Twierdzenia o granicach funkcji.
14
15
3

1. CIĄGI LICZBOWE
4
1. CIĄGI LICZBOWE
Definicja 1.1.
Ciągiem nieskończonym nazywamy każdą funkcję f określoną na zbiorze
liczb naturalnych.
Wartości tej funkcji nazywamy wyrazami ciągu i oznaczamy
a
n
≡ f(n),
n
∈ N.
Ciąg o wyrazach a
n
zapisujemy symbolem
(a
n
) lub a
1
, a
2
, . . . ,
zaś zbiór wartości ciągu oznaczamy przez
{a
n
}
n
∈N
.
Ciągi, których wyrazy są liczbami nazywamy ciągami liczbowymi (np. ciągi liczbowe o
wyrazach rzeczywistych, ciągi liczbowe o wyrazach zespolonych). Ciągi, których wyrazy są
funkcjami nazywamy ciągami funkcyjnymi.
1.1. Własności
ciągów
liczbowych o wyra-
zach rzeczywistych: monotoniczność, ogra-
niczoność, zbieżność.
Definicja 1.2.
a) Ciąg (a
n
) jest rosnący
def
⇔
V
n
∈N
a
n+1
> a
n
.
b) Ciąg (a
n
) jest niemalejący
def
⇔
V
n
∈N
a
n+1
a
n
.
c) Ciąg (a
n
) jest malejący
def
⇔
V
n
∈N
a
n+1
< a
n
.
d) Ciąg (a
n
) jest nierosnący
def
⇔
V
n
∈N
a
n+1
¬ a
n
.
Twierdzenie 1.3.
Jeśli a
n
> 0 dla n
∈ N, to
ciąg (a
n
) jest rosnący
⇔
V
n
∈N
a
n+1
a
n
> 1.
Ćwiczenie 1.4. Sformułować analogiczne własności dla ciągu niemalejącego, malejącego i nie-
rosnącego.
Definicja 1.5.
a) Ciąg (a
n
) jest ograniczony z dołu
def
⇔
W
m
∈R
V
n
∈N
a
n
m.
b) Ciąg (a
n
) jest ograniczony z góry
def
⇔
W
M
∈R
V
n
∈N
a
n
¬ M.
c) Ciąg (a
n
) jest ograniczony
def
⇔ (a
n
) jest ograniczony z dołu i z góry.

1. CIĄGI LICZBOWE
5
Ćwiczenie 1.6. Zbadać własności ciągów o wyrazach ogólnych:
a) a
n
=
√
n;
c) a
n
=
(
−1)
n
n
−1
;
b) a
n
= (
−3)
n
;
d) a
n
=
1
n
2
+ 1
.
Definicja 1.7.
Ciąg liczbowy (a
n
) jest zbieżny do a
∈ R, gdy
V
ε>0
W
K
∈N
V
n
K
|a
n
− a| < ε,
czyli
V
ε>0
W
K
∈N
V
n
K
a
− ε < a
n
< a + ε.
Liczbę a nazywamy granicą właściwą ciągu (a
n
) i zapisujemy
lim
n
→∞
a
n
= a lub a
n
→ a.
Przykład 1.8. Wykazać, że lim
n
→∞
1
n
= 0.
Definicja 1.9.
a) Ciąg (a
n
) jest rozbieżny do +
∞, gdy
V
ε>0
W
K
∈N
V
n
K
a
n
> ε.
b) Ciąg (a
n
) jest rozbieżny do
−∞, gdy
V
ε>0
W
K
∈N
V
n
K
a
n
<
−ε.
Zapisujemy odpowiednio:
lim
n
→∞
a
n
= +
∞ lub lim
n
→∞
a
n
=
−∞.
Jeśli ciąg (a
n
) nie posiada granicy (właściwej lub niewłaściwej), to mówimy, że jest rozbieżny.
Przykład 1.10. Wykazać, że lim
n
→∞
n
2
= +
∞.
Twierdzenie 1.11.
Każdy ciąg posiada conajwyżej jedną granicę (właściwą lub niewłaściwą).
Definicja 1.12.
Podciągiem ciągu (a
n
) nazywamy każdy ciąg (a
k
n
), gdzie (k
n
) jest dowolnym
rosnącym ciągiem liczb naturalnych.
Np. Podciągami ciągu (a
n
) są ciągi:
a
1
, a
3
, a
5
, . . .
a
2
, a
4
, a
6
, . . .
a
3
, a
4
, a
5
, . . .
(a
2n
−1
)
∞
n=1
(a
2n
)
n
∈N
(a
n
)
n
3
Twierdzenie 1.13.
Każdy podciąg ciągu zbieżnego jest zbieżny i ma tę samą granicę, co dany
ciąg.
Przykład 1.14. Wykazać, że nie istnieją granice:
a) lim
n
→∞
(
−1)
n
,
b) lim
n
→∞
cos
nπ
2
.
Ćwiczenie 1.15. Wykazać, że:

1. CIĄGI LICZBOWE
6
a) lim
n
→∞
a
n
=
±∞ ⇒ lim
n
→∞
1
a
n
= 0;
{
1
±∞
= 0
}
b) lim
n
→∞
a
n
= 0
⇒ lim
n
→∞
1
a
n
=
(
+
∞, gdy a
n
> 0 dla prawie wszystkich n
∈ N,
−∞, gdy a
n
< 0 dla prawie wszystkich n
∈ N.
{
1
0
+
= +
∞}
{
1
0
−
=
−∞}
Ćwiczenie 1.16. Wykazać, że
a) lim
n
→∞
q
n
=
nie istnieje dla q
¬ −1,
0
dla q
∈ (−1; 1),
1
dla q = 1,
+
∞
dla q > 1.
b) lim
n
→∞
n
α
=
0
dla α < 0,
1
dla α = 0,
+
∞ dla α > 0.
1.2. Twierdzenia o ciągach zbieżnych i roz-
bieżnych.
Twierdzenie 1.17.
Jeśli ciąg liczbowy jest zbieżny, to jest ograniczony.
Uwaga 1.18. Twierdzenie odwrotne do Tw.1.17 nie jest prawdziwe.
Twierdzenie 1.19 (Bolzano-Weierstrassa).
Jeśli ciąg liczbowy jest ograniczony, to istnieje
podciąg zbieżny. Jeśli ciąg liczbowy jest nieograniczony, to posiada podciąg rozbieżny do
−∞
lub +
∞.
Twierdzenie 1.20.
Jeśli ciąg liczbowy jest ograniczony i monotoniczny, to jest zbieżny.
Lemat 1.21. Jeśli ciągi (a
n
), (b
n
) są zbieżne oraz
W
K
∈N
V
n
K
a
n
¬ b
n
,
to lim
n
→∞
a
n
¬ lim
n
→∞
b
n
.
Twierdzenie 1.22 (o trzech ciągach).
Załóżmy,że
(
∗)
W
K
∈N
V
n
K
a
n
¬ b
n
¬ c
n
,
a) Jeśli lim
n
→∞
a
n
= lim
n
→∞
c
n
= a, to istnieje granica ciągu (b
n
), przy czym lim
n
→∞
b
n
= a.
1. CIĄGI LICZBOWE
7
b) Jeśli lim
n
→∞
a
n
= +
∞, to lim
n
→∞
b
n
= +
∞.
c) Jeśli lim
n
→∞
c
n
=
−∞, to lim
n
→∞
b
n
=
−∞.
Twierdzenie 1.23.
Jeśli lim
n
→∞
a
n
= a oraz c
6= 0, to
lim
n
→∞
c
· a
n
=
(
c
· a, gdy a ∈ R,
±∞, gdy a = ±∞.
W szczególności dla c > 0
{c · (+∞) = +∞}
oraz
{c · (−∞) = −∞}
Twierdzenie 1.24.
Jeśli lim
n
→∞
a
n
= a oraz
lim
n
→∞
b
n
= b, to
Twierdzenie 1.25.
Jeśli lim
n
→∞
a
n
= a,
lim
n
→∞
b
n
= b oraz b
n
6= 0 dla n ∈ N, to
Twierdzenie 1.26.
Jeśli lim
n
→∞
a
n
= a,
lim
n
→∞
b
n
= b oraz b
n
0 dla n ∈ N, to

1. CIĄGI LICZBOWE
8
Symbole nieoznaczone:
∞ − ∞ 0 · ∞
∞
∞
0
0
0
0
∞
0
1
∞
1.3. Zbieżność pewnych ciągów specjalnych.
Liczba
e.
Twierdzenie 1.27.
a) lim
n
→∞
n
√
n = 1.
b) lim
n
→∞
n
√
a = 1.
c) Jeśli a
n
0 dla każdego n ∈ N oraz lim
n
→∞
a
n
= a > 0, to lim
n
→∞
n
√
a
n
= 1.
Uwaga 1.28. Tw. 1.27 c) nie zachodzi w przypadku, gdy a = +
∞.
Twierdzenie 1.29.
Ciąg a
n
= (1 +
1
n
)
n
dla n
∈ N jest ograniczony i monotoniczny.
Definicja 1.30.
Liczbą e nazywamy granicę ciągu (1 +
1
n
)
n
, n
∈ N.
Twierdzenie 1.31.
a)
∗
lim
n
→∞
n
X
k=0
1
k!
= e.
b) Liczba e jest liczbą niewymierną.
e = 2, 7182818284 . . .
Twierdzenie 1.32.
Jeśli a
n
6= 0 dla każdego n ∈ N oraz lim
n
→∞
a
n
=
±∞, to lim
n
→∞
(1 +
1
a
n
)
a
n
= e.
Definicja 1.33.
Logarytm o podstawie równej e nazywamy logarytmem naturalnym i ozna-
czamy symbolem ln.
ln x
def
= log
a
x dla x > 0

1. CIĄGI LICZBOWE
9
1.4. Zbiory ograniczone na prostej. Kresy gór-
ny i dolny.
Definicja 1.34.
Niech E
⊂ R, E 6= ∅.
a) Zbiór E jest ograniczony z góry, gdy
∨
M
∈R
∧
x
∈E
x
¬ M.
Lczbę M nazywamy ograniczeniem górnym zbioru E.
b) Zbiór E jest ograniczony z dołu, gdy
∨
m
∈R
∧
x
∈E
x
m.
Liczbę m nazywamy ograniczeniem dolnym zbioru E.
c) Zbiór E jest ograniczony, gdy zbiór E jest ograniczony z góry i z dołu.
Definicja 1.35.
Niech E
⊂ R, E 6= ∅.
a) Liczbę M
0
∈ E taką, że
∧
x
∈E
x
¬ M
0
nazywamy elementem największym w zbiorze E i oznaczamy przez max E.
b) Liczbę m
0
∈ E taką, że
∧
x
∈E
x
m
0
nazywamy elementem najmniejszym w zbiorze E i oznaczamy przez min E.
Definicja 1.36.
Niech E
⊂ R, E 6= ∅.
a) Jeśli zbiór E jest ograniczony z góry, to liczbę M
∈ R taką, że
(1)
∧
x
∈E
x
¬ M,
(2)
∧
M
1
<M
∨
x
∈E
x > M
1
nazywamy kresem górnym zbioru E i oznaczamy przez sup E.
(Liczba sup E jest najmniejszym ograniczeniem górnym zbioru E.)
W przypadku gdy E nie jest ograniczony z góry przyjmujemy sup E = +
∞.
b) Jeśli zbiór E jest ograniczony z dołu, liczbę m
∈ R taką, że
(1)
∧
x
∈E
x
m,
(2)
∧
m
1
>m
∨
x
∈E
x < m
1
nazywamy kresem dolnym zbioru E i oznaczamy przez inf E.

1. CIĄGI LICZBOWE
10
(Liczba inf E jest największym ograniczeniem dolnym zbioru E.)
W przypadku gdy E nie jest ograniczony z dołu przyjmujemy inf E =
−∞.
Twierdzenie 1.37.
Każdy niepusty zbiór E
⊂ R posiada kresy górny i dolny, które należą do
zbioru R.
Twierdzenie 1.38.
a) Jeśli ciąg (a
n
) jest niemalejący, to
sup
{a
n
: n
∈ N} = lim
n
→∞
a
n
,
inf
{a
n
: n
∈ N} = a
1
.
b) Jeśli ciąg (a
n
) jest nierosnący, to
sup
{a
n
: n
∈ N} = a
1
,
inf
{a
n
: n
∈ N} = lim
n
→∞
a
n
.

2. GRANICE FUNKCJI
11
2. GRANICE FUNKCJI
2.1. Podstawowe definicje.
Niech X
⊂ R, X 6= ∅.
Definicja 2.1.
Niech x
0
∈ R.
• Sąsiedztwem punktu x
0
nazywamy każdy zbiór
S(x
0
) = (a, x
0
)
∪ (x
0
, b),
gdzie a, b
∈ R, a < x
0
< b.
Zbiory
S
−
(x
0
) = (a, x
0
),
S
+
(x
0
) = (x
0
, b),
nazywamy odpowiednio lewostronnym i prawostronnym sąsiedztwem punktu x
0
.
• Otoczeniem punktu x
0
nazywamy zbiór
U (x
0
) = S(x
0
)
∪ {x
0
}.
Zbiory
U
−
(x
0
) = S
−
(x
0
)
∪ {x
0
},
U
+
(x
0
) = S
+
(x
0
)
∪ {x
0
}.
nazywamy odpowiednio lewostronnym i prawostronnym otoczeniem punktu x
0
.
• Sąsiedztwem −∞ nazywamy zbiór
S(
−∞) = (−∞, b), gdzie b ∈ R.
• Sąsiedztwem +∞ nazywamy zbiór
S(+
∞) = (a, +∞), gdzie a ∈ R.
Definicja 2.2.
• Punkt x
0
∈ R jest punktem skupienia zbioru X, jeśli istnieje ciąg (x
n
) taki, że
{x
n
} ⊂ X \ {x
0
} oraz
lim
n
→∞
x
n
= x
0
.
• Jeśli x
n
< x
0
dla n
∈ N (x
n
> x
0
dla n
∈ N), to x
0
nazywamy lewostronnym
(prawostronnym) punktem skupienia zbioru X.
• Punkty zbioru, które nie są jego punktami skupienia nazywamy punktami izolowanymi.
Zbiór punktów skupienia (lewostronnych, prawostronnych punktów skupienia) zbioru X ozna-
czamy przez X
d
(X
d
−
, X
d+
).

2. GRANICE FUNKCJI
12
Definicja 2.3 (Heinego granicy funkcji w +
∞).
Niech f : X
→ R, X− zbiór nieograniczony z dołu.
a) Liczba g jest granicą właściwą funkcji f w +
∞, gdy
∧
(x
n
),
{x
n
}⊂X
[ lim
n
→∞
x
n
= +
∞ ⇒
lim
n
→∞
f (x
n
) = g].
Zapisujemy
lim
x
→+∞
f (x) = g
b) Funkcja f ma w +
∞ granicę niewłaściwą +∞, gdy
∧
(x
n
),
{x
n
}⊂X
[ lim
n
→∞
x
n
= +
∞ ⇒
lim
n
→∞
f (x
n
) = +
∞].
Zapisujemy
lim
x
→+∞
f (x) = +
∞
Analogicznie definiujemy lim
x
→+∞
f (x) =
−∞, lim
x
→−∞
f (x) = g oraz lim
x
→−∞
f (x) =
±∞.
Definicja 2.4 (Heinego granicy funkcji w punkcie).
Niech f : X
→ R oraz x
0
∈ X
d
.
a) Liczba g jest granicą właściwą funkcji f w x
0
, gdy
∧
(x
n
),
{x
n
}⊂X\{x
0
}
[ lim
n
→∞
x
n
= x
0
⇒ lim
n
→∞
f (x
n
) = g].
Zapisujemy
lim
x
→x
0
f (x) = g
b) Funkcja f posiada w x
0
granicę niewłaściwą +
∞, gdy
∧
(x
n
),
{x
n
}⊂X\{x
0
}
[ lim
n
→∞
x
n
= x
0
⇒ lim
n
→∞
f (x
n
) = +
∞].
Zapisujemy
lim
x
→x
0
f (x) = +
∞
Analogicznie definiujemy lim
x
→x
0
f (x) =
−∞.
Definicja 2.5.
Niech f : X
→ R.
a) Niech x
0
∈ X
d
−
. Liczba g jest lewostronną granicą właściwą funkcji f
w punkcie
x
0
, gdy
∧
(x
n
),
{x
n
}⊂X∩(−∞,x
0
)
[ lim
n
→∞
x
n
= x
0
⇒ lim
n
→∞
f (x
n
) = g].
Zapisujemy

2. GRANICE FUNKCJI
13
lim
x
→x
−
0
f (x) = g lub f (x
−
0
) = g
b) Niech x
0
∈ X
d+
. Liczba g jest prawostronną granicą właściwą funkcji f w punkcie
x
0
, gdy
∧
(x
n
),
{x
n
}⊂X∩(x
0
,+
∞)
[ lim
n
→∞
x
n
= x
0
⇒ lim
n
→∞
f (x
n
) = g].
Zapisujemy
lim
x
→x
+
0
f (x) = g lub f (x
+
0
) = g
Analogicznie definiujemy lewostronną i prawostronną granicę niewłaściwą funkcji w punkcie.
Definicja 2.6 (Cauchy’ego granicy funkcji w +
∞).
Niech f : X
→ R, X− zbiór nieograniczony z dołu.
a) Liczba g jest granicą właściwą funkcji f w +
∞, gdy
∧
ε>0
∨
δ>0
∧
x
∈X
[x > δ
⇒ |f(x) − g| < ε].
b) Funkcja f ma w +
∞ granicę niewłaściwą +∞, gdy
∧
ε>0
∨
δ>0
∧
x
∈X
[x > δ
⇒ f(x) > ε].
c) Funkcja f ma w +
∞ granicę niewłaściwą −∞, gdy
∧
ε>0
∨
δ>0
∧
x
∈X
[x > δ
⇒ f(x) < −ε].
Podobnie definiujemy granicę właściwą i niewłaściwą w +
∞.
Definicja 2.7 (Cauchy’ego granicy funkcji w punkcie).
Niech f : X
→ R oraz x
0
∈ X
d
.
a) Liczba g jest granicą właściwą funkcji f w punkcie x
0
, gdy
∧
ε>0
∨
δ>0
∧
x
∈X
[0 <
|x − x
0
| < δ ⇒ |f(x) − g| < ε].
b) Funkcja f ma w punkcie x
0
granicę niewłaściwą +
∞, gdy
∧
ε>0
∨
δ>0
∧
x
∈X
[0 <
|x − x
0
| < δ ⇒ f(x) > ε].
c) Funkcja f ma w punkcie x
0
granicę niewłaściwą
−∞, gdy
∧
ε>0
∨
δ>0
∧
x
∈X
[0 <
|x − x
0
| < δ ⇒ f(x) < −ε].
Twierdzenie 2.8.
Odpowiadające sobie definicje Heinego i Cauchy’ego granic funkcji są rów-
noważne.
Twierdzenie 2.9 (warunek konieczny i wystarczający istnienia granicy).
Jeśli x
0
∈ X
d
−
∩ X
d+
, to
lim
x
→x
0
f (x) = g
⇔
lim
x
→x
−
0
f (x) = lim
x
→x
+
0
f (x) = g.
2. GRANICE FUNKCJI
14
2.2. Twierdzenia o granicach funkcji.
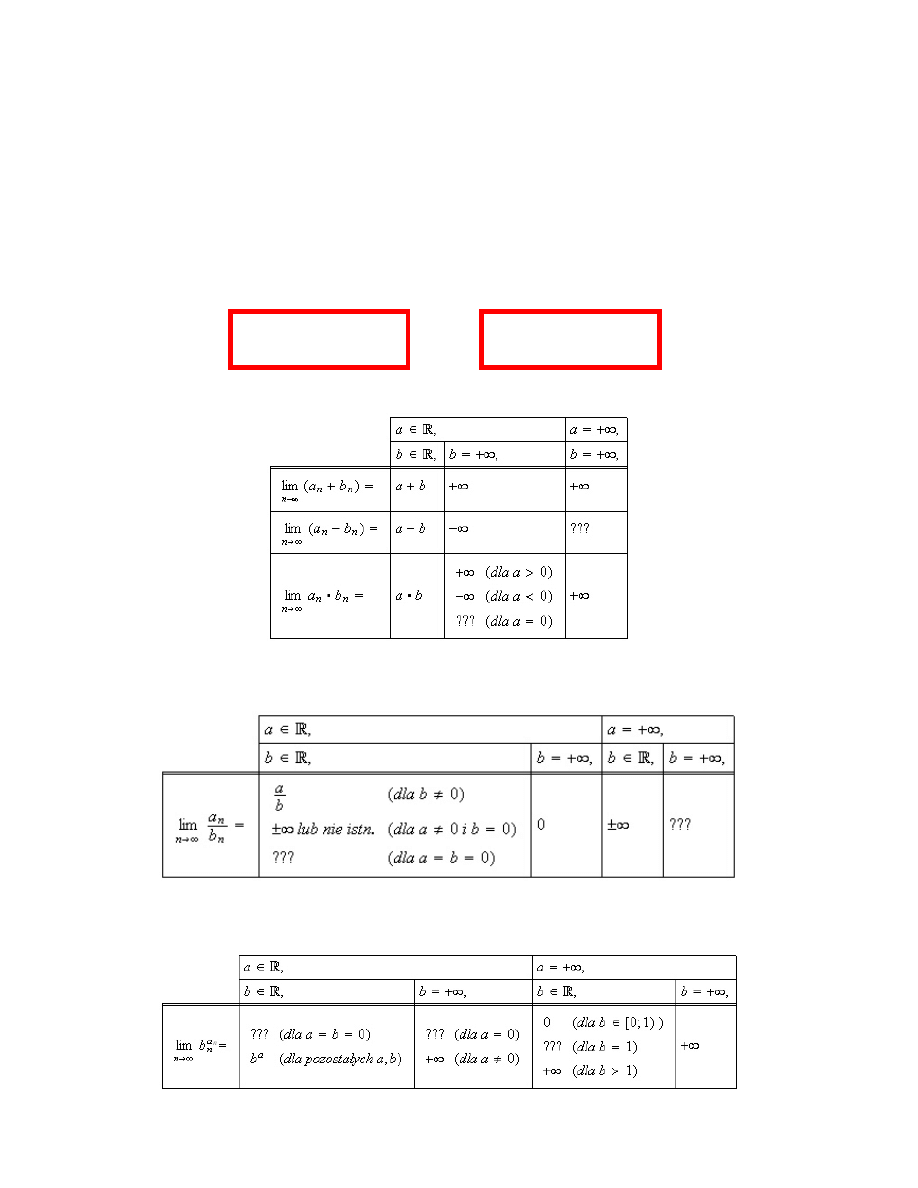
Twierdzenie 2.10 (o arytmetyce granic właściwych funkcji).
Jeśli f, g : X
→ R, lim
x
→x
0
f (x) = a oraz lim
x
→x
0
g(x) = b, to
a) lim
x
→x
0
(c
· f(x)) = c · a dla dowolnego c ∈ R;
b) lim
x
→x
0
(f (x)
± g(x) = a ± b;
c) lim
x
→x
0
(f (x)
· g(x)) = a · b;
d) lim
x
→x
0
f (x)
g(x)
=
a
b
, o ile b
6= 0;
e) lim
x
→x
0
(g(x))
f (x)
= b
a
, o ile b > 0 i a
6= 0.
Twierdzenie 2.11 (o arytmetyce granic niewłaściwych funkcji).
a +
∞ = +∞ dla −∞ < a ¬ +∞
a
· (+∞) = +∞ dla −∞ < a ¬ +∞
a
∞
= 0 dla
−∞ < a < +∞
a
0
+
= +
∞ dla 0 < a ¬ +∞
b
∞
= 0 dla 0
+
¬ b < 1,
b
∞
= +
∞ dla 1 < b ¬ +∞
∞
a
= 0 dla
−∞ ¬ a < 0,
∞
a
= +
∞ dla 0 < a ¬ +∞
Twierdzenie 2.12 (o granicy funkcji złożonej).
Niech f : X
→ Y ⊂ R, g : Y → R. Jeśli
(1)
lim
x
→x
0
f (x) = a,
(2)
f (x)
6= a dla każdego x ∈ S(x
0
),
(3)
lim
x
→a
g(x) = b,
to lim
x
→x
0
g(f (x)) = b.
2. GRANICE FUNKCJI
15
Twierdzenie 2.13 (o trzech funkcjach).
Jeśli funkcje f, g, h : X
→ R spełniają warunki
(1)
∧
x
∈S(x
0
)
f (x)
¬ g(x) ¬ h(x),
(2)
lim
x
→x
0
f (x) = lim
x
→x
0
h(x) = a,
to lim
x
→x
0
g(x) = a.
Twierdzenie 2.14 (o dwóch funkcjach).
Niech f, g : X
→ R oraz
∧
x
∈S(x
0
)
f (x)
¬ g(x).
Jeśli lim
x
→x
0
f (x) = +
∞, to lim
x
→x
0
g(x) = +
∞.
Jeśli lim
x
→x
0
g(x) =
−∞, to lim
x
→x
0
f (x) =
−∞.
Powyższe twierdzenia o granicach funkcji zachodzą zarówno dla granic w punkcie, jak i dla
granic jednostronnych oraz granic w
±∞.
Twierdzenie 2.15.
lim
x
→0
sin x
x
= 1.
Twierdzenie 2.16.
lim
x
→0
(1 + x)
1
x
= e.
2.3. Asymptoty funkcji.
Definicja 2.17.
Niech f : X
→ R, x
0
∈ X
d
.
a) Prosta x = x
0
jest lewostronną (prawostronną) asymtotą pionową wykresu funkcji
f , jeśli
lim
x
→x
−
0
f (x) =
±∞ ( lim
x
→x
+
0
f (x) =
±∞).
b) Prosta x = x
0
jest obustronną asymtotą pionową wykresu funkcji f, jeśli jest jedno-
cześnie jego lewostronną i prawostronną asymptotą pionową.
Definicja 2.18.
Niech f : X
→ R, X− zbiór nieograniczony z dołu. Prosta y = ax + b jest
asymptotą ukośną wykresu funkcji f w
−∞, gdy
lim
x
→−∞
[f (x)
− (ax + b)] = 0.
Analogicznie definiujemy asymptotę ukośną w +
∞.
Przykład 2.19. Wykazać, że prosta y = x
− 1 jest asymptotą ukośną wykresu funkcji f(x) =
x
2
x+1
.
Twierdzenie 2.20.
a) Prosta y = ax + b jest asymptotą ukośną wykresu funkcji f w
−∞ ⇔
a = lim
x
→−∞
f (x)
x
oraz
b = lim
x
→−∞
(f (x)
− ax).
b) Prosta y = Ax + B jest asymptotą ukośną wykresu funkcji f w +
∞ ⇔
A = lim
x
→+∞
f (x)
x
oraz
B = lim
x
→+∞
(f (x)
− Ax).
Document Outline
Wyszukiwarka
Podobne podstrony:
2012 AMI wyklad print cz1
2007 AMI wyklad print
AMI Wyklad1 rozdz9
ami wyklad1 11
2010 AMI wyklad
2012 AMI wyklad print
002 Analiza AMI Wyklad r1 id 59 Nieznany (2)
2007 AMI wyklad print4 id 55147 Nieznany (2)
002 Analiza, 2007 AMI wyklad print
2007 AMI wyklad print 1 7
002 Analiza 2007 AMI wyklad pri Nieznany (2)
2007 AMI wyklad print 1 7
2012 AMI wyklad print
więcej podobnych podstron