Kurs na Studiach Doktoranckich Politechniki Wrocławskiej (wersja: styczeń 2007)
________________________________________________________________________________________

100

XII. LEPKOSPRĘŻYSTOŚĆ

1. Liniowe ciała z pamięcią

Ciało liniowo sprężyste posiada pamięć prostą, czyli pamięta jedną konfigurację którą jest bez-
odkształceniowy stan początkowy. Istnieją materiały, które pamiętają przeszłość. Wśród tej gru-
py materiałów można wyróżnić takie dla których przyczyna i skutek są liniowo zależne.

W rozdziale tym rozważane są materiały, dla których zależność pomiędzy naprężeniem i od-
kształceniem jest liniowa ale jednocześnie zależna od czasu. Dla tej klasy materiałów aktualny
stan odkształcenia zależy od całej historii obciążenia. Materiały takie zwane są materiałami lep-
kosprężystymi.

Jako ilustrację problemu rozważamy przykład pręta rozciąganego siłą osiową F jak to pokazano
na rys. 12.1. W chwili t siła o wartości F(t) wywoła wydłużenie u(t). Wydłużenie u(t) zależy od
historii obciążenia aż do chwili t. Gdy funkcja F(t) jest ciągła i różniczkowalna, to w ciągu nie-
skończenie małego przedziału czasu dτ w chwili τ<t przyrost obciążenia wyniesie (dF/dt)dτ.
Przyrost ten działa na pręt wywołując przyrost wydłużenia du(t) w chwili t ze współczynnikiem
proporcjonalności C zależnym od wielkości przedziału czasu t

−

τ. Zatem

τ

τ

−

=

τ

=

d

d

d

)

(

)

(

d

t

t

F

t

C

t

u

,

(12.1)

gdzie

τ

=

t

t

F

d

d

jest wartością pochodnej w chwili t=τ; pochodna ta jest równa

τ

τ

d

)

(

dF

jeśli zmien-

ną t zastąpimy przez τ przed różniczkowaniem.

Ponieważ siła osiowa F(t) jest proporcjonalna do naprężenia a przemieszczenie u(t) proporcjo-
nalne do odkształcenia, w dalszym ciągu będziemy używali wielkości lokalnych, a w takim razie
równanie (1) zapiszemy w postaci

τ

σ

τ

−

=

ε

τ

=

d

d

d

)

(

)

(

d

t

t

t

c

t

,

(12.2)

Sumując przyrosty odkształceń w ciągu całej historii otrzymujemy

τ

σ

τ

−

=

ε

τ

=

∫

d

d

d

)

(

)

(

0

t

t

t

t

c

t

.

(12.3)

Jeżeli „obciążeniem” pręta będzie zmienne w czasie odkształcenie (przemieszczenie) to wów-
czas odwracają się role odpowiednio naprężenia i odkształcenia w równaniu (3), stąd

Rys. 12.1.

Konderla P. Mechanika ośrodków ciągłych

________________________________________________________________________________________

101

τ

ε

τ

−

=

σ

τ

=

∫

d

d

d

)

(

)

(

0

t

t

t

t

k

t

.

(12.4)

Powyższe równania są liniowe, przy czym

ƒ c(t) – funkcja pełzania; jest wydłużeniem wywołanym nagłym przyłożeniem naprężenia o

intensywności jednostkowej w chwili t=0,

),

(

)

(

t

H

t

=

σ

ƒ k(t) – funkcja relaksacji; jest naprężeniem wywołanym odkształceniem jednostkowym za-

danym w chwili t=0,

),

(

)

(

t

H

t

=

ε

gdzie funkcja Heaviside’a jest równa

⎪

⎩

⎪

⎨

⎧

<

=

>

=

0

dla

0

0

dla

2

/

1

0

dla

1

)

(

t

t

t

t

H

.

(12.5)

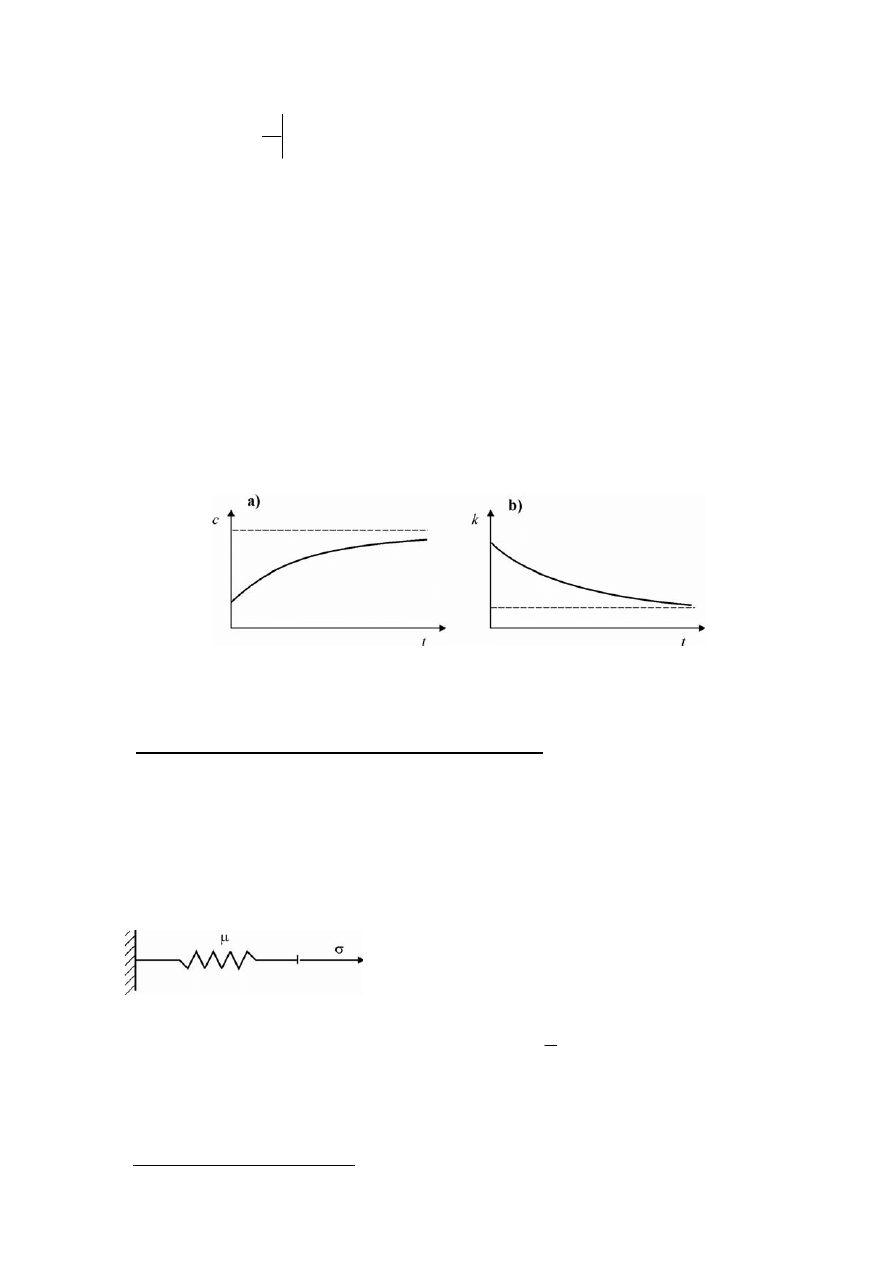
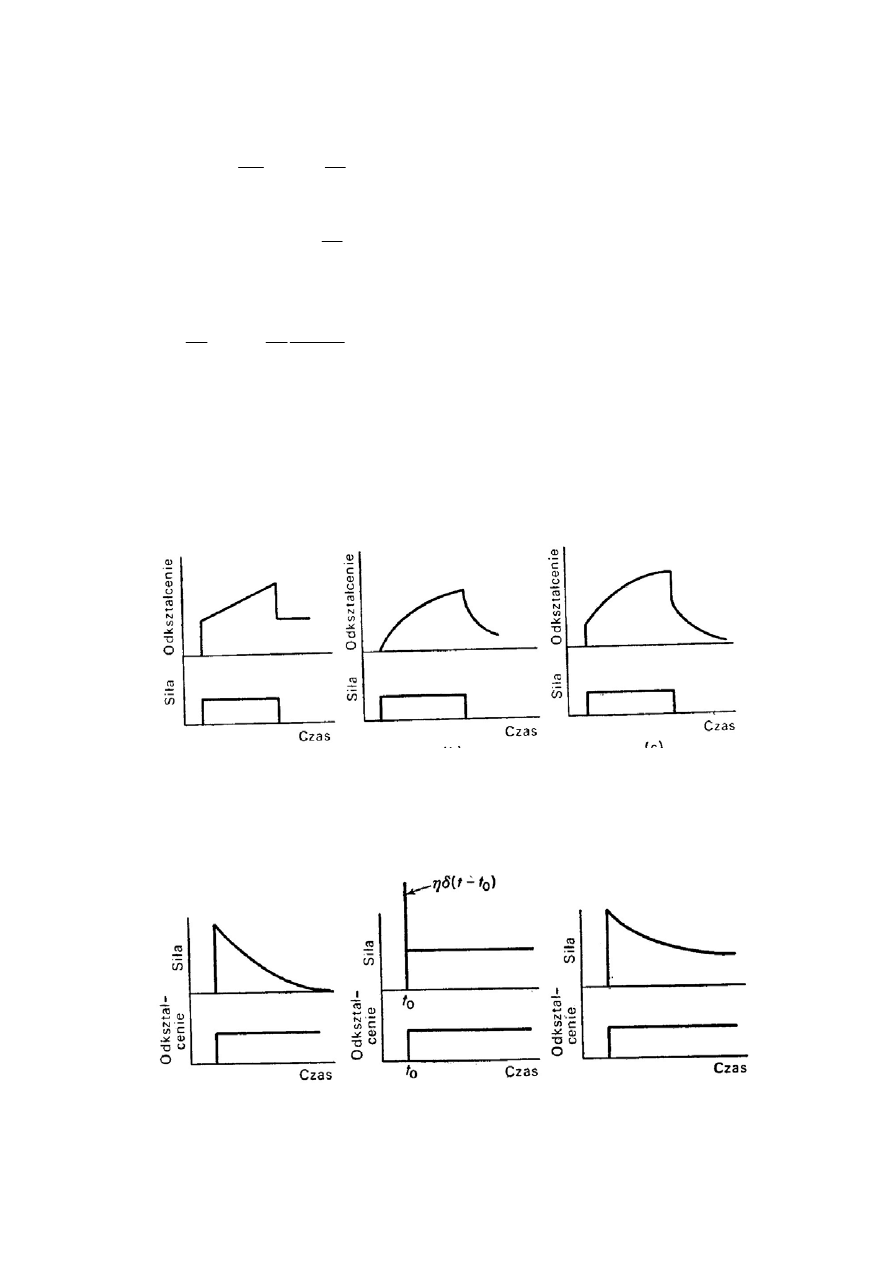
Dla materiału wykazującego cechy sprężyste i lepkie typowe funkcje pełzania i relaksacji są po-
kazane na rys. 12.2.

2. Mechaniczne modele materiału lepkosprężystego

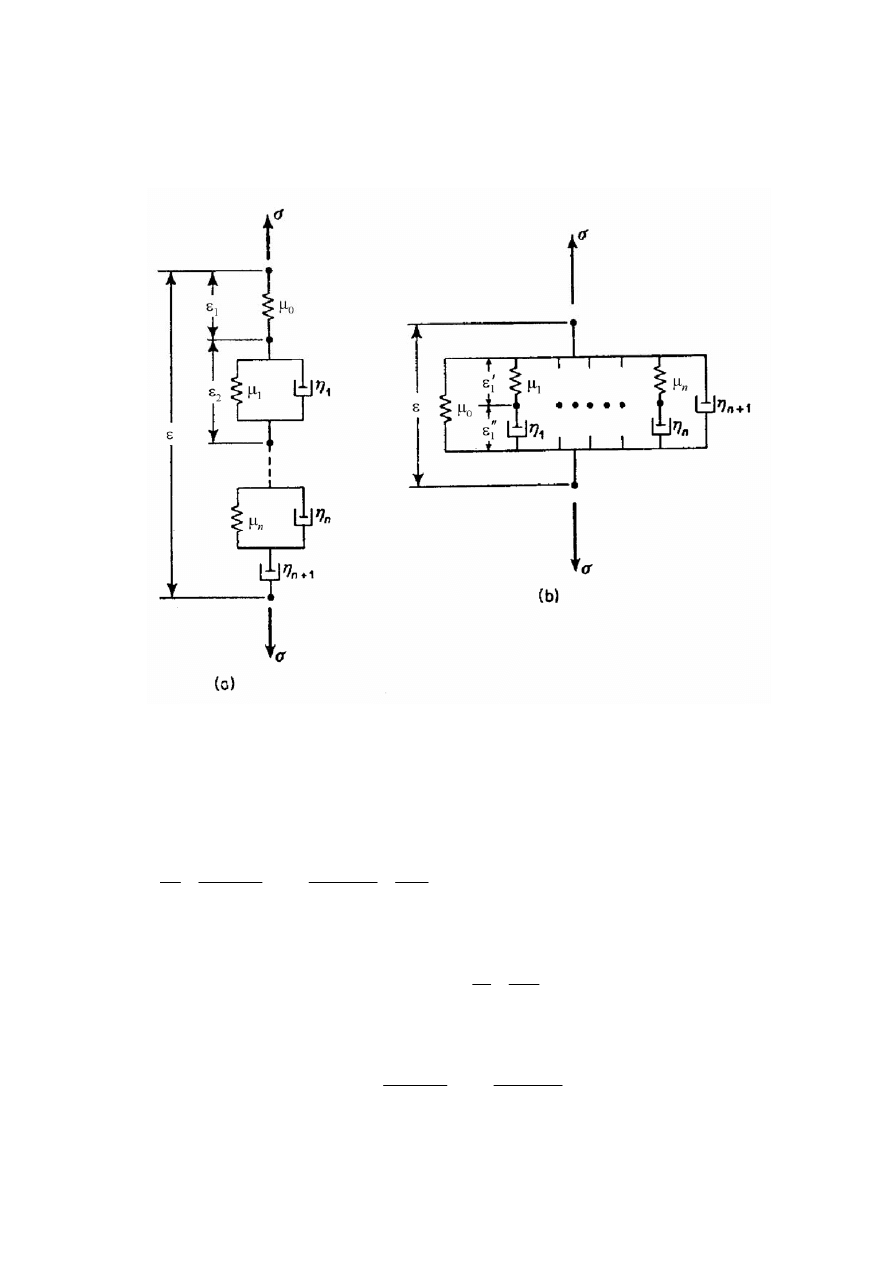
Na wstępie rozważamy mechaniczne modele lepkosprężyste materiału, których budowę można
zilustrować graficznie. Podstawowymi elementami modeli lepkosprężystych są: model materiału
idealnie sprężystego i model materiału idealnie lepkiego

a) Model materiału idealnie sprężysty

Równanie konstytutywne:

με

=

σ

,

(12.6)

gdzie

μ - moduł sprężystosci.

Funkcja pełzania

μ

=

1

c

.

(12.7)

Funkcja relaksacji

μ

=

k

. (12.8)

b) Model materiału idealnie lepki

Rys. 12.2. Typowa funkcja pełzania (a) oraz funkcja relaksacji (b)

Rys. 12.3. Model sprężysty materiału

Kurs na Studiach Doktoranckich Politechniki Wrocławskiej (wersja: styczeń 2007)
________________________________________________________________________________________

102

Równanie konstytutywne:

η

σ

=

ε&

, (12.9)

gdzie

η − współczynnik lepkości.

Funkcja pełzania

η

= /

)

(

t

t

c

. (12.10)

Funkcja relaksacji

Odkształcenie przyjmujemy w postaci:

)

(

)

(

t

H

t

=

ε

,

po podstawieniu do (9) mamy

)

(

)

(

)

(

t

t

H

t

k

ηδ

=

η

=

ε

η

=

&

&

,

(12.11)

gdzie δ(t) - funkcja Diraca

⎪

⎩

⎪

⎨

⎧

>

ε

=

≠

=

∫

ε

ε

−

0

dla

)

0

(

d

)

(

)

(

0

dla

0

)

(

f

t

t

t

f

t

t

δ

δ

(12.12)

Wykorzystując podstawowe modele opisane wyżej możemy budować złożone modele lepko-
sprężyste, łącząc elementy podstawowe równolegle i/lub szeregowo. Poniżej pokazano niektóre
z takich modeli.

c) Model Maxwella

Równanie konstytutywne

Odkształcenie jest superpozycją odkształcenia elementu lepkiego i sprężystego, stąd

μ

σ

+

η

σ

=

ε

+

ε

=

ε

μ

η

&

&

&

&

.

(12.13)

Funkcja pełzania

Podstawiając funkcję jednostkowego naprężenia )

(

)

(

t

H

t

=

σ

do (13) i całkując po czasie

)

(

1

)

(

t

H

t

t

c

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

μ

+

η

=

.

(12.14)

Funkcja relaksacji

Rozwiązując równanie różniczkowe

)

(t

H

k

k

μ

=

η

μ

+

&

(12.15)

Rys. 12.3. Model sprężysty materiału

Rys. 12.5. Schemat modelu Maxwella

Konderla P. Mechanika ośrodków ciągłych

________________________________________________________________________________________

103

otrzymano

)

(

)

(

)

/

(

t

H

e

t

k

t

η

μ

−

μ

=

.

(12.16)

W materiale o modelu Maxwella nagłe przyłożenie siły wywołuje natychmiastowe odkształcenie
dzięki elementowi sprężystemu. W dalszych chwilach obserwuje się pełzanie związane z istnie-
niem elementu tłumika. Również nagłe odkształcenie wywołuje natychmiastową reakcję (naprę-
żenie) elementu sprężystego, której wartość zmniejsza się wykładniczo z czasem na skutek zja-
wiska relaksacji naprężeń. Czynnik η/µ o wymiarze czasu nazywamy czasem relaksacji – jest
miarą szybkości zanikania naprężenia w elemencie sprężystym.

d) Model Voigta

Równanie konstytutywne

Naprężenie jest sumą naprężenia w ele-
mencie lepkiem i sprężystym, stąd

με

+

ε

η

=

σ

+

σ

=

σ

μ

η

&

. (12.17)

Funkcja pełzania

Podstawiając funkcję jednostkowego na-
prężenia

)

(

)

(

t

H

t

=

σ

do (17) i całkując po

czasie mamy

(

)

)

(

1

1

)

(

)

/

(

t

H

e

t

c

t

η

μ

−

−

μ

=

. (12.18)

Funkcja relaksacji

Podstawiając bezpośrednio do równania (...)

)

(

)

(

t

H

t

=

ε

mamy

)

(

)

(

)

(

t

H

t

t

k

μ

+

ηδ

=

.

(12.19)

W materiale o modelu Voigta nagłe przyłożenie naprężenia (siły) nie wywoła natychmiastowego
odkształcenia (wydłużenie) ponieważ element tłumiący wstawiony równolegle z elementem
sprężystym nie pozwala na natychmiastowe odkształcenie. Odkształcenie zaczyna natychmiast
narastać ale stopniowo, dopóki element sprężysty nie przejmie całego naprężenia (obciążenia).
Relaksacja tłumika ma charakter wykładniczy a η/µ jest czasem relaksacji (obrazuje szybkość
zanikania odkształcenia (przemieszczania tłoka tłumika)).

e) Model liniowy standardowy

Równanie konstytutywne

Model standardowy jest szeregowym połą-
czeniem modelu Maxwella i modelu sprę-
żystego. Naprężenie jest sumą naprężenia
w elemencie Maxwella i sprężystym, stąd

E

M

E

M

ε

=

ε

=

ε

σ

+

σ

=

σ

.

(12.20)

Z równania (13) mamy

Rys.12.6. Schemat modelu Voigta

Rys.12.7. Schemat modelu standardowego

Kurs na Studiach Doktoranckich Politechniki Wrocławskiej (wersja: styczeń 2007)
________________________________________________________________________________________

104

2

2

M

2

M

M

D

s

ημ

η

+

μ

σ

=

ε

⇒

μ

σ

+

η

σ

=

ε

M

M

&

&

, (12.21)

gdzie oznaczono operator różniczkowy

t

d

/

d

D

≡

.

Wyznaczając

σ

M

z (21) oraz podstawiając do (20

1

) mamy

ε

⎥

⎦

⎤

⎢

⎣

⎡

η

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

μ

μ

+

+

μ

=

σ

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

μ

η

+

⇒

ε

η

+

μ

μ

+

ημ

=

σ

η

+

μ

⇒

ε

μ

+

ε

η

+

μ

ημ

=

σ

D

1

D

1

D)]

(

D

[

D)

(

D

D

2

1

1

2

2

1

2

2

1

2

2

(12.22)

a po rozpisaniu pochodnych otrzymujemy równanie konstytutywne w postaci równania róż-
niczkowego

ε

η

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

μ

μ

+

+

ε

μ

=

σ

μ

η

+

σ

&

&

2

1

1

2

1

.

(12.23)

Funkcja pełzania

Podstawiając funkcję jednostkowego naprężenia

)

(

)

(

t

H

t

=

σ

do (23) mamy

)

(

)

(

1

2

2

1

1

t

H

t

H

c

c

&

&

μ

η

+

=

η

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

μ

μ

+

+

μ

.

(12.24)

Korzystając z transformacji Laplace’a mamy

3

c

s

c

s

c

⇒

μ

η

+

=

η

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

μ

μ

+

+

μ

2

2

1

1

1

1

,

(12.25)

gdzie

)]

(

[

)

(

t

c

s

c

L

=

jest transformatą Laplaca

4

funkcji pełzania. Po dokonaniu odwrotnej

transformaty mamy

⎟

⎟

⎠

⎞

⎜

⎜

⎝

⎛

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

μ

+

μ

−

μ

+

μ

+

μ

=

η

μ

μ

+

μ

μ

−

t

e

t

c

2

2

1

1

1

1

1

1

)

(

2

1

1

2

1

. (12.26)

Funkcja relaksacji

Podobnie jak wyżej podstawiając do równania (23)

)

(

)

(

t

H

t

=

ε

oraz przyjmując )

(

)

(

t

k

t

≡

σ

mamy

)

(

1

)

(

2

1

1

2

t

H

t

H

k

k

&

&

η

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

μ

μ

+

+

μ

=

μ

η

+

.

(12.27)

Korzystając z transformacji Laplace’a można otrzymać rozwiązanie równania (27) w postaci

(

)

)

(

1

)

(

)

(

)

/

(

1

2

1

)

/

(

2

1

2

2

t

H

e

t

H

e

t

k

t

t

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

μ

μ

+

μ

=

μ

+

μ

=

η

μ

−

η

μ

−

. (12.28)

3

wg [10] Roylance D.: Engineering Viscoelasticity.

4

Transformata Laplace’a:

∫

∞

−

=

=

0

d

)

(

)

(

)]

(

[

t

e

t

f

s

f

t

f

st

L

.

Konderla P. Mechanika ośrodków ciągłych

________________________________________________________________________________________

105

W literaturze funkcje pełzania i relaksacji przedstawiane są również w równoważnej postaci

)

(

1

1

1

)

(

/

R

t

H

e

E

t

c

t

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

τ

τ

−

−

=

σ

τ

−

σ

ε

,

(12.29)

)

(

1

1

)

(

/

R

t

H

e

E

t

k

t

⎥

⎦

⎤

⎢

⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

τ

τ

−

−

=

ε

τ

−

ε

σ

.

(12.30)

gdzie stałe

1

2

1

2

2

'

μ

μ

+

μ

μ

η

=

τ

μ

η

=

τ

σ

ε

(12.31)

są odpowiednio czasem relaksacji obciążenia przy stałym odkształceniu i czasem relaksacji od-
kształcenia przy stałym obciążeniu, natomiast gdy

t→∞ element tłumiący doznaje całkowitej

relaksacji, zatem zależność naprężenie-odkształcenie staje się podobna jak dla elementu spręży-
stego i charakteryzuje ją stała

E

R

=

μ

1

nazywana modułem sprężystym relaksacji.

Dla porównania funkcje pełzania i relaksacji dla modeli Maxwella, Voigta i modelu standardo-
wego pokazane są odpowiednio na rys. 12.8 i rys. 12.9.

Rys.12.9. Funkcje relaksacji dla modelów (a) Maxwella, (b) Voigta, (c) standardowego.

Rys.12.8. Funkcje pełzania dla modelów (a) Maxwella, (b) Voigta, (c) standardowego.

Kurs na Studiach Doktoranckich Politechniki Wrocławskiej (wersja: styczeń 2007)
________________________________________________________________________________________

106

Rys. 12.10. Złożone modele materiału lepkosprężystego

Na podobnej zasadzie jak to pokazano dla modelu standardowego można budować bardziej zło-
żone modele lepkosprężyste. Przykładowo na rys. 12.10 pokazano schematy złożonych modeli
mechanicznych materiału lepkosprężystego.

Dla modelu pokazanego na rys. 12.10a, będący uogólnieniem modelu Kelvina, mamy

,

...

oraz

...

,

D

,

2

1

2

1

2

1

1

0

n

ε

+

+

ε

+

ε

=

ε

σ

=

ε

η

+

ε

μ

σ

=

ε

μ

(12.32)

stąd

.

1

D

1

...

D

1

1

1

1

1

0

ε

=

σ

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

μ

+

η

+

μ

+

+

η

+

μ

+

μ

+

n

n

n

(12.33)

Analogicznie dla modelu pokazanego na rys. 12.10b (uogólnienie modelu Maxwella) mamy

...

,

D

1

1

,

D

,

1

1

1

1

1

1

1

1

1

1

1

σ

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

η

+

μ

=

ε′′

+

ε′

=

ε

⇒

σ

=

ε′′

η

σ

=

ε′

μ

(12.34)

stąd

.

D

D

D

...

D

D

...

1

1

1

1

1

0

1

1

0

ε

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

η

+

η

+

μ

η

μ

+

+

η

+

μ

η

μ

+

μ

+

=

σ

+

+

σ

+

σ

=

σ

+

+

n

n

n

n

n

n

(12.35)

Aby otrzymać jawną postać konstytutywnego równania różniczkowego z równań (33) i (35) na-
leży przedstawić je w postaci wielomianu eliminując mianowniki ułamków, a następnie iloczyny

Konderla P. Mechanika ośrodków ciągłych

________________________________________________________________________________________

107

operatora różniczkowego D i funkcji naprężenia oraz odkształcenia traktować jako pochodne po
czasie.

3. Równania konstytutywne ciała lepkosprężystego

Zależności między naprężeniem a odkształceniem sformułowane w poprzednich rozdziałach
uogólniono na kontinuum trójwymiarowe. W tym celu zastąpiono zależność naprężenie-
odkształcenie zależnością tensorową.

Przyjęto, że układem odniesienia będzie kartezjański układ współrzędnych i promień wektor
dowolnego punktu ma współrzędne

(

)

3

2

1

,x

,x

x

=

= x

r

.

Wprowadza się następujące oznaczenia: tensor naprężenia σ

ij

, tensor odkształcenia

ε

ij

w każdym

punkcie x ciała w przedziale czasu

(

)

+∞

<

<

∞

−

t

. Zakłada się że pole odkształceń

ε

ij

(x

,t), pole

przemieszczeń

u

i

(x,

t) i pole prędkości v

i

(x,

t) są nieskończenie małe.

Stąd pochodna cząstkowa względem czasu

t

ij

∂

ε

∂

jest równa pochodnej materialnej

ij

ε& z dokład-

nością do nieskończenie małych pierwszego rzędu.

Liniowy materiał lepkosprężysty dla kontinuum trójwymiarowe dla ciągłego i różniczkowalnego
pola odkształceń można zdefiniować następująco:

τ

τ

τ

∂

ε

∂

τ

−

=

σ

∫

∞

−

d

)

,

(

)

,

(

)

,

(

x

t

x

G

t

x

t

kl

ijkl

ij

(12.36)

Jest to prawo naprężenie-odkształcenie typu relaksacyjnego.

G

ijkl

jest polem tensorowym 4-tego

rzędu

− tensorową funkcją relaksacyjną. Równanie postaci (36) w literaturze nosi nazwę splotu

całkowego funkcji

G

ijkl

oraz

ε

ij

.

Jeżeli przyjąć, że dla

t<0 naprężenie

σ

ij

=0 i

ε

ij

=0 oraz

ε

ij

≠0 dla

t=0 wówczas równanie (36)

przyjmuje postać

τ

τ

τ

∂

ε

∂

τ

−

+

ε

=

σ

∫

+

d

)

,

(

)

,

(

)

0

,

(

)

,

(

)

,

(

0

x

t

x

G

x

t

x

G

t

x

t

kl

ijkl

kl

ijkl

ij

(12.37)

W przypadku występowania nieciągłości pola odkształceń w postaci „skoków” pola odkształceń,
wówczas dla każdej takiej nieciągłości pola odkształcenia o wartość

ij

ε

Δ w chwili t=ξ równanie

(37) należy dodatkowo uzupełnić o człon

)

(

)

,

(

)

,

(

ξ

−

ξ

ε

Δ

t

H

x

t

x

G

kl

ijkl

.

Podobnie definiujemy prawo naprężenie-odkształcenie typu pełzania (uzupełniając to równanie
w dodatkowe człony w przypadku nieciągłości pola naprężeń)

τ

τ

τ

∂

σ

∂

τ

−

=

ε

∫

∞

−

d

)

,

(

)

,

(

)

,

(

,

x

t

x

J

t

x

t

l

k

ijkl

ij

(12.38)

gdzie

J

ijkl

jest polem tensorowym 4-tego rzędu

− tensorową funkcją pełzania.

W dalszym ciągu dla uproszczenia zapisu wprowadza się skrócony zapis iloczynu splotowego.
Oznaczając przez

φ i ψ funkcje określone odpowiednio w przedziałach 0≤ t <∞ i -∞< t <∞ moż-

Kurs na Studiach Doktoranckich Politechniki Wrocławskiej (wersja: styczeń 2007)
________________________________________________________________________________________

108

na przedstawić następujące wyrażenie całkowe

)

0

(

)

(

)

(

d

d

)

(

)

(

0

ψ

ϕ

+

τ

τ

τ

ψ

τ

−

ϕ

=

∫

t

d

t

t

I

t

.

(12.39)

Jeśli całka istnieje dla każdego

t z przedziału (0,∞) to funkcja I(t) nazywana jest splotem φ i ψ i

w skrócie jest oznaczana jako

ψ

∗

ϕ

=

d

)

(t

I

.

(12.40)

Iloczyn splotowy ma następujące własności:

– przemienność:

ϕ

ψ

=

ψ

∗

ϕ

d

*

d

,

– łączność:

θ

ψ

∗

ϕ

=

θ

ψ

∗

ϕ

d

*

)

d

(

)

d

*

d(

, (12.41)

– rozdzielność:

θ

ϕ

+

ψ

∗

ϕ

=

θ

+

ψ

∗

ϕ

d

*

d

)

d(

.

Zatem wzory (36) oraz (38) można zapisać następująco:

ijkl

kl

kl

ijkl

ij

G

G

d

d

∗

ε

=

ε

∗

=

σ

,

(12.42)

ijkl

kl

kl

ijkl

ij

J

J

d

d

∗

σ

=

σ

∗

=

ε

.

(12.43)

Aksjomat o nieistnieniu wstecznego działania mówi, że dla czasu

−∞< t <0

G

ijkl

= 0 oraz

J

ijkl

=

0.

(12.44)

W przypadku materiału izotropowego tensor

G

ijkl

charakteryzuje się niezmienniczością wzglę-

dem obrotu układu współrzędnych. Zatem

G

ijkl

musi być tensorem izotropowym i wówczas

można go przedstawić w postaci

(

)

jk

il

jl

ik

kl

ij

ijkl

G

G

G

G

δ

δ

+

δ

δ

+

δ

δ

−

=

2

3

1

1

2

,

(12.45)

gdzie G

1

, G

2

są funkcjami skalarnymi spełniającymi warunek (44) i nazwane funkcjami relaksa-

cyjnymi dla ścinania i izotropowe ściskania. Funkcje te są odpowiednikami modułu Kirchhoffa
μ oraz modułu ściśliwości K dla ciał sprężystych izotropowych.

W takim razie dla materiału izotropowego związek konstytutywny (42) można zapisać równo-
ważnie jako prawo zmiany postaci i prawo zmiany objętości

kk

kk

kk

ij

ij

ij

G

G

G

G

ε

∗

=

∗

ε

=

σ

ε

∗

=

∗

ε

=

σ

d

d

'

d

d

'

'

2

2

1

1

(12.46)

gdzie

ij

ij

'

,

'

ε

σ

są składowymi dewiatora naprężenia i odkształcenia:

kk

ij

ij

ij

kk

ij

ij

ij

ε

δ

−

ε

=

ε

σ

δ

−

σ

=

σ

3

1

'

,

3

1

'

(12.47)

Analogicznie prawo naprężenie-odkształcenie typu pełzania dla ciała izotropowego ma postać

kk

kk

kk

ij

ij

ij

J

J

J

J

σ

∗

=

∗

σ

=

ε

σ

∗

=

∗

σ

=

ε

d

d

'

'

d

d

'

'

2

2

1

1

(12.48)

gdzie

J

1

, J

2

– funkcje pełzania dla ścinania i izotropowe ściskania.

Konderla P. Mechanika ośrodków ciągłych

________________________________________________________________________________________

109

Jeśli

G

ijkl

,

J

ijkl

lub

G

1

, G

2

,

J

1

, J

2

są funkcjami Heaviside’a (ze względu na czas) to związki kon-

stytutywne redukują się do związków konstytutywnych dla ciała liniowo sprężystego.

4. Równania konstytutywne w formie równań różniczkowych

W przypadku, kiedy funkcja relaksacyjna składa się ze skończonego widma, wówczas możliwe
jest przedstawienie równań konstytutywnych dla materiału lepkosprężystego w postaci równania
różniczkowego.

Niech D

k

oznacza się operator różniczkowania względem czasu

k

k

k

t

t

f

f

∂

∂

=

)

(

D

.

(12.49)

Definiujemy wielomianowe operatory różniczkowe postaci

,

D

Q

,

D

P

,

D

Q

,

D

P

2

2

1

1

0

0

2

2

m

0

k

1

0

1

∑

∑

∑

∑

=

=

=

=

=

=

=

=

n

k

m

k

k

k

k

k

k

k

n

k

k

k

d

c

b

a

(12.50)

gdzie

a

k

,

b

k

,

c

k

,

d

k

są funkcjami rzeczywistymi współrzędnych przestrzennych

x

1

,

x

2

,

x

3

, przy

czym współczynniki główne

a

n

1

,

b

m

1

,

c

n

2

,

d

m

2

są różne od zera, tak więc wielomiany P

1

, P

2

, Q

1

,

Q

2

są odpowiednio rzędu

n

1

,

n

2

,

m

1

,

m

2

.

Na podstawie powyższych założeń równania konstytutywne dla izotropowego liniowego mate-
riału lepkosprężystego (46) można przedstawić w równoważnej postaci

⎩

⎨

⎧

ε

=

σ

ε

=

σ

kk

kk

ij

ij

2

2

1

1

Q

P

'

Q

'

P

(12.51)

Jeśli równanie konstytutywne dla danego materiału może być wyrażone w postaci całkowej i
różniczkowej to można określić zależność między funkcją relaksacyjną (lub pełzania) a operato-
rami różniczkowymi.

1. Dokonujemy transformacji Laplace’a równań

5

(46) i (48)

),

(

)

(

)

(

),

(

'

)

(

)

(

'

2

1

s

s

G

s

s

s

s

G

s

s

kk

kk

ij

ij

ε

=

σ

ε

=

σ

(12.52)

).

(

)

(

)

(

),

(

'

)

(

)

(

'

2

1

s

s

J

s

s

s

s

J

s

s

kk

kk

ij

ij

σ

=

ε

σ

=

ε

(12.53)

2. Podobnie transformujemy równania (51)

5

Transformacja Laplace’a splotu: L[f *g] = L[f] L[g]

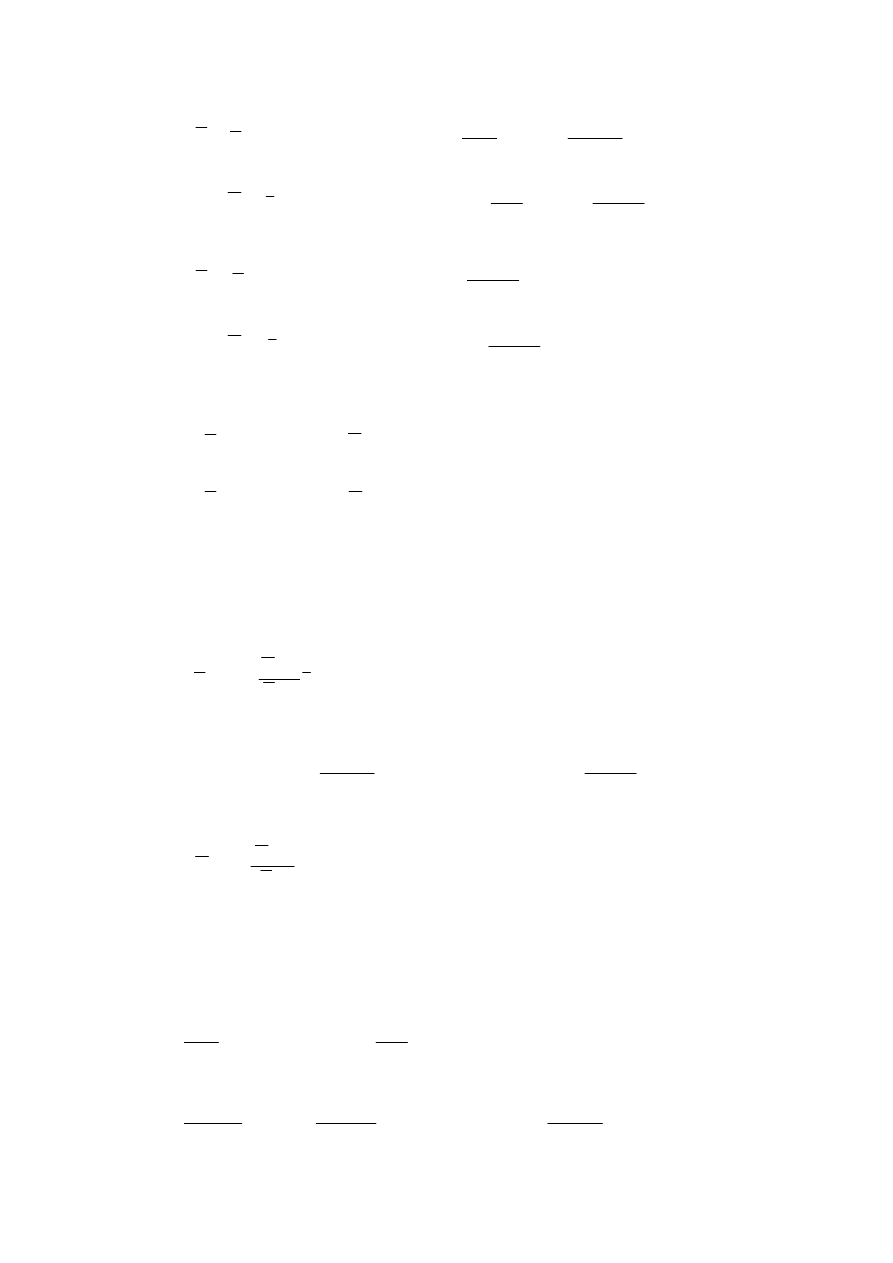
Kurs na Studiach Doktoranckich Politechniki Wrocławskiej (wersja: styczeń 2007)
________________________________________________________________________________________

110

,

)

0

(

'

)

0

(

'

)

0

(

'

)

(

'

)

(

)

0

(

'

)

0

(

'

)

0

(

'

)

(

'

)

(

1

1

1

1

1

2

1

1

1

1

2

1

1

1

∑

∑

=

−

−

−

−

−

−

−

−

=

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

∂

ε

∂

+

+

∂

ε

∂

+

ε

−

ε

=

=

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

∂

σ

∂

+

+

∂

σ

∂

+

σ

−

σ

m

k

k

ij

k

ij

k

ij

k

k

ij

k

ij

k

ij

k

ij

k

n

k

k

ij

t

t

s

s

b

s

s

Q

t

t

s

s

a

s

s

P

L

L

(12.54)

,

)

0

(

)

0

(

)

(

)

(

)

0

(

)

0

(

'

)

(

'

)

(

2

2

1

1

1

1

2

1

1

1

1

2

∑

∑

=

−

−

−

−

−

−

=

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

∂

ε

∂

+

+

ε

−

ε

=

=

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

∂

σ

∂

+

+

σ

−

σ

m

k

k

jj

k

jj

k

k

jj

k

ij

k

jj

k

n

k

k

jj

t

s

d

s

s

Q

t

s

c

s

s

P

L

L

(12.55)

gdzie

⎪

⎪
⎩

⎪

⎪
⎨

⎧

=

=

=

=

∑

∑

∑

∑

=

=

=

=

2

2

1

1

0

0

2

2

m

0

k

1

0

1

)

(

,

)

(

)

(

,

)

(

n

k

m

k

k

k

k

k

k

k

n

k

k

k

s

d

s

Q

s

c

s

P

s

b

s

Q

s

a

s

P

(12.56)

3. To czy równania (54) i (55) mogą być traktowane jako prawo relaksacyjne czy pełzania zale-

ży od tego czy odpowiednio

n

1

≥m

1

,

n

2

≥m

2

.

4. Jeśli

n

1

≥m

1

wtedy (54) ma postać:

)

(

'

)

(

)

(

)

(

'

1

1

s

s

P

s

Q

s

ij

ij

ε

=

σ

,

(12.57)

jeżeli spełniony jest warunek początkowy

0

)

0

(

'

)

0

(

'

)

0

(

'

)

0

(

'

1

1

1

1

1

1

1

1

1

1

≡

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

∂

ε

∂

+

+

ε

−

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

∂

σ

∂

+

+

σ

∑

∑

=

−

−

−

−

−

−

=

m

k

k

ij

k

ij

k

k

k

ij

k

ij

k

n

k

k

t

s

b

t

s

a

L

L

. (12.58)

Wówczas równanie (57) można traktować jako prawo relaksacyjne gdzie

)

(

)

(

)

(

1

1

1

s

P

s

s

Q

s

G

=

.

(12.59)

5. Warunek początkowy (58) jest wielomianem wielkości

s. Każdy współczynnik wielomianu

musi być równy zero.

Tak więc gdy

n

1

=m

1

to

⎪

⎪

⎪

⎪

⎩

⎪⎪

⎪

⎪

⎨

⎧

ε

+

+

∂

ε

∂

=

σ

+

+

∂

σ

∂

+

∂

σ

∂

ε

+

∂

ε

∂

=

σ

+

∂

σ

∂

ε

=

σ

−

−

−

−

−

−

−

−

−

).

0

(

'

)

0

(

'

)

0

(

'

)

0

(

'

)

0

(

'

),

0

(

'

)

0

(

'

)

0

(

'

)

0

(

'

),

0

(

'

)

0

(

'

1

1

1

1

2

2

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

ij

n

ij

n

n

ij

n

ij

n

n

n

ij

n

n

ij

n

ij

n

ij

n

ij

n

ij

n

ij

n

b

t

b

a

t

a

t

a

b

t

b

a

t

a

b

a

K

K

L

(12.60)

Jeśli

m

1

<n

1

wtedy współczynniki w równaniach (58) ze wskaźnikami

k>m

1

muszą być zastą-

Konderla P. Mechanika ośrodków ciągłych

________________________________________________________________________________________

111

pione przez zera.

6. Jeśli

n

1

≤m

1

wtedy (54) ma postać:

)

(

'

)

(

)

(

)

(

'

1

1

s

s

Q

s

P

s

ij

ij

σ

=

ε

(12.61)

jeśli zachodzi warunek początkowy (58).
Wówczas równanie (57) można traktować jako prawo pełzania gdzie

)

(

)

(

)

(

1

1

1

s

Q

s

s

P

s

J

=

.

(12.62)

7. Jeśli

n

1

=m

1

wtedy materiał może być zdefiniowany przez prawo konstytutywne typu pełzania

lub relaksacyjnego.

5. Zagadnienie graniczne (początkowo-brzegowe)

Ruch ciała lepkosprężystego podporządkowany jest prawom zachowania masy i pędu, zależno-
ściom między naprężeniem i odkształceniem, warunkom brzegowym i początkowym.

Oznaczamy przez

u

i

,

ε

i

, σ

ij

,

X

i

odpowiednio składowe kartezjańskie przemieszczenia, odkształ-

cenia, naprężenia i sił masowych na jednostkę objętości, a przez

ρ – gęstość masy. Dla ciał lep-

kosprężystych jednorodnych izotropowych i nieskończenie małych przemieszczeń możemy za-
pisać następujące równania

definicja

odkształcenia

(

)

i

j

j

i

ij

u

u

,

,

2

1

+

=

ε

,

(12.63)

równanie

ciągłości

0

=

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

ρ

∂

∂

+

∂

ρ

∂

t

u

x

t

i

i

,

(12.64)

równanie ruchu

2

2

,

t

u

X

i

i

j

ij

∂

∂

=

+

ρ

σ

,

ji

ij

σ

σ

=

, (12.65)

równania konstytutywne w trzech możliwych sformułowaniach:

a) prawo relaksacyjne

1

'

'

dG

ij

ij

∗

ε

=

σ

2

dG

kk

kk

∗

ε

=

σ

(12.66a)

b) prawo pełzania

1

'

'

dJ

ij

ij

∗

σ

=

ε

2

dJ

kk

kk

∗

σ

=

ε

(12.66b)

c) w postaci równań różniczkowych

kk

kk

ij

ij

ε

=

σ

ε

=

σ

2

2

1

1

Q

P

'

Q

'

P

(12.66c)

warunki

początkowe dla stanu naturalnego:

0

=

σ

=

ε

=

ij

ij

ij

u

dla

-∞<t<0

(12.67)

W przypadku stosowania równań (66c) w chwili początkowej

t=0 zachodzi skok ciągłości de-

Kurs na Studiach Doktoranckich Politechniki Wrocławskiej (wersja: styczeń 2007)
________________________________________________________________________________________

112

wiatora odkształcenia bądź naprężenia, wówczas warunki początkowe muszą określać pole od-
kształcenia i pochodne tego pola w chwili początkowej

),

0

(

'

...

),

0

(

'

),

0

(

'

+

+

+

∂

ε

∂

∂

ε

∂

ε

n

ij

n

ij

ij

t

t

(12.68)

jak również pole naprężenia i jego pochodne

),

0

(

'

...

),

0

(

'

),

0

(

'

+

+

+

∂

σ

∂

∂

σ

∂

σ

n

ij

n

ij

ij

t

t

(12.69)

a ponadto powyższe wartości muszą spełniać warunki konieczne (60)

,

,...,

2

,

1

dla

)

0

(

'

)

0

(

'

n

r

t

b

t

a

r

k

ij

r

k

n

r

k

k

r

k

ij

r

k

n

r

k

k

=

∂

ε

∂

=

∂

σ

∂

+

−

−

=

+

−

−

=

∑

∑

(12.70)

gdzie

n jest liczbą większą z dwóch liczb będących stopniami wielomianu P

1

i Q

1

.

Warunki brzegowe mogą mieć postać albo zadanych sił powierzchniowych na powierzchni

S

σ

z

normalną zewnętrzną

n

i

(warunki kinetyczne)

i

j

ij

p

n

=

σ

na

S

σ

,

(12.71)

albo zadanych przemieszczeń na powierzchni

S

u

i

i

z

u

= na S

u

,

(12.72)

gdzie

p

i

, z

i

są z góry danymi funkcjami miejsca i czasu oraz

S = S

σ

+ S

u

.

Zagadnienie teorii lepkosprężystości liniowej polega na wyznaczeniu

u

i

,

e

ij

,

σ

ij

dla zadanych

X

i

,

p

i

,

z

i

oraz danych warunków początkowych. Z wyjątkiem prawa konstytutywnego (prawa naprę-

żenie-odkształcenie) identyczne równania mamy w liniowej teorii sprężystości.