CZĘŚĆ 1. POZNANIE NAUKOWE JAK PRZEDMIOT ANALIZY

PODZIAŁ NAUK

Ze względu na metodę:

•

DEDUKCYJNE - posługują się metodami dedukcyjnymi, czyli niezawodnymi (matematyka i logika)

•

INDUKCYJNE - posługują się (obok metod dedukcyjnych) również metodami indukcyjnymi, czyli nie-niezawodnymi

Ze względu na zależność od doświadczenia:

•

APRIORYCZNE = niezależne od doświadczenia. Np. "każda liczba podzielna przez 4 jest podzielna przez 2"

•

APOSTERIORYCZNE = zależne od doświadczenia. Np. "Odległość między Warszawą i Paryżem wynosi 1500km"

Ze względu na przedmiot poznania:

•

REALNE (o rzeczywistości, np. fizyka, historia)

•

FORMALNE (o wytworach umysłu: matematyka, logika)

Nauki formalne są jednocześnie dedukcyjne i aprioryczne.

Nauki realne są jednocześnie indukcyjne i aposterioryczne.

Ze względu na stawiane zadania:

•

TEORETYCZNE (zajmujące się poznaniem)

•

PRAKTYCZNE (zajmujące się działaniem)

- prakseologiczne - teorie skutecznego działania (jak działać aby osiągnąć cel?);
- aksjologiczne - uzasadniające działania (dlaczego należy postępować w taki właśnie sposób?).

NAUKI EMPIRYCZNE

Są to nauki realne, indukcyjne, aposterioryczne, czyli nauki, które formułują twierdzenia dotyczące świata realnego i sprawdzają
(testują) je w oparciu o doświadczenie lecz ich twierdzenia nigdy nie są pewne (choć mogą być bardzo mocno potwierdzone przez
fakty). Przeciwieństwem są nauki nieempiryczne, takie jak matematyka i logika. Jako wzorzec metodologiczny dla nauk empirycznych
wskazuje się zwykle fizykę ale nie wszystkie nauki mogą być uprawiane tak jak fizyka. Dziś wskazuje się często, że innym wzorcem stają
się nauki biologiczne.

PODZIAŁ NAUK EMPIRYCZNYCH

Ze względu na charakter formułowanych twierdzeń

•

NOMOTETYCZNE - formułujące prawa mówiące o istnieniu ogólnych zależności ( np. prawa fizyki).

•

IDIOGRAFICZNO-TOPOLOGICZNE
- idiograficzne (opisowe) – zajmujące się opisem zjawisk - np. historia wojen napoleońskich
- typologiczne – ustalające typy (wzory) zjawisk – np. kultura renesansu

Ze względu na rodzaj podejmowanych problemów

•

PODSTAWOWE – np. badanie problemów ogólnych, np. badanie mechanizmu modyfikowania aktywności mięśni
szkieletowych za pomocą biofeedbacku.

•

STOSOWANE – np. stosowanie wiedzy ogólnej do rozwiązywania problemów szczegółowych): np. zastosowanie EMG-
biofeedbacku do leczenia napięciowego bólu głowy.

Ze względu na przedmiot

•

PRZYRODNICZE: o przyrodzie nieożywionej i ożywionej. Istnieją duże różnice metodologiczne między naukami o
przyrodzie nieożywionej i ożywionej, na przykład – między takimi naukami jak fizyka i biologia. Świadomość tych różnic
istniała od dawna. Przykładowo, w XVII wieku, w okresie narodzin współczesnej nauki, stosowano podział nauk
przyrodniczych (o naturze) na filozofię naturalną (np. fizyka, astronomia) i historię naturalną (np. botanika, zoologia).

•

HUMANISTYCZNE: o człowieku i społeczeństwie, wytworach kultury oraz dziejach człowieka i jego wytworów

W literaturze anglosaskiej termin "SCIENCE" oznaczał początkowo tylko nauki przyrodnicze. Dziś używa się go w szerszym
znaczeniu i określa nim wszystkie NAUKI EMPIRYCZNE a czasem nawet wszystkie nauki empiryczne i nieempiryczne (formalne).

Nadal jednak podkreśla się opozycję: filozofia – nauka. PSYCHOLOGIA jest dyscypliną empiryczną z pogranicza nauk
humanistycznych i przyrodniczych (biologicznych).

NAUKI O NAUCE

EMPIRYCZNE - badające naukę jako wytwór kultury

•

psychologia nauki - psychologiczne uwarunkowania twórczości naukowej

•

socjologia nauki - Społeczne uwarunkowania rozwoju nauki

•

historia nauki - dzieje nauki, dzieje instytucji naukowych, itp.

•

polityka naukowa - jak kierować instytucjami naukowymi

FILOZOFICZNE

•

Metodologia nauki - zajmuje się analizą metod naukowych i wytworów działalności naukowej

•

Filozofia nauki - bada najbardziej podstawowe problemy poznania naukowego (np. przedmiot poznania naukowego,
wartość poznania naukowego, podstawowe założenia poznania naukowego)

METODOLOGIA NAUK

•

APRAGMATYCZNA - o wytworach działalności naukowej (teoria systemów dedukcyjnych, analiza teorii w naukach
empirycznych)

•

PRAGMATYCZNA - o czynnościach naukowych: jak się uprawia lub jak powinno się uprawiać naukę (np. jak dobierać próbę do
badań) – podział wg Ajdukiewicza

- OGÓLNA - zajmuje się metodami stosowanymi we wszystkich naukach (np. zasady wnioskowania indukcyjnego)
- SZCZEGÓŁOWA - zajmuje się metodami specyficznymi dla poszczególnych nauk (np. zasady konstrukcji testów

psychologicznych)

- OPISOWA - jak (faktycznie) uprawia się naukę
- NORMATYWNA - jak powinno się uprawiać naukę

CZYM JEST A CZYM NIE JEST NAUKA?



Dąży do poznania prawdy (stworzenia możliwe dokładnej reprezentacji rzeczywistości)



Dąży do wyjaśniania zjawisk i tworzenia spójnych systemów wyjaśniających (teorii)



Poddaje swoje twierdzenia systematycznej kontroli empirycznej

Nauka (empiryczna) udziela odpowiedzi na pytania:

•

jak jest (opis)

•

dlaczego tak jest (wyjaśnianie)

•

czego można oczekiwać w przyszłości (przewidywanie)

•

co należy zrobić aby osiągnąć dany cel (funkcja praktyczna)

Nauka nie jest jednak w stanie udzielać odpowiedzi na pytania wartościujące, np.: co jest dobre? jak należy postępować? do jakiego
celu należy dążyć? (może natomiast wskazywać metody prowadzące do osiągnięcia jakiegoś celu jeśli cel ten został wcześniej
wskazany ). Nauka pozostawia te problemy innym dziedzinom refleksji (np. filozofii, teologii)

Wiedza naukowa nie jest też:

•

mądrością (jak osiągnąć szczęście? odnaleźć sens życia?)

•

światopoglądem (tzw. „światopogląd naukowy” zawiera zawsze obok elementów naukowych elementy pozanaukowe)

CZĘŚĆ 2. POJĘCIA I ICH DEFINIOWANIE

NIEKTÓRE POJĘCIA LOGICZNE UŻYWANE W WYKŁADZIE

~ lub ¬

negacja ( ~p ; nieprawda że p)



koniunkcja ( p q ; p



i q, zarówno p jak q)



alternatywa ( p q ; p



lub q, co najmniej jedno z dwóch p lub

lub ,



 

implikacja ( p q ;



jeśli p to q; jeśli p to wykluczone że nie q)



tożsamość (p q; p



zawsze wtedy i tylko wtedy gdy q)

P(x)

(P od x) ; x ma własność P (np. „x jest studentem”)

~P(x)

nieprawda że x ma własność P

xRx lub R(x,y)

relacja R zachodzi między przedmiotami x i y (np.: x jest

większy od y)

lub





kwantyfikator duży (ogólny)

x P(x) –



dla każdego x, P od x; (inaczej: każdy przedmiot x z

rozważanej dziedziny ma własność P; np. każdy człowiek jest

rozumny)

lub





kwantyfikator mały (szczegółowy)

x P(x) –



istnieje takie x, że x ma własność P

x y P(x,y) –

 

dla każdego x istnieje takie y, że x pozostaje w

relacji P do y

Np. Dla każdej liczby naturalnej x istnieje liczba naturalna y taka,

że x jest mniejsze od y.

ZAGADNIENIA WSTĘPNE

Teoria znaków (w tym – językowych) nazywa się semiotyką. Podstawowe działy semiotyki:

•

SYNTAKTYKA zajmuje się relacjami zachodzącymi między wyrażeniami (przykład: sprzeczność między dwoma zdaniami)

•

SEMANTYKA zajmuje się relacjami między wyrażeniami a rzeczywistością do której się one odnoszą (przykład: oznaczanie,
prawda)

•

PRAGMATYKA zajmuje się relacjami między wyrażeniami a ich użytkownikami, tj. nadawcami i odbiorcami wyrażeń (przykład:
rozumienie wyrażeń).

KATEGORIE SYNTAKTYCZNE WYRAŻEŃ I ICH CHARAKTERYSTYKA

ZDANIA

NAZWY

FUNKTORY

1. ZDANIE

W sensie logicznym to wyrażenie, któremu przysługuje wartość logiczna (w logice dwuwartościowej: prawda lub fałsz). Inaczej –
wyrażenie, które coś stwierdza (zdanie kategoryczne). Jeśli jest tak jak stwierdza zdanie p, zdanie p jest prawdziwe. Jeśli tak nie
jest - zdanie p jest fałszywe. Nie wszystkie zdania w sensie gramatycznym są zdaniami

w sensie logicznym. Nie są nimi:

•

pytania (zdania pytajne), np. Czy dzisiaj jest wtorek?

•

oceny, np. Zdrowie jest rzeczą dobrą.

•

dyrektywy, np. Należy myć zęby.

Ze względu na sposób rozstrzygania prawdziwości zdań można je podzielić na:

•

Zdania a priori (przed doświadczeniem) - zdania których prawdziwość jest niezależna od doświadczenia (na
przykład, twierdzenia logiki i matematyki).

•

Zdania a posteriori (po doświadczeniu) – zdania których prawdziwość ustalana jest w oparciu o doświadczenie
(przykład: zdania obserwacyjne, prawa indukcyjne).

−

zdania analityczne - są prawdziwe na mocy znaczenia jakie posiadają w danym języku. Zdaniu
takiemu nie można zaprzeczyć bez popadnięcia w wewnętrzną sprzeczność. Przykład: „centymetr
jest setną częścią metra”. Zdaniami analitycznymi są, w szczególności, wszystkie prawa logiki.
Zdania analityczne nie stwierdzają nic o rzeczywistości ani też nie można z nich takiej wiedzy
wydedukować.

−

zdania syntetyczne - stwierdzają coś, co wykracza poza samo znaczenie zawartych w nim
terminów. Ich zaprzeczenie nie prowadzi do wewnętrznej sprzeczności. Przykład: „Sevilla leży nad
rzeką Guadalquivir”.

Stary problem filozoficzny: czy istnieją zdania syntetyczne a priori? Dominuje pogląd, że wszystkie zdania analityczne są a priori
(tzn. ich prawdziwość nie zależy od doświadczenia, nie posiadają bowiem treści empirycznej), a wszystkie zdania syntetyczne są
a posteriori (ich prawdziwość zależy od zgodności z doświadczeniem). Kant uważał że istnieją zdania syntetyczne a priori,
stanowiące fundament nauki (np. „wszystko ma swoją przyczynę”). Ich podstawą są transcendentalne, aprioryczne kategorie
umysłu, które nie wywodzą się z doświadczenia zmysłowego ale warunkują to doświadczenie.

Kategorie Kanta (za Heller, 2005)



kategorie ilości: jedność wielość, całość



kategorie jakości: rzeczywistość, negacja, ograniczenie



kategorie stosunku: substancja i przypadłość, przyczyna i skutek, akcja i reakcja



kategorie modalności: możliwość i niemożliwość, istnienie i nieistnienie, konieczność i względność

Stanowisko Kanta znalazło nową interpretację na gruncie ewolucyjnej teorii poznania. Selekcja ewolucyjna „faworyzowała”
organizmy, które potrafiły najlepiej wykorzystać informację o środowisku. Sposób odbioru i oceny informacji jest częściowo
ukształtowany filogenetycznie (filogenetyczne a posteriori) i determinuje aktywność poznawczą osobnika (ontogenetyczne a
priori wiedza wrodzona)



2. NAZWA

Wyrażenie, które może pełnić w zdaniu funkcję podmiotu lub orzecznika (np. WARSZAWA jest STOLICĄ POLSKI). To także
wyrażenie które pełni funkcję oznaczania swoich desygnatów (desygnat – przedmiot o którym można nazwę zgodnie z prawdą
orzec (np. „to jest stół” - nazwę stół orzekamy o tym oto przedmiocie).

RODZAJE NAZW



INDYWIDUALNE (INDYWIDUOWE) - przysługują konkretnym, indywidualnym obiektom. Przykłady: Jan Kowalski,
Warszawa



GENERALNE (UNIWERSALNE) - przysługują pewnej klasie obiektów ze względu na jakąś ich cechę (w szczególnym
przypadku klasa ta może być jednoelementowa lub pusta). Przykłady: stół, najwyższa góra świata, krasnoludek.

Ten sam obiekt może być desygnatem nazwy indywiduowej i generalnej, np.:

- ostatni król Polski (nazwa generalna)
- Stanisław August Poniatowski (nazwa indywidualna)

Podział nazw ze względu na liczbę desygnatów



OGÓLNE – wiele desygnatów



JEDNOSTKOWE – jeden desygnat

Podział ze względu na istnienie desygnatów



NIEPUSTE (istnieją desygnaty), np. człowiek.



PUSTE (nie istnieją desygnaty), np. krasnoludek.

2.2 ELEMENTY TEORII NAZW

•

DESYGNATY NAZWY – przedmioty o których orzekamy nazwę

•

ZAKRES NAZWY (denotacja) – zbiór wszystkich jej desygnatów

Nazwa jest ostra (lub zakres nazwy jest ostry) jeśli o każdym przedmiocie można powiedzieć czy jest czy nie jest
desygnatem nazwy. Nazwa ostra dzieli uniwersum na dwie klasy: przedmioty należące i nie należące do zakresu nazwy.
Przykład nazwy nieostrej: młodzieniec.

Stosunki zachodzące między zakresami dwóch nazw:

•

równoważność (równość) zakresów,

•

podrzędność / nadrzędność,

•

krzyżowanie się,

•

wykluczanie się

TREŚĆ NAZWY - zbiór cech przysługujących desygnatom nazwy.

Znaczenie nazwy (sposób rozumienia nazwy) nazywamy POJĘCIEM. Znaczenie nazw jest problemem ogromnie
złożonym. Istnieje wiele koncepcji znaczenia nazwy. ZNACZENIE nazwy jako KONOTACJA – zespół cech
charakterystycznych dla zakresu nazwy, za pomocą których myślimy o jej desygnatach. Ta sama nazwa może być
rozumiana w różny sposób (nazwy wieloznaczne) i – zależnie od tego – może oznaczać różne przedmioty (mieć różny
zakres). Przykład: zamek jako budowla i zamek jako urządzenie do zamykania drzwi. Należy więc mówić o zakresie nazwy
przy określonym jej znaczeniu.

3. FUNKTORY

Wyrażenia które razem z innymi wyrażeniami (tzw. argumentami) tworzą wyrażenia bardziej złożone. Przykłady:

•

"i" -- funktor zdaniotwórczy od dwóch argumentów zdaniowych, np. "Jan jest przystojny i Jan jest studentem"

•

"idzie" -- funktor zdaniotwórczy od jednego argumentu nazwowego, np. "Jan idzie"

•

"ładny" -- funktor nazwotwórczy od jednego argumentu nazwowego, np. "ładny dzień"

DEFINICJE

Ścisłe definiowanie pojęć umożliwia precyzyjne formułowanie sądów o rzeczywistości. Precyzyjne sądy są łatwiejsze do weryfikacji /
falsyfikacji. Ścisłe definiowanie pojęć pozwala unikać sporów pozornych (sporów werbalnych o pozorach sporów rzeczowych, czyli
sporów w których różnica stanowisk wynika z różnego rozumienia tych samych słów). Definicja (najogólniej) to krótkie określenie
czegoś.

Trzy zasadnicze funkcje definicji (wg H. Mortimerowej):



podawać charakterystykę przedmiotu (d. realna);



umożliwiać przekład jednego wyrażenia na inne;



być postulatem znaczeniowym (wprowadzać nowe wyrażenia do języka w oparciu o konwencje językowe).

DEFINICJE NOMINALNE

Definicja NOMINALNA - definicje słów - wprowadza do danego języka wyrażenie za pomocą innych wyrażeń znajdujących się już
w tym języku. Podział definicji nominalnych:

•

Definicja SPRAWOZDAWCZA – zdaje sprawę z zastanego sposobu rozumienia słowa w danym języku. Definicja taka
jest zdaniem rzeczowym (zdaniem w sensie logicznym).

•

Definicje PROJEKTUJĄCE – oparte na konwencji terminologicznej, ustanawiającej sposób rozumienia nowego
wyrażenia. Konwencja terminologiczna nie jest zdaniem w sensie logicznym ale wyraża pewien akt woli, w rodzaju:
„słowo A będę rozumiał w taki to a taki sposób”. Definicja oparta o konwencję terminologiczną nazywa się też
POSTULATEM ZNACZENIOWYM JĘZYKA. Definicje projektujące są zdaniami analitycznymi – nie można im zaprzeczyć
nie popadając w wewnętrzną sprzeczność. Nie są też zależne od doświadczenia (są zdaniami a priori). Wymaga się
natomiast podania „dowodu istnienia” tj. wykazania, że istnieje przedmiot, który tę definicję spełnia.
Wprowadzanie do języka nazw pustych może rodzić problemy logiczne (np. problem wartości logicznej zdań
zawierających nazwy puste).

•

Definicja KONSTRUKCYJNA – definicja podająca nowe znaczenie słowa. Przykład: „Manipulacja eksperymentalna to
przyporządkowanie różnych (co najmniej dwóch) wartości zmiennej niezależnej grupom zrandomizowanym”.

•

Definicja REGULUJĄCA – definicja modyfikująca znaczenie słowa już istniejącego w danym języku (wyostrzająca jego
zakres lub eliminująca wieloznaczność). Przykłady: „Dziecko (w rozumieniu PKP) to osobnik do lat 3”, „Rak, w
rozumieniu niniejszej ustawy, jest rybą”.

NAJWAŻNIEJSZE RODZAJE DEFINICJI NOMINALNYCH

NORMALNE

Definicja NORMALNA jest definicją nominalną, która pozwala wyeliminować w dowolnym zdaniu nowo wprowadzone
wyrażenie przez inne wyrażenia, już istniejące w danym języku. Może mieć postać równości lub równoważności.Definicja
równościowa:

A =

Lewy człon (definiowany) nazywa się definiendum. Prawy człon (definiujący) nazywa się defiens. Znak

nazywa się

równością definicyjną. Przykład: „kwadrat to prostokąt równoboczny”. Definicja normalna której definiendum składa
się tylko z wyrażenia definiowanego nazywa się definicją WYRAŹNĄ. Jeśli definiendum zawiera inne wyrażenia obok
wyrażenia definiowanego mówimy o definicji KONTREKSTOWEJ (lewy człon definicji nazywa się wtedy definitum), np:

kwadrat liczby = a

iloczyn liczby a pomnożonej przez nią samą

Każdą definicję RÓWNOŚCIOWĄ można przekształcić w definicję ROWNOWAŻNOŚCIOWĄ. Definicja równoważnościowa
ma postać równoważności dwóch zdań (gdzie Q jest terminem definiowanym), np:

Qx Px



Figura jest kwadratem zawsze wtedy i tylko wtedy gdy jest prostokątem równobocznym.

WARUNKI POPRAWNOŚCI DEFINICJI NORMALNYCH (w naukach formalnych):



warunek eliminowalności (zastępowalności) - każdą formułę (wyrażenie), zawierającą zdefiniowane wyrażenie,
można zastąpić przez równoważną formułę nie zawierającą tego wyrażenia



warunek nietwórczości - definicja nie powinna być aksjomatem - czegokolwiek można dowieść w teorii T z
dodaną do niej definicją, można też dowieść bez tej definicji.



warunek niesprzeczności - definicja dołączona do systemu (niesprzecznego) nie powinna prowadzić do
sprzeczności.

Definicje w naukach formalnych są ekstensjonalne: znaczenie wyrażenia jest funkcją jego zakresu (jeśli dwa wyrażenia
mają ten sam zakres to mają też to samo znaczenie). Język potoczny nie jest ekstensjonalny (jest intensjonalny).

Przykład: „Jan wie że, ...”

•

Warszawa to Stolica Polski.

•

Warszawa to miasto liczące ponad 1 milion mieszkańców, położone na 21 długości geograficznej wschodniej



i 52 25’ szerokości geograficznej północnej”.



Zakres definiensa jest w obu definicjach (a i b) identyczny. Ale zdanie „Jan wie że Warszawa to A” może okazać się
prawdziwe, gdy A zastąpimy definiensem pierwszej definicji nazwy Warszawa a fałszywe, gdy zastąpimy je definiensem
drugiej definicji.

PRZEZ ABSTRAKCJE

Każdy stosunek równości (równoważności) wyznacza pewien rodzaj (rodzinę) cech. Dwa przedmioty są równe pod
względem pewnej cechy P (mają tę samą cechę P) gdy zachodzi między nimi odpowiedni stosunek równościowy R.

Przykłady:

•

Dwa odcinki mają tę samą (konkretną) długość P gdy są ze sobą przystające (pozostają względem siebie w
relacji przystawania R). Długość (jako taką) można z kolei zdefiniować jako rodzinę (wszystkich) długości

•

Liczbę (określoną) możemy zdefiniować jako cechę przysługującą wszystkim zbiorom równolicznym z danym
zbiorem. Np. liczba pięć jest cechą wszystkich zbiorów równolicznych z liczbą palców jednej ręki. Liczba jako
taka (liczba kardynalna) to rodzina wszystkich (konkretnych) liczb. Tak definiowane cechy nazywa się
RODZINAMI CECH ABSTRAKCJI do stosunku równości (równoważności).

AKSJOMATYCZNE

Definicje aksjomatyczne (inaczej: definicje przez postulaty) służą do definiowania terminów pierwotnych w rachunkach
formalnych. Dzięki takim definicjom unika się sytuacji, kiedy terminy pierwotne pozostają niezdefiniowane (jest to
jednak możliwe tylko w naukach formalnych, np. w logice). Definicja aksjomatyczna polega na odpowiednim użyciu
terminów pierwotnych w aksjomatach (zdaniach pierwotnych systemu). Zdania są dobrane tak, aby (przy założeniu ich
prawdziwości) ograniczały możliwe interpretacje użytych w nich terminów. Definicje aksjomatyczne zalicza się do
definicji

Przykład:

1) x R x
2) x R y  y R x
3) (x R y y R z) x R z





Jeśli zdania 1, 2 i 3 są prawdziwe, to termin R musi oznaczać jakiś rodzaj równości.

Od definicji aksjomatycznej wymaga się aby:

•

układ postulatów określał jednoznacznie rozumienie terminu definiowanego.

•

układ postulatów był niesprzeczny

W języku naturalnym i literaturze naukowej mamy często do czynienia z sytuacją, gdy jakiś termin nie jest zdefiniowany
wprost, natomiast możemy domyślić się jego znaczenia z kontekstu. Z kontekstu uczymy się też najczęściej znaczenia
wyrażeń języka ojczystego.

4. CZĄSTKOWE

Definicje cząstkowe są wyrażeniami w postaci okresu warunkowego (ogólnie: Ax Bx), podającymi tylko



NIEKTÓRE

kryteria stosowalności terminu definiowanego.

Okres warunkowy (zdanie warunkowe) podaje:

•

albo warunek wystarczający (wystąpienie P jest warunkiem wystarczającym dla wystąpienia Q)

Px Qx



„Jeśli x ukończył uniwersytet (P), x ma wyższe wykształcenie (Q)”.

•

albo warunek konieczny (wystąpienie P jest warunkiem koniecznym dla wystąpienia Q, czyli jeśli nie wystąpi P to
nie wystąpi Q):

(~Px ~Qx) (Qx Px)







„Warunkiem (koniecznym) zaliczenia roku (Q) jest zdobycie 60 punktów ECTS (P)”.

Definicje cząstkowe pozwalają orzec definiowany termin tylko o CZĘŚCI przedmiotów – o tych mianowicie, które
spełniają warunek podany w poprzedniku definicji. O pozostałych przedmiotach nie można natomiast orzec czy
posiadają definiowaną cechę. Definicji cząstkowych używamy wtedy, gdy nie jest możliwe podanie definicji
równościowej (równoważnościowej).

Forma definicji cząstkowych:

•

Definicje CZĄSTKOWE w postaci prostego zdania warunkowego

Jeśli żarówka świeci, to żarówka jest dobra”
(ogólnie: Px Qx, gdzie Q jest terminem definiowanym).



Jeśli jednak nie świeci to nie wiadomo czy jest dobra czy nie (mógł się przepalić bezpiecznik, uszkodzić

przewód itp.)

„Jeśli figura nie ma kątów równych to figura nie jest kwadratem” (~Px ~Qx)



Ale jeśli ma kąty równe to nie wiadomo czy jest kwadratem (może być prostokątem).

•

Definicje REDUKCYJNE (zdania redukcyjne) – szczególna postać definicji cząstkowych, wprowadzona
przez Carnapa,. Służą do definiowania terminów teoretycznych za pomocą terminów empirycznych
(„redukują terminy teoretyczne do terminów obserwacyjnych”).

– jednostronne zdanie redukcyjne (Q – termin definiowany):

x (Sx (Px Qx)





– obustronne zdanie redukcyjne:

x (Sx (Px Rx)







•

Definicja operacyjna - rodzaj definicji redukcyjnej wskazującej operacje (czynności) jakie
należy wykonać aby stwierdzić, czy przedmiot ma definiowaną cechę. W szczególności,
definicja operacyjna może wskazywać metodę pomiaru („rozumieć co znaczy dana cecha
to wiedzieć jak ją zmierzyć”). Przykład definicji (w postaci zdania redukcyjnego) w oparciu
o operację pomiarową

„Jeśli osoba dorosła poddana zostanie badaniu testem Ravena to osoba ta ma wysoką

inteligencję zawsze wtedy i tylko wtedy gdy rozwiąże poprawnie co najmniej n zadań

testowych”.

Ogólnie: Jeśli wykonana zostanie na x operacja O, to x ma cechę C zawsze wtedy i tylko
wtedy gdy x uzyska wynik W.

x (Ox  (Cx  Wx)

Definicja operacyjna nie odwołująca się do pomiaru:

„Jeśli umieścimy x w pobliżu opiłków metalu to x jest magnesem zawsze wtedy i tylko

wtedy gdy x przyciąga opiłki”.

Operacjonizm – stanowisko zgodnie z którym pojęcia naukowe powinny być definiowane
za pomocą definicji operacyjnych (Bridgman).

INNE RODZAJE DEFINICJI

1. Definicja REALNA

Jest pojęciem niejasnym i różnie definiowanym. Zgodnie z jednym z ujęć, definicja realna podaje jednoznaczną
charakterystykę jakiegoś przedmiotu. (zakłada się przy tym, że zbiór przedmiotów, o których mowa w definiendum, jest
dobrze określony, tzn. wiadomo jakie przedmioty należą do tego zbioru a jakie nie należą; np. wiadomo co jest
człowiekiem a co nim nie jest nim). Według Marciszewskiego, definicja realna podaje cechy istotne definiowanego
przedmiotu (tzw. definicja istotnościowa). Przykład: „człowiek to istota rozumna”. Powstaje jednak pytanie jak rozumieć
„cechę istotną”. Szczególną postacią definicji realnej jest definicja KLASYCZNA – tzn. definicja przez rodzaj i różnicę
gatunkową (per genus et differentia specifica).

Przykład: „kwadrat to prostokąt równoboczny”.

Niektórzy autorzy nie godzą się na traktowanie definicji jako twierdzeń rzeczowych (czyli twierdzeń o rzeczywistości) i
akceptują tylko definicje nominalne, tj. określające zakres i znaczenie słów. Wg Poppera definicje takie powinny być
czytane „od prawej do lewej”.

Przykład: „szczeniak to młody pies”.

Definicja ta nie udziela odpowiedzi na pytanie „co to jest szczeniak”, ale odpowiada na pytanie „jak nazywamy młodego
psa”.

Pojecie definicji istotnościowej i istoty zjawiska wywodzi się z tradycji sokratejsko-platońsko-arystotelesowskiej (por.
Heller, 2005). Sokrates zastanawiał się nad istotą cnót moralnych (co to jest sprawiedliwość?) a Platon i Arystoteles nad
tym, jak to się dzieje, że rzeczy się zmieniają a jednocześnie zachowują swą tożsamość. Uznali, że zmieniają się
przygodne (niekonieczne) cechy przedmiotów (bytów) a ich istota pozostaje niezmienna. Ta niezmienna istota rzeczy
była określana mianem idei (Platon) substancji i formy (Arystoteles). Celem nauki miało być dociekanie istoty zjawisk
(Arystoteles: „poznanie każdej rzeczy sprowadza się do poznania jej istoty”), czyli szukanie odpowiedzi na pytania w
rodzaju: co to jest czas?, co to jest człowiek?, etc. Odpowiedzi na takie pytania ujmowane były w formę definicji
istotnościowych. Opisane wyżej podejście nazywa się esencjalizmem.

Zdaniem Poppera, nauka nie bada istoty przedmiotów czy zjawisk ale ich zachowanie, bądź zachodzące między nimi
relacje. Nie dociekamy tego jaka jest istota czasu, ale jak go mierzyć, bądź w jakich relacjach pozostaje on do innych
zjawisk bądź procesów. Tworzenie precyzyjnych definicji jest ważne dla zwięzłości języka (dłuższe określenia
zastępujemy krótszymi) i sprawnego komunikowania się, ale nie poszerza wiedzy o świecie. Definicje nie zawierają w
sobie żadnej wiedzy o świecie. Wiedza o świecie zawarta jest w sądach (teoriach naukowych). Pełne zdefiniowanie
wszystkich terminów naukowych jest zresztą niemożliwe (regressus ad infinitum) a ich znaczenie zmienia się z postępem
nauki.

2. Definicje OSTENSYWNE - (inaczej: „dejktyczne”, „przez pokazywanie”).

Służą do definiowania terminów obserwacyjnych, np:

„To (pokazujemy dany przedmiot) jest KOŃ”

NIEKTÓRE BŁĘDY DEFINIOWANIA

Nieostrość

Definicja (równościowa lub równoważnościowa) jest NIEOSTRA jeśli o niektórych przedmiotach nie można orzec czy są czy też nie są
desygnatami definiowanego wyrażenia.

Np.: „Dziecko to osobnik młody”

Jeśli zakresy definiendum i definiensa pokrywają się definicję nazywamy adekwatną. Jeśli zakres definiensa obejmuje przedmioty nie
należące do definiendum – definicja ZA SZEROKA (np. kwadrat to figura prostokątna). Jeśli zakres definiensa nie obejmuje wszystkich
przedmiotów należących do definiendum definicja jest ZA WĄSKA (np. student to osoba ucząca się na uniwersytecie). Może się zdarzyć,
że człony definicji krzyżują się (definicja taka jest jednocześnie za wąska i za szeroka)

Idem per idem (to samo przez to samo) lub błędne koło w definiowaniu (circulus in definiendo)

Błąd polegający na użyciu w definiensie wyrażenia definiowanego.

Przykład: „Definicja to zdanie podające definicję wyrażenia”

Zwykle mamy do czynienia z błędnym kołem pośrednim: termin a definiujemy za pomocą terminu b, b za pomocą c, c za pomocą ... a.
Ponieważ jednak nie można iść w definiowaniu pojęć w nieskończoność (regressus ad infinitum) pewne pojęcia muszą pozostać
niezdefiniowane.

Błąd ignotum per ignotum (nieznane przez nieznane)

Definiowanie słowa nieznanego odbiorcy za pomocą innych wyrażeń również mu nieznanych. Jest to błąd ze względu na odbiorcę
definicji - ta sama definicja może być zrozumiała dla jednego odbiorcy a niezrozumiała dla innego.

„Wariancja to kwadrat odchylenia standardowego”

„Wariancja to miara zróżnicowania jakiegoś zbioru wyników”

TERMINY TEORETYCZNE A TERMINY OBSERWACYJNE



Terminy OBSERWACYJNE - odnoszą się do własności obserwowalnych (np. „X jest wysoki”).



Terminy TEORETYCZNE - odnoszą się do tego co nieobserwowalne (np. „X ma silne ego”).

Terminy obserwacyjne służą do przedstawiania wyników badań. Budowanie teorii wymaga terminów teoretycznych. Dziś uważa się
jednak, że terminy obserwacyjne są obciążone teorią (język obserwacyjny jest „uteoretyzowany”). Znaczenie pojęć obserwacyjnych
zależy od znajomość teorii. Na przykład, znaczenie wyniku pomiaru dokonanego testem psychologicznym zależy od znajomości teorii
testów i teorii mierzonej cechy. Podział pojęć naukowych na terminy teoretyczne i obserwacyjne, choć pożyteczny, jest więc nieostry.
Mamy tu raczej do czynienia z różnym stopniem nasycenia terminów obserwacyjnych teorią.

Terminy teoretyczne mogą mieć różną formę.



Terminy dyspozycyjne – mają bardzo ubogą treść. „x ma cechę dyspozycyjną (ukrytą) D” jeśli w określonych warunkach x
ujawnia pewną cechę obserwowalną O.

Przykład: rozpuszczalny, cecha lęku w koncepcji lęku Charlesa D. Spielbergera (State-Trait Anxiety Inventory).



Konstrukty teoretyczne -- pojęcia teoretyczne których treść wykracza poza zaobserwowane fakty. Mówi się, że konstrukt
teoretyczny ma tzw. nadwyżkę znaczenia
(surplus meaning)

JAK POWSTAJĄ KONSTRUKTY TEORETYCZNE? Przykład (fikcyjny i bardzo uproszczony)

Zaobserwowano, że osoby które lepiej wykonują zadanie (1) wykonują też lepiej zadania (2), (3) i (4).

(1) 12 + 27 =
(2) 1, 4, 7, 10, ...

(3) , , , , , .....

b) 
a) 
c) 

(4) Co to jest sztaluga? ..............

Konstrukt: inteligencja.

Definicja (teoretyczna) inteligencji: „zdolność adaptacji do nowych warunków i do wykonywania nowych zadań” (Stern). Z tak
zdefiniowanej inteligencji można wydedukować wiele nowych cech, zarówno obserwowalnych jak i (wcześniej)
nieobserwowalnych, np. osoby o wyższej inteligencji:

•

mają większe sukcesy zawodowe

•

szybciej się uczą

•

łatwiej rozwiązują problemy

Postulowane przez teorię własności osób inteligentnych, które nie zostały jeszcze zweryfikowane empirycznie (a niektóre z nich,
być może, nigdy nie zostaną zweryfikowane), stanowią NADWYŻKĘ ZNACZENIA (surplus meaning) pojęcia „inteligencja”.

DEFINIOWANIE TERMINÓW TEORETYCZNYCH ZA POMOCĄ TERMINÓW OBSERWACYJNYCH

Terminy obserwacyjne są zasadniczo przyjmowane bez definicji (jako zrozumiałe same przez się). Mogą być też definiowane
ostensywnie.
Terminy teoretyczne mogą być definiowane za pomocą innych terminów teoretycznych (lub słów z języka potocznego). Uważa
się natomiast, że terminy teoretyczne nie dają się zdefiniować w sposób zupełny za pomocą terminów obserwacyjnych, lecz
jedynie w sposób cząstkowy.

KRYTERIA STOSOWALNOŚCI TERMINÓW TEORETYCZNYCH

Na jakiej podstawie mogę orzec że x posiada jakąś nieobserwowalną (teoretyczną) własność W?

Ponieważ chodzi o powiązanie terminów teoretycznych z obserwacyjnymi, jest to pytanie o SENS EMPIRYCZNY terminów teoretycznych.

W fizyce mówi się o REGUŁACH KORESPONDENCJI, czyli o procedurach pozwalających powiązać terminy teoretyczne z obserwacyjnymi
(mogą to być np. procedury pomiarowe) Procedury takie są zwykle czymś dużo bardziej złożonym niż definicje operacyjne. Hempel
mówi o „zasadach łączących” terminy teoretyczne i obserwacyjne.

W psychologii mówi się o OPERACJONALIZACJI zmiennych teoretycznych (nie należy mylić operacjonalizacji z operacjonizmem jako
stanowiskiem metodologicznym).
Operacjonalizacja pojęć teoretycznych należy do najbardziej złożonych problemów w naukach empirycznych. Jest bardzo wiele, nieraz
trudnych do zaklasyfikowania, sposobów wiązania pojęć teoretycznych z pojęciami obserwacyjnymi.

1. DEFINICJE CZĄSTKOWE

Definicje cząstkowe (np. w postaci zdań redukcyjnych) służą (częściowemu) przekładaniu pojęć teoretycznych na pojęcia
empiryczne. Sens redukcyjnego definiowania terminów teoretycznych można (za Przełęckim) przedstawić następująco: choć
terminy teoretyczne są nieobserwowalne, to jednak w pewnych, ściśle określonych warunkach „ujawniają się” w zjawiskach
obserwowalnych.

PROBLEMY z operacyjnym definiowaniem pojęć:



Reguły korespondencji mogą przyporządkowywać temu samemu pojęciu teoretycznemu WIELE pojęć
obserwacyjnych. Przykładowo, fizyka zna wiele metod pomiaru długości a w psychologii istnieje wiele testów
inteligencji, wiele procedur manipulacji poziomem motywacji, itp. Przyjęcie sztywnego, wąsko rozumianego
stanowiska operacjonalistycznego prowadzi do konkluzji: „ile operacji tyle pojęć” (zwłaszcza gdy wyniki różnych
operacji nie są zgodne ze sobą).



Pojęcia definiowane operacyjnie mają sens tylko w tych warunkach w których operacje są wykonalne. Pojęcie „1 metr”
definiowane jako cecha przedmiotów przystających do wzorca (sztaby) metra, jest pozbawione znaczenia w
przypadku wielkich odległości kosmicznych. Iloraz inteligencji II = 100, zdefiniowany za pomocą pomiaru skalą
Wechslera, nie ma sensu tam, gdzie test Wechslera nie jest znany.



Wiele terminów teoretycznych to konstrukty o bardzo bogatej treści, nie dające się satysfakcjonująco zdefiniować za
pomocą definicji operacyjnych. Dziś uważa się, pełne zdefiniowanie pojęć teoretycznych w terminach pojęć
obserwowalnych jest nieosiągalne. Z drugiej strony, może istnieć bardzo wiele kryteriów stosowania terminów
teoretycznych, wyznaczających równie wiele implikacji testowych tych pojęć (Hempel).

W psychologii unika się definicji operacyjnych. Terminy teoretyczne operacjonalizuje się zwykle za pomocą różnych, mniej lub
bardziej złożonych procedur (przykład: operacjonalizacja pojęcia huśtawki emocjonalnej w eksperymentach Dolińskiego).
Ważną rolę wśród tych procedur odgrywają tzw. wskaźniki.

2. WSKAŹNIKI

W jest wskaźnikiem zjawiska wskazywanego I (indicatum) jeśli na podstawie zaobserwowania W możemy wnioskować o
zjawiska I, tzn.:

•

z faktu wystąpienia W możemy wnioskować
o wystąpieniu I (zjawiska jakościowe), lub

•

z natężenia W możemy wnioskować o natężeniu I (zjawiska ilościowe).

Podstawą wnioskowania o I na podstawie W jest zachodzenie związku między W i I. Zdanie stwierdzające zachodzenie takiego
związku nazywa się ZDANIEM WPROWADZAJĄCYM WSKAŹNIK.

Związek między W i I może być związkiem (podział S. Nowaka):

•

definicyjnym: wskaźnik DEFINICYJNY

•

rzeczowym: wskaźnik RZECZOWY.

Wskaźniki rzeczowe dzielimy na:

•

wskaźniki EMPIRYCZNE (W i I są obserwowalne)

•

wskaźniki INFERENCYJNE (I jest nieobserwowalne)

Zdanie wprowadzające wskaźnik definicyjny nie różni się od definicji operacyjnej. Jest ono postulatem terminologicznym
(zdaniem analitycznym) opartym na pewnej konwencji (umowie) terminologicznej: będę traktował W jako wskaźnik I (np. będę
traktował rodzinę z jednym lub dwojgiem dzieci jako rodzinę małą).

Zdanie wprowadzające wskaźnik rzeczowy jest zdaniem syntetycznym, które stwierdza zachodzenie zależności między dwoma
zjawiskami. Zdanie to może być prawdziwe (jeśli między W i I rzeczywiście zachodzi odpowiedni związek) lub fałszywe (jeśli
związek nie zachodzi). Zakłada się przy tym, że pojęcie wskazywane zostało już wcześniej zdefiniowane (wskaźnik rzeczowy nie
pełni funkcji definicji).

Przykład: Jeśli przyjmiemy, że test wynik testu T jest wskaźnikiem rzeczowym inteligencji a okaże się że osoby z wysoką
inteligencją (określoną w jakiś inny sposób) osiągają w teście T niskie wyniki, to będzie to znaczyło, że test T nie jest dobrym
wskaźnikiem inteligencji (a zdanie mówiące o istnieniu związku między W i I jest zdaniem fałszywym).

2.2 WSKAŹNIKI EMPIRYCZNE I INFERENCYJNE

Wskaźniki empiryczne stosuje się zazwyczaj wtedy, gdy W i I są obserwowalne ale zaobserwowanie zjawiska W jest
łatwiejsze,

prostsze,

wygodniejsze

niż

zaobserwowanie

zjawiska I. Na przykład, badacz może przyjąć że posiadanie mieszkania własnościowego w dobrej dzielnicy będzie
wskaźnikiem zamożności (rozumianym jako posiadanie określonych dochodów rocznych). Posiadanie mieszkania jest
łatwiejsze do zaobserwowania niż wysokość dochodów. Większość cech psychologicznych (np. siła ego, poziom
inteligencji) to konstrukty teoretyczne, musimy więc stosować wskaźniki inferencyjne. Powstaje problem jak wykazać że
zachodzi związek miedzy W i I, jeśli I jest nieobserwowalne?

Ustalanie związku między zjawiskiem nieobserwowalnym a jego wskaźnikiem INFERENCYJNYM przypomina testowanie
teorii.

•

Z teorii cechy C (konstruktu teoretycznego) dedukujemy pewne obserwowalne konsekwencje (jakie
obserwowalne zachowania powinien przejawiać ktoś, kto ma cechę C).

•

Następnie możemy sprawdzić do jakiego stopnia przewidywania zgadzają się z teorią (tzn. potwierdzają ją lub jej
przeczą)

W przypadku wskaźnika inferencyjnego, z teorii cechy wskazywanej (indicatum) dedukujemy jakie związki powinny
zachodzić między danymi obserwacyjnymi a następnie obserwujemy czy faktycznie tak jest. Na przykład, z teorii
inteligencji możemy wydedukować hipotezy, że osoby o wysokiej inteligencji powinny osiągać lepsze wyniki na studiach,
mieć większe sukcesy zawodowe, itp. Jeśli nie stwierdzimy takich faktów u osób z wysokimi wynikami w teście T to
możemy wyciągnąć wniosek, że test T nie jest dobrym wskaźnikiem inteligencji (ewentualnie, że niedobra jest teoria na
której oparty jest test T).

3. WSKAŹNIK A DEFINICJA OPERACYJNA

Definicja operacyjna określa sposób rozumienia wyrażenia. Jest to zdanie analityczne (postulat terminologiczny), któremu nie
można zaprzeczyć bez popadania w wewnętrzną sprzeczność. Zdanie wprowadzające wskaźnik rzeczowy jest zdaniem
rzeczowym, które stwierdza, że między dwoma zjawiskami (W i I) zachodzi zależność. Fakty mogą potwierdzić lub obalić takie
zdanie. Zdanie wprowadzające wskaźnik rzeczowy nie definiuje natomiast terminu I (termin I musi być zdefiniowany oddzielnie).
Inne są konsekwencje nie potwierdzenia przewidywań wydedukowanych z przyjętych wskaźników lub definicji operacyjnych.

Jeśli mamy dwa WSKAŹNIKI rzeczowe (W1 i W2) cechy Q (np. dwa testy inteligencji) i wskaźniki te nie korelują ze sobą (osoby
uzyskujące wysokie wyniki w jednym teście uzyskują niskie wyniki w drugim teście), to znaczy to, że:

•

co najmniej jeden wskaźnik jest nietrafny, a tym samym:

•

co najmniej jedno zdanie wprowadzające wskaźnik jest fałszywe.

Jeśli natomiast mamy dwie niezgodne ze sobą definicje operacyjne (tzn. definiujemy cechę Q za pomocą własności W1 i W2,
które nie korelują ze sobą) to musimy przyjąć, że definicje te definiują dwie rożne cechy (jakieś: Q1 i Q2).

Psychologowie unikają zazwyczaj operacyjnego definiowania cech psychologicznych explicite. Ślady takiego definiowania można
jednak dostrzec w sformułowaniach typu: „inteligencja mierzona testem T ...”. Sugerują one, że test T definiuje jakiś szczególny
rodzaj inteligencji, inny niż inteligencja mierzona innym testem.

3.3 OPERACJONALIZACJA ZMIENNYCH MANIPULOWALNYCH

Operacjonalizacja może dotyczyć zmiennych mierzalnych i zmiennych manipulowalnych.

Operacjonalizacja zmiennych manipulowalnych
Chcemy np. wykazać eksperymentalnie, że lęk obniża poziom wykonania zadań złożonych. Musimy WYTWORZYĆ za
pomocą odpowiedniego oddziaływania (O) co najmniej dwa różne poziomy lęku (zmiennej manipulowalnej - X). W
jaki sposób wykazać, że oddziaływanie spowodowało rzeczywiście zmianę tej zmiennej X o którą nam chodzi?

•

Niekiedy, można użyć niezależnych wskaźników zmiennej X (np. testów mierzących stan leku)

•

Analiza wpływu oddziaływania (O) na zmienną zależną (Z);

O X Y

 

Jeśli manipulacja O powoduje oczekiwaną zmianę Y nie przesądza to jeszcze o trafności manipulacji zmienna X.
Zaufanie do hipotezy „O X” wzrasta, gdy zaobserwujemy, że inne efekty stosowanej manipulacji są zgodne z



teorią.

Zmienne pośredniczące w badaniach eksperymentalnych

Jeśli efekt oddziaływania może być wyjaśniony za pomocą różnych zmiennych teoretycznych (X i X’), wybiera się nieraz
zmienną (konstrukt) o większej mocy wyjaśniającej.
O  X

 Y

O  X

 Y

Zdarza się, że alternatywne teorie, wyjaśniające tę samą zależność empiryczną O Z, są niewspółmierne (twierdzeń



jednej teorii nie da się przełożyć na twierdzenia drugiej). Np. gorsze zapamiętywanie „brzydkich słów” może być
tłumaczone jako hamowanie reakcji dla uniknięcia kary (teoria uczenia) albo jako stłumienie („zepchnięcie do
podświadomości”) niepożądanych zachowań (psychoanaliza).

Eksperyment krzyżowy (experimentum crucis) – ma rozstrzygać między konkurującymi ze sobą teoriami, tzn.
definitywnie potwierdzić jedną i obalić drugą. Możliwość takich eksperymentów kwestionuje się jednak, m.in. ze
względu na niewspółmierność teorii.

Definicje projektujące, służące do definiowania pojęć teoretycznych (typu: „osobowość jest to ...”), nie są zdaniami w
sensie logicznym (nie są ani prawdziwe ani fałszywe) i nie zawierają żadnej wiedzy o świecie. Są zdaniami analitycznymi,
opartymi na pewnej konwencji terminologicznej. Na pytanie „co to jest osobowość?” nie ma więc odpowiedzi, chyba
żeby rozumieć je następująco: „co naukowiec X lub społeczność naukowa Y rozumie przez pojęcie osobowość?” Nie
znaczy to jednak, że dowolnie (ale formalnie poprawnie) zdefiniowane pojęcie teoretyczne jest z poznawczego punktu
widzenia równie dobre jak każde inne. Może się bowiem okazać, że jakaś (w określony sposób zdefiniowana) zmienna
pozostaje w nadzwyczaj interesujących relacjach do innych ważnych zmiennych.

Wybór pojęć za pomocą których formłujemy jakiś problem nazywa się KONCEPTUALZACJĄ problemu. Niekiedy nowa
konceptualizacja pozwala rozwiązać problem, który wcześniej wydawał się niemożliwy do rozwiązania.

CZĘŚĆ 3. TWIERDZENIA I ICH UZASADNIANIE

SYSTEMY AKSJOMATYCZNE W NAUKACH FORMALNYCH

TERMINY i ich definiowanie:



Pojęcia PIERWOTNE (niezdefiniowane, lub zdefiniowane za pomocą definicji aksjomatycznych) i WTÓRNE (zdefiniowane za
pomocą pojęć pierwotnych lub innych pojęć zdefiniowanych przy ich pomocy)



Pojęcia pierwotne są dokładnie wymienione



Dąży się do tego, aby pojęć pierwotnych było jak najmniej

ZDANIA i ich uzasadnianie:



Zdania (tezy) systemu dzieli się na zdania PIERWSZE (AKSJOMATY), przyjęte bez dowodu, i zdania WTÓRNE – wydedukowane
ze zdań pierwszych za pomocą niezawodnych (dedukcyjnych) reguł wnioskowania.



Aksjomaty są zazwyczaj wyraźnie wymienione.



Dąży się aby liczba aksjomatów była jak najmniejsza.



Zbór aksjomatów powinien być niezależny.

Zbiór aksjomatów jest niezależny, gdy żadnego aksjomatu nie da się wydedukować z pozostałych.

REGUŁY wnioskowania:



Reguły wnioskowania, które wychodząc od prawdziwych przesłanek prowadzą zawsze do prawdziwych wniosków, nazywamy
niezawodnymi lub dedukcyjnymi.

NIEKTÓRE FORMALNE WŁASNOŚCI TEORII



NIESPRZECZNOŚĆ

System jest NIESPRZECZNY gdy wśród jego tez nie ma pary zdań sprzecznych: p i ~p. Zwykle system nie zawiera zdań sprzecznych
wśród swych aksjomatów, może się jednak zdarzyć, że takie zdania dadzą się wydedukować z aksjomatów. Sprzeczność teorii jest
bardzo poważną wadą, ponieważ z pary zdań sprzecznych wynika dowolne zdanie:

∧

~p)

⊃



ROZSTRZYGALNOŚĆ

System jest ROZSTRZYGALNY gdy istnieje metoda, która pozwala o każdym zdaniu z danej dziedziny rozstrzygnąć w skończonej liczbie
kroków czy jest prawdziwe ono czy nie. Przykład zdania nierozstrzygalnego:
"Liczba gwiazd we wszechświecie jest parzysta"



ZUPEŁNOŚĆ

System jest ZUPEŁNY gdy z jego aksjomatów dadzą się wydedukować wszystkie zdania prawdziwe w danej dziedzinie (każde zdanie
prawdziwe jest tezą systemu).

Jeśli jakieś zdanie prawdziwe nie da się wydedukować, można usunąć ten mankament przyjmując dodatkowe aksjomaty. Wtedy jednak
pojawiają się zwykle nowe zdania, które nie dadzą się wydedukować z aksjomatów. Kurt Gödel udowodnił, że wszystkie bogatsze teorie
w naukach formalnych (tzn. teorie zawierające w sobie arytmetykę liczb naturalnych) są niezupełne. Wynik Gödla (nad)interpretuje się
często jako dowód na istnienie granic ludzkiego poznania: nie da się zbudować takiej teorii która wyjaśniałaby wszystko.

TEORIE W NAUKACH EMPIRYCZNYCH

Przez teorię rozumie się pojedyncze zdanie teoretyczne albo system powiązanych ze sobą zdań teoretycznych. Zdanie teoretyczne to
zdanie zawierające terminy teoretyczne, których desygnaty nie są bezpośrednio obserwowalne (w przeciwieństwie do zdania
obserwacyjnego, opisującego wyniki obserwacji).

FUNKCJE TEORII NAUKOWYCH

•

FUNKCJA DESKRYPTYWNA (OPIS) – teoria dostarcza terminów do opisu rzeczywistości.

Np. lekarz może powiedzieć, że u badanego "występują objawy paranoidalne i niepokój ruchowy, badany nie potrafi
nawiązać kontaktu emocjonalnego z otoczeniem i jest stale napięty”.

Dziś podkreśla się, że język obserwacyjny jest uteoretyzowany a interpretacja wyników obserwacji zależy od teorii. Tym
samym, podział pojęć na obserwacyjne i teoretyczne przestaje być ostry.

•

FUNKCJA PRAKTYCZNA (WSKAZYWANIE REGUŁ DZIAŁANIA) - teoria mówi jak postępować aby osiągnąć jakiś cel
(spowodować zmianę rzeczywistości). Funkcja praktyczna to zastosowanie teorii.

Dyrektywy praktyczne można też formułować bez teorii, na podstawie doświadczenia. Dyrektywy takie mają jednak
ograniczony zakres zastosowania.

•

FUNKCJA EKSPLANACYJNA (WYJAŚNIANIE) i FUNKCJA PREDYKTYWNA (PRZEWIDYWANIE)

Wyjaśnianie, sprawdzanie (hipotez) i przewidywanie to, w sensie logicznym, wnioskowania odwołujące się do stosunku
wynikania, w najprostszej formie – do relacji: p

→

•

Przewidywanie to szukanie następnika dla uznanego poprzednika (szukanie zdania q, które wynika z uznanego
zdania p); w szczególności jest to dedukowanie zdań obserwacyjnych z uznanego prawa (praw) i pewnych
przesłanek szczegółowych.

„Jeśli zaszło X to (przewidujemy, że) zajdzie Y”

•

Wyjaśnianie to szukanie poprzednika dla uznanego następnika (szukanie zdania p, z którego można

wydedukować uznane zdanie q); w szczególności: szukanie prawa (praw) z których można wydedukować inne
prawo lub zdanie obserwacyjne.

EXPLANANS - człon wyjaśniający
EXPLANANDUM - człon wyjaśniany

"Dlatego zaszło Y (explanandum) że zaszło X (explanans)"

Potwierdzenie empiryczne przewidywań wynikających z teorii traktuje się jako argument przemawiający za tym, że
teoria dobrze wyjaśnia zjawiska w danej dziedzinie, natomiast niezgodność faktów z przewidywaniami może świadczyć o
tym, że wyjaśnienie proponowane przez teorię jest błędne. Na przykład to, że potrafimy bardzo dokładnie przewidzieć
ruchy ciał niebieskich, jest argumentem przemawiającym za tym, że współczesna teorie astronomiczne dobrze
wyjaśniają ruchy tych ciał. Przewidywanie nie jest jednak tym samym co wyjaśnianie. Na przykład:

•

Znając wysokość słońca (kąt pod jakim padają promienie słoneczne) i wysokość masztu można wydedukować
długość cienia a znając wysokość słońca i długość cienia można wydedukować wysokość masztu. Ale, o ile
długość masztu wyjaśnia długość cienia to nie uważamy, aby długość cienia wyjaśniła długość masztu.

•

Jeśli ekstrawersja i lęk są ze sobą skorelowane, to możemy przewidywać ekstrawersję na podstawie
znajomości lęku i lęk na podstawie znajomości ekstrawersji. Nie jest jednak pewne czy którekolwiek z tych
wnioskowań jest wyjaśnianiem (poziom obu tych zmiennych może być spowodowany jakimś trzecim
czynnikiem).

RODZAJE WYJAŚNIEŃ

Wyjaśnianie jako logiczne wywnioskowywanie (niekiedy – dedukowanie) faktów z teorii lub teorii mniej ogólnych z teorii bardziej
ogólnych. Do tego rodzaju wyjaśnień zaliczamy:

1. NOMOLOGICZNO-DEDUKCYJNE

2. INDUKCYJNO-STATYSTYCZNE

2.1 FUNKCJONALNE

– jaką rolę (funkcję) pełni element X w systemie S?

2.2 GENETYCZNE

– jak doszło do powstania zjawiska x?

2.3 INTENCJONALNE

– jaka była intencja lub cel działania podmiotu?

WYJAŚNIANIE NOMOLOGICZNO-DEDUKCYJNE (Hempel i Oppenheimer, 1948)

•

Wyjaśnianie faktów: z dwojakiego rodzaju przesłanek: praw ogólnych (nomos) i warunków początkowych (Initial
Conditions), czyli zdań szczegółowych stwierdzających fakty, dedukujemy wystąpienie jakiegoś faktu (ewentualnie –
prawa empirycznego)

PRAWA OGÓLNE

WARUNKI POCZĄTKOWE
---- (dedukcja) -------------
KONKLUZJA (EXPLANANDUM)

(P): Dla każdego x, jeśli x ma cechę P to x ma cechę Q
(WP): Ten oto (konkretny) x

ma cechę P

Konkluzja: x

ma cechę Q

Przykład:

Dla każdego x (Jeśli x jest miedzią to x przewodzi prąd)
Ten oto kawałek drutu x

jest wykonany z miedzi

przewodzi prąd

Aby można było wyjaśniać fakty na podstawie praw (teorii) potrzebne są zasady wiążące terminy teoretyczne z
terminami obserwacyjnymi (podające zasady interpretacji terminów teoretycznych, wyposażające terminy
teoretyczne w treść empiryczną) – por. operacjonalizacja pojęć teoretycznych

•

Wyjaśnianie praw: wyjaśniane mogą być zarówno jednostkowe fakty jak i prawa. W szczególności, często
poszukujemy teoretycznego wyjaśnienia praw empirycznych. Dzięki takim wyjaśnieniom powstaje spójny system
powiązanych ze sobą praw (teorii). Nomologiczno-dedukcyjne wyjaśnianie praw polega na ich dedukowaniu z praw
bardziej ogólnych lub z teorii.

Przykłady:

Każde ciało lżejsze od wody pływa
Lód jest ciałem lżejszym od wody
Lód pływa

PROBLEMY ZWIĄZANE Z WYJAŚNIANIEM NOMOLOGICZNO-DEDUKCYJNYM

Nie każde wnioskowanie, formalnie zgodne z modelem nomologiczno-dedukcyjnym, stanowi rzeczywiste wyjaśnienie
faktów. Aby wyeliminować problemy związane z tym modelem nakłada się na wyjaśnianie N-D dodatkowe warunki:



Warunek ASYMETRII WYJAŚNIANIA: wyjaśnianie nie może zachodzić w obie strony.

Przykład:

Widząc że wskazówka barometru spada można wywnioskować że nadejdzie burza. Ale to nadejście

burzy wyjaśnia ruch wskazówki a nie na odwrót.

Znając kąt padania promieni światła i długość cienia można wywnioskować jaka jest wysokość

masztu. Uważamy jednak, że to wysokość masztu wyjaśnia długość cienia a nie na odwrót.



Prawa (przesłanki wnioskowania) nie mogą być PRZYPADKOWYMI UOGÓLNIENIAMI



Przesłanki powinny być PRZYCZYNOWO ISTOTNE dla wniosku (relevance)

Przykład:

Jeśli ktoś bierze pigułki antykoncepcyjne to nie zachodzi w ciążę
Jan Kowalski brał pigułki antykoncepcyjne
-------------------------------------------------------
Jan Kowalski nie zaszedł w ciążę

Pojawia się jednak problem jak rozumieć y określenie „przyczynowo istotne”. Pojęcie przyczyny, choć
powszechnie używane, nie jest jasne. Bywa też krytykowane ze względu na swój potencjalnie
„metafizyczny” charakter (por. teorię przyczyn Arystotelesa). Zdaniem Lazarsfelda (za: Babbie, 2007)
aby można było uznać A za przyczynę B muszą być spełnione co najmniej dwa warunki:

−

A poprzedza w czasie B

−

między A i B zachodzi zależność empiryczna

−

Skutek nie może dać się wyjaśnić za pomocą jakiejś trzeciej zmiennej (inaczej: zależność
między A i B nie może być zależnością pozorną)

Warunki te można uznać za operacyjną definicję przyczyny.



Wyjaśnianie naukowe nie może być WYJAŚNIANIEM „AD HOC” (wyjaśnianiem za pomocą „hipotez ad
hoc”)

Hipotezą „ad hoc” („do tego”) jest taka hipoteza, z której nie da się wydedukować żadnych
sprawdzalnych faktów poza tym jednym, dla którego wyjaśnienia hipoteza została sformułowana.

Hipoteza H stworzona dla wyjaśnienia faktu Z powinna pozwalać na predykcje innych faktów. Predykcje
takie stanowią „niezależne testy hipotezy H”. Jeśli predykcje takie nie są możliwe, hipotezę należy
traktować jako nieweryfikowalną (nienaukową).

Doskonały przykład wyjaśniania ad hoc (wyjaśniania dlaczego księżyc ma kształt doskonale kulisty
pomimo tego, że na jego powierzchni można zobaczyć góry i doliny) podaje Chalmers (1993, ss. 78-79).

2. WYJAŚNIANIE INDUKCYJNO-STATYSTYCZNE (PROBABILISTYCZNE)

Podobne do nomologiczno-dedukcyjnego z tą jednak różnicą, że przesłankami są nie prawa deterministyczne ale prawa
probabilistyczne. W takim przypadku explanandum nie wynika z przesłanek dedukcyjnie. Można mówić jedynie o (odpowiednio
wysokim) prawdopodobieństwie z jakim zajdzie zdarzenie o którym mowa w explanandum.

Przykłady:

Jest wysoce prawdopodobne, że jeśli x jest ekstrawertykiem to x jest osobą towarzyską
Jan jest ekstrawertykiem
Jest wysoce prawdopodobne, że Jan jest osobą towarzyską

Polon ma połowiczny czas rozpadu równy 3,05 minuty
W próbce jest 1 mg Polonu
Po upływie 3,05 minuty w próbce pozostanie 0,5 mg Polonu

W tym ostatnim przypadku, prawdopodobieństwo zajścia przewidywanego wyniku jest tak duże, że wniosek można
traktować jako „praktycznie pewny”.

Pierwotnie Hempel uważał, że stosowanie wyjaśniania indukcyjno-statystycznego jest wynikiem niedoskonałości naszej wiedzy.
W miarę pogłębiana się tej wiedzy, wyjaśnienie indukcyjno-statystyczne powinno się zbliżać do nomologiczno–dedukcyjnego.
Potem jednak zmienił pogląd uznając, że:
„wiele ważnych praw i teoretycznych zasad nauk przyrodniczych ma charakter probabilistyczny...”

W szczególności, prawa psychologiczne (tzn. prawa będące wynikiem badań psychologicznych) mają charakter probabilistyczny.

2.1 WYJAŚNIANIE FUNKCJONALNE

Odpowiada na pytanie jaką rolę (funkcję) pełni zjawisko X w określonym systemie S?
Wyjaśnianie funkcjonalne koncentruje się na relacjach zachodzących między systemem a jego elementami. Na przykład:

"Jaka funkcję pełni układ sercowo-naczyniowy w organizmie zwierzęcym?"
"Jaką funkcję pełni tabu kazirodztwa w regulacji zachowania społecznego?"

Funkcję można rozumieć jako własność lub proces ważne (czasem konieczne) dla funkcjonowania jakiegoś systemu.
W naukach inżynierskich funkcję definiuje się jako własność urządzenia, która jest niezbędna do realizacji jego

celu

, tzn.

do tego, do czego zostało ono skonstruowane lub do czego jest używane. Gadomski: „funkcja to własność procesu lub
systemu konieczna do realizacji jego celu”. Przykładowe: „reflektory samochodowe służą do oświetlania drogi”.
Wyjaśnienie funkcjonalne zjawisk naturalnych (przyrodniczych) nie zakłada celowości. W biologii przyjmuje się
natomiast (nieraz milcząco) założenie, że zachowanie lub cechy strukturalne organizmów żywych są zasadniczo
adaptacyjne. Jeśli np. odkryjemy jakąś nową strukturę w mózgu to nie pytamy czy jest ona potrzebna ale do czego jest
potrzebna (jaką pełni funkcję). Założenie to zapożyczone jest z teorii ewolucji zgodnie z którą, jeśli jakiś gatunek przeżył
to znaczy, że okazał się „przystosowany” – to co istnieje ma wartość adaptacyjną (ma znaczenie dla przeżywalności
organizmów) a przynajmniej nie jest nieadaptacyjne. Założenie takie pełni również funkcję heurystyczną – skłania do
poszukiwania adaptacyjnej funkcji struktur, właściwości lub procesów.

Zdaniem Nagela (1961, ss. 346, i.n.) wyjaśnianie funkcjonalne można zasadniczo zastąpić wyjaśnianiem N-D, tzn.
wyjaśnianiem odwołującym się do praw stwierdzających warunki konieczne lub wystarczające dla przebiegu danego
procesu lub zaistnienia jakiegoś zjawiska. Przykładowo zdanie „Funkcją chlorofilu znajdującego się w roślinach zielonych
jest umożliwienie im fotosyntezy” można zastąpić zdaniem „Fotosynteza zachodzi w roślinach tylko wtedy, gdy
zawierają chlorofil” lub zdaniem „Niezbędnym warunkiem zachodzenia fotosyntezy w roślinach jest obecność w nich
chlorofilu”.
Każde z tych sformułowań kładzie nacisk na inny aspekt relacji między systemem a jego częściami składowymi.
Sformułowanie pierwszego rodzaju wskazują na następstwa (skutki) jakie ma dla systemu zachodzenia pewnego
procesu lub posiadania pewnego elementu strukturalnego, sformułowanie drugiego rodzaju natomiast wskazują
warunki konieczne lub wystarczające i konieczne (przyczyny) w jakich system zachowuje swe charakterystyczne
czynności i organizację. Powstaje jednak wątpliwość czy wyjaśnianie N-D nie zaciera tego, co jest specyficzną cechą
wyjaśniania funkcjonalnego, tj. badania roli jaką w funkcjonowaniu systemu pełnią jego elementy składowe.

2. 2 WYJAŚNIANIE GENETYCZNE

Jest pytaniem o genezę jakiegoś zjawiska Z, pytaniem o to, w jaki sposób doszło do zaistnienia zjawiska Z, jaki był
przebieg (trajektoria) procesów, które doprowadziły do zaistnienia zjawiska Z. Na przykład:

"W jaki sposób doszło do powstania płuc u zwierząt lądowych?"
"W jaki sposób doszło do powstania objawów nerwicowych u Jasia?"

Wyjaśnianie genetyczne stosuje się do zjawisk, których przebieg jest wyjątkowy i niepowtarzalny, takich jak np.
powstawanie gatunków biologicznych, historia procesów społecznych, przebieg życia danej jednostki, itp. a więc takich,
których nie da się wyjaśnić satysfakcjonująco za pomocą praw ogólnych.

Prawa ogólne stosują się do zjawisk powtarzalnych - stwierdzają one, że zawsze kiedy zachodzi zjawisko A zachodzi też
zjawisko B. Przedmiotem wyjaśnień genetycznych są natomiast procesy niepowtarzalne. Na każdym etapie takiego
procesu mogą działać różne czynniki przyczynowe ale żaden z nich nie wyznacza w sposób jednoznaczny następnego
etapu procesu. Proces ten można jedynie opisać (zrekonstruować jego przebieg ex post) jak ma to np. miejsce w
wypadku ewolucji gatunków biologicznych. Opis taki nazywany jest narracją historyczną. Narracje historyczne różnią się
więc zasadniczo od wyjaśniania zjawisk za pomocą praw. Opisywane przez nie procesy nie dadzą się wydedukować w
sposób pewny z praw (nawet jeśli wyjaśnianie powołuje się jakieś prawa). Narracje nie pozwalają też na przewidywanie
przebiegu opisywanych procesów (chyba że na zasadzie ekstrapolacji aktualnych trendów). Narracje historyczne można
by więc określić jako opis ex post procesów, których przebieg nie da się ująć w prawa i który jest nieprzewidywalny.

2.3 WYJAŚNIANIE INTENCJONALNE

Przez wskazanie intencji (zamiaru) lub celu działania. Na przykład:

„Dlaczego Jaś się uczy? Bo chce dobrze zdać egzamin”

Powszechnie uznaje się, że człowiek jest zdolny do działań celowych. Niektóre zachowania zwierząt przypominają
zachowania celowe człowieka (np. używanie narzędzi przez szympansy). Interpretacja takich zachowań bywa sprawą
dyskusyjną. W sposób przenośny zachowaniem celowym (goal-oriented behavior) określa się reakcje instrumentalne
(np. szczur naciska na dźwignie „bo chce dostać pokarm”). Istnieje problem (filozoficzny, światopoglądowy) czy można
mówić np. o celowości w odniesieniu do świata pozaludzkiego (np. o celowości świata jako takiego). Wyjasnienie
odwolujące się do tego rodzaju celowości nazywa się teleologicznym. Zachowaniem celowym w znaczeniu ścisłym
nazywamy zachowanie, które jest świadomie ukierunkowane na cel. „Celowe” zachowanie zwierząt (goal-oriented
behavior) można natomiast uznać za realizację pewnego programu, który został wyselekcjonowany przez ewolucję.
Ewolucja nie zakłada jednak

żadnego

celu.

W psychologii rozróżnia się tradycyjnie:

•

Zachowania reaktywne, typu: bodziec

→

reakcja (S-R). Na przykład:

"x cofnął palec gdy dotknął do gorącego pieca"

Wyjaśnianie zachowań reaktywnych zakłada zwykle determinizm zjawisk.

•

Zachowania celowe (zwane „czynnosciami” przez prof. Tomaszewskiego), tj. zachowania podejmowane po to,
aby osiągnąć jakiś cel. Na przykład:

„Jan uczy się bo chce zostać psychologiem”

Czy można mówić o celu nieświadomym (np. dziecko płacze, bo chce zwrócić na siebie uwagę)? Wskazywanie na „cel”
działania, którego podmiot sobie nie uświadamia, jest podobne do wyjaśniania funkcjonalnego (pytamy raczej: jaką
funkcję pełni płacz dziecka?). W humanistyce pojawia się jeszcze inne rozumienie wyjaśniania:

•

Wyjaśnianie jako INTERPRETACJA (odkrywanie znaczenia)

Zgodnie z poglądem reprezentowanym przez niektóre kierunki współczesnej filozofii (hermeneutyka,
postmodernizm) wyjaśnienie zjawisk społecznych polega na odkrywaniu znaczenia jakie ludzie nadają lub
przypisują różnym zjawiskom, w szczególności – zjawiskom społecznym lub wytworom ludzkim. Zjawiska te
można, wg tego ujęcia, traktować jak TEKST posiadający określone znaczenie. Żeby zrozumieć tekst trzeba umieć
odczytać jego ZNACZENIE (SENS). Hermeneutyka poszukuje raczej uniwersalnych reguł interpretacji
doświadczenia ludzkiego natomiast postmodernim podkreśla pluralizm i relatywizm zasad interpretacyjnych (w
związku z załamaniem się narracji uniwersalistycznych, czyli tzw. „metanarracji”). Psychologia jako nauka
empiryczna nie zajmuje się sensem doświadczenia ludzkiego jako takim. Ponieważ jednak ludzie przypisują różne
subiektywne znaczenie zdarzeniom które ich spotykają (różnie interpretują te zdarzenia) i ma to wpływ na ich
zachowanie, relacja między spostrzeganym znaczeniem zdarzeń a zachowaniem może być przedmiotem badań
psychologicznych.

PRAWA NAUKOWE

Barrow: prawo naukowe (teorię) można traktować jako „kompresję informacji”. Prawo przedstawia w sposób skrócony informację
zawartą w bardzo długich szeregach danych obserwacyjnych. W takim ujęciu zaciera się różnica między opisem i wyjaśnianiem
(wyjaśnianie jest syntetycznym opisem faktów). Ale prawa zawierają terminy nieobserwacyjne („masa”, „entropia”, „motywacja”, „siła
ego”). Prawa zawierające takie terminy są czymś więcej niż samym opisem faktów (wykraczają poza zaobserwowane fakty).

Prawa naukowe są zasadniczo zdaniami warunkowymi (choć samo sformułowanie prawa może niekiedy maskować jego
warunkowy/charakter). Przykład:

Zdanie „wszystkie kruki są czarne” znaczy faktycznie:
„dla każdego x (jeśli x jest krukiem to x jest czarny)”

∧

x (Px

⊃

Qx)

Słowo „prawo” ma utrwalone tradycją miejsce w języku nauki ale czasem rodzi niepożądanie skojarzenia z prawem (nakazem, normą)
moralnym czy politycznym. Lepiej byłoby więc mówić nie o prawach ale o regularnościach zachodzących w przyrodzie.

PRAWA OGÓLNE W NAUKACH PRZYRODNICZYCH I WARUNKI JAKIE SIĘ TRADYCYJNIE NA NIE NAKŁADA



Powinny być zdaniami ogólnymi (tzn. dotyczyć WSZYSTKICH przedmiotów danej klasy);

∧

x (Px

⊃

Qx)



Nie mogą zawierać nazw indywiduowych. Przykład (negatywny):

„Wszystkie żony Kowalskiego były rude”



Powinny być zdaniami uniwersalnymi, nie zawierającymi ograniczeń czasowo-przestrzennych. Zdania zawierające takie
ograniczenia nazywają się generalizacjami historycznymi, np.:

„Wszyscy królowie, panujący w Polsce w latach 1386-1572, pochodzili z dynastii Jagiellonów”.
„Poziom dochodów w Polsce jest (obecnie) wyższy w mieście niż na wsi”.

Mówi się, że zdanie takie jak „Miedź przewodzi prąd” jest prawdziwe zawsze i wszędzie. Natomiast zdanie "Poziom
dochodów ..." odnosi się do zdarzeń w danym miejscu i czasie.

Popper: nie istnieją w ogóle „prawa rozwoju historycznego” a bieg historii ludzkości jest nieprzewidywalny, m.in. dlatego,
że nieprzewidywalny jest rozwój wiedzy (co nie wyklucza możliwości krótkoterminowego prognozowania zjawisk
społecznych). Pogląd głoszący możliwość formułowania praw historycznych (głoszony np. przez Hegla i Marksa) nazywał
Popper „historycyzmem”. Warunek 3, wysuwany pod adresem praw fizyki, jest za mocny dla teorii w naukach
biologicznych, a tym bardziej – dla teorii w naukach społecznych.



Prawo naukowe nie może być „przypadkowym ogólnieniem”(accidental generalization).

Czasem mówi się, że prawa powinny wyrażać prawdy konieczne ale jest to wymóg niejasny, bo nie wiadomo co ma
znaczyć określenie „konieczne”. Stawia się natomiast warunek, że prawo naukowe powinno nadawać się na
uzasadnienie tzw. hipotetycznego (nierzeczywistego, kontrfaktycznego) okresu warunkowego.

Przykład (negatywny) Hempla: "Każdy przedmiot ze szczerego złota ma masę mniejszą niż 100 ton". Zdaniu temu
odpowiada okres warunkowy: „Dla każdego x, gdyby x był ze złota, to x musiałby ważyć mniej niż 100 ton".

Przykład pozytywny: „Miedź przewodzi prąd” („Dla każdego x, gdyby x był z miedzi to x przewodziłby prąd”).

Uznamy drugi okres warunkowy ale nie uznamy pierwszego, bo nie ma takiego prawa z którego wynikałoby, że nie może
istnieć przedmiot ze złota o wadze równej/większej niż 100 ton.

KLASYFIKACJA PRAW NAUKOWYCH

JAKOŚCIOWE – ILOŚCIOWE

•

JAKOŚCIOWE– mówią o występowaniu pewnych zdarzeń

•

ILOŚCIOWE – wyrażają wielkość pewnej zmiennej jako funkcję wielkości innej zmiennej.

TEORETYCZNE – EMPIRYCZNE (EKSPERYMENTALNE)

•

TEORETYCZNE - zawierają terminy teoretyczne, np.

„Entropia układu zamkniętego nie może maleć”
„Ludzie dążą do redukcji dysonansu poznawczego”

•

EMPIRYCZNE - formułowane wyłącznie przy pomocy terminów obserwacyjnych (często stanowią proste uogólnienie
zdań obserwacyjnych – tzw. „generalizacje empiryczne”), np.:

„wszystkie kruki są czarne”
„miedź topi się w temperaturze 1083

C”

Prawo Ohma: U = R I

PRAWA NASTĘPSTWA I PRAWA WSPÓŁISTNIENIA

•

PRAWA NASTĘPSTWA mówią o następowaniu jednych zdarzeń po innych (skutków po przyczynach), np.:

„frustracja prowadzi do agresji”

•

PRAWA WSPÓŁISTNIENIA mówią o współwystępowaniu pewnych zjawisk lub własności, np.: prawo Boyla-Mariotta o
zależności miedzy objętością i ciśnieniem gazu: PV = const.

4. DETERMINISTYCZNE I STATYSTYCZNE (PROBABILISTYCZNE)

•

DETERMINISTYCZNE – stwierdzają jednoznaczną (bezwyjątkową) zależność między zdarzeniami (przyczyną i
skutkiem) typu: ilekroć zachodzi A, tylekroć zachodzi B.

Zdanie „miedź topi się w temperaturze 1083

C” znaczy: „każdy kawałek miedzi, ilekroć zostanie podgrzany do

temperatury 1083

C, tylekroć przejdzie w stan płynny”.

Klasyczne sformułowanie zasady determinizmu podał Laplace (1820), który uważał, że gdyby jakaś potężna
inteligencja znała wszystkie prawa przyrody i aktualny stan świata, to mogłaby przewidzieć bezbłędnie jego stan
przyszły.

„Powinniśmy patrzeć na obecny stan świata jako na wynik jego stanu poprzedniego i przyczynę stanu
późniejszego. Inteligencja, która by znała wszystkie siły działające w przyrodzie w danym momencie i chwilowe
położenie wszystkich przedmiotów we wszechświecie byłaby w stanie ująć w jedną formułę ruchy zarówno
największych ciał w świecie, jak i najlżejszych atomów, pod warunkiem, że byłaby to inteligencja zdolna poddać
wszystkie te dane analizie; nic nie byłoby dla niej niepewne, widziałaby przeszłość i przyszłość. Doskonałość jaką
umysł ludzi zdołał nadać astronomii jest słabym odbiciem takiej inteligencji. Odkrycia w zakresie mechaniki i
geometrii wraz z odkryciami w zakresie powszechnego ciążenia zbliżyły nasz umysł do możliwości ujęcia w jednej
formule analitycznej przeszłości i przyszłości naszego świata. Wszystkie wysiłki ludzkiego umysłu, ażeby poznać
prawdę, zbliżają go do inteligencji, jaką sobie przed chwilą wyobraziliśmy, jakkolwiek zawsze będziemy
nieskończenie od niej dalecy”. (Laplace, Théorie de analitique des probabilités, Paris, 1820; za: Nagel, 1961, ss.
248-249)

•

STATYSTYCZNE – mówią o prawdopodobieństwie jakiegoś zdarzenia. Mówią jak zachowa się pewna zbiorowość,
ale nie pozwalają przewidzieć jak się zachowa konkretny przedmiot.

Dziś uznaje się, że prawa probabilistyczne odgrywają doniosłą rolę w nauce. Wiele praw naukowych ma
charakter explicite probabilistyczny, np. prawo połowicznego rozpadu pierwiastków, prawa termodynamiki
statystycznej (temperatura gazu to średnia energia kinetyczna cząsteczek, a ciśnienie gazu to średni pęd
cząsteczek gazu). Praktycznie wszystkie prawa psychologiczne (tzn. te które są wynikiem badań
psychologicznych) mają charakter probabilistyczny. Twierdzenie: „frustracja prowadzi do agresji” nie znaczy, że
każdy człowiek poddany frustracji zareaguje agresją ale że agresja pojawia się częściej u osób poddanych
frustracji niż nie poddanych frustracji. Probabilistyczny charakter praw może być wyrażony explicite (np. prawo
połowicznego rozpadu pierwiastków) bądź implicite (podane wyżej twierdzenie o wpływie frustracji na agresję).

Dwa poglądy na naturę praw probabilistycznych:

•

są „przybliżeniem” praw deterministycznych (Hempel
w swych wczesnych pismach);

•

odzwierciedlają probabilistyczną naturę zjawisk.

Ernst

Mayr

podkreśla

np.,

że

przedmiotem

badań

biologicznych

są zróżnicowane populacje osobników. Jeśli zróżnicowana populacja poddana zostanie jakiemuś oddziaływaniu
to efekty tego oddziaływania będą zazwyczaj również zróżnicowane. Efekty takie dadzą się przedstawić tylko w
kategoriach statystycznych a nie deterministycznych. Zdaniem Stanisława Lema prawa statystyczne pojawiły się
w nauce bardzo późno, gdyż z różnych powodów (psychologicznych, filozoficznych) ludzie z trudem akceptują
probabilistyczny porządek rzeczy (Einstein: „Pan Bóg nie gra w kości”).

5. FAKTUALNE I IDEALIZACYJNE

•

FAKTUALNE – dotyczą obiektów rzeczywistych (np. miedź przewodzi prąd).

•

IDEALIZACYJNE dotyczą obiektów idealnych bądź warunków idealnych, spełniających pewne upraszczające
założenia, np. „każde ciało, na które nie działa żadna siła, ....”. Zastosowanie praw idealizacyjnych do obiektów
rzeczywistych wymaga konkretyzacji prawa, czyli uchylenia założeń upraszczających.

Twierdzenia psychologiczne mają często charakter idealizacyjny, np. „idealny ekstrawertyk to ...”; „gdyby nie działały
inne zmienne, to ...”.

UZASADNIANIE ZDAŃ W NAUKACH EMPIRYCZNYCH

Dwie metody uzasadniania zdań:

•

UZASADNIANIE BEZPOŚREDNIE – przez odwołanie się wprost do subiektywnych doświadczeń (boli mnie głowa) lub
obserwacji (jest ciemno).

•

UZASADNIANIE POŚREDNIE - na podstawie innych zdań

Istnieje (uproszczony) pogląd, że zdania obserwacyjne są uzasadniane wyłącznie w oparciu o obserwację (bezpośrednio) a zdania
teoretyczne są uznawane pośrednio, na podstawie zdań obserwacyjnych i innych zdań teoretycznych.

UZASADNIANIE ZADAŃ OBSERWACYJNYCH

Co powinny stwierdzać zdania obserwacyjne?

Koncepcja zdań protokolarnych (sprawozdawczych) opisujących proste fakty, dostępne bezpośredniej obserwacji (Kolo
Wiedeńskie). Faktami takimi mogą być:

•

doznania podmiotu (interpretacja subiektywna psychologiczna), np. „widzę stół”.

•

obiektywny stan rzeczy (interpretacja przedmiotowa, antypsychologiczna), np. „tu oto stoi stół”.
Podkreśla się, że zdania obserwacyjne powinny być intersubiektywnie sensowne i intersubiektywnie
sprawdzalne.

•

fizykalizm - zdania obserwacyjne powinny być formułowane w obiektywnym języku fizyki. W
psychologii zbliżone stanowisko głosili skrajni behawioryści – kwestionowali oni prawomocność
danych introspekcyjnych.

•

Czy istnieją czyste zdania obserwacyjne?

W obserwacji zawarta jest zwykle teoria. Przykładowo, interpretacja wyników pomiaru zależy od teorii na której oparta
jest budowa instrumentu. Interpretacja wyniku testu psychologicznego nie jest możliwa bez znajomości teorii testów i
teorii mierzonej cechy. Uważa się więc, że podział zdań na zdania obserwacyjne i zdania teoretyczne jest nieostry.
Można co najwyżej mówić, że pewne zdania są bardziej a inne mniej nasycone teorią (bardziej lub mniej
„uteoretyzowane”).

Kryteria uznawania zdań obserwacyjnych?

Czy sama obserwacja gwarantuje prawdziwość zdań obserwacyjnych? Przeciw takiej tezie przemawiają m.in.:

•

błędy, pomyłki, złudzenia percepcyjne

•

przypadki, kiedy kwestionujemy wyniki obserwacji na podstawie teorii.
Na przykład, nie uznamy za prawdziwe zdania mówiącego że temperatura ciała pacjenta wynosiła 80

bo jest to niezgodne z wiedzą (teorią) fizjologiczną.
Choć obserwując zachodzące słońce widzimy, że nad samym horyzontem obniża się szybciej niż
wcześniej, przyjmujemy że jest to złudzenie a ruch słońca jest jednostajny.

•

niezgodne wyniki badań empirycznych.

Według Poppera: zdania BAZOWE (zdania o faktach mające stanowić empiryczną bazę nauki) nie są uzasadniane w
oparciu o bezpośrednie doświadczenie. Są uznawane na mocy decyzji przez społeczność naukowców, w oparciu o
dotychczasowe wyniki badań i ich konfrontację z teorią.

UZASADNIANIE ZDAŃ TEORETYCZNYCH

1. Podejście INDUKCYJNE

Teoria to wynik uogólniania obserwacji. Obserwacje te stanowią jednocześnie uzasadnienie teorii. Indukcja
enumeracyjna (przez wyliczenie):

przedmiot x

ma własność A

przedmiot x

ma własność A

przedmiot x

ma własność A

nie zaobserwowano żadnego przedmiotu
x który nie ma własności A
------------------------------------------
każdy x ma własność A

Argumenty przeciwko prawomocności indukcji:



Wnioskowanie indukcyjne nie jest niezawodne: żadna liczba obserwacji nie gwarantuje prawdziwości wniosku.
Wyjątkiem jest tzw. indukcja zupełna (tj. uzupełniona o przesłankę, że zaobserwowane X-y, to wszystkie X-y jakie
istnieją”) ale indukcja taka nie ma praktycznie zastosowania przy uzasadnianiu teorii naukowych.

Przykład: „Długo sądzono że ryby trzonopłetwe wyginęły ok. 70 mln lat temu. Tymczasem 22 grudnia 1938
wyłowiono w Oceanie Indyjskim egzemplarz takiej ryby (nazwanej Latimeria Chalumnae) a potem dalsze
egzemplarze. Fakty te podważyły wcześniejszą teorię mimo, że była ona oparta na bardzo licznych danych
obserwacyjnych.”



Podejście indukcyjne kłóci się z praktyką badawczą. Nie można dokonywać obserwacji bez teorii. Teoria
ukierunkowuje badania, mówi jakie fakty są ważne, co należy obserwować (nie można obserwować
wszystkiego). Fakt jest kwalifikowany jako ważny nie ze względu na problem ale ze względu na hipotezę. Fakt jest
ważny ze względu na hipotezę H jeśli z hipotezy tej wynika, że (w określonych warunkach) fakt taki powinien
wystąpić lub nie powinien wystąpić. Pewne fakty mogą zostać w ogóle nie zaobserwowane dopóki nie pojawi się
hipoteza dla której są one ważne.

2. Podejście HIPOTETYCZNO-DEDUKCYJNE (hypothetico-deductive model)

Naukowcy wymyślają HIPOTEZY (generują pomysły) a potem poddają je sprawdzeniu (testowi) empirycznemu (schemat:
„pomysł i test”). Testowanie teorii polega na DEDUKOWANIU z niej przewidywań (obserwowalnych faktów lub praw
empirycznych) i konfrontowaniu ich z rzeczywistością: „Jeśli rzeczywiście jest tak, jak mówi teoria T, to powinniśmy
zaobserwować fakt Z. Sprawdźmy więc (przeprowadźmy badanie), czy rzeczywiście zdarzy się Z”. Testowanie hipotez
teoretycznych wymaga powiązania terminów teoretycznych z obserwacyjnymi (operacjonalizacji zmiennych
teoretycznych).

Kontekst odkrycia i kontekst uzasadnienia (koncepcja Reichenbacha)

•

Kontekst odkrycia – odnosi się generowania teorii.

•

Kontekst uzasadnienia – odnosi się do testowania teorii.

Generowanie hipotez (teorii) jest procesem twórczym i stanowi przedmiot zainteresowania raczej nauk
empirycznych (np. psychologii) niż metodologii nauk. Jeśli jednak teoria zostanie już sformułowana można ją
poddać racjonalnej rekonstrukcji i ocenić obiektywnie (zgodnie z zasadami metodologii) jej wartość, tzn. jej
poprawność formalną, wartość wyjaśniającą oraz zgodność z faktami.

Dwie logiczne reguły wnioskowania oparte na stosunku wynikania :

modus ponendo ponens

modus tollendo tollens

⊃

----------

-------------

~ p

Tylko druga reguła (modus tollendo tolens) jest niezawodna (dedukcyjna), tzn. gwarantuje, że wychodząc od
prawdziwych przesłanek dojdziemy ZAWSZE do prawdziwych wniosków.

W zastosowaniu do testowania teorii oznacza to, że za pomocą faktów (F) można wykazać fałszywość teorii (T),
nie można natomiast wykazać jej prawdziwości. Inaczej mówiąc: teorie są falsyfikowalne empirycznie ale nie są
weryfikowalne empirycznie. Teza ta stanowi postawę koncepcji falsyfikacjonizmu Poppera.

⊃

~Fi

----------

-------------

Faktycznie sytuacja jest bardziej złożona, ponieważ nigdy nie dedukujemy faktów z jednej przesłanki, lecz z wielu
przesłanek: zdań teoretycznych (T) i reguł korespondencji (RK) ustalających związki między terminami
teoretycznymi i obserwacyjnymi (operacjonalizujących teorię). Jeśli przewidywania nie potwierdzają się, to
wiadomo, że przynajmniej jedna z przesłanek wnioskowania jest fałszywa, ale nie wiadomo która (bądź które) z
nich. W szczególności nie wiadomo, czy fałszywa jest właśnie testowana przez nas teoria

Przykład: testujemy hipotezę mówiąca że frustracja prowadzi do agresji. Frustrację wywołujemy
eksperymentalnie dając badanym do wykonania nierozwiązywalne zadanie umysłowe, agresję mierzymy testem
agresji

Jeśli wynik (poprawnie przrowadzonego) eksperymentu okaże się negatywny, to nie wiadomo, np. czy:

•

testowana hipoteza jest nieprawdziwa;

•

nieprawdziwa jest teoria frustracji lub teoria agresji na której oparta jest hipoteza;

•

nieprawdziwa jest teoria testów psychologicznych;

•

zastosowana procedura eksperymentalna nie wywołuje
faktycznie frustracji;

•

test T nie jest trafną i rzetelną miarą agresji;
itd.

Niektórzy twierdzą, że twierdzeń naukowych nie da się falsyfikować pojedynczo; falsyfikować można jedynie
zespoły twierdzeń. Quine idzie jeszcze dalej i mówi, że sens empiryczny przysługuje nie pojedynczym zdaniom ale
nauce jako całości.

3. WNIOSKOWANIE DO NAJLEPSZEGO WYJAŚNIENIA zwane też wyjaśnianiem ABDUKCYJNYM.

Hipotezę która (spośród wszystkich innych dostępnych hipotez ) dostarcza najlepszych wyjaśnień zjawisk w
rozpatrywanej dziedziny należy uznać za przypuszczalnie prawdziwą.

Wyjaśnienie najlepsze to takie, które odsłania mechanizm danego zjawiska, ma największą moc wyjaśniającą (dotyczy
najobszerniejszej klasy zjawisk, sprzyja więc unifikacji teorii)
i jest najbardziej precyzyjne (por. Grobler, 2002).

Wyjaśnianie abdukcyjne pozwala uniknąć niektórych problemów jakie stwarza:

•

z jednej strony wnioskowanie indukcyjne: nawet największa liczba faktów zgodnych z teorią nie jest
wstanie zagwarantować prawdziwości tej teorii,

•

z drugiej zaś falsyfikacjonizm: wskazując na warunki, w których teoria powinna być odrzucona, nie
wyjaśnia dlaczego naukowcy akceptują określone teorie i to nawet wtedy, gdy są one niezgodne z
faktami a niekiedy odrzucają teorie, które nie zostały sfalsyfikowane. Falsyfikacjonizm nie wyjaśnia też
dlaczego naukowcy przykładają tak wielką wagę do wyników potwierdzających teorie (por. Grobler,
2006).

Wyjaśnienie abdukcyjne zgadza się z poglądem, że w nauce nie ma pewności, jest natomiast postęp, tj. zastępowanie
gorszych teorii lepszymi.

CZĘŚĆ 4. WYBRANE KONCEPCJE Z FILOZOFII NAUKI DOTYCZĄCE STATUSU TEORII W NAUKACH EMPIRYCZNYCH

KONCEPCJA FALSYFIKACJONIZMU POPPERA

Karl R. Popper (1934/1959/2002). Logika odkrycia naukowego. Warszawa: PWN.

PROBLEM DEMARKACJI: co różni wiedzę naukową od wiedzy nienaukowej?

Kryterium naukowości teorii jest jej FALSYFIKOWALNOŚĆ („wywrotność”). Teoria jest falsyfikowalna jeśli można wskazać fakty, które
(gdyby zaszły) byłyby z nią niezgodne. Obserwacyjnie można stwierdzić tylko zaistnienie jakiegoś faktu. Nie można stwierdzić
empirycznie, że coś nie istnieje (to, że jakiegoś faktu dotąd nie zaobserwowano nie przesądza wcale, że nie zaobserwujemy go w
przyszłości). Zatem, aby teoria była falsyfikowalna muszą z niej wynikać negatywne przewidywania. Teoria naukowa musi mówić co jest
niemożliwe, co się nie może zdarzyć. Jeśli taki (według teorii niemożliwy) fakt stwierdzimy, będzie to oznaczać, że teoria jest błędna. Im
więcej negatywnych przewidywań da się wydedukować z teorii tym jest ona bardziej falsyfikowalna (bardziej naukowa).

W szczególności, teoria jest tym bardziej falsyfikowalna im:

•

jest bardziej precyzyjna;

•

jest bardziej ogólna (tj. wynika z niej więcej faktów);

•

jest bardziej śmiała (wynikające z niej predykcje są, na gruncie dotychczasowej wiedzy, nowatorskie)

Dyrektywy postępowania naukowca wg Poppera:

•

Zadaniem naukowca jest tworzenie śmiałych teorii a następnie poddawanie ich możliwie jak najsurowszym testom (tj.
podejmowanie prób obalenia teorii). Pozytywne wyniki testów nie przesądzają o prawdziwości teorii. W szczególności,
nie ma sensu robić badań, jeśli z góry wiadomo, że dadzą one wynik pozytywny (jeśli wiadomo z góry że "wyjdzie").

•

Jeśli teoria wytrzyma testy ("corroboration"), tzn. nie uda się jej sfalsyfikować, nasze zaufanie do niej wzrasta i
TYMCZASOWO akceptujemy teorię.

•

Jeśli teoria nie wytrzyma testów ("refutation") - szukamy nowej, lepszej teorii (w szczególności – może być to
zmodyfikowana wersja dotychczasowej teorii).

Koncepcja Poppera:

•

jest normatywna (wskazuje jak powinno się postępować przy testowaniu teorii);

•

kładzie większy nacisk na kryteria odrzucania niż na kryteria uznawania teorii; tymczasem teorie są akceptowane przede
wszystkim ze względu na swoje sukcesy;

•

Nie wyjaśnia też jakimi kryteriami kierują się naukowcy wybierając jedną spośród istniejących teorii.

KONCEPCJA REWOLUCJI NAUKOWYCH KUHNA

Thomas S. Kuhn (1962/2001). Struktura rewolucji naukowych. Warszawa: PWN.

Jak faktycznie postępują badacze testując teorie? (podejście historyka nauki): historia nauki pokazuje, że nawet wiele wyników
niezgodnych z teorią nie prowadzi do jej odrzucenia gdy jest to teoria ważna, wysokiego stopnia ogólności. Jeśli pojawiają się fakty
niezgodne z teorią naukowcy modyfikują teorię aby zachować jej zgodność z faktami ("lepsza zła teoria niż żadna"). Teorii nie mogą
obalić fakty tylko inna, lepsza od niej teoria. Bardziej rozwinięte nauki osiągnęły etap nauki normalnej (instytucjonalnej).

Etapy rozwoju nauki normalnej:

Pre-nauka (faza przed-pragmatyczna)

Faza paradygmatyczna

•

istnieje uznany paradygmat

•

naukowcy zajmują się rozwiązywaniem zagadnień szczegółowych w ramach obowiązującego
paradygmatu (tzw. „rozwiązywanie łamigłówek”)

•

naukowcy modyfikują teorię gdy pojawiają się fakty nie dające się z nią uzgodnić (tzw. anomalie)

•

kryzys (duża liczba anomalii)

Zmiana paradygmatu (rewolucja naukowa)

4. Nowa faza nauki normalnej

PARADYGMAT to „powszechnie uznane osiągnięcia naukowe, dostarczające społeczności uczonych modelowych problemów i

rozwiązań”. Pojęcie „paradygmat” zrobiło ogromną karierę i bywa obecnie różnie rozumiane, w szczególności:

•

szerzej – jako ogół przekonań podzielanych przez daną
grupę naukowców;

•

bardziej wąsko (rozumienie właściwe) – jako powszechnie uznawane przez badaczy okazy owocnej praktyki badawczej,
wyznaczające wzorce postępowania przy rozwiązywaniu problemów naukowych.

Koncepcja Kuhna kwestionuje:

•

Naiwny falsyfikacjonizm (odrzucamy teorie dlatego, że są niezgodne z faktami)

•

Pogląd, że rozwój nauki jest kumulatywny (polega na dokładaniu nowych faktów i nowych teorii do wcześniej uznanych).
Rozwój nauki polega raczej na nowym uporządkowaniu faktów, na zmianie ich interpretacji.

•

Pogląd, że rozwój nauki ma charakter ciągły -- ważne zmiany w nauce zachodzą w sposób skokowy, rewolucyjny. Po
rewolucji naukowej następuje faza nauki normalnej.

Dziś wysuwane są argumenty, że nie wszystkie nauki rozwijają się według schematu podanego przez Kuhna (tzn. poprzez rewolucje
naukowe).

KONCEPCJA PROGRAMÓW BADAWCZYCH LAKATOSA

Imre Lakatos (1978/1995). Pisma z filozofii nauk empirycznych. Warszawa: PWN.

Teorii naukowych nie można rozpatrywać jako izolowanych twierdzeń. Uznanie teorii zależy od uznania innych teorii. Stąd, pojedynczy
fakt niezgodny z teorią nie musi obalać tej teorii. Teorie ukierunkowują rozwój badań -- są

PROGRAMAMI BADAWCZYMI.

Na program badawczy składa się:

•

TWARDY RDZEŃ złożony z najbardziej ogólnych hipotez. Twardy rdzeń jest niefalsyfikowalny -- kto atakuje twardy rdzeń
wychodzi poza program badawczy.

•

OCHRONNY PAS HIPOTEZ POMOCNICZYCH -- jeśli pojawiają się anomalie, modyfikuje się hipotezy pomocnicze aby
uchronić twardy rdzeń programu.

•

HEURYSTYKA POZYTYWNA - jak rozwijać program (techniki, metody, dyrektywy, specyficzne dla danego programu).

•

HEURYSTYKA NEGATYWNA - co jest zabronione.

W każdym programie zabronione jest:

•

atakowanie twardego rdzenia programu

•

modyfikowanie programu za pomocą hipotez "ad hoc".

Teorie (programy) konkurują ze sobą. Programy POSTĘPOWE wypierają programy DEGENERUJĄCE SIĘ. O tym, który program jest
bardziej postępowy, można jednak rozstrzygnąć dopiero po fakcie (z perspektywy historycznej). W historii nauki zdarzało się nieraz, że
programy, które wydawały się zdegenerowane, zaczynały potem na nowo inspirować badania (np. atomizm).

Program jest postępowy:

•

Teoretycznie - gdy potrafi generować nowe przewidywania,

•

Empirycznie - gdy przynajmniej niektóre z przewidywań zostaną potwierdzone empirycznie,

•

Heurystycznie - gdy oferuje nowe metody rozwiązywania problemów.

Program badawczy zyskuje szczególnie dużo w konkurencji z innymi programami, jeśli potrafi przewidzieć jakieś nowe, nie znane
wcześniej fakty. Predykcje nowych faktów są silniejszym argumentem na rzecz programu niż wyjaśnianie faktów już znanych (czyli
wyjaśnianie "ex post").

KONTROWERSJA INSTRUMENTALIZM - REALIZM (koncepcją podobną do instrumentalizmu jest konwencjonalizm)

O tym, która teoria jest lepsza, nie rozstrzygają same fakty. Teorię zawsze można zmodyfikować tak, aby pasowała do faktów.
Niektórym pojęciom teoretycznym prawdopodobnie nie odpowiada nic w rzeczywistości. Służą jedynie temu, by uczynić teorię bardziej
spójną. Przykład: pojęcie eteru w koncepcji elektromagnetyzmu Maxwella.

Zdaniem niektórych autorów „przedmioty teoretyczne” (typu „masa” „siła”, „siła ego”) to pomysłowe fikcje pozwalające w sposób
formalnie prosty i wygodny opisywać i przewidywać obserwowalne rzeczy i zdarzenia. Zdania zawierające terminy teoretyczne nie są
zdaniami o świecie realnym (nie są ani prawdziwe ani fałszywe) ale stanowią wygodną i pożyteczną aparaturę symboliczną (instrument
poznawczy), umożliwiającą wyprowadzanie pewnych faktów fizycznych z innych faktów (cytaty za Hempel, 2002). O wyborze teorii
decydują nie tylko fakty, ale również takie cechy teorii jak: użyteczność, prostota ("brzytwa" Okhama), czy elegancja.

Co przemawia przeciw instrumentalizmowi? Teorie pozwalają przewidywać fakty, które wcześniej nie były znane (np. odkrycie Plutona
na podstawie teorii Newtona). Trudno jest wyjaśnić takie odkrycia jeśli przyjmuje się, że teorie nie dotyczą realnego świata.

ANARCHIZM EPISTEMOLOGICZNY PAULA K. FEYERABENDA

Paul K. Feyerabend (1996). Przeciw metodzie. Wrocław: Siedmioróg.

Historia nauki pokazuje że nie istnieje żaden standard wspólny dla wszystkich poczynań naukowych. Narzucanie takiego standardu jest
szkodliwe bo hamuje postęp naukowy. Jedyna zasada, która nie hamuje postępu, brzmi: "NIC ŚWIĘTEGO" (ANYTHING GOES). Nie ma
takiej reguły metodologicznej której naukowcy by nie naruszali. Wiele wielkich wydarzeń naukowych zaistniało dlatego, że badacze
świadomie lub nieświadomie naruszyli jakąś zasadę metodologiczną (np. negowali dobrze potwierdzone fakty lub formułowali hipotezy
ad hoc). Gdyby badacze stosowali się rygorystycznie do dyrektyw metodologicznych, wiele ważnych teorii by nie przetrwało lub w ogóle
nie powstało.

Ocena teorii nie jest nigdy zupełnie obiektywna a na jej sukces wpływają często względy pozaracjonalne (np. przekonania filozoficzne,
światopoglądowe, oczekiwania środowiska). Wiele teorii przetrwało nie dzięki racjonalnym argumentom, ale dzięki wierze i
entuzjazmowi zwolenników tych teorii. Należy rozwijać teorie alternatywne nawet jeśli są niezgodne
z pewnymi faktami bądź uznanymi teoriami (zasada kontrindukcji). Istnienie alternatywnych teorii stymuluje rozwój nauki.

FILOZOFIA NAUK BIOLOGICZNYCH W UJĘCIU ERNSTA MAYRA

Współczesna filozofia nauki jest zdominowana przez filozofię fizyki. Zgodnie z poglądami wielu filozofów fizyki, prawa naukowe
powinny być BEZWYJĄTKOWE I UNIWERSALNE (BEZ OGRANICZEŃ PRZESTRZENNYCH I CZASOWYCH). Zdaniem Mayra, taki model nie
pasuje do nauk biologicznych.

Jeśli mówimy, że miedź przewodzi prąd to mamy na myśli to, że każdy kawałek miedzi (bezwyjątkowo) przewodzi prąd . Dzieje się tak,
ponieważ każdy kawałek miedzi jest identyczny. Każdy osobnik tego samego gatunku biologicznego jest natomiast inny, wyjątkowy i
niepowtarzalny. Zróżnicowanie to jest efektem zróżnicowania puli genetycznej a także innych czynników, w szczególności – uczenia się.
Zróżnicowanie populacji jest nieodłączną cechą organizmów żywych i jest podstawą ewolucji gatunków (doboru naturalnego i doboru
płciowego). Jeśli jakiś czynnik oddziałuje na zróżnicowaną populację osobników, to efekty takiego oddziaływania są zazwyczaj również
zróżnicowane. Efekty te dadzą się opisać tylko za pomocą praw statystycznych (probabilistycznych).

Uważa się że prawa fizyki są niezmienne w czasie: prawidłowości które zachodzą dziś, zachodziły też w przeszłości
i będą zachodziły w przyszłości. Gatunki biologiczne są natomiast efektem ewolucji, która jest procesem historycznych, mającym
przebieg unikatowy i nieprzewidywalny. Zjawisk wyjątkowych i niepowtarzalnych nie da się wydedukować z praw przyrody. Aby je
wyjaśnić należy przedstawić ich genezę (wyjaśnianie genetyczne), tj. zrekonstruować scenariusz zdarzeń które doprowadziły do ich
zaistnienia (narracja historyczna).

Uważa się, że prawa fizyki są niezmienne w przestrzeni. Jeśli odkryjemy na jakiejś odległej planecie węgiel to będzie to taki sam węgiel
jaki istnieje na ziemi. Nie ma jednak podstaw aby sądzić, że jeśli odkryjemy na innej planecie żywe organizmy
(jeśli w ogóle je odkryjemy) to będą one takie same jak na ziemi, tzn. będą miały taki sam kod genetyczny, taki sam metabolizm, takie
same mechanizmy reprodukcji, itp.
W złożonych systemach biologicznych na wyższych poziomach organizacji pojawiają się nowe właściwości, nie dające się przewidzieć na
podstawie wiedzy o ich elementach na niższym poziomie organizacji. Określa się to mianem „emergencji”. Istnienie zjawiska emergencji
ogranicza stosowanie wyjaśniania redukcjonistycznego (przynajmniej w biologii). „Całość jest czymś więcej niż sumą części”.

Przez prawo deterministyczne rozumie się prawo ustalające jednoznaczny związek między zjawiskami (np. między wcześniejszym i
późniejszym stanem jakiegoś układu). Laplace twierdził np. że gdyby jakaś potężna inteligencja znała wszystkie prawa przyrody i
aktualny stan świata, to mogłaby przewidzieć bezbłędnie jego stan przyszły. Zjawiska biologiczne nie są deterministyczne: te same
przyczyny mogą wywoływać różne skutki a podobne skutki mogą mieć różne przyczyny. Zjawisk takich nie da się wyjaśnić poprzez
wydedukowanie ich z ogólnych praw przyrody (praw uniwersalnych). Konieczne jest odwołanie się do wyjaśnień genetycznych (narracji
historycznych). Teoria ewolucji wyjaśnia mechanizm ewolucji życia biologicznego (generowanie różnorodności, dziedziczenie i selekcja
przez środowisko) natomiast sam przebieg ewolucji (historia świata biologicznego) jest nieprzewidywalny.

CZĘŚĆ 4: POMIAR

Metody pomiaru można przedstawiać w różnych ujęciach – najłatwiej wyjaśnić go w ujęciu teorii relacji.

ELEMENTY TEORII RELACJI

Uwaga: o elementach teorii relacji nie będzie mówił na wykładzie, bo jest ona przedmiotem wykładu z logiki i nie będzie ona
przedmiotem egzaminu. Wykład właściwy zaczyna się od izomorfizmu relacji.

x pozostaje w relacji (stosunku) R do y

co zapisujemy:

x R y lub R(x,y)

Relacja zachodzi zawsze w jakimś zbiorze, co zaznaczamy zapisem:

∧

x, y

∈

(x R y). Dwa sposoby określania relacji (na przykładach):

•

relacja „większości” w zbiorze licz naturalnych;

•

relacja "jest większy od" w zbiorze liczb naturalnych.

Elementy między którymi zachodzi relacja nazywają się ARGUMENTAMI relacji. Ze względu na liczbę argumentów możemy podzielić
relacje na dwu-, trój- i więcej argumentowe. Wszystkie relacje omawiane w dalszej części rozdziału są relacjami dwuargumentowymi.
Przykłady:

•

relacje dwuargumentowe:

"x jest większy od y",
"Jan kocha Marię".

•

relacja trójargumentowa:

"x leży pomiędzy y i z".

Element x, pozostający w relacji R do y, nazywa się POPRZEDNIKIEM relacji, a zbiór wszystkich poprzedników relacji -- DZIEDZINĄ relacji.
Element y nazywa się NASTĘPNIKIEM relacji, a zbiór wszystkich następników -- PRZECIWDZIEDZINĄ relacji. Zbiór wszystkich
poprzedników i następników relacji to POLE relacji.

WYBRANE CECHY RELACJI DWUARGUMENTOWYCH

Relację zachodzącą w danym zbiorze można scharakteryzować za pomocą różnych cech (można badać czy konkretna relacja
posiada określone cechy).

•

ZWROTNOŚĆ

Relacja R zachodząca w zbiorze A jest ZWROTNA jeśli zachodzi między dowolnym elementem tego zbioru a nim
samym.

∧

∈

(x R x)

Przykład: relacja równości w zbiorze liczb naturalnych (każda liczba naturalna jest równa sobie samej)
Jeśli relacja nigdy nie zachodzi miedzy danym elementem a nim samym mówimy że jest ona PRZECIWZWROTNA.

∧

∈

~(x R x)

Przykład: relacja większości w zbiorze licz naturalnych (żadna liczba nie jest większa od niej samej)

•

SYMETRYCZNOŚĆ

Relacja jest SYMETRYCZNA wtedy gdy, jeśli zachodzi między dwoma dowolnymi elementami zbioru w jedną
stronę to zachodzi też zawsze w drugą stronę (np. relacja „x jest krewnym y”).

∧

x,y

∈

((x R y)

⊃

(y R x))

Relacja jest NIESYMETRYCZNA (ASYMETRYCZNA) gdy zachodząc w jedną stronę nie zawsze zachodzi w drugą
stronę (np. „x kocha y”)

∨

x,y

∈

~((xRy)

⊃

(yRx))

∨

x,y

∈

((xRy)

∧

~ (yRx))

Relacja jest PRZECIWSYMETRYCZNA (ANTYSYMETRYCZNA) gdy zachodząc w jedną stronę nigdy nie zachodzi w
drugą stronę (np. „x jest ojcem y”):

∧

x,y

∈

((xRy)

⊃

~(yRx))

•

PRZECHODNIOŚĆ

∧

x,y,z

∈

((x R y)

∧

(y R z))

⊃

(x R z)

Przykład: „jest większy” w zbiorze liczb

•

SPÓJNOŚĆ

Relacja R jest spójna w zbiorze Z jeśli zachodzi w jedną lub drugą stronę między dwoma dowolnymi elementami
tego zbioru:

∧

x,y

∈

((xRy)

∨

(yRx))

Relacje zwrotne, symetryczne i przechodnie nazywamy relacjami RÓWNOŚCIOWYMI.

Relacje antysymetryczne, przechodnie i spójne SILNIE PORZĄDKUJĄ zbiór.

Relacja która jest antysymetryczna i przechodnia ale nie jest spójna, natomiast spójna jest jej alternatywa z relacją równościową,
CZĘŚCIOWO PORZĄDKUJE zbiór (porządkuje wszystkie elementy z wyjątkiem równych).

RELACJA JEDNOZNACZNA (WIELO-JEDNOZNACZNA)

Dla każdego x istnieje tylko jeden y

∧

x,y,z

∈

((xRy

∧

xRz)

⊃

(y=z))

Przykład: funkcje (np. y =

) , „każde dziecko ma jedną matkę”

RELACJA ODWROTNIE JEDNOZNACZNA (JEDNO-WIELOZNACZNA)

Dla każdego y istnieje tylko jeden x

∧

x,y,z

∈

((xRy

∧

zRy)

⊃

(x=z))

Przykład: „X jest matką Y”, „jedna matka może mieć wiele dzieci)

RELACJA WZAJEMNIE JEDNOZNACZNA (JEDNO-JEDNOZNACZNA)

Dla każdego x istnieje tylko jeden y i dla każdego y istnieje tylko jeden x (relacja która jest zarazem jednoznaczna
i odwrotnie jednoznaczna).

Przykład: „X pozostaje w związku małżeńskim z Y” w zbiorze małżeństw monogamicznych.

IZOMORFIZM I HOMOMORFIZM RELACJI

Niech będą dane dwa zbiory:

•

zbiór A złożony z elementów a

, a

, ..., a

, między którymi zachodzi relacja R

•

zbiór B złożony z elementów b

, b

, ..., b

między którymi zachodzi relacja S

Niech będzie dana relacja T taka, że jej dziedziną są elementy zbioru A a przeciwdziedziną elementy zbioru B.

R, A

S, B

...

….

Relacja T odwzorowuje IZOMORFICZNIE relację R na relację S (R jest izomorficzna z S) zawsze wtedy i tylko wtedy gdy T jest relacją
wzajemnie jednoznaczną, której dziedziną jest pole relacji R a przeciwdziedziną pole relacji S, przy czym:

Jeśli relacja T przyporządkowuje elementowi

element

a elementowi

element

to relacja R zachodzi między

i i

zawsze wtedy i tylko wtedy, gdy relacja S zachodzi między

Gdy przyporządkowanie elementów obu zbiorów jest jednoznaczne (wielo-jednoznaczne) mówimy o odwzorowaniu
HOMOMORFICZNYM.

Mamy zbiór numerków do szatni (n

, n

, ... n

) i zachodzącą między nimi relacje "jest mniejszy od". Mamy zbiór okryć

oddawanych do szatni (o

, o

, .. o

) i zachodzącą między nimi relację "zostało oddane do szatni wcześniej niż". Jeśli

szatniarka przydziela numerki okryciom według kolejności oddawania ich do szatni to każdy numerek jest przydzielony do
jednego okrycia i każde okrycie ma przydzielony jeden numerek. Jeśli numerek

jest mniejszy od numerka

j to okrycie

, któremu przydzielono numerek

, zostało oddane do szatni wcześniej niż okrycie

któremu przydzielono numerek

j . Wtedy relacja między numerkami palt i numerków będzie odwzorowana izomorficznie.

Jeśli jednak szatniarka będzie wieszała kilka okryć razem (dając im ten sam numerek) to odwzorowanie relacji między
numerkami na relację między okryciami będzie homomorficzne.

Tak samo stosunki między liczbami są izomorficznie odwzorowane na stosunki na linijce (dwie liczby są równe = dwa odcincki
są równe).

POMIAR

Pomiar jest to obserwacja ilościowa. Narzędziem pomiaru jest skala pomiarowa. Skala pomiarowa jest to system relacyjny, złożony z
systemu matematycznego i systemu empirycznego, zbudowany w taki sposób, że określone relacje między liczbami odwzorowane są
izomorficznie na określone relacje między cechami przedmiotów.

Funkcja przyporządkowująca liczby cechom nazywa się FUNKCJĄ POMIAROWĄ. Liczbę przyporządkowaną danej cesze przez funkcję
pomiarową nazywamy MIARĄ LICZBOWĄ tej cechy.

POMIAR to przyporządkowanie liczb obiektom (pod względem jakiejś cechy) w taki sposób aby (wybrane) relacje miedzy liczbami
odzwierciedlały relacje między cechami (obiektami). POMIAR (konkretnej cechy) CECHY to znalezienie jej miary liczbowej.

RODZAJE POMIARU

•

Jeśli istnieje funkcja która bezpośrednio przyporządkowuje liczby mierzonym wielkościom (np. pomiar długości przez
porównanie obiektu z wzorcem mierzonej wielkości) to mówimy o pomiarze PODSTAWOWYM.

•

Jeśli mierzymy jakąś wielkość jako funkcję innej wielkości mówimy o pomiarze POŚREDNIM (POCHODNYM) (np.
pomiar temperatury za pomocą pomiaru wysokości słupka rtęci w termometrze.

•

Jeśli mierzymy cechę C za pomocą innej cechy W będącej wskaźnikiem cechy C, mówimy o pomiarze
WSKAŹNIKOWYM.

Nie możemy mierzyć bezpośrednio cech psychologicznych, nie możemy też stosować pomiaru pośredniego (pochodnego).
Pomiar cech psychologicznych można traktować jako pomiar wskaźnikowy pod warunkiem, że pojęcie wskaźnika będziemy
rozumieli odpowiednio szeroko, obejmując nim również wskaźniki inferencyjne).

POZIOMY POMIARU (SKALE POMIAROWE)

Skala pomiarowa odwzorowuje określone relacje między liczbami na relacje między cechami. Zależnie od tego jakie relacje
między liczbami są odwzorowywane na relacjach między cechami możemy mówić o różnych poziomach pomiaru (rodzajach skal
pomiarowych).

Podział skal w/g Stevensa:

Skala nominalna (n) - nazwowa

Skala porządkowa ( p ) - inaczej: rangowa

Skala interwałowa ( i ) - inaczej: przedziałowa (róźnice dwóch wielkości) i skala stosunkowa (s) - inaczej:
ilorazowa, metryczna

1. SKALA NOMINALNA

Przyporządkowuje cechom liczby w taki sposób, że stosunek równości / nierówności między liczbami zostaje
odwzorowany na stosunek równości / nierówności między cechami. Pomiar za pomocą skali nominalnej jest klasyfikacją
obiektów do rozłącznych klas.

Przykłady: klasyfikacja chorób (numery chorób) klasyfikacja przestępstw (paragrafy kodeksu), klasyfikacja
podstawowych emocji (gniew, strach, zadowolenie, itp.)

2. SKALA PORZĄDKOWA

Przyporządkowuje cechom liczby w taki sposób, że stosunki równości/nierówności oraz większości/mniejszości między
liczbami zostają odwzorowane na stosunki równości/nierówności i większości/mniejszości między cechami.

Przykłady: kolejność zawodnika na mecie, stopnie (rangi) oficerskie

3. SKALA STOSUNKOWA i INTERWAŁOWA

Skala STOSUNKOWA przyporządkowuje cechom liczby w taki sposób, że stosunki (w znaczeniu: ilorazy) między liczbami
zostają odwzorowane na stosunki między cechami. Dla zbudowania skali stosunkowej wystarczy wykazać, że funkcja
pomiarowa odwzorowuje stosunek sumy miedzy cechami na stosunek sumy arytmetycznej miedzy liczbami. Np.
kolejność dojechania do mety zawodników.

W skali INTERWAŁOWEJ stosunki między cechami nie są odwzorowane na stosunki miedzy liczbami, natomiast stosunki
między interwałami są odwzorowane na stosunki między liczbami (interwał = różnica między dwiema cechami).
Przyporządkowanie jakiejś cesze liczby 1 jest równoznaczne z ustaleniem JEDNOSTKI POMIARU. Jednostka pomiaru jest
zawsze umowna. Wynik pomiaru nie zależy od wyboru jednostki. Jednostkę można zmienić mnożąc ją przez stałą.

W skali stosunkowej i interwałowej mamy do czynienia z jednostką pomiaru (wzorcem danej wielkości) oraz jej miarą
liczbową (np. 1 metr). W skalach interwałowej i stosunkowej wystarczy jeden wzorzec. Dzięki operacjom dodawania i
powielania (wyznaczania krotności danej wielkości) można tworzyć jednostki większe i mniejsze od jednostki
podstawowej. Na przykład, mając wzorzec metra można tworzyć jednostki wielokrotne (np. kilometry) i pod-wielokrotne
(np. milimetry).

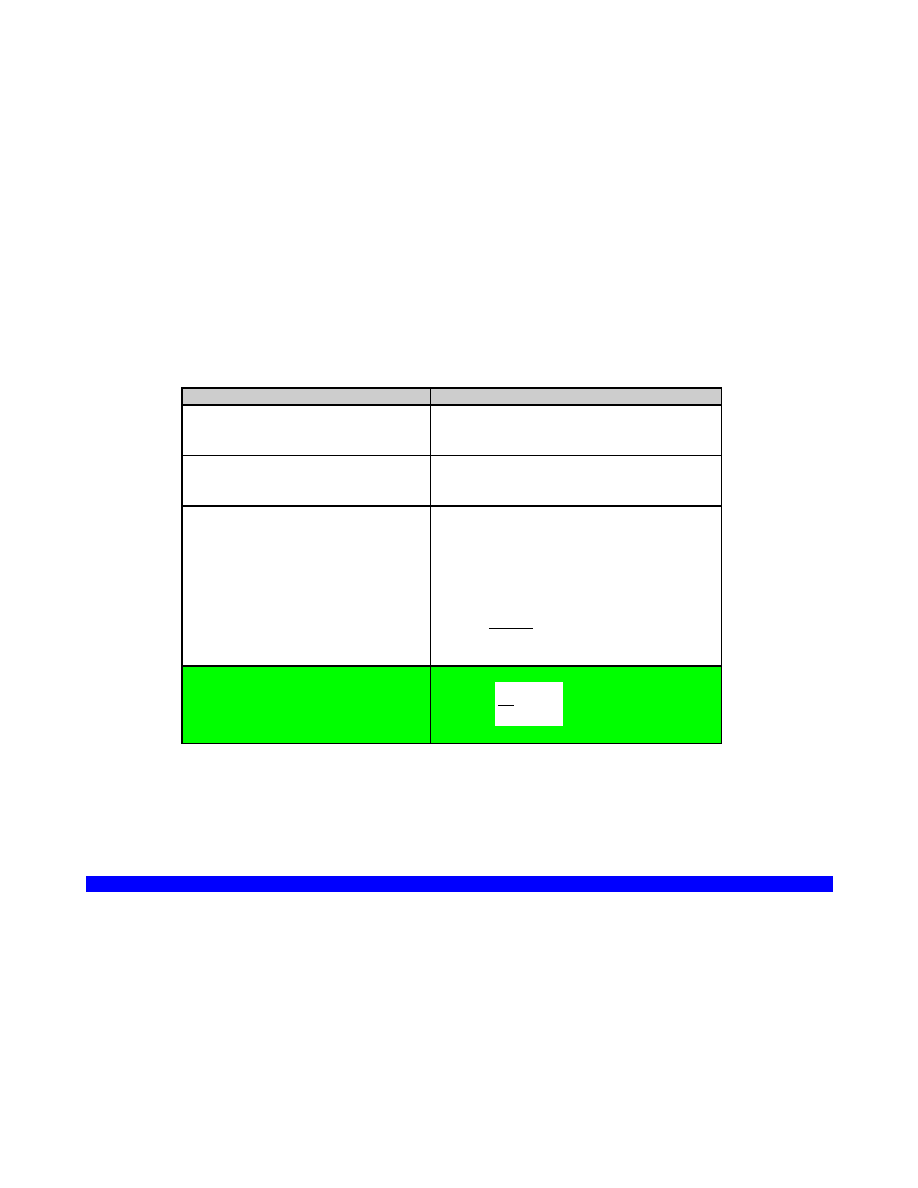
Dodawanie odpowiada matematycznej funkcji dodawania, powielanie - operacji mnożenia i dzielenia (pochodnych od
operacji dodawania). Przykłady operacji na obiektach empirycznych: dodawanie mas - równoważenie ciężarów na
wadze, powielanie mas - za pomocą dźwigni.

W skalach nominalnej i porządkowej nie mamy jednego wzorca mierzonej cechy. Należy stworzyć tyle wzorców ile jest
wartości na skali.

Skala STOSUNKOWA (w odróżnieniu od interwałowej) wymaga naturalnego zera (zero oznacza absolutny brak
mierzonej wielkości). Skala INTERWAŁOWA można potraktować jako pewną transformację skali metrycznej, polegająca
na przesunięciu naturalnego punktu zerowego (albo inaczej – ustaleniu zera umownego). W skali tej różnice miedzy
wielkościami tworzą metryczną skalę interwałów.

Przykłady skal:

•

skala stosunkowa: długość, masa, napięcie, temperatura absolutna (skala Kelvina)

•

skala interwałowa: czas kalendarzowy, temperatura w skali Celsjusza lub Fahrenheita

Tabela. Relacje między wielkościami o których można orzekać w poszczególnych typach skal

Skala

Relacje

Nominalna

a=b; a

≠

Porządkowa

j/w oraz:
a>b; a<b

Interwałowa

j/w oraz:

(a-b) = (c-d); (a-b)

≠

(c-d)

(interwał A-B jest równy interwałowi C-D)
(a-b) > (c-d); (a-b) < (c-d)

−

Stosunkowa

j/w oraz:

OD CZEGO ZALEŻY POZIOM SKALI?

Aby skonstruować skalę pomiarową należy dysponować operacją pozwalającą wykazać, że między wielkościami istnieje relacja
izomorficzna z jakąś relacją między liczbami.

•

Aby stworzyć skalę NOMINALNĄ należy dysponować operacją pozwalającą stwierdzić równość / nierówność między
wielkościami (np. w diagnostyce, porównywanie objawów choroby z objawami wzorcowymi).

•

Aby stworzyć skale PORZĄDKOWĄ należy dysponować operacją pozwalającą stwierdzić zachodzenie stosunku większości /
mniejszości (np. operacja zarysowywania w skali twardości minerałów)

•

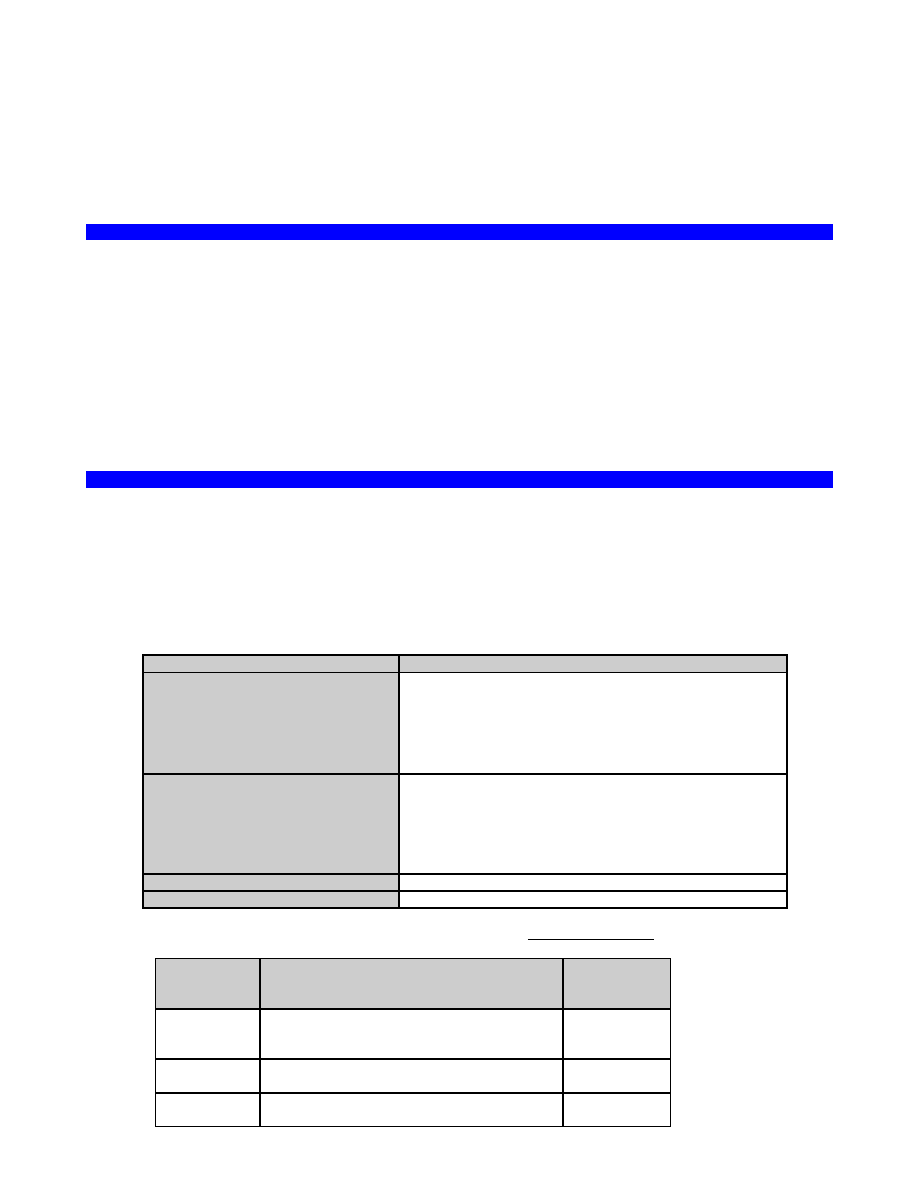
W skali INTERWAŁOWEJ i STOSUNKOWEJ należy dysponować operacją pozwalającą na dodawanie mierzonych wielkości (tzn.
operacją izomorficzną z dodawaniem liczb). np. ważenia na wadze szalkowej pozwala stwierdzić zachodzenie następujących
relacji między ciężarami (przedmiotami):

−

większości: (a przeważa b)

-- skala R

−

sumy fizycznej: (a + b równoważą się z c) -- skala S

−

równości: (dwa przedmioty się równo-ważą) -- skala N

Wielkości psychologiczne są zasadniczo nieaddytywne – interwałowy charakter skali pomiarowej wykazujemy więc pośrednio.

POMIAR CECH PSYCHOLOGICZNYCH

Nie możemy wykonywać operacji bezpośrednio na wielkościach psychologicznych (co najwyżej na ich wskaźnikach). Nie możemy też
stosować pomiaru pochodnego. Istnieją również wątpliwości czy skale do pomiaru cech psychologicznych spełniają wymagania skal
interwałowych (a tym bardziej stosunkowych). Można jednak wykazać, że niektóre z nich mają pewne właściwości skal interwałowych
(np. że odchylenie standardowe może być traktowane jako (równa) jednostka wyrażająca odległość wyniku od środka rozkładu) co daje
podstawę (przy spełnieniu innych, dodatkowych założeń) do stosowania statystyk parametrycznych.

Wielkim osiągnięciem Alfreda Binet, twórcy pierwszego testu inteligencji, było pokazanie, że można wykonywać operacje na
(wskaźnikach) inteligencji (a właściwie – wskaźnikach poziomu umysłowego) i na tej podstawie ustalać relacje między różnymi
wartościami tej zmiennej. Dając dzieciom do wykonania standardowy zestaw zadań umysłowych Binet był w stanie ustalić czy poziom
umysłowy dziecka jest równy przeciętnemu, wyższy od przeciętnego, czy też niższy od przeciętnego. We współczesnych skalach
inteligencji zmienną tę „mierzy się” w odchyleniach standardowych, które traktowane są jako (równe) „jednostki” a skonstruowane w
ten sposób skale traktuje się jako skale interwałowe.

DOPUSZCZALNE PRZEKSZTAŁCENIA WIELKOŚCI LICZBOWYCH

Niekiedy dokonujemy transformacji wielkości pomiarowych, zamieniając np. metry na centymetry, centymetry na cale, wyniki surowe
testu na steny, itp. Jakie warunki muszą spełniać takie transformacje?

Tabela. Transformacje wartości liczbowych dopuszczalne w poszczególnych typach skal pomiarowych (transformacje dozwolone w
danym typie skali są też dozwolone w skalach od niej słabszych).

Skala

Dopuszczalne transformacje

Nominalna

Transformacje wzajemnie jednoznaczne. Jeśli np. przed
transformacją zachodziło:
x

= x

i x

≠

to po transformacji (przejściu x w x’) relacje te muszą być
zachowane:
x

’ = x

’ i x

’

≠

’

Porządkowa

Monotoniczne (stale rosnące)
Po transformacji zachowane muszą być stosunki równości i
mniejszości między liczbami, np.:
x

= x

’ = x

’

> x

’ > x

’

< x

’ < x

’

Interwałowa

x’ = a + bx

Stosunkowa

x’ = bx

Zadania: przekształcenia liczbowe dopuszczalne w poszczególnych typach skal (będzie na egzaminie!)

Pierwotny zbiór
danych:

A B C D E

3, 5, 7, 9, 3

Zbiory
przekształcone
(poniżej):

Transformacja

dopuszczalna

w skali?

zbiór 1

6, 10, 14, 18, 6

zbiór 2

4, 6, 8, 10, 4

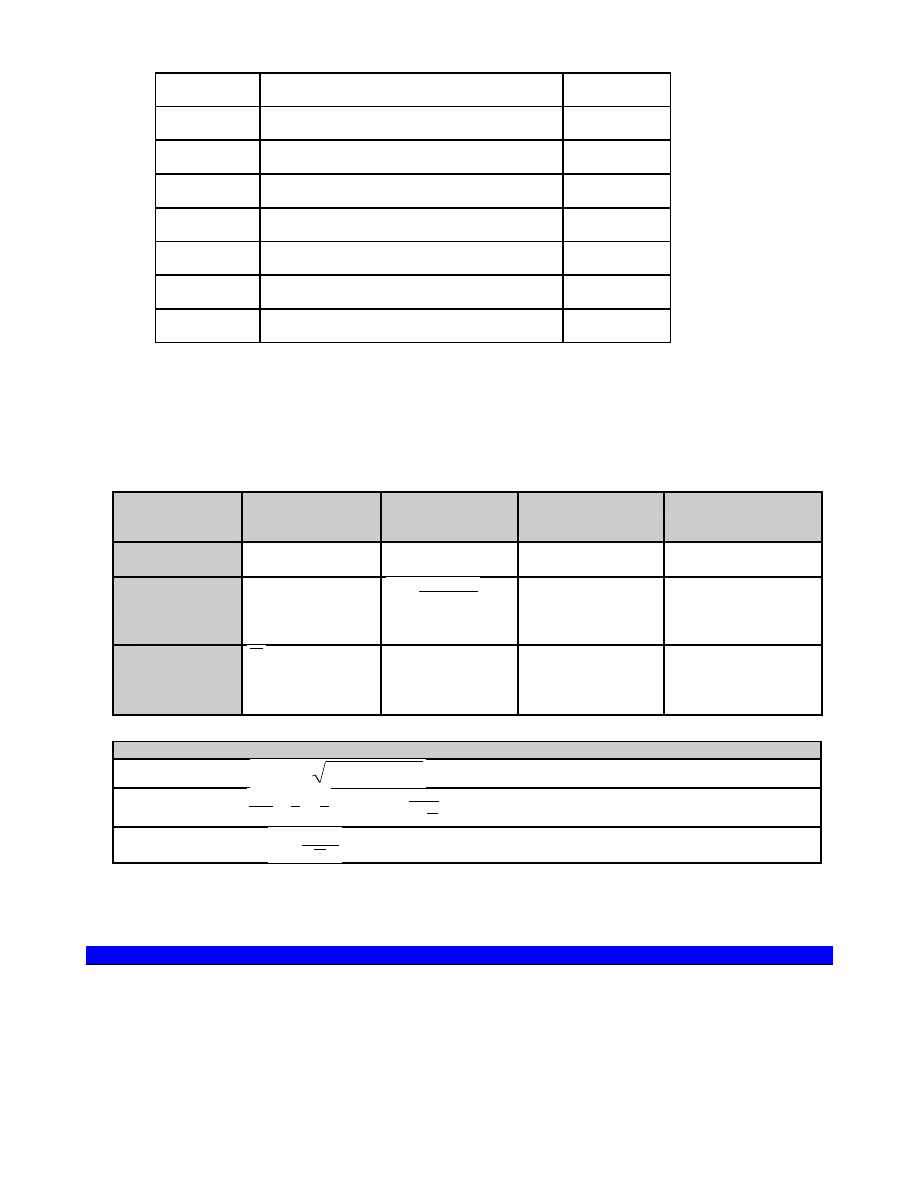
zbiór 3

31, 51, 71, 91, 31

zbiór 4

5, 3, 2, 7, 5

zbiór 5

37.4, 41, 44.6, 48.2, 37.4

zbiór 6

9, 25, 49, 81, 9

zbiór 7

4, 8, 12, 16, 4

zbiór 8

16, 20, 24, 28, 16

zbiór 9

13, 11, 9, 7, 13

zbiór 10

23, 25, 27, 100, 23

Przykłady statystyk dozwolonych w poszczególnych typach skal (statystyki dozwolone w danym typie skali są też dozwolone w
skalach od niej mocniejszych). Nie dotyczy to egzaminu, bo wykracza poza dotychczasową wiedzę ;)s

Rodzaj

skali

Miary
tendencji
centralnej

Miary
rozpro-szenia

Miary
współ-
zmienności

Testy
istotności

Nominalna

Mo
Modalna

-- brak --

phi (

)

V-Cramera

chi

(

)

porządkowa

Me
Mediana

−

Odchylenie
ćwiartkowe

tau (

)

Kendalla;
ro (

)

Spearmana;

U Manna-Witneya;
Test
Wilcoxona.

interwałowa
i
stosunkowa

Średnia
arytme-
tyczna

s, s

, (

)

Odchylenie
standardowe;
Wariancja

r ( r

);

R ( R

);

Stosunek korelacyjny
eta (

)

t Studenta;
ANOVA;
MANOVA;
Analiza regresji; inne

Statystyki dopuszczalne tylko w skali stosunkowej

Średnia geometryczna:

⋅

(pierwiastek n-tego stopnia z iloczynu n pomiarów)

Średnia harmoniczna:

∑

;

∑

(odwrotność średniej odwrotności pomiarów)

Współczynnik zmienności:

100

CZĘŚĆ 5. PLANOWANIE I ANALIZA BADAŃ EMPIRYCZNYCH. PROBLEMY, HIPOTEZY, ZMIENNE; TESTOWANIE HIPOTEZ

BADANIA EKSPERYMENTALNE; PLANOWANIE I ANALIZA BADAŃ JAKO PROBLEM KONTROLI WARIANCJI

PROBLEMY I HIPOTEZY BADAWCZE

PROBLEM: pytanie na które poszukujemy odpowiedzi

PYTANIA ROZSTRZYGNIĘCIA: Czy ... ? (Tak, Nie)

np. Czy X wpływa na Y?

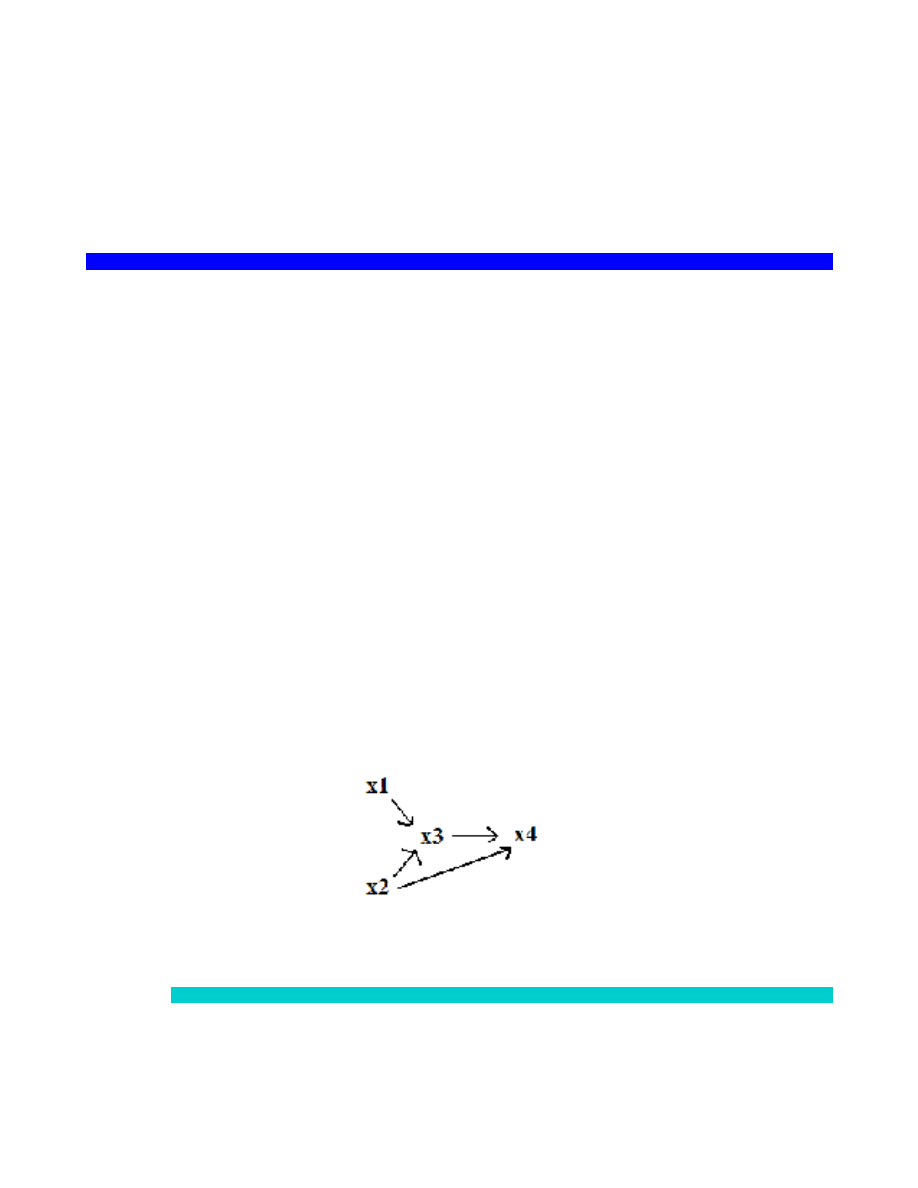
Pytanie rozstrzygnięcia sugeruje hipotezę badawczą (Czy prawdziwa jest hipoteza mówiąca że “X wpływa na

Y”?)

PYTANIA DOPEŁNIENIA: Co / który / jak .... ?

np. Co jest przyczyną Y? Przyczyną Y jest .... (wiele możliwych odpowiedzi)

4. HIPOTEZA: proponowana (prowizoryczna) ODPOWIEDŹ NA PYTANIE (do sprawdzenia).

ZMIENNE I ICH RODZAJE

Taka wartość, która może przybierać różne wartości.

•

Zmienna jest MANIPULOWALNA – jeśli możemy dowolnie przyporządkować badanym różne wartości tej zmiennej.

•

Zmienna jest OBSERWOWALNA (w szczególnym przypadku –MIERZALNA) – jeśli możemy tylko obserwować (mierzyć)
wartość zmiennej.

Niektóre zmienne (np. płeć, iloraz inteligencji) są z natury niemanipulowalne. Inne (np. stan lęku) mogą pełnić rolę zmiennych
manipulowalnych jak i obserwowalnych.

Pojęcie zmiennej NIEZALEŻNEJ I ZALEŻNEJ odnoszą się do PLANU BADANIA i SPOSOBU ANALIZY DANYCH (w konkretnym badaniu).
Pojęcia przyczyny i skutku - odnoszą się do INTERPRETACJI wyników.

Przy dwóch zmiennych, zmienną niezależną oznaczamy zwyczajowo symbolem X, zmienną zależną – symbolem Y.

Jeśli pytamy: „czy A wpływa na B?” traktujemy A jako zmienną niezależną, a B jako zmienną zależną. Zmienna która w jednym badaniu
analizowana jest jako zmienna zależna (od jakiejś innej zmiennej), w innym badaniu może być traktowana jako zmienna niezależna.

Przykład.
Jeśli przewidujemy wzrost na podstawie wagi ciała, zmienną niezależną będzie waga ciała, zmienną zależną - wzrost. Jeśli
przewidujemy wagę ciała na podstawie wzrostu -- zmienną niezależną będzie wzrost, zmienną zależną - waga ciała. Nie oznacza to
jednak że traktujemy różnice we wzroście jako przyczynę różnic w wadze ani na odwrót.

W bardziej złożonych modelach teoretycznych mogą występować zmienne pośredniczące (mierzalne lub niemierzalne), np.:

RODZAJE ZMIENNYCH NIEZALEŻNYCH

•

Zmienna niezależna GŁÓWNA -- zmienna istotna z merytorycznego punktu widzenia (z punktu widzenia
analizowanego zagadnienia), stanowiąca główny przedmiot badania (badanie zostało podjęte właśnie dla oceny jej
wpływu na zmienną zależną). Przykładowo, jeśli przedmiotem badania jest wpływ nagrody na poziom wykonania
zadań, zmienną główną będzie nagroda.

•

Zmienna niezależna UBOCZNA -- zmienna istotna z merytorycznego punktu widzenia (z punktu widzenia teorii
danej zmiennej), nie będąca jednak głównym przedmiotem zainteresowania badacza w danym badaniu. Badacz

musi się jednak liczyć z jej wpływem na zmienną zależną i (jeśli to możliwe) kontrolować go. W przykładzie
podanym wyżej, zmienną uboczną mógłby być np. poziom inteligencji badanych osób. Choć badacza nie interesuje
wpływ inteligencji na poziom wykonania zadań to musi się liczyć z tym, że taki wpływ może mieć miejsce i że różnice
indywidualne w inteligencji mogą powodować dodatkowe zróżnicowanie wyników (wzrost wariancji wewnątrz
grup).

•

Zmienna niezależna ZAKŁÓCAJĄCA -- zmienna nieistotna z merytorycznego punktu widzenia, związana z samym
przebiegiem badania (np. różna pora dnia rozwiązywania zadań, stan zdrowia osób badanych, itp.).

OPERACJONALIZACJA ZMIENNYCH: POMIAR I MANIPULACJA

Celem badań empirycznych jest ustalanie zależności między zmiennymi: zmienną niezależną (zmiennymi niezależnymi) i
zmienną zależną (zmiennymi zależnymi). Zazwyczaj badacza interesuje związek między zmiennymi teoretycznymi. Ustalenie
takiego związku wymaga operacjonalizacji zmiennych teoretycznych.

•

Operacjonalizacja zmiennych mierzalnych (zależnych lub niezależnych): dobór odpowiednich (obserwowalnych,
mierzalnych) wskaźników zmiennej zależnej.

Przykład: badamy wpływ motywacji na poziom wykonania. Operacjonalizacja “poziomu wykonania” może
polegać na zastosowaniu jakiegoś testu umysłowego -- wynik w teście będzie miarą poziomu wykonania

•

Operacjonalizacja zmiennych niezależnych manipulowalnych: dobór procedur pozwalających stworzyć dwa lub
więcej poziomów zmiennej niezależnej.

Przykład: procedura polegająca na nagradzaniu jednej grupy za dobre wyniki a nie nagradzaniu drugiej grupy
może wywołać różne poziomy motywacji do wykonywania zadania.

BADANIA PODSTAWOWE I STOSOWANE

•

Badania PODSTAWOWE - poszukiwanie zależności ogólnych.

•

Badania STOSOWANE - dotyczą zastosowania wiedzy ogólnej do konkretnych problemów.

Podział ten nie jest ostry.

•

Badania KONFIRMACYJNE – mają na celu testowanie hipotez (udzielenie odpowiedzi na pytanie czy testowana
hipoteza jest prawdziwa?) Hipoteza ukierunkowuje zbieranie danych: zbieramy takie dane, które są istotne z
punktu widzenia testowanej hipotezy.

•

Badania EKSPLORACYJNE (bez hipotez) – ukierunkowane na poszukiwanie nowych zależności empirycznych.

Jeśli nowa (nie przewidywana wcześniej) zależność zostanie zaobserwowana, wymaga ona później "interpretacji" – czyli
sformułowania hipotezy wyjaśniającej. Jeśli jednak hipoteza H wyjaśniająca fakt X została sformułowana "ex post", (po
zaobserwowaniu faktu X), fakt X nie może być traktowany jako potwierdzenie hipotezy H. Hipoteza “ex post” musi być
poddana niezależnym testom w kolejnych badaniach (badaniach konfirmacyjnych).
W rzeczywistości, badacz zbierając dane, zawsze kieruje się jakąś hipotezą (np. jakie zmienne warto obserwować?), ale może
być ona bardzo ogólnikowa i nieprecyzyjna.

TESTOWANIE HIPOTEZ STATYSTYCZNYCH

1. PRÓBA A POPULACJA

POPULACJA: zbiorowość do której chcemy odnosić wyniki badań.
PRÓBA: część populacji którą badamy.

Zdarza się, że badamy całą populację (np. spis powszechny). Najczęściej jednak badamy próbę i na tej podstawie formułujemy
wnioski dotyczące populacji.

Aby można było wnioskować o populacji na podstawie próby, próba musi być:



REPREZENTATYWNA dla populacji (statystyki obliczone z próby muszą być możliwie bliskie parametrom
populacji).



odpowiednio DUŻA (przy małych próbach następują duże wahania wyników z próby na próbę)

-3

-2

-1

-0

male proby
duze proby

Parametry: μ, σ, ρ, ...
Statystyki: M, s, r, …

1.1. PRÓBA. LOSOWY DOBÓR PRÓBY

Próba losowa to próba WYLOSOWANA z populacji. Metody losowego doboru próby

•

losowanie indywidualne (nieograniczone, systemowe)

•

losowanie warstwowe (dzielimy populacje na warstwy, a następnie losujemy osoby z każdej warstwy

•

losowanie grupowe (losujemy grupy osób, np. szkoły)

•

losowanie wielostopniowe (mieszane).

Inne zasady doboru próby

•

dobór incydentalny (badamy osoby które są dostępne).

•

dobór ochotniczy (kto się zgłosi)

Losowy dobór próby jest kosztowny i pracochłonny. W psychologii próby losowe stosuje się zazwyczaj przy szacowaniu
parametrów (np. opracowywanie norm testowych). W badaniach eksperymentalnych bada się zwykle (ze względów
technicznych) próby incydentalne. Liczebność prób też nie jest zazwyczaj zbyt duża (15-20 przypadków). Oczekuje się
natomiast, że wyniki badań zostaną zreplikowane w sposób niezależny (na innej próbie, w innym laboratorium). Należy
odróżniać losowość doboru próby (z populacji) od losowego podziału próby na grupy eksperymentalne, czyli –
randomizacji.

2. INDUKCJA STATYSTYCZNA

Dwa rodzaje wnioskowania statystycznego(indukcji statystycznej):

•

SZACOWANIE PARAMETRÓW

•

TESTOWANIE HIPOTEZ STATYSTYCZNYCH

PARAMETR charakteryzuje rozkład zmiennej w populacji. Wielkości charakteryzujące rozkład zmiennej w próbie nazywają się
STATYSTYKAMI.

Szacowanie parametrów jest wnioskowaniem indukcyjnym (czyli nie-niezawodnym) mającym na celu ocenę wartości
parametrów populacji na podstawie statystyk z próby.

Na przykład:

•

Ile zadań testu Ravena rozwiązują średnio 12-letnie dzieci polskie?

•

Jaki procent (populacji) wyborców będzie głosował w wyborach prezydenckich na kandydata X?

Testowanie hipotez jest wnioskowaniem indukcyjnym mającym na celu weryfikację hipotez, mówiących o istnieniu w populacji
zależności między zmiennymi.

HIPOTEZY STATYSTYCZNE

•

Hipoteza zerowa: Ho

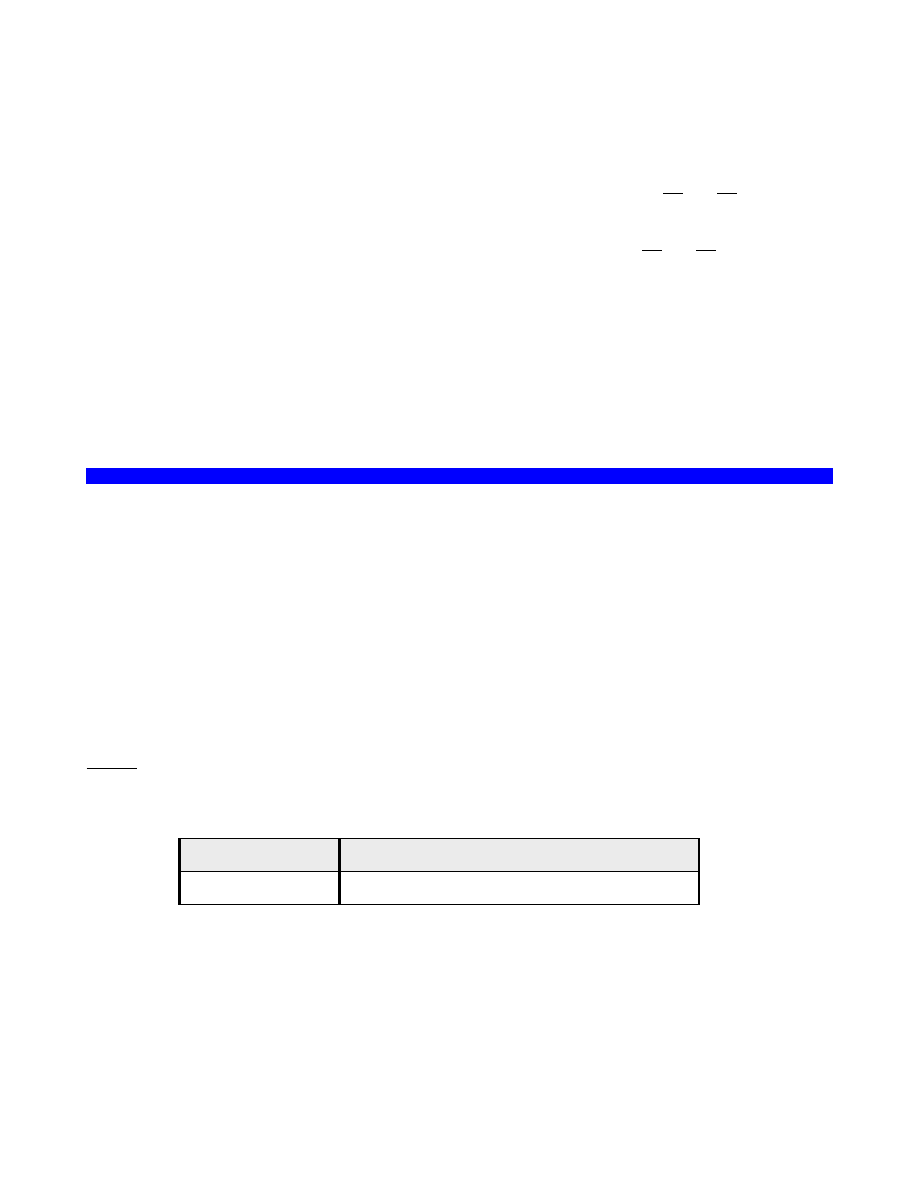
Nie istnieje zależność między zmiennymi w populacji. Zależność zaobserwowana w próbie powstała w sposób
losowy.

•

Hipoteza alternatywna: H1

W populacji istnieje zależność miedzy zmiennymi. Jej efektem jest zależność zaobserwowana w próbie.

Przykład 1:

Ho: Średnie w populacji nie różnią się:

1 =

2 . Różnica między średnimi w próbie (np.

) powstała

losowo.

H1: Średnie w populacji różnią się (np.

1 >

2). Różnica między średnimi w próbie (

) jest wynikiem

istnienia różnicy między średnimi w populacji.

Przykład 2:

Ho: Korelacja miedzy zmiennymi X i Y w populacji wynosi 0 (

= 0). Korelacja między zmiennymi w próbie

(r > 0) powstała losowo.

H1: Korelacja miedzy zmiennymi w populacji jest różna od zera (np.

> 0). Korelacja zaobserwowana w próbie

(r > 0) wynika z istnienia korelacji w populacji.

SCHEMAT WNIOSKOWANIA INDUKCYJNEGO PRZY TESTOWANIU HIPOTEZ STATYSTYCZNYCH

Jeśli zaobserwowano zależność między zmiennymi w próbie to można przyjąć, że zachodzi jedno z dwóch:

•

Nie istnieje zależność między zmiennymi w populacji (Ho) a wynik zaobserwowany w próbie powstał losowo.

Istnieje zależność między zmiennymi w populacji (H1) i dlatego zaobserwowano zależność w próbie.

Indukcja statystyczna opiera się na następującym schemacie wnioskowania:

Zakładamy prowizorycznie Ho i próbujemy ją odrzucić.

Jeśli nie uda się odrzucić Ho to uznajemy, że wynik zaobserwowany w próbie postał losowo.

Jeśli uda się odrzucić Ho to uznajemy, że zależność zaobserwowana w próbie nie powstała losowo.

4. Przyjmujemy wtedy H1 mówiącą, że istnieje zależność między zmiennymi w populacji.

Problem: czy wyrzucenie 8 orłów w 10 rzutach monetą powstało losowo?

Tabela 1. Rozkład dwumianowy: liczba orłów uzyskana w 10 rzutach rzetelną monetą (całkowita liczba możliwych zdarzeń =
210 = 1024)

zdarzenie
(liczba orłów)

0 1 2 3 4 5 6 7 8 9 10

częstość

1 10 45 120 210 252 210 120 45 10 1

Prawdopodobieństwo otrzymania w sposób losowy 8 orłów w 10 rzutach wynosi: 45/1024

≈

0,04.

Przy testowaniu hipotez interesuje nas prawdopodobieństwo z jakim może się pojawić losowo określony wynik i wyniki bardziej
od niego skrajne, np.:

Jakie jest prawdopodobieństwo że ktoś uzyskał w sposób losowy 8 lub więcej orłów w 10 rzutach?

Półprosta (x

≥

8) nazywa się OBSZAREM KRYTYCZNYM. W naszym przypadku prawdopodobieństwo (p) losowego otrzymania

wyniku, który mieści się w obszarze krytycznym (x

≥

8) wynosi:

p= 45/1024+ 10/1024 + 1/1024 = 56/1024

≈

0,05468..

≈

0,05

Rozkład dwumianowy

obszar krytyczny dla p ≈ 0,05 (test jednostronny)
i dla p ≈ 0,1 (test dwustronny)

ETAPY TESTOWANIA HIPOTEZY STATYSTYCZNEJ

SFORMUŁOWANIE PROBLEMU (PYTANIA)

Na przykład: Czy wynik "8 orłów w 10 rzutach" powstał losowo, czy też nie powstał losowo (np. nierzetelna moneta
wyjątkowe uzdolnienia rzucającego, itp.)?

HIPOTEZY ZEROWEJ I ALTERNATYWNEJ

Ho: otrzymany wynik powstał w sposób losowy.
H1: otrzymany wynik nie powstał w sposób losowy.

WYBÓR MODELU STATYSTYCZNEGO

1 0

1 20

21 0

252

21 0

1 20

1 0 1

1 00

1 50

200

250

300

1 0

Liczba orłów

0,1

1 1 ,7

2 0,5

24,6

20,5

1 1 ,7

0,1

1 0

1 5

ów

1 0

liczba orłów

Wybieram model statystyczny który (zakładam!) dobrze opisuje badane zjawisko. W omawianym przykładzie zakładam,
że rozkład losowy rzutów monetą jest zgodny z rozkładem dwumianowym.

Dysponując modelem statystycznym jesteśmy w stanie ocenić prawdopodobieństwo uzyskania określonego wyniku
w sposób losowy. W naszym przykładzie, prawdopodobieństwo uzyskania 8 lub więcej orłów w 10 rzutach wynosi: p
= 0,05

3a. Podjęcie decyzji co do strategii odrzucania hipotezy zerowej (wybór poziomu alfa)

3b. Obliczenie wartości statystyki

3c. Podjęcie decyzji o odrzuceniu lub nie odrzuceniu h0.

Przybliżone procenty powierzchni pod krzywą rozkładu normalnego dla różnych przedziałów na osi wyników (oś wyników w
jednostkach odchylenia standardowego).

4. PODJĘCIE DECYZJI CO DO STRATEGII ODRZUCANIA HIPOTEZY ZEROWEJ

Sposób wnioskowania:

•

Jeśli prawdopodobieństwo losowego otrzymania określonego wyniku jest odpowiednio niskie, podejmujemy decyzję, że
wynik ten nie powstał losowo.

•

Jeśli prawdopodobieństwo to jest odpowiednio wysokie, przyjmujemy, że wynik mógł powstać w sposób losowy.

Należy podjąć decyzję, przy jakim prawdopodobieństwie p będziemy uznawali wynik za nielosowy. Inaczej mówiąc -- przy jakim
p będziemy odrzucali Ho. Najczęściej przyjmuje się, że Ho należy odrzucić jeśli p ≤ 0,05. Stosuje się też ostrzejsze kryteria (p ≤
0,001; p ≤ 0,001). W badaniach pilotażowych można stosować bardziej liberalne kryteria (np. p ≤ 0,10).

Jeśli wynik pozwala na odrzucenie Ho, to mówimy że jest ISTOTNY STATYSTYCZNIE.

Podejmując DECYZJĘ o odrzuceniu Ho musimy się zawsze liczyć z ryzykiem popełnienia błędu.

Przykładowo, jeśli podejmiemy decyzję, o uznawaniu za nielosowe zdarzeń, które mogłyby się zdarzyć losowo z
p = 5/100 (takich jak np. wyrzucenie 8 lub więcej orłów w 10 rzutach) to musimy się liczyć z tym, że 5 razy na 100 taki właśnie
wynik może się pojawić losowo i nasza decyzja będzie wtedy błędna.

Podjęcie błędnej decyzji, polegającej na odrzuceniu Ho gdy jest ona prawdziwa, nazywa się BŁĘDEM ALFA (

Podjęcie błędnej decyzji, polegającej na nie odrzuceniu Ho gdy jest ona fałszywa, nazywa się BŁĘDEM BETA (

Czym większe jest prawdopodobieństwo popełnienia błędu

tym mniejsze prawdopodobieństwo popełnienia błędu beta.

Należy jednak pamiętać, że:

≠

-3,5

-3

-2,5

-2

-1 ,5

-1

-0,5

0,5

1 ,5

2,5

3,5

w ynik (w odc hye niac h s tandardow yc h)

9.2

19.1

1.7

9.2

4.4

15.0

Prawdopodobieństwo przyjęcia hipotezy H1 gdy jest ona prawdziwa równa się 1 –

, i jest nazywane mocą statystyczną testu.

Moc testu to inaczej jego zdolność do wykrycia zależności miedzy zmiennymi, kiedy zależność taka rzeczywiście istnieje.

Prawdopodobieństwo błędu α i błędu β

Wartość krytyczna testu
moc statystyczna testu = 1– β

Prawdopodobieństwo zdarzenia (p) a błąd alfa (

)

p jest PRAWDOPODOBIEŃSTWEM jakiegoś zdarzenia, oszacowanym na podstawie modelu statystycznego (oczywiście
oszacowanie to może być również błędne, jeśli np. dane empiryczne nie spełniają założeń modelu statystycznego). Alfa (

)

oznacza PRAWDOPODOBIEŃSTWO PODJĘCIA BŁĘDNEJ DECYZJI, polegającej na odrzucaniu Ho wtedy, gdy jest ona prawdziwa.

•

Każda decyzja o odrzuceniu Ho może być błędna.

•

Błąd alfa nie odnosi się do pojedynczej decyzji, ale do pewnej STRATEGII PODEJMOWANIA DECYZJI.

Wybierając alfa = 0.10 wybieram strategię obarczoną 10% prawdopodobieństwem błędu, tzn. w długiej serii decyzji będę
błędnie odrzucał Ho nie częściej niż 10 razy na 100. Wybierając mniejsze alfa, np.

< 0,001, wybieram strategię mniej

ryzykowną: w długiej serii decyzji będę błędnie odrzucał Ho nie częściej niż 1 raz na 1000 (choć będę częściej przyjmował Ho,
mimo

że

jest

ona

fałszywa).

Jednakże, niezależnie od wybranego alfa, nigdy nie mogę być pewien czy KONKRETNA decyzja o odrzuceniu Ho jest trafna, czy
też nie. Testowanie hipotez jest szczególnym przypadkiem wnioskowania indukcyjnego, jest więc zawsze obarczone ryzykiem
błędu.

Przykład: test t-Studenta
Interesuje nas istotność różnicy między średnimi. W praktyce, nie szacujemy istotności różnic wyrażonych w jednostkach
surowych (takich, w jakich mierzona była zmienna). Bezwzględna wielkość takich różnic zależna jest od rodzaju zmiennej i
jednostek pomiaru. Na przykład, różnica wzrostu może być wyrażona bądź w metrach bądź w centymetrach – w pierwszym
wypadku bezwzględna wielkość różnicy będzie 100 razy mniejsza niż w drugim. Żeby uniknąć takich kłopotów budujemy
specjalne statystyki, pozwalające na ocenę DOWOLNEJ różnicy między średnimi.

n n

−

(

)

P rawdziwa Ho
P rawdziwa H1

Znając rozkład statystyki t (jest on zbliżony do normalnego) możemy oszacować prawdopodobieństwo z jakim określona
wartość testu t może pojawić się w sposób losowy. W analizie wariancyjnej stosuje się test F. Pozwala on szacować istotność
różnic między więcej niż dwiema średnimi (dla dwóch średnich: F = t2).

BADANIA EKSPERYMENTALNE; PLANOWANIE I ANALIZA BADAŃ JAKO PROBLEM KONTROLI WARIANCJI

Eksperyment jest schematem badawczym który pozwala na celowe oddziaływanie na zmienną zależną a jednocześnie stwarza najlepsze
możliwości kontroli zmiennych ubocznych. Eksperyment polega na stworzeniu takiego układu izolowanego, w którym na zmienną
zależną wpływa jedna lub kilka zmiennych niezależnych (głównych) natomiast wpływ innych zmiennych (ubocznych i zakłócających) jest
wyeliminowany lub dobrze kontrolowany. Eksperyment powinien być tak zaplanowany i przeprowadzony, aby grupy eksperymentalne
nie różniły się między sobą od siebie niczym, poza poziomem zmiennej niezależnej (zmiennych niezależnych).

•

MANIPULACJA EKSPERYMENTALNA: przyporządkowanie różnych (co najmniej dwóch) poziomów zmiennej niezależnej
grupom zrandomizowanym.

•

RANDOMIZACJA: losowy podział próby na grupy eksperymentalne.

•

EKSPERYMENT to badanie w którym manipulujemy co najmniej jedną zmienną niezależną, kontrolujemy zmienne uboczne i
eliminujemy zmienne zakłócające.

P o d z ia ł p la n ó w b a d a w c z y c h

R ANDO MIZ AC J A

ek s perym ent

B R AK ra ndom iz a c ji

qua s i-ek s perym e nt

O DDZ IAŁ Y WANIE

(tre a tm e nt)

B R AK oddz ia ływa nia

(wyłą c z nie z m ienne m ierz one)

ba da nie e x-pos t fa c to

ZMIENNA ZALEŻNA JEST ZMIENNĄ MIERZONĄ.

TRAFNOŚĆ WEWNĘTRZNA I ZEWNĘTRZNA PLANU EKSPERYMENTALNEGO

Plan jest trafny WEWNĘTRZNIE gdy:

•

umożliwia udzielenie odpowiedzi na postawione pytanie.

•

umożliwia testowanie hipotezy eksperymentalnej, eliminując jednocześnie wszystkie hipotezy alternatywne
(alternatywne wyjaśnienia uzyskanych wyników).

Przykład:
Testujemy hipotezę mówiącą, że "nagroda podwyższa poziom wykonania zadań umysłowych". Zastosowano plan dwu-
grupowy, jak niżej.

Grupa 1: kobiety

Grupa 2: mężczyźni

Nagroda

Brak nagrody

Gdybyśmy zaobserwowali wyższy poziom wykonania w grupie 1 niż w grupie 2, nie moglibyśmy rozstrzygnąć czy różnica ta
została spowodowana nagrodą (hipoteza badawcza) czy też płcią osób badanych (hipoteza alternatywna). Plan jest
nietrafny wewnętrznie. Byłby on trafny wewnętrznie wtedy, gdyby zaobserwowanej różnicy między grupami nie można było
wyjaśnić NICZYM INNYM, lecz jedynie działaniem nagrody (zmiennej niezależnej).

Koniecznym warunkiem trafności wewnętrznej planu eksperymentalnego jest randomizacja. Jeśli grupy nie są zrandomizowane,
nigdy nie wiemy, czy nie różnią się między sobą pod względem jakiejś ważnej zmiennej.

Plan jest trafny ZEWNĘTRZNIE gdy pozwala generalizować (uogólniać) wyniki uzyskane w próbie na populację.

Generalizacja może dotyczyć:

•

badanych osób – np. czy wyniki uzyskane na 20 kobietach i 20 mężczyznach można uogólnić na wszystkie kobiety i
mężczyzn?

•

zmiennej manipulowalnej – czy wyniki uzyskane z zastosowaniem nagany jako kary można uogólnić na wszystkie rodzaje
kar?

W badaniach eksperymentalnych bardzo rzadko bada się próby reprezentatywne (stosuje się natomiast powtarzanie badań na
różnych próbach). Nie jest to jednak mankament tak ważny jak brak reprezentatywności próby przy szacowaniu parametrów.
Nie chodzi tu bowiem o ocenę, ile wynosi wartość określonego parametru zmiennej, ale o to, czy manipulacja eksperymentalna
POWODUJE ZMIANĘ zmiennej zależnej. Oczywiście trzeba się liczyć z tym, że efekty manipulacji mogą być różne zależnie od
populacji.

ELEMENTY ANALIZY WARIANCJI (rozwiązanie klasyczne, oparte na sumach kwadratów)

B adania ek sper ym entalne

g łó w n e

- - - - - - - - - - - - - - - - - - - - -

m a n ip u la c ja

k o n tro la

s ta ty s ty c z n a

k o n tro la

e k s p e ry m e n ta ln a

u b o c z n e

- - - - - - - - - - - - - - - - - - - - - - -

k o n tro la

z a k łó c a ją c e

- - - - - - - - - - - - - - - - - - - - - -

e lim in a c ja

Z m ie n n e

n ie z a le ż n e

•

suma kwadratów (odchyleń od średniej) / sum of squares – SS

•

stopnie swobody / degree of freedom – df

•

średni kwadrat / mean square (MS) = wariancja –

Tabela 2. Obliczanie wariancji

X -

= x

-4

-2

14 4 16

Próba:

Populacja:

obliczanie wariancji w próbie:

= SS/n;

= 40/5 = 8

szacowanie (estymacja) wariancji w populacji:

ˆs

= SS/df (df = n – 1);

ˆs

= 40/4=10

(często używa się jednak symbolu

zamiast

ˆs

)

Tabela 3. Porównanie wariancji w czterech zbiorach*

Zbiór:

Z1 Z2

Z3 Z4

6 16

12 7

16 7

20 10

24 13

28 13

100

100 50

20 10

5 5

0 0

(SS)

160 36

160

(MS)

40 9

*wariancja jest szacowana na podstawie wzoru: S2=

/ (n-1)

Zbiór 2 powstał ze zbioru 1 przez dodanie stałej = 10. Dodanie stałej nie zmienia wariancji.
Zbiór 3 powstał ze zbioru 1 przez pomnożenie wartości zmiennej przez stałą = 2. Mnożenie przez stałą (np. zmiana jednostki
pomiaru) zmienia wariancję.
Zauważ, że zbiory 1, 4 i 5 mają tę samą średnią ale różne wariancje.

Tabela 4. Analiza wariancji (ANOVA) -- plan dwugrupowy.

Zbiór wyników: 1

1 + 2

6 16 6 16

100

150

330

liczba osób w grupie: i=1, 2, ..., n; liczba grup: j=1, 2, ..., k.

= (

) + (

)

m g

. .

w g

. .

SUMY KWADRATÓW

między grupami:

m g

. .

∑

−

)

(

wewnątrz grup:

w g

. .









−

∑

)

(

całkowita:

∑

−

)

(

m g

. .

= 5 [ (10-15)2 + (20-15)2 ] = 5 (52 + 52) = 250

w g

. .

= 40 + 40 = 80;

= 330;

330 = 250 + 80

Stopnie swobody (df) dla MS

między grupami = k-1
wewnątrz grup = k (n-1)
całkowity = N-1 = (kn-1)

m g

. .

m g

. .

/df =

m g

. .

/k-1 = 250/1 = 250

w g

. .

w g

. .

/df =

w g

. .

/k(n-1) = 80/8 = 10

m g

w g

. .

250

Uzyskany wynik zapisalibyśmy: F(1/8) = 25, p = 0,001

Sumy kwadratów są addytywne (całkowita suma kwadratów jest sumą cząstkowych sum kwadratów) ale nieporównywalne ze
sobą (zależą od wielkości zbioru). Wariancje nie są addytywne ale porównywalne (test f jest porównaniem dwóch wariancji).

Analiza wariancji opiera się na założeniu, że porównywane zbiory (w szczególności: grupy eksperymentalne) mogą się różnić
pod względem średnich nie mogą się różnić pod względem wariancji (wariancje w zbiorach muszą być równe).

Znając rozkład testu F możemy oszacować jakie jest prawdopodobieństwo uzyskania w sposób losowy określonej wartości F
przy określonej liczbie stopni swobody. Generalnie, czym większa wartość F, tym mniejsze prawdopodobieństwo że uzyskana
została ona w sposób losowy.

F jest tym większe, im:

•

większa jest wariancja między zbiorami (między grupami),

•

mniejsza jest wariancja w zbiorach (wewnątrz grup).

Wariancja między zbiorami nazywana jest wariancją KONTROLOWANĄ - jest to wariancja wywołana celowym działaniem
eksperymentatora.
Wariancja w zbiorach nazywana jest wariancją NIEKONTROLOWANĄ, wariancją RZESZTOWĄ, (residuals) lub wariancją BŁĘDU
(error). Wariancja w zbiorach stanowi oszacowanie wariancji zmiennej w populacji. Jest ona spowodowana wieloma różnymi
czynnikami, nad którymi (w danym badaniu) nie mamy kontroli.

DYREKTYWY EFEKTYWNEJ MANIPULACJI

•

MAKSYMALIZUJ wariancję kontrolowaną! -- staraj się, aby różnice między średnimi dla zbiorów (grup) były jak największe.

•

MINIMALIZUJ wariancję niekontrolowaną! -- staraj się, aby zmienność wyników wewnątrz zbiorów (grup) była jak
najmniejsza.

Sposoby minimalizowania wariancji wewnątrz grup:

•

ELIMINACJA wpływu zmiennych ubocznych, przez dobór odpowiedniego planu badawczego lub dobór osób badanych (np.
badanie tylko jednej płci);

•

Uczynienie niektórych niekontrolowanych zmiennych ubocznych (np. pewnych cech indywidualnych) ZMIENNYMI
KONTROLOWANYMI, dzięki:

−

kontroli eksperymentalnej – wbudowanie zmiennych ubocznych w plan eksperymentalny (np. plan w blokach
kompletnie zrandomizowanych);

−

kontroli statystycznej – np. zastosowanie analizy kowariancji (ANCOVA) ze zmienną uboczną jako zmienną towarzyszącą
(inaczej: współzmienną, kowariantem).

PLANOWANIE I ANALIZA BADAŃ EMPIRYCZNYCH. PLANY EKSPERYMENTALNE

PRZEGLĄD TYPOWYCH PLANÓW EKSPERYMENTALNYCH

1. Plany w grupach kompletnie zrandomizowanych.

1.1. Plany jednoczynnikowe (jedna zmienna niezależna).

1.1.1. dwa poziomy zmiennej niezależnej;

1.1.2. wiele poziomów zmiennej niezależnej.

1.2. Plany wieloczynnikowe (wiele zmiennych niezależnych): oddziaływania addytywne i interakcja.

2. Plany z powtarzanymi pomiarami.

3. Plany oparte na kwadracie łacińskim.

4. Plany w blokach kompletnie zrandomizowanych.

5. Analiza kowariancji.

W ANALIZIE WARIANCJI (ANOVA) ZMIENNE NIEZALEŻNE NAZYWANE SĄ CZYNNIKAMI (STĄD: PLANY JEDNOCZYNNIKOWE,
DWUCZYNNIKOWE, ITP.) W ANOVA MAMY ZAWSZE JEDNĄ ZMIENNĄ ZALEŻNĄ (TZW. ANALIZA JEDNOZMIENNOWA, UNIVARIATE). JEŚLI
ZMIENNYCH ZALEŻNYCH JEST WIĘCEJ PRZEPROWADZAMY DLA KAŻDEJ Z NICH ODDZIELNĄ (JEDNOZMIENNOWĄ) ANALIZĘ.

PLANY W GRUPACH KOMPLETNIE ZRANDOMIZOWANYCH

1.1.1 PLANY JEDNOCZYNNIKOWE, DWUGRUPOWE (DWA POZIOMY ZMIENNEJ NIEZALEŻNEJ

Tabela 5c.1. Klasyczny eksperyment dwugrupowy

Grupy zrandomizowane:

zmienna niezależna (X):

zmienna zależna (Y):

Stosując analizę wariancji otrzymujemy test F jako oszacowanie istotności różnicy między średnimi

1 i

Przy dwóch grupach możemy też zastosować test t-studenta (dla dwu grup: F = t

Zakładamy, że (dzięki randomizacji) grupy eksperymentalne nie różniły się między sobą przed eksperymentem. Jeśli
mamy co do tego wątpliwości, możemy zastosować pomiar początkowy (por. plan Solomona)

Jeśli nie było różnic między grupami przed eksperymentem, a pojawiły się po zastosowaniu manipulacji zmienną X, to
mamy prawo wnioskować że X wpływa na Y (działanie zmiennej X jest przyczyną zmian zmiennej Y).

Tabela 5c.2. Czterogrupowy plan Solomona

Grupy

Pomiar Oddziały- Pomiar
początkowy wanie końcowy

G 1: Kontrolna

---- ---- Yk1

G 2: Kontrolna

Yp2 ---- Yk2

G 3: Eksperymentalna

---- X Yk3

G 4: Eksperymentalna

Yp4 X Yk4

Plan ten pozwala ocenić efektywność randomizacji oraz wpływ pomiaru początkowego i zmiennej głównej (X) na pomiar
końcowy (Y). Oszacowania efektu zmiennej X i pomiaru początkowego dokonujemy przez PORÓWNANIE POMIARÓW
KOŃCOWYCH. Porównania między pomiarami początkowymi i końcowymi mają znaczenie pomocnicze gdyż nie
gwarantują takiej kontroli zmiennych ubocznych jak porównania między grupami zrandomizowanymi.

ZACHOWANIE BADACZA MOŻE BYĆ STRONNICZE. ABY WYELIMINOWAĆ TEN EFEKT I EFEKT PLACEBO, STOSUJE SIĘ TZW.
PLAN EKSPERYMENTALNY ŚLEPY (SINGLE-BLIND), W KTÓRYM OSOBY BADANE NIE MAJĄ DOSTĘPU DO INFORMACJI

MOGĄCYCH WPŁYNĄĆ NA WYNIK BADANIA (NP. DO INFORMACJI, KTÓRA GRUPA JEST KONTROLNA A KTÓRA
EKSPERYMENTALNA), PLAN PODWÓJNIE ŚLEPY (DOUBLE-BLIND), W KTÓRYM INFORMACJE TAKIE SĄ NIEDOSTĘPNE DLA
EKSPERYMENTATORA (OSOBY KONTAKTUJĄCEJ SIĘ Z BADANYMI), LUB NAWET POTRÓJNIE ŚLEPY (TRIPLE-BLIND), W
KTÓRYM INFORMACJE TE SĄ NIEDOSTĘPNE DLA OSOBY ANALIZUJĄCEJ WYNIKI.

1.1.2 PLANY JEDNOCZYNNIKOWE, WIELOGRUPOWE (WIELE POZIOMÓW ZMIENNEJ NIEZALEŻNEJ

Tabela 5c.3. Eksperyment jednoczynnikowy, czterogrupowy

Grupy zrandomizowane:

G1 G2 G3 G4

zmienna niezależna (X): X

zmienna zależna (Y):

Wielokrotne porównania między średnimi

Zbiorczy test F (omnibus F test) dla jednoczynnikowego planu wielogrupowego testuje hipotezę zerową:
H

: μ

= μ

= ... μ

Jeśli uda się odrzucić tę hipotezę (F okaże się istotne) to nie wiemy, które średnie różnią się miedzy sobą a które nie. Do
analizy różnic między poszczególnymi średnimi (grupami, pomiarami) służy analiza kontrastów.

KONTRASTY

POST HOC (A POSTERIORI)

Stosuje się je wówczas, gdy badacz nie ma jasnej hipotezy co kierunku zależności miedzy zmiennymi. Szacujemy
wówczas istotność różnic między wszystkimi możliwymi parami średnich (multiple comparisons). Do porównań takich
nie należy używać tradycyjnego testu t Studenta, ale specjalnych testów (kontrastów post hoc), takich np. jak:

•

test Tukeya

•

test Duncana

•

test Scheffego (najbardziej konserwatywny test post hoc)

PROCEDURA BONFERRONIEGO
Do wielokrotnych porównań między parami średnich (dla danych skorelowanych jak i nieskorelowanych) można
zastosować test t Studenta z tzw. poprawką Bonferroniego. Poprawka ta polega na tym, że wartość p dla tradycyjnego
testu t Studenta (wyszukaną w tablicach, lub podaną przez komputerowy program statystyczny) mnożymy przez liczbę
dokonywanych porównań między średnimi.

Przykład:
Mamy pięć średnich i dokonujemy czterech porównań (każdą z czterech pierwszych średnich porównujemy z
ostatnią). Dla różnicy między średnimi M

i M

otrzymaliśmy t(30) = 2,80, p < 0,01. Istotność testu t z poprawką

Bonferroniego wynosi: 0,01 x 4 = 0,04 (

≈

0,05).

Procedura Bonferroniego jest łatwa w stosowaniu ale bardzo konserwatywna (różnice oszacowane innymi metodami
jako istotne, mogą okazać się nieistotne przy zastosowaniu metody Bonferroniego), szczególnie gdy liczba porównań
jest duża.

Wady wielokrotnych porównań między średnimi:

•

Jeśli porównujemy ze sobą wszystkie średnie, to liczba możliwych porównań bardzo szybko rośnie ze wzrostem
liczby średnich. Liczba takich porównań wynosi:
k (k-1)/2 (gdzie k = liczba średnich). Np. dla 5 średnich mamy 5(5-1)/2 = 10 porównań.

•

Jeśli porównujemy parami dużą liczbę średnich, otrzymujemy w wyniku mało przejrzysty i trudny do interpretacji
obraz zależności między zmiennymi.

KONTRASTY PLANOWANE (A PRIORI) (

SPSS

jako:

KONTRASTY)

Kontrasty planowane (inaczej a priori) przeznaczone są do testowania istotności tylko wybranych różnic między
średnimi, tych mianowicie, o których mowa w hipotezie (hipotezach) teoretycznych. Jeśli liczba średnich równa się k, to
możemy poddać analizie nie więcej niż k-1 kontrastów planowanych. Na przykład, dla 6 średnich mamy 15 możliwych
kontrastów post hoc, ale nie więcej niż 5 kontrastów planowanych. Kontrasty planowane mają większą moc niż
kontrasty post hoc: ta sama różnica miedzy średnimi może się okazać istotna, jeśli jest analizowana jako kontrast
planowany, a nieistotna - jeśli jest analizowana jako kontrast post hoc. Przy kontrastach post hoc liczba porównań jest
większa, więc prawdopodobieństwo losowego pojawienia się dużej różnicy miedzy średnimi jest większe. Testy post hoc
zawierają „poprawkę” na taki efekt. W SPSS można wybrać z menu gotowe (już zdefiniowane) kontrasty planowane lub
samodzielnie je zdefiniować używając odpowiednich współczynników (por. następna strona).

Jeśli analizujemy kontrasty planowane, nie musimy liczyć ogólnego testu F.

Przykłady kontrastów:
Po lewej stronie podano przykładowe hipotezy dotyczące różnic miedzy grupami (A, B, C, itd.), po prawej –
współczynniki kontrastów zdefiniowanych tak aby sprawdzić te hipotezy. Suma współczynników dla każdego
kontrastu musi równać się zero.

1) Współczynniki dla kontrastów prostych (każdą grupę porównujemy z grupą odniesienia; tu – z grupą D):
A > D

1, 0, 0, -1; suma = 0

B > D

0, 1, 0, -1; suma = 0

C > D

0, 0, 1, -1;

suma = 0

2) Współczynniki dla kontrastów zdefiniowanych
po lewej stronie:
A = B

1, -1, 0, 0;

suma = 0

C = D

0, 0, 1, -1;

suma = 0

(A+B) > (C+D)

1, 1, -1, -1; suma = 0

3) Współczynniki dla kontrastów zdefiniowanych po lewej stronie:
A > B,C

2, -1, -1;

suma = 0

B = C

0, 1, -1;

suma = 0

Wśród kontrastów planowanych wyróżnia się tzw. kontrasty ortogonalne. Dla kontrastów ortogonalnych (i tylko dla
nich) zachodzi równość:

+ SS

+ ... SS

= SS

czynnik

Dwa kontrasty są ortogonalne jeśli suma iloczynów ich współczynników (suma iloczynów współczynników przypisanych
tym samym grupom) równa się zero, np.:

2, -1, -1;

suma = 0

0, 1, -1;

suma = 0

Suma iloczynów (0) + (-1) + (1) = 0

Jeśli liczba kontrastów > 2, to suma iloczynów ich współczynników musi równać się zero dla każdej pary kontrastów.
Zauważ, że kontrasty proste, podane wyżej, nie są ortogonalne.

Analiza trendów (wielomianowych) (w SPSS jako: kontrasty > wielomianowe)

Trendy wielomianowe są szczególnym przypadkiem kontrastów ortogonalnych. Analiza trendów ma na celu
oszacowanie, czy zależność między zmiennymi (niezależną i zależną) da się przybliżyć za pomocą wielomianu n-tego
stopnia, a graficznie – przedstawić jako linia prosta (trend liniowy) lub jakaś linia krzywa (trend krzywoliniowy). Analiza
trendów wymaga aby zmienna niezależna była ciągła, mierzona na skali interwałowej, a jej kolejne, dyskretne wartości
(zastosowane w badaniu) były rozłożone w równych odstępach. Do analizy trendów można stosować zarówno ANOVA-ę
jak i analizę regresji wielokrotnej. Ilustrację graficzną wielomianu n-tego stopnia stanowi linia (łącząca średnie) mająca
n-1 zgięć (tzn. n-1 razy zmieniająca kierunek, por rycina 1 i 2). Na przykład, ilustracją trendu stopnia drugiego
(„kwadratowego”) jest linia zmieniająca jeden raz swój kierunek. Dla wykrycia trendu n-tego stopnia potrzeba co
najmniej n+1 średnich (grup). Np. aby wykryć trend 2-go stopnia potrzebne są co najmniej trzy średnie.
Znalezienie istotnego trendu, dobrze dopasowanego do danych, może wskazywać na istnienie ogólnej zależności między
zmiennymi.

Rycina 1a. Przykładowe dane

0.1

0.2

0.3

100 db

80 db

60 db

40 db

20 db

Rycina 1b. Trend liniowy

0.1

0.2

0.3

100 db

80 db

60 db

40 db

20 db

Rycina 2a. Przykładowe dane

czas pracy (w godzinach)

Rycina 2b. Trend kwadratowy (2-go stopnia)

czas pracy (w godzinach)

Ocena wielkości (siły) efektu (effect size)

Czym innym jest pytanie o to, czy różnica między średnimi w ogóle istnieje (istotność różnicy) a czym innym pytanie o to,
ja duża jest ta różnica (wielkość efektu). Na przykład, dysponując precyzyjną wagę laboratoryjną możemy wykazać że

waga dwóch przedmiotów różni się o 10 mg, a dysponując tylko wagą towarową możemy nie być w stanie wykazać, że
waga dwóch ciężarówek różni się o 10 kg.

Istotność testu statystycznego zależy od wielkości próby. Nawet niewielka różnica między średnimi będzie istotna jeśli
próba będzie bardzo duża, a duża różnica między średnimi może okazać się nieistotna gdy próba będzie bardzo mała.
Istotność różnicy nie wskazuje więc, czy różnica ta jest mała czy duża. Ogólnie: istotność statystyczna efektu nie
wskazuje czy jest on silny czy słaby. Dziś coraz częściej wymaga się aby podawać nie tylko istotność efektu ale i jego
wielkość.

W analizie regresji miarą siły efektu zm. niezależnej (lub zmiennych niezależnych w regresji wielokrotnej) jest
współczynnik determinacji, tzn. kwadrat współczynnika korelacji: r

lub R

. Jeśli np. R

= 0,40 to znaczy to, że 40% sumy

kwadratów zmiennej zależnej można przewidzieć na podstawie znajomości zmiennych niezależnych

W ANOVA można stosować różne miary siły wpływu czynnika eksperymentalnego. Jedną z najlepszych jest
współczynnik

(„omega kwadrat”). Na przykład, w eksperymencie jednoczynnikowym, siłę wpływu czynnika A można

policzyć wg wzoru::

100

)

(

⋅

−

cala

Wzory na

dla innych planów eksperymentalnych podaje Brzeziński.

W menu programu SPSS nie ma współczynnika

, jest natomiast współczynnik η

(eta kwadrat), który interpretuje się

podobnie jak

, tzn. jako procent zmienności (sumy kwadratów) zmiennej zależnej, wywołanej wpływem czynnika

eksperymentalnego.

Jeśli

np.

eksperymencie

= 0,20 dla czynnika A, to znaczy to, że 20% zmienności zmiennej zależnej wywołana została działaniem czynnika A.

Najprostsza wersja współczynnika η

ma postać:

total

effect

Inna wersja wzoru (dostępna w SPSS) ma postać:

error

effect

(w wypadku eksperymentu jednoczynnikowego oba wzory dają ten sam wynik).

Współczynnik η

(w wersji dostępnej w SPSS) można stosować do porównywania efektu tej samej zmiennej w różnych

badaniach. Jeśli natomiast oceniamy efekty różnych czynników w tym samym eksperymencie to może się okazać, że
suma wszystkich η

(tzn. oszacowanych dla wszystkich czynników eksperymentalnych) będzie większa od 1.

Przykład: CUD – efekt Poffenbergera (1912) (por. Wolski 2005)

Ruch prawej ręki kontroluje lewa półkula mózgu, ruch lewej ręki – prawa półkula. Czas reakcji motorycznej jest
krótszy jeśli bodziec wzrokowy eksponowany jest do tej samej półkuli, która kontroluje ruch reagującej ręki niż
wtedy, gdy jest kierowany do półkuli przeciwnej (bodziec eksponuje się w taki sposób aby trafiał tylko do jednej,
wybranej połowy pola widzenia). Średnia różnica między czasem prostej reakcji skrzyżowanej i nieskrzyżowanej
(crossed-uncrossed difference – CUD) miała wynosić wg Poffenbergera 4 milisekundy, dziś szacuje się ją na 3 ms. CUD
jest efektem bardzo słabym. Aby wykazać jego istotność statystyczną potrzeba wielkiej liczby (kilkuset ) prób. Wolski
w swoich badaniach (eksperyment 2001, 2003) stosował 6 sesji po 240 prób (ekspozycji bodźców) w każdej sesji,
czyli: 6 x 240 = 1440 prób dla każdej z około 40 osób badanych.

1.2. PLANY WIELOCZYNNIKOWE W GRUPACH KOMPLETNIE ZRANDOMIZOWANYCH

Tabela 5c.4. Schemat eksperymentu: AxB (2 x 2)

= SS

+ SS

= SS

+ SS

AxB

Dzieląc sumy kwadratów przez stopnie swobody otrzymamy następujące oszacowania wariancji:

(MS

; MS

AxB

) i MS

Dzieląc MS dla efektów przez MSwg trzymamy odpowiednie testy F:

- dla różnic między grupami: F = MS

/ MS

- dla czynnika A: F = MS

/ MS

- dla czynnika B: F = MS

/ MS

- dla interakcji A x B: F = MS

AxB

/ MS

ODDZIAŁYWANIA ADDYTYWNE i INTERAKCJA: EFEKTY GŁÓ

E I EFEKTY PROSTE

Przykład planu eksperymentalnego A x B (2 x 3)

Brak interakcji

2) Interakcja

Efekt główny i efekt prosty mogą być różne definiowane, zależnie od metody analizy. Najprościej można je zdefiniować
jako różnice między dwiema średnimi.

A2 A

B1 B2 B3 M

A1 10 30 50 30

A2 10 20 30 20

10 25 40 25

1 0

A1
A2

1 0

A1
A2

Efekt GŁÓWNY (main effect) danej zmiennej to różnica między jej wartościami brzegowymi w tabeli (zacienionymi).
Ogólnie – jest to efekt danej zmiennej uśredniony po wszystkich poziomach drugiej zmiennej (np. efekt zmiennej A
uśredniony po wszystkich poziomach zmiennej B).

Efekt PROSTY (simple effect) danej zmiennej to różnica między jej wartościami w polach tabeli (niezacienionymi).
Ogólnie – jest to efekt jednej zmiennej zachodzący dla wybranego poziomu drugiej zmiennej (np. efekt zmiennej A
zachodzący dla B1, B2, itd.). Efekt prosty nazywany jest też efektem warunkowym (A/B1, A/B2, A/B3 lub B/A1, B/A2).

Jeśli wszystkie efekty proste są sobie równe (a tym samym są równe efektowi głównemu) to nie ma interakcji (linie
łączące średnie są wtedy równoległe). Przykładowo, w Tab. 1 efekty proste zmiennej A są sobie równe:

.). Liczbowo wynosi to: (20 - 10) = (30 - 20) = (40 – 30)

W Tabeli. 2 efekty proste nie są równe:

≠

, (a linie łączące średnie nie są równoległe), co łatwo sprawdzić.

Czynniki eksperymentalne pozostają w INTERAKCJI jeśli efekt jednego czynnika na zmienną zależną zależy od poziomu
innego czynnika. Nie analizujemy wtedy efektów głównych, tylko efekty PROSTE.

Jeśli wpływ jednego czynnika nie zależy od poziomu drugiego czynnika, to nie zachodzi interakcja. Analizujemy wówczas
tylko efekty GLÓWNE. Przy braku interakcji łączny efekt obu zmiennych jest sumą ich efektów głównych (efekty te są
ADDYTYWNE):

= SS

+ SS

Jeśli zachodzi interakcja, w równaniu pojawia się dodatkowy czynnik:

= SS

+ SS

AxB

Jeśli nie ma interakcji, wyniki eksperymentu n-czynnikowego są równoważne wynikom n eksperymentów
jednoczynnikowych. Jeśli zachodzi interakcja, konieczny jest eksperyment wieloczynnikowy.

ANALIZA WARIANCJI 2 X 3 (przykład liczbowy SPSS)

anova Z by A (1,3) B (1,2) / statistics=3.

* * * C E L L M E A N S * * *

B 1 2
A 1 6.00 6.00

2 6.00 10.00

3 6.00 14.00

* * * A N A L Y S I S O F V A R I A N C E * * *

Sum of Mean Signif.
Source of Variation Squares DF Square F of F
Main Effects 80.000 3 26.667 10.000 .009
A 32.000 2 16.000 6.000 .037
B 48.000 1 48.000 18.000 .005
2-way Interactions 32.000 2 16.000 6.000 .037
A x B 32.000 2 16.000 6.000 .037

Explained 112.000 5 22.400 8.400 .011
Residual 16.000 6 2.667
Total 128.000 11 11.636

Graficzna prezentacja efektów głównych i interakcji

Rycina 3a. Efekty główne czynnika A (trudność zadania) i czynnika B (nagroda)

Trudne

S rednie

L atwe

bez nag rody
nag roda

Rycina 3b. Efekty główne czynnika A (trudność zadania)

T rudne

S rednie

L atw e

Rycina 3c. Efekty główne czynnika B (nagroda)

Bez

nagrody

Nagroda

Rycina 4a. Interakcja czynników A i B (ilustracja danych z wydruku SPSS)

Rycina 4b. Interakcja czynników A i B

Rycina 4c. Interakcja czynników A i B

Interakcja zmiennej kategorialnej i ciągłej

Przykład: wpływ poziomu reaktywności (X1) i sytuacji stresowej (X2) na wielkość reakcji na stres (Y).

Miarą wpływu reaktywności (zmienna ciągła) jest nachylenie linii regresji; miarą wpływu sytuacji stresowej (zmienna
kategorialna) jest różnica między liniami regresji dla obu grup.

Oszacowane średnie brzegowe - REAKCJA1

REAKTYWN

90,00

80,00

70,00

60,00

STRES

,00

1,00

Rysunek 1a. Brak interakcji

Oszacowane średnie brzegowe - REAKCJA2

REAKTYWN

90,00

80,00

70,00

60,00

STRES

,00

1,00

Rysunek 1b. Interakcja

Interakcja zmiennych ciągłych

Przykład: Wpływ dwóch mierzonych zmiennych niezależnych (plan ex-post facto): inteligencji (V1)
i poziomu motywacji (V2) na poziom wykonania zadań umysłowych (V3).

Brak interakcji: Wpływ jednej zmiennej niezależnej nie zależy od poziomu drugiej zmiennej. Inaczej – nachylenie linii
regresji V3 względem V1 jest takie same dla wszystkich wartości V2, a nachylenie regresji V3 względem V2 jest takie
same dla wszystkich wartości V1.

Interakcja: Wpływ jednej zmiennej niezależnej zależy od poziomu drugiej zmiennej. Inaczej – nachylenie linii regresji V3
względem V1 jest różne dla różnych wartości X2 lub nachylenie regresji V3 względem V2 jest różne dla różnych
wszystkich wartości V1.

2. PLANY Z POWTARZANYMI POMIARAMI

•

Plan w grupach zrandomizowanych - na każdej osobie dokonujemy JEDNEGO pomiaru zmiennej zależnej.

•

Plan z powtarzanymi pomiarami - na każdej osobie dokonujemy KILKU (co najmniej dwóch) pomiarów
zmiennej zależnej.

2,036

2,473

2,909

3,345

3,782

4,218

4,655

5,091

5,527

5,964

above

3D Surface Plot (NEW.STA 10v*10c)

Distance Weighted Least Squares

2,556

3,3

4,045

4,789

5,534

6,278

7,022

7,767

8,511

9,256

above

3D Surface Plot (NEW.STA 10v*10c)

Distance Weighted Least Squares

Tabela 5c.5a. Plan jednoczynnikowy w grupach kompletnie zrandomizowanych

Zm. Niezależna (A):

Grupy:

gr 1

gr 2

gr 3

Tabela 5c.5b. Plan jednogrupowy z powtarzanymi pomiarami.

Zm. Niezależna (A):

Pomiary (ta sama grupa):

pom 1

pom 2

pom 3

Tabela 5c.6. Plan jednoczynnikowy, dwugrupowy (grupy zrandomizowane) z powtarzanymi pomiarami.

Pomiar

zmiennej

zależnej Y

Grupa 1 (X1)

Grupa 2 (X2)

Np. Sprawdzamy jak długo trwają efekty leku (X1) w porównaniu do placebo (X2). Efekt działania leku mierzymy
trzykrotnie (Y1, Y2, Y3), np. co godzinę. Oszacowania efektów manipulacji dokonujemy przez PORÓWNANIE MIĘDZY
GRUPAMI. Stosowanie powtarzanych pomiarów NIE JEST MANIPULACJĄ EKSPERYMENTALNĄ !!! Porównania między
pomiarami nie zapewniają takiej kontroli zmiennych ubocznych jak porównania między grupami zrandomizowanymi.
Dlatego wnioski oparte na podstawie porównań między pomiarami są mniej wiarygodne niż wnioski oparte na
porównaniach międzygrupowych.

Zalety i wady planów z powtarzanymi pomiarami

Zalety

•

Są bardziej ekonomiczne (mniej badanych osób).

•

Łatwiej uzyskać wysoką wartość testu F, gdyż możemy wyłączyć z wariancji błędu różnice między osobami.

•

Niektóre problemy wymagają stosowania powtarzanych pomiarów, np. badanie habituacji, reminiscencji
(zjawisko Ballarda). Ma to miejsce najczęściej wtedy, gdy badane zjawisko polega na zmianach w czasie.

Wady

•

Silniejsze (trudniejsze do spełnienia) założenia modelu statystycznego;

•

Słabsza (niż w wypadku planów w grupach zrandomizowanych) kontrola zmiennych ubocznych.

Jednym z problemów jest kontrola KOLEJNOŚCI poziomów zmiennej niezależnej. Jeśli poziomy zmiennej niezależnej
eksponowane są w stałej kolejności trzeba się liczyć z:

•

wpływem czynników działających w czasie trwania pomiaru (np. habituacja, zmęczenie)

•

wpływem wcześniejszych pomiarów na pomiary późniejsze (np. uczenie się, zmiana nastawienia do badania).

•

niektóre zmienne niezależne mogą wykluczać (lub ograniczać) stosowanie powtarzanych pomiarów (por.
klasyczne eksperymenty z manipulacją wiarygodnością informatora).

3. PLANY OPARTE NA KWADRACIE ŁACIŃSKIM

Załóżmy, że w eksperymencie z powtarzanymi pomiarami zmienną niezależną jest rodzaj zadania. Stosujemy trzy
rodzaje zadań (A, B, C) i chcemy wykluczyć wpływ kolejności rozwiązywania zadań na zmienną zależną.

Tabela 5c.7. Plan oparty na permutacji elementów

Osoba badana
(grupa osób) próba 1

próba 2 próba 3

Przy sześciu osobach badanych, każda z nich wykonuje zadania w innej kolejności. Możemy też przebadać większą liczbę
osób (tzn. wielokrotność liczby 6).

Wadą schematu z tabeli 5c-7 jest to, że liczba permutacji rośnie bardzo szybko z liczbą elementów permutowanych.

liczba permutacji (n!)

120

3 628 800

Kwadrat łaciński pozwala planować badania z dużą liczbą poziomów zmiennej niezależnej a jednocześnie małą liczbą
badanych osób.

Tabela 5c.8. Plan trójczynnikowy (osoby x próby x zadania) oparty na kwadracie łacińskim 4 x 4. Kontrolujemy kolejność
czterech zadań (A, B, C, D) badając tylko cztery osoby (lub wielokrotność tej liczby).

Osoba badana

(grupa osób)

próba 1

próba 2

próba 3

próba 4

* Nazwa "łaciński" pochodzi liter alfabetu łacińskiego którymi oznacza się pola kwadratu.

Jak widać:

•

Każde zadanie występuje tylko raz w każdym wierszu (osoba badana) i każdej kolumnie (próba).

•

Każdy poziom każdego czynnika spotyka się dokładnie jeden raz z każdym z poziomów każdego innego
czynnika.

•

Każda ze zmiennych musi mieć taką samą liczbę poziomów, równą wymiarowi kwadratu. Gdyby liczba
zadań wynosiła przykładowo 10, kwadrat (10 x 10) musiałby mieć 10 wierszy (osób) i 10 kolumn (prób).

W kwadrat łaciński można wbudować dodatkową, czwartą zmienną (a nawet więcej zmiennych). Przy czterech
zmiennych otrzymujemy tzw. kwadrat "grecko-łaciński" (od liter alfabetu greckiego i łacińskiego).

Tabela 5c.9. Kwadrat grecko-łaciński, czteroczynnikowy, „4 x 4”

Kwadraty łacińskie, o wymiarach od „3 x 3” do „12 x 12” można znaleźć w pracy: Ryszard Zieliński (1972). Tablice
statystyczne (tablica 57 i 58). Warszawa: PWN.

4. PLANY W BLOKACH KOMPLETNIE ZRANDOMIZOWANYCH.

Randomizacja zapewnia kontrolę zmiennych ubocznych w tym sensie, że zmienne te działają we wszystkich grupach tak
samo (rozkład zmiennej zależnej powinien być taki sam we wszystkich grupach). Randomizacja nie ma jednak wpływu
na WIELKOŚĆ wariancji w zbiorach (wariancji niekontrolowanej). W przypadku porównań międzygrupowych ważnym
źródłem wariancji wewnątrz-grupowej są różnice indywidualne. Plan w BLOKACH kompletnie ZRANDOMIZOWANYCH
polega na tym, że wybraną zmienną indywidualną czynimy zmienną eksperymentalną (kontrolowalną). Tym samym
minimalizujemy wielkość wariancji niekontrolowanej (wewnątrzgrupowej).

Tabela 5c.-10. Plan w blokach kompletnie zrandomizowanych.

Zmienna blokowa (I.I.) Zmienna manipulowalna
Bloki

grupa 1 grupa 2

blok 1

( 78 < II < 82)

blok 2

( 88 < II < 92)

blok 3

( 98 < II < 102)

blok 4

(108 < II < 112)

blok 5

(118 < II < 122)

Y – wynik pomiaru zmiennej zależnej

Plan w blokach kompletnie zrandomizowanych:

Sposób doboru osób do grup eksperymentalnych

•

Najpierw dobieramy osoby w bloki pod względem wybranej zmiennej indywidualnej (blokowej). Następnie
przydzielamy losowo (randomizacja) osoby z każdego bloku do grup eksperymentalnych.

•

Osoby w tym samym bloku powinny być jak najbardziej podobne do siebie pod względem zmiennej blokowej,
natomiast osoby w różnych blokach - jak najbardziej różnić się od siebie.

Schemat blokowy pozwala:

•

ocenić siłę wpływu wybranej zmiennej indywidualnej (zmiennej blokowej) na zmienną zależną i ewentualnej
interakcji zmiennej blokowej ze zmienną niezależną;

•

minimalizować wariancję niekontrolowaną wywołaną zmienną blokową;

Efektywność planu blokowego zależy od siły związku między zmienną blokową a zmienną zależną. Plan blokowy jest
stosunkowo pracochłonny (dobór osób do bloków!). Alternatywą (jeśli nie ma interakcji zmiennej blokowej ze zmienną
niezależną) jest zastosowanie analizy kowariancji z użyciem zmiennej indywidualnej jako zmiennej towarzyszącej
(kowariantu)

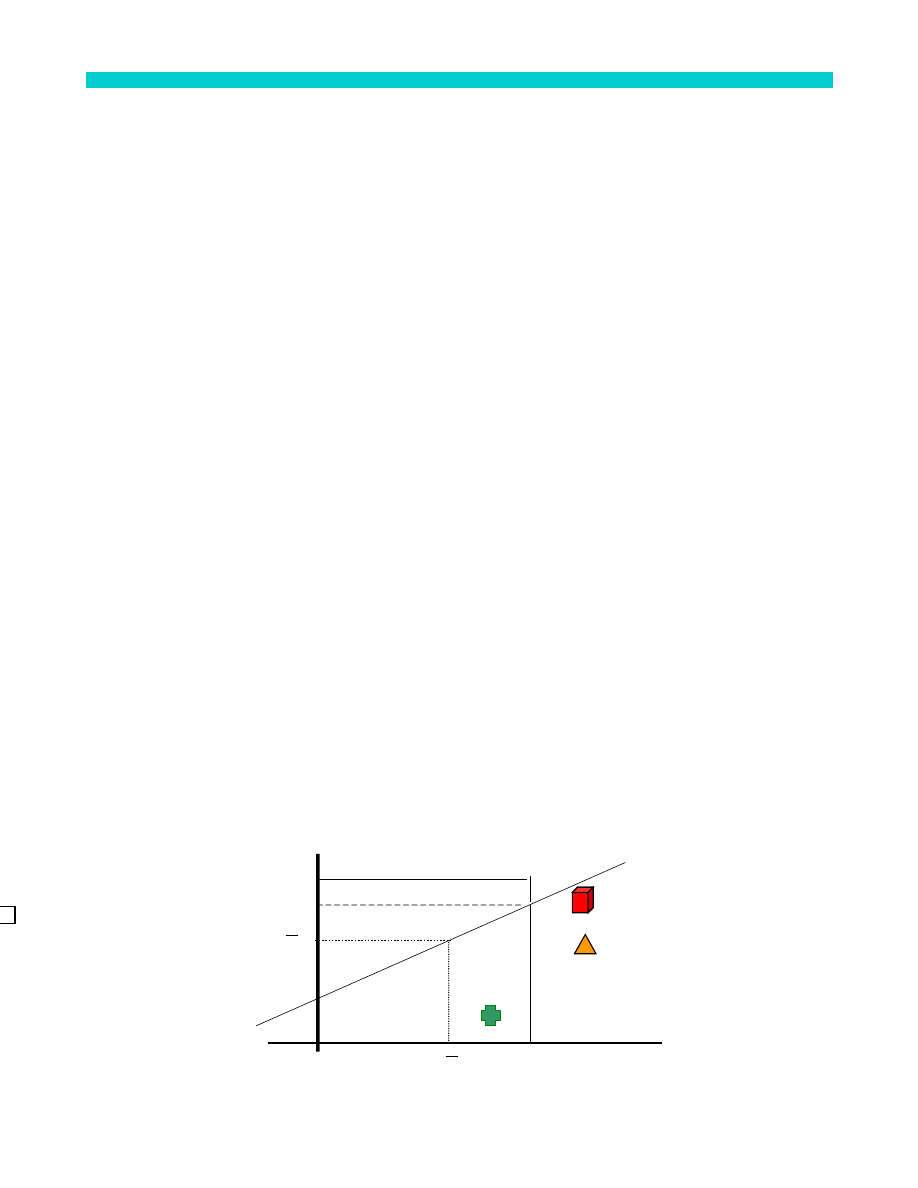
5. ANALIZA KOWARIANCJI.

Oceniając wpływ zmiennej niezależnej (X) na zmienną zależną (Y) stwierdzamy, iż Y jest wysoko skorelowana z jakąś
zmienną uboczną (C). Chcielibyśmy wyeliminować wpływ zmiennej ubocznej, gdyż utrudnia ona precyzyjne oszacowanie
wpływu X na Y (zwiększa wariancję błędu).

Przykład fikcyjny (poglądowy).
Różne pociągi pokonują różne trasy (A

, A

, ... A

) w różnym czasie (t

, t

..., t

). Jest to spowodowane tym, że trasy

mają różną długość oraz tym, że pociągi jeżdżą z różną szybkością. Ponieważ istnieje związek miedzy szybkością
pociągu i czasem przejazdu danej trasy, możemy łatwo obliczyć w jakim czasie pociągi pokonywałyby różne trasy
gdyby wszystkie jeździły z jednakową szybkością (czyli: gdyby wyeliminować wpływ szybkości pociągów)

Przykład psychologiczny.
Badamy wpływ metody nauczania (X) na poziom znajomości języka obcego uczniów (Y). Stwierdzamy jednak, że
poziom zmiennej Y zależy od poziomu inteligencji badanych (C). Chcemy wyeliminować wpływ różnic indywidualnych
w poziomie inteligencji aby bardziej precyzyjnie oszacować wpływ metody nauczania. Nie mamy możliwości takiego
doboru uczniów, aby wszyscy mieli jednakową inteligencję (badamy jakąś rzeczywistą szkołę), możemy jednak
wyeliminować wpływ inteligencji drogą analizy statystycznej.

Analiza kowariancji (analysis of covariance - ANCOVA) pozwala, drogą czysto STATYSTYCZNĄ, wyeliminować wpływ
zmiennej ubocznej na zmienną zależną. Polega to (mówiąc w uproszczeniu) na przekształceniu wyników do takiej
postaci, jak gdy wszyscy badani mieli identyczny poziom zmiennej ubocznej (np. identyczny poziom inteligencji w
przykładzie powyżej). Eliminowana w taki sposób zmienna uboczna nazywa się: zmienną towarzyszącą, współzmienną
lub kowariantem.

W szczególności, ANOCOVA pozwala:

•

Oszacować wpływ zmiennej towarzyszącej na zmienną zależną.

•

Oszacować wpływ zmiennej niezależnej na zmienną zależną z wyeliminowaniem wpływu zmiennej
towarzyszącej (jak gdyby badani nie różnili się pod względem zmiennej towarzyszącej).

•

Zmniejszyć wariancję niekontrolowaną a tym samym -- bardziej precyzyjnie oszacować wpływ zmiennej
niezależnej na zmienną zależną.

•

Skorygować średnie grupowe (tzw. adjusted means), tj. oszacować jakie byłyby średnie grupowe (poziom
zmiennej zależnej) gdyby nie wpływała na nie zmienna towarzysząca (tzn. gdyby poziom zmiennej
towarzyszącej był we wszystkich grupach jednakowy).

Efektywność ANCOVA-y zależy od siły związku (korelacji) między zmienną zależną i kowariantem. Jeśli korelacja ta jest
bardzo niska, wynik analizy kowariancji nie będzie się wiele różnił od wyniku zwykłej analizy wariancji. W ANCOVA
wymagane jest aby:

•

korelacja zmiennej zależnej i kowariantu (czyli: współczynnik regresji b dla kowariantu) była taka sama we
wszystkich grupach (korygowanie wyników we wszystkich grupach można wówczas przeprowadzić w oparciu o
identyczne równanie regresji);

•

pomiar kowariantu był wolny od wpływu manipulacji eksperymentalnej. W wypadku badań eksperymentalnych
oznacza to np., że kowariant powinien być mierzony przed podaniem instrukcji eksperymentalnej.

Analiza kowariancji: korygowanie danych surowych

′

Ogólne równanie regresji (dla jednego predyktora – X):

Y = a + bX

a – stała (constant, intercept ) równania regresji
b – współczynnik nachylenia linii regresji

Różnica między wynikiem otrzymanym Y

a wynikiem oczekiwanym Y

’

dla

osoby i :

(

)

(

)

−

′ −

− ′

Obliczanie średnich skorygowanych (adjusted mean) :

gdzie:

średnia skorygowana zmiennej Y w grupie i
średnia nieskorygowana zmiennej Y w grupie i
średnia zmiennej X dla grupy i
średnia całkowita zmiennej X (dla całej próby)
współczynnikiem regresji dla kowariantu (zmiennej towarzyszącej).

Zakładamy tu, że współczynnik b (nachylenie linii regresji) jest jednakowy we wszystkich grupach a zatem wszystkie
wyniki możemy korygować w oparciu o ten sam współczynnik b.

BADANIA QUASI – EKSPERYMENTALNE

Badania quasi-eksperymentalne („niby-eksperymentalne”) mają wszelkie cechy badań eksperymentalnych (włącznie z celowym
oddziaływaniem na osoby badane – treatment) za wyjątkiem RANDOMIZACJI. Brak randomizacji jest poważnym mankamentem planów
quasi eksperymentalnych gdyż oznacza ograniczoną kontrolę nad zmiennymi ubocznymi. Dlatego też, jeśli jest to tylko możliwe należy
stosować randomizację i plany eksperymentalne.

Plan 1. Plan jednogrupowy z powtarzanymi pomiarami

Pomiar
początkowy
zmiennej
zależnej

Oddziaływanie

Pomiar końcowy zmiennej
zależnej

Jedna
grupa

Przykład:
Porównujemy ciśnienie krwi przed (Yp) i po (Yk) zastosowaniu leku. Jeśli zaobserwujemy różnicę między Yp i Yk nie możemy
być nigdy pewni czy spowodowana została ona lekiem (zmienna niezależna) czy też innymi czynnikami, takimi jak np.
spontaniczne około-dobowe wahania ciśnienia, psychologiczny efekt terapii („efekt placebo”), wpływ pomiaru
początkowego na pomiar końcowy, itp.

Plan z powtarzanymi pomiarami stosuje się często dla oceny zmian w czasie (dynamiki zmian) zmiennej zależnej. Plan taki nie
zapewnia jednak dostatecznej kontroli zmiennych ubocznych. Jeśli jest to możliwe, należy zastosować plan eksperymentalny
(np. dwugrupowy, patrz niżej) z powtarzanymi pomiarami. Podstawą oceny skuteczności leku byłyby wtedy porównania
MIĘDZY GRUPAMI zrandomizowanymi w kolejnych pomiarach.

Grupy Zrando-
mizowane

Pomiar początkowy

Oddziaływ
a-nie (np.
lek)

Pomiar
końcowy 1

Pomiar
końcowy 2

Grupa 1

k1 1

. .

k1 2

. .

)

(

)

(

adj

−

Grupa 2

k 2 1

. .

k 2 2

. .

Plan 2. Porównania między grupami niezrandomizowanymi

Przykład: porównujemy dwie metody nauczania stosując każdą z nich w innej szkole: metodę M1 w szkole A, metodę M2 w
szkole B.

Grupy

niezrandomizowane

zmienna

niezależna

zmienna

zależna

szkoła A

szkoła B

Jeśli zaobserwujemy różnicę między grupami nie będziemy mogli być pewni czy jest to rzeczywiście efekt metody czy też efekt
innych, nie kontrolowanych czynników:

•

różnic między grupami (tu: szkołami);

•

interakcji grupy i oddziaływania (tu: szkoły i metody);

Mankament ten można częściowo zminimalizować dokonując pomiaru ważnych zmiennych ubocznych i kontrolując (drogą
statystyczną, np. stosując ANCOVA) ich wpływ na zmienną zależną. Musimy jednak wiedzieć przed rozpoczęciem zbierania
danych jakie zmienne uboczne są ważne. Szczególnym przypadkiem omawianego planu są badania w których grupę kontrolną
dobiera się na zasadzie tzw. „doboru parami” (zamiast randomizacji). Np. do każdego chorego dobiera się osobę „kontrolną” o
tej samej płci, wieku, wykształceniu itp.

Plan 3. Porównania między grupami niezrandomizowanym z pre-testem i post-testem.

Grupy
niezrandomizowane

Pomiar
początkowy

Oddziały-wanie

Pomiar końcowy

Grupa 1

Grupa 2

Zastosowanie pomiaru początkowego w planie wielogrupowym pozwala ocenić, czy porównywane grupy nie różnią się przed
badaniem poziomem zmiennej zależnej. Jeśli grupy nie są równoważne, rekomendowanym sposobem analizy jest analiza
kowariancji (ANCOVA) z użyciem pomiaru początkowego jako zmiennej towarzyszącej (kowariantu).

Mankamentem planów z pomiarem początkowym jest jego potencjalny wpływ na pomiar końcowy. Do oszacowania wpływu
pomiaru początkowego na pomiar końcowy można użyć planu Solomona.

BADANIA EX POST FACTO: PORÓWNANIA MIĘDZYGRUPOWE

BADANIA EKSPERYMENTALNE A BADANIA EX-POST FACTO
W badaniach NIEEKSPERYMENTALNYCH (EX-POST FACTO) badacz nie manipuluje zmiennymi ani nie oddziałuje w żaden sposób na
badanych (na zmienna zależną) lecz jedynie dokonuje POMIARU zmiennych. Na podstawie analizy statystycznej staramy się ustalić
relacje między mierzonymi zmiennymi a niekiedy –zależności przyczynowe. Ponieważ oddziaływania przyczynowe musiały mieć miejsce
przed rozpoczęciem badań, mówimy o analizie ex-post facto („po fakcie”).

Zalety badań eksperymentalnych:

•

możliwość celowego wywoływania zjawisk

•

lepsza kontrola zmiennych

•

łatwiejsza interpretacji przyczynowa

Ograniczenia badań eksperymentalnych:

•

Nie wszystkie hipotezy dają się badać eksperymentalnie:

- nie wszystkie zmienne są manipulowalne;
- manipulacja może być niemożliwa lub trudna ze względów technicznych;
- manipulacja może być niedopuszczalna ze względów etycznych;

•

Istnieje problem generalizacji wyników badań eksperymentalnych (zwłaszcza laboratoryjnych) na warunki naturalne.

Porównanie badań eksperymentalnych i ex-post facto na przykładzie porównań międzygrupowych

Plan eksperymentalny

Grupy
zrandomizowane

Zmienna niezależna
manipulowalna

Zmienna zależna

Grupa 1

Grupa 2

KONTROLA zmiennych ubocznych. Jeśli porównujemy grupy zrandomizowane (i potrafimy wyeliminować zmienne zakłócające) to
możemy przyjąć, że przed manipulacją grupy eksperymentalne nie różnią się między sobą systematycznie (tzn. wartość oczekiwana
każdej zmiennej jest taka sama dla wszystkich grup; im mniejsze grupy jednak, tym większe prawdopodobieństwo pojawienia się
znacznych odchyleń średnich grupowych od wartości oczekiwanych) pod względem ŻADNEJ ZMIENNEJ. Jeśli więc stwierdzimy w
pomiarze końcowym różnicę między grupami, to nie da się jej wyjaśnić systematycznym wpływem żadnej zmiennej za wyjątkiem
zmiennej którą manipulujemy.
Wyjaśnianie PRZYCZYNOWE: jeśli nie było różnicy między grupami na początku badania (randomizacja!) a pojawiła się w pomiarze
końcowym, to przyczyną tej różnicy może być tylko wpływ zmiennej X – przesądza o tym sam plan badania.

Plan ex-post facto

Przykład: badamy uprzedzenia etniczne (Y) w grupach różniących się pod względem zmiennej osobowościowej autorytaryzmu (X).

Grupy kryterialne,
dobrane pod względem zmiennej X

Druga mierzona zmienna:
Y

Grupa 1 (X1)

Grupa 2 (X2)

KONTROLA zmiennych ubocznych. Grupy różniące się pod względem zmiennej X mogą się też różnić pod względem innych zmiennych,
skorelowanych z X (np. grupy różniące się autorytaryzmem mogą się też różnić pod względem sposobu wychowania, statusu
społecznego, poziomu lęku, itp.).
Wyjaśnianie PRZYCZYNOWE. Jeśli nawet istnieje związek statystyczny między X i Y, to ani plan badania ani sposób analizy danych nie
przesądza o tym, czy X jest przyczyną Y, czy Y przyczyną X, czy też, być może, istnieje inna zmienna -- Z , która wpływa zarówno na X jak i
na Y. Zależność statystyczną która nie jest zależnością przyczynową nazywa się „zależnością pozorną”. Dla interpretacji przyczynowej
wyników badań ex-post facto konieczne są dodatkowe przesłanki natury zarówno statystycznej (kontrola ważnych zmiennych
ubocznych) jak i merytorycznej.

Zależnością pozorną nazywamy zależność statystyczną, która nie ma charakteru przyczynowego.

Np. stwierdzono zależność statystyczna między liczbą bocianów i liczbą urodzeń (w gminach, w których żyje więcej bocianów rodzi
się więcej dzieci). Zależność ta znika gdy uwzględnimy rodzaj gminy (miejska/wiejska): w gminach wiejskich jest więcej dzieci i
więcej bocianów niż w gminach miejskich.

 liczba bocianów (X)
rodzaj gminy (Z)
 liczba urodzeń (Y)

Zależności między Z i X oraz między Z i Y są zależnościami przyczynowymi. Zależność między X i Y jest zależnością pozorną.

Aby wykazać że zależność między zmiennymi X i Y jest pozorna należy znaleźć odpowiednią zmienną kontrolną (Z) której uwzględnienie
w analizie eliminuje zależność statystyczną między X i Y (por. przykład na następnych stronach).

Przykład (fikcyjny) zależności pozornej (dane liczbowe z pracy Jahoda, Deutsch i Cook, 1955)

Mierzymy liczbę dzieci i liczbę bocianów w 480 gminach.

Tabela 1. Dane pierwotne

Duża liczba bocianów

Mała liczba bocianów

Razem

Duża liczba dzieci

110

200

Mała liczba dzieci

190

280

Razem

200

280

480

Analiza danych w tabeli 1 wskazuje na istnienie zależności statystycznej między liczbą dzieci i liczbą bocianów.

Tabela 2. Uwzględnienie zmiennej kontrolnej (charakter gminy)

Gmina wiejska

Gmina miejska

Liczba
dzieci

Duża liczba
bocia-nów

Mała liczba
bocia-now

Razem

Duża liczba
bocia-nów

Mała liczba
bocia-nów

Razem

Duża

120

Mała

180

240

Razem

120

160

240

320

Po uwzględnieniu w analizie dodatkowej zmiennej (gmina (miejska / wiejska), czyli zmiennej KONTROLNEJ, stwierdzona wcześniej
zależność znika. Jeśli analizujemy dane oddzielnie dla gmin miejskich i oddzielnie dla gmin wiejskich nie stwierdzamy zależności między
liczbą bocianów a liczbą dzieci. Stwierdzona wcześnie zależność statystyczna nie jest więc zależnością przyczynową, ale zależnością
POZORNĄ. Jeśli nie uda się wykazać że zależność między X i Y jest zależnością pozorną, może to wskazywać że:

•

mamy do czynienia z zależnością przyczynową;

•

nie uwzględniliśmy w analizie właściwej zmiennej kontrolnej (w momencie zbierania danych musimy wiedzieć jakie zmienne
uboczne są ważne dla analizowanego problemu).

Aby wykazać że zależność statystyczna jest rzeczywiście zależnością przyczynową potrzebne są przesłanki merytoryczne (np.
wyjaśniające jaki jest mechanizm zaobserwowanej zależności między zmiennymi).

PLANY EX-POST FACTO

1. Porównania międzygrupowe

2. Analiza korelacyjna (i pochodne od niej)
3. Inne, na przykład:
- badania podłużne (longitudinal)
- studium przypadku (case study)

PORÓWNANIA MIĘDZYGRUPOWE

Tworzymy grupy kryterialne w oparciu o jedną zmienną obserwowalną (mierzalną) lub kombinację kilku zmiennych
a następnie porównujemy grupy pod względem innej zmiennej.

W badaniach ex-post facto grupy kryterialne mogą być tworzone zarówno w oparciu o zmienne NIEZALEŻNE jak i zmienne
ZALEŻNE. Przykładowo, jeśli interesuje nas wpływ inteligencji na osiągnięcia szkolne uczniów możemy:

•

stworzyć grupy różniące się poziomem inteligencji i porównać ich osiągnięcia szkolne

•

stworzyć grupy różniące się osiągnięciami szkolnymi i porównać ich wyniki w teście inteligencji.

O wyborze schematu analizy decyduje często wygoda a nie kierunek zależności. Na przykład, łatwiej jest dobrać grupy uczniów
różniących się osiągnięciami szkolnymi i następnie przebadać ich testem inteligencji niż zastosować procedurę odwrotną.

Rodzaje analizy danych

Plan 1. Dwie zmienne nominalne (klasyfikacyjne) – tabela kontyngencji

B1 (palą)

B2 (nie palą)

Razem

A1 (kobiety)

A2 (mężczyźni)

Razem

120

Do oszacowania istotności zależności między zmiennymi w takiej postaci (dane maja postać liczebności grup) możemy użyć test

2 , a do oceny siły związku między zmiennymi – współczynnik korelacji

(dla tablicy 2 x 2) , lub C wielodzielcze (dla tablicy

większej, np. 2 x 3); oba współczynniki korelacji oblicza się na podstawie

Plan 2. Jedna zmienna niezależna – nominalna (klasyfikacyjna), druga zmienna – ciągła:

Zmienna 1 (płeć)

Zmienna 2

grupa 1 (kobiety) grupa 2
(mężczyźni)

Test: porównywanie średnich (np. test t-studenta), lub jakiś test nieparametryczny (np. U Manna-Whitneya)

Plan 3. Jedna zmienna niezależna ciągła, wtórnie zdychotomizowana, druga zmienna ciągła.

Dzielimy badanych na dwie lub więcej grup na podstawie wartości jednej zmiennej ciągłej (np. mierzonej testem
psychometrycznym) a następnie porównujemy utworzone grupy pod względem rozkładu drugiej zmiennej.

Zmienna 1 Zmienna 2

Grupa 1 (wyniki testu T1 wyższe od a)

Grupa 2 (wyniki testu T1 niższe od b)

Czy dychotomizować zmienne ciągłe czy analizować je w postaci oryginalnej (jako zmienne ciągłe)?

Dychotomizowanie zmiennych ciągłych ma poważne wady:

•

utrata części informacji – zamieniamy mocniejszą skalę pomiarową (interwałową lub porządkową) na słabszą,
(nominalną);

•

eliminowanie z analizy części próby (analizujemy tylko grupy skrajne a eliminujemy środek rozkładu) .

Za dychotomizacją przemawia tylko jeden argument: pozwala ona ograniczyć liczbę osób badanych (ważne, jeśli pomiar
zmiennej zależnej jest bardzo pracochłonny (np. badania metodą rezonansu magnetycznego grupy ekstrawertyków i
introwertyków).

Plan 4. Plany wieloczynnikowe w badaniach ex-post facto.

Załóżmy, że w badaniach ex-post facto mamy dwie lub więcej zmiennych niezależnych (np. płeć i poziom wykształcenia) a
zmienna zależna jest zmienną interwałową. Czy możemy użyć analizy wariancji? np. jak niżej

Powodem stosowania ANOVA-y jest to, że pozwala ona analizować interakcję zmiennych niezależnych (jeśli nie ma interakcji, plan n-
czynnikowy może być zastąpiony przez n planów jednoczynnikowych). Argumentem „przeciw” jest to, że ANOVA opiera się na
założeniu, że zmienne niezależne są nieskorelowane (ortogonalne). W badaniach eksperymentalnych założenia to jest spełnione
automatycznie (pod warunkiem że grupy są równoliczne). W badaniach nie-eksperymentalnych założenie to rzadko jest spełnione. W
związku z tym wyniki analizy statystycznej będą obciążone trudnym do oszacowania błędem. Jeśli w badaniach nie-eksperymentalnych
(zwłaszcza: ex post facto) analizujemy bezpośredni wpływ kilku zmiennych niezależnych na zmienną zależną, właściwą metodą analizy
będzie analiza regresji wielokrotnej (multiple regression analysis). Jeśli analizujemy bardziej skomplikowane zależności między
zmiennymi można skorzystać z takich metod jak LISREL czy AMOS.

Zalety analizy regresji:

•

dopuszcza istnienie korelacji między zmiennymi niezależnymi.

•

daje możliwość jednoczesnego analizowania zmiennych niezależnych kategorialnych i ciągłych oraz interakcji między nimi.
Jeśli zmienna kategorialna ma dwie wartości (0 i 1), może być wprost włączona do analizy. Jeśli ma więcej niż dwie wartości
musi być w odpowiedni sposób zakodowana (w postaci odpowiednich wektorów).”

•

jest metodą znacznie prostszą niż AMOS i LISREL

BADANIA EX POST FACTO: KORELACJA I REGRESJA

Analiza korelacji i regresji jest bardzo uniwersalną metoda analizy. Dla przykładu, wszystko co można policzyć analizą wariancji można
też policzyć analizą regresji ale nie na odwrót. Istnieje też wiele metod analizy danych
pochodnych od analizy korelacyjnej, w szczególności:

•

analiza regresji prostej – jedna zmienna niezależna (zwana tez predyktorem) i jedna zmienna zależna

•

analiza regresji wielokrotnej – wiele zmiennych niezależnych (predyktorów);

•

analiza ścieżkowa;

•

analiza dyskryminacyjna;

•

analiza czynnikowa;

•

model równań strukturalnych (LISREL).

KORELACJA

Istnieje wiele metod korelacji. Największe możliwości interpretacyjnych daje współczynnik korelacji według momentu
iloczynowego (współczynnik r Pearsona). Wymaga on pomiaru zmiennych na skali co najmniej interwałowej oraz tzw.
dwuwymiarowego rozkładu normalnego. U każdego obiektu (np. osoby) pochodzącego z danej (jednej!) próby mierzymy co
najmniej dwie zmienne. Korelacja oznacza związek (zależność statystyczną) między zmiennymi. Nie przesądza jednak o istnieniu
zależności przyczynowej.

KORELACJA I REGRESJA PROSTA

Współczynnik korelacji stanowi miarę współzmienności dwu zmiennych (powiedzmy: X i Y). Współczynnik korelacji może
przybierać wartości od r= -1 (perfekcyjna zależność ujemna), poprzez r=0 (doskonałą niezależność zmiennych), do r= 1
(perfekcyjny związek dodatni). Wyrażenie r

, nazywane jest współczynnikiem DETERMINACJI. Oznacza ono procent sumy

kwadratów jednej zmiennej, który można przewidzieć na podstawie drugiej zmiennej.

Przykład 1a. Silny związek między zmiennymi

Przykład 1b: Silny związek między zmiennymi – linia regresji.

Przykład 2: Słaba korelacja dodatnia

x
x
x x
x x
x x x
x
x x
x
x x
x

Przykład 3: Silna korelacja ujemna

Przykład 4: Korelacja zerowa (brak związku między zmiennymi): dla wszystkich X taka sama przewidywana wartość Y

Przykład 5: Korelacja zerowa (brak związku między zmiennymi): nie można wykreślić linii (regresji) najlepiej dopasowanej do
danych (każda linia jest równie (nie)dobra)

x
x x
x x
x x
x x x

x x
x
x
x

x
x
x x
x x

x
x x
x

x x x x x x x

x x

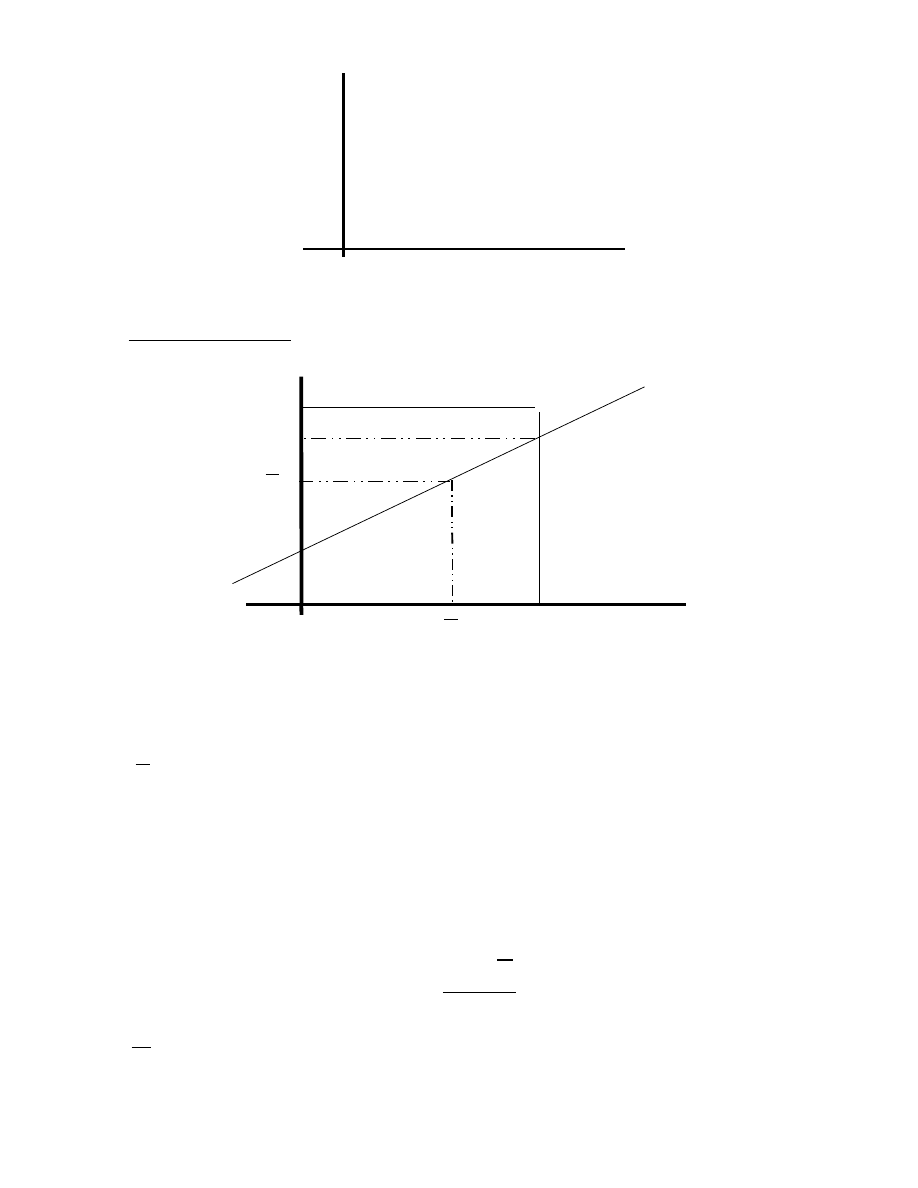
REGRESJA I PRZEWIDYWANIE
Równanie regresji pozwala przewidywać wartość zmiennej zależnej Y na podstawie znajomości zmiennej niezależnej X.

Rysunek 5f-1. Linia regresji prostej

Równanie regresji prostej: Y = a + bX + e lub: Y’ = a + b X;

Y – wartość rzeczywista zmiennej zależnej;
Y’ – wartość przewidywana zmiennej zależnej;

– wartość średnia zmiennej zależnej

e – błąd przewidywania;
b – współczynnik nachylenia (slope) – wyznacza kąt
nachylenia linii regresji;
a – stała równania regresji (constant, intercept) – wyznacza
wysokości linii regresji. Jeśli X = 0, to Y = a; czyli a to
wysokość linii regresji (wartość Y) w punkcie X = 0.

Analizowane dane (zmienna zależną niezależną) możemy przedstawić w postaci standaryzowanej (jako odchylenia
poszczególnych wyników od średniej całkowitej):

−

Dane w postaci standaryzowanej mają, z założenia, średnią:

= 0 i wariancję:

= 1. Dla danych standaryzowanych równanie regresji ma postać:

Y’ =

(opuszczamy w równaniu a, gdyż wynosi ono zero).

x x x

x x x x x

x x xx xxx x x

x x x x x x

x x x x x

x x x x

′

Równanie regresji w postaci standaryzowanej jest bardzo wygodne gdyż eliminuje wpływ jednostek pomiaru na wartość
zmiennych. Wszystkie zmienne wyrażone są w tych samych jednostkach: jednostkach odchylenia standardowego. Analiza
regresji umożliwia (analogicznie jak w wypadku ANOVA) rozłożenie sumy kwadratów (SS) zmiennej zależnej Y (

) na dwie

składowe:

•

SS przewidywaną na podstawie równania regresji -

reg

•

SS nie przewidywalną przez równanie regresji – SS błędu (SS

error

) lub SS resztową (residual --

res

(porównaj rysunek na poprzdeniej stronie)

Ponieważ dwa wyrażenia po prawej stronie równania (w nawiasach) są nieskorelowane ze sobą, zachodzi równość:

∑

−

)

(

)

(

)

(

= SS

reg

+ SS

res

res

reg

Jak widać z ostatniego wzoru, r

informuje o tym, jaką proporcję całkowitej sumy kwadratów zmiennej zależnej można

przewidzieć na podstawie zmiennej niezależnej (i równania regresji). Z wzoru tego widać też, że im większe jest SS

reg

(tzn. im

bliżej linii regresji położone są punkty na wykresie, por. strony 4 i 5) tym wyższa jest korelacja (r i r

). Istotność współczynnika

regresji dana jest wzorem:

F =

res

reg

)

−

res

reg

k= liczba zmiennych niezależnych, N = wielkość próby (dla jednej zm. niezależnej: df

= 1, df

= N - 2). Jeśli istotne jest r to istotne

jest też r

(przy identycznym alfa).

Istnieją metody analizy regresji krzywoliniowej, analizujące rozrzut punktów względem jakieś krzywej.

KORELACJA I REGRESJA WIELOKROTNA (multiple correlation and regression)

Analiza regresji wielokrotnej pozwala przewidywać wartość zmiennej zależnej Y na podstawie wielu zmiennych niezależnych
(predyktorów): X

, X

, ... X

Predyktory

te:

•

mogą być wzajemnie skorelowane ze sobą;

•

mogą być zmiennymi ciągłymi jak i dyskretnymi (skokowymi). Poza przypadkiem, kiedy predyktory dyskretne przybierają
wartości: 0 i 1, muszą być one, przed włączenie do analizy, zakodowane w specjalny sposób. Najczęściej jednak
analizowana jest zależność między zmiennymi ciągłymi.

Równanie regresji wielokrotnej ma postać (czasem zamiast a pisze się b

Y’ = a + b

, + b

, + ... + b

Jeśli równanie regresji przedstawione jest w postaci standaryzowanej (patrz niżej), współczynniki beta (

) mogą być traktowane

jako wagi zmiennych niezależnych. Informują one jak duży wpływ ma dana zmienna niezależna na zmienną zależną. Wielkości
współczynników b są nieporównywalne, bo zależą od skali pomiarowej (zmiana jednostki pomiaru powoduje zmianę
współczynnika b).

(

)

(

)

−

′ −

− ′

Y’ =

, +

, + ... +

Analiza regresji pozwala

•

Wybrać zbiór predyktorów (zmiennych niezależnych), spośród wszystkich predykatorów poddanych analizie, który
zapewnia najlepsze przewidywanie zmiennej Y; przy doborze predyktorów brane jest pod uwagę ich wzajemne
skorelowanie.

•

Ocenić wagi poszczególnych predyktorów.

•

Oszacować jaki procent całkowitej sumy kwadratów zmiennej zależnej można przewidzieć na podstawie wszystkich
zmiennych niezależnych uwzględnionych w równaniu regresji. Miarą tego efektu jest współczynnik determinacji (r

lub

Dla odróżnienia od korelacji prostej (r) współczynnik korelacji wielokrotnej oznacza się symbolem R. Współczynnik R jest miarą
siły związku miedzy zmienną zależną a wszystkimi predyktorami uwzględnionymi w modelu analizy.

Warto pamiętać, że analiza regresji jest przede wszystkim narzędziem PREDYKCJI. Niekiedy mówi się, że zmienne niezależne,
analizowane za pomocą analizy regresji, WYJAŚNIAJĄ określony procent zmienności zmiennej zależnej. Interpretacja taka nie
zawsze jest uzasadniona a zawsze wymaga dodatkowych przesłanek statystycznych i merytorycznych.

Przykład:
Szukamy czynników pozwalających najlepiej przewidywać ryzyko zachorowania na chorobę wieńcową. Analizujemy (za
pomocą regresji wielokrotnej) następujące predyktory (czynniki ryzyka):

•

Palenie papierosów;

•

Picie alkoholu;

•

Dieta (zawartość tłuszczów i cukru);

•

Aktywność ruchowa;

•

Płeć;

•

Czynnik genetyczny (występowanie choroby w rodzinie)

•

Wiek (liczba lat życia);

•

Rok urodzenia.

Można oczekiwać (na podstawie dostępnej dotąd wiedzy), że trafność przewidywania ryzyka zachorowania będzie się zwiększała w miarę
jak będziemy uwzględniali kolejne predyktory: 1, 2, ..., 7. Natomiast dołączenie zmiennej 8 nie polepszy trafności przewidywań ponieważ
nie dostarcza ona żadnej nowej informacji o badanym (informuje o tym, co już wiemy na podstawie zmiennej 7). Fakt, że zmienna 8 jest
bardzo wysoko (tu: perfekcyjnie) skorelowana ze zmienną 7 sprawia, że jest ona z bezużyteczna (redundantna) dla prognozy zmiennej
zależnej. Najlepszymi predyktorami zmiennej zależnej są takie zmienne niezależne, które wysoko korelują ze zmienną zależną (kryterium) i
jednocześnie nisko korelują wzajemnie ze sobą.

ANALIZA DYSKRYMINACYJNA

O ile celem analizy regresji jest znalezienie układu predyktorów pozwalających najlepiej przewidywać WARTOŚĆ zmiennej
zależnej Y, to celem analizy dyskryminacyjnej jest znalezienie zbioru predyktorów pozwalających najlepiej przewidywać
PRZYNALEŻNOŚĆ BADANYCH DO JEDNEJ Z GRUP kryterialnych. Najlepiej jeśli grupy kryterialne tworzone są w oparciu o „mocne”
kryteria (np. kobiety / mężczyźni, chorzy / zdrowi).

Przykład zastosowania analizy dyskryminacyjnej

Analizujemy dwie grupy badanych: zdrowych i chorych (np. na choroby krążenia). Interesuje nas które zmienne (spośród
dużego zbioru analizowanych zmiennych, takich jak np.: wiek, płeć, waga ciała, palenie papierosów, itp.) pozwalają najlepiej
przewidywać ryzyko zachorowania na chorobę układu krążenia, czyli to, czy dana osoba znajdzie się (np. po pięciu latach) w
grupie osób zdrowych czy też w grupie osób chorych.

PROBLEM ZALEŻNOŚCI PRZYCZYNOWYCH W BADANIACH NIEEKSPERYMENTALNYCH : ANALIZA ŚCIEŻKOWA

Budujemy MODEL teoretyczny wyjaśniający zależności przyczynowe w pewnym zbiorze zmiennych a następnie sprawdzamy w
jakim stopniu dane empiryczne (uzyskane w badaniach korelacyjnych) potwierdzają ten model (podejście konfirmacyjne). Do
analizy takiej można wykorzystać analizę regresji wielokrotnej.

Charakterystyka analizy ścieżkowej

•

zakłada się, że zależności między zmiennymi są jednokierunkowe.

•

zmienne egzogenne—zmienne nie wyjaśniane przez pozostałe zmienne uwzględnione w modelu;

•

zmienne endogenne - zmienne wyjaśniane przez inne zmienne uwzględnione w modelu.

•

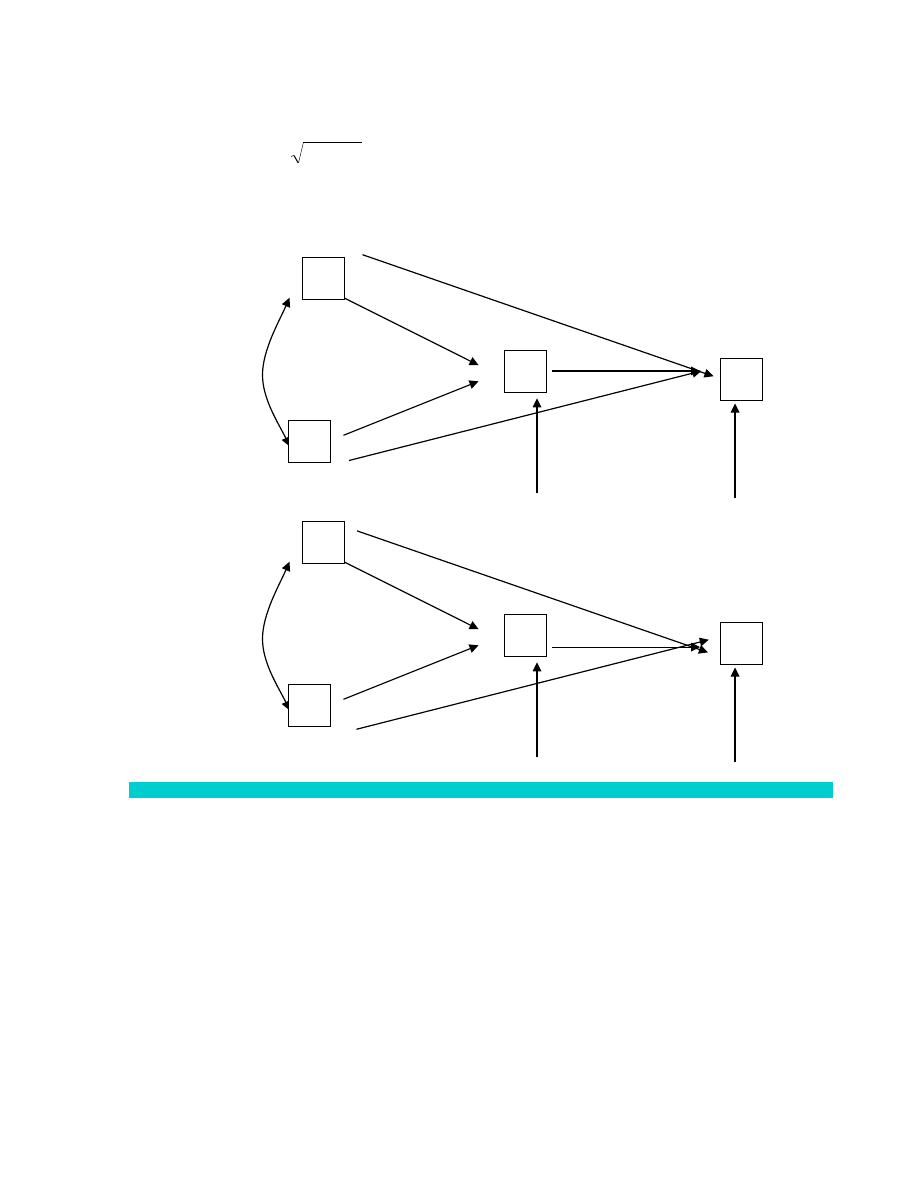
współczynnik ścieżkowy (path coefficient - p) – miara bezpośredniego wpływu danej zmiennej (endogennej lub
egzogennej) na zmienną endogenną. wartość współczynnika ścieżkowego równa się współczynnikowi beta równania
regresji.

•

wariancja resztowa (residual - e) -- wariancja zmiennej endogennej nie wyjaśniana przez inne zmienne uwzględnione w
modelu (e równa się

−

Do podobnych, lecz bardziej zaawansowanych analiz wykorzystuje się programy LISREL (J

˙˙o

reskog) i AMOS

Przykład diagramu ścieżkowego : nna rysunku górnym zaznaczono nazwy ścieżek, na rysunku dolnym – wartości
współczynników ścieżkowych oraz (w nawiasach) korelacje między zmiennymi.

ANALIZA CZYNNIKOWA

Analiza czynnikowa ma na celu poszukiwanie zmiennych ukrytych (czynników) mogących wyjaśnić zależności między pewną
(zazwyczaj dużą) liczbą skorelowanych zmiennych mierzonych. Aby wyjaśnić całą wariancję n zmiennych mierzonych potrzeba
zawsze n czynników. Zazwyczaj jednak potrafimy wyjaśnić bardzo znaczny procent wariancji zmiennych mierzonych za pomocą
stosunkowo niewielkiej liczby czynników (por. podany niżej przykład liczbowy). Wiele etapów analizy czynnikowej (np. decyzja
co do liczby czynników) oraz interpretacja psychologiczna otrzymanych czynników mają charakter mniej lub bardziej arbitralny.

•

Analiza czynnikowa KONFIRMACYJNA ma na celu testowanie hipotez wyjaśniających zależności między mierzonymi
zmiennymi. Hipotezy te mogą dotyczyć liczby czynników, korelacji między czynnikami, ładunków czynnikowych, itp.
(ładunek czynnikowy to korelacja między czynnikiem a zmiennymi mierzonymi).

•

Analiza czynnikowa EKSPLORACYJNA -- nastawiona na poszukiwanie zmiennych ukrytych (czynników) mogących
wyjaśnić zależności między zmiennymi mierzonymi. Jeśli takie czynniki zostaną wykryte powinny być traktowane jako
hipotezy do sprawdzenia w kolejnych badaniach.

Analiza czynnikowa stosowana w sposób ateoretyczny określana jest jako podejście „garbage in -- garbage out”, tzn. „śmiecie
wkładamy – śmiecie otrzymujemy”.

p41

p31

p43

p32

p42

(.3

.009 (.33)

.398 (.41)

.416 (.50)

.041 (.16)

.501 (.57)

.710

.911

MODEL EKSPERYMENTALNY A KORELACYJNY

Kryteria

Model

eksperymentalny

Model

korelacyjny

Przedmiot analizy

Różnice między warunkami

Współzmienność zmiennych (siła związku między
zmiennymi)

Wymagania

Możliwie jednorodna próba, podzielona losowo
na grupy badane w różnych warunkach
(różnice między osobami = błąd
eksperymentalny)

Możliwie duża i zróżnicowana próba, badana w
identycznych warunkach

zalety

Łatwość kontroli zmiennych ubocznych
(randomizacja)

Łatwiejsze wnioskowanie
o zależnościach przyczynowych

Łatwość zbierania danych (łatwość pomiaru
dużej liczby zmiennych)

ograniczenia

Zbytnie zwiększanie liczby zmiennych
niezależnych (np. liczby grup) jest zwykle bardzo
kosztowne

Ograniczona trafność ekologiczna (zwłaszcza
badań laboratoryjnych)

Trudność kontroli zmiennych ubocznych

Trudność wnioskowania
o zależnościach przyczynowych. Analiza
zależności przyczynowych (causal analysis)
wymaga zwykle bardzo zaawansowanej
statystyki

Document Outline

A2
A2
Teoria znaków (w tym – językowych) nazywa się semiotyką. Podstawowe działy semiotyki:
2.2 ELEMENTY TEORII NAZW
Ocena wielkości (siły) efektu (effect size)
Y12
Y13
Y = a + bX

Wyszukiwarka

Podobne podstrony:
Metodologia ?dań opracowanie
Metodologia wykłady - opracowanie na egzamin, studia różne, Opracowania
pytania na metodologie wraz z opracowaniem, metodologia
metodologia?dań lit opracowanie
Metodologia - badań - opracowanie, PSYCHOLOGIA, Psychologia II semestr, Metodologia badań psychologi
METODOLOGIA?DAŃ SPOŁECZNYCH opracowanie
Metodologia ?dań opracowanie
Metodologia badań społecznych - opracowanie, Pedagogika resocjalizacyjna
opracowane pytania metodologia III cz
METODOLOGIA opracowane zagadnienia pdf
Dewey Jak myślimy opracowanie, Metodologia
Biologia opracowane slajdy
metodologia opracowanie10 12, komunikacja społeczna, metodologia
moje opracowanie egzaminu z metodologii 2014

więcej podobnych podstron

Metodologia slajdy opracowane

Document Outline