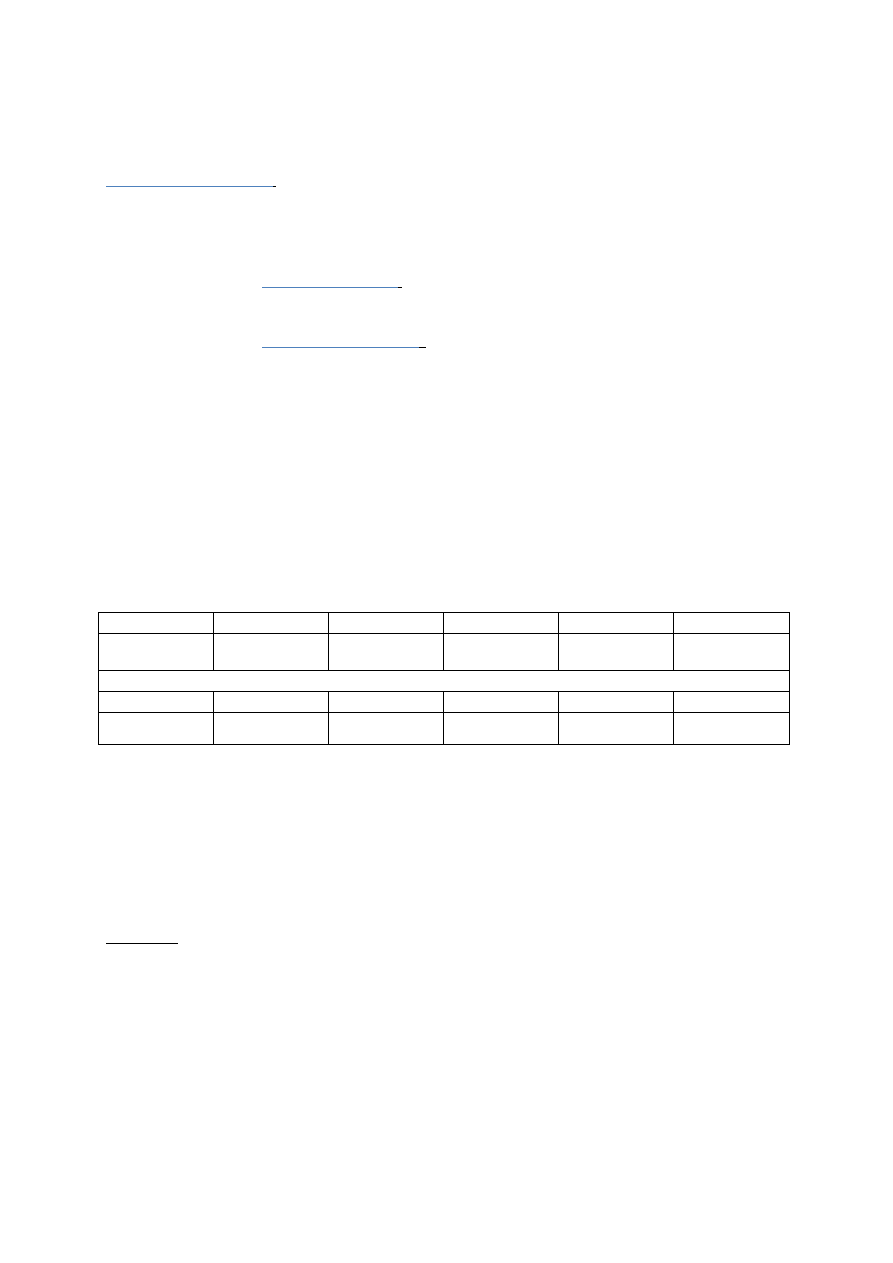
Permutacja  ciągu (1,…,n) 

-ciąg złożony z tych samych liczb lecz w innej kolejności 
 

Permutacja elementarna

 – permutacja polegająca na zamianie miejsc dwóch elementów, 

np. 1,2,3,4,5,6 → 1,2,6,4,5,3 
 
Złożenie permutacji też jest permutacją. 
 
Permutację nazywamy 

permutacją parzystą

 jeżeli jest złożeniem parzystej ilości permutacji 

elementarnych. 
 
Permutację nazywamy 

permutacją nieparzystą

  jeżeli jest złożeniem nieparzystej ilości złożeniem 

permutacji elementarnych. 
Przykład: 
(1,2,3,4,5,6) → 

(2,6,5,3,1,4)

 

(

2

,

1

,3,4,5,6)      

(1,6,5,3,2,4)

 

(2,

6

,3,4,5,

1

)      

(1,2,5,3,6,4)

 

(2,6,

5

,4,

3

,1)      

(1,2,3,5,6,4)

 

(2,6,5,

3

,

4

,1)      

(1,2,3,4,6,5)

 

(2,6,5,3,

1

,

4

)      

(1,2,3,4,5,6)

 

 
Permutacją g ciągu (1,…,n) nazywamy permutacją odwrotną do permutacji f jeżeli złożenie g◦f = f◦g 
jest permutacją identycznościową. 
 

Tw.

 Jeżeli permutacja f jest parzysta (nieparzysta) to permutacja f

-1

 jest parzysta (nieparzysta). 

5 

1 

4 

6 

3 

2 

1 

2 

3 

4 

5 

6 

(klocki) 
1 

2 

3 

4 

5 

6 

2 

6 

5 

3 

1 

4 

 
                     {1, jeżeli (i1,…,i1) jest parzystą permutacją ciągu (1,…,n) 
δ(i1,…,in)= {-1, jeżeli ciąg (i1…in) jest nieparzystą permutacją ciągu (1,…,n) 
                     {0, jeżeli  ciąg (i1,…,in) nie jest permutacją ciągu (1,…,n) 
 

Df

. Formą wieloliniową antysymetryczną określoną na kolumnach macierzy kwadratowej A wymiary 

nxn, która na kolumnach macierzy jednostkowych przyjmuje wartość 1 nazywamy wyznacznikiem a 
jej wartość na kolumnach macierzy A nazywamy wyznacznikiem macierzy A i oznaczamy detA lub |A|. 
 
Własności: 

1° 

 det I=1 

2° i 3◦   wyznacznik jest liniowy względem każdej kolumny oddzielnie 
4°  

wyznacznik macierzy zawierającej kolumnę zer wynosi zero. 

5° 

wyznacznik macierzy, w której 2 kolumny są identyczne wynosi 0 

6° 

zamiana miejscami dwóch kolumn macierzy skutkuje pomnożeniem wyznacznika           
przez -1 

7° 

do kolumny macierzy można dodać inna kolumnę pomnożoną przez dowolną stałą, 
nie zmieniając wyznacznika 

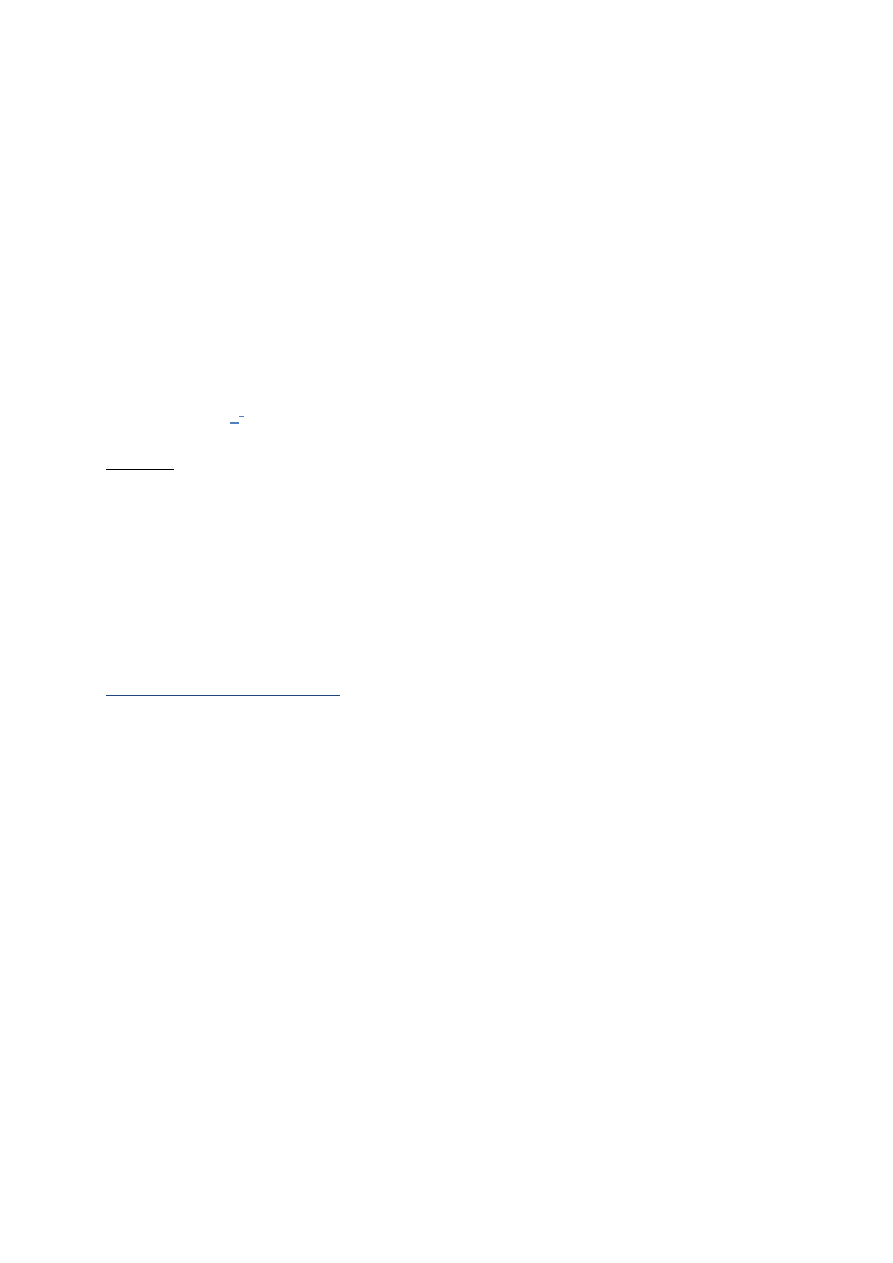
8° 

 

 

=

…

∗ … ∗

det( , … , )  = 

∗ … ∗

( , … , ) 

 

 

9° 

 

 

 

=

…

∗ … ∗

( , … , ) = 

= 

∗ … ∗

( , … , ) =  

…

∗ … ∗

( , … , )

=

 

10°  

Własności 2°-7° dotyczą także wierszy macierzy. 

 

We wzorze 8° jest 

n

n

 n!

 mnożeń. 

 
Przykłady: 
1°  

A=a

11

, detA=a

11 

 

2° 

A= 

 , det A = a

11

a

22 

-a

21

a

12 

 

3° 

A=

 , det A = a

11

a

22

a

33

 - a

21

a

12

a

33

 + a

21

a

32

a

13

 - a

31

a

22

a

13

 + a

31

a

12

a

23

 - a

11

a

32 

a

23 

 

 

 

 

reguła Sarrusa 

(dotyczy tylko wyznaczników 3x3)

 

 
 

Rozwinięcie Laplace’a wyznacznika 
 

(a

1,1 

,   a

1,2 

, … ,     a

1,n 

)           (a

1,1 

,   a

1,2 

,  … , a

1,n   

)                  (a

1,1   

,  … ,  a

1,n-1 

,   a

1,n   

) 

(  

⋮       ⋮                 ⋮     )           (  ⋮         ⋮              ⋮    )                  (    ⋮                ⋮          ⋮    )                   

(a

i-1,1 

,  a

i-1,2 

, … ,  a

i-1,n

)           (a

i-1,1 

, a

i-1,2 

, … , a

i-1,n 

)                  (a

i-1,1 

,  … , a

i-1,n-1  

, a

i-1,n  

) 

      det  (

a

i,1 

,    a

i,2 

, … ,    a

i,n    

) = det(

a

i,1

,     0,      …,     0

   ) + … + det

(   0  ,   … ,      0    , a

i,n     

)  

= 

(a

i+1,1 

, a

i+1,2 

, … , a

i+1,n

)           (a

i+1,1 

, a

i+1,, 

, … , a

i+1,n

)                  (a

i+1,1  

, … , a

i+1,n-1 

, a

i+1,n 

) 

(  

⋮           ⋮              ⋮   )           (  ⋮         ⋮               ⋮    )                  (     ⋮               ⋮          ⋮    )                   

(a

n,1 

,   a

n,2 

, … ,   a

n,n   

)           (a

n,1 

,   a

n,2 

,  … ,  a

n,n  

)                  (a

n,1    

, … ,  a

n,n-1 

,   a

n,n    

) 

 
              (a

11     

,  a

12 

,  … ,   a

1n    

)                (a

11

  , a

12

 ,  … , a

1n

 )                           

              (  

⋮          ⋮              ⋮     )                (  ⋮       ⋮             ⋮    )            

              (a

i-1,1

 , a

i-1,2

 , … , a

i-1,n 

 )                ( a

i-1,1

 , 1 , … , a

i-1,n

 ) 

=a

i1

det( 1   ,       0   , …  ,   0    ) + a

i,n

det(   0                     1   )  =  

             (a

i+1,1 

 , a

i+1,2

 , … , a

i+1,n

)                (a

i+1,1

 , 1 , … , a

i+1,n

 ) 

             (  

⋮           ⋮               ⋮    )                (  ⋮       ⋮            ⋮     )            

             (a

n,1

  ,   a

n,2

  ,  ... , a

n,n  

)                (a

n,1

 , a

n,2

 , … , a

n,n

 ) 

 
 
 
 
 
 

                                         (a

11

    , … , a

1,j-1

  ,  a

1,j+1

 ,  … ,  a

1,n

   ) 

                                         (  

⋮                                               ⋮     )            

                                         

(a

i-1,1 

 , … , a

i-1,j-1 

 , a

i-1,j+1

 , … , a

i-1,n 

 ) 

= 

∑

(−1)

 

 (a

i+1,1

 , … , a

i+1,j-1

 , a

i+1,j+1

 , … , a

i+1,n

 ) =

∑

(−1)

 

! =

∑

=

 

                                         (  

⋮                                                ⋮    )            

                                         (a

n,1

  ,  … , a

n,j-1

  ,  a

n,j+1

  , … ,  a

n,n

   ) 

                                                 ↑Minor nr ij 

 

=

∑

=

 

~dopełnienie algebraiczne element macierzy A