Statystyczna kontrola procesu – karty kontrolne Shewharta.
Każde przedsiębiorstwo produkcyjne, dąży do tego, aby produkty które wytwarza były
jak najlepszej jakości. W dzisiejszych czasach, to właśnie jakość pozwala utrzymać się na
rynku, gdzie konkurencja jest bardzo duża. Ponieważ, jakość oznacza zarówno wydajność,
niezawodność, trwałość, kompatybilność, czyli ogół właściwości obiektu wiążących się z
jego zdolnością do zaspokojenia potrzeb stwierdzonych lub oczekiwanych, na potrzeby
niniejszego referatu, zainteresowaniem zostanie objęta jedynie jakość wykonania, czyli
zgodność wyrobu z wymaganiami projektu.
Ponieważ zmienne występujące w procesie sterowania jakością są zmiennymi
losowymi, rola metod statystycznych odgrywa w niej dominującą rolę. Podstawowe
znaczenie mają metody i narzędzia należące do tzw. wielkiej siódemki SPC (
magnificent seven
od Statistical Process Control
) w skład której wchodzą:
1. diagram przebiegu procesu (
process flow diagram
)
2. karta kontrolna (
control chart
)
3. arkusz kontrolny
(checksheet)
4. diagram Ishikawy (
cause and defect diagram, Fishbone diagram
)
5. diagram Pareto (
Pareto diagram
)
6. histogram (
histogram
)
7. punktowy diagram korelacji
(scatter plot)
Podstawową rolę w działaniach sterowania jakością odgrywają karty kontrolne. Są to
podstawowe i najwcześniejsze historycznie narzędzie SPC. Należą do metod bieżących
kontroli jakości, a jednocześnie przy właściwym stosowaniu mają bardzo duże znaczenie przy
poprawie jakości produkcji.
Praktyczne zastosowanie kart kontrolnych nastąpiło w 1924 roku w Bell Laboratories.
Pomysł kart zawdzięczamy Walter’owi Shewhart’owi, od którego nazwiska nazywa się je
często kartami kontrolnymi Shewhart’a (KKS). Wykorzystują one prawa rachunku
prawdopodobieństwa i statystyki matematycznej pozwalają wychwycić ewentualne
rozregulowanie proces. Jeśli są takie sygnały, wówczas podejmuje się decyzję o ewentualnym
przerwaniu produkcji i przeprowadzenia jego regulacji.
Projektowanie KKS opiera się na założeniu, ze każdy proces jest poddawany działaniu
dwóch rodzajów czynników zakłócających:
- naturalnych – są to czynniki nierozerwalnie związane z procesem. Jest ich
zazwyczaj wiele, ale żaden nie odgrywa dominującej roli,
- nieprzypadkowa – związana jest z przyczynami które można wyjaśnić np.
zmęczenie robotników. Jest ona szczególnie niepożądana, ponieważ jest oznaką
nieprawidłowego przebiegu procesu i znacznie obniża jakość.
Głównym elementem każdej karty kontrolnej jest diagram przeglądowy, służący do
monitorowania procesu. Na osi poziomej, oznaczonej symbolem t, odkłada się numer
kolejnej próbki pobranej do badania. Na osi pionowej odkłada się natomiast wartości
obserwowanej charakterystyki. Charakterystyka ta jest zmienną losową. Istotnym elementem
jest linia centralna (center line). Jest to najczęściej taka wartość charakterystyki, wokół której
powinny losowo oscylować kolejne wartości parametru. Linia ta wyznaczana jest na
podstawie tzw. próby pilotażowej, bądź wyznaczona z góry przez normy dotyczące danego
procesu.
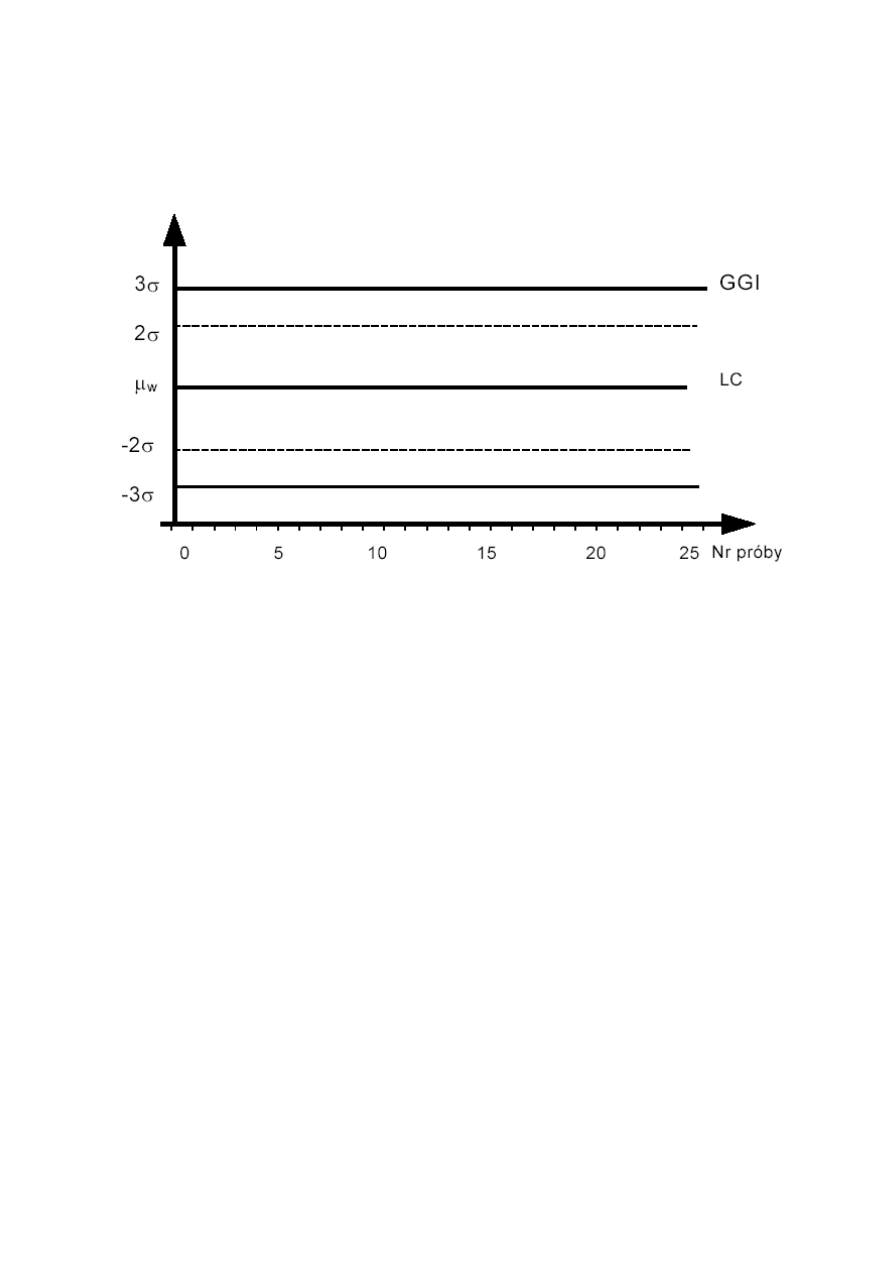
W zależności od potrzeb badania stosuje się dwustronny, bądź jednostronny schemat
kontrolny. W takiej sytuacji na diagramie wykreśla się granice kontrolne (control limits).
Graficzną prezentację konstrukcji kart kontrolnych przedstawiono na rysunku 1.1.
Rys. 1.1 Idea karty kontrolnej.
Źródło: Opracowanie własne
Decyzje podejmowane przy użyciu karty kontrolnej oparte są na podstawie weryfikacji
hipotez statystycznych przy danym
α
. Należy podkreślić, ze w miarę jak rosną wymagania
jakościowe w stosunku do procesów i wyrobów rozszerza się również zakres stosowania
nowoczesnych kart kontrolnych, określanych często kartami kontrolnymi z możliwością
akceptacji procesu, a więc z określoną explicite wartością
β
.
W zależności od rodzaju produkcji, oraz wymagań dotyczących jakości stosuje się różne
karty kontrolne lub inne bardziej zaawansowane techniki. Karty kontrolne można podzielić ze
względu na rodzaj badanej cechy jak również liczbę kontrolowanych parametrów.
W zależności od rodzaju kontrolowanej cechy karty kontrolne dzieli się na:
1) karty kontrolne dla cech ocenianych liczbowo
2) karty kontrolne dla cech ocenianych alternatywnie
Karty dla cech ocenianych alternatywnie, stosuje się przy cechach jakościowych, ale
możliwe jest wykorzystanie ich również przy kontroli cech mierzalnych, zwłaszcza gdy sam
proces przeprowadzenia pomiaru jest długi bądź kosztowny. Niemniej jednak stosując skalę
alternatywną traci się dużo informacji, które ograniczać mogą poszukiwanie zakłóceń
procesu.
W zależności od liczby kontrolowanych parametrów karty dzieli się na:
1) jednotorowe
2) dwutorowe
3) wielotorowe
Dla kart jednotorowych konstruuje się jeden wykres dla obserwowanego parametru, a
dla kart dwu i wielotorowych prowadzi się ich odpowiednio więcej.
Większość kart zakłada iż rozkład cechy jest rozkładem normalnym.
GGO
DGO
DLK
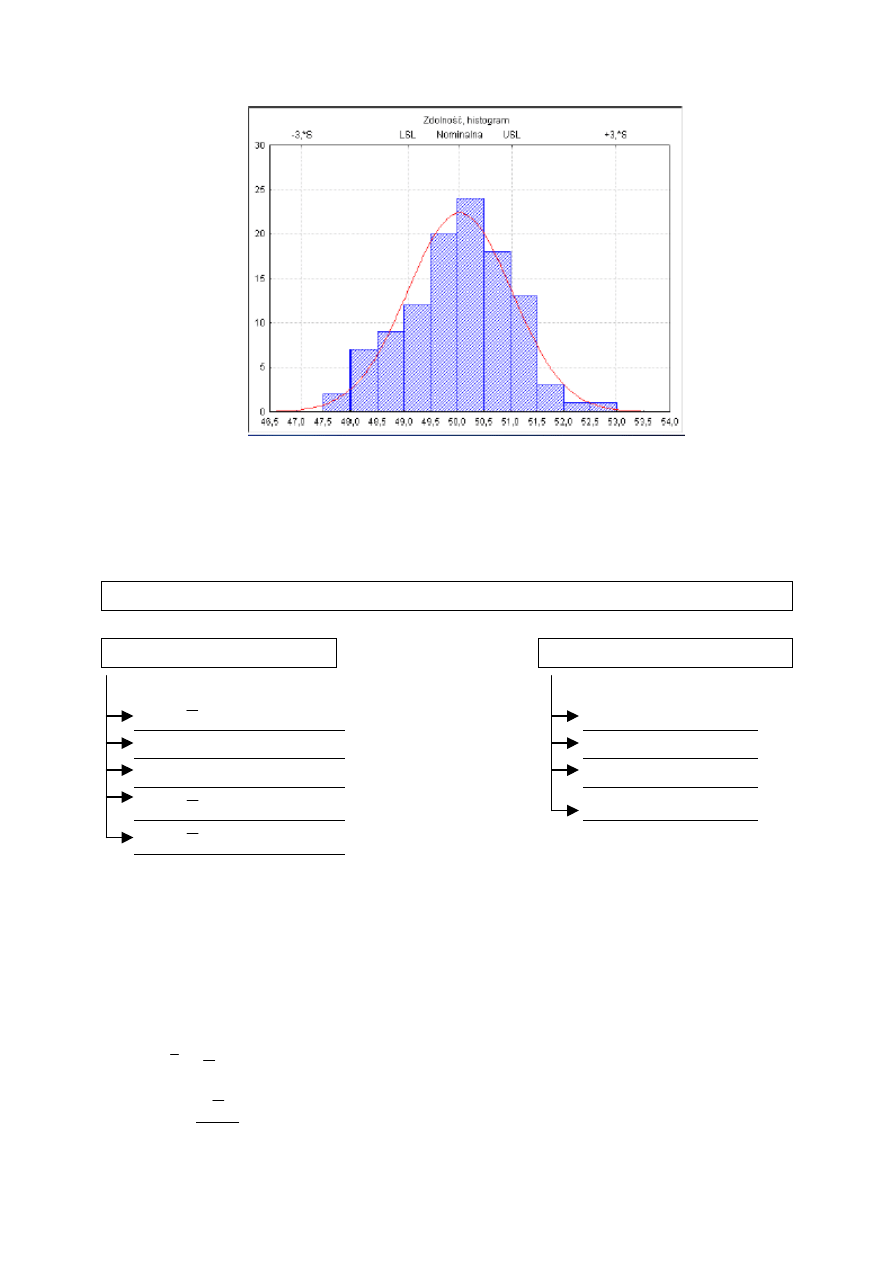
Rys. 1.1. Badanie zgodności rozkładu z rozkładem normalnym
Typy najczęściej stosowanych kart kontrolnych Shewharta przedstawia rysunek 1.2.
Rys. 1.2 Typy najczęściej stosowanych kart kontrolnych Shewarta
KARTY KONTROLNE SHEWARTA
Przy ocenie liczbowej
Przy ocenie alternatywnej
Karta
X
Karta p
Karta X
Karta np
X
max
-X
min
(R)
Karta c
Karta
R
X
−
Karta u
Karta
S
X
−
Źródło: Opracowanie własne
Konstrukcja linii kontrolnych przy tworzeniu kart występuje w dwóch przypadkach.
Mianowicie, gdy znamy parametry projektowe wyrobu (średnia, odchylenie, a także GLC i
DLK) tzw. wartości normatywne , oraz gdy parametrów tych nie znamy i należy je
oszacować. Najczęściej szacuje się średnią, odchylenie lub rozstęp. Estymatory
wykorzystywane do wspomnianych parametrów są następujące:
1)
∑
=
=
n
j
ij
i
x
n
x
1
1
ij
x - j-ta obserwacja w i-tej próbie
(1.1)
2)
)
(
ˆ
2
n
d
R
=
σ
d
n
(n) – tzw. współczynnik Hartley’a (wartość stablicowana)
(1.2)
3)
)
(
ˆ
4
n
c
S
=
σ
,
∑
=
=
k
i
i
S
k
S
1
1
,
3
4
)
1
(
4
)
(
4
−
−
=
n
n
n
c
dla n>25 (wsp. korygujący) (1.3)
Zależność 2) może być stosowana w przypadku gdy liczebność próbki n
≤12 (dla n>12
rozstęp nie jest dobrym estymatorem zmienności) oraz gdy zmienność w próbce jest mniejsza
od zmienności średniej między próbami.
Przy konstruowaniu linii kontrolnych dla poszczególnych, jak wspomniano wcześniej,
istnieją dwa przypadki. Przy prezentacji poszczególnych kart, zostaną uwzględnione obydwie
metody. Pierwsza z nich, gdy znane są wartości normatywne, czyli parametry rozkładu
normalnego tj.
µ oraz σ, oraz drugi, gdy tych wartości nie są znane, a zostaną oszacowane na
za pomocą estymatorów (1.1)-(1.3). Dla wszystkich kart przyjęto obszar zmienności +/- 3
σ.
Wyznaczenie linii kontrolnych dla Karty
X
1) dla znanych wartości normatywnych
n
m
GLK
σ
3
+
=
m
LC
=
n
m
DLK
σ
3
−
=
2) dla nieznanych wartości normatywnych (szacowanie 1.1 oraz 1.2)
R
n
A
x
R
n
n
d
x
GLK
)
(
)
(
3
2
2
+
=
+
=
x
LC
=
R
n
A
x
R
n
n
d
x
DLK
)
(
)
(
3
2
2
−
=
−
=
3) dla nieznanych wartości normatywnych (szacowanie 1.1 oraz 1.3)
S
n
A
x
n
n
c
S
x
GLK
)
(
)
(
3
3
4
+
=
+
=
x
LC
=
S
n
A
x
n
n
c
S
x
DLK
n
)
(
)
(
3
4
−
=
+
=
3
4
)
1
(
4
)
(
4
−
−
=
n
n
n
c
Położenie linii kontrolnych na karcie X obliczane jest na podstawie miar rozproszenia
(odchylenia lub rozstępu). Dlatego jeśli nie można założyć niezmienności rozproszenia w
czasie, konieczne jest prowadzenie dodatkowo karty kontrolnej S lub karty kontrolnej R.
Wyznaczenie linii kontrolnych dla karty S
1) dla znanych wartości normatywnych
σ
σ
)
(
)
(
1
3
)
(
6
2
4
4
n
B
n
c
n
c
GLK
=
−
+
=
σ
)
(
4
n
c
LC
=
σ
σ
)
(
)
(
1
3
)
(
5
2
4
4
n
B
n
c
n
c
DLK
=
−
−
=
)
(
1
3
)
(
)
(
2
4
4
5
n
c
n
c
n
B
−
−
=
)
(
1
3
)
(
2
4
4
6
n
c
n
c
B
−
+
=
2) dla nieznanych wartości normatywnych (szacowanie 1.3)
)
(
)
(
1
)
(
3
4
2
4
4
n
B
S
n
c
n
c
S
S
GLK
=
−
+
=
S
LC
=
)
(
)
(
1
)
(
3
3
2
4
4
n
B
S
n
c
n
c
S
S
DLK
=
−
−
=
)
(
1
)
(
3
1
)
(
2
4
4
4
n
c
n
c
n
B
−
+
=
)
(
1
)
(
3
1
)
(
2
4
4
3
n
c
n
c
n
B
−
−
=
Wyznaczenie linii kontrolnych dla karty R
1) dla znanych wartości normatywnych
σ
)
(
3
)
(
3
2
n
d
n
d
GLK
+
=
σ
)
(
2
n
d
LC
=
σ
)
(
3
)
(
3
2
n
d
n
d
DLK
−
=
2) dla nieznanych wartości normatywnych
R
n
D
n
d
R
n
d
R
GLK
)
(
)
(
)
(
3
4
2
3
=
+
=
R
LC
=
R
n
D
n
d
R
n
d
R
DLK
)
(
)
(
)
(
3
3
2
3
=
−
=
)
(
)
(
3
1
)
(
2
3
4
n
d
n
d
n
D
+
=
)
(
)
(
3
1
)
(
2
3
3
n
d
n
d
n
D
−
=
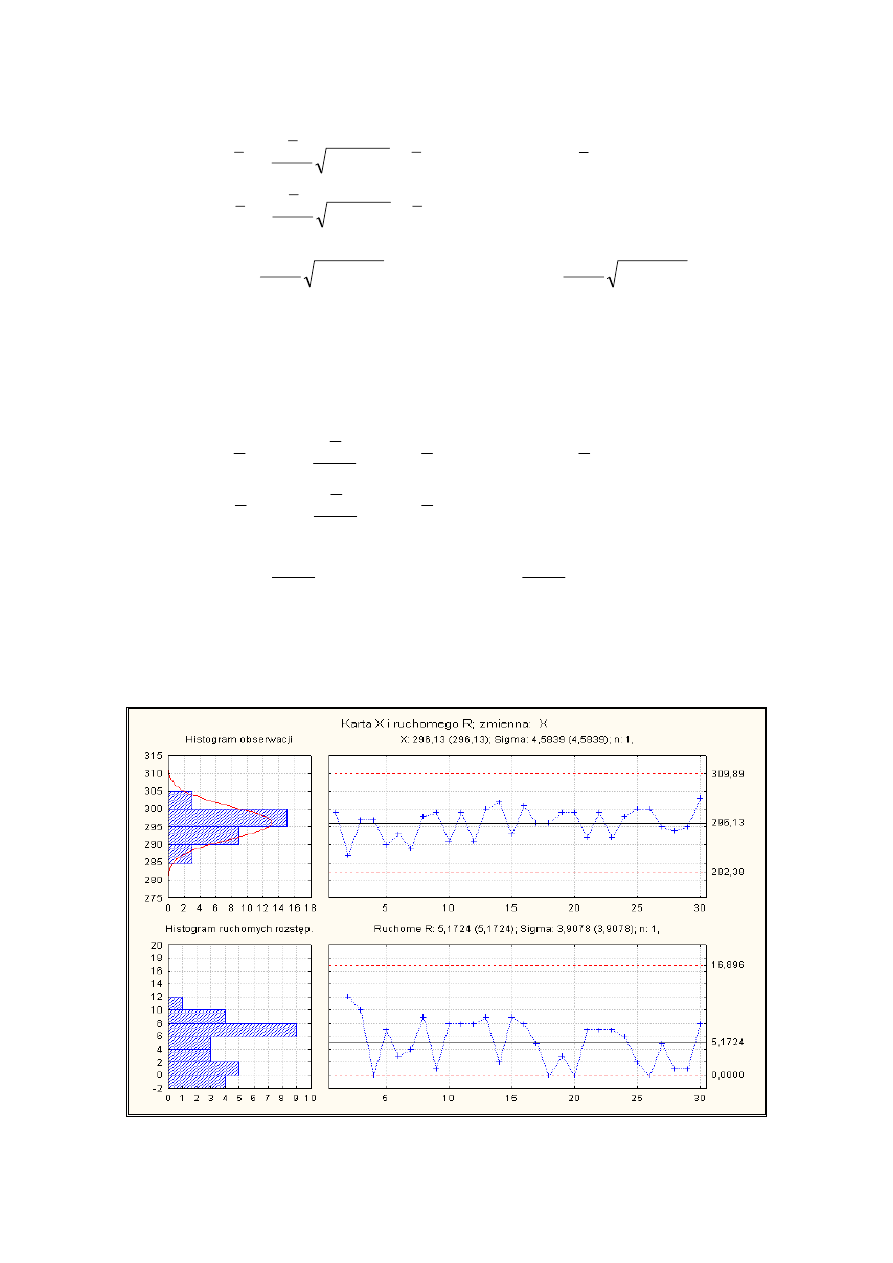
Rys. 1.2 Przykład karty kontrolnej ujawniającej stabilność procesu
Źródło: www.statsoft.pl
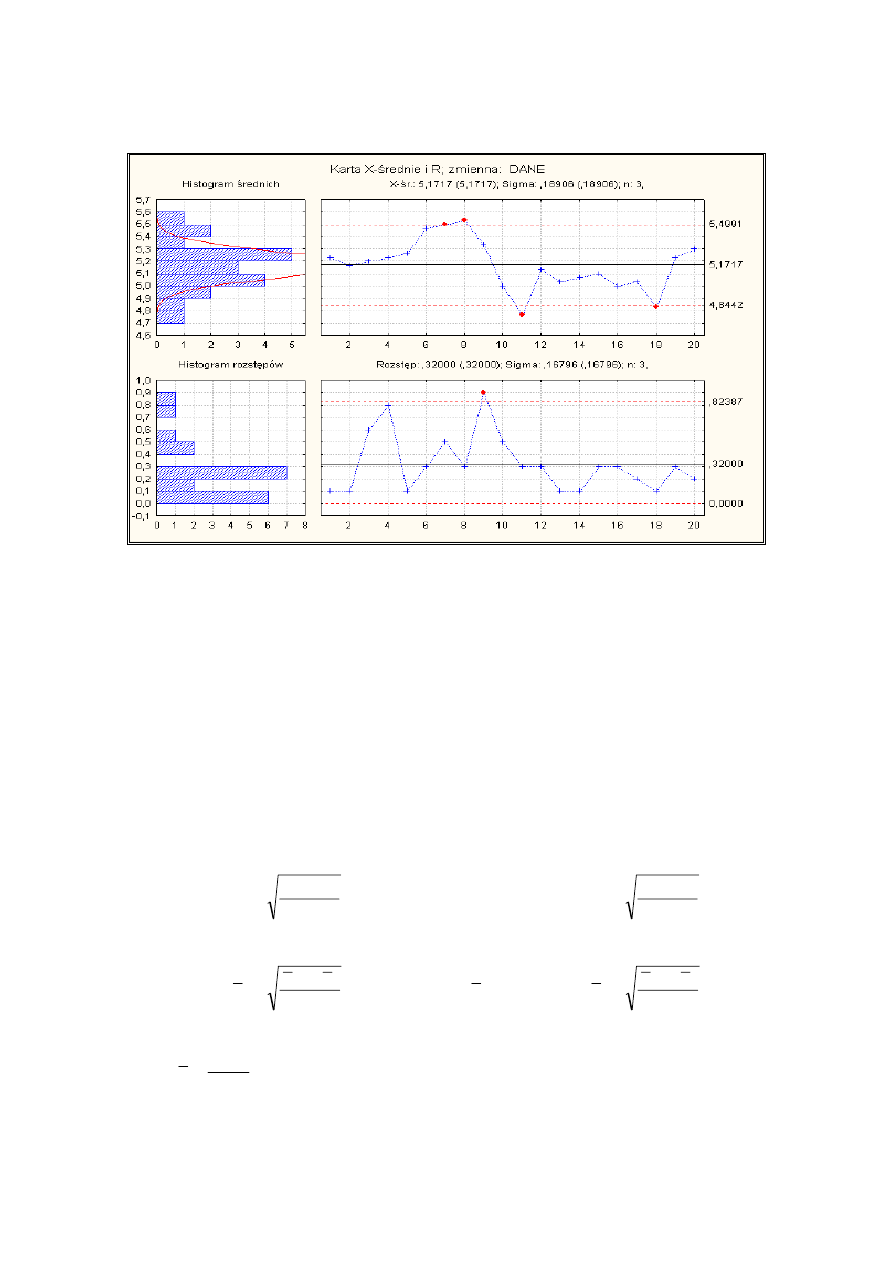
Rys. 1.3. Przykład karty kontrolnej ujawniającej niestabilność procesu
Źródło: www.statsoft.pl
Kolejnym rodzajem kart, są karty oparte na ocenie alternatywnej. Podobnie jak we
wcześniejszych kartach, rozważane są dwa przypadki w wyznaczaniu linii kontrolnych
procesu: dla znanych wartości normatywnych, oraz dla ich nieznanych parametrów.
Podstawowe typy kart kontrolnych dla zmiennych binarnych są następujące:
Karta kontrolna p
Polega na określeniu frakcji wadliwych elementów procesu. Dla poszczególnych
przypadków linie kontrolne wyznacza się:
1) przy znanej wadliwości procesu (p)
n
p
p
p
GLK
)
1
(
3
−
+
=
p
LC
=
n
p
p
p
DLK
)
1
(
3
−
−
=
2) przy nieznanej wadliwości procesu
n
p
p
p
GLK
)
1
(
3
−
+
=
p
LC
=
n
p
p
p
DLK
)
1
(
3
−
−
=
, gdzie
m
p
p
m
i
i
∑
=
=
1
ˆ
i
pˆ - frakcja w i-tej próbie
Karta kontrolna np.
Jest modyfikacją karty kontrolnej p, polegającą na tym, iż zamiast rozpatrywania frakcji
elementów wadliwych, określa się ich liczbę. Dla poszczególnych przypadków linie kontrolne
są następujące:
1) przy znanej wadliwości procesu
)
1
(
3
p
np
np
GLK
−
+
=
np
LC
=
)
1
(
3
p
np
np
DLK
−
−
=
2) przy nieznanej wadliwości procesu
)
1
(
3
p
p
n
p
n
GLK
−
+
=
p
n
LC
=
)
1
(
3
p
p
n
p
n
DLK
−
−
=
Karta kontrolna c
Określa liczbę wad w jednostce wyrobu. Jeżeli Z jest zmienną losową przyjmującą
wartości określające liczbę wad w produkcie, to jej rozkład jest zgodny z rozkładem Poissona
z parametrem
λ. Niekiedy karta ta jest wykorzystywana do badania liczby wadliwych
produktów w próbie. Linie kontrolne wyznaczane są:
1) przy znanej średniej liczbie wadliwych elementów
c
c
GLK
3
+
=
c
LC
=
c
c
DLK
3
−
=
2) przy nieznanej wadliwości procesu
c
c
GLK
3
+
=
c
LC
=
c
c
DLK
3
−
=
Karta kontrolna u
Pozwala na kontrolę braków w zestawie produktów. Średnią liczbę wad w zestawie
oblicza się następująco:
n
c
u
= , gdzie
n- liczba wszystkich produktów
c- liczba wszystkich wad
Linie kontrolne określa się następująco:
n
u
u
GLK
3
+
=
u
LC
=
n
u
u
DLK
3
−
=
W przypadku gdy liczebność próby jest różna linie kontrolne wyznacza się następująco:
i
n
u
u
GLK
3
+
=
u
LC
=
i
n
u
u
DLK
3
−
=
Wykorzystanie kart kontrolnych pozwala na wykrycie niestabilności produkcji wyrobu
w trakcie jego wytwarzania. Pozwala to nie tylko na zmniejszenie kosztów gwarancji, lecz
także na zwiększenie niezawodności produktu, a co za ty, idzie zadowolenia klienta i
zdobycia przewagi na rynku. Oprócz zaprezentowanych podstawowych kart, istnieją jeszcze
inne, nieco bardziej skomplikowane. Powstawały one wraz z rozwojem statystyki
matematycznej, jak również były odpowiedzią na coraz to bardziej złożone procesy
produkcyjne. Do tych kart można zaliczyć między innymi wielowymiarowe karty T
2
Hotellinga.
Bibliografia:
1) Hamrol A., Mantura W., Zarządzanie jakością – teoria i praktyka, Wydawnictwo
Naukowe PWN, 2002 Warszawa
2) Iwasiewicz A., Zarządzanie jakością, Wydawnictwo Naukowe PWN, 1999
Warszawa
3) Kończak G., Wykorzystanie kart kontrolnych w sterowaniu jakością w toku
produkcji, AEiKA, 2000 Katowice
Statystyczna kontrola procesu – karty kontrolne Shewharta
Ewelina Kowalska
Koło Naukowe Metod Ilościowych
Przy Katedrze Statystyki
Wydział Zarządzania
Uniwersytet Gdański