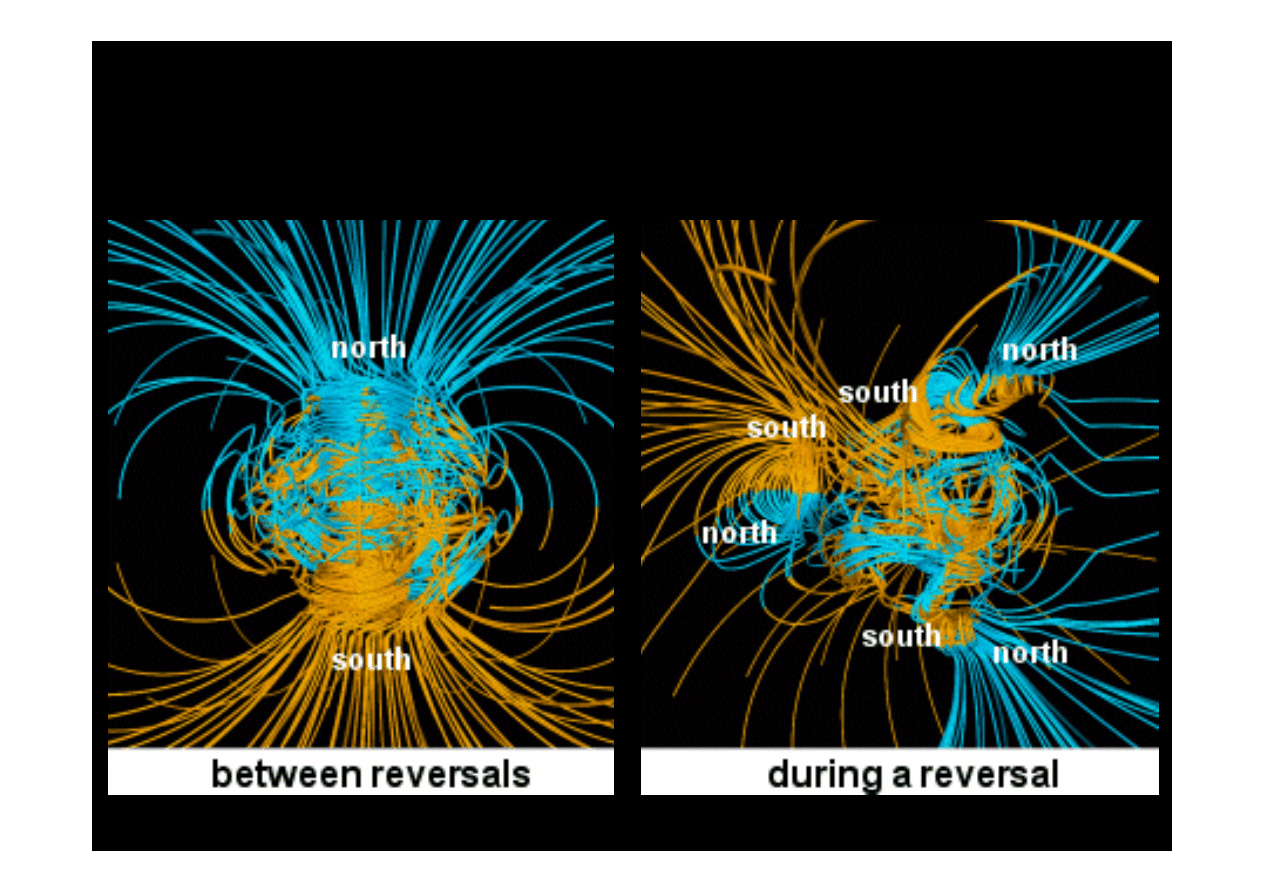
Pole magnetyczne

Obserwacja

Ładunki elektryczne

w spoczynku

⇒ oddziaływania

elektrostatyczne; pole E

Ładunki elektryczne

w ruchu

⇒ oddziaływania

elektryczne i magnetyczne; pole E i B

Źródło pola magnetycznego :

elementarne:

⇒

elementarny ładunek elektryczny
poruszający się z prędkością v

praktyczne:

⇒

prąd elektryczny

pole B ?

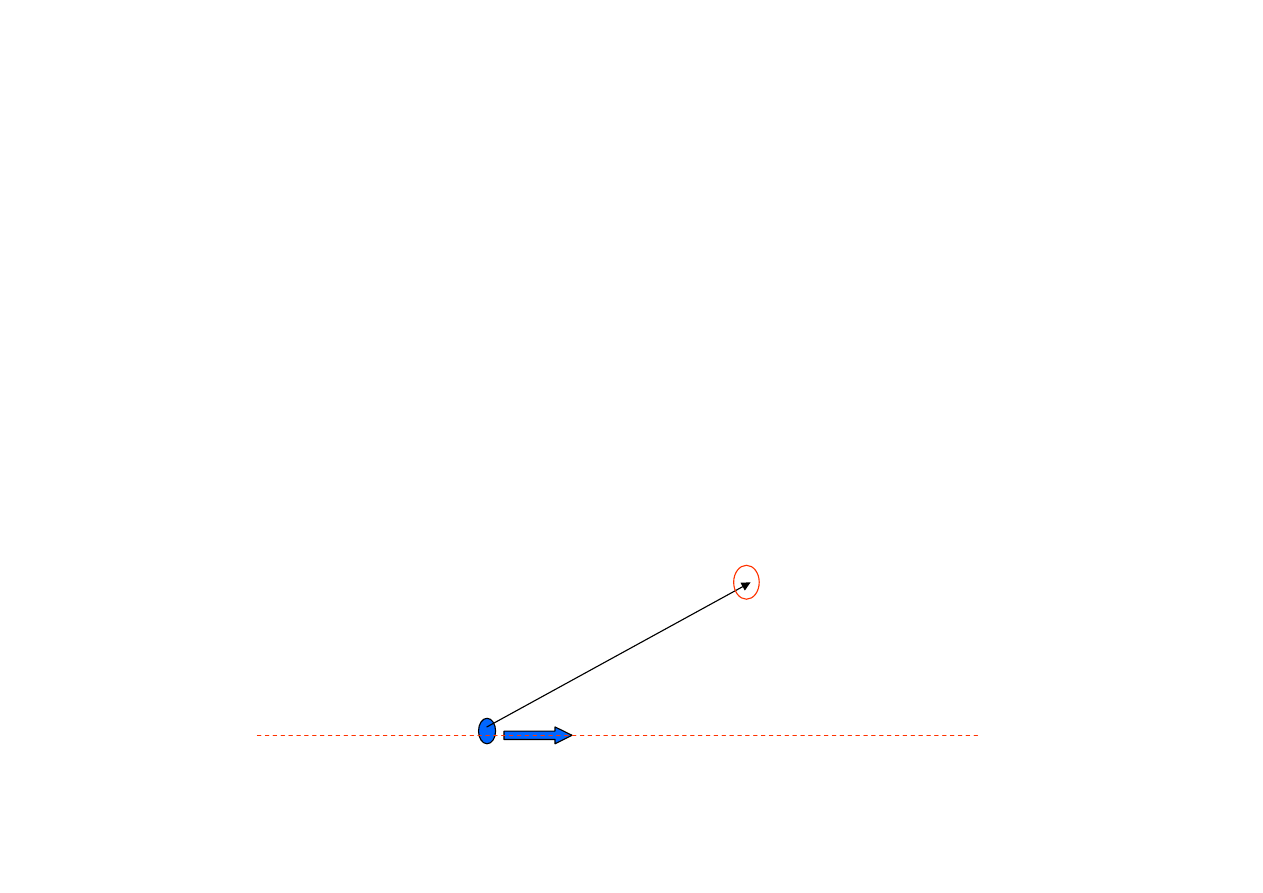
Jakie pole B wytwarza poruszający się ładunek?

Argumenty logiki i symetrii

1. „złamanie” izotropowości przestrzeni – wyróżniony kierunek,
2. B= f(q,v, r)

Wnioski: symetria osiowa pola B,

B~ q(v x r), B~ 1/r

2

v

r

q

Jakie pole B wytwarza poruszający się ładunek?

Wyniki doświadczenia (v

<<c)

(ładunek q poruszający się z prędkością v)

,

(

μ

o

= 4

π 10

-7

H/m)

3

)

(

4

r

r

x

v

q

B

o

r

r

r

π

μ

=

Uwaga1

Wielkość B jest pseudowektorem

Uwaga 2

Wektor B podlega superpozycji: B

w

=

Σ

B

i

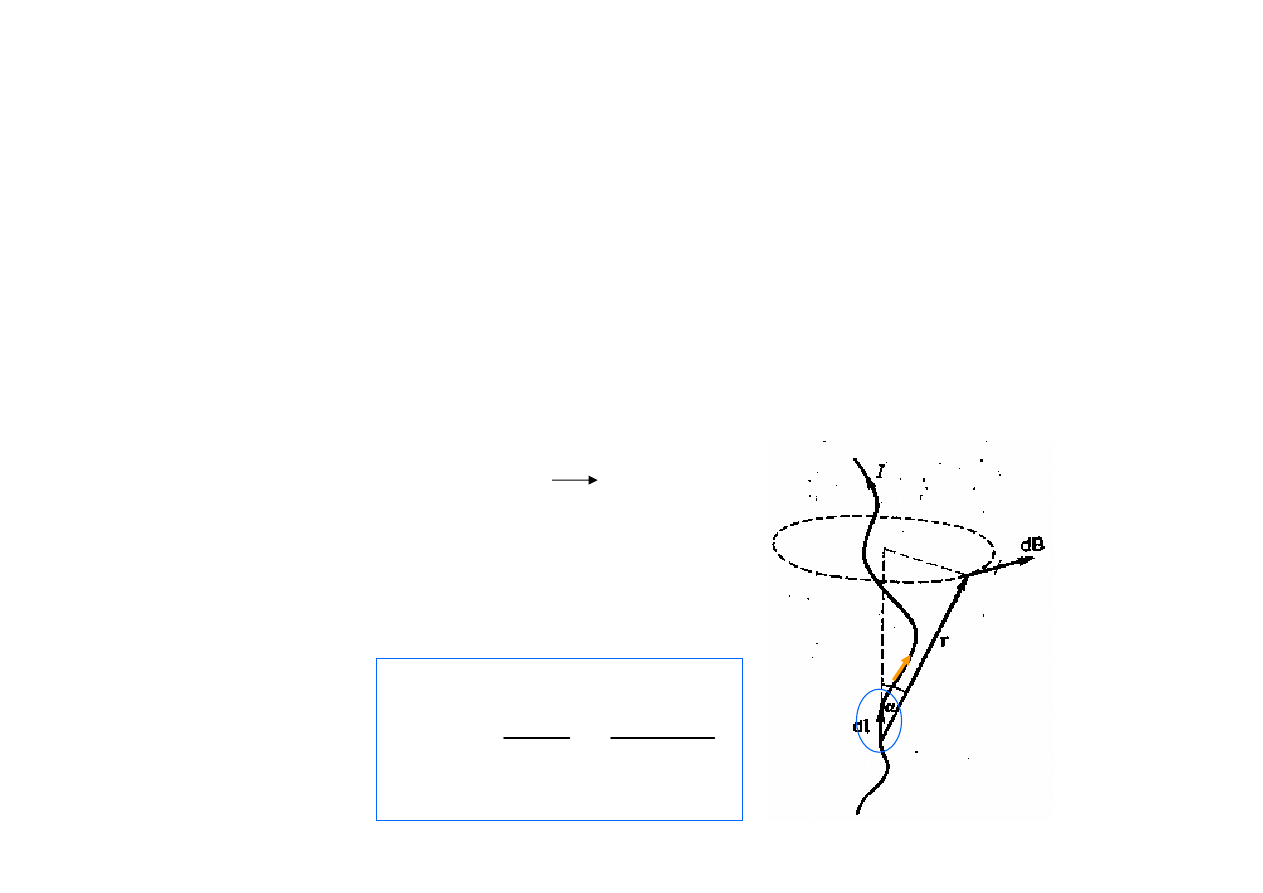
Pole B wytwarzane przez prąd I:

Prawo Biota-Savarta-Laplace’a

(q·v)

(I ·dl)

Dla prądu o natężeniu I:

dB

=

3

4

r

r

x

l

d

I

o

r

r

π

μ

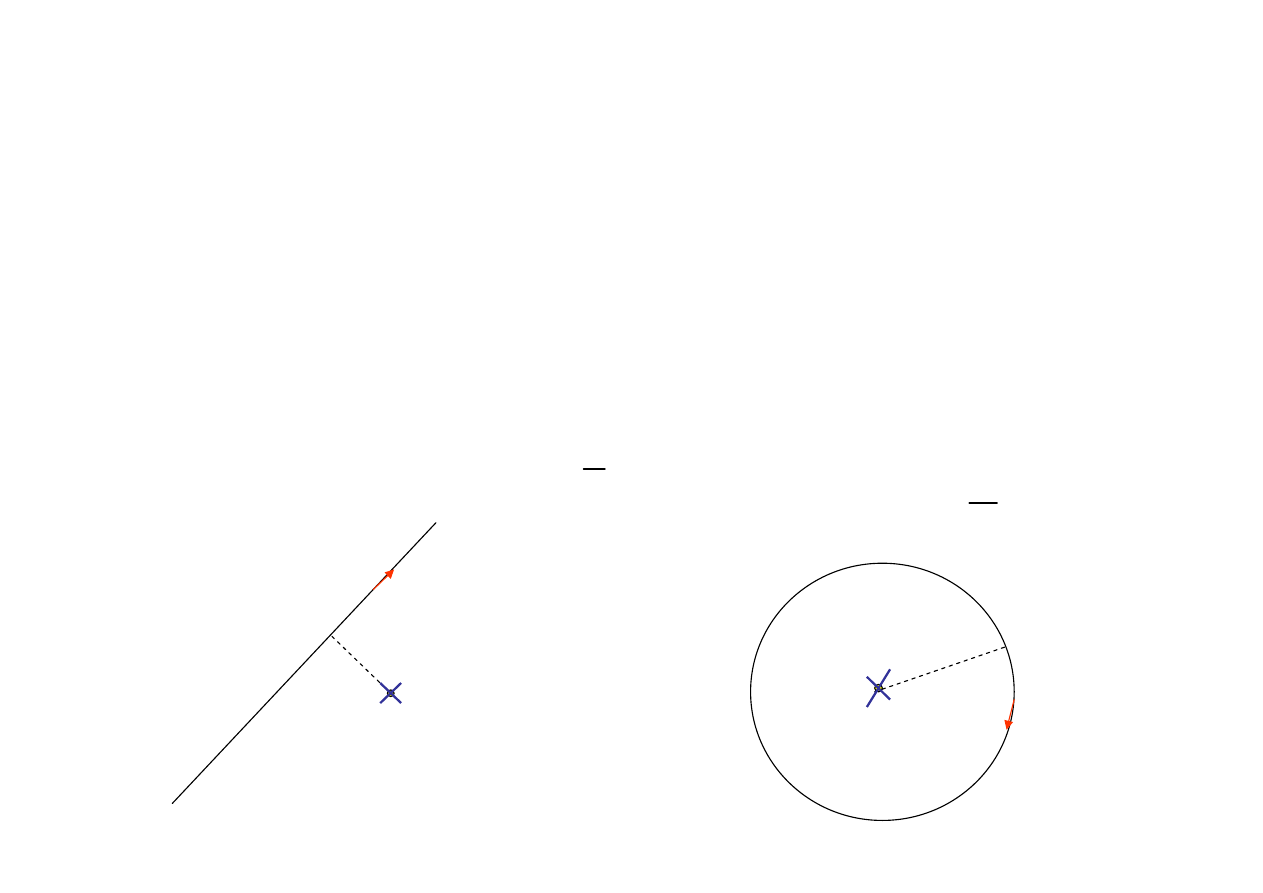
Uwaga

Pole magnetyczne może również być reprezentowane przez linie
pola, równoległe do B

Przykłady źródeł pola magnetycznego

- prąd prosty B=

2(

μ

o

/4

π)

b

I

R

I

B

B

I

b

- prąd kołowy (w środku)

B=

2

π(μ

o

/4

π)

I

R

Siła oddziaływania pola B na poruszający się ładunek q:

obserwacja:

Ładunki elektryczne w ruchu generują pole B

pole B oddziałuje tylko na ładunki elektryczne w ruchu

F

B

= ?

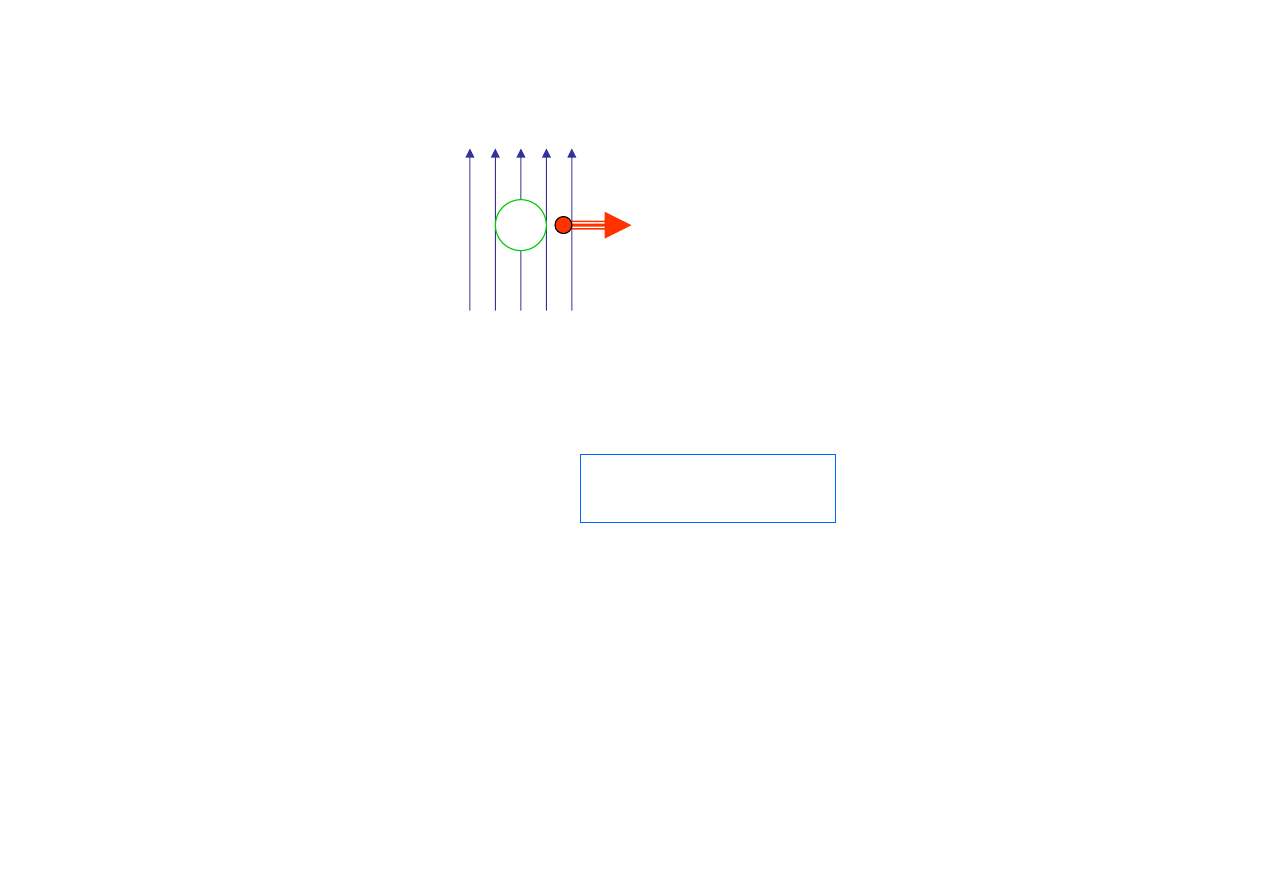
Siła oddziaływania pola B na poruszający się ładunek q

:

Wyniki doświadczenia

(v

<<c)

Siła Lorentza: F

q,B

=q v x B

Uwaga

Siła magnetyczna F

q,B

nie wykonuje pracy nad ładunkiem,

ponieważ

F

q,B

⊥ v

(o ile się pojawia)

v

B

F

•

Gdy prędkość ładunku

v

⊥

jest prostopadła

do pola magnetycznego B, to

F

q,B

= q

v

⊥

x B = q

v

⊥

B

= max

Definicja

Indukcją magnetyczną B nazywamy pseudowektor

B = F

q,B

/q v

⊥

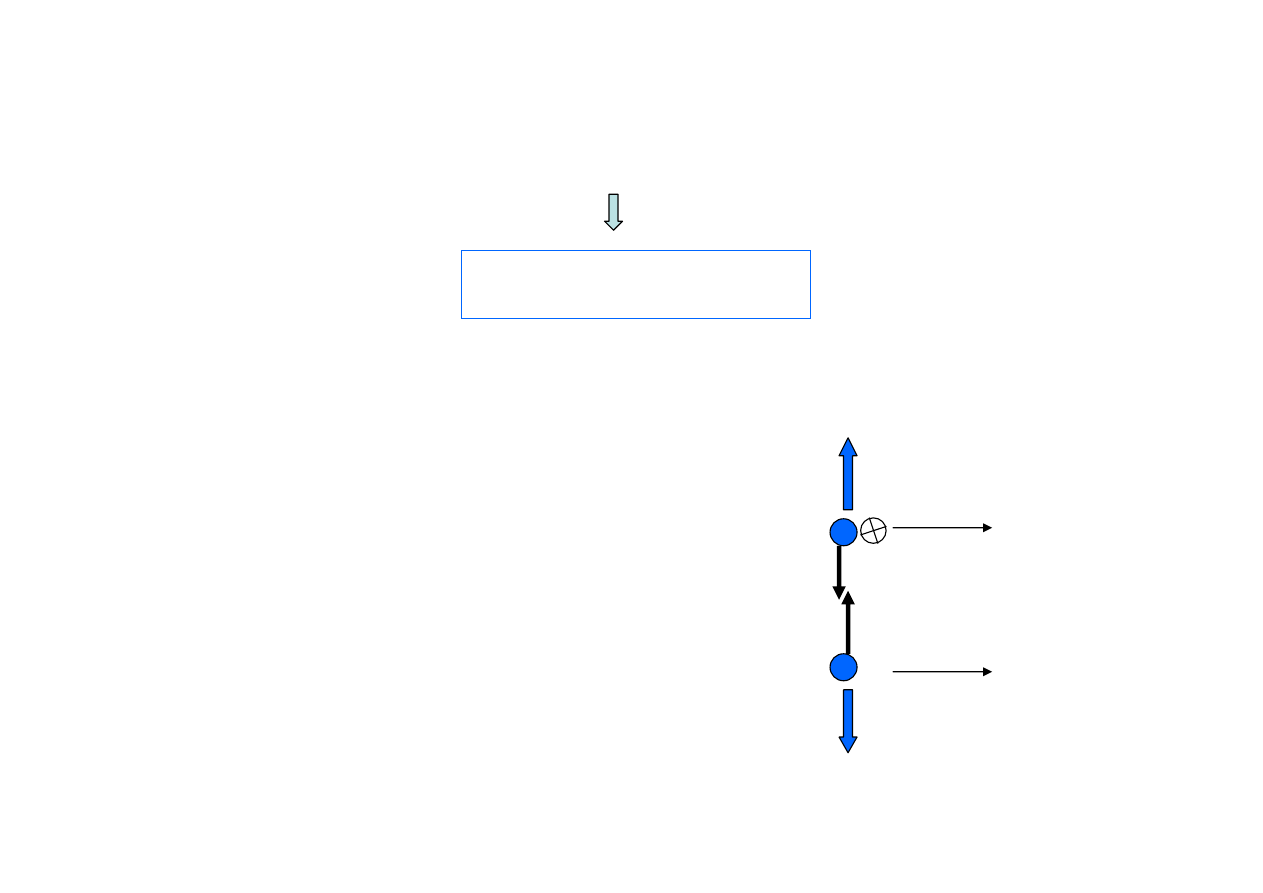
W przypadku, gdy naładowana cząstka porusza się

z prędkością

v

w polach

B

i

E

, doznaje działania siły

F = qE + q v x B

Uwaga :

F

q,B

/

F

e

= (v

2

/c

3

)

v

F

qB

F

e

B

-q

-q

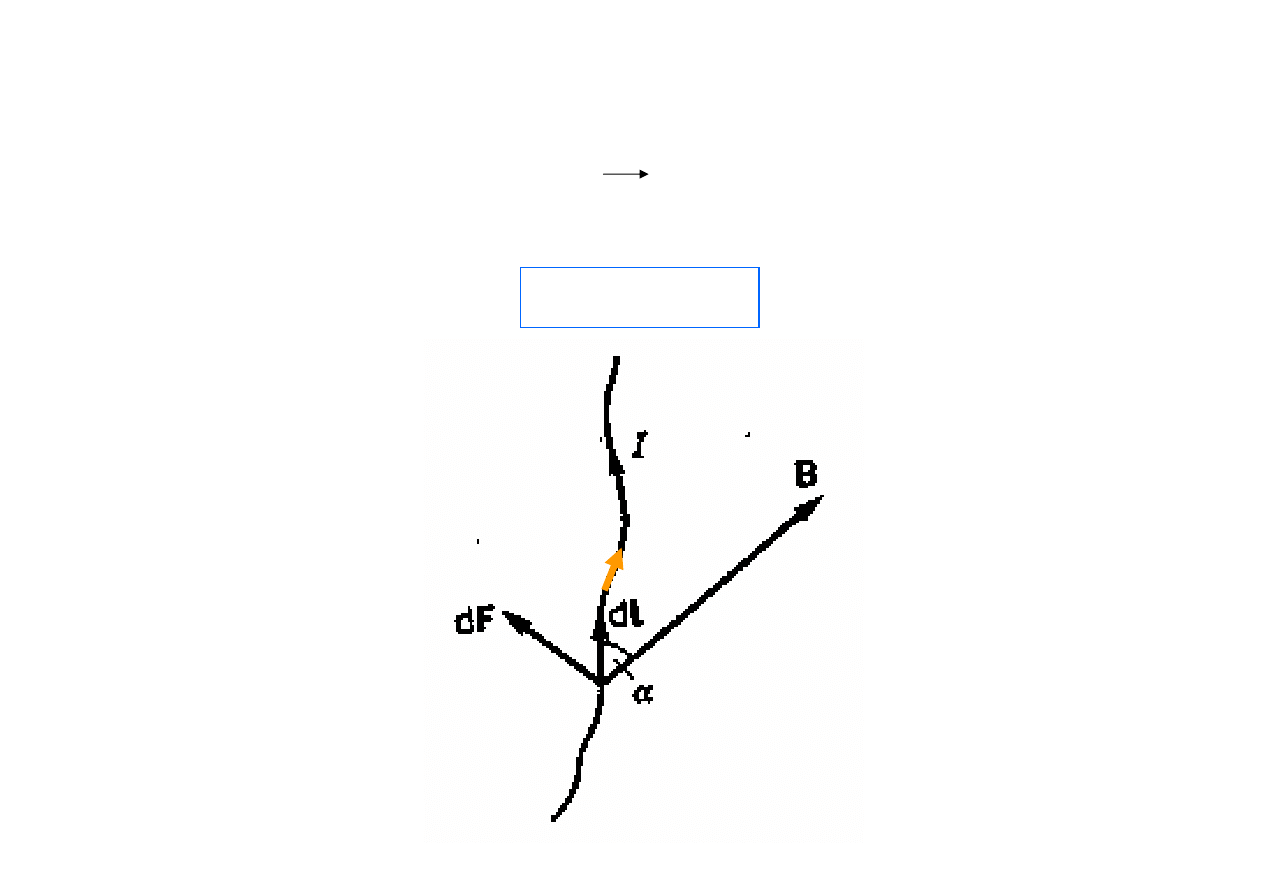
Siła oddziaływania pola B na prąd o natężeniu I

(q

·

v I

·

dl):

Prawo Ampere’a:

dF = I dl x B

Definicja

Momentem magnetycznym p

m

płaskiego obwodu zamkniętego z prądem

I

nazywa się wielkość wektorową

p

m

= I dS

,

(dS = n

+

dS)

n

+

I

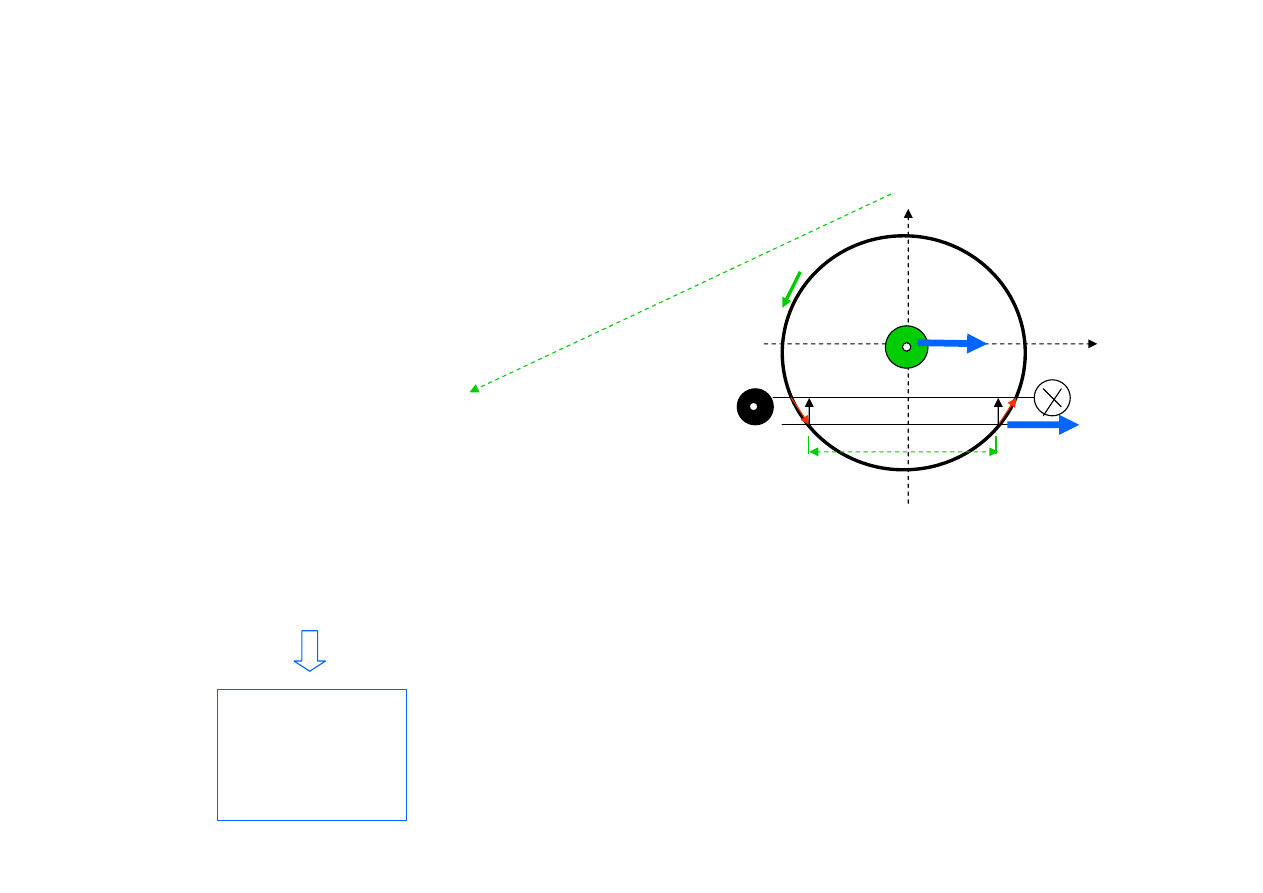
Obwód z prądem w polu magnetycznym

dF = I dlxB, dF = IB dl sin

α = IB

dl cos

β

= (IB

dy)

Moment pary sił dF:
dN = r

FF

x dF,

dN = 2

x

dF = I(2

x

dy

)B

dN = I dSxB

ogólnie N = I S x B ;

p

m

= IS moment magnetyczny

więc N = p

m

xB {analogia do dipola elektrycznego N=

μ

e

xE}

oraz W

m

=-p

m

•B

”

W

e

=-

μ

e

•E

∫

∫

∫

=

=

=

=

B

x

S

I

xB

S

d

I

B

x

S

Id

N

d

N

r

r

r

r

r

r

r

dF =

I

dl

x

B

y

x

I

dl

dF

dF

B

x

n

dy

Prawo Gaussa dla pola B

(twierdzenie o strumieniu wektora B)

Strumień wektora indukcji magnetycznej przez dowolną

powierzchnię zamkniętą jest równy zeru:

φ

B

=

= 0

korzystając z Tw. O-G uzyskuje się

div B (=

∇B) = 0

∫∫

S

S

d

B

r

r

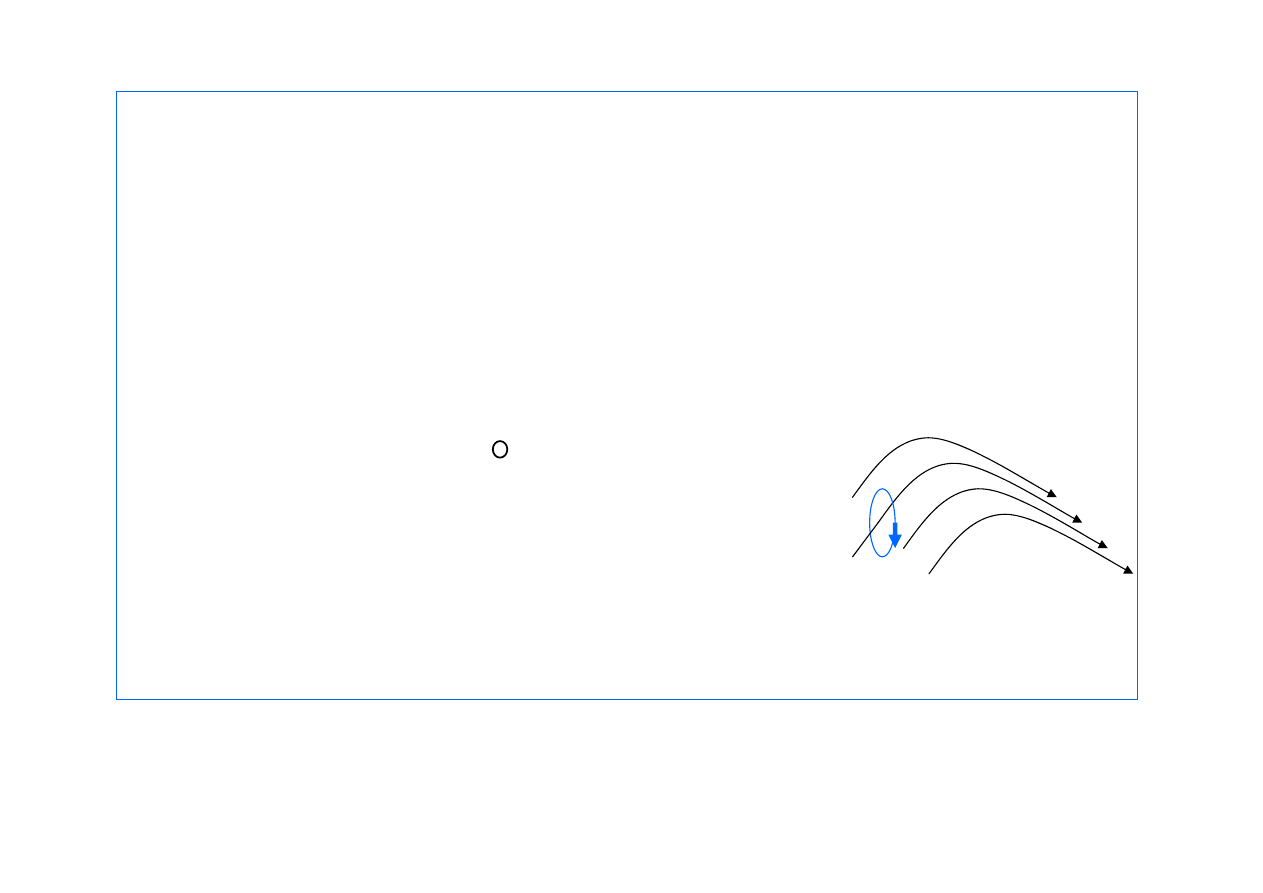
Twierdzenie o cyrkulacji wektora B :

Cyrkulacja wektora indukcji magnetycznej po dowolnym
konturze zamkniętym jest równa - z dokładnością do stałej-
prądowi obejmowanemu przez ten kontur:

korzystając z Tw. S.

uzyskuje się:

rot B (=

∇

xB) =

μ

o

j

∫

Γ

=

I

l

d

B

o

μ

r

r

•

Γ

I

Wniosek

Pole magnetyczne B jest polem wirowym bezźródłowym
Pole magnetyczne B nie jest polem zachowawczym

Uwaga 6

Ze względu na w/w Wniosek
nie istnieje funkcja potencjału* pola magnetycznego

Pole magnetyczne w materii

Namagnesowanie

Założenie Ampere’a:
molekularne prądy kołowe I

cz

o gęstości j

cz

;

pod wpływem

zewnętrznego pola B

o

proces:

chaos

⇒ orientacja,

od prądów I

cz

powstaje pole

B’

(wewnętrzne)

Zatem całkowite pole wewnątrz materii: B =B

o

+ B’

rot B =

μ

o

( j+ j

cz

)

n

+

I

n

+

n

+

I

n

+

n

+

I

n

+

n

+

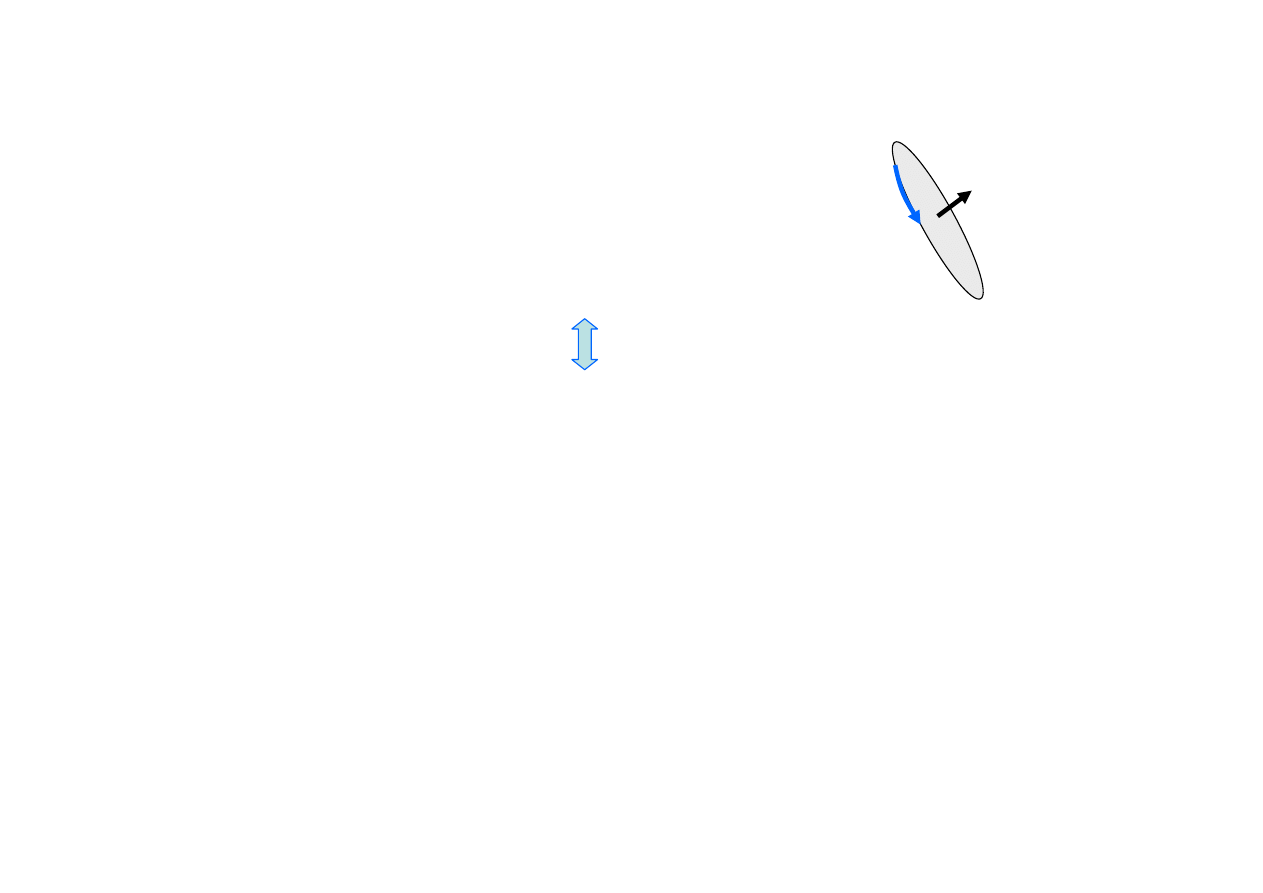
p

m

= I dS ,

(dS = n

+

dS)

Definicja

Namagnesowanie

J

jest sumą momentów magnetycznych jednostki objętości materiału

J = (1/V)

Σ

V

p

m

n

+

I

Definicja

Natężeniem pola magnetycznego H

nazywamy wielkość:

H

= (B

o

/

μ

o

) – J

Założenie:

J =

χ H,

χ

- podatność magnetyczna,

stąd

H = B/

μ

o

–

χ H,

lub

H (1 +

χ) = B/μ

o

B =

μ

o

(

1 +

χ

) H

Definicja 6
Bezwymiarową wielkość

μ

= (

1 +

χ

) nazywa się względną

przenikalnością magnetyczną (przenikalnością magnetyczną) substancji;

wobec tego:

B =

μ

μ

o

H

Uwaga 7

Podatność magnetyczna

χ

może być liczbą dodatnią lub ujemną,

wobec tego przenikalność magnetyczna

μ

może być większa lub mniejsza od jedności

W próżni brak dipoli

→ J = χ H =0

χ = 0

μ = (1 + χ) =1

B =

μ μ

o

H

→

B

o

=

μ

o

H

W magnetyku

→ B = μ μ

o

H ;

μ<1, μ>1

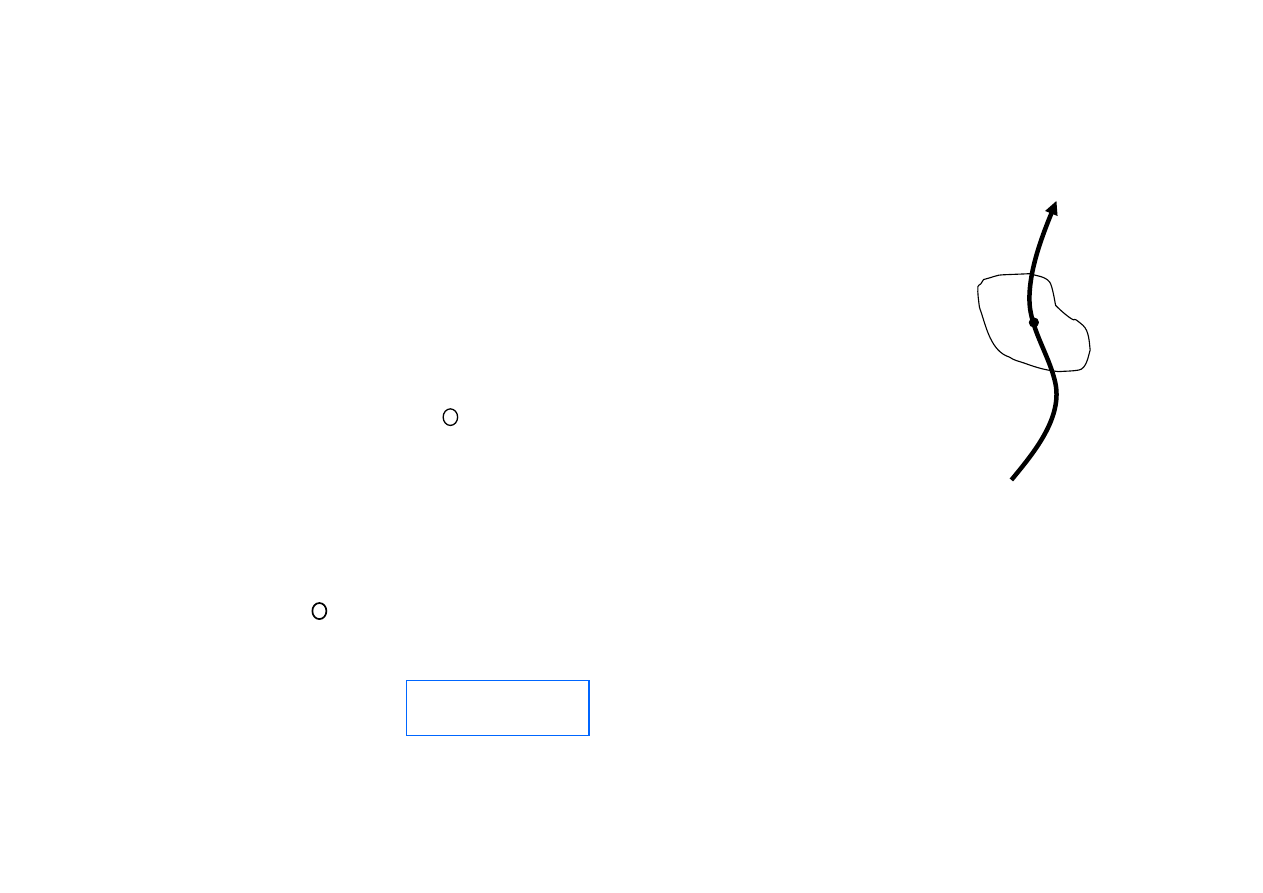
Twierdzenie o cyrkulacji wektora natężenia pola

magnetycznego H

Cyrkulacja

wektora

natężenia pola magnetycznego H

po dowolnym konturze zamkniętym jest równa
algebraicznej sumie prądów (makroskopowych)
obejmowanych przez ten kontur :

H dl = I

(ponieważ cyrkulacja wektora indukcji magnetycznej B

po dowolnym konturze zamkniętym jest równa :

B dl =

μ μ

o

I oraz H = B /

μ μ

o

)

lub (tw.S.): rot H = j

tylko prądy makroskopowe!

∫

L

I

L

∫

L

Twierdzenie o strumieniu

wektora natężenia pola magnetycznego H

Strumień wektora natężenia pola magnetycznego

przez dowolną powierzchnię zamkniętą jest równy zeru:

φ

H

=

= 0

korzystając z tw. O-G uzyskuje się

div H (=

∇H) = 0

∫∫

S

S

d

H

r

r

Rodzaje magnetyków

1. diamagnetyki

⇒ χ< 0, χ ≈ 10

-10

m

3

/mol, (

μ ≤ ≈ 1),

np. woda

μ

=0,999991

2. paramagnetyki

⇒ χ> 0, χ ≈ 10

-10

m

3

/mol, (

μ ≥ ≈ 1),

np. glin m=1,000008

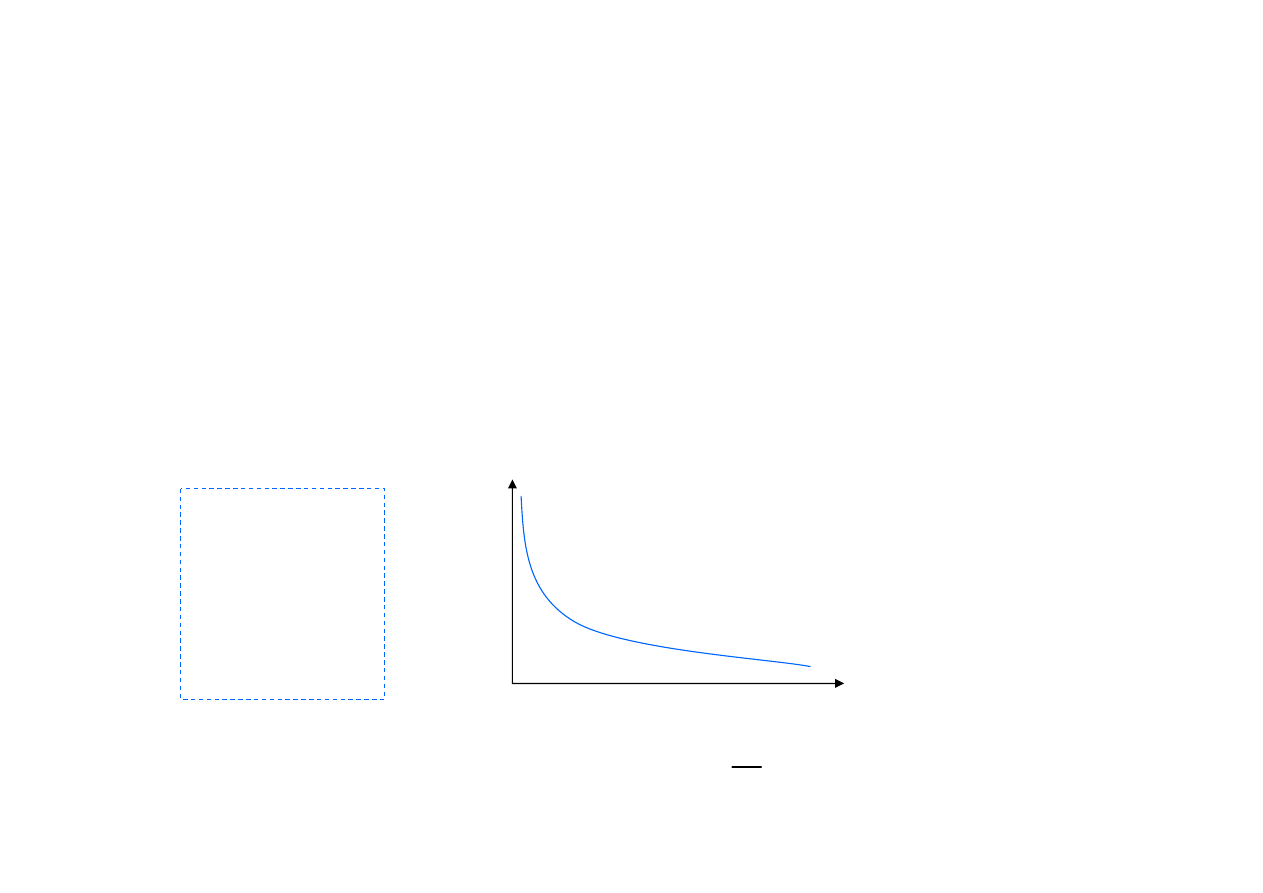
Prawo Curie:

(C – stała Curie)

χ

T

w ośrodku
B =

μ

μ

o

H

w próżni
B =

μ

o

H

T

C

=

χ

χ=

μ

-1

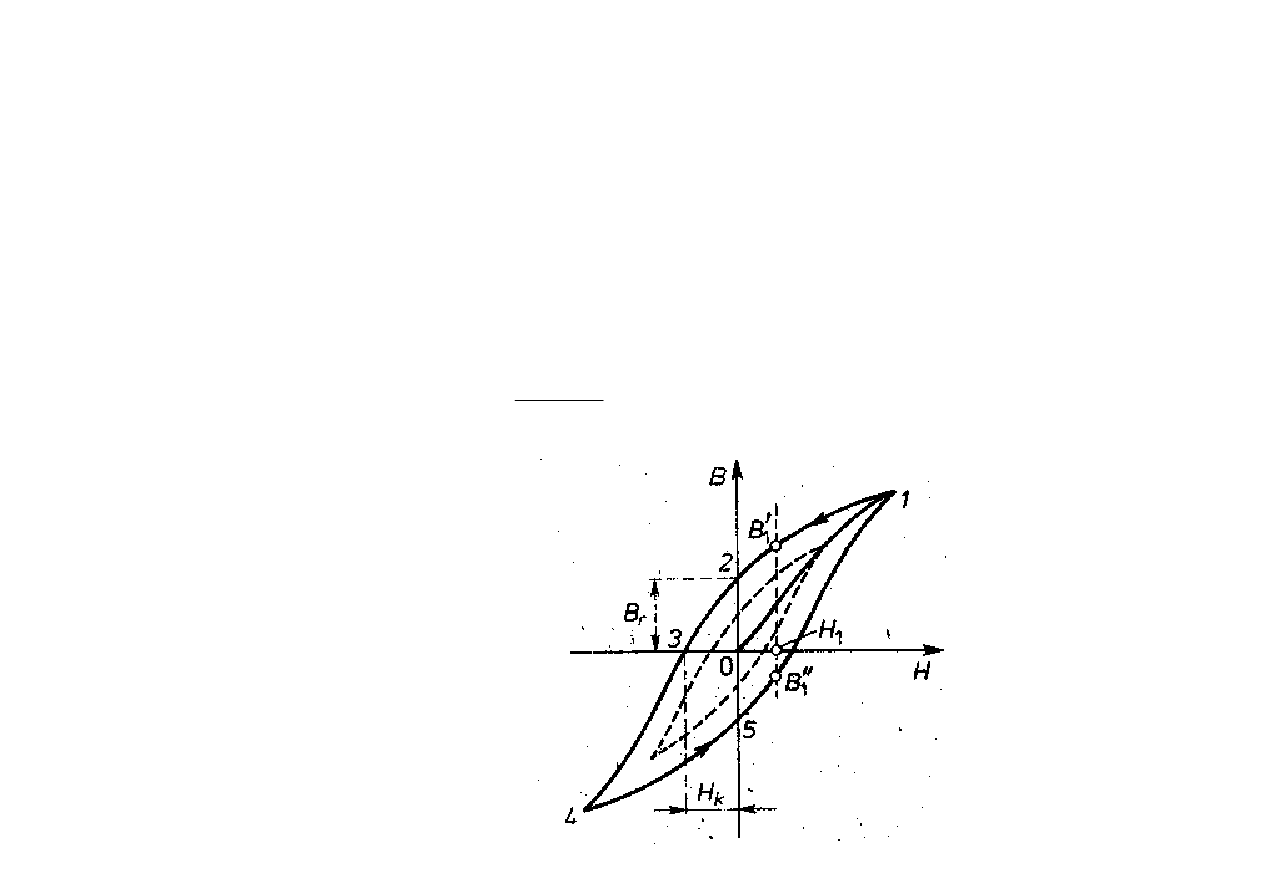
3. Ferromagnetyki

⇒ χ ≈ 1 m

3

/mol,

¾

wysoka przenikalność

μ (kilka tysięcy),

¾

μ(H), t.zn. J(H), B(H), jest funkcją nieliniową,

¾

histereza J(H), B(H).
np. stal

μ

=300 (zależy od natężenia pola)

Prawo Curie-Weissa

,

(T

c

- temperatura Curie)

4. antyferromagnetyki

ferromagnetyk

c

T

T

C
−

=

χ

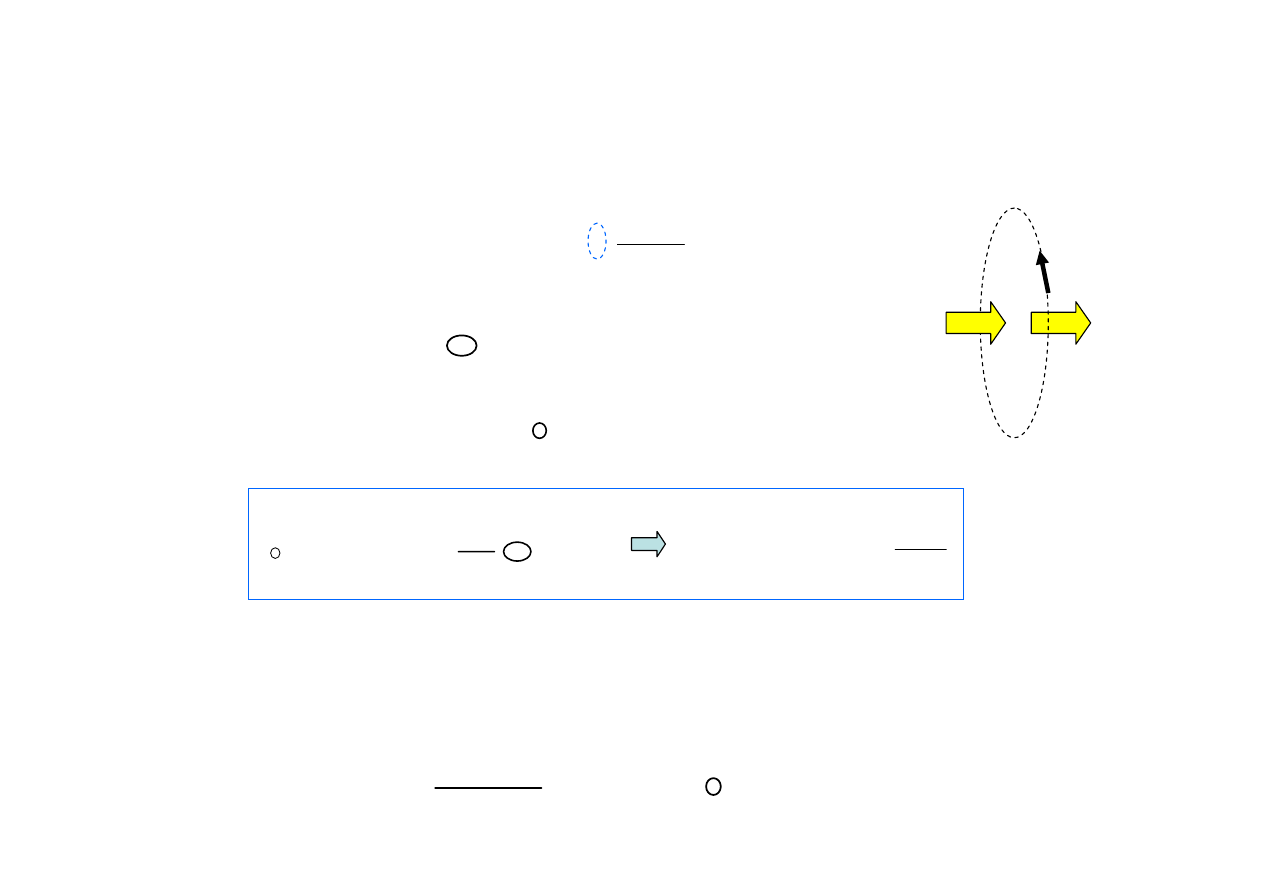
Indukcja elektromagnetyczna

Michael Faraday (1831)

SEM

ind

(=

ΔV

ind

) = -

[volt],

Uwaga

SEM

ind

nie jest pochodzenia elektrostatycznego i nie tworzy

pola potencjalnego:

dt

d

B

Φ

]

/

[

2

m

Wb

S

d

B

S

B

∫∫

=

Φ

L

r

r

l

d

E

r

r

∫

=

Δ

L

ind

ind

V

0

l

d

E

≠

∫

r

r

L

ind

=

Δ

=

Φ

−

ind

B

V

dt

d

Φ

B

L

S

l

d

E

r

r

∫

L

ind

∫∫

−

=

S

S

d

B

dt

d

r

r

t

B

∂

∂

−

=

r

r

ind

E

rot

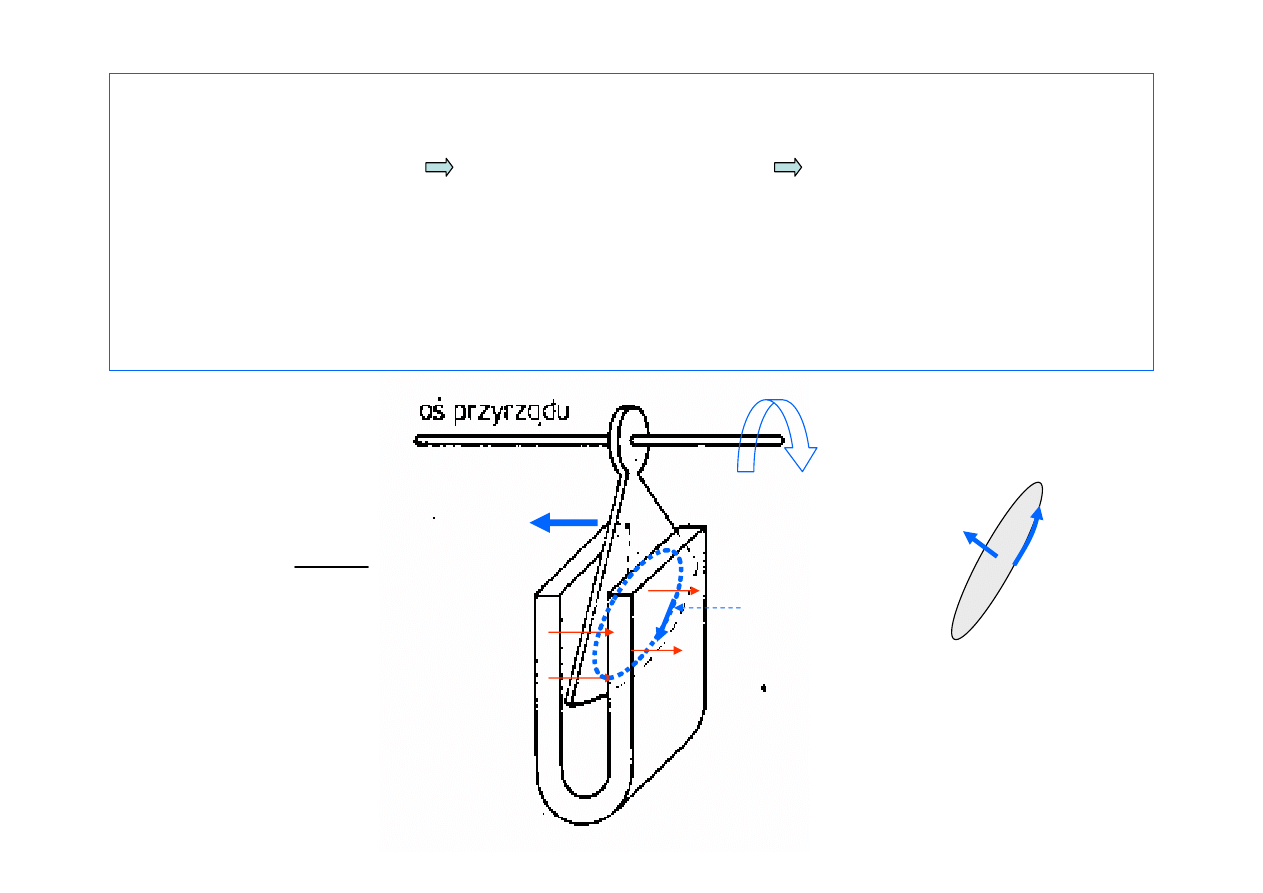
Reguła Lenza

SEM

ind

(=

ΔV

ind

)

(ośrodek przew.

σ

)

prąd indukcyjny

I

ind

Prąd indukcyjny jest zawsze skierowany tak, aby przeciwdziałać

przyczynie, która go wywołuje

(-)

⇒

prądy Foucaulta

B,

Φ

B

SEM

ind

dt

d

SEM

B

ind

Φ

−

=

p

m

W

m

=-p

m

•B

p

m

I

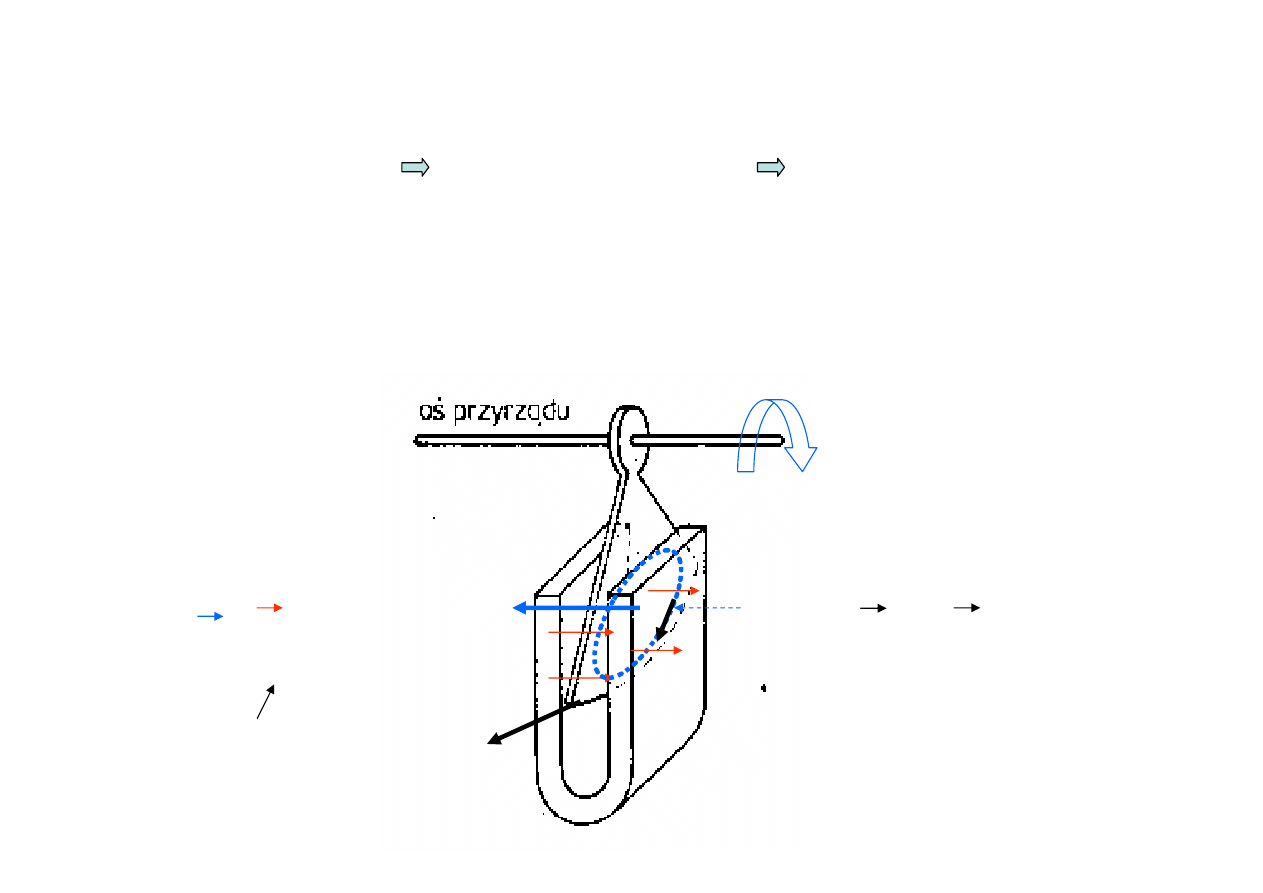
Reguła Lenza

SEM

ind

(=V

ind

)

(ośrodek przew.

σ

)

prąd indukcyjny

I

ind

Prąd indukcyjny jest zawsze skierowany tak, aby przeciwdziałać

przyczynie, która go wywołuje (-)

⇒

prądy Foucaulta

B,

Φ

B

SEM

ind

I

ind

-B

-B, p

m

W

m

=-

p

m

•

B

=

+

p

m

•

B ,

F = -

∇W

F

Zjawisko samoindukcji

dI

⇒ dB ⇒ dφ

B

⇒ SEM

ind

⇒ - dI

ind

w tym samym obwodzie

ponieważ (dla nie-ferromagnetyków):

B

∼ I

⇒

φ = L• I

, L [H-henr]– indukcyjność

obwodu

L=const(I),

zależy od kształtu prądu, tj. obwodu,

⇒

SEM

samoind

= - L

Uwaga
Indukcyjność L zależy od geometrii obwodu (kształtu i rozmiarów);

dt

dI