Analiza widmowa
czyli
powrót na ziemię
Transformata Fouriera
f(t) — dowolna funkcja (dystrybucja)
Transformata Fouriera f(t)
( )
{ }
( )
( )
– j
e
d
j
t
f t
f t
t
F
ω
ω
+∞
∞
=
∫
≜
F
–
∞
∫
Odwrotna transformata Fouriera funkcji F(j
ω
)
( )
( )
{
}
( )
–1
j
d
j
j
e
2π
t
f t
F
F
ω
ω
ω
ω
+∞
−∞
=
=
∫
F
Istnienie i jednoznaczność przekształcenia Fouriera
Twierdzenie 1.
Jeżeli f(t) jest funkcją bezwzględnie całkowalną w przedziale (–
∞
,
∞
),
tzn.
to całka
( )
j
e
d
t
f t
t
ω
∞
−
−∞
∫
( )
d
,
f t
t
∞
−∞
< ∞
∫
jest zbieżna dla wszystkich wartości
ω
. Transformata Fouriera funkcji f(t)
jest ciągłą funkcją
ω
, oraz
−∞
∫
( )
( )
{ }
j
,
F
f t
ω
=
F
( )
lim
j
0.
F
ω
ω
→±∞
=
Bezwzględna całkowalność f(t) jest warunkiem dostatecznym istnienia
transformaty Fouriera.

Twierdzenie 2.
Jeżeli f
1
(t) i f
2
(t) są funkcjami bezwzględnie całkowalnymi, to
( )
{
}
( )
{
}
( )
( )
1
2
1
2
f t
f
t
f t
f
t
=
⇔
=
F
F
1. Ponieważ
( )
( )
∞
∞
Wnioski:
więc wszystkie sygnały o skończonej energii (w szczególności
przebiegi impulsowe) spełniają warunki dostateczne istnienia
transformaty Fouriera.
2. Nie są transformowalne funkcje stałe i okresowe. Będzie
jednak
dla
nich
istnieć
dystrybucyjne
przekształcenie
Fouriera.
( )
( )
2
d
d
f
t
t
f t
t
∞
∞
−∞
−∞
< ∞
⇒
< ∞
∫
∫

Własności przekształcenia Fouriera
Stosować będziemy oznaczenia:
( )
{ }
( )
( )
( )
( )
{ }
( )
( )
( )
j
j
j
j
f t
F
f t
F
g t
G
g t
G
ω
ω
ω
ω
=
⇔
=
⇔
⇌
⇌
F
F
1. Liniowość
( )
( )
( )
( )
1
2
1
2
j
j
a f t
a g t
a F
a G
ω
ω
+
+
⇌
( )
( )
( )
( )
1
2
1
2
⇌
2. Przesunięcie w dziedzinie czasu
(
)
( )
0
j
0
j
e
t
f t
t
F
ω
ω
−
−
⇌
3. Przesunięcie w dziedzinie
ω
( )
(
)
0
j
0
0
e
j
,
t
f t
F
ω
ω ω
ω
−
∈
⇌
ℝ
4. Różniczkowanie (dystrybucyjne) w dziedzinie czasu
( )
( )
d
j
j
d
f t
F
t
ω
ω
⇌
5. Splot w dziedzinie czasu
( ) ( )
( ) (
)
( ) ( )
d
j
j
f t
g t
f
g t
F
G
τ
τ τ
ω
ω
∞
−∞
∗
=
−
∫
⇌
6. Mnożenie w dziedzinie czasu
( ) ( )
( ) ( )
( ) (
)
1
1
j
j
j
j
d
f t g t
F
G
F
G
ω
ω
η
ω η
η
∞
∗
=
−
∫
⇌
( ) ( )
( ) ( )
( ) (
)
1
1
j
j
j
j
d
2π
2π
f t g t
F
G
F
G
ω
ω
η
ω η
η
−∞
∗
=
−
∫
⇌
7. Symetria
( )
( )
j
2π
F
t
f
ω
−
⇌
8. Zmiana skali czasu
( )
(
)
j
,
0
t
f
a F
a
a
a
ω
≠
⇌
Przykład 1.
( ) ( )
δ
f t
t
=
( )
( )
{ }
( )
j
j
δ
e
d
1
t
F
f t
t
t
ω
ω
∞
−
−∞
=
=
=
∫
F
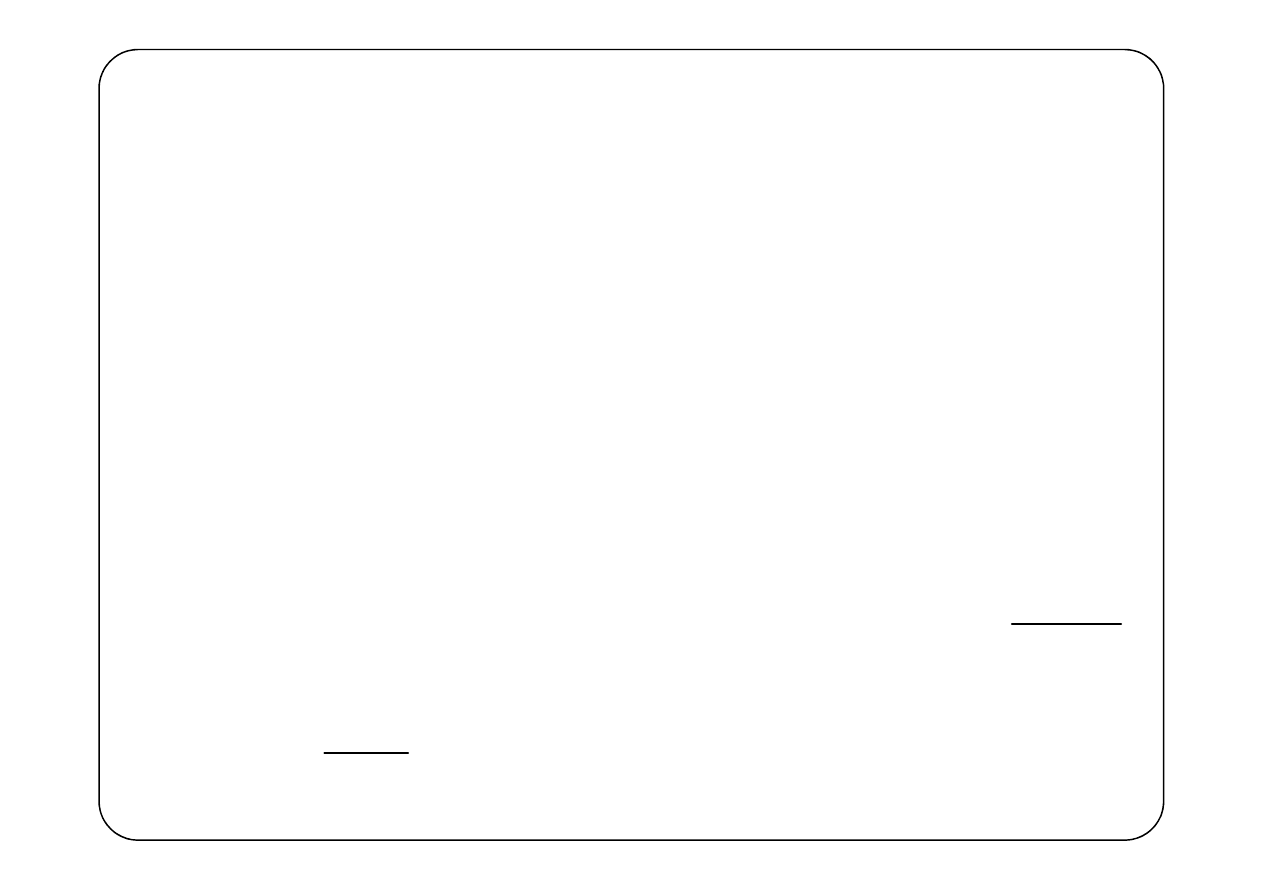
Przykład 2.
( )
( )
e
,
0
at
f t
t
a
−
=
>
1
( )
( )
{ }
( )
(
)
j
j
0
1
j
e
e
d
e
d
j
a
t
a t
t
F
f t
t
t
t
a
ω
ω
ω
ω
∞
∞
− +
−
−
−∞
=
=
=
= +
∫
∫
1
F
( )
{ }
1
f t
s
a
= +
L
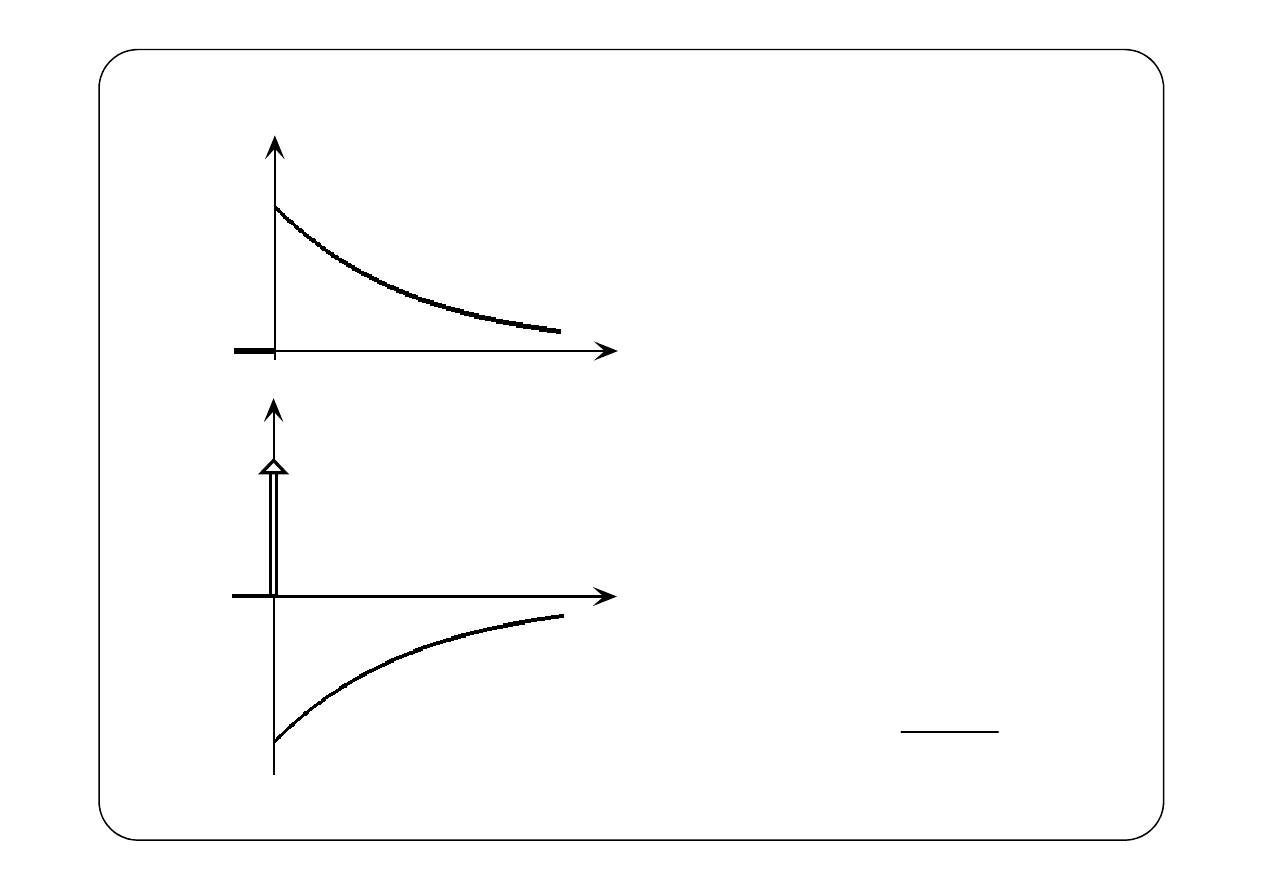
( )
f
t
′
t
1
( )
f t
e
a t
−
⇌
( )
j
F
ω
( )
f
t
′
Inaczej
⇌
( )
( )
j
j
1
j
F
aF
ω
ω
ω
= −
( )
1
j
j
F
a
ω
ω
= +
t
– a
e
a t
a
−
−
( )
δ t
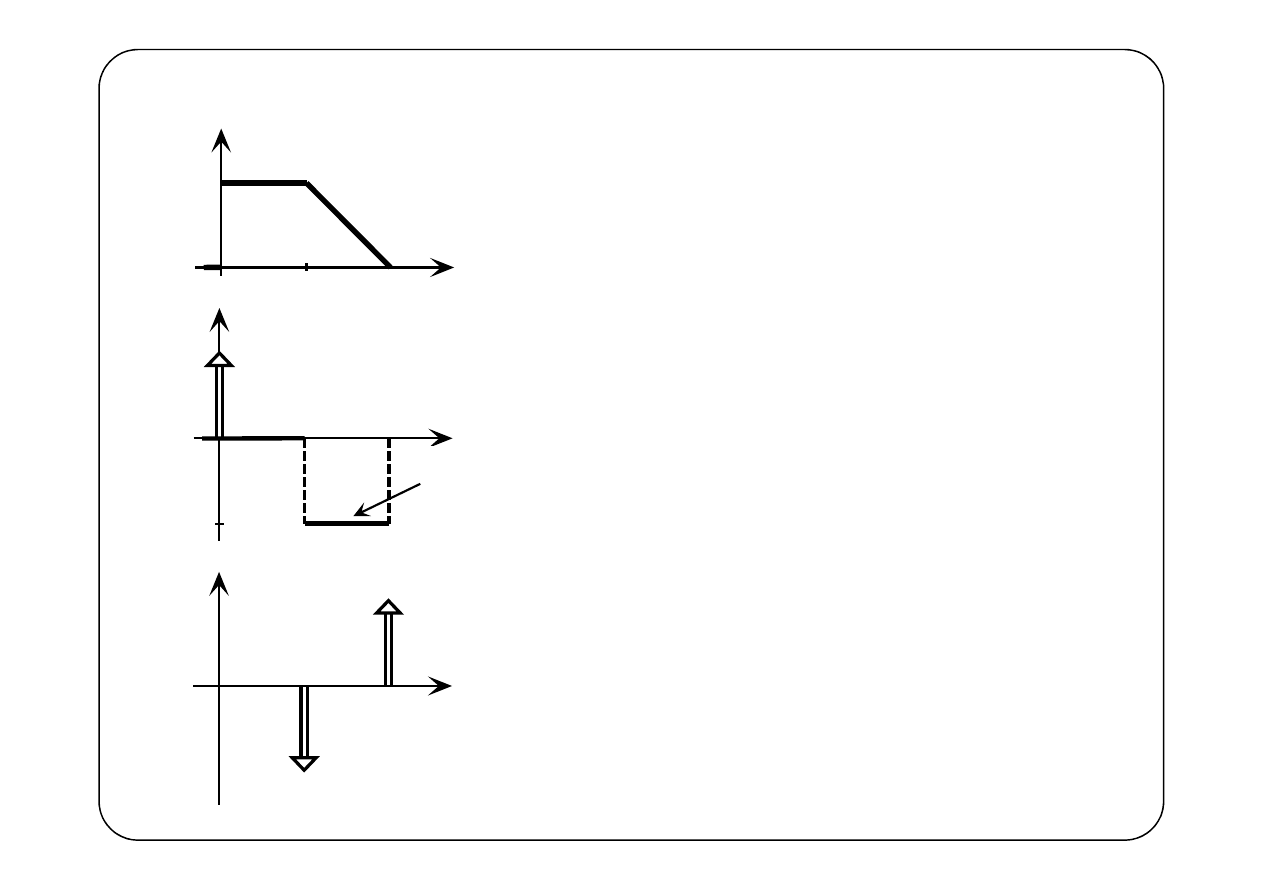
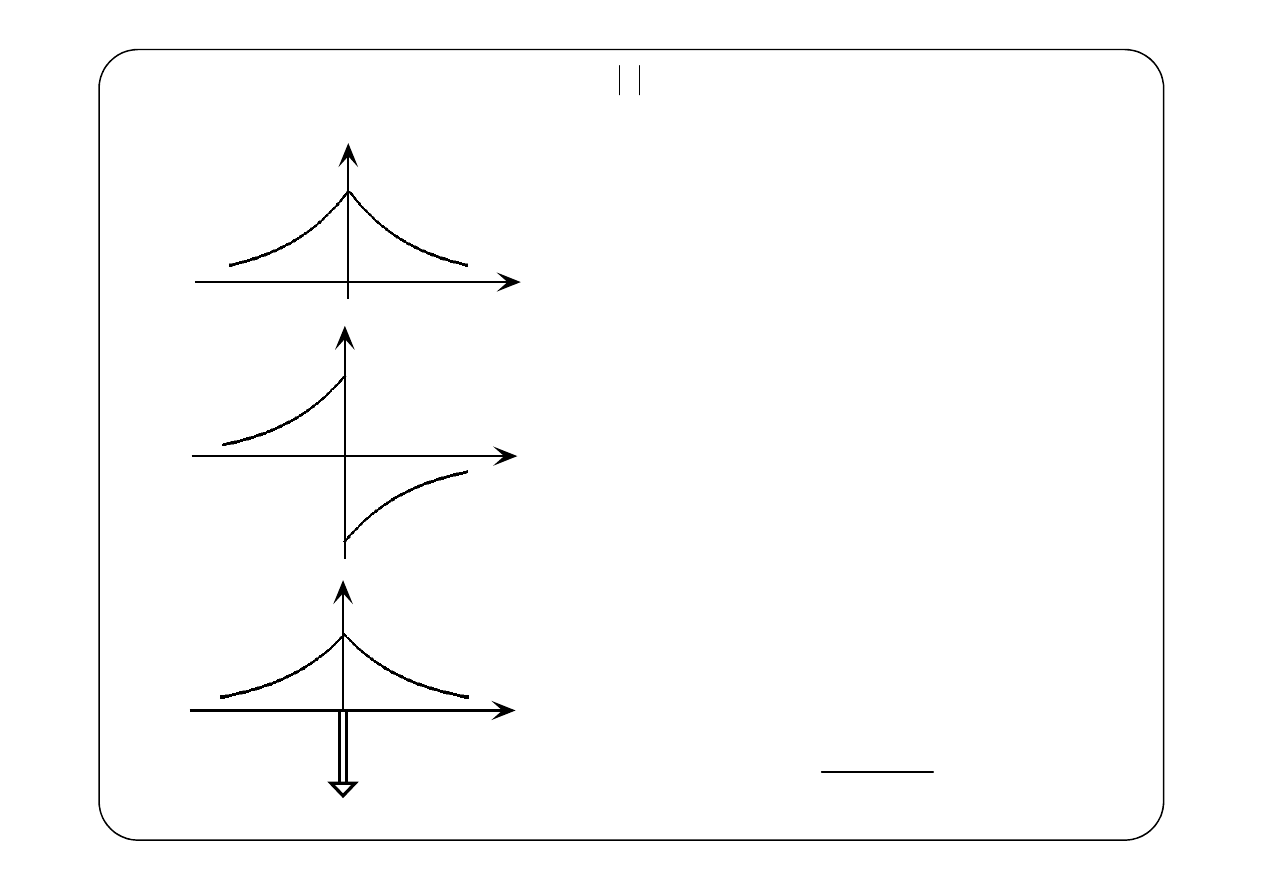
Przykład 3.
1
2
1
f(t)
t
2
1
f
'
(t)
t
( )
δ t
⇌
( )
j
F
ω
⇌
( )
( )
j
j
1
j
F
G
ω
ω
ω
= +
–1
( )
g t
2
1
t
( )
g t
′
( )
δ
1
t
−
−
(
)
δ
2
t
−
⇌
( )
( )
j
j
1
j
F
G
ω
ω
ω
= +
( )
( )
{ }
j
G
g t
ω
=
F
⇌
( )
j
2 j
j
j
e
e
G
ω
ω
ω
ω
−
−
= −
+
( )
j
2 j
e
e
j
j
G
ω
ω
ω
ω
−
−
−
+
=
( )
j
2 j
e
e
j
j
1
j
F
ω
ω
ω
ω
ω
−
−
−
+
= +
( )
j
2 j
j
2 j
j
e
e
1
e
e
j
F
ω
ω
ω
ω
ω
ω
−
−
−
−
−
+
−
+
=
+
=
( )
( )
2
2
j
e
e
1
e
e
j
j
j
F
ω
ω
ω
ω
ω
−
+
−
+
=
+
=
−
( )
{ }
2
2
2
2
2
1
e
e
e
e
s
s
s
s
s
f t
s
s
s
s
−
−
−
−
−
+
= −
+
=
L
( )
f t
t
e
a t
−
e
a t
1
Przykład 4.
( )
f
t
′
t
e
a t
a
a
( )
e
a t
f t
−
=
⇌
( )
j
F
ω
⇌
( )
j
j
F
ω
ω
e
a t
a
−
−
–a
( )
f
t
′′
t
2
e
a t
a
−
2
e
a t
a
( )
2 δ
a
t
−
⇌
( )
j
j
F
ω
ω
⇌
( )
( )
2
2
j
2
j
F
a
a F
ω
ω
ω
−
= − +
( )
2
2
2
j
a
F
a
ω
ω
=
+
Związek z transformatą Laplace’a
( )
{ }
( )
( )
( )
{ }
( )
( )
0
j
e
d
e
d
j
s t
t
f t
f t
t
F s
f t
f t
t
F
ω
ω
∞
−
−
∞
−
−∞
=
=
=
=
∫
∫
L
F
Jeżeli
( )
0
dla
0
f t
t
≡
<
to
to
( )
( )
j
j
s
F
F s
ω
ω
=
=
pod warunkiem, że oś j
ω
ωω
ω
należy do obszaru zbieżności
transformaty Laplace’a.
Warunek ten jest spełniony gdy
czyli jest warunkiem istnienia transformaty Fouriera.
( )
0
d
,
f t
t
∞
−
< ∞
∫
Twierdzenie
Jeżeli f(t) jest funkcją przyczynową, czyli
a jej transformatą Laplace’a jest wymierna funkcja
której mianownik jest wielomianem Hurwitza (czyli F(s) nie ma
biegunów w domkniętej prawej półpłaszczyźnie zmiennej s), to
istnieje transformata Fouriera funkcji f(t) i jest równa
( )
0
dla
0,
f t
t
≡
<
( )
( )
{ }
,
F s
f t
=
L
( )
( )
{ }
( )
j
j
s
F
f t
F s
ω
ω
=
=
=
F
( )
( )
( )
( )
1
1
e
,
j
1
1
j
t
f t
t
F s
F
s
ω
ω
−
=
=
⇒
=
+
+
1
( )
( )
( )
( )
2
2
2
2
j
2
e
cos
,
j
4
5
5
4 j
t
s
f t
t
t
F s
F
s
s
ω
ω
ω
ω
−
+
+
=
⋅
=
⇒
=
+
+
−
+
1
( )
( )
( )
(
)
( )
(
)
3
10
4
4
6
6
e
,
j
10
10
j
t
f t
t
t
F s
F
s
ω
ω
−
=
=
⇒
=
+
+
1
( )
( )
( )
( )
( )
( )
( ) ( )
( )
2
2
1
sin
,
1
1
e
,
2
1
,
t
f t
t
t
F s
s
f t
t
F s
s
f t
t
F s
s
=
⋅
=
+
=
=
−
=
=
1
1
1
Transformaty Fouriera nie istnieją.
Nie wolno
podstawić s = j
ω
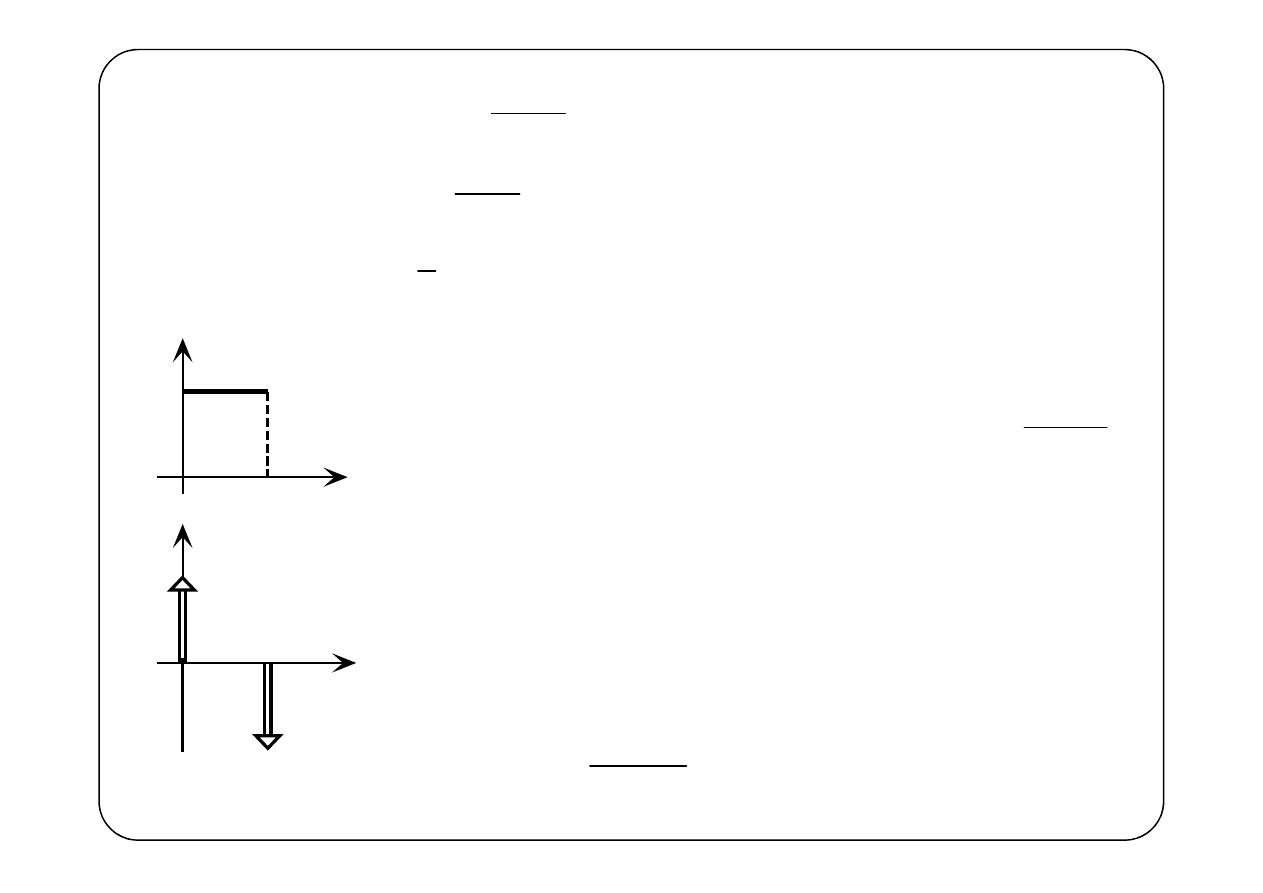
t
1
( )
f t
⇌
( )
j
F
ω
( )
{ }
( )
1 e
s
f t
F s
s
−
−
=
=
L
t
1
( )
f
t
′
t
1
( )
δ t
( )
δ
1
t
−
−
⇌
⇌
( )
j
F
ω
( )
j
j
j
1 e
F
ω
ω
ω
−
= −
( )
j
1 e
j
j
F
ω
ω
ω
−
−
=
( )
{ }
( )
s
L
( )
0
lim
1
s
F s
→
=
F(s) nie jest funkcją wymierną
Punkt s = 0 nie jest
biegunem funkcji F(s)
Interpretacja fizyczna
( )
( )
( )
(
)
(
)
{
}
j
j
j
–1
d
d
d
j
e
j
e
j
e
2π
2π
2π
j
t
t
t
f
t
F
F
F
F
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
∞
∞
∞
−
→−
−∞
−∞
−∞
∗
∗
∗
∗
∗
=
=
=
−
=
=
−
∫
∫
∫
F
Jeżeli
( )
( )
f t
f
t
∗
=
to
to
(
)
( )
( )
(
)
j
j
czyli
j
j
F
F
F
F
ω
ω
ω
ω
∗
∗
−
=
=
−
(funkcja hermitowska zmiennej rzeczywistej
ω
)
( )
( )
( )
( )
( )
j
j
j
e
,
arg
j
F
F
F
ξ ω
ω
ω
ξ ω
ω
=
=
( )
(
)
( )
( )
j
j
F
F
ω
ω
ξ ω
ξ ω
=
−
= − −
funkcja parzysta
funkcja nieparzysta
( )
( )
( )
( )
( )
( )
(
)
( )
( )
( )
( )
( )
( )
(
)
( )
(
)
( )
( )
0
j
j
j
j
j
0
0
j
j
j
j
0
j
j
0
0
d
d
d
j
e
j
e
e
j
e
e
2π
2π
2π
d
d
j
e
e
j
e
e
2π
2π
d
d
j
e
e
2
j
cos
2π
2π
t
t
t
t
t
f t
F
F
F
F
F
F
F
ξ ω
ξ ω
ω
ω
ω
ξ ω
ξ ω
ω
ω
ω ξ ω
ω ξ ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω ξ ω
∞
∞
−∞
−∞
∞
−
−
∞
∞
∞
+
−
+
=
=
+
=
−
=
−
+
=
=
+
=
+
∫
∫
∫
∫
∫
∫
∫
Funkcję f(t) można przedstawić jako nieskończoną, nieprzeliczalną
sumę przebiegów sinusoidalnych o ,,amplitudach”
(
) ( )
d
π
j
,
F
ω
ω
sumę przebiegów sinusoidalnych o ,,amplitudach”
i zmieniających się w sposób ciągły pulsacjach
ω
i fazach
początkowych
ξ
(
ω
).
(
) ( )
d
π
j
,
F
ω
ω
( )
( )
( )
j
j
F
F
ω
ω
ξ ω
— zespolone widmo sygnału f(t)
— widmo amplitudowe (widmowa gęstość amplitudy)
— widmo fazowe
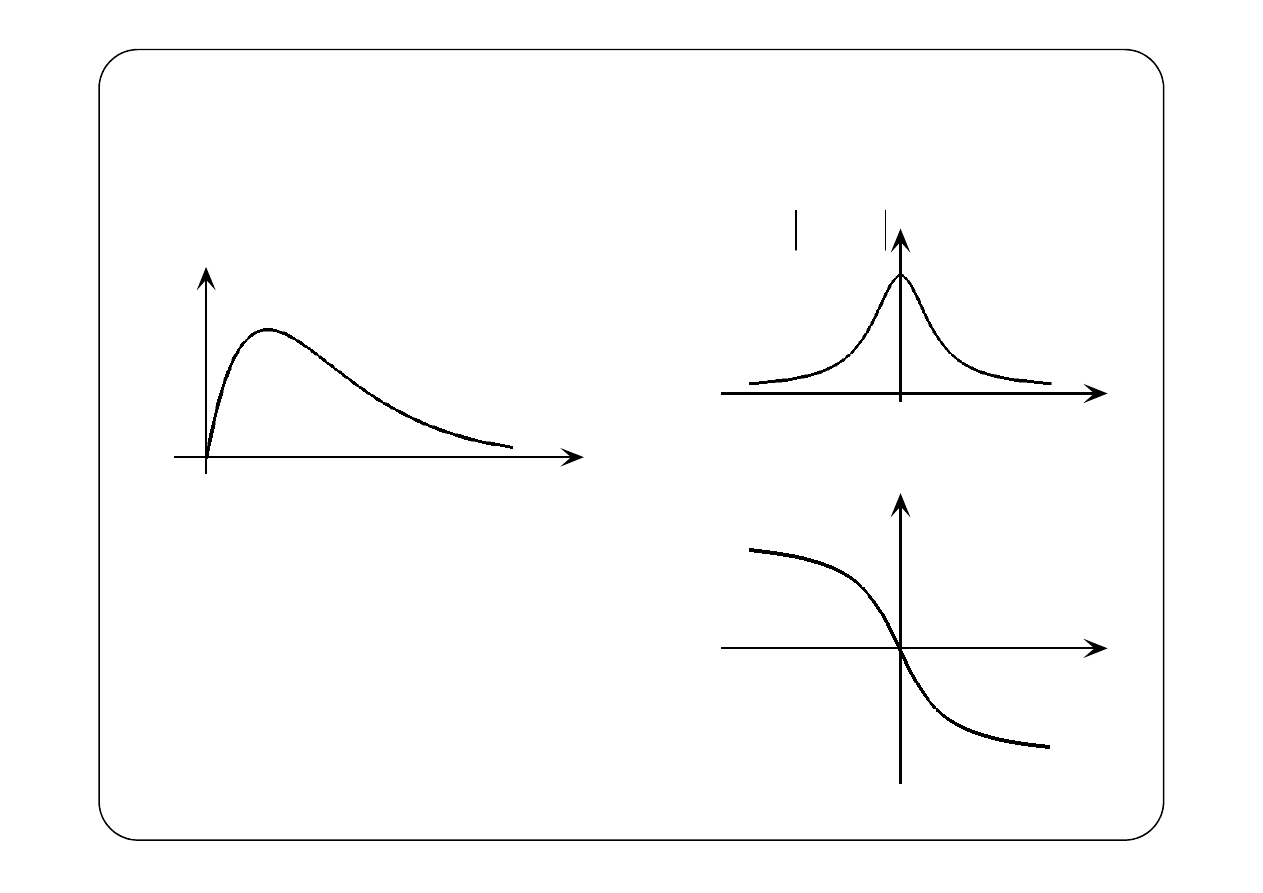
( )
f t
t
( )
j
F
ω
ω
Alternatywny opis sygnałów
W dziedzinie czasu
W dziedzinie częstotliwości
( )
ξ ω
ω

Energia sygnału
( )
2
d
W
f
t
t
∞
−∞
∫
≜
( ) ( )
( )
( )
( ) ( )
( )
( )
j
j
j
d
d
j
e
d
2π
d
d
j
e
d
j
e
d
2π
2π
t
t
t
W
f t f
t
t
f t
F
t
f t F
t
F
f t
t
ω
ω
ω
ω
ω
ω
ω
ω
ω
∞
∞
∞
−∞
−∞
−∞
∞ ∞
∞
∞
−
−
−∞ −∞
−∞
−∞
∗
∗
∗
∗
=
=
=
=
=
=
∫
∫
∫
∫ ∫
∫
∫
( ) ( )
( )
2
2π
2π
d
d
j
j
j
2π
2π
F
F
F
ω
ω
ω
ω
ω
−∞ −∞
−∞
−∞
∞
∞
−∞
−∞
∗
=
=
∫
∫
( )
( )
( )
2
2
2
0
d
d
d
j
2
j
2π
2π
f
t
t
F
F
ω
ω
ω
ω
∞
∞
∞
−∞
−∞
=
=
∫
∫
∫
Równość Parsevala

( )
2
j
2π
F
ω
— widmowa gęstość energii
( )
2
j
2π
F
ω
ω
ω
2
ω
−
1
ω
−
1
ω
2
ω
Energia sygnału — powierzchnia pod krzywą
Energia zawarta w paśmie (
ω
1
,
ω
2
)
( )
2
1
2
d
2
j
2π
W
F
ω
ω
ω
ω
∆ =
∫
Efektywna szerokość pasma sygnału — przedział pulsacji,
w którym zawarta jest założona część całkowitej energii sygnału,
czyli
ω
g
tak wybrane, aby
( )
( )
g
g
g
2
2
0
d
d
j
2
j
2π
2π
F
F
W
ω
ω
ω
ω
ω
ω
ω
κ
−
=
≥
∫
∫
Zwykle przyjmuje się
(
)
0, 9 0, 99
κ
=
÷
Przykład
1
∞
−
∫
( )
( )
e
,
0,
at
f t
t
a
−
=
>
1
2
0
1
e
d
2
at
W
t
a
−
=
=
∫
( )
( )
2
2
2
1
1
j
,
j
,
j
F
F
a
a
ω
ω
ω
ω
=
=
+
+
2
2
d
1
arc tg
a
a
a
ω
ω
ω
=
+
∫
( )
g
g
2
2
0
1
d
1
π
2
tg
2π
2
2
a
a
a
ω
ω κ
ω
κ
ω
≥
⇒
≥
+
∫
g
g
0,95
12, 7
0,99
63, 7
a
a
κ
ω
κ
ω
=
⇒
≥
=
⇒
≥
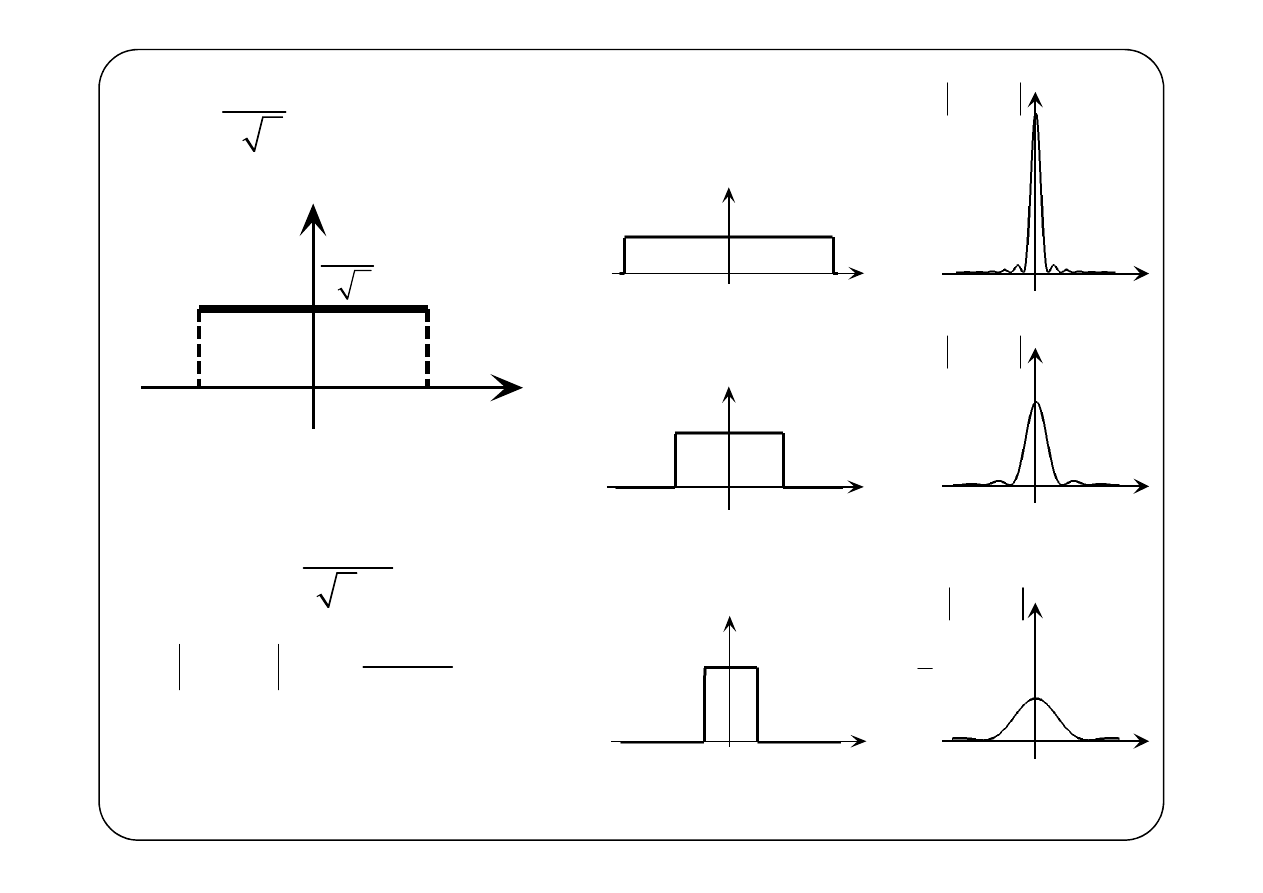
( )
f t
( )
f t
t
( )
2
j
F
ω
( )
2
j
F
ω
2
a
=
1
a
=
ω
( )
(
) (
)
1
2
f t
t
a
t
a
a
=
+ −
−
1
1
( )
f t
1
2 a
a
−
a
t
( )
f t
t
t
( )
2
j
F
ω
1
2
a
=
ω
ω
1
W
=
( )
( )
( )
2
2
sin
j
sin
j
a
F
a
a
F
a
a
ω
ω
ω
ω
ω
ω
=
=
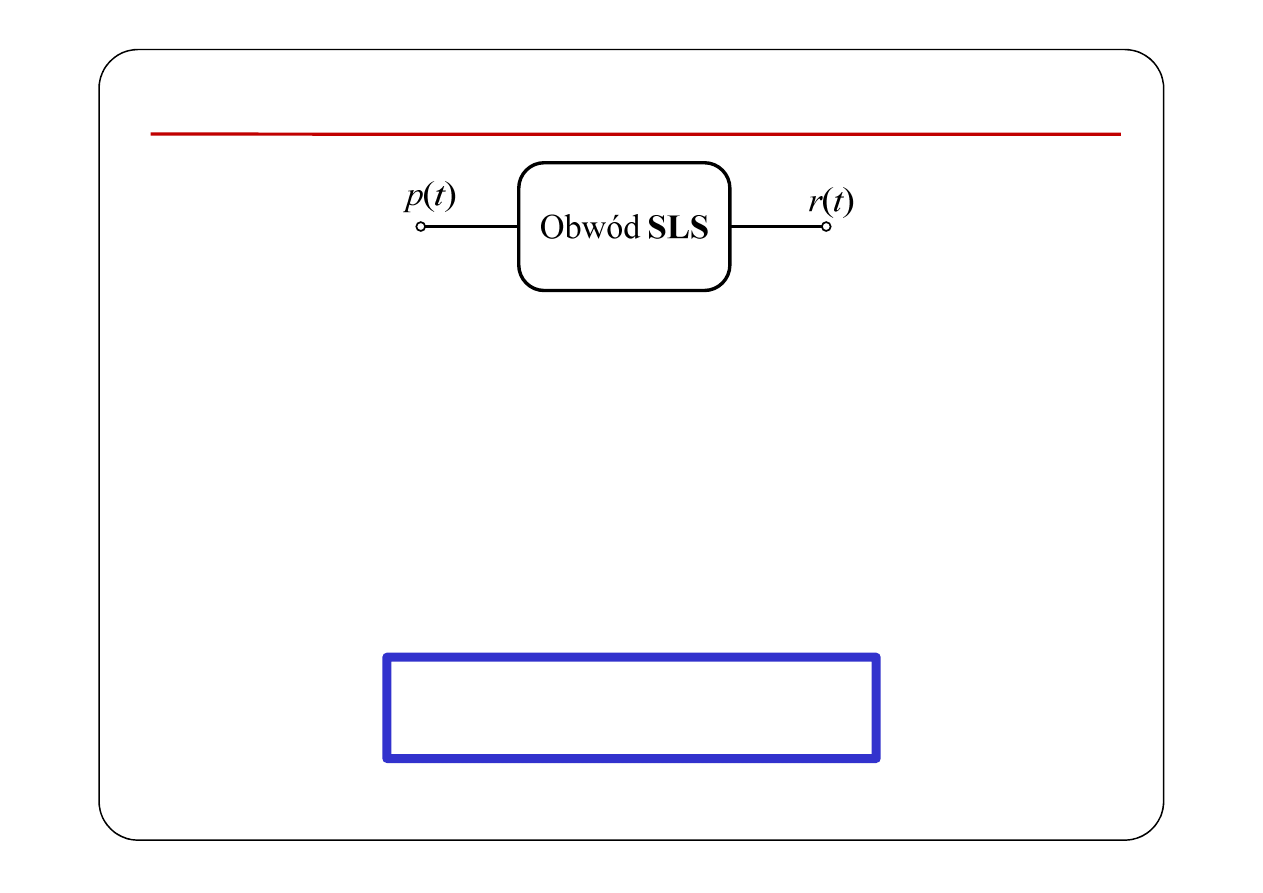
Charakterystyki widmowe układów SLS
( ) ( ) ( )
( ) (
)
(
) ( )
0
d
d
t
r t
h t
p t
h
p t
h t
p
τ
τ τ
τ
τ τ
∞
+
−
−∞
=
∗
=
−
=
−
∫
∫
Jeżeli istnieją transformaty Fouriera
Jeżeli istnieją transformaty Fouriera
( )
( )
{ }
( )
( )
{ }
j
j
P
p t
H
h t
ω
ω
=
=
F
F
to
( )
( ) ( )
j
j
j
R
H
P
ω
ω
ω
=
Niech
( )
( )
( )
0
δ
h t
a
t
h t
=
+
Transformata Fouriera będzie istnieć gdy
czyli gdy układ będzie BIBO stabilny.
( )
0
0
d
,
h t
t
∞
< ∞
∫
— charakterystyka widmowa układu
( )
( )
{ }
j
H
h t
ω
=
F
Jeżeli H(s) jest operatorową transmitancją układu BIBO stabilnego, to
( )
( )
j
j
s
H
H s
ω
ω
=
=
Charakterystyka widmowa istnieje tylko
wtedy gdy układ jest BIBO stabilny!!!
Podstawienia s = j
ω
wolno dokonać tylko wtedy, gdy funkcja H(s)
nie ma biegunów w prawej domkniętej półpłaszczyźnie zmiennej s.
( )
( )
( )
j
j
e
H
A
θ ω
ω
ω
=
( )
( )
( )
( )
( )
( )
j
j
j
j
e
,
j
j
e
P
P
R
R
ξ ω
η ω
ω
ω
ω
ω
=
=
( )
( ) ( )
( ) ( ) ( )
j
j
R
A
P
ω
ω
ω
η ω
θ ω ξ ω
=
=
+
( )
( )
j
A
H
ω
ω
=
— charakterystyka amplitudowa
( )
( )
j
A
H
ω
ω
=
— charakterystyka amplitudowa
Określa w jaki sposób modyfikowane jest widmo amplitudowe
pobudzenia
( )
( )
arg
j
H
θ ω
ω
=
— charakterystyka fazowa
Określa w jaki sposób modyfikowane jest widmo fazowe
pobudzenia
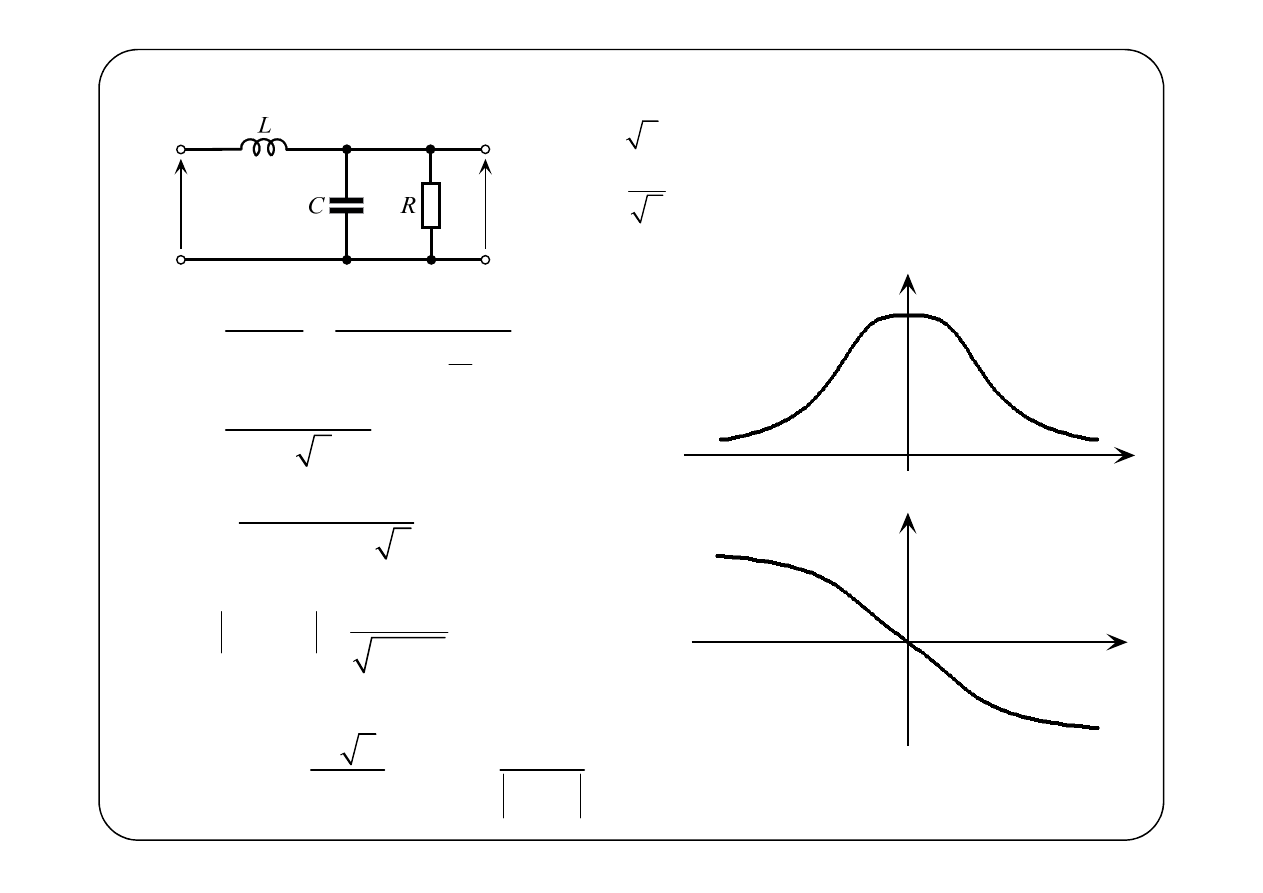
( )
A
ω
ω
Przykład 1.
( )
1
U
s
( )
2
U
s
( )
( )
( )
2
2
1
1
1
U
s
H s
L
U
s
s LC
s
R
=
=
+
+
2 H,
1
F,
2
1 Ω.
L
C
R
=
=
=
( )
2
1
2 1
H s
s
s
=
+
+
ω
( )
θ ω
ω
( )
2
2 1
s
s
+
+
( )
2
1
j
1
j
2
H
ω
ω
ω
=
−
+
( )
( )
( )
( )
4
2
2
2
1
j
,
1
arg
j
2
1
arc tg
arccos
sgn( )
1
1
A
H
H
ω
ω
ω
θ ω
ω
ω
ω
ω
ω
ω
=
=
+
=
=
−
= −
−
⋅
−
−

Przykład 2.
( )
1
U s
( )
2
U
s
( )
( )
( )
2
2
1
2
2
1
1
1
sC
U
s
R
s
H s
C
C
U
s
s
s
−
−
=
=
=
+
+ +
1
2
3
1
2
1
1Ω,
Ω,
2 Ω,
3
1F,
1F.
R
R
R
C
C
=
=
=
=
=
( )
( )
2
2
1
2
1
1
2
3
3
1
2
2
1
1
1
C
C
U
s
s
s
s C C
s
R
R
R
R
+
+ +
+
+
+
( )
( )
(
)
( )
2
2
2
2
2
j
j
2
j
2
2
arc tg
π sgn
H
A
ω
ω
ω
ω
ω
ω
ω
ω
ω
θ ω
ω
ω
−
=
−
+
=
−
+
−
=
−
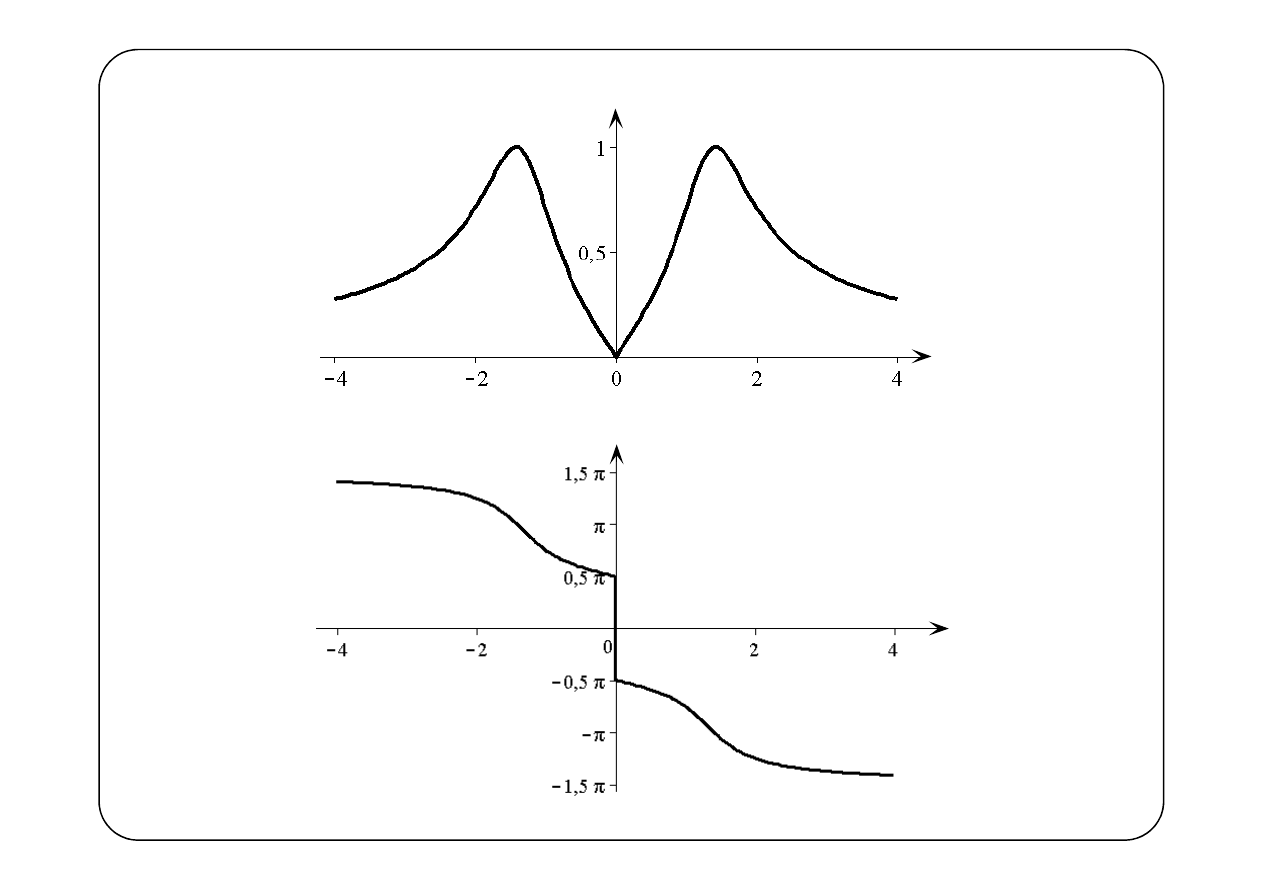
( )
A
ω
ω
( )
θ ω
ω
( )
θ ω

Przykład 3.
( )
1
U s
( )
2
U
s
1
2
1Ω,
1Ω,
1Ω,
1 F.
R
R
R
C
=
=
=
=
( )
( )
( )
2
2
1
1
1
R
sC
U
s
R R
s
H s
−
−
=
= −
= −
+
( )
θ ω
ω
( )
A
ω
( )
( )
1
1
1
1
1
s
H s
s
U
s
sC
R
−
=
= −
= −
+
+
( )
( )
( )
1
j
j
1+j
1
π
2arctg
H
A
ω
ω
ω
ω
θ ω
ω
−
= −
=
= − −
( )
θ ω
ω
Filtr wszechprzepustowy
(all-pass filter)
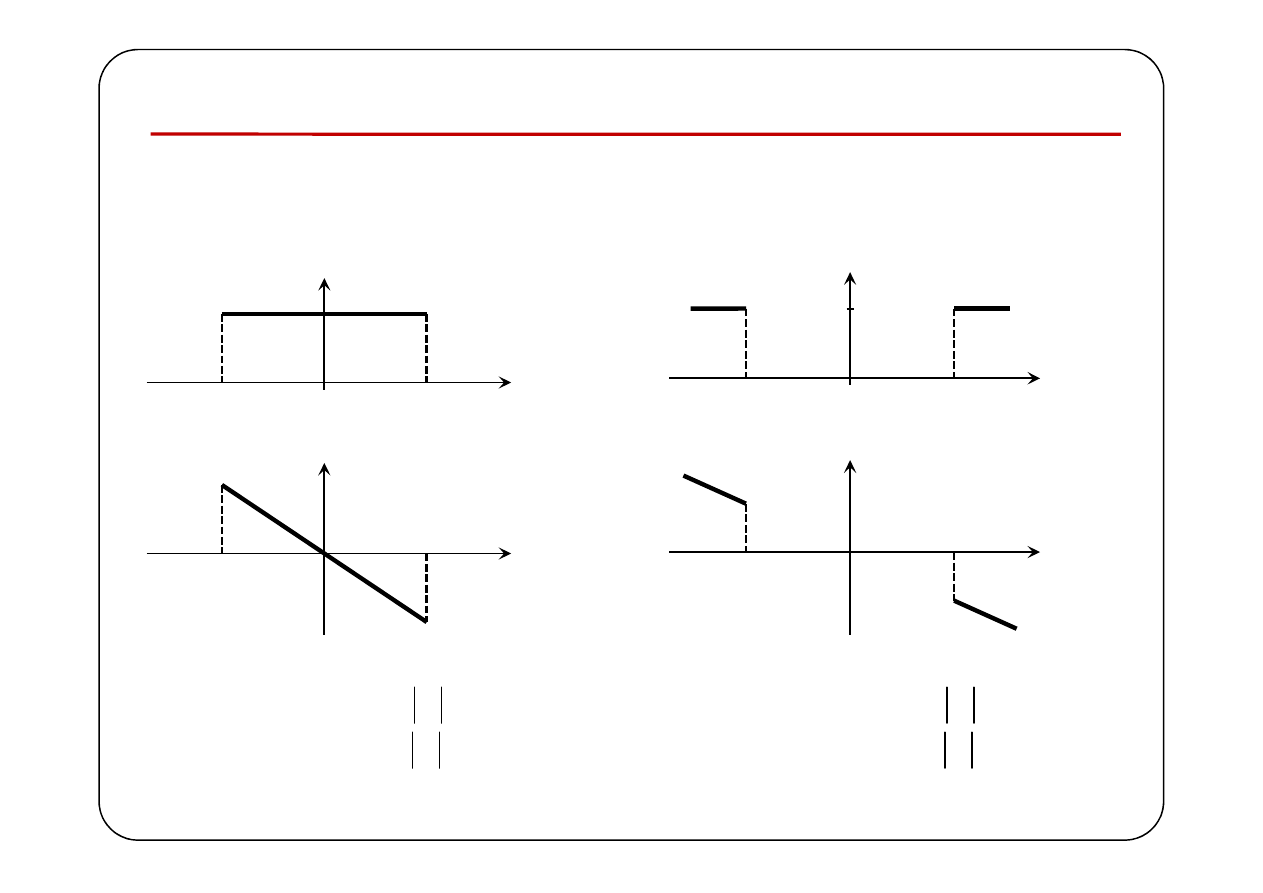
Podstawowe typy filtrów idealnych
( )
θ ω
ω
( )
A
ω
g
ω
−
g
ω
1
Filtr dolnoprzepustowy
( )
θ ω
ω
( )
A
ω
g
ω
−
g
ω
1
Filtr górnoprzepustowy
( )
θ ω
ω
g
ω
−
g
ω
( )
0
j
g
g
e
dla
j
0
dla
t
H
ω
ω ω
ω
ω ω
−
≤
=
>
( )
θ ω
ω
g
ω
−
g
ω
( )
0
j
g
g
e
dla
j
0
dla
t
H
ω
ω ω
ω
ω ω
−
≥
=
<
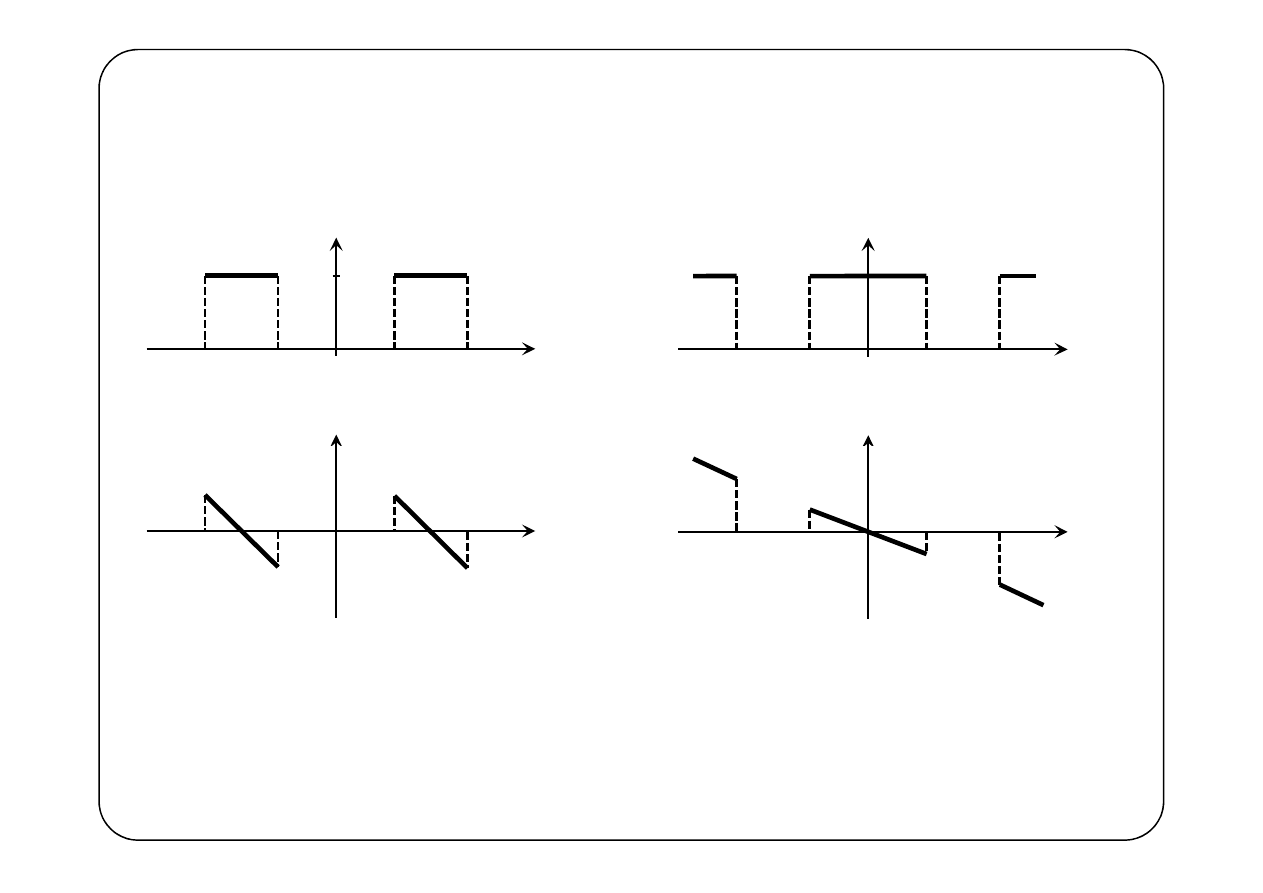
( )
θ ω
ω
( )
A
ω
g1
ω
−
g1
ω
1
g 2
ω
−
g 2
ω
Filtr pasmowoprzepustowy
( )
θ ω
ω
( )
A
ω
g1
ω
−
g1
ω
1
g 2
ω
−
g 2
ω
Filtr pasmowozaporowy
ω
g 2
ω
−
g1
ω
−
g1
ω
g 2
ω
ω
g 2
ω
−
g1
ω
−
g1
ω
g 2
ω
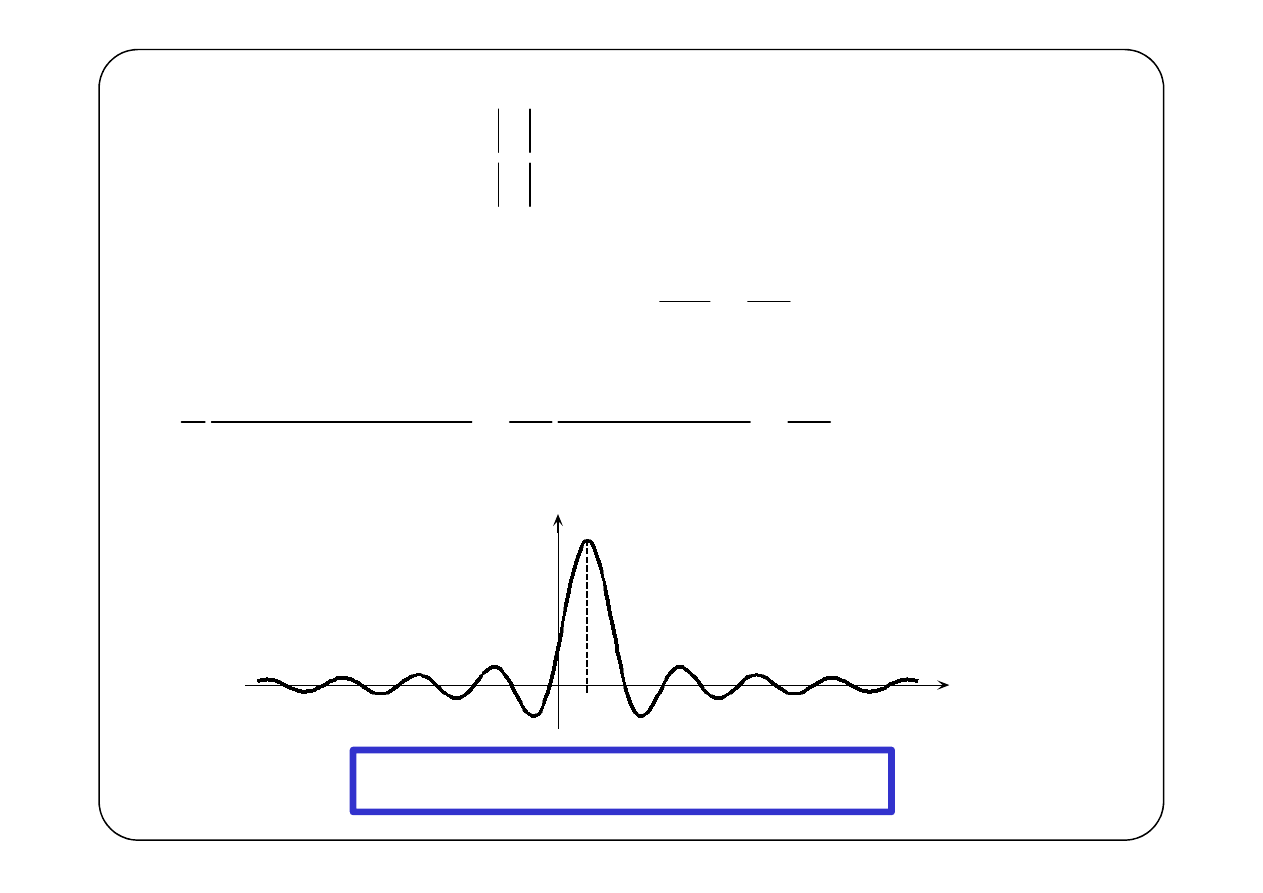
( )
0
j
g
g
e
dla
j
0
dla
t
H
ω
ω ω
ω
ω ω
−
≤
=
>
( )
( )
{
}
(
)
(
)
(
)
(
)
(
)
(
)
(
)
g
g
0
0
g
g
0
g
0
g
j
j
–1
j
j
j
g
g
0
g
g
0
d
1
j
e
e
e
d
2π
2π
sin
1 e
e
Sa
π
π
π
2 j
t t
t
t
t t
t t
h t
H
t
t
t
t
t
t
t
t
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
−
−
−
−
−
− −
=
=
=
=
−
−
=
=
=
−
−
−
∫
∫
F
(
)
(
)
0
g
0
π
π
π
2 j t
t
t
t
ω
−
−
h(t)
t
0
t
Układ nie jest przyczynowy!!!

Kryterium Paley’a-Wienera
Jeżeli charakterystyka amplitudowa A(
ω
) spełnia warunek
to istnieje funkcja
θ
(
ω
), taka, że charakterystyka widmowa
jest realizowalna fizycznie.
( )
2
ln
d
,
1
A
ω
ω
ω
∞
−∞
< ∞
+
∫
( )
( )
( )
j
j
e
H
A
θ ω
ω
ω
=
( )
A
ω
( )
A
ω
ω
( )
A
ω
ω
Nierealizowalne
( )
A
ω
ω
ω
( )
A
ω
Realizowalne
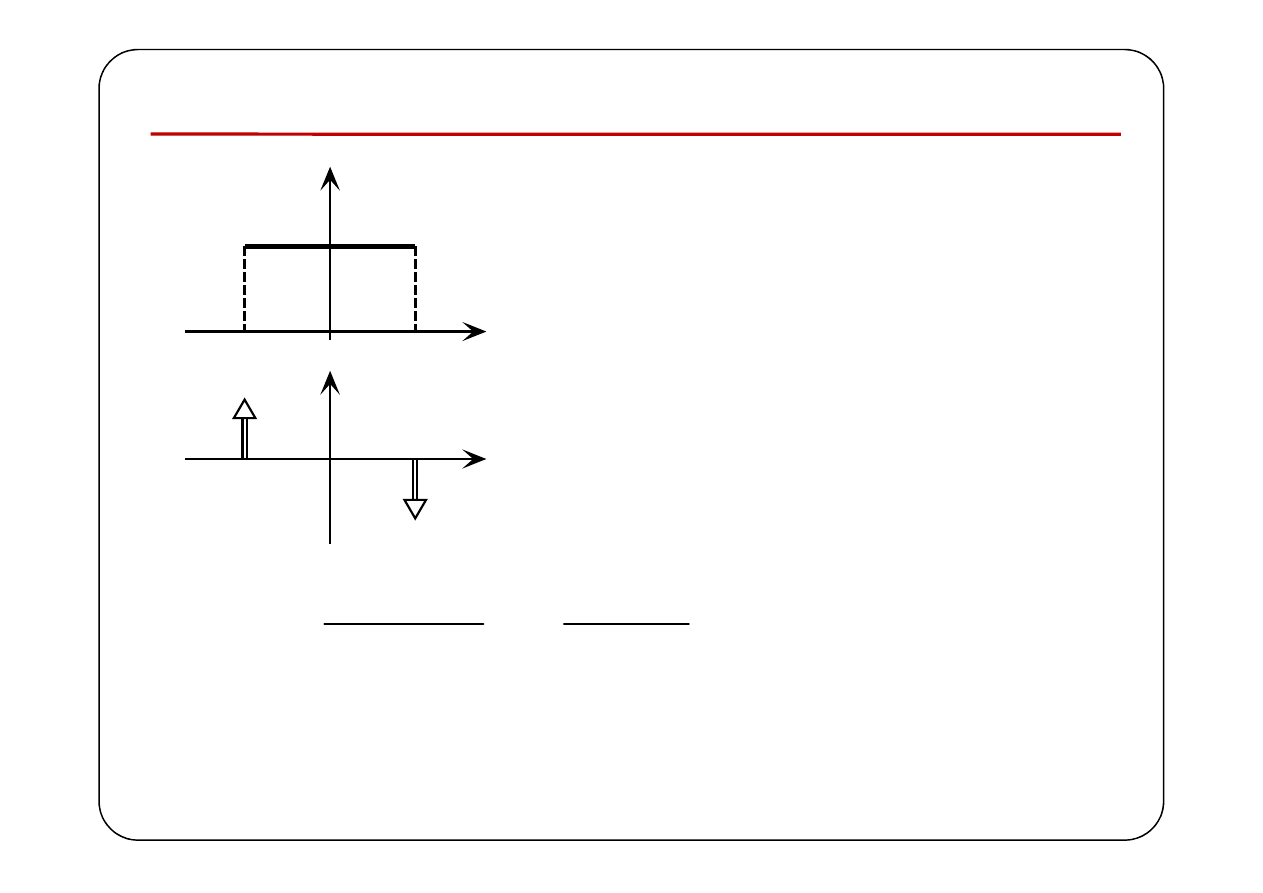
Dystrybucyjna transformata Fouriera
f(t)
t
–a
a
1
t
a
f
'
(t)
(
)
δ t
a
+
⇌
( )
j
F
ω
⇌
( )
j
j
j
j
e
e
a
a
F
ω
ω
ω
ω
−
=
−
t
–a
a
(
)
δ t
a
−
−
⇌
( )
j
j
e
e
F
ω
ω
=
−
( )
( )
j
j
sin
e
e
j
2
j
a
a
a
F
a
a
ω
ω
ω
ω
ω
ω
−
−
=
=

( )
( )
sin
j
2
a
F
a
a
ω
ω
ω
=
1
a
=
2
a
=
3
a
=
( )
( ) ( )
sin
sin
2
d
2
d
a
a
a
a
K
a
a
ω
ω
ω
ω
ω
ω
∞
∞
−∞
−∞
=
=
∫
∫
( )
{
}
( )
–1
j
d
δ
δ
e
t
K
K
K
ω
ω
ω
ω
∞
=
=
∫
F
{ }
( )
?
1
δ
K
ω
=
F
( )
1
a
f t
→ ∞
⇒
→
4
a
=
5
a
=
( )
{
}
( )
–1
j
d
δ
δ
e
2
π
2
π
t
K
K
K
ω
ω
ω
ω
−∞
=
=
∫
F
1
2π
2π
K
K
=
⇒
=
{ }
( )
1
2πδ
ω
=
F

( )
e
dla
0
e
dla
0
t
t
t
f t
t
ε
ε
−
>
=
−
<
1
–
1
e
t
ε
−
e
t
ε
−
( )
f t
t
⇌
( )
j
F
ω
1
( )
f
t
′
( )
2δ t
e
t
ε
ε
−
e
t
ε
ε
−
−
t
( )
g t
( )
g t
′
2
e
t
ε
ε
−
2
e
t
ε
ε
−
t
⇌
⇌
( )
( )
j
j
2
j
F
G
ω
ω
ω
= +
( )
( )
2
j
j
j
G
F
ω
ω
ε
ω
=

( )
( )
( )
( )
2
2
2
2
j
j
j
2
j
j
j
2
j
2 j
j
F
F
F
F
ε
ω
ω
ω
ω
ε
ω
ω
ω
ω
ω
ω ε
= +
−
=
−
=
+
( )
1,
0
sgn
t
f t
t
ε
→
>
→
=
( )
j
j
F
ω
0
ε
→
( )
0
sgn
1,
0
f t
t
t
ε
→
→
=
−
<
0
2
2
2
,
0
2 j
j
0,
0
ε
ω
ω
ω
ω ε
ω
→
≠
−
→
+
=
ω
{
}
2
sgn
j
t
ω
=
F
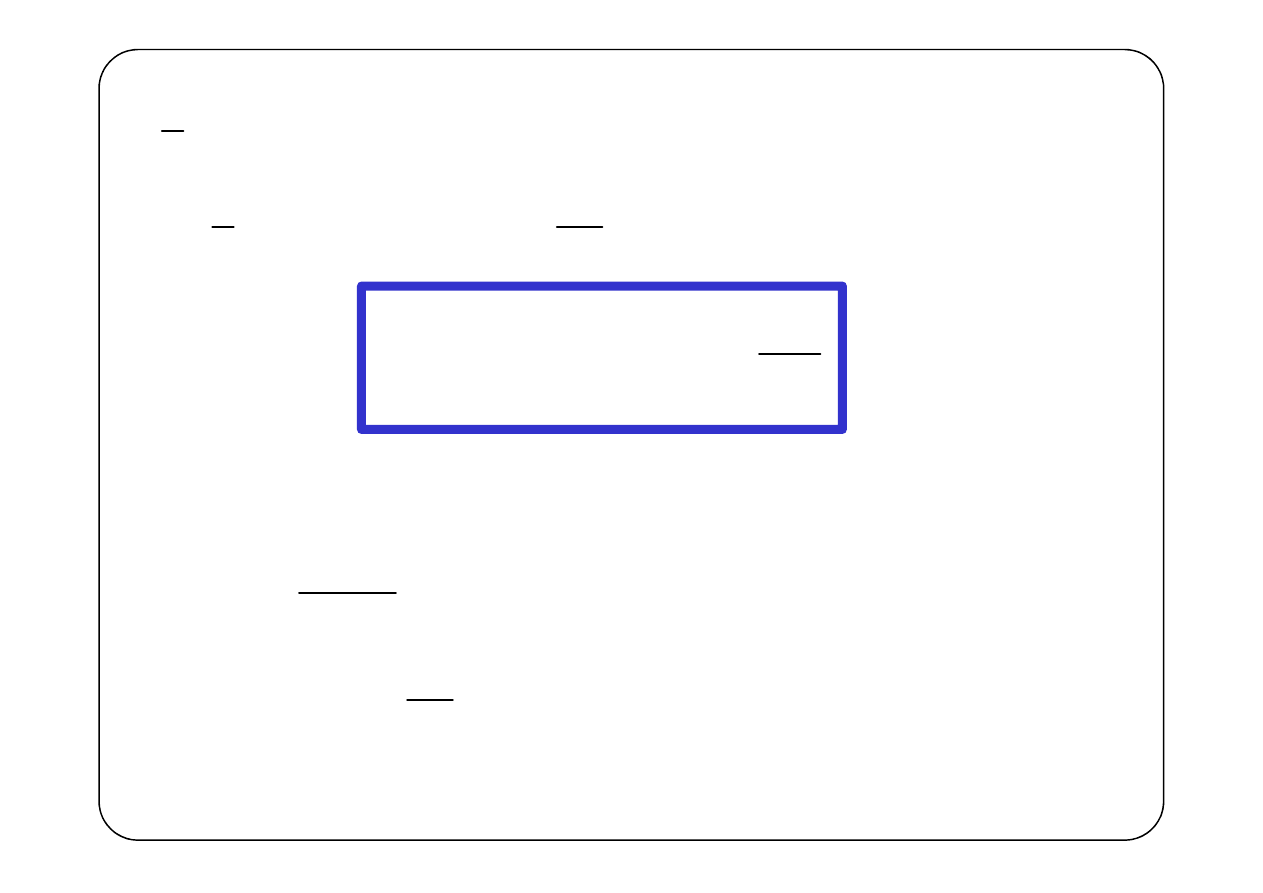
(
) ( )
1
1 sgn
2
t
t
+
=
1
(
)
{
}
( )
1
1
1 sgn
πδ
2
j
t
ω
ω
+
=
+
F
( )
{ }
( )
1
πδ
j
t
ω
ω
=
+
1
F
( )
( )
( )
( )
( )
0
e
,
1
j
j
t
f t
t
f t
t
F
ε
ε
ω
ε
ω
−
→
=
→
= +
1
1
( )
0
1
,
j
0
?
0
j
F
ε
ω
ω
ω
ω
→
≠
→
=
Dla
ω
= 0 granica w zwykłym
sensie nie istnieje!
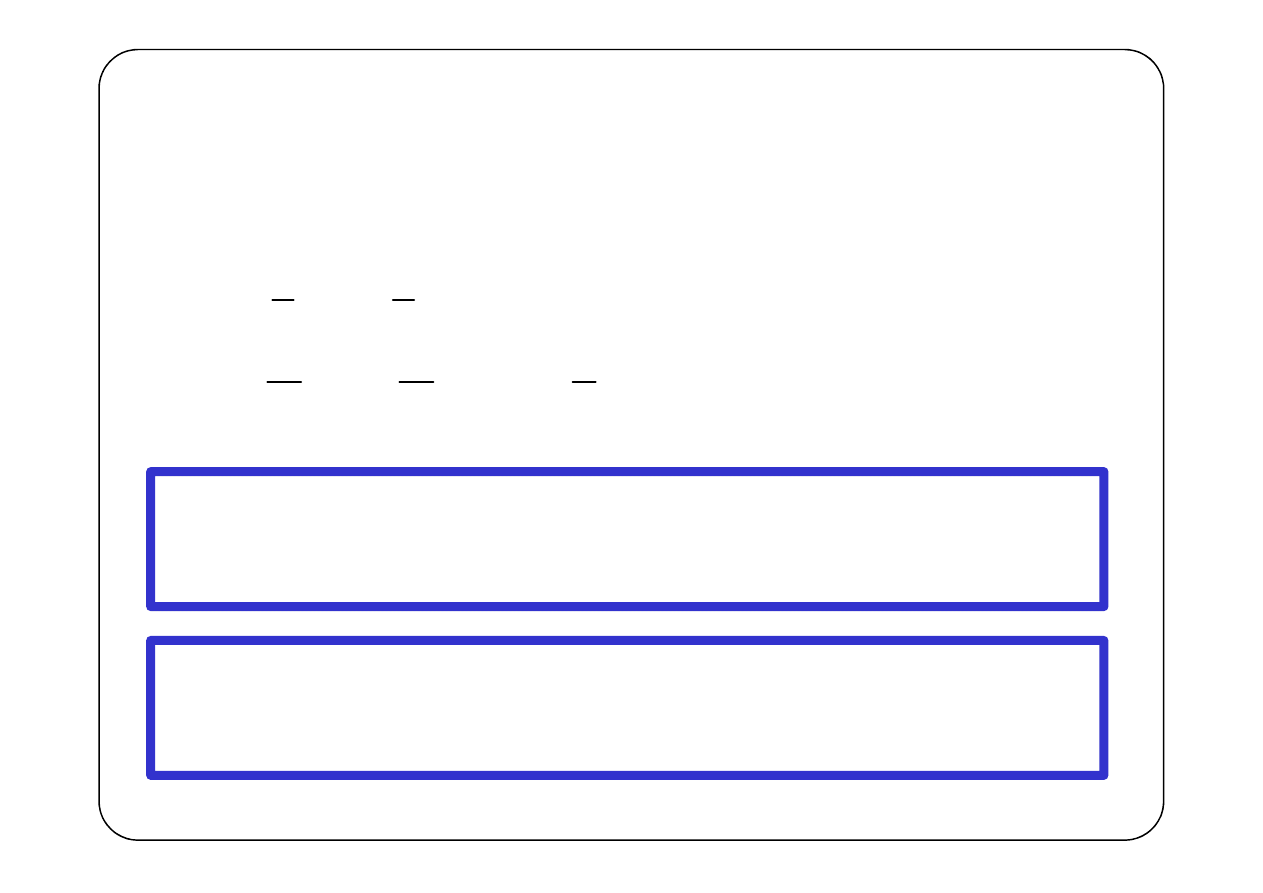
( )
(
)
(
)
(
) (
)
(
) (
)
0
0
0
0
0
0
j
0
j
0
j
j
0
0
0
j
j
0
0
0
1
2πδ
e
2πδ
e
2πδ
1
1
cos
e
e
π δ
δ
2
2
1
1
π
sin
e
e
δ
δ
2 j
2 j
j
t
t
t
t
t
t
t
t
ω
ω
ω
ω
ω
ω
ω
ω ω
ω ω
ω
ω ω
ω ω
ω
ω ω
ω ω
−
−
−
−
+
=
+
−
+
+
=
−
−
−
+
⇌
⇌
⇌
⇌
⇌
{
}
(
) (
)
0
0
0
sin
jπ δ
δ
t
ω
ω ω
ω ω
= −
−
−
+
F
{
}
(
) (
)
0
0
0
cos
π δ
δ
t
ω
ω ω
ω ω
=
−
+
+
F
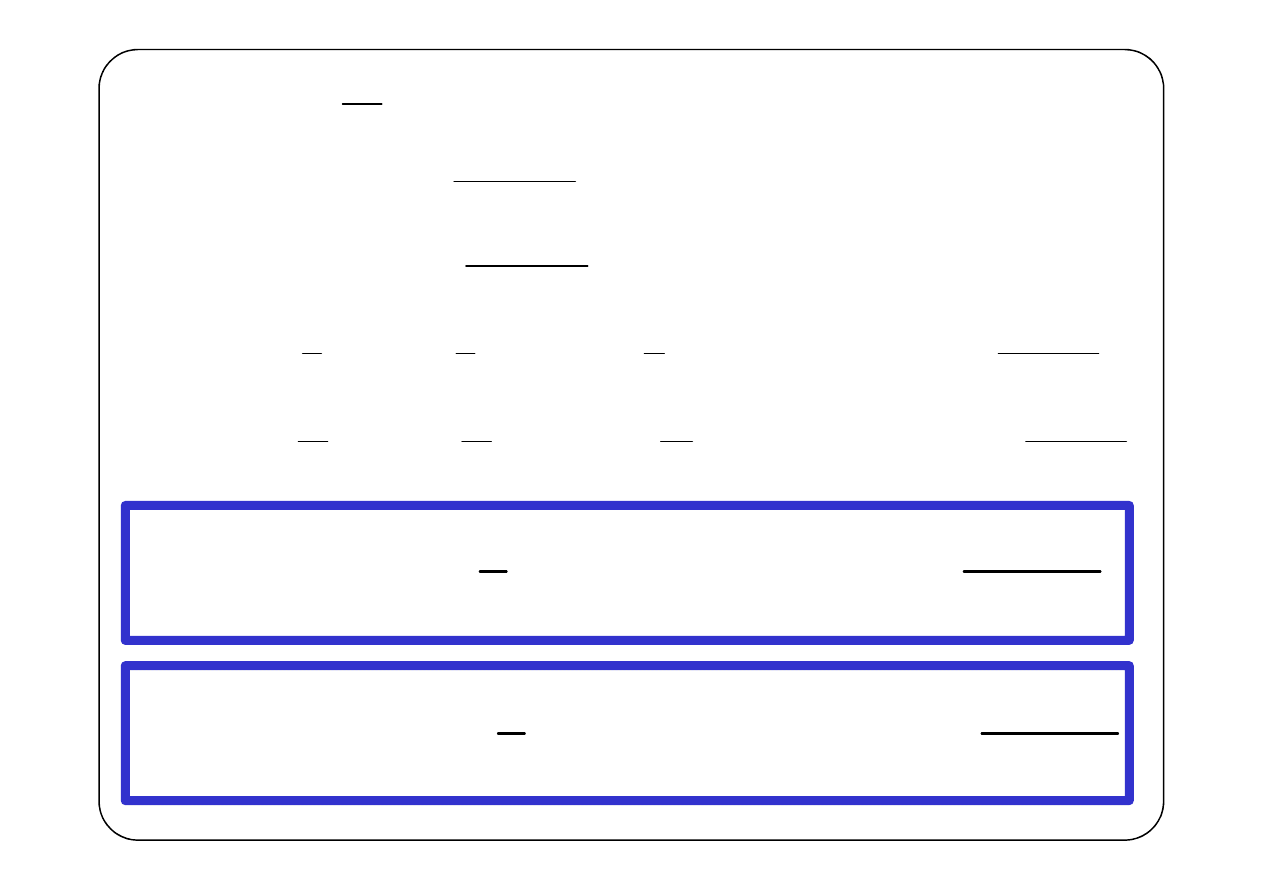
( )
( )
( )
(
) (
)
( )
(
) (
)
( )
( )
( )
(
) (
)
( )
( )
( )
(
) (
)
0
0
0
0
0
0
j
0
0
j
0
0
j
j
0
0
0
2
2
0
j
j
0
0
0
0
2
2
1
πδ
j
1
e
πδ
j
1
e
πδ
j
j
1
1
π
cos
e
e
δ
δ
2
2
2
1
1
π
sin
e
e
δ
δ
2 j
2 j
j2
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
ω
ω
ω
ω
ω
ω
ω
ω
ω ω
ω ω
ω ω
ω ω
ω
ω
ω ω
ω ω
ω ω
ω
ω
ω ω
ω ω
ω ω
−
−
−
+
−
+
−
+
+
+
=
+
−
+
+
+
−
=
−
−
−
+
+
−
1
1
1
1
1
1
1
1
1
⇌
⇌
⇌
⇌
⇌
( )
( )
( )
(
) (
)
0
0
0
2
2
0
sin
e
e
δ
δ
2 j
2 j
j2
t
t
t
t
ω
ω ω
ω ω
ω ω
=
−
−
−
+
+
−
1
1
1
⇌
( )
{
}
(
) (
)
0
0
0
2
2
0
j
π
cos
δ
δ
2
t
t
ω
ω
ω ω
ω ω
ω ω
⋅
=
−
+
+
+
−
1
F
( )
{
}
(
) (
)
0
0
0
0
2
2
0
π
sin
j
δ
δ
2
t
t
ω
ω
ω ω
ω ω
ω ω
⋅
= −
−
−
+
+
−
1
F
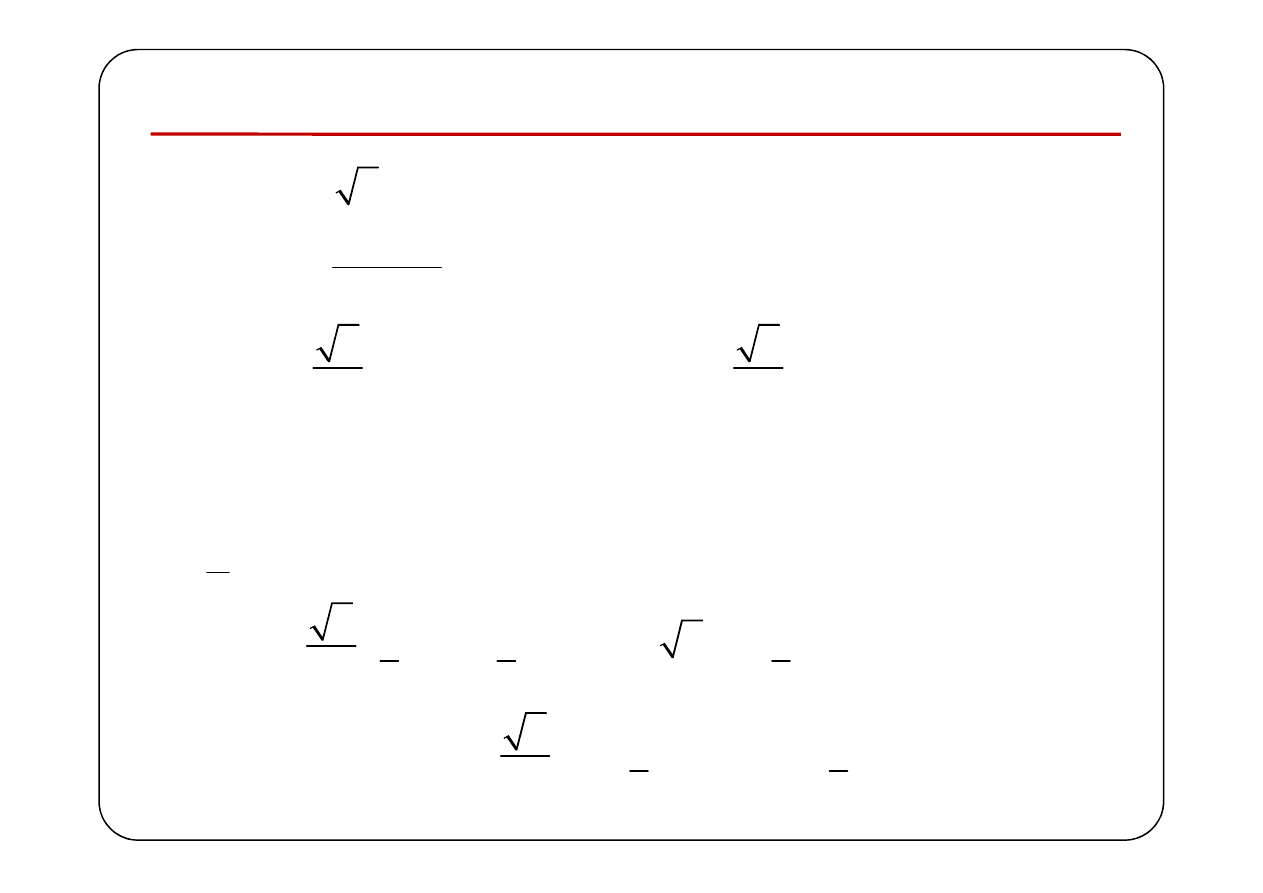
Przebieg sinusoidalny jako pobudzenie
( )
(
)
(
)
0
0
0
0
j
j
j
j
j
j
2
2
e
e
e e
e
e
2 j
2 j
t
t
t
t
p t
P
P
P
P
ω ϕ
ω ϕ
ω
ω
ϕ
ϕ
+
−
+
−
−
=
−
=
−
{ }
j
j
j
e
e
sin
Im e
2 j
x
x
x
x
−
−
=
=
( )
(
)
0
2 sin
p t
P
t
ω
ϕ
=
+
Oznaczmy
j
e
P
P
ϕ
≜
( )
{
}
0
0
0
j
j
j
2
e
e
2 Im
e
2 j
t
t
t
p t
P
P
P
ω
ω
ω
−
∗
=
−
=
( )
( )
{ }
(
)
(
)
0
0
2
j
2π
δ
δ
2 j
P
p t
P
P
ω
ω ω
ω ω
∗
=
=
⋅
−
−
+
F
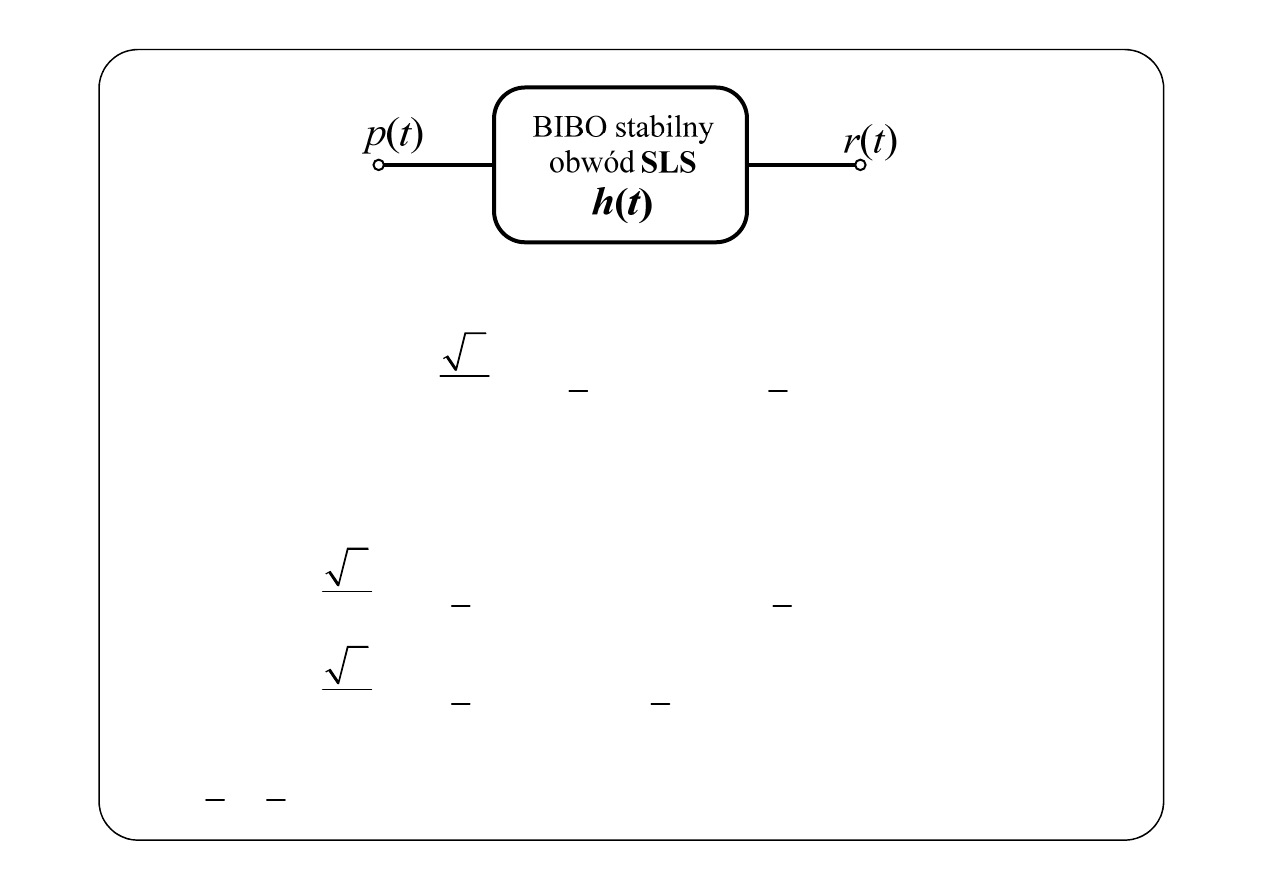
( )
( ) ( )
( )
( )
{ }
j
j
j
,
j
R
H
P
H
h t
ω
ω
ω
ω
=
=
F
( )
( )
(
)
(
)
0
0
2
j
j
2π
δ
δ
2 j
R
H
P
P
ω
ω
ω ω
ω ω
∗
=
⋅
−
−
+
( )
(
)
( ) (
)
j
δ
j
δ
H
H
ω
ω ω
ω
ω ω
−
=
−
( )
(
)
( ) (
)
( )
(
)
(
) (
)
( ) (
)
0
0
0
0
0
0
0
0
j
δ
j
δ
j
δ
j
δ
j
δ
H
H
H
H
H
ω
ω ω
ω
ω ω
ω
ω ω
ω
ω ω
ω
ω ω
∗
−
=
−
+
=
−
+
=
+
( )
( ) (
)
( ) (
)
(
)
(
)
0
0
0
0
0
0
2
j
2π
j
δ
j
δ
2 j
2
2π
δ
δ
2 j
R
PH
P H
R
R
ω
ω
ω ω
ω
ω ω
ω ω
ω ω
∗ ∗
∗
=
⋅
−
−
+
=
=
⋅
−
−
+
( )
j
0
j
e
R
PH
R
ψ
ω
=
≜

( )
{
}
0
0
0
j
j
j
2
e
e
2 Im
e
2 j
t
t
t
r t
R
R
R
ω
ω
ω
−
∗
=
−
=
( )
(
)
(
)
(
)
0
0
j
j
0
2
e
e
2 sin
2 j
t
t
r t
R
R
R
t
ω ψ
ω ψ
ω
ψ
+
−
+
=
−
=
+
( )
(
)
{
}
( )
(
)
{
}
0
0
j
0
j
Jeżeli
2 sin
2 Im
e
to
2 sin
2 Im
e
t
t
p t
P
t
P
r t
R
t
R
ω
ω
ω
ϕ
ω
ψ
=
+
=
=
+
=
Podsumowanie:
( )
(
)
{
}
0
j
0
2 sin
2 Im
e
t
r t
R
t
R
ω
ω
ψ
=
+
=
j
j
e
e
P
P
R
R
ϕ
ψ
=
=
— wartość skuteczna zespolona pobudzenia
— wartość skuteczna zespolona reakcji
( )
( )
0
0
j
,
j
s
R
H P
H
H
H s
ω
ω
=
= ⋅
=
=
( )
( )
( )
0
j
0
0
j
j
e
H
H
H
θ ω
ω
ω
=
=
— transmitancja zespolona

SLS
( )
1
p t
( )
2
p t
( )
r t
( )
( )
( )
( )
2
0
p t
=
=
∗
( )
( )
( )
( )
1
0
p t
=
=
∗
( )
(
)
{
}
( )
(
)
{
}
0
0
j
1
1
1
0
1
j
2
2
2
0
1
2 sin
2 Im
e
2 sin
2 Im
e
t
t
p t
P
t
P
p t
P
t
P
ω
ω
ω
ϕ
ω
ϕ
=
+
=
=
+
=
Zakładamy, że układ jest BIBO stabilny oraz
p
1
(t) i p
2
(t) mają takie same pulsacje!
( )
( )
( )
( )
( )
{
}
0
1
1
1
1
1
1
1
0
j
1
1
j
1
1
j
2 Im
e
e
t
r t
h t
p t
R
H
P
r t
R
R
R
ω
ψ
ω
=
∗
=
=
=
( )
( )
( )
( )
( )
{
}
0
2
2
2
2
2
2
2
0
j
2
2
j
2
2
j
2 Im
e
e
t
r t
h t
p t
R
H
P
r t
R
R
R
ω
ψ
ω
=
∗
=
=
=
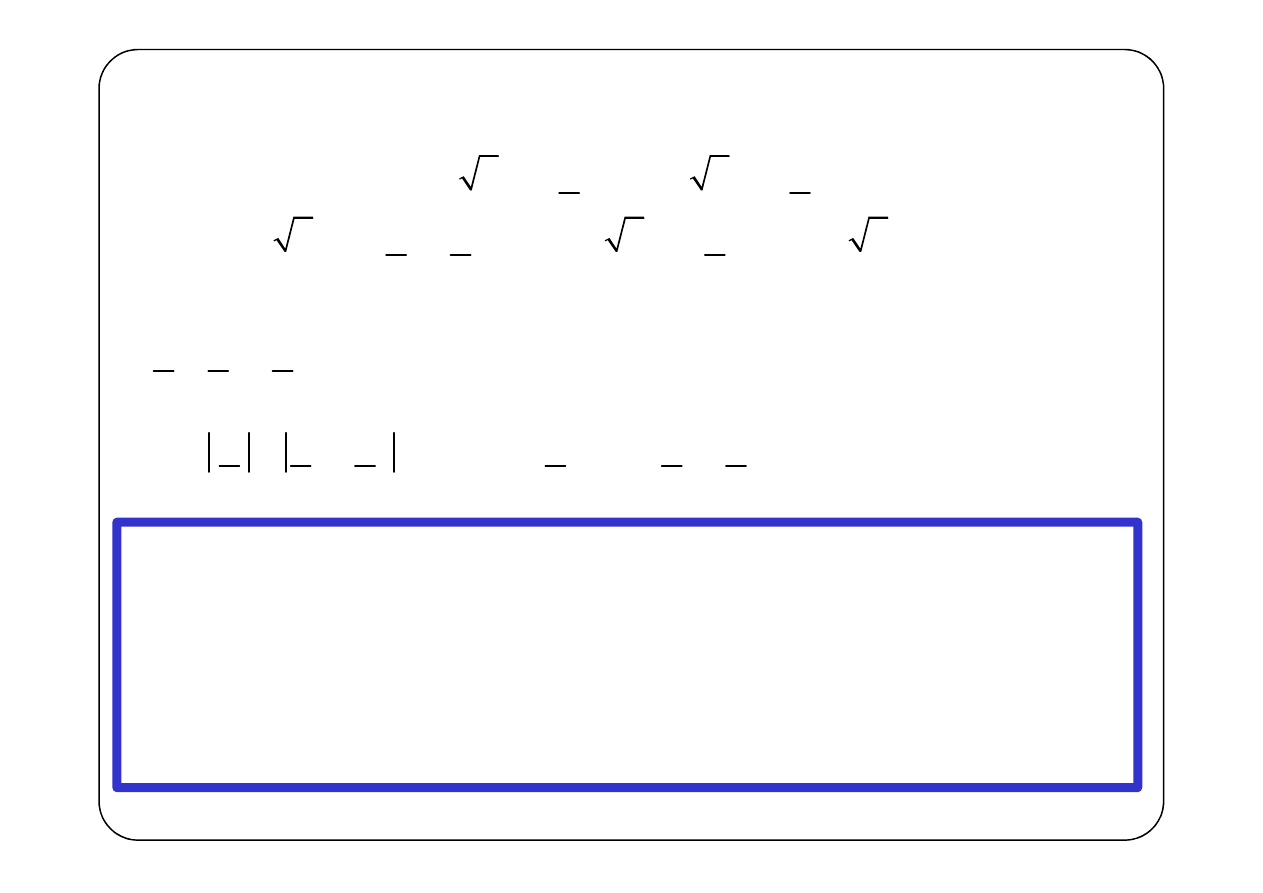
Na podstawie twierdzenia o superpozycji:
( ) ( )
( )
{
}
{
}
(
)
{
}
{
}
(
)
0
0
0
0
j
j
1
2
1
2
j
j
1
2
0
2 Im
e
2 Im
e
2 Im
e
2 Im
e
2 sin
t
t
t
t
r t
r t
r t
R
R
R
R
R
R
t
ω
ω
ω
ω
ω
ψ
=
+
=
+
=
=
+
=
=
+
gdzie
(
)
1
2
czyli
,
arg
arg
R
R
R
R
R
R
R
R
R
R
ψ
=
+
=
=
+
=
=
+
Wniosek:
Jeżeli wszystkie pobudzenia w obwodzie są przebiegami
sinusoidalnymi o takiej samej pulsacji
ω
0
, to w stanie
ustalonym reakcja jest również przebiegiem sinusoidalnym
o pulsacji
ω
0
.
(
)
1
2
1
2
,
arg
arg
R
R
R
R
R
R
R
ψ
=
=
+
=
=
+
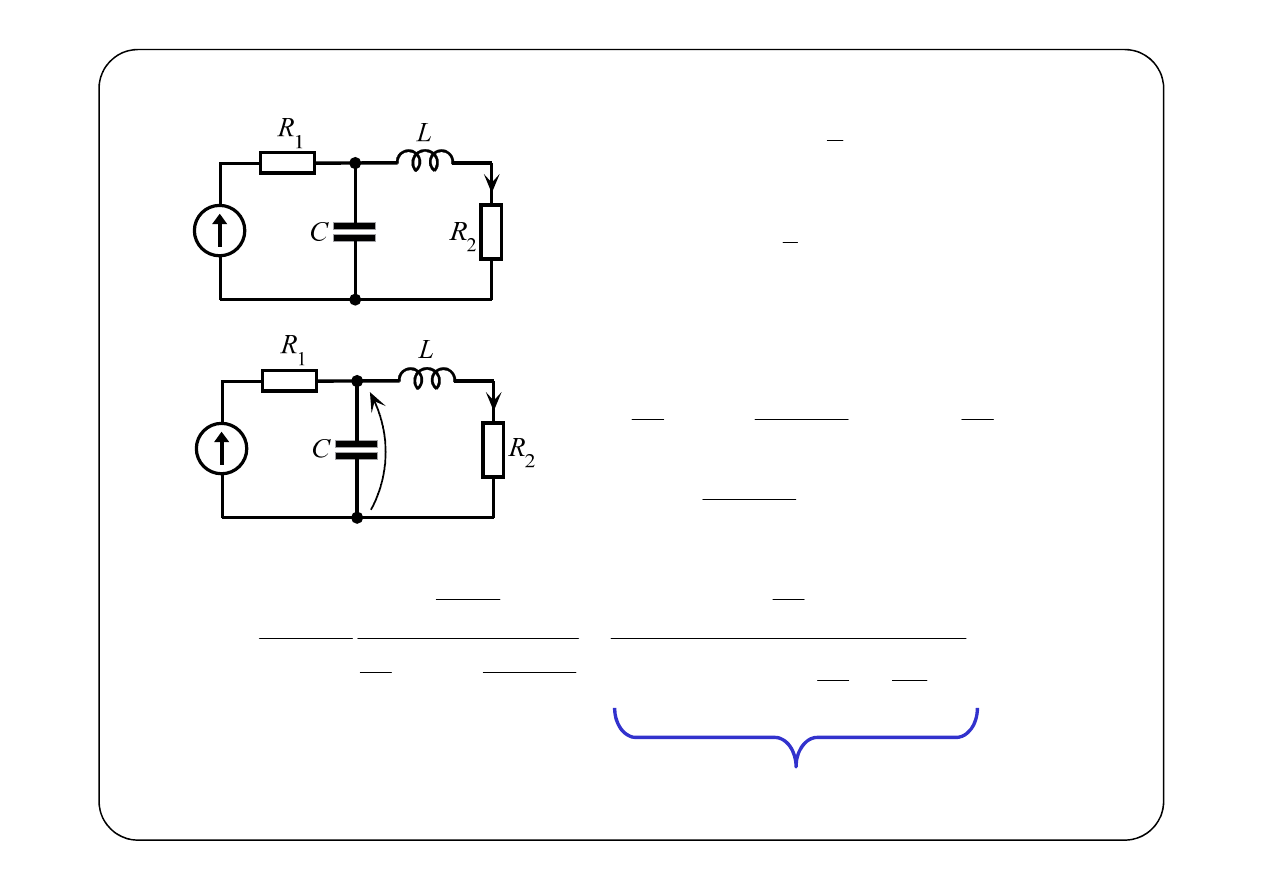
Przykład
( )
e t
( )
i t
( )
(
)
( )
1
2
π
4
1
2
10 sin 2
V,
1Ω,
4 Ω,
1H,
F.
?
e t
t
R
R
L
C
i t
=
+
=
=
=
=
=
( )
E s
( )
I s
( )
U s
( )
( )
1
2
1
1
1
1
sC
U s
E s
R
sL
R
R
+
+
=
+
( ) ( )
( ) ( )
p t
e t
r t
i t
=
=
( )
E s
( )
U s
( )
( )
1
2
1
2
1
R
sL
R
R
I s
U s
sL
R
+
=
+
( )
( )
( )
1
1
2
2
2
2
1
2
1
1
1
1
1
1
1
E s
R
R
I s
E s
sL
R
R
L
sC
s LC
s CR
R
sL
R
R
R
=
=
+
+
+
+
+
+
+
+
( )
H s
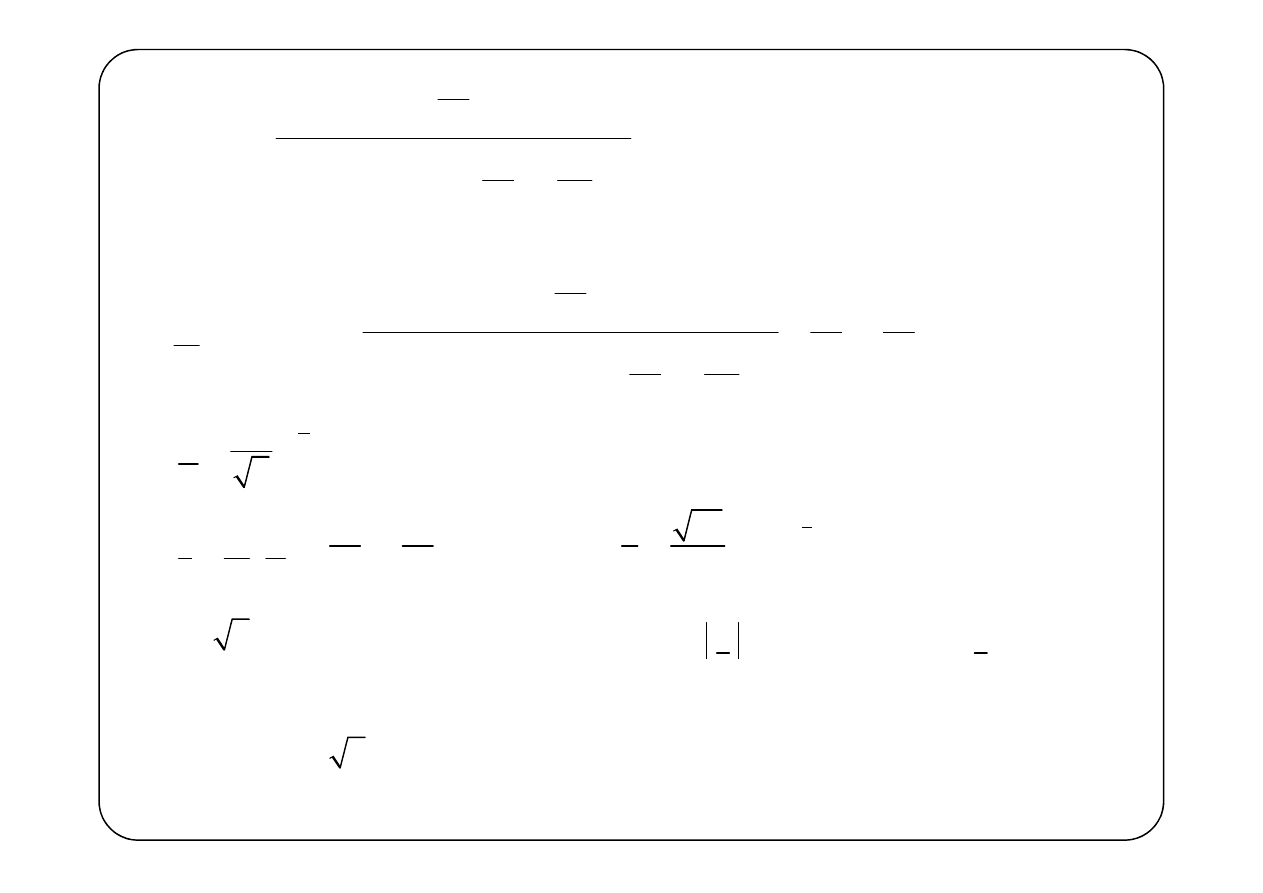
( )
1
2
2
2
1
1
1
1
R
H s
R
L
s LC
s CR
R
R
=
+
+
+
+
0
j
j2
s
ω
=
=
( )
2
1
0
2
0
0
2
1
1
1
1
2
j
j
15
15
j
1
R
H
H
R
L
LC
CR
R
R
ω
ω
ω
=
=
=
−
−
+
+
+
+
π
j
4
10
e
5
j5
E
=
= +
4
10
e
5
j5
2
E
=
= +
(
)
(
)
1
jarctg
j 0,3217
3
10
1
2
1
j
5
j5
1
j
e
1, 054e
15
15
3
3
I
H E
−
−
= ⋅ =
−
+
= −
=
≈
( )
(
)
0
0
2 sin
,
gdzie
2,
1, 054,
arg
0, 3217
i t
I
t
I
I
I
ω
ψ
ω
ψ
=
+
=
=
=
=
= −
czyli
( )
(
)
1, 054 2 sin 2
0, 3217 A.
i t
t
=
−
A gdyby tak od początku pisać
0
0
j
j
sL
L
sC
C
ω
ω
→
→
Wówczas
0
1
0
2
1
1
1
1
j
j
C
U
E
R
L
R
R
ω
ω
+
+
=
+
( )
( )
( )
E s
E
U s
U
I s
I
→
→
→
Czy zawsze
wolno tak zrobić
1
0
2
1
0
2
j
1
j
R
L
R
R
I
U
L
R
ω
ω
+
=
+
2
j 0,3217
1
2
0
0
2
1
1
1
1
1
j
1, 054e
3
j
1
E
R
I
R
L
LC
CR
R
R
ω
ω
−
=
= −
≈
−
+
+
+
+
( )
(
)
1, 054 2 sin 2
0, 3217 A.
i t
t
=
−
Wyszukiwarka
Podobne podstrony:
analiza notatki 3 id 559208 Nieznany (2)
analiza ilosciowa 6 id 60541 Nieznany (2)
Analiza struktury id 61534 Nieznany (2)
analiza ilosciowa 2 id 60539 Nieznany
Analiza czynnikowa id 59935 Nieznany (2)
Darfur analiza kryzysu id 13186 Nieznany
Analiza Finansowa 3 id 60193 Nieznany (2)
Analiza finansowhga id 60398 Nieznany (2)
IMW W02 analiza stanow id 21233 Nieznany
Analiza krancowa id 60743 Nieznany (2)
analiza skupien id 61367 Nieznany
Analiza termiczna id 61671 Nieznany (2)
Analiza biochemiczna id 59863 Nieznany
analiza wzory id 61812 Nieznany (2)
analiza kationow 2 id 60685 Nieznany
analizaf 7I id 61960 Nieznany (2)
analiza chem 2 id 59885 Nieznany (2)
Analiza matematyczna 2 id 60894 Nieznany
więcej podobnych podstron