- 1 -

Automated NMR structure calculation

P

ETER

G

ÜNTERT

Tatsuo Miyazawa Memorial Program, RIKEN Genomic Sciences Center, 1-7-22 Suehiro,
Tsurumi, Yokohama 230-0045, Japan

e mail: [e-mail]
telephone: [phone]
fax: [phone]

© 2005 Peter Güntert. All Rights reserved.

Contents

1 Introduction .......................................................................................................................................... 2

2 Principles of automated NOE assignment ............................................................................................ 3

2.1 Chemical shift assignment ............................................................................................................. 3

2.2 Requirements on input data ........................................................................................................... 4

2.3 Ambiguity of chemical shift-based NOE assignment.................................................................... 7

2.4 Ambiguity of structure-based NOE assignment ............................................................................ 8

2.5 Network-anchoring ........................................................................................................................ 8

2.6 Ambiguous distance restraints ..................................................................................................... 11

2.7 Partial NOE assignment............................................................................................................... 11

2.8 Calibration of distance restraints ................................................................................................. 12

2.9 Constraint combination................................................................................................................ 13

2.10 Removal of erroneous restraints by violation analysis .............................................................. 15

2.11 Error-tolerant target function ..................................................................................................... 15

2.12 Refinement in explicit solvent ................................................................................................... 16

2.13 Quality control ........................................................................................................................... 17

2.14 Troubleshooting......................................................................................................................... 19

3 Implementations of automated NOESY assignment .......................................................................... 20

3.1 Semiautomatic methods ............................................................................................................... 20

3.2 The NOAH algorithm .................................................................................................................. 21

3.3 The ARIA algorithm.................................................................................................................... 21

3.4 The CANDID algorithm .............................................................................................................. 23

3.5 CYANA ....................................................................................................................................... 23

3.6 The AUTOSTRUCTURE algorithm ........................................................................................... 26

3.7 The KNOWNOE algorithm ......................................................................................................... 27

4 Assignment-free structure calculation ................................................................................................ 27

- 2 -

1 Introduction

NMR protein structure determination has remained until recently a laborious undertaking that

occupied a trained spectroscopist over several months for each new protein structure. It has

been recognized that many of the time-consuming interactive steps carried out by an expert

during the process of spectral analysis could be accomplished by automated, computational

methods (Moseley and Montelione, 1999; Altieri and Byrd, 2004; Baran et al., 2004;

Gronwald and Kalbitzer, 2004), and many approaches have already been proposed in order to

automate parts of NMR protein structure determination. Today automated methods for NMR

structure calculation are playing a more and more prominent role and will most likely

supersede the conventional manual approaches to solving three-dimensional protein structures

in solution. This chapter gives an introduction to the current state of automated NMR

structure calculation.

So far, all de novo NMR protein structure determinations have followed the “classic way”

(Wüthrich, 1986) that proceeds through the successive steps of sample preparation, NMR

measurements, NMR data processing, peak picking, chemical-shift assignment, NOESY

assignment and collection of other conformational restraints, structure calculation, and

structure refinement. Section 2 is devoted to basic aspects of the principles and problems of

automated NOESY assignment and structure calculation, including questions of reliability,

quality control and troubleshooting. Section 3 presents a selection of various specific

implementations of automated NOESY assignment and structure calculation for which either

the literature bears testimony of widespread use or that embody concepts of particular interest

and future potential. Alternatives to the classic approach that bypass the potentially

cumbersome chemical shift and NOESY assignment steps have been proposed, and will be

discussed in Section 4.

For consistency and simplicity, the following conventions will be used: An interaction

between two or more atoms is manifested by a signal in a multidimensional spectrum. A peak

refers to an entry in a peak list that has been derived from an experimental spectrum by peak

picking. A peak may or may not represent a signal, and there may be signals that are not

represented by a peak. Chemical shift assignment is the process and the result of attributing a

specific chemical shift value to an atom. Peak assignment is the process and the result of

- 3 -

identifying in each spectral dimension the atom(s) that are involved in the signal represented

by the peak. NOESY assignment is peak assignment in NOESY spectra.

2 Principles of automated NOE assignment

Because of resonance and peak overlap it is in practice not straightforward to obtain a

comprehensive set of distance restraints from a NOESY spectrum. NOESY assignment

instead becomes an iterative process in which preliminary structures, calculated from limited

numbers of distance restraints, serve to reduce the ambiguity of the cross peak assignments.

In addition to this problem, considerable difficulties may arise from spectral artifacts and

noise, and from the absence of expected signals because of fast relaxation. These inevitable

shortcomings of NMR data collection are the main reason why until recently laborious

interactive procedures have dominated 3D protein structure determinations. Automated

procedures follow the same general scheme as the interactive approach but do not require

manual intervention during the assignment/structure calculation cycles (Figs. 1 and 2). Two

main obstacles have to be overcome by an automated method starting without any prior

knowledge of the structure: First, based on chemical shifts alone the number of NOESY cross

peaks with unique assignment based on chemical shifts is in general not sufficient to define

the fold of the protein. Therefore, automated methods should have the ability to make use also

of NOESY cross peaks that cannot yet be assigned unambiguously. Second, the automated

program must be able to cope with erroneously or inaccurately picked peaks and with the

incompleteness of the chemical shift assignment of typical experimental data sets. An

automated procedure needs devices to substitute the intuitive decisions made by an

experienced spectroscopist in dealing with imperfect experimental NMR data.

2.1 Chemical shift assignment

In de novo three-dimensional structure determinations of proteins by NMR, the key

conformational data are upper distance limits derived from nuclear Overhauser effects

(NOEs) (Solomon, 1955; Macura and Ernst, 1980; Kumar et al., 1980; Neuhaus and

Williamson, 1989). In order to extract distance restraints from a NOESY spectrum, its cross

peaks have to be assigned, i.e. the pairs of interacting hydrogen atoms have to be identified.

The assignment of NOESY cross peaks requires as a prerequisite the knowledge of the

chemical shifts of the spins from which NOEs are arising. There have been many attempts to

- 4 -

automate this chemical shift assignment step that conventionally has to precede the collection

of conformational restraints and the structure calculation. These methods have been reviewed

recently (Moseley and Montelione, 1999; Altieri and Byrd, 2004; Baran et al., 2004;

Gronwald and Kalbitzer, 2004), and will not be discussed in detail here. Some automated

approaches (Friedrichs et al., 1994; Hare and Prestegard, 1994; Olson and Markley, 1994;

Buchler et al. 1996; Li and Sanctuary, 1997a; Lukin et al., 1997; Zimmerman et al., 1997;

Leutner et al., 1998; Atreya et al., 2000; Bailey-Kellog et al., 2000; Güntert et al., 2000;

Bhavesh et al., 2001; Moseley et al., 2001; Tian et al., 2001; Andrec and Levy, 2002;

Chatterjee et al., 2002; Coggins and Zhou, 2003) target the question of assigning the

backbone and, possibly,

β chemical shifts, usually on the basis of triple resonance

experiments that delineate the protein backbone through one- and two-bond scalar couplings.

Other algorithms (Chin et al., 1992; Xu et al., 1993, 1994; Oschkinat and Croft, 1994; Bartels

et al., 1996, 1997; Choy et al., 1997; Croft et al., 1997; Li and Sanctuary, 1997b; Gronwald et

al., 1998; Pristovšek et al., 2002; Hitchens et al., 2003) are concerned with the more

demanding problem of complete assignment of the amino acid backbone and side-chain

chemical shifts. In most cases, these algorithms require peak lists from a specific set of NMR

spectra as input, and produce lists of chemical shifts of varying completeness and correctness,

depending on the quality and information content of the input data and the capabilities of the

algorithm.

2.2 Requirements on input data

A limiting factor for the application of automated NOE assignment methods is that they rely

on the availability of an essentially complete list of chemical shifts from the preceding

sequence-specific resonance assignment. At present, chemical shift assignment remains

largely the domain of interactive or semi-automated methods, despite of the aforementioned

promising attempts towards automation. Experience shows that in general the majority of the

chemical shifts can be assigned readily whereas others pose difficulties that may require a

disproportionate amount of the spectroscopist’s time. Hence, NMR structure determination

would be speeded up significantly if NOE assignment and structure calculation could be

based on incomplete lists of assigned chemical shifts, provided that the reliability and

robustness of the NMR method for protein structure determination is not compromised.

- 5 -

The influence of incomplete chemical shift assignments on the reliability of NMR structures

obtained by automated NOESY cross peak assignment has been investigated in detail (Jee and

Güntert, 2003) using the program CYANA for combined automated NOESY assignment with

the CANDID algorithm (Herrmann et al., 2002a; see Section 3.4) and torsion angle dynamics-

based structure calculations (Güntert et al., 1997). Various degrees of completeness of the

chemical shift assignment were simulated by randomly omitting entries from the experimental

1

H chemical shift lists that had been used for the earlier, conventional structure

determinations of two proteins. Overall, the results showed that for reliable automated

NOESY assignment with the CYANA program, and, presumably, other NOE assignment

algorithms based on the same principles, around 90% completeness of the chemical shift

assignments for the backbone amide and non-labile protons is required. Furthermore, the

input data must be self-consistent in the sense that the peak lists are faithful representations of

the NOESY spectra and that the positions of the NOESY cross peaks fit the chemical shift

lists within the specified error ranges. The chemical shift tolerances should not significantly

exceed 0.02 ppm for

1

H when working with homonuclear [

1

H,

1

H]-NOESY spectra, or 0.03

ppm when working with heteronuclear-resolved 3D or 4D NOESY spectra, and 0.6 ppm for

15

N and

13

C shifts (Herrmann et al., 2002a). The algorithm was more tolerant against the lack

of chemical shift assignments when using data from a uniformly

13

C- and

15

N-labelled protein

than in the case of homonuclear data for a much smaller protein. This is due to the availability

of

13

C and

15

N chemical shifts that allow resolving many

1

H chemical shift degeneracies such

that the probability of accidental, erroneous NOE assignments is decreased compared to the

case of homonuclear data. In certain cases the lack of a small number of “essential” chemical

shifts can lead to a significant deviation of the structure. For example, the lack of aromatic

chemical shifts was in general found to be more harmful to the outcome of a structure

calculation than that of a similar number of other protons, presumably because aromatic

protons tend to be located in the hydrophobic core of the protein where they give rise to a

higher-than-average number of NOEs. With exclusively homonuclear data significant

deviations from the reference structure of more than 2 Å were sometimes observed already at

the omission of 20% of the aromatic chemical shifts, which corresponds to an overall

omission ratio of less than 2% of all assigned

1

H chemical shifts. On the other hand, in

practice the algorithm might be expected to tolerate a slightly higher degree of

incompleteness in the chemical shift assignments than the simulations of Jee and Güntert

(2003) suggested if most missing assignments are of “unimportant” chemical shifts that are

- 6 -

involved in few NOEs only. This is usually the case because the chemical shifts of protons

that are involved in many NOEs are intrinsically easier to assign than those exhibiting only

few NOEs.

CYANA uses network-anchoring and constraint combination, two devices that have been

designed and shown to be effective in minimizing the impact of incomplete and/or erroneous

pieces of input data (see Sections 2.5 and 2.9). Chemical shift assignment-based automated

NOE assignment without network-anchoring and constraint combination can be more

susceptible to the deleterious effects from missing chemical shift assignments or artifacts in

the input data.

Instead of using an invariable, fixed list of user-supplied chemical shift assignments,

programs may try to find additional chemical shift assignments during automated NOESY

assignment and the structure calculation. Such methods have been proposed and applied when

a preliminary structure was available (Hare and Wagner; 1999): Starting from nearly

complete chemical shift assignments for the backbone and for 348 side-chain protons of the

28 kDa single-chain T cell receptor protein, the chemical shifts of 40 additional side-chain

protons could be found by a combination of chemical shift prediction with the program

SHIFTS (Ösapay and Case, 1991; Sitkoff and Case, 1997) and NOE assignment with ARIA

(Nilges et al., 1997).

In contrast to the susceptibility against missing chemical shift assignments, automated

structure calculation with the CYANA program was found to be tolerant with respect to

incomplete NOESY peak picking (Jee and Güntert, 2003). The algorithm tolerated the

omission of up to 50% of the NOESY cross peaks that were used for the conventional

structure determinations with only a moderate decrease in the precision and accuracy of the

resulting structure. Even when half of the NOESY peaks were omitted from the experimental

input peak lists from 3D NOESY spectra, RMSD values to the reference structure remained in

the region of 2 Å. Similar behavior was observed when only homonuclear data was available,

albeit with a somewhat more pronounced dependence on the omission rate and RMSD bias

values occasionally exceeding 2 Å in runs with 30% NOESY peak omission ratio. These

findings suggest that it is better to strive for correctness than for ultimate completeness of the

input NOESY peak lists.

- 7 -

2.3 Ambiguity of chemical shift-based NOE assignment

Because of the limited accuracy of experimentally determined chemical shift values and peak

positions many NOESY cross peaks cannot be attributed to a single, unique spin pair but have

an ambiguous NOE assignment comprising multiple spin pairs. A simple mathematical model

of the NOESY assignment process by chemical shift matching gives insight into this problem

(Mumenthaler et al., 1997). It assumes a protein with n hydrogen atoms, for which complete

and correct chemical shift assignments are available, and N cross peaks picked in a 2D

[

1

H,

1

H]-NOESY spectrum with an accuracy of the peak position of

∆ω, i.e. the position of the

picked peak differs from the resonance frequency of the underlying signal by no more than

∆ω in both spectral dimensions. Under the simplifying assumption of a uniform distribution

of the proton chemical shifts over a spectral width

∆Ω, the chemical shift of a given proton

falls within an interval of half-width

∆ω about a given peak position with probability

∆Ω

∆

=

ω

2

p

. Peaks with unique chemical shift-based assignment have in both spectral

dimensions exactly 1 out of all n proton shifts inside the tolerance range

∆ω from the peak

position. Their expected number is

∆Ω

∆

−

−

−

=

≈

−

=

/

4

2

2

2

unique

)

1

(

ω

n

np

n

Ne

Ne

p

N

N

. (1)

N

unique

decreases exponentially with increasing size of the protein (n) and increasing chemical

shift tolerance range (

∆ω). For a typical small protein with, for instance, n = 500 proton

chemical shifts within a range of

∆Ω = 10 ppm and chemical shift accuracies of ∆ω = 0.01,

0.02 or 0.03 ppm, respectively, Eq. 1 predicts that only 14%, 1.8% or 0.25% of the NOEs can

be assigned unambiguously based solely on chemical shift information, which is generally

insufficient to calculate a preliminary three-dimensional structure. For peak lists obtained

from

13

C- or

15

N-resolved 3D [

1

H,

1

H]-NOESY spectra, the ambiguity in one of the proton

dimensions can usually be resolved by reference to the hetero-spin, so that Eq. 1 is replaced

by

∆Ω

∆

−

−

=

≈

/

2

unique

ω

n

np

Ne

Ne

N

. (2)

With regard to assignment ambiguity, 3D NOESY spectra are thus equivalent to homonuclear

NOESY spectra from a protein of half the size or with twice the accuracy in the determination

of the chemical shifts and peak positions.

- 8 -

The influence of chemical shift tolerances on NMR structure calculations using ARIA

protocols for assigning NOE data has been assessed systematically by Fossi et al. (2005).

2.4 Ambiguity of structure-based NOE assignment

Once available, a preliminary three-dimensional structure may be used to resolve ambiguous

NOE assignments. The ambiguity is resolved if only one out of all chemical shift-based

assignment possibilities corresponds to an interatomic distance shorter than the maximal

NOE-observable distance, d

max

. Assuming that the hydrogen atoms are evenly distributed

within a sphere of radius R that represents the protein, the probability q that two given

hydrogen atoms are closer to each other than d

max

can be estimated by the ratio between the

volumes of two spheres with radii d

max

and R, respectively:

3

max

)

/

(

R

d

q

=

. Using d

max

= 5 Å,

one obtains q ≈ 4% for a nearly spherical protein with a radius of about 15 Å. Thus, under

ideal conditions about 96% of the peaks with two assignment possibilities can be assigned

uniquely by reference to the protein structure. Even by reference to a perfectly refined

structure, however, it is impossible to resolve all assignment ambiguities, since the

probability q will always be larger than 0.

2.5 Network-anchoring

Network-anchoring (Herrmann et al., 2002a) exploits the observation that the correctly

assigned restraints form a self-consistent subset in any network of distance restraints that is

sufficiently dense for the determination of a protein 3D structure. In contrast, the erroneously

assigned restraints are randomly distributed in space, generally contradicting each other.

Network-anchoring evaluates the self-consistency of NOE assignments independent from any

previous knowledge on the 3D protein structure and can thus compensate for the absence of

3D structural information at the outset of a de novo structure determination (Fig. 3). Network-

anchoring is important for finding a well-defined, essentially correct structure already in the

first cycle of the structure calculation and is a major factor for the robustness of automated

NOESY assignment with the program CYANA (Herrmann et al., 2002a; Güntert, 2004). The

requirement that each NOE assignment must be embedded in the network of all other

assignments makes network-anchoring a sensitive approach for detecting erroneous restraints.

These may also include “lonely” restraints that artificially constrain unstructured parts of the

protein. Since such lonely restraints do not lead to systematic restraint violations during the

- 9 -

structure calculation, they could not be detected and eliminated by 3D structure-based peak

filters.

In the CANDID algorithm, the network-anchoring score N

αβ

for a given initial assignment of

a NOESY cross peak to an atom pair (

α,β) is calculated by searching all atoms γ in the same

or in the neighboring residues of either

α or β that are connected simultaneously to both

atoms

α and β (Herrmann et al., 2002a). The connection may either be an initial assignment

of another peak (in the same or in another peak list) or the fact that the covalent structure

implies that the corresponding distance must be short enough to give rise to an observable

NOE. Each such indirect path contributes to the total network-anchoring score for the

assignment (

α,β) an amount given by the product of the generalized volume contributions

(Herrmann et al., 2002a) of its two parts,

α→γ and γ→β. N

αβ

has an intuitive meaning as the

number of indirect connections between the atoms

α and β through a third atom γ, weighted

by their respective generalized volume contributions.

In the program CYANA, network-anchoring is implemented in the probabilistic NOE

assignment algorithm. The program calculates the probability P

network

that a given initial

assignment to an atom pair (

α,β) corresponds to a distance d

αβ

shorter than the upper distance

bound u derived from the NOESY cross peak volume. The network-anchoring based

probability is computed from individual probabilities, P

1

, P

2

,… , defined below, that represent

different possible ways to confirm that the assignment (

α,β) corresponds to a short enough

distance:

L

)

1

)(

1

(

1

2

1

network

P

P

P

−

−

−

=

. (3)

P

network

is always larger than the individual probabilities, P

1

, P

2

,… Therefore, network-

anchoring requires that some (not necessarily all) individual probabilities are high. The

individual probabilities include the following cases:

(a) The a priori probability that two atoms in a protein of radius R are closer than the upper

limit u is

3

1

)

/

(

)

(

R

u

u

d

P

=

≤

αβ

. (4)

(b) The covalent structure may imply that the distance d

αβ

is shorter than an upper bound, c:

(

)

1

,

)

/

(

min

)

(

3

2

c

u

u

d

P

=

≤

αβ

. (5)

- 10 -

This applies to short-range assignments.

(c) Another NOE, e.g. a symmetry-related peak, exists with probability P’ of having the same

assignment, (

α,β),

(

)

1

,

)

'

/

(

min

)

'

(

'

)

(

3

3

u

u

u

d

P

u

d

P

⋅

≤

=

≤

αβ

αβ

.

(6)

)

'

(

'

u

d

P

≤

αβ

is the probability that the assignment (

α,β) is correct for symmetry-related peak

with upper distance bound u’.

(d) Two NOEs exist that connect atoms

α and β through a third atom, γ:

)

,

;

(

)

(

)

(

)

(

4

βγ

αγ

βγ

βγ

αγ

αγ

αβ

u

u

u

f

u

d

P

u

d

P

u

d

P

⋅

≤

⋅

≤

=

≤

,

(7)

)

(

αγ

αγ

u

d

P

≤

and )

(

βγ

βγ

u

d

P

≤

denote the probabilities that the assignments (

α,γ) and (β,γ)

of the two “indirect” NOEs with upper distance bounds u

αγ

and u

βγ

are correct. The function f

is a geometric factor that describes the probability for the distance d

αβ

to be shorter than the

upper bound u, given that the two distances d

αγ

and d

βγ

are shorter than u

αγ

and u

βγ

,

respectively. One of the two NOEs can be replaced by a covalently constrained distance. In

this case the NOE-derived upper bound is replaced by the one implied by the covalent

structure and the corresponding probability is set to 1.

(e) The atoms

α and β are close in the covalent structure to atoms α’ and β’, respectively, that

are connected by an NOE:

)

,

,

;

(

)

(

)

(

'

'

'

'

'

'

'

'

5

β

α

ββ

αα

β

α

β

α

αβ

u

c

c

u

g

u

d

P

u

d

P

⋅

≤

=

≤

.

(8)

)

(

'

'

'

'

β

α

β

α

u

d

P

≤

and g are defined as the analogous quantities in Eq. 7. c

αα

’

and c

ββ

’

are the

upper bounds derived from the covalent structure for the distances d

αα

’

and d

ββ

’

.

The overall network-anchoring probability can include in the product of Eq. 3 multiple terms

of types (c)-(e) that reflect multiple indirect paths. The calculation of the network-anchoring

probability is recursive in the sense that its calculation for a given peak requires the

knowledge of the probabilities from other peaks, which in turn involve the corresponding

network-anchoring probabilities. Therefore, the calculation of these quantities is iterated until

convergence. Note that the peaks from all peak lists contribute simultaneously to network-

anchored assignment.

- 11 -

2.6 Ambiguous distance restraints

Ambiguous distance restraints (Nilges, 1993, 1995) are an important and powerful concept

for the handling of ambiguities in NOESY cross peak assignments. When using ambiguous

distance restraints, each NOESY cross peak is treated as the superposition of the signals from

each of its multiple assignments, using relative weights proportional to the inverse sixth

power of the corresponding interatomic distance. A NOESY cross peak with a unique

assignment possibility gives rise to an upper bound b on the distance d(

α,β) between two

hydrogen atoms,

α and β. A NOESY cross peak with n > 1 assignment possibilities can be

seen as the superposition of n degenerate signals and interpreted as an ambiguous distance

restraint,

b

d

≤ , with

6

/

1

1

6

−

=

−

⎟

⎠

⎞

⎜

⎝

⎛

=

∑

n

k

k

d

d

. (9)

Each of the distances d

k

= d(

α

k

,

β

k

) in the sum of Eq. 9 corresponds to one assignment

possibility to a pair of hydrogen atoms,

α

k

and

β

k

. Because the “r

-6

-summed distance” d is

always shorter than any of the individual distances d

k

, an ambiguous distance restraint is

never falsified by including incorrect assignment possibilities, as long as the correct

assignment is present.

2.7 Partial NOE assignment

Despite of the property of ambiguous distance restraints that additional, even wrong

assignment possibilities added to an ambiguous distance restraint that contains one or several

correct assignments do not render the restraint incompatible with the correct structure, it is

important to keep the ambiguity of NOE assignments small in order to obtain a well-defined

structure. This is because additional assignment possibilities “dilute” the information

contained in an ambiguous distance restraint and make it more difficult for the structure

calculation algorithm to find the correct structure.

To this end, the “volume contribution”, i.e. the relative contribution C

k

of each assignment

possibility k to the total peak intensity, is estimated from the three-dimensional structure from

the previous cycle by (Nilges et al., 1997)

- 12 -

6

−

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

d

d

C

k

k

, (10)

where

L

denotes the average over the individual conformers of the structure bundle.

Alternatively, when spin diffusion is taken into account by a relaxation matrix treatment, the

volume contributions C

k

are obtained from the back-calculated NOE intensities (Linge et al.,

2004a). In either case, the volume contributions are normalized such that the sum over all

contributions to a given peak equals 1. A partial assignment is then achieved by ordering the

contributions by decreasing size, and discarding the smallest contributions such that

p

C

p

N

k

k

>

∑

=1

, (11)

where p is the “assignment cutoff” and N

p

the number of contributions to the peak necessary

to account for a fraction of the peak volume larger than p (Nilges et al., 1997). For instance,

in the ARIA algorithm the parameter p is decreased from cycle to cycle and typically takes

the values 1.0, 0.9999, 0.999, 0.99, 0.98, 0.96, 0.93, 0.9, 0.8 in cycles 0 to 8, respectively

(Linge et al., 2001). To give an intuitive meaning to the assignment cutoff p, a cross peak

with two assignments may be considered (Nilges and O’Donoghue, 1998): If the shorter of

the two distances is 2.5 Å, a value p = 0.999 will exclude a second distance of 7.9 Å, a value

p = 0.95 a second distance of 4.1 Å, and a value p = 0.8 a second distance of 3.3 Å. If the

shorter distance is 4 Å, the corresponding minimal excluded distances are 12.6, 6.6 and 5.2 Å,

respectively.

2.8 Calibration of distance restraints

Under the assumption of isolated spin pairs in a rigid molecule, the target distances d

NOE

can

be obtained from the cross peak volume V by a simple calibration function,

6

/

1

NOE

)

(

−

= CV

d

.

The calibration constant C can be set by the user or determined automatically, for example by

setting

∑

−

=

NOEs

6

/V

d

C

, where the sum runs over all NOEs with a corresponding average

distance d smaller than a cutoff of typically 6 Å (Linge et al., 2001). In the ARIA

algorithm, an upper bound

2

NOE

NOE

d

d

u

ε

+

=

and a lower bound

2

NOE

NOE

d

d

l

ε

−

=

(typically

ε

= 0.125 Å

−1

) are derived from each target distance d

NOE

(Linge et al., 2001). Most other

algorithms apply only an upper bound. Alternatively, spin diffusion effects (Kalk and

- 13 -

Berendsen, 1980) can be taken into account by a relaxation matrix approach based on the

simulation of the NOE spectrum rather than the direct use of the individual distances d

(Linge et al., 2004a). A fast matrix squaring scheme performs the potentially time-consuming

relaxation matrix analysis efficiently, and the deviation of the calculated NOE from the value

resulting from the isolated spin pair approximation is used to derive a correction factor for the

target distance. In this way, severe cases of spin diffusion can be detected and corrected

within the framework of the automated algorithm.

2.9 Constraint combination

In NMR structure determinations of biological macromolecules spurious distance restraints

may arise from misinterpretation of noise and spectral artifacts. This situation is particularly

critical at the outset of a structure determination, before the availability of a preliminary

structure for 3D structure-based filtering of restraint assignments. Constraint combination

(Herrmann et al., 2002a) aims at minimizing the impact of such imperfections on the resulting

structure at the expense of a temporary loss of information. It is typically applied in the first

two cycles of automated NOESY assignment with the program CYANA and consists of

generating distance restraints with combined assignments from different, in general unrelated,

cross peaks (Fig. 4). The basic property of ambiguous distance restraints—that the restraint

will be fulfilled by the correct structure whenever at least one of its assignments is correct,

regardless of the presence of additional, erroneous assignments—then implies that such

combined restraints have a lower probability of being erroneous than the corresponding

original restraints, provided that the fraction of erroneous original restraints is smaller than

50%.

Two basic modes of constraint combination are “2→1” combination of all assignments of two

long-range peaks each into a single restraint and “4→4” pairwise combination of the

assignments of four long- range peaks into four restraints (Herrmann et al., 2002a). Let A, B,

C, D denote the sets of assignments of four peaks. Then, 2→1 combination replaces two

restraints with assignment sets A and B, respectively, by a single ambiguous restraint with

assignment set A

∪ B, the union of sets A and B. 4→4 pairwise combination replaces four

restraints with assignments A, B, C and D by four combined ambiguous restraints with

assignment sets A

∪ B, A ∪ C, A ∪ D and B ∪ C, respectively. In both cases constraint

combination is not applied to the short-range peaks, because in case of error their effect on

- 14 -

the global fold of a protein is minimal (Nabuurs et al., 2003). The number of long-range

restraints is cut in half by 2→1 combination but stays constant upon 4→4 pairwise

combination. The latter approach thus preserves more of the original structural information,

and can furthermore take into account that certain peaks and their assignments are more

reliable than others, because the peaks with assignment sets A, B, C, D are used 3, 2, 2, 1

times, respectively, to form combined restraints. To this end, the peaks included in constraint

combination are sorted according to their total residue-wise network-anchoring score

(Herrmann et al., 2002a) and 4→4 combination is performed by selecting the assignments A,

B, C, D from the first, second, third, and fourth quarter of the sorted list.

The effect of constraint combination on the expected number of erroneous distance restraints

in the case of 2→1 combination can be estimated quantitatively by assuming an original data

set containing N long-range peaks, and a uniform probability p

<< 1 that a long-range peak

would lead to an erroneous restraint. By 2→1 constraint combination, these are replaced by

N/2 restraints that are erroneous with probability p

2

. In the case of 4→4 combination, it may

be assumed that the same N long-range peaks can be classified into four equally large classes

with probabilities

αp, p, p,

p

)

2

(

α

−

respectively, that they would lead to erroneous restraints.

The overall probability for an input restraint to be erroneous is again p. The parameter

α,

1

0

≤

≤

α

, expresses how much “safer” the peaks in the first class are compared to those in

the two middle classes, and in the fourth, “unsafe” class. After 4→4 combination, there are

still N long-range restraints but with an overall error probability of

2

2

)

4

/

)

1

(

(

p

α

α

−

+

, which

is smaller than the probability p

2

obtained by simple 2→1 combination provided that the

classification into more and less safe classes was successful (

α < 1). For instance, 4→4

combination will transform an input data set of 900 correct and 100 erroneous long-range

cross peaks (i.e., N = 1000, p = 0.1) that can be split into four classes with

α = 0.5 into a new

set of approximately 993 correct and 7 erroneous combined restraints. Alternatively, 2→1

combination will yield under these conditions approximately 495 correct and 5 erroneous

combined restraints. Unless the number of erroneous restraints is high, 4→4 combination is

thus preferable over 2→1 combination in the first two NOESY assignment and structure

calculation cycles.

The upper distance bound b for a combined restraint is formed from the two upper distance

bounds b

1

and b

2

of the original restraints either as the r

-6

-sum,

6

/

1

6

2

6

1

)

(

−

−

−

+

=

b

b

b

, or as the

maximum,

)

,

max(

2

1

b

b

b

=

. The first choice minimizes the loss of information if two already

- 15 -

correct restraints are combined, whereas the second choice avoids the introduction of too

small an upper bound if a correct and an erroneous restraint are combined.

2.10 Removal of erroneous restraints by violation analysis

Experimental peak lists can in practice not be assumed to be completely free of errors,

especially in the early stages of a structure determination or if they originate from automatic

peak picking. In addition, if the chemical shift assignment is incomplete, even the most

carefully prepared peak list will contain peaks that cannot be assigned correctly, namely those

involving unassigned spins, because most automated NOE assignment algorithms do not

attempt to extend or modify the chemical shift assignments provided by the user. When

building a three-dimensional structure from NOE data, most erroneous distance restraints will

be inconsistent with each other and with the correct ones. The erroneous restraints can

therefore, in principle, be detected by analyzing the violations of restraints with respect to the

bundle of three-dimensional structures from the previous cycle of calculation. The problem is

to distinguish violations arising from incorrect restraints from those of correct restraints that

appear as a result of insufficient convergence of the structure calculation algorithm, or as an

indirect effect of structural distortions caused by other erroneous restraints. Violations due to

incorrect restraints can be expected to occur in the majority of conformers rather than

sporadically. Therefore, a violation analysis can be performed by counting the conformers in

which a given restraint is violated by more than a cutoff that is decreased gradually from an

initial large value of 1–2 Å in the second cycle to about 0.1 Å in the final cycle of the

automated structure calculation. If this is the case for a given restraint in more than, say, 50%

of all conformers, several options are possible (Mumenthaler and Braun, 1995; Linge et al.,

2001; Herrmann et al., 2002a): The peak may either be reported as a problem but still used

without change, or the upper distance bound may be increased, or the restraint may be

removed from the input for the structure calculation in the current cycle. Obviously, this kind

of violation analysis can be applied only after a first preliminary structure has been obtained.

2.11 Error-tolerant target function

In order to reduce distortions in the structures resulting from erroneous distance restraints that

passed undetected through the violation analysis, the contribution to the target function from a

severely violated restraint should be limited (Mumenthaler and Braun, 1995). For instance,

- 16 -

ARIA uses in the structure calculation with CNS a target function with a linear asymptote for

large violations which limits the maximal force exerted by a violated distance restraint. The

target function for a single distance restraint is (Nilges and O’Donoghue, 1998):

⎪

⎪

⎪

⎩

⎪⎪

⎪

⎨

⎧

+

≥

−

+

−

−

+

−

+

<

<

−

≤

≤

<

−

=

.

if

)

(

)

2

(

)

2

3

(

;

if

)

(

;

if

0

;

if

)

(

)

(

2

2

2

a

u

d

u

d

u

d

a

a

a

a

a

u

d

u

u

d

u

d

l

l

d

l

d

d

f

γ

γ

γ

(12)

Here,

d

denotes the r

-6

-summed distance of Eq. 9, l and u are the lower and upper distance

bounds,

γ is the slope of the asymptotic potential, and a is the violation at which the potential

switches from harmonic to asymptotic behavior.

The use of NOE pseudo-potential energy function that is linear in the size of the restraint

violation for each individual assignment possibility has been proposed by Kuszewski et al.

(2004). In this approach, a violated restraint for a given assignment results in a force of

constant magnitude, independent of the size of the restraint violation.

As an alternative, implemented in the program CYANA, the idea of ambiguous distance

restraints can be extended in order to confine the actual contribution of a strongly violated

restraint to the target function in an intuitive way to a certain maximum value, v

max

, regardless

of the actual size of the large violation. When violation confinement is active, the effective

distance, d of Eq. 9, to be compared with the upper distance bound, b, is calculated as

6

/

1

1

6

6

max

)

(

−

=

−

−

⎟

⎠

⎞

⎜

⎝

⎛

+

+

=

∑

n

k

k

d

v

b

d

. (13)

The basic property of ambiguous distance restraints implies that

max

v

b

d

+

<

and thus

confines the apparent distance restraint violation to less than v

max

.

2.12 Refinement in explicit solvent

Strongly simplified, “soft” force fields are generally used for the de novo calculation of NMR

structures. There are two reasons for this: Computational efficiency and the need to allow for

a reasonably smooth folding pathway of the polypeptide chain from a random initial structure

to the native conformation. This pathway should not be obstructed by high energy barriers as

they occur if steep, divergent potentials such as the Lennard-Jones potential of standard

- 17 -

classical molecular dynamics force fields are used. The stiffness incurred by potentials that

impede the interpenetration of parts of the molecule during the initial stages of the simulated

annealing procedure would result in most conformers being trapped far from the native

structure in local minima with unfavorable energies.

However, since the physical reality of the non-bonded attractive and repulsive interactions is

only crudely approximated in this way, the resulting structures have often appeared to be of

low quality when submitted to structure validation programs that put much emphasis on such

features as the appearance of the Ramachandran plot, staggered rotamers of side-chain torsion

angles, covalent and hydrogen bond geometry, and electrostatic interactions. To remedy this

situation, a short molecular dynamics trajectory in explicit solvent (Allen and Tildesley, 1987;

Leach, 2001) may be used to refine the final structure in ARIA (Linge et al. 2004b). It could

be shown that a thin layer of solvent molecules around the protein is sufficient to obtain a

significant improvement in validation parameters over unrefined structures, while maintaining

reasonable computational efficiency (Linge et al., 2004b; Spronk et al., 2002).

2.13 Quality control

A variety of methods and criteria for the validation of NMR protein structures have been

proposed or are in use (Spronk et al., 2004), and their importance has recently been assessed

by a large-scale effort to recalculate NMR solution structures for which the experimental

restraints have been deposited in the Protein Data Bank (Nederveen et al., 2005).

Final structures from an automatic algorithm that have a low RMSD within the bundle of

conformers but differ significantly from the “correct” structure are problematic because,

without knowledge of a reference structure, they may appear at first glance as good, well-

defined solutions. In a conventional structure calculation based on manual NOESY

assignment, incomplete or inconsistent input data will be manifested by large RMSD and/or

target function values of the final structure bundle, which will prompt the spectroscopist to

correct and/or complete the input data for a next round of structure calculation. The test

calculations of Jee and Güntert (2003) showed that for structure calculation with automated

NOE assignment neither the RMSD value of the final structure nor the final target function

value are suitable indicators to discriminate between correct and biased results. Other criteria

are needed to evaluate the outcome.

- 18 -

On the basis of the initial experience with the CANDID algorithm, guidelines for successful

runs were proposed (Herrmann et al., 2002a). These comprised six criteria that should be met

simultaneously: (1) average CYANA target function value of cycle 1 below 250 Å, (2)

average final CYANA target function value below 10 Å

2

, (3) less than 20% unassigned

NOEs, (4) less than 20% discarded long-range NOEs, (5) RMSD value in cycle 1 below 3 Å,

and (6) RMSD between the mean structures of the first and last cycle below 3 Å. Criterion (4)

refers to the percentage of NOEs discarded by the CANDID algorithm among all NOEs with

assignments exclusively between atoms separated by 4 or more residues along the

polypeptide sequence. Criteria (3) and (4) impose a limit on the number of NOEs that are not

used to generate distance restraints for the final structure calculation, and thus measure the

completeness with which the picked NOE cross peaks can be explained by the resulting

structure.

The validity of the original guidelines as sufficient conditions for successful CYANA runs

was confirmed by the fact that all the structure calculations in the systematic study of Jee and

Güntert (2003) with an RMSD bias (Güntert, 1998) to the reference structure of more than 2

Å violated one or several of the six criteria. On the other hand, these test calculations revealed

a certain redundancy among the six original criteria. Provided that the input peak lists do not

deliberately misinterpret the underlying NOESY spectra (to which the algorithm has no direct

access), the aforementioned criteria of Herrmann et al. (2002a) can be replaced by only two

conditions for successful structure calculation with automated NOESY assignment: Less than

25% of the long-range NOEs have been discarded by the automated NOESY assignment

algorithm for the final structure calculation, and the backbone RMSD to the mean coordinates

for the structure bundle of the first cycle does not exceed 3 Å.

The percentage of discarded long-range NOEs cannot be calculated readily outside the

program that generates the NOE assignments, because it requires knowledge of the possible

assignments also for the NOESY cross peaks that were excluded from the generation of

conformational restraints. In this case, an overall percentage of unused cross peaks of less

than 15 % can be used as an alternative criterion that is straightforward to evaluate from the

final assigned output peak lists, in which unused cross peaks remain unassigned. Among these

two alternatives, the percentage of discarded long-range NOEs is a slightly more sensitive

indicator of the accuracy of the final structure than the overall percentage of unused cross

peaks because the latter includes also peaks with short-range assignment or with no

- 19 -

assignment possibility at all that are expected to have little distorting effect on the resulting

structure.

The ability of the program to find a well-defined structure in the initial cycle of NOE

assignment and structure calculation, as measured by the RMSD within the structure bundle

in cycle 1, is an important factor that strongly influences the accuracy of the final structure.

This can be understood by considering the iterative nature of the automated NOE assignment

algorithm, in which each cycle except cycle 1 is dependent on the structure obtained in the

preceding cycle. A low precision of the structure from cycle 1 may hinder convergence to a

well-defined final structure, or, more dangerously, opens the possibility of a structural drift in

later cycles towards a precise but inaccurate final structure.

2.14 Troubleshooting

If the output of a structure calculation based on automated NOESY assignment does not

fulfill the aforementioned guidelines, the structure will in many cases still be essentially

correct, but should not be accepted without further validation. The normal approach in this

case is to improve the quality of the input chemical shift and peak lists, and to perform a new

complete structure calculation, until the criteria are met. Usually, this can be achieved

efficiently because the output from an unsuccessful run, even though the structure cannot be

trusted, clearly points out problems in the input, e.g. peaks that cannot be assigned and might

therefore be artifacts or indications of erroneous or missing sequence-specific assignments.

The program CYANA provides for each peak informational output that greatly facilitates this

task: the list of its chemical shift-based assignment possibilities, the assignment(s) finally

chosen, and the reasons why an assignment is chosen or not, or why a peak is not used at all.

In addition, even when the criteria of the previous section are met already, a higher precision

and accuracy of the structure might still be achieved by further improving the input data. A

completely refined input data set should contain well below 5% of peaks that cannot be

assigned and used by the program.

- 20 -

3 Implementations of automated NOESY assignment

3.1 Semiautomatic methods

Semiautomatic NOESY assignment methods relieve the spectroscopist from the burden of

checking the two straightforward criteria for NOESY assignments, i.e. the agreement of

chemical shifts and the compatibility with a preliminary structure, while entrusting the

assignment decisions to the spectroscopist who may have additional relevant information at

his disposal. Such approaches (e.g. Güntert et al., 1993; Meadows et al., 1994; Duggan et al.,

2001) use the chemical shifts and a model or preliminary structure to provide the user with

the list of possible assignments for each cross peak. The user decides interactively about the

assignment and/or temporary removal of individual NOESY cross peaks, possibly taking into

account supplementary information such as line shapes or secondary structure, and performs a

structure calculation with the resulting input. In general, several cycles of NOESY assignment

and structure calculation are required to obtain a high-quality structure.

A prototype of this semiautomatic approach is the program ASNO (Güntert et al., 1993). The

input for ASNO consists of a list of the proton chemical shifts, a peak list containing the

chemical shift coordinates of the cross peaks in the NOESY spectrum, and a bundle of

conformers calculated using a previous, in general preliminary set of input of NOE distance

restraints. Alternatively, the structural input can consist of the crystal structure of the protein

under investigation or originate from a homologous protein. In that case care must be

exercised to rule out possible bias by the imported reference data. In addition, the user

specifies the maximally allowed chemical shift differences between corresponding cross peak

coordinates and proton chemical shift values to be used for chemical shift-based assignments,

the maximal proton-proton distance d

max

in the structure that may give rise to an observable

NOE, and the minimal number of conformers for which a given proton–proton distance must

be shorter than d

max

for an acceptable NOE assignment. For each NOESY cross peak ASNO

first determines the set of all possible chemical shift-based assignments. These are then

checked against the corresponding

1

H–

1

H distances in the group of preliminary conformers

and retained only if the distance between the two protons is shorter than d

max

in at least the

required number of conformers. After several rounds of structure calculation, NOE

assignment with ASNO, and interactive checking and refinement of the assignments, a final,

high-quality structure is obtained.

- 21 -

The program SANE (Structure Assisted NOE Evaluation) (Duggan et al., 2001) is an

alternative protocol in which ambiguous distance restraints are generated for cross peaks with

multiple possible assignments. The user is directly involved in violation analysis after each

round of structure calculation. Throughout the structure determination the user provides input

that can help to circumvent erroneous local structures and reduce the number of iterations

required to reach acceptable structures. Like ASNO, the SANE program includes a distance

filter that is based on an initial search model structure, which may be an X-ray structure, an

ensemble of solution structures, or even a homology-modeled structure. To minimize the

problem of multiple possible assignments SANE makes use of a suite of filters that take into

account existing partial assignments, the average distance between protons in one or more

structures, relative NOE contributions calculated from the structures, and the expected

secondary structure in order to iterate to an accurately assigned NOE cross peak list,

including both unambiguous and ambiguous NOEs for the structure calculation.

3.2 The NOAH algorithm

In a first approach and proof of feasibility of automated NOESY assignment, the programs

DIANA (Güntert et al., 1991) and DYANA (Güntert et al., 1997) were supplemented with the

automated NOESY assignment routine NOAH (Mumenthaler and Braun, 1995; Mumenthaler

et al., 1997). In NOAH, the multiple assignment problem is treated by temporarily ignoring

cross peaks with too many (typically, more than two) assignment possibilities and instead

generating independent distance restraints for each of the assignment possibilities of the

remaining, low-ambiguity cross peaks, where one has to accept that part of these distance

restraints may be incorrect. In order to reduce the impact of these incorrect restraints on the

structure, an error-tolerant target function is used. NOAH requires high accuracy of the input

chemical shifts and peak positions. It makes use of the fact that only a set of correct

assignments can form a self-consistent network, and convergence towards the correct

structure has been achieved for several proteins (Mumenthaler and Braun, 1995;

Mumenthaler et al., 1997; Xu et al., 1999; 2001; Oezguen et al., 2002).

3.3 The ARIA algorithm

The widely used automated NOESY assignment procedure ARIA (Nilges et al., 1997; Nilges

and O’Donoghue, 1998; Linge et al., 2001, 2003) has been interfaced initially with the

- 22 -

program XPLOR (Brünger, 1992) and later with the program CNS (Brünger et al., 1998) for

the structure calculation. ARIA introduced many new concepts, most importantly the use of

ambiguous distance restraints (Nilges, 1993, 1995; see Section 2.6) for handling ambiguities

in the initial, chemical shift-based NOESY cross peak assignments. Prior to the introduction

of ambiguous distance restraints, in general only unambiguously assigned NOEs could be

used as distance restraints in the structure calculation. Since the majority of NOEs cannot be

assigned unambiguously from chemical shift information alone, this lack of a general way to

directly include ambiguous data into the structure calculation considerably hampered the

performance of automatic NOESY assignment algorithms.

ARIA starts from lists of peaks and chemical shifts in the formats of the common spectral

analysis programs ANSIG (Kraulis 1989; Helgstrand et al., 2000), NMRView (Johnson and

Blevins, 1994), PIPP (Garrett et al., 1991) or XEASY (Bartels et al., 1995) and proceeds in

cycles of NOE assignment and structure calculation. Constraints on dihedral angles, J-

couplings, residual dipolar couplings, disulfide bridges and hydrogen bonds can be used in

addition, if available. In each cycle, ARIA calibrates and assigns the NOESY spectra, merges

the restraint lists from different spectra, and calculates a bundle of (typically 20) conformers

with the program CNS. Normally, an extended “template” structure is used in the initial cycle

0. In all later cycles, NOE assignment, calibration and violation analysis are based on the

average

1

H-

1

H distances d calculated from the (typically 7 out of 20) lowest energy

conformers from the previous cycle.

The ARIA algorithm is particularly efficient for improving and completing the NOESY

assignment once a correct preliminary polypeptide fold is available. To obtain a correct fold

in the initial phase of a de novo structure determination when the powerful structure-based

filters for the elimination of erroneous cross peak assignments cannot be active yet, it can be

of help if the user supplies a limited number of already assigned long-range distance

restraints. ARIA has been used in the NMR structure determinations of many proteins (Linge

et al., 2001, 2003). Similar algorithms that also relies on ambiguous distance restraints and

the program XPLOR for the structure calculation has been implemented (Gilquin et al., 1999;

Savarin et al., 2001; Kuszewski et al., 2004).

- 23 -

3.4 The CANDID algorithm

The CANDID algorithm (Herrmann et al., 2002a) in the programs DYANA (Güntert et al.,

1997) and CYANA version 1.0 (Güntert, 2004) combines features from NOAH and ARIA,

such as the use of three-dimensional structure-based filters and ambiguous distance restraints,

with the new concepts of network-anchoring and constraint combination that further enable

an efficient and reliable search for the correct fold in the initial cycle of de novo NMR

structure determinations. Automated structure calculation with CYANA proceeds in iterative

cycles of NOE assignment followed by structure calculation. Between subsequent cycles,

information is transferred exclusively through the intermediary three-dimensional structures,

in that the molecular structure obtained in a given cycle is used to guide the NOE assignments

in the following cycle. Otherwise, the same input data are used for all cycles, that is, the

amino acid sequence of the protein, one or several chemical shift lists, and one or several lists

containing the positions and volumes of cross peaks in 2D, 3D or 4D NOESY spectra. The

assignment of NOEs with CANDID is based on the concept of “generalized volume

contributions” (Herrmann et al., 2002a). The original, “physical” volume contribution of a

given assignment to the total intensity of a peak (Eq. 10) is generalized in CANDID by

factors that reflect the covalent structure of the protein, the presence of transposed peaks, and

network-anchoring.

The CANDID method has been evaluated in test calculations (Herrmann et al., 2002a, b; Jee

and Güntert, 2003) and used in many de novo structure determinations, including four

variants of the human prion protein (Calzolai et al., 2001; Zahn et al., 2003), two distinct

forms of the pheromone binding protein from Bombyx mori (Horst et al., 2001; Lee et al.,

2002), the calreticulin P-domain (Ellgard et al., 2001, 2002), the class I human ubiquitin-

conjugating enzyme 2b (Miura et al., 2002), the heme chaperone CcmE (Enggist et al., 2002)

(Fig. 2), the nucleotide-binding domain of Na,K-ATPase (Hilge et al., 2003).

3.5 The CYANA algorithm

A new, probabilistic automated NOE assignment algorithm has been implemented in program

CYANA, version 2.0. Input chemical shift lists can be in the formats of XEASY (Bartels et

al., 1995) or the BioMagResBank (Doreleijers et al., 2003). NOESY peak lists can be

prepared either using interactive spectrum analysis programs such as XEASY, NMRView

(Johnson and Blevins, 1994), ANSIG (Kraulis 1989; Helgstrand et al., 2000), or automated

- 24 -

peak picking methods such as AUTOPSY (Koradi et al., 1998) or ATNOS (Herrmann et al.,

2002b) that allow to start the NOE assignment and structure calculation process directly from

the NOESY spectra. The input may further include previously assigned NOE upper distance

restraints or other previously assigned conformational restraints. These will not be modified

during automated NOE assignment but used for the CYANA structure calculation. An

automated CYANA structure calculation typically comprises seven cycles (Figs. 1 and 2),

each of which consists of the following steps:

1. Read experimental input data: Amino acid sequence; chemical shift list from sequence-

specific resonance assignment; list(s) of NOESY cross peak positions and volumes; and,

optionally, conformational restraints from other sources for use in addition to the input

from automated NOE assignment.

2. Calibrate distance bounds. From the NOESY peak volumes or intensities upper distance

bounds are derived.

3. Create initial assignment list. For each NOESY cross peak, one or several initial

assignments are determined based on chemical shift agreement within a user-defined

tolerance range.

4. Filter initial assignments. For each initial assignment of a NOESY cross peak an overall

probability for its correctness is calculated as the product of three probabilities that reflect

(a) the agreement between the values of the chemical shift list and the peak position, (b)

self-consistency within the entire NOE network (see Section 2.5), and, if available (i.e. in

cycles 2, 3,...), (c) the compatibility with the three-dimensional structure from the

preceding cycle (Fig. 3). Initial assignments with overall probability below a given

threshold are discarded.

5. Create distance restraints. Distance restraints are created for all cross peaks with at least

one assignment with overall probability above the threshold. Peaks with a single accepted

assignment yield unambiguous distance restraints, those with more than one accepted

assignment result in ambiguous distance restraints.

6. Constraint combination. In cycles 1 and 2 groups of (2 or) 4, a priori unrelated long-range

distance restraints are combined into new virtual distance restraints that carry each the

assignments from two of the original restraints (see Section 2.9).

7. Structure calculation. Using simulated annealing (Kirkpatrick et al., 1983) driven by

torsion angle dynamics (Jain et al., 1993; Güntert et al., 1997) a 3D structure of the protein

is calculated that is added to the input for the following cycle. Distance restraints from

- 25 -

NOEs with multiple assignments and those resulting from constraint combination are

introduced as ambiguous distance restraints into the structure calculation.

8. Return to Step 1.

In the first cycle, the structure-independent NOE self-consistency check has a dominant

impact on the filtering of individual assignment possibilities (step 4) and entire distance

restraints (step 5), since structure-based criteria cannot be applied yet. The second and

subsequent cycles differ from the first cycle by the use of an additional probability for NOE

assignments and cross peaks that exploit the protein 3D structure from the preceding cycle.

Since the precision of the structure determination normally improves with each subsequent

cycle, the criteria for accepting assignments (step 4) are tightened in more advanced cycles of

the structure calculation.

The output from a cycle includes a listing of all NOESY cross peak assignments, comments

about individual assignment decisions that can help to recognize potential artifacts in the

input data, and a three-dimensional structure in the form of a bundle of conformers. A final

structure calculation is performed with unique assigned distance restraints only, in order to

allow their direct use in subsequent refinement and analysis programs that cannot handle

ambiguous distance restraints.

A complete automated CYANA structure calculation requires the calculation of 7 x 100

individual conformers, and hence a substantial amount of computation. Because of the

efficiency of the CYANA torsion angle dynamics algorithm (Jain et al., 1993; Güntert et al.,

1997) it is nevertheless possible to perform a complete automated structure calculation with

CYANA in short time. For instance, the computation time for the calculation of one

conformer of the 136-residue heme chaperone protein CcmE on the basis of 2453 NOE upper

distance bounds and 56 torsion angle restraints (Enggist et al., 2002) using 10000 torsion

angle dynamics steps on a single processor is less than one minute on modern hardware:

Linux PC, Pentium IV, 3.06 GHz:

29 s

Linux PC, Pentium IV, 1.8 GHz:

42 s

Compaq Alpha Server GS 320:

23 s

Silicon Graphics, R16000, 700 MHz:

39 s

Silicon Graphics, R12000, 400 MHz:

59 s

Time-consuming structure calculations are most efficiently performed in parallel. Since an

NMR structure calculation always involves the computation of a group of conformers, it is

highly efficient and straightforward with CYANA to run calculations of multiple conformers

- 26 -

in parallel, for example on clusters of Linux computers using the Message Passing Interface

MPI for interprocess communication (Gropp et al., 1996) or on shared-memory

multiprocessor systems. Nearly ideal speedup, i.e., an overall computation time almost

inversely proportional to the number of processors, can be achieved with CYANA (Güntert et

al., 1997).

The CYANA algorithm has been used for a large number of the NMR protein structures

determined by the RIKEN Structural Genomics/Proteomics Initiative, and elsewhere. These

structure determinations have confirmed that network-anchored assignment and restraint

combination enable reliable, truly automated NOESY assignment and structure calculation

without prior knowledge about NOESY assignments or the three-dimensional structure.

NOESY assignments and the corresponding distance restraints for these de novo structure

determinations were made using CYANA, confining interactive work to the stage of the

preparation of the input chemical shift and peak lists. If used sensibly, automated NOESY

assignment with CYANA has no disadvantage compared to the conventional, interactive

approach but is a lot faster, and more objective. Network-anchored assignment and constraint

combination render automated NOE assignment with CYANA stable also in the presence of

the imperfections typical for experimental NMR data sets. Using CYANA, the evaluation of

NOESY spectra is no longer the time-limiting step in protein structure determination by

NMR.

3.6 The AUTOSTRUCTURE algorithm

An approach that uses rules for assignments similar to the ones used by an expert to generate

an initial protein fold has been implemented in the program AUTOSTRUCTURE and applied

to protein structure determination (Huang et al., 2003, 2005; Greenfield et al., 2001; Moseley

and Montelione, 1999). AUTOSTRUCTURE is aimed to identify iteratively self-consistent

NOE contact patterns, without using any 3D structure model, and to delineate secondary

structures, including alignments between

β-strands, based upon a combined pattern analysis

of secondary structure-specific NOE contacts, chemical shifts, scalar coupling constants, and

slow amide proton exchange data. The software generates conformational restraints, e.g.

distance, dihedral angle and hydrogen bond restraints, automatically and submits parallel

structure calculations with the program DYANA (Güntert et al., 1997). The resulting

- 27 -

structure is then refined automatically by iterative cycles of self-consistent assignment of

NOESY cross peaks and regeneration of the protein structure with the program DYANA.

3.7 The KNOWNOE algorithm

The program KNOWNOE (Gronwald et al., 2002) presents a “knowledge-based” approach to

the problem of automated assignment of NOESY spectra that is, in principle, devised to work

directly with the experimental spectra without interference of an expert. Its central part is a

“knowledge-driven Bayesian algorithm” for resolving ambiguities in the NOE assignments.

NOE cross peak volume probability distributions were derived for various classes of proton-

proton contacts by a statistical analysis of the corresponding interatomic distances in more

than 300 protein NMR structures. For a given cross peak with n possible assignments

n

A

A

,

,

1

K

, the conditional probabilities P(Ak, a|V) that an assignment Ak is responsible for at

least a fraction a of the cross peak volume V can then be calculated from the volume

probability distributions using Bayes’ theorem. Peaks with one assignment Ak with a

probability P(Ak, a|V

0

) higher than a cutoff, typically in the range 0.8 to 0.9, are transiently

considered as unambiguously assigned. Note that no preliminary structure is needed to

achieve this discrimination that yields a higher number of unambiguous assignments as would

be possible based on chemical shifts alone (see Section 2.4). With this list of unambiguously

assigned peaks a set of structures is calculated. These structures are used as input for a next

cycle in which only assignments are accepted that correspond to distances shorter than a

threshold d

max

, which is decreased from cycle to cycle until

5

max

=

d

Å, the assumed

detection limit for NOEs. Since this algorithm essentially relies on the unambiguously

assigned NOEs in order to calculate the intermediate structures (only for the final structure

calculation some ambiguous distance restraint are used), it requires, like NOAH (see Section

3.2), a high accuracy of the chemical shifts of typically 0.01 ppm. The program KNOWNOE

was tested successfully on 2D NOESY spectra of the 66 amino acid cold shock protein from

Thermotoga maritima for which automated NOESY assignment resulted in a structure of

comparable quality to the one obtained from manual data evaluation (Gronwald et al., 2002).

4 Assignment-free structure calculation

It is almost universally assumed that a protein structure determination by NMR requires the

sequence-specific resonance assignments (Wüthrich, 1986). However, the chemical shift

- 28 -

assignment by itself has no biological relevance. It is required only as an intermediate step in

the interpretation of the NMR spectra. Several attempts have been made to devise a strategy

for NMR protein structure determination that circumvents the tedious chemical shift

assignment step. There is a loose analogy between these approaches and the direct phasing

methods in X-ray crystallography (Drenth, 1994). Although until today no de novo NMR

protein structure determination has been accomplished without prior chemical shift

assignment, an introduction into the concepts assignment-free NMR structure calculation is

warranted because recent progress in this field may open the avenue to an alternative strategy

of NMR structure determination.

The underlying idea of assignment-free NMR structure calculation methods is to exploit the

fact that NOESY spectra provide distance information even in the absence of any chemical

shift assignments. This proton-proton distance information can be exploited to calculate a

spatial proton distribution. Since there is no association with the covalent structure at this

point, the protons of the protein are treated as a gas of unconnected particles. Provided that

the emerging proton distribution is sufficiently clear, a model can then be built into the proton

density in a manner analogous to X-ray crystallography in which the structural model is

constructed into the electron density.

This general idea was first tested by Malliavin et al. (1992) with simulated NOEs between

backbone amide protons of lysozyme. From simulations with synthetic NOE data for BPTI

and combining metric matrix distance geometry with graph theoretical approaches to identify

secondary structure elements and, eventually, sequence-specific assignments, Oshiro and

Kuntz (1993) concluded that “this approach is only useful with excellent quality stereo-

resolved data”.

By then the most thorough attempt at simultaneous protein structure determination and

sequence-specific assignment of

13

C and

15

N-separated NOE data using “a novel real-space

ab initio approach” came with Per Kraulis’ ANSRS algorithm (Kraulis, 1994). The input data

are a list of NOESY cross peaks including knowledge of the chemical shifts of the

13

C or

15

N

atoms covalently bound to the protons that make the NOE (i.e., a 4D NOESY peak list), and a

complete but unassigned list of the chemical shifts of all detectable

1

H-

13

C and

1

H-

15

N

moieties. The ANSRS algorithm then proceeds in three stages. First,

1

H spin 3D real-space

structures are calculated using dynamical simulated annealing. Second, a list for each residue

type of plausible

1

H spin combinations with probability scores is generated in a recursive

combinatorial search with spatial restraints. Finally, the sequence-specific assignment and a

- 29 -

low-resolution 3D structure are obtained by Monte Carlo simulated annealing. With simulated

data for two small proteins of 32 and 58 residues the resulting average 3D real-space

1

H spin

structures were within less than 2 Å RMSD from the previously known 3D structure, and the

ANSRS procedure was able to determine the sequence-specific assignments for more than

95% of the spins. Despite these encouraging figures, the ANSRS program has not become a

routine tool for NMR structure determination, presumably because the requirements on the

quality of the input data are still formidable from the experimental point of view, and because

the algorithm has no facilities to deal with overlap among

1

H-X chemical shift pairs.

Atkinson and Saudek proposed an interesting algorithm for direct fitting of structure and

chemical shift data to NMR spectra (Atkinson and Saudek, 1997). Optimization of four

variables per atom, three Cartesian coordinates and the chemical shift value, directly against

the NOESY spectrum, rather than peak lists, by simulated annealing was shown to succeed in

finding sets of coordinates (i.e. structures) and chemical shifts that match the reference

configuration, albeit only in the case of a peptide fragment with six atoms. Subsequently, the

same authors realized that the direct determination of protein structures by NMR without

chemical shift assignment is not restricted to using only NOESY spectra, but can incorporate,

in a natural way, data from the same set of heteronuclear and dipolar coupling experiments as

normally used in the conventional approach (Atkinson and Saudek, 2002). NOEs are again

interpreted as distances between unassigned and unconnected atoms, while cross peaks in all

other spectra are also interpreted as distances instead of being used for assignment purposes.

For example, a

15

N-

1

H HSQC peak yields a distance equal to the N-H bond length between

the two corresponding atoms, and the HNCA spectrum yields, for each N-H pair, four

distances to the two adjacent C

α

atoms. RMSD values to the crystal structure below 2 Å were

obtained when using simulated peak lists for the protein ubiquitin with no prior assignment of

any spectral resonance or cross peak, but every hydrogen atom in the structure was labeled by

both its own chemical shift and that of the attached heavy atom.

The most recent approach to NMR structure determination without chemical shift assignment

is the CLOUDS protocol of Grishaev and Llinás (2002a, b). For the first time, the feasibility

of the assignment-free structure determination concept could be demonstrated using

experimental data rather than simulated data sets. The CLOUDS method relies on precise and

abundant inter-proton distance restraints calculated via a relaxation matrix analysis of sets of

experimental NOESY cross peaks (Madrid et al., 1991). A gas of unassigned, unconnected

- 30 -

hydrogen atoms is condensed into a structured proton distribution (cloud) via a molecular

dynamics simulated annealing scheme in which the inter-nuclear distances and van der Waals

repulsive terms are the only active restraints. Proton densities are generated by combining a

large number of such clouds, each computed from a different trajectory. After filtering by

reference to the cloud closest to the mean, a minimal dispersion proton density (“family of

clouds”) is identified that affords a quasi-continuous hydrogen-only probability distribution

and conveys immediate information on the shape of the protein. The NMR-generated proton

density provides a template to which the molecule has to be fitted to derive the structure. The

primary structure is threaded through the unassigned proton density by a Bayesian approach,

for which the probabilities of sequential connectivity hypotheses are inferred from likelihoods

of H

N

-H

N

, H

N

-H

α

, and H

α

-H

α

interatomic distances as well as

1

H NMR chemical shifts, both

derived from public databases. Once the polypeptide sequence is identified, directionality

becomes established, and the N and C termini are recognized. Side chain hydrogen atoms are

found by a similar procedure. The folded structure is then obtained via a direct molecular

dynamics embedding into mirror image-related representations of the proton density and

selected according to a lowest energy criterion.

The feasibility of the method was tested with experimental NMR data measured for two

globular proteins of 60 and 83 residues, for which excellent unambiguously identified

homonuclear NOESY peak lists were available from the previous, conventional structure

determinations. At the outset of a de novo structure determination it may not be

straightforward to produce a NOESY peak list of such completeness and quality. In

particular, it was assumed that the NOEs can be identified unambiguously, i.e. that it is

known with certainty whether any two NOESY peaks involve the same proton or not. The

resulting structures deviated by 1.0–1.4 Å RMSD for the backbone heavy atoms from the

previously reported X-ray and NMR structures (Grishaev and Llinás, 2002b). These results

show that assignment-free NMR structure calculation can successfully generate 3D protein

structures from experimental data.

As for all NMR spectrum analysis, resonance overlap presents a major difficulty also in

applying “no assignment” strategies. Indeed, if two resonances from nuclei that are far apart

in the structure have identical chemical shifts but distinct sets of neighbors they would be

represented by a single atom with one set of neighbors, leading to a gross distortion of the

calculated structure. In that respect, the use of heteronuclear-edited NOESY spectra

- 31 -

drastically reduces the likelihood of overlap. At present, a full de novo protein structure

determination by the assignment-free approach has not been reported yet, and it remains to be

seen whether the assignment-free approach will be able to provide the reliability and the

structure quality of the conventional method.

References

Abe H, Braun W, Noguti T, Gō N (1984) Rapid calculation of first and second derivatives of conformational energy with

respect to dihedral angles in proteins. General recurrent equations. Computers & Chemistry 8:239–247

Allen MP, Tildesley, DJ (1987) Computer Simulation of Liquids. Clarendon Press, Oxford

Altieri AS, Byrd RA (2004) Automation of NMR structure determination of proteins. Curr. Opin. Struct. Biol. 14: 547–553.

Andrec M, Levy RM (2002) Protein sequential resonance assignments by combinatorial enumeration using 13Ca chemical

shifts and their (i, i

−1) sequential connectivities. J. Biomol. NMR 23:263–270

Atkinson RW, Saudek V (1997) Direct fitting of structure and chemical shift to NMR spectra. J. Chem. Soc. Faraday Trans.

93:3319–3323

Atkinson RW, Saudek V (2002) The direct determination of protein structure by NMR without assignment. FEBS Lett.

510:1–4

Atreya HS, Sahu SC, Chary KVR, Govil G (2000) A tracked approach for automated NMR assignments in proteins

(TATAPRO). J. Biomol. NMR 17:125–136

Bailey-Kellogg C, Widge A, Kelley JJ, Berardi MJ, Bushweller JH, Donald BR (2000) The NOESY JIGSAW: Automated

protein secondary structure and main-chain assignment from sparse, unassigned NMR data. J. Comp. Biol. 7:537–558

Baran MC, Huang YJ, Moseley HNB, Montelione GT (2004) Automated analysis of protein NMR assignments and

structures. Chem. Rev. 104: 3541-3555

Bartels C, Xia, TH, Billeter M, Güntert P, Wüthrich K (1995) The program XEASY for computer-supported NMR-spectral

analysis of biological macromolecules. J. Biomol. NMR 6:1–10

Bartels C, Billeter M, Güntert P, Wüthrich K (1996) Automated sequence-specific NMR assignment of homologous proteins

using the program GARANT. J. Biomol. NMR 7:207–213

Bartels C, Güntert P, Billeter M, Wüthrich K (1997) GARANT-A general algorithm for resonance assignment of

multidimensional nuclear magnetic resonance spectra. J. Comp. Chem. 18:139–149

Berendsen HJC, Postma JPM, van Gunsteren WF, DiNola A, Haak JR (1984). Molecular dynamics with coupling to an

external bath. J. Chem. Phys. 81:3684–3690

Bhavesh NS, Panchal SC, Hosur RV (2001) An efficient high-throughput resonance assignment procedure for structural

genomics and protein folding research by NMR. Biochemistry 40:14727–14735

Brünger AT (1992) X-PLOR version 3.1. A system for X-ray crystallography and NMR. Yale University Press, New Haven

Brünger AT, Adams PD, Clore GM, DeLano WL, Gros P, Grosse-Kunstleve RW, Jiang JS, Kuszewski J, Nilges M, Pannu

NS, Read RJ, Rice LM, Simonson T, Warren GL (1998) Crystallography & NMR system: A new software suite for

macromolecular structure determination. Acta Crystallogr. D 54: 905–921

Calzolai L, Lysek DA, Güntert P, von Schroetter C, Riek R, Zahn R, Wüthrich K (2000) NMR structures of three single-

residue variants of the human prion protein. Proc. Natl. Acad. Sci. USA 97:8340–8345

Buchler, NEG, Zuiderweg ERP, Wang H, Goldstein RA (1997) Protein heteronuclear NMR assignments using mean-field

simulated annealing. J. Magn. Reson. 126:34–42

- 32 -

Chatterjee A, Bhavesh NS, Panchal SC, Hosur RV (2002) A novel protocol based on HN(C)N for rapid assignment in (

15

N,

13

C) labeled proteins: implications to structural genomics, Biochem. Biophys. Res. Commun. 293:427–432

Chin Y, Hwang JF, Chen TB, Soo VW (1992) RUBIDIUM, a program for computer-aided assignment of 2-dimensional

NMR-spectra of polypeptides. J. Chem. Inf. Comput. Sci. 32:183–187

Choy WY, Sanctuary BC, Zhu G (1997) Using neural network predicted secondary structure information in automatic

protein NMR assignment. J. Chem. Inf. Comput. Sci 37:1086–1094

Coggins BE, Zhou P (2003) PACES: Protein sequential assignment by computer-assisted exhaustive search. J. Biomol. NMR

26:93–111

Croft D, Kemmink J, Neidig KP, Oschkinat H (1997) Tools for the automated assignment of high-resolution three-

dimensional protein NMR spectra based on pattern recognition techniques. J. Biomol. NMR 10:207–219

Doreleijers JF, Mading S, Maziuk D, Sojourner K, Yin L, Zhu J, Markley JL, Ulrich EL (2003) BioMagResBank database

with sets of experimental NMR constraints corresponding to the structures of over 1400 biomolecules deposited in the

Protein Data Bank. J. Biomol. NMR 26:139–146

Drenth J (1994) Principles of protein X-ray crystallography. Springer, New York

Duggan BM, Legge GB, Dyson HJ, Wright PE (2001) SANE (Structure Assisted NOE Evaluation): An automated model-

based approach for NOE assignment. J. Biomol. NMR 19:321–329

Ellgaard L, Riek R, Herrmann T, Güntert P, Braun D, Helenius A, Wüthrich K (2001) NMR structure of the calreticulin P-

domain. Proc. Natl. Acad. Sci. USA 98:3133–3138

Ellgaard L, Bettendorff P, Braun D, Herrmann T, Fiorito F, Jelesarov I, Herrmann T, Güntert P, Helenius A, Wüthrich K

(2002) NMR structures of 36 and 73-residue fragments of the calreticulin P-domain. J. Mol. Biol. 322, 773–784

Enggist E, Thöny-Meyer L, Güntert P, Pervushin K (2002) NMR structure of the heme chaperone CcmE reveals a novel

functional motif. Structure 10:1551–1557

Friedrichs MS, Mueller L, Wittekind M (1994) An automated procedure for the assignment of protein

1

HN,

15

N,

13

C

α

,

1

H

α

,

13

C

β

and

1

H

β

resonances. J. Biomol. NMR 4:703–726

Fossi M, Linge J, Labudde D, Leitner D, Nilges M, Oschkinat H (2005) Influence of chemical shift tolerances on NMR

structure calculations using ARIA protocols for assigning NOE data. J. Biomol. NMR 31:21–34

Garrett DS, Powers R, Gronenborn AM, Clore GM (1991) A common-sense approach to peak picking in 2-dimensional, 3-

dimensional, and 4-dimensional spectra using automatic computer-analysis of contour diagrams. J. Magn. Reson. 95:214–

220

Gilquin B, Lecoq A, Desné F, Guenneugues M, Zinn-Justin S, Ménez A (1999) Conformational and functional variability

supported by the BPTI fold: Solution structure of the Ca2+ channel blocker calcicludine. Proteins 34:520–532

Greenfield NJ, Huang YJ, Palm T, Swapna GVT, Monleon D, Montelione GT, Hitchcock-DeGregori SE (2001) Solution

NMR structure and folding dynamics of the N terminus of a rat non-muscle alpha-tropomyosin in an engineered chimeric

protein. J. Mol. Biol. 312:833–847

Grishaev A, Llinás M (2002a) CLOUDS, a protocol for deriving a molecular proton density via NMR. Proc. Natl. Acad. Sci.

USA 99:6707–6712

Grishaev A, Llinás M (2002b) Protein structure elucidation from NMR proton densities. Proc. Natl. Acad. Sci. USA

99:6713–6718

Gronwald W, Kalbitzer HR (2004) Automated structure determination of proteins by NMR spectroscopy. Prog. NMR

Spectrosc. 44:33–96.

Gronwald W, Willard L, Jellard T, Boyko RE, Rajarathnam K, Wishart DS, Sonnichsen FD, Sykes BD (1998) CAMRA:

Chemical shift based computer aided protein NMR assignments. J. Biomol. NMR 12:395–405

- 33 -

Gronwald W, Moussa S, Elsner R, Jung A, Ganslmeier B, Trenner J, Kremer W, Neidig KP, Kalbitzer HR (2002) Automated

assignment of NOESY NMR spectra using a knowledge based method (KNOWNOE). J. Biomol. NMR 23:271–287

Gropp W, Lusk E, Doss N, Skjellum, A (1996) A high-performance, portable implementation of the MPI message passing

interface standard. Parallel Computing 22:789–828

Güntert P (2004) Automated NMR protein structure calculation with CYANA. Meth. Mol. Biol. 278:353–378

Güntert P (2003) Automated NMR protein structure calculation. Prog. NMR Spectrosc. 43:105–125

Güntert P (1998) Structure calculation of biological macromolecules from NMR data. Q. Rev. Biophys. 31:145–237

Güntert P, Braun W, Wüthrich K (1991) Efficient computation of three-dimensional protein structures in solution from

nuclear magnetic resonance data using the program DIANA and the supporting programs CALIBA, HABAS and GLOMSA.

J. Mol. Biol. 217:517–530

Güntert P, Berndt KD, Wüthrich K (1993) The program ASNO for computer-supported collection of NOE upper distance

constraints as input for protein structure determination. J. Biomol. NMR 3:601–606

Güntert P, Mumenthaler C, Wüthrich K (1997) Torsion angle dynamics for NMR structure calculation with the new program

DYANA. J. Mol. Biol. 273:283–298

Güntert P, Salzmann M, Braun D, Wüthrich K (2000) Sequence-specific NMR assignment of proteins by global fragment

mapping with the program MAPPER. J. Biomol. NMR 18:129–137.

Hare BJ, Prestegard JH (1994) Application of neural networks to automated assignment of NMR structures of proteins. J.

Biomol. NMR 4:35–46

Hare BJ, Wagner G (1999) Application of automated NOE assignment to three-dimensional structure refinement of a 28 kDa

single-chain T cell receptor. J. Biomol. NMR 15:103–113

Helgstrand M, Kraulis P, Allard P, Härd T (2000) ANSIG for Windows: An interactive computer program for semiautomatic

assignment of protein NMR spectra J. Biomol. NMR 18:329–336

Herrmann T, Güntert P, Wüthrich K (2002a) Protein NMR structure determination with automated NOE assignment using

the new software CANDID and the torsion angle dynamics algorithm DYANA. J. Mol. Biol. 319:209–227

Herrmann T, Güntert P, Wüthrich K (2002b) Protein NMR structure determination with automated NOE-identification in the

NOESY spectra using the new software ATNOS. J. Biomol. NMR 24:171–189

Hilge M, Siegal G, Vuister GW, Güntert P, Gloor SM, Abrahams JP (2003) ATP-induced conformational changes of the

nucleotide binding domain of Na,K-ATPase. Nat. Struct. Biol. 10:468–474

Hitchens TK, Lukin JA, Zhan YP, McCallum SA, Rule GS (2003) MONTE: An automated Monte Carlo based approach to

nuclear magnetic resonance assignment of proteins. J. Biomol. NMR 25:1–9

Horst R, Damberger F, Luginbühl P, Güntert P, Peng G, Nikonova L, Leal WS, Wüthrich K (2001) NMR structure reveals

intramolecular regulation mechanism for pheromone binding and release. Proc. Natl. Acad. Sci. USA 98:14374–14379

Huang YJ, Swapna GVT, Rajan PK, Ke H, Xia B, Shukla K, Inouye M, Montelione GT (2003) Solution NMR structure of

ribosome-binding factor A (RbfA), a cold-shock adaptation protein from Escherichia coli. J. Mol. Biol. 327:521-536

Huang YJ, Moseley HNB, Baran MC, Arrowsmith C, Powers R, Tejero R, Szyperski T, Montelione GT (2005) An

integrated platform for automated analysis of protein NMR structures. Meth. Enzymol. 394: 111-141

Jain A, Vaidehi N, Rodriguez G (1993) A fast recursive algorithm for molecular dynamics simulation. J. Comp. Phys.

106:258–268

Jee JG, Güntert P (2003) Influence of the completeness of chemical shift assignments on NMR structures obtained with

automated NOE assignment. J. Struct. Funct. Genom. 4:179-189

Johnson BA, Blevins RA (1994) NMR View - a computer program for the visualization and analysis of NMR data. J.

Biomol. NMR 4:603–614

Kalk A, Berendsen HJC (1976) Proton magnetic-relaxation and spin diffusion in proteins J Magn. Reson. 24:343–366

- 34 -

Kirkpatrick S, Gelatt Jr CD, Vecchi, MP (1983) Optimization by simulated annealing. Science 220:671–680

Koradi R, Billeter M, Wüthrich K (1996) MOLMOL: a program for display and analysis of macromolecular structures. J.

Mol. Graph. 14:51–55

Koradi R, Billeter M, Engeli M, Güntert P, Wüthrich K (1998) Towards fully automatic peak picking and integration of

biomolecular NMR spectra. J. Magn. Reson. 135:288–297

Kraulis PJ (1989) ANSIG - a program for the assignment of protein 1H 2D NMR spectra by interactive computer graphics. J.

Magn. Reson. 24:627–633

Kraulis PJ (1994) Protein 3-dimensional structure determination and sequence-specific assignment of 13C-separated and

15N-separated NOE data—a novel real-space ab-initio approach. J. Mol. Biol. 243:696–718

Kumar A, Ernst RR, Wüthrich K (1980) A two-dimensional nuclear overhauser enhancement (2D NOE) experiment for the

elucidation of complete proton-proton cross-relaxation networks in biological macromolecules. Biochem. Biophys. Res.

Commun. 95:1–6

Kuszewski J, Schwieters CD, Garrett DS, Byrd RA, Tjandra N, Clore GM (2004) Completely automated, highly error-

tolerant macromolecular structure determination from multidimensional nuclear overhauser enhancement spectra and

chemical shift assignments. J. Am. Chem. Soc. 126:6258–6273

Leach AR (2001) Molecular modeling. Principles and applications. 2

nd

edition. Prentice Hall, Harlow, UK

Lee D, Damberger FD, Peng G, Horst R, Güntert P, Nikonova L, Leal WS, Wüthrich K (2002) NMR structure of the

unliganded Bombyx mori pheromone-binding protein at physiological pH. FEBS Lett. 531:314–318

Leutner M, Gschwind RM, Liermann J, Schwarz C, Gemmecker G, Kessler H (1998) Automated backbone assignment of

labeled proteins using the threshold accepting algorithm. J. Biomol. NMR 11:31–43

Li KB, Sanctuary BC (1997a) Automated resonance assignment of proteins using heteronuclear 3D NMR. 1.Backbone spin

systems extraction and creation of polypeptides. J. Chem Inf. Comput. Sci. 37:359–366

Li KB, Sanctuary BC (1997b) Automated resonance assignment of proteins using heteronuclear 3D NMR. 2. Side chain and

sequence-specific assignment. J. Chem Inf. Comput. Sci. 37:467–477

Linge JP, O’Donoghue SI, Nilges M (2001) Automated assignment of ambiguous nuclear Overhauser effects with ARIA.

Meth. Enzymol. 339:71–90

Linge JP, Habeck M, Rieping W, Nilges M (2003) ARIA: automated NOE assignment and NMR structure calculation.

Bioinformatics 19:315–316

Linge JP, Habeck M, Rieping W, Nilges M (2004a) Correction of spin diffusion during iterative automated NOE assignment.

J. Magn. Reson. 167:334–342

Linge JP, Williams MA, Spronk CAEM, Bonvin AMJJ, Nilges M (2004b) Refinement of protein structures in explicit

solvent. Proteins 50:496–506

Lukin JA, Gove AP, Talukdar SN, Ho C (1997) Automated probabilistic method for assigning backbone resonances of

(

13

C,

15

N)-labeled proteins. J. Biomol. NMR 9:151–166

Macura, S, Ernst, RR (1980) Elucidation of cross relaxation in liquids by 2D NMR spectroscopy. Mol. Phys. 41:95–117

Madrid M, Llinás E, Llinás M (1991) Model-independent refinement of interproton distances generated from 1H-NMR

Overhauser intensities. J. Magn. Reson. 93:329–346

Malliavin TE, Rouh A, Delsuc M, Lallemand JY (1992) Approche directe de la détermination de structures moléculaires à

partir de l’effet Overhauser nucléaire. Compt. Rend. Acad. Sci. Serie II 315:635–659

Meadows RP, Olejniczak ET, Fesik SW (1994) A computer-based protocol for semiautomated assignments and 3D structure

determination of proteins. J. Biomol. NMR 4:79–96

Miura T, Klaus W, Ross A, Güntert P, Senn H (2002) The NMR structure of the class I human ubiquitin-conjugating enzyme

2b. J. Biomol. NMR, 22:89–92

- 35 -

Moseley, HNB, Montelione, GT (1999) Automated analysis of NMR assignments and structures for proteins. Curr. Op.

Struct. Biol. 9:635–642

Moseley, HNB, Monleon D, Montelione, GT (2001) Automatic determination of protein backbone resonance assignments

from triple resonance nuclear magnetic resonance data. Meth. Enzymol. 339:91–107

Mumenthaler C, Braun W (1995) Automated assignment of simulated and experimental NOESY spectra of proteins by

feedback filtering and self-correcting distance geometry. J. Mol. Biol. 254:465–480

Mumenthaler C, Güntert P, Braun W, Wüthrich K (1997) Automated procedure for combined assignment of NOESY spectra

and three-dimensional protein structure determination. J. Biomol. NMR 10:351–362

Nabuurs SB, Spronk CAEM, Krieger E, Maassen H, Vriend G, Vuister GW (2003) Quantitative evaluation of experimental

NMR restraints. J. Am. Chem. Soc. 125:12026–12034.

Nederveen AJ, Doreleijers JF, Vranken W, Miller Z, Spronk CAEM, Nabuurs, SB, Güntert P, Livny M, Markley JL, Nilges

M, Ulrich EL, Kaptein R, Bonvin AMJJ (2005) RECOORD: a REcalculated COORdinates Database of 500+ proteins from

the PDB using restraints from the BioMagResBank. Proteins 59:662–672.

Neuhaus D, Williamson MP (1989) The nuclear Overhauser effect in structural and conformational analysis. VCH,

Weinheim

Nilges M (1993) A calculation strategy for the structure determination of symmetric dimers by

1

H NMR. Proteins 17:297–

309

Nilges M (1995) Calculation of protein structures with ambiguous distance restraints. Automated assignment of ambiguous

NOE crosspeaks and disulphide connectivities. J. Mol. Biol. 245:645–660

Nilges M, O’Donoghue SI (1998) Ambiguous NOEs and automated NOE assignment. Prog. NMR Spectrosc. 32:107–139

Nilges M, Macias M, O’Donoghue SI, Oschkinat H (1997) Automated NOESY interpretation with ambiguous distance

constraints: The refined NMR solution structure of the pleckstrin homology domain from

β-spectrin. J. Mol. Biol. 269:408–

422

Oezguen N, Adamian L, Xu Y, Rajarathnam K, Braun W (2002) Automated assignment and 3D structure calculations using

combinations of 2D homonuclear and 3D heteronuclear NMR spectra. J. Biomol. NMR 22:249–263

Olson Jr JB, Markley JL (1994) Evaluation of an algorithm for the automated sequential assignment of protein backbone

resonances - a demonstration of the connectivity tracing assignment tools (CONTRAST) software package. J. Biomol. NMR

4:385–410

Ösapay K, Case DA (1991) A new analysis of proton chemical shifts in proteins. J. Am. Chem. Soc. 113:9436–9444

Oshiro CM, Kuntz ID (1993) Application of distance geometry to the proton assignment problem. Biopolymers 33:107–115

Oschkinat H, Croft D (1994) Automated assignment of multidimensional nuclear-magnetic-resonance spectra. Meth.

Enzymol. 239:308–318

Pristovšek P, Rüterjans H, Jerala R (2002) Semiautomatic sequence-specific assignment of proteins based on the tertiary

structure—the program st2nmr. J. Comput. Chem. 23:335–340

Savarin P, Zinn-Justin S, Gilquin B (2001) Variability in automated assignment of NOESY spectra and three-dimensional

structure determination: A test case on three small disulfide-bonded proteins. J. Biomol. NMR 19:49–62

Sitkoff D, Case DA (1997) Density functional calculations of proton chemical shifts in model peptides. J. Am. Chem. Soc.

119:12262–12273

Solomon I (1955) Relaxation processes in a system of two spins. Phys. Rev. 99:559–565

Spronk CAEM, Nabuurs SB, Krieger E, Vriend G, Vuister GW (2004) Validation of protein structures derived by NMR

spectroscopy. Prog. NMR Spectrosc. 45:315–347

Spronk CAEM, Linge JP, Hilbers CW, Vuister GW (2002) Improving the quality of protein structures derived by NMR

spectroscopy. J. Biomol. NMR 22: 281–289

- 36 -

Tian F, Valafar H, Prestegard JH (2001) A dipolar coupling based strategy for simultaneous resonance assignment and

structure determination of protein backbones. J. Am. Chem. Soc. 123:11791–11796

Wüthrich K (1986) NMR of proteins and nucleic acids. Wiley, New York

Xu J, Strauss SK, Sanctuary BC, Trimble L (1993) Automation of protein 2D proton NMR assignment by means of fuzzy

mathematics and graph-theory. J. Chem. Inf. Comput. Sci. 33:668–682

Xu J, Strauss SK, Sanctuary BC, Trimble L (1994) Use of fuzzy mathematics for complete automated assignment of peptide

1

H 2D NMR-spectra. J. Magn. Reson. B 103:53–58

Xu Y, Wu J, Gorenstein D, Braun W (1999) Automated 2D NOESY assignment and structure calculation of

crambin(S22/I25) with the self-correcting distance geometry based NOAH/DIAMOD programs. J. Magn. Reson. 136:76–85

Xu Y, Jablonsky MJ, Jackson PL, Braun W, Krishna NR (2001) Automated 2D NOESY assignment and structure calculation

of crambin(S22/I25) with the self-correcting distance geometry based NOAH/DIAMOD programs. J. Magn. Reson. 148:35–

46

Zahn R, Güntert P, von Schroetter C, Wüthrich K (2003) NMR structure of a human prion protein with two disulfide bridges.

J. Mol. Biol. 326:225–234

Zimmerman DE, Kulikowski CA, Huang YP, Feng WQ, Tashiro M, Shimotakahara S, Chien CY, Powers R, Montelione GT

(1997) Automated analysis of protein NMR assignments using methods from artificial intelligence. J. Mol. Biol. 269:592–

610

Figure captions

Fig. 1 General scheme of automated combined NOESY assignment and structure calculation.

Fig. 2 Structures of the heme chaperone CcmE (Enggist et al., 2002) obtained with the program CYANA in

seven consecutive cycles of combined automated NOESY assignment and structure calculation using torsion

angle dynamics. The backbones of the 10 conformers with lowest target function value in each cycle were

drawn with the program MOLMOL (Koradi et al., 1996).

Fig. 3 Three conditions that must be fulfilled by a valid assignment of a NOESY cross peak to two protons A

and B in the automated NOESY assignment with CYANA: (a) Agreement between chemical shifts and the peak

position, (b) network-anchoring, and (c) spatial proximity in a (preliminary) structure.

Fig. 4 Schematic illustration of the effect of constraint combination (Herrmann et al., 2002a) in the case of two

distance restraints, a correct one connecting atoms A and B, and a wrong one between atoms C and D. A

structure calculation that uses these two restraints as individual restraints that have to be satisfied simultaneously

will, instead of finding the correct structure (a), result in a distorted conformation (b), whereas a combined

restraint that will be fulfilled already if one of the two distances is sufficiently short leads to an almost

undistorted solution (c).

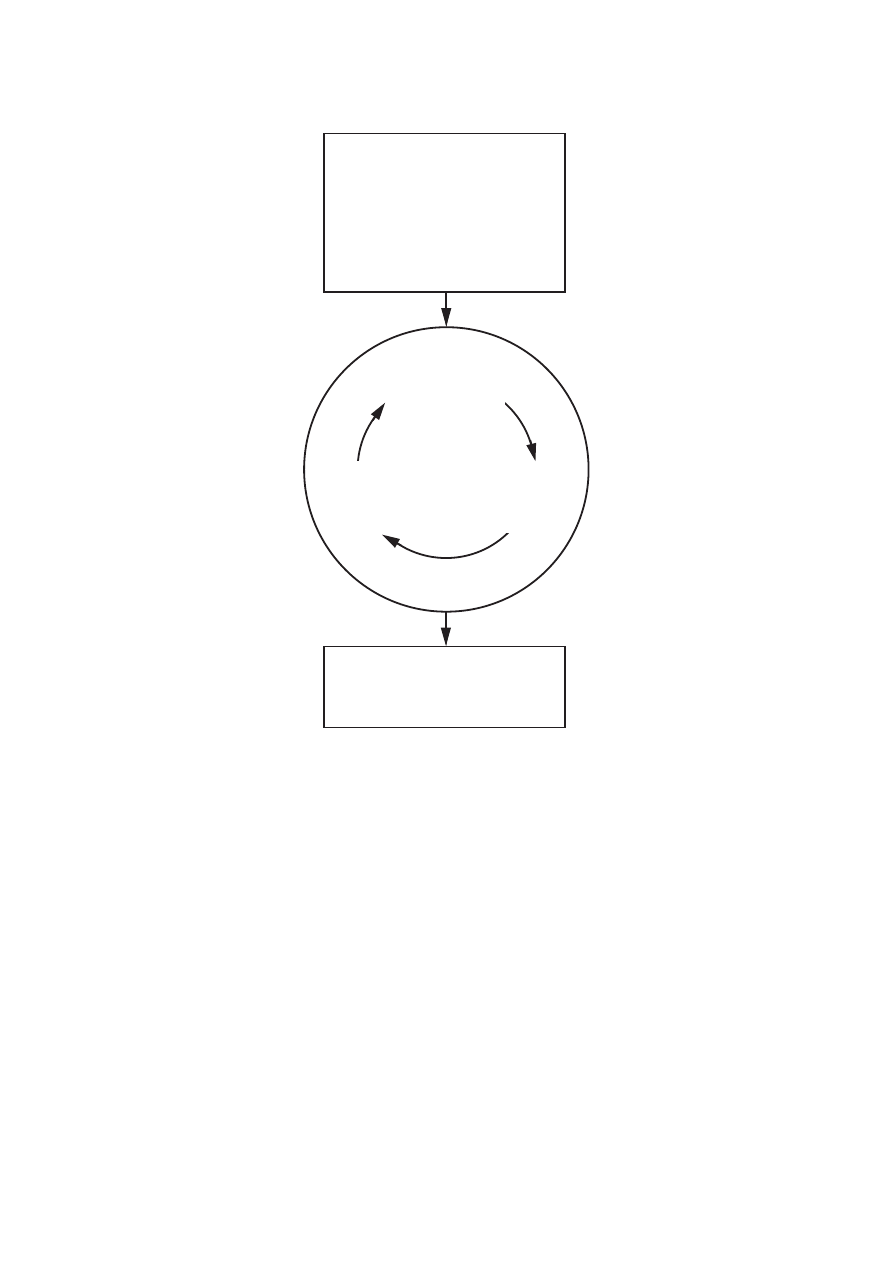
Find NOE

assignments

Evaluate NOE

assignments

Structure

calculation

Amino acid sequence

Sequence-specific

NOESY cross peak

positions and volumes

NOE assignments

3D Structure

assignments

Figure 1 (Güntert)

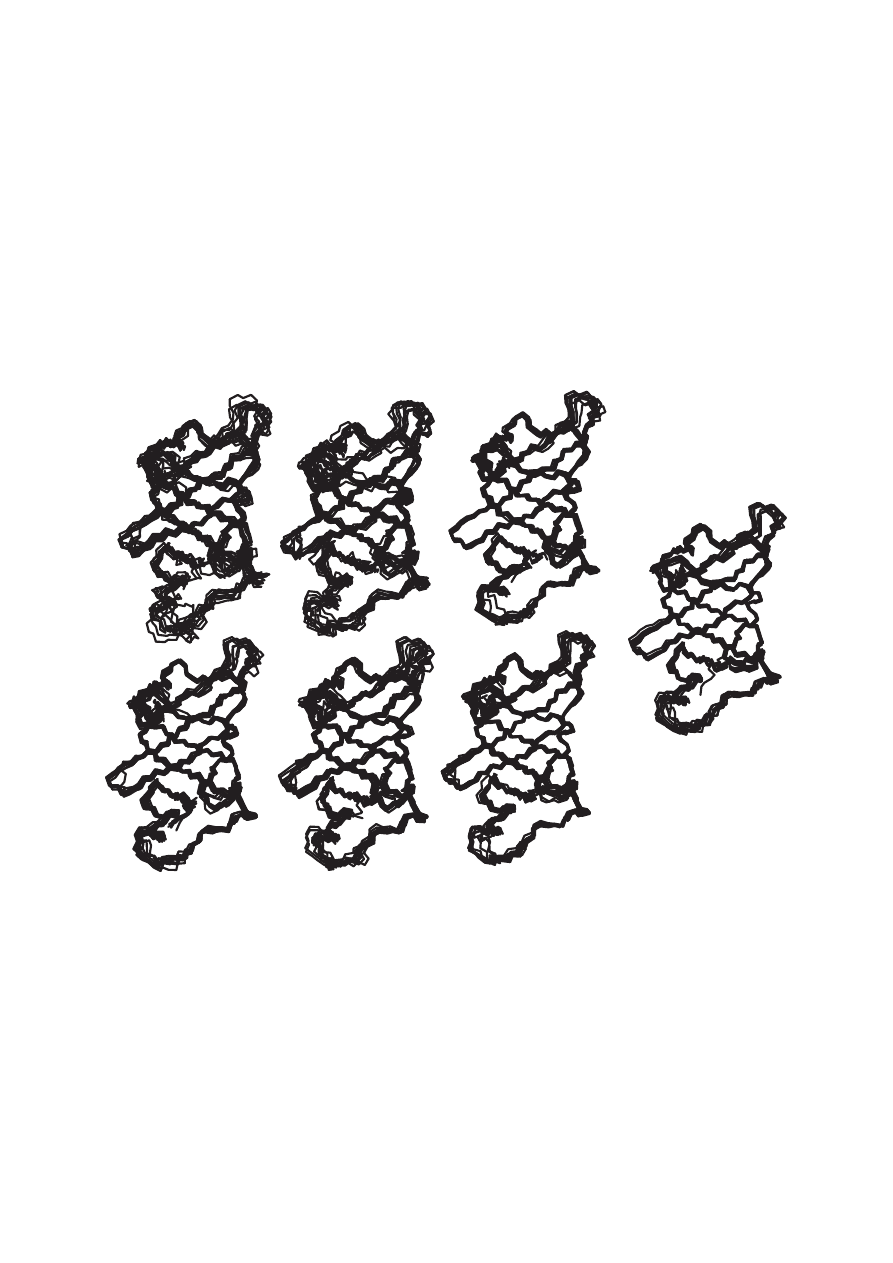
Cycle 1

Cycle 7

Cycle 6

Cycle 5

Cycle 4

Cycle 3

Cycle 2

Final structure

Figure 2 (Güntert)

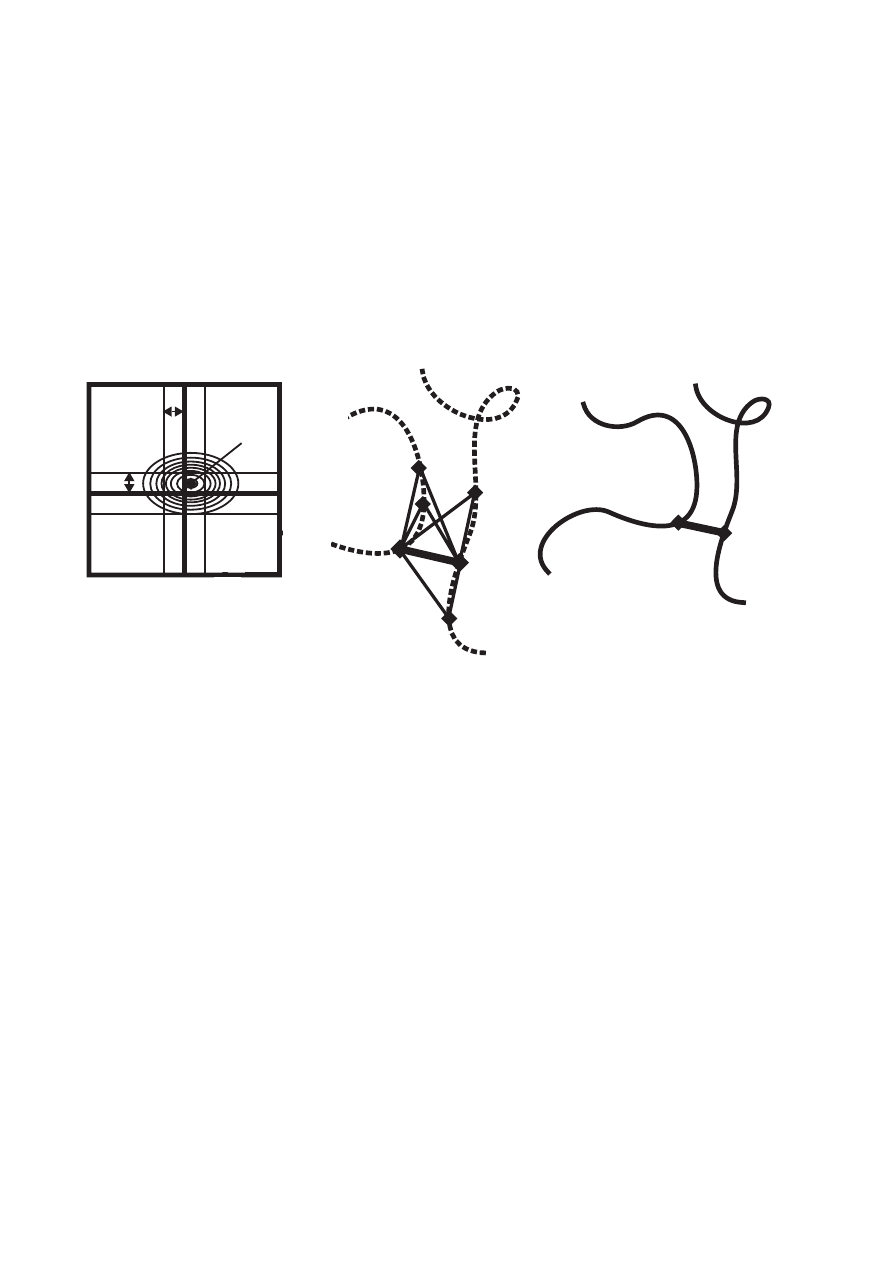
∆ω

Peak at
(

ω

1

,

ω

2

)

ω

A

ω

A

w

B

d

AB

< d

max

atom A

atom B

|ω

1

− ω

A

| < ∆ω |ω

2

− ω

B

| < ∆ω

ω

B

∆ω

(a)

(c)

(b)

A

B

Figure 3 (Güntert)

A

B

C

D

Correct

A

B

C

D

A

B

C

D

Combined

Individual

constraint

constraints

structure

A–B (correct)

C–D (wrong)

(unknown)

(a)

(c)

(b)

(ambiguous)

Figure 4 (Güntert)