PROJEKT NR 3 – KOMPUTEROWA METODA PRZEMIESZCZEŃ
POLITECHNIKA POZNAŃSKA
WYDZIAŁ BUDOWNICTWA I INśYNIERII ŚRODOWISKA
INSTYTUT KONSTRUKCJI BUDOWLANYCH
ZAKŁAD MECHANIKI BUDOWLI
PROJEKT NR 3 – KOMPUTEROWA METODA PRZEMIESZCZEŃ
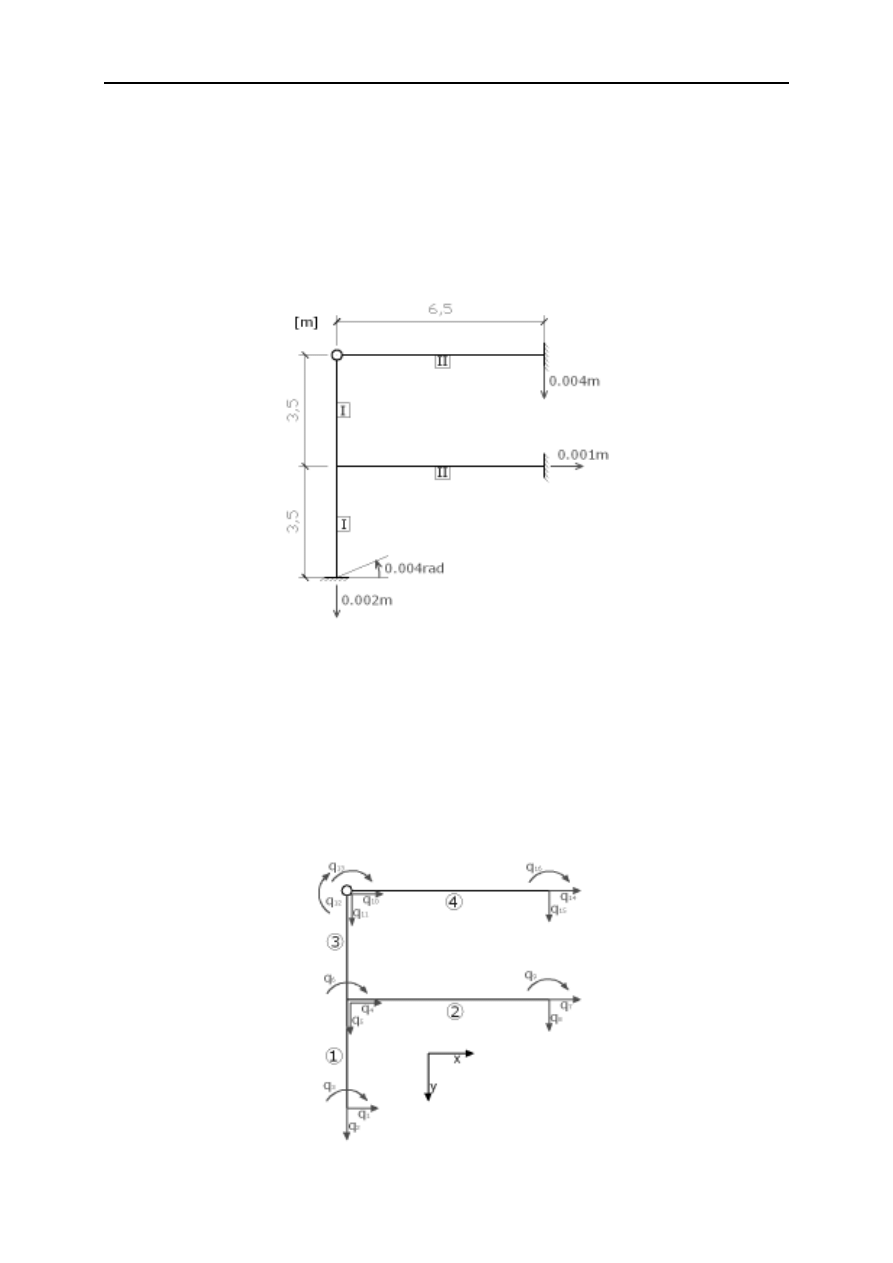
TEMAT: Dla układu przedstawionego na rysunku obliczyć rozkład sił wewnętrznych, korzystając z
komputerowej metody przemieszczeń.
schemat konstrukcji
Dane:
E=205 GPa
Pręty pionowe (I)
I200
A
I
=33,5 cm
2
EA
I
=686750 kN
I
I
=2140,0 cm
4
EI
I
=4387,0 kNm2
Pręty poziome (II)
I220
A
II
=39,6 cm
2
EA
II
=811800 kN
I
II
=3060,0 cm
4
EI
II
=6273,0 kNm2
Określenie SGN:
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Grzegorz Kamyszek KBI 1
1/8
PROJEKT NR 3 – KOMPUTEROWA METODA PRZEMIESZCZEŃ
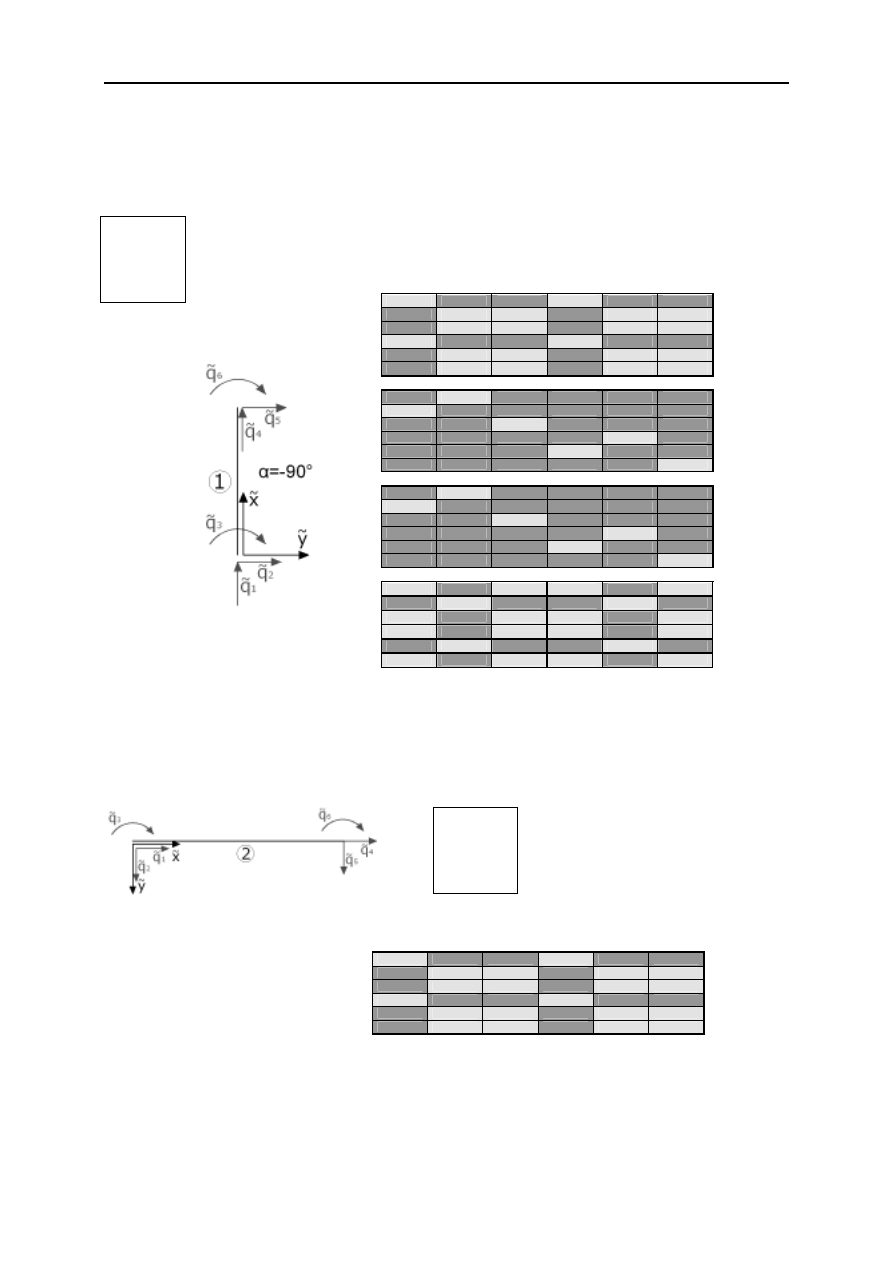
MACIERZE SZTYWNOŚCI POSZCZEGÓLNYCH PRĘTÓW:
T
K
T
K
T
~
=
Pręt 1 – pręt obustronnie utwierdzony
Macierz sztywności pręta w układzie lokalnym:
196214,3
0
0
-196214,3
0
0
0
1227,8
2148,7
0
-1227,8
2148,7
K`(1)=
0
2148,7
5013,7
0
-2148,7
2506,9
-196214,3
0
0
196214,3
0
0
0
-1227,8
-2148,7
0
1227,8
-2148,7
0
2148,7
2506,9
0
-2148,7
5013,7
0
-1
0
0
0
0
1
0
0
0
0
0
T=
0
0
1
0
0
0
0
0
0
0
-1
0
0
0
0
1
0
0
0
0
0
0
0
1
0
1
0
0
0
0
-1
0
0
0
0
0
T
T
=
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
-1
0
0
0
0
0
0
0
1
1227,8
0
2148,7
-1227,8
0
2148,7
0
196214,3
0
0
-196214,3
0
K(1)=
2148,7
0
5013,7
-2148,7
0
2506,9
-1227,8
0
-2148,7
1227,8
0
-2148,7
0
-196214,3
0
0
196214,3
0
2148,7
0
2506,9
-2148,7
0
5013,7
Macierz sztywności pręta w układzie globalnym
Pręt 2 – pręt obustronnie utwierdzony
Macierz sztywności pręta w układzie lokalnym/globalnym:
124892,3
0
0
-124892,3
0
0
0
274,1
890,8
0
-274,1
890,8
K(2)=
0
890,8
3860,3
0
-890,8
1930,2
-124892,3
0
0
124892,3
0
0
0
-274,1
-890,8
0
274,1
-890,8
0
890,8
1930,2
0
-890,8
3860,3
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Grzegorz Kamyszek KBI 1
2/8
dane:
l=
3,5
EI=
4387
EA=
686750
dane:
l=
6,5
EI=
6273
EA=
811800
PROJEKT NR 3 – KOMPUTEROWA METODA PRZEMIESZCZEŃ
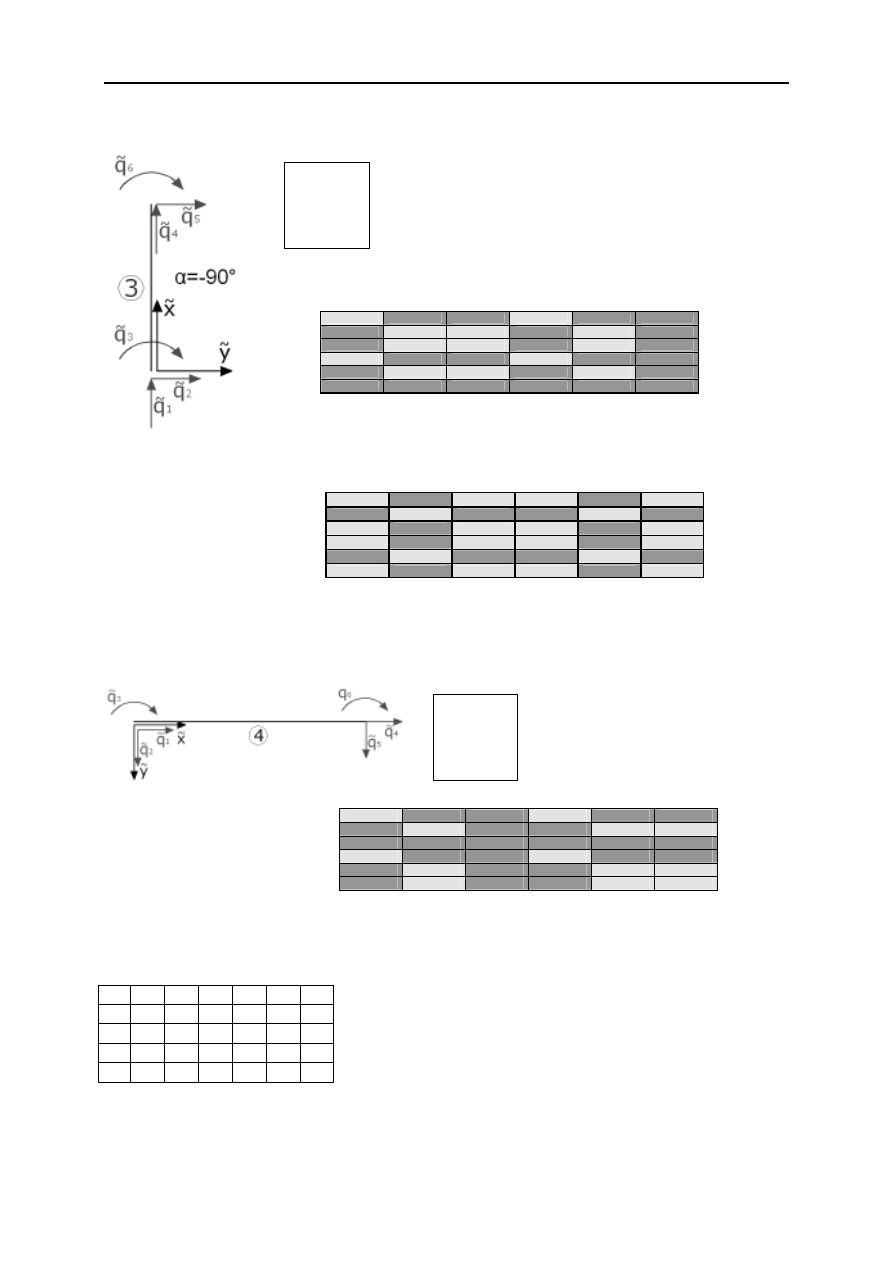
Pręt 3 – pręt z przegubem na prawym końcu
Macierz sztywności pręta w układzie lokalnym:
Macierz transformacji jak dla pręta 1
Macierz sztywności pręta w układzie globalnym:
307,0
0
1074,4
-307,0
0
0,0
0
196214,3
0
0
-196214,3
0
K(3)=
1074,4
0
3760,3
-1074,4
0
0,0
-307,0
0
-1074,4
307,0
0
0,0
0
-196214,3
0
0
196214,3
0
0,0
0
0,0
0,0
0
0,0
Pręt 4 – pręt z przegubem na lewym końcu
TABELA POWIĄZAŃ
124892,3
0
0
-124892,3
0
0
0
68,5
0
0
-68,5
445,4
K(4)=
0
0
0
0
0
0
-124892,3
0
0
124892,3
0
0
0
-68,5
0
0
68,5
-445,4
0
445,4
0
0
-445,4
2895,2
Tabela powiązań:
Nr 1 2 3 4 5 6
1
1
2
3
4
5
6
2
4
5
6
7
8
9
3
4
5
6 10 11 12
4
10 11 13 14 15 16
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Grzegorz Kamyszek KBI 1
3/8
dane:
l=
3,5
EI=
4387
EA=
686750
196214,3
0
0
-196214,3
0
0
0
307,0
1074,4
0
-307,0
0
K`(3)=
0
1074,4
3760,3
0
-1074,4
0
-196214,3
0
0
196214,3
0
0
0
-307,0
-1074,4
0
307,0
0
0
0
0
0
0
0
dane:
l=
6,5
EI=
6273
EA=
811800

PROJEKT NR 3 – KOMPUTEROWA METODA PRZEMIESZCZEŃ
MACIERZ SZTYWNOŚĆI DLA CAŁEGO UKŁADU:
W wierszu 4, 5, 6 i kolumnie 4, 5, 6 należy dodać do siebie macierze 1, 2, 3.
W wierszu 10, 11 i kolumnie 10, 11 należy dodać do siebie macierze 3 i 4.
Obliczenie wektora P:
0
R
P
P
W
−
=
0
=
W
P
-
brak obciążenia zewnętrznego
Pręt 1:
)
1
(
~
)
1
(
~
)
1
(
0
~
q
K
R
=
transformacja do układu globalnego
Pręt 2:
)
2
(
~
)
2
(
~
)
2
(
0
~
q
K
R
=
układ nie wymaga transformacji
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Grzegorz Kamyszek KBI 1
4/8
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
1227,8
0
2148,7
-1227,8
0
2148,7
0
0
0
0
0
0
0
0
0
0
2
0
196214,3
0
0
-196214,3
0
0
0
0
0
0
0
0
0
0
0
3
2148,7
0
5013,7
-2148,7
0
2506,9
0
0
0
0
0
0
0
0
0
0
4
-1227,8
0
-2148,7
126427,1
0
-1074,4
-124892,3
0
0
-307,0
0
0
0
0
0
0
5
0
-196214,3
0
0
392702,7
890,8
0
-274,1
890,8
0
-196214,3
0
0
0
0
0
6
2148,7
0
2506,9
-1074,4
890,8
12634,3
0
-890,8
1930,2
-1074,4
0
0
0
0
0
0
7
0
0
0
-124892,3
0
0
124892,3
0
0
0
0
0
0
0
0
0
8
0
0
0
0
-274,1
-890,8
0
274,1
-890,8
0
0
0
0
0
0
0
9
0
0
0
0
890,8
1930,2
0
-890,8
3860,3
0
0
0
0
0
0
0
10
0
0
0
-307,0
0
-1074,4
0
0
0
125199,3
0
0
0
-124892,3
0
0
11
0
0
0
0
-196214,3
0
0
0
0
0
196282,8
0
0
0
-68,5
445,4
12
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
13
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
14
0
0
0
0
0
0
0
0
0
-124892,3
0
0
0
124892,3
0
0
15
0
0
0
0
0
0
0
0
0
0,0
-68,5
0
0
0
68,5
-445,4
16
0
0
0
0
0
0
0
0
0
0,0
445,4
0
0
0
-445,4
2895,2
macierz sztywno
ś
ci pr
ę
ta 1
macierz sztywno
ś
ci pr
ę
ta 3
macierz sztywno
ś
ci pr
ę
ta 2
macierz sztywno
ś
ci pr
ę
ta 4
027
,
10
594
,
8
429
,
392
055
,
20
595
,
8
43
,
392
0
0
0
004
,
0
0
002
,
0
)
1
(
~
)
1
(
0
~
−
−
−
−
=
−
−
=
K
R
)
1
(
0
~
0
)
(
R
T
R
T
e
=
027
,
10
43
,
392
594
,
8
055
,
20
43
,
392
595
,
8
)
(
0
−
−
−
−
=
e
R
0
0
892
,
124
0
0
89
,
124
0
0
001
,
0
0
0
0
)
2
(
~
)
2
(
0
~
−
=
=
K
R
)
2
(
0
~
0
)
(
R
R
e
=

PROJEKT NR 3 – KOMPUTEROWA METODA PRZEMIESZCZEŃ
Pręt 3:
)
3
(
~
)
3
(
~
)
3
(
0
~
q
K
R
=
układ nie wymaga transformacji
Pręt 4:
)
4
(
~
)
4
(
~
)
4
(
0
~
q
K
R
=
układ nie wymaga transformacji
Wektor P po agregacji:
7817
,
1
16
2741
,
0
15
0
14
0
13
0
12
2741
,
0
11
0
10
0
9
0
8
89
,
124
7
027
,
10
6
429
,
392
5
297
,
116
4
055
,
20
3
43
,
392
2
595
,
8
1
0
−
−
−
=
−
=
R
P
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Grzegorz Kamyszek KBI 1
5/8
0
0
0
0
0
0
0
0
0
0
0
0
)
3
(
~
)
3
(
0
~
=
=
K
R
)
3
(
0
~
0
)
(
R
R
e
=
782
,
1
274
,
0
0
0
274
,
0
0
0
004
,
0
0
0
0
0
)
4
(
~
)
4
(
0
~
−
−
=
=
K
R
)
4
(
0
~
0
)
(
R
R
e
=
PROJEKT NR 3 – KOMPUTEROWA METODA PRZEMIESZCZEŃ
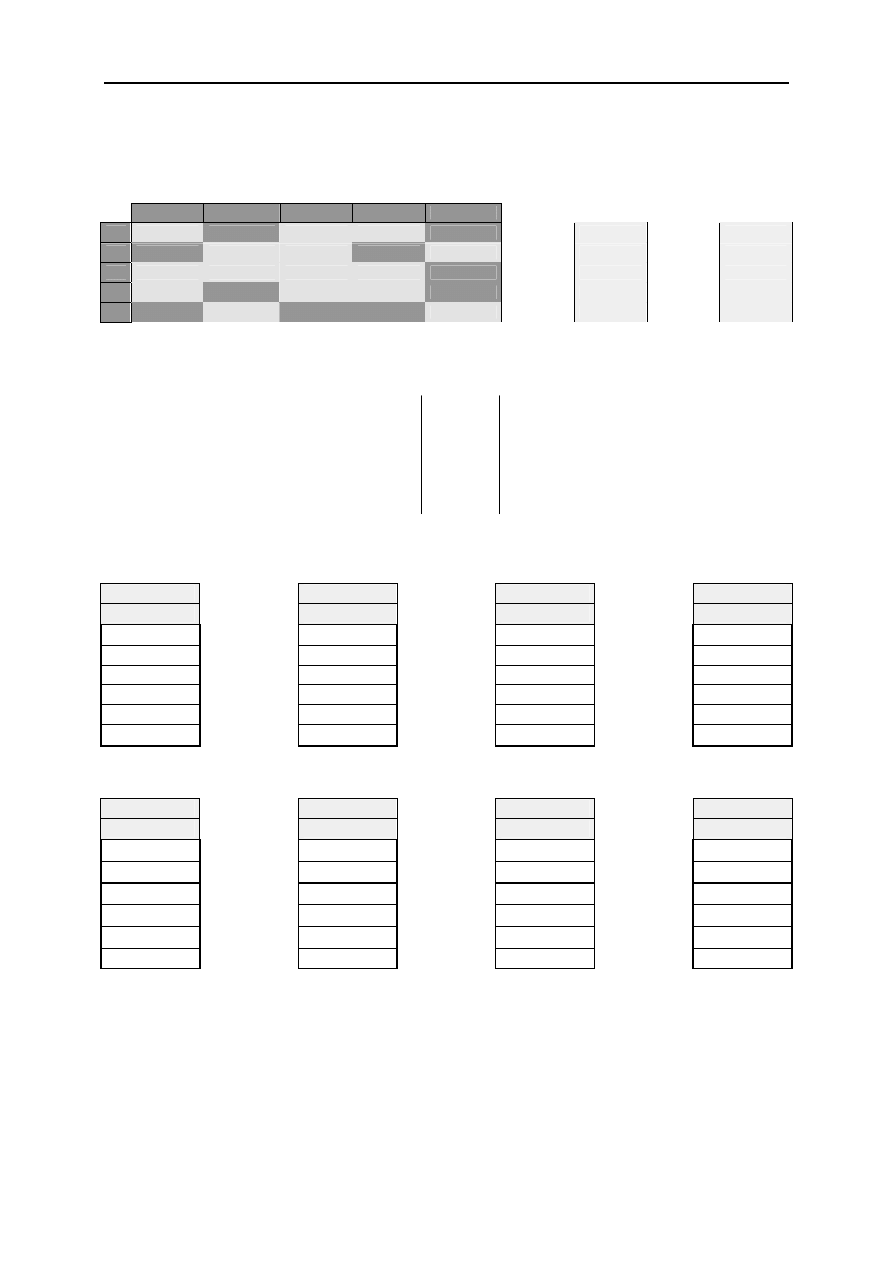
Po uwzględnieniu warunków podparcia (wykreśleni wierszy oraz kolumn nr 1, 2, 3, 7, 8, 9, 14, 15, 16 oraz
redukcji prętów 3 i 4 otrzymuję układ:
]
1
5
[
]
1
5
[
]
5
5
[
x
x
x
P
q
K
=
⋅
K
q
P
4
5
6
10
11
4
126427,1
0
-1074,4
-307,0
0
q1
116,2974
5
0
392702,7
890,8
0
-196214,3
q2
392,4286
6
-1074,4
890,8
12634,3
-1074,4
0
*
q3
=
10,02743
10
-307,0
0
-1074,4
125199,3
0
q4
0
11
0
-196214,3
0
0
196282,8
q5
0,274105
Po rozwiązaniu układu otrzymujemy wektor przemieszczeń węzłowych:
001995
,
0
000009
,
0
000733
,
0
001995
,
0
000926
,
0
=
P
Wektory przemieszczeń globalne dla poszczególnych prętów:
pr
ę
t1
pr
ę
t2
pr
ę
t3
pr
ę
t4
q
(1)
q
(2)
q
(3)
q
(4)
0
0,000926
0,000926
0,000009
0
0,001995
0,001995
0,001995
0
0,000733
0,000733
1
0,000926
0
0,000009
0
0,001995
0
0,001995
0
0,000733
0
1
0
Wektory przemieszczeń lokalne dla poszczególnych prętów
)
(
)
(
~
e
e
q
T
q
⋅
=
:
pr
ę
t1
pr
ę
t2
pr
ę
t3
pr
ę
t4
q
~(1)
q
~(2)
q
~(3)
q
~(4)
0
0,000926
-0,001995
0,000009
0
0,001995
0,000926
0,001995
0
0,000733
0,000733
1
-0,00199
0
-0,001995
0
0,000926
0
0,000009
0
0,000733
0
1
0
W macierzy przemieszczeń w pręcie 3 oraz 4 występuje niewiadoma powstała w wyniku redukcji tych
prętów, ponieważ nie wpływa ona na dalsze obliczenia można w tym miejscu wpisać dowolna liczbę aby
umożliwić dalsze obliczenia w programach kalkulacyjnych. Tu wpisano liczbę 1.
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Grzegorz Kamyszek KBI 1
6/8
PROJEKT NR 3 – KOMPUTEROWA METODA PRZEMIESZCZEŃ
Wektory reakcji węzłowych:
)
(
0
~
)
(
~
)
(
~
)
(
~
e
e
e
e
R
q
K
R
+
⋅
=
pr
ę
t1
pr
ę
t2
pr
ę
t3
pr
ę
t4
R`1
R`2
R`3
R`4
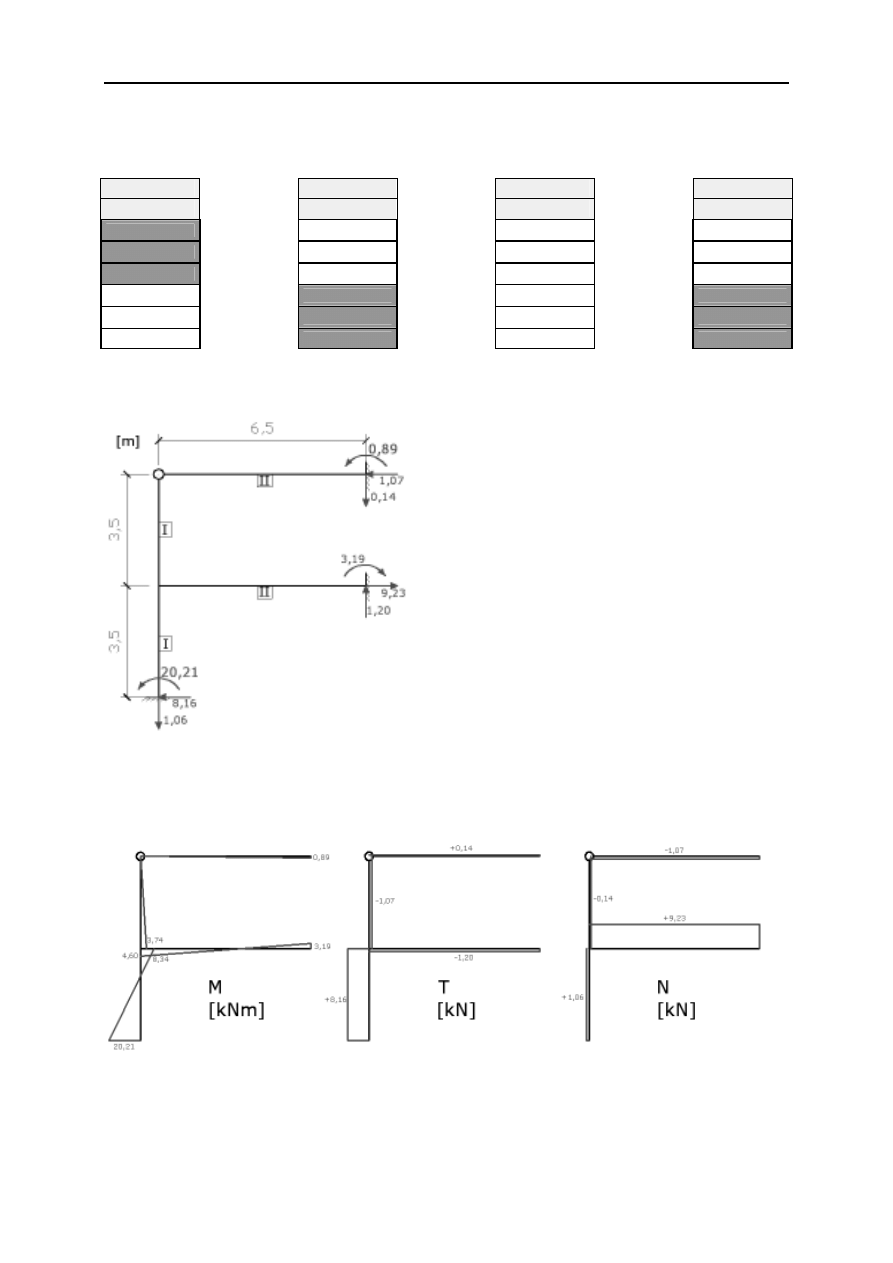
-1,06
-9,23
0,14
1,07
-8,16
1,20
1,07
-0,14
-20,21
4,60
3,74
0,00
1,06
9,23
-0,14
-1,07
8,16
-1,20
-1,07
0,14
-8,34
3,19
0,00
-0,89
Reakcje więzów:
Kontrola statyczna:
∑
=
+
−
−
=
0
23
,
9
07
,
1
16
,
8
X
∑
=
−
+
−
=
0
14
,
0
20
,
1
06
,
1
Y
∑
=
⋅
−
⋅
+
⋅
−
⋅
+
−
+
−
=
015
,
0
5
,
6
20
,
1
5
,
3
23
,
9
7
07
,
1
5
,
6
14
,
0
89
,
0
19
,
3
21
,
20
1
M
Wykresy sił wewnętrznych:
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Grzegorz Kamyszek KBI 1
7/8
PROJEKT NR 3 – KOMPUTEROWA METODA PRZEMIESZCZEŃ
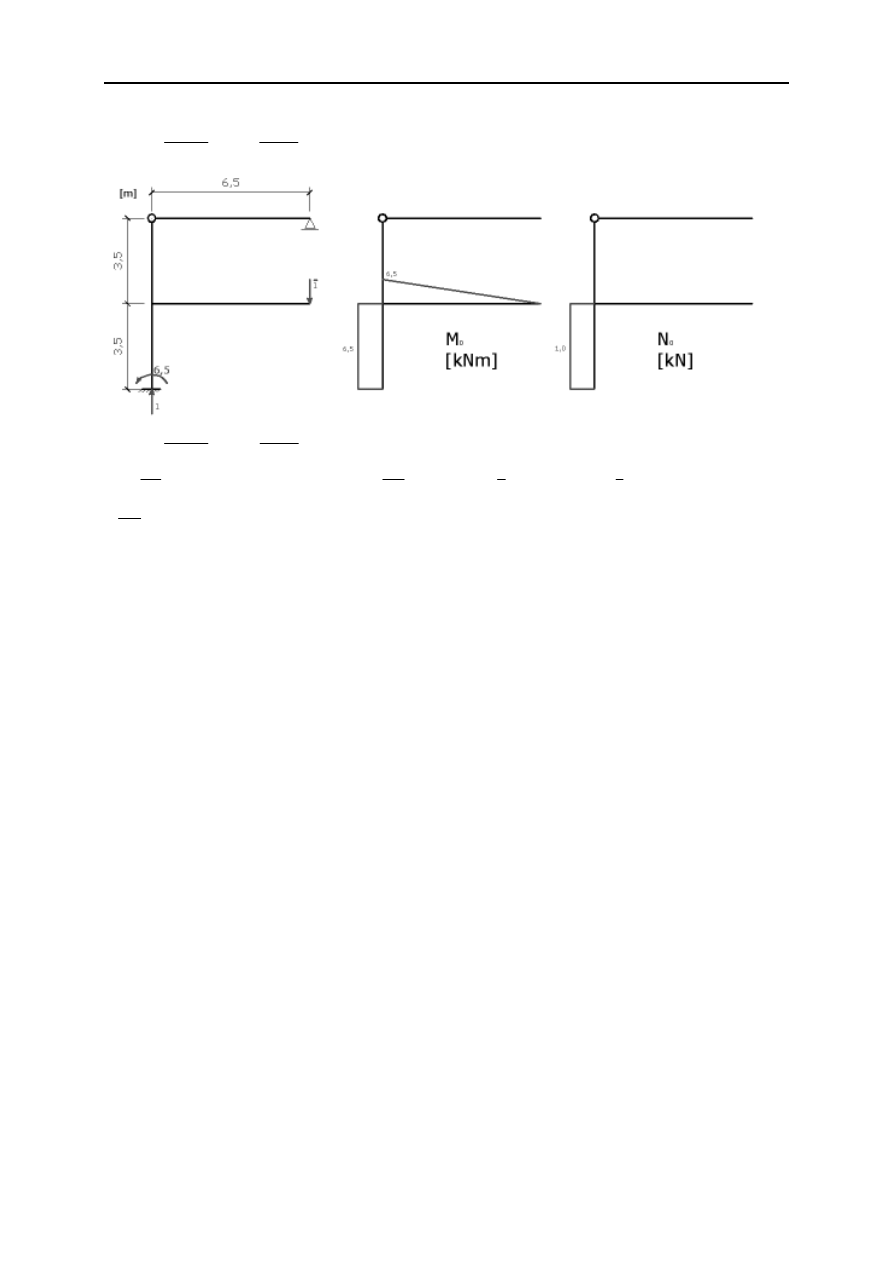
Kontrola kinematyczna:
∆
−
+
=
⋅
∑
∑∫
∑∫
−
−
−
i
n
n
R
dx
EA
N
N
dx
EI
M
M
V
0
0
1
=
∆
−
+
=
⋅
∑
∑∫
∑∫
−
−
−
i
n
n
R
dx
EA
N
N
dx
EI
M
M
V
0
0
1
[
]
[
]
%
04
,
0
000014
,
0
024
,
0
000005402
,
0
006769
,
0
03075
,
0
]
004
,
0
5
,
6
002
,
0
1
[
1
5
,
3
06
,
1
1
5
,
6
3
1
5
,
6
19
,
3
5
,
0
5
,
6
3
2
5
,
6
61
,
4
5
,
0
1
5
,
6
5
,
3
35
,
8
5
,
0
5
,
6
5
,
3
21
,
20
5
,
0
1
1
1
2
1
≈
−
=
−
+
−
=
⋅
+
⋅
−
−
⋅
⋅
+
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
−
+
⋅
⋅
⋅
−
⋅
⋅
⋅
=
⋅
−
EA
EI
EI
V
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Grzegorz Kamyszek KBI 1
8/8
Wyszukiwarka
Podobne podstrony:
proj156 id 397568 Nieznany
proj158 id 397570 Nieznany
proj157 id 397569 Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
analiza ryzyka bio id 61320 Nieznany
pedagogika ogolna id 353595 Nieznany
Misc3 id 302777 Nieznany
więcej podobnych podstron