Konspekt nr 2 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”

1

Rozkład jednowymiarowej zmiennej losowej i jej podstawowe

parametry charakterystyczne

1.

Pojęcie zmiennej losowej

Zmienna losowa w ujęciu intuicyjnym (związana z pewnym doświadczeniem), to taka

zmienna, która w wyniku doświadczenia przyjmuje pewną wartość liczbową, a więc nie dają-

cą się ustalić przed przeprowadzeniem doświadczenia. Formalna definicja jest następująca.

Mamy dowolną przestrzeń probabilistyczną (Ω, T, P)

I

.

Zmienna losową nazywamy do-

wolną funkcję X, której dziedziną są elementy ω przestrzeni zdarzeń elementarnych Ω, a

przeciwdziedziną (czyli wartości jakie ta funkcja może przyjmować) zbiór liczb rzeczywi-
stych R

, mającą następujące własności: dla dowolnej, ustalonej liczby rzeczywistej x zbiór

zdarzeń elementarnych ω, dla których spełniona jest nierówność X(ω) < x, jest zdarzeniem
losowym, czyli

( )

{

}

T

∈

<

ω

ω

x

X

:

dla ka

żdego

R

∈

x

(1).

Zmienne

losowe oznaczamy dużymi literami np.: X, Y, Z, S, T a ich wartości odpowiedni-

mi małymi literami: x, y, z, s, t, czasami z indeksami.

PRZYKŁAD 1. W pewnym zakładzie pracy zatrudnionych jest N osób. Załóżmy, że interesuje nas taka ce-

cha pracowników jak ich wiek. Oznaczmy go przez X. Dokonujemy losowego wyboru jednego pracownika spo-

śród wszystkich N osób. Oczywiście przed wybraniem pracownika nie jesteśmy w stanie dokładnie powiedzieć

jaki będzie on miał wiek. A więc wiek pracownika będzie zmienna losową, którą oznaczyliśmy przez X, a kon-
kretny wiek wylosowanej osoby oznaczamy przez x.

Rozróżniamy dwa typy zmiennych losowych:

− zmienne losowe skokowe (dyskretne),
− zm

ienne losowe ciągłe.

Zmienne losowe skokowe mogą przyjmować wartości wyrażające się tylko niektórymi

liczbami rzeczywistymi z określonych przedziałów. Najczęściej są to liczby całkowite nie-
ujemne.

Zbiór wszystkich wartości jakie może przyjmować zmienna losowa skokowa jest

zawsze przeliczalny

II

PRZYKŁAD 2. Przykładem zmiennej losowej skokowej o przeliczalnym zbiorze wartości może być liczba

wypadków komunikacyjnych w określonym przedziale czasowym w danym kraju, liczba cykli do momentu

zniszczenia próbki w próbie zmęczeniowej, liczba kontuzji zawodników w ciągu roku w danym klubie sporto-

wym itp. Każda z tych zmiennych losowych może przyjmować wartości wyrażające się liczbami całkowitymi

nieujemnymi. W żaden jednak sposób nie da się ściśle ustalić jaką może ona przyjąć wartość największą.

a niekiedy skończony.

PRZYKŁAD 3. Zmienną losową skokową ze skończonym zbiorem wartości może być przykładowo liczba

wadliwych sztuk

w danej partii produktu. Taka zmienna nie może oczywiście przyjąć wartości większej niż ilość

sztuk.

Zmienne losowe ciągłe przyjmują wartości wyrażające się dowolnymi liczbami rzeczywi-

stymi z określonych przedziałów.

I

Pojęcie przestrzeni probabilistycznej nie będzie zdefiniowana w niniejszym opracowaniu. Należy jedynie wie-

dzieć, że jest to trójka składająca się z następujących elementów: przestrzeni zdarzeń elementarnych Ω, pola
zdarzeń T, oraz prawdopodobieństwa P.

II

Zbiór przeliczalny intuicyjnie można zdefiniować jako zbiór, którego elementy można uporządkować w ciąg

(skończony bądź nie), tzn. „wypisać je po kolei”, „ponumerować”. Zbiór licz rzeczywistych R nie jest zbiorem

przeliczalnym.

Konspekt nr 2 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”

2

PRZYKŁAD 4. Za przykład zmiennej losowej ciągłej może posłużyć temperatura jakiegoś ciała, stężenie

procentowe roztworu, czas bezawaryjnej pracy jakiegoś urządzenia itp. Jeżeli temperaturę ciała będziemy mie-

rzyć w kelwinach, to wówczas może ona wyrazić się dowolną liczbą rzeczywistą z przedziału [-273, T

r

], gdzie T

r

oznacza temperaturę termicznego rozkładu materiału. Stężenie roztworu wyraża sie dowolną liczbą rzeczywistą

z przedziału [0, 100] a czas bezawaryjnej pracy urządzenia - liczbą rzeczywistą z przedziału [0, +∞).

Przedstawiony podział na zmienne losowe skokowe i ciągłe ma znaczenie tylko meryto-

ryczne. W praktyce wszystkie zmienne losowe są skokowe. Niektóre z nich jak np. tempera-
t

ura ciała jest zmienną losową, której wartości zmieniają się z krokiem równym dokładności

termometru za pomocą, którego dokonujemy pomiaru. Można jednak użyć termometru o

jeszcze większej dokładności i ta sama zmienna losowa będzie zmieniać się z jeszcze mniej-

szych krokiem. Pomijając ograniczenia fizyczne, można użyć termometru o dowolnej dokład-

ności, dlatego pod względem matematycznym taka zmienna jest traktowana jako ciągła.

2. Charakterystyki jednowymiarowej zmiennej losowej

Każda zmienna losowa przedstawiona w postaci (1) jest funkcją, która zdarzeniom loso-

wym przyporządkowuje wartości liczbowe. Zdarzenia te realizują się z prawdopodobień-

stwem określonym przez zespół warunków, w którym się ono odbywa. W konsekwencji, po-

szczególne wartości zmiennej losowej realizują się z takimi samymi prawdopodobieństwami

jak odpowiadające im zdarzenia losowe. Regułę, według której jednostkowa masa prawdopo-

dobieństwa rozłożona jest na poszczególne wartości zmiennej losowej, albo na pewne skupi-

ska tych wartości, nazywamy rozkładem prawdopodobieństwa zmiennej losowej.
2.1. Funkcja prawdopodobieństwa oraz funkcja gęstości prawdopodobieństwa

Dla zmiennej losowej skokowej rozkład prawdopodobieństwa może być dany za pomocą

funkcji prawdopodobieństwa

(

) ( )

i

i

i

p

x

x

X

=

=

=

P

P

dla i = 1, ...,k

(2)

takiej, że

*

∑

=

=

k

i

i

p

1

1

(3)

Funkcja (2)

przyporządkowuje wartości prawdopodobieństwa p

i

poszczególnym warto-

ściom x

i

zmiennej losowej X

. Jeżeli zmienna losowa X przyjmowałaby nieskończenie wiele

wartości, to granicę sumowanie w (3) należy zamienić z k na ∞.

PRZYKŁAD 1. Na podstawie długotrwałych obserwacji procesu produkcji pewnych odlewów stwierdzono,

że:

70% odlewów spełnia warunki jakościowe i należy do gatunku pierwszego (zdarzenie losowe A

1

),

25% odlewów spełnia warunki jakościowe i należy do gatunku drugiego (zdarzenie losowe A

2

),

5% odlewów nie odpowiada wymogom jakościowym (zdarzenie losowe A

3

).

Określmy następującą zmienną losową:











−

−

−

=

.

zdarzenie

zachodzi

gdy

3

,

zdarzenie

zachodzi

gdy

2

,

zdarzenie

zachodzi

gdy

1

3

2

1

A

A

A

X

Funkcja prawdopodobieństwa tej zmiennej losowej przedstawia się następująco:

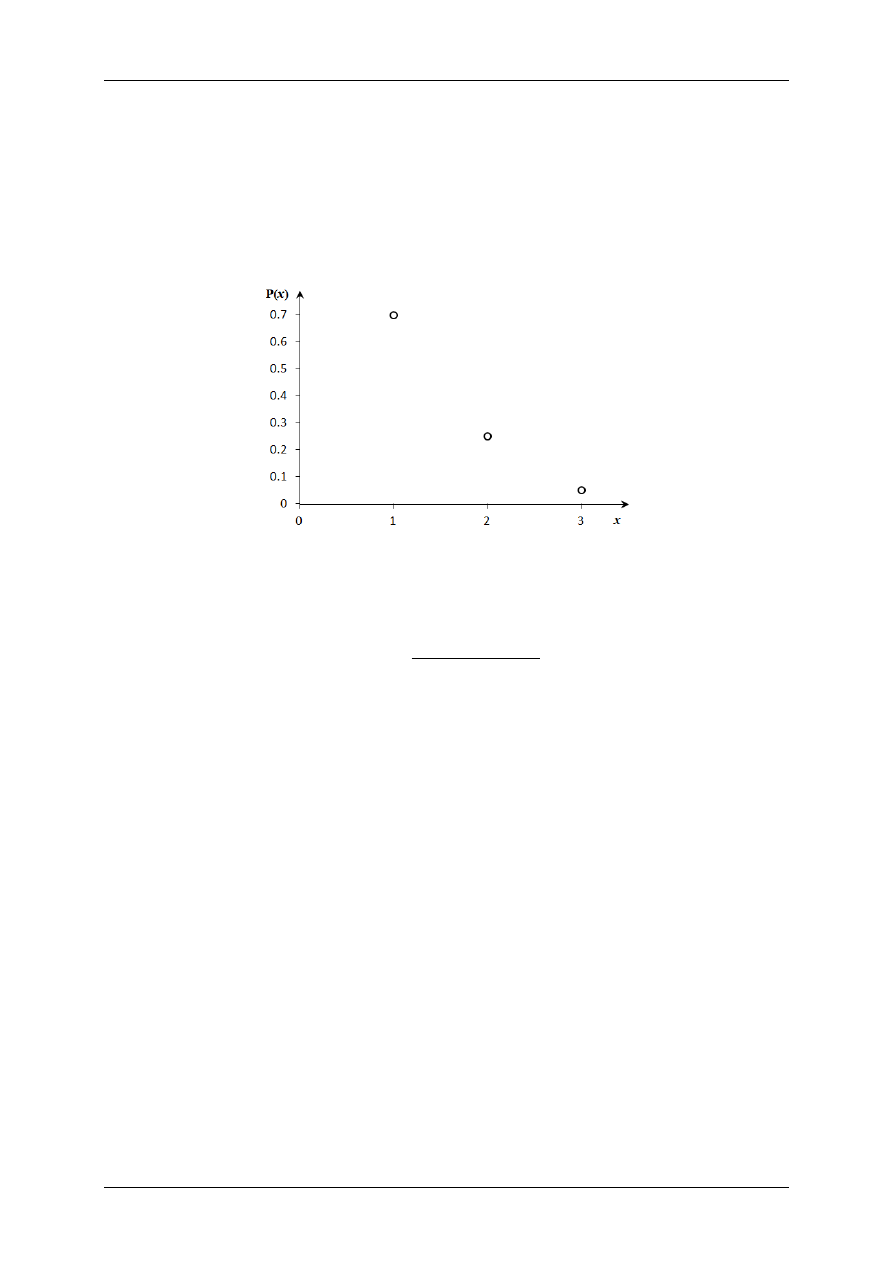
Konspekt nr 2 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”

3

(

)

(

)

(

)

.

05

.

0

3

P

,

25

.

0

2

P

,

70

.

0

1

P

=

=

=

=

=

=

X

X

X

Wykres tej funkcji przedstawiony jest na rys. 1.

Rys. 1.

Przykład funkcji prawdopodobieństwa dla zmiennej losowej skokowej

W przypadku zmiennej losowej ciągłej zamiast funkcji prawdopodobieństwa określa się

funkcję gęstości prawdopodobieństwa f(x), która zdefiniowana jest w następujący sposób

( )

(

)

x

x

x

X

x

x

f

x

∆

∆

+

<

≤

=

→

∆

P

lim

0

(4),

przy czym

*

( )

∫

=

b

a

dx

x

f

1

(5).

Granice

całkowania a i b oznaczają kres dolny i kres górny zmienności zmiennej losowej

X.

Bardzo często zamiast granic a, b w zmiennej losowej ciągłej w rozważaniach teoretycz-

nych

występuje całkowanie od -∞ do +∞. W praktyce oczywiście wiemy, że zmienna przyj-

muje

skończoną wartość, jednak bardzo często nie jesteśmy w stanie w sposób ścisły ustalić

kresu dolnego i górnego zmienności zmiennej losowej X.

Dowodzi się, że prawdopodobieństwo zdarzenia losowego polegającego na tym, że

zmienna losowa

ciągła X przyjmie wartość równą konkretnej liczbie rzeczywistej x

0

, jest zaw-

sze równe zeru, co zapisuje się następująco

(

)

0

P

0

=

= x

X

(6).

Stwierdzenie to ma intuicyjne wytłumaczenie. W każdym przedziale liczbowym na osi

rzeczywistej i

stnieje nieskończenie wiele liczb. Zatem skoro zmienna losowa ciągła może

przyjąć dowolną wartość rzeczywistą z danego przedziału, to mamy nieskończenie wiele wy-

borów, a więc prawdopodobieństwo tego, że wybierzemy tą jedną konkretną wartość wynosi
zero.

Konspekt nr 2 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”

4

2.2. Dystrybuanta

Dystrybuanta zmiennej losowej X

definiowana jest w następujący sposób

*

( ) (

)

x

X

x

F

<

= P

, dla x

∈ R

(7).

Wartościami dystrybuanty są prawdopodobieństwa zdarzeń losowych polegające na tym,

że zmienna losowa X przyjmie wartość mniejszą niż liczba rzeczywista x. Dla zmiennych

losowych skokowych, w powyższym równaniu, stosuje się niekiedy słabą nierówność, czyli

≤.

Dystrybuanta zmiennej losowej ma następujące właściwości:

1.

( )

1

0

≤

≤

x

F

, dla wszystkich x,

2.

jeśli x

2

> x

1

, to

( )

( )

1

2

x

F

x

F

≥

,

3.

( )

0

lim

=

−∞

→

x

F

x

,

4.

( )

1

lim

=

+∞

→

x

F

x

.

Między dystrybuantą a funkcją prawdopodobieństwa i funkcją gęstości prawdopodobień-

stwa zachodzą następujące związki

*

( )

∑

<

=

x

x

i

i

p

x

F

(8),

*

( )

( )

∫

∞

−

=

x

du

u

f

x

F

(9).

Ze wzoru (9)

wynika, że

*

( )

( )

x

F

x

f

'

=

(10),

czyli pochodna dystrybuanty zmiennej

losowej ciągłej równa jest funkcji gęstości prawdopo-

dobieństwa. Należy zauważyć, że w równaniu (9) zamieniono oznaczenie zmiennej całkowa-

nia, tak aby nie była taka sama jak górna granica całkowania.

PRZYKŁAD 1. Na podstawie funkcji prawdopodobieństwa zmiennej losowej X z przykładu 1 w rozdziale 2,

wyznaczyć jej dystrybuantę oraz narysować jej wykres.

Zmienna losowa X

jest skokowa i może przyjmować wartości 1, 2 lub 3 z odpowiednimi prawdopodobień-

stwami tj. 0.70, 0.25 lub 0.05. Aby wyliczyć jej dystrybuantę posługujemy się wzorem (8).

−

prawdopodobieństwo tego, że zmienna losowa X przyjmie wartość mniejszą od 1

( )

0

1

1

=

=

∑

<

i

x

i

p

F

,

−

prawdopodobieństwo tego, że zmienna losowa przyjmie wartość mniejszą od 2

( )

(

)

70

.

0

1

P

2

2

=

=

=

=

∑

<

X

p

F

i

x

i

,

−

prawdopodobieństwo, że zmienna losowa przyjmie wartość mniejszą od 3

( )

(

) (

)

95

.

0

25

.

0

70

.

0

2

P

1

P

3

3

=

+

=

=

+

=

=

=

∑

<

X

X

p

F

i

x

i

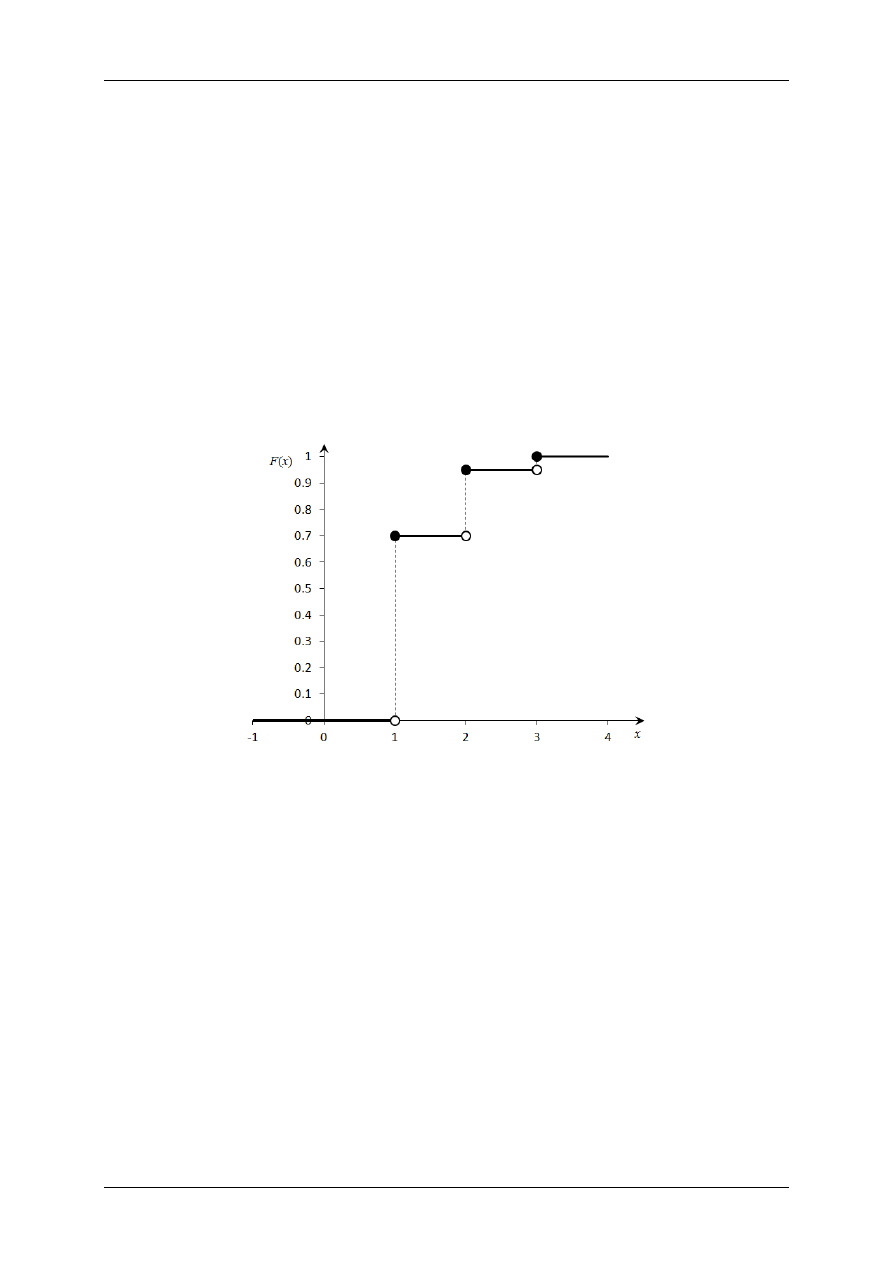
Konspekt nr 2 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”

5

−

oraz prawdopodobieństwo tego, że zmienna losowa przyjmie wartość większą lub równą od 3

(

)

(

) (

) (

)

1

05

.

0

25

.

0

70

.

0

3

P

2

P

1

P

3

3

=

+

+

=

=

+

=

+

=

=

=

≥

∑

≥

X

X

X

p

x

F

i

x

i

.

Zbierając powyższe wyniki otrzymujemy

( )













≥

<

≤

<

≤

<

=

3

dla

1

3

2

dla

95

.

0

2

1

dla

70

.

0

1

dla

0

x

x

x

x

x

F

Wykres dystrybuanty będzie wyglądał następująco

Rys. 2. Wykres dystrybuanty zmiennej losowej X typu skokowego

Zamalowane kropki na wykresie oznaczają, że funkcja w tym punkcie przyjmuje właśnie taką wartość.

3. Podstawowe parametry jednowymiarowej zmiennej losowej

Podstawowymi parametrami jednowymiarowej zmiennej losowej są:

−

wartość oczekiwana (nadzieja matematyczna, wartość przeciętna),

− wariancja,

− odchylenie standardowe.

Wartość oczekiwana zmiennej losowe X definiowana jest w następujący sposób:

− dla zmiennej losowej skokowej

*

( )

∑

=

i

i

i

p

x

X

E

(11),

−

dla zmiennej losowej ciągłej

Konspekt nr 2 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”

6

*

( )

( )

∫

+∞

∞

−

⋅

=

dx

x

f

x

X

E

(12).

W niektórych podręcznikach można spotkać oznaczenie wartości oczekiwanej małą literą

m.

Wariancj

ę, którą będziemy oznaczać przez D

2

(X)

III

− dla zmiennej losowej skokowej

, zmiennej losowej X zdefiniowana jest

następująco:

*

( )

( )

(

)

∑

−

=

i

i

i

p

X

E

x

X

D

2

2

(13),

−

dla zmiennej losowe ciągłej

*

( )

( )

(

) ( )

∫

+∞

∞

−

−

=

dx

x

f

X

E

x

X

D

2

2

(14).

W przypadku liczenia wariacji dla dużej ilości zmiennych losowych, wygodniej jest po-

służyć się przekształceniem wzoru (13) do postaci

*

( )

( )

( )

(

)

2

2

2

X

E

X

E

X

D

−

=

(15).

Odchylenie standardowe, niezależnie od rodzaju zmiennej losowej, obliczamy jako nie-

ujemny pierwiastek kwadratowy z wariancji

( )

( )

X

D

X

D

2

=

(16).

Innym oznaczeniem, spotykanym w książkach, odchylenia standardowego jest grecka litera σ.

PRZYKŁAD 1. Na podstawie funkcji prawdopodobieństwa zmiennej losowej X z przykładu 1 w rozdziale 2,

obliczyć jej wartość oczekiwaną, wariancję i odchylenie standardowe.

Aby obliczyć wartość oczekiwaną zmiennej losowej X korzystamy ze wzoru (11). Sumujemy po wszystkich

wartościach i = 1, 2, 3

( )

∑

=

=

⋅

+

⋅

+

⋅

=

=

3

1

35

.

1

05

.

0

3

25

.

0

2

70

.

0

1

i

i

i

p

x

X

E

.

Wariancję wyliczamy w oparciu o równanie (13)

( )

( )

(

)

(

)

(

)

(

)

∑

=

=

−

+

−

+

−

=

−

=

3

1

2

2

2

2

2

3275

.

0

05

.

0

35

.

1

3

25

.

0

35

.

1

2

70

.

0

35

.

1

1

i

i

i

p

X

E

x

X

D

.

Wy

liczmy jeszcze raz wariancję tym razem korzystając ze wzoru(15). Wyliczmy najpierw wartość oczeki-

waną z kwadratu zmiennej losowej

( )

∑

=

=

⋅

+

⋅

+

⋅

=

=

3

1

2

2

2

2

2

15

.

2

05

.

0

3

25

.

0

2

70

.

0

1

i

i

i

p

x

X

E

.

III

Inne spotykane oznaczenia wariancji to: V(X) i σ

2

.

Konspekt nr 2 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”

7

Podstawiając wartości do wzoru (15) otrzymujemy

( )

( )

( )

(

)

3275

.

0

35

.

1

15

.

2

2

2

2

2

=

−

=

−

=

X

E

X

E

X

D

.

Odchylenie standardowe wg równania (16)

( )

( )

5723

.

0

3275

.

0

2

=

=

=

X

D

X

D

.

PRZYKŁAD 2. Funkcja gęstości prawdopodobieństwa pewnej zmiennej losowej Y typu ciągłego podana

jest następującym wzorem

( )













≤

<

≤

+

−

<

≤

−

<

=

y

y

y

y

y

y

y

f

6

dla

0

6

4

dla

5

.

1

25

.

0

4

2

dla

5

.

0

25

.

0

2

dla

0

.

Obliczyć:

a)

wartość oczekiwaną,

b)

wariancję,

c) odchylenie standardowe,
d)

dystrybuantę w punktach załamania wykresu f(y) wykres.

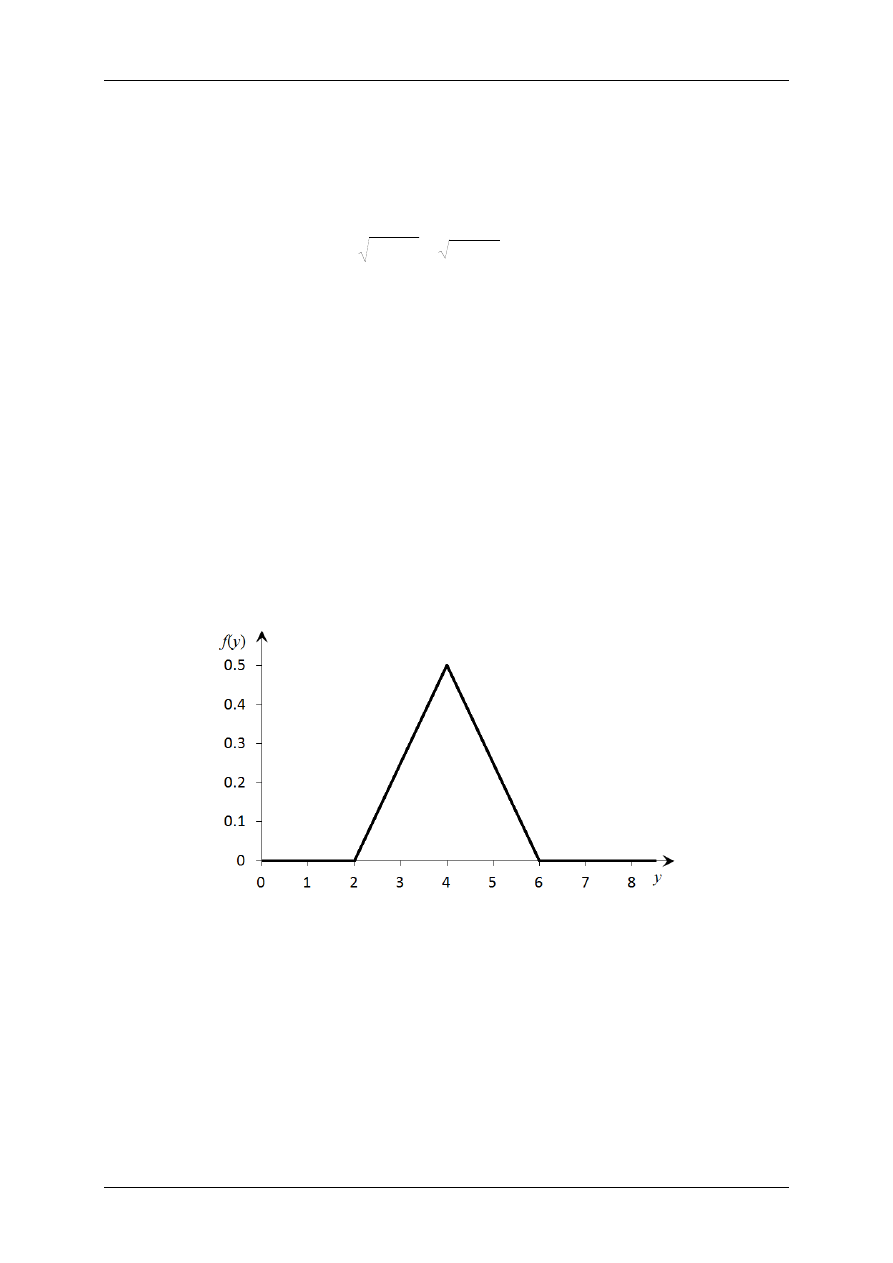
Zanim przejdziemy do obliczeń, wygodniej będzie przedstawić sobie funkcję f(y) na wykresie

Rys. 3. Wykres funkcji

gęstości prawdopodobieństwa zmiennej losowej Y

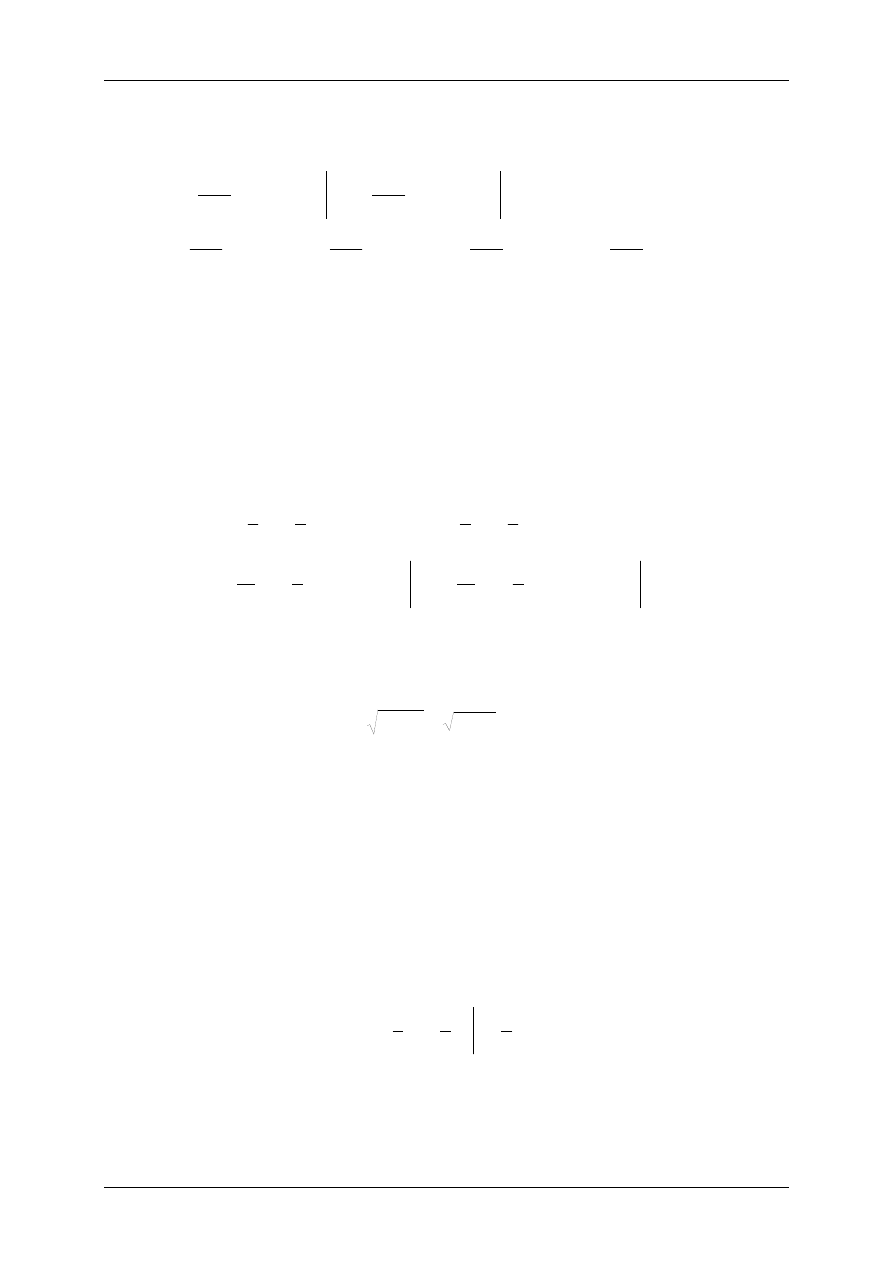
Ad. a). Wartość oczekiwaną liczymy ze wzoru (12) rozbijając całkę na cztery części. Ponieważ nasza funk-

cja dla y < 2 oraz 6

≤ y jest zerowa, to jej całka oznaczona też będzie zerowa. Zatem pozostaje nam obliczyć

dwie całki w zakresie od 2 do 4 oraz od 4 do 6

( )

(

)

(

)

∫

∫

+

−

+

−

=

6

4

4

2

5

.

1

25

.

0

5

.

0

25

.

0

dy

y

y

dy

y

y

Y

E

Konspekt nr 2 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”

8

( )

(

)

(

)

( )

( )
( )

4

4

75

.

0

4

3

25

.

0

6

75

.

0

6

3

25

.

0

2

25

.

0

2

3

25

.

0

4

25

.

0

4

3

25

.

0

75

.

0

3

25

.

0

25

.

0

3

25

.

0

5

.

1

25

.

0

5

.

0

25

.

0

2

3

2

3

2

3

2

3

6

4

2

3

4

2

2

3

6

4

2

4

2

2

=

⋅

−

+

⋅

+

−

⋅

+

−

⋅

−

=













+

−

+













−

=

+

−

+

−

=

∫

∫

Y

E

Y

E

y

y

y

y

Y

E

dy

y

y

dy

y

y

Y

E

Ad. b). Wa

riancję liczymy ze wzoru (14) rozbijając całkę na cztery części. Dwie całki zerują się dla tych

wartości, gdzie funkcja f(y) przyjmuje wartości zerowe. Obliczamy dwie pozostałe

( ) (

) (

)

(

) (

)

( )

(

)

(

)

(

)

(

)

( )

( )

( )

667

.

0

24

8

6

7

16

1

8

4

6

5

16

1

24

16

2

7

4

1

8

8

2

5

4

1

5

.

1

25

.

0

16

8

5

.

0

25

.

0

16

8

5

.

1

25

.

0

4

5

.

0

25

.

0

4

2

6

4

2

3

4

4

2

2

3

4

2

6

4

2

3

4

2

2

3

2

6

4

2

4

2

2

2

6

4

2

4

2

2

2

=













+

−

+

−

+













−

+

−

=













+

−

+

−

+













−

+

−

=

+

−

⋅

+

−

+

−

⋅

+

−

=

+

−

−

+

−

−

=

∫

∫

∫

∫

∫

∫

Y

D

y

y

y

y

y

y

y

y

Y

D

dy

y

y

y

dy

y

y

y

Y

D

dy

y

y

y

dy

y

y

y

Y

D

dy

y

y

dy

y

y

Y

D

.

Ad. c). Odchylenie standardowe

( )

( )

817

.

0

667

.

0

2

=

=

=

Y

D

Y

D

.

Ad. d). Korzystamy ze wzoru (9)

− dla y < 2

( )

( )

∫

∞

−

=

=

2

0

2

dy

y

f

F

,

− dla 2

≤ y < 4

( )

( )

(

)

( )

2

1

2

1

8

1

0

4

5

.

0

25

.

0

4

4

2

2

4

2

2

=













−

+

=

−

+

=

∫

∫

∞

−

y

y

F

dy

y

dy

y

f

F

.

− dla 4

≤ y < 6

Konspekt nr 2 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”

9

( )

( )

( )

(

)

( )

( )

1

2

1

2

1

0

6

2

3

8

1

2

1

0

6

5

.

1

25

.

0

6

6

4

2

6

4

4

2

2

=

+

+

=













+

−

+

+

=

+

−

+

+

=

∫

∫

∫

∞

−

F

y

y

F

dy

y

dy

y

f

dy

y

f

F

.

− dla 6

≤ y

(

)

( )

( )

( )

( )

( )

1

0

2

1

2

1

0

6

6

6

6

4

4

2

2

=

+

+

+

=

+

+

+

=

≤

∫

∫

∫

∫

+∞

∞

−

F

dy

y

f

dy

y

f

dy

y

f

dy

y

f

y

F

.

LITERATURA

W. Krysicki, J. Bartos, W. Dysza, K. Królikowska, M. Wasilewska: Rachunek prawdopo-

dobieństwa i statystyka matematyczna w zadaniach. Wydawnictwo Naukowe PWN, Warsza-
wa 2005.

A. Iwasiewicz, A. Paszek: Statystyka z elementami statystycznych metod monitorowania

procesów. Wydawnictwo Akademii Ekonomicznej w Krakowie, Kraków 2004.

W. Kordecki:

Rachunek prawdopodobieństwa i statystyka matematyczny. Oficyna Wy-

dawnicza GiS, Wrocław 2003.