Konspekt nr 3 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”
1
Wybrane rozkłady zmiennych losowych
1.
Rozkład dwumianowy
Załóżmy, że wykonujemy n prób losowych. Każda próba losowa jest niezależna tzn. na
i-ty
wynik nie wpływa to co zdarzyło się w innych próbach. W każdej pojedynczej próbie
losowej
może zajść interesujące nas zdarzenie (sukces) lub może nie zajść (porażka). Załóż-
my też, że znamy prawdopodobieństwo zajścia sukcesu w pojedynczej próbie, i że jest ono
stałe we wszystkich n próbach. Prawdopodobieństwo to oznaczmy przez p, natomiast praw-
dopodobieństwo porażki przez q = 1 – p. Pytamy, jakie jest prawdopodobieństwo zdarzenia
polegające na tym, że wśród n prób sukces wystąpi k razy. Prawdopodobieństwo tego zdarze-
nia, oznaczane przez P(k),
można obliczyć z poniższego wzoru
( )
k
n
k
q
p
k
n
k
−
=
P
(1).
Wzór (1)
nosi nazwę wzoru dwumianowego Bernoulliego, a samo sformułowanie zagad-
nienia – schematu Bernoulliego.
PRZYKŁAD 1. Niech, prawdopodobieństwo tego, że sztuka wybrana losowo z partii towaru jest dobra, wy-
nosi p
= 0.98. Załóżmy, że losowanie sztuki z partii towaru dokonujemy za każdym razem ze zwrotem, tak aby
zdarzenia polegające na losowaniu sztuk były niezależne. Należy obliczyć prawdopodobieństwo tego, że na 100
losowo wybranych sztuk 98, 99, 100 będzie dobrych.
Zadanie rozwiązujemy korzystając ze wzoru (1) podstawiając odpowiednio: n = 100, p = 0.98, q = 1 – p =
0.02 oraz kolejno k = 98, 99 i 100
( )
(
)
( )
(
)
273
.
0
02
.
0
98
.
0
!
98
100
!
98
!
100
98
P
!
!
!
P
98
100
98
≈
⋅
−
=
=
−
=
−
−k
n
k
q
p
k
n
k
n
k
,
( )
27
.
0
99
P
≈
,
( )
133
.
0
100
P
≈
.
PRZYKŁAD 2. Rzucamy 10 razy symetryczną monetą. Obliczyć jakie jest prawdopodobieństwo tego,
że orzeł wypadnie 5 razy.
W rozwiązaniu przyjmujemy n = 10 oraz k = 5. Prawdopodobieństwo sukcesu (wypadnięcia orła) w poje-
dynczym rzucie wynosi p
= 1/2 a porażki q = 1/2. Podstawiając do wzoru (1) otrzymujemy
( )
(
)
246
.
0
2
1
2
1
!
5
10
!
5
!
10
5
P
5
10
5
≈
⋅
−
=
−
.
W schemacie Bernoulliego zmienną losową jest liczba oznaczająca ilość sukcesów w n
próbach. Oznaczmy tą zmienną losową przez K, natomiast małą literą k będziemy oznaczać
konkretną wartość jaką ta zmienna losowa może przyjąć. Oczywiście K przyjmuje tylko war-
tości całkowite od zera do n, czyli k = 0, 1, 2, ..., n.
Jak
wygląda rozkład prawdopodobieństwa P(K=k, n, p)
I
I
W niektórych podręcznikach do oznaczenia funkcji prawdopodobieństwa P(k) dodaje się jeszcze n i p, stąd
oznaczenie P(K=k, n, p).
zmiennej losowej K? Spróbujmy
to pokazać na przykładzie doświadczenia losowego polegającego na rzuceniu 20 razy syme-
tryczną kostką do gry. Interesuje nas prawdopodobieństwo wypadnięcia szóstki k razy. Wia-
do
mo, że prawdopodobieństwo sukcesu w pojedynczym rzucie wynosi p = 1/5, a prawdopo-
dobieństwo porażki, czyli wypadnięcia czegokolwiek oprócz szóstki, wynosi q = 1 – p = 5/6.
Aby narysować rozkład zmiennej losowej K należy wykonać obliczenia dla każdej wartości k.
Konspekt nr 3 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”
2
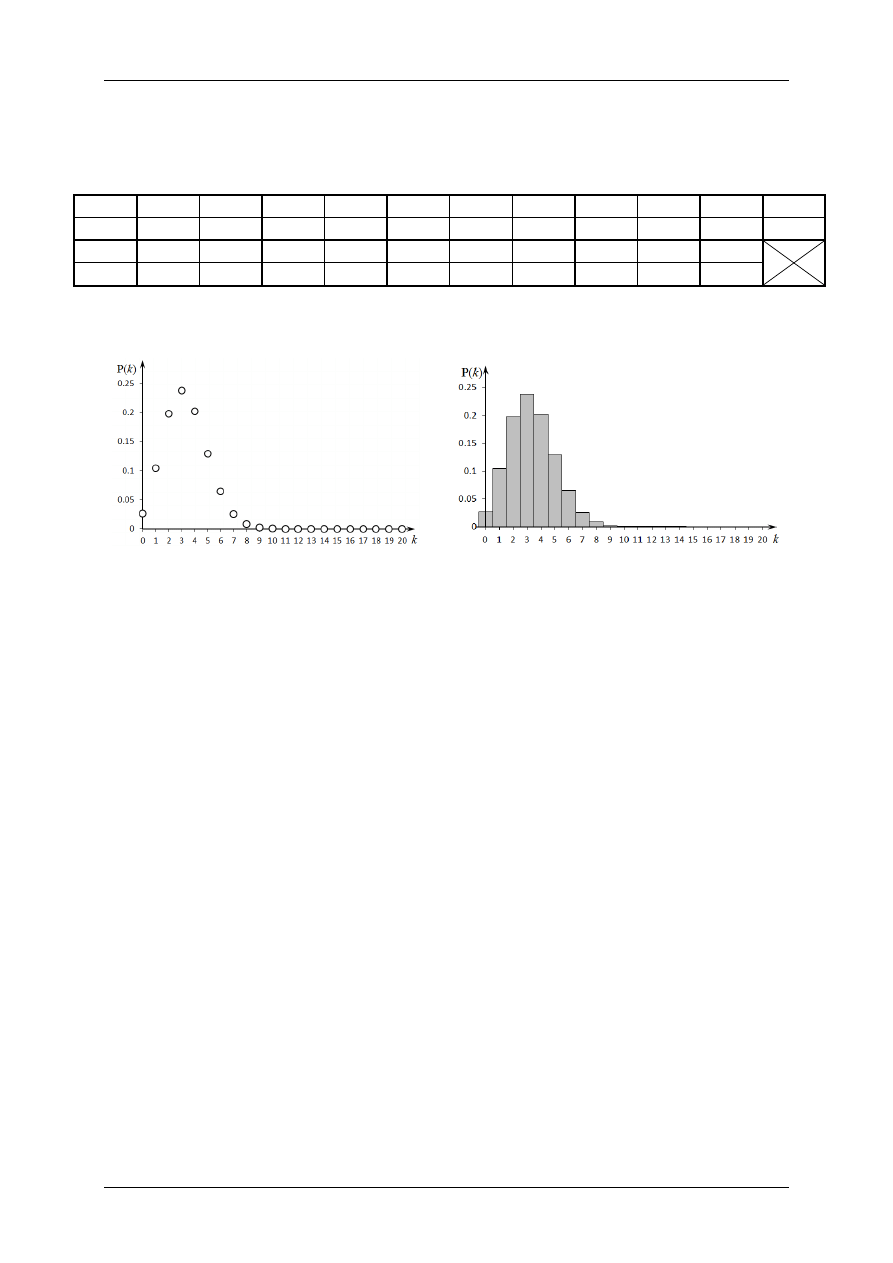
Zestawienie wyników
obliczeń umieszczono w tabeli 1, natomiast wykres funkcji prawdopo-
dobieństwa P(k) przedstawiono w dwóch formach na rys. 1 i 2.
Tab. 1
. Zestawienie prawdopodobieństw zmiennej losowej K w rozkładzie dwumianowym
k
0
1
2
3
4
5
6
7
8
9
10
P(k)
0.026
0.104.
0.198
0.238
0.202
0.129
0.065
0.026
0.008
0.002
4.93
∙10
-4
k
11
12
13
14
15
16
17
18
19
20
P(k)
8.97
∙10
-5
1.35
∙10
-5
1.66
∙10
-6
1.66
∙10
-7
1.33
∙10
-8
8.28
∙10
-10
3.90
∙10
-11
1.30
∙10
-12
2.74
∙10
-14
2.74
∙10
-14
Rys. 1
. Prawdopodobieństwo P(k) w rozkładzie
dwumianowym przy p = 1/6, n = 20
Rys. 2
. Prawdopodobieństwo P(k) w rozkładzie
dwumianowym (przy p = 1/6, n = 20)
przedstawione w postaci histogramu
Wysokość słupków na histogramie (rys. 2) odpowiada liczbowo wartości P(k) a szerokość
każdego prostokąta wynosi 1 tak aby suma pól wszystkich prostokątów wynosiła 1.
Analizując przedstawiony wykres rozkładu zmiennej losowej K widać, że P(k) najpierw
rośnie, a następnie od pewnej wartości k (k
max
) maleje. Przyb
liżoną wartość k
max
, przy której
P(k
) jest największe, dla małych wartości n (n < 30) można obliczyć z następującego wzoru
q
np
k
−
≈
max
(2),
natomiast dla n
≥ 30 człon q w powyższym równaniu można opuścić dostając
np
k
≈
max
(3).
Wielkość k
max
, obliczona z powyższych równań, w niektórych przypadkach może przyjąć
wartość rzeczywistą mimo tego, że k jest liczbą całkowitą od 0 do n.
Dystrybuanta zmiennej losowej K
ma postać
( )
>
≤
≤
<
=
∑
<
−
n
x
n
x
q
p
k
n
x
x
F
x
k
k
n
k
K
dla
1
0
dla
0
dla
0
(4).
W powyższym równaniu dopisano indeks dolny „K” tak aby zaznaczyć, że dystrybuanta
dotyczy właśnie tej zmiennej losowej. Zmienna x jest dowolną liczbą rzeczywistą. Przypo-
mnijmy, że dystrybuanta to taka funkcja, która określa jakie jest prawdopodobieństwo tego,
że zmienna losowa, w naszym przypadku K, przyjmie wartość mniejszą od x.
Zmienna losowa K
ma wartość oczekiwaną
Konspekt nr 3 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”
3
( )
np
K
E
=
(5)
oraz wariancję
( )
npq
K
D
=
2
(6).
2.
Rozkład Poissona
Zmienna losowa Z
ma rozkład Poissona, jeśli może przyjmować wartości wyrażające się
liczbami całkowitymi nieujemnymi (z = 0, 1, 2, ...), z prawdopodobieństwami
(
)
λ
−
λ
=
λ
=
e
z
z
Z
z
!
,
P
(7)
gdzie
λ = np
jest parametrem tego rozkładu
II
Dystrybuanta zmiennej losowej Z
w rozkładzie Poissona przedstawia się następująco
.
( )
>
λ
≤
=
∑
<
λ
−
0
dla
!
0
dla
0
x
e
z
x
x
F
x
z
z
Z
(8)
a wartość oczekiwana i wariancja
( )
( )
np
Z
D
Z
E
=
=
2
(9).
Rozkład Poissona jest rozkładem granicznym dla rozkładu dwumianowego. Jeśli n rośnie
nieograniczenie, a p
zmienia się wraz z n w ten sposób, że iloczyn np jest stały, to dla każde-
go z zachodz
i zbieżność rozkładu dwumianowego do rozkładu Poissona. Oznacza to, że w
niektórych przypadkach możemy przybliżyć rozkład dwumianowy, który dla dużych n wy-
maga sporego nakładu obliczeń, rozkładem Poissona. Przyjmuje się zwykle, że przybliżenie
to jest wyst
arczająco dobre, gdy n ≥ 20 i jednocześnie p ≤ 0.2.
Rozkład Poissona często nazywany jest rozkładem zdarzeń rzadkich. Stosowany jest tam
gdzie prawdopodobieństwo sukcesu jest małe.
3.
Rozkład normalny
Mówimy, że zmienna losowa X ma rozkład normalny, jeśli jej funkcja gęstości prawdopo-
dobieństwa
III
ma postać
( )
(
)
σ
µ
−
−
π
σ
=
2
exp
2
1
2
x
x
f
(10),
przy czym
μ = E(X), σ = D(X).
Parametry
μ i σ są niezależne. Parametr μ określa położenie funkcji (10) na osi licz rze-
czywistych w tym sensie, że funkcja ta osiąga maksimum w punkcie x = μ. Parametr σ określa
kształt krzywej. Im większa jest wartość σ, tym bardziej spłaszczona jest krzywa dzwonowa.
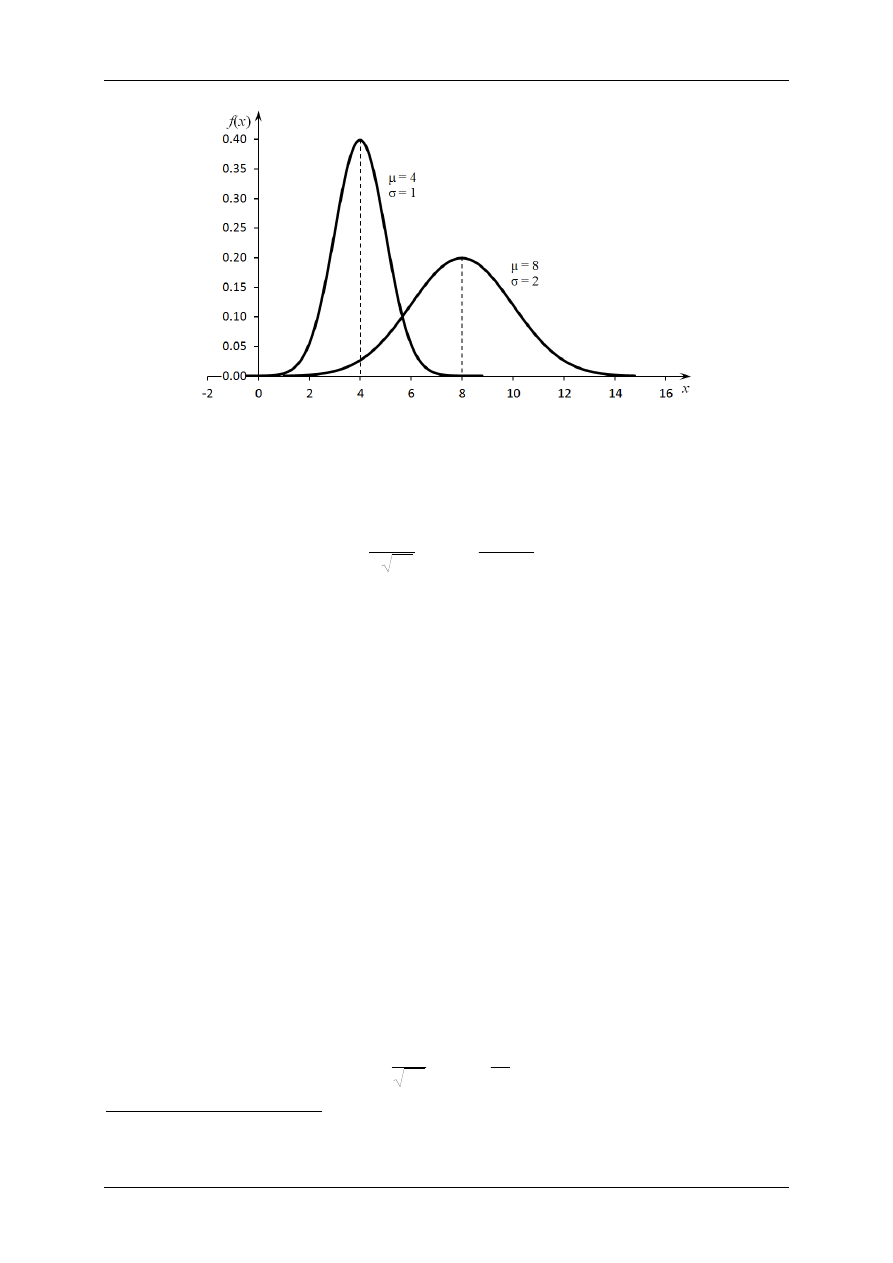
Na rys. 3 przedstawiono wykresy funkcji (10)
dla dwóch różnych wartości μ i σ.
II
Zmienne n i p oznaczają to samo co w rozkładzie dwumianowym.
III
Rozkład normalny jest typu ciągłego, dlatego mówimy o funkcji gęstości prawdopodobieństwa. W przypadku
gdy zmienna losowa jest typu skokowego, jak w przypadku rozkładu dwumianowego i Poissona, posługujemy
się pojęciem funkcji prawdopodobieństwa.
Konspekt nr 3 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”
4
Rys. 3.
Funkcje gęstości prawdopodobieństwa rozkładu normalnego dla dwóch wartości μ i σ
Pole powierzchni pod wykresem funkcji (10) jest zawsze równe 1 (patrz; Konspekt nr 2
równanie 5).
Dystrybuanta zmiennej losowej X
o rozkładzie normalnym określona jest wzorem
( )
(
)
dx
x
x
F
x
∫
∞
−
σ
µ
−
−
π
σ
=
1
2
exp
2
1
2
1
(11).
Dla przypomnienia, dystrybuanta to tak funkcja, która mówi jakie jest prawdopodobie
ń-
stwo tego, że zmienna losowa X przyjmie wartość mniejszą od jakiejś liczby rzeczywistej x
1
.
Można to zapisać w taki sposób F(x
1
) = P(X < x
1
).
Aby to prawdopodobieństwo obliczyć na-
leży scałkować pole powierzchni wykresu funkcji (10) w granicach od -∞ do x
1
, co zapisane
jest w równaniu (11)
. Przykładowo, aby obliczyć prawdopodobieństwo tego, że zmienna lo-
sowa, przedstawiona graficznie na rys. 3
(dla μ = 8 i σ = 2), przyjmie warto
ść mniejszą od
x
1
=
8 należy obliczyć pole powierzchni pod krzywą w granicach od -∞ do x
1
= 8. Ponieważ
krzywa dzwonowa jest symetryczna, a x
1
= μ w tym przypadku, i pole powierzchni pod całą
krzywą równe jest 1, to całka (11) równa jest 1/2. Wynika stąd, że parametr μ ma charakter
wartości średniej.
Funkcja (11)
nie ma rozwiązania analitycznego (dokładnego). Jej rozwiązanie można zna-
leźć w tablicach statystycznych, przy czym znajdują się tam wyniki dla tzw. znormalizowa-
nej
IV
(11)
zmiennej losowej
o wartości średniej μ = 0 i odchyleniu standardowym σ = 1. Normali-
zacji tej do
konuje się poprzez zastosowanie, do całki
, następującego podstawienia
u
x
σ
=
µ
−
(12).
Obliczając różniczkę z powyższego równania mamy
du
dx
σ
=
(13).
Ostatecznie po podstawieniu (12) i (13) do (11) dostajemy
( )
du
u
u
u
∫
∞
−
−
π
=
Θ
1
2
exp
2
1
2
1
(14).
IV
Niekiedy można spotkać się z pojęciem standaryzowana zmienna losowa lub unormowana zmienna losowa.
Wszystkie one oznaczają to samo.
Konspekt nr 3 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”
5
Obecnie, gdy dostęp do komputerów jest powszechny, rzadziej korzysta się z tablic staty-
stycznych
niż to maiło miejsce dawniej. Nie jest konieczne już normalizowanie zmiennej lo-
sowej. War
tość dystrybuanty (11) można wyliczyć przykładowo korzystając z funkcji, znaj-
du
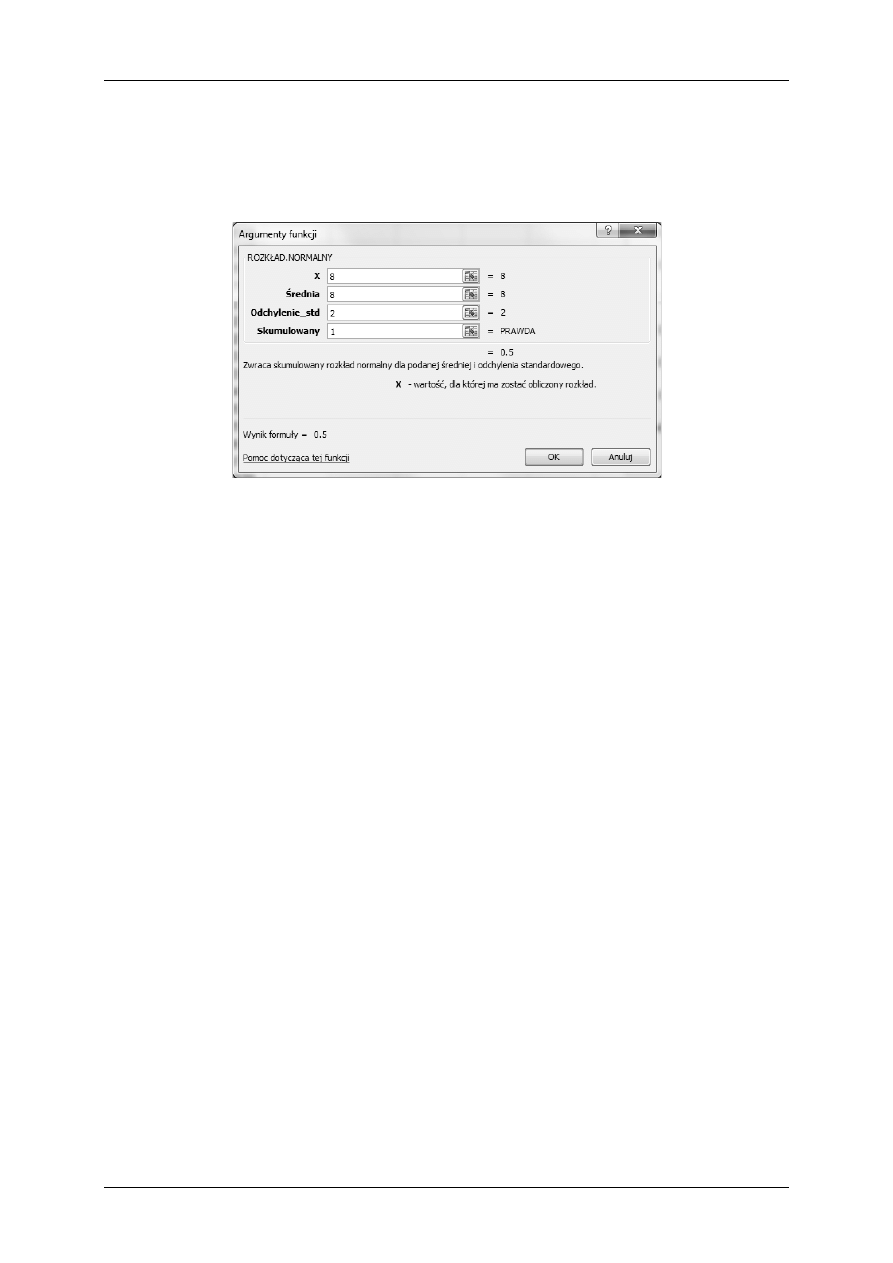
jącej się w arkuszu kalkulacyjnym MS Excel, o nazwie ROZKŁAD.NORMALNY. Przy-
kład okna kreatora funkcji z wprowadzonymi danymi x
1
= 8, μ = 8, σ = 2 pokazano na rys. 4.
Rys. 4. Kreator funkcji w MS Excel do wyliczenia dystrybuanty zmiennej losowej X = x
1
= 8
o rozkładzie normalnym dla parametrów: wartość średnia μ = 8, odchylenie standardowe
σ = 2
Wyjaśnienia wymaga parametr ”Skumulowany”. Przyjmuje on dwie wartości tj. 0
(FAŁSZ) lub 1 (PRAWDA). Jeśli posiada on wartość 1 to zostaje wyliczona wartość dystry-
buanty, a więc całka (11). Dla 0 liczona jest wartość funkcji (10).
Rozkład normalny, zwany też rozkładem Gaussa, występuje bardzo często w przyrodzie.
Przykładem zmiennych losowych o rozkładzie Gaussa mogą być: wzrost i waga człowieka,
iloraz inteligencji, natężenie światła, błędy pomiarowe.
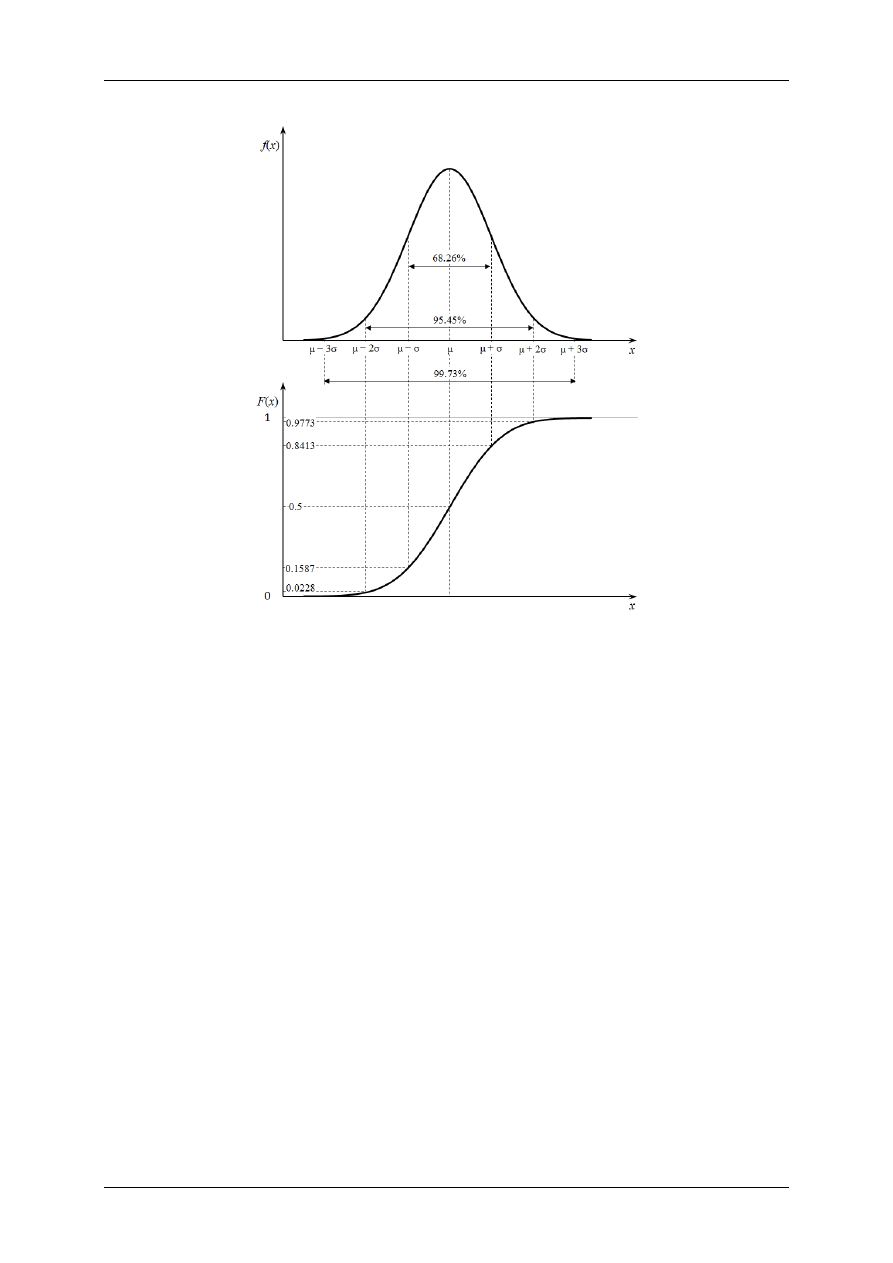
Rys. 5
pokazuje podstawowe własności funkcji gęstości prawdopodobieństwa oraz dys-
trybuanty zmiennej losowej X
, a także relacje między tymi charakterystykami rozkładu.
Na uwagę zasługują następujące własności rozkładu normalnego
(
)
6826
.
0
P
=
σ
+
µ
<
<
σ
−
µ
X
(15),
(
)
9545
.
0
2
2
P
=
σ
+
µ
<
<
σ
−
µ
X
(16),
(
)
9973
.
0
3
3
P
=
σ
+
µ
<
<
σ
−
µ
X
(17).
Jedna z podstawowych cech r
ozkładu normalnego jest fakt, że niemal wszystkie realizacje
zmiennej losowej X
należą do przedziału (μ – 3σ; μ – 3σ), mimo że dziedziną funkcji (10) jest
c
ały zbiór licz rzeczywistych R. Jest to tzw. reguła trzech sigm.
Konspekt nr 3 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”
6
Rys. 5.
Funkcja gęstości prawdopodobieństwa i dystrybuanta zmiennej losowej X
o
rozkładzie normalnym
PRZYKŁAD 1.W pewnej szkole zmierzono wszystkim uczniom wzrost (zmienna losowa X). Z pomiarów
ob
liczono wartość średnią μ = 170.3 cm, oraz odchylenie standardowe σ = 5.9 cm. Obliczyć jakie jest prawdo-
po
dobieństwo tego, że przypadkowo wybrany uczeń z tej szkoły będzie miał wzrost mieszczący się w przedziale
(x
1
= 160; x
2
= 175) cm.
Obliczmy najpierw prawdopodobieństwo tego, że przypadkowo wybrany uczeń będzie miał wzrost mniejszy
od 175 cm, czyli jest to warto
ść dystrybuanty F(x
2
) = P(X < x
2
= 175) danej równaniem (11). Ca
łkę tą rozwiązu-
jemy pos
ługując się funkcją ROZKŁAD.NORMALNY znajdującą się w arkuszu kalkulacyjnym MS Excell. Do
kreatora funkcji podstawiamy nast
ępujące dane: X = x
2
= 175;
Średnia = μ = 170.3; Odchylenie_std = σ = 5.9;
Skumulowany = 1. Wynik dostajemy następujący F(175) = 0.787.
Obliczmy teraz prawdopodobie
ństwo tego, że wzrost ucznia będzie mniejszy od 160 cm, czyli
F(x
1
) = P(X < x
1
= 160). Wynik jest nast
ępujący F(160) = 0.040.
Aby dosta
ć ostateczny wynik należy odjąć F(x
2
) od F(x
1
)
(
)
( ) ( )
(
)
747
.
0
040
.
0
787
.
0
175
160
P
P
1
2
2
1
=
−
=
<
<
−
=
<
<
X
x
F
x
F
x
X
x
.
Konspekt nr 3 z laboratoriów „Statystyka i rachunek prawdopodobieństwa”
7
LITERATURA
W. Krysicki, J. Bartos, W. Dysza, K. Królikowska, M. Wasilewska: Rachunek prawdopo-
dobieństwa i statystyka matematyczna w zadaniach. Wydawnictwo Naukowe PWN, Warsza-
wa 2005.
A. Iwasiewicz, A. Paszek: Statystyka z elementami statystycznych metod monitorowania
procesów. Wydawnictwo Akademii Ekonomicznej w Krakowie, Kraków 2004.
W. Kordecki: Rachunek pra
wdopodobieństwa i statystyka matematyczny. Oficyna Wy-
dawnicza GiS, Wrocław 2003.
Document Outline