Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

2. Wstęp do matematyki

2.2. Produkt kartezjański

Dla dowolnych elementów

i

parę

uporządkowaną (

) definiujemy jako zbiór

{ { }}. Oznacza to ustawienie tych elementów

w kolejności takiej, że element

jest pierwszy, a

element

jest drugi.

Z powyższej definicji wynika, że:

( ) ( ). (2.47)

Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

Iloczynem kartezjańskim dowolnych zbiorów

i

nazywamy zbiór

{( ) }. (2.51)

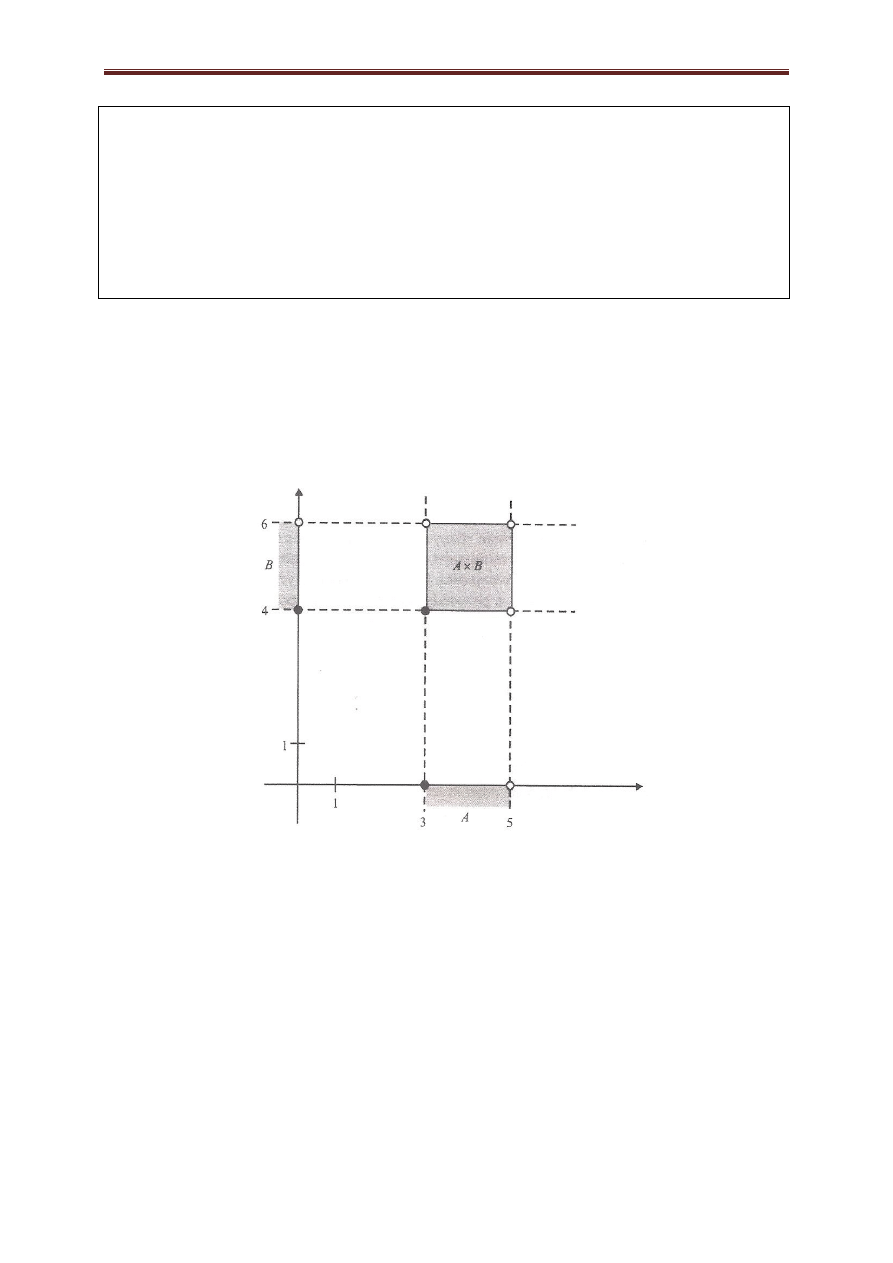
Przykład 2.6. Na rysunku 2.6 przedstawiono

iloczyn

, gdzie 〈 ) i 〈 ).

Rysunek 2.6.



Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

2.3. Funkcje

Funkcją

przekształcającą zbiór

w zbiór

nazywamy dowolne

przypisanie każdemu elementowi

dokładnie jednego elementu

.

Oznacza to, że obrazem formalnym

dowolnej funkcji

jest wykres

funkcji

spełniający warunki:

( ) , (2.52)

((

) (

) )

. (2.53)

Jeśli (

) , to wtedy zapisujemy:

( ) (2.54)

i w ten sposób argumentowi funkcji

jest przypisana wartość funkcji

.

Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

Dla dowolnej funkcji

zbiór ( )

nazywamy

dziedziną

funkcji

(zbiorem

argumentów funkcji).

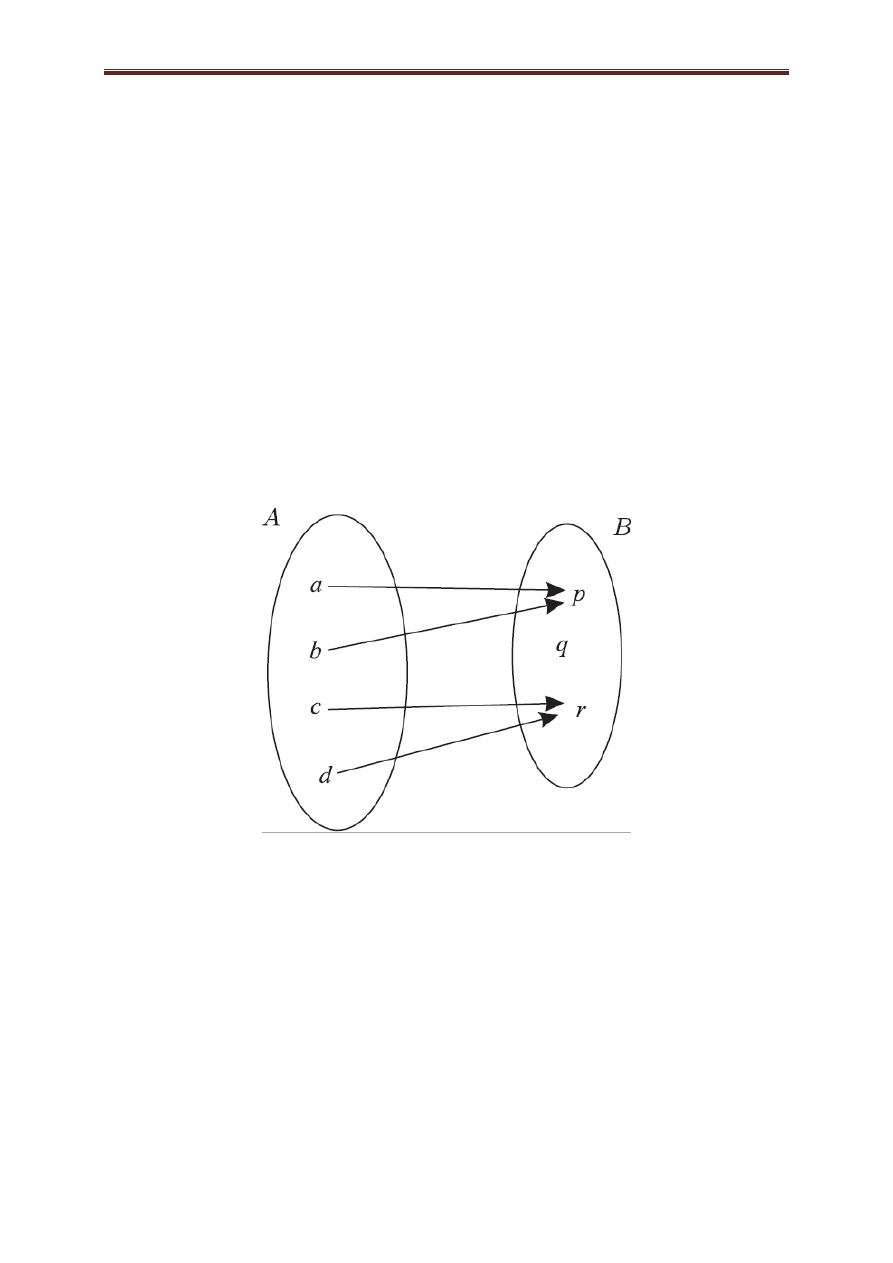
Przykład 2.7. Na rysunku 2.7 przedstawiono wykres

funkcji

określonej na zbiorze { }.

Za pomocą strzałek poszczególnym elementom zbioru

przypisano tam elementy ze zbioru { }.

Wykres tej funkcji jest dany jako zbiór

{( ) ( ) ( ) ( )}. Wykres ten możemy też

opisać za pomocą zależności:

( ) ( )

( ) ( ) .



Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

Zbiór wartości funkcji (przeciwdziedziną

funkcji) określany, jako:

̅( ) { ( )} (2.55)

Jeśli jest spełniony warunek:

̅( ) , (2.56)

to funkcja

przekształca

na

, co

zapisujemy

→ .

Jeśli jest spełniony warunek:

(

)

(

) (

),

to

nazywamy

funkcją

różnowartościową.

Każdą różnowartościową funkcję

→

nazywamy izomorfizmem i oznaczamy za pomocą

symbolu

→ .

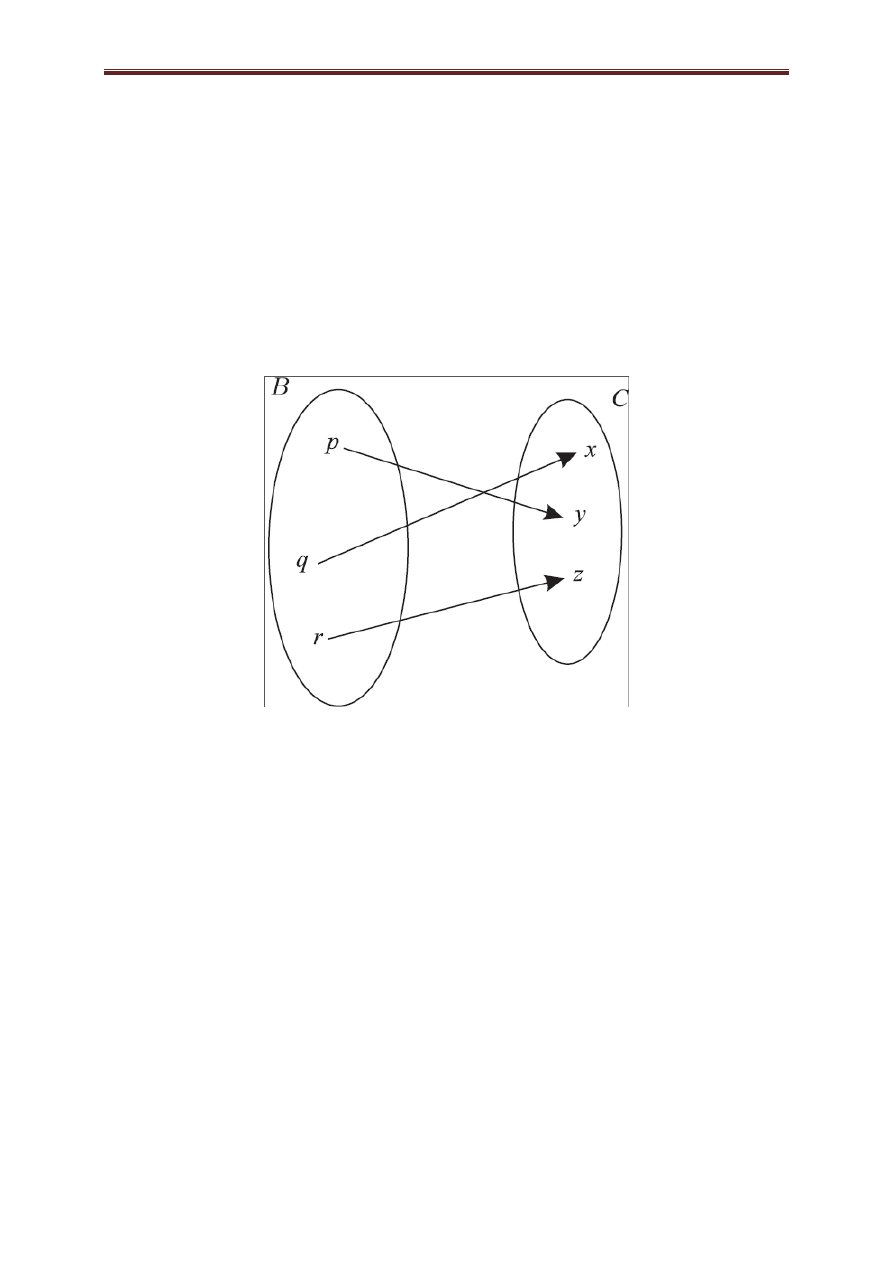
Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

Przykład 2.8. Funkcja

określona w

przykładzie 2.7 nie jest funkcją przekształcającą na

zbiór

, gdyż zbiór jej wartości

̅( ) { } . Nie

jest to też funkcja różnowartościowa, gdyż nie spełnia

ona warunku (2.57).

Rys. 2.8

Na rysunku 2.8 przedstawiono funkcję

przekształcającą zbiór

{ } na zbiór

{ }. Jest to funkcja różnowartościowa. Wszystko to

oznacza, że funkcja

→ jest izomorfizmem.



Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

Złożeniem funkcji

i

nazywamy funkcję

określoną za

pomocą tożsamości:

( ) ( ) ( ).

Funkcję

nazywamy

funkcją

wewnętrzną, zaś funkcję

nazywamy

funkcją zewnętrzną.

Opisana powyżej funkcja złożona nie zawsze

istnieje. Warunkiem koniecznym i dostatecznym

na to, aby istniała funkcja złożona

jest zawieranie się przeciwdziedziny

̅( ) funkcji

wewnętrznej

w

dziedzinie

( ) funkcji

zewnętrznej.

Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

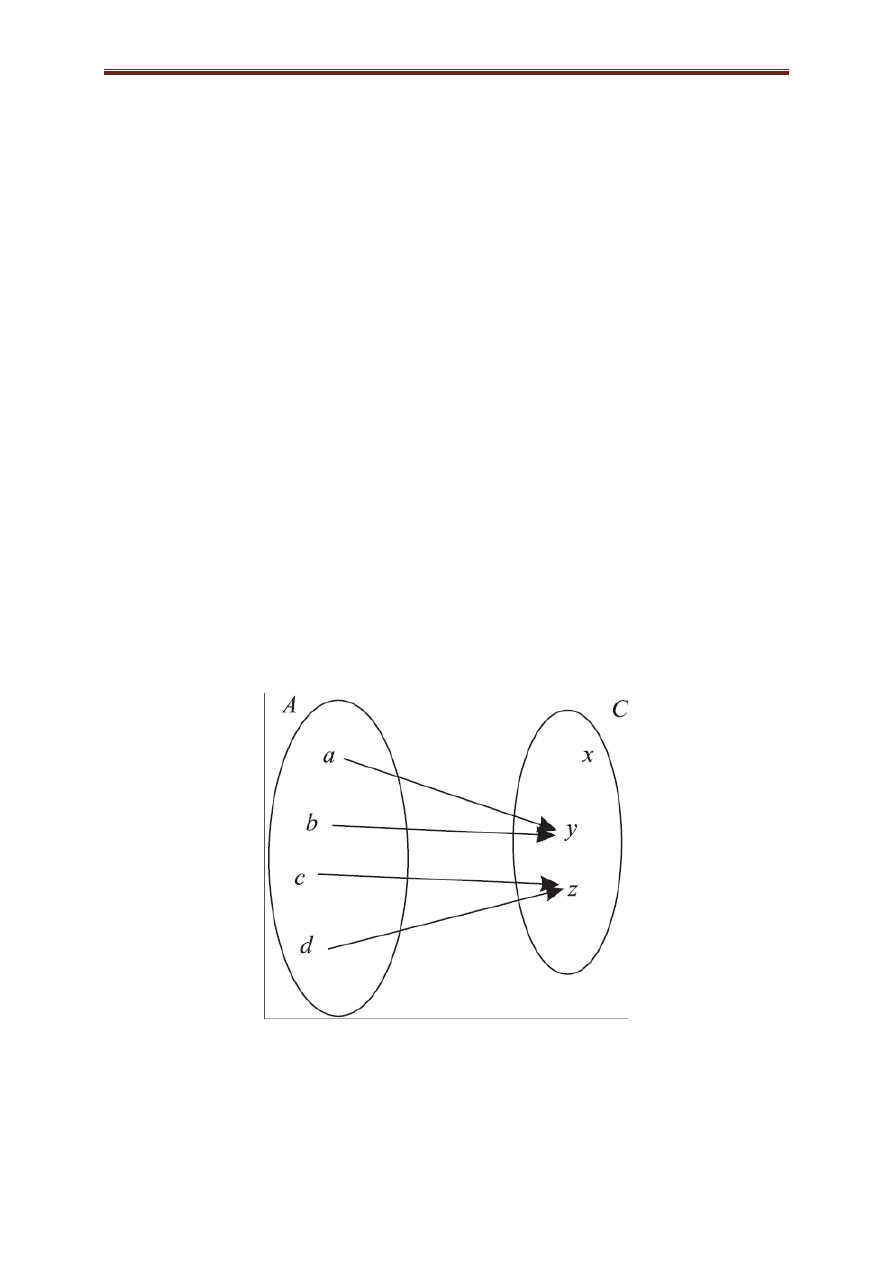
Przykład 2.9. Wyznaczmy złożenie

funkcji opisanych w poprzednich przykładach.

jest funkcją wewnętrzną, zaś funkcja

jest funkcją zewnętrzną. Wyznaczamy

kolejne wartości funkcji złożonej:

( ) ( ) ( ),

( ) ( ) ( ),

( ) ( ) ( ),

( ) ( ) ( ).

Uzyskana funkcja złożona jest przedstawiona poniżej

Rysunek 2.9

Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

Na marginesie tych rozważań zauważmy, że

̅( )

( ) . W tej sytuacji nie istnieje złożenie funkcji
. Oznacza to między innymi, że w

ogólnym przypadku składanie funkcji nie jest

przemienne.



Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

2.4. Ciągi

Ciągiem nazywamy każdą funkcję

przekształcającą zbiór indeksów

w dowolny zbiór wartości

. W ten sposób

każdemu indeksowi

jest przyporządkowany

wyraz ciągu:

( ). (2.59)

Ciąg taki oznaczamy za pomocą symbolu {

}

.

(

), to wtedy nazywamy ciągiem

nieskończonym i oznaczamy symbolem {

}

lub symbolem {

}

, lub symbolem {

} .

(

{ }), to wtedy ciąg

nazywamy ciągiem m-elementowym lub ciągiem

skończenie elementowym i oznaczamy symbolem
{

}

.

Określenie ciągu za pomocą zależności (2.59)

nazywamy analityczną definicją ciągu.

Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

Jeśli jest dany ciąg {

}

początkowych

wartości, to wtedy dowolny ciąg {

}

może być

też określony za pomocą zależności:

(

) . (2.60)

Taki sposób

określenia ciągu nazywamy

rekurencyjną definicją ciągu.

Przykład 2.10. Symbolem (

) oznaczamy resztę

z dzielenia przez 3 zadanej liczby naturalnej

.

Ciąg przekształcający zbiór liczb naturalnych

na

zbiór

{ } jest określony za pomocą funkcji:

( ) {

( )

( )

( )

Jest to analityczna definicja tego ciągu. Początkowe

wyrazy tego ciągu przedstawiają się następująco:

(*)

Zanim wprowadzimy definicję rekurencyjną tego

ciągu, określamy funkcję

. Funkcja ta jest

dana za pomocą zależności:

Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

( ) {

gdzie

. Definicja rekurencyjna ciągu (*)

przyjmuje wtedy postać:

,

,

(

).

Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

Szczególnym przypadkiem ciągów rozważanym w

matematyce są ciągi liczbowe określone jako

funkcje postaci

. Przykładem

ciągu liczbowego jest ciąg {

}

określony

rekurencyjnie:

, (2.61)

( ) . (2.62)

jest nazywana silnią liczby

.

symbol Newtona:

(

)

( )

.

Implementacja WOLFRAM

wartość

Wyznaczamy, wydając polecenie:

Fact[n].

Wartość

(

) wyznaczamy, wydając polecenie:

Bin[n,k]. █

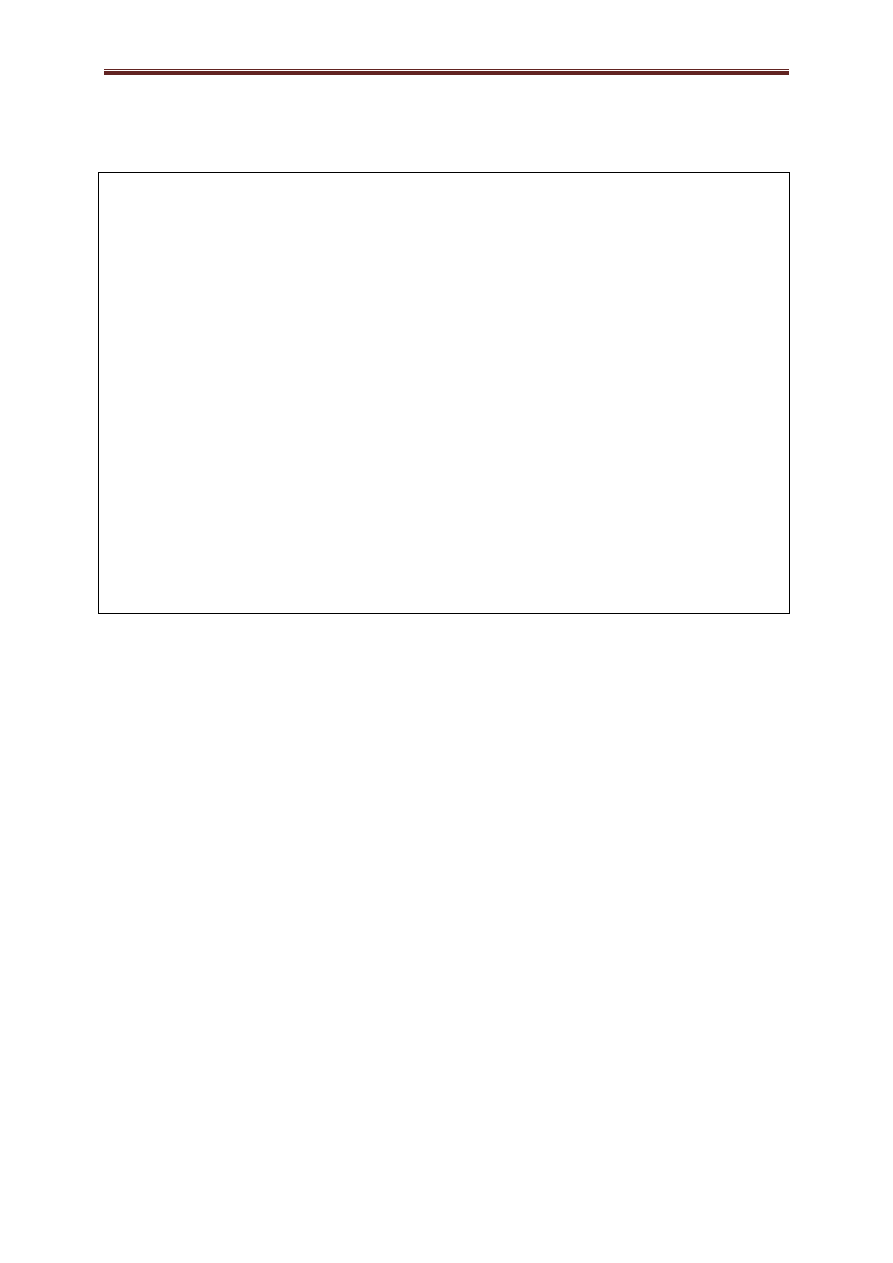
Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

2.5. Tablice

Tablicą prostokątną o

wierszach i kolumnach

nazywamy każdą funkcję

przekształcającą

zbiór

par

indeksów

{ } { } w dowolny zbiór

wartości

. W ten sposób każdej parze indeksów

( ) jest przyporządkowany element tablicy

.

Tablicę taką oznaczamy za pomocą symboli

[

].

Każdą tablicę możemy zapisać w postaci ujętego w

nawiasy kwadratowe prostokąta elementów:

[

] (2.64)

(

)

i-ty

wiersz

tablicy.

(

) j-ta kolumną tablicy. element

macierzy

jest oznaczony przez dwa indeksy:

pierwszy jest numerem wiersza, a drugi numerem

kolumny.

Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

Przykład 2.11. Przykładem tablicy o elementach

pochodzących ze zbioru

{ } jest prostokąt

figur geometrycznych:

[

] .



Tablicę

kwadratową

[

],

której

elementy spełniają warunek:

(2.62)

nazywamy tablicą symetryczną.

Przykład 2.12. Przykładem tablicy symetrycznej o

elementach pochodzących ze zbioru

{ } jest

kwadrat figur geometrycznych:

[

] .



Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

3. Grafy i digrafy

3.1. Grafy

Grafem

nazywamy parę:

( ( )), (3.1)

gdzie

{

}

jest

zbiorem

wierzchołków, a

( ) {

} –

zbiorem krawędzi

{

} .

Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

Przykład 3.1. Przedstawić na rysunku graf

( ( ))

({

} {

}) ,

gdzie

{

},

{

},

{

},

{

},

{

}. Kolejność wierzchołków

nie ma znaczenia. Dzięki temu możemy na przykład

zapisać

{

} {

}.

Rysunek 3.1



Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

3.2. Digrafy

Digrafem

nazywamy parę:

( ( )), (3.5)

gdzie

{

}

jest

zbiorem

wierzchołków, a

( ) {

} –

zbiorem łuków

(

) .

Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

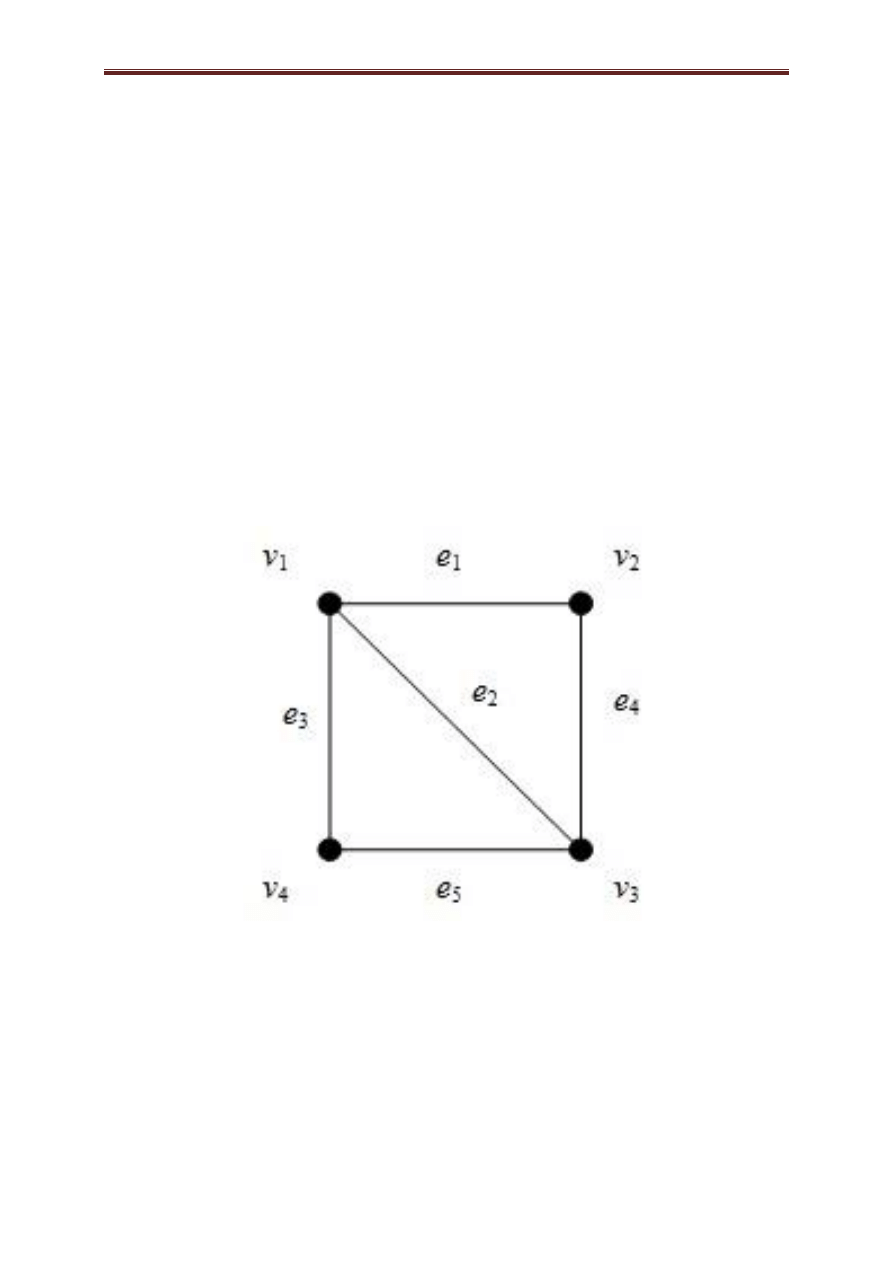
Przykład 3.10. Na rysunku 3.3 przedstawiono

przykładowy digraf.

Rysunek 3.3

Zbiór wierzchołków tego digrafu to

{

},

zaś zbiór łuków

( ) {

}, gdzie

(

)

(

)

(

)

(

)

(

)

W przypadku digrafu istotna jest kolejność

wierzchołków. Dzięki temu możemy na przykład

zapisać

(

) (

)



Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

Tablicą przyległości digrafu

( ( ))

opisanego przez (3.5) nazywamy kwadratową

tablicę

( ) [

]

elementów:

{

(

) ( )

(

) ( )

(3.8)

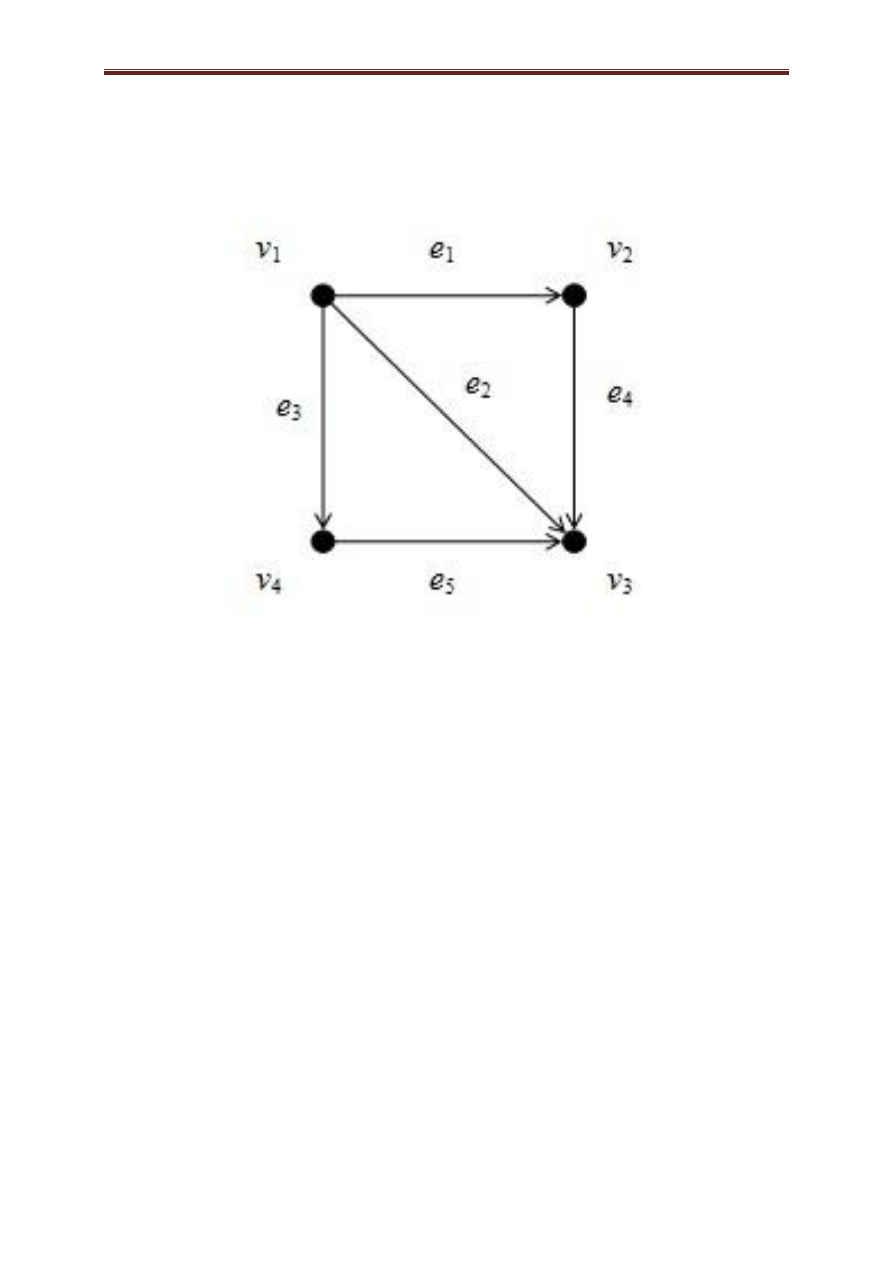
Przykład 3.15. Tablica przyległości

( ) grafu z

rysunku 3.3 ma postać:

( ) [

].



Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

Grafem (digrafem) obciążonym nazywamy

każdą trójkę (

) taką, że para

( ) jest grafem (digrafem). Wartość (

)

nazywamy wagą krawędzi (łuku)

.

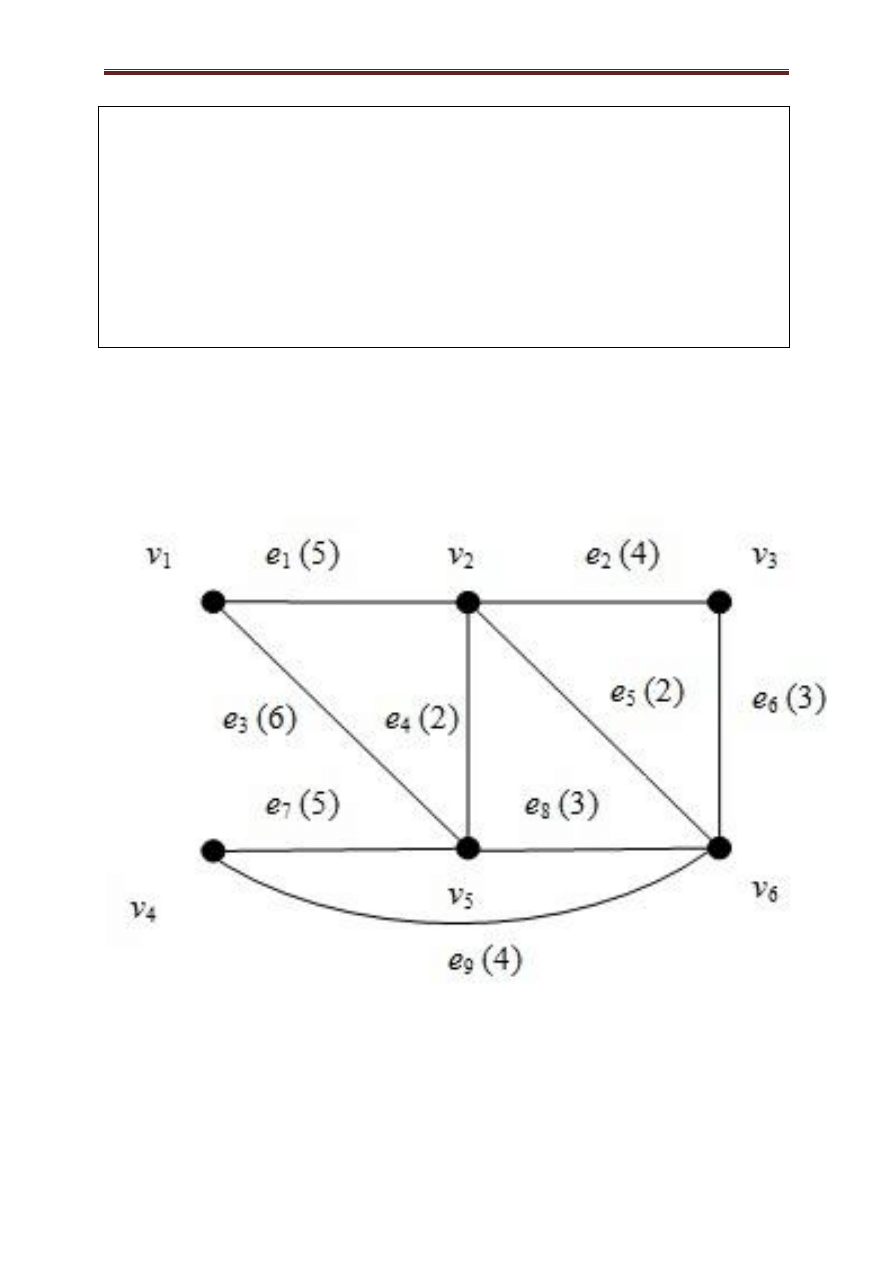
Przykład 3.33. Na rysunku 3.11 przedstawiono

przykład graf obciążonego. Na rysunku 3.13

przedstawiono przykład digrafu obciążonego.



Rysunek 3.11

Opracowano na podstawie K. Piasecki, M. Anholcer, K. Echaust: e-Matematyka wspomagająca ekonomię, C.H. Beck 2013

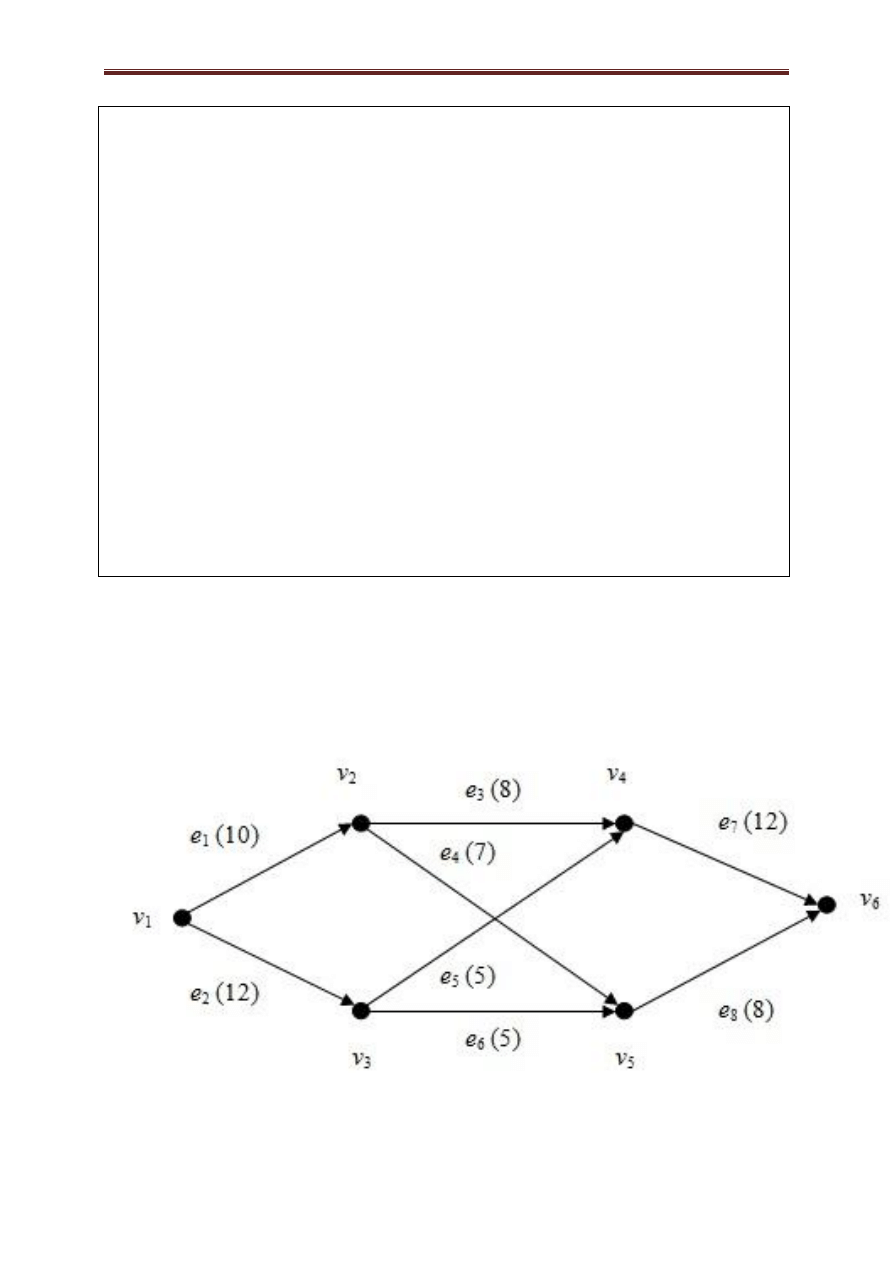
Siecią nazywamy digraf spełniający warunki:

węzeł niebędący końcem żadnego łuku i

nazywany źródłem sieci.

węzeł, niebędący początkiem żadnego łuku i

nazywany ujściem sieci.

skierowana ścieżka ze źródła do każdego innego

węzła sieci

ścieżka do ujścia z każdego innego węzła sieci.

.

Przykładową sieć przedstawia rysunek 3.13. Źródłem

jest węzeł s = v

1

, zaś ujściem t = v

6

. W nawiasach

podano wagi łuków.

Rysunek 3.13