1. Wielościany w rzutach prostokątnych

Konstruowanie wielościanów rzutach prostokątnych jest zagadnieniem stosunkowo prostym i
sprowadza się do ustalania rzutów poszczególnych wierzchołków i krawędzi. Zagadnieniem, które
wymaga nieskomplikowanej analizy jest tzw. widoczność krawędzi. Zakładając, że ściany
wielościanu są nieprzezroczyste należy ustalić, które z krawędzi są widoczne w poszczególnych
rzutach, a które są niewidoczne. W Graficznym zapisie konstrukcji krawędzie niewidoczne
zapisywane są przy pomocy linii kreskowej w odróżnieniu do widocznych, które zapisujemy przy
pomocy linii ciągłej grubej.

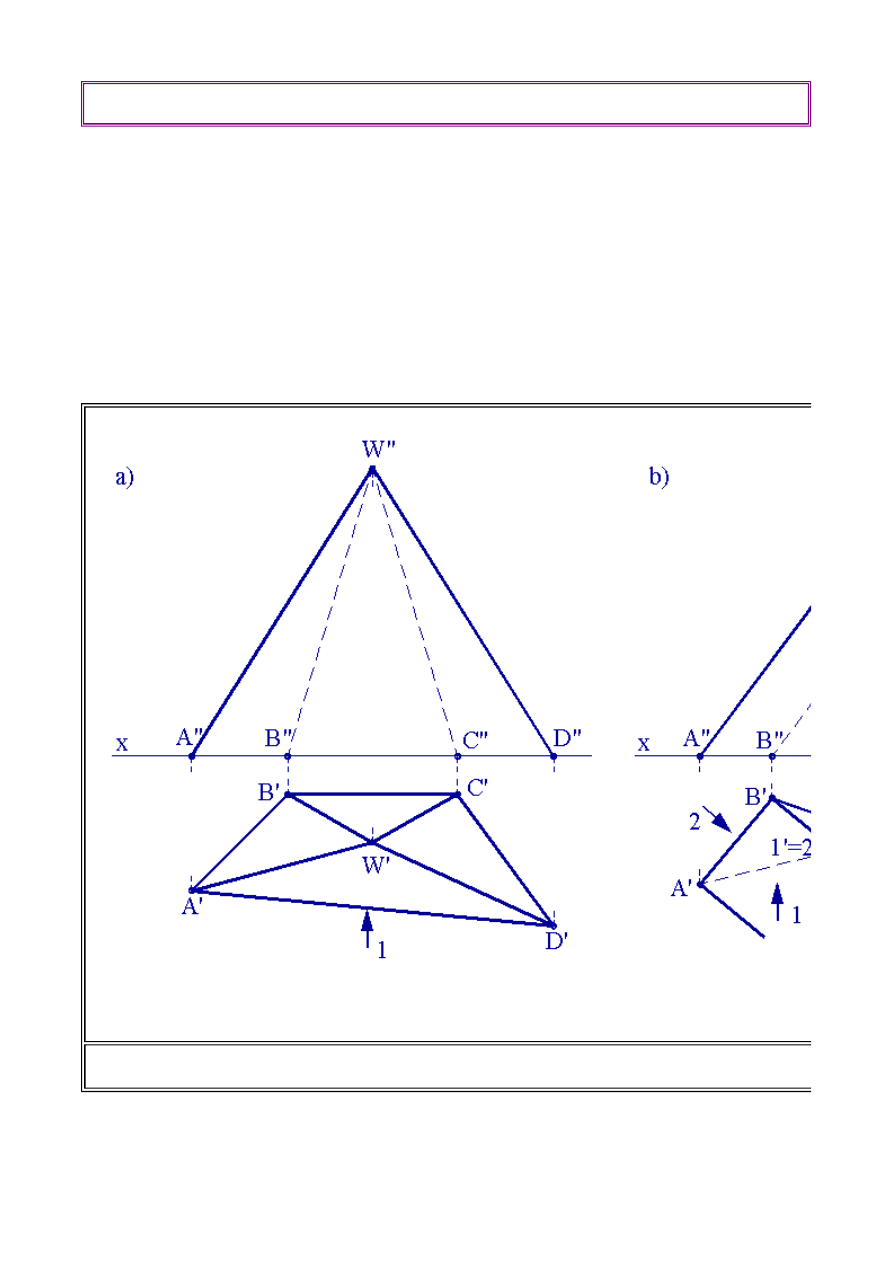
Widoczność w rzucie pionowym ustalamy analizując rzut poziomy z kierunku prostopadłego do
osi x (patrz: rys.2.1 - strzałki "1" prostopadłe do osi x). Z analizy tej można wysnuć wniosek, iż w

(1.1) Budowa brył przestrzennych stojących na rzutniach

Rys.2.1. Wielościany stojące na rzutni poziomej a) Ostrosłup prosty o podstawie czworokąta.
trójkąta.

Informatyka 4 - Lekcja 2

przypadku ostrosłupa ściana

ADW

przysłania wszystkie ściany pozostałe. Krawędzie tej ściany będą

widoczne i zapisane w rzucie pionowym linią ciągłą grubą. W przypadku graniastosłupa ściana

AC,

w rzucie pionowym, przysłania ściany

AB

i

BC

. Wspólna krawędź tych ścian

B

będzie

niewidoczna, zapiszemy ją zatem linią kreskową. Pozostałe dwie krawędzie, jako skrajne ściany

AC

będą widoczne i zostaną zapisane liniami ciągłymi grubymi. W przypadku rzutów poziomych
wielościanów, ocenę taką możemy dokonać również na rzucie poziomym, obserwując ten rzut z
kierunku oznaczonego strzałką "2". Dla ostrosłupa widać wyraźnie, że niewidoczna jest podstawa

ABCD

stojąca na rzutni poziomej, ponieważ jest przysłaniana przez pozostałe ściany ostrosłupa.

Jednak poszczególne boki podstawy:

AB, BC, CD

i

DA

będą widoczne, ponieważ są skrajnymi

bokami ścian widocznych. Dla oceny widoczności krawędzi graniastosłupa, pomocne będą dwa
punkty obrane na przecięciu się krawędzi

A'C

' i krawędzi

B'

. Punkt

1

leżący na krawędzi

B

będzie

widoczny, ponieważ ma większa wysokość niż punkt

2

leżący na boku podstawy

AB

. Punkt

1

ma

zatem większą odległość od rzutni poziomej, musi być zatem widoczny. Odcinek oznaczony w
rzucie poziomym

A'C'

będzie niewidoczny.

Istotnym zagadnieniem w rzutowaniu prostokątnym jest rozdział dotyczący tzw.

ELEMENTÓW

WSPÓLNYCH

.

Przykładem może być wyznaczanie krawędzi przecięcia się dwu płaszczyzn. Na rys.2.2
przedstawiono rozwiązanie tego zagadnienia w przypadku, gdy są one zadane w postaci śladów. W
celu wyznaczenia wspólnej krawędzi płaszczyzny

a

i

b

należy ustalić dwa punkty wspólne tych

płaszczyzn, ponieważ one jednoznacznie określają prostą, w tym przypadku będącą krawędzią
wspólną płaszczyzn.

(1.2) Elementy wspólne – krawędzie przecięcia się płaszczyzn

Informatyka 4 - Lekcja 2

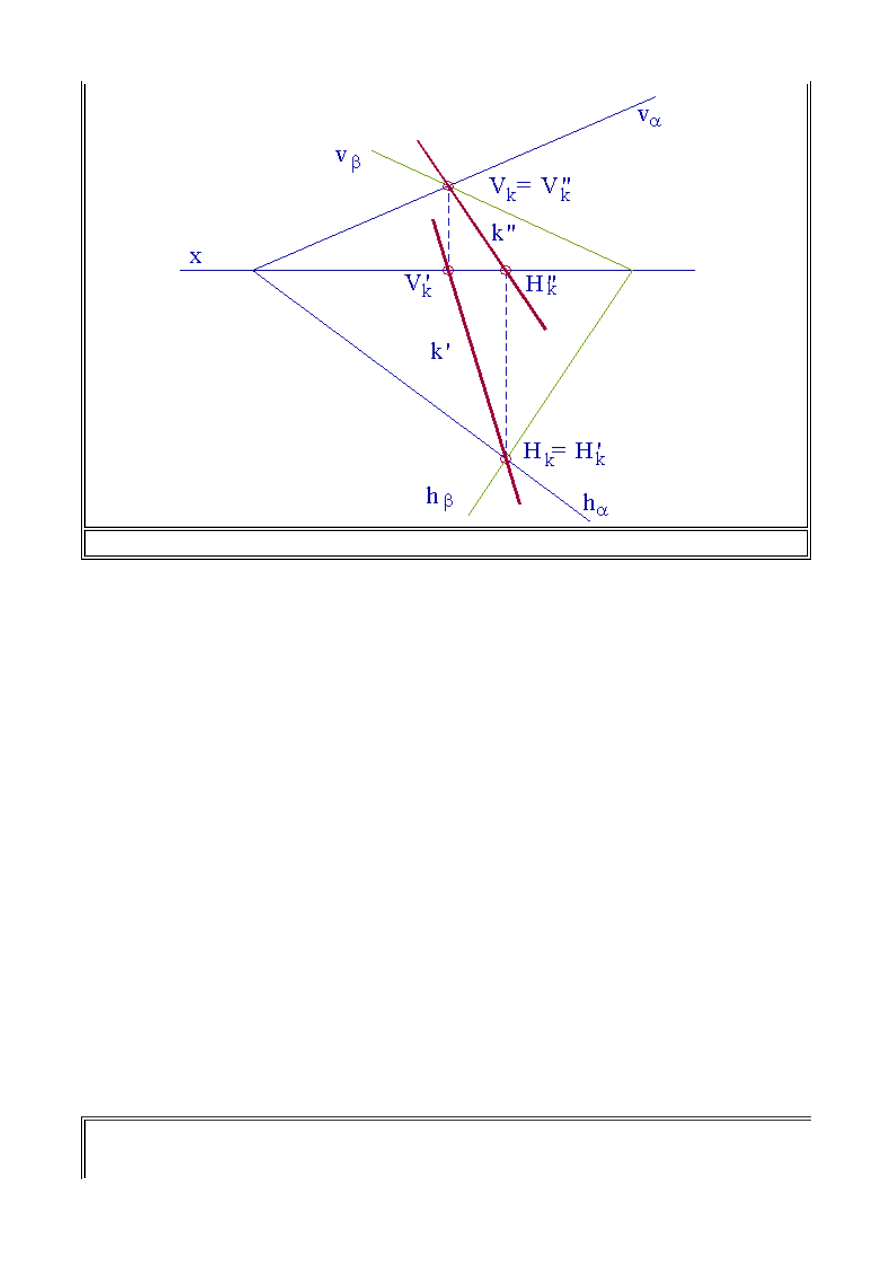
Punkty te łatwo ustalić, ponieważ ślady płaszczyzn są to proste należące do tych płaszczyzn i
jednocześnie leżące na rzutniach. Punkty przecięcia się jednoimiennych śladów wyznaczają nam
ślady wspólnej prostej "

k

" , zwanej krawędzią przecięcia się płaszczyzn. Mając ślady krawędzi

V

k

i

H

k

można wyznaczyć rzuty śladów. Rzut pionowy śladu pionowego pokrywa się ze śladem

pionowym, rzut poziomy tego śladu znajduje się na osi x. Podobnie rzut poziomy śladu poziomego
pokrywa się ze śladem poziomym, natomiast rzut pionowy tego śladu znajduje się na osi x. W
konsekwencji rzuty

k'

i

k"

krawędzi otrzymamy łącząc jednoimienne rzuty śladów.

Wyznaczanie krawędzi przecięcia się płaszczyzn w konstrukcjach bezśladowych zostaną omówione
w dalszej części wykładu.

Kolejny element wspólny jaki powinniśmy rozpatrzyć to punkt przebicia płaszczyzny prostą.
Wyznaczanie punktów przebicia zilustrowane zostało schematycznie na rys.2.3.a.

W celu wyznaczenia punktu przebicia płaszczyzny

a

prostą

l

należy przez prosta poprowadzić

dowolną płaszczyznę

b,

a następnie wyznaczyć krawędź przecięcia się płaszczyzn

k.

W miejscu

przecięcia się dwóch prostych

k

i

l

otrzymamy punkt

P

- wspólny dla prostej

l

i płaszczyzny

a

.

Punkt

P

stanowi zatem punkt przebicia płaszczyzny

a

przez prostą l.

Rys.2.2. Krawędź przecięcia się dwu płaszczyzn

a i b.

(1.3) Elementy wspólne – punkty przebicia figur płaskich prostą

Informatyka 4 - Lekcja 2

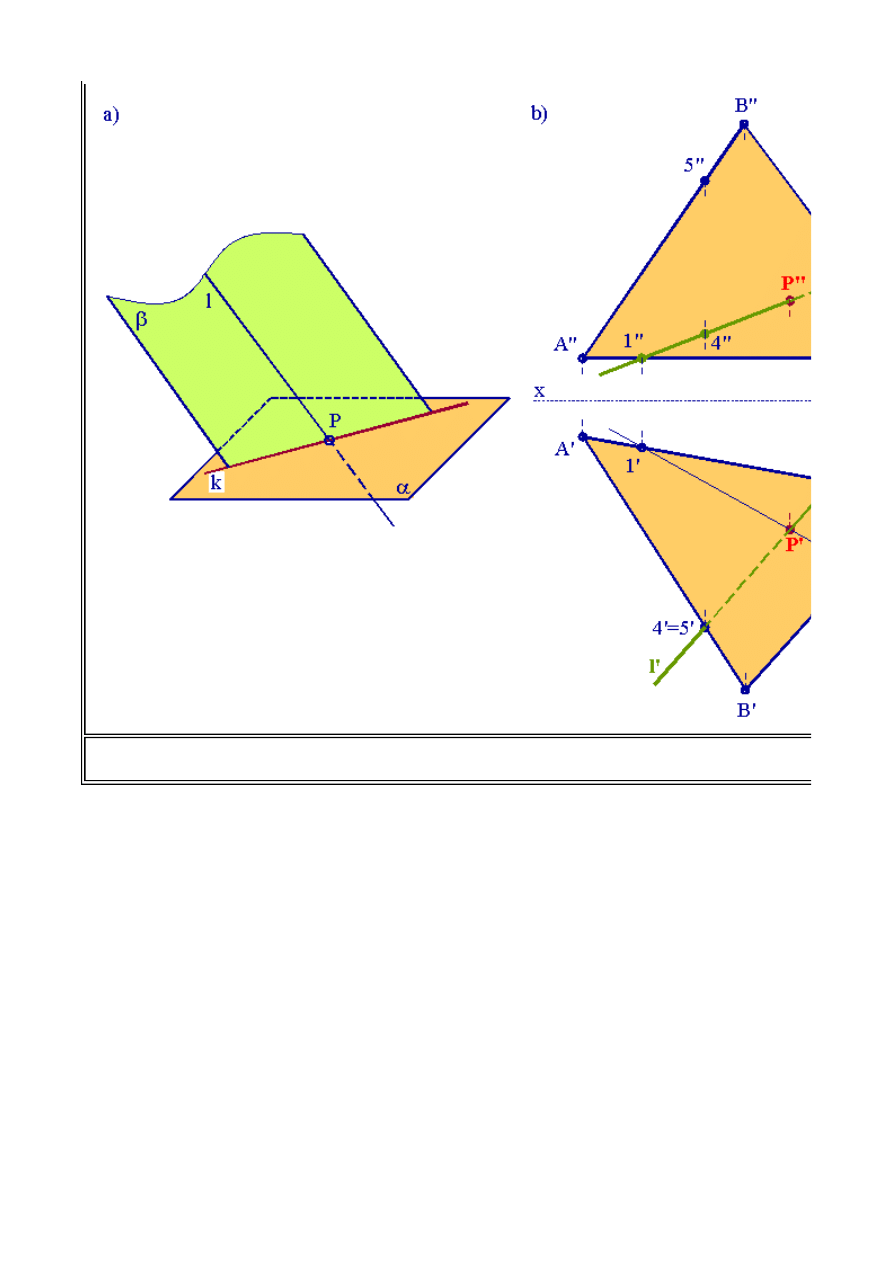
Na rys. 2.3.b przedstawiony został przykład wyznaczania punktu przebicia prostej

l

z płaszczyzną

D

(ABC).

Zgodnie z wcześniej omówionym schematem postępowania, w pierwszej kolejności przez

daną prostą

l

poprowadzimy płaszczyznę pionowo - rzutującą

b

. Jeżeli prosta ma leżeć w

płaszczyźnie

b

to rzut pionowy płaszczyzny, będący jednocześnie śladem pionowym płaszczyzny

powinien pokrywać się z rzutem pionowym prostej

l''

.

Każdy element płaski leżący w płaszczyźnie

pionowo - rzutującej będzie miał rzut pionowy pokrywający się ze śladem pionowym (rzutem
pionowym) płaszczyzny. Kolejny etap - to wyznaczenie krawędzi przecięcia się płaszczyzn

a

i

b

.

Oczywiście rzut pionowy krawędzi wyznaczymy natychmiast, ponieważ musi on, zgodnie z
wcześniejszymi ustaleniami, leżeć na rzucie pionowym płaszczyzny

b

. Otrzymaliśmy zatem rzut

pionowy krawędzi

k''

. Ponieważ krawędź

k

jest prostą leżącą w płaszczyźnie trójkąta musi zatem

przecinać boki tego trójkąta. Punkty przecięcia rzutu pionowego krawędzi

k''

z rzutami pionowymi

boków oznaczono cyframi odpowiednio

1''

i

2''

. Rzuty poziome tych punktów

1'

i

2'

, które

wyznaczymy na odpowiednich rzutach poziomych boków trójkąta pozwolą wyznaczyć rzut poziomy

Rys. 2.3. Punkt przebicia płaszczyzny prostą. a) schemat postępowania. b) wyznaczanie punk
prostą.

Informatyka 4 - Lekcja 2

krawędzi

k'

. Ostatni etap tego zadania to poszukiwanie punktu

P

- przecięcia się krawędzi

k

z prostą

l

, który jest punktem przebicia prostej

l

z płaszczyzną

a

. W rzucie pionowym proste

k"

i

l"

pokrywają się, ale w rzucie poziomym punkt przecięcia jest wyraźnie widoczny. Oznaczając rzut
poziomy punktu

P'

możemy następnie wyznaczyć jego rzut pionowy, poprzez przecięcie się

odnoszącej prostopadłej do osi

x

z rzutem pionowym prostej

k''

. Przyjmując założenie, że

płaszczyzna trójkąta jest nieprzezroczysta powinniśmy oznaczyć jeszcze

widoczność

prostej.

Widoczność w poszczególnym rzucie oznaczamy analizując rzut drugi. I tak, chcąc rozpatrzyć
widoczność prostej w rzucie poziomym analizujemy rzut pionowy. Ocenimy, czy punkt

2

leżący na

boku

BC

ma większą odległość od rzutni pionowej niż punkt

3

leżący na prostej

l

. Ocenę tego faktu

możemy zaobserwować w rzucie poziomym. Punkt 2 leżący na boku

BC

jest bardziej oddalony od

rzutni pionowej (ma większa głębokość), zatem bok

BC

w rzucie pionowym jest widoczny, prosta

l

natomiast, na której leży punkt

3

jest niewidoczna. Podobną analizę możemy przeprowadzić dla

rzutu poziomego, oceniając wysokość punktów 4 i 5 (w rzucie pionowym) należących odpowiednio
do prostej

l

i boku

AB

. Prosta

l

będzie niewidoczna, natomiast bok

AB

w rzucie poziomym będzie

widoczny.

Przykład

Wyznaczyć punkt przebicia prostej

a

z płaszczyzną

a

określoną śladami.

Zadanie to rozwiążemy analogicznie jak w poprzednim przypadku. Przez prostą

a

poprowadźmy

płaszczyznę pionowo - rzutującą

b

. Następnie wyznaczymy krawędź przecięcia się dwu płaszczyzn

a

i

b

. Tam, gdzie krawędź

k

przetnie prostą

a

otrzymamy szukany punkt

P

przebicia prostej

a

z

płaszczyzną

a

.

Informatyka 4 - Lekcja 2

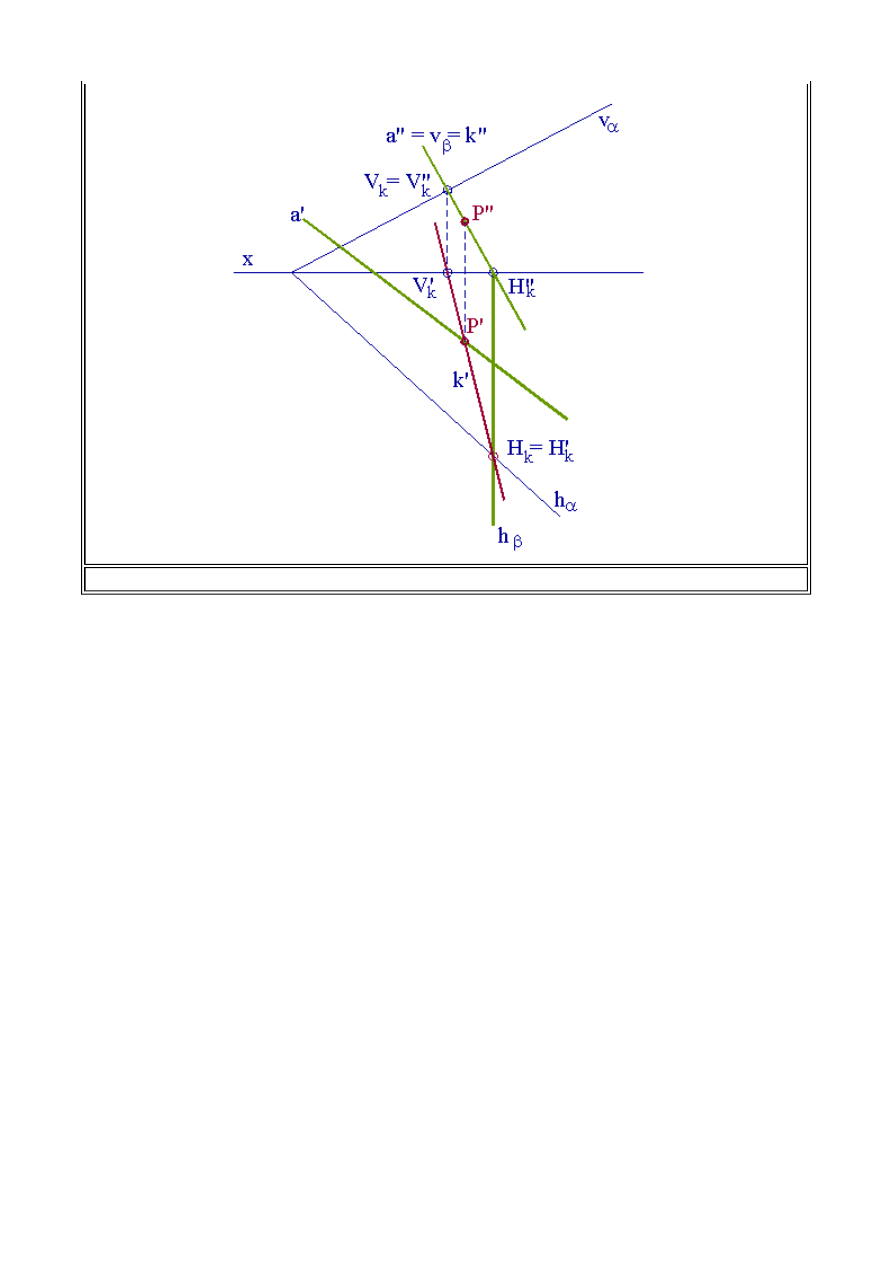
Punkt przebicia P w rzucie poziomym jest miejscem przecięcia się rzutów poziomych prostych

l'

i

k'.

Wyznaczenie krawędzi przecięcia się płaszczyzn jest konstrukcją, którą realizowaliśmy w p-cie

1.2. niniejszego rozdziału.

Rys.2.4. Punkt przebicia prostej z płaszczyzną.

Informatyka 4 - Lekcja 2

2. Przenikanie figur płaskich i przekroje wielościanów

płaszczyznami rzutującymi

Przenikanie się płaskich i przestrzennych obiektów technicznych stanowi dla konstruktorów
istotny problem, umożliwia bowiem ocenę współpracy podzespołów i mechanizmów jeszcze na
etapie projektowania.

Rozpatrzymy te zagadnienia dla podstawowych obiektów przestrzennych, zapisanych w rzutach
prostokątnych.

Przykład 1

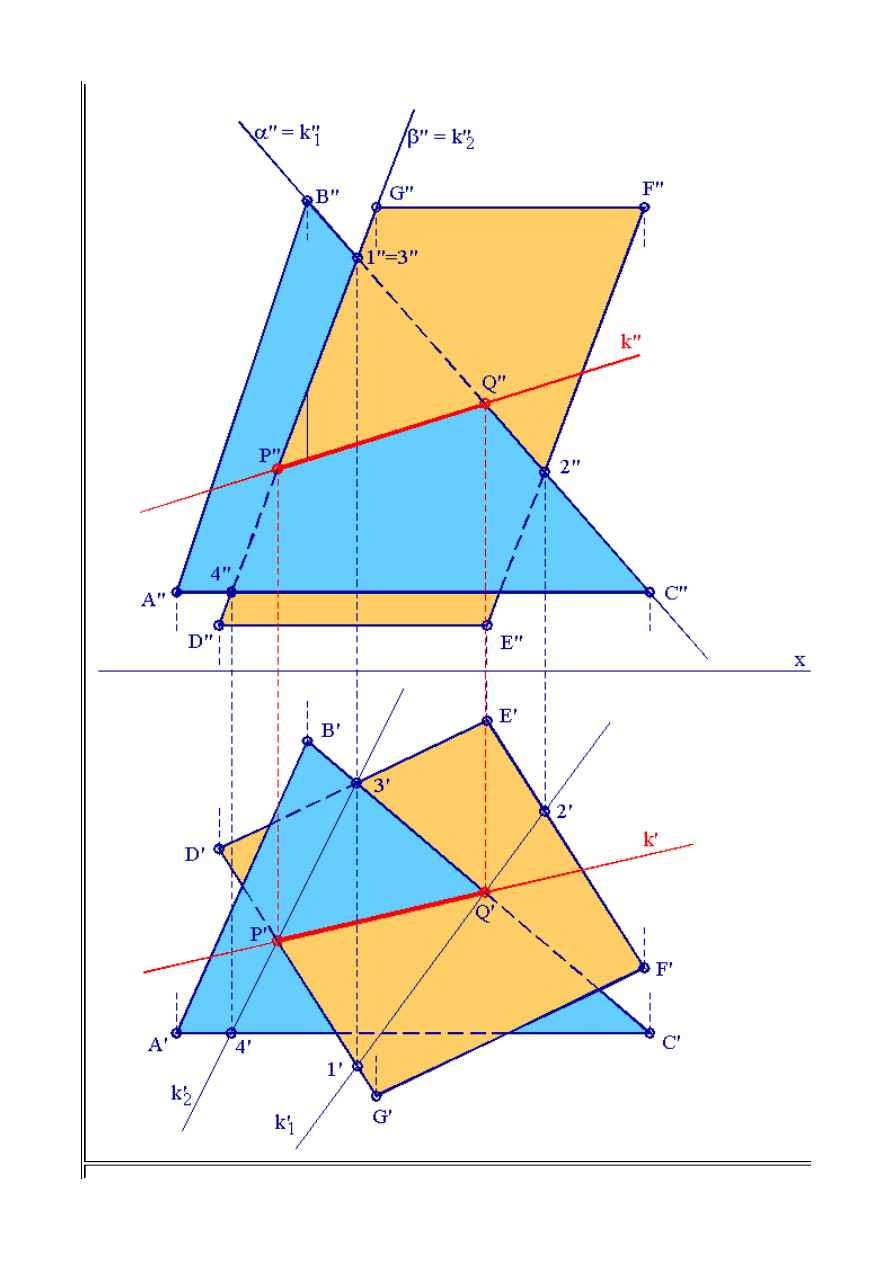
Wyznaczyć linie przenikania dwóch wielokątów płaskich: trójkąta ABC i równoległoboku DEFG.
Przyjmując płaszczyzny za nieprzezroczyste ustalić widoczność krawędzi.

Linia przenikania figur płaskich to nic innego jak odcinek krawędzi przecięcia się płaszczyzn,
zdefiniowanych przez te figury, wspólny dla obu płaszczyzn. Należy zatem wyznaczyć wspólną
krawędź przecięcia się płaszczyzn reprezentowanych przez trójkąt i równoległobok. Krawędź
wyznaczymy metodą pośrednią, poszukując punktów przebicia boku jednej z figur z płaszczyzną
drugiej figury. Wyznaczenie dwóch punktów przebicia, czyli dwóch punktów wspólnych tych
płaszczyzn określi nam krawędź przecięcia się płaszczyzn (dwa punkty, jednoznacznie, określają
prostą).

1) Wyznaczmy punkt przebicia boku BC trójkąta z płaszczyzną równoległoboku. W tym celu
podobnie jak w rozdz. 1.3 niniejszej lekcji poprowadzimy płaszczyznę pionowo - rzutującą

a

przez

bok

BC

trójkąta. Płaszczyzna jest rzutująca, a więc krawędź przecięcia się tej płaszczyzny z

płaszczyzną równoległoboku

k

1

będzie leżała w płaszczyźnie

a,

ale

również w płaszczyźnie

równoległoboku. Rzut pionowy krawędzi będzie pokrywał się z rzutem pionowym płaszczyzny

a

oraz z rzutem pionowym boku

B"C"

. Jeżeli leży w płaszczyźnie równoległoboku, to oznacza, że

punkty

1"

i

2"

są rzutami punktów przecięcia się krawędzi z rzutami boków

D"G"

oraz

E"F"

.

Rzuty poziome tych punktów znajdziemy na przecięciu się odnoszących prostopadłych do osi x z
rzutami poziomymi boków równoległoboku

D'G'

oraz

E'F'

. W ten sposób znaleźliśmy rzuty

krawędzi

k"

1

oraz

k'

1

. W rzucie poziomym otrzymamy szukany punkt przebicia

Q'

boku

B'C'

trójkąta z płaszczyzną równoległoboku. Rzut pionowy tego punktu wyznaczymy na przecięciu się
odnoszącej z rzutem pionowym krawędzi

k"

1

oraz boku

B"C"

.

(2.1) Przenikanie figur płaskich

Informatyka 4 - Lekcja 2

Informatyka 4 - Lekcja 2

2) Podobną konstrukcję przeprowadzamy z inną parą boków, np. równoległoboku oraz płaszczyzny
trójkąta

ABC.

Przyjmijmy do rozważań bok

DG

równoległoboku, przez który poprowadzimy

płaszczyznę

b,

a następnie w drodze postępowania analogicznego jak poprzednio wyznaczymy

krawędź przecięcia się płaszczyzny

b

z

płaszczyzną trójkąta oraz w konsekwencji punkt przebicia

P"

boku

DG

z trójkątem

ABC.

3) Podobnie jak w przypadku opisanym w rozdz.1.3 ustalamy widoczność poszczególnych
krawędzi analizując odpowiednio wysokość i głębokość punktów znajdujących się na przecięciu się
rzutów poszczególnych boków figur płaskich.

Przekroje wielościanów płaszczyznami są konstrukcjami prostymi. Dla zilustrowania tego
zagadnienia rozpatrzmy dwa przykłady.

Przykład 2

Wyznaczyć rzuty przekroju ostrosłupa ABCW stojącego na rzutni poziomej płaszczyzną pionowo -
rzutującą

a".

Zbudujmy w rzutach prostokątnych ostrosłup prosty o podstawie trójkąta stojący na rzutni poziomej
oraz przyjmijmy płaszczyznę pionowo - rzutującą określoną śladami

v

a

i

h

a

. Ponieważ płaszczyzna

a

jest rzutująca to wszystkie elementy płaskie znajdujące się w płaszczyźnie, w rzucie pionowym

będą znajdować się na rzucie pionowym płaszczyzny

a

, czyli na śladzie pionowym płaszczyzny

a

.

Tak więc przekrój w rzucie pionowym wyznaczymy w postaci punktów przecięcia się śladu

v

a

z

rzutami pionowym krawędzi ostrosłupa

A"W"

,

B"W"

i

C"W"

. Przekrój w rzucie pionowym

będzie wyznaczony przez rzuty punktów

1"

,

2"

i

3"

.

Rys.2.5. Linia przenikania trójkąta z równoległobokiem

(2.2) Przekroje ostrosłupów i graniastosłupów płaszczyznami rzutującymi

Informatyka 4 - Lekcja 2

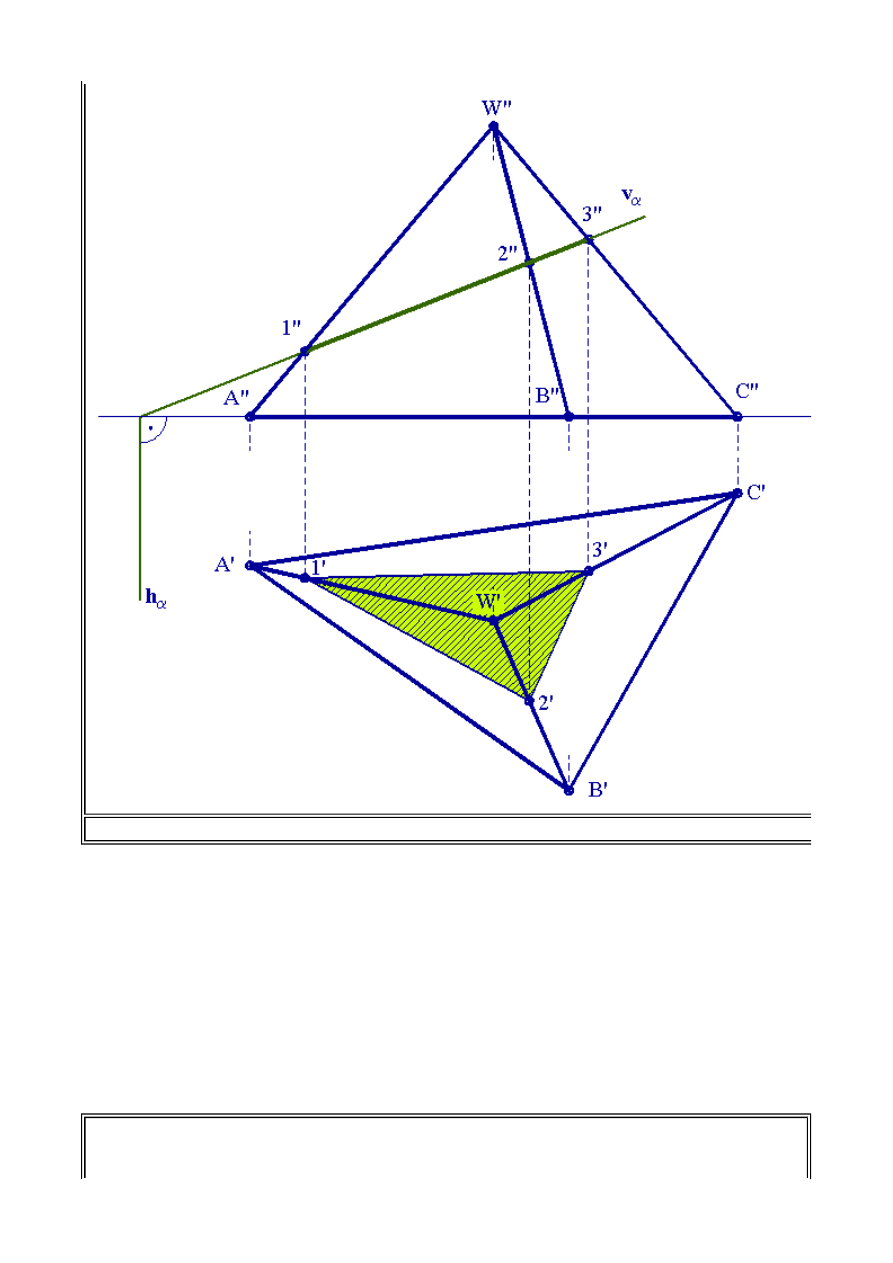
Rzut poziomy przekroju wyznaczymy oczywiście na rzutach poziomych krawędzi

A'W'

,

B'W'

i

C'W'.

Przykład 3

Wyznaczyć rzuty przekroju graniastosłupa pochyłego ABC stojącego na rzutni poziomej
płaszczyzną pionowo - rzutującą

a".

Przy rozwiązywaniu tego przykładu postępujemy analogicznie jak dla przykładu 2.

Rys.2.6. Przekrój ostrosłupa płaszczyzną pionowo - rzutującą

Informatyka 4 - Lekcja 2

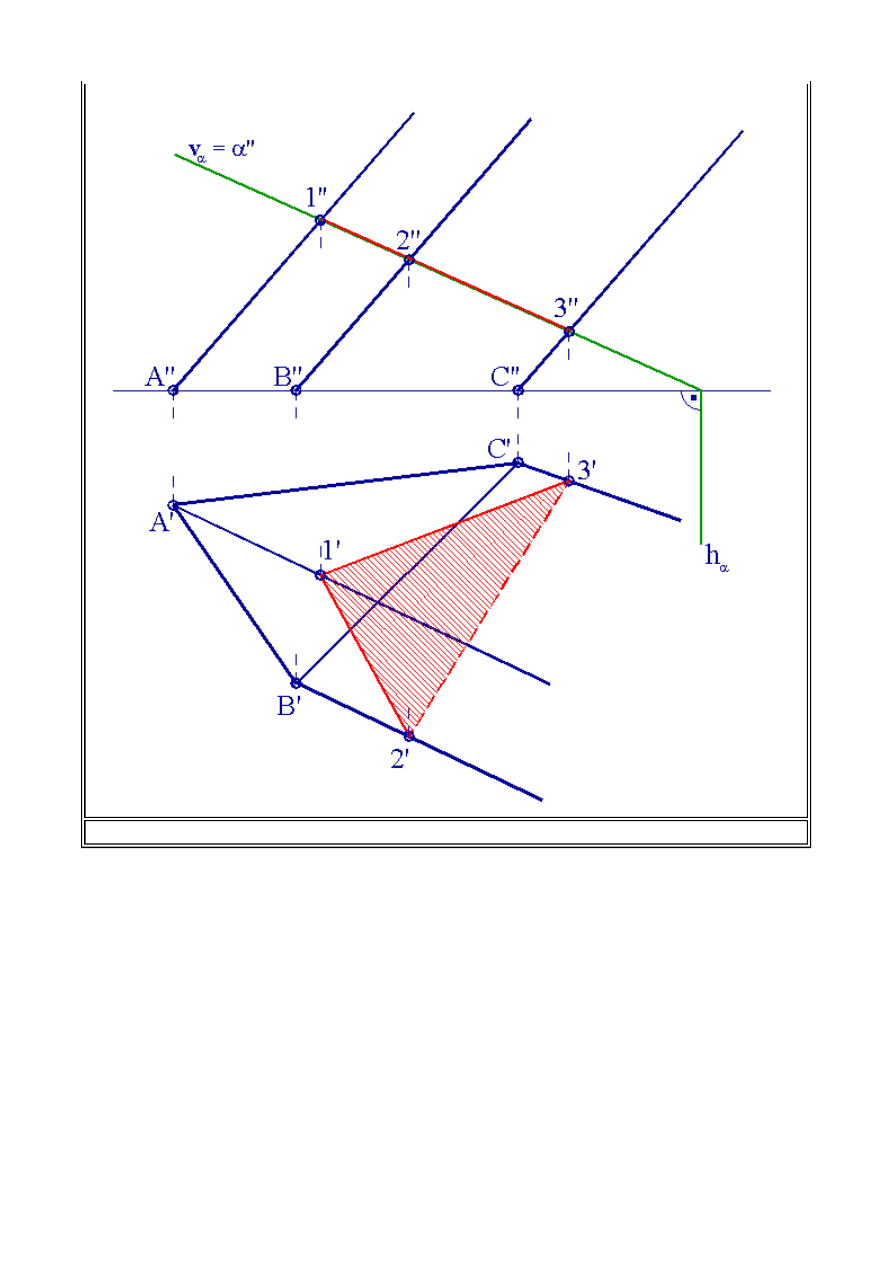
Po wyznaczeniu rzutów przekroju należy zwrócić uwagę na widoczność krawędzi. Zagadnienie
to było już omawiane wcześniej, przypomnijmy zatem, iż analizę widoczności dla rzutu pionowego
przeprowadzamy analizując rzut poziomy z kierunku prostopadłego do osi x, natomiast widoczność
w rzucie poziomym przeprowadzamy w rzucie poziomym analizując go od strony osi x w kierunku
zgodnym z kierunkiem krawędzi graniastosłupa.

Rys.2.7. Przekrój graniastosłupa pochyłego płaszczyzną pionowo - rzutującą

Informatyka 4 - Lekcja 2

3. Przekroje i przenikanie wielościanów

Przekroje wielościanów płaszczyznami dowolnym omówione w rozdz. 2 niniejszej lekcji są
konstrukcjami mało skomplikowanymi. Bardziej złożone są konstrukcje przekrojów płaszczyznami
dowolnymi. W celu uproszczenia postępowania przy wyznaczaniu takich przekrojów wprowadzimy
operację, która pozwoli nam sprowadzić zagadnienie do prostego postępowania opisanego
wcześniej. Operację tą nazywać będziemy

transformacją.

Definicja

Transformacją nazywamy zmianę układu odniesienia. W wyniku transformacji otrzymujemy
możliwość rzutowania na trzecią (lub więcej) rzutnię prostopadłą do rzutni poziomej lub pionowej.

Transformacja pozwala zatem tak zmienić układ odniesienia, aby np. płaszczyzna dowolna w
nowym układzie odniesienia stała się płaszczyzną rzutującą, co jak wiadomo zdecydowanie
upraszcza konstrukcje.

Poniżej zostaną omówione zasady transformacji (zmiany układu odniesienia) przy rzutowaniu
podstawowych elementów płaskich jak: punkt, prosta i płaszczyzna. Transformacja elementów
podstawowych umożliwi oczywiście rozpatrywanie obiektów przestrzennych, które są zwykle z nich
stworzone.

W celu dokonania transformacji punktu obieramy płaszczyznę

p

3

, która jest prostopadła np. do

rzutni poziomej, a następnie dokonujemy rzutowania prostokątnego na tą właśnie rzutnię. Na rys.
2.8a przykład ten zilustrowano w rzucie aksonometrycznym. Jak widać poza dwoma rzutami:
pionowym i poziomym otrzymaliśmy trzeci rzut punktu oznaczany przez

P'''

. Trzecią rzutnię

obracamy następnie dookoła osi transformacji, czyli krawędzi przecięcia się trzeciej rzutni z rzutnią
poziomą, do położenia pokrywającego się z rzutnią poziomą. Przenosząc to rozważnie do układu
rzutów prostokątnych, w celu wyznaczenia trzeciego rzutu punktu po dokonaniu transformacji
układu odniesienia należy:

1. obrać w sposób dowolny oś transformacji (ślad, krawędź przecięcia się nowej rzutni

p

3

z rzutnią

poziomą. Oś transformacji oznaczać będziemy

x

1/3

.

2. trzeci rzut punktu będzie leżał na odnoszącej prostopadłej do osi transformacji, co wynika z
rozłożenia układu trzeciej rzutni

p

3

na rzutnie poziomą

p

1

. Odległość w jakiej będzie się znajdował

trzeci rzut punktu

P'''

będzie odległy od osi x o wielkość równą wysokości punktu

P

, czyli

odległości punktu od rzutni poziomej. Ta odległość jest oczywiście analogiczna jak odległość rzutu

(3.1) Transformacja układu odniesienia

(3.2) Transformacja punktu

Informatyka 4 - Lekcja 2

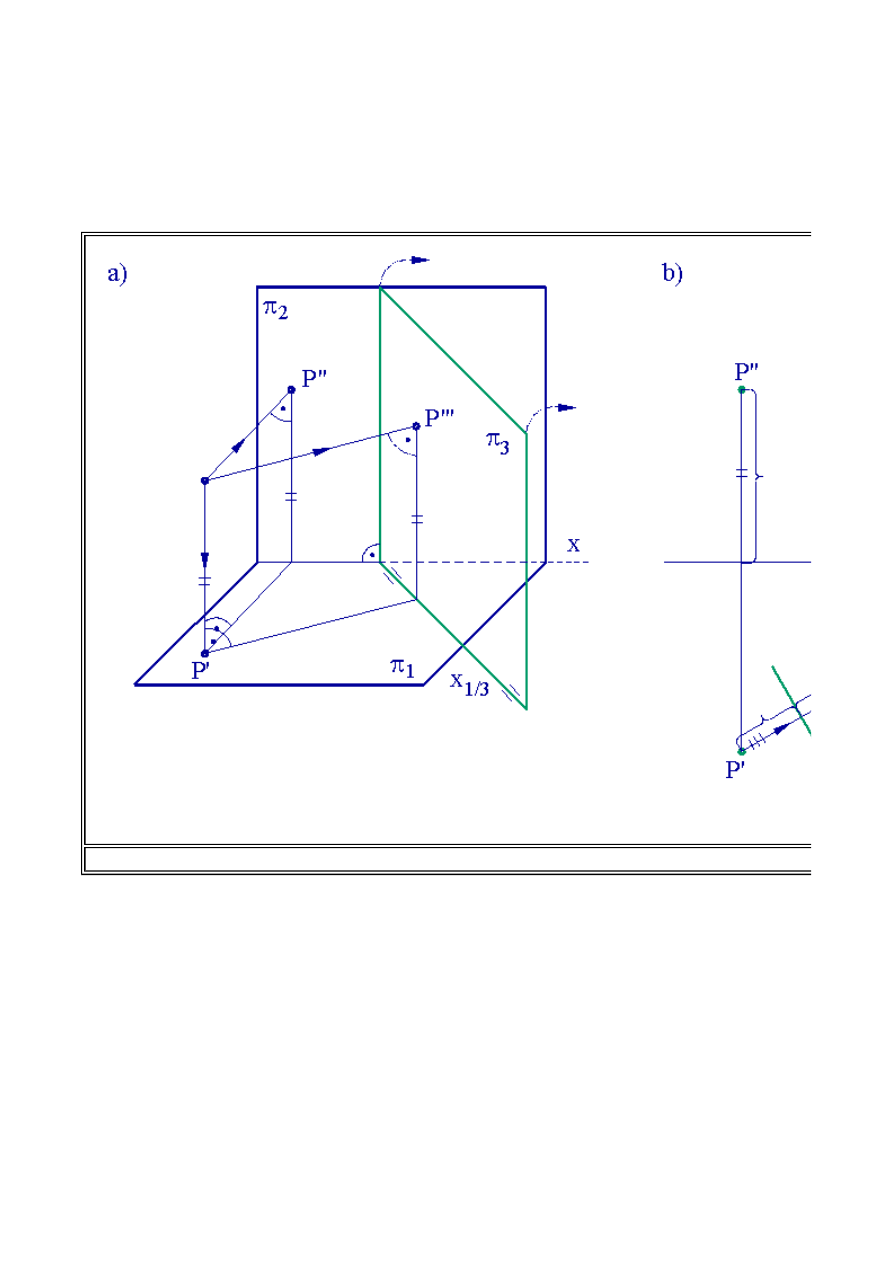
pionowego punktu

P"

od osi

x.

Można zatem stwierdzić, iż odmierzamy od osi

x

1/3

odległość

poprzedniego rzutu punktu (

P"

) od poprzedniej osi (

x

).

3. taką operację możemy powtarzać w miarę potrzeby wielokrotnie, zachowując opisane powyżej
zasady. Na rys. 2.8.b przedstawiono dwie kolejne transformacje punktu

P

.

Transformacja prostej, to nic innego jak transformacja dwóch punktów należących do
niej. Transformację prostej wykonujemy w określonym celu. Zwykle dotyczy to sprowadzania
prostej do położenia rzutującego, to znaczy do położenia prostopadłego do rzutni. Takie położenie
prostej może być wykorzystywane do rozwiązywania szeregu konstrukcji (np. wyznaczania
rzeczywistej odległości dwu prostych skośnych). Sprowadzenie prostej do położenia rzutującego za
pomocą transformacji uwarunkowane jest położeniem danej prostej. Położenie równoległe do rzutni
umożliwia dokonanie takiej operacji za pomocą jednej transformacji. W tym bowiem przypadku
jesteśmy w stanie zaproponować trzecią rzutnię prostopadle do prostej (oś transformacji będzie

Rys.2.8 Transformacja punktu

(3.3) Transformacja prostej i płaszczyzny

Informatyka 4 - Lekcja 2

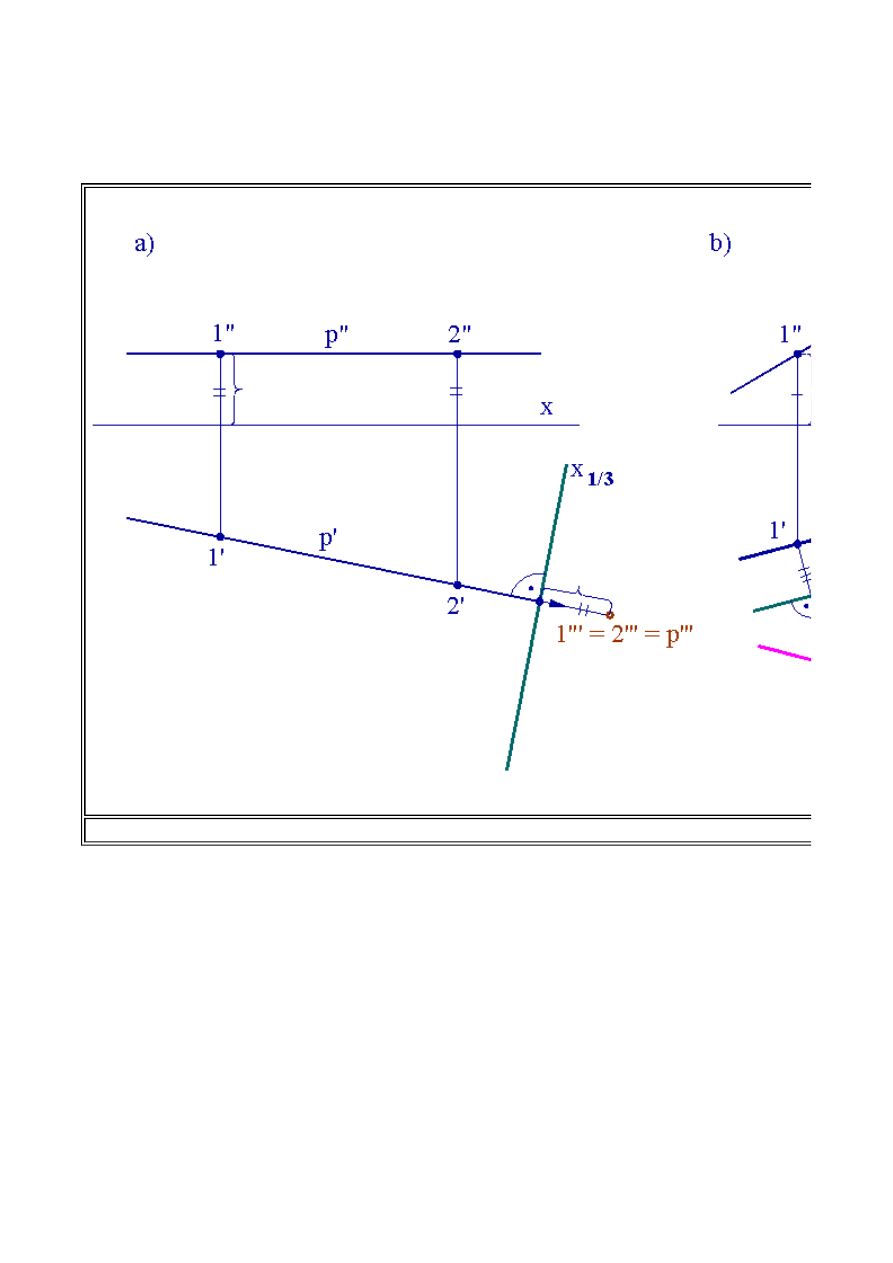
prostopadła do rzutu poziomego prostej, jeżeli prosta jest równoległa do rzutni poziomej lub
prostopadła do rzutu pionowego, jeżeli jest ona równoległa do rzutni pionowej). Na rys.2.9 a
przedstawiono transformację prostej poziomej (równoległej do rzutni poziomej).

Prosta p jest prostą poziomą, wiec sprowadzenie jej do położenia rzutującego (do punktu) jest
możliwe za pomocą jednej transformacji o osi

x

1/3

prostopadłej do rzutu poziomego prostej.

Dokonując transformacji prostej, należy dokonać transformacji dwóch dowolnych punktów
należących do niej. Obieramy dwa punktu

1

i

2

, a następnie dokonujemy transformacji tych

punktów o osi

x

1/3

. Odmierzając na odnoszącej przechodzącej przez punkty

1'

i

2'

i prostopadłej do

osi transformacji odległość równą wysokości punktów

1

i

2

(odległość

1"

i

2"

od osi x)

wyznaczymy trzecie rzuty punktów

1'''

i

2'''

, a tym samym i trzeci rzut prostej

p'''

.

Sprowadzenie prostej w położeniu dowolnym do położenia rzutującego (do punktu) możliwe
jest za pomocą podwójnej transformacji. W pierwszej sprowadzamy prostą do położenia
równoległego z trzecią rzutnią, a następnie za pomocą rzutni czwartej prostopadłej do trzeciego rzutu

Rys.2.9. Transformacja prostej. a) prosta pozioma b) Prosta dowolna.

Informatyka 4 - Lekcja 2

sprowadzamy ją do położenia rzutującego. W pierwszej transformacji przyjmujemy trzecią rzutnię
równolegle do prostej (oś transformacji

x

1/3

będzie równoległa do rzutu poziomego prostej

a')

. Druga

transformacja o osi

x

3/4

będzie prostopadła do trzeciego rzutu. Odmierzając od osi

x

3/4

odległość rzutu

poziomego

a'

od pierwszej osi transformacji otrzymamy czwarte rzuty punktów oraz czwarty rzut

prostej

p

IV

, który również będzie punktem.

Transformacja płaszczyzny to transformacja trzech punktów należących do niej.

Transformacja płaszczyzny ma na celu sprowadzenie jej do położenia rzutującego (do prostej).
Szereg konstrukcji w rzutach prostokątnych rozwiązuje się w sposób nieskomplikowany jeżeli
mamy do czynienia z płaszczyzną w położeniu rzutującym. Zatem zmiana układu odniesienia w taki
sposób, aby rozważana płaszczyzna była w położeniu rzutującym daje wymierne korzyści, albowiem
wszystkie elementy płaskie znajdujące się w tej płaszczyźnie będą rzutowały się w trzecim rzucie na
trzeci rzut płaszczyzny.

Definicja

Aby sprowadzić płaszczyznę dowolną do położenia rzutującego należy oś transformacji wybrać
prostopadle do śladu poziomego płaszczyzny, w przypadku transformacji na płaszczyznę
prostopadłą do rzutni poziomej lub prostopadle do śladu pionowego płaszczyzny, jeżeli
dokonujemy transformacji na płaszczyznę prostopadłą do rzutni pionowej.

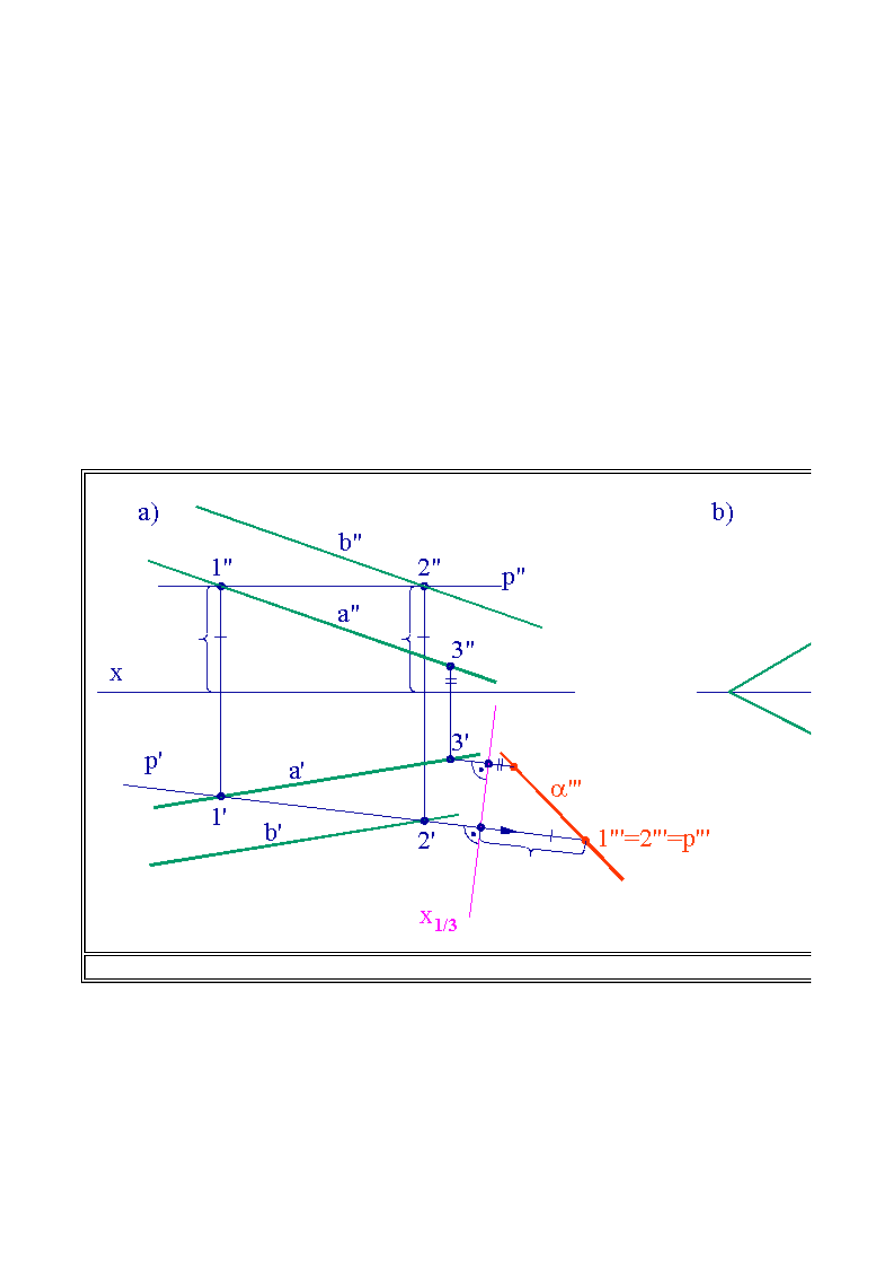
Rys.2.10. Transformacja płaszczyzny. a) Płaszczyzna określona przez dwie proste równoległe.

Informatyka 4 - Lekcja 2

Mając do czynienia z płaszczyzną określoną bezśladowo prostopadłość osi transformacji musimy
zapewnić odpowiednio do rzutu poziomego prostej poziomej, w I przypadku, lub do rzutu
pionowego prostej czołowej w II przypadku. Zatem wstępną czynnością będzie ustalenie rzutów
prostej poziomej (czołowej) leżącej w analizowanej płaszczyźnie. Na rys. 2.10 przedstawiono
konstrukcję zmiany układu odniesienia za pomocą transformacji dla płaszczyzny określonej dwoma
prostymi równoległymi (2.10a) oraz określonej śladami (rys.2.10b).

W przypadku sprowadzania płaszczyzny określonej przez dwie proste równoległe do położenia
rzutującego obieramy prostą poziomą leżącą w tej płaszczyźnie. Rzut pionowy prostej poziomej

p"

będzie równoległy do osi x. Na rzutach poziomych prostych

a'

i

b'

znajdziemy rzuty punktów

1'

i

2'

należących do tych prostych oraz w konsekwencji wyznaczymy rzut poziomy prostej

p'.

Wyznaczając oś transformacji

x

1/3

, podobnie jak w p.3.3 ustalimy trzecie rzuty punktów 1''' i 2''' oraz

p'''. Wystarczy zatem obrać jeszcze jeden punkt (np.3) nie współliniowy z punktami 1 i 2, aby po
przeprowadzeniu transformacji tego punktu wyznaczyć jego trzeci rzut, przy tej samej osi
transformacji. Rzuty punktów 1''', 2''' oraz 3''' wyznaczają nam trzeci rzut płaszczyzny, który będzie
prostą. Trzeci rzut płaszczyzny jest więc położeniem rzutującym płaszczyzny

a(a||b)

.

Przy sprowadzaniu płaszczyzny określonej śladami do położenia rzutującego postępujemy bardzo
podobnie. W tym przypadku oś transformacji

x

1/3

będzie prostopadła do śladu poziomego

płaszczyzny

a

. Ponieważ ślad poziomy płaszczyzny jest szczególnym położeniem prostej poziomej

leżącej w płaszczyźnie, to punkt przecięcia się śladu poziomego z osią transformacji

x

1/3

-

oznaczony

X

a

'''

, zwany węzłem płaszczyzny będzie punktem należącym do trzeciego rzutu płaszczyzny.

Należy zatem obrać jeszcze jeden punkt nie należący do śladu poziomego (np. p-kt 1) , aby po
dokonaniu transformacji tego punktu, przy tej samej osi

x

1/3

, ustalić jego trzeci rzut. Punkty

1'''

i

X

a

'''

wyznaczą nam trzeci rzut płaszczyzny

a'''

.

Zmiana układu odniesienia zwana transformacją pozwoli w prostszy sposób rozwiązywać złożone
konstrukcje w rzutach prostokątnych. Dotyczy to w szczególności przekrojów brył przestrzennych
płaszczyznami w położeniu dowolnym. W tym przypadku rozwiązanie zagadnienia będziemy
poprzedzali zmianą układu odniesienia, tak aby płaszczyzna przekroju, po dokonaniu transformacji,
była w położeniu rzutującym.

Przykład 1

Wyznaczyć linię przenikania równoległoboku z ostrosłupem prostym o podstawie trójkąta, stojącym
na rzutni poziomej.

Wyznaczmy rzuty pionowe i poziome ostrosłupa oraz równoległoboku. Dla uproszczenia
równoległobok określimy przy pomocy podstawy

PQ

oraz dwóch prostych równoległych

a

i

b

.

Drugą podstawę pominiemy, albowiem nie będzie brała udziału w konstrukcji. Zadaniem naszym

(3.4) Przekroje wielościanów płaszczyzną dowolną

Informatyka 4 - Lekcja 2

jest wyznaczenie linii przenikania równoległoboku z ostrosłupem, co oznacza, że powinniśmy
wyznaczyć przekrój ostrosłupa płaszczyzną równoległoboku, a następnie oraz ustalić części wspólne
przekroju dla ostrosłupa i równoległoboku. Na rys.2.11 przedstawiona została konstrukcja
rozwiązania tego przykładu.

Przystępując do rozwiązania powyższego zadania w pierwszej kolejności dokonamy zmiany układu
odniesienia przy pomocy transformacji. Sprowadzenie płaszczyzny równoległoboku do położenia
rzutującego rozpoczniemy od obrania właściwej osi transformacji układu. Oś

x

1/3

powinna być

prostopadła do rzutu poziomego prostej poziomej leżącej w płaszczyźnie. W tym przypadku boki
równoległoboku

a

i

b

są właśnie w takim położeniu, zatem oś transformacji

x

1/3

będzie prostopadła

do rzutów poziomych

a'

i

b'

.

Informatyka 4 - Lekcja 2

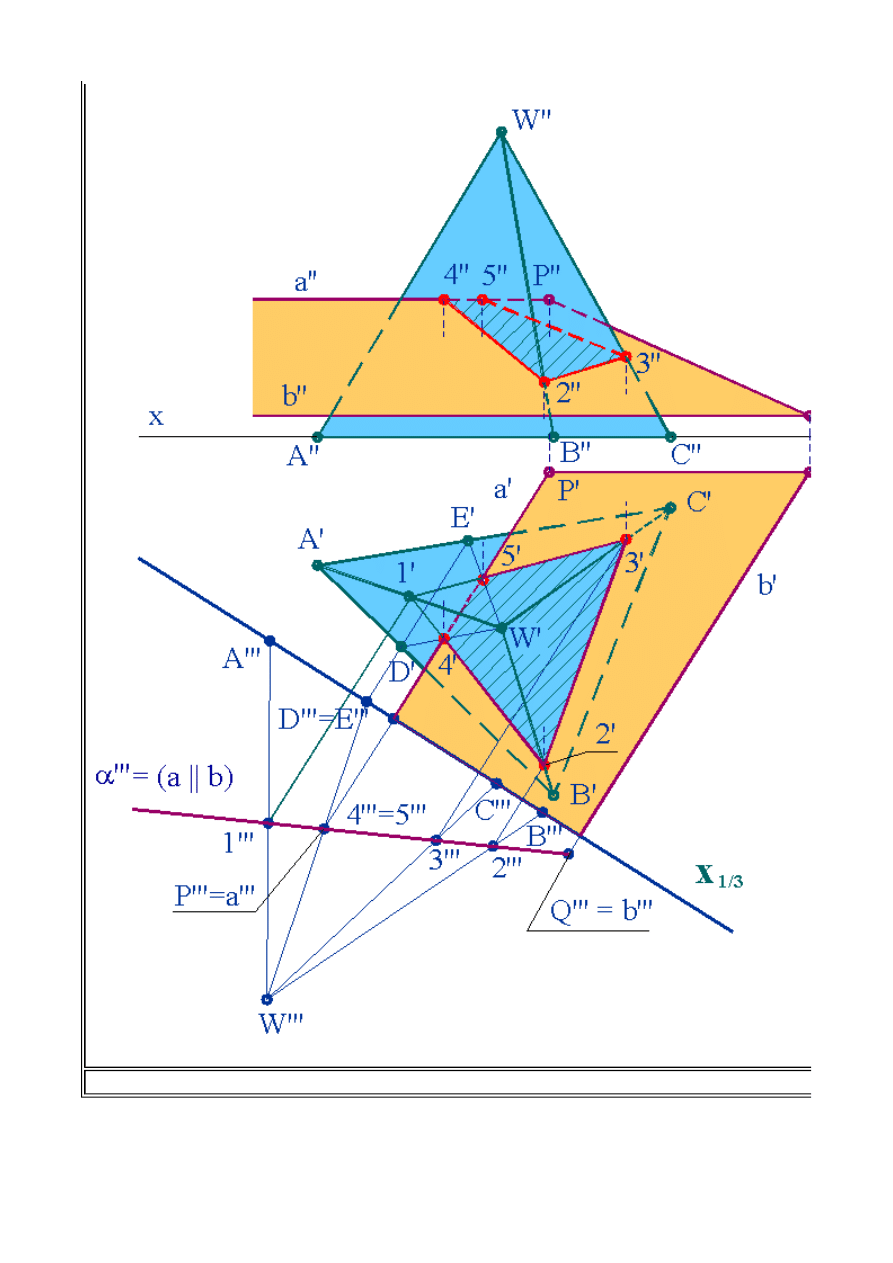
Wyznaczamy trzeci rzut płaszczyzny równoległoboku

a'''(a||b)

ustalając kolejno trzecie rzuty

prostej

a'''

i

b'''

, odmierzając od osi transformacji wysokość punktów

P

i

Q

znajdujących się na

Rys.2.11. Przekrój ostrosłupa płaszczyzną równoległoboku.

Informatyka 4 - Lekcja 2

prostych. Następnie dokonujemy transformacji ostrosłupa. Podstawa ostrosłupa

A''B''C''

będzie

znajdować się na osi transformacji, ponieważ podstawa stoi na rzutni poziomej (wysokość
wierzchołków podstawy wynosi zero). Wierzchołek

W'''

będzie odległy od osi transformacji o

odległość

W''

od osi

x

. (wysokość wierzchołka

W

). Otrzymaliśmy założenia zadania w nowym

układzie odniesienia. Płaszczyzna

a'''(a||b)

jest w położeniu rzutującym, więc wyznaczenie

punktów przebicia krawędzi ostrosłupa z płaszczyzną równoległoboku (szukany przekrój ostrosłupa)
w trzecim rzucie otrzymamy w punktach przecięcia krawędzi

A'''W'''

,

B'''W'''

, i

C'''W'''

z

płaszczyzną

a'''(a||b)

punkty

1'''

,

2'''

i

3'''

. Jak widać w trzecim rzucie punkt

1

znajduje się poza

równoległobokiem, nie będzie zatem tworzył linii przenikania, ale będzie należał do przekroju. Linie
przekroju będą ograniczone zatem prostą

a

, która jest bokiem równoległoboku. Trzeci rzut prostej

a

wyznaczy punkty

4'''

i

5'''

, przebicia prostej

a

ze ścianami ostrosłupa. Rzuty poziome tych punktów

4'

i

5'

wyznaczymy prowadząc przez nie tworzące ostrosłupa

DW

i

EW

i

ustalając rzuty tych

tworzących. Po wyznaczeniu tych punktów możemy wykreślić linię przenikania, która ograniczona
będzie punktami

2

,

3

,

4

,

5

. Mając rzuty poziome tych punktów można wyznaczyć rzuty pionowe.

Rzuty punktów

2''

i

3''

będą leżały odpowiednio na krawędziach ostrosłupa, natomiast

4''

i

5''

na

boku

a

równoległoboku. Przyjmując, że ściany ostrosłupa i płaszczyzna równoległoboku są

nieprzezroczyste możemy ustalić widoczność poszczególnych krawędzi. Sposób ustalania
widoczności został opisany w poprzednich rozdziałach. Efekt rozwiązania przedstawiony na rys.2.11
wyraźnie pokazuje wzajemne przenikanie się krawędzi równoległoboku ze ścianami ostrosłupa.

W technice często mamy do czynienia z zagadnieniem przenikania się powierzchni regularnych
wielościanów. Ustalenie linii przenikania - konstrukcyjnie pozwala konstruktorowi przewidzieć
szereg kwestii technicznych wynikających z tego tytułu. Wykorzystując metody przedstawione w
dotychczasowych rozdziałach omówimy przykładowe przenikanie się dwóch wielościanów.

Przykład 2

Wyznaczyć linię przenikania ostrosłupa KLNW z graniastosłupem prostym stojącym na rzutni
poziomej oraz podstawie ABCD.

Na rysunku 2.12a przedstawione zostały założenia do niniejszego zadania. Graniastosłup, którego
podstawa

ABCD

stoi na rzutni poziomej, a więc jego ściany są w położeniu rzutującym względem

tej rzutni. Wszystkie elementy płaskie leżące na ścianach graniastosłupa, w rzucie poziomym, będą
znajdowały się na rzucie poziomym boków podstawy

A'B'

,

B'C'

,

C'D'

,

D'A'

. Dla ułatwienia i

czytelności rysunku nie oznaczymy górnej podstawy graniastosłupa, która jak widać z rzutu
pionowego nie bierze udziału w tworzeniu linii przenikania. Położenie ostrosłupa wymaga ustalenia
widoczności jego krawędzi. Widoczność tą powinniśmy ustalić w rzucie pionowym, ponieważ w
rzucie poziomym krawędzie podstawy pokrywają się. W tym celu wykorzystamy punkty

EF

leżące

odpowiednio:

E

na boku podstawy

LN

oraz

F

na krawędzi

KW

ostrosłupa. Rzuty pionowe tych

(3.5) Przenikanie wielościanów

Informatyka 4 - Lekcja 2

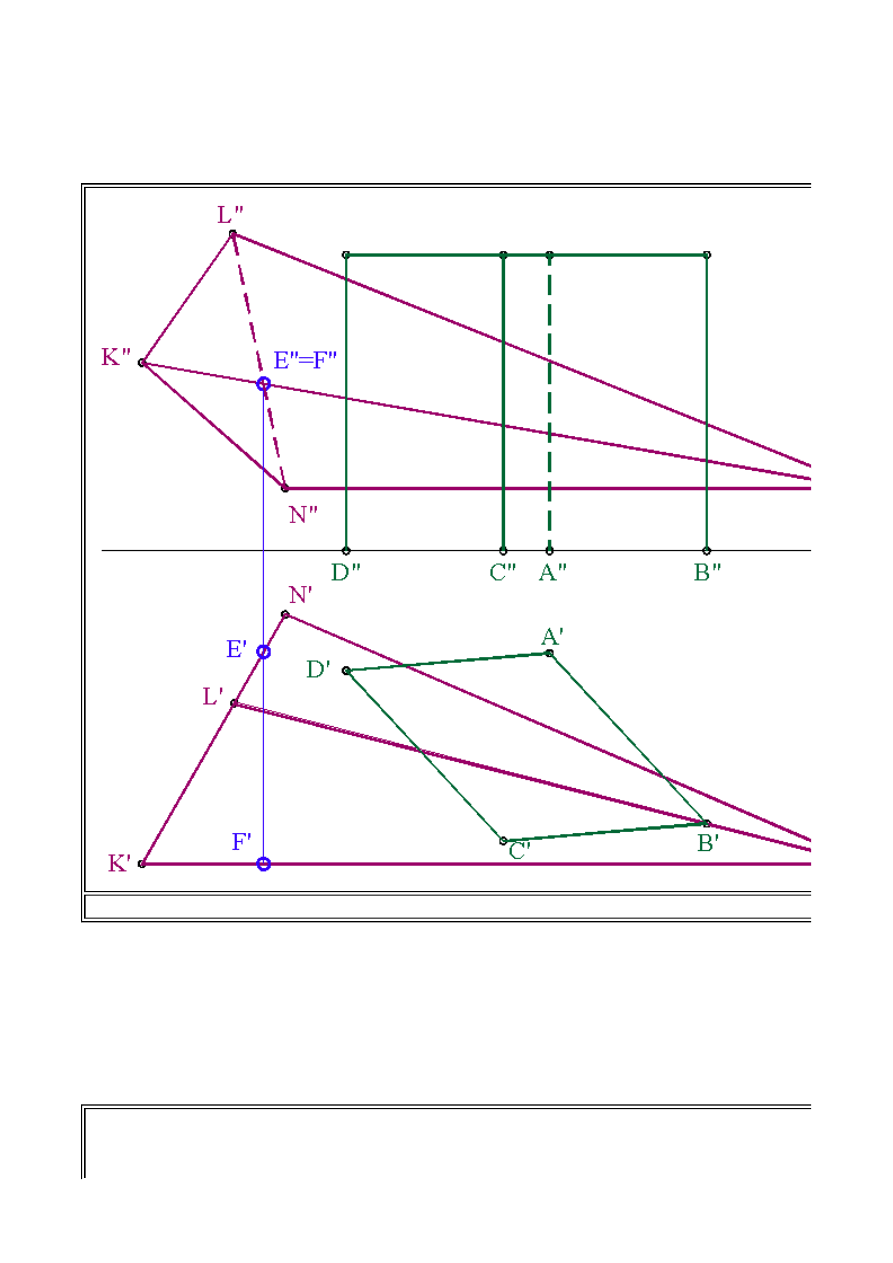
punktów pokrywają się. Ustalając, że punkt

F

należący do krawędzi

KW

ma większa głębokość

(większą odległość od rzutni pionowej) można stwierdzić, iż w rzucie pionowym bok podstawy
ostrosłupa

L''N''

będzie niewidoczny, co zaznaczamy linią kreskową.

Linia przenikania wielościanów związana jest z wyznaczaniem punktów przebicia jednego z
wielościanów ze ścianami drugiego wielościanu. Na rys. 2.12 b, w rzucie poziomym możemy

zaobserwować, które krawędzie jednego z wielościanów przebijają ściany drugiego wielościanu.

Krawędź

A

graniastosłupa leży poza ostrosłupem i nie bierze udziału w tworzeniu poszukiwanej linii

przenikania. Pozostałe krawędzie graniastosłupa przebijają ściany ostrosłupa. Krawędź

B

przecina

krawędź

LW

oraz ścianę

KNW

ostrosłupa, krawędź

C

graniastosłupa przebija ściany

KNW

i

KLW

ostrosłupa. Krawędź

D

graniastosłupa przebija ściany

LNW

oraz

KNW

.

Rys.2.12 a. Przenikanie ostrosłupa z graniastosłupem prostym -założenia do zadania.

Informatyka 4 - Lekcja 2

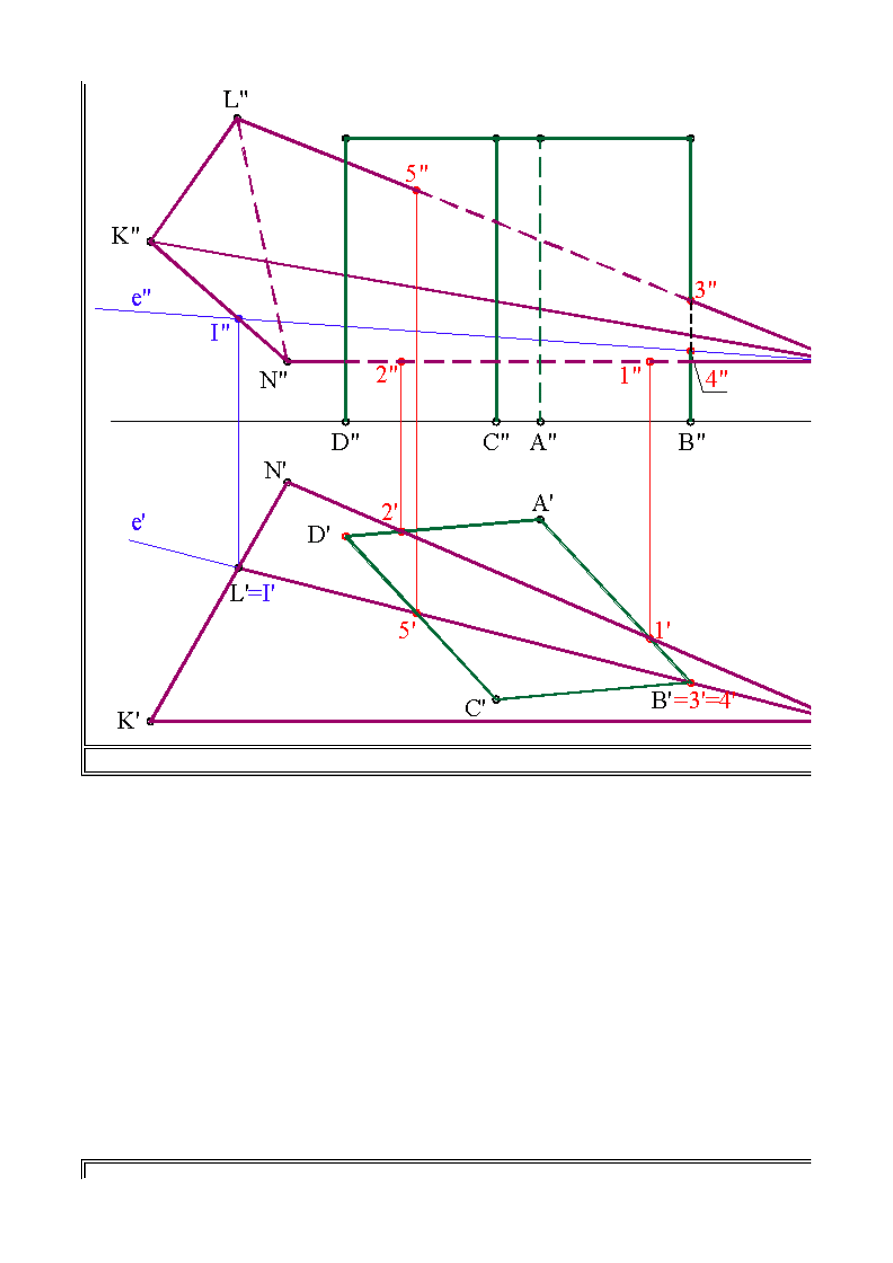
Podobnie można ocenić, które krawędzie ostrosłupa przebijają ściany graniastosłupa. Krawędź

NW

ostrosłupa przebija ścianę

DA

i

AB

graniastosłupa, natomiast krawędź

LW

przebija ścianę

CD

oraz przecina (opisaną wcześniej) krawędź

B

graniastosłupa. Krawędź

KW

nie bierze udziału w

tworzeniu linii przenikania. Po takiej analizie możemy przystąpić do wyznaczania poszczególnych

punktów linii przenikania.

Oznaczmy poszczególne punkty przebicia i przecięcia krawędzi ostrosłupa ze ścianami i
krawędzią graniastosłupa, opisane powyżej, w rzucie poziomym kolejno punktami

1'

,

2'

,

3'

,

4'

,

5'

.

Rzuty pionowe punktów

1''

,

2''

,

3''

,

5''

znajdziemy bezpośrednio na rzucie pionowym krawędzi

ostrosłupa. Jedynym problem do rozwiązania jest rzut pionowy punktu

4''

, który znajduje się na

ścianie

KNW

ostrosłupa. W celu wyznaczenia jego położenia poprowadźmy przez rzut poziomy

wierzchołka

W'

ostrosłupa i rzut poziomy punktu

4'

tworzącą

e'

, leżącą na ścianie

K'N'W'

.

Następnie wyznaczymy rzut pionowy tworzącej

e''

, korzystając pośrednio z rzutów punktów

I'

i

II''

przecięcia tworzącej z bokiem

KN

podstawy ostrosłupa, na rzucie pionowym

e''

wyznaczymy

poszukiwany rzut pionowy punktu

4''

. W etapie I ustalone zostały punkty przebicia krawędzi

ostrosłupa ze ścianami graniastosłupa. W etapie II zajmiemy się punktami przecięcia krawędzi

graniastosłupa ze ścianami ostrosłupa (patrz rys. 2.12c).

Rys.2.12 b. Przenikanie ostrosłupa z graniastosłupem prostym - wyznaczanie linii przenikania

Informatyka 4 - Lekcja 2

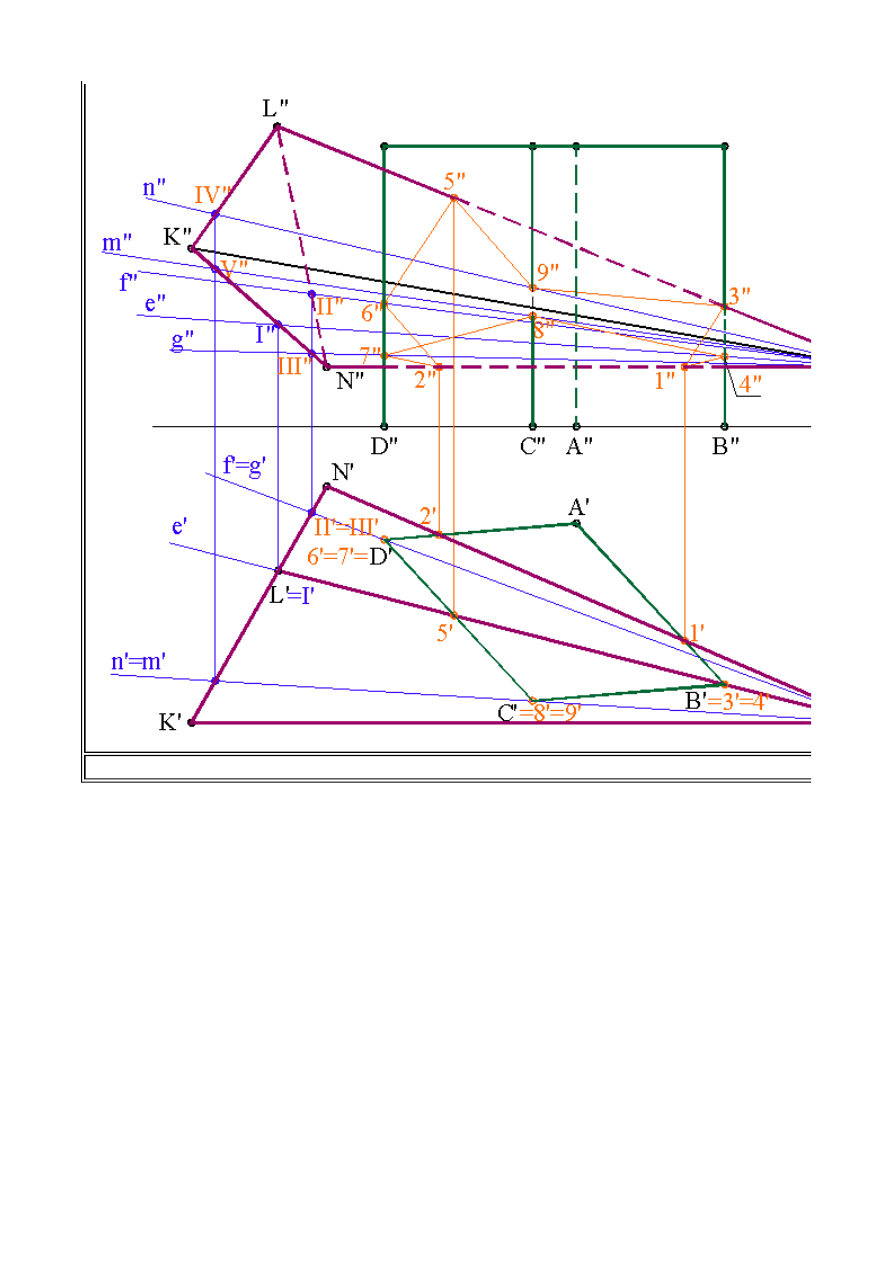
Kolejne punkty przecięcia krawędzi graniastosłupa ze ścianami ostrosłupa to: Punkt

6

i

7

przebicia krawędzi

D

ze ścianami odpowiednio

NLW

i

NKW

oraz punkty

8

i

9

przebicia krawędzi

C

ze ścianami

KLW

i

KNW

. Rzuty pionowe tych punktów wyznaczymy po ustaleniu rzutów

pionowych poszczególnych tworzących przechodzących przez te punkty.

Kolejny problem to ustalenie kolejności połączenia punktów tworzących linie przenikania. W tym

celu zbudujemy tzw.

siatkę znaków.

Rozetnijmy poszczególne wielościany wg jednej z krawędzi

(najlepiej według krawędzi nie biorącej udziału w tworzeniu linii przenikania) i oznaczmy te
krawędzie symbolicznie na przedstawionej siatce, powtarzając pierwszą krawędź, tak aby zamknąć

powierzchnię boczną danego wielościanu. Na tak stworzonej siatce nanosimy symbolicznie
poszczególne punkty linii przenikania od

1

do

9

. Np. punkt

1

znajduje się na krawędzi

N

ostrosłupa

oraz ścianie

AB

graniastosłupa. Podobnie postępujemy z następnymi punktami. Końcowym

akcentem tego etapu jest wyznaczanie linii przenikania, a więc ustalenie, które punkty należy
połączyć ze sobą, tak aby utworzyły zamkniętą linię przenikania. Zasada łączenia ze sobą

poszczególnych punktów polega na łączeniu ze sobą jedynie w obrębie jednego kwadratu. Powstała
zatem zamknięta linia przenikania. Może się zdarzyć, że otrzymamy dwie, pozornie otwarte linie

przenikania, wtedy gdy przecięcie wielościanu nastąpi wzdłuż krawędzi zaangażowanej w procesie

konstrukcji linii przenikania. Pamiętając jednak, że powierzchnie boczne wielościanów są zamknięte

Rys.2.12 c. Przenikanie ostrosłupa z graniastosłupem prostym - wyznaczanie linii przenikania -

Informatyka 4 - Lekcja 2

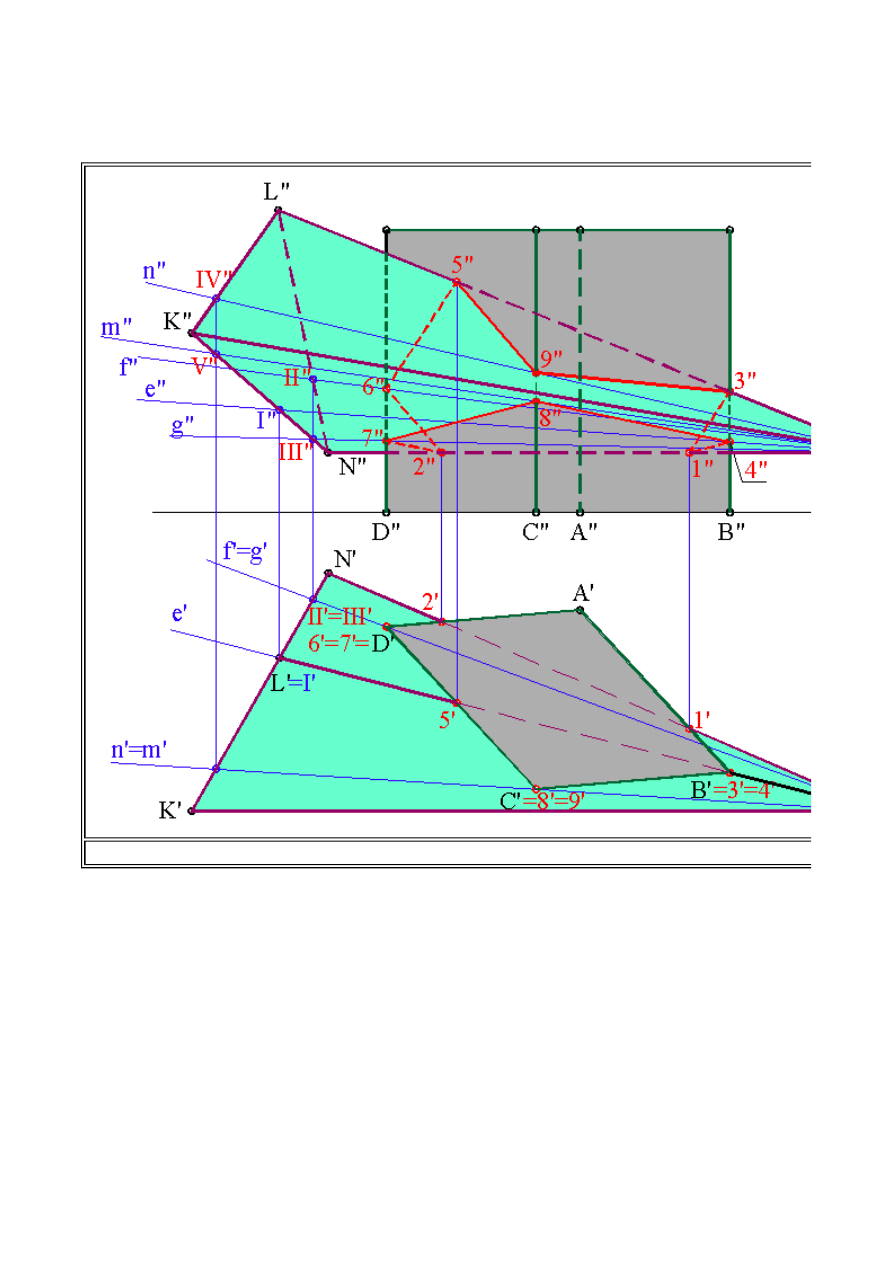
oraz, że na końcu siatki powtarzamy pierwsza krawędź, zawsze otrzymamy linie zamkniętą. Tak

otrzymane połączenia punktów linii przenikania nanosimy następnie, cienką linią, na rysunek
konstrukcyjny.

Ostatni III etap związany jest z widocznością linii przenikania w rzucie pionowym. Analizując rzut

poziomy wielościanów ustalimy, które ze ścian są widoczne, a które są niewidoczne w rzucie
pionowym. Analizę taka przeprowadzamy odrębnie dla każdego z wielościanów. W przypadku

graniastosłupa niewidocznymi są ściany

AB

i

DA

, co zaznaczamy znakiem (-), a następnie całą

ścianę na siatce znaków kreskujemy. Dla ostrosłupa niewidoczna jest ściana

LN

, którą również

oznaczamy znakiem (-) i całą ścianę kreskujemy. Otrzymaliśmy zatem pola kwadratów, w których

znajdująca się linia przenikania jest niewidoczna oraz pola, w których jest ona widoczna. Tak

otrzymaną, na siatce znaków, sytuację nanosimy na układ rzutów prostokątnych wielościanów.
Ostatecznie przyjmując, że ściany wielościanów są nieprzezroczyste możemy uwypuklić wzajemne

przenikanie się brył za pomocą cieniowania każdej z nich osobno. Zadanie powyższe zostało
rozwiązane.

Rys.2.12 d. Przenikanie ostrosłupa z graniastosłupem prostym - wyznaczanie linii przenikania

Informatyka 4 - Lekcja 2