
1. Odwzorowanie postaci geometrycznej w rzutach
środkowym i równoległym
Celem zapisu konstrukcji jest identyfikacja obiektu przestrzennego (urządzenia technicznego) za
pomocą metod zrozumiałych dla ludzi profesjonalnie zajmujących się techniką. Proponowane w
Graficznym zapisie konstrukcji metody umożliwiają również zapis pozwalający identyfikować
obiekty przestrzenne przez osoby nie mające związków z tą dziedziną wiedzy. Identyfikacja tych
obiektów dokonywana jest:
l
w pierwszym przypadku za pomocą tzw.
rzutowania prostokątnego
na wzajemnie
prostopadłe płaszczyzny zwane rzutniami oraz
l
w drugim przypadku za pomocą tzw.
rzutu aksonometrycznego.
Odwzorowania elementów przestrzennych na płaszczyźnie muszą spełniać szereg podstawowych
warunków:
·
zapisy konstrukcji muszą być absolutnie jednoznaczne, co oznacza, iż obiektowi
przestrzennemu przypisany jest jeden rysunek lub zespół rysunków dokładnie opisujący jego
właściwości geometryczne oraz na odwrót na podstawie rysunku lub zespołu rysunków
można absolutnie jednoznacznie odtworzyć dany obiekt przestrzenny;
·
zapisy konstrukcji powinny umożliwiać czytającemu rysunek analizę obiektu
przestrzennego, łącznie z identyfikacją wszystkich właściwości geometrycznych (wymiary,
kształt, szczegóły konstrukcyjne) oraz niektórych właściwości technologicznych (rodzaj
obróbki, tolerancje i pasowania powierzchni).
Informatyka 4 - Lekcja 1
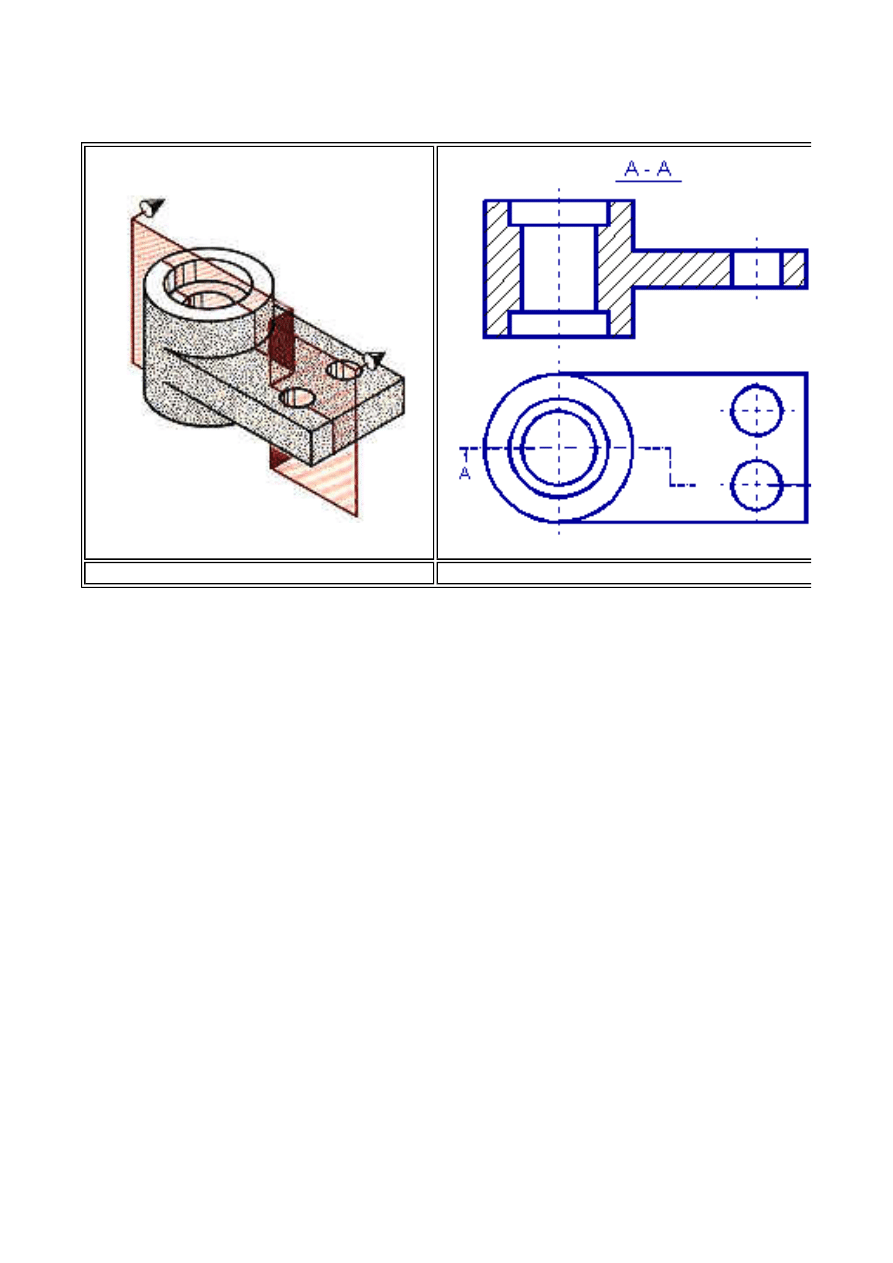
Poniżej przedstawiono zapis przykładowej konstrukcji mechanicznej w formie rzutu
aksonometrycznego oraz rzutów prostokątnych na dwie wzajemnie prostopadłe rzutnie.
Jak widać na rys. 1.1. forma rysunku aksonometrycznego pozwala czytelnikowi na dość
precyzyjną identyfikację geometryczną obiektu przestrzennego. Rysunek 1.2 wymaga już od
czytelnika znajomości zasad i metod odwzorowań przestrzennych. Wymaga również
wyobraźni przestrzennej do poprawnego odczytu konstrukcji. Temu celowi poświecone będą
dwa pierwsze z pośród trzech podstawowych bloków przedmiotu.
Przedmiot Informatyka 4 - CAD w Graficznym zapisie konstrukcji składa się z trzech
podstawowych bloków tematycznych:
1. Blok związany z podstawami odwzorowań przestrzennych na płaszczyźnie za pomocą rzutu
równoległego oraz rzutu prostokątnego.
2. Blok związany z teorią zapisu konstrukcji mechanicznych i elektromechanicznych
3. Blok związany z niezbędnymi narzędziami komputerowymi służącymi do komputerowego
tworzenia rysunków płaskich i przestrzennych, ich zapisu, edycji i modyfikacji.
Pierwszy blok dotyczy podstaw odwzorowań, a w szczególności tych elementów, które
związane są z prostokątnymi rzutami Monge’a oraz rzutami aksonometrycznymi brył
przestrzennych. Wiadomości z tej dziedziny kształtują wyobraźnie przestrzenna słuchacza oraz
pozwalają na swobodne operowanie podstawowymi elementami przestrzeni euklidesowej W
3
.
Blok drugi dotyczy szczegółowych zasad zapisu konstrukcji mechanicznych i
elektromechanicznych. Wiedza z tego zakresu pozwoli tworzyć i odczytywać techniczny zapis
konstrukcji elementów maszyn. Pozwala również zapoznać się słuchaczowi z metodami uproszczeń
stosowanych w zapisie. Blok ten przygotowuje słuchacza do samodzielnego zapisu projektowanej
konstrukcji.
Rys.1.1 Rzut aksonometryczny części maszynowej
Rys. 1.2 Rzuty prostokątne części maszynowej przedstawionej na rys.1.1.
Informatyka 4 - Lekcja 1
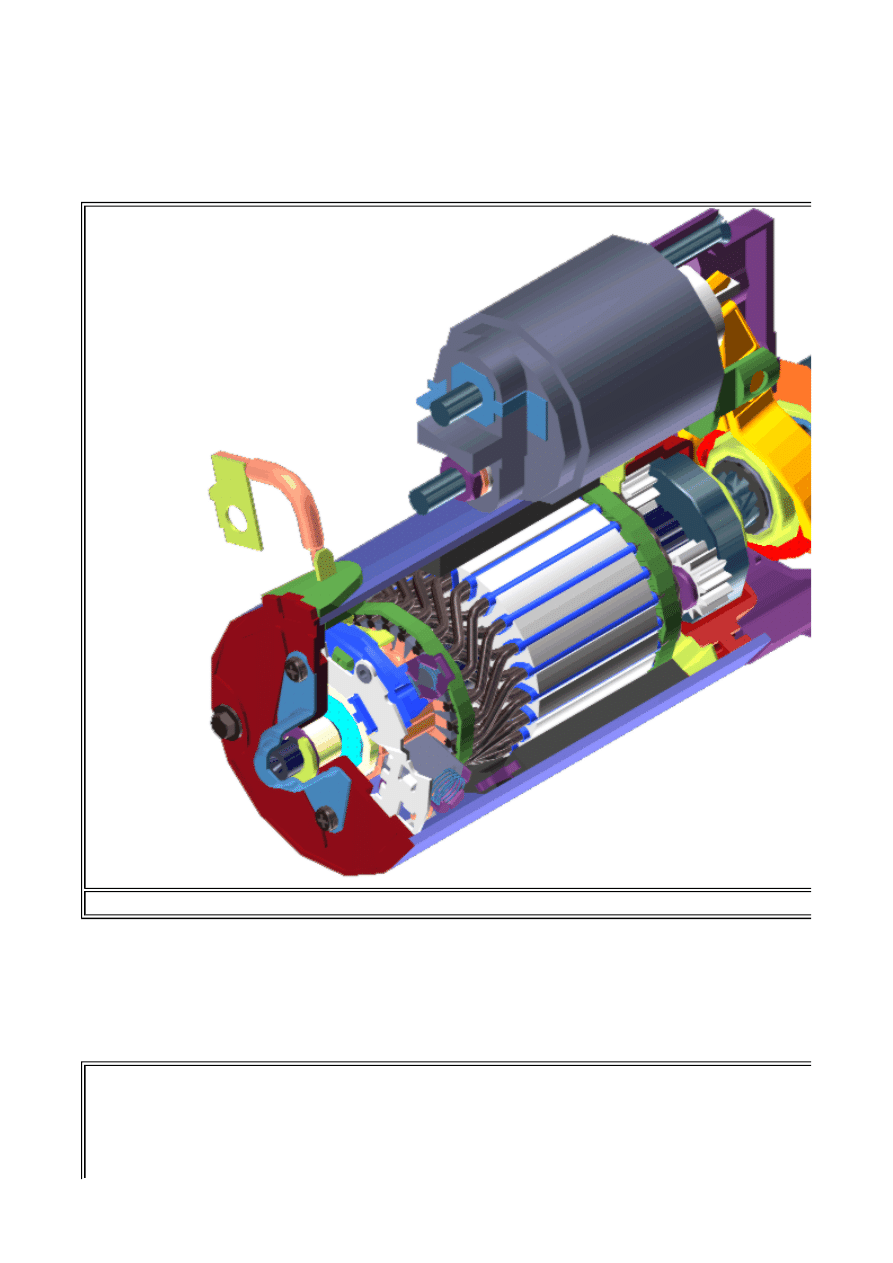
Blok trzeci to poznanie narzędzia umożliwiającego prace nad projektem. Narzędzia w dobie
dostępu do techniki komputerowej związane są z metodami CAD (Computer Aided Design). Na
fotografii 1.1 przedstawiony został przykładowy rysunek przekroju elektrycznego rozrusznika
samochodowego w wymiarze przestrzennym 3D. Tak przygotowany model rozrusznika składa się z
szeregu elementów projektowanych oddzielnie, składanych i współpracujących ze sobą.
Stosowane metody CAD umożliwiają prezentację modeli urządzeń bardziej zrozumiałą dla
użytkowników. W tym przypadku przedstawia się rysunki podzespołów przygotowanych do
montażu, co jest bardziej czytelne dla człowieka bez przygotowania technicznego. Na fot.1.2
przedstawiony został rysunek modelu rzeczywistego, elipsoidalnego, samochodowego projektora
oświetleniowego nowej generacji w takiej właśnie formie.
Fot.1.1. Widok aksonometryczny modelu samochodowego rozrusznika magnetoelektrycznego w wy
Informatyka 4 - Lekcja 1

Poznanie trzech wyżej wymienionych zagadnień pozwoli słuchaczowi na twórczą pracę w
konkretnej dziedzinie techniki. Szczególną uwagę pragniemy zwrócić na poznanie współczesnych
narzędzi do zapisu projektowanych konstrukcji. Stanowią one dla projektanta bazę ułatwiającą
konstruktorowi trudną prace twórczą nad projektowaniem coraz bardziej skomplikowanych urządzeń
technicznych. Narzędzie, któremu poświęciliśmy uwagę w BLOKU 3 niniejszego przedmiotu jest
program graficzny amerykańskiej firmy Autodesk AutoCAD 2000 w polskiej wersji językowej.
Przedstawiony w załączeniu dysk CD z programem jest wersją trialową tego programu ważną
jedynie 30 dni. Zalecamy zatem
nie uruchamiać jej dopóty, dopóki nie poznamy zasad i metod
omówionych w BLOKU 1 i 2.
Fot.1.2. Widok samochodowego projektora oświetleniowego nowej generacji, przygotowanego do m
3D
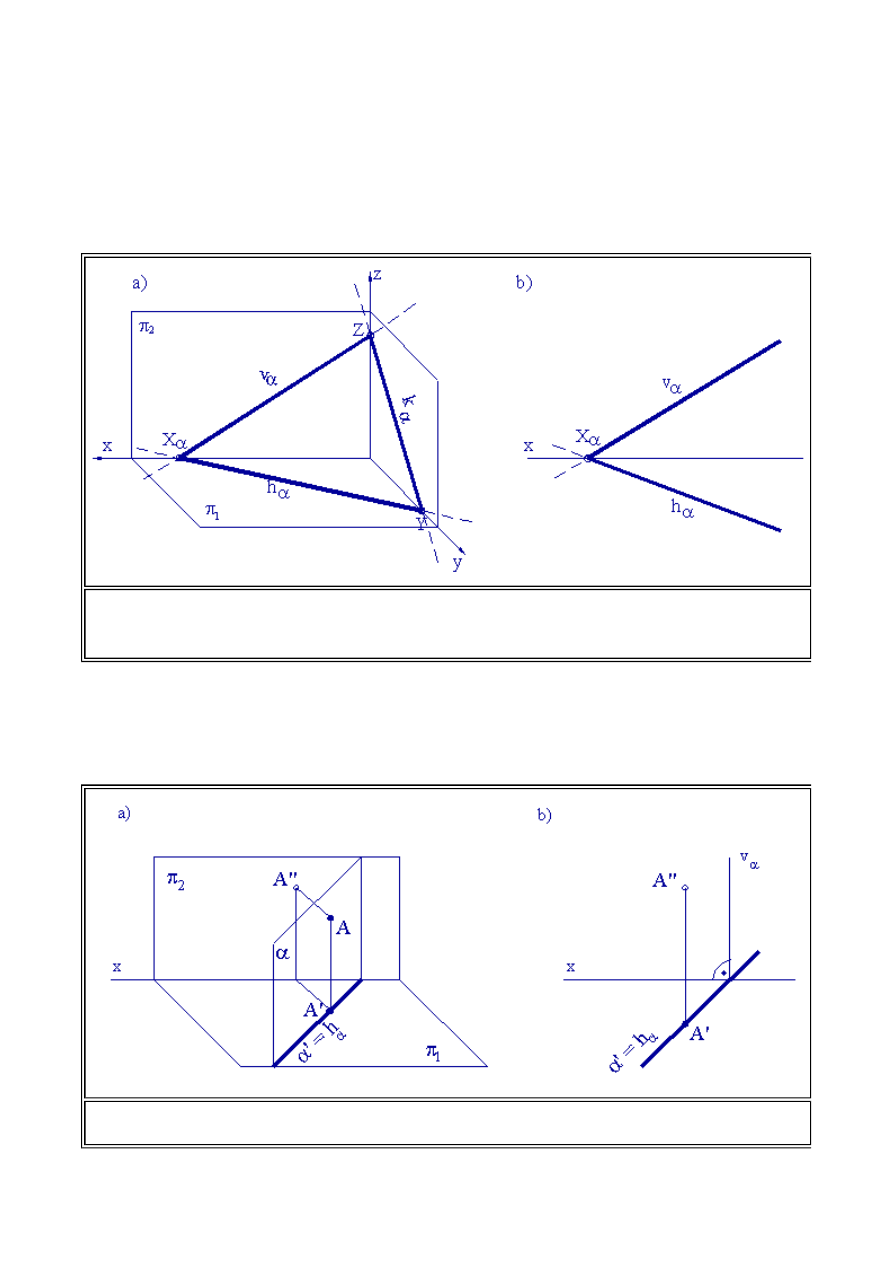
(1.1) Rzutowanie środkowe i równoległe w zapisie konstrukcji
Informatyka 4 - Lekcja 1
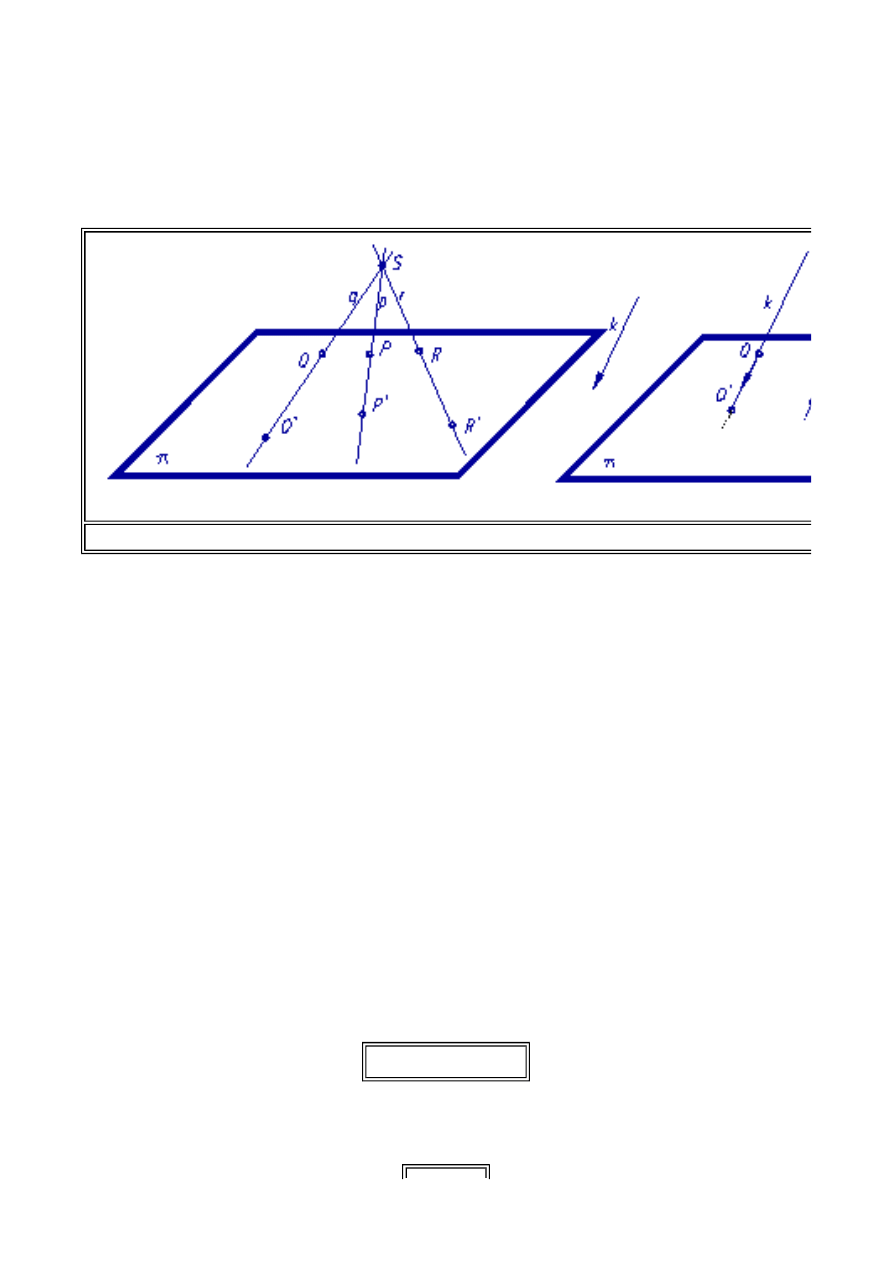
Operacja rzutowania jest podstawową operacją w odwzorowaniach przestrzennych na płaszczyźnie.
Niech w trójwymiarowej przestrzeni euklidesowej W
3
ustalona będzie płaszczyzna
p , zwana dalej
rzutnią oraz punkt S lub prosta k (kierunek rzutowania) nie należące do rzutni
p . Zespół złożony z rzutni,
punktu S - zwanego środkiem rzutowania nazywamy aparatem rzutowania środkowego, lub zastępując
środek rzutu kierunkiem rzutowania k - aparatem rzutowania równoległego i oznaczamy.
Rzuty środkowe punktów P, Q, R otrzymamy prowadząc promienie rzutujące p, q, r
wychodzące z środka rzutowania S i przechodzące przez te punkty, aż do przecięcia się z rzutnią
p.
Punkty przebicia promieni rzutujących z rzutnia wyznaczą rzuty środkowe tych punktów. W
przypadku rzutu równoległego postępujemy podobnie. Jednak promienie rzutujące są równoległe do
zadanego kierunku rzutowania k. Rozważając w geometrii zasady rzutowania równoległego często
mamy do czynienia z elementami niewłaściwymi, które zdefiniujemy dla zrozumienia zapisów
umownych stosowanych w rzutowaniu.
W geometrii euklidesowej dwie proste leżące na płaszczyźnie przecinają się lub są równoległe.
Prosta nie leżąca w płaszczyźnie przebija ją lub jest do niej równoległa. Rozważania byłyby
prostsze, gdyby dwie proste leżące w płaszczyźnie zawsze przecinały się, zaś prosta zawsze
przebijała płaszczyznę. Wprowadzając określenie punktu niewłaściwego możemy uzyskać takie
własności podstawowych elementów przestrzennych Do zbioru punktów właściwych, leżących na
prostej, dołączymy zatem jeden punkt niewłaściwy w taki sposób, aby:
l
proste równoległe miały wspólny punkt niewłaściwy,
l
proste nierównoległe miały różne punkty niewłaściwe.
Można zatem powiedzieć, iż proste równoległe "przecinają się" w jednym punkcie niewłaściwym.
Analogiczne rozumowanie możemy przeprowadzić w stosunku do dwóch płaszczyzn równoległych,
które miałyby "wspólną" krawędź przecięcia, zwaną prostą niewłaściwą. Punkty niewłaściwe
oznaczać będziemy symbolem punktu właściwego ze znakiem "nieskończoność":
Prostą niewłaściwą opisujemy przy pomocy odcinka prostej zakończonej strzałką, określającą
kierunek prostej oraz punktem niewłaściwym n p.:
Rys.1.3. Rzut środkowy i równoległy punktów leżących w przestrzeni W
3
.
:
np. A
:
, B
:
Informatyka 4 - Lekcja 1

Rzutowanie równoległe elementów przestrzennych na jedną rzutnię nie jest odwzorowaniem
jednoznacznym w obydwu kierunkach. A więc, jeżeli punktowi w przestrzeni odpowiada jeden i
tylko jeden rzut równoległy punktu na określoną rzutnię, to niestety rzutowi temu nie odpowiada
jeden i tylko jeden punkt w przestrzeni W
3
. Z punktu widzenia potrzeb techniki taki rzut nie może
być podstawą jednoznacznych odwzorowań na płaszczyźnie i odwrotnie. Wprowadzenie
odpowiednich własności tego rzutu może doprowadzić do odwzorowań jednoznacznych, a więc
przydatnych w graficznym zapisie konstrukcji technicznych. Oznacza to, iż określona ewolucja
własności rzutowania równoległego może być przydatna w technice. Przywołując zdefiniowane
przez Euklidesa pewne zapisy o charakterze podstawowym w teorii geometrii jak
określenia,
pewniki i postulaty
można sformułować podobne definicje określające własności rzutu w
rzutowaniu równoległym. Własności te, przedstawione poniżej pozwolą na wykorzystywanie zasad
rzutowania równoległego do zapisu złożonych konstrukcji technicznych.
Zwykle rzutowanie na jedną rzutnię nie jest odwzorowaniem jednoznacznym. W celu
dostosowania takiego rzutu do praktyki technicznej należy wprowadzić pewne własności, które tą
jednoznaczność odwzorowań zapewnią. Uogólniając należy stwierdzić, iż własności rzutu tworu G'
nie są identyczne jak własności samego tworu G. Wynika to z faktu, że twór może być bryłą
przestrzenną, natomiast jego rzut równoległy zawsze jest figurą płaską. Jednak niektóre własności
tych tworów nie ulegają zmianie po dokonaniu operacji rzutowania równoległego. Własności te
nazwane zostały
niezmiennikami rzutu równoległego.
Do niezmienników rzutowania równoległego
zaliczamy zatem:
1. współliniowość punktów (rzuty punktów leżących na prostej będą leżały na rzucie tej
prostej),
2. przynależności elementów (jeżeli punkt leży na prostej, to rzut tego punktu leży na rzucie tej
prostej),
3. równoległość prostych (rzutami prostych równoległych są proste równoległe),
4. stosunek długości odcinków równoległych (jeżeli długości odcinków równoległych
pozostają w określonym stosunku do siebie to długości ich rzutów pozostają w stosunku
identycznym),
5. stosunek podziału odcinka (jeżeli punkt A dzieli odcinek w określonym stosunku, to rzut
punktu A' dzieli rzut tego odcinka w takim samym stosunku),
6. długość odcinków równoległych do rzutni (długość odcinka równoległego do rzutni jest taka
sama jak długość rzutu tego odcinka),
7. kąt o obu ramionach równoległych do rzutni (wielkość kąta, którego obydwa ramiona są
równoległe do rzutni jest taka sama jak wielkość rzutu tego kąta),
8. związki miarowe w płaszczyźnie równoległej do rzutni (długości odcinków, kąty oraz
wielkości figur leżących na płaszczyźnie równoległej do rzutni zachowują się po dokonaniu
operacji rzutowania).
(1.2) Niezmienniki rzutu równoległego
Informatyka 4 - Lekcja 1
Niezmienniki rzutowania równoległego stanowią własności o charakterze podstawowych, które będą
wykorzystywane do zapisu konstrukcji technicznych na płaszczyźnie.
Znany z geometrii elementarnej układ osi współrzędnych, zwany układem kartezjańskim, jest
układem przestrzennym i składa się z osi x, y, z oraz początku układu współrzędnych. Osie są
położone pod kątami 90
o
względem siebie. Umieszczony w takim układzie punkt P będzie miał
współrzędne P(x
o
, y
o
, z
o
). Analogicznie można zdefiniować położenie wektora i innych elementów
w przestrzeni. Rzuty aksonometryczne są formą rzutów równoległych, które pozwalają
przetransponować układ przestrzenny 0, x, y, z na układ płaski, a więc układ umożliwiający
odwzorowanie tworów przestrzennych na płaszczyźnie. Takim zagadnieniem jesteśmy
zainteresowani z punktu widzenia
graficznego zapisu konstrukcji
. Rozwijając teorię rzutowania
równoległego przyjmiemy twierdzenie, które otworzy możliwości wyodrębnionego zapisu tworów
przestrzennych zwanego
rzutem aksonometrycznym
(dowód twierdzenia znajdzie czytelnik w
literaturze przedmiotowej).
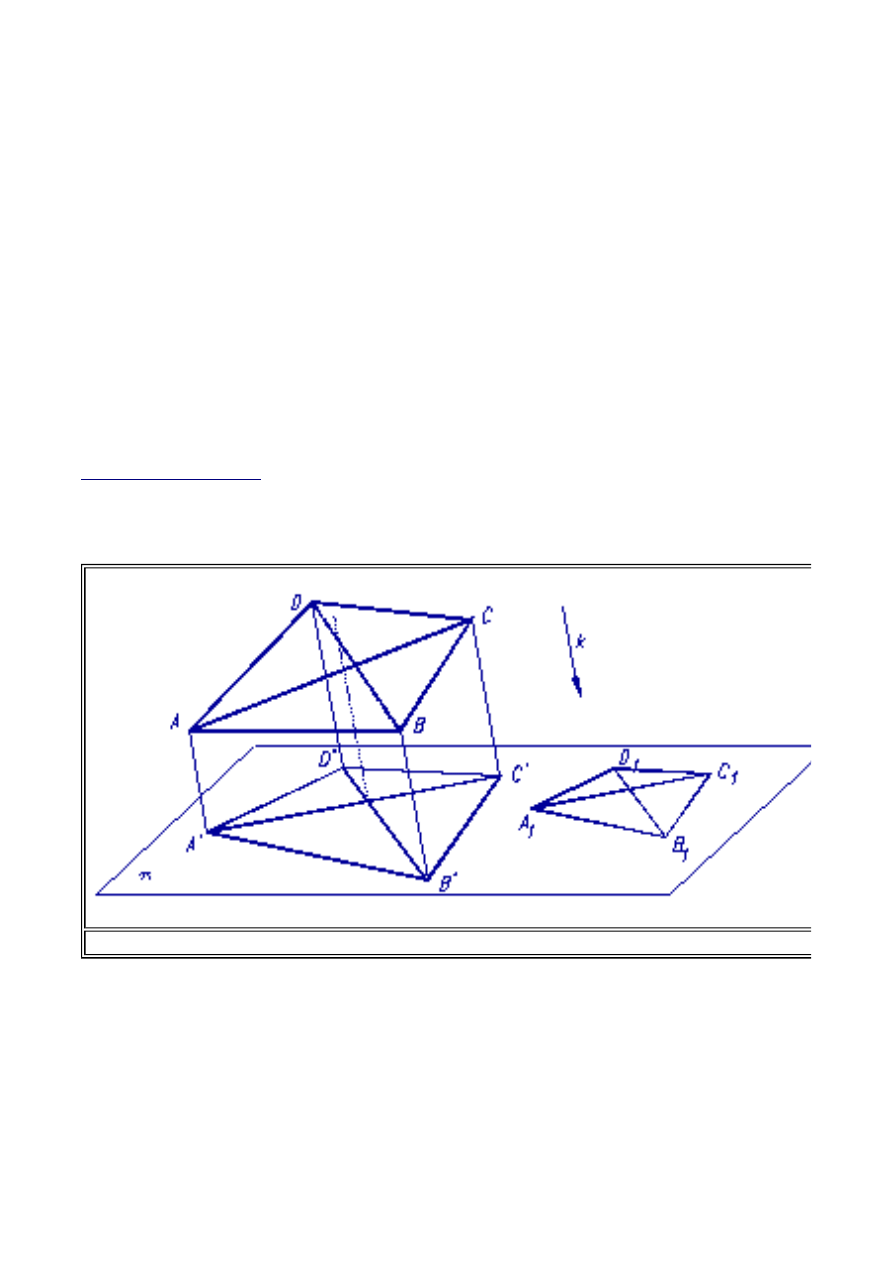
Twierdzenie Pohlkie'go
Każdy czworościan (bryła przestrzenna) można zrzutować, za pomocą rzutowania równoległego,
na czworokąt podobny do z góry zadanego czworokąta zupełnego (patrz Rys.1.4).
Twierdzenie to umożliwia przenoszenie brył przestrzennych do zupełnie dowolnych układów
płaskich zwanych układami aksonometrycznymi. Stanowi to dla inżyniera źródło możliwości
różnorodnego eksponowania swoich twórczych projektów.
Przyjmując do wiadomości ustalenia twierdzenia Pohlkie'go można układ współrzędnych
(1.3) Rzuty aksonometryczne jako wyodrębniona forma rzutowania
równoległego
Rys. 1.4. Ilustracja twierdzenia Pohlkie'go.
(1.4) Układy aksonometryczne
Informatyka 4 - Lekcja 1
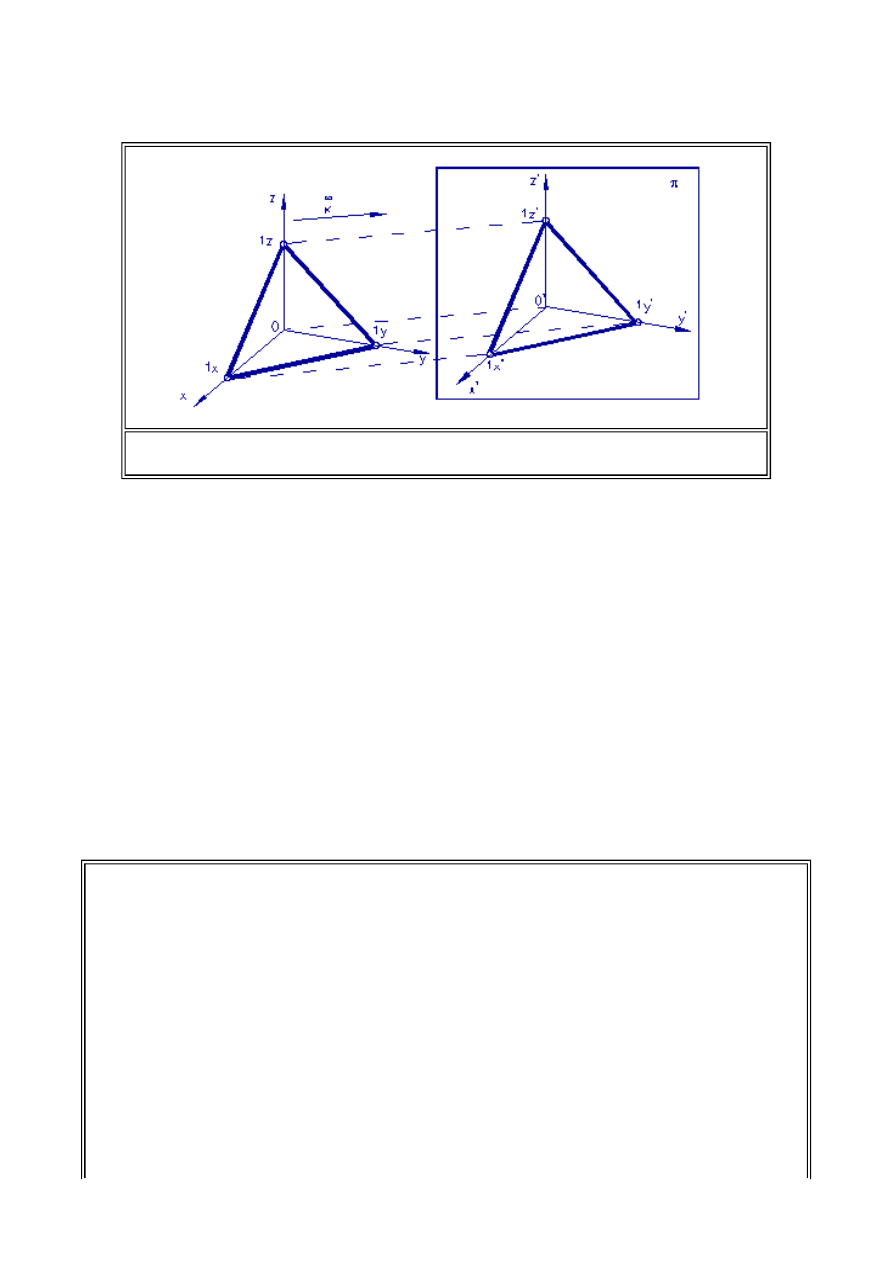
kartezjańskich, za pomocą rzutu równoległego, przetransponować na dowolny układ płaski. Ilustruje
to rys.1.5.
Na osiach układu przestrzennego (0, x, y, z) odłożono odcinki jednostkowe [01
x
,
01
y
,
01
z
],
które po dokonaniu rzutowania równoległego z kierunku K
:
, utworzą rzuty jednostkowe tych
odcinków w nowym układzie płaskim. Nowy układ osi 0'x'y'z' wraz z ich odcinkami jednostkowymi
0'1'
x'
, 0'1'
y'
, ,0'1'
z'
nazywamy
aksonometrycznym układem współrzędnych
. Stosunek długości
odcinków jednostkowych w układzie przestrzennym do długości ich rzutów w układzie płaskim
nazywamy
skrótem aksonometrycznym
i dla poszczególnej osi współrzędnych układu
aksonometrycznego powinien być zdefiniowany odrębnie. Ma to istotne znaczenie, albowiem jak
wynika z wcześniejszych ustaleń można zdefiniować układ o dowolnie położonych osiach oraz
dowolnych skrótach aksonometrycznych. Skróty aksonometryczne dla poszczególnych osi
l
x'
,
l
y'
,
l
z'
, w różnych źródłach literaturowych mogą być definiowane w różny sposób, co jest dopuszczalne
i nie budzi zastrzeżeń z punktu widzenia teorii rzutowania równoległego.
Dla potrzeb Graficznego zapisu konstrukcji, w wyniku doświadczeń praktycznych, zaproponowano
cztery najbardziej używane i przydatne w technice układy aksonometryczne. Poniżej przedstawiono
praktyczne układy aksonometryczne.
Rys. 1.5. Rzut równoległy przestrzennego układu (0, x, y, z) na układ płaski (0',
x', y', z').
Informatyka 4 - Lekcja 1
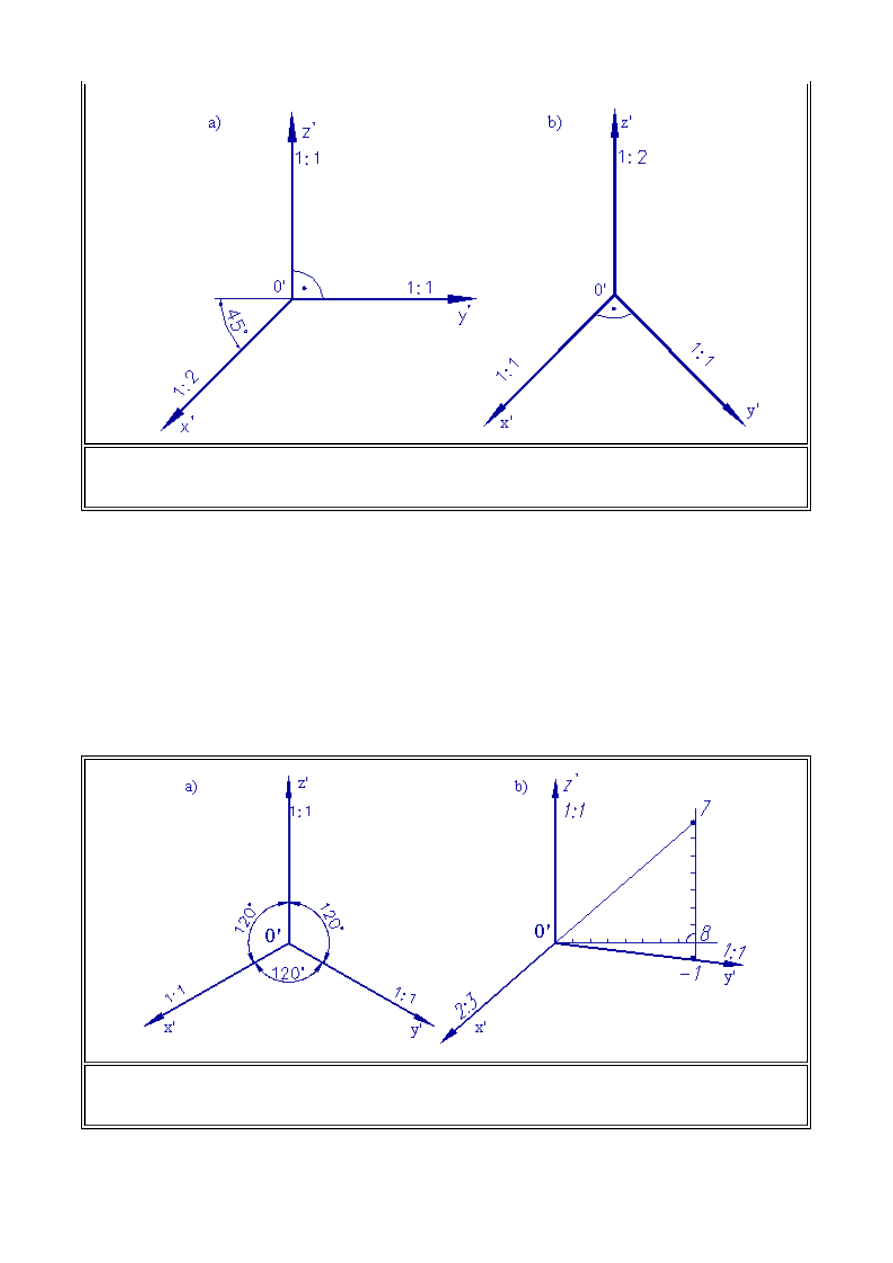
W układzie perspektywy kawalerskiej osie y' i z' położone są względem siebie pod kątem 90
o
.
Oś x' położona po kątem 135
o
względem y' i z'. Układ umożliwia zapis bez zniekształceń w pł. (0,
y', z').
W układzie dimetrii wojskowej oś z'" układu jest pionowa, skrót zmniejsza wymiary w tym
kierunku dwukrotnie. Osie x', y' pod kątem 135
o
względem osi z'. Skróty nie zmieniają
wymiarów w kierunku tych osi.
Układ izometrii równokątnej jest układem regularnym. Osie x', y', z' pod kątem 120
o
względem
Rys. 1.6. Układy aksonometryczne. a) Układ dimetrii (perspektywy) kawalerskiej (
l
x
= 1:2,
l
y
= 1:1,
l
z
= 1:1). b) Układ dimetrii wojskowej (
l
x'
= 1:1,
l
y'
=1:1,
l
z'
= 1:2)..
Rys. 1.7. Układy aksonometryczne. a) Układ izometrii równokątnej (
l
x
= 1:1,
l
y
=1:1,
l
z
=
1:1). b) Układ dimetrii prawie prostokątnej (
l
x'
= 2:3,
l
y'
=1:1,
l
z'
= 1:1).
Informatyka 4 - Lekcja 1
siebie. Skróty nie zmieniają wymiarów w każdej osi.
Tworzenie trzech pierwszych układów nie sprawia żadnych problemów. Komentarza wymaga
tworzenie układu dimetrii prawie prostokątnej. Oś z' jest osią pionową. Pozostałe osie x' i y'
tworzymy w sposób następujący:
l
na pomocniczej linii poziomej odmierzamy osiem odcinków jednostkowych otrzymując na
niej punkt, przez który prowadzimy pomocniczą prostą pionową.
l
odmierzając następnie na tej prostej w kierunku góry 7 odcinków jednostkowych oraz 1 w dół
otrzymamy dwa punkty,
l
łącząc otrzymane punkty z środkiem układu wyznaczymy położenie osi x' i y'.
Rysowanie technicznych obiektów przestrzennych w rzutach aksonometrycznych pozwala
przygotować zapis konstrukcji, który może być zrozumiały dla każdego czytelnika oraz przydatny
do dalszych zapisów technicznych. Dla pokazania przykładu zapisu w takim rodzaju rzutowania
rozwiążemy poniższe zadanie.
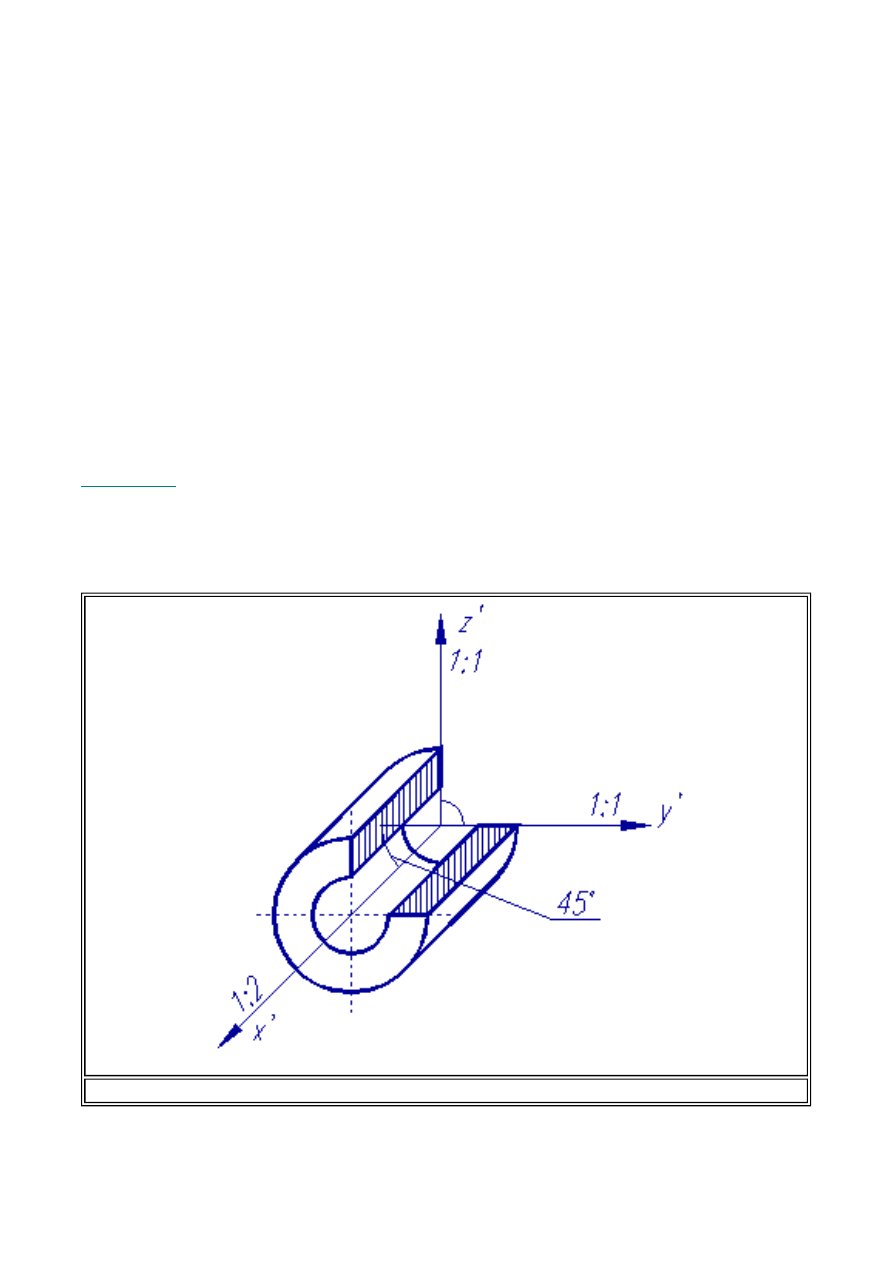
Zadanie 1.1.
W układzie perspektywy kawalerskiej narysować rzut rury z wyciętą ćwiartką na całej długości.
Rozwiązanie tego zadania przedstawiono na rys. 1.8.
Rys. 1.8. Rysunek odcinka rury walcowej w układzie aksonometrii kawalerskiej.
Informatyka 4 - Lekcja 1

Rozpoczynając rozwiązywanie powyższego zadania zwróćmy uwagę na umiejscowienie modelu
bryły w układzie współrzędnych aksonometrycznych. Widok z kierunku prostopadłego do osi
wzdłużnej rury jest dwoma współśrodkowymi okręgami. Jeżeli chcemy, aby okręgi te nie uległy
deformacji na elipsy, których precyzyjna konstrukcja jest trudniejsza od prostej konstrukcji okręgu,
należy w taki sposób umiejscowić rurę w układzie, który zapewni rysunek bez zniekształceń (układ
osi 0y' i 0z' - zapewnia taką sytuację, ponieważ położenie osi jest względem siebie prostopadłe, a
skróty aksonometryczne wynoszą odpowiednio
l
y'
= 1:1,
l
z'
= 1:1.)
Informatyka 4 - Lekcja 1
2. Odwzorowania przestrzenne w rzutach prostokątnych
Rzutowanie prostokątne elementów przestrzennych jest podstawową forma odwzorowań
stosowanych w technice. Zastosowanie trzech wzajemnie prostopadłych rzutni umożliwia
jednoznaczne odwzorowanie elementów przestrzennych na płaszczyźnie i odwrotnie. Tego typu
rzutowanie jest podstawą
graficznego i komputerowego zapisu konstrukcji
. Rzut prostokątny jest
rodzajem rzutu równoległego. Zatem znane są zasady rzutowania prostokątnego. Umieszczony twór
przestrzenny rzutowany jest za pomocą promieni rzutujących prostopadłych do rzutni. Poniżej
przedstawiono zasady powstawania rzutów w odniesieniu do podstawowych tworów
geometrycznych tzn. punktu, prostej i płaszczyzny. Poznanie zasad w odniesieniu do tych
elementów, zwanych także prymitywami umożliwi zapis konstrukcji bardziej złożonych o dużym
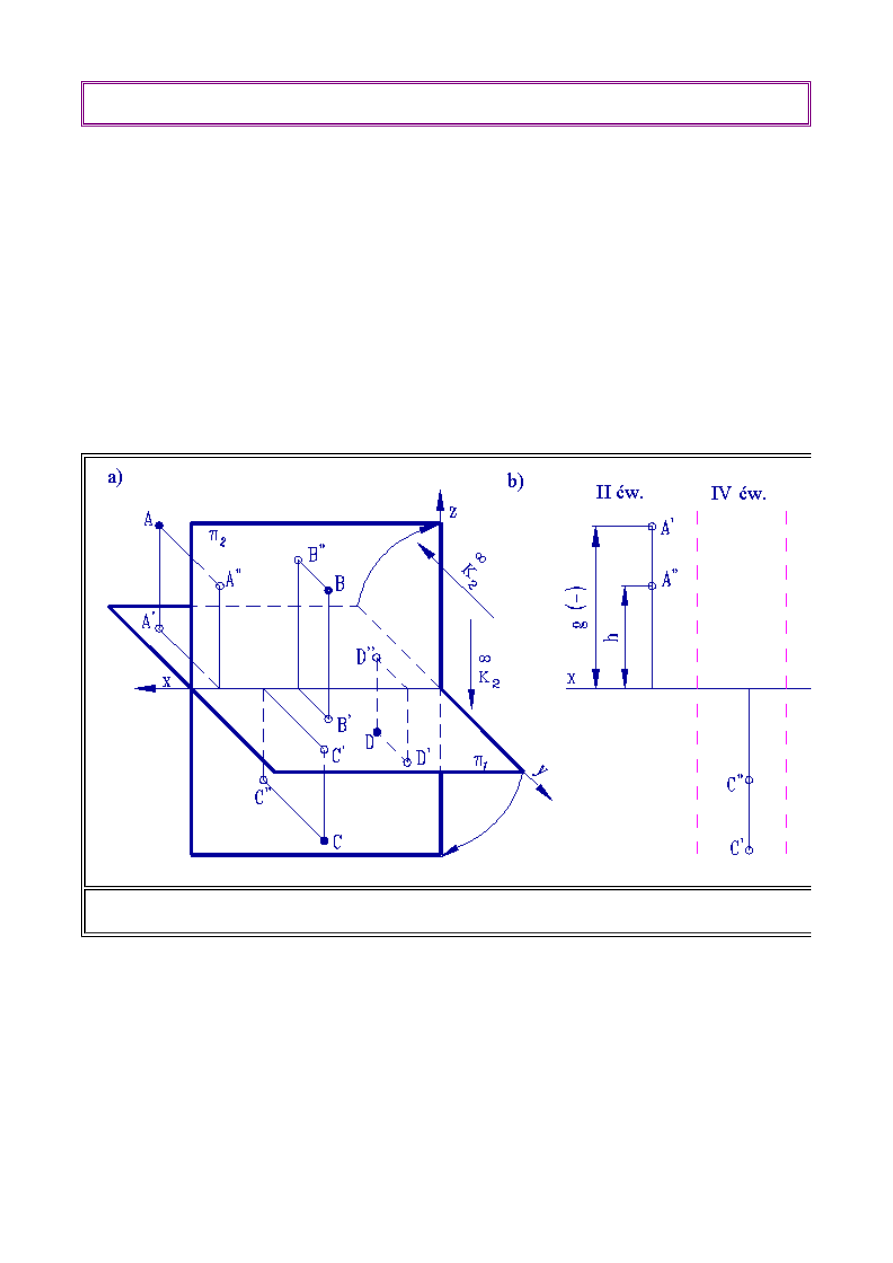
stopniu uszczegółowienia. Na rys. rys 1.6a i 1.6b przedstawiono zasady tworzenia rzutów (zapis w
rzutach aksonometrycznych) oraz rzuty prostokątne punktów A, B, C, D umieszczonych w różnych
obszarach przestrzennych.
Przestrzeń W
3
podzielona została na cztery obszary zwane ćwiartkami za pomocą dwóch
przecinających się płaszczyzn - pionowej i poziomej. Płaszczyzny te po złożeniu do jednej
płaszczyzny pozwalają nas jasne i jednoznaczne odwzorowania przestrzenne na płaszczyźnie
rysunku.
l
Ćwiartka I jest obszarem położonym przed rzutnią pionową i nad rzutnią poziomą,
l
Ćwiartka II jest obszarem położonym za rzutnią pionową i nad rzutnią poziomą.
l
Ćwiartka III jest obszarem położonym za rzutnią pionową i pod rzutnią poziomą.
l
Ćwiartka IV jest obszarem położonym przed rzutnią pionową i pod rzutnią poziomą.
(2.1) Odwzorowanie punktów
Rys. 1.9. Rzutowanie prostokątne punktów a) Ilustracja rzutowania prostokątnego w układzie akso
prostokątne punktów położonych w czterech ćwiartkach
Informatyka 4 - Lekcja 1
Złożenie dwóch płaszczyzn do wspólnego położenia, po obrocie dookoła osi x, będącej ich
krawędzią przecięcia pozwala rozmieścić rzuty na jednej wspólnej płaszczyźnie. Odległość punktu
od rzutni poziomej nazywamy wysokością i oznacza się literą "h", natomiast odległość punktu od
rzutni pionowej nazywamy głębokością i oznacza się "g". Wysokość jest dodatnia w ćwiartce I i II,
a więc nad rzutnią poziomą, głębokość jest dodatnia w ćwiartce I i IV, a więc przed rzutnią
pionową. W przypadku zaistnienia potrzeby wprowadzenia trzeciego parametru identyfikującego
obiekty przestrzenne można wprowadzić trzecią rzutnię, prostopadłą do rzutni poziomej i pionowej.
W tym przypadku odległość punktu od trzeciej rzutni nazywamy szerokością punktu "s".
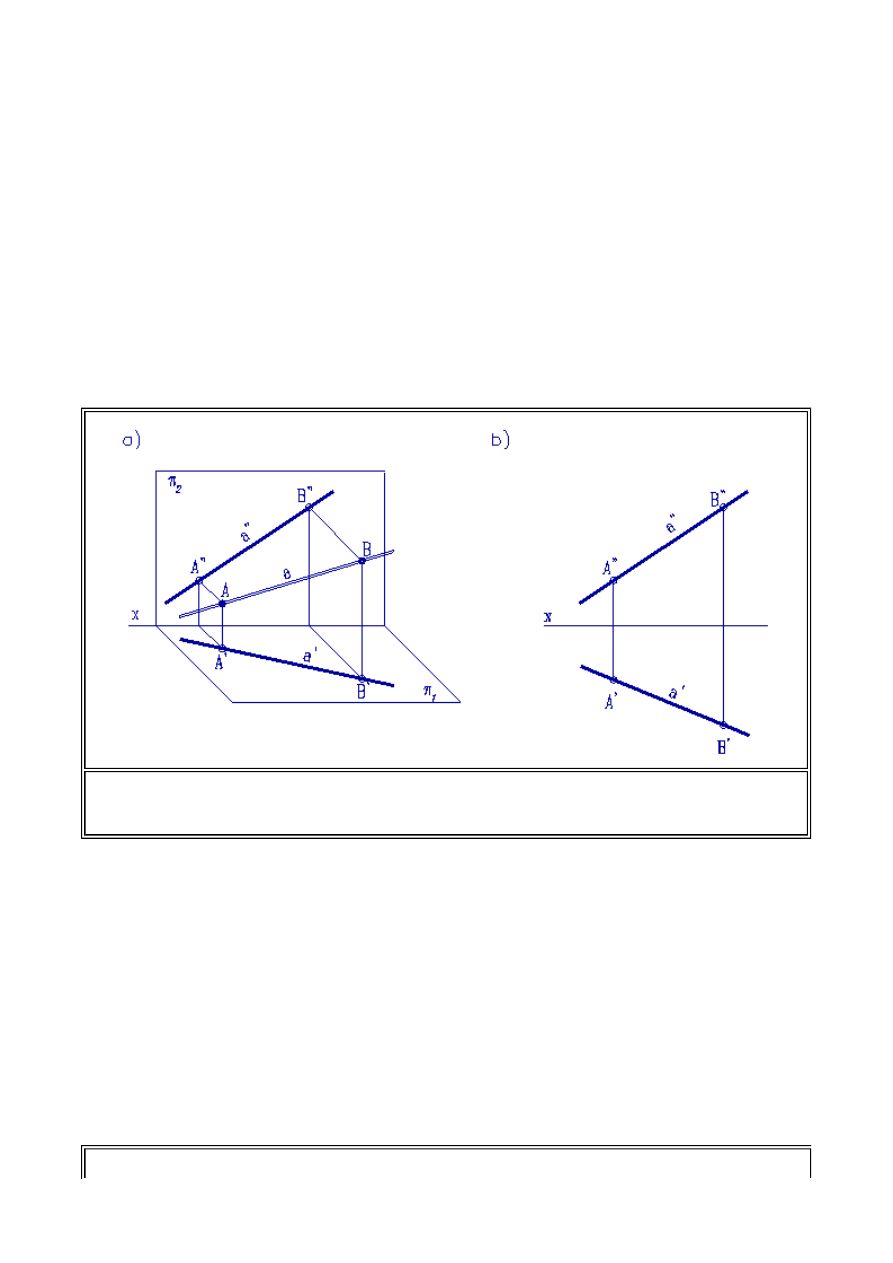
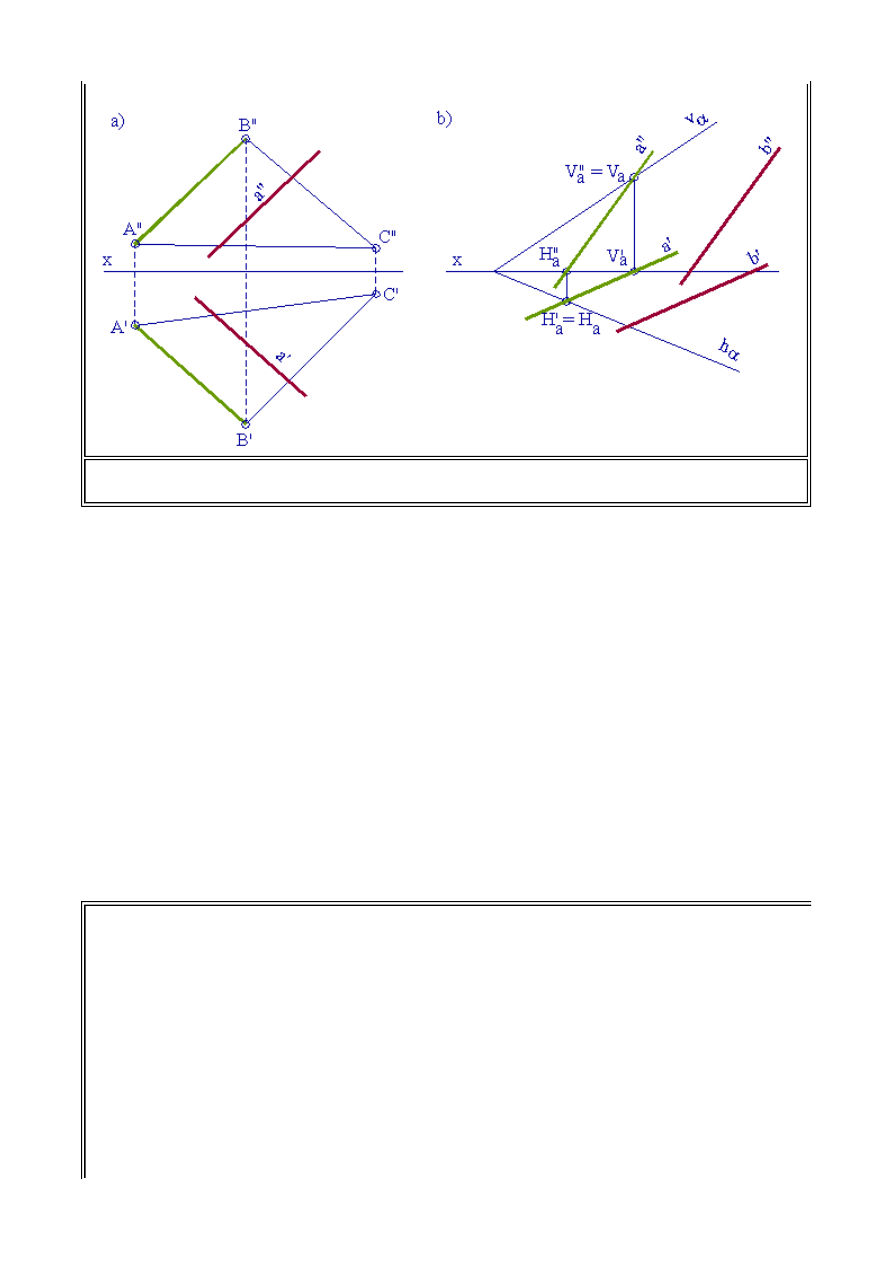
Rozważmy obecnie rzutowanie kolejnego elementu jakim jest prosta. Prostą "a" można opisać
jednoznacznie za pomocą dwóch punktów. Zatem rzuty prostej można wyznaczyć łącząc
jednoimienne rzuty punktów A i B leżących na tej prostej. Zasady tworzenia rzutów prostej
przedstawia rys.1.10.
Prosta określona jednoznacznie za pomocą dwóch punktów może być określona w rzutach za
pomocą rzutów punktów o szczególnym położeniu względem rzutni. Takimi punktami są ślady
prostej. Śladami prostej nazywamy punkty przebicia prostej z rzutniami. Zatem możemy mówić o
śladzie pionowym prostej opisywanej literą V
a
(od słowa vertical) oraz o śladzie poziomym H
a
(od
słowa horizontal). Punkty V
a
i H
a
oczywiście w rzutach określone są za pomocą ich rzutów
pionowych i poziomych. Rzut pionowy śladu pionowego V
a
'' pokrywa się ze śladem pionowym,
natomiast rzut poziomy tego śladu V
a
' znajduje się na osi x (rzuty poziome wszystkich punktów
leżących na rzutni pionowej znajdują się na osi x). Rzut poziomy śladu poziomego H
a
'
pokrywa się
ze śladem poziomym, natomiast rzut pionowy tego śladu H
a
'' znajduje się na osi x (rzuty pionowe
wszystkich punktów leżących na rzutni poziomej znajdują się na osi x). Opisanie prostej za pomocą
ich śladów przedstawiono na rys. 1.11.
(2.2) Odwzorowanie prostych
Rys. 1.10. Rzutowanie prostokątne prostej oraz punktów leżących na niej a) Ilustracja
rzutowania prostokątnego prostej w układzie aksonometrycznym b) Rzuty prostokątne
prostej
Informatyka 4 - Lekcja 1
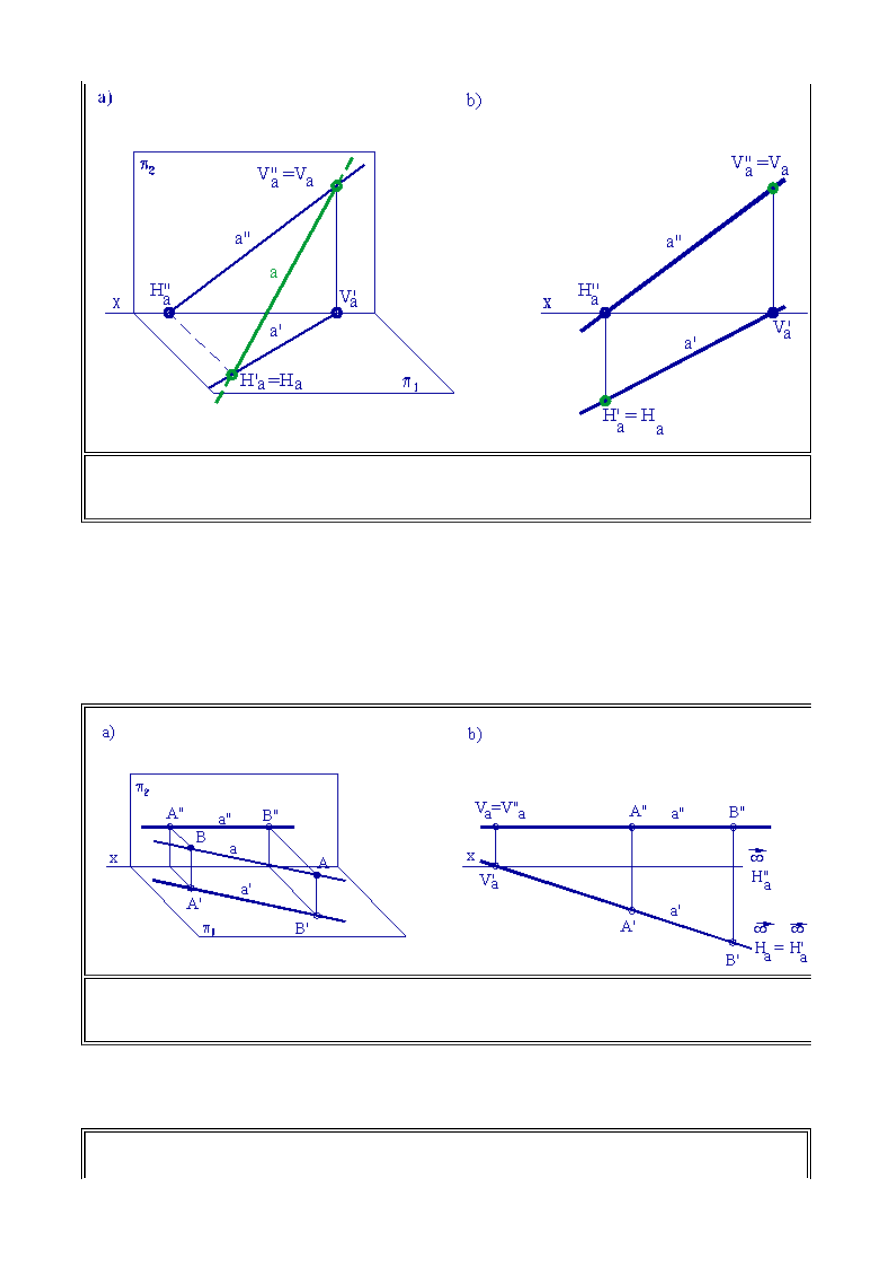
Przedstawione powyżej rzuty prostej dotyczą jej położenia ogólnego. W konstrukcjach
przestrzennych często wykorzystywane są inne, szczególne położenia prostych, których rzuty można
łatwo przewidzieć, bez konieczności żmudnych konstrukcji pomocniczych. Do takiego położenia
prostych można zaliczyć n. p. proste poziome - równoległe do rzutni poziomej
p
1
oraz proste
czołowe - równoległe do rzutni pionowej
p
2
. Rzuty prostych w położeniu szczególnym
przedstawiono na rys.1.12. i 1.13.
Jak widać na rysunku 1.12. rzut pionowy prostej poziomej ma położenie zawsze równoległe do osi x,
co jest wygodną informacją przy rozwiązywaniu konstrukcji bardziej złożonych.
Rys. 1.11. Rzutowanie prostokątne prostej określonej przy pomocy śladów a) Ilustracja
rzutowania prostokątnego prostej oraz jej śladów w układzie aksonometrycznym b) Rzuty
prostokątne prostej oraz jej śladów
Rys. 1.12. Rzutowanie prostokątne prostej prostej poziomej a) Ilustracja rzutowania
prostokątnego prostej poziomej w układzie aksonometrycznym b) Rzuty prostokątne prostej
poziomej
Informatyka 4 - Lekcja 1
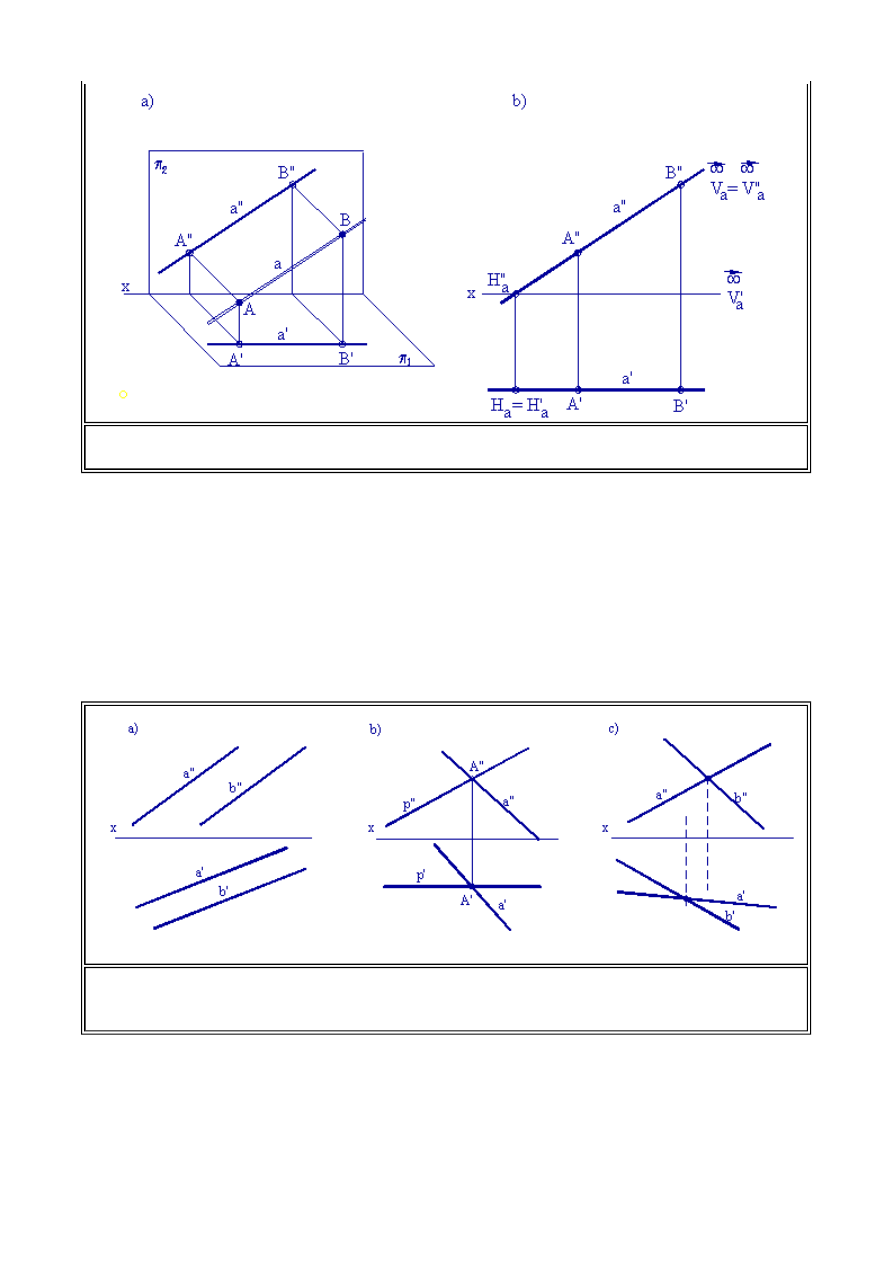
Jak wynika z rysunku 1.13. rzut poziomy prostej czołowej ma położenie zawsze równoległe do osi x,
co będzie wykorzystywane przy rozwiązywaniu konstrukcji złożonych.
Proste w przestrzeni mogą przecinać się ze sobą, być równoległe lub być skośne względem siebie.
Dwie proste przecinające się i dwie proste równoległe jednoznacznie określają płaszczyznę. W tym
przypadku mówimy, że płaszczyzna określona jest bezśladowo. Na rys. 1.14. przedstawiono trzy
przypadki położenia dwu prostych względem siebie.
Proste przedstawione na rys.1.14c nie przecinają się ze sobą. Punkty przecięcia rzutów nie leżą na
jednej odnoszącej prostopadłej do osi x (patrz linia kreskowa).
Rys. 1.13. Rzutowanie prostokątne prostej czołowej a) Ilustracja rzutowania prostokątnego
prostej czołowej w układzie aksonometrycznym. b) Rzuty prostokątne prostej czołowej
(2.3) Wzajemne położenie prostych
Rys. 1.14. Wzajemne położenie prostych względem siebie w rzutach prostokątnych a) Rzuty
dwu prostych równoległych b) Rzuty dwu prostych przecinających się c) Rzuty dwu
prostych skośnych
(2.4) Odwzorowanie płaszczyzn
Informatyka 4 - Lekcja 1
Płaszczyzny odwzorowywane są w rzutach prostokątnych w sposób umowny. Nie budzą żadnych
wątpliwości płaszczyzny określone bezśladowo ( tak jak przedstawione na rys. rys. 1.14 a i b.).
Jednak ogólnie ujmując zagadnienie należy stwierdzić, iż rzutem płaszczyzny jest płaszczyzna.
Zapis w tym przypadku byłby utrudniony. Płaszczyzna zatem może być określona za pomocą śladów
- pionowego v
a
i poziomego h
a
. Ślady w tym przypadku są krawędziami przecięcia się
płaszczyzny
a z rzutniami pionową i poziomą. Ilustracje odwzorowania płaszczyzny dowolnej w
rzutach prostokątnych przedstawiono na rys. 1.15.
Duże znaczenie w rozwiązywaniu konstrukcji geometrycznych maja płaszczyzny o szczególnym
położeniu względem rzutni. Do płaszczyzn tych należą płaszczyzna pionowo - rzutująca i
płaszczyzna poziomo - rzutująca przedstawione na rys. rys. 1.16 i 1.17. Są to płaszczyzny
prostopadłe do rzutni.
Rys. 1.15. Odwzorowanie płaszczyzny w położeniu ogólnym w rzutach prostokątnych a)
Ilustracja śladów płaszczyzny w rzucie aksonometrycznym b) Odwzorowanie płaszczyzny
a
przy pomocy śladów
Rys. 1.16. Rzuty i ślady płaszczyzny poziomo rzutującej a) Rzut aksonometryczny
płaszczyzny b) Rzut prostokątny płaszczyzny
Informatyka 4 - Lekcja 1
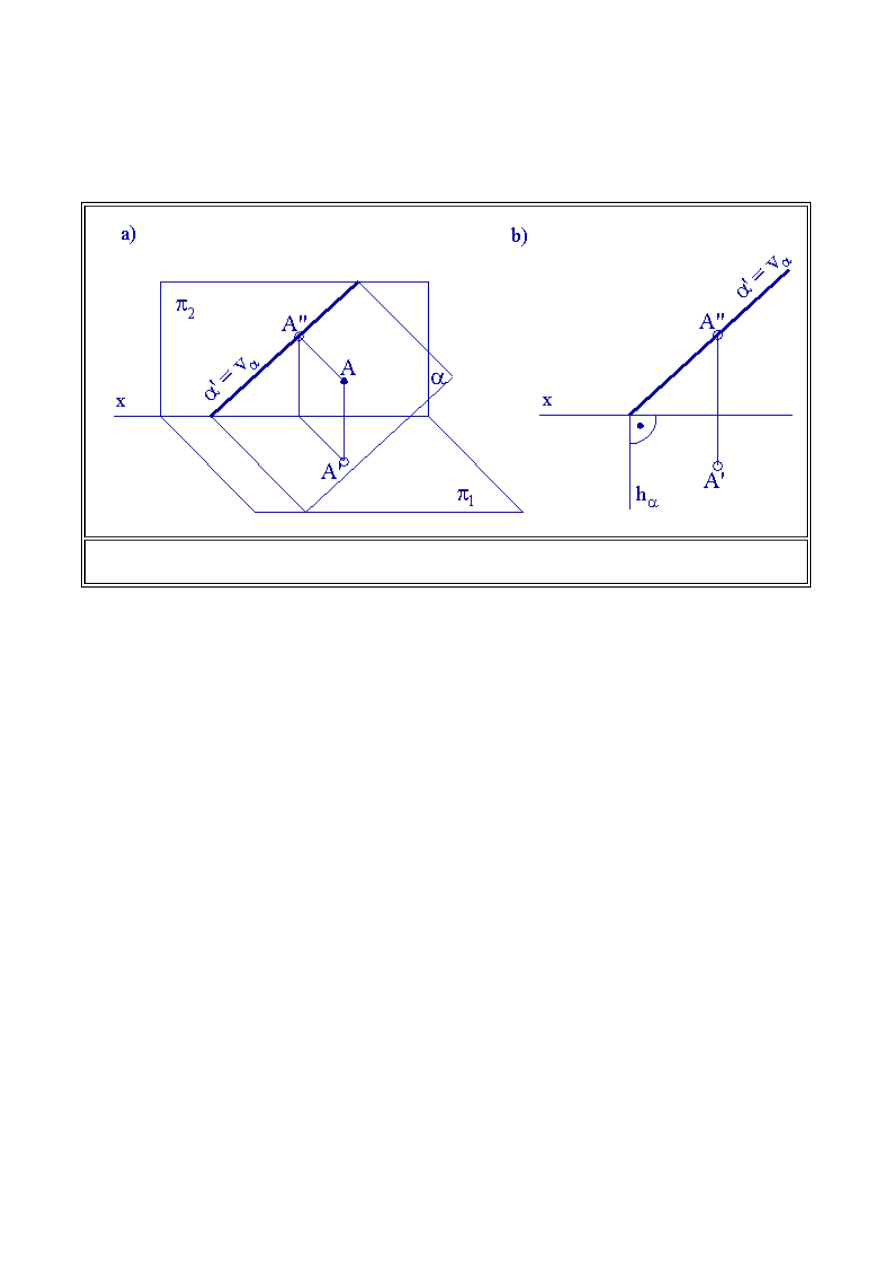
Położenie płaszczyzny poziomo - rzutującej jest niezwykle interesujące z punktu widzenia
realizacji konstrukcji złożonych. Wszystkie elementy płaskie znajdujące się w tej płaszczyźnie
odwzorowują się w rzucie poziomym na ślad poziomy płaszczyzny (czyli w tym przypadku na rzut
poziomy płaszczyzny). Umożliwia to w szybki sposób przewidzieć położenie tych rzutów, bez
konieczności stosowania konstrukcji pomocniczych.
Podobnie sytuacja przedstawia się z płaszczyzną pionowo - rzutującą. Wszystkie elementy płaskie
znajdujące się w tej płaszczyźnie odwzorowują się w rzucie pionowym na ślad pionowy płaszczyzny
(czyli na rzut pionowy płaszczyzny). Skraca to pracochłonność konstrukcji złożonych, a więc są to
płaszczyzny, z których konstruktorzy chętnie korzystają.
Rys. 1.17. Rzuty i ślady płaszczyzny pionowo - rzutującej. a) Rzut aksonometryczny
płaszczyzny. b) Rzut prostokątny płaszczyzny.
Informatyka 4 - Lekcja 1
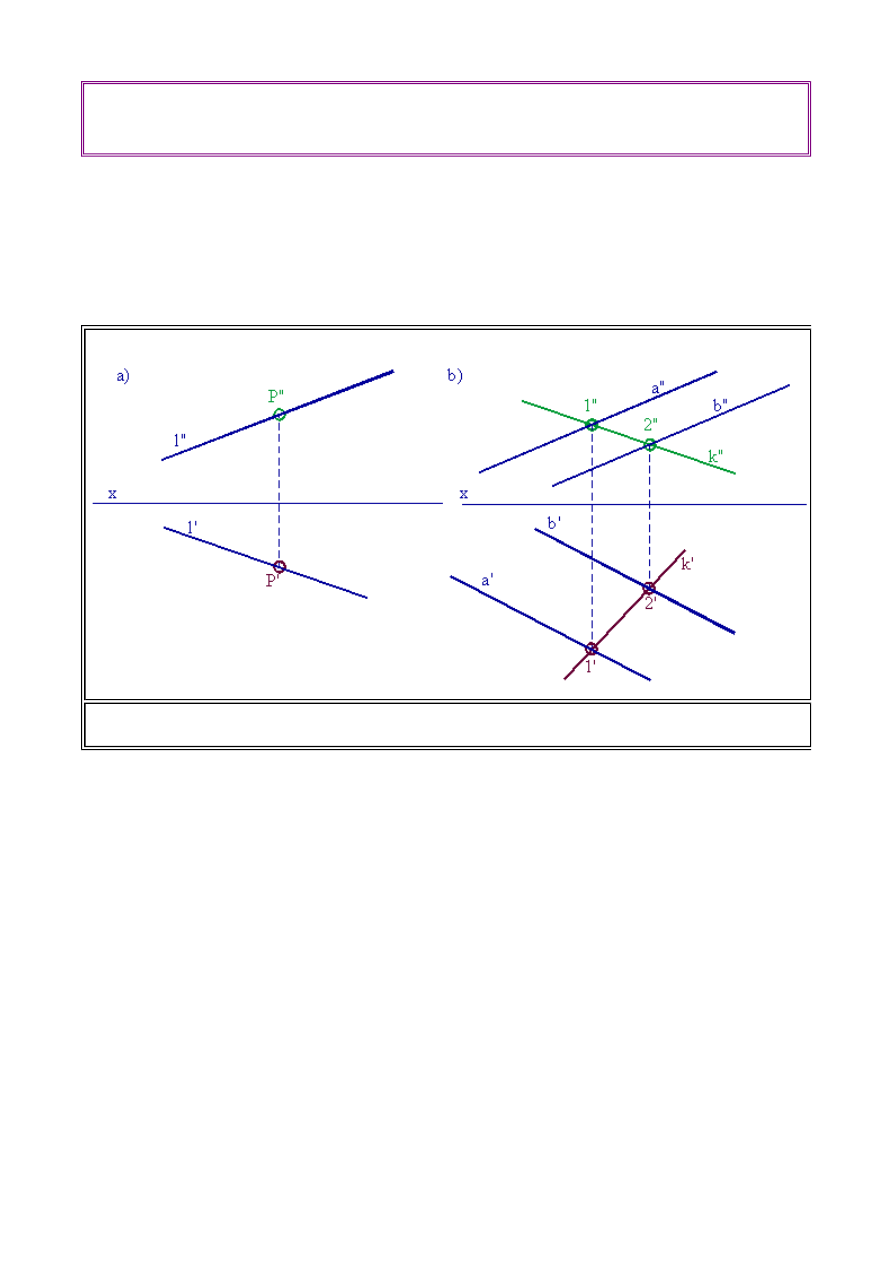
3. Elementy przynależne i równoległe w rzutowaniu
prostokątnym
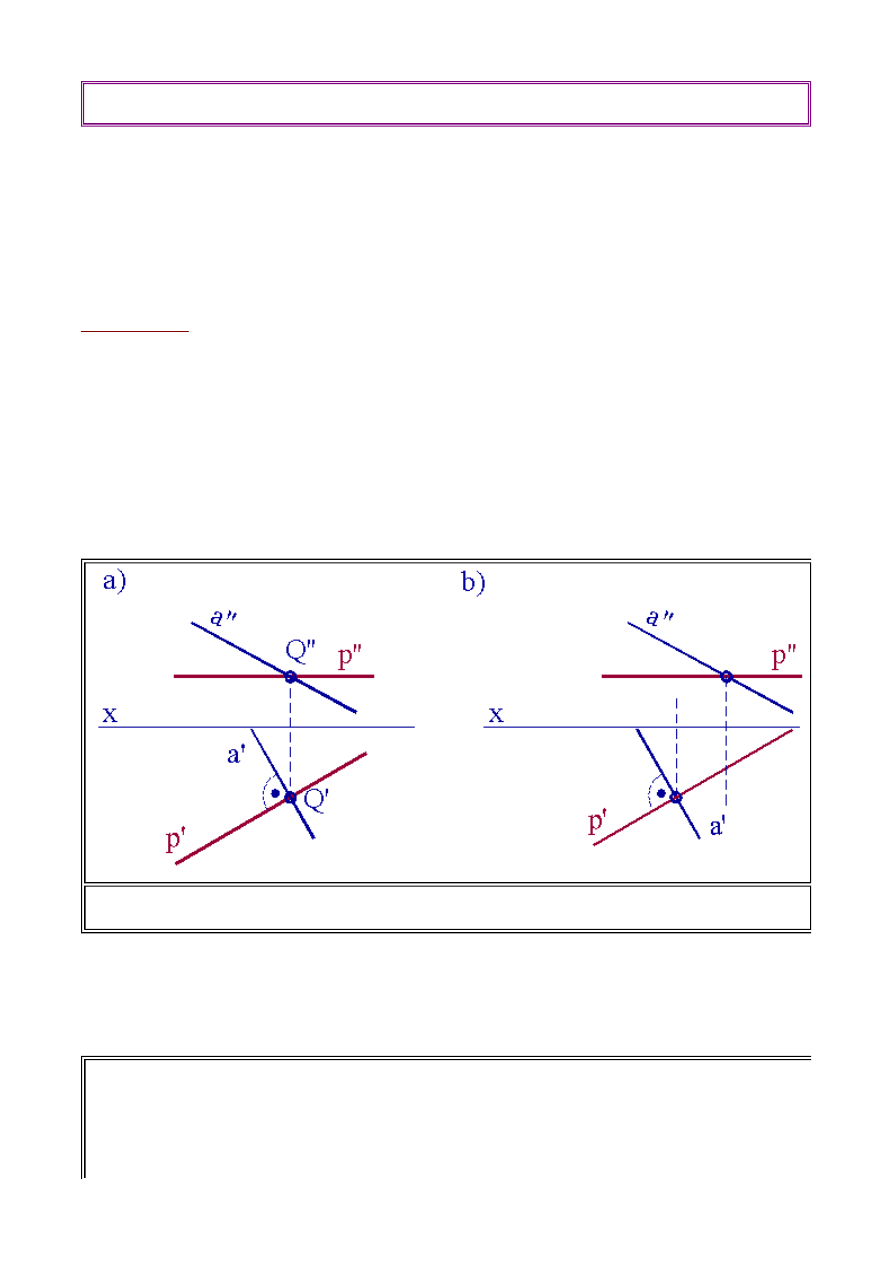
Definicja
W rzutach prostokątnych, podobnie jak w rzutach równoległych, jeżeli punkt
przynależy do prostej to rzuty tego punktu przynależą do rzutów prostej.
Można to zilustrować na rys. 1.18a.
Zakładając, że punkt
P
leży na prostej
l
obieramy punkt
P''
leżący na rzucie pionowym prostej
l''
.
Rzut poziomy tego punktu,
P'
będzie leżał na odnoszącej prostopadłej do osi x i rzucie poziomym
prostej
l'
. Analogiczne rozumowanie można przeprowadzić dla przynależności prostej do
płaszczyzny (Rys.1.18b). Zakładając, że prosta
k
leży w płaszczyźnie dwóch prostych
a
i
b
,
obieramy dowolny rzut pionowy prostej -
k''
. Prosta
k''
przecina proste
a" i b"
w punktach
1'' i 2''
.
Rzuty poziome tych punktów będą leżały odpowiednio na odnoszących prostopadłych do osi x oraz
rzutach poziomych prostych
a'
i
b'
.
Punkt jest przynależny do płaszczyzny jeżeli przynależy do prostej leżącej w płaszczyźnie.
Obierzemy dowolny punkt
A,
przyjmując jego rzut pionowy
A''
jak na rys. 1.19, i założymy, że
leży on na płaszczyźnie dwóch przecinających się prostych
(a x b)
. Aby wyznaczyć drugi rzut tego
punktu powinniśmy skorzystać z cytowanej powyżej definicji przynależności. Poprowadźmy przez
rzut pionowy punktu
A''
dowolną prostą
p''
, która będzie leżała w płaszczyźnie dwóch prostych
(a x
b)
. Jeżeli tak, to prosta
p''
przetnie nam proste
a''
i
b''
w punktach odpowiednio
2''
i
1''.
Rzuty
poziome tych punktów
1'
i
2'
znajdziemy na przecięciu się odnoszących prostopadłych do osi x z
rzutami poziomymi prostych
a'
i
b'
. Rzuty poziome punktów
1'
i
2'
wyznacza nam rzut poziomy
prostej
p'
, leżącej w płaszczyźnie prostych (a x b). Ponieważ prostą
p
prowadziliśmy przez punkt
A
(3.1) Przynależność punktu do prostej i prostej do płaszczyzny
Rys.1.18. Przynależność elementów a) Przynależność punktu do prostej b) Przynależność
prostej do płaszczyzny
(3.2) Przynależność punktu do płaszczyzny
Informatyka 4 - Lekcja 1
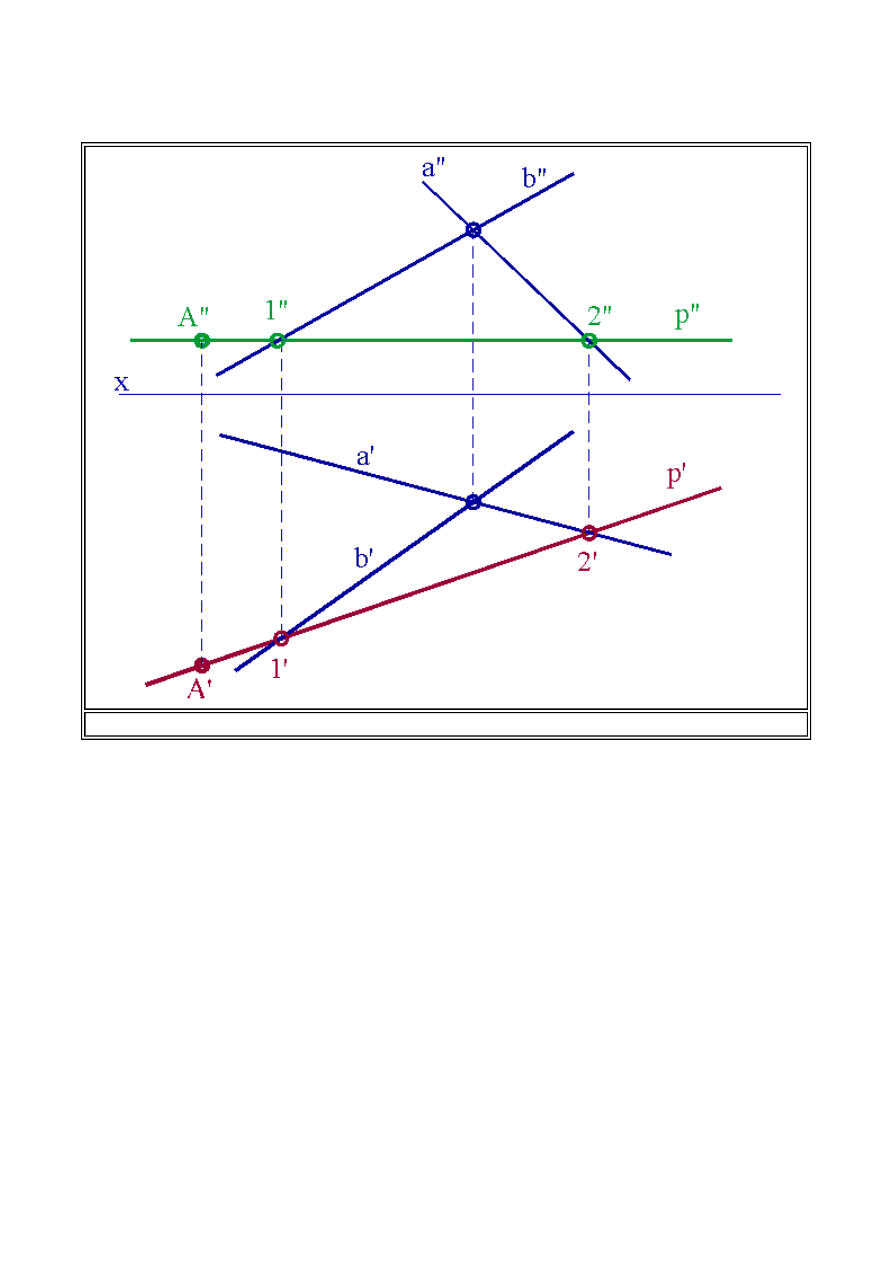
można jego rzut poziomy
A'
wyznaczyć na przecięciu się odnoszącej, prostopadłej do osi x, i rzutu
poziomego prostej
p'.
Analogiczne zagadnienie można rozpatrzyć, zakładając iż dana płaszczyzna określona jest śladami
v
a
i h
a
(patrz rys. 1.20a,b). Przyjmijmy dowolny rzut poziomy punktu A'. Zakładając, iż punkt
należy do płaszczyzny
a, z definicji przynależności wyznaczymy drugi rzut punktu. Przez rzut
poziomy punktu prowadzimy rzut poziomy prostej l (l'), dla której zakładamy przynależność do
płaszczyzny
a. Możemy zdefiniować przynależność prostej do płaszczyzny w sposób następujący:
Definicja
Prosta należy do płaszczyzny, jeżeli ma z nią co najmniej dwa punkty wspólne. W konstrukcjach
śladowych prosta leży na płaszczyźnie, jeżeli ślady prostej leżą na śladach płaszczyzny.
Rzut pionowy punktu
A''
wyznaczymy pośrednio poprzez wyznaczenie drugiego rzutu prostej
l''
.
Wyznaczamy ślad poziomy prostej
l
-
H
l
oraz pokrywający się z nim rzut poziomy tego śladu
H'
l
.
Rzut pionowy śladu poziomego
H''
l
prostej
l
będzie leżał na przecięciu się z osią x, odnoszącej
prostopadłej do osi x wystawionej ze śladu poziomego prostej
l.
Rzut poziomy śladu pionowego
V'
l
będzie leżał na przecięciu się rzutu poziomego prostej
l
z osią x. Rzut pionowy śladu pionowego
V''
l
będzie leżał na przecięciu się odnoszącej, prostopadłej do osi x, wystawionej z tego punktu, aż
do przecięcia się z rzutem pionowym prostej
l.
Otrzymaliśmy w ten sposób rzuty pionowe śladów
Rys.1.19. Przynależność punktu do płaszczyzny określonej bezśladowo
Informatyka 4 - Lekcja 1
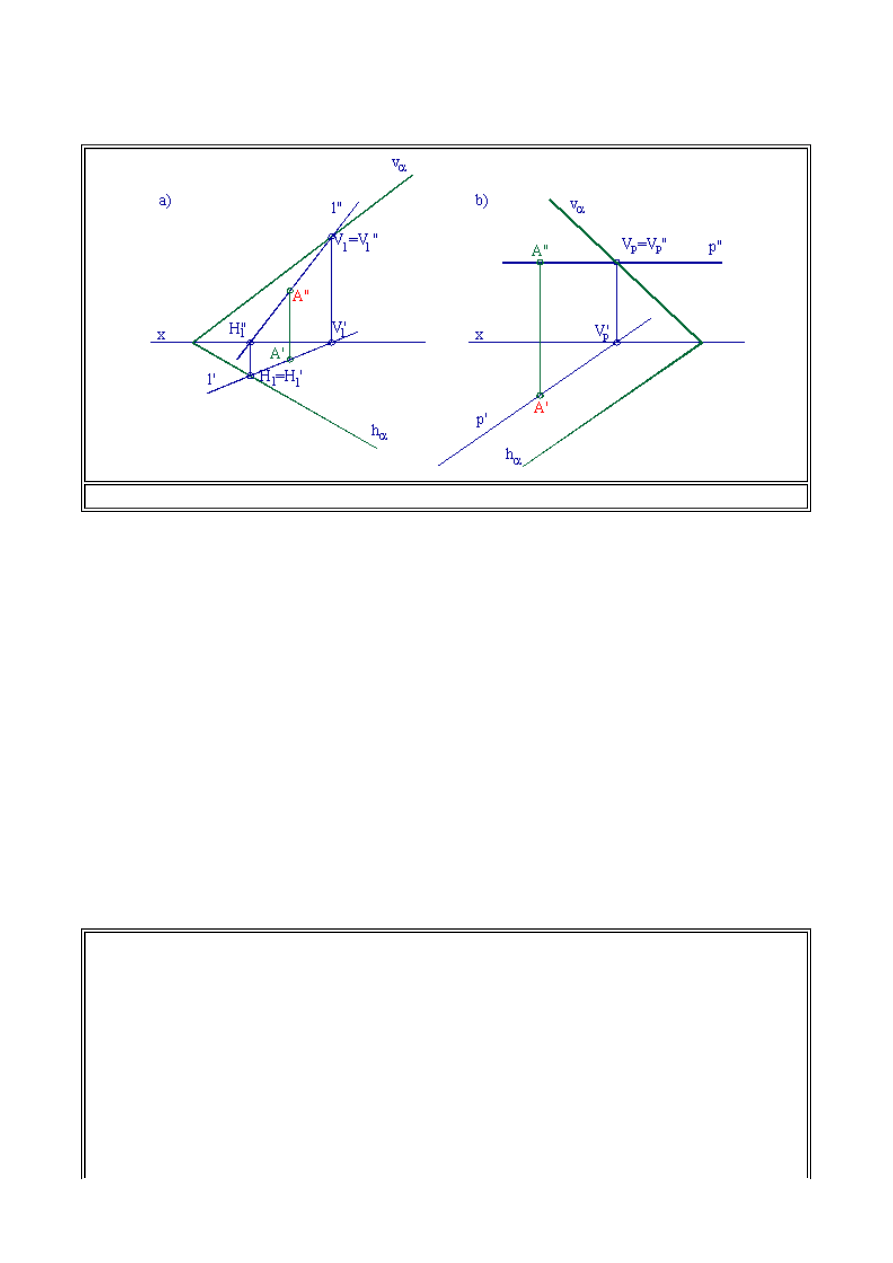
prostej
l
, które wyznaczają rzut pionowy prostej
l''
. Na rzucie tym leży oczywiście szukany rzut
punktu
A''
, który będzie należał na płaszczyźnie
a
.
Na rys.1.20b. Przedstawiono analogiczną konstrukcję, korzystając z pośrednictwa prostej poziomej
p
leżącej w płaszczyźnie
a
.
Dwie proste są do siebie równoległe jeżeli ich rzuty są równoległe. Definicje równoległości prostych
przedstawiono na rys. 1. 14. Zagadnienie to wydaje się oczywiste, wynika bowiem z niezmienników
rzutu równoległego.
Definicja
Prosta jest równoległa do płaszczyzny jeżeli jest równoległa do dowolnej prostej leżącej w tej
płaszczyźnie.
Oczywiście w konstrukcjach bezśladowych równoległość ta wydaje się oczywista i sprowadza się do
równoległości dwóch prostych, którą opisano wcześniej. Przykład równoległości prostej do
płaszczyzny trójkąta przedstawiono na rys. 1.21a. Prosta
a
jest równoległa do płaszczyzny trójkąta
ponieważ jest równoległa do boku
AB
D (ABC) (a" || AB" oraz a' || AB').
Rys.1.20. Przynależność punktu do płaszczyzny określonej śladami
(3.3) Równoległość prostych oraz prostej do płaszczyzny
Informatyka 4 - Lekcja 1
Bardziej złożona jest konstrukcja równoległości prostej do płaszczyzny w przypadku, gdy
płaszczyzna określona jest śladami. Wynika to z konieczności wyznaczenia najpierw prostej
a
leżącej w płaszczyźnie. Przypomnijmy tu warunek przynależności prostej do płaszczyzny (ślady
prostej muszą leżeć na śladach płaszczyzny). Po wyznaczeniu rzutów prostej
a
leżącej w
płaszczyźnie
a
, bez trudu wyznaczyć rzuty prostej
b ||
a
.
Równoległość płaszczyzn w rzutach prostokątnych można zdefiniować w sposób następujący:
Definicja
Jeżeli dwie przecinające się proste są równoległe do dwóch innych, przecinających się prostych, to
płaszczyzny jakie tworzą te proste są do siebie równoległe.
Można to przedstawić na rys. 1.22a. Jedna z płaszczyzn jest określona przez dwie proste
przecinające się, druga również, lecz w postaci trójkąta.
Rys.1.21. Równoległość prostej do płaszczyzny a) Prosta równoległa do płaszczyzny trójkąta
ABC b) Prosta równoległa do płaszczyzny określonej śladami.
(3.4) Równoległość płaszczyzn
Informatyka 4 - Lekcja 1
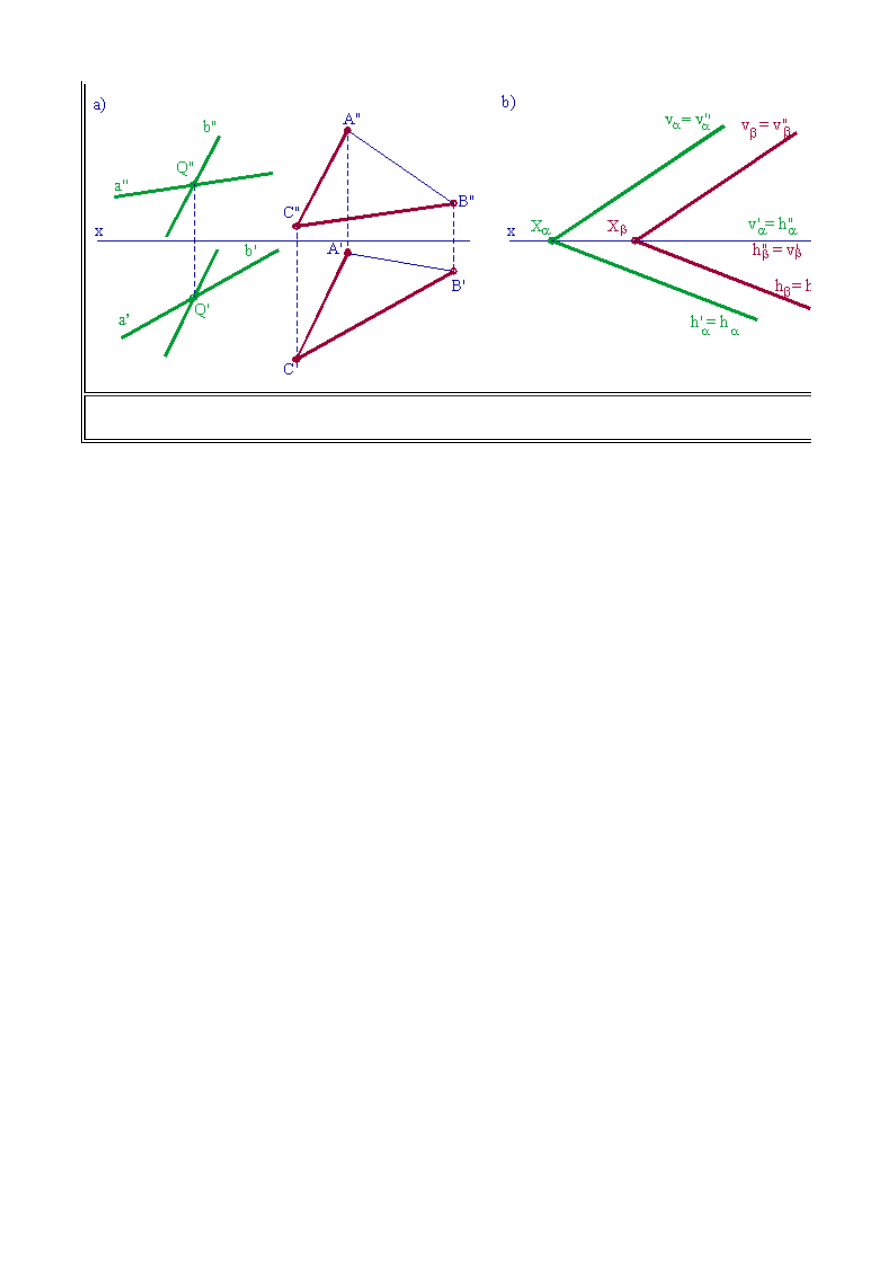
W konstrukcjach śladowych warunkiem równoległości płaszczyzn jest równoległość ich
jednoimiennych śladów, przecinających się w punkcie właściwym na osi x. To oznacza, że aby dwie
płaszczyzny były do siebie równoległe to ich ślady pionowe muszą być do siebie równoległe oraz
ślady poziome również muszą być do siebie równoległe. Definicja ta jest zgodna z poprzednią,
ponieważ ślady płaszczyzny to nic innego jak rzuty dwóch wzajemnie przecinających się prostych,
spełniających jedynie warunek położenia na rzutniach (patrz:
definicja śladów płaszczyzn
)
Przypomnijmy tu jednak fakt, iż ogólnie nie można stwierdzić, że płaszczyzny, których ślady są
odpowiednio równoległe, są do siebie równoległe. Przykładem mogą tu być dwie płaszczyzny
równoległe do osi x. Ich ślady są do siebie równoległe, lecz płaszczyzny wcale nie muszą być
równoległe. Istotnym zatem jest tu drugi warunek, aby ślady przecinały się na osi x. Na rys. 1.22a
płaszczyzna określona przy pomocy dwóch prostych
(a x b)
przecinających się w punkcie
Q
jest
równoległa do płaszczyzny
D (ABC)
ponieważ rzuty prostych
a i b
są odpowiednio równoległe do
rzutów boków
D (ABC)
,
a mianowicie
AC i CB.
Rys. 1.22. Równoległość płaszczyzn. a) Rzuty dwóch płaszczyzn równoległych określonych
dwiema prostymi równoległymi b) Równoległość płaszczyzn określonych śladami
Informatyka 4 - Lekcja 1
4. Prostopadłość prostych i płaszczyzn
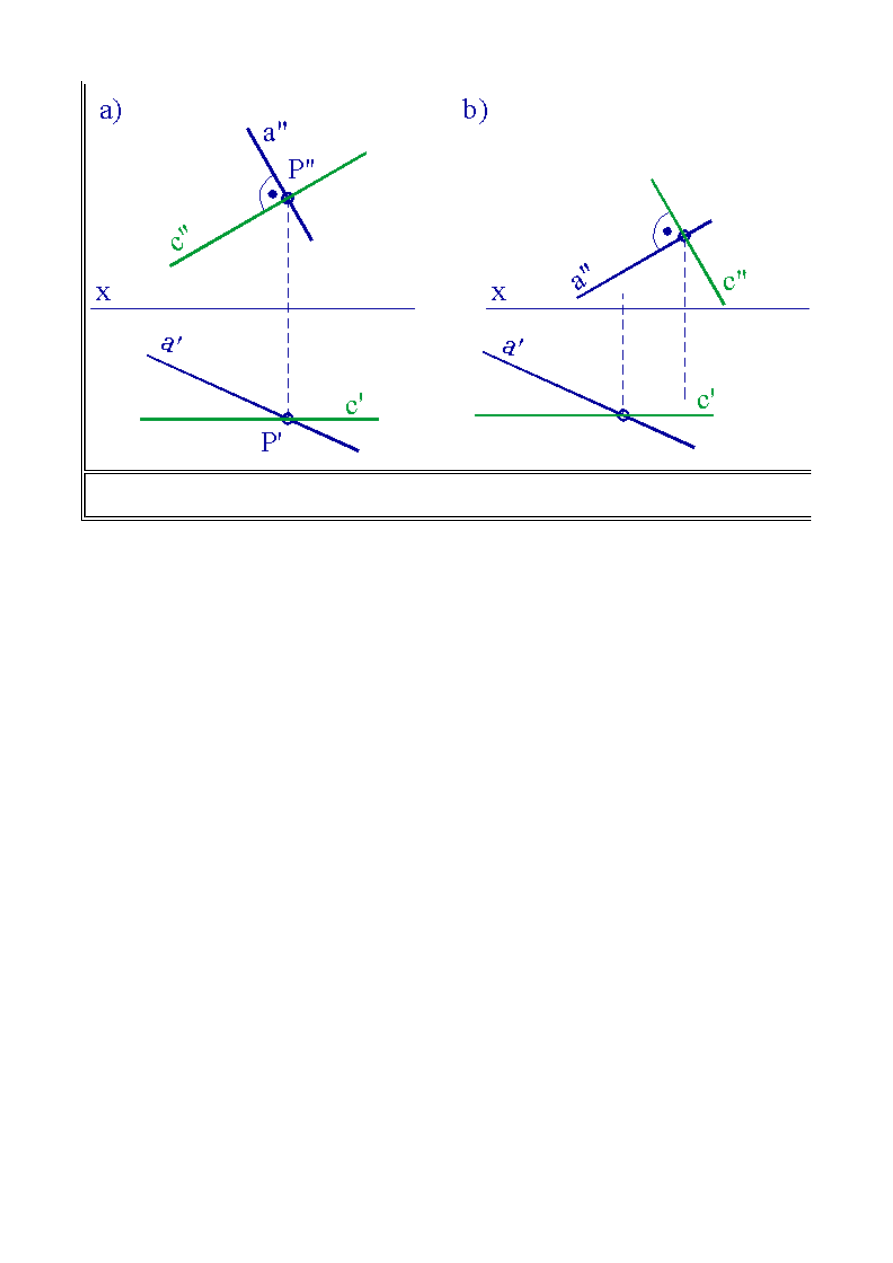
Ogólnie, jeżeli dwie proste są do siebie prostopadłe, to w rzutach prostokątnych ich rzuty,
zwykle, nie są prostopadłe. Są jednak przypadki szczególne dla których prostopadłość wybranych
rzutów jest zachowana. Wynika to oczywiście z niezmienników rzutowania równoległego. Można
nawet powiedzieć, iż dodatkowy 9 niezmiennik dotyczy właśnie prostopadłości prostych w rzutach
prostokątnych. Niezmiennik ten można sformułować w sposób następujący:
Niezmiennik 9
Kąt prosty, którego jedno z ramion jest równoległe do rzutni zachowuje swą prostopadłość po
dokonaniu rzutowania na tą właśnie rzutnię.
Proste równoległe do rzutni to odpowiednio: pozioma (równoległą do rzutni poziomej) oraz
czołowa (równoległa do rzutni
pionowej). Jeżeli zatem jedno z ramion kąta prostego jest prostą
poziomą lub czołową, to rzutem tego kąta, odpowiednio poziomym dla prostej poziomej i pionowym
dla prostej czołowej, będą kąty proste. Przedstawiono to na rys. 1.23.
Podobnie można rozważyć kwestię kąta prostego, którego jedno z ramion jest równoległe do
rzutni pionowej. W rzucie pionowym otrzymamy wówczas kąt prosty, co jest dowodem
prostopadłości prostych. Rzuty prostokątne prostych prostopadłych
a
i
c
przedstawiono na rys.
1.24.
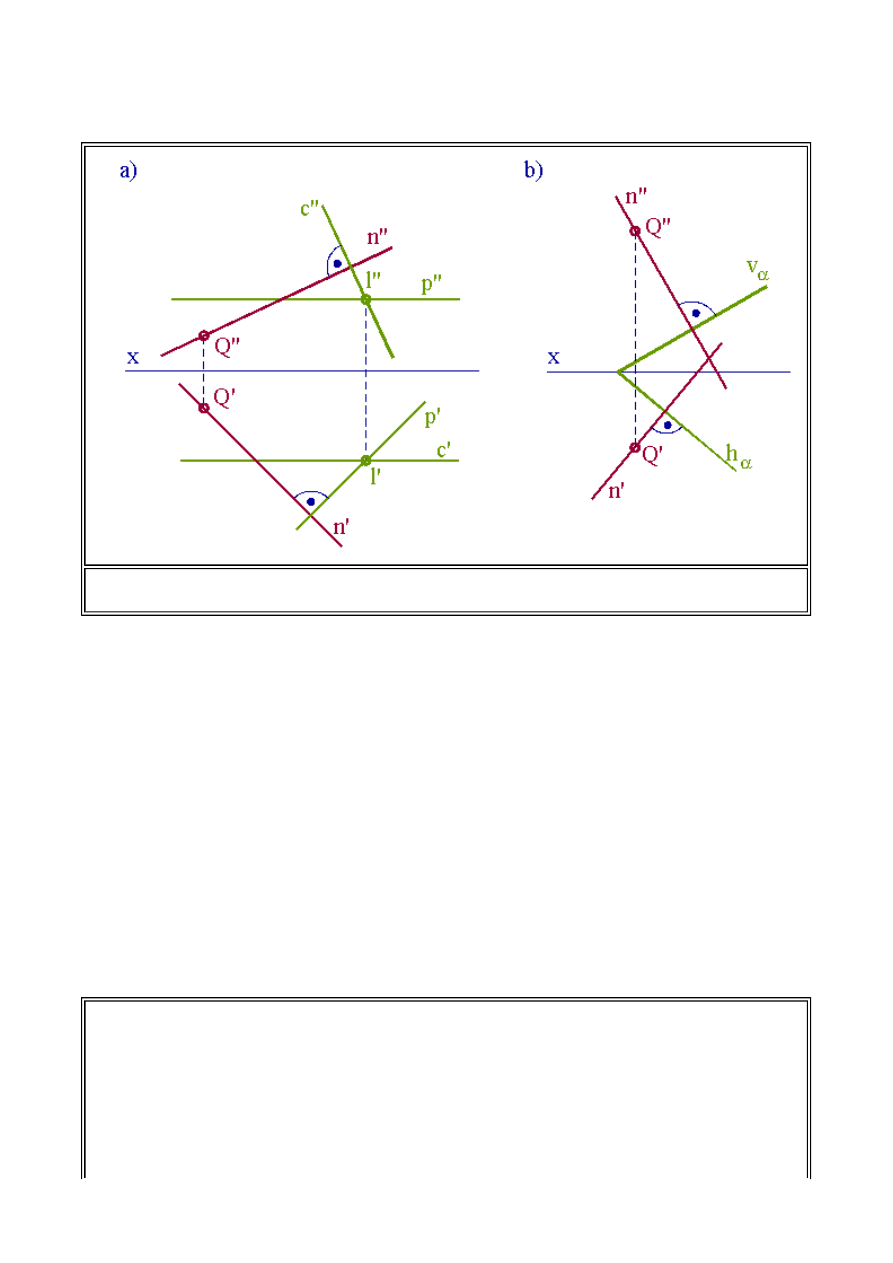
(4.1) Prostopadłość prostych
Rys.1.23. Rzuty prostych prostopadłych, z których jedna jest równoległa do rzutni poziomej.
a) Proste przecinające się b) Proste skośne.
Informatyka 4 - Lekcja 1
Definicja
Prosta jest prostopadła do płaszczyzny jeżeli jest prostopadła do dwóch przecinających się prostych
leżących w tej płaszczyźnie.
Prostopadłość prostej do płaszczyzny ustalana jest w rzutach prostokątnych poprzez konstrukcję
prostopadłości dwu prostych. Rzuty prostej prostopadłej do danej płaszczyzny, zgodnie z
ustaleniami w p. 4.1. powinny być zatem prostopadłe odpowiednio do rzutu poziomego prostej
poziomej leżącej w płaszczyźnie oraz do rzutu pionowego prostej czołowej leżącej w płaszczyźnie.
Aby zatem poprowadzić prosta prostopadłą do płaszczyzny określonej bezśladowo należy
wyznaczyć dwie przecinające się proste (poziomą i czołową) leżące w tej płaszczyźnie. Umożliwi to
nam wyznaczenie prostej, która będzie prostopadła do jednej i drugiej prostej. Oczywiście, w sensie
ogólnym, prosta jest prostopadła do płaszczyzny, jeżeli jest prostopadła do dowolnych
przecinających się prostych leżących w płaszczyźnie, jednak konstrukcję taką można zbudować w
rzutowaniu prostokątnym tylko wtedy jeżeli oprzemy się na prostych szczególnych, ponieważ ich
pojedyncze ramiona są równoległe do rzutni.
Zamiast wyznaczać proste szczególne leżące w płaszczyźnie, możemy samą płaszczyznę
zbudować z dwóch przecinających się prostych - poziomej i czołowej. Na rys. 1.25a. przedstawiono
konstrukcję płaszczyzny
a
(
p
x
c
) złożonej z dwóch prostych: poziomej i czołowej przecinających
się w punkcie
1
. Prosta
n
jest prostopadła do płaszczyzny
a
, ponieważ jej rzuty są odpowiednio
prostopadłe do rzutu pionowego prostej czołowej i rzutu poziomego prostej czołowej.
W przypadku płaszczyzny określonej śladami konstrukcja prostej prostopadłej do płaszczyzny jest
znacznie prostsza, ponieważ rzuty prostej powinny być prostopadłe do odpowiednich śladów
płaszczyzny. Nie kłóci się to z poprzednimi ustaleniami, albowiem ślady płaszczyzny są szczególnie
położonymi prostymi: poziomą i czołową, które leżą w płaszczyźnie i jednocześnie leżą na
Rys.1.24. Rzuty prostych prostopadłych, z których jedna jest równoległa do rzutni pionowej.
a) Proste przecinające się. b) Proste skośne.
(4.2) Prostopadłość prostej do płaszczyzny
Informatyka 4 - Lekcja 1
rzutniach. Ślady te oczywiście są prostymi, które przecinają się na osi x, spełniają więc wszystkie
warunki do realizacji konstrukcji prostopadłości prostej do płaszczyzny.
Na rys. 1.25 b przedstawiono konstrukcję prostej
n
prostopadłej do płaszczyzny
a
określonej
śladami. Prosta prostopadła do płaszczyzny przechodzi przez z góry określony punkt
Q
w
przestrzeni.
Definicja
Dwie płaszczyzny są do siebie prostopadłe, jeżeli jedna z nich zawiera prostą prostopadłą do
drugiej płaszczyzny.
Można zatem stwierdzić, że każda płaszczyzna przechodząca przez prostą prostopadłą do
płaszczyzny jest do niej prostopadła. A więc przez prostą prostopadłą do płaszczyzny można
poprowadzić cały pęk płaszczyzn, które będą prostopadłe do danej płaszczyzny
.
Na rys. 1.26 a, b
przedstawiono płaszczyzny prostopadłe do z góry zadanych płaszczyzn.
Rys.1.25. Prosta prostopadła do płaszczyzny a) Płaszczyzna określona bezśladowo b)
Płaszczyzna określona śladami
(4.3) Prostopadłość płaszczyzn
Informatyka 4 - Lekcja 1
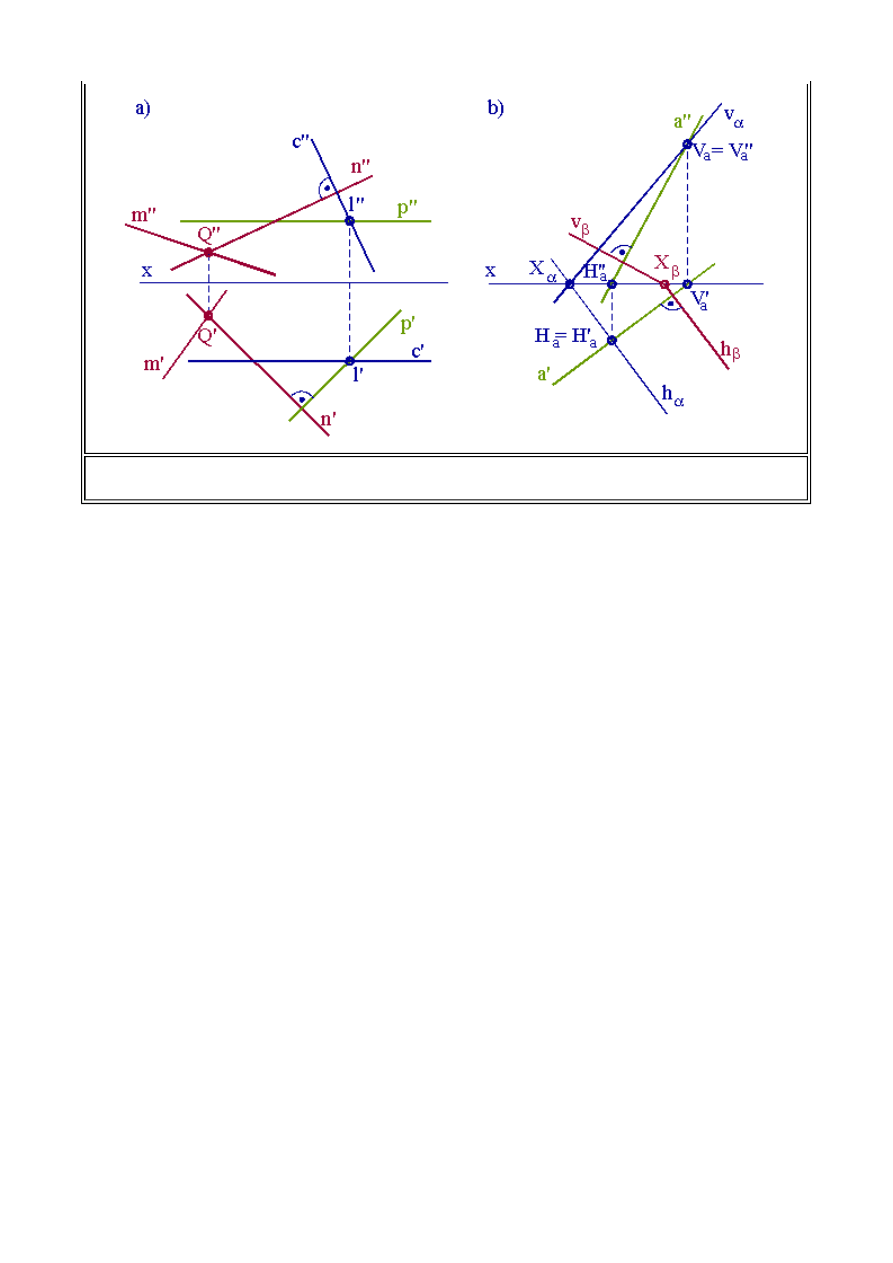
Na rys. 1.26a dana jest płaszczyzna określona za pomocą dwóch przecinających się w punkcie
1
prostych
p
i
c
. Druga płaszczyzna prostopadła do pierwszej określona została za pomocą również
dwóch prostych
m
i
n
przecinających się w punkcie
Q
, przy czym jedna z nich jest prostopadła do
płaszczyzny utworzonej przez proste
p
i
c
. Wynika to z faktu, iż proste
p
i
c
są odpowiednio
równoległe do rzutni poziomej (prosta pozioma
p
) i rzutni pionowej (prosta czołowa
c
), a więc
prosta n będzie prostopadła do płaszczyzny utworzonej przez te proste, jeżeli rzut pionowy prostej
n"
będzie prostopadły do rzutu pionowego prostej czołowej
c"
, a rzut poziomy prostej
n'
będzie
prostopadły do rzutu poziomego prostej poziomej
p'
.
W przypadku konstrukcji śladowych ( rys.1.26 b) w dowolnej płaszczyźnie
a
określonej śladami
v
a
i
h
a
obieramy dowolną prostą
a
leżącą w płaszczyźnie, a więc jej ślady
V
a
i
H
a
będą leżały
na śladach płaszczyzny. W ten sposób skonstruowane rzuty prostej
a
leżącej w płaszczyźnie
a
powinny być prostopadłe odpowiednio do jednoimiennych śladów płaszczyzny
b
. Ślady te
oczywiście muszą przecinać się w punkcie
X
a
na osi x. Zatem możemy stwierdzić, że płaszczyzna
b
jest prostopadła do
a
, ponieważ jest prostopadła do prostej
a
, która leży w płaszczyźnie
a
.
Rys.1.26. Płaszczyzny wzajemnie prostopadłe. a). Płaszczyzny określone bezśladowo. b).
Płaszczyzny określone śladami.
Informatyka 4 - Lekcja 1
Wyszukiwarka
Podobne podstrony:
komputerowe wspomaganie projektowania lekcja 8
komputerowe wspomaganie projektowania lekcja 4
komputerowe wspomaganie projektowania lekcja 2
komputerowe wspomaganie projektowania lekcja 6
komputerowe wspomaganie projekt Nieznany
Labolatorium projektowania układów i systemów sterowania, Narzędzia komputerowego wspomagania projek
sciaga ze wspomagania, Politechnika Lubelska, Studia, Semestr 6, sem VI, Komputerowe wspomaganie pro
Komputerowe wspomaganie projektowania w3
komputerowe wspomaganie projekt Nieznany (6)
więcej podobnych podstron