Egzamin z matematyki dla Ochrony Środowiska II stopieo 

 

Imię i nazwisko:…………………………………………………………………………………………………………………… 

nr albumu:………………………………………………. 

Specjalnośd:…………………………………………………………………………………………………………………………… 

 

1.  Na odcinku *0,1+ umieszczono losowo i niezależnie dwa punkty x i y. Niech A będzie 

zdarzeniem, że x>y+0.5 , natomiast B, że x<0.5 . Czy zdarzenia A i B są niezależne? 

2.  W rodzinie jest czwórka dzieci. Prawdopodobieostwo, że dziecko jest chłopcem 

wynosi 0.51. Wylicz prawdopodobieostwo zdarzenia, że w rodzinie są sami chłopcy, 
jeśli wiadomo, że w tej rodzinie jest co najmniej jeden chłopiec. 

3.  Wiedząc, że zmienna losowa X ma funkcję gęstości  ( )   {

                               

        

 

           

                               

 , 

wyznacz wartośd parametru a oraz oblicz EX. 

4.  Przy założeniu, że ciśnienie w komorze spalania silnika rakietowego ma rozkład 

normalny wyznacz 99% realizację przedziału ufności dla średniego ciśnienia w 
komorze spalania tego silnika, jeżeli dokonano 7 pomiarów ciśnienia otrzymując: 
31.85, 31.36, 30.32, 30.90, 31.70, 32.40, 31.60. 

5.  Wylosowano 120 sztuk pewnego wyrobu wyprodukowanego starą technologią i 

otrzymano 12 sztuk wadliwych, a wśród 160 sztuk wyprodukowanych nową 
technologią było 20 sztuk wadliwych. Na poziomie istotności =0.05 sprawdź 
hipotezę o jednakowych procentach braków przy produkcji obu metodami, wobec 
hipotezy, że jakośd produkcji nową technologią jest lepsza. 

6.  Wykonano 200 serii po 6 niezależnych rzutów monetą i uzyskano następujące wyniki: 

Liczba orłów w serii  0  1 

2 

3 

4 

5  6 

Liczba serii 

7  18  45  60  46  19  5 

 

Na poziomie istotności =0.05 zweryfikuj hipotezę, że liczba orłów wyrzuconych w 

serii rzutów ma rozkład dwumianowy z prawdopodobieostwem sukcesu p=

 
 

. 

 

 

1 

2 

3 

4 

5 

6 

Suma 

 

 

 

 

 

 

 

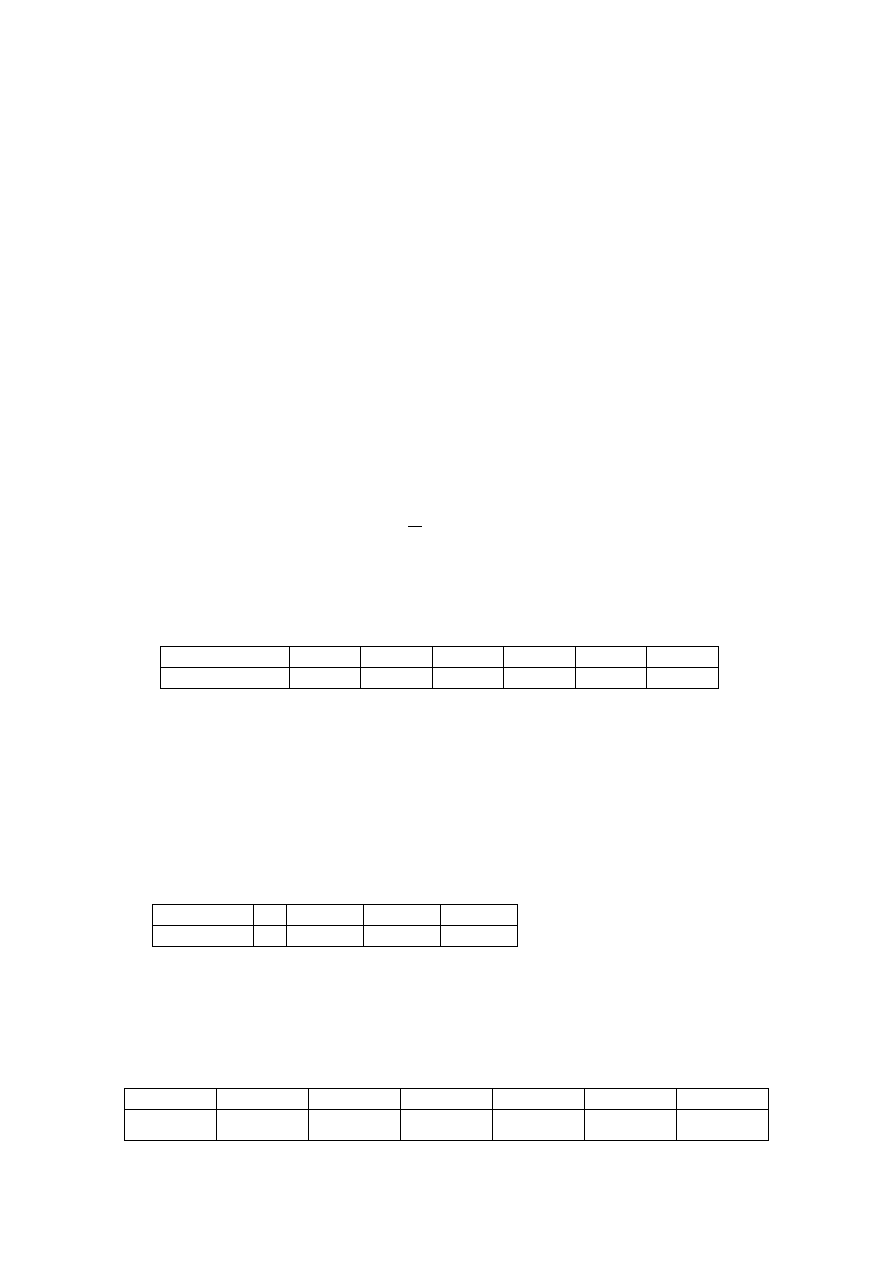
Egzamin z matematyki dla Ochrony Środowiska II stopieo 

 

Imię i nazwisko:…………………………………………………………………………………………………………………… 

nr albumu:………………………………………………. 

Specjalnośd:…………………………………………………………………………………………………………………………… 

 

1.  Z kwadratu [0,1][0,1] wybieramy losowo punkt o współrzędnych (p,q). Oblicz 

prawdopodobieostwo, że równanie  

 

             będzie miało pierwiastki rzeczywiste. 

2.  W pierwszej urnie są dwie białe kule i jedna czarna, a w drugiej jedna biała i dwie czarne. Z 

pierwszej urny losujemy jedną kulę i przekładamy do drugiej. Następnie z drugiej urny 
losujemy dwie kule. Oblicz prawdopodobieostwo, że będą to dwie białe kule. 

3.  Zysk netto osób prowadzących działalnośd gospodarczą w pewnym regionie jest zmienną 

losową X z funkcją gęstości  ( )   {

                     

 

  

            

                     

 . Wyznacz dystrybuantę tego rozkładu i 

oblicz prawdopodobieostwo, że zysk osoby prowadzącej taką działalnośd będzie od 4 do 6. 

4.  W celu oszacowania średniej wytrzymałości na ściskanie pewnego typu betonu, dokonano 80 

niezależnych pomiarów wytrzymałości tego betonu otrzymując wyniki: 

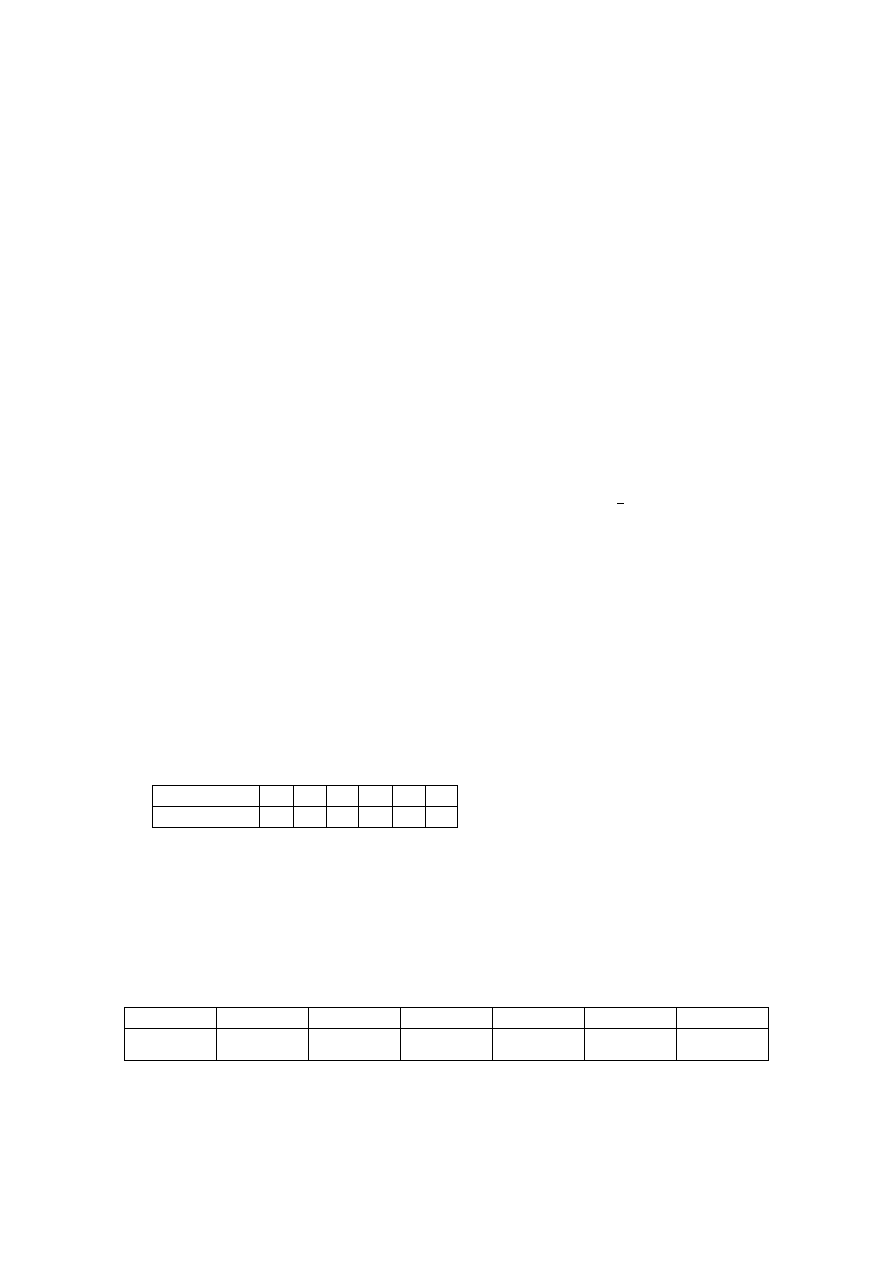
Wytrzymałośd 

190-194  194-198  198-202  202-206  206-210  210-214 

Liczba pomiarów  6 

12 

26 

20 

11 

5 

Wyznacz 99% realizację przedziału ufności dla średniej wytrzymałości na ściskanie tego 
betonu. 

5.  W pewnym instytucie hodowli roślin wysiano 800 ziaren grochu nowej odmiany i 

zaobserwowano, że wykiełkowało 728 ziaren. Na poziomie istotności =0.01 zweryfikuj 
hipotezę, że siła kiełkowania grochu tej odmiany wynosi 85%, wobec hipotezy, że jest 
mniejsza. 

6.  Przeprowadzono ewidencję awarii urządzeo technicznych w zakładzie produkcyjnym w ciągu 

kolejnych 100 dni roboczych, uzyskując wyniki: 

Liczba awarii  0 

Poniżej 2  Poniżej 3  Poniżej 4 

Liczba dni 

20  65 

95 

100 

Na poziomie istotności =0.05 zweryfikuj hipotezę, że rozkład liczby awarii jest rozkładem 
Poissona (z parametrem = ̅ ). 

 

 

1 

2 

3 

4 

5 

6 

Suma 

 

 

 

 

 

 

 

Egzamin z matematyki dla Ochrony Środowiska II stopieo 

 

Imię i nazwisko:…………………………………………………………………………………………………………………… 

nr albumu:………………………………………………. 

Specjalnośd:…………………………………………………………………………………………………………………………… 

 

1.  Na kartce egzaminacyjnej jest 5 pytao i 3 możliwe odpowiedzi na każde z pytao. Zdający 

losowo wybiera odpowiedź na każde z pytao. Oblicz prawdopodobieostwo otrzymania 4 
poprawnych odpowiedzi. 

2.  Z odcinka [-1,1+ wybrano losowo i niezależnie dwie liczby x i y. Oblicz prawdopodobieostwo, 

że   

 

   

 

        , jeśli wiadomo, że  

 

   

 

       . 

3.  Znajdź wartośd oczekiwaną zmiennej losowej X, o gęstości  ( )   {

                   

 
 

            

                   

 . 

4.  Z 400 przebadanych zakładów produkcyjnych danego regionu w pewnym roku 330 zapłaciło 

kary umowne za niedotrzymanie umów korporacyjnych. Znajdź 95% realizację przedziału 
ufności dla procentu zakładów produkcyjnych w tym regionie w danym roku, które zapłaciły 
kary umowne. 

5.  Zmierzono w dwóch ulach średnice komórek plastrów zbudowanych przez pszczoły . Dla 7 

wylosowanych komórek z pierwszego ula otrzymano: 5.36, 5.20, 5.28, 5.16, 5.30, 5.08, 5.23 , 
a dla drugiego ula: 5.15, 5.04, 5.30, 5.22, 5.19, 5.24, 5.12. Na poziomie istotności =0.05 
zweryfikuj hipotezę, że odchylenia standardowe średnic komórek plastra są jednakowe, 
wobec  hipotezy, że są różne. 

6.  Wykonano 120 rzutów sześcienną kostką do gry otrzymując wyniki: 

Liczba oczek 

1 

2 

3 

4 

5 

6 

Liczba rzutów  11  30  14  10  33  22 

Na poziomie istotności =0.05 zweryfikuj hipotezę, że kostka jest symetryczna (tzn. 
prawdopodobieostwo wyrzucenia każdej liczby oczek jest takie samo). 

 

 

1 

2 

3 

4 

5 

6 

Suma