12 Zginanie płaskie belek prostych.doc

131

ZGINANIE PŁASKIE BELEK PROSTYCH

WYKRESY SIŁ POPRZECZNYCH I MOMENTÓW

ZGI

NAJĄCYCH

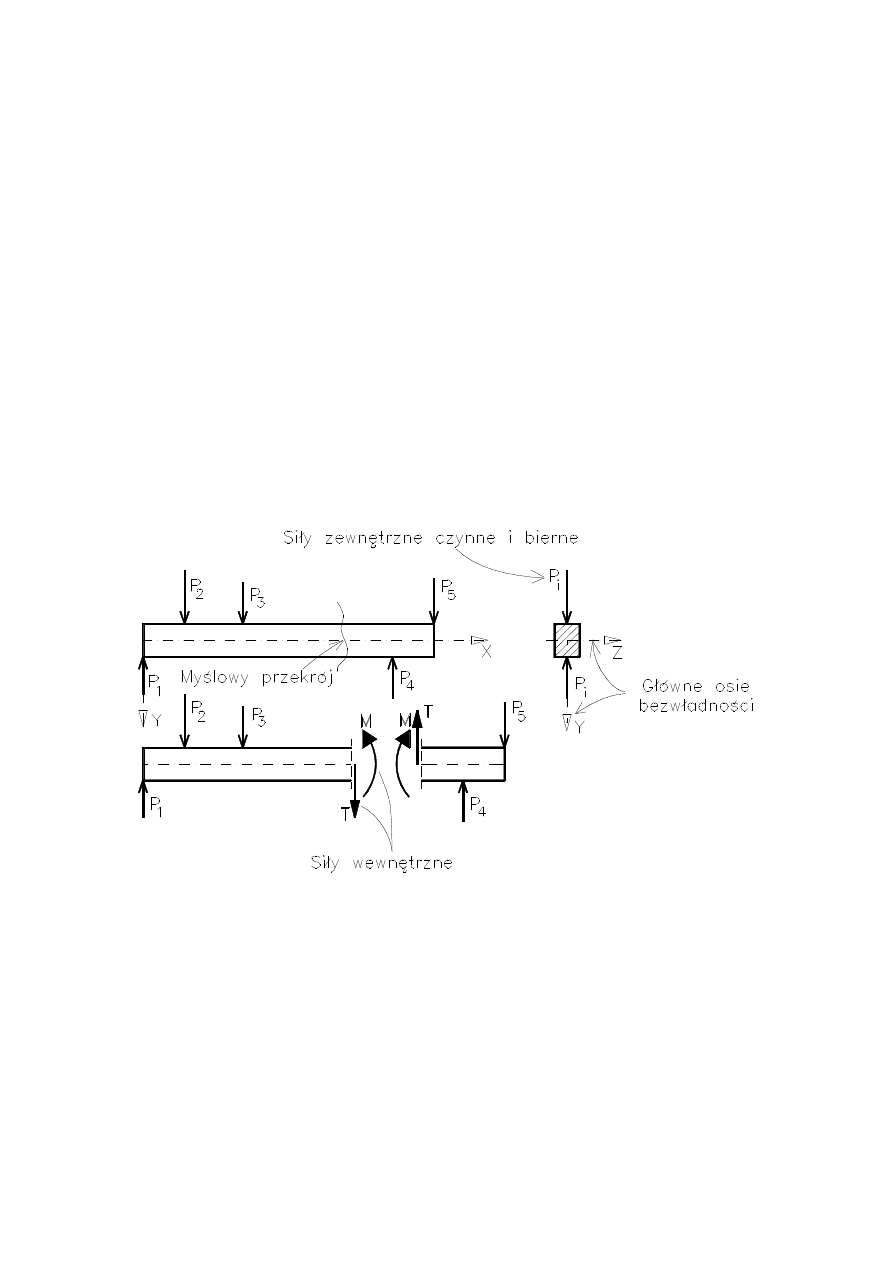
Zginanie płaskie: wszystkie siły zewnętrzne czynne (obciąże-
nia) i bierne (reakcje) leżą w jednej wspólnej płaszczyźnie prze-
chodzącej przez oś belki

Zginanie proste: kier

unek wektora momentu zginającego po-

krywa się z kierunkiem osi symetrii przekroju poprzecznego
belki.

Do wyznaczania sił wewnętrznych wykorzystuje się me-

todę myślowych przekrojów. Przy stałym przekroju belki gra-
nicami odcinków, w których należy dokonać myślowych prze-
kro

jów, są punkty przyłożenia sił zewnętrznych – czynnych i

biernych (reakcji podporowych). Na rysunku pokazano zasto-
sowanie metody myślowych przekrojów, układ współrzędnych
(

oś Y skierowana jest w dół, oś X wzdłuż osi belki) oraz siły

we

wnętrzne w belce.

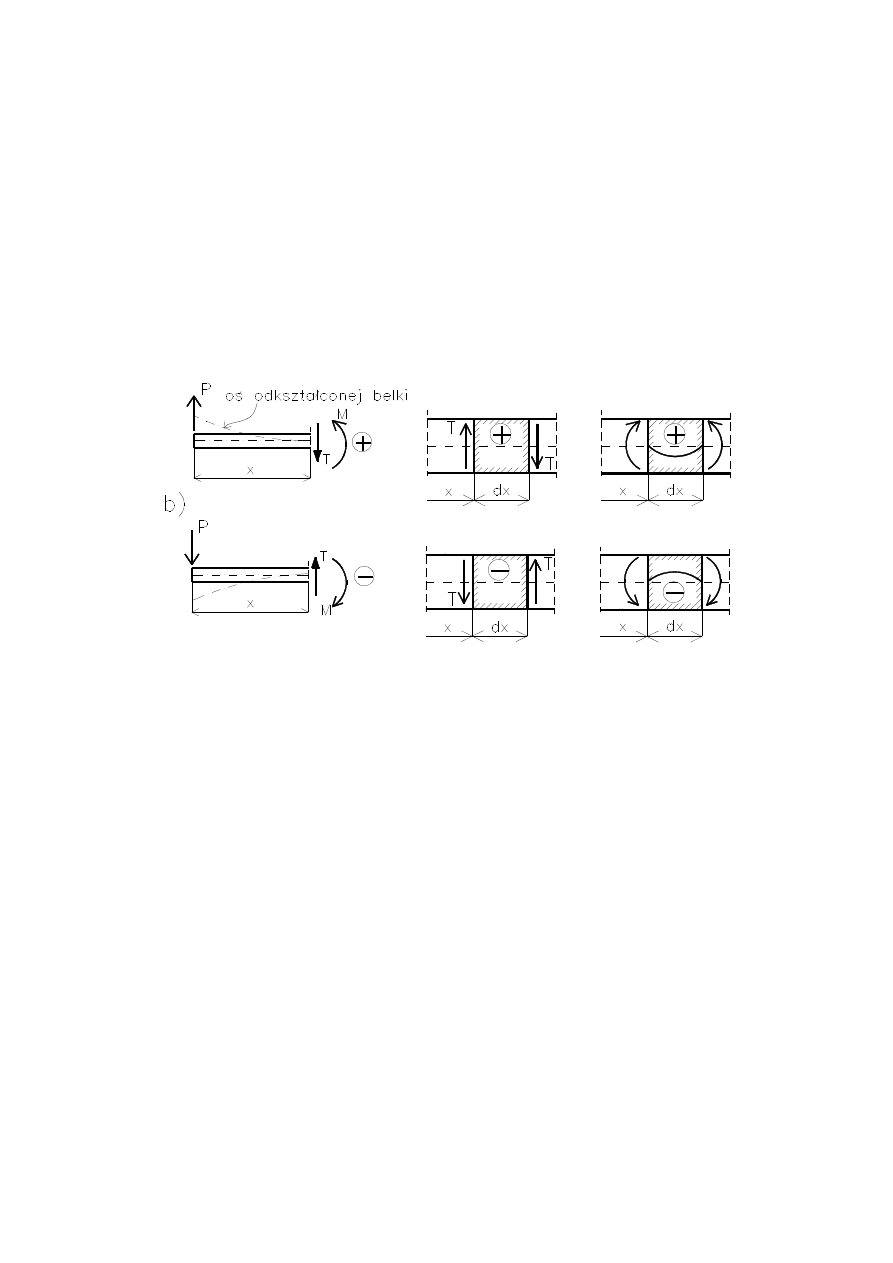
12 Zginanie płaskie belek prostych.doc

132

W odróżnieniu od rozciągania i skręcania, w zginaniu wystę-

pują dwie siły wewnętrzne – siła poprzeczna T w płaszczyźnie
obciążenia XY oraz moment zginający M, którego wektor jest
prostopadły do płaszczyzny XY. W obliczeniach wytrzymało-
ściowych belek rzeczą podstawową jest wyznaczenie rozkła-
dów T i M. Maksymalne wartości tych sił wskazują na przekroje
najbardziej ob

ciążone, na przekroje niebezpieczne. Umowne

określenie znaków sił wewnętrznych pokazano na rysunku.

UMOWA:
Belka zginana „wypukłością w dół” – dodatnie siły wewnętrzne.
Belka zginana „wypukłością w górę” – ujemne siły wewnętrzne.

12 Zginanie płaskie belek prostych.doc

133

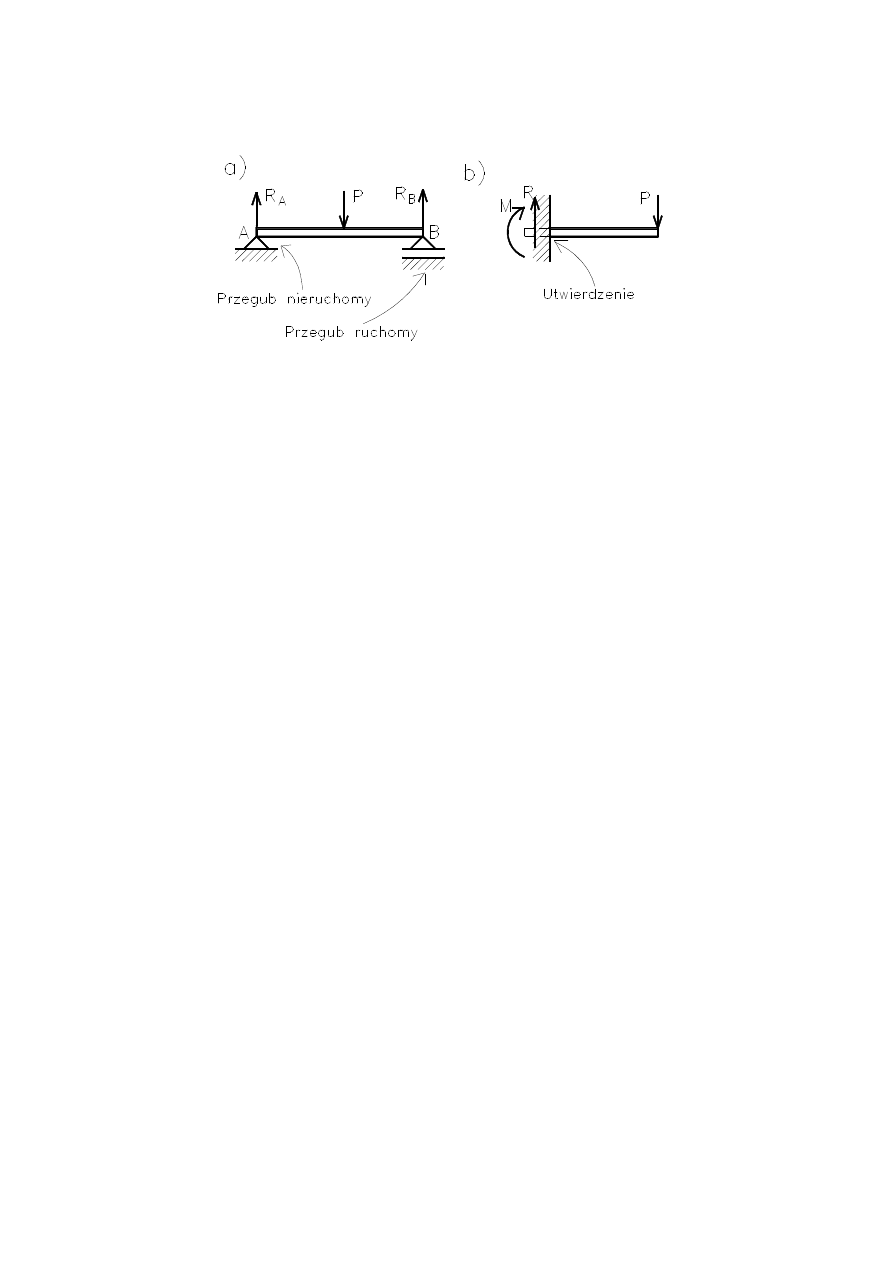
RÓWNANIA STATYKI

Sposoby podparcia belek

Układy sił:

a)

Płaski układ sił równoległych z dwoma równaniami sta-
tyki.

b)

Płaski układ sił dowolnych z dwoma równaniami statyki
(suma rzutów sił na oś poziomą nieaktywna).

Dla wyznaczania reakcji podporowych można sformułować

dwa układy równań równowagi, zawierające po dwa równa-
nia.

(1)













n

1

i

n

1

i

i

0

yi

,

0

M

,

0

P

0

– dowolny punkt.

(2)













n

1

i

Bi

n

1

i

Ai

.

0

M

,

0

M

UWAGA PRAKTYCZNA: korzystnie jest stosować układ (2).
Dla sprawdzania

poprawności obliczeń można wykorzystać

dodat

kowo drugie równanie układu (1).

12 Zginanie płaskie belek prostych.doc

134

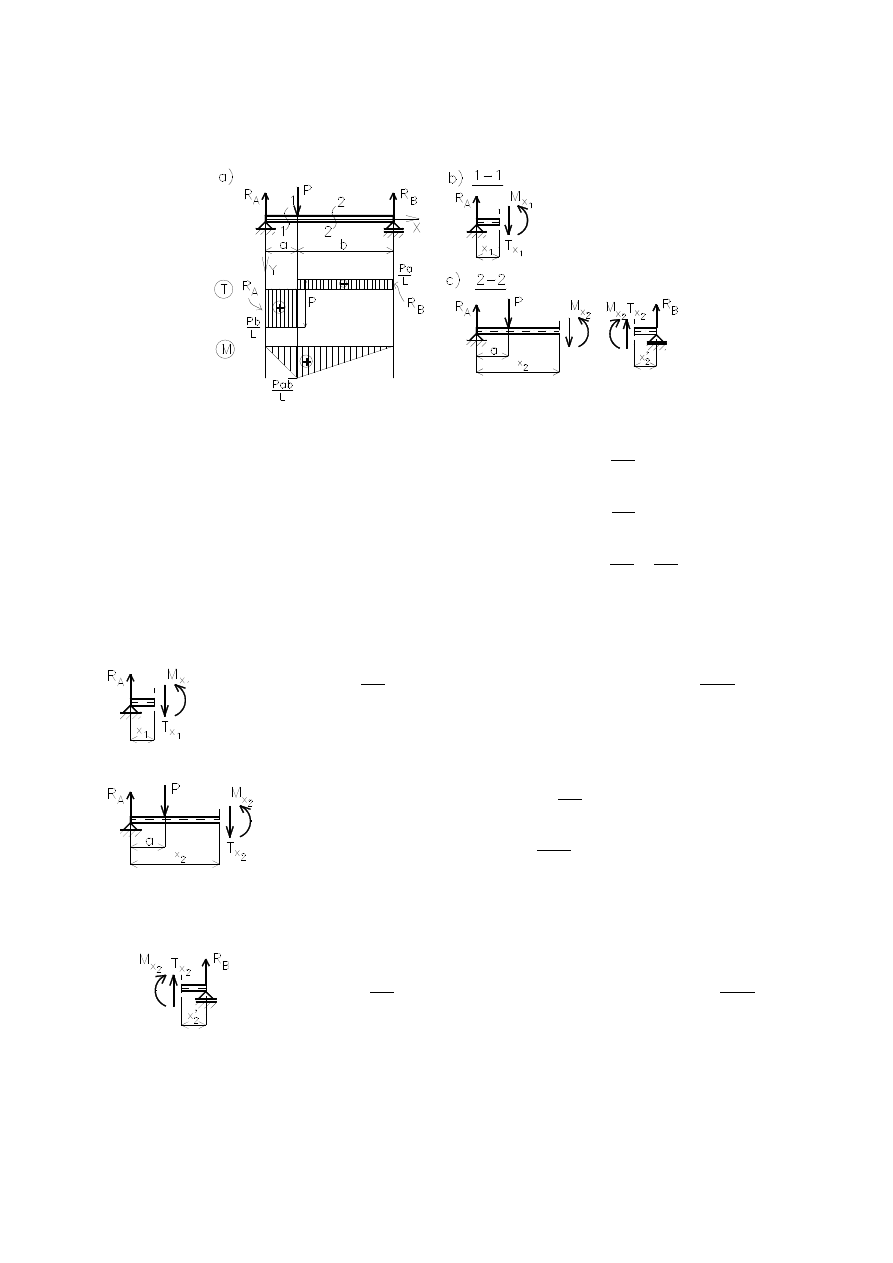
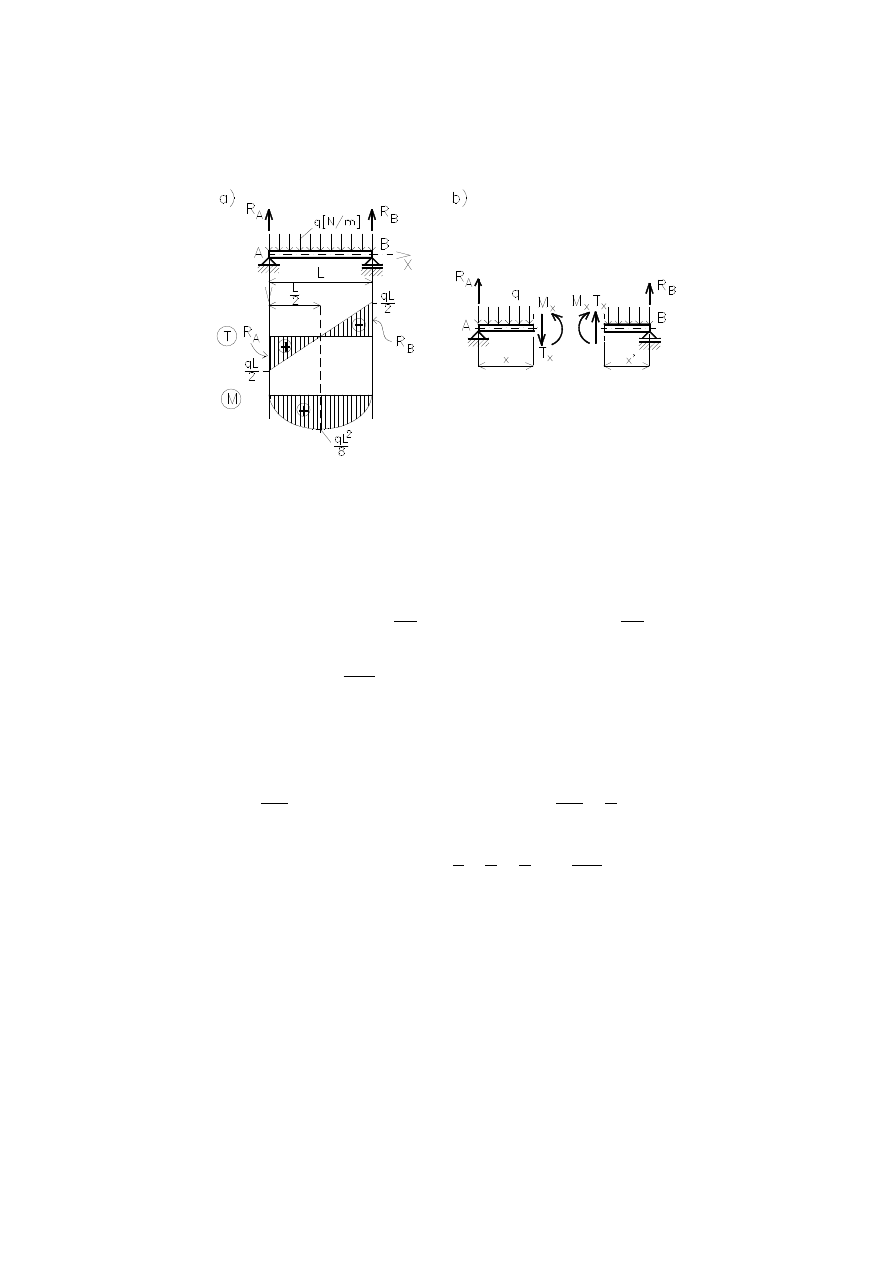
Przykład

Dla belki przedstawionej na rysunku wyko

nać wykresy sił poprzecznych i momen-

tów zginających.

Zadanie jest statycznie wyznaczalne. Dla L = a + b reakcje podporowe (rys. a):

























.

L

Pb

R

0

Pb

L

R

0

M

,

L

Pa

R

0

Pa

L

R

0

M

A

A

B

B

B

A

Sprawdzenie

prawidłowości obliczeń:

 













P

L

Pa

L

Pb

R

R

0

y

P

B

A

Ponieważ belka ma stały przekrój poprzeczny, myślowe przekroje wyznacza się w

przedziałach ograniczonych punktami przyłożenia obciążeń (rys. b,c):
Przedział 1–1:

0



x

1



a

.

L

Pab

M

,

0

M

;

x

R

M

,

L

Pb

R

T

a

x

0

x

1

A

x

A

x

1

1

1

1















Przedział 2–2:

a



x

2



a + b





.

0

M

,

L

Pab

M

,

a

x

P

x

R

M

,

L

Pa

R

P

R

T

b

a

x

a

x

2

2

A

x

B

A

x

2

2

2

2





























Podobnie jak dla prętów i wałów, aby sprawdzić poprawność obliczeń, należy

sprawdzić prawy koniec belki (rys. c).
Prze

dział 2’–2’: 0



2

'

x



b

.

L

Pab

M

,

0

M

,

x

R

M

,

L

Pa

R

T

b

x

0

x

'

2

B

x

B

x

'

2

'

2

'

2

'

2

















Wykresy T oraz M pokazano na rys. a. Analizując je należy pamiętać, że na wy-

kresach sił wewnętrznych muszą być widoczne wszystkie siły zewnętrzne. Na wykre-
sie T uskoki odpowiadają siłom P, R

A

i R

B

. Na podpor

ach A i B moment musi być

równy zeru – na podparciu przegubowym nie ma momentu zewnętrznego. Musi być
także zachowana ciągłość wykresu M na końcu I i początku II przedziału.

12 Zginanie płaskie belek prostych.doc

135

P

RZYKŁAD

Dla belki obciążonej w sposób ciągły obciążeniem o stałej intensywności q wyko-

nać wykresy sił poprzecznych i momentów zginających.

Obciążenie ciągłe q = const działające na odcinku L można zastąpić siłą wypad-

kową q



L, przyłożoną w połowie długości odcinka (wypadkowa układu sił równole-

głych). Z sumy momentów względem podpór A i B otrzymuje się R

A

= R

B

= qL/2

(rys. a). W belce wystarczy roz

patrzyć tylko jeden przedział 0



x



L, w którym

.

0

M

,

0

M

;

2

qx

x

R

M

,

2

qL

qL

R

T

,

2

qL

R

T

;

qx

R

T

L

x

o

x

2

A

x

A

L

x

A

0

x

A

x

































Do wykonania wykresu momentów potrzebny jest trzeci punkt, który można otrzy-

mać, obliczając ekstremum funkcji opisującej moment zginający:

.

8

qL

2

L

q

2

1

2

L

R

M

M

,

L

2

1

q

R

x

0

T

qx

R

dx

dM

2

2

A

x

x

max

A

m

x

A

m





































Ekstremum momentu występuje w przekroju, w którym siła poprzeczna jest

równa zeru (por. zależności różniczkowe pomiędzy obciążeniem a siłami wewnętrz-
ny

mi). Sprawdzenie poprawności obliczeń można przeprowadzić rozpatrując prawy

koniec belki (rys. b).

12 Zginanie płaskie belek prostych.doc

136

P

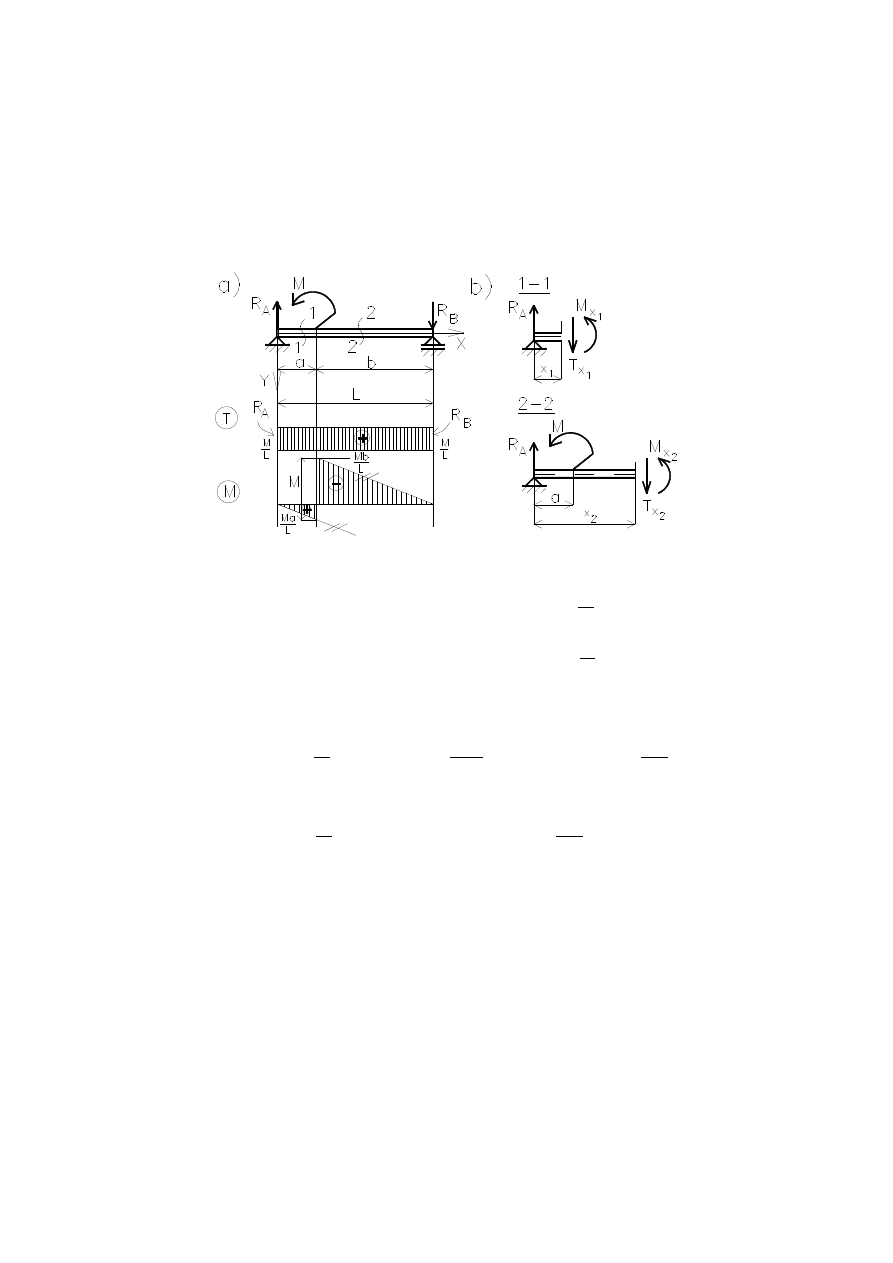
RZYKŁAD

Dla belki obciążonej momentem M wykonać wykresy sił poprzecznych i momen-

tów zginających.

Z równań statyki oblicza się reakcje podporowe (rys. a):

























.

L

M

R

0

M

L

R

,

0

M

,

L

M

R

0

M

L

R

,

0

M

A

A

B

B

B

A

Sprawdzenie: R

A

– R

B

= 0.

W przedziale 1

–1 (0



x

1



a) siły wewnętrzne wynoszą (rys. b):

,

L

Ma

M

,

0

M

,

L

Mx

x

R

M

,

L

M

R

T

a

x

0

x

1

1

A

x

A

x

1

1

1

1

















natomiast w przedziale 2

–2 (a



x

2



L):

.

0

M

,

L

Mb

M

,

M

x

R

M

,

L

M

R

T

L

x

a

x

2

A

x

A

x

2

2

2

2



















Wykresy sił wewnętrznych pokazano na rys. a.

12 Zginanie płaskie belek prostych.doc

137

P

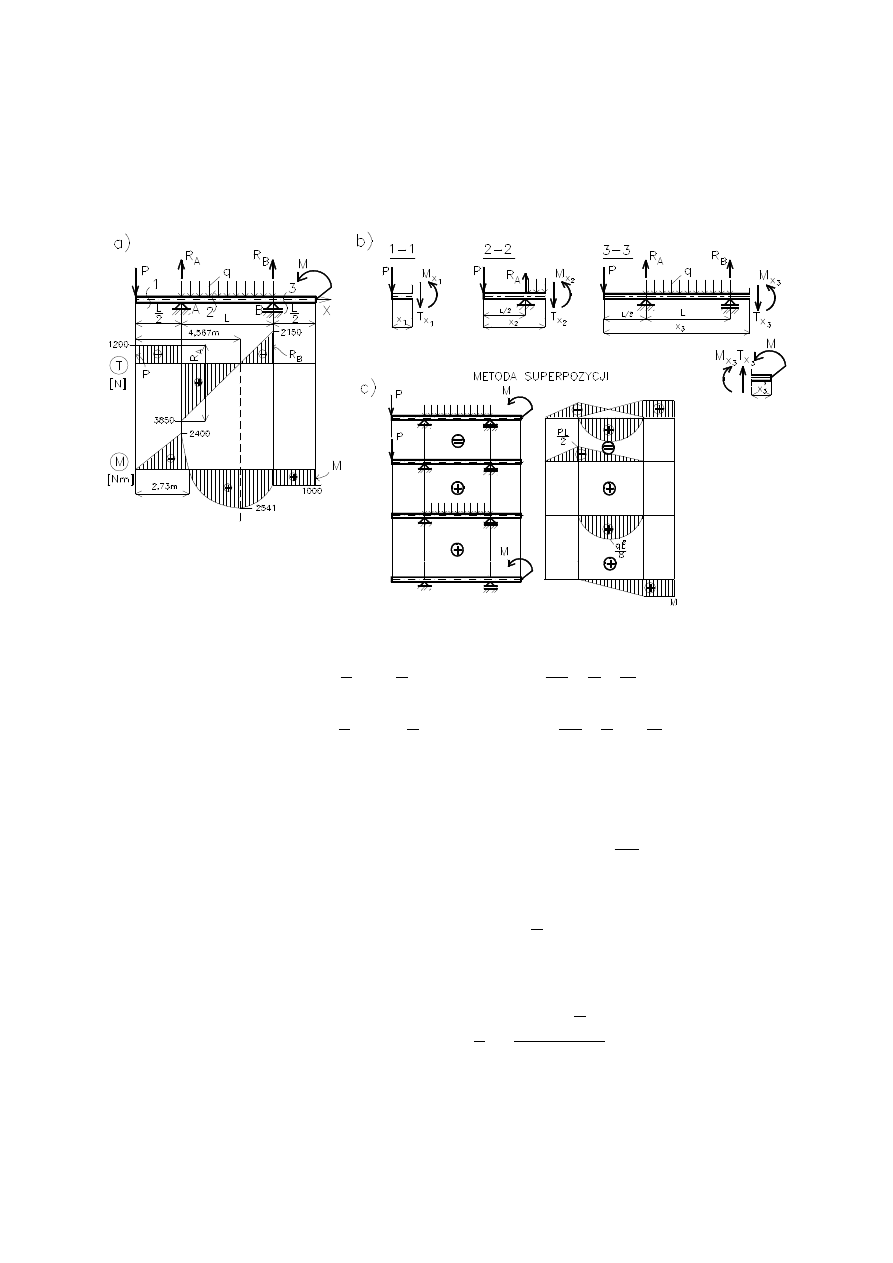
RZYKŁAD

Dla belki przedstawionej na rysunku

wykonać wykresy sił poprzecznych oraz mo-

mentów zginających. Przyjąć dane: P = 1200 N, q = 1500 N/m, M = 1000 N



m,

L = 4

m. Wykonać dodatkowo wykres momentów, korzystając z zasady superpozycji.

Równania statyki (rys. a):

















































.

N

5050

L

M

P

2

3

2

qL

R

0

M

2

L

qL

L

2

3

P

L

R

,

0

M

,

N

2150

L

M

2

P

2

qL

R

0

M

2

L

qL

2

L

P

L

R

,

0

M

A

A

B

B

B

A

Sprawdzenie: R

A

+ R

B

= P + qL = 7200 N.

Siły wewnętrzne w trzech myślowych przekrojach (rys. b):

Prze

dział 1–1: 0



x

1



L/2

.

m

N

2400

2

PL

M

,

0

M

;

Px

M

,

N

1200

P

T

2

/

L

x

0

x

1

x

x

1

1

1

1





























Przedział 2–2: L/2



x

2



3/2L

,

2

L

x

q

R

P

T

2

A

x

2























,

N

2150

4

1500

5050

1200

T

,

N

3850

5050

1200

T

L

2

/

3

x

2

/

L

x

2

2



























,

2

2

L

x

q

2

L

x

R

Px

M

2

2

2

A

2

x

2





































,

m

N

2400

2

1200

M

2

/

L

x

2















12 Zginanie płaskie belek prostych.doc

138

.

m

N

1000

12000

20200

7220

2

4

1500

4

5050

4

2

3

1200

M

2

L

2

/

3

x

2



























Ponieważ w przedziale II siła poprzeczna zmieniła swój znak, można wniosko-

wać, że w przekroju, w którym T = 0 moment osiągnie w tym przedziale wartość eks-
tremalną

.

m

N

2541

M

M

,

m

567

,

4

q

P

R

2

L

x

0

T

2

L

x

q

R

P

dx

dM

567

,

4

x

max

x

A

m

2

x

2

A

2

x

2

2

2

2













































Przekrój, w którym moment jest równy zeru obliczyć można rozwiązując trójmian

kwadratowy i wybierając pierwiastek znajdujący się w granicach drugiego przedziału

.

m

73

,

2

x

0

2

2

L

x

q

2

L

x

R

Px

M

20

2

2

2

A

2

x

2











































Przekrój 3–3: 3/2L



x

3



2L





.

m

N

1000

M

,

m

N

1000

M

,

L

x

qL

L

2

3

x

R

2

L

x

R

Px

M

,

0

qL

R

R

P

T

L

2

x

L

2

/

3

x

3

3

B

3

A

3

x

B

A

x

3

3

3

3

































































Siły wewnętrzne w przedziale III można również określić w prostszy sposób,

przyjmując granice przedziału 0



x’

3





L/2 (patrz rys. b). Sposób ten umożliwia rów-

nież sprawdzenie poprawności obliczeń.

Wykresy sił wewnętrznych przedstawiono na rys. a. Analizując te wykresy należy

po raz kolejny zwrócić uwagę, że wszystkie siły zewnętrzne muszą być na nim
widoczne.

W przekrojach, w których nie ma sił zewnętrznych (czynnych i bier-

nych) obowiązuje ciągłość odpowiednich wykresów.

Wykres momentów zginających w bardzo prosty sposób można otrzymać stosując

zasadę superpozycji. Na rysunku c pokazano sposób rozdzielenia obciążenia na trzy
proste przypadki oraz sumowania odpowiadających tym przypadkom wykresów mo-
mentów zginających. Przedstawiony sposób otrzymywania wykresów M ma duże
znaczenie praktyczne.

12 Zginanie płaskie belek prostych.doc

139

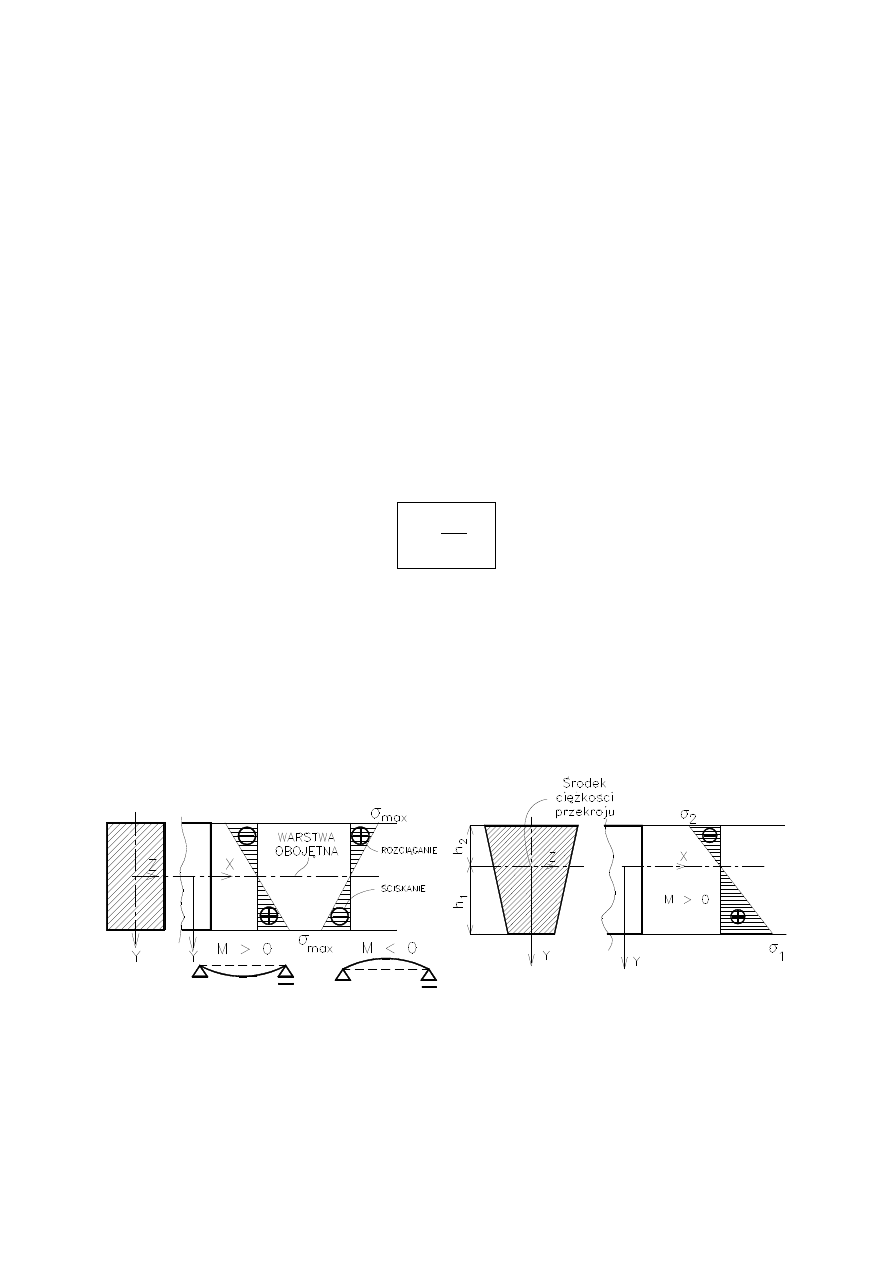
NAPRĘŻENIA NORMALNE W ZGINANEJ BELCE

Moment zginający



naprężenia normalne

Siła poprzeczna



naprężenia styczne (ze względów prak-

tycznych

– pomijane).

Założenia: hipoteza płaskich przekrojów. Z doświadczenia: W

zginanej belce istnieje

warstwa obojętna, prostopadła do

płaszczyzny działania momentu zginającego, w której włókna
nie ulegają odkształceniom



naprężenia = 0.

Naprężenia normalne w warstwie odległej o y od warstwy obo-
jętnej:

.

y

J

M

Z





J

Z

– osiowy moment bezwładności przekroju porzecznego belki.

Naprężenia normalne są liniową funkcją odległości od osi ob-

ojętnej. Maksymalne wartości naprężeń normalnych występują
w włóknach skrajnych, najbardziej oddalonych od osi obojętnej.
Rozkład naprężeń normalnych pokazano na rysunku.

Naprężenia normalne w zginanej

belce o przekroju prostokątnym

Naprężenia normalne w zginanej

belce o przekroju trapezowym

12 Zginanie płaskie belek prostych.doc

140

Dla belki o przekroju trapezowym: p

o wyznaczeniu położenia

środka ciężkości przekroju znane są odległości skrajnych włó-
kien od osi obojętnej. Na rysunku przyjęto, że odległości skraj-
nych włókien h

1

> h

2

, stąd |



1

| > |



2

|. Naprężenia te wynoszą:

.

h

J

M

,

h

J

M

2

Z

2

1

Z

1









Maksymalne naprężenia normalne przy zginaniu:

.

W

M

Z

max





W

z

– wskaźnik wytrzymałości przekroju na zginanie, zdefi-

niowany jako iloraz momentu bezwładności oraz maksymalnej
od

ległości skrajnego włókna od osi obojętnej.

.

h

J

W

max

Z



WARUNEK WYTRZYMAŁOŚCIOWY dla zginanej belki o rów-
nej wytrzymałości na rozciąganie i na ściskanie ma postać

.

W

M

dop

Z

max









Z warunku wytrzymałościowego można wyznaczyć:

– obciążenia dopuszczalne dla zadanego przekroju belki,
– wymaganą wielkość przekroju dla zadanego obciążenia.

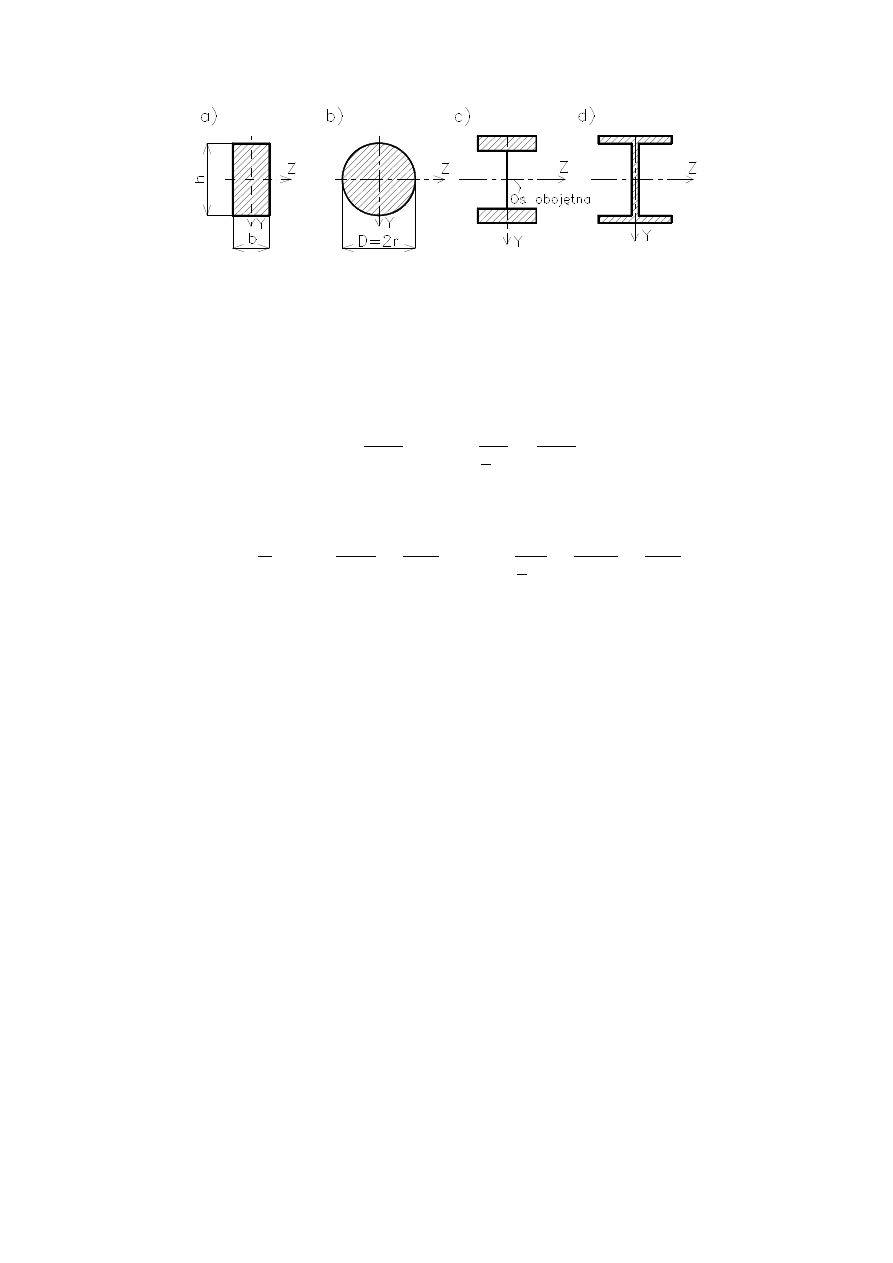
12 Zginanie płaskie belek prostych.doc

141

Przykłady przekrojów belek

Dla przekroju prostokątnego (rys. a) moment bezwładności

względem osi Z (oś obojętna) oraz wskaźnik wytrzymałości
przekroju na zginanie wynoszą:

.

6

bh

h

J

W

,

12

bh

J

2

2

1

Z

Z

3

Z







Dla przekroju okrągłego (rys. b)

.

4

r

32

D

D

J

W

,

4

r

64

d

W

2

1

J

3

3

2

1

Z

Z

4

4

0

Z





















O wytrzymałości belki decyduje moment bezwładności prze-

kroju względem osi obojętnej. Z wytrzymałościowego punktu
widzenia naj

bardziej korzystne są te przekroje, których większa

część pola powierzchni położona jest możliwie daleko od osi
obojętnej (rys. c). W praktyce przekrojami przeznaczonymi do
pracy w warunkach zginania są przekroje dwuteowe (na rys. d
pokazano model takiego przekroju). Przekroje dwuteowe (rów-
nież teowe, ceowniki, kątowniki itp.) są przekrojami znormali-
zowanymi (patrz tabele w

yrobów hutniczych). Warto zwrócić

uwagę, że niewłaściwe usytuowanie dwuteownika znacznie
zmniejsza zdolność konstrukcji do przenoszenia obciążeń, np.
obrócenie dwuteownika z rys. d o kąt 90



spowoduje znacz

ące

obniżenie wytrzymałości rzędu kilkudziesięciu procent.

12 Zginanie płaskie belek prostych.doc

142

P

RZYKŁAD

Dla belki wspornikowej obliczyć wymiary
przekroju poprzecznego. Przyjąć naprę-
żenia dopuszczalne



dop

= 140 MPa.

Z wykresu momentów zginających wi-
dać, że maksymalny moment w utwier-
dzeniu wynosi M

max

= P



L = 8 kN



m.

Warunek wytrzymałościowy ma postać:

.

W

M

dop

max









P = 10 kN

L = 0,8 m

d

d=

0,

8d

P



L

Z warunku tego wyznacza się wartość liczbowa wskaźnika wytrzymałości na zginanie:

.

cm

14

,

57

10

140

8

M

W

3

3

dop

max











Dla belki o przekroju pierścieniowym wskaźnik ten wynosi:





.

d

058

,

0

W

,

d

02898

,

0

64

)

d

8

,

0

(

d

J

,

d

5

,

0

J

W

3

4

4

4













Z zależności 0,058 d

3

= 57,14 otrzymuje się: d = 9,95 cm.

P

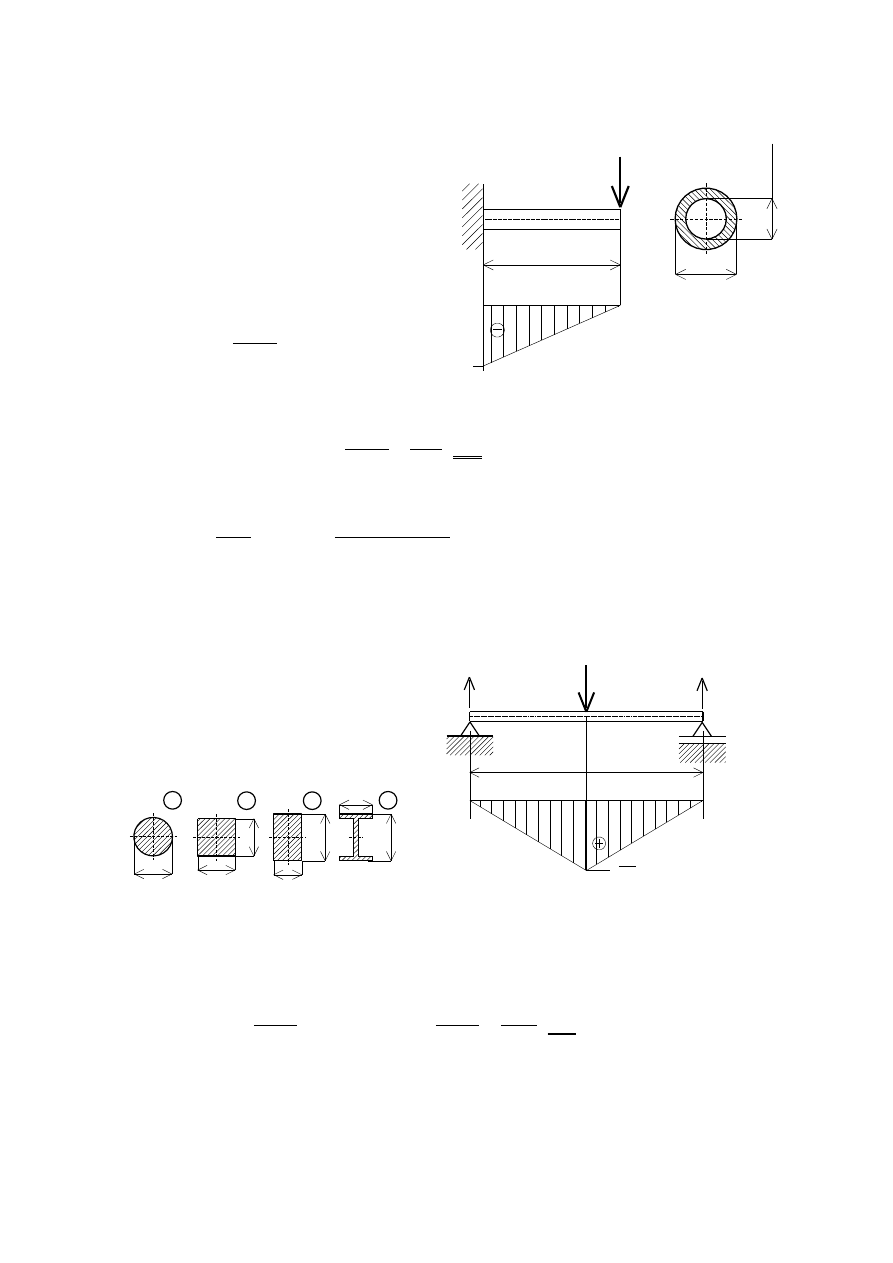
RZYKŁAD

Dla belki jednoprzęsłowej obciążonej
siłą skupioną P określić wymiary 4 ty-
pów przekrojów poprzecznych pokaza-
nych na rysunku. Wybrać przekrój naj-
lepszy z ekonomicznego punktu wi-
dzenia.

d

a

b

2b

h

t

a

1

2

3

4

P = 50 kN

L = 3 m

R

A

B

R

PL

4

= 0,5 P

= 0,5 P

Do obliczeń przyjąć



dop

= 150 MPa.

Z wykresu momentów zginających określić można maksymalna wartość momentu
zginającego M

max

= PL/4 = 50



3/4 = 37,5 kN



m. Z warunku wytrzymałościowego wy-

znacza się wymaganą wartość wskaźnika wytrzymałości na zginanie:

.

cm

250

10

150

5

,

37

M

W

,

W

M

3

3

dop

max

dop

max



















Dla porównania przekrojów wykorzystane zostaną ich pola powierzchni. Dla po-
szczególnych przekrojów otrzymano następujące wartości.

12 Zginanie płaskie belek prostych.doc

143

1. Przekr

ój kołowy

.

cm

46

,

146

4

d

F

,

cm

66

,

13

250

32

W

32

d

,

32

d

W

2

2

1

3

3

3

























2. Przekrój kwadratowy

.

cm

1

,

131

a

F

,

cm

45

,

11

250

6

W

6

a

,

6

a

W

2

2

2

3

3

3

















3. Przekrój prostokątny

.

cm

104

b

2

F

,

cm

21

,

7

250

2

3

W

2

3

b

,

3

b

2

6

)

b

2

(

b

W

2

2

3

3

3

3

2



















4. Przekrój dwuteowy: z tabel wyrobów hutniczych (Polskie Normy) znajduje się dwu-
teownik I220, posiadający wskaźnik W = 278 cm

3

(h = 220 mm, t = 98 mm). Pole po-

wierzchni tego dwuteownika wynosi F

4

= 39,6 cm

2

.

Z porównania pól powierzchni w odniesieniu do dwuteownika

F

1

: F

2

: F

3

: F

4

= 3,70 : 3,31 : 2,63 : 1,00

wynika, że przekrój dwuteowy jest najlżejszy (to porównanie ma więc aspekt eko-
nomiczny).

W zginanej belce występują naprężenia normalne

dop

Z

max

W

M









oraz

naprężenia styczne obliczane ze wzoru

dop

Z

max

max

b

J

S

T













(S

max

– max moment statyczny przekroju). Dla

belki o przekroju dwuteowym na rysunku pokazano rozkłady
naprężeń. W punktach 1 i 3 sprawdzane są warunki na



max

i



max

. Szczególnej uwagi wymaga punkt 2, w którym występują

razem duże wartości



i



- tutaj znajduje zastosowanie hipote-

za Hubera:

.

3

dop

2

2

2

2

red















Rozkłady naprężeń normalnych i

stycznych w dwuteowniku

Z pra

ktyki wiadomo, że naprę-

żenia styczne mają znacznie
mniejszy wpływ niż naprężenia
normal

ne, jednakże sprawdzenie

warunku na maksymalne napr

ę-

żenia styczne



max

, a przede

wszystkim sprawdzenie punk

tów,

w których działają łącznie naprę-
żenia normalne i styczne jest ko-
nieczne.

12 Zginanie płaskie belek prostych.doc

144

ODKSZTAŁCENIA BELEK

Odkształceniami belki są:
– ugięcie belki y, zdefiniowane jako pionowe przemieszczenie

środka ciężkości przekroju poprzecznego belki,

– kąt obrotu przekroju

.

tg

dx

dy









, zdefiniowany jako kąt obrotu

normalnej do przekroju poprzecznego belki lub ze wzgl

ędów

praktycznych

– prostopadłej do normalnej.

Odkształcenia zginanej belki

Obliczanie odkształceń belek możliwe jest za pomocą metody

całkowania tzw. równania różniczkowego linii ugięcia belki. Me-
toda ta pozwala na wyznaczanie ugięcia oraz kata obrotu w
dowolnym przekroju x. W praktyce inżynierskiej stosowane są
również uproszczone metody wyznaczania odkształceń belek.
Jedną z metod jest metoda superpozycji.

Metoda superpozycji obliczania odks

ztałceń belki

Metoda superpozycji

pozwala wyznaczać odkształcenia tylko

w wybranych punktach (np. poparcia, końce belki). Dla szybkie-
go stosowania metody należy korzystać z gotowych rozwiązań
dla podstawowych typów prostych belek (patrz tabela).

12 Zginanie płaskie belek prostych.doc

145

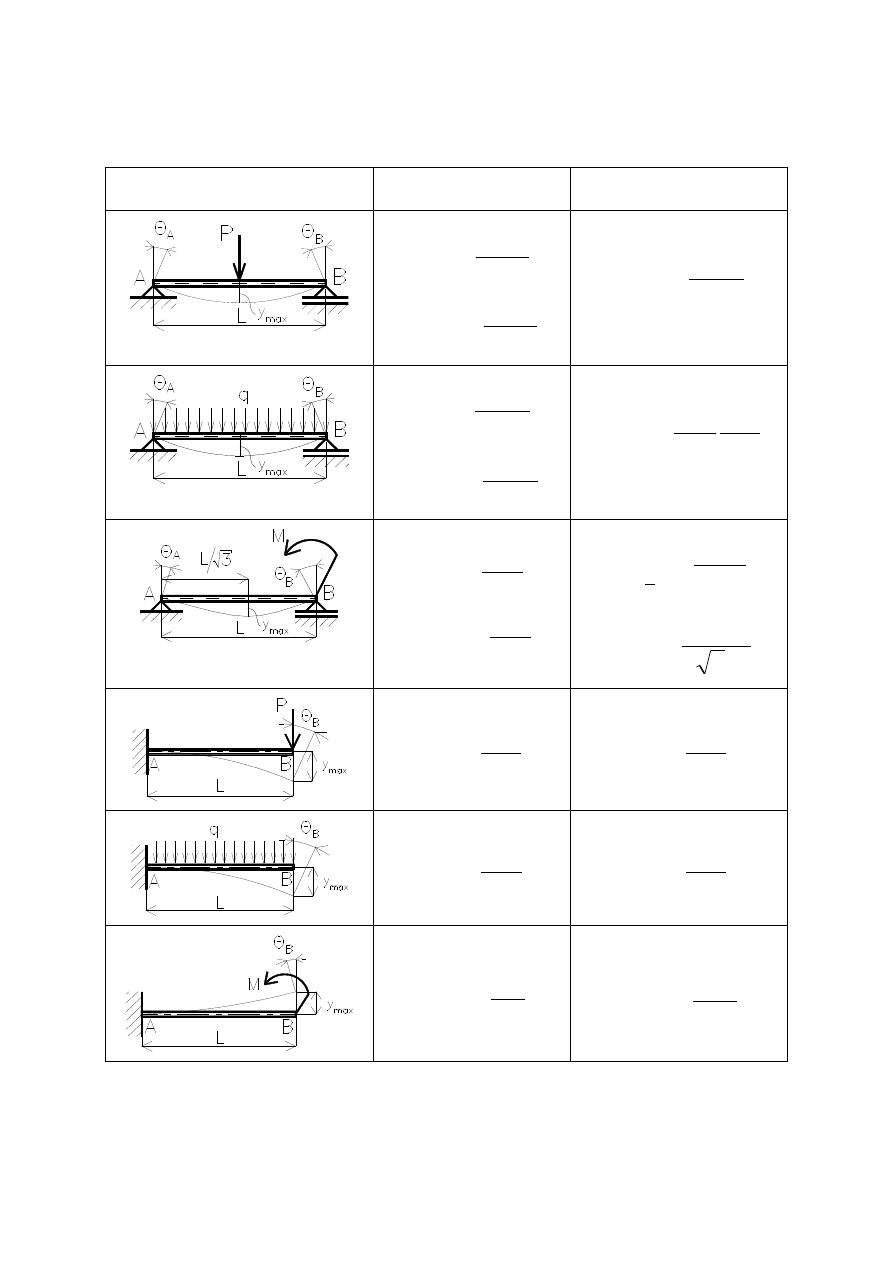
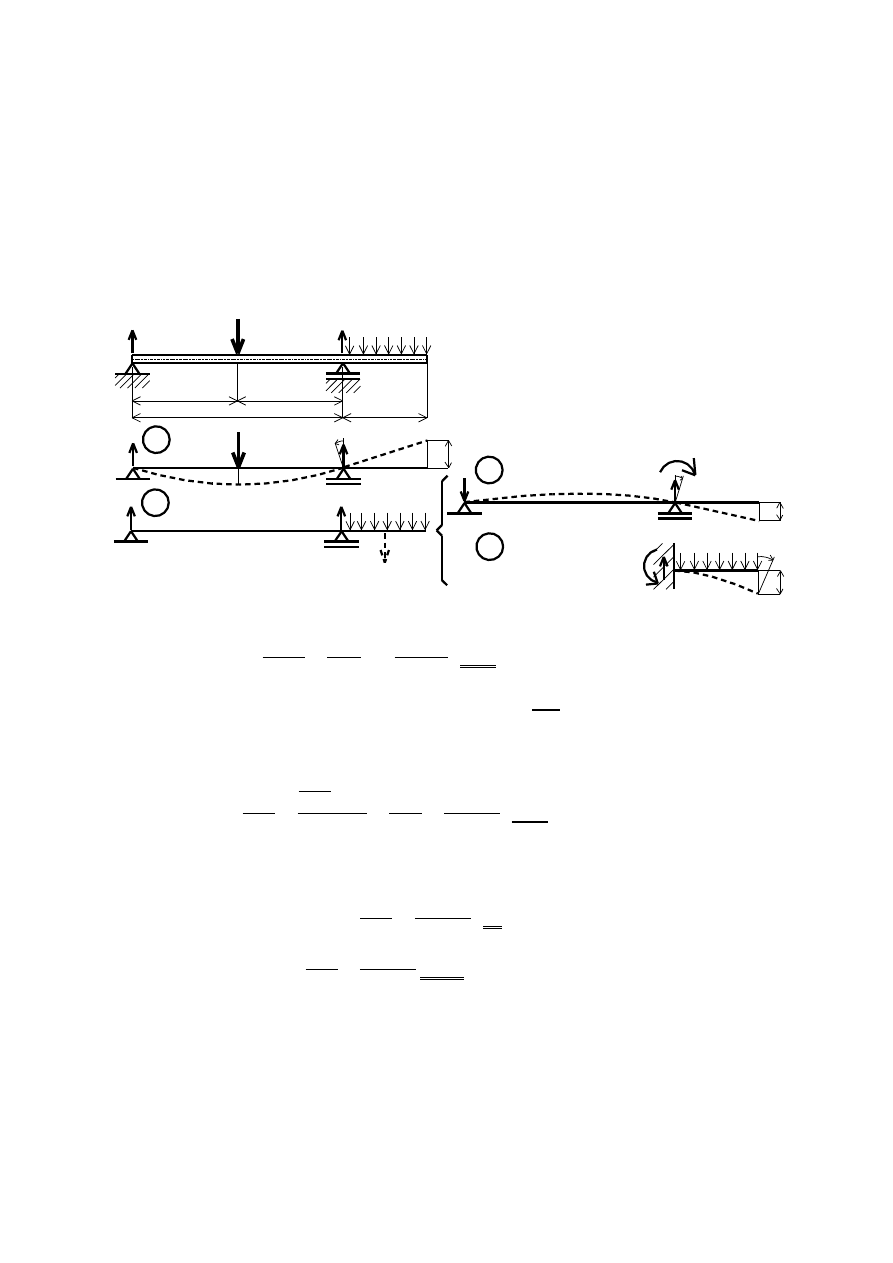
Przemieszczenia prostych belek

Belka

Kąt obrotu

Przemieszczenie

EJ

16

PL

EJ

16

PL

2

B

2

A











EJ

48

PL

y

3

max



dla x = L/2

EJ

24

qL

EJ

24

qL

3

B

3

A











EJ

qL

384

5

y

4

max



dla x = L/2

EJ

3

ML

EJ

6

ML

B

A











EJ

3

9

ML

y

EJ

16

ML

y

2

max

2

L

2

1

x







EJ

2

PL

2

B





EJ

3

PL

y

3

B



EJ

6

qL

3

B





EJ

8

qL

y

4

B



EJ

ML

B







EJ

2

ML

y

2

B





12 Zginanie płaskie belek prostych.doc

146

P

RZYKŁAD

7.8

Dla belki przedstawionej na rysunku

obliczyć ugięcie i kąt obrotu punk-

tu C. Przyjąć: P = 40 kN, q = 2,5 kN/m, EJ = 50 MNm

2

.

Aby zastosow

ać metodę superpozycji, należy rozdzielić obciążenia na

siłę skupioną P oraz obciążenia ciągłe q. Ponieważ q działa na części
belki znajdującej się poza podporami, należy uwzględnić moment M od-
działujący na część belki AB.

A

B

P = 40 kN

L

a = 5 m

b = 4 m

a = 5 m

q = 5 kN/m

R

A

B

R

B1



B2a



B2b



P

1

y

y

2a

2b

y

(qb)

q

q

M = qb /2

2

1

2

2a

2b

1.

Belka obciążona siłą P:





.

mm

20

10

005

,

0

4

a

tg

a

y

,

29

,

0

rad

005

,

0

10

50

4

5

40

EJ

4

Pa

EJ

16

PL

3

1

B

1

B

1

3

2

2

2

1

B





















































2. Belka obciążona rozłożoną równomiernie siłą q.

2a. Odkształcenie przęsła AB:

 

,

12

,

0

rad

00208

,

0

10

50

3

5

5

,

2

EJ

3

qa

EJ

3

a

2

2

qa

EJ

3

ML

3

3

3

2

a

2

B

























.

mm

3

,

8

10

00208

,

0

4

a

y

3

a

2

B

a

2















2b. Odkształcenie wspornika BC:

,

mm

16

10

50

8

4

5

,

2

EJ

8

qa

y

4

4

b

2













.

03

,

0

rad

00053

,

0

10

50

6

4

5

,

2

EJ

6

qa

3

3

3

b

2

B





















Całkowite ugięcie końca C:

.

mm

3

,

4

16

3

,

8

0

,

20

y

y

y

y

b

2

a

2

1

C

















Kąt obrotu przekroju belki na podporze B:





.

17

,

0

12

,

0

29

,

0

a

2

B

1

B

B



























Kąt obrotu przekroju belki na końcu C:

.

17

,

0

03

,

0

17

,

0

b

2

B

B

b

2

B

a

2

B

1

B

C







































12 Zginanie płaskie belek prostych.doc

147

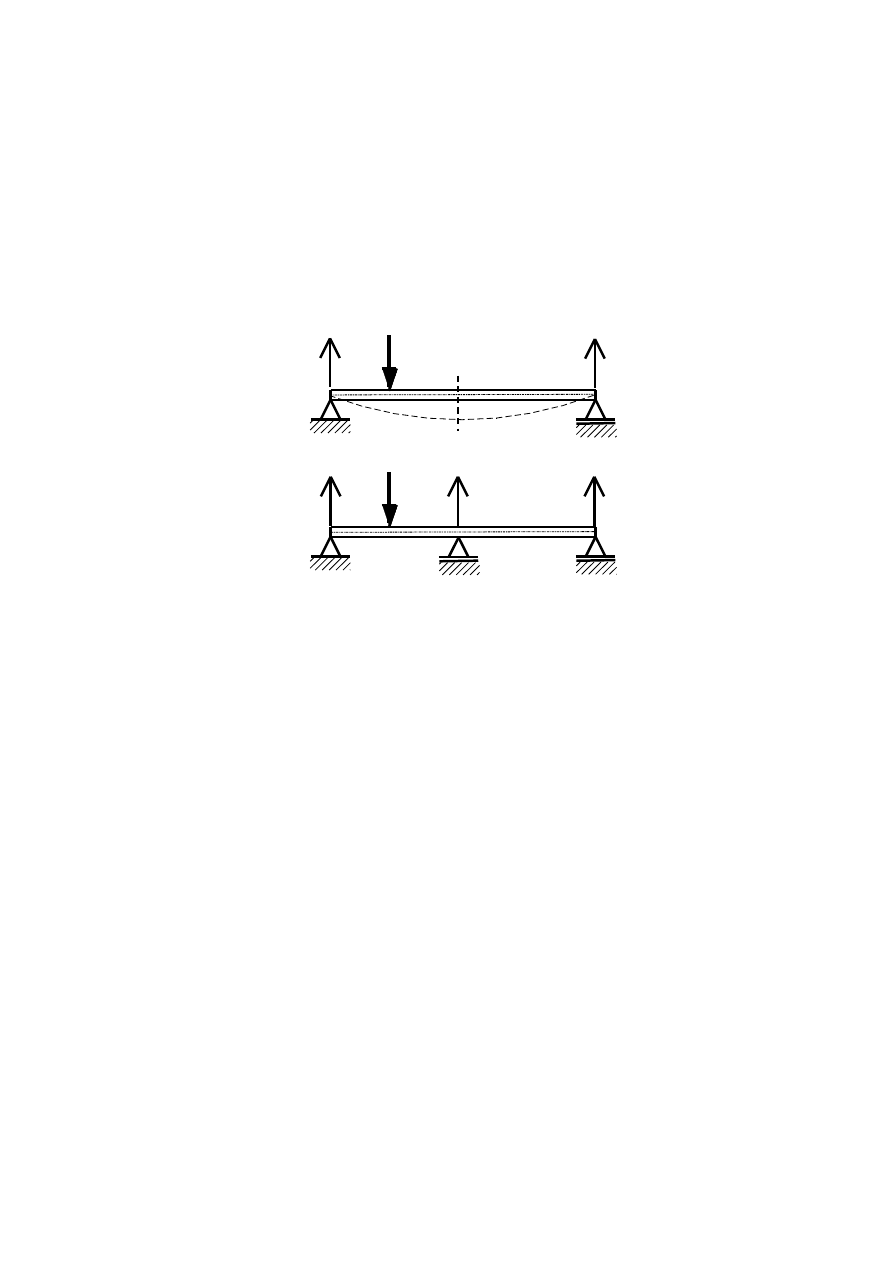
BELKI STATYCZNIE NIEWYZNACZALNE

W belce statycznie niewyznaczalnej liczba niewiadomych reakcji pod-

porowych jest większa od liczby równań statyki. Różnica pomiędzy tymi
wielkościami określa stopień statycznej niewyznaczalności zadania.
Rysunek pokazuje, jak belka statyczne wyznaczalna staje się belką sta-
tycznie niewyznaczalną.

A

C

P

A

B

B

C

P

C

R

A

R

A

R

R

B

R

B

a)

b)

Belka statycznie wyznaczalna i statycznie niewyznaczalna

Belka pokazana na rysunku a jest belką statycznie wyzna-

czalną (płaski układ sił równoległych). Z dwóch równań statyki
wyznacza się reakcje R

A

i R

B

. Ze względów konstrukcyjnych

może się okazać, że ugięcie belki w przekroju C przekracza
wartości dopuszczalne i konieczne jest podparcie belki w tym
punkcie (rys. b). Skutkiem dodatkowego podparcia jest poja-
wienie się trzeciej reakcji R

C

i belka staje się jednokrotnie sta-

tycznie niewyznaczalna.

12 Zginanie płaskie belek prostych.doc

148

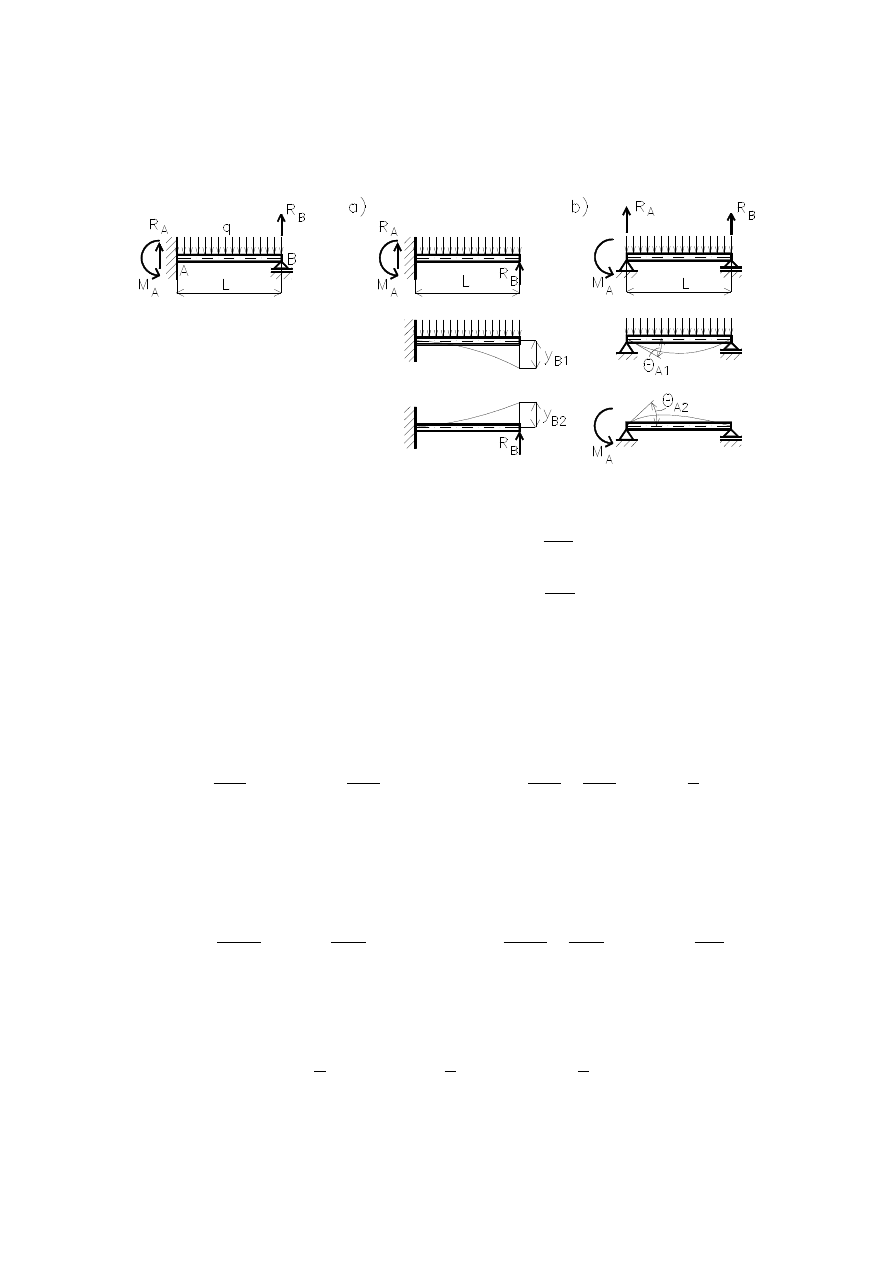
Przykład

Dla belki pokazanej na rysunku

wyznaczyć reakcje, korzystając z me-

tody superpozycji.

Równania równowagi:

,

0

2

qL

M

L

R

0

M

)

1

(

2

A

B

A

























.

0

2

qL

M

L

R

0

M

)

2

(

2

A

A

B

Zdanie jest jednokrotnie statycznie wyznaczalne

– należy ułożyć jedno

równanie geometryczne. Zadanie rozwiązano dwoma sposobami.

1.

Równanie geometryczne y

B

= 0 (rys. a).

Po uwolnieniu belki z podparcia B należy obliczyć jej ugięcie wywołane
obciążeniem q oraz siłą R

B

.

qL

8

3

R

EJ

3

L

R

EJ

8

qL

y

y

,

EJ

3

L

R

y

,

EJ

8

qL

y

B

B

4

2

B

1

B

B

2

B

4

1

B















2.

Równanie geometryczne



A

= 0 (rys. b).

Po uwolnieniu belki z utwierdzenia, należy porównać kąty obrotu na
podporze A:

.

8

qL

M

EJ

3

L

M

EJ

24

qL

,

EJ

3

L

M

,

EJ

24

qL

2

A

A

3

2

A

1

A

A

2

A

3

1

A























Z układu dwóch równań statyki oraz jednego z przedstawionych wyżej

równań geometrycznych otrzymuje się:

.

qL

8

1

M

,

qL

8

3

R

,

qL

8

5

R

2

A

B

A





