Opracowanie zagadnień na egzamin z Nauki o

Materiałach 2009/2010

Agnieszka Wilk, Juliusz Dąbrowa

W opracowaniu tym znajduje się 170 odpowiedzi na pytania podane przez profesora Lisa.
Każde z zagadnień ma w opisie zawarte odniesienia do źródeł, z których korzystano podczas
opracowywania, lub w których można znaleźć inne informacje na dany temat. Odniesienia te
są podane w sposób następujący:

Wykład- W, numer wykładu, numery slajdów

Książki- tytuł, strony

Używane materiały:

CCS- Jerzy Dereń, Jerzy Haber, Roman Pampuch „Chemia ciała stałego” 1975

BiW- Roman Pampuch „Budowa i właściwości materiałów ceramicznych” 1995

MC- Roman Pampuch „Materiały ceramiczne” 1988

ZNoM- Roman Pampuch „Zarys nauki o materiałach. Materiały ceramiczne” 1977

WMC- Roman Pampuch „Współczesne materiały ceramiczne” 2005

Inne źródła są opisywane bezpośrednio.

Celem tego opracowania jest umożliwienie łatwiejszej nauki (nie mylić z żadną). W związku z
tym prosimy, jeśli już ktoś by z tego korzystał, aby nie przerabiać tego tekstu na „pomoce
naukowe” stosowane na egzaminie, zwłaszcza, że odnalezienie paru takich samych ściąg
przez egzaminatora mogło by mieć dość negatywny wydźwięk. Chodzi też o zwykły szacunek
dla cudzej pracy. Jest tego jedna piąta pampucha, to naprawdę nie jest tak dużo.

Autorzy

1.Wymień i zapisz typy defektów punktowych w związku MeX

Defektami punktowymi nazywamy zaburzenia struktury krystalicznej (w porównaniu do idealnej sieci

przestrzennej),których zasięg nie przekracza rozmiarów atomu (jonu). Można wyróżnić:



Wakancje (V) – brak atomu w węźle sieci: V

Me

X, MeV

X



Atom (jon) w niewłaściwym położeniu: MeX→XMe



Atomy (jony) w położeniach międzywęzłowych: Me

i

, X

i



Defekty ładunków: elektrony e

-

i dziury h

•

W przypadku kryształów jonowych, konieczne jest zachowanie stosunku liczby kationów i anionów (musi być zachowana
elektroobojętność), w związku z czym powstają defekty będące kombinacją prostych defektów punktowych.



Defekt Frenkla- powstaje kation międzywęzłowy: Me

M

→

+



Defekt Antyfrenkla- powstaje anion międzywęzłowy: X

X

→ +



Defekt Schottkie’go- wyjście atomów na powierzchnię: zero→

+



Defekt Antyschottkie’go- wejście atomów w pozycje międzywęzłowe: MeX→

+

Te defekty, które występują w nieobecności atomów obcych (domieszek), nazywamy defektami

rodzimymi. W każdym krysztale występuje określone stężenie defektów, co wynika z dążenia

do stanu równowagi. Mianowicie wywołany przez obecność defektów przyrost entropii

konfiguracyjnej powoduje, że -przy niewielkim wzroście entropii- entalpia swobodna

krystalicznego materiału obniża się. Wynika to ze wzoru: ∆G= H-T∆S . Człon T∆S rośnie szybciej

niż H, G maleje co jest korzystne energetycznie (ciut dokładniej-punkt 3.).

W2,7-8; WMC s46; BiW s51-52; MC s42-43

2.Podaj znane Ci właściwości tworzyw zależne od rodzaju i stężenia defektów punktowych.

Podstawowe właściwości fizykochemiczne danego związku można w szerokich granicach modyfikować,

wprowadzając do jego sieci krystalicznej odpowiednie domieszki. Można stwierdzić, że dodatek jonu metalu o
wartościowości wyższej od wartościowości kationów macierzystych powoduje w przypadku związków typu Me

1+y

X lub

MeX

1-y

spadek stężenia kationów międzywęzłowych lub luk anionowych przy równoczesnym wzroście stężenia swobodnych

elektronów (półprzewodnik typu n), podczas gdy dodatek kationów o wartościowości niższej wywiera wpływ odwrotny. W
przypadku związków typu Me

1-y

X lub MeX

1+y

dodatek jonów o wartościowości wyższej powoduje wzrost stężenia luk

kationowych lub międzywęzłowych anionów przy równoczesnym spadku stężenia dziur elektronowych. Dodatek natomiast
kationów o wartościowości niższej wywiera wpływ przeciwny. Domieszki muszą jednak tworzyć z kryształem roztwór stały
oraz zajmować położenie węzłowe. Tworzeniu się defektów typu Schottky’ego towarzyszy zmniejszanie się gęstości
kryształu (rośnie objętość kryształu). Powstanie defektów typu Frenkla lub anty-Frenkla nie powoduje zmiany gęstości
kryształu. Bez defektów nie istniałaby elektronika, metale byłyby silniejsze, ceramika nie pękałaby, kryształy byłyby
bezbarwne.

Defekty mogą wpłynąć w dwojaki sposób na przewodnictwo elektryczne:

I. mogą zmniejszyć przewodnictwo metalu (zwiększyć jego opór)

II mogą zwiększyć przewodnictwo:

1. mogą zwiększyć przewodnictwo elektronowe (w półprzewodnikach, czyli materiałach kowalencyjnych);

2. mogą zwiększyć przewodnictwo jonowe (w materiałach jonowych).

Defekty są niezbędne aby zachodziły zjawiska dyfuzji.

Domieszki absorbują (i emitują) światło o innej długości fali niż idealna substancja krystaliczna. Wskutek tego domieszki
mogą zmienić kolor kryształu.

3.Jak stężenie wakacji zależy od temperatury?

Jak było już napisane w każdym krysztale występuje określone stężenie defektów, co wynika z dążenia do stanu

równowagi. Entropia konfiguracyjna układu S

k

jest miarą logarytmu naturalnego liczby możliwych konfiguracji P, za

pomocą których można zrealizować dany stan: S

k

=k lnP gdzie k- stała Boltzmanna. W krysztale zbudowanym tylko z

jednego rodzaju atomów istnieje tylko jeden możliwy ich układ, dlatego, że atomy są traktowane jako nierozróżnialne-
obojętnie gdzie damy atom Jaś i tak cała struktura to same Jasie więc to bez znaczenia. Jeśli natomiast mamy w krysztale n
defektów punktowych np. wakancji, to możemy je ułożyć w węzłach sieci przestrzennej na wiele rozróżnialnych sposobów.
Wywołany tym przyrost S

k

dany jest: S

k

=-k[N ln{N/(n+N)}+n ln{n/(N+n)}] gdzie N- liczba atomów, n- liczba wakancji.

Zdefektowanie punktowe powoduje wzrost entalpii kryształu ∆H

v

, więc można teraz zapisać zmianę entalpii swobodnej

spowodowaną przez powstanie wakancji: ∆G

v

=n∆H

v

-T(n∆S

osc

+∆S

k

) (wzór ∆G=H-T∆S )czyli

∆G

v

=n∆H

v

-nT∆S

osc

+kT[N ln{N/(n+N)}+n ln{n/(N+n)}] gdzie T- temperatura w [K], ∆S

osc

- zmiana entropii oscylacyjnej atomów

sąsiadujących z wakancją. W tym ostatnim składniku liczniki w logarytmach są mniejsze od mianowników, więc wartości
logarytmu będą ujemne-zatem im większa będzie liczba wakancji n tym bardziej ujemny będzie ten czynnik. Zatem cała ta
funkcja opisująca zależność entalpii swobodnej od liczby wakancji przechodzi gdzieś przez minimum przy jakiejś wartości n.

Warunek minimum można zapisać jako: =0, odpowiada to stanowi równowagi i po rozwiązaniu mamy że

n/(n+N)=[V

v

]=exp(∆S

osc

/k)exp(-∆H

v

/kT) gdzie [V

v

] to stężenie wakancji jako ułamek molowy. Utworzenie wakancji niewiele

zmienia objętość kryształu, ∆H

v

jest praktycznie równe energii tworzenia jednej wakancji E

v

, więc po pół strony

niepotrzebnych rzeczy można zapisać że [V

v

]

~

exp(-E

v

/kT). Im większe wartości T będziemy wstawiać, tym większą wartość

będzie miało całe wyrażenie- ze wzrostem temperatury wzrasta stężenie wakancji.

W2,9; WMC s46; BiW s52 ; MC s43-45

4.Scharakteryzuj defekty liniowe.

Defektem liniowym (dyslokacją)nazywamy zakłócenie periodycznej budowy sieci krystalicznej rozciągające się

wzdłuż pewnej linii atomów lub jonów. Istnieją dwa podstawowe typy defektów liniowych:



Dyslokacja krawędziowa



Dyslokacja śrubowa

W dyslokacji krawędziowej, pod linią O-O zwana także linia dyslokacji, kryształ ma

niezaburzoną budowę. W tym rodzaju dyslokacji przesuniecie następuje w kierunku

prostopadłym do linii dyslokacji. Wzdłuż dyslokacji krawędziowej można wyróżnić linię

atomów z których każdy ma o jeden skoordynowany atom mniej niż w przypadku

struktury idealnej. W dyslokacji śrubowej, przesunięcie następuje natomiast

równolegle do linii dyslokacji, wzdłuż tej dyslokacji nie zmienia się

liczba skoordynowanych atomów, natomiast skręceniu ulegają płaszczyzny atomowe

a zespoły koordynacyjne są zniekształcone. Aby charakteryzować defekty liniowe,

można użyć tzw. wektora Burgersa. Używamy do tego pętli z odcinków

równych wektorowi translacji kryształu, leżących w płaszczyźnie

prostopadłej do linii translacji. Obwód Burgers ulega zamknięciu gdy

w obwiedzionym obszarze nie ma dyslokacji. Jeśli jest, to do zamknięcia

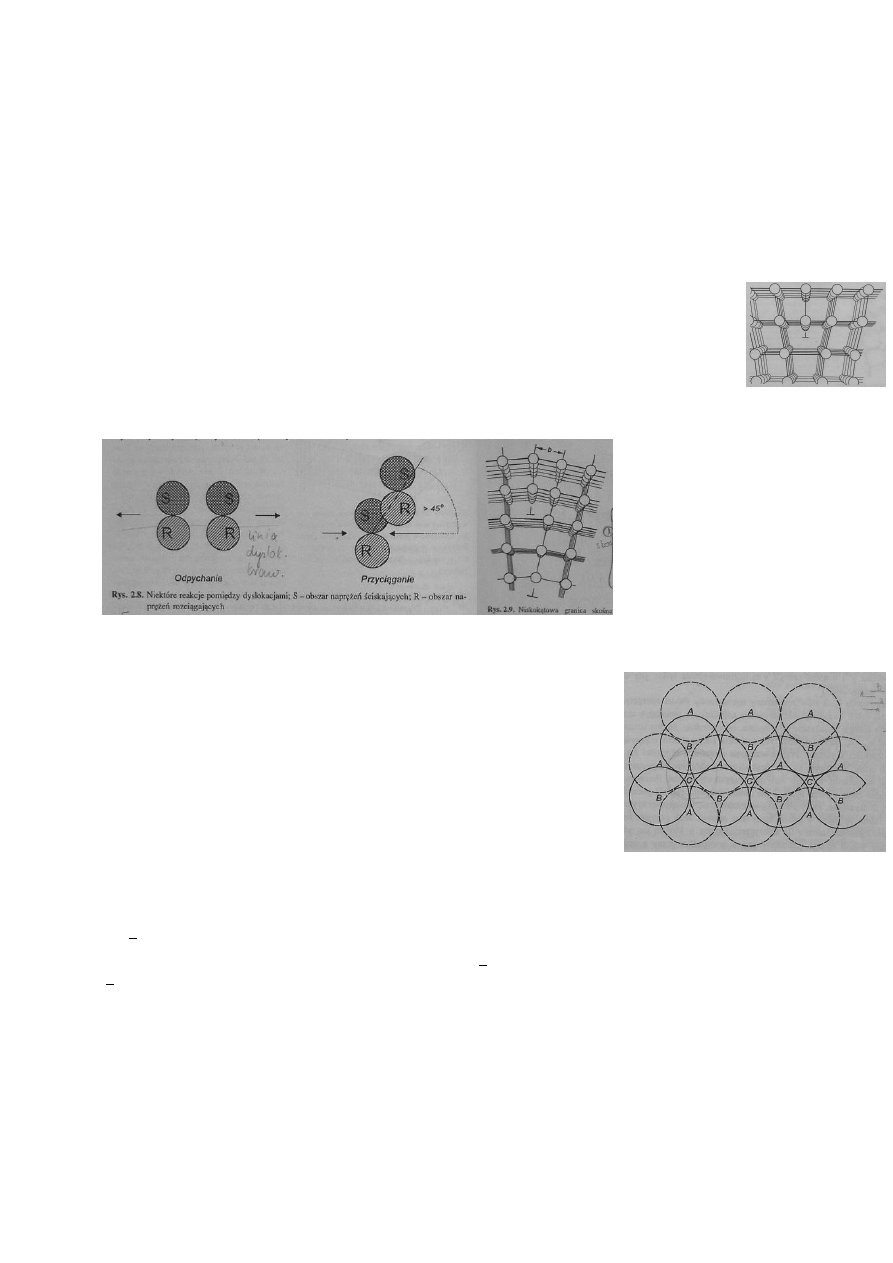
obwodu potrzeba wektora zwanego wektorem Burgersa (s). Dla dyslokacji śrubowej jest on zwrócony

równolegle do linii dyslokacji, dla krawędziowej-prostopadle. Ze względu na statystyczne rozmieszczenie

dyslokacji w krysztale można zakładać, że liczba dyslokacji przecinających jednostkową powierzchnię kryształu równa jest
ich gęstości.

W2,12; BiW s55-57; WMC s47-49; MC s55-66

5.Scharakteryzuj defekty płaskie.

Defekty płaskie maja swoje źródło w defektach liniowych. Rozpatrzmy przypadek dyslokacji

krawędziowej. Jak widać na obrazku obok, odległości międzyatomowe nad linia dyslokacji są mniejsze, a pod linia
większe od równowagowych. Oznacza to że w jednym obszarze mamy naprężenia ściskające w drugim
rozciągające. Dyslokacje o podobnych rozkładach naprężeń będą się odpychać, ponieważ nałożenie się obszarów
identycznych naprężeń zwiększałoby energię. Jeśli natomiast dyslokacje występują na różnych poziomach
struktury to przyciągają się bowiem nałożenie pola rozciągającego ze ściskającym zmniejsza wielkość naprężeń i
obniża energię. To przyciąganie powoduje układanie się dyslokacji jedne nad drugimi-powstają defekty płaskie. Można
wyróżnić parę rodzajów:



Niskokątowe granice daszkowe -rozdzielają nanostrukturę na dwie części w których płaszczyzny atomów są do

siebie nachylone pod niewielkim kątem. Pochodne dyslokacji krawędziowych.



Niskokątowe granice skręcenia. Pochodne dyslokacji śrubowych

Tworzenie się defektów płaskich powoduje, że rzeczywista struktura krystaliczna składa
się z wielu bloków o różnej orientacji tworząc tzw. strukturę mozaikową. Istnieje jeszcze
jeden rodzaj defektów płaskich- błędy ułożenia.

Weźmy płaszczyznę kryształu, określając środki jej atomów literą A. Drugą warstwę atomów
można

ustawić na niej tak, że środki jej atomów znajdą się w punktach B lub C. Jeśli położymy np.
w punktach B,

to możemy następną, trzecia warstwę znów ułożyć w punktach A. Uzyskamy sekwencje
ABABAB

(typowe dla kierunku [0001] w układzie heksagonalnym]. Równie dobrze można trzecia
warstwę położyć

w punktach C. Powstanie sekwencja ABCABC ([111] regularny). Jednak mogą się pojawić zaburzenia,

np. w układzie heksagonalnym powstanie sekwencja ABABCBCB, a w układzie regularnym może wystąpić sekwencja
ABCACBA. Można zauważyć w tym drugim przypadku, że środkowy atom jest czymś w rodzaju lustra.

Rezultatem tego jest powstawanie po dwóch stronach płaszczyzny A, struktur będących lustrzanym odbiciem względem
A- powstanie tzw. granica bliźniacza. Oprócz tego trzeba pamiętać, iż każda zewnętrzna powierzchnia kryształu jest
defektem płaskim.

W2,13-15; MC s66-73; BiW s57-60\

6.Podaj znane ci właściwości tworzyw zależne od występowania defektów liniowych i
płaskich.

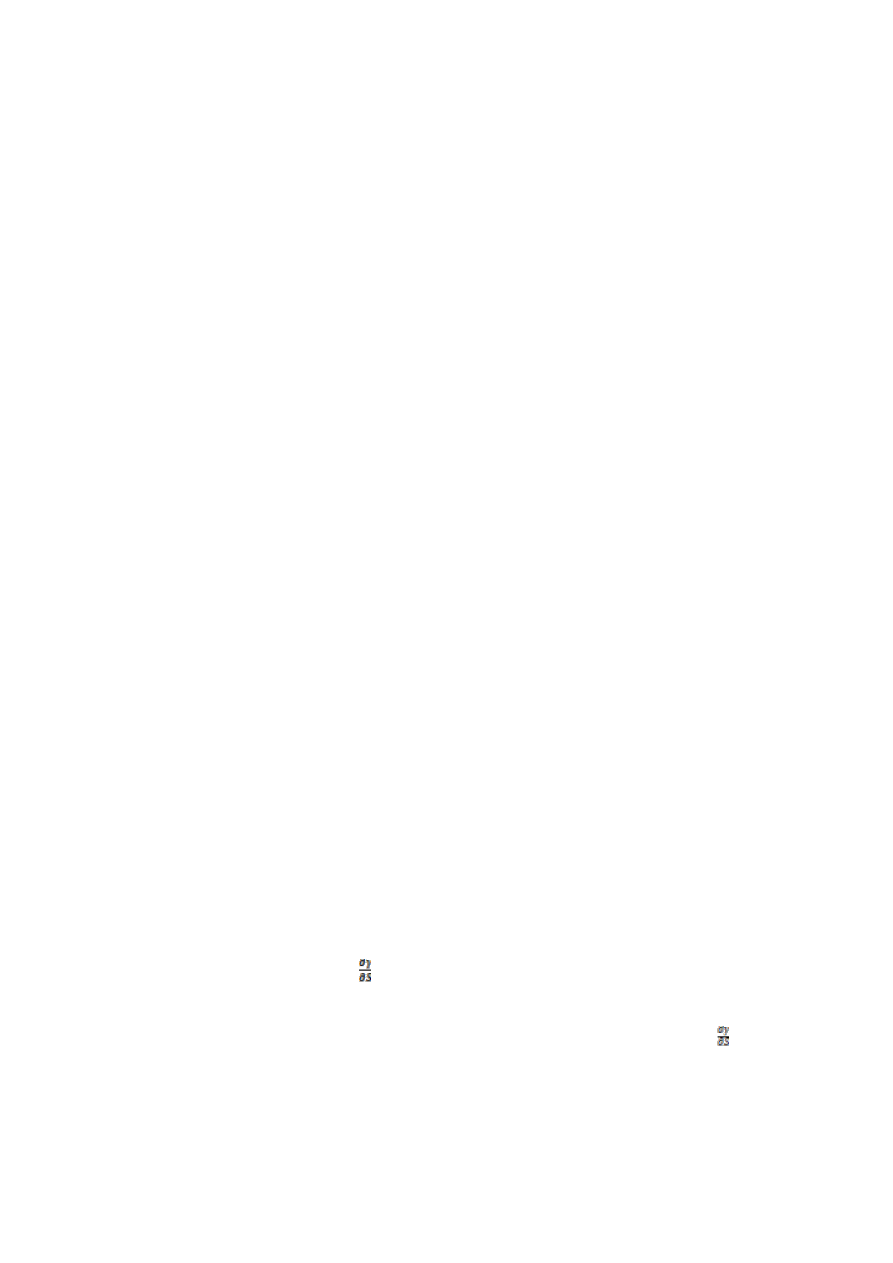
Dyslokacje mają swój udział w deformacji plastycznej ciał stałych, a w szczególności metali. Ich obecność wpływa

również na kinetykę wzrostu kryształów oraz na takie właściwości jak przewodnictwo elektryczne oraz ruchliwość
poszczególnych elementów sieci. Obecność dyslokacji w ciele stałym pogarsza jego właściwości sprężyste np. chlorek
srebrowy w temperaturze pokojowej ma konsystencję ciasta i można go walcować na cienki warstwy. Podobnie kryształy
aluminium. Obliczenia granic sprężystości kryształów, oparte na założeniu idealnej budowy sieci krystalicznej, doprowadziły
do wartości 10

3

-10

4

razy większych od wartości obserwowanych. Znaczne przesycenie konieczne do wzrostu kryształów

doskonałych wiąże się z trudnością powstania nowej płaszczyzny sieciowej, na równej powierzchni kryształu. Trudność ta
nie występuje, gdy występują dyslokacje śrubowe-następuje spiralne rozbudowanie się schodka dyslokacji śrubowej.
Obecność defektów liniowych w krysztale może być przyczyną defektów punktowych, mogących poruszać się w sieci
krystalicznej ruchem dyfuzyjnym. Wiadomo, że wytrzymałość pojedynczych kryształów jest mniejsza niż materiałów
polikrystalicznych, ponieważ zaburzenia budowy sieciowej na granicach ziaren umacniają metal. Wiadomo też, że kryształy
zawierające dużą liczbę defektów są bardziej wytrzymałe od kryształów z małą liczbą defektów. Dzieje się tak dlatego, że w
przypadku dużej liczby defektów sieciowych ruch dyslokacji jest hamowany na skutek wzajemnego przecinania się dyslokacji
(powstają dyslokacje nie tylko równolegle do siebie, ale również umiejscowione w różnych płaszczyznach i o różnych
kierunkach), ich grupowania się, a także obecności przeszkód w postaci innych defektów sieciowych, np. obcych atomów.
Wynika z tego, że wytrzymałość rzeczywista metali zmniejsza się wraz ze zwiększaniem liczby (gęstości) dyslokacji i innych
defektów sieciowych, tylko do pewnej granicy i po osiągnięciu minimalnej wartości, przy tzw. krytycznej gęstości dyslokacji
zaczyna ponownie wzrastać.

7.Co to jest energia powierzchniowa?

Energia powierzchniowa jest zmiana całkowitej energii kryształu w wyniku utworzenia jednostkowej

powierzchni granicy rozdziału ciało stałe- próżnia. Jak już powiedziano powierzchnia kryształu jest defektem. Na atom we
wnętrzu struktury działają ze wszystkich stron siły wzajemnego oddziaływani z sąsiadami. Atomy powierzchniowe części
tych sąsiadów nie posiadają. Tworząc wiązania atom zmniejsza energie swoich elektronów, zatem atom powierzchniowy
nie mogąc wytworzyć wszystkich wiązań z braku kolegów, musi mieć nadmiarowa energie względem nich. Można
powiedzieć, że entalpia swobodna każdego ciała stałego składa się z dwóch składowych: entalpii swobodnej struktury
krystalicznej, oraz nadmiarowej entalpii swobodnej warstw przypowierzchniowych. Ten nadmiar w przeliczeniu na
jednostkę powierzchni nazywamy energia powierzchniową. Energia powierzchniowa γ jest wielkością skalarną, jej
jednostką jest J/m

2

. Przykładowe wartości dla niektórych materiałów:



ZrO

2

(M)-1,13



Diament-5,3-9,8 (zależnie od płaszczyzny krystalograficznej)



Szkło kwarcowe-0,44



γ-TiC-4,6

W2,16-17; MC s73

8.Co to jest napięcie powierzchniowe, podaj relację pomiędzy energia powierzchniową a
napięciem powierzchniowym.

Jest to wielkość wektorowa. O ile energia powierzchniowa jest zmiana całkowitej energii kryształu w wyniku

utworzenia jednostkowej powierzchni granicy rozdziału ciało stałe- próżnia o tyle napięcie powierzchniowe γ’ jest siłą
potrzebna do zwiększenia wielkości powierzchni o jednostkę. Moduł napięcia powierzchniowego można powiązać z

energia powierzchniową zależnością: Iγ’I=γ+S

gdzie S to wielkość powierzchni. Gdy rozciągamy powierzchnię powoduje

to zwiększanie się odległości międzyatomowych, zaś liczba atomów pozostaje taka sama-czyli na większą powierzchnie
przypada po rozciągnięciu tyle samo atomów co wcześniej-maleje zatem N

p

(atomy/powierzchnie). O ile dla cieczy czy

gazów N

p

nie ulega zmianie, ze względu na ruchliwość atomów (trudno rozciągać powierzchnie cieczy), a zatem

=

0 i Iγ’I=γ,

o tyle dla ciał stałych N

p

będzie się zmieniać, więc ten drugi człon będzie znaczący. W przypadku ciał stałych napięcie i

energia są sobie liczbowo równe wtedy tylko, gdy zmiany rozwinięcia powierzchni zachodzą wskutek powolnych
procesów o prędkościach porównywalnych z dyfuzją, tzn. gdy procesy uzupełniania liczby atomów powierzchniowych
zachodzą podobnie jak w cieczy czy gazie. Trochę to zagmatwane.

MC s77-78.

9.Wyprowadź zależność na siłę napędową krystalizacji.

Siłą napędową procesu krystalizacji jest obniżanie się entalpii swobodnej układu. Dowolna przemianę fazową

możemy opisać wyrażeniem ∆G

r

= (μ

1

-μ

2

)∆n + γS, gdzie μ- potencjały chemiczne faz, ∆n- liczba moli tworzącej się fazy, γ-

energia powierzchniowa i S-powierzchnia. Pierwszy człon określa zmianę energii swobodnej związaną z powstawaniem
objętości nowej fazy, drugi człon natomiast, określa prace potrzebną do utworzenia granicy rozdziału fazy tworzącej się i
pierwotnej. Czyli ogólnie można to zapisać tak: ∆G

r

= ∆G

v

+∆G

s

. Teraz musimy uczynić parę założeń:



Zarodek nowej fazy krystalicznej powstaje w formie kulistych zarodków



Zmniejszenie energii swobodnej dzięki powstaniu fazy stałej o mniejszej energii swobodnej jest proporcjonalne
do objętości zarodka.



Wzrost energii swobodnej wskutek powstania granicy miedzy fazami jest proporcjonalny do powierzchni zarodka

oraz do energii powierzchniowej γ.

Możemy teraz zapisać, że ∆G

v

= πr

3

∆G gdzie ∆G to zmiana potencjału termodynamicznego podczas przejścia objętości fazy

nietrwałej w trwałą, oraz że ∆G

s

=4πr

2

γ. Zatem składając całość do kupy, otrzymujemy że zmiana entalpii swobodnej

towarzysząca zarodkowaniu wynosi ∆G

r

= πr

3

∆G+4πr

2

γ

W2,22-23; CCS s406; wykład z politechniki wrocławskiej

10.Wyprowadź zależność na wielkość zarodka krytycznego krystalizacji.

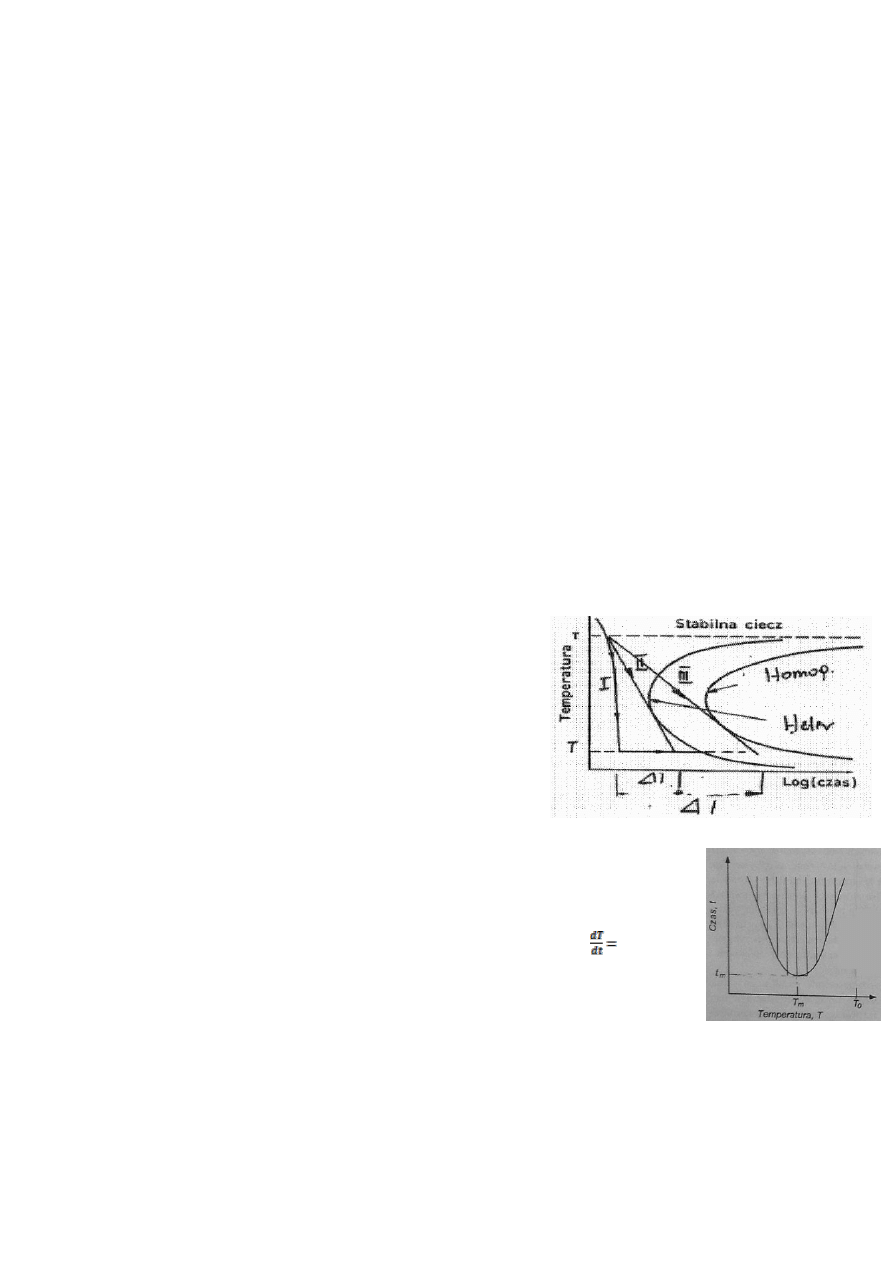
Aby zrozumieć jak wielkość zarodka wpływa na samorzutność krystalizacji warto przytoczyć wykres ∆G(r).

Jeśli zarodek jest kulisty, to zmianę potencjału termodynamicznego ∆G

r

towarzyszącą utworzeniu

zarodka fazy ciekłej o promieniu r można wyrazić równaniem: ∆G

r

= πr

3

∆G+4πr

2

γ gdzie ∆G to zmiana

potencjału termodynamicznego podczas przejścia objętości fazy nietrwałej w trwałą. Pierwszy człon
jest związany z tworzeniem się objętości fazy o niższym potencjale termodynamicznym (∆G<0) zatem
ze wzrostem r człon ten będzie bardzo gwałtownie maleć (r jest w potędze trzeciej, ∆G jest ujemne),
drugi z tworzeniem się powierzchni rozdziału (powierzchnia rośnie ze wzrostem promienia, ale r jest tylko
w drugiej potędze). Zatem sumarycznie: po przekroczeniu pewnej krytycznej wartości r*, pierwszy,
ujemny człon zacznie przeważać- ∆G

r

będzie maleć, czyli proces stanie się samorzutny. Natomiast w

początkowej fazie wzrostu zarodka, przy małym zarodku następuje przyrost ∆G- zarodki mogą się
tworzyć tylko tam gdzie atomy maja wyższą energie niż średnia energia atomów w objętości- np.
w wyniku fluktuacji ciepła. Te małe zarodki maja tendencje do zanikania, aby mogły urosnąć do tej
krytycznej wielkości r* trzeba im dostarczyć dość energii -po przekroczeniu r* reszta idzie z górki. Wielkość przyrostu
potencjału termodynamicznego (naszego ∆G

r

), potrzebną do utworzenia zarodka o promieniu r*, możemy uzyskać

przyrównując pochodną

do 0 (jeśli pochodna się zeruje to mamy ekstremum, w tym wypadku nasza wartość ∆G

r

zaznaczona na wykresie). No więc wstawiamy do naszego równania na ∆G

r

, r=r* i robimy

pochodną:

=0=4π(r*)

2

∆G+8πr*γ ,z której łatwo policzyć że r*=-

Dodatkowo patrząc do wykładu, można zapisać,

że ∆G=-

(T-T

m

),( gdzie T

m

-temperatura topnienia) co można wstawić do otrzymanego wcześniej wyniku.

W2,22-23; ZNoM s211-212

11.Przedstaw wykres zależności szybkości tworzenia zarodków od temperatury

Ten i następny punkt są niestety dosyć dziwne i nie do końca wiadomo czy w punkcie 12 nie ma odpowiedzi na 11.

12.Przedstaw wykres zależności szybkości wzrostu kryształów od temperatury

Wykres ten możemy rozbić na dwie części-opisującą V

1

i opisującą V

2

.

V

1

-Popatrzmy na pierwszy człon równania z punktu 10. Występuje w nim czynnik

∆G. Im większe będzie przechłodzenie układu, tym ten czynnik będzie bardziej ujemy-
oznacza to, że zarówno r* jak i bariera potencjału ∆G

r

ulegną zmniejszeniu-ponieważ

łatwiej jest utworzyć mniejszy zarodek, to w miarę wzrostu przechłodzenia układu,
coraz łatwiej będą powstawać zarodki o rozmiarach krytycznych, zatem krystalizacja
będzie łatwiejsza i szybsza. Jednak w pewnym momencie (w punkcie d), wzrost
przechłodzenia nie pociąga już za sobą wzrostu prędkości krystalizacji. Przyczyna jest
prosta-aby mógł powstać jakikolwiek zarodek atomy muszą się ruszać, tworzyć
ugrupowania. W niskiej temperaturze, spada ruchliwość atomów, zarodki tworzą się
coraz trudniej z powodu niedostatecznego dopływu koniecznych do wzrostu atomów. Można zapisać że:

V

1~

exp(

)

oraz

V

2~

exp(

) gdzie T

m

-temperatura topnienia

Zatem szybkość tworzenia się zarodków jest wypadkową tych dwóch prędkości i posiada ekstremum w punkcie d.
W2,24; ZNoM s211

13.Podaj regułę określającą szybkość wzrostu ścian kryształu (Gibbsa-Curie-Wulffa)

Reguła GCW mówi, że ściany kryształu rosną z szybkościami proporcjonalnymi do ich energii

powierzchniowej: V

1

:V

2

:V

3

=γ

1

:γ

2

:γ

3.

Wynika to z faktu, iż

pewne ściany przyłączają dużo łatwiej atomy niż

inne, czynnikiem o tym decydującym jest stosunek liczby najbliższych sąsiadów danego atomu w płaszczyźnie
równoległej do granicy rozdziału (oznaczamy tą liczbę literą w) do liczby najbliższych sąsiadów danego atomu
po przyłączeniu do struktury krystalicznej (u= w + sąsiedzi w podłożu krystalicznym do którego atom się
przyłączył). Ten stosunek w/u, decyduje o tym, jak łatwo będzie się tworzył występ na gładkiej powierzchni
kryształu. Stadium tworzenia się takiego występu determinuje natomiast ogólną szybkość rozrostu całej
ściany kryształu, im łatwiej tworzy się występ tym szybciej rośnie ściana. Takie występy (zarodki
dwuwymiarowe), tworzą się łatwiej jeśli stosunek w/u jest mały, w związku z czym na początku najszybciej
będą rosnąć ściany spełniające ten warunek. Jeśli przyłączany atom, ma niski stosunek w/u,
oznacza to, że wytwarza on mało wiązań-ma zatem dużą energię. Czyli jest powiązanie między V a γ. W
początkowym stadium rozwoju będą zatem dominować ściany o dużej energii powierzchniowej- dużej prędkości wzrostu.
Z czasem jednak, zaczynają w zewnętrznym pokroju kryształu dominować ściany wolniej rosnące, co obrazuje rysunek.
Ogólnie napisane to jest w wielkim skrócie, więcej informacji o wyprowadzeniu całej tej zależności, można znaleźć w ZNoM
na stronach 213-219.
ZNoM s218; W2,26-27; CCS s416

14.Opisz metody tyglowe otrzymywania monokryształów.

Znów nie za bardzo wiadomo o co chodzi, następne 3 punkty o tym są.

15.Omów metodę Bridgmana otrzymywania monokryształów.

Metoda Bridgmana jest metodą pozwalającą na uzyskanie

monokryształów wszystkich podstawowych grup materiałów-metali,
stopów, półprzewodników, tlenków, materiałów organicznych,
kryształów jonowych. Jej przebieg jest opisany na rysunku.
Zalety:



Kształt kryształu zależy od kształtu naczynia



Małe naprężenia termiczne-mało dyslokacji indukowanych



Proces nie wymaga dużej dbałości



Niski poziom konwekcji

Wady



Wzrost jest ograniczony przez ciśnienie jakie wywiera

pojemnik na kryształ w czasie chłodzenia



Trudności w produkcji na dużą skale-trzeba przygotować zarodki,

uszczelnić tygle itd.

16.Omów metodę Czochralskiego otrzymywania monokryształów.

Metoda Czochralskiego jest procesem otrzymywania monokryształów, bardzo często używanym do otrzymywania

monokryształów krzemu na skalę przemysłową, ale również można ja stosować do otrzymywania monokryształów metali i
stopów. Tygiel w którym znajduje się materiał jest zazwyczaj zbudowany z grafitu, kwarcu, lub innego żaroodpornego
materiału nie wchodzącego w reakcje ze stopem, który utrzymywany jest tuz powyżej temperatury topnienia. Otrzymywane
w tej metodzie kryształy cechuje wysoka czystość i doskonałość. Otrzymywany monokryształ ma orientacje
krystalograficzną zarodka.

Zalety



Wzrastający kryształ jest ciągle widoczny-łatwa kontrola



Otrzymywane kryształy są duże-łatwo produkował na wielka skalę



Otrzymywane kryształy mają określona orientacje krystalograficzną



Wysoka czystość

Wady



Duże naprężenia termiczne



Konieczność ciągłej kontroli i wysokiej staranności



Konieczność rotacji kryształu

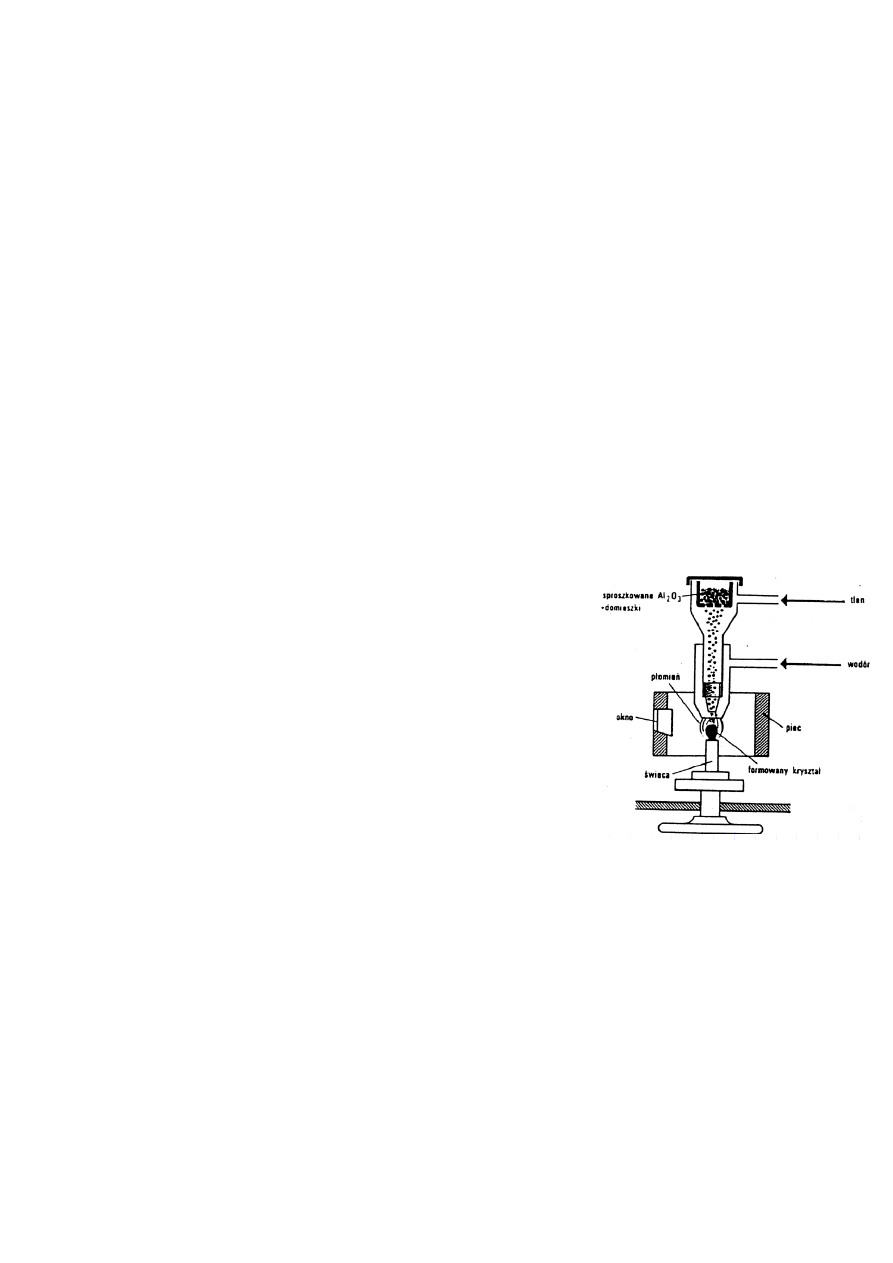
17. Omów metodę Verneuila otrzymywania monokryształów.

Metoda Verneuila - polega na topieniu silnie rozdrobnionego materiału i

jego krystalizacji ze stopu. W metodzie tej pierwotnie polikrystaliczny, drobno
rozmielony materiał dozowany jest cienką strużką na płomień palnika, najczęściej
tlenowodorowego, gdzie ulega stopieniu, a następnie otrzymana ciecz opada na
monokrystaliczny podkład, którym jest najczęściej naturalny kryształ minerału - np.
rubinu. Wzrost dopływu tlenu powoduje wzrost temperatury i rozszerzenie podstawy
kryształu. Po wytworzeniu się oczekiwanej wielkości kryształu (tzw. gruszki o długości
kilku centymetrów i średnicy około centymetra) następuje jego stopniowe chłodzenie i
odprężanie przez wygrzewanie w wysokiej temperaturze i bardzo powolne
ochładzanie. W metodzie tej punkt krystalizacji powinien być nieruchomy względem
palnika, a jego przemieszczenie jest najczęstszą przyczyną niepowodzenia tego
procesu. Nowo powstały kryształ rośnie, więc aby punkt krystalizacji był
nieruchomy, cały podkład z monokryształem musi być obniżany, można go również
obracać. Dotychczas tą metodą zdołano opanować syntezę monokryształów ponad stu
różnych substancji. Metoda Verneuila pozwala uzyskiwać duże monokryształy o umiarkowanej jednorodności i czystości,
zawierające dość często drobne wtrącenia nadtopionego substratu. Otrzymuje się w niej ferryty, korund, spinele, granaty,

tlenki metali przejściowych i ziem rzadkich

.

18. Dla jakich właściwości i w jakich zastosowaniach celowe jest stosowanie materiałów w
postaci monokryształów? Odpowiedź uzasadnij przykładami.

Monokryształy są poszukiwane ze względu na swoje cechy:



Małe zdefektowanie



Wysoka sztywność i twardość



Wysoka wytrzymałość



Izotropia właściwości



Rozszczepienie i załamanie światła



Przeźroczystość (jonowe i kowalencyjne)

Przykładami zastosowań mogą być:



Elektronika



Jubilerstwo



Optoelektronika



Elementy maszyn i urządzeń

W elektronice najczęściej wykorzystywanym materiałem są monokryształy krzemu. Otrzymuje się je przy pomocy metody
Czochralskiego, w której dostaje się kryształy o długości do 2 metrów i średnicy ponad 20cm. Takie kryształy tnie się na
płytki, będące podłożem dla układów scalonych. Innym zastosowaniem monokryształów są lasery. Przykładem tutaj może
być monokryształ azotku galu, (polska specjalność zresztą) wykorzystywany w niebieskich laserach. Zastosowanie
monokryształu jest tu celowe, dzięki znacznie mniejszym stężeniom defektów niż w polikrysztale, które to defekty prowadzą
w za dużym stężeniu, do strat optycznych i rozpraszania światła. Kolejnym zastosowaniem monokryształów są łopatki w
turbinach silników odrzutowych. Pracują one w bardzo wysokich temperaturach, w których najgroźniejszym czynnikiem jest
zjawisko pełzania. Pełzanie jest inicjowane w tych warunkach w granicach międzyziarnowych, jednym z rozwiązań tego
problemu jest ich wyeliminowanie- użycie monokryształu.

19. Podaj klasyczna definicje szkła.

Szkło według Maxwella (definicja genetyczna)- jest nim każda substancja która w wyniku chłodzenia przeszła w

sposób ciągły od stanu ruchliwej fazy ciekłej do stanu stałego, przekraczając w pewnej temperaturze zwanej temperatura
witryfikacji, lepkość 10

13

Puaza.

Obecnie ta definicja ma znaczenie historyczne, bowiem istnieją metody otrzymywania szkieł (np. metoda zol-żel), które
pozwalają otrzymać szkło nie przechodząc w toku powstawania przez fazę ciekłą.

W3,5; Profesor Handke

20. Co to jest wykres T-T-T (Time-Temperature-
Transformation)?

O tym czy z fazy ciekłej powstanie ciało stałe krystaliczne czy

amorficzne, decydują warunki otrzymywania. Rozpatrując przemianę faza
ciekła-krystaliczna, można określić warunki sprzyjające powstawaniu faz
amorficznych. W skrócie TTT jest to wykres przemiany od czasu i
temperatury. Linia na wykresie TTT jest miejscem geometrycznym czasu i
temperatury, przy których w fazie ciekłej powstaje określony udział
objętościowy fazy krystalicznej. Określa kinetyczne warunki zajścia
przemiany fazowej. Pole zakreskowane, odpowiada większej częstości
tworzenia się zarodków krystalicznych, a więc większym udziałom fazy
krystalicznej. Pole białe natomiast odpowiada udziałom fazy krystalicznej mniejszym niż te określone przez
linię TTT- czyli jeśli określimy że linia odpowiada 10

-4

% udziału kryształów w fazie stałej, to w białym polu

udział ten będzie mniejszy niż ta liczba-a więc składa się głównie z fazy amorficznej. Powstawaniu fazy
amorficznej będzie sprzyjać szybkie ochładzanie -uporządkowana struktura krystaliczna nie zdąża się
wtedy wykształcić. Szybkość tą można odczytać z wykresu. Dla naszego wykresu oznaczmy T

m

i t

m

jako

odpowiednio temperatura i czas odpowiadające minimum na wykresie. Jeśli stop znajduje się w
temperaturze początkowej T

0

, to jeśli będziemy go ochładzać z szybkością większą niż :

(T

0-

T

m

)/t

m

(tą

wartość nazywamy krytyczną prędkością chłodzenia) układ nigdy nie znajdzie się w obszarze
zakreskowanym-czyli odpowiadającym tworzeniu się struktur krystalicznych o większym udziale niż ten
zadany linią. Oczywiście w zależności od mechanizmu zarodkowania homo- lub heterogenicznego, krzywa
TTT będzie miała różne parametry. Za bardziej odpowiadające rzeczywistym, przyjmuje się te dla
heterogenicznego-zachodzi znacznie częściej w prawdziwych stopach. Wbrew pozorom to wszystko pokrywa się z
informacjami z wykładu. Wykres z wykładu odpowiada sytuacji gdy T

0

=T

topnienia

, osie są tu zamienione miejscami. Reszta

rozumowania jest ta sama. Warto zauważyć że wykres TTT jest lustrzanym odbiciem wykresu szybkości zarodkowania w
funkcji stopnia przechłodzenia.

W3,7-8; BiW s48-49

21.Co to jest krytyczna prędkość chłodzenia dla krystalizacji, podaj różnicę tej wielkości dla
zarodkowania homo i heterogenicznego.

Jak wynika z poprzedniego punktu, krytyczna prędkość chłodzenia, jest równa V

k

=

(T

0-

T

m

)/t

m

. W zależności

od rodzaju zarodkowania, jej wartość będzie się zmieniać. Rozróżniamy zarodkowanie homo i heterogeniczne.
Zarodkowanie homogeniczne, jest to tworzenie się zarodków w jednorodnej fazie-zarodki zbudowane są z tej samej
substancji która będzie krystalizować z roztworu, maja formę kulistą, wymagają dużych przechłodzeń by powstać. Wróćmy

na moment do punktu 10, otrzymaliśmy dwa równania na ∆G: ∆G

r

= πr

3

∆G+4πr

2

γ , oraz na wielkość zarodka krytycznego:

r*=-

. Wstawiając to drugie do pierwszego otrzymamy, że ∆G

r

=

-to równanie opisuje przypadek zarodkowania

homogenicznego. Zarodkowanie heterogeniczne, polega na utworzeniu zarodka nowej fazy na obcym podłożu (np. jakieś
obce cząstki) lub na defekcie. Zarodek ma wtedy kształt czaszy kulistej, scharakteryzowanej przez promień krzywizny oraz
kat zwilżania Θ. Występujące tu obniżenie bariery ∆G wiąże się z obniżeniem wkładu energii potrzebnej do utworzenia
granicy rozdziału faz, tzn. ze zmniejszeniem członu powierzchniowego: 4πr

r

γ (Bo kula zawsze będzie miała większą

powierzchnię, niż czasza kulista o podobnym promieniu). Prowadzi to w konsekwencji do obniżenia granicy zarodkowania
∆G

r

. Mamy tu warunek aby nowo tworząca się faza, zwilżała powierzchnie obcych cząstek. Dla kąta zwilżania Θ możemy

zapisać: ∆G

r

=

. Dla dowolnej wartości kąta Θ mniejszej od 180

o

(dla Θ=180

o

nie będzie zwilżania-

czyli czasza będzie kula, nawias =1), wyrażenie w nawiasie będzie mniejsze od 1, czyli bariera zarodkowania będzie
mniejsza niż dla zarodkowania jednorodnego. Ponieważ dla zarodkowania heterogenicznego bariera zarodkowania jest
mniejsza, wymagane będzie mniejsze przechłodzenie-czyli na wykresie TTT wartość T

m

będzie mniejsza niż dla

homogenicznego (wykres jest „głębszy”). Zatem wartość V

k

=

(T

0-

T

m

)/t

m

wzrośnie-czyli aby uzyskać szkło, w wypadku

zarodkowania heterogenicznego, musimy obniżać temperaturę szybciej niż dla zarodkowania homogenicznego.

W3,7; BiW s49; ZNoM s212-214

22. Wymień znane ci grupy składników szkłotwórczych.

Składnikami szkłotwórczymi nazywamy związki tworzące więźbę szkła. Maja zdolność do tworzenia stopu o

wysokiej lepkości w temperaturze topnienia lub likwidusu. Rodzaje składników szkłotwórczych:



Polimery nieorganiczne-należą tu szkłotwórcze tlenki: SiO

2

,GeO

2

,B

2

O

3

,P

2

O

5

,As

2

O

5

,V

2

O

5

,Sb

2

O

5

,Nb

2

O

5

a także

BeF

2

. Ważną role odgrywa w tej grupie występowanie mostków tlenowych lub fluorowych, o niskiej liczbie

koordynacyjnej elementu mostkotwórczego (czyli np. tlenu)



Związki z grupa hydroksylową- woda(trudno przechodzi w stan szklisty), alkohol etylowy, gliceryna, glukoza (b.

łatwo). Analogicznie do mostków z poprzedniej grupy, tutaj występują wiązania wodorowe.

Obie te grupy w stanie szklistym są typowymi niemetalami oraz izolatorami. Istnieją jednak także substancje mające w tym
stanie właściwości półprzewodnikowe oraz leżące w trójkącie wiązań w obszarze pola metaloidów:



Selenki i tellurki arsenu. Jeśli do złożonych szkieł boranowych, germanianowych czy fosforanowych,

wprowadzimy tlenki będące w stanie czystym półprzewodnikami, otrzymamy szkła o wł. półprzewodnikowych
(np. CoO,MnO,TiO

2

)



Pierwiastki w stanie szklistym- półmetale o strukturze polimerycznej łańcuchowej(spiralnie zwinięte łańcuchy w

heksagonalnym selenie) lub warstwowej (arsen, antymon, bizmut). Również niemetale mogą występować w
stanie szklistym, np. siarka, przy czym pierścienie siarki współwystępują tu z łańcuchami spiralnymi podobnymi do
tych w selenie.

W3,15; CCS s167-169

23.Wymień grupy składników szkieł tlenkowych.



Tlenki szkłotwórcze- tworzą więźbę szkła- SiO

2

,GeO

2

,B

2

O

3

,P

2

O

5

,As

2

O

5

,V

2

O

5

,Sb

2

O

5

,Nb

2

O

5



Tlenki modyfikujące-zwykle są to atomy wprowadzane w postaci tlenków, które wiążą się z więźbą

bezkierunkowymi wiązaniami jonowymi. Odznaczają się dużymi rozmiarami kationów i niskim ładunkiem (mała
elektroujemność). Ponieważ atomy tlenu dość słabo wiążą się z metalami, są one odciągane przez atomy krzemu
o silniejszym polu dodatnim. W wyniku tego wzrasta stosunek liczby tlenu do krzemu w więźbie, co prowadzi do
zrywania mostków tlenowych. Zachodzi depolimeryzacja, w wyniku której więźba staje się luźniejsza-ułatwia to
wprowadzanie kationów w pozycje śródwięźbowe, wysycając przy tym lokalne niedobory ładunku. Oprócz tego
łączą fragmenty więźby gdy nie jest ona w pełni przestrzennie spolaryzowana(to z wykładu).



Tlenki pośrednie-tlenki Al, Pb ,Ti ,Zn ,Cd ,Be ,Zr- w stanie czystym nie tworzą szkła, natomiast nabierają

właściwości szkłotwórczych w obecności innych tlenków, zastępując jony więźby, co modyfikuje właściwości szkła.



Barwniki-tlenki metali przejściowych- Co ,Ni, Cu, Cr, Fe- oprócz tego mogą to także być metale szlachetne w

formie roztworów koloidalnych- Ag, Au, Cu. Związki te tworzą centra barwne w szkłach.

CCS s180; W3,15-16; Wykład z propedeutyki nauk materiałowych o szkle

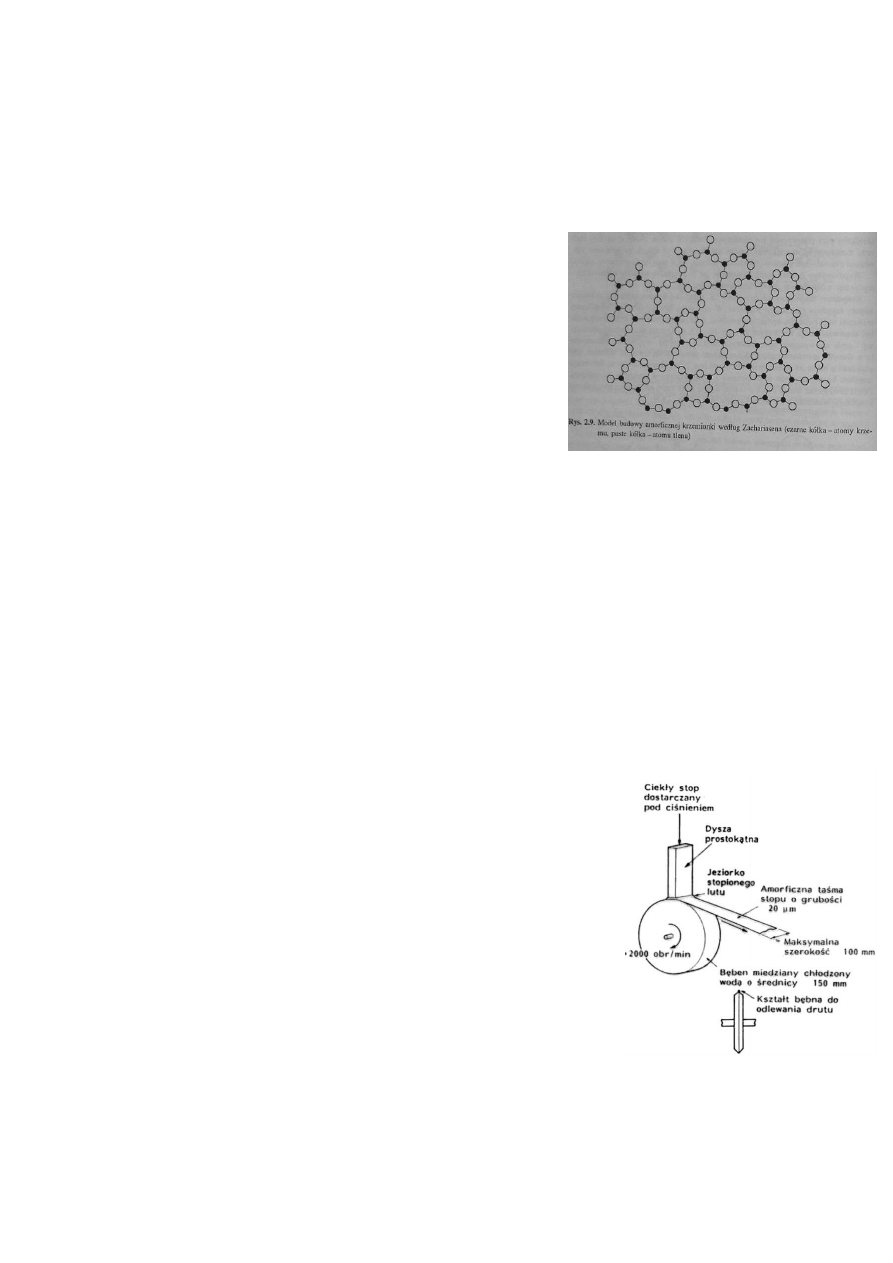
24. Opisz model budowy szkła według Zachariasena.

Zachariasen w swoim modelu budowy szkła zakłada uporządkowanie

tylko na poziomie tetraedru SiO

4

. Występuje tu struktura więźby-przestrzennej

sieci wiązań. W tej koncepcji płaski rzut tetraedrycznych zespołów
koordynacyjnych krzemu i 4 sąsiadujących z nim atomów tlenu jest
przedstawiony w postaci trójkątnych utworów. W amorficznej krzemionce te
zespoły są identyczne, lecz ich powiązanie jest nieregularne. Pozwala to na
utworzenie ciągłej więźby, ale o mniej gęstym ułożeniu atomów niż w
strukturze krystalicznej. W konsekwencji w amorficznej krzemionce musza
występować w porównaniu do krystalicznej, pustki niezapełnione przez atomy.
Dzięki temu można w takie przestrzenie wprowadzać atomy modyfikujące
właściwości więźby.

BiW s23-24; WMC s52-53; W3,13

25. Wymień podstawowe cechy szkieł krzemianowych.

Szkła krzemianowe jako jednostkę strukturalna posiadają tetraedr [SiO

4

]

4-

, otrzymujemy je ze stopów stosunkowo ubogich

w tlen (stosunek O:Si≈ 2), w wyników ich chłodzenia powstaje szkło krzemianowe o wykształconej więźbie- przestrzennym
wiązaniu (ciągłej sieci przestrzennej). Szkła krzemianowe cechuje:



Wysoka temperatura mięknięcia (około 1200⁰C),



Duża stabilność



Duża wytrzymałość mechaniczna



Mała rozszerzalność ciepła- duża odporność na wstrząsy termiczne



Wysoka lepkość

Nie wiadomo za bardzo co tu pisać i o co dokładnie chodzi pytającemu
W3,11-14; Ashby „Materiały inżynierskie” s211

26. Warunki otrzymywania i podstawowe cechy szkieł metalicznych.

Ze względu na dużą ruchliwość elementów stopu, metale wykazują naturalna

zdolność do krystalizacji, nie tworząc faz bezpostaciowych. Aby otrzymać z nich stan
szklisty, konieczne są bardzo duże prędkości chłodzenia: >10

10

[K/s]. Jest to bardzo trudne

do osiągnięcia i wymaga odpowiednich technik, jedna z nich przedstawiono na rysunku. W
metodzie tej ciekły stop dostarczany pod ciśnieniem, ulega błyskawicznemu chłodzeniu na
miedzianym bębnie, który jest ciągle chłodzony. Aby jak najbardziej skrócić czas kontaktu
bębna z metalem, obraca się on z bardzo wysoka częstotliwością, dzięki czemu nie ulega tak
łatwo nagrzaniu, co pozwala dalej prowadzić proces. Amorficzny metal uzyskuje się w
postaci taśmy (lub drutu zależnie od użytego bębna). Obecnie istnieją nowe technik i nowe
stopy, które umożliwiają uzyskanie szkieł metalicznych przy znacznie niższych prędkościach
chłodzenia (nawet rzędu 100K/s). Udało się również otrzymać stal amorficzną (nie wykazuje
wł. magnetycznych w T

pokojowej

). Innymi przykładami mogą być stopy Cu(50)-Zr(50), Pd(80)-

Si(20) czy magnetyczny Fe(40)-Ni(40)-P(14)-B(6). Szkło amorficzne ma wiele zalet:



Brak granic międzyziarnowych



Brak plastyczności



Wysoka twardość



Nadprzewodnictwo



Bardzo dobre właściwości magnetyczne



Odporność na korozję

Ich wady wynikają z zalet:



Kruchość



Brak plastyczności



Trudne w otrzymaniu

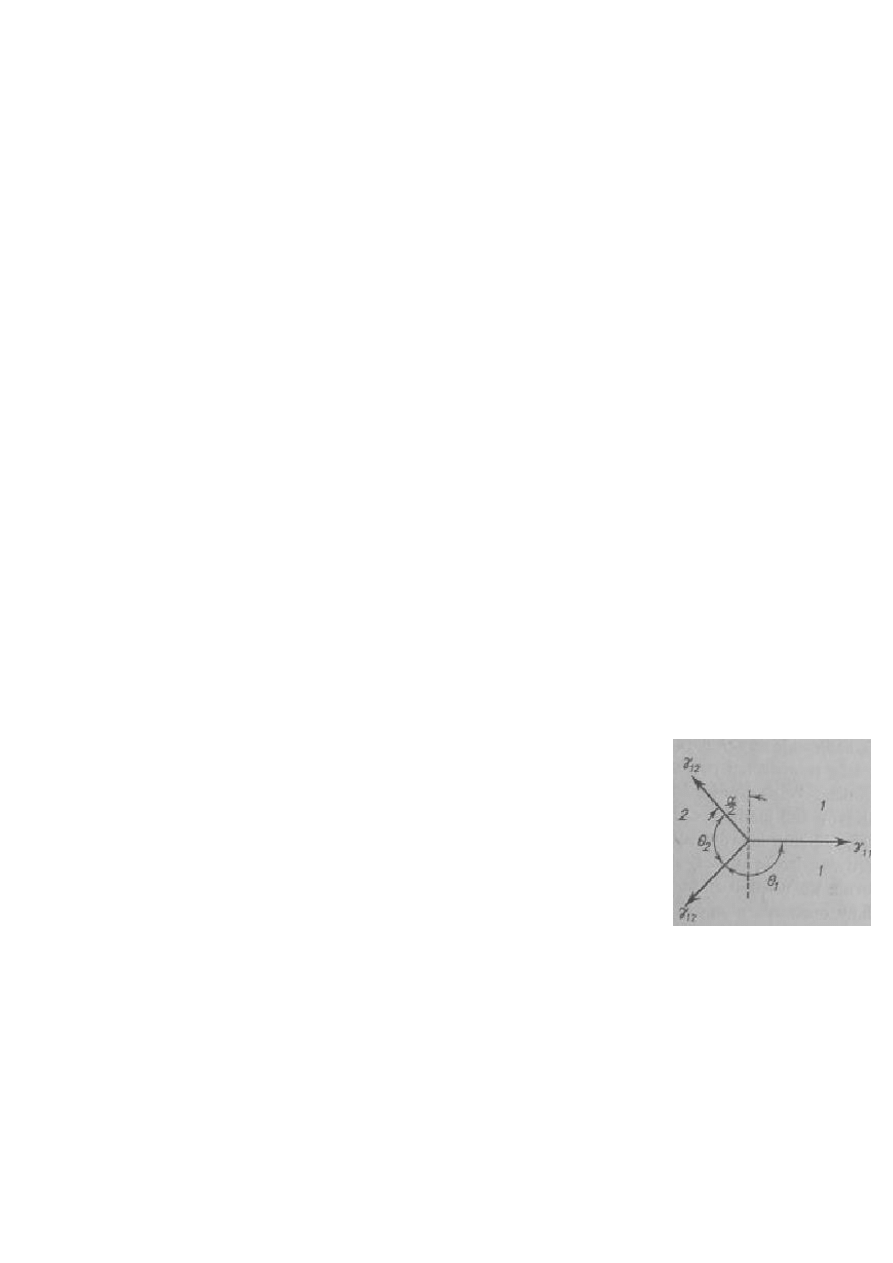
W3,36-38

27. Dla jakich właściwości i w jakich zastosowaniach celowe jest stosowanie materiałów w
postaci szkła? Odpowiedź uzasadnij przykładami.

Szkła mają liczne, unikalne właściwości takie jak:



Izotropia właściwości i budowy



Łatwość formowania kształtów- łatwo można uzyskać np. tafle- zastosowania w budownictwie (chociażby okna),

zdobnictwo.



Odporność chemiczna- szkła laboratoryjne



Wysoka wytrzymałość cieplna- szkło laboratoryjne, naczynia żaroodporne



Twardość



Odporność na ściskanie



Przepuszczalność światła inne właściwości optyczne (załamanie, odbicie)- soczewki optyczne, światłowody



Właściwości izolacyjne (elektryczne)



Właściwości termoizolacyjne- np. szkło piankowe jest stosowane w budownictwie, energetyce jądrowej ze

względu na właściwości termoizolacyjne i odporność chemiczna.

28. Podaj definicje i znane ci elementy budowy polikryształu.

Polikryształ –materiał o złożonej budowie, którego podstawą są połączone trwale (granicami fazowymi) różnie

zorientowane elementy krystaliczne. Taka budowa powoduje, iż o ich właściwościach w dużej mierze decyduje obecność
silnie rozwiniętych powierzchni rozdziału ciało stałe- ciało stałe oraz granic gaz- ciało stałe. Elementy budowy:



Ziarna- pojedyncze kryształy oddzielone granicami międzyziarnowymi. W polikrysztale mogą znajdować się ziarna

wielu faz.



Pory- puste przestrzenie miedzy ziarnami wypełnione faza gazową



Faza amorficzna- występuje jako oddzielne elementy mikrostruktury lub w postaci warstw na granicach ziaren



Wtrącenia dyspersyjne-małe kryształy występujące w objętości ziaren.

W4,9-10

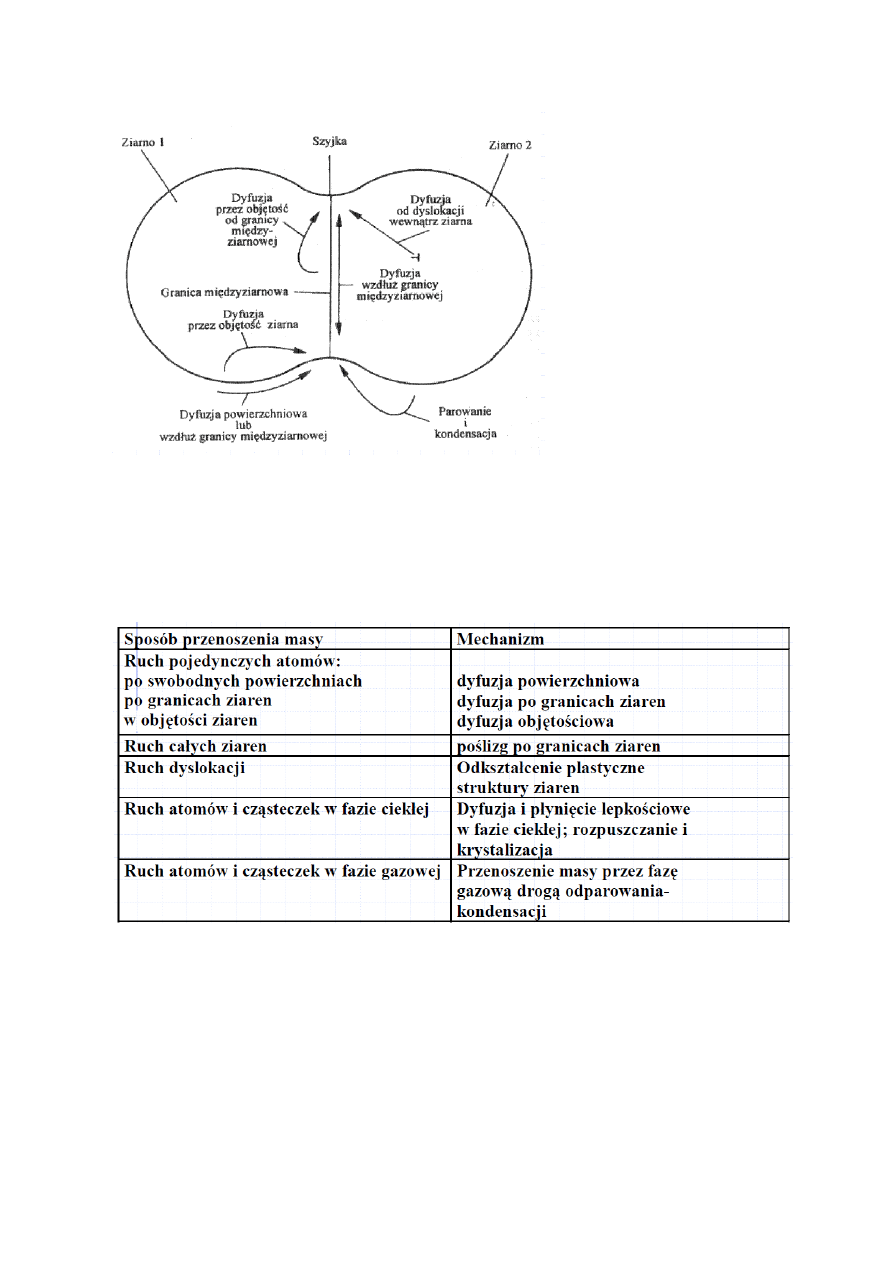
29. Wyprowadź zależność na równowagowa wielkość kąta dwuściennego w miejscu styku
trzech ziaren w polikrysztale.

Polikryształy nie osiągają stanu równowagi poza zlokalizowanymi obszarami w pobliżu granic

międzyziarnowych. Idealny kształt ziaren i kąty między nimi musza zatem wynikać z ustalania się
równowagi energii granic międzyziarnowych. Oprócz tego, kształt ziaren musi pozwalać na
wypełnienie bez reszty całej objętości polikryształu. Rozpatrzmy dwuwymiarowy przekrój wycinka
polikryształu. Dla uproszczenia możemy przyjąć, że energia granic rozdziału jest izotropowa i dwa
identyczne ziarna stykają się z trzecim. To ostatnie może być ziarnem tej samej fazy ale o innej
orientacji. Przy nieskończenie małym przesunięciu się trzech granic rozdziału o dx wzdłuż granicy 1/1,
„powierzchnia” tej granicy zmniejsza się o dx, natomiast powierzchnia pozostałych dwóch granic 1/2
zwiększa się o dx sin(α/2). Ponieważ układ ma być w stanie równowagi, to temu przesunięciu nie
może towarzyszyć zmiana energii, zatem:
-γ

11

dx+2γ

12

dx sin(α/2)=0 czyli γ

11

=2γ

12

sin(α/2) ponieważ

cos(90˚-α/2)=sin(α/2)=cos(Θ/2) to γ

11

=2γ

12

cos(Θ/2)

Wcześniej zrobiliśmy założenie że energia jest izotropowa: γ

11

=γ

12

=γ. Gdy wstawimy to do naszego

równania, otrzymamy że nasz cos(Θ/2)=0,5 z czego wynika że nasze kąty dwuścienne w przekroju polikryształu mają
120˚.

W4,12-15; MC s95; BiW s79-80; ZnOM s68-69

30. Opisz budowę idealnego kryształu jednofazowego.

Z poprzedniego punktu można wnioskować, że najtrwalszym układem jest układ w którym trzy granice miedzy

ziarnowe tworzą między sobą kąty równe lub zbliżone do 120˚. Gdyby ziarna miały jednakowe wymiary, to granice
miedzy ziarnowe wychodzące z tych punktów potrójnych są wtedy proste, a wszystkie ziarna maja dwuwymiarowy
przekrój w kształcie regularnych sześcioboków. Układ taki jest nieskończenie meta trwały, bowiem każde przemieszczenie
którejkolwiek granicy powodowałoby wzrost energii układu. Niestety w rzeczywistości polikryształy powstają ze zbiorów

ziaren o niejednakowych wymiarach, więc bardziej realnym modelem będzie taki składający się z wielu
różnych wieloboków. Część z nich będzie miała więcej niż 6 boków, część mniej. Taki układ również
będzie dążył do równowagi. Gdyby na przykład były punkty, w których stykałby się 4 granice miedzy
ziarnowe lub więcej, to będą one nietrwałe i dysocjują drogą małych przemieszczeń do konfiguracji
trwałej, z 3 stykającymi się granicami(drugi rysunek). Z kolei taka konfiguracja dalej będzie chciała obniżać
swoja energię, więc układ będzie dążył do uzyskania kata 120˚ między granicami. Jak wspomnieliśmy, w
realnym polikrysztale większość wieloboków nie jest 6-katem, więc aby ich granice mogły się zbiegać
pod katem 120˚, musza mieć one zakrzywione boki (te z >niż 6 kątami wklęsłe, te z <6 wypukłe). Mimo
wszystko, takie zakrzywione granice nie są trwałe, jest więc możliwe przenoszenie masy poprzez nie-granice
będą chciały się prostować. Oznacza to że wieloboki o granicach wklęsłych, będą wzrastać kosztem tych o
granicach wypukłych (pierwszy rysunek, strzałki). Jednak jest to proces bardzo wolny. Ogólnie w
polikryształach będzie występować budowa taka jak na większym rysunku- osiągamy meta trwała równowagę
tylko w lokalnych obszarach, zazwyczaj na przecięciu 3 granic. Cały ten wywód dotyczył dwuwymiarowego przekroju, dla
trójwymiarowego sprawa wygląda dość podobnie. Taki trójwymiarowy zbiór również cechują tylko lokalne stany
równowagi na przecięciach ziaren, granice będą tu się zbiegać albo po 3 (120˚) albo po 4 (około 109˚ ). Nie istnieją
żadne regularne wielościany spełniające te warunki i mogące wypełniać w całości przestrzeń, natomiast pasuje tu
tzw. 14-ścian Kelvina, mający 8 ścian sześciokątnych i 6 kwadratowych. Dodatkowo jego krawędzie są nieco

zniekształcone, aby zachować odpowiednie kąty. Można policzyć, że średnio na jedna ścianę takiej bryły wypada 5

ściany, co pokrywa się z obserwacjami doświadczalnymi. W przypadku silnego zróżnicowania wartości energii
powierzchniowej na poszczególnych płaszczyznach krystalograficznych w polikrysztale, mogą powstawać ziarna o
dominacji ścian o najniższej energiach zorientowanych tak, aby wystąpiła największa koincydencja sieci-czyli węzły
sieci dwóch sąsiednich ziaren są wspólne, ziarna maja wspólne atomy. (występuje to zwłaszcza w materiałach o wiązaniach
kowalencyjnych)

W4,14-18; MC s94-98; ZNoM s69-71 BiWs79-80 o koincydencji s81

31. Wyprowadź zależność na równowagową wielkość kąta dwuściennego w miejscu styku
dwóch ziaren z fazą szklistą w polikrysztale.

Faza szklista powstaje w polikryształach, zazwyczaj w wyniku zestalania się stopionych faz w

procesie powstawania polikryształu. Forma i sposób rozprowadzenia fazy szklistej zależy od stopnia
zwilżania ciała stałego przez fazę szklista oraz udziału objętościowego fazy szklistej. Gdy ciecz i ciało stałe
znajdują się w równowadze w nieobecności fazy gazowej można zapisać wzór z punktu 29: γ

11

=2γ

12

cos(Θ/2)

w postaci

=2

cos(φ/2) ,(zakładamy że energia powierzchniowa γ równa się napięciu

powierzchniowemu γ’) gdzie φ- kąt dwuścienny zaznaczony na rysunku,

- napięcie powierzchniowe na

granicy rozdziału ciało stałe-ciało stałe,

-to samo tyle że ciało stałe-ciecz. Wynika z tego że kąt

dwuścienny dla układów dwufazowych zależy od stosunku

: cos(φ/2) = 0,5

W4,24; BiW s84; MC s99-100

32. Przedstaw schematycznie mikrostrukturę polikryształów z faza szklista o różnym kacie
zwilżania.

Jest to kontynuacja poprzedniego punktu. Patrząc na otrzymane w nim równanie cos(φ/2) = 0,5

widać, że jeśli

napięcie sc jest większe od ss, to kąt φ jest większy lub równy 120˚, a faza ciekła tworzy tylko odizolowane krople na
przecięciu granic międzyfazowych. Gdy kąt ten jest w przedziale 60˚-120˚, faza ciekła zaczyna penetrować wzdłuż granicy

ziaren, natomiast gdy φ jest mniejsze niż 60˚-faza ciekła rozpływa się wzdłuż granic międzyziarnowych.

Mikrostruktury polikryształów:

,

Dla rysunku tuz nad; przypadek a) opisuje sytuacje gdy w podwyższonej temperaturze, prosta struktura z ziaren fazy stałej
znajduje się w równowadze ze stopem, φ=120˚. Natomiast b) pokazuje sytuacje gdy dwie fazy stale A i B powstały w wyniku
reakcji, np. rozkładu termicznego jakiegoś związku. Łączy je zastygła faza niskotopliwa np. ich eutektyk, występuje tu mały
kąt φ. Jest to dość popularna struktura, cechuje np. układy MgO-SiO

2

-CaO W c) mamy układ w którym wytrąca się wtórna

faza stała w wyniku przesycenia roztworów stałych i stopów podczas obniżania temperatury. Występuje to np. w przypadku
wytrącania się MgFe

2

O

4

z roztworu stałego FO w MgO. Dla wielu glinokrzemianowych materiałów ceramicznych

charakterystyczne jest powstawanie wtórnej fazy krystalicznej w wyniku krystalizacji przesyconych stopów bogatych w
krzemionkę, dla materiałów szamotowych i porcelanowych taka wtórna faza krystaliczna jest mulit(faza B na rysunku d)).

W4,25-29; MC s99-101; ZnOM s72-74; BiW s84

33. Wymień znane ci metody otrzymywania polikryształów.



Krystalizacja ze stopów- jest to podstawowa metoda otrzymywania polikryształów, otrzymuje się nią większość

materiałów metalicznych. Występujące w tej metodzie warunki sprzyjają krystalizacji wielozarodkowej.



Krystalizacja szkieł- materiały szkło krystaliczne (następny punkt)



Spiekanie proszków- punkty od 36, generalnie jest to proces polegający na przekształceniu zbioru drobnych ziaren

w lity polikryształ w sposób trwały, w temperaturze niższej od temperatury topnienia.



Wiązanie chemiczne i hydratacja

o

Reakcyjne wiązanie w wysokich temperaturach-otrzymywanie tworzyw ceramiki specjalnej, azotku

krzemu- SHS (wysokotemperaturowa synteza samorozwijająca)- technika ta polega na wykorzystaniu
ciepła wydzielanego w toku reakcji egzotermicznej do samoogrzania się reagującego układu do wysokich
temperatur niezbędnych do zajścia syntezy.

o

Wiązanie tworzyw droga hydratacji- tworzywa polikrystaliczne można otrzymać droga wiązania

chemicznego w temperaturze pokojowej, przykładem może być hydratacja cementu portlandzkiego.
Jego podstawowymi składnikami są albit (3CaO SiO

2

czyli C

3

S) i belit (C

2

S). W wyniku hydratacji tych

związków zachodzi proces wiązania cementu: 2C

3

S + 6H = C

3

S

2

H

3

+ 3CH oraz 2C

2

S + 5H = C

2

S

2

H

4

+ CH

powstające fazy C-S-H o zmiennym składzie początkowo występują w formie żelu, a następnie w formie
wydłużonych igieł, powodują stężenie zaczynu i wiążąc ziarna kruszywa powodują powstanie trwałej
struktury betonu.

W5:3,9,34-37; Wykład z propedeutyki „Materiały ceramiczne”

34.Podaj definicję i wymień podstawowe metody otrzymywania tworzyw szklano
krystalicznych (pyroceram) oraz

35.Jakie wady i zalety posiadają tworzywa szklano krystaliczne w porównaniu ze szkłem .

Jest to szkło do którego wprowadzono zarodki krystaliczne w celu sztucznego wywołania krystalizacji i

otrzymania materiału o wyższej odporności mechanicznej. Szkło w zwykłych warunkach jest termodynamicznie
metatrwałe. Procesy krystalizacji są bardzo wolne ze względu na wysoką lepkość szkła. Należy je więc ułatwić. Wprowadza
się więc zarodki, które tworzą liczne granice rozdziału faz co ułatwia krystalizacje. Jednocześnie krystalizacje ułatwia
wprowadzanie jonów które obniżają lepkość szkła poprzez rozbicie jego ciągłej więźby na mniejsze domeny-mogą to
robić jony modyfikujące, np. Ti

4+

. Inna metoda jest wprowadzenie zarodków drugiej fazy szklistej powstałych w skutek

likwacji. Po wprowadzenie przeprowadzamy obróbkę cieplną, najczęściej dwustopniową dla wzrostu krystalitów. Otrzymany
materiał jest polikryształem szkło-krystalicznym, faza krystaliczna stanowi w nim 5-95%, wielkość nieprzeźroczystych ziaren
jest z zakresu 0,02-2µm. Materiał ten jest nieporowaty. Przykładowe składy takich materiałów: SiO

2

-Al

2

O

3

-LiO

2

-z metalami

szlachetnymi, SiO

2

-Al

2

O

3

-MgO-z metalami lub TiO

2

, dla typu miki (o wyglądzie porcelany):58% SiO

2

-16% Al

2

O

3

-12% CaO.

Właściwości tworzyw szklano krystalicznych:



Wysoka wytrzymałość



Wyższa niż szkła odporność na pękanie



Odporność na szoki termiczne



Nieprzeźroczystość- jest raczej wadą

W5,4-8; WMC s264-268

36. Co to jest spiekanie?

Spiekanie jest podstawowym procesem w technologiach otrzymywania materiałów ceramicznych i w metalurgii

proszków zachodzącym podczas operacji wypalania. W trakcie spiekania zbiór drobnych ziaren przekształca się w sposób
trwały w lity polikryształ, przy czym proces zachodzi w temperaturze niższej od temperatury topnienia (0,5-0,8 T

top

).

Spiekanie jest procesem samorzutnym, gdyż wiąże się z obniżaniem nadmiarowej energii powierzchniowej układu-
sumaryczna energia powierzchni swobodnej proszku jest bowiem większa niż energii powstających w polikrysztale granic
międzyziarnowych.

W5,9; BiW s74; ZNoM s181

37.Wymien podstawowe etapy otrzymywania wyrobów metodą spiekania.



Proszek wyjściowy



Kształtka po prasowaniu



Kształtka po doprasowaniu izostatycznym



Kształtka po spiekaniu



Kształtka po obróbce mechanicznej

W5,10

38.Skad powstają siły napędowe procesu spiekania?

Siłą napędową spiekania jest dążenie układu do obniżenia energii powierzchniowej.

Można to omówić na przykładzie dwóch ziaren początkowo stykających się w sposób punktowy.

Ziarna te są niewielkich rozmiarów, mają duże rozwinięcie powierzchni (powierzchnia stykająca się z gazem). Taka
powierzchnia charakteryzuje się nadmiarową entalpia swobodną (energią powierzchniową) γ

sg

. Występuje tu tendencja

do zbliżania się środków tych ziaren, w wyniku czego część powierzchni ciało stałe-gaz zamienia się w powierzchnię ciało
stałe-ciało stałe. Oznaczając energie powierzchniową granic rozdziału ciało stałe-ciało stałe jako γ

ss

, możemy zapisać że

∆γ=γ

ss

-2γ

sg.

Z rozważań na temat kata dwuściennego w polikrysztale, można powiedzieć, że 2 γ

sg

> γ

ss

(Ponieważ w stanie

równowagi 0= γ

ss

- 2γ

sg

cos(Θ/2), a 2γ

sg

cos(Θ/2)< 2γ

sg

-przynajmniej tak mi się wydaje że stąd to się bierze), a zatem nasze

∆γ<0 co oznacza że proces jest samorzutny. Proces obniżania energii powierzchniowej trwa tak długo, aż zostanie
zrównoważony przez przyrost energii odkształcenia sprężystego wywołanej przez wzrastające odkształcenie obu kul. Na
wykładzie było powiedziane, że lokalne siły napędowe wynikają ze zróżnicowania wartości potencjału chemicznego, które z
kolei wynika z różnicy krzywizn powierzchni ziaren w miejscu kontaktu. Szczerze mówiąc nie mam pojęcia skąd to się bierze,
sprawdziłem 5 pampuchów i nic na ten temat nie znalazłem.

W5,12; ZNoM s181-183; MC s192-193; BiW s74-76

39.Układ naprężeń w miejscu styku ziaren i jego konsekwencje w procesie spiekania.

Omówionemu wcześniej zbliżaniu centrów towarzyszy sprężyste odkształcenie się cząstek-

materia w obszarze kontaktu zagęszcza się, natomiast w obwodzie kontaktu-rozrzedza. Taki stan pociąga
za sobą występowanie naprężeń-tam gdzie mamy większe zagęszczenie-ściskających, na zewnątrz-
rozciągających(patrz rysunek). Ponieważ naprężenia zwiększają entalpie swobodną układu, naprężenia te
będą limitować zbliżanie się centrów ziaren. Jednak możliwe jest dalsze zbliżanie się centrów, bowiem w
temperaturze spiekania intensywnie zachodzi dyfuzja atomów. Występowanie stanu naprężeń pociąga za
sobą istnienie gradientu stężeń atomów. W związku z tym na atomy podlegające dyfuzji działa siła F związana
z gradientem chemicznym (którego szczególnym przypadkiem jest gradient stężenia atomów ∂c/∂x). Dla
gradientu w jednym kierunku można zapisać: F

x

=- ∂c/∂x .Ponieważ stężenie atomów jest większe w

centrum ich kontaktu, a siła działa wbrew gradientowi, to wystąpią strumienie dyfuzyjne atomów, od
centrum kontaktu na zewnątrz, co powoduje dalsze zbliżanie się centrów. Naprężenia ściskające w centrum
kontaktu powodują jeszcze jedno zjawisko-transport całych ziaren, co prowadzi do ich przegrupowania.
Ponieważ ziarna są rozmieszczone przypadkowo, to naprężenia miedzy nimi również takie będą. Jest to
sytuacja równoważna działaniu wszechstronnego ciśnienia hydrostatycznego. Powoduje ono tendencje do
zmniejszania objętości zajmowanej przez zbiór ziaren- przyjmują one bardziej gęste ułożenie (drugi rysunek).
Pominąłem tu naprężenia gdy w układzie występuje dodatkowo faza ciekła, jak ktoś chce można doczytać.

W5,14-15; BiW s76-77; MC od s194(nie polecam)

40.Zaznacz na schematycznym rysunku spiekających się ziaren podstawowe mechanizmy
spiekania.

Transport masy jest powodowany przez różne czynniki, jego rodzaj zależy od tych czynników.



Różnice potencjału chemicznego atomów w obszarach ściskanych i rozciąganych

∆µ= -2γΩ/r -stąd dyfuzja objętościowa i po granicach ziaren (Ω- objętość atomowa).



Różnice potencjału chemicznego atomów na powierzchni wypukłej i płaskiej

∆µ= -γΩ/r -stąd dyfuzja po powierzchni



Różnice prężności par nad powierzchnia zakrzywiona i płaską

Ln (p/p

0

)= γΩ/(kTr) -stąd transport masy typu parowanie kondensacja (w wysokich temperaturach)



Różnice aktywności ziaren o różnej krzywiźnie w kontakcie z fazą ciekłą

Ln(a/a

0

)= Kγ/kTr -stąd rozpuszczanie-krystalizacja

W5,16-17 –w pampuchach tez można znaleźć ale jest to rozrzucone

41.Podaj które mechanizmy przenoszenia masy powodują, a które nie powodują
zagęszczenia w toku spiekania.

Mechanizmy nie zagęszczające-dyfuzja po powierzchni (zmienia tylko kształt kontaktów ziaren, istotna w początkowym
okresie spiekania), odparowanie-kondensacja (również zmienia tylko kształt kontaktów ziaren, istotna w początkowym
okresie spiekania)

Mechanizmy zagęszczające-ruch całych ziaren, dyfuzja objętościowa, dyfuzja po granicach ziaren, ruch dyslokacji

W5,18-23; Dr.Rączka

42.Jak faza ciekła wpływa na spiekanie?

Temat ten jest bardzo zagmatwany i niespójny. Każde źródło mówi co innego, tutaj opierać się będę głównie o

„Chemię ciała stałego”. W przypadku małych udziałów fazy ciekłej, gdy jest ona fazą niezwilżającą, lub słabo zwilżającą

ziarna, możemy ja traktować jako dodatkową fazę stałą, niemal nic nie zmienia się w modelu spiekania. Faza ta jest w
takich warunkach faza nieciągłą, tworzy odizolowane krople w polikrysztale. Wtrącenia te mogą tylko w pewnym stopniu
wpływać na szybkość procesów rozrostu ziaren i utrudniać ruch granic międzyziarnowych. Gdy mamy do czynienia z cieczą
zwilżającą, sytuacja się zmienia. Rozpatrzmy dwa różne ziarna, które reagując ze sobą w podwyższonej temperaturze,
tworząc fazę ciekłą w punkcie styku. Powstaje „szyjka”, na jej obwodzie mamy naprężenia rozciągające, w jej centrum
natomiast- ściskające. Ciecz tworzy cienka warstewkę rozgraniczająca ziarna, ziarna nią przegrodzone zachowują się
względem siebie idealnie sprężyście. Obecność cieczy na granicach ziaren (ciecz ma niższą lepkość niż warstwy granic
międzyziarnowych), powoduje łatwiejsze przemieszczanie się ziaren względem siebie (przegrupowanie a w konsekwencji
zagęszczenie) i proces ten może zachodzić w niższych temperaturach. Sytuacja się ponownie zmienia, gdy objętość fazy
ciekłej jest znacznie większa niż ta potrzebna do wytwarzania warstewek miedzy ziarnami (np. około 30%), bowiem
oprócz ich tworzenia, faza ciekła może tutaj zapełniać puste przestrzenie miedzy ziarnowe w proszku, po zakończeniu
przegrupowywania się ziaren (czyli zanikają pory). Obecność większych udziałów cieczy pozwala uzyskać zagęszczenie
materiału już w znacznie niższych temperaturach lub po krótszym czasie niż podczas spiekania w jedynie fazy stałej. Gdy
udział fazy ciekłej jest niewystarczający do wypełnienia wszystkich porów (np. 10%), to i tak może odbywać się dalsze
zagęszczanie materiału, jeśli tylko faza ciekła odznacza się dużą zdolnością rozpuszczania fazy stałej. Wtedy atomy drogą
dyfuzji w fazie ciekłej będą przechodzić do innych miejsc układu, a w konsekwencji zachodzić będzie zbliżanie się środków
ziaren (czyli dalsza eliminacja porów).

W5,25-26; CCS s496-499; BiW s77-78

43.Co to jest proces witryfikacji, podaj przykłady.

Witryfikacja zwana zeszkleniem jest procesem otrzymywania szkła. Zwykle podczas ochładzania fazy ciekłej,

ulega ona przemianie w fazę stała krystaliczną, a transformacji tej towarzyszy skokowa zmiana funkcji termodynamicznych

entropii i entalpii (można również powiedzieć że zachodzi ciągła zmiana wartości potencjału chemicznego µ=

oraz

skokowa zmiana pierwszych pochodnych µ: entropii entalpii)-taki proces nazywamy przemiana fazowa I rzędu. Możliwe
jednak jest, że ciecz zamiast krystalizować ulega przechłodzeniu, powstaje wtedy metastabilna ciecz przechłodzona,
która w niższej od T

krystalizacji

, T

witryfikacji

ulegnie przemianie, bez skokowej zmiany entalpii w fazę szklistą. Proces ten

nazywamy witryfikacją. Jest to przemiana pseudofazowa, bowiem nie prowadzi od przejścia ze stanu równowagi w stan
równowagi (ani ciesz przechłodzona ani szkło stanem równowagi nie jest), T

wit

nie jest temperatura charakterystyczna,

zależy od sposobu prowadzenia procesu (szybkości przechładzania) oraz nie ma skokowej zmiany entalpii. Proces ten jest
odwracalny, lepkość materiału zmienia się w sposób ciągły od lepkości ruchliwej cieczy (logη=1) do lepkości ciała stałego
(logη=25), przy czym punkt przegięcia logη=13 znajduje się w T

wit

–stad definicja szkła.

Krystalografia i krystalochemia dla ceramików s275-277

44.Wymień techniki otrzymywania polikryształów porowatych.

Materiały porowate to materiały w których celowo wprowadzono duży udział porów. Powodem są ich

właściwości- np. niskie przewodnictwo cieplne spowodowane gazem w porach. Ze względu na budowę i udział
objętościowy porów możemy je podzielić na 3 grupy:



Ziarniste-są wytwarzane z surowców rozdrobnionych do wielkości ziaren powyżej 1µm, które spieka się po

uformowaniu w odpowiednie kształtki. W zależności od ułożenia ziaren objętość porów V

p

wacha się od 0,26

(dla ułożenia piramidalnego, pierwszy rysunek) do 0,47 (dla ułożenia luźnego, drugi rysunek). Stanowią
większość materiałów ogniotrwałych.



Materiały komórkowe- uzyskujemy je przez wprowadzanie do rozdrobnionych surowców substancji, które

ulegają spaleniu podczas spiekania. Gdy się wypalą, na ich miejscu zostają pory. Taki materiał zawiera
izolowane, nie przecinające się ze sobą pory. Maksymalny ich udział (gdy pory stykają się punktowo), wynosi
0,678. Jeśli udział porów jest większy powstaje materiał komórkowy o kapilarnym modelu mikrostruktury- pory są
w nim połączone kanalikami o różnych promieniach r, średnicy d i długości b.



Materiały piankowe-otrzymujemy je, jeśli w toku wypalania materiału, stworzy się warunki

umożliwiające wydzielanie się gazów w całej objętości materiału znajdującego się w stanie
plastycznym w podwyższonej temperaturze. Gaz wydzielający się w wyniku spalania tworzy
wówczas banieczki w stopionej masie. Ponieważ ciśnienie i naprężenie jest jednakowe we wszystkich
porach, powstaje mikrostruktura piany o V

p

=0,9-0,95 . Z tych materiałów wywodzą się ceramiczne

materiały porowate o budowie plastra miodu.

W4,21-24; BiW s89-91; MC s103-106

45.Podaj podział układów zdyspergowanych.

Układy zdyspergowane, to takie w których faza stała występuje w postaci bardzo małych cząstek stałych

(krystalicznych lub amorficznych) w gazowym lub ciekłym ośrodku rozpraszającym. Cząstki te maja rozmiary od 10

-9

m

(roztwory koloidalne) do 1µm. Wszystkie układy zdyspergowane można podzielić na 3 podstawowe grupy:



Układy dwufazowe: zdyspergowane cząstki stale-gazowy ośrodek dyspergujący (s-g)-rysunki b, f i c. Typowymi

przedstawicielami takich układów są proszki ceramiczne służące jako materiał izolacyjny lub materiał do
otrzymywania polikryształów drogą spiekania, pigmenty ceramiczne, maty i filce złożone z cienkich włókien
(rysunek f). Układy te często są produktami końcowymi procesów i reakcji w układach s-c i s-c-g, np. wiążące
materiały budowlane.



Układy dwufazowe: zdyspergowane cząstki stałe- ciekły ośrodek dyspergujący (s-c)- rysunek a. Takimi układami

są pasty i zawiesiny stosowane w klasycznej technologii ceramiki szlachetnej, pasty i zawiesiny wykorzystywane
przy otrzymywaniu warstw ceramicznych (np. elementy elektroniczne)



Układy trójfazowe: zdyspergowane cząstki stałe-ciekły ośrodek dyspergujący-gazowy ośrodek dyspergujący

(s-c-g)- rysunki d i e. Układy te tworzą się zwykle z układów s-c przy zmniejszaniu się np. podczas suszenia,
udziału objętościowego fazy ciekłej do ilości, przy których ciecz tworzy kapilarne meniski pomiędzy stałymi
cząstkami. Do tego typu należą masy ceramiczne przygotowane do prasowania tzw. metoda półsuchą w
technologii materiałów ogniotrwałych i ceramiki szlachetnej.

W6,4-5; MC s118-120; BiW s67-68

46.Wymien podstawowe parametry charakteryzujące proszki.

W zależności od wielkości i stężenia cząstek w fazie gazowej wyróżniamy 3 rodzaje układów ciało stałe-gaz,

jednym z nich są proszki:



Dymy- cząstki poniżej 10

-7

m, silnie rozproszone



Pyły- cząstki 10

-7

do 10

-6

, silnie rozproszone



Proszki- cząstki do rzędu 10

-3

m, stężone

Podstawowymi parametrami charakteryzującymi proszek są wielkość i forma jego cząstek. Trzeba przy tym pamiętać że
pojecie cząstka nie jest jednoznaczne- proszek ma bowiem budowę niejednorodną a cząstki tworzą trudne do rozdzielenia
większe elementy- agregaty i aglomeraty. W związku z tym pod pojęciem ziarno proszku rozumiemy najmniejszy lity
element proszku możliwy do identyfikacji metodami mikroskopowymi lub mechanicznymi. Proszki są populacjami
złożonymi z wielkiej liczby elementów, charakteryzuje je występowanie rozkładu wielkości ziaren. Ze względu na kształt
dzielimy cząstki na:



Kuliste



Płatkowe



Włókniste



Dendrytyczne



Iglaste



Globularne



Wielościenne



Granulkowe



Nieregularne

Innym parametrem jest omówiona dalej powierzchnia właściwa.

W6,5-8; norma PN-EN ISO 3252:2002

47.Powierzchnia właściwa proszku: definicja, metody badania, przykłady wielkości.

Powierzchnia właściwa proszku jest ilorazem powierzchni zewnętrznej cząstek proszku i ich masy: S

w

= S/m

[m

2

/g]. Parametr ten w sposób generalny określa stopień dyspersji proszku- im większa powierzchnia właściwa tym

drobniejszy proszek. Powierzchnia ta może również służyć jako miara reaktywności proszku w reakcjach chemicznych w
tym spiekaniu, hydratacji i innych. Istnieje wiele metod pomiaru tej wielkości: metody siecznych przypadkowych (metoda
punktowa i metoda liniowa), metody Blaina i Fischera oraz metody sorpcyjne np. BET. Metoda BET cechuje się wysoka
czułością i dokładnością. Aby pomiar był dokładny należy określić ilość cząstek zaadsorbowanych na monowarstwie oraz
znać średnią powierzchnie zajmowaną przez cząstkę adsorbatu. W przypadku proszku zazwyczaj do naczynia z proszkiem,
wewnątrz którego panuje próżnia, wprowadza się znana objętość absorbatu (gaz, pary). Po ustaleniu się równowagi mierzy
się ciśnienie końcowe panujące w naczyniu. Znając objętość naczynia, oraz ciśnienie jakie wywierałby gaz gdyby nie
zachodziła adsorpcja, liczy się jej wielkość. Przykładowe wielkości:

W6,9-10; źródła w Internecie, w tym jedno jest wykładem z AGH.

48.Podaj przykłady zastosowania proszków jako materiałów inżynierskich.

Proszki jako surowce do wytwarzania wyrobów litych



Proszki do spiekania (ceramiczne i metaliczne)



Proszki polimerowe do formowania termoplastycznego i chemicznego



Materiały wiążące i betony



Pasty dla elektroniki

Proszki jako wypełniacze tworzyw



Farby



Wypełniacze w polimerach



Faza rozproszona w kompozytach

Proszki jako materiały



Proszki izolacyjne



Proszki polerskie

W6,11

49.Wymien podstawowe zalety materiałów w postaci włókien.

Włóknem nazywamy mono-(tzw. wiskery) lub polikrystaliczne ciało stałe, w którym stosunek minimalnej

długości do maksymalnej średnicy poprzecznej jest większy niż 10:1. Włókna cechują unikalne właściwości, które
umożliwiają ich wykorzystanie w wielu sytuacjach. Mają one elastyczna postać i „nieskończony” wymiar-można je giąć,
nawijać, tkać z nich. Oprócz tego cechuje je duże rozwinięcie powierzchni co ma wpływ na ich właściwości sorpcyjne i
katalityczne. Ich zdyspergowany charakter i mały wymiar poprzeczny powodują ich znakomite właściwości izolacyjne, oraz
umożliwiają rozprowadzenie w ciągłym medium (np. osnowie w kompozycie). Jednak ich najważniejszą cecha są bardzo
wysokie właściwości mechaniczne. Wynikają one właśnie z budowy- w małej objętości włókna jest znacznie mniejsze
prawdopodobieństwo wystąpienia defektu, niż dla np. płyty. W przypadku włókien szklanych, ich duża wytrzymałość w
porównaniu do szkła wynika dodatkowo z mniejszej ilości mikrowydzieleń bogatych w alkalia. Stan naprężeń wokół takich
wydzieleń jest źródłem powstawania kulistych pęknięć przy obciążeniu mechanicznym. Również bardzo małe we włóknach
są wtrącenia obcych stałych cząstek. W przypadku wiskerów, właściwości mechaniczne są wyjątkowo wysokie, gdyż nie
występują w nich praktycznie defekty takie jak dyslokacje- ich budowa jest prawie doskonałą struktura krystaliczną,
przez co uzyskiwane przez nie wytrzymałości osiągają poziom teoretyczny. Włókna cechują również specyficzne
właściwości optyczne. Występujące we włóknach szklanych wewnętrzne odbicie, wykorzystano w konstrukcji
światłowodów.

W6,12-13; MC s111-113

50.Charakterystka i podział warstw oraz

51.Metody otrzymywania warstw.

Warstwa to warstwa na powierzchni z grubsza. Właściwości materiałów występujących na powierzchni w postaci

warstw są zależne od właściwości materiału warstwy (struktury i mikrostruktury), charakteru oddziaływania z podłożem
oraz od właściwości samego podłoża. Zadaniem warstw jest ochrona materiału przed środowiskiem, zwiększanie
wytrzymałości materiału oraz jego dekoracja. W elektronice wykorzystuje się także warstwy jako wyroby techniczne. Podział
warstw



Powłoki-emalie, farby itp. Spełniające rolę tylko ochronna i dekoracyjną



Warstwy- które w istotny sposób zmieniają właściwości podłoża lub pełnia samodzielna funkcje jako wyrób:

-cienkie warstwy 10-10

4

nm

-grube warstwy >10

4

nm



Połączenia warstwowe np. ceramika-metal

Otrzymywanie warstw:



Chemiczna krystalizacja z fazy gazowej CVD- warstwy osadzane są w wyniku reakcji chemicznej gazowych

reagentów na ogrzanym podłożu.



Fizyczna krystalizacja z fazy gazowej PVD- warstwy osadzane są w wyniku osadzania reagentów na podłożu w

toku przemian fizycznych: parowania, sublimacji itp.



Warstwy grube nanoszone plazmowo- technologia wykorzystująca gorącą plazmę (2500-3000˚C). ziarna proszku

wprowadzanego do płomienia plazmotronu ulegają częściowemu nadtopieniu i osadzając się na podłożu krzepną
tworząc warstwę. Wykorzystuje się tą technikę do nanoszenia warstw ochronnych na narzędzia.

Przykłady zastosowania cienkich warstw



Elektronika(warstwy czynne-Si, Ge oraz bierne-azotki, tlenki SiO

2

)



Optoelektronika- światłowody



Warstwy antyrefleksyjne- okulary, szyby



Warstwy ochronne- narzędzia skrawające, szkło

Grube warstwy



Emalie



Szkliwa



Złącza ceramika-metal

W6,22-30

52.Definicja i podział materiałów kompozytowych.

Kompozyt jest to materiał zbudowany w sposób świadomy z dwu lub więcej tworzyw i posiadający właściwości

inne niż poszczególne materiał składowe. W kompozytach można łączyć różne rodzaje materiałów jak metale, polimery i
tworzywa ceramiczne wykorzystując ich specyficzne cechy, a także materiały tego samego typu miedzy sobą. Obecnie
wyróżnia się 3 podstawowe rodzaje kompozytów:



Ziarniste (cząstkowe)



Włókniste



Warstwowe (laminaty)

Właściwości kompozytów są wypadkową właściwości i udziału objętościowego poszczególnych faz. Zależności te mogą
mieć charakter modelowy lub empiryczny. Do niektórych właściwości kompozytów można stosować prawo mieszanin, np.
do gęstości. Ogólnie wygląda ono tak: W=W

1

V

1

+W

2

V

2

gdzie W

n

właściwość danej fazy, V

n

- udział objętościowy danej fazy,

W- właściwość całego materiału.

W7,5-7

53.Kompozyty ziarniste; budowa i podstawowe zalety.

Materiały zbudowane z ciągłej osnowy, w której rozprowadzone są izometryczne ziarna drugiej fazy, o

wymiarach nm- µm nazywamy kompozytami ziarnistymi. Podstawowymi zmiennymi, od których zależy efektywność
działania zdyspergowanych w osnowie cząstek, są średnia droga swobodna w osnowie pomiędzy cząstkami l oraz odstęp
miedzy nimi D

cz

.Wielkości te są związane ze sobą średnicą cząstek d i ich udziałem objętościowym V

cz

następującymi

zależnościami;

l=(2d/3V

cz

)(1-V

cz

) i D

cz

=(2d

2

/3V

cz

)

0,5

(1-V

cz

)

Kolejną wielkością charakteryzująca kompozyty ziarniste jest próg perkolacji. Określa on maksymalny udział fazy
ziarnistej, przy którym pozostaje ona równomiernie rozmieszczona i nie występują w postaci aglomeratów. Z obliczeń
teoretycznych wynika, iż powinien on wynosić 18-22%. Cząstki mogą mieć wiele zastosowań, np. ziarna mogą
przeciwdziałać ruchowi dyslokacji w osnowie co pozwala zachować większa sztywność materiału (kompozyty o
metalicznej osnowie i ceramicznych ziarnach na przykład), ograniczają ruchy makrocząstek w materiałach, większe cząstki
(powyżej 0,1µm) mogą przenosić obciążenia z osnowy (hamują jej odkształcanie)

W7,8; WMC s169-175, MC 106-107; wykład z politechniki gdańskiej

54.Które właściwości materiałów można szczególnie poprawić stosując kompozyty ziarniste?
Odpowiedź uzasadnij.

W przypadku kompozytów ziarnistych ceramiczno-ceramicznych,

można wyróżnić dwie grupy graniczne-pierwszą w której obserwuje się wzrost
wytrzymałości materiału z niewielkim wzrostem wytrzymałości na kruche
pękanie i drugą, dokładnie odwrotną. Dla pierwszej grupy, wzrost
wytrzymałości wiąże się ze zmniejszaniem krytycznej długości pęknięcia, dla
drugiej jest znów przeciwnie-wzrost K

1c

wynika ze zwiększenia krytycznej

długości pęknięcia. Tłumaczy się to na podstawie tworzenie się pęknięć w
materiale na skutek resztkowych naprężeń cieplnych. Naprężenia te powstają w
kompozycie gdy ochładzamy go do temperatury pokojowej i wynikają z różnych
współczynników rozszerzalności osnowy(α

m

) i cząstek(α

p

). Gdy α

m

>α

p

w

materiale powstają krótkie pęknięcia wzdłuż linii łączących dwa ziarna. Im
więcej ziaren tym krótsze linie-im więcej cząstek tym lepsza wytrzymałość σ.
Gdy α

m

<α

p

, tworzące się pęknięcia biegną naokoło ziaren- wydłużają się-

wzrasta K

1c

. W tej grupie, bardzo popularne są kompozyty z częściowo

stabilizowanym ZrO

2

(są to tak właściwie ziarna roztworu stałego CeO

2

, Y

2

O

3

lub MgO w ZrO

2

). W temperaturze pokojowej ZrO

2

występuje w postaci nietrwałej odmiany tetragonalnej. W warunkach

obciążenia rozciągającego w ziarnach, ZrO

2

przechodzi w odmianę jednoskośną. W obciążonym materiale wierzchołek

rozprzestrzeniającego się w osnowie pęknięcia poprzedza obszar, w którym na pole znacznych naprężeń rozciągających,
nakłada się pole maksymalnych naprężeń ścinających. Gdy ten obszar dojdzie do ziarna, może inicjować wspomniana
przemianę. Odmiana jednoskośna ma większą objętość od tetragonalnej, w rezultacie czego w najbliższym otoczeniu ziarna
powstają naprężenia ściskające. Pęknięcie o którym wcześniej mówiliśmy zaczyna się więc rozprzestrzeniać w polu naprężeń
ściskających, które przeciwdziałają rozwieraniu się pęknięcia- wzrasta jego odporność na kruche pękanie.

WMC s170-175; MC s107

55.Kompozyty włókniste: budowa i podstawowe zalety.

Są to materiały wielofazowe, których składowymi elementami struktury są osnowa oraz włókna (krótkie lub

długie). Osnowa w której są umieszczone włókna, nadaje kompozytowi jego zewnętrzną postać i makroskopowo
monolityczną budowę. Jej funkcja polega na przejmowaniu zewnętrznych obciążeń mechanicznych i przekazywaniu ich
włóknom. Włókna dzięki ich strukturze i postaci (punkt 49), cechuje wytrzymałość rząd lub dwa większa
od litych polikryształów z tego samego materiału. Takie właściwości włókien pozwalają nadąć
kompozytowi sztywność, wytrzymałość i odporność na kruche pękanie większe niż jest to możliwe dla
czystej osnowy. Najczęściej spotykanymi włóknami są włókna szklane, węglowe, wiskery SiC i Al

2

O

3

. Jako

osnowy zwykle służą polikrystaliczne materiały ceramiczne, polimery organiczne i metale. Dla
kompozytów o silnie związanych osnowie i włóknach można zapisać regułę mieszanin: E= E

wł

V

wł

+ E

os

V

os

, gdzie E-moduł

Younga, V-udział objętościowy a indeksy

wł

,

os

odnoszą się do odpowiednich faz. Aby uzyskać jak najwyższe właściwości,

udział włókien powinien być możliwie duży. Znaczny wpływ na właściwości kompozytu ma także granica rozdziału
osnowa-włókno. Ocenę stopnia wypełnienia przez włókno objętości osnowy można
oprzeć o model (rysunek) układu włókien, złożony z wyprostowanych włókien o średnicy
d, zorientowanych swoją osią w trzech kierunkach w przestrzeni i= x, y, z. Jeśli odległość
między osiami włókien w poszczególnych kierunkach wynosi odpowiednio t

x

, t

y

, t

z

, to

stosunek odległości pomiędzy osiami włókien w dwu wzajemnie prostopadłych w
przestrzeni kierunkach można zapisać jako; K

y

= t

x

/t

y

, K

z

= t

x

/t

z

, K

x

= t

y

/t

x.

Udział przestrzeni

dostępnej dla włókien zorientowanych w i-tym kierunku dany jest przez współczynnik Z

i

.

Granicznymi wartościami są Z

i

=0, gdy nie ma włókien ułożonych równolegle do i-tego kierunku oraz Z

i

=1, gdy wszystkie

położenia dostępne dla włókien w danym i-tym kierunku są zajęte. Przy danych wartościach Ki i Zi można zapisać:
t

x

=(d/2)(πW)

0,5

, gdzie W=(Z

x

K

y

K

z

+Z

y

K

z

+Z

z

K

y

)/(V

wł

). Gdy np. ułożymy włókna krzyżowo, najgęściej jak to możliwe, w dwu

kierunkach x i y, to Z

z

=0, Z

x

=Z

y

=1,t

x

=d, t

y

=2d, to otrzymamy ze wzoru że V

wł

wynosi 0,79. Jedynym ustawieniem o

porównywalnym udziale włókien jest ustawienie z włóknami równoległymi ustawionymi tylko w jednym kierunku. Przy
izotropowym rozłożeniu włókien w 3 kierunkach, można uzyskać V

wł

=0,59. Trzeba pamiętać że jeśli ułożymy włókna w

danym kierunku, ten kierunek będzie miał lepsze właściwości. Dlatego zwykle stosuje się trójwymiarowe ułożenia
włókien, zyskując izotropowość kompozytu kosztem jego właściwości. Przejdźmy do zagadnień związanych z granica
rozdziału włókno-osnowa. Można wyróżnić parę typów:

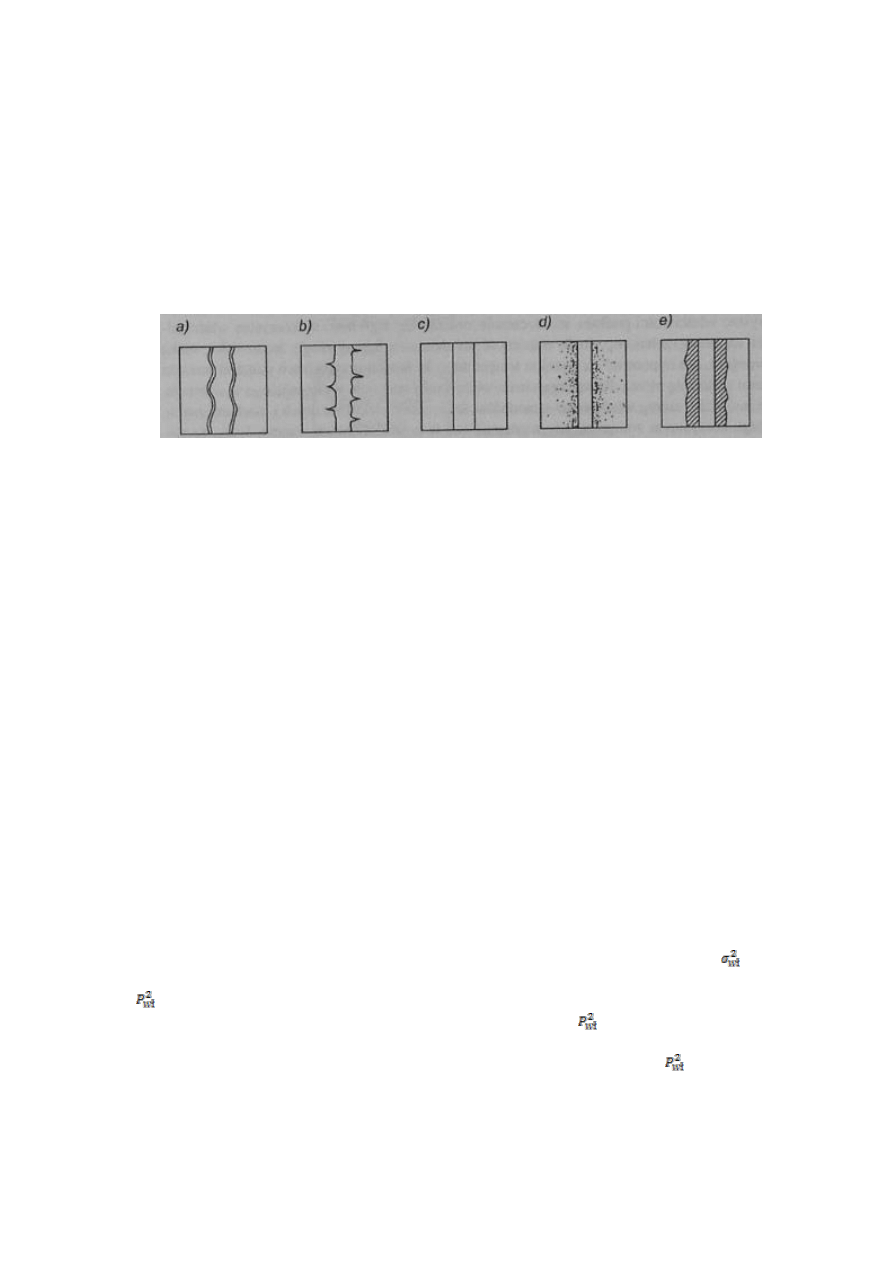
a) Włókno klinuje się w czysto mechaniczny sposób w osnowie- rzadko spotykane
b)Włókno ma postać drutu kolczastego- częste gdy używamy wiskerów, daje dobre powiązanie mechaniczne
włókna i osnowy.
c)Włókno gładkie, nie reagujące z osnową- więź włókno- osnowa jest słaba, pogarszają się właściwości materiału.
Aby temu zaradzić wprowadza się na granice organiczne substancje sprzęgające, łączące się chemicznie z zarówno
włóknami jaki i osnową.
d)Włókna rozpuszczane w osnowie, tworzą w niej roztwór stały- częste w osnowach ceramicznych i metalicznych.
e)Włókno reaguje z osnową, na granicy rozdziału tworzy się warstwa produktu ich reakcji- wzmacnia więź włókno-
osnowa, ale wskutek różnych właściwości sprężystych włókien i warstwy reakcyjnej łatwo powstają i
rozprzestrzeniają się tu
pęknięcia.

Zalety użycia włókien:



Podwyższają sztywność



Zwiększają udarność



Zwiększają odporność na kruche pękanie



Zwiększają wytrzymałość materiału

W7,9-12; BiW s92-96; MC s115-116; WMC s175-178 (dużo informacji o osnowach ceramicznych)

56. Które właściwości materiałów można podnieść stosując kompozyty włókniste.
Odpowiedź uzasadnij. Oraz

91.Opisz mechanizm podwyższania energii pękania w kompozytach włóknistych.

Stosując kompozyty włókniste możemy podwyższyć moduł Younga materiału. Jak było napisane w poprzednim

punkcie, dla kompozytów o silnie związanych osnowie i włóknach można zapisać regułę mieszanin: E= E

wł

V

wł

+ E

os

V

os

, gdzie

E-moduł Younga, V-udział objętościowy a indeksy

wł

,

os

odnoszą się do odpowiednich faz. Jeśli włókna maja wyższy moduł

Young (a mają), moduł Younga materiału znacznie rośnie w porównaniu do czystej osnowy. Oprócz tego kompozyty
charakteryzuje mała gęstość, dzięki czemu maja dużą wytrzymałość i sprężystość właściwą- czyli stosunek wytrzymałości i
modułu sprężystości do gęstości. Inną właściwością która ulega poprawieniu jest odporność materiału na kruche pękanie.
Ponieważ granice rozdziału faz, wskutek zaburzonej budowy maja zwykle niższą wytrzymałość, gdy główne pękniecie
dochodzi do granicy osnowa-włókno, następuje lokalne rozwarstwienie materiału. Gdy obciążenia są równoległe do osi
włókien, rozwarstwienia na granicy rozdziału są równoległe do kierunku naprężeń, maja ograniczoną długość i nie
przechodzą przez cały materiał. Następuje w związku z tym pochłoniecie energii oddziaływań sprężystych bez dekohezji.
Można powiedzieć że włókna spinają(mostkują) główne pękniecie, powstrzymując je przed rozprzestrzenianiem. Wynika
to z tego, że aby wzrost szerokości u pęknięcia był możliwy, włókno musi się na odcinku l

db

rozciągnąć o tą zmianę

szerokości czyli ∆u. Powstaje tutaj energia odkształceń sprężystych o wartości na jednostkowa powierzchnię w=(

/2E

wł

)l

db

Efekt mostkowania będzie tak długo aktywny, jak długo trzyma się włókno, zatem górna wartość tej energii wynosić będzie
w

m

= (

/2E

wł

)l

db

gdzie P

wł

- wytrzymałość włókna na rozciąganie. Dla udziału objętościowego włókien V

wł

energia

zmagazynowana w materiale na jednostkę powierzchni wynosić będzie w

m

= V

wł

(

/2E

wł

)l

db

Energia ta jest

pochłaniana przy rozprzestrzenianiu się pęknięcia. Będzie ona częścią efektywnej energii powierzchni. Można więc napisać,
że odporność na kruche pękanie kompozytu w którym jest mostkowanie wynosi: K

c

=(Eγ

ef

)

0,5

=(E(γ+ V

wł

(

/2E

wł

)l

db

)

0,5

.

Włókna gdy zostanie przekroczona ich wysoka wytrzymałość ulegają dekohezji, jednak trzeba pamiętać, że zaczyna się
ona w miejscach występowania defektów, a te nie zawsze leżą na osi pęknięcia- czyli uszkodzenie może być w innym
fragmencie włókna, np. w takim które w całości jest w osnowie. Aby uległo ono dekohezji, trzeba je z włókna „wyciągnąć”.
Praca potrzebna na wyciągniecie włókien przez naprężenia ścinające występujące na granicy rozdziału włókno-osnowa

wynosi τ(l

po

/r)

2

gdzie l

po

- długość elementu włókna którego wyciągniecie spowoduje eliminacje mostkowania, τ- naprężenia

ścinające, r- promień włókna. Przy udziale włókien wyciąganych V

po

, maksymalna wartość energii odkształcenia sprężystego

na jednostkowa powierzchnię, pochłanianej w procesie wyciągania włókien wynosi γ

po

=V

po

r τ(l

po

/r)

2

. Cały ten mechanizm

jest w kompozytach włóknistych wyjątkowo efektywny.

W7,9-12; WMC s175-178; MC s107-110; BiW s92-96

57.Kompozyty warstwowe (laminaty): budowa i podstawowe zalety

Laminat jest to kompozyt powstający z połączenia naprzemiennych warstw różnego

rodzaju w sposób trwały. Zazwyczaj składa się z ułożonych naprzemiennie warstw dwóch
materiałów, jednej o wyższej wytrzymałości i drugiej znajdującej się pomiędzy warstwami
pierwszej (może pełnić role lepiszcza). Laminaty cechuje anizotropowość właściwości-
wytrzymałość i sztywność zależą od położenia kierunku warstwy. Przykładem takiego materiału
może być laminat z warstw SiC- warstwy wytrzymałe, ale kruche i sztywne, oraz z warstw
grafitu- słabszego i nie tak sztywnego. Podczas obciążania, laminat zaczyna pękać w miejscu
występowania defektów w sztywnej warstwie o wysokim module Younga E. Pękniecie dochodzi
następnie do mniej sztywnej warstwy i rozprzestrzenia się w niej. Lokalny zanik spójności tej warstwy, umożliwia wzajemne
przemieszczenie sąsiednich warstw, co oznacza zmniejszenie oporności laminatu na
rozprzestrzenianie się pęknięcia . Następnie pękniecie znów trafia na sztywna warstwę, co
powoduje ponowny wzrost R. Proces ten powtarza się aż zostanie spełniony warunek dla
katastrofalnego rozwoju pęknięcia. I

σ=const

=

, gdzie R- oporność materiału, G- siła

rozprzestrzeniająca pękniecie, a- długość pęknięcia, σ- naprężenie. Na drugim rysunku warunek
ten jest spełniony przy pękaniu trzeciej sztywnej warstwy. Stabilne zwiększanie się długości
pęknięcia- czyli bez zapoczątkowania jego katastrofalnego rozprzestrzeniania się, jest
równoznaczne ze zwiększeniem krytycznej długości pęknięcia a

c

i odporności na kruche pękanie

K

Ic

, ponieważ (G

Ic

E’)

0,5

= (RE’)

0,5

=K

Ic

=σ

c

a

c

- krytyczna długość pęknięcia, G

Ic

- krytyczna siła

rozprzestrzeniająca pęknięcie o tej długości, E’- dla płaskiego stanu naprężeń E’= E(1-v), gdzie E- moduł Younga, v- liczba
Poissona.

Obecnie najczęściej stosowane laminaty to laminaty poliestrowo-szklane (PS) (na przemian tkaniny szklane i

warstwa żywice, łatwe w wyrobie, dość tanie), laminaty epoksydowe (ES) oraz laminaty szklano-epoksydowe. (Powstają w
wyniku nasycenia żywicą epoksydową tkaniny szklanej i sprasowaniu jej w układzie warstwowym. Maja b. wysokie
właściwości mechaniczne- wytrzymałość na zginanie i ściskanie)

W7,13; WMC s178-180; Wikipedia; Niestety autor tego opracowania sam nie rozumie o co w tym chodzi, materiał jest w
podręcznikach praktycznie niewyjaśniony.

58.Uzasadnij celowość stosowania kompozytów warstwowych. Podaj przykłady.

Laminat(kompozyt warstwowy) składa się z faz, które występują w postaci dwu lub wielu warstw łączonych ze

sobą w sposób trwały (połączenia są nieskończenie cienkie-odkształcenia przebiegają po grubości kompozytu i żadna
warstwa nie może się przemieszczać względem innej). Warstwy w laminacie są tak ustawione względem siebie i zarazem
przyjętego układu odniesienia, aby uzyskać takie charakterystyki sztywnościowe laminatu, które umożliwiają

formowanie elementów konstrukcyjnych zdolnych do przenoszenia obciążenia o dowolnym kierunku. O wytrzymałości
laminatu decydują następujące czynniki :

1) charakterystyki wytrzymałościowe warstwy

2) charakterystyki sztywnościowe warstwy

3) charakterystyki temperaturowe (współczynniki rozszerzalności cieplnej) warstwy

4) sekwencja ułożenia warstw i ich udział objętościowy.

Skoro o właściwościach laminatów decydują indywidualne właściwości warstw, to można je dobrać w taki sposób, aby
uzyskać potrzebne optymalne właściwości kompozytu w zależności od zastosowania.

Laminaty charakteryzują się więc: wysoką wytrzymałością mechaniczną, wysoką odpornością na warunki atmosferyczne,
wysoką twardością powierzchni, odpornością na zabrudzenia, odpornością na środki chemiczne, niektóre z nich są
produktami naturalnego pochodzenia.

Przykład:

- Nowoczesne konstrukcje pancerzy to wielowarstwowe elementy kompozytowe zawierające warstwy ceramiczne,
metaliczne i polimerowe. Ceramika konstrukcyjna ma dużą twardość powiązaną z małą gęstością. Rolą warstwy ceramiki
jest rozproszenie i pochłonięcie energii pocisku, w trakcie jej fragmentacji. Oprócz tego istotną cechą ceramicznych warstw
ochronnych jest zmiana toru wnikania pocisku podczas ich przebijania. Zmiana kierunku penetracji pocisku w przebijanej
ceramice jest podstawą do takiego sposobu zaprojektowania warstwy lub kilku warstw ceramicznych w konstrukcji
pancerza kompozytowego, aby móc skutecznie rozproszyć energię kinetyczną pocisków przeciwpancernych.

- kondensator Al-mika –duża stałość pojemności w czasie, ściśle określony temperaturowy współczynnik pojemności

- kompozyt gradientowy FGM- element pancerza ceramicznego

Internet

59.Opisz materiały gradientowe (FGM).

Są kompozytami o budowie warstwowej, jednak w odróżnieniu od laminatów, idąc od jednej powierzchni

materiału do drugiej skład zmienia się w sposób ciągły. Przykładem FGM może być materiał metaliczno-ceramiczny
działający w wysokiej temperaturze zewnętrznej. W związku z tym na działanie temperatury wystawimy koniec ceramiczny-
o wysokiej odporności termicznej. Trzeba jednak pamiętać, że w związku z tym mogą w materiale wystąpić duże gradienty
temperatur. Na wskutek tego w wyniku różnicy współczynników rozszerzalności cieplnej (α) ceramiki i metalu tworzą się
na ich styku naprężenia. Jeśli nie zostaną one rozładowane, w materiale pozostaną naprężenia resztkowe. Także wewnątrz
samych warstw powstają naprężenia. Aby zminimalizować ten problem, kolejne warstwy materiału powinny mieć małą
grubość, a ich skład zmienia się w kolejnych warstwach w sposób płynny, od warstwy czysto ceramicznej do czysto
metalicznej. Dzięki temu wskroś materiału występują płynne zmiany α,
a także współczynnika przewodnictwa cieplnego λ i sztywności
charakteryzowanej przez moduł Younga E. Dodatkowo aby zmniejszyć
naprężenia cieplne, można w warstwach środkowych wprowadzić pory,
które pozwalają na swobodne rozszerzanie i skurcz (oczywiście tylko do
pewnego stopnia) części o różnej temperaturze. Taki materiał FGM łączy
w sobie wysoka wytrzymałość termiczna faz ceramicznych i mechaniczną
faz metalicznych. Oprócz materiały o funkcjonalnym gradiencie składu
maja zastosowanie w wojsku (metaliczno-ceramiczne, jako pancerze),
biomateriałach (hydroksyapatyt- kolagen) a także w przezroczystych
materiałach o gradiencie współczynnika załamania światła.

W7,14-16; WMC s 180-181; BiW s87-88

60. Porównaj na wybranym przykładzie kompozyt (sztuczny) z odpowiadającym mu
materiałem naturalnym wytwarzanym przez przyrodę.

Przykładem takiego kompozytu może być kompozyt, którego naukowcy (prof. Ślusarczyk) mają zamiar

wykorzystać jako implant kostny (zamiast tkanki kostnej). Jest on zbudowany z materiału organicznego- polimeru
cukrowego i nieorganicznego hydroksyapatytu. Kompozyt taki doskonale łączy się z naturalną tkanką kostną. Kompozyt ma
strukturę podobną do kości. W stanie suchym jest twardy. Po nasączeniu staje się miękki i można go odpowiednio do
potrzeb kształtować, aby uzupełniać nim różnego rodzaju ubytki kostne. Naturalne kości nie są wystarczająco elastyczne aby
się dopasować do ubytków. Kompozyt daje się dobrze sterylizować, możemy go również nasączać substancjami
antybakteryjnymi (np. antybiotykami) albo czynnikami wzrostowymi. Badania kompozytu wykazały, że nie jest toksyczny.
Składniki są również kompatybilny biologicznie z tkanką kostną, nie są rakotwórcze i nie mają właściwości alergizujących.
Kompozyt o tak unikalnych właściwościach mógłby być wykorzystywany m.in. w uzupełnianiu ubytków kostnych u ludzi, np.
po usunięciu fragmentów zajętych przez komórki rakowe, czy w stomatologii, np. jako materiał wypełniający zębodół, na
którym można by osadzać implanty zębów. Kość zbudowana więc z takie kompozytu byłaby wytrzymalsza, odporniejsza na
uszkodzenia i choroby. Mogłaby też pełnić dodatkowe funkcje-na przykład mogłaby być nośnikiem leków.

61.Wyjasnij pojęcie nanokompozyty.

Nanokompozyty są to wielofazowe materiały, w których jedna z faz ma co najmniej jeden wymiar mniejszy niż

100nm. Cechują je unikalne właściwości, wynikające z bardzo wysokiego stosunku powierzchni nanocząstek do ich
objętości. Obecnie rozróżnia się 3 rodzaje nanokompozytów ze względu na osnowę:



O osnowie metalicznej



O osnowie ceramicznej



O osnowie polimerowej

W zależności od dodawanych cząstek uzyskuje się różne efekty:



Montmorylonit- dobre właściwości barierowe (gazy, zapachy)



Fulereny i nanorurki- wzrost właściwości mechanicznych, elektrycznych oraz trwałości.



Krzemionki- podwyższenie właściwości mechanicznych i odporności termicznej



Metale i ich związki- podwyższają przewodność elektryczna i cieplną, działają jako katalizatory. Srebro działa

bakteriobójczo



Nanopory- zmniejszenie masy

Wykład z politechniki poznańskiej: http://www.dmef.put.poznan.pl/download/NANOKOMPOZYTY15_10_05.pdf

62.Scharakteryzuj na wykresie cechy odkształcenia sprężystego i plastycznego w ujęciu
reologicznym.

Odkształcenie sprężyste- jest to odkształcenie odwracalne, gdy zachodzi to po odjęciu obciążenia materiał wraca do
swojej pierwotnej postaci w sposób natychmiastowy (chyba że mamy ciało o sprężystości opóźnionej). Odkształcenie
liniowo zależy tu od naprężenia, zgodnie z prawem Hooke’a: σ= Eε

Odkształcenie plastyczne-Odkształcenie tutaj jest trwałe, materiał po odjęciu obciążenia, zachowuje nadana przezeń
formę.

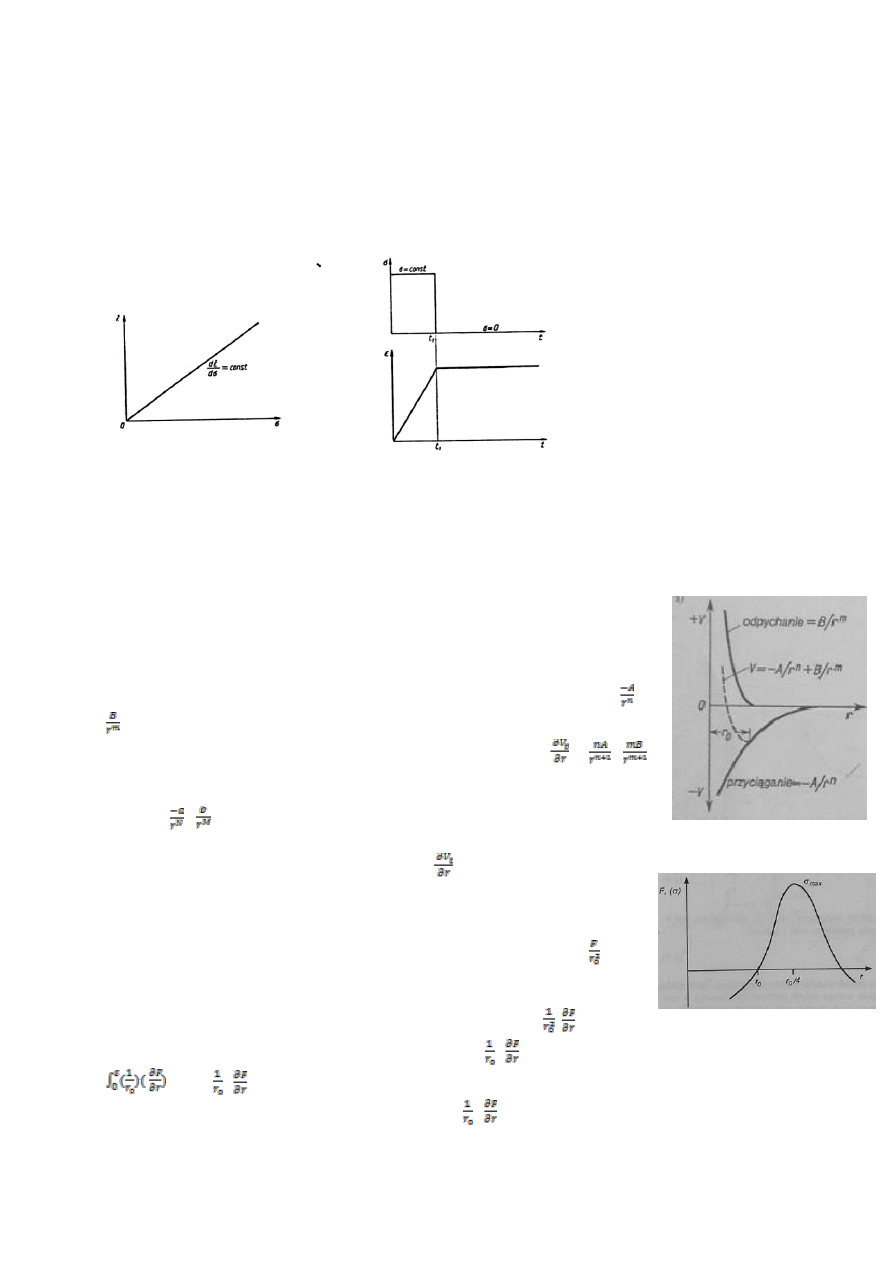
W8,9-10; BiW s98-99

63.Scharakteryzuj na wykresie cechy odkształcenia lepkościowego w ujęciu reologicznym.

Jak można wywnioskować z powyższych wykresów w wyniku odkształcenia lepkościowego długość materiału

zwiększa się proporcjonalnie do wielkości działającego naprężenia. Poza tym naprężenia działające w czasie początkowym
są stałe aż nastąpi trwałe odkształcenie materiału. Wtedy naprężenie spadają do 0. Ponadto w początkowym czasie
zaobserwować liniowy wzrost wartości odkształcenia- w chwili t

a

osiąga ono wartość maksymalną. W czasie t> t

a

wykres

odkształcenia od czasu jest stały.

64.Wyprowadź zależność na teoretyczną wartość stałych sprężystości w
ujęciu modelowym dwu atomów.

Przyczyny sprężystego odkształcania, można wyjaśnić rozpatrując zmiany energii

potencjalnej atomów w zależności od odległości międzyatomowej r. Energia potencjalna atomu V

p

wynika z występowania sił przyciągania i odpychania między atomami. Można to wyrazić; V

p

=

+

(1) gdzie A i B- stałe proporcjonalności dla sił odpychania i przyciągania, m i n- wykładniki

potęgowe. Konkretna siłę działającą na atom można obliczyć z gradientu V

p

: F = -

= -

+

Znak minus, oznacza, że siła działa w kierunku od większej do mniejszej energii potencjalnej.
Następnie przyjmujemy, że nA= a, mB= b, n+1= N oraz m+1=M. Mając takie dane można zapisać

siłę jako: F=

+

(2). Równaniom 1 i 2 odpowiadają krzywe, nazywane krzywymi Condona-

Morse’a. Odległość odpowiadającą minimum energii potencjalnej nazywamy równowagową odległością międzyatomową

r

0

. W tej odległości siła działająca na atom wynosi 0, bo F= -

= 0, bo pochodna w minimum się

zeruje. Jeśli na atom w położeniu równowagi zacznie działać zewnętrzne obciążenie
mechaniczne powodujące przesuniecie atomu z tej pozycji o dr, to na atom zaczyna działać
wewnętrzna siła skierowana przeciwnie do kierunku przesunięcia. Wywołuje to tendencje

atomu do powrotu w pozycje równowagi- pojawiają się zatem naprężenia o wartości σ= . Układ

pozostaje w stanie naprężonym tak długo jak działa obciążenie. Po odjęciu obciążenia atom
wraca do pozycji równowagowej, co jest korzystne energetycznie- stąd sprężyste zachowanie

kryształów. Przyrost naprężenia które wywoływaliśmy można zapisać jako: dσ=( )( )

r=ro

dr. Ponieważ odkształcenie można

wyrazić za pomocą odkształcenia względnego ε, to dr=r

0

dε stąd: dσ=( )(

)

r=ro

dε czyli aby otrzymać σ musimy scałkować:

r=ro

dε = ( )(

)

r=ro

ε Teraz mając nasz σ, potrzebujemy określić współczynnik kierunkowy krzywej stycznej do

krzywej F(r) w pobliżu r

0

- wprowadzamy stałą sprężystości C: C=( )(

)

r=ro

Dla małych odkształceń względnych,

odkształcenie jest liniową funkcja naprężenia σ, C natomiast można uznać za stałą otrzymując równanie σ=Cε.

W8,16-18; MC s139-141; BiW s99-100; ZNoM s80-81

65.Narysuj krzywe σ= f(ε) dla typowych materiałów ceramicznych, metalicznych i polimerów.

Punkt F dla każdego z tych materiałów oznacza dekohezję. Szkło podobnie jak niemal wszystkie materiały

ceramiczne cechuje kruche pękanie- materiał traci spójność bez wystąpienia wcześniej znaczniejszych odkształceń.
Wykres ten będzie miał różną wartość F dla próbki materiału ceramicznego, ze względu na mechanizm dekohezji- decydują
o niej pęknięcia, pory, rysy, nieciągłości, będące zależne od właściwości konkretnej próbki. Dla metalu sytuacja wygląda
nieco inaczej. Początkowo rozciągamy go sprężyście, zgodnie z prawem Hooke’a, aż do osiągnięcia granicy plastyczności.
Od tego punktu materiał zaczyna zachowywać się plastycznie, odkształcenia są trwałe. W przypadku kauczuku mówimy o
materiale lepko sprężystym. Oznacza to, że materiał równocześnie wykazuje cechy sprężyste jak i lepkie. Odkształcenie
lepko sprężyste bowiem, podobnie jak sprężyste jest odwracalne, jednak z powodu cech lepkościowych, materiał powraca
do dawnej postaci dopiero po dłuższym czasie.

Artykuł z IMIR-u; BiW s98-99; MC s134

66.Podaj znane ci stałe materiałowe charakteryzujące odkształcenia
sprężyste.

Stałymi materiałowymi są ; moduł Younga E, moduł sztywności G, liczba Poissona v. Niestety

aby je wyprowadzić trzeba użyć stałych sprężystości C oraz stałych podatności sprężystej S. Możliwe że
nie jest to zupełnie potrzebne, ale wyprowadźmy to. Kontynuując punkt 64, można przypadek modelu
dwuatomowego, przenieść na wieloatomowy monokryształ. Aby go opisać należy podać szereg stałych
sprężystości. Opiszmy wokół dowolnego punktu w strukturze nieskończenie mały sześcian o
współrzędnych x

1

, x

2

, x

3

. Dzięki temu obciążenie dowolnie skierowane względem powierzchni sześcianu

można rozłożyć na składowe prostopadłe(normalne) i styczne do jego 6 ścian. W tym ujęciu dowolne
obciążenie można scharakteryzować przez jedną składową normalna i dwie styczne (rysunek, 3
składowe po jednej na kierunek). Zakładamy, że odkształcenia i naprężenia na ścianach przeciwległych i
naprężenia są identyczne. W związku z tym zostają nam 3 ściany, które łącznie mają 3 składowe normalne i 6 stycznych. Przy
odkształceniach statycznych, następuje dalsza redukcja, bowiem styczne składowe naprężenia i odkształcenia na wzajemnie
prostopadłych ścianach są sobie równe- czyli łącznie zostaje nam 6 wielkości. Teraz dla pojedynczego kryształu możemy
zapisać równania, równoważne prawu Hooke’a: (σ

i

)=(C

ij

)(ε

j

) gdzie i,j=1,2…6. Ponieważ mamy 6 naprężeń, dla każdego

musimy zapisać równanie, co daje nam 6 równań z 36 stałymi C

ij

:

Układ ten można dalej uprościć, bowiem C

ij

=C

ji

(i≠j). Ogólnie można przyjąć że im wyżej symetryczny jest układ, tym mniej

stałych C (dla regularnego np. są tylko 3, bowiem struktura jest izotropowa i wszystkie kierunki są równoważne, czyli
C

11

=C

22

=C

33

itd). Ponieważ polikryształy są również izotropowe, więc obowiązują je takie same zasady jak kryształy

regularne. Otrzymujemy układ 3 równań dla naprężeń normalnych i jednego równania dla naprężeń ścinających.;

σ

1

= C

11

ε

1

+C

12

ε

2

+C

12

ε

3

σ

2

= C

12

ε

1

+C

11

ε

2

+C

11

ε

3

σ

3

= C

12

ε

1

+C

12

ε

2

+C

11

ε

3

σ

4

= C

44

ε

4

przy czym ε

4

= ε

5

= ε

6

Obok stałych sprężystości można zdefiniować stałe podatności sprężystej S

ij

, dostając odwrotne równanie macierzowe:

ε

1

=S

11

σ

1

+ S

12

σ

2

+ S

12

σ

3

ε

1

=S

12

σ

1

+ S

11

σ

2

+ S

12

σ

3

ε

1

=S

12

σ

1

+ S

12

σ

2

+ S

11

σ

3

ε

1

=S

44

σ

4

Więc dochodząc do sedna sprawy, charakteryzując sprężystość stosujemy stale inżynierskie. Charakteryzujemy je jako:

E=(∂σ

i

/∂ε

j

) (i=j=1,2,3)

G=(∂σ

i

/∂ε

j

) (i=j=4,5,6)

V=-(∂ε

i/

∂ε

j

)

σi σk

Dla materiałów izotropowych, otrzymuje się

E=(∂σ

1

/∂ε

1

) = 1/S

11

G=(∂σ

4

/∂ε

4

) = 1/s

44

=C

44

V=-(∂ε

2/

∂ε

1

)

σ2 σ3

=…

=-(∂ε

3/

∂ε

2

)

σ1 σ3

=-

S

12

/S

11

Ponieważ stałe podatności sprężystej musza być identyczne w każdym kierunku, to można wyprowadzić

S

44

=2(S

11

-S

12

)

Dodatkowo gdy się złoży wszystko w kupę, to otrzymamy zależności miedzy stałymi:

E=2G(1+v)

W8,19; MC s141-146; BiW s100-103; ZNoM s83-86

67.Podaj warunki i postać uogólnionego prawa Hooke’a.

Dla ciał izotropowych oraz kryształów regularnych, korzystając z wyprowadzonych w poprzednim punkcie stałych

materiałowych, można zapisać układ równań zawierający stałe podatności sprężystej w inny sposób:

ε

1

=

- (σ

2

+σ

3

)

ε

2

=

- (σ

1

+σ

3

)

ε

3

=

- (σ

1

+σ

2

)

ε

4

=

Taki układ równań nazywamy uogólnionym prawem Hooke’a.

MC s146; BiW s103; ZNoM s86; WMC s77

68.Moduł Younga, sztywności i liczba Poissona: definicja i zakres wartości(podaj przykłady).

Moduł Younga E- jest hipotetycznym naprężeniem, które wystąpiłoby przy dwukrotnym wydłużeniu próbki

materiału, przy założeniu, że jej przekrój nie ulegnie zmianie (założenie to spełnione jest dla hipotetycznego materiału o
współczynniku Poissona v = 0). Ogólnie można powiedzieć, że jest współczynnikiem proporcjonalności pomiędzy
naprężeniem a odkształceniem w prawie Hooke’a. Według niego E = [N/m

2

] ( a dokładniej E=(∂σ

i

/∂ε

j

) (i=j=1,2,3), jeśli

wszystkie naprężenia normalne są równe zeru z wyjątkiem jednego, i-tego naprężenia). W materiałach anizotropowych,
jego wartość zależy od kierunku w materiale. Przykładowe wartości:



Stal- 200 [GPa]



Diament- 1035 [GPa]



βSiC- 352 [GPa]



Drewno dębowe- 11[GPa]

Moduł sztywności G- zwany także modułem Kirchoffa, jest współczynnikiem uzależniającym odkształcenie postaciowe
(odkształcenie postaciowe to zmiana kształtu ośrodka ciągłego przy zachowaniu długości odcinków równoległych do osi
układu współrzędnych- np. ścinanie) materiału od naprężenia, jakie w nim występuje. Jednostką modułu Kirchhoffa jest

paskal. Jest to wielkość określająca sprężystość materiału. G = [N/m

2

] gdzie τ- naprężenie ścinające, γ- odkształcenie

postaciowe. (G=(∂σ

i

/∂ε

j

) (i=j=4,5,6)). Przykładowe wartości:



Stal- 79,3 [GPa]



Diament- 575 [GPa]



βSiC- 232 [GPa]

Liczba Poissona- Podczas jednoosiowego rozciągania idealnie sprężystego ciała stałego, obok wydłużenia wzdłuż osi
działania naprężeń występuje również skurcz poprzeczny. Jeśli odkształcenie w kierunku działania naprężenia jest równe ε,
to odkształcenie w kierunku poprzecznym wynosi –vε. Współczynnik Poissona jest zatem stosunkiem odkształcenia
poprzecznego do odkształcenia podłużnego przy osiowym stanie naprężenia. Jest wielkością bezwymiarową i nie określa

sprężystości materiału, a jedynie sposób w jaki się on odkształca. v=

. Przykładowe wartości:



Stal- 0,27 do 0,30



Szkło- 0,18 do 0,30



Guma> 0,5

W8,14/19; MC s133-134; BiW s98, 103, 105; Wikipedia

69.Narysuj wykres zależności odkształcenia od czasu dla odkształcenia sprężystego ze
zjawiskiem relaksacji. Oraz

70.Podaj definicje zrelaksowanego i niezrelaksowanego modułu Younga.

Odkształcenie sprężyste wiąże się z przemieszczeniem atomów, które wymaga czasu. W pewnych warunkach

możliwe więc jest, że moment osiągnięcia maksymalnego odkształcenia może być opóźniony w stosunku do momentu
przyłożenia obciążenia. Obciążony materiał ulega natychmiastowemu odkształceniu ε

U

, które nazywamy odkształceniem

niezrelaksowanym. Jeśli utrzymamy stałe obciążenie to w miarę upływu czasu odkształcenie stopniowo przyrasta do
wartości ε

R

- odkształcenia zrelaksowanego. Podobnie wygląda powrót do pierwotnych wymiarów po odjęciu obciążenia.

Zależne od czasu odkształcenie można zapisać jako ε

a

=ε

a max

[1-exp(-t/Θ)] gdzie ε

a

- część odkształcenia zależna od czasu,

ε

a max

- jego końcowa, maksymalna wartość, Θ- czas relaksacji. Aby dostać wyrażenie na pełne odkształcenie materiału,

trzeba dodać ε

U

: ε(t)= ε

U

+ ε

a

= ε

U

+ ε

a max

[1-exp(-t/Θ)]. Ponieważ ε

a max

= ε

R

-ε

U

, oraz σ

0

/E

i

= ε

i

(dla i zrelaksowanego R i

niezrelaksowanego U), po podstawieniu dostaniemy:

ε(t)= (σ

0

/E

R

)+[(σ

0

/E

U

) - (σ

0

/E

R

)]exp(-t/Θ)

(70)Wynika z tego, że moduł Younga E

i

(i= U, R) zależy od stosunku czasu działania obciążeń do czasu relaksacji. Jeśli czas

działania obciążeń jest bardzo mały, to t/Θ będzie dążyć do zera, a zatem exp(-t/Θ) e

0

1. Jak wstawimy to do równania,

(σ

0

/E

R

) się skróci i zostanie ε=σ

0

/E

U

. Moduł Younga wyznaczony w takich warunkach nazywać będziemy nazywać

modułem niezrelaksowanym. Gdy natomiast sytuacja jest odwrotna i czas obciążenia jest długi w porównaniu do czasu
relaksacji, to exp(-t/Θ) przyjmować będzie bardzo małe wartości, zatem istotny będzie tylko człon σ

0

/E

R

,więc ε= σ

0

/E

R

. Tak

wyznaczony moduł Younga nazywamy modułem zrelaksowanym. Ponieważ ε

R

>ε

U,

to E

R

<E

U

. Czas relaksacji wynika z

opóźnienia przy dostosowywaniu się położeń atomów (nawet ziaren) do położeń wymuszanych przez naprężenia. Dla
atomów jest to średnio 10

-3

s, podczas gdy w powszechnie stosowanych metodach statycznych pomiarów, czas obciążenia

to 10

0

-10

2

s. W tych metodach mierzymy moduł zrelaksowany. Jeśli natomiast wywoływane obciążenia trwają 10

-3

s do 10

-

6

s jak ma to miejsce w przypadku metody ultradźwiękowej, to wtedy mierzony jest moduł niezrelaksowany.

W8,29-31; BiW s109-110; MC s135-136

71.Wyprowadź wzór na energię oddziaływań sprężystych.

Pytanie to jest trochę nie na miejscu, bowiem zarówno na wykładzie jak i w literaturze wyprowadza się głownie

gęstość energii. Zakładam że profesor miał to na myśli. Energią oddziaływań sprężystych, nazywamy pracę wykonaną
przez obciążenia i zmagazynowaną w odkształconym sprężyście materiale. Jej gęstość oznaczamy jako w i wyrażamy w
J/m

3

. Ogólnie gęstość zmagazynowanej energii odkształcenia sprężystego wynosi: w=

dla odkształcenia

osiowego o ε

1

pod naprężeniem σ

1

(σ

2

=σ

3

=0). Gdy weźmiemy z uogólnionego prawa Hooke’a

ε

1

=

- (σ

2

+σ

3

)

i

wstawimy do całki (Jak widać wstawiamy samo

,

bo σ

2

+σ

3

= 0) to uzyskamy że w=0,5E

=0,5(σ

2

/E) (podstawiając z

normalnego Hooke’a). Natomiast w materiale płasko odkształconym pod działaniem naprężeń σ

1

i σ

2

: w=2

=

=

Można zauważyć ogólna prawidłowość, że gęstość energii odkształcenia sprężystego jest proporcjonalna do iloczynu
modułu Younga i kwadratu odkształcenia względnego. Szczegółowa postać wyrażeń na gęstość tej energii zależy od
konkretnego stanu naprężeń i odkształceń.

W8,22; BiW s104; WMC s77-78

72.Wyprowadź zależność na E dla materiału dwufazowego w ujęciu modelu równoległego.

Przypadek kompozytu w którego osnowie 1 znajdują się silnie z nią powiązane włókna 2 ułożone

równolegle do kierunku działającej siły jest najprostszym przypadkiem z punktu widzenia analizy właściwości
sprężystych. W modelu przyjmujemy że E

1

≠E

2

ale liczba Poissona v

1

=v

2

=v. Przy wydłużaniu wzdłuż osi włókien

obie fazy ulęgają identycznemu odkształceniu ε

1

=ε

2

=ε. Ponieważ odkształcenie kompozytu jest jednorodne, to

energia odkształcenia sprężystego jest sumą energii odkształcenie sprężystego obu faz:

(V’

1

+V’

2

)=

V’

1

+

V’

2

gdzie E-moduł Younga całości, E

1

,E

2

- moduły odpowiednich faz, V

1

, V

2

- objętości odpowiednich faz.

Jeśli na granicach włókno-osnowa nie występuje żaden poślizg i cały kompozyt odkształca się jednakowo ε

1

=ε

2

=ε, to można

skrócić to wyrażenie do E=E

1

V

1

+E

2

V

2

gdzie V

1

, V

2

to udziały objętościowe (bo dzielimy pierwsze równanie obustronnie przez

(V’

1

+V’

2

)). Czyli dla tego modelu moduł Younga jest średnią ważona modułów obydwu faz. Tak policzona wartość jest

dolna granicą modułu Younga kompozytu, ponieważ zazwyczaj liczby Poissona są dla osnowy i włókien różne. W związku
z tym przy identycznym wydłużeniu w kierunku równoległym do osi włókien, powiązanie ze sobą osnowy i włókien
powoduje zmniejszenie poprzecznego kurczu w fazie o większej oraz zwiększenie tego skurczu w fazie o mniejszej liczbie
Poissona w porównaniu do stanu gdy obie fazy są oddzielnie. W związku z tym w obydwu fazach na granicy rozdziału
występują naprężenie rozciągające prostopadle do tych granic, co dostarcza dodatkowej energii odkształceń sprężystych,
przez co E>E

1

V

1

+E

2

V

2

W8,23; MC s146; ZNoM s89-90

73.Wyprowadź zależność na E dla materiału dwufazowego w ujęciu modelu szeregowego.

W modelu szeregowym sytuacja jest nieco inna. Ze względu na ułożenie warstw, ich względne

odkształcenie różni się miedzy sobą, natomiast naprężenie w każdej fazie wynosi tyle samo (czyli ε

1

≠ε

2

i

σ

1

=σ

2

=σ).

Przekształcając wzór:



=E



uzyskujemy, że



=



/E. Podstawiając to do wzoru

(V’

1

+V’

2

)=

V’

1

+

V’

2

otrzymujemy:

(V’

1

+V’

2

)=

V’

1

+

V’

2 .

gdzie E-moduł Younga całości, E

1

,E

2

- moduły odpowiednich

faz, V

1

, V

2

- objętości odpowiednich faz. Upraszczając powyższe wyrażenie otrzymujemy: 1/E=V

1

/E

1

+V

2

/E

2.

74.Napisz zależność E od porowatości uwzględniającą zjawisko koncentracji
naprężeń.

Korzystając z zależności dla kompozytów możemy potraktować pory, jako fazę o module

E=0. Zatem z reguły faz otrzymamy, że: E=E

1

V

1

+0 V

2

a ponieważ V

1

=1-V

2

, to otrzymamy, że E=E

1

(1-V

2

).

Jest to jednak tylko przybliżenie, bowiem wszelkie nieciągłości fazy stałej (np. pory) powodują
koncentrację naprężeń i zwiększenie gęstości zmagazynowanej energii odkształcenia sprężystego w tej
fazie w pobliżu nieciągłości. Można to prześledzić na rysunku. Podczas rozciągania łańcuchów
atomowych w materiale, występuje w nich jednolity przyrost odległości międzyatomowych. Jeśli teraz
część łańcuchów ulegnie zerwaniu, to nie mogą one przenosić obciążeń, musza to za nie robić sąsiedzi a
konkretnie obciążenia wędrują przez łańcuch na czubku pęknięcia. Czyli obciążenie wzrośnie
parokrotnie, a siła wystarczająca do zerwania tego wiązania zmaleje tyle samo razy. W litym,
jednorodnym materiale panuje w całej objętości naprężenie σ, w naszym wielkość naprężenia w pobliżu

wierzchołka σ

max

jest większa i wynosi: σ

max

=σ(1+2

)≈2σ

gdzie c- długość pęknięcia wzdłuż osi

równikowej, ρ- promień krzywizny wierzchołka. Zatem nasz wzór na moduł Younga ulegnie zmianie i

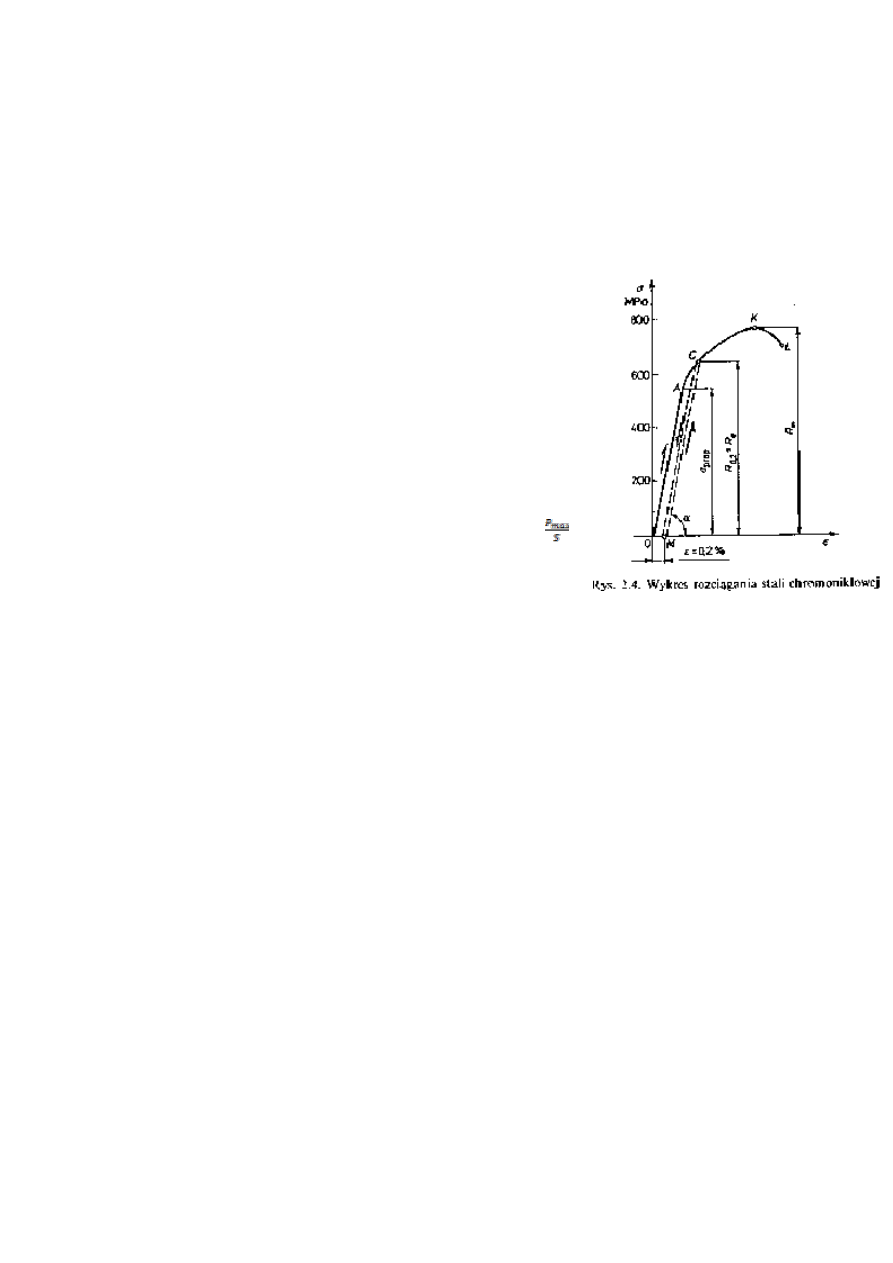
będzie wyglądał tak: E= E

1

(1-kV

2

), gdzie k- współczynnik koncentracji naprężeń równy σ/σ

max

. Jak widać z naszego wzoru na

σ

max

, koncentracja naprężeń zależy od kształtu poru. Ponieważ pory nie zawsze są kuliste (czyli nasze c będzie się zmieniać

w zależności od ułożenia poru), trzeba uwzględnić orientację poru względem kierunku obciążeń. Zrobił to Rossi, według
którego k=(5/4)(a/c)+(3/4) gdzie a- długość osi poru w płaszczyźnie prostopadłej, a c- równoległej do kierunku obciążeń.
Podane wzory są prawdziwe dla udziału porów do 0,2- powyżej tej wielkości pola naprężeń wokół porów zaczynają się
nakładać, co bardzo utrudnia ich analizę.

W8,25-27; BiW s106-108; MC s148-151

75.Zaznacz na wykresie σ= f(ε) dla metali, charakterystyczne
punkty określające odkształcenia plastyczne.

W początkowej fazie rozciągania, zachowana jest proporcjonalność

odkształcenia do naprężenia wynikająca z prawa Hooke’a. Następnie wydłużenia
stopniowo stają się coraz większe i początkowo prosty odcinek wykresu rozciągania
przechodzi w linie zakrzywioną. Brak tu wyraźnej granicy plastyczności, dlatego
używamy pojęcia umownej granicy plastyczności. Jest to taka wartość obciążenia,
która po jej odjęciu, zostawia materiał wydłużony trwale o 0,2%. Punkt ten na
wykresie oznaczony jest C. W punkcie A natomiast, mamy granice proporcjonalności-
czyli stosowalności prawa Hooke’a. W punkcie K, mamy wytrzymałość na rozciąganie

R

m

. Jest to maksymalna wartość obciążenia jaka może znieść próbka, jej wzór to

,

gdzie P

max

- maksymalna wartość siły, S- początkowy przekrój rozciąganej próbki.

Michał Niezgodziński „Wytrzymałość materiałów” s20-24

76. Opisz mechanizm dyslokacyjny odkształcenia plastycznego.

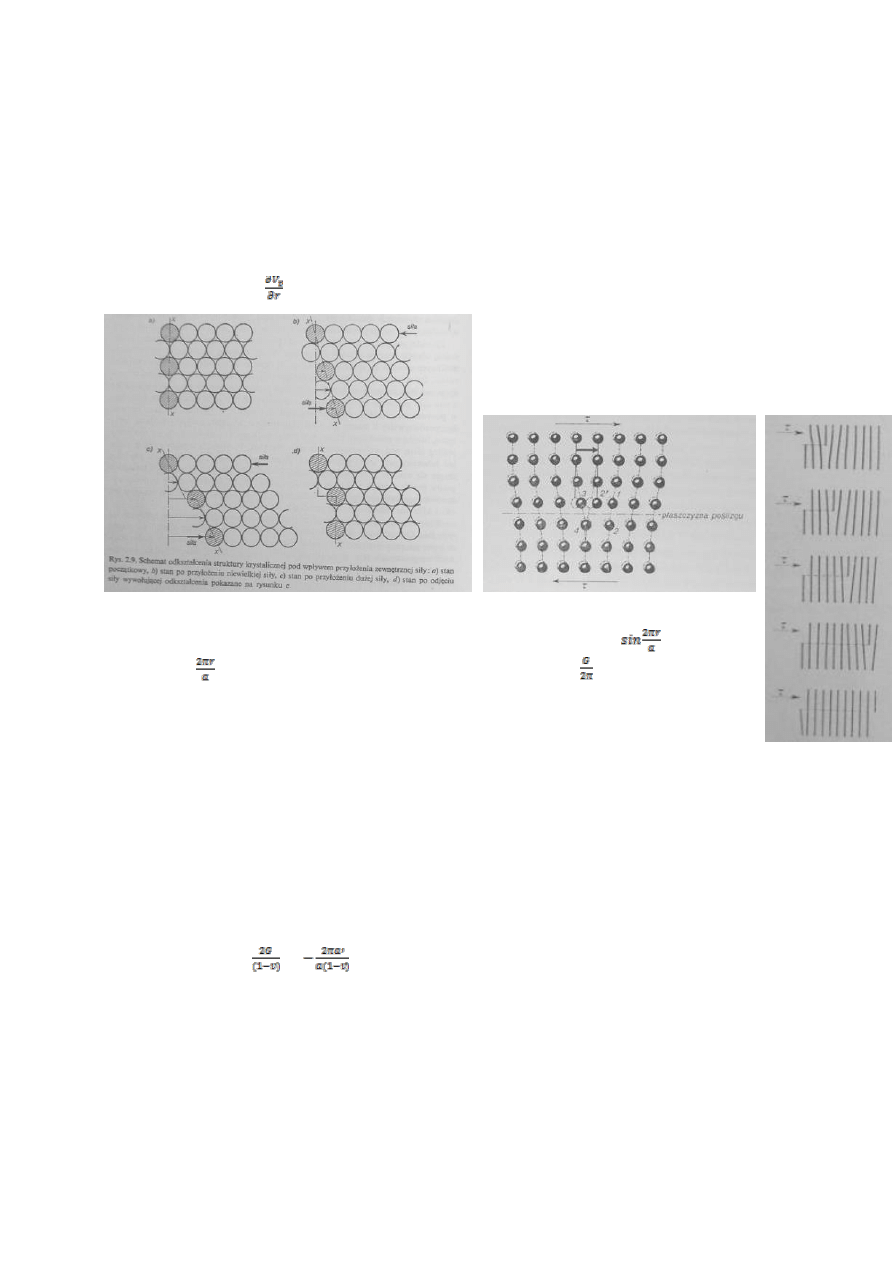
Trwałe odkształcenia następuje gdy część atomów tworzących fragment materiału przemieści względem reszty

w nowe pozycje równowagowe. Proces ten może zachodzić min. przez ruch dyslokacji w materiale. Rozpatrzmy idealny
kryształ pozbawiony defektów liniowych i płaskich. Jeśli przyłoży się siłę wywołującą naprężenia ścinające w materiale, to
gdy siła będzie niewielka, to atomy oddalają się jedynie nieznacznie od położenia równowagi i wracają doń po odjęciu
obciążenia. Jeśli siła jest wystarczająco duża, może spowodować trwałe przemieszczenie atomów do sąsiednich stanów
równowagi (w których znów maja minimum energii więc jest to pozycja trwała). Takie odkształcenie pozostaje po odjęciu
obciążenia. Proces taki nazywamy poślizgiem, a płaszczyzna położona nad obydwiema przemieszczającymi się częściami
kryształu- płaszczyzna poślizgu. Popatrzmy na to od strony energii. W toku przemieszczania atomów, maksimum energii jest
osiągane w połowie drogi miedzy pozycjami równowagowymi czyli w a/2 (patrz wykres). W tym miejscu wartość naprężenia

ścinającego wynosi 0 (bo τ=-(

) (r= a/2) a ponieważ V

p

ma maksimum to pochodna się musi zerować). Ponieważ

„siedzimy” na maksimum będąc w tej odległości a/2, to teraz obojętnie w która stronę ruszymy względem siebie
atomy, będziemy obniżać energię. Patrząc na wykres τ®, widać, że maksimum naprężeń przypada na odległość a/4- te

naprężenia są wtedy równe granicy plastyczności idealnego kryształu. Możemy napisać że τ=τ

0

a w

przybliżeniu τ=τ

0

(bo sinus ma małą wartość). Z prawa Hooke’a τ= Gr/a, a zatem τ

0

= czyli około 1/6 G.

Niestety w rzeczywistych kryształach granica plastyczności jest około 10

-5

G, więc widać że cos jest nie tak.

Tłumaczy się te rozbieżności występowaniem dyslokacji, w obecności których poślizg i odkształcenie kryształu
odbywa się z przemieszczeniem tylko małej liczby atomów położonych na linii dyslokacji- czyli potrzebne są dużo
mniejsze naprężenia bo nie przesuwamy wielkiego kawałka kryształu tylko maleńki wycinek. Można to rozpatrzyć na
przykładzie zachowawczego poślizgu dyslokacji czysto krawędziowej. W wyniku tego procesu dodatkowa półpłaszczyzna
(zakończona w 3), przesunęła się do nowej pozycji, położonej o jeden odstęp międzyatomowy dalej w prawo (2).
Wielokrotne powtórzenie tego procesu zaowocuje przesuwaniem dyslokacji w prawo, aż w końcu wyjdzie ona na
powierzchnie kryształu (patrz rysunki). Na ostatnim rysunku mamy płaska strukturę z dwu rzędów atomów. Załóżmy
poślizg, który spowoduje, że atom nr 9, przesunie się w pozycje 8, ale 1 pozostanie na miejscu (czyli na górze mamy
upchnięte 9 atomów w miejscu 8). Poza 1 i 9 wszystkie górne atomy nie są w pozycjach równowagowych. W 5 mamy
dyslokacje krawędziową, atom 5 jest bowiem przesunięty dokładnie o a/2 z pozycji równowagowej, atomy 2,3,4 o mniej niż
a/2 atomy 6,7,8 o więcej niż a/2. 6,7,8 zatem chcą iść dalej w prawo, do następnych pozycji równowagowych, 2,3,4 maja
bliżej do swoich własnych wiec chcą wrócić do nich. Oba te trendy nawzajem się znoszą, więc aby zaburzyć ta równowagę

trzeba minimalnej sily: τ

0

=

exp[

] gdzie a’- odległość miedzy płaszczyznami atomowymi równoległymi do

płaszczyzny poślizgu.

W9,7-13; ZNoM s95-99; WMC s79-80; MC s151-155

77.Definicja i przykłady systemów poślizgu.

Poślizg w strukturach krystalograficznych, zachodzi wzdłuż uprzywilejowanych płaszczyzn i określonych

kierunków, charakteryzujących się największą gęstością upakowania (ponieważ energia potrzebna do przesunięcia
dyslokacji jest tym mniejszy, im mniejszy jest wektor translacji). Kombinacje takiego kierunku i płaszczyzny nazywamy
systemem poślizgu. Systemy poślizgu występują w tzw. rodzinach, przy czym systemy poślizgu z tej samej rodziny
uruchamiane są przez takie samo naprężenie ścinające. Systemy poślizgu występują tylko w kryształach o symetrii wyższej
niż trójskośna. Poślizg z udziałem więcej niż jednego systemu, może wywołać czyste odkształcenie plastyczne materiału (ale
nie musi, np. może wywołać tylko rotacje kryształu)- dzieje się to np. gdy poślizg zachodzi przez systemy [011](0

) i

[0

](011). Do oceny plastyczności kryształów konieczna jest znajomość systemów poślizgu które wywołują czyste

odkształcenie plastyczne. Ponieważ odpowiednie kombinacje różnych systemów mogą wywołać ten sam efekt co inne,
wprowadzamy pojęcie liczby niezależnych systemów- wywołujących różne rodzaj czystego odkształcenia. Występująca w
strukturze regularnej płasko centrowanej liczba 5 niezależnych systemów jest liczba maksymalną, pozwala bowiem na
odkształcenie plastyczne kryształu w dowolnych warunkach obciążenia- czyli 5 systemów= materiał ciągliwy. W
kryształach o strukturze regularnej, najbardziej uprzywilejowana rodzina systemów jest [1 0](111), taka rodzina posiada 5

systemów niezależnych. Jednak nie zawsze poślizg zachodzi wzdłuż płaszczyzny teoretycznie najbardziej uprzywilejowanej,
zależy to od charakteru wiązań i ułożenia jonów w krysztale. Liczba niezależnych systemów poślizgu w kryształach rośnie
wraz z temperaturą, co tłumaczy dlaczego np. MgO czy NaCl w wyższych temperaturach są plastyczne (osiągają liczbę 5
sys.niezal.).

W9,16-17; MC s158-162; BiW s113-114; ZNoM s102-106

78.Wymień zjawiska podwyższające i obniżające granicę plastyczności materiałów.

Aby dokonać odkształcenia plastycznego, konieczne jest występowanie dyslokacji i ich łatwe przemieszczanie.

Przesuwaniu dyslokacji towarzyszy zrywanie i odtwarzanie poszczególnych wiązań, co wymaga pokonania pewnej siły.
Siłę minimalną, potrzebna do uruchomienia dyslokacji nazywamy krytycznym naprężeniem poślizgu dyslokacji. Zjawiska
które ją zwiększają nazywamy mechanizmami umocnienia materiału:



Występowanie ukierunkowanych wiązań które nie mogą ulegać znacznej deformacji (wiązania kowalencyjne, w

np. ceramice kowalencyjnej)- wiązania ukierunkowane mogą odkształcać się o b. mały kat, bez zerwania ciągłości
materiału, stąd naprężenia potrzebne do ruchu dyslokacji są tu bardzo wysokie, często większe od wytrzymałości
materiałów- zachodzi wtedy kruche pękanie, bez odkształcenia plastycznego



Umocnienia roztworowe i dyspersyjne- występowanie domieszek obcych atomów utrudnia ruch dyslokacji, a wiec

obniża plastyczność (np. stopy metali, z różnych atomów, mają mniejszą plastyczność niż czyste metale)



Umocnienie odkształceniowe- w tym procesie, dyslokacje ulegają spiętrzenie- zbierają się w kupę i zachodzi ich

splatanie- nawzajem się unieruchamiają. W efekcie dyslokacje nie wędrują, mamy umocnienie materiału. Aby
materiał potem był znów plastyczny, należy go wyżarzyć.



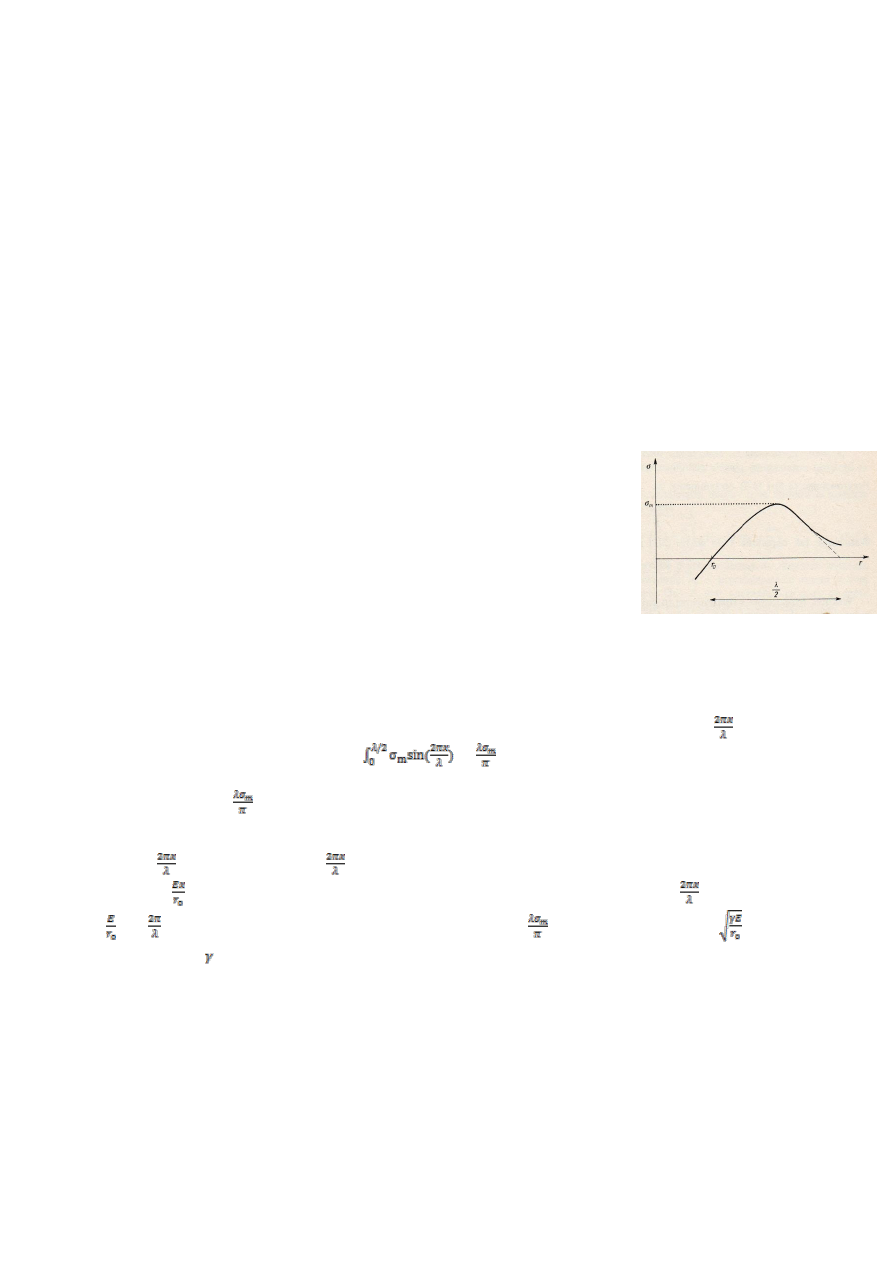
Umocnienie w polikrysztale- jeśli granice miedzy ziarnowe są słabe, to ruch dyslokacji przez nie jest utrudniony, co

w efekcie obniża plastyczność. Druga możliwość, to takie ustawienie ziaren, by ich systemy poślizgu były
odchylone od kierunku działania naprężeń zewnętrznych R

e

=3τ

y

(wsp. Taylora)

Zjawiska zwiększające plastyczność- obniżające granice plastyczności



Temperatura- wraz z temperatura rośnie ruchliwość defektów punktowych a wraz z nimi możliwość ruchów

dyfuzyjnych dyslokacji. W takich warunkach nawet materiały kruche mogą być plastyczne- nadplastyczność.

W9,18-23

79.Wymień znane Ci wielkości określające wytrzymałość i podaj warunki ich pomiaru.

-wytrzymałość na rozciąganie –R

m

-wytrzymałość na ściskanie

-wytrzymałość na zginanie
Wytrzymałość wyznaczana jest w standardowych (normowych) warunkach zniszczenia
materiału

80.Wyprowadź zależność na wytrzymałość teoretyczna kryształu oraz

81.Podaj zależność na wytrzymałość teoretyczną kryształu i opisz
występujące wielkości.

Wytrzymałością teoretyczną nazywamy wytrzymałość wiązań międzyatomowych

na zerwanie pod wpływem obciążenia. Rozpatrzmy zatem oddzielenie atomów na odległość
większą od efektywnego zasięgu sił wzajemnego przyciąganie między nimi. Użyjemy do tego wykresu σ(r). Zwiększenie
odległości międzyatomowej wymaga początkowego wzrostu naprężeń. Naprężenia osiągają maksymalna wartość σ

m

w

odległości r

0

+ ∆r. Od tego momentu, dalszy wzrost odległości powoduje zmniejszenie naprężeń. Zerwanie wiązania,

następuje dla naprężeń większych lub równych σ

m

, czyli σ

m

jest maksymalna wytrzymałością wiązania na rozciąganie. Jej

wartość liczymy jako energię (pracę) potrzebną do takiego rozdzielenia atomów. Praca w będzie równa polu pod krzywą σ(r)

od 0 (r

0

) do λ/2 (r

0

+ ∆r). Ponieważ krzywa w przybliżeniu jest sinusoidą o okresie λ, to można zapisać: σ= σ

m

sin(

) gdzie x=

r-r

0

czyli jak to scałkujemy to otrzymamy w: w=

dx=

Rozdzieleniu atomów w krysztale towarzyszy

powstanie dwóch nowych powierzchni o nadmiarowej energii γ, można więc powiedzieć, że wykonana praca w zostaje

zużyta w tym celu; 2γ=

. Teraz trzeba λ zastąpić jakimiś mierzalnymi wartościami. W tym celu zakładamy, że dla małych

przemieszczeń kątowych, sin a= a, czyli

σ= σ

m

sin(

) można uprościć do σ= σ

m

(

). Dla małych przemieszczeń atomów oprócz tego spełnione jest prawo Hooke’a

czyli σ= Eε= gdzie E-moduł Younga, x/r

0

= ε czyli odkształcenie względne. Jak przyrównamy to z σ= σ

m

(

), to otrzymamy

= σ

m

. Teraz do tego równania podstawiamy λ wyliczone z równania 2γ=

. W efekcie otrzymamy, że σ

m

=

gdzie

E- moduł Younga, -energia powierzchniowa, r

0

- odległość pomiędzy dwoma pozycjami równowagowymi (długość wiązania

w krysztale).

W10,7-8; ZNoM s108-110; BiW s121-122

82.Podaj wzór na wytrzymałość teoretyczną kryształu ze szczeliną (wzór Griffitha), opisz
występujące wielkości.

Wzór Griffitha został wyprowadzony na podstawie bilansu energetycznego. Według Griffitha pęknięcie może

rozwijać się wówczas, gdy towarzyszące temu rozładowanie energii zachodzi z równą lub większą szybkością od
pochłaniania energii w celu wykształcenia nowych powierzchni. Innymi słowy rozprzestrzenianie się pęknięcia i niszczenie

zwartego materiału jest możliwe tylko wówczas, gdy procesom pękania towarzyszy stałe zmniejszanie się energii
potencjalnej kryształu dzięki rozładowywaniu się energii odkształceń sprężystych. Dla szczeliny o długości c warunek ten, w

przypadku naprężeń płaskich, można sformułować: σ

z

≥

ZNoM s113

83.Podaj wzór i scharakteryzuj pojęcie „współczynnik intensywności naprężeń K

c

” oraz

84.Porównaj pojęcia: współczynnik intensywności naprężeń i krytyczny współczynnik
intensywności naprężeń.

Rozpatrzmy płaskie odkształcenie płyty, która zawiera w centrum eliptyczne pęknięcie, będące pod wpływem

obciążenia rozciągającego w kierunku x

2

prostopadłym do długiej osi pęknięcia. Jest to przypadek, w którym mamy

warunki najbardziej sprzyjające rozprzestrzenianiu się pęknięcia- mamy najsilniejszą koncentrację naprężeń
rozwierających szczelinę. Maksymalnymi naprężeniami w płycie będą te styczne do wierzchołka pęknięcia. Z teorii Inglisa

możemy zapisać: σ

max

=P[1+2

] gdzie to promień krzywizny wierzchołka szczeliny. Zakładając że c/ρ>>1, można to

uprościć do σ

max

=2

. Gdy przemnożymy obie strony przez czynnik (πρ)

0,5

i przekształcając otrzymamy że:

0,5σ

max

(πρ)

0,5

=P

. Ponieważ P i c są wielkościami mierzalnymi, to stosowanie K

c

będzie wygodnym parametrem do

określania odporności materiału na kruche pękanie. Można mianowicie (tutaj kopia z następnego punktu) powiedzieć, że
kiedy- przy określonej długości pęknięcia c

c

, i obciążenia P

c

–osiągane w materiale naprężenie σ

max

osiąga wartość

wytrzymałości teoretycznej materiału σ

m

to odpowiada to maksymalnej wartości współczynnika K

c

mianowicie K

Ic

.

Współczynnik K

Ic

określany jest odpornością na kruche pękanie. Współczynnik intensywności naprężeń K

I

osiąga swą

wartość krytyczną w momencie zapoczątkowania katastrofalnego rozprzestrzeniania się pęknięcia obecnego w materiale

W10,13; BiW s125-126

85. Podaj sens fizyczny wielkości K

IC

, w czym ją wyrażamy.

Można powiedzieć, że kiedy- przy określonej długości pęknięcia c

c

, i obciążenia P

c

–osiągane w materiale

naprężenie σ

max

osiąga wartość wytrzymałości teoretycznej materiału σ

m

to odpowiada to maksymalnej wartości

współczynnika K

I

(współczynnika intensywności naprężeń) mianowicie K

Ic

. Współczynnik K

Ic

określany jest odpornością na

kruche pękanie. Współczynnik intensywności naprężeń K

I

osiąga swą wartość krytyczną w momencie zapoczątkowania

katastrofalnego rozprzestrzeniania się pęknięcia obecnego w materiale. K

Ic

jest stałą materiałową charakterystyczną dla

danego tworzywa. Możemy go traktować jako miarę energii odkształcenia sprężystego, która jest pochłaniana w toku
rozprzestrzeniania się pęknięcia. Jest to bardzo ważny parametr decydujący o wytrzymałości tworzyw kruchych (zwłaszcza
ceramicznych). K

Ic

zwany jest także wiązkością lub krytyczną szybkością uwalniania energii. Zależy on od stałych

materiałowych:

K

Ic

2

=E



ef

 K

Ic

= (E



ef

)

1/2

=



m

(πc

c

)

1/2

, ponieważ



ef

=

K

Ic

2

/E

dla PSN

K

Ic

2

=E



ef

/1-



2

dla PSO

PSN- płaski stan naprężeń

PSO- płaski stan odkształceń

W10,9-10; BiW s126-127; MC s220

86. Podaj zakres wielkości K

IC

dla ceramiki i

metali.

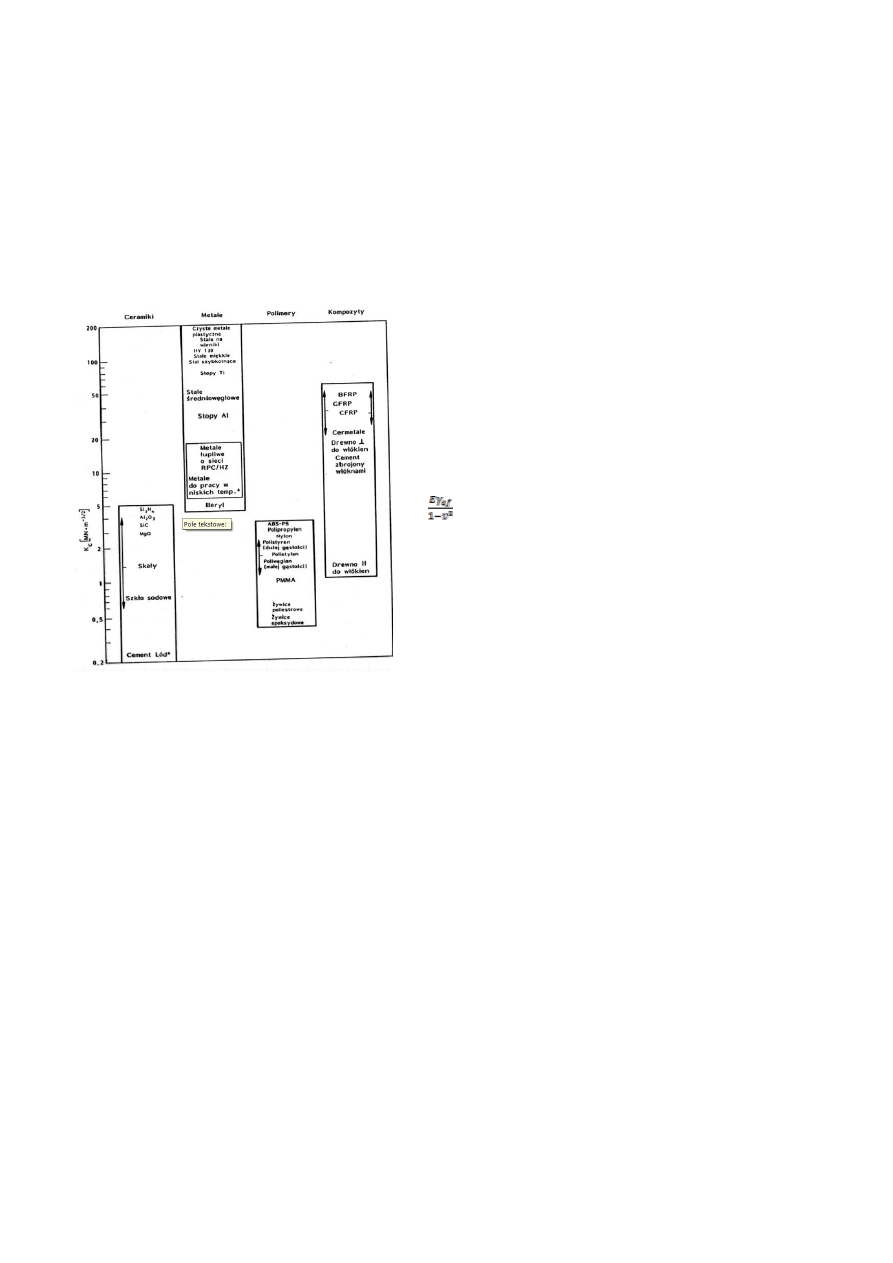
Można zauważyć że wartości K

Ic

dla materiałów ceramicznych amorficznych i polikrystalicznych nie przekraczają 6[MPam

0,5

].

Wartości wyliczone i praktyczne dla normalnych materiałów ceramicznych wykazują dużą zbieżność, więc można uznać że
dekohezja w nich zachodzi w skutek prostego rozprzestrzeniania się pęknięć o długości krytycznej c

c

, odbywającego się bez

przeszkód. Można również zauważyć podwyższenie wartości K

Ic

dla materiałów „ulepszonych”.

W10,15; BiW s127-128

87. Podaj zależność od K

IC

od energii pękania.

K

IC

jest stałą materiałową która zależy od energii pękania



ef

.

Energia pękania jest tutaj w postaci energii efektywnej (patrz pkt.
88), uwzględniającej wszystkie mechanizmy mające wpływ na
pochłanianie energii oddziaływań sprężystych. Zależność odporności
na kruche pękanie od energii pękania dana jest wzorem:

K

c

2

=E



ef

 K

c

= (E



ef

)

1/2

-płaski stan naprężeń

K

Ic

=

- płaski stan odkształceń

W10,14-16; BiW s127; MC s 218

88. Podaj sens fizyczny wielkości „energii pękania”,
w czym ją wyrażamy.

W wielu materiałach ceramicznych, wartość odporności

na kruche pękanie jest większa niż można by się tego spodziewać.

Wynika to z występowania dodatkowych zjawisk pochłaniających energię odkształceń sprężystych w trakcie pękania
takich jak: zjawisko mostkowania (kompozyty), tworzenie się sieci mikropęknięć i rozgałęzianie, przemiany fazowe
(materiały TZP). Do ważniejszych czynników decydujących o wytrzymałości i ciągliwości materiałów należy również stan ich
powierzchni. W najczystszej postaci występuje w przypadku szkieł dobrej jakości (które nie zawierają defektów). Drobne
rysy i szkła usuwa się drogą trawienia powierzchni szkła, dewitryfikacji , hartowania powierzchni. Rozważając odporność na
kruche pękanie energię powierzchniową



należy zastąpić efektywną energią powierzchniową (energią pochłanianą w

czasie powstania spękania niszczącego materiał), albo lepiej energią pękania:



ef

=



+



p

+



r

+



pf

+



i



-energia powierzchniowa



p

-energia odkształcenia plastycznego



r

-energia powstania dodatkowych spękań



pf -

energia pochłaniana w toku przemian fazowych



i

-wszelkie inne procesy pochłaniania energii

Efektywna energia pękania decyduje o odporności materiału na kruche pękania. Energią pękania podwyższają wszystkie
procesy pochłaniające energię w toku pękania. Efektywną energię pękania wyraża się w kJ/m

2

W10,16; BiW s127; MC s 218

89. Scharakteryzuj mechanizm Cooke’a –Gordona hamowania spękań w polikrysztale.

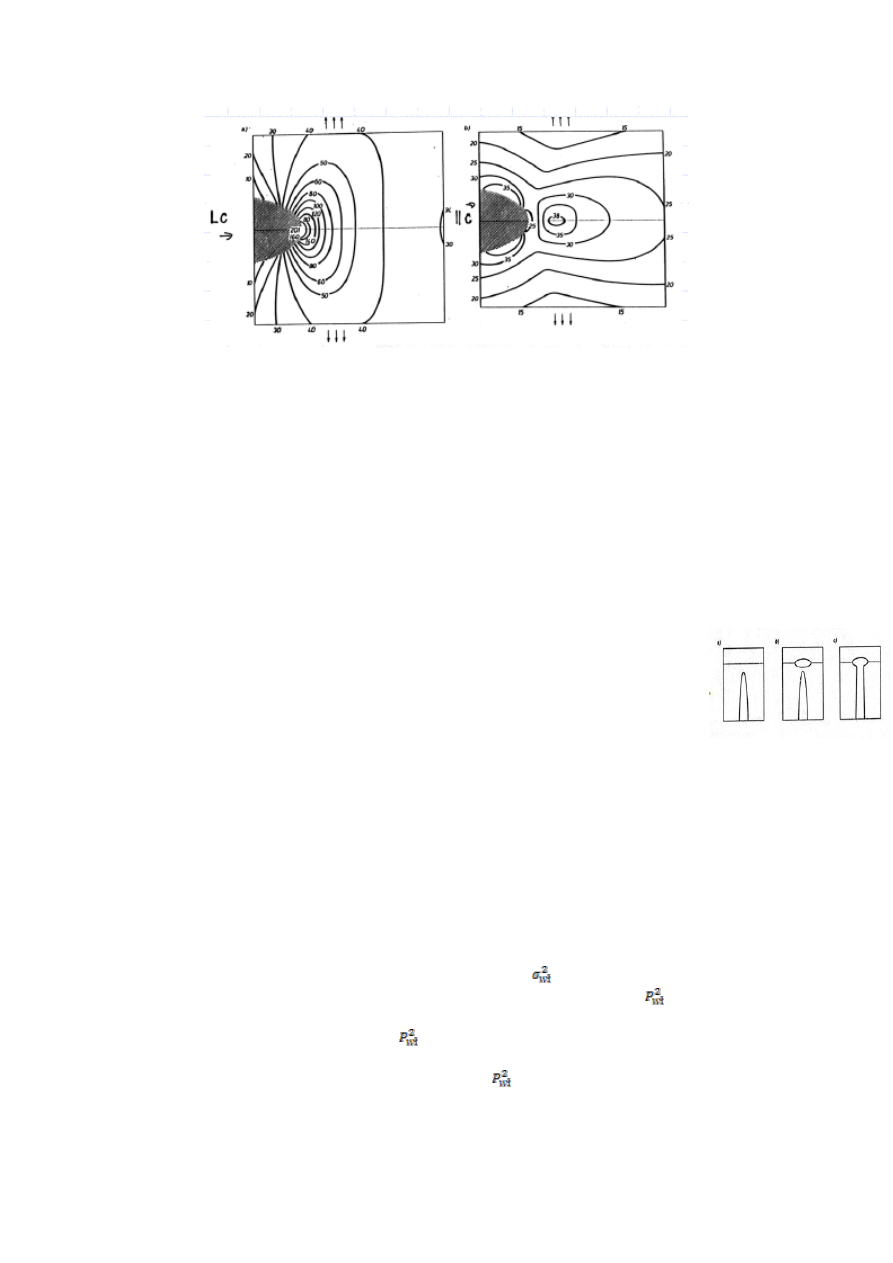
Polikryształy charakteryzuje większa odporność na kruche pękanie niż w monokryształy. Wynika to przede

wszystkim z obecności granic międzyziarnowych. Na rysunku przedstawiono mapy naprężeń według Cooka i Gordona
a)naprężenia prostopadłe do płaszczyzny pęknięcia dążące do jego do jego rozwarcia i dalszego rozprzestrzeniania się w
głąb ziarna .
b) mapa naprężeń równoległych do płaszczyzny pęknięcia czyli prostopadłych do kierunku naprężeń rozwierających
szczelinę, w przeciwieństwie do nich mają zerową wartość przy wierzchołku pęknięcia.
Niezależnie od promienia krzywizny wierzchołka pęknięcia, rozmiarów pęknięcia i sposobu przykładania naprężeń
zewnętrznych, stosunek maksymalnych naprężeń równoległych i prostopadłych do powierzchni spękania ma stałą
wartość równą 1/5. Przy takim rozkładzie naprężeń wewnętrznych istotne znaczenie dla rozprzestrzeniania się pęknięcia
ma fakt istnienia w materiale granic międzyziarnowych lub międzyfazowych. Gdy obszar maksymalnych naprężeń
równoległych do płaszczyzny pęknięcia, wyprzedzający wierzchołek pęknięcia, dociera do granicy międzyziarnowej
prostopadłej do płaszczyzny pęknięcia występuje tendencja do rozwarstwiania się materiału wzdłuż granicy
międzyziarnowej i tym samym do rozgałęzienia pęknięcia. Jeżeli:
-wytrzymałość granicy międzyziarnowej >1/5 wytrzymałości objętości fazy krystalicznej (naszego ziarna), materiał nie
ulega rozwarstwieniu na granicy i pękniecie rozprzestrzenia się dalej przez granicę w sąsiednim ziarnie
-wytrzymałość granicy międzyziarnowej<1/5 wytrzymałości ziaren krystalicznych to pod wpływem naprężeń
równoległych granica międzyziarnowa ulega rozwarstwianiu przed dojściem do niej wierzchołka pęknięcia (rys. b na
dole). Wtedy pierwotne pęknięcie łączy się z nowo powstałym pęknięciem poprzecznym i kierunek
rozprzestrzeniania się pęknięcia ulega odchyleniu w kierunku równoległym do działania naprężeń. Hamuje
to rozprzestrzenianie się pęknięć, ponieważ tendencja do rozprzestrzeniania się pęknięć równoległych do
kierunku przyłożone siły zewnętrznej jest znikoma. W najgorszym przypadku zwiększa się udział energii
rozproszonej przy rozprzestrzenianiu się pęknięcia czyli trudniej zniszczyć materiał. Mechanizm ten pozwala
przewidywać, że drobno ziarniste polikryształy (maja więcej granic) będą miały wyższą wytrzymałość
mechaniczną, co jest zgodne z doświadczeniem.

W10,19; ZNoM s118-120; MC s215-217

91. Opisz mechanizm podwyższania energii pękania w kompozytach włóknistych (z pkt.56).

Odporność materiału na kruche pękanie znacząco wzrasta w kompozytach włóknistych. Ponieważ granice

rozdziału faz, wskutek zaburzonej budowy maja zwykle niższą wytrzymałość, gdy główne pękniecie dochodzi do granicy
osnowa-włókno, następuje lokalne rozwarstwienie materiału. Gdy obciążenia są równoległe do osi włókien, rozwarstwienia
na granicy rozdziału są równoległe do kierunku naprężeń, maja ograniczoną długość i nie przechodzą przez cały materiał.
Następuje w związku z tym pochłoniecie energii oddziaływań sprężystych bez dekohezji. Można powiedzieć że włókna
spinają(mostkują) główne pękniecie, powstrzymując je przed rozprzestrzenianiem. Wynika to z tego, że aby wzrost
szerokości u pęknięcia był możliwy, włókno musi się na odcinku l

db

rozciągnąć o tą zmianę szerokości czyli ∆u. Powstaje tutaj

energia odkształceń sprężystych o wartości na jednostkowa powierzchnię w=(

/2E

wł

)l

db

Efekt mostkowania będzie tak

długo aktywny, jak długo trzyma się włókno, zatem górna wartość tej energii wynosić będzie w

m

= (

/2E

wł

)l

db

gdzie P

wł

-

wytrzymałość włókna na rozciąganie. Dla udziału objętościowego włókien V

wł

energia zmagazynowana w materiale na

jednostkę powierzchni wynosić będzie w

m

= V

wł

(

/2E

wł

)l

db

Energia ta jest pochłaniana przy rozprzestrzenianiu się

pęknięcia. Będzie ona częścią efektywnej energii powierzchni. Można więc napisać, że odporność na kruche pękanie
kompozytu w którym jest mostkowanie wynosi: K

Ic

=(Eγ

ef

)

0,5

= (E(γ+ V

wł

(

/2E

wł

)l

db

)

0,5

. Włókna gdy zostanie przekroczona

ich wysoka wytrzymałość ulegają dekohezji, jednak trzeba pamiętać, że zaczyna się ona w miejscach występowania
defektów, a te nie zawsze leżą na osi pęknięcia- czyli uszkodzenie może być w innym fragmencie włókna, np. w takim które
w całości jest w osnowie. Aby uległo ono dekohezji, trzeba je z włókna „wyciągnąć”. Praca potrzebna na wyciągniecie

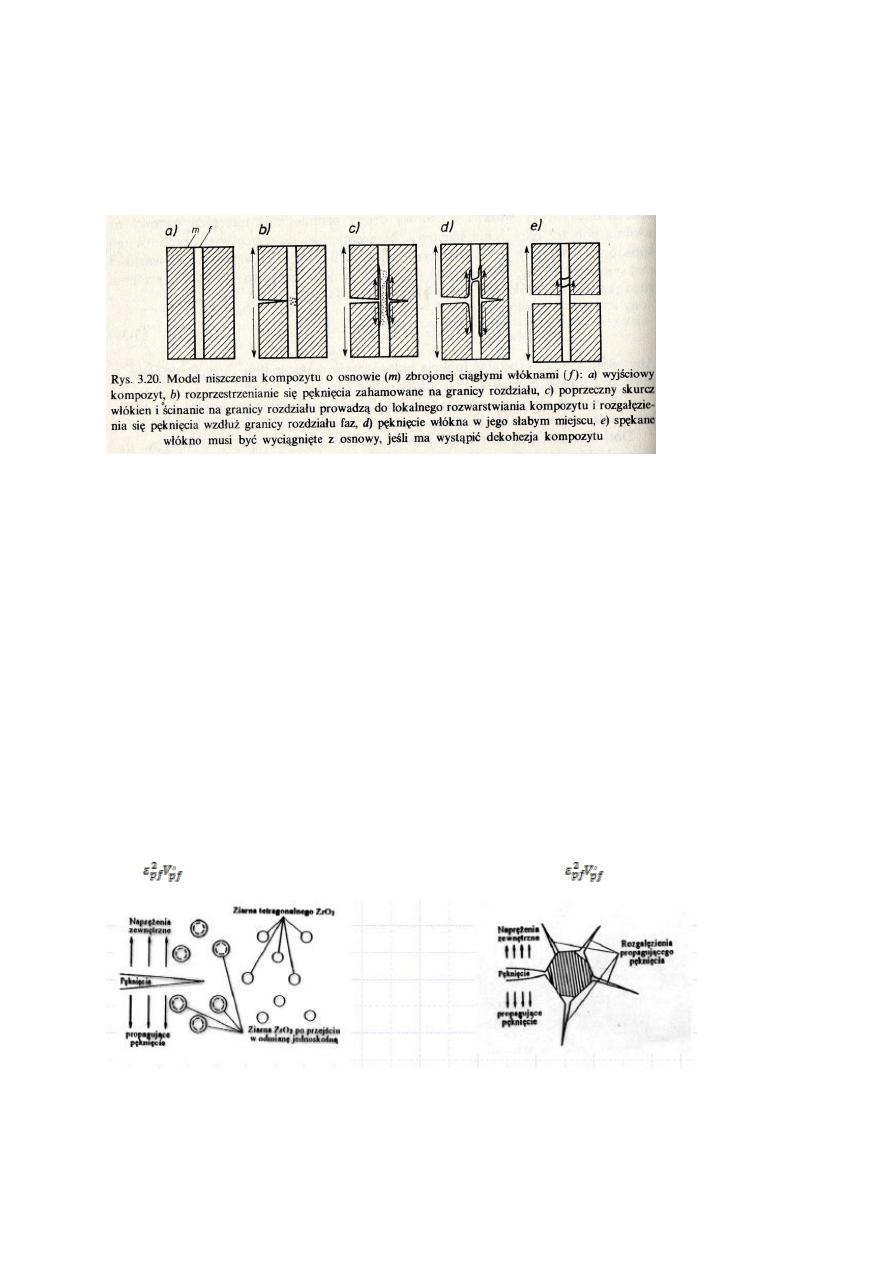
włókien przez naprężenia ścinające występujące na granicy rozdziału włókno-osnowa wynosi τ(l

po

/r)

2

gdzie l

po

- długość

elementu włókna którego wyciągniecie spowoduje eliminacje mostkowania, τ- naprężenia ścinające, r- promień włókna.
Przy udziale włókien wyciąganych V

po

, maksymalna wartość energii odkształcenia sprężystego na jednostkowa

powierzchnię, pochłanianej w procesie wyciągania włókien wynosi γ

po

=V

po

r τ(l

po

/r)

2

. Cały ten mechanizm jest w

kompozytach włóknistych wyjątkowo efektywny.

W10,20; BiW s128-130; ZNoM s124-125; WMC s175-178 (dużo informacji o osnowach ceramicznych)

92.Opisz mechanizm podwyższania energii pękania w wyniku przemian fazowych wtrąceń
ziarnistych ZrO

2

K

ompozyty z częściowo stabilizowanym ZrO

2

(są to tak właściwie ziarna roztworu stałego CeO

2

, Y

2

O

3

lub MgO w

ZrO

2

) zyskały dużą popularność ze względu na podwyższona odporność na kruche pękanie.. W temperaturze pokojowej

ZrO

2

występuje w postaci nietrwałej odmiany tetragonalnej. W warunkach obciążenia rozciągającego w ziarnach, ZrO

2

przechodzi w odmianę jednoskośną. W obciążonym materiale wierzchołek rozprzestrzeniającego się w osnowie pęknięcia
poprzedza obszar, w którym na pole znacznych naprężeń rozciągających, nakłada się pole maksymalnych naprężeń
ścinających. Gdy ten obszar dojdzie do ziarna, może inicjować wspomniana przemianę. Odmiana jednoskośna ma większą
objętość właściwą od tetragonalnej a co za tym idzie większe odległości międzyatomowe. Wzrost w wyniku przemiany tych
odległości w rezultacie czego w najbliższym otoczeniu ziarna powstają naprężenia ściskające. Pęknięcie o którym wcześniej
mówiliśmy zaczyna się więc rozprzestrzeniać w polu naprężeń ściskających, które przeciwdziałają rozwieraniu się tego
pęknięcia- wzrasta odporność materiału na kruche pękanie. Obszar pomiędzy czubkiem pęknięcia a polem naprężeń które
może wywołać przemianę (w odległości r od czubka) nazywamy strefa procesową. W całym tym procesie zachodzi
pochłanianie energii γ

pf

której wartość można policzyć, na podstawie równania mówiącego że gęstość energii odkształcenia

sprężystego wynosi: w=AEε

2

gdzie A jest bezwymiarową stałą. Jeżeli więc wprowadzimy odkształcenie materiału w trakcie

przemiany fazowej ε

pf

oraz V’

pf

–udział objętościowy fazy tetragonalnej która ulega przemianie w jednoskośną w strefie

procesowej o promieniu r, to spadek gęstości energii odkształcenia sprężystego na jednostkę powierzchni wyniesie
γ

pf

= AE

r a odporność na kruche pękanie można zapisać jako K

Ic

=[E(γ+ AE

r)]

0,5

.

W10,21; WMC s174-175; BiW s130-131

93. Podaj znane Ci równania opisujące zależność wytrzymałości od porowatości

Wytrzymałość materiałów ulega obniżeniu wraz ze wzrostem porowatości i zależy od kształtu porów. Zależności

mają postać podobną do tych, które opisują moduł Younga:



=



0

(1-kV

p

)



0

-wytrzymałość materiału nieporowatego

V

p

- udział objętościowy porów

k- współczynnik koncentracji zależny od kształtu i ukierunkowania poru względem naprężeń
Wzór ten opisuje zależności prawdziwe dla większości polikryształów o niskiej porowatości. Empirycznie zaobserwowano w
pewnych kryształach pewne odchylenia od tej zależności liniowej, można je przybliżać równaniami empirycznymi np.
postaci:



=



0

exp(1-bV

p

),



=



0

[1-AV

p

-B(V

p

)

2

…]

W skutek koncentracji naprężeń w otoczeniu porów materiał znajduje się w tych miejscach w stanie większych naprężeń
wewnętrznych niż nieporowaty. Im większy jest udział objętościowy porów tym większa objętość materiału podlega
działaniu uwielokrotnionych naprężeń i tym mniejsza jest wytrzymałość mechaniczna porowatego materiału.

W10,22; ZNoM s121-122; MC s230

94. Podaj na rysunku typową zależność wytrzymałości od wielkości ziaren dla polikryształów
ceramicznych.

W polikryształach ceramicznych (pękanie kruche) możliwy jest zróżnicowany mechanizm pękania z
przewagą pękania po granicach ziaren ( międzyziarnowego) lub poprzez ziarna
(wewnątrzziarnowe). Ten pierwszy mechanizm dominuje w przypadku ziaren o małych rozmiarach
(<1µm), przy większych, częstszy jest ten drugi (patrz wykres). Źródła tych mechanizmów są różne:
1- Lokalne pękanie międzyziarnowe powoduje zwiększenie energii pękania i energia ta rośnie z
wielkością ziaren. Pękanie międzyziarnowe związane jest głównie z różnicą wydłużeń stykających się
z sobą ziaren przy obciążeniu mechanicznym materiału. Stykające się ze sobą ziarna są zorientowane
z punktu widzenia struktury. Mają one inne właściwości sprężyste i wykazują różną tendencję do
wydłużania w tym samym kierunku. Mikropęknięcia rozprowadzone są statystycznie.
2 -Pękanie poprzez ziarna wiąże się z podwyższaniem energii pękania w skutek występowania
mechanizmu Cooke’a-Gordona- pęknięcie które przeszło przez ziarno natrafia na granicę międzyziarnowe, im więcej granic
tym większe pochłanianie energii, a więcej granic oznacza mniejsze ziarna.
3- Sumarycznie często występuje ekstremum energii pękania –wytrzymałość polikryształu dla pewnej wielkości ziaren.

W10,23; MC 228-230

95.Podaj założenia statystycznej teorii wytrzymałości Weibulla.

Statystyczna teoria wytrzymałości jest próbą analizy statystycznych aspektów kruchego pękania. Jej założenia:

1. Materiał posiada charakter izotropowy i posiada statystyczny rozkład defektów
2.Prawdopodobieństwo znalezienia defektu o wielkości krytycznej jest w całej objętości materiału identyczne
3.Materiał ma charakter kruchy a jego zniszczenie następuje wskutek rozprzestrzeniania się defektu krytycznego
4.Liczba defektów w materiale jest duża

W10,25; BiW s135

96. Scharakteryzuj wielkość moduł (stała) Weibulla.

Współczynnik m, nazywany modułem Weibulla wiąże się z gęstością prawdopodobieństwa

występowania defektu np. szczeliny o długości c. Im większa jest wartość m, tym węższy jest przedział
wielkości szczeliny i tym mniejsze są wielkości najczęściej występujących szczelin. W związku z tym
również i rozrzut prawdopodobieństwa kruchego zniszczenia poszczególnych próbek maleje ze
wzrostem modułu Weibulla- czyli mamy mniejszy przedział obciążeń które mogą próbkę rozwalić. Dla m
dążącego do nieskończoności (a w praktyce >>100) krzywa rozkładu wytrzymałości mechanicznej

próbek przechodzi w postać załamanej linii prostej, której pionowa część odpowiada odciętej



0

. Wytrzymałość przestaje

być wielkością statystyczną i staje się wielkością stałą. Empirycznie wyznaczone wartości modułu Weibulla dla materiałów
ceramicznych mieszczą się w przedziale 5<m<30, natomiast dla stali jest to 50<m<100, co stanowi liczbową ilustrację
twierdzenia o większej reprezentatywności próbek w przypadku metali- czyli jest bardzo prawdopodobne że jak zbadamy
następne 10 próbek stali to będą miały takie same właściwości jak ta pierwsza.

W10,26; BiW s135-136; MC 223-224

97. Narysuj zależność P(V

0

)=f(



) wg statystycznej teorii Weibulla dla tworzyw plastycznych i

kruchych

Niech jednostkowa objętość materiału V, będzie poddana działaniu obciążenia rozciągającego P, które wywołuje w

materiale jednorodne naprężenie rozciągające σ. Prawdopodobieństwo kruchej dekohezji P(V

0

) przy obciążeniu P

c

dane jest

przez:
P(V

0

)= 1- exp[-V(σ-σ

u

)/σ

0

)]

m

dla σ>σ

u

P(V

0

)= 0 dla σ<σ

u

Przy czym σ

u

jest naprężeniem, dla którego prawdopodobieństwo zniszczenia próbki jest równe zero, σ

0

- stała

normalizująca, m- stała Weibulla
Nie było to nigdzie jasno sprecyzowane, ale jako tworzywo plastyczne w opinii autora powinno się traktować materiały o
wysokim m, ich skrajnym przypadkiem jest sytuacja gdy m→∞, wtedy wykres przyjmuje kształt schodka. Materiałami
kruchymi będą te o niewielkim m, kształtem ich wykresu jest „zbocze”.

W10,26; BiW s135-136

98. Podaj zależność wytrzymałości materiałów kruchych od objętości próbki.

Ze statystycznej teorii wytrzymałości wynikają ważne wnioski. Przeciętna wytrzymałość na zerwanie próbek
kruchego materiału ceramicznego jest odwrotnie proporcjonalna do V

1/m

. Im bardziej jednorodny jest materiał z punktu

widzenia rozprowadzenia szczelin tym bardziej reprezentatywny dla całości materiału jest zbiór defektów występujących w
małej próbce. W tym przypadku zwiększenie objętości próbek wpływa nieznacznie na wytrzymałość. Dla materiałów
bardziej niejednorodnych prawdopodobieństwo wystąpienia defektów o wielkości krytycznej jest w małej próbce
mniejsze niż w dużej objętości. Z punktu widzenia doświadczalnej oceny wytrzymałości materiału oznacza to, że średnia
wytrzymałość materiałów kruchych oszacowana na podstawie wytrzymałości małych próbek będzie się zmniejszać ze
wzrostem liczby zbadanych próbek. Z tego względu próbki poddawane są badaniom próbnym- wszystkie kształtki
materiałów ceramicznych przeznaczonych do użytkowania poddawane są wstępnemu obciążeniu, wyższemu od obciążenia
występującego w toku użytkowania tych kształtek.



1

/



2

=(V

2

/V

1

)

1/m

W10,28; MC 224-225

99.Wymień mechanizmy przenoszenia ciepła.

Procesy przenoszenia ciepła można podzielić na trzy szerokie grupy:



konwekcja- ciepło przenosi się w wyniku transportu cząsteczek obdarzonych energią cieplną, mechanizm ten jest

szczególnie ważny w przypadku gazów, nie odgrywa natomiast poważniejszej roli w ciałach stałych (mała
ruchliwość atomów w tym stanie)-



promieniowanie- energia cieplna jest wymieniana pomiędzy oddalonymi od siebie powierzchniami stałymi

promieniowania i absorpcji (istotny w temperaturze powyżej 1000



C oraz dla materiałów porowatych)



przewodnictwo cieplne-proces wymiany ciepła między ciałami pozostającymi ze sobą w bezpośrednim kontakcie,

ma podstawowe znaczenie dla materiałów ceramicznych. Teoria przewodnictwa cieplnego w kryształach i
substancjach amorficznych nawiązuje do zjawisk przewodnictwa w gazach. Przenoszenie ciepła w gazach jest
możliwe przez zderzenia obdarzonych energią molekuł, które wykazują chaotyczne ruchy. Gęstość strumienia
ciepła płynącego w czasie dt prostopadle do płaszczyzny o jednostkowej powierzchni A można wyrazić jako
funkcję siły napędowej, którą jest tu gradient temperatury, w kierunku x.

q

x

=

= -λ

przepływ ciepła ustaje, gdy zanika gradient temperatury, a przy istnieniu gradientu temperatury jest do niego
proporcjonalny. λ jest tu stała proporcjonalności- przewodnością cieplną. Jest to stała zależna od temperatury.

W11,12; BiW s140

100.Scharakteryzuj współczynnik przewodnictwa cieplnego (przewodność cieplną), podaj
zakres wartości dla tworzyw ceramicznych.



-przewodność cieplna, współczynnik proporcjonalności który charakteryzuje zdolność materiału do przenoszenia ciepła

pod wpływem gradientu . W tych samych warunkach więcej ciepła przepłynie przez substancję o większym

współczynniku przewodności cieplnej . Jest to stała zależna od temperatury.

Jeżeli temperatura w dowolnym punkcie układu zmienia się z czasem, to przewodnictwo cieplne zależy od stosunku



do

pojemności cieplnej na jednostkę objętości tj. od iloczynu gęstości



i ciepła właściwego c. Stosunek ten to współczynnik

przewodnictwa temperaturowego. W przypadku gazów przewodność cieplną można wyrazić prostymi zależnościami.
Energia cieplna molekuł gazu w danej temperaturze jest proporcjonalna do ciepła właściwego c

p

w stałej objętości. Na

podstawie kinetycznej teorii gazów:



=1/3



c

v

- średnia prędkość molekuł gazu, - średnia droga pomiędzy zderzeniami,



-gęstość gazu

W przypadku ciał stałych ciepło przekazywane jest także drogą wymiany energii między atomami. Atomy są jednak silnie
powiązane i wykonują tylko ruchy drgające wokół swych pozycji równowagi. Ruchy drgające atomów są ze sobą
skorelowane, drgania atomów mają charakter fal-fononów:



=1/3



c

v

, gdzie -średnia prędkość fononów, -średnia droga

swobodna. W zakresie podwyższonych temperatur, w którym obowiązuje prawo Dulonga-Petita c

v

=3R, c

v

=const a nie

zależy od temperatury zmiany przewodności cieplnej zależą od zmian długości drogi swobodnej fononów . Droga fononów

zależy natomiast od prawdopodobieństwa ich oddziaływania. Procesy przerzutu „Umklapp”(Lecą dwie fale o małej
długości fali w jednym kierunku, interferują ze sobą. Fala interferencyjna powstała przez nakładania się fal o dużej
częstotliwości nie może istnieć- jej długość byłaby mniejsza od wymiarów komórki elementarnej, drgania atomów można
jednak opisywać falami dozwolonymi w krysztale, które poruszają się przeciwnie do kierunku fali interferencyjnej)
skracają drogę swobodną fononów i zmniejszają przewodność cieplną. Zachodzi tutaj przedłużenie czasu przenoszenia
energii w krysztale, co jest równoważne zwiększeniu liczby zderzeń, co z kolei jest równoważne skróceniu i obniżeniu λ.

Przewodność cieplna jest wielkością charakterystyczną substancji w danym stanie skupienia i jego fazie. Dla substancji
niejednorodnych jest zależna od ich budowy, porowatości itp. Dla małych zakresów temperatur w technice przyjmuje się, że
przewodność cieplna nie zależy od temperatury. W rzeczywistości jednak przewodność cieplna zależy od temperatury.
Substancjami najlepiej przewodzącymi ciepło są metale, najsłabiej gazy.

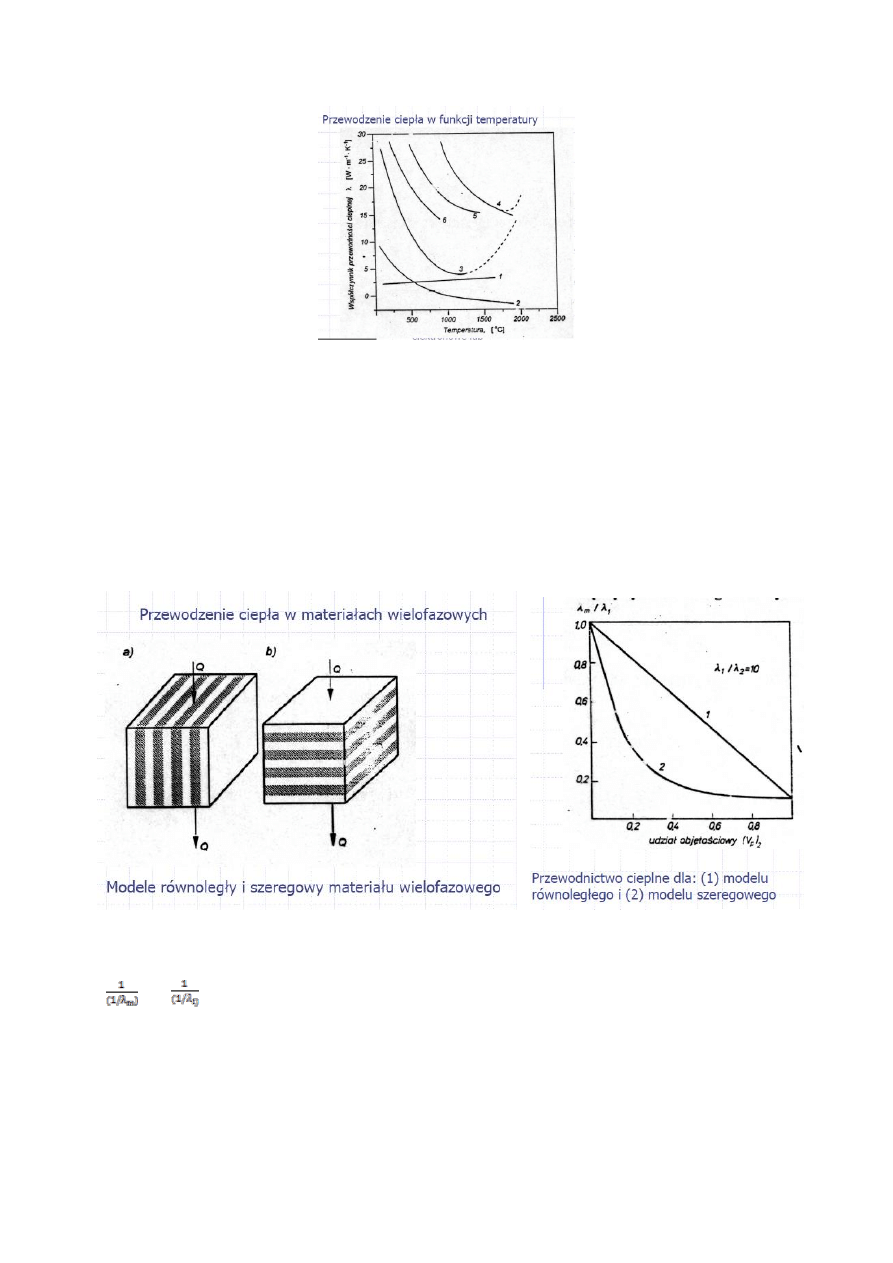
Dla materiałów ceramicznych wartość przewodności cieplnej wynosi od 2W/mK dla ZrO2 do 2000 W/mK dla diamentu.

W11,12-13; BiW s140-144

101 i 102.Współczynnik przewodzenia ciepła materiałów dwufazowych w ujęciu modelu
równoległego i szeregowego.

Istotny wpływ na przenoszenie ciepła przez materiał mają pory obecne w materiale ponieważ dla gazu zawartego w porach



0. Można więc rozważyć 2 modele matematyczne będąca przypadkami skrajnymi (rzeczywiste materiały mają

właściwości pośrednie):

1. W modelu równoległym strumień cieplny jest równoległy do warstw . Przy założeniu, że w całym materiale występuje
ten sam gradient temperatury:

=



i=1

Dla układu dwufazowego:



m

=



1

v

1

+



2

v

2

 ponieważ



1

>>



2

(bo dla gazu λ

2

jest bliska zeru) to



m

=



1

v

1

v

i

- udział objętościowy i-tej fazy; m,1,2- odpowiednio cały materiał, faza stała i gazowa

Zatem w modelu równoległym przewodnictwo cieplne odbywa się głównie przez lepszy przewodnik ciepła (faza stała).

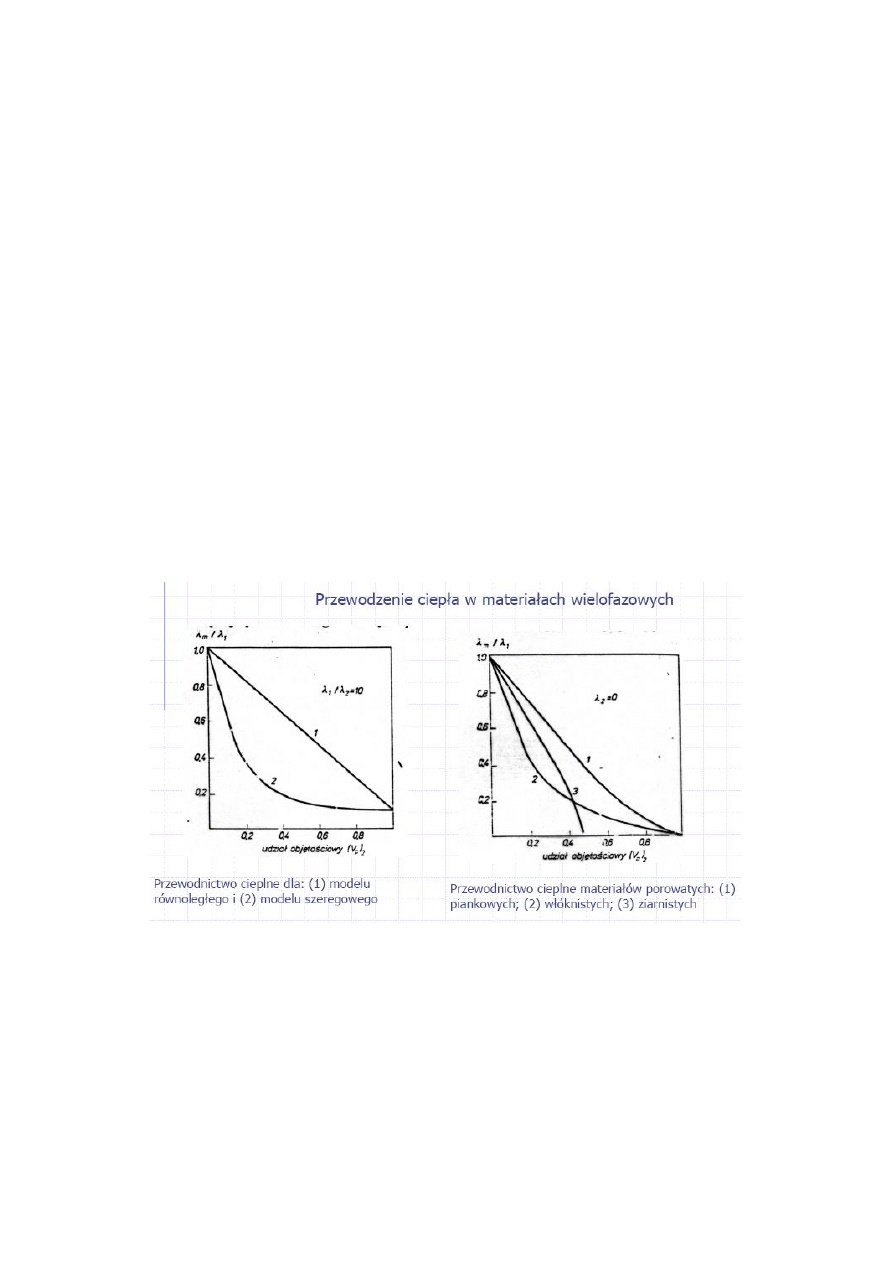
W modelu warstw prostopadłych(inaczej- model szeregowy) gęstość strumienia cieplnego w każdej warstwie jest
jednakowa. Gradienty temperatury są w tej sytuacji różne, ze względu na odmienny współczynnik przewodnictwa ciepła
obu warstw.

1/



m

=v

1

/



1

+v

2

/



2

po sprowadzeniu do wspólnego mianownika 1/



m

=



1



2

/(



2

v

1

+



1

v

2

) 

Ponieważ ponownie



1

>>



2

zatem w przybliżeniu



m

=



2

/v

2

Przewodność cieplna jest tu ustalona przez przewodność gorszego przewodnika (gaz w porach). Jak już wspomniano są to
modele matematyczne, zbliżać do nich się będą materiały piankowe (równoległy model) i materiały włókniste (szeregowy.
W porowatych materiałach ceramicznych może wystąpić przenoszenie ciepła drogą promieniowania między
powierzchniami ciała stałego (znaczący dopiero w wysokich temperaturach). Gęstość strumienia promieniowania energii
cieplnej rośnie wtedy z T

m

3



T gdzie



T=T

1

-T

2

T

m

=(T

1

-T

2

)/2

W11,14-17; BiW s144-146; MC s248-251

103. Określ wpływ porowatości na przewodnictwo cieplne rzeczywistych tworzyw
porowatych.

Eksperymentalnie wyznaczona przewodność cieplna rzeczywistych materiałów porowatych mieści się pomiędzy dwoma
granicznymi przypadkami (szeregowym i równoległym). Przewodność cieplna materiałów piankowych zbliża się do
przewodności modelu równoległego (dominacja przewodnictwa cieplnego przez fazę stałą), a przewodność materiałów
włóknistych do przewodności modelu szeregowego (dominacja przewodnictwa cieplnego przez fazę gazową w porach).

Przewodność cieplna jest tu ustalona przez przewodność gorszego przewodnika (gaz w porach). Ciekawym przypadkiem są
materiały ziarniste, znajdują się one jakby pomiędzy modelami, a przy V

p

około 30% można zaobserwować drastyczny

spadek wartości przewodnictwa, aż do wartości przewodnictwa gazu w porach przy V

p

około 50%. Ten ostatni udział

objętościowy odpowiada bowiem sytuacji, gdy pory staja się w materiale niemal fazą ciągłą. W porowatych materiałach
ceramicznych może wystąpić przenoszenie ciepła drogą promieniowania między powierzchniami ciała stałego (znaczący
dopiero w wysokich temperaturach, tak właściwie to nawet to nie dotyczy tego punktu). Gęstość strumienia
promieniowania energii cieplnej rośnie z Tm

3



T gdzie



T=T

1

-T

2

T

m

=(T

1

-T

2

)/2 BM 145-146, wykład

W11, 17; BiW s145-146; MC s249-251

104. Podaj zakres temperatur topnienia i sublimacji podstawowych materiałów
metalicznych, ceramicznych i polimerów.

Temperatury sublimacji:

Diament 3600

SiC 2800

Tlenek glinu 2000

Ogólnie to straszna bieda, można znaleźć w necie.

W11,3

105. Co to jest pełzanie?

Pełzanie jest to powolne, trwałe i ciągłe odkształcenie materiału w czasie pod wpływem niewielkich naprężeń

niższych od granicy plastyczności. W przypadku metali odkształcenie takie wywołane jest dyfuzyjnym wspinaniem się
dyslokacji, w materiałach ceramicznych, w których dyslokacje są raczej nieruchawe, musi wiązać się z transportem masy
wskutek migracji indywidualnych atomów drogą dyfuzji, której wystąpienie nie wymaga przyłożenia obciążeń. Dyfuzja
jest procesem termicznie aktywowanym i zachodzi w mierzalnym stopniu dopiero w podwyższonych temperaturach. Tym
samym i pełzanie dyfuzyjne jest możliwe w zakresie wyższych temperatur (metale 0,3-0,4 T

top

, ceramika 0,4-0,5 T

top

).

Wielkość odkształcenia wywołanego pełzaniem zależy od naprężenia, temperatury i czasu:



=f(



, t, T)pełzanie.

Odkształcenie tu ma charakter płynięcia lepkościowego, zatem w przeciwieństwie do odkształcenia sprężystego pełzanie
większości metali i ceramiki w temperaturze pokojowej praktycznie zależy od czasu.

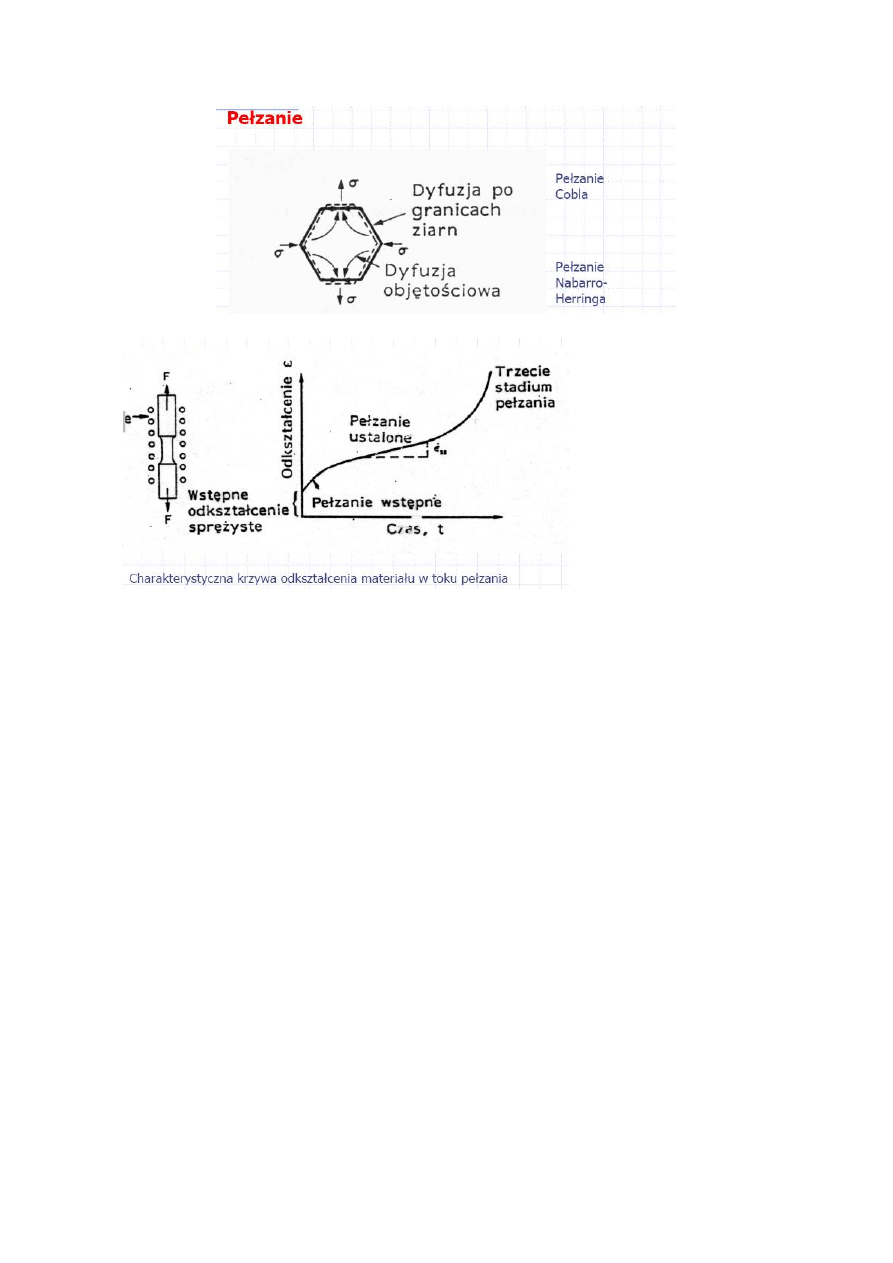
Zjawiska podobne jak w procesie

spiekania. Pełzanie bada się

teoretycznie-nie ma uniwersalnych

metod wyznaczania pełzania.

W11,5-7; BiW s115; MC s182

106. Fenomenologiczne równanie pełzania.

W czasie pełzania ustalonego (II etap na wykresie wyżej) szybkość pełzania jest stała. Równanie pełzania opisuje

się zależnością analogiczną do odkształcenia lepkościowego:



=B



n

B- stała typu współczynnika lepkości

n- stała zależna od mechanizmu pełzania czyli typu procesu zachodzącego w materiale.

Dla procesu dyfuzyjnego najbardziej typowymi mechanizmami są:

I Pełzanie Nabarro-Herringa typu dyfuzji objętościowej

II Pełzanie Cobla typu dyfuzji po granicach ziaren

W11,8- jedyne źródło tak o tym mówiące

107. Podaj i zaznacz na schemacie dyfuzyjne mechanizmy pełzania tworzyw ceramicznych.

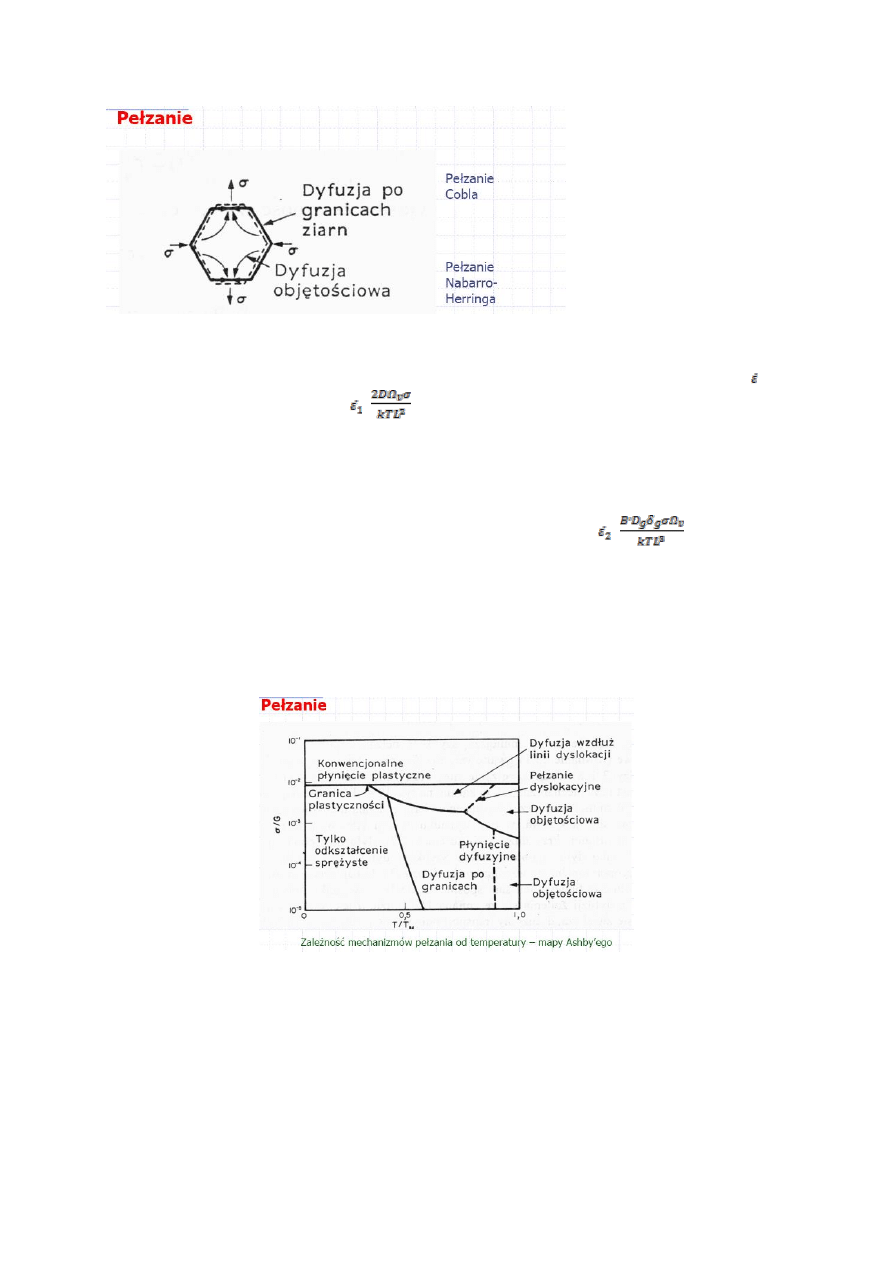
I Pełzanie Nabarro-Herringa typu dyfuzji objętościowej- gdy ogrzany kryształ znajduje się pod wpływem zewnętrznych
obciążeń. Następuje wtedy ukierunkowana dyfuzja atomów od obszarów w stanie naprężeń ściskających do rozciągających
(czyli od obszarów o większym potencjale chemicznym do obszarów o mniejszym potencjale). Szybkość odkształcenia jest

tutaj liniową funkcją naprężenia dana przez: =

gdzie D- współczynnik samodyfuzji, Ω

v

- objętość wakancji, σ-

naprężenie, L- wymiar ziaren polikryształu, k- stała Boltzmanna, T- temperatura.

II Pełzanie Cobla typu dyfuzji po granicach ziaren- mechanizm ten cechuje niższa energia aktywacji, niż poprzedni, w
związku z czym dominować będzie w niższych temperaturach. Innym czynnikiem od którego zależy ten mechanizm jest
wielkość ziaren w polikrysztale- im mniejsze ziarna, tym więcej granic, tym więcej masy przenoszonej nimi. Gdy dyfuzja

zachodzi od obszarów w stanie naprężeń ściskających do rozciągających możemy zapisać: =

gzie B’=150/π, D

g

-

współczynnik samodyfuzji wzdłuż ziaren, δ

g

- szerokość granic międzyziarnowych.

W11,10; ZNoM s130-131; MC s184-185; BiW s119

108. Co to są mapy Ashby’ego dla pełzania?

Mapy Ashby’ego sporządzane są w układzie: względne naprężenie ścinające



/G oraz temperatura względna(stosunek

temperatury bezwzględnej do temperatury bezwzględnej topnienia). Poszczególne pola map odpowiadają zakresom
naprężeń i temperatur względnych, w których dominują określone mechanizmy odkształcenia nieodwracalnego (plastyczne
lub lepkościowe).

W11,11; BiW s120-121; MC s190-191; ZNoM s131-132

109. Jak współczynnik rozszerzalności cieplnej zależy od rodzaju wiązań?

Materiały zmieniają swoje wymiary wraz z temperaturą. Do określania tych zmian używamy współczynnika

rozszerzalności cieplnej α. Z praktycznego punktu widzenia interesuje nas
związek współczynnika rozszerzalności cieplnej z rodzajem wiązań
międzyatomowych. Na wykresie mamy zmiany energii potencjalnej V

p

z

odległością międzyatomową dla substancji o wiązaniach kowalencyjnych
(w tej roli H

2

) oraz jonowych (NaCl). Pokazuje on, że ze wzrostem

jonowości wiązania obserwuje się zwiększenie asymetrii krzywej energii
potencjalnej V

p

= f(r), gdzie r- odległość międzyatomowa, czemu

towarzyszy wzrost wartości współczynników rozszerzalności cieplnej
(rośnie (r

2

-r

1

)/



T)

Odległość międzyatomowa w temperaturze T

1

oscyluje pomiędzy

położeniami A

1

i B

1

, a jej średnia długość dana jest przez r

1

. Odległość

międzyatomowa w temperaturze T

2

oscyluje pomiędzy położeniami A

2

i

B

2

-wtedy jej średnie położenie opisuje r

2

>r

1

- współczynnik rozszerzalności

cieplnej zwiększa się. Czyli w skrócie im większa jonowość, tym większa
asymetria, im większa asymetria tym większe

tym większe α.

Obok rodzaju wiązań atomowych istotną rolę odgrywa również budowa materiałów. Szkła, odznaczające się wiązaniami o
pewnym stopniu jednorodności, wykazują bardzo niski współczynnik rozszerzalności cieplnej ( istotny wpływ ma również to,
że drgania atomów w takich materiałach , ze względu na ich małą gęstość mogą odbywać się bez większych przeszkód- jest
tam dużo miejsca).

W11,20; BiW s146-147; ZNoM s136-137

110. Współczynnik rozszerzalności cieplnej: definicje, miara, zakres wielkości dla tworzyw
ceramicznych.

Jak już wspomnieliśmy materiały zmieniają swe wymiary z temperaturą. Zmiany te określa właśnie

współczynnik rozszerzalności cieplnej α. Liniowy współczynnik rozszerzalności cieplnej wyraża względne wydłużenie
materiału występujące podczas ogrzania materiału o jeden stopień (objętościowy analogicznie dla objętości). Określa on
zmiany wymiarów z temperaturą.

dla liniowych zmian wymiarów:

dla objętości:

V

0,

l

0

-pierwotna objętość i długość

Dla ciał izotropowych, lub pojedynczych kryształów regularnych występuje prosta zależność między rozszerzalnością
objętościowa a liniową:

= 3

. Współczynniki te zmieniaja się z temperaturą, dlatego korzystając z nich należy podawać

zakres temperaturowy dla współczynnika rozszerzalności.

Współczynnik rozszerzalności cieplnej mierzymy w jednostkach: [1/K] lub [1/



C].

Jego wartość wynosi od 0,05-0,07*10

-6

dla szkła kwarcowego do 13,5-13,8*10

-6

dla MgO i 10,2 do 10,7 dla ZrO

2

.

W11,19-20; BiW s146; ZNoM s136

111. Wyprowadź zależność na wielkość naprężeń cieplnych w ujęciu modelowym
„utwierdzonej płyty”.

Rozpatrzmy mały element materiału w postaci bardzo cienkiej płytki o pomijalnie małych

wymiarach w kierunku z, która może swobodnie zmieniać wymiary tylko w kierunku y, w kierunku x
jest bowiem przymocowana do sztywnego podłoża. Płytka o początkowej temperaturze T

0

zostaje

ochłodzona równomiernie do temperatury T< T

0

. Wymiary w kierunku x nie mogą ulec zmianie mimo że by chciały, więc

płytce pojawiają się wskutek tego naprężenia cieplne w kierunku x. Możemy je policzyć. Nasza chłodzona płytka jakby
mogła, zmniejszyłaby się o



x

=



L

(T

0

-T)-płytka w kierunku x powinna się kurczyć. Aby uzyskać stan taki jaki mamy, trzeba

dodać naprężenia rozciągające w kierunku x:



x

= E



x

= E



L



T= E



L

(T

0

-T)



y

=



z

=0.

W kierunku x powstają naprężenia rozciągające zależne od modułu Younga i współczynnika rozszerzalności cieplnej
materiału płytki. Naprężenia rozciągające mają znak plus a ściskające minus. W kierunku y płytka może się kurczyć lub
rozszerzać swobodnie i nie powstają żadne naprężenia.

Gdyby nasz płytka miała zauważalny rozmiar w kierunku z, który tez jest przymocowany, a więc są tu także naprężenia, wzór
ulega modyfikacji z uwzględnieniem liczby Poissona



x

=



z

= E



L

(T

0

-T)/(1-



)



-liczba Poissona.

W modelu przyjęto sprężyste zachowanie materiału (dopuszczalne przy gwałtownych zmianach temperatury, które nas
zresztą najbardziej interesują).

W11,24; BiW s148-149; ZNoM s138-139

112. Podaj definicję naprężeń cieplnych I i II rodzaju.

W materiale poddawanym zmianom temperatury w obszarze odkształceń sprężystych możliwe jest

nierównomierne rozszerzanie cieplne w różnych obszarach:

Naprężenia I rodzaju- naprężenia wynikające z anizotropii rozszerzalności cieplnej poszczególnych ziaren lub anizotropii
modułu Younga E. Wielkość tych naprężeń zależy od własności sprężystych i współczynników rozszerzalności cieplnej
sąsiadujących składników. Gdy wartość powstałych naprężeń przekroczy wytrzymałość tworzywa, następuje jego pękanie.
Naprężenia I rodzaju występują na granicach stykających się ziaren, mają charakter lokalny i maleją nagle w miarę oddalania
się od granicy międzyziarnowej. Wywołane przez nie spękania mają charakter lokalny- w konsekwencji nie następuje
zniszczenie tworzywa, lecz tylko lokalne spękanie.

Naprężenia II rodzaju- naprężenia wynikające z nierównomiernego rozkładu temperatury w objętości (materiał jest
nierównomiernie ogrzany). Niemożliwa jest swobodna rozszerzalność poszczególnych elementów objętości materiału, w
obrębie którego istnieje zróżnicowanie temperatury-swobodna ekspansja każdego z obszarów prowadziłaby do ich
rozdzielenia. Ponieważ są one „uwięzione” w objętości tego samego ciała muszą powstać naprężenia II rodzaju. Prowadzą
one w przypadku przekroczenia wytrzymałości materiału do jego spękań i zniszczenia. Mogą powstać zarówno w
materiałach ceramicznych, metalicznych oraz kompozytowych.

W11,21-24; BiW s148,153-154; Skrypt do laboratorium z NOMu s97-98

113. Od czego zależy wartość naprężeń cieplnych w warunkach nieustalonego przepływu?
Oraz

114.Co to jest liczba Biota?

Przy nieskończenie dużej wartości współczynnika przenikania ciepła h (umożliwiający obliczanie ciepła

przenikającego przez przegrodę cieplną),temperatura powierzchni gorącej kształtki wrzucanej do zimnego ośrodka,
natychmiast osiąga temperaturę tego ośrodka, natomiast środek pozostaje gorący. W tej sytuacji maksymalne naprężenia
występują już w pierwszej chwili , po czasie t0, na powierzchni. Jeśli współczynnik przenikania ciepła jest natomiast
skończony, wówczas maksymalne naprężenia cieplne występują wprawdzie również na powierzchni, osiągane są dopiero po

pewnym czasie. Czas ten jest tym dłuższy im mniejszą wartość ma liczba Biota



- β= r

m

(r

m

- typowy wymiar próbki, np.

promień) W warunkach niestacjonarnego przepływu warunki cieplne określa właśnie liczba Biota, a naprężenia cieplne są
jej funkcją. Funkcja ta ma różną postać w zależności od wielkości



, np. jeśli



<1 to jest to funkcja liniowa:

Zatem można powiedzieć, że warunkach nieustalonego przepływu rozkład temperatury w kształtce zależy od czasu oraz:

-współczynnika wnikania ciepła do materiału

-współczynnika przewodnictwa cieplnego



-wymiarów kształtki r

A wszystkie te wielkości powiązane są w liczbie Biota β. Ogólnie



T



gdy h





r



W11,27-28; BiWs150-152

115. Scharakteryzuj pojęcie: „odporność materiału na wstrząs cieplny”.

Mamy sytuacje taką jak w punkcie 113- wrzucamy gorąca kształtkę do zimnego ośrodka. Jak już napisaliśmy

powstają naprężenia cieplne drugiego rodzaju, które mogą wywołać spękanie materiału, jeśli osiągną jego wartość
wytrzymałości na rozciąganie. Analogicznie jak dla cienkiej płyty, w przypadku kształtki o formie walca można zapisać
naprężenia jako :

P

c

= σ=

Różnice T

mat

-T

ośr

można zapisać jako ∆T. Przekształcając powyższe równanie, dla naprężeń równych wytrzymałości uzyskamy

maksymalną różnicę temperatury:

∆T

max

= R

1

=

R

1

nazywamy współczynnikiem odporności na kruche pękanie w warunkach naprężeń cieplnych. Pod tym pojęciem rozumie

się maksymalną różnicę temperatury, przy której maksymalne naprężenia cieplne są równe wytrzymałości tworzywa czyli:



T=



T

max

gdy



cieplne

=



wytrzymałościowe.

Gdy zatem



T=



T

max

, kształtka zaczyna pękać. Po przekroczeniu



T

max

następuje mniej lub bardziej gwałtowne obniżenie

wytrzymałości materiału na rozciąganie.

W11,25; BiW s150-151

116. Które tworzywa ceramiczne posiadają najwyższą odporność na wstrząs cieplny.
Odpowiedź uzasadnij. Podaj przykłady.

Najwyższą odporność na wstrząsy cieplne posiadają szkła np. szkło kwarcowe 2500⁰C i szkło wapniowo sodowe

500, Si

3

N

4

- 400-500 oraz kompozyty ziarniste i porowate: Al

2

O

3

i ZrO

2

- 800-1000.

∆T

max

= R

1

=

Wiele spośród materiałów o wysokiej odporności na wstrząs cieplny można przewidzieć z tego wzoru. Szkła np. cechuje
niska rozszerzalność cieplna, stosunkowo niskie E, zatem można się spodziewać wysokich wartości ∆T. Zastosowanie

materiałów porowatych obniża natomiast E i G, co również ma pozytywny wpływ na odporność na wstrząs cieplny

.

MC s407; BiW s157- strasznie mało jest na ten temat

117. Zależność



T od właściwości mechanicznych materiału.

Tak właściwie to ten punkt i poprzedni to przynajmniej dla mnie niemal to samo. Dla cienkiego walca kołowego,

którego temperatura T

1

jest w całej objętości jednakowa i którego umieścimy w płynie o wyższej temperaturze T

2

można

przyjąć, że rozszerzalność liniowa jest taka sama we wszystkich kierunkach a jej wartość wynosi:



y

=



x

=



T. Tendencjom do

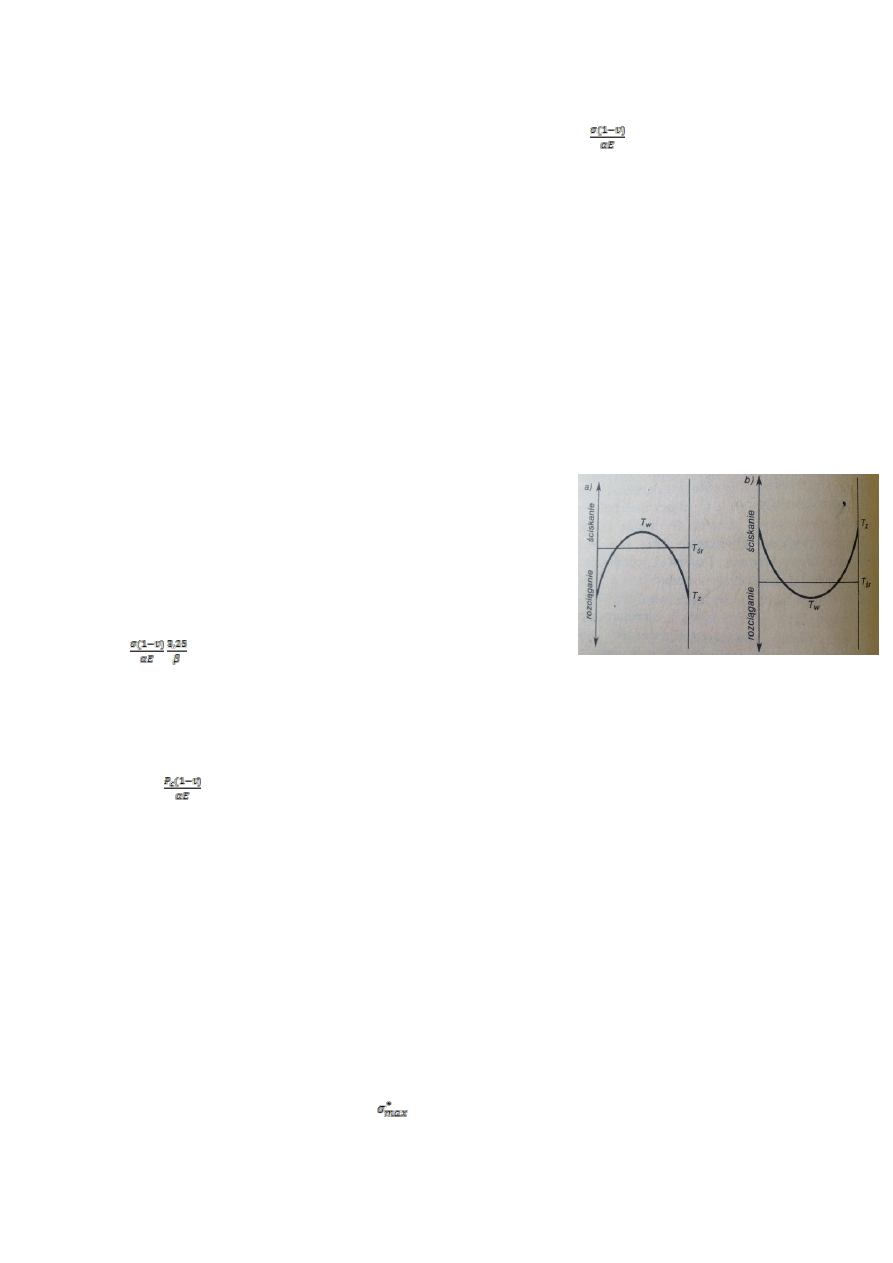
zmiany przekroju przeciwstawiają się naprężenia, których wartość można obliczyć z prawa Hooke’a. Dla płaskiego układu

naprężeń



x

=1/E(



x

-



y

) i



y

=1/E(



y

-



x

). Ponieważ



x

=



y

to



x

=



y

=



. Otrzymujemy ∆T =



T- jest różnicą temperatury rozpatrywanego punktu i T

śr

.



T maleje więc ze wzrostem liczby Poissona i modułu Younga.

W11,25; BiW s150-151; skrypt s98-100

118. Zależność



T od właściwości cieplnych materiału.

Dla walca rozpatrywanego w punkcie 114 temperatura w określonym punkcie wewnętrznym walca uzależniona

jest od szybkości wnikania ciepła przez powierzchnię (charakteryzowana współczynnikiem h), od zdolności przewodnictwa
cieplnego walca (charakteryzowana współczynnikiem



) oraz odległości tego punktu od powierzchni- często równoznacznej

z typ[owym rozmiarem próbki r

m

–a wszystkie te wielkości połączone są w liczbie Biota. Jeżeli pominąć wymianę ciepła

przez wolne końce walca, które w istotny sposób zmieniają tylko rozkład temperatury w ich pobliżu, rozkład temperatury w
czasie t jest w kształtce osiowo symetryczny i nie zależy od współrzędnej w kierunku osiowym. Rozkład temperatury wzdłuż
osi walca jest paraboliczny o średniej temperaturze T

śr

( średnia kalorymetryczna, taka jaką miałby walec, gdyby ilość ciepła

wymieniona z otoczeniem przyjmowana była z jednakową szybkością przez całą objętość walca). Izotermy temperatury w
walcu dla przekroju poprzecznego mają kształt kół współśrodkowych.

a)płyta chłodzona,

b)płyta ogrzewana.

Podsumowując, można powiedzieć że naprężenia cieplne są funkcja liczby Biota a
co za tym idzie wartość ∆T również będzie od tej liczby zależeć. Teraz w zależności
od wartości β można wyprowadzać różne równania na ∆T, np. dla β<1:

∆T=

∙

W11,27-28; BiW s151-152; MC s260-262, skrypt s100-102

119. Jakimi parametrami określamy odporność materiału na wstrząs cieplny?

Kształtka zaczyna pękać, gdy różnica początkowej temperatury kształtki i temperatury otoczenia osiągnie wartość:



T

max

=R

1

=

gdzie P

C

- wartość wytrzymałości materiału na rozciąganie. R

1

to pierwszy współczynnik odporności na

naprężenia cieplne (współczynnik odporności na pękanie w warunkach naprężeń cieplnych).

Inaczej sytuacja wygląda gdy wszystko dzieje się warunkach niestacjonarnego przepływu, na szczęście wyrażenia
analityczne konieczne w tym przypadku mogą być uproszczone przez:

-wprowadzenie bezwymiarowego względnego naprężenia maksymalnego



max

*

- wykorzystanie zależności między



max

* i



.



max

*=



max

/



max

0

przy czym



max

-naprężenia występujące gdy h ma małą wartość,



max

0

-gdy h dąży do nieskończoności.

Dla naszej ulubionej kształtki o postaci walca:



max

0

=



L

E(T

śr

-T

p

)/(1-



)

Można zatem zapisać na podstawie zależności na

że



max

* =



max

T

p

- temperatura powierzchni

Przy założeniu że β<2 można zapisać przedział:

3,25/



< 1/



max

* < 4/







max

*= r

m

h/3,7







T

max

=

∙

Jak widać z tego równania, przy małych wartościach h istotną rolę zaczyna odgrywać



. Wprowadza się drugą stałą

materiałową-drugi współczynnik odporności na pękanie w warunkach naprężeń cieplnych R

2

. R

2

= R

1



-charakteryzuje on

odporność materiału na pękanie pod wpływem naprężeń cieplnych w warunkach powolnego chłodzenia i ogrzewania.

Aby materiał uległ dekohezji, pęknięcia powstałe pod wpływem naprężeń cieplnych muszą się rozprzestrzeniać w materiale.
Trzeba pamiętać że w przypadku naprężeń termicznych, gdy rozwijają się pęknięcia to wartość tych naprężeń spada. Prace
Hasselman’a pozwoliły wyprowadzić współczynnik wyrażający odporność materiału na rozprzestrzenianie się pęknięć w

warunkach naprężeń cieplnych: R

3

=

=(K

Ic

/P

C

)

2

gdzie K

Ic

-odporność na kruche pękanie.

BiW s150-153

120.Jak wyznaczamy krzywą Haselmana, podaj przykłady tej krzywej dla różnych typów
tworzyw.

W materiale przy ∆T>∆T

max

pojawiają się spękania. Te spękania obniżają wytrzymałość mechaniczna materiału.

Badając zatem zależność wytrzymałości materiału σ w funkcji ∆T, możemy zauważyć że w punkcie ∆T

max

następuje

obniżenie tej wytrzymałości, (gwałtowność zmiany zależy od rodzaju materiału). Krzywa Hasselmana to eksperymentalne
wyznaczona zależność wytrzymałości od wielkości wstrząsu cieplnego



T.



=f(



T)

W11,26; Skrypt s100-101

121. Przeanalizuj wpływ porowatości na odporność materiału na wstrząsy cieplne.

Przykładem materiału porowatego używanego w gwałtownie zmieniających się temperaturach, mogą być

ziarniste materiały ogniotrwałe. Udział objętościowy porów w materiałach ziarnistych, jest znaczny i wynosi od 0,2-0,3.
Przy takich udziałach objętościowych ziarna stykają się ze sobą tylko na ograniczonej powierzchni. Wytrzymałość materiału
można opisać za pomocą równania Rumpffa: P

C

=(9/8)[(1-V

p

)/V

p

](F

k

/d

2

) gdzie F

k

jest siłą potrzebną do rozerwania wiązań

między ziarnami. Ponieważ mikrostruktura materiałów ziarnistych jest niejednorodna, występuje tu nierównomierny
rozkład F

k

. Jeśli siła kohezji kontaktów jest zróżnicowana to naprężenia cieplne powodują powstanie lokalnych pęknięć,

mianowicie tylko tam, gdzie występują kontakty międzyziarnowe o niższej kohezji. Tym samym powstają tu zlokalizowane
mikropęknięcia, na których rozprasza się nagromadzona energia sprężystą i zmniejsza się niebezpieczeństwo dekohezji
materiału. Materiały porowate typu komórkowego obniżają natomiast E i G co zwiększa ich odporność na wstrząs
termiczny kosztem pewnego obniżenia wytrzymałości mechanicznej. Pory mogą zostać wypełnione napełniaczem

przewodzącym ciepło i uchodzącym z materiału podczas ogrzewania(powłoki ablacyjne)-obniża się dzięki temu temperaturę
powierzchni nagrzanego materiału wskutek pochłaniania ciepła przez parowanie wypełniacza. Inna metodą jest też
tworzenie porowatej warstwy zewnętrznej- zmniejsza się dzięki temu dopływ ciepła do wewnętrznych warstw spełniających
rolę konstrukcji nośnej.

BiW s157-158; MC s266

122. Podaj prawo Ohma w ujęciu makroskopowym i elementarnym- określ występujące
pojęcia.

Prawo Ohma w ujęciu makroskopowym: U= RI

U-napięcie I- natężenie R- opór

Oznaczając l-długość przewodnika, S- pole przekroju,



-opór właściwy,



-przewodność właściwa (konduktywność)

R

U= I ∙ przyjmując j= I/S- gęstość strumienia prądu oraz E= U/l- natężenie pola elektrycznego

Otrzymujemy: j=



E - II postać prawa Ohma- elementarną (mikroskopową)

W ujęciu elementarnym strumień prądu to ruch ładunków prądu w polu elektrycznym:

J=



i

n

i

evz

i

,gdzie ni-gęstość nośników, e- elementarny ładunek, v-średnia prędkości ruchu ładunków w kierunku pola, z

i

-

liczba elementarnych ładunków ( w jednostce objętości)

Σ- Konduktywność (przewodnictwo właściwe, przewodność elektryczna właściwa) to miara zdolności materiału do
przewodzenia prądu elektrycznego. [



]=S/m=1/(



m).



=



i

n

i

ez

i

(v/E)=b - ruchliwość ładunku w polu

Ostatecznie:



=



i

n

i

ez

i

b

i

- postać dyfuzyjna prawa Ohma

Konduktywność (przewodnictwo właściwe, przewodność elektryczna właściwa) to miara zdolności materiału do
przewodzenia prądu elektrycznego. [



]=S/m=1/(



m).

W12,4; wikipedia

123. Wymień znane Ci rodzaje nośników
prądu elektrycznego.

Nośniki ładunku:

a) elektrony swobodne (metale)

b) dziury elektronowe i elektrony (półprzewodniki i izolatory)

c) jony (w przypadku ciał stałych o wiązaniach jonowych)

W12,7; BiW s180

124. Podaj podstawy teorii pasmowej
przewodnictwa elektrycznego materiałów.

W atomie poszczególne elektrony mogą znajdować się w określonych, dyskretnych stanach energii. Dodatkowo

w ciele stałym, atomy są związane, co nakłada dodatkowe ograniczenia. Dozwolone poziomy energetyczne odizolowanych
atomów, w krysztale, na skutek oddziaływań z innymi atomami, ulegają przesunięciu- wiele atomów ma minimalnie

różniące się wartości energii- powstają tzw. pasma dozwolone. Pozostałe pasma nazywamy wzbronionymi. To czy dany
elektron może mieć określona energię można określić z warunku Bragga. Można to zrozumieć przez analogię. Wiadomo, że
np. promieniowanie rentgenowski nie rozprzestrzenia się w krysztale, tylko ulega odbiciu, gdy spełniony jest wspomniany
warunek; n’λ= 2dsinθ (d-stała sieciowa, n’



C). Ponieważ ruch elektronu ma cechy falowe a elektronowi można przypisać

pewną długość fali: p= m



=h/



, gdzie h- stała Plancka, to fale elektronowe mogą ulegać odbiciu w strukturze krystalicznej.

Będzie się to działo, gdy tzw. liczba falowa K= n’π/d , lub gdy długość fali wynosi λ= 2d/n’. Elektrony spełniające te warunki
nie będą mogły rozprzestrzeniać się w krysztale, tworząc strefę energii wzbronionych.

Strefa energii wzbronionych (przerwy energetycznej)- przedział energii odpowiadającej energii elektronów niezdolnych do
przemieszczania się w krysztale.

Pasma walencyjne- Zakresy energii odpowiadające mogącym się ruszać elektronom są zakreskowany na rysunku i
oddzielone od siebie strefami energii wzbronionych. Można wyróżnić pasma położone niżej w widmie energii- odpowiadają
one elektronom na orbitalach wewnętrznych, i położone wyżej- orbitale zewnętrzne, z elektronami tworzącymi wiązania
międzyatomowe. Te wszystkie poziomy są w pełni zapełnione, a elektrony w nich nie mogą zmieniać swojej energii
kinetycznej- czyli jak przyłożymy pole elektryczne to nie mogą one uczestniczyć w przewodzeniu prądu.

Pasmo przewodnictwa- jest to pasmo dozwolone, o energii wyższej niż najwyższe pasmo walencyjne. Elektrony z tego
pasma walencyjnego, mogą przechodzić do pasma przewodnictwa na wskutek wzbudzenia- dostarczenia energii. W paśmie
przewodnictwa elektrony mogą prac udział w przewodzeniu prądu. Przejście z miedzy pasami powoduje, że w paśmie
walencyjnym tworzą się dziury po elektronach, które podlegają takim samym zasadom ruchu co elektrony.

BiW s182-183; wikipedia

125.Co to jest energia strefy wzbronionej, podaj klasyfikację materiałów według wielkości
energii strefy wzbronionej.

Dolna granica pasma przewodnictwa jest położona wyżej (wyższa energia) niż górna granica pasma walencyjnego

(niższa energia). Przerwa energetyczna pomiędzy tymi pasmami jest nazywana pasmem zabronionym (wzbronionym) lub
przerwą zabronioną (energia ta jest oznaczana przez W

g

)- przedział energii odpowiadający energii elektronów niezdolnych

do przemieszczania się w krysztale. Żeby w danym materiale mógł płynąć prąd elektryczny muszą istnieć swobodne nośniki -
pojawią się one, gdy elektrony z pasma walencyjnego przejdą do pasma przewodnictwa. Musi więc zostać z zewnątrz
dostarczona energia co najmniej tak duża, jak przerwa zabroniona.

-metale (przewodniki, ci d) nie mają pasma
zabronionego (pasmo walencyjne i
przewodnictwa zachodzą na siebie lub w paśmie
walencyjnym występują swobodne elektrony-
pełni ono rolę pasma przewodnictwa)

-izolator (a) –energia rzędu 10eV- dostarczenie
takiej dużej energii oznaczałoby zniszczenie

izolatora

-półprzewodnik- energia mniejsza niż 2eV ( choć istnieją półprzewodniki o energii większej)

W12,10; BiW s182

126. Podaj różnicę między półprzewodnikiem samoistnym a domieszkowanym, podaj
przykłady.

Półprzewodnik samoistny jest to półprzewodnik, którego materiał jest idealnie czysty, bez żadnych

zanieczyszczeń struktury krystalicznej. Powstają w nim pary: elektron w paśmie przewodnictwa- dziura w paśmie
walencyjnym, powstające w wyniku przeniesienia elektronu przez wzbudzenie z pasma walencyjnego do
przewodnictwa. Są to kryształy o strukturze diamentu(Si,Ge) , sfalerytu(GeAs, GaP, pite) i wurcytu(Sic, CdS).
Wiązania mają charakter głównie kowalencyjny. Charakteryzują się szerokimi pasmami walencyjnymi i
przewodnictwa tzn. posiadają dużą ruchliwość nośników. Przewodnictwo rośnie z temperaturą w skutek zwiększania
się liczby nośników prądu.

Półprzewodniki samoistne mają mało ładunków swobodnych (co objawia się dużą rezystywnością), dlatego też
stosuje się domieszkowanie. Materiały uzyskane przez domieszkowanie nazywają się półprzewodnikami
niesamoistnymi lub półprzewodnikami domieszkowanymi.

W półprzewodniku poziom Fermiego położony jest podobnie jak w przypadku izolatorów, jednak przerwa
energetyczna (szerokość pasma wzbronionego) jest niewielka (umownie za półprzewodnik przyjmuje się ciało, w którym
szerokość pasma wzbronionego jest mniejsza niż 2 eV). W półprzewodnikach samoistnych część elektronów przechodzi do
pasma przewodnictwa dzięki energii termicznej lub np. wzbudzeń fotonowych. Przewodnictwo w półprzewodnikach
samoistnych ma charakter pół na pół elektronowo-dziurowy.

Półprzewodniki typu n

Jeżeli wprowadzany atom domieszki będzie chętnie oddawał elektrony do pasam przewodnictwa, to nazywamy go
donorem. Jeżeli np. do półprzewodnika (będącego pierwiastkiem grupy 14) wprowadzimy pierwiastek z grupy 15
nadmiarowe elektrony w strukturze krystalicznej utworzą nowy poziom - poziom donorowy, który znajduje się tuż
poniżej pasma przewodnictwa. Elektrony z poziomu donorowego (na który łatwiej wrzucić elektrony niż na pasmo
przewodnictwa) niewielkim kosztem energetycznym mogą przenosić się do pasma przewodnictwa. W
półprzewodnikach typu n główny wkład do przewodnictwa pochodzi od elektronów (ale efekty opisane dla
spontanicznych też grają role).

La

Ba

x

La



Ba

+e’

Półprzewodniki typu p

Analogicznie do półprzewodników typu n, jeżeli wprowadzimy pierwiastek grupy 13 to tuż powyżej pasma
walencyjnego pojawia się wolny poziom, zwany akceptorowym. Spontaniczne przejście elektronów na ten poziom
powoduje powstawanie dziur, które są nośnikiem dominującym.

Mg

Si

xx

+2e’ Mg

Si

’’+2h



W12,16; MC s339; Wikipedia

127. Co to są półprzewodniki tlenkowe?

Związki jonowe o charakterze niestechiometrycznym lub związki jonowe z domieszkami zawierające defekty punktowe i
elektronowe (elektrony i dziury).

Przykładem takich półprzewodników mogą być tlenki metali grup przejściowych, zawierające kationy z niezapełnionymi
orbitalami d, a więc kationy zdolne przy wzajemnych zbliżeniach do utworzenia niezapełnionych pasm np. ZnO, NiO, ZnS.
Budowa większości półprzewodników jest bardziej lub mniej jonowa, a ta związana jest z bardzo wąskimi pasmami zarówno
przewodnictwa jak i walencyjnym. Pasma energii stają się coraz węższe przy zmniejszającym się stopniu nakładania orbitali
kationów-liczba stanów energetycznych dostępnych dla elektronów zdolnych do przemieszczania się w krysztale ulega
zmniejszeniu. W granicznym przypadku kryształ związku tlenowego o niewielkiej szerokości strefy energii wzbronionej
charakteryzuje się występowaniem odizolowanych od siebie poziomów energii elektronów związanych z kationami (
zmniejsza się ruchliwość elektronów i dziur). Należy przyjąć występowanie mechanizmu „skaczących elektronów”, w
których nośnik ładunku może przejść przez kryształ na drodze kolejnych, odizolowanych od siebie przeskoków. Ruchliwość
taka znacznie wzrasta ze wzrostem temperatury- półprzewodniki tlenkowe uzyskuje się do otrzymywania rezystorów
zmniejszających silnie swą rezystywność z temperaturą. Mechanizm przeskoków:

I etap: Ni

2+

Ni

3+

Ni

3+

II etap: Ni

3+

Ni

2+

Ni

3+

III etap: Ni

3+

Ni

3+

Ni

2+

W12,17; BiW s186-187; ZNoM s254-255; WMC s119-120

128. Dlaczego typowe materiały ceramiczne są izolatorami elektrycznymi?

W materiałach ceramicznych szerokość strefy energii wzbronionych (4-10 eV)jest większa i poziomy związane z

obcymi domieszkami są tu położone dość daleko od dna pasma przewodnictwa i pułapu pasma walencyjnego. W
większości materiałów ceramicznych stężenie defektów punktowych jest znikome, więc mamy małe stężenie nośników
które są przezeń generowane. Oprócz tego jonizacja takich materiałów wymaga większego wkładu energii. Związane z
domieszkami elektrony i dziury elektronowe, występują na tych poziomach przez dłuższy czas i spędzają tylko krótki okres
czasu w paśmie przewodnictwa lub walencyjnym, gdzie mogą poruszać się pod wpływem pola. Następstwem jest znaczne
zmniejszenie się ruchliwości elektronowych nośników ładunku i zmniejszenie przewodnictwa elektrycznego . Sytuacja taka
jest tym bardziej prawdopodobna im szersza jest strefa energii wzbronionych.

W12,9; MC s346; BiW s185-186

129.Wymień mechanizmy polaryzacji elektrycznej.

Indukcja momentów dipolowych możliwa jest w skutek:



a) polaryzacji elektronowej polegającej na przesunięciu elektronów względem

dodatniego ładunku rdzenia atomu (wszystkie rodzaje materiałów)



b) polaryzacji jonowej, występującej w materiale złożonym z jonów, polegającej

na rozsunięciu środków ciężkości ładunku dodatniego kationów i ujemnego
anionów



c)polaryzacji orientacyjnej która powstaje w wyniku oddziaływania pola

elektrycznego bądź na materiały zawierające polarne molekuły bądź
spolaryzowane zespoły defektów punktowych. Dipole ulegają orientacji pod
wpływem przyłożonego pola elektrycznego.



D) polaryzacja ładunku przestrzennego

Omówione rodzaje polaryzacji mogą wystąpić w wyniku:

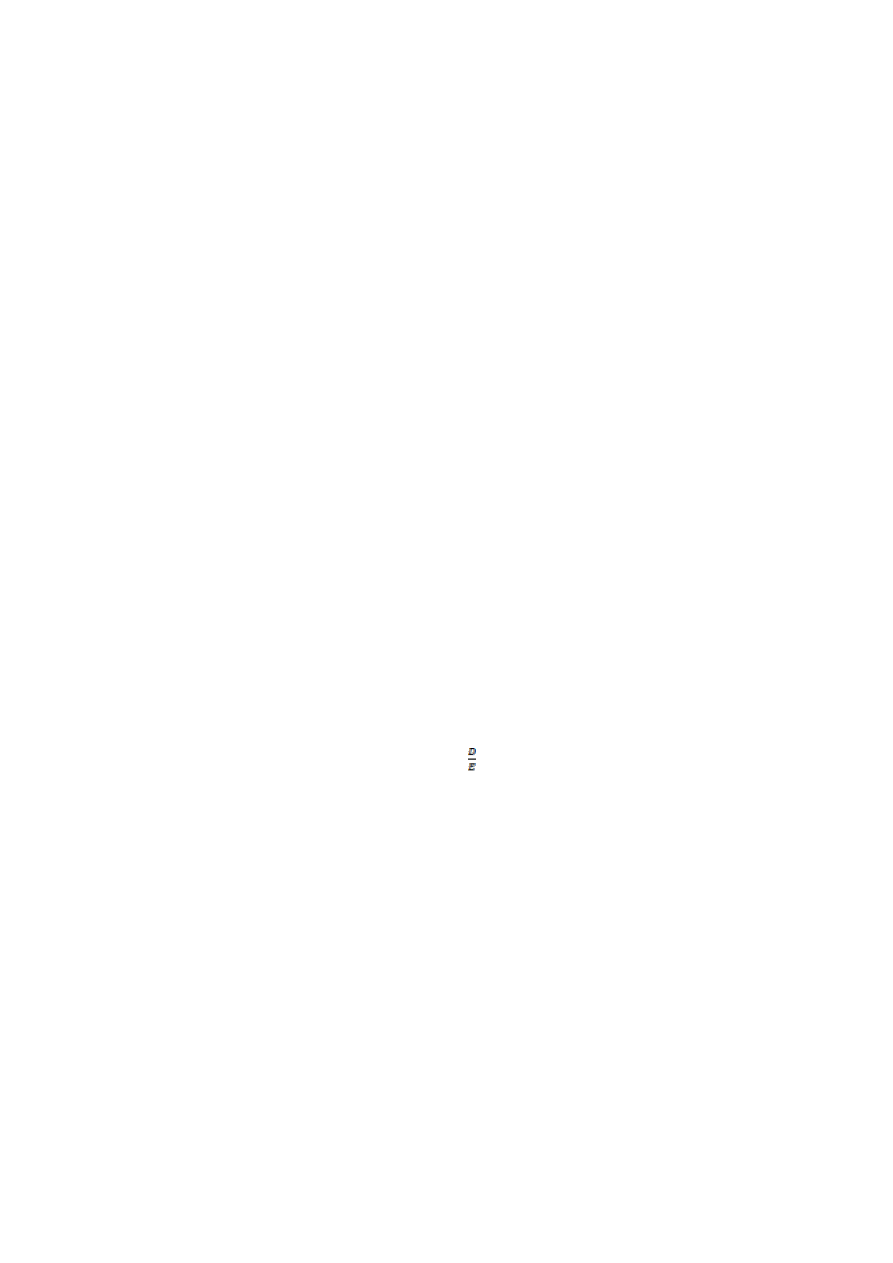
-polaryzacji sprężystej- rozsunięcie punktów ciężkości ładunku elektrycznego następuje wyłącznie wskutek dostosowania
się położeń naładowanych elementów do kierunku przyłożonego pola elektrycznego, czemu przeciwdziałają siły sprężyste
wywołane przez przemieszczanie się tych elementów względem pozycji równowagowych

-polaryzacji cieplnej- wiążę się z przemieszczaniem się słabo związanych elektronów lub dziur elektronowych,
występujących przy poziomach donorowych lub akceptorowych. Pod wpływem energii cieplnej elektrony i dziury
elektronowe przeskakują z pozycji na pozycję w sposób chaotyczny, lecz przyłożenie zewnętrznego pola elektrycznego
przeskoki te ukierunkowuje i wywołuje polaryzację elektronową (podobny efekt- ukierunkowanie ruchu defektów,
naładowanych względem struktury krystalicznej, pod wpływem pola elektrycznego- polaryzacja jonowa.

Polaryzacja sprężysta i cieplna w tym związana z ładunkiem przestrzennym różnią się czasem dostosowania się do działania
pola elektrycznego-czasem relaksacji.

W12,22; MC s312-313; BiW s160-161

130. Jakie parametry charakteryzują właściwości dielektryczne materiałów?

- przenikalność dielektryczna materiałów

-stała dielektryczna materiałów



s

=



0



r

- wytrzymałość na przebicie -największa wartość natężenia pola elektrycznego, jaka może istnieć w dielektryku (izolatorze)
bez wywołania przebicia. Jednostką jest V/m

- rezystywność- to miara oporu z jakim materiał przeciwstawia się przepływowi prądu elektrycznego

- maksymalna temperatura zastosowania

-temperatura Curie

Wikipedia- lipne źródło ale jak na to pytanie się nadaje

131. Co to jest przenikalność dielektryczna materiałów?

Przenikalność elektryczna (stała dielektryczna) jest to wielkość fizyczna, oznaczana grecką literą ε (epsilon),

charakteryzująca właściwości elektryczne środowiska. Dla substancji izotropowych jest to wielkość skalarna, równa

stosunkowi indukcji pola elektrycznego do natężenia tego pola: ε= .Wymiarem przenikalności elektrycznej w układzie SI

jest F∙m

-1

(farad na metr). Spośród wszystkich ośrodków, najmniejszą przenikalność elektryczną wykazuje próżnia. Wartość

ta, oznaczana ε

0

, jest równa: ε

0

= 8,854187817*10

-12

[F/m]

Przenikalność poszczególnych ośrodków często określa się poprzez bezwymiarową wartość przenikalności względnej,
oznaczanej ε

r

. Wielkość ta wskazuje, ile razy przenikalność (bezwzględna) ośrodka jest większa od przenikalności próżni:

ε= ε

r

∙ε

0.

Współczynnik ε

r

, zwany dawniej stałą elektryczną ośrodka, przyjmuje wartości od 1 (dla próżni i silnie rozrzedzonych gazów)

do dziesiątek tysięcy (dla ferroelektryków). Wartości względnej stałej dielektrycznej, zazwyczaj wyznacza się poprzez analizę
zjawisk w kondensatorach. Jeżeli w przestrzeni pomiędzy dwiema naładowanymi, przewodzącymi płytkami, położonymi
względem siebie równolegle, znajduje się próżnia to pomiędzy wektorem natężenia pola elektrycznego E

a

, którego źródłem

są ładunki na okładkach, a wektorem indukcji elektrycznej D występuje związek D=



0

E

a

, natomiast, gdy pomiędzy płytkami

znajduje się materiał ulegający polaryzacji to wektor indukcji elektrycznej dany jest przez D=



s

E

a



s

-jest stałą dielektryczną

materiału, którą można wyrazić jako krotność



0

:



s

=



s



r

,

MC s315-316; BiW s162; wikipedia

132 . Co to są materiały ferroelektryczne?

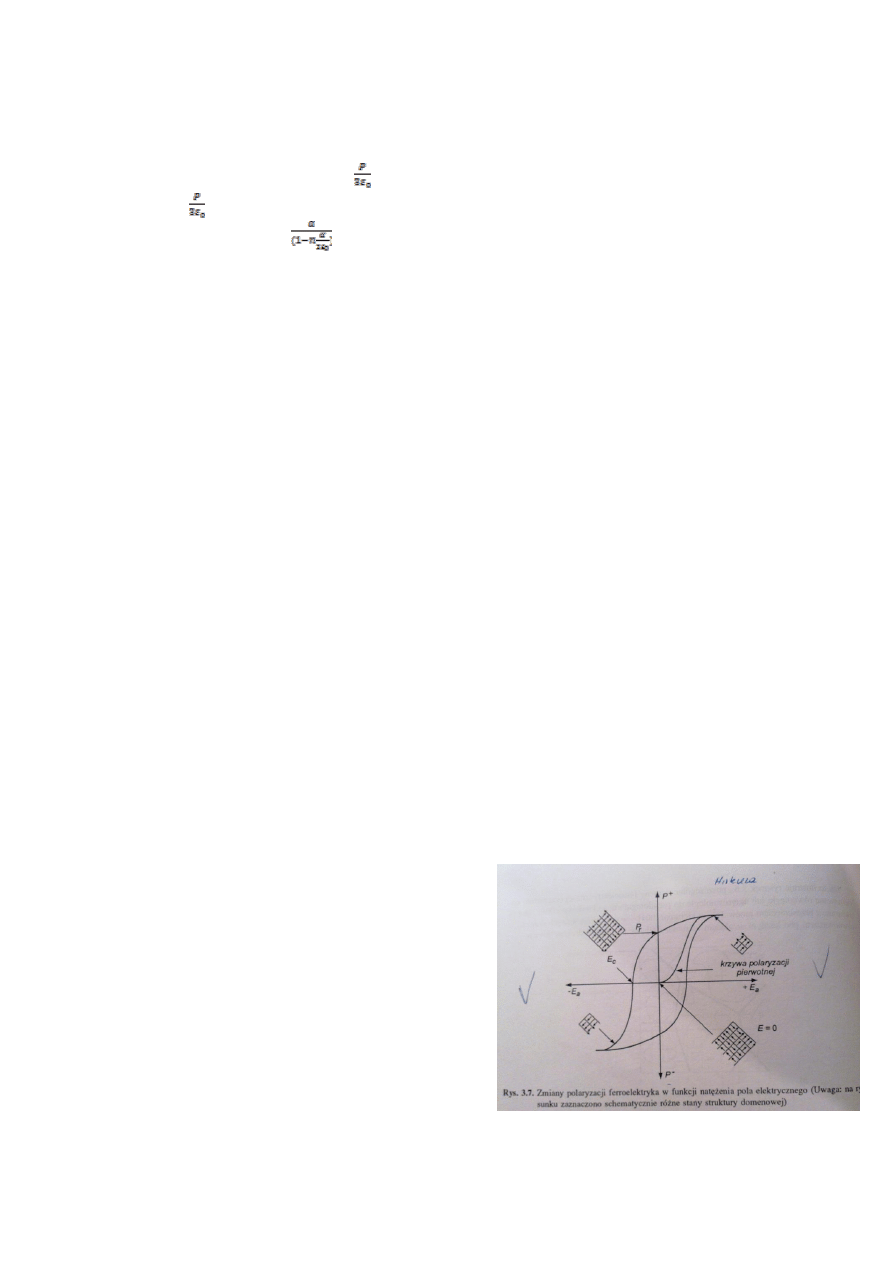
Ferroelektryki to specyficzna grupa dielektryków o dużej względnej stałej dielektrycznej. Ulegają one

samorzutnie polaryzacji w nieobecności pola elektrycznego lub przy bardzo małych wartościach jego natężenia.
Wychodząc ze wzorów na polaryzacje materiału P= nαE

loc

gdzie E

loc

jest to natężenie pola działającego lokalnie na każdy

dipol, oraz ze wzoru na właśnie E

loc

: E

loc

= E

a

+

, (n- liczba dipoli na jednostkę objętości, E

a

- natężenie zewnętrznego pola

elektrycznego,

- natężenie pochodzące od pozostałych dipoli, α- polaryzowalność) podstawiając drugi wzór do

pierwszego można uzyskać: P= [n

] E

a

. Zakładając że stężenie dipoli jest bardzo duże (co mam miejsce w

ferroelektrykach) to mianownik dąży do zera, zaś P dąży do nieskończoności. Czyli już dla bardzo małych E

a

mamy duże P-

mogą wystąpić duże wartości polaryzacji przy znikomo małych wartościach natężenia pola elektrycznego (np. BaTiO

3

, PZT-

tez z tytanem coś). W wysokich temperaturach ferroelektryki mają strukturę perowskitu, gdzie jony Ti

4+

znajdują się w

centrum oktaedrów tlenowych. Poniżej określonej temperatury nazywanej temperaturą ferroelektryczną Curie ta
symetryczna struktura przechodzi w przypadku BaTiO

3

w niżej symetryczną strukturę o symetrii tetragonalnej w wyniku

sprzężonych małych przesunięć jonów tytanu z kierunku <001>. W skutek tego punkty ciężkości dodatniego ładunku jonów
tytanu nie zbiegają się w strukturze w centrum oktaedrów ujemnie naładowanych jonów tlenu. Wystąpiła samorzutna
polaryzacja bez wpływu zewnętrznego pola elektrycznego. Oprócz tego występuje polaryzacja związana z występowaniem
domen ferroelektrycznych.

W12,25-26; BiW s161-162,167-168

133. Dlaczego BaTiO

3

ma właściwości ferroelektryczne?

W BaTiO

3

Jony Ti

4+

znajdują się w centrum oktaedrów tlenowych. Jak wcześniej napisaliśmy, poniżej określonej

temperatury nazywanej temperaturą ferroelektryczną Curie ta symetryczna struktura przechodzi w przypadku BaTiO

3

w

niżej symetryczną strukturę o symetrii tetragonalnej w wyniku sprzężonych małych przesunięć jonów tytanu z kierunku
<001>. W skutek tego punkty ciężkości dodatniego ładunku jonów tytanu nie zbiegają się w strukturze w centrum
oktaedrów ujemnie naładowanych jonów tlenu. Wystąpiła samorzutna polaryzacja bez wpływu zewnętrznego pola
elektrycznego. Jeśli krystaliczny BaTiO

3

nie znajdował się wcześniej w zewnętrznym w polu elektrycznym wówczas

makroskopowa polaryzacja związana z występowaniem domen ferroelektrycznych jest niewielka. Domeny
ferromagnetyczne mają zwykle wymiary od 10

-6

do 10

-4

. Są to obszary o jednakowej orientacji dipoli. Jednak, przynajmniej

w mojej opinii, kwestia domen nie dotyczy tego pytania.

W12,25; BiW s168

134. Narysuj krzywą histerezy dla ferroelektryków.

W przypadku materiałów o budowie domenowej przyłożenie zewnętrznego pola elektrycznego powoduje

zmiany tej budowy. Początkowo przy niewielkich natężeniach pola występuje rozrost domen, w których kierunek
polaryzacji jest najbliższy kierunkowi pola (przesunięcie granic międzyziarnowych). Po osiągnięciu przez materiał polaryzacji
równej maksymalnej polaryzacji spontanicznej w domenach, pole elektryczne może indukować dalszy przyrost polaryzacji
materiału zwiększając momenty dipolowe w porównaniu z
momentami powstającymi spontanicznie (duży wkład energii i duże
natężenie pola). Ostatni przyrost zanika przy odłączeniu
zewnętrznego pola i polaryzacji nieco spada, do poziomu polaryzacji
remanencji P

r

. Dla sprowadzenia polaryzacji materiału do zera,

konieczne jest zadziałanie pola o kierunku przeciwnym do
poprzednio przyłożonego (E

c

- natężenie pola koercji). Dalszy wzrost

natężenia (powyżej E

c

) pozwala odwrócić kierunek polaryzacji

materiału. Omówione zjawiska powodują, ze w przebiegu polaryzacji
w zależności od natężenia pola elektrycznego występuje pętla
histerezy.

W12,25; BiW s169-170; WMC s131-132

135. Na czym polega budowa domenowa
ferroelektryków?

Domeny ferroelektryczne są to występujące w ziarnach o

ferroelektrycznych właściwościach małe obszary o wymiarach
rządu od 10

-6

do 10

-4

przy czym w danej domenie występuje

jednakowa orientacja dipoli. Poszczególnie domeny
ferroelektryczne są przeważnie zorientowane równolegle lub
antyrównolegle do kierunku <001>. Przeciwnie zorientowane
momenty dipolowe domen sąsiadujących ze sobą w ziarnie znoszą
się w dużym stopniu. Taka antyrównoległa orientacja tyczy około
80% wszystkich domen. Tworzenie struktury domenowej wynika ze
względów energetycznych. Jednorodna polaryzacja całej objętości
kryształu spowodowałaby wystąpienie na ścianach ziarna dużej
liczby ładunków związanych jednego rodzaju i o przeciwnym ładunku na przeciwległych ścianach. Pole elektryczne
wytworzone przez powierzchniowe ładunki z jednej strony przeciwdziała polaryzacji a z drugiej podnosi energię układu.
Natężenie pola i energia układu mogą ulec zmniejszeniu, jeśli duża liczna linii pola w pobliżu kryształu zostanie „zwarta na
krótko” dzięki pojawieniu się na danej powierzchni obok siebie przeciwnych ładunków związanych, a więc gdy w krysztale
utworzą się domeny o antyrównolegle zorientowanych dipolach elektrycznych.

W12,26; BiW s169; WMC s129-130

136. Scharakteryzuj wielkość: przenikalność magnetyczna materiałów

Przenikalność magnetyczna jest to wielkość określająca zdolność danego materiału (ośrodka) do zmiany indukcji
magnetycznej pod wpływem natężenia pola magnetycznego.

W celu fenomenologicznego określenia pola magnetycznego wprowadza się wielkość zwaną indukcją magnetyczną B. Zależy
ona od natężenia pola magnetycznego H, a z drugiej strony od współczynnika charakteryzującego ośrodek podlegający
działaniu pola magnetycznego- czyli właśnie przenikalność:

B=



0

H



0

-przenikalność magnetyczna próżni (1,2566*10

-8

Vs/Am)

Jeśli w polu magnetycznym znajdzie się dowolny materiał to B=



H, gdzie



- absolutna przenikalność magnetyczna materiału

i ośrodka.



=



0



r



r

- względna przenikalność magnetyczna. MC 294

MC s294; BiW s201

137. Podaj podział materiałów ze względu na właściwości magnetyczne, określ przenikalność
magnetyczną dla każdego typu tworzyw.

Diamagnetyki- każdy atom ma zerowy moment magnetyczny (np. Cu) (przenikalność jest nieco mniejsza od jedności (czyli
od μ

0

, mówimy powiem o przenikalności względnej). Większość materiałów ceramicznych oraz półprzewodników

samoistnych. Należą do nich także nadprzewodniki wysokotemperaturowe (w nich pole magnetyczne jest całkowicie
wypierane, μ

r

=0)

Paramagnetyki- momenty magnetyczna są zorientowane przypadkowo i się znoszą (np. Cr) (przenikalność nieco wyższa od
jedności)

Ferromagnetyki- momenty magnetyczne są uporządkowane wewnątrz każdej domeny (np. Fe) (względna przenikalność
osiąga wartości rzędu 10

5

). Są to np. metale grup przejściowych- Fe, Co, Ni

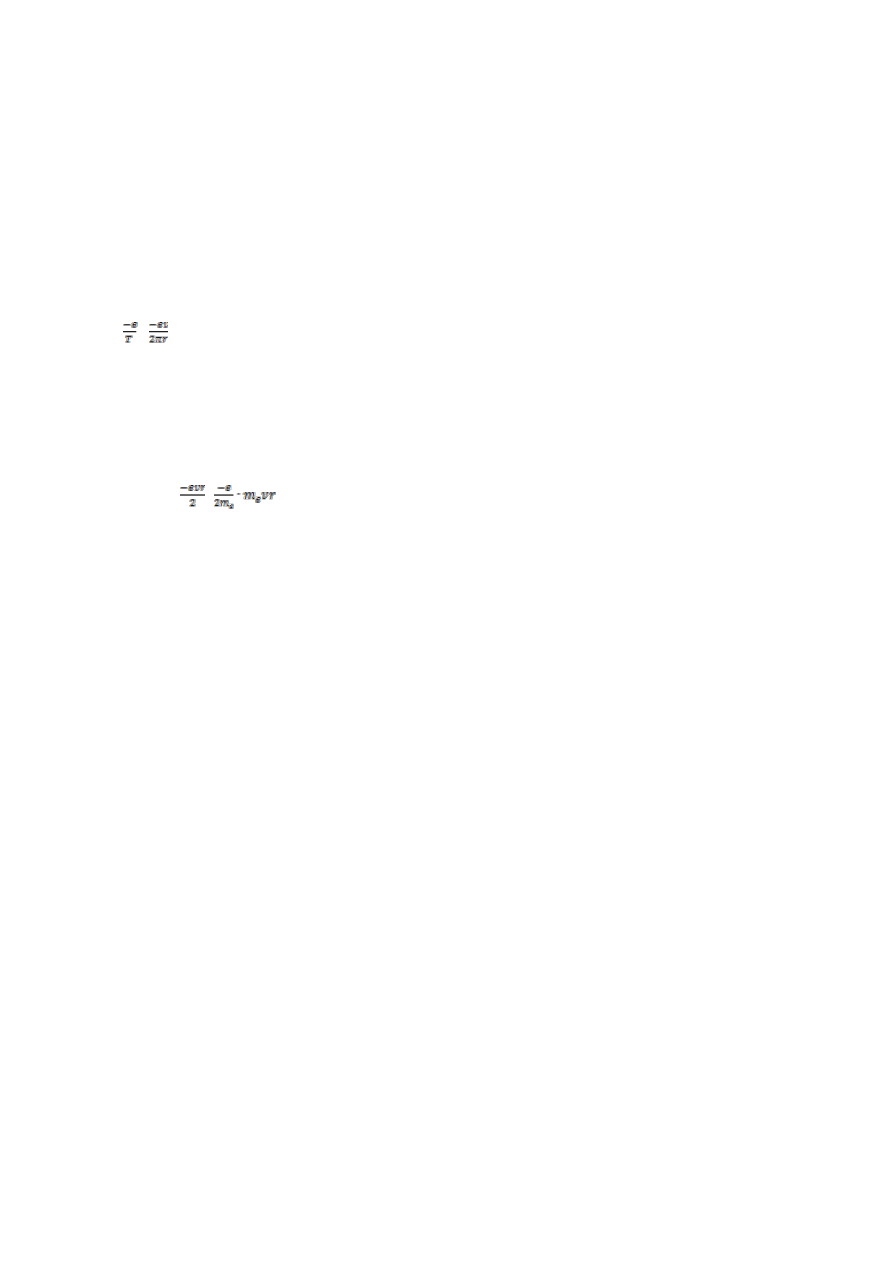
Ferrimagnetyki- istnieją podstruktury posiadające zorientowane jednakowo i zróżnicowane momenty magnetyczne (np.
spinele). Zaliczamy do nich min. materiały ceramiczne o wiązaniu jonowym w których strukturze występują kationy grup
przejściowych.

W13,6; MC s299; BiW s201

138. Przyczyny powstania nieskompensowanego momentu magnetycznego w materiałach

.

Paramagnetyzm występuje w materiałach, w których poszczególne składowe atomy mają własne wypadkowe momenty
magnetyczne. Wszystko wynika z faktu, że poruszający się ładunek elektryczny, np. elektron, wywołuje pole magnetyczne.
Niech pojedynczy elektron o ładunku –e i masie m

e

krąży po orbicie o promieniu r. Wywołany prąd I dany jest wzorem:

I

=

=

v- prędkość liniowa krążącego elektronu, T- okres obrotu

Prąd kołowy I tworzy w ten sposób pole magnetyczne prostopadłe do swej trajektorii (elektron jest równoważny małemu
magnesowi).

Moment magnetyczny m

m

prostopadły do zamkniętego obwodu prądu tworzącego powierzchnię A=



r

2

jest równy IA.

m

m

=IA=I



r

2

=

=

gdzie m

e

vr= L - mechaniczny moment pędu

Moment magnetyczny wytwarzany przez elektron poruszający się po orbicie jest zatem proporcjonalny do jego
mechanicznego momentu pędu.

W świetle mechaniki kwantowej elektron może się jednak poruszać tylko po orbitach, dla których rzuty momentów pędu na
kierunek pola są całkowitymi wielokrotnościami h/2



czyli po ludzku musi być skwantowany.

Jeśli wprowadzi się pojęcie elementarnego momentu magnetycznego nazywanego magnetonem Bohra
m

B

=(h/2



)(e/2m

e

)=9,27*10

-24

J/T to całkowity moment magnetyczny atomu m

m

=-m

B

L

Elektron charakteryzuje się również wewnętrznym ruchem (spinem-ruchem kołowym elektronów w orbicie), który również
prowadzi do powstania momentu magnetycznego. W przypadku momentu magnetycznego związanego ze spinowym
momentem pędu, dla jednego elektronu o niesparowanym spinie m

ms

= +/-0,5m

B

W przypadku gdy mamy więcej niż jeden elektron na niezapełnionych całkowicie orbitalach 3d lub 4f, spinowy moment
magnetyczny jest równy m

e,ef

=-2m

B

(S(S+1))

1/2

W13,8; BiW s201-203; WMC s149-151; MC 295-296- te wyprowadzenia znacznie między sobą się różnią.

139. Zależność przenikalności magnetycznej od temperatury.

Można wyprowadzić zależność, mówiącą że (1+



m

)=



r

, gdzie µ

r

- względna przenikalność magnetyczna materiału,

χ

m

- podatność magnetyczna materiału. Korzystając z tej informacji, można omówić zależność przenikalności magnetycznej

od temperatury. Występują 2 przypadki:

1. Mamy materiał w którym momenty magnetyczne poszczególnych jonów ułożone są chaotycznie. Po umieszczeniu
materiału w polu magnetycznym występuje w nim tendencja do orientacji momentów atomów równolegle do linii
zewnętrznego pola magnetycznego. Ruchy cieplne atomów przeciwdziałają równoległemu ułożeniu momentów. W związku
z tym, temperatura będzie miała wpływ na przenikalność. Im wyższa temperatura tym mniejsza podatność magnetyczna i
przenikalność magnetyczna (bo tym silniejsze są przeszkadzające nam ruchy cieplne). Równanie Curie:



m

=C/T C-stała Curie

2. W wysokich temperaturach kryształ zachowuje się jak typowy paramagnetyk. Poniżej określonej temperatury tak zwanej
ferromagnetyczną temperaturą Curie T

c

energia wzajemnych oddziaływać pomiędzy elementarnymi dipolami

magnetycznymi może zrównoważyć energię ruchów cieplnych ( może to wystąpić nawet bez zewnętrznego pola
elektrycznego). Dipole magnetyczne o jednakowym momencie układają się równolegle- poniżej T

c

podatność magnetyczne i

przenikalność magnetyczna gwałtownie wzrasta. Takie zachowanie występuje u ferromagnetyków.

Wzór Curie-Weissa



m

=C/(T-T

c

) T

c

- ferromagnetyczna temperature Curie

MC s298-299

140. Podaj specyficzne cechy materiałów ferromagnetycznych.

Przykładem ferromagnetyków są żelazo, kobalt, nikiel, pierwiastki ziem rzadkich.

Ferromagnetyki posiadają wysokie wartości nieskompensowanych momentów magnetycznych a w ich kryształach w
niskich temperaturach poniżej tak zwanej temperatury Curie powstają obszary posiadające wypadkowy silny moment
magnetyczny-domeny.

Pod wpływem zewnętrznego pola magnetycznego następuje porządkowanie domen wskutek ich obrotu i rozrostu.

W temperaturach powyżej temperatury Curie efekt ten zanika

Charakterystyczne stałe materiałowe:

- przenikalność magnetyczna początkowa- stosunek B/H na początkowym odcinku pierwotnej krzywej namagnesowania

-indukcja nasycenia- maksymalna wartość indukcji na krzywej histerezy

-pole koercji ( energia rozmagnesowania)- natężenie pola magnetycznego niezbędnego do obniżenia do zera
namagnesowania szczątkowego (resztkowego), czyli tzw. pozostałości

Wykład 13,10; MC s298; BiW s205

141. Narysuj krzywe histerezy magnetycznej dla materiałów magnetycznych miękkich i
magnetycznych twardych, określ podstawowe różnice, podaj przykłady i zastosowania takich
tworzyw.

Podobnie jak działo się w przypadku właściwości elektrycznych, również w przypadku własności magnetycznych

występuje pętla histerezy. Sam proces również jest analogiczny. Materiał posiada budowę domenową, ferryt o takiej
budowie, jeśli wcześniej nie był w polu magnetycznym, ma indukcję równą 0. Gdy indukcja w polu rośnie, zaczyna się
rozrost domen o momencie magnetycznym równoległym do linii pola magnetycznego. Po zakończeniu wzrostu tych domen,
przy dużych natężeniach można osiągnąć dalszy wzrost indukcji. Analogicznie jak dla histerezy elektrycznej, mamy indukcję
nasycenia B

r

, natężenie pola koercji H

c

, indukcję remanencji B

r

. Oprócz tego występuje również przenikalność magnetyczna

początkowa µ

rp

= przy H dążącym do zera. Ze względu na wartości tych parametrów, możemy ferryty podzielić na miękkie

i twarde.

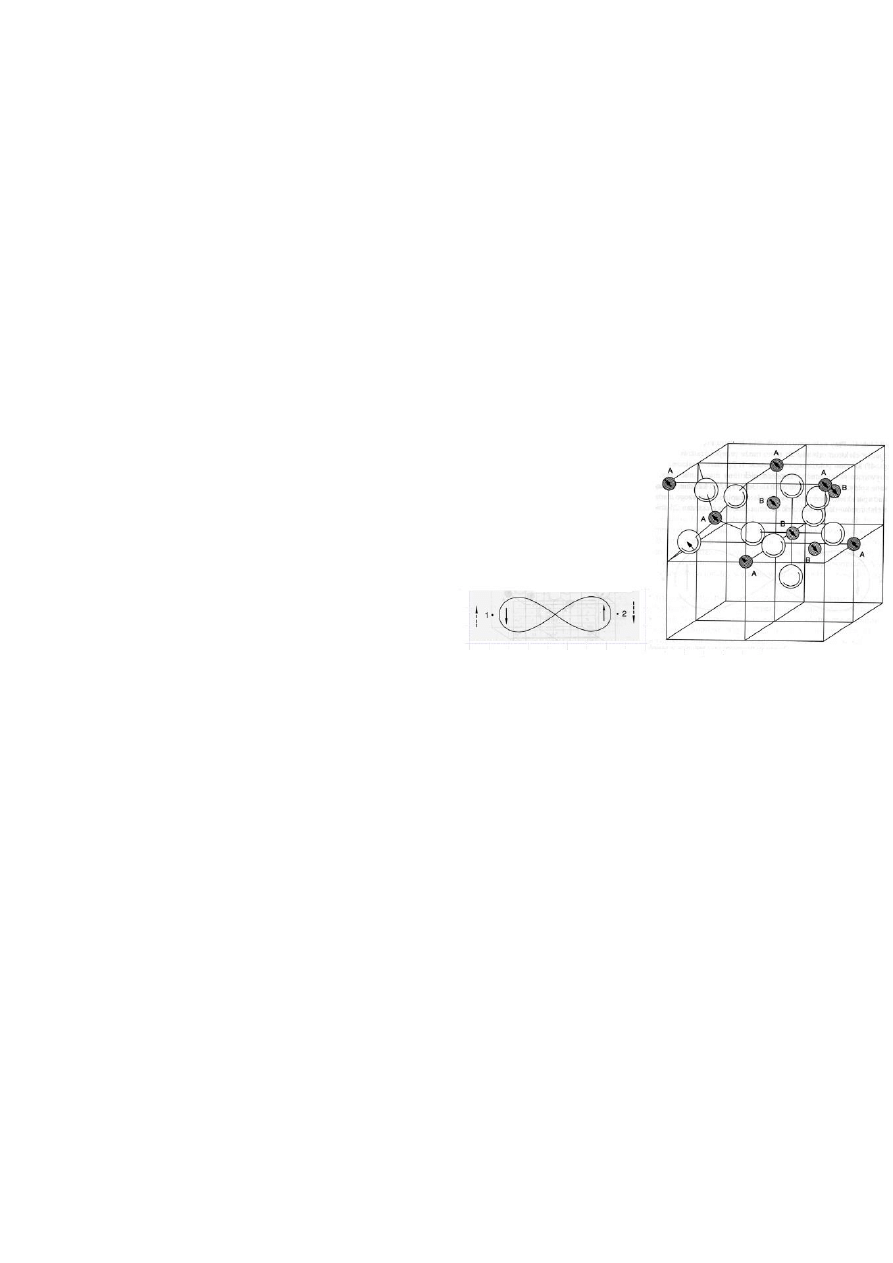
Ferryty magnetyczne miękkie ulegają łatwo namagnesowaniu, odznaczając się stosunkowo dużymi wartościami
początkowej przenikalności magnetycznej µ

rp

(dla pól o małym i średnim natężeniu) i małymi wartościami natężenia

powściągającego H

c.

Oznacza to stosunkową wąską pętlę histerezy i małe straty energii. Namagnesowanie i

przemagnesowanie wiąże się przede wszystkim z przemieszczaniem się ścian domen. Znajdują one zastosowanie jako
magnetyczne rdzenie anten oraz w innym elementach radiotechnicznych, telewizyjnych i telekomunikacyjnych. Specjalną
grupę ferrytów miękkich stanowią ferryty o prawie prostokątnej pętli histerezy(znaczna indukcja przy nieznacznych
natężeniach zewnętrznego pola). 70%-tlenek żelaza i 30% inne tlenki np. MgO, MnO

Ferryty magnetyczne twarde zachowują w znacznym stopniu swe namagnesowanie po odjęciu zewnętrznego pola lub
zmianie jego kierunku. Odznaczają się szeroką pętlą histerezy, dużą wartością H

c

i pozostałości magnetycznej B

r

. W procesie

magnesowania dominują procesy obrotu domen- aby domeny ładnie rosły, obracamy je tak by były równolegle do linii pola.
Przy ich pomocy można wytwarzać silne statyczne pola magnetyczne(magnesy trwałe, pamięci ferrytowe). Y

3

Fe

5

O

12

,

BaFe

12

O

19

W13,11; MC s308-309; WMC s155

142. Budowa spinelu

.

Struktura spinelu ma ogólny wzór A[B

2

]O

4

gdzie B

jest na ogół Fe

3+

. W regularnej strukturze spinelu kationy

znajdują się albo w środku tetraedrów albo w środku
oktaedrów tworzonych przez gęsto upakowane jony tlenu.
Pierwszą z tych pozycji oznacza się zwyczajowo A, a drugą
symbolem B. Ta ostatnia podawana jest w sumarycznym
wzorze

chemicznym

spinelu

wewnątrz

nawiasów

kwadratowych. Dzięki pośrednictwu anionów tlenu, kationy
spinelu mogą wzajemnie silnie oddziaływać, szczególnie w
triadach A-O-B (superwymiana kwantowo-mechaniczna).

W13,12-13; BiW s204; WMC s152-153; MC s300-302

143. Co to są ferryty? Podaj przykład takich tworzyw i obszary zastosowania.

Ferryty - niemetaliczne materiały ceramiczne o właściwościach ferrimagnetycznych(przy antyrównoległej orientacji

momentów kationów występuje wypadkowy moment magnetyczny). Łączy je występowanie nich kationów Fe

3+ (

Fe

2

O

3

).

Zazwyczaj można je opisać wzorem ogólnym Me

x

Fe

1-x

[Me

1-x

Fe

1+x

O

4

]. (Fe

2

O

3

z tlenkami metali jedno-,dwu- i

trójwartościowych, a czasem nawet czterowartościowych). Jak już było to omówione w punkcie 141 ferryty możemy
podzielić na miękkie i twarde, występuje w nich pętla histerezy magnetycznej. Występują u nich 3 typy struktury:



spinelu(MeFe

2

O

4

),



granatu(Y

2

Fe

5

O

12

),



magnetoplumbitu(MeFe

12

O

19

).

Spinele to ferryty miękkie, a granaty i magnetoplumbity- twarde.

Zastosowania ferrytów.
-radiotechnika
-technika wysokich częstości
-technika ultradźwięków
-jako rdzenie cewek, transformatorów, anten magnetycznych
Ze względu na duży opór elektryczny ferrytów ich stosowanie w aparaturze dużych częstości gwarantuje małe straty na
prądy wirowe
-technika prowadzenia mikrofal w falowodach poprzez wykorzystanie zjawiska Faradaya (zjawisko skręcenia płaszczyzny
polaryzacji mikrofal) i zjawiska rezonansu ferrimagnetycznego

-ferryty o prostokątnej pętli histerezy jako elementy magnetycznej pamięci cyfrowej
-ferryty magnetycznie twarde do budowy magnesów trwałych

Ferryty są polikryształami ceramicznymi otrzymywanymi droga spiekania z proszków. Ich właściwości zależą zarówno od
struktury: budowa krystalicznai skład pierwiastkowy; jak i mikrostruktury: gęstość, porowatość, wielkość i kształt ziaren i
porów. (to z wykładu)

W13,12-19; BiW s203; WMC s152

144. Scharakteryzuj wymianę kwantowo-mechaniczną w ferrytach.

Jak wspomnieliśmy, w spinelach występują triady A-O-B. Kationy w pozycjach A i B mogą ze sobą oddziaływać

w sposób nazywany superwymianą kwantowo-mechaniczną. Omówmy ten mechanizm na schemacie. Na rysunku
zaznaczono obydwa orbitale tlenu 2p

x

oraz zwrot obydwu elektronów tlenu na tym orbitalu. W punktach 1 i 2, mamy

odpowiednio kationy w pozycji A i B (według struktury spinelu). Załóżmy że każdy z nich ma po jednym niesparowanym
elektronie 3d lub 4f. Jeden z elektronów orbitalu 2p tlenu, może przejść czasowo do orbitalu 3d (orbitale bowiem nakładają
się). Zgodnie z zakazem Pauliego, elektrony w tej samej przestrzeni muszą mieć różne spiny- elektron orbitalu 3d/4f, musi
mieć zatem spin przeciwny do spinu elektronu tlenu. Gdy atom tlenu, pozbędzie się już jednego elektronu, staje się
magnetyczny. Wtedy ten drugi, pozostały tlenowi, niesparowany elektron 2p, może oddziaływać z elektronem kationu B-
czyli znów elektron kationu musi być przeciwny do tego tlenu. Podsumowując, ponieważ spiny obu elektronów tlenu, z
orbitalu 2p muszą być przeciwne, zatem na skutek oddziaływań tych elektronów z elektronami kationów, elektrony
kationów też są względem siebie przeciwne. Teraz, jeśli obydwa kationy, A i B, mają taki sam moment magnetyczny, to
wypadkowy moment triady wynosi 0 (antyferromagnetyki). W ferrimagnetykach, momenty kationów A i B są różne, zatem
triada A-O-B, posiada jakiś wypadkowy
moment magnetyczny. Im wyższa jest
siła superwymiana, tym wyższą
temperatura Curie- czyli temperatura
Curie odzwierciedla siłę wzajemnych
oddziaływań momentów
magnetycznych w materiale.

W13,13; MC s300-303; BiW s204-205

145.Wpływ mikrostruktury na właściwości magnetyczne ferrytów.

W przypadku ferrytów magnetycznych miękkich, stwierdza się wzrost przenikalności magnetycznej z wielkością

ziaren oraz obniżenie przy wzroście udziału objętościowego porów i wtrąceń lub wydzieleń wtórnych faz stałych.
Przemieszczanie się ścian Blocha (ścian domen) wewnątrz ziaren jest bowiem utrudnione przy występowaniu zaburzeń
struktury wewnątrz ziaren-czyli gorzej się magnesuje. Zmniejszanie się wymiarów ziaren zmniejsza wartość początkowej
przenikalności magnetycznej (liczba elementarnych magnesów może stać się zbyt mała, aby zrównoważyć energię
potrzebną do utworzenia ścian Blocha, domeny musiałyby się rozprzestrzeniać poprzez granice międzyziarnowe). W
związku z tym małe ziarna są zazwyczaj jednodomenowe. Tworzenie się zarodków domen o przeciwnym kierunku
namagnesowania jest uprzywilejowane w pobliżu nieciągłości budowy polikryształu (np. pory wtrącenia). Zatem
podstawowym warunkiem uzyskania prostokątnej pętli histerezy jest mały udział objętościowy porów i jednorodność
roztworów stałych-bo im mniej nieciągłości tym lepiej w tym wypadku. Małe wymiary ziaren sprzyjają osiągnięciu dużej
wartości B

r

. Duże wartości H

c

są przejawem utrudnionego ruchu ścian Blocha więc wartość H

c

rośnie ze zmniejszeniem się

wielkości ziaren ferrytów względem wielkości domen. Ponadto mały rozrzut wielkości ziaren, duża jednorodność roztworów
stałych oraz duża gęstość pozwala na uzyskanie maksymalnych dla danego materiału parametrów magnetycznych.

146. W jakim zakresie długości fali i energii fotonów mieści się światło widzialne,
podczerwień i nadfiolet.

Energie fotonów można bardzo prosto wyliczyć ze wzoru, znając długość fali λ, ze wzoru E=

gdzie h- stała Plancka, c-

prędkość światła. Wartości te są przybliżone- zakresy λ są różne w zależności od źródła.

promieniowanie

długość fali λ

energia [eV]

nadfiolet

100-380 [nm]

3,26-12,4

światło widzialne

380-780 [nm]

1,59-3,26

podczerwień

780 [nm]-1 [mm]

0,0012-1,59

WMC s134; Wikipedia

147. Co to jest współczynnik załamania światła, absorpcji i transmisji?

Z elektromagnetycznej teorii światła wynika, że współczynnik załamania równy jest stosunkowi prędkości

rozchodzenia się światła w próżni c i prędkości rozchodzenia się światła w materiale
v.

n

1

=c/v=(



r



)

1/2

Gdzie ε

r

- względna stała dielektryczna materiału, µ- względna przenikliwość

magnetyczna materiału. Dla materiałów nie będących ferro- i ferroelektrykami, dla
których µ jest zbliżone do 1 : n

1

=c/v=(



r

)

1/2

Jeżeli wiązka światła pada na gładką powierzchnię izotropowego materiału to cześć
promieniowania ulega odbiciu, podczas gdy pozostała cześć penetruje to materiału i
ulega absorpcji w mniejszym lub większym stopniu. Między tymi wiązkami zachodzi
zależność:



0

=



0

’ sin



0

/sin



1

=n

1

/n

0

n

1

,n

0

- współczynnik załamania światła w materiale i w próżni.

Aby opisać zachowanie się ośrodków absorbujących światło, wprowadza się dodatkową stałą materiałową- współczynnik
absorpcji światła a, który charakteryzuje tłumienie amplitudy światła w materiale (a jest ekspotencjalną miarą czynnika
tłumienia). Współczynnik załamania i absorpcji łączy się często w postaci zespolonego współczynnika załamania światła:
n’=n+ia

Współczynnik transmisji określany jest jako stosunek natężenia fali przepuszczonej przez ośrodek do natężenia fali na
niego padającej.

1=



+



+





- współczynnik absorpcji



- współczynnik odbicia



-współczynnik transmisji

BiW s210-211; MC s355-356; W14,5-8

148. Podaj przykłady współczynników załamania światła dla wybranych materiałów.



Diament- 2,42



Si- 4,18



αAl

2

O

3

- 1,64



PbO- 2,66



Szkło CROWN- 1,52



GaAs- 4,04

W14,6

149. Dlaczego metale są nieprzezroczyste dla światła widzialnego?

Dla metali przy braku przerwy energetycznej (metale mają bardzo małe różnice między sąsiednimi poziomami

energetycznymi) możliwe jest pochłanianie kwantów energii promieniowania praktycznie w całym zakresie

promieniowania widzialnego. Metale są więc nieprzeźroczyste dla światła widzialnego. Niektóre metale mogą mieć barwę
na skutek selektywnego odbicia światła (złoto, miedź- pochłaniają tylko wyższe częstotliwości). Metale można wypolerować
tak by odbiły całe światło (lustro).

MC s359; W14,10

150. W jakim zakresie promieniowania przeźroczyste są materiały półprzewodnikowe i
dlaczego?

Półprzewodniki są dla oka ludzkiego nieprzeźroczyste. W skutek małych szerokości strefy energii wzbronionych(1-

4eV), odpowiadających energii fotonów promieniowania w zakresie widzialnego, są one zdolne do absorpcji
promieniowania tego zakresu. Wiele półprzewodników może być ciałami przezroczystymi dla promieniowania zakresu
podczerwonego (Bo ciała mogą adsorbować tylko fotony o energii większej od wartości przerwy energetycznej, zatem
podczerwieni nie).

BiW s215; MC s359; W14,9 i 11

151. W jakim zakresie promieniowania przeźroczyste są monokryształy ceramiczne i
dlaczego?

W typowych kryształach jonowych i kowalencyjnych o właściwościach izolacyjnych, złożonych z jonów o

konfiguracji elektronowej gazów szlachetnych, wszystkie poziomy energii elektronów w paśmie walencyjnym są obsadzone.
Szerokość strefy energii wzbronionych elektronów w czystych i mało zdefektowanych kryształach typowych izolatorów
dochodzą do 10eV. Zakres ten odpowiada energii fotonów nadfioletu. Kryształy np. halogenków litowców nie absorbują
zatem promieniowania w zakresie od bliskiej podczerwieni (1eV) do nadfioletu (10eV) i w naturalnym świetle
słonecznym są dla oka ludzkiego bezbarwne i przeźroczyste. Taka sytuacja dotyczy monokryształów halogenków litowców,
a przypadku faz ceramicznych monokryształów Al

2

O

3

, MgO czy SiO

2

. Polikryształy nie zachowują tych właściwości (mają

pory, na których zachodzi rozpraszanie fal świetlnych).

MC s358-359; BiW s214-215; W14,11

152. Kiedy polikrystaliczne tworzywa ceramiczne mogą być przeźroczyste dla światła
widzialnego?

Polikrystaliczne materiały ceramiczne mogą być przeźroczyste dla światła, kiedy ich przerwa energetyczna jest

na tyle szeroka, że nie mogą one absorbować światła w zakresie widzialnym. Absorpcja światła nie wystąpi jeżeli
elementy mikrostruktury taki jak ziarna i pory, mają wymiary mniejsze od długości światła (Jeśli mają większe lub
porównywalne, to wystąpi absorpcja światła na tych elementach). W praktyce polikryształy ceramiczne są nieprzezroczyste
barwy białej.

W14,11; BiW s215

153. Co to jest barwa światła?

Selektywna absorpcja lub odbicie światła powodująca wyeliminowanie części promieniowania prowadzi do odczucia

barwy przez oko ludzkie. Można powiedzieć, że naturalna barwa materiałów w świetle słonecznym, które jest zbiorem
fotonów odpowiadających wszystkim barwom światła widzialnego, jest wówczas mieszaniną barw odpowiadających tym
fotonom światła, które nie uległy absorpcji. Barwa światła to promieniowanie elektromagnetyczne o długości fali od 380 do
780nm. Nierozróżnialne w zakresie od 380-400 i od 700-780nm, dlatego zwęża się do zakresu od 400-700nm. Określone
długości fali odpowiadają barwom prostym (nasyconym):



Fioletowa 380-430



Niebieska 430-490



Zielona 490-570



Żółta 570-600



Pomarańczowa 600-610



Czerwona 610-780

Światło białe to różne składowe w odpowiednich proporcjach. Każda długość fali emituje energię, a widzialne światło
zawiera wszystkie długości fal z różną energią

W14,12; WMC s134; MC s359-360

154. Wymień typy centrów barwnych w materiałach ceramicznych

.

Centra barwne to dodatkowe poziomy donorowe lub akceptorowe w strefie energii wzbronionych odległe od

pasma walencyjnego lub przewodnictwa o 1-3eV, co odpowiada fotonom światła widzialnego. Poziomy te mogą tworzyć
centra barwne w postaci:

-zespołów elektronów i dziur elektronowych oraz odpowiednich defektów punktowych

-jonów domieszkowych o budowie odbiegającej od budowy jonów typu gazu szlachetnego- czyli np. jony metali grup
przejściowych posiadające nieobsadzone wewnętrzne orbitale.

Dzięki nim zachodzi absorpcja światła w zakresie widzialnym.

W14,13-15; MC s360; WMC s215

155. Podaj schematycznie ideę powstawania centrów barwnych z udziałem defektów
punktowych

.

Jeśli stechiometryczny kryształ izolatora o odpowiedniej

liczbie defektów punktowych i wiązaniach jonowych podda się
napromieniowaniu fotonami o odpowiedniej energii to część
podstawowych atomów kryształu zostanie pozbawiona zewnętrznych
elektronów, które przechodzą do pasma przewodnictwa
(pozostawiając równoważną liczę dziur elektronowych). Elektrony
ulegają po krótkiej chwili rekombinacji z dziurami- elektrony wracają
do atomów i odtwarza się pierwotny stan przed napromieniowaniem.
Zanim to jednak nastąpi swobodne elektrony mogą przebiegać w
pobliżu wakacji anionowych lub domieszkowych kationów. Dzięki
przyciąganiu kulombowskim te dodatnio naładowane defekty
punktowe mogą wiązać elektrony przez pewien okres. Również dodatnio naładowane dziury, które uniknęły eliminacji i
wędrują przez kryształ mogą być schwytane przed ujemnie naładowane defekty. Można wymienić centrum utworzone po
schwytaniu elektronu przez międzywęzłowy kation, lub dziury schwytane przez międzywęzłowy anion. Elektrony takie mają
większą energię niż z zapełnionego pasma walencyjnego. Napromieniowanie za pomocą fotonów może wywołać
wzbudzenie elektronów centrów i ich przejście do pasma przewodnictwa. Zachodzi absorpcja fotonów w zakresie światła
widzialnego.

W14,15; WMC s360; BiW s215-216

156. Podaj ideę powstania centrów barwnych wskutek domieszki jonów metali
przejściowych.

Szczególną grupę centrów powodujących zabarwienie kryształów i szkieł

stanowią jony pierwiastków grup przejściowych układu okresowego
(V,Cr,Mn,Fe,Co,Ni)- cechuje je bowiem posiadanie niecałkowicie zapełnionych
orbitali, albo pierwiastków ziem rzadkich. Występują one jako domieszki lub
kationy rodzime danego kryształu. Rozpatrzmy tą sytuację dla jonu Ti

3+

, w którym

jest jeden elektron na nieuczestniczącym w wiązaniu orbitalu 3d. Jeśli w strukturze
krystalicznej, ten jon jest otoczony przez ujemne ligandy tak, że tworzą one pole
centro symetryczne, to nic się nie dzieje- wszystkie orbitale 3d na których może być
elektron maja tą samą energię. Inaczej sytuacja wygląda gdy pole jest tetra lub
oktaedryczne. Ponieważ ligandy są naładowane ujemnie, będą one „odpychały” te
orbitale z ujemnym elektronem, które są w ich kierunku zorientowane (np. dla pola
oktaedrycznego najbardziej odpychany będzie orbital 3d

x2-y2

) . Występowanie tej siły

odpychania podwyższa energię tych orbitali, zatem zachodzi rozszczepienie poziomów
energetycznych różnych orbitali 3d. Wielkość rozszczepienia oznaczamy Δ, dla
większości jonów grup przejściowych wartość ta wynosi 1-3ev- czyli pokrywa się z
zakresem energii fotonów światła widzialnego, może więc zachodzić ich absorpcja, co
prowadzi do efektu barwy.

W14,14; BiW s216-217; MC s364-366

157. Co to jest optoelektronika?

Optoelektronika to dziedzina techniki, która wykorzystuje specyficzne właściwości światła w celu pozyskiwania,

gromadzenia, przesyłania, obróbki i prezentacji informacji. Wykorzystuje światło do transmisji sygnałów w elektronice i
telekomunikacji. Optoelektronika zajmuje się także konstrukcją i zastosowaniem urządzeń i aparatów do emisji i detekcji
światła, zapisem danych na dyskach optycznych. Zastosowania obejmują różne dziedziny techniki, a także medycyny.
Zastosowanie światła pozwala zwiększyć szybkość transmisji, pojemność łączy i zmniejszyć straty energii. Zadania
optoelektroniki względem informacji (pozyskiwanie - detektory fotoelektryczne, gromadzenie - CD,DVD, przesyłanie -
technika światłowodowa, IrDA, obróbka - komputery optyczne, ciekłokrystaliczne wyświetlacze LCD, monitory, matryce
diod LED).
-elektroluminescencyje źródło światła
-światłowód
-fotoodbiornik.

Wikipedia; W14,16-17

158. Idea budowy światłowodu.

Transmisja światła jest możliwa dzięki zastosowaniu światłowodu

wykorzystującego zjawisko całkowitego wewnętrznego odbicia. Typowe światłowody
zbudowane są z szeregu włókien szklanych o współczynniku załamania światła n

1

, każde z

tych włókien znajduje się w płaszczu wykonanym z materiału optycznie rzadszego od
szkła, czyli o niższym n=n

0

np. z polimeru. Ponieważ w tej sytuacji sinα

1

= [

-

]

0,5

to już

przy niewielkich różnicach n

1

i n

0

, uzyskamy znaczny kąt α, pozwalający na całkowite

wewnętrzne odbicie- czyli wiązka idzie wewnątrz włókna jak na rysunku. Wpadająca do
światłowodu wiązka światła, jest przenoszona odbiciami wewnętrznymi, z prędkością
równą v= c/n

1

na drugi koniec włókna. Materiał światłowodu powinien charakteryzować się dużym współczynnikiem

załamania światła n (szkła na bazie krzemionkowej, szkła selenowe). Włókna pokrywa się warstwami materiałów nie
przepuszczających światło, które chronią równocześnie przed uszkodzeniami mechanicznymi i korozją. Światłowody muszą
odznaczać się minimalną absorpcją promieniowania.

W14,18; BiW s212; WMC s136

159. Idea budowy i zastosowanie laserów.

Lasery wykorzystują w swoim działaniu zjawisko luminescencji. Laser, jest to materiał emitujący koherentne,

silnie wzmocnione, tworzące wiązkę rozchodzącą się w danym kierunku światło. Poprzez absorpcje energii zewnętrznej, w
materiale zachodzą przejścia optyczne elektronów z poziomu wzbudzonego na podstawowy. Działa to tak, że wzbudzamy
elektron dostarczając mu energię wyższą od stanu E

1

, otrzymawszy taki nadmiar energii, elektron spada z wyższego

energetycznie poziomu E

1

na niższy poziom podstawowy E

2

, po drodze emitują foton o energii równej hv= E

1

-E

2

. Warunkiem

emitowania światła przez laser, jest doprowadzenie do sytuacji, gdy N

1

(E

1

)>N

2

(E

2

) gdzie N jest to gęstość obsadzenia danego

poziomu. Normalnie w materiale więcej elektronów obsadza poziom podstawowy niż wzbudzony, naszym celem jest
poprzez doprowadzenie energii wykonać inwersję tych obsadzeń. Mając już potrzebny nam stan, wymuszamy „spadnięcie”
wzbudzonych elektronów do poziomu podstawowego, poprzez doprowadzenie fotonu o energii E

1

-E

2

. Wywołuje on

kaskadę- każdy taki foton, powoduje spadek sąsiada itd. Światło (strumień fotonów) tak wywołane będzie miał taką spójną
fazę, kierunek i polaryzację. W rzeczywistości jest to ciut bardziej skomplikowane, patrz WMC s142. Możemy wyróżnić 2
rodzaje laserów:
- lasery półprzewodnikowe-po wytworzeniu nierównowagowego stężenia nośników ładunku nadmiarowe elektrony
przewodnictwa oraz dziury elektronowe rekombinują się ze sobą w centrach tworzonych przez atomy domieszek
- lasery w których aktywatorami są jony pierwiastków ziem rzadkich lub pierwiastków grup przejściowych
Budowa:

Fotony zostają odbite w lustrze i wracając przez kryształ kontynuują wzbudzanie promieniowania. Fotony emitowane pod
kątem do osi krystalicznego pręta ulegają rozproszeniu.

Zastosowanie: poligrafia, znakowanie produktów, obróbka mechaniczna-cięcie metali, wojsko np. czujniki, medycyna,
telekomunikacja-nadajniki, geodezja-pomiary.

WMC s141-143

160. Zjawisko luminescencji i jego zastosowanie w technice.

Tak właściwie to pojęcie to wyjaśniliśmy w poprzednim punkcie o laserze, który jest jej szczególnym

przypadkiem. Poprzez absorpcje energii zewnętrznej, w materiale zachodzą przejścia optyczne elektronów z poziomu
wzbudzonego na podstawowy. Działa to tak, że wzbudzamy elektron dostarczając mu energię wyższą od stanu E

1

,

otrzymawszy taki nadmiar energii, elektron spada z wyższego energetycznie poziomu E

1

na niższy poziom podstawowy

E

2

, po drodze emitują foton o energii równej hv= E

1

-E

2

. Czyli powrotowi elektronu z pasma o wyższej do pasam o niższej

energii towarzyszy strata nadmiarowej energii kwantów promieniowania-fotonów. Wyróżnia się fluorescencję
(natychmiastowa emisja) i fosforescencję (dłuższy odstęp między wzbudzeniem i emisją). Luminescencję można wywołać
poprzez bombardowanie kryształu prędkimi elektronami (umieszczenie kryształu w polu elektrycznym-
elektroluminescencja, katodoluminescencja-wzbudzenie strumieniem fotonów), przez napromieniowanie kryształu
odpowiednimi fotonami (światła nadfioletowego-fotoluminescencja). W większości przypadków luminescencja wymaga
obecności defektów punktowych w krysztale. Jony domieszek stanowią poziomy akceptorowe. Pod wpływem fotonów
nastąpi wzbudzenie elektronów pasma walencyjnego do pasma przewodnictwa (powstają elektrony przewodnictwa i dziury
elektronowe). Błądząca w krysztale dziura elektronowa wskutek przeciwnego znaku swego ładunku w porównaniu z

centrum utworzonym przez poziom akceptorowy może uleć rekombinacji. Centrum staje się elektrycznie obojętne i może
się do niego przyłączyć swobodny elektron w paśmie przewodnictwa, czemu towarzyszy emisja fotonu o energii E=h



.

Zastosowanie: lasery, spektrofluorymetria, mikroskopia konfokalna

Internet; WMC s141-143; MC s370-373

161. Fotodioda i fotoprzewodnik-idea budowy i zastosowanie.

Oba te urządzenia działa na skutek występowania zjawiska fotoprzewodnictwa. Jak już wiemy, materiał może

absorbować fotony, których energia jest równa lub większa od wartości przerwy energetycznej. W przypadku światła
widzialnego jest to około 1,6-3,3 eV. Taka przerwa występuje tylko w półprzewodnikach. Gdy naświetlamy
półprzewodnik, elektrony z pasma walencyjnego zostają wzbudzone przez fotony do pasma przewodnictwa, a zatem
zwieksza się stężenie elektronów przewodnictwa. Jeśli w tym momencie przyłożymy pole elektryczne, to zaobserwujemy
wzrost jego natężenia- efekt ten nazywamy właśnie fotoprzewodnictwem.

Fotodioda – dioda półprzewodnikowa pracująca jako fotodetektor. Fotodiody wykonane są jako elementy złącza p-n lub p-i-
n, z warstwą samoistną (niedomieszkowaną). Fotony padające na złącze są absorbowane (zjawisko fotoelektryczne
wewnętrzne) w rezultacie czego elektron zostaje przeniesiony do pasma przewodnictwa i powstaje para elektron-dziura.
Elektrony swobodne są przyciągane przez dodatni ładunek przestrzenny na granicy obszaru typu n, dziury zaś wędrują do
obszaru typu p. Prąd przewodzenia złącza p-n zwiększa się wraz ze wzrostem strumienia świetlnego. Złącze musi być
polaryzowane zaporowo z zewnętrznego źródła napięcia. Przy braku polaryzacji dioda pracuje jako źródło prądu
elektrycznego, przy oświetleniu w złączu powstaje siła elektromotoryczna wywołująca prąd elektryczny. Przy polaryzacji
zaporowej do diody podłączone jest napięcie w kierunku zaporowym, dioda pełni rolę rezystora którego opór zależy od
oświetlenia. Zastosowanie: jako baterie słoneczne (przy braku polaryzacji) lub nieliniowe rezystory ( przy polaryzacji
zaporowej), przy odtwarzaniu zapisu dźwiękowego z taśmy filmowej, w urządzeniach automatyki przemysłowej.

Fotoopornik- jest elementem światłoczułym. Jego rezystancja zmienia się pod wpływem padającego promieniowania i nie
zależy od kierunku przyłożonego napięcia, podobnie jak rezystancja zwykłego rezystora. Oświetlenie fotorezystora
powoduje zwiększenie przepływającego prądu (zmniejsza się jego rezystancja). Prąd będący różnicą całkowitego prądu
płynącego przez fotorezystor i prądu ciemnego (prąd płynący przez fotorezystor przy braku oświetlenia) nazywamy prądem
fotoelektrycznym. Jego wartość zależy od natężenia oświetlenia. Fotorezystory wykonuje się najczęściej w postaci cienkich
półprzewodnikowych warstw monokrystalicznych lub polikrystalicznych naniesionych na izolacyjne np. szklane podłoże .
Materiał światłoczuły rozdzielają dwie metalowe elektrody mające wyprowadzenia. Elektrody te często mają kształt
grzebieniowy. Nad powierzchnią światłoczułą umieszcza się okienko i zamyka w obudowie, chroniącej przed uszkodzeniami,
a niekiedy umożliwiającej pracę w obniżonej temperaturze (naczynie Dewara). Zastosowanie: do pomiaru temperatury
poprzez pomiar natężenia promieniowania, ostrzegania w systemach przeciwpożarowych, wykrywania zanieczyszczeń rzek i
zbiorników wodnych, detekcji strat ciepła przez izolację termiczną budynków.

WMC s140-141; MC 367-369

162. Zmęczenie materiału – definicja zjawiska i metody badania.

Zmęczeniem materiałów nazywamy zmiany zachodzące w tworzywie pod wpływem zmiennych, niekiedy

okresowych naprężeń, niższych niż granica plastyczności ujawniających się zmniejszeniem wytrzymałości lub
zniszczeniem. Pęknięcia mogą po prostu powstać rosnąc z małą szybkością przy obciążeniach mniejszych od obciążeń
krytycznych, jeśli mają one charakter zmienny lub gdy otoczenie materiału jest środowiskiem korodującym. Zmęczenie jest
najczęstszą przyczyną niszczenia metali stosowanych do części maszyn.

Badania zmęczenia przeprowadza się podając materiał cyklicznym naprężeniom o zmiennej częstotliwości lub/i
amplitudzie. Do takich badań służą maszyny hydrauliczne lub ciśnieniowe.

W15,3

163. Mechanizmy zniszczenia zmęczeniowego metali

.

Jednym z mechanizmów jest wzrost istniejących spękań w skutek łączenia się
defektów i pustek przed czołem spękania.

W czystych metalach lub polimerach (lewa część rysunku) obciążenie
rozciągające powoduje powstanie strefy uplastycznionej przed czołem
pęknięcia. To z kolei powoduje otwarcie się pęknięcia o wartości



-powstaje

nowa powierzchnia pęknięcia. Natomiast w trakcie ściskania materiał zostaje
ściśnięty i pęknięcie zamyka się. Nowo utworzona powierzchnia przyrasta (o



).

Podoba sytuacja powtarza się w kolejnych cyklach obciążenia, pęknięcie
stopniowo narasta z szybkością wynoszącą w przybliżeniu



.

Rzeczywiste materiały zawsze zawierają małe wtrącenia. Rozwój pęknięcia
opisuje prawa część rysunku. W strefie uplastycznia powstają pustki łączące się
ze sobą i z czołem pęknięcia. Z powodu ich obecności pęknięcie rośnie szybciej.

Drugim mechanizmem jest rozrost spękań powierzchniowych wzdłuż płaszczyzny
poślizgu.

W elementach poddanych zmęczeniu niskocyklowemu, odkształcenie plastyczne
szybko powoduje wzrost chropowatości ich powierzchni i pęknięć
powierzchniowych , które początkowo rosną wzdłuż płaszczyzny poślizgu
(pęknięcia fazy I). Następnie zaczynają rosnąć w kierunku prostopadłym do osi
rozciągania.

Zmęczenie wysokocyklowe przebiega w odmienny sposób. Zakres żywotności
materiału jest związany z okresem inicjowania pęknięcia. Występują odkształcenia
lokalne w miejscach koncentracji naprężeń ( karby, rysy, zmiany przekroju
elementu). W tych miejscach dochodzi do powstania pęknięcia, które rozrasta się
(początkowo wolno, potem szybko) do momentu zniszczenia elementu.

Ashelby tom1 s175

164. Mechanizmy zniszczenia zmęczeniowego ceramiki.

Materiały kruche są bardzo mało odporne na zmęczenie. Zjawiska te związane są że zmniejszaniem się K

Ic

może

zwiększać korozja gazowa, chemiczna lub pełzanie, powodując zwiększanie się wielkości defektów w materiale. Dla
materiałów ceramicznych występuje
minimalna wartość K

I0

- granica zmęczenia

statycznego

W15,8-9

165. Ścieranie i mechanizmy zużycia tribologicznego.

Ścieranie jest to zużycie powierzchni na skutek tarcia. Tarcie jest to siła oporu występująca podczas przemieszczania się
stykających się powierzchni materiałów.

F=



P , gdzie F- siła tarcia statycznego lub dynamicznego ,



-współczynnik tarcia statycznego (rzędu 0,5) lub

dynamicznego (mniejszy), P- nacisk

Wartość współczynnika tarcia zależy od stanu powierzchni
i jej rodzaju.

Tarciem i jego skutkami zajmuje się nauka- tribologia
(tribos=tarcie).

Mechanizmy zużycia tribologicznego:

- zużycie ścierne – przy nierównych powierzchniach:

Fragmenty materiału, które uległy zużyciu adhezyjnemu odrywają się od powierzchni materiału i mogą łatwo ulec utlenieniu
( tlenem z substancji smarujących) w wyniku czego powstają twarde cząstki tlenku, które działają jak papier ścierny. Twardy
materiał działa jak „pług” odrywając fragmenty miękkiego materiału. Podobne efekty daje
obecność między powierzchniami zanieczyszczeń (np. piasku). Zużycie ścierne zmniejsza się
przez zmniejszenie obciążenia lub zwiększenie twardości materiału.

- zużycie adhezyjne- następuje adhezja gładkich powierzchni i wyrywanie cząstek materiału
mniej odpornego.

Jeżeli metal A jest bardziej miękki starty materiał będzie z niego usuwany. Jeżeli metale A i B są jednakowo miękkie, obie
powierzchnie będą ulegały zużyciu. Aby zmniejszyć adhezję należy zmniejszyć nacisk.

- zużycie przez utlenianie lub spajanie- tarciu i ścieraniu towarzyszy wydzielania się ciepła. Możliwy jest bardzo wysoki
wzrost temperatury aż do utlenienia powierzchni, reakcji z materiałem chłodzącym lub spajanie powierzchni.

166. Metody badania ścieralności materiałów.

W znormalizowanych warunkach nacisku i czasu (ilość cykli) bada się zużycie powierzchni materiału mierzone stratą masy
( lub inne np. badanie płytek ceramicznych).

Ścieralność oznacza się min. na tarczy Böhmego, jako zmniejszenie wysokości próbki podczas badania normowego.

s = (M/A)*(1/



p

) [cm]

w którym:

M – strata masy próbki po 440 obrotach tarczy, [g], A – powierzchnia próbki, [cm

2

],



p

– gęstość pozorna próbki, [ g/cm

3

].

W15,13; Wykład z IMIRu

167. Udarność materiałów- definicja, metody badania i przykłady.

Znormalizowaną miarą odporności na zniszczenia w warunkach dynamicznych jest udarność mierzona wartością pracy
zużytej na dynamiczne złamanie próbki o znormalizowanych wymiarach:

KC=K/A [J/cm

2

]

K- praca zniszczenia A-powierzchnia

Metodami badania udarności za pomocą
młotów wahadłowych są metoda
Charpy’ego, Izoda lub Schoba-Nitchego-
Salewskiego .

Metoda Charciego:

W próbkę podpartą końcami na dwóch
podporach uderzają środkowo wahadła.
Praca łamania K jest różnicą energii
potencjalnej młota w położeniu
początkowych K

max

i końcowym K

min

.

Młot Charpy'ego składa się z podstawy i dwóch słupów w których łożyskowane jest wahadło z bijakiem. Do słupów
przymocowane są podpory, na których umieszcza się próbkę w taki sposób aby karb usytuowany był od strony przypór.

Metoda Izoda różni się od metody Charpy'ego sposobem zamocowania próbki, wymiarami próbek oraz prędkość uderzenia
wahadła młota. Bada się wyłącznie próbki z karbem. Próbkę mocuje się pionowo, jednym końcem w uchwycie podstawy
młota i łamie ostrzem walcowym wahadła młota w określonej odległości od krawędzi uchwytu. Udarność określa praca
zużyta na dynamiczne złamanie próbki z karbem odniesiona do początkowego przekroju poprzecznego w miejscu karbu,
wyrażona w kJ/m

2

.

W15,16-17; Internet

168. Co to jest odporność balistyczna materiałów.

Odporność balistyczna jest to odporność materiału na działanie czynników wysokich energii (pociski, fala detonacyjna,
wybuchy). Odporność tą mierzymy minimalną grubością warstwy która nie uległa zniszczeniu.

W15,18

169. Mechanizm działania odpornościowego pancerza ceramicznego

.

Nowoczesne konstrukcje pancerzy to wielowarstwowe elementy kompozytowe zawierające warstwy

ceramiczne, metaliczne i polimerowe. Pancerze ceramiczne o grubości 100mm zastępują ok. 500mm RHA (stal pancerna) a
w układzie kompozytowym zwielokrotniają ochronę nawet 2-3 razy.
Działanie pancerza ceramicznego:
- zniszczenie (stępienie pocisku) dzięki dużej twardości
-zmiana kierunku pocisku (odbicie)
-pochłanianie energii w wyniku kruchego rozpadu na części (fragmentacja, piaskowanie).
Najbardziej skuteczne są twarde i wytrzymałe materiały borkowe i węglikowe.

Ceramiczne warstwy antybalistyczne - służą do ochrony sprzętu wojskowego i innych obiektów specjalnych przed
działaniem czynnika niszczącego. Ich zastosowanie umożliwia obniżenie masy pojazdów (korzystne kiedy wymagany jest ich
transport powietrzny). Ceramika konstrukcyjna ma dużą twardość powiązaną z małą gęstością. Rolą warstwy ceramiki jest
rozproszenie i pochłonięcie energii pocisku, w trakcie jej fragmentacji. Oprócz tego istotną cechą ceramicznych warstw
ochronnych jest zmiana toru wnikania pocisku podczas ich przebijania. Zmiana kierunku penetracji pocisku w przebijanej
ceramice jest podstawą do takiego sposobu zaprojektowania warstwy lub kilku warstw ceramicznych w konstrukcji
pancerza kompozytowego, aby móc skutecznie rozproszyć energię kinetyczną pocisków przeciwpancernych. Stwierdzono
również, iż nie tylko grubość danego rodzaju ceramiki ma istotny wpływ na jej zdolność ochronną, ale i to, czy ceramika o
danej grubości jest monolitem, czy składa się z kilku oddzielnych płytek. Kilka płytek ceramicznych, stykających się ze sobą,
stanowi moduł ochronny mniej skuteczny niż jedna płyta ceramiczna o łącznej grubości tych płytek. Jest to ważny szczegół
technologiczny, ponieważ wynika z niego, że pancerz służący do ochrony przed pociskami o wysokiej energii powinien
zawierać jedynie płytki ceramiczne o dużej grubości i powierzchni. Powyższe spostrzeżenia stały się przesłanką do podjęcia
prac nad gradientowymi warstwami ochronnymi.

W15;18-25; Wikipedia

170. Podaj przykład zniszczenia materiału wskutek erozji cząstek wysokiej energii.

Elementami, które ulegają zniszczeniu wskutek erozji cząstek wysokiej energii są np. wykładziny w kominie

elektrowni. Narażone są one na erozję mechaniczną, sublimację (rozkład w wysokiej temperaturze), utlenianie i utlenianie z
pasywacją. Cząstki (elementy nieopalone, pyły) o małych wymiarach rzędu



m i dużej prędkości do setek km/h uderzają o

powierzchnię wykładziny. Praca uderzenia powoduje wyrwania, spękania i odkształcenia. Erozja połączona jest z korozją
chemiczną na skutek oddziaływania agresywnego medium

W15,26-28