Kolokwium 1

- ODPOWIEDZI

grupa I

Zadanie 1: Zdecydować, czy podane liczby są zapisane w postaci trygonometrycznej (a-c) lub
kanonicznej (d-f). Jeśli nie są, doprowadzić do tej postaci.

a) –

,

b)

- poprawnie,

c)

,

d)

- poprawnie,

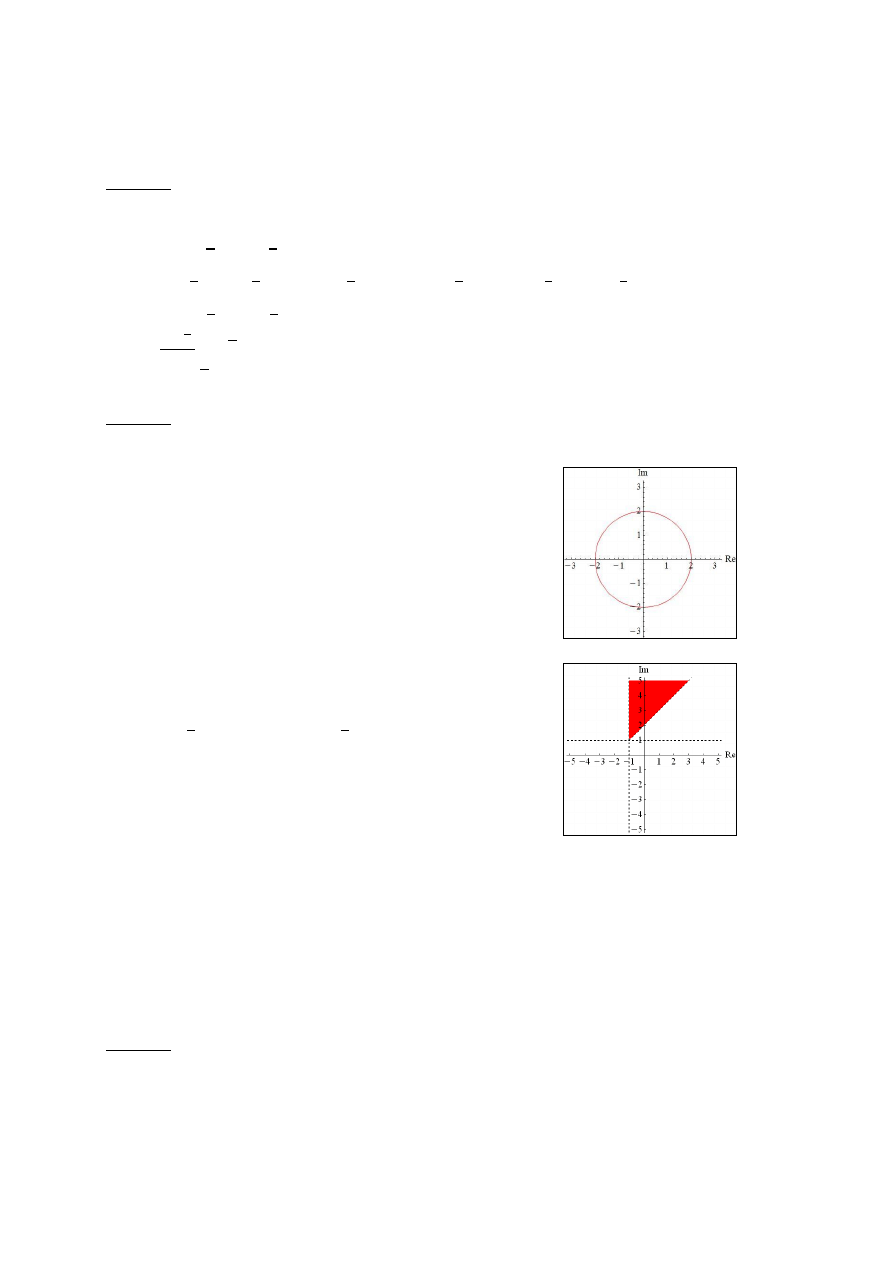
Zadanie 2: Na płaszczyźnie zespolonej narysować następujące obszary:

a)

,

Niech .

– okrąg o promieniu 2 i środku

w punkcie

b)

.

Funkcja przesunięta o wektor .

oraz dowieść:

.

Niech

oraz

.

Wtedy

Zadanie 3: Rozważmy zbiór dwuelementowy z dodawaniem określonym
równościami:

, ,
, ,

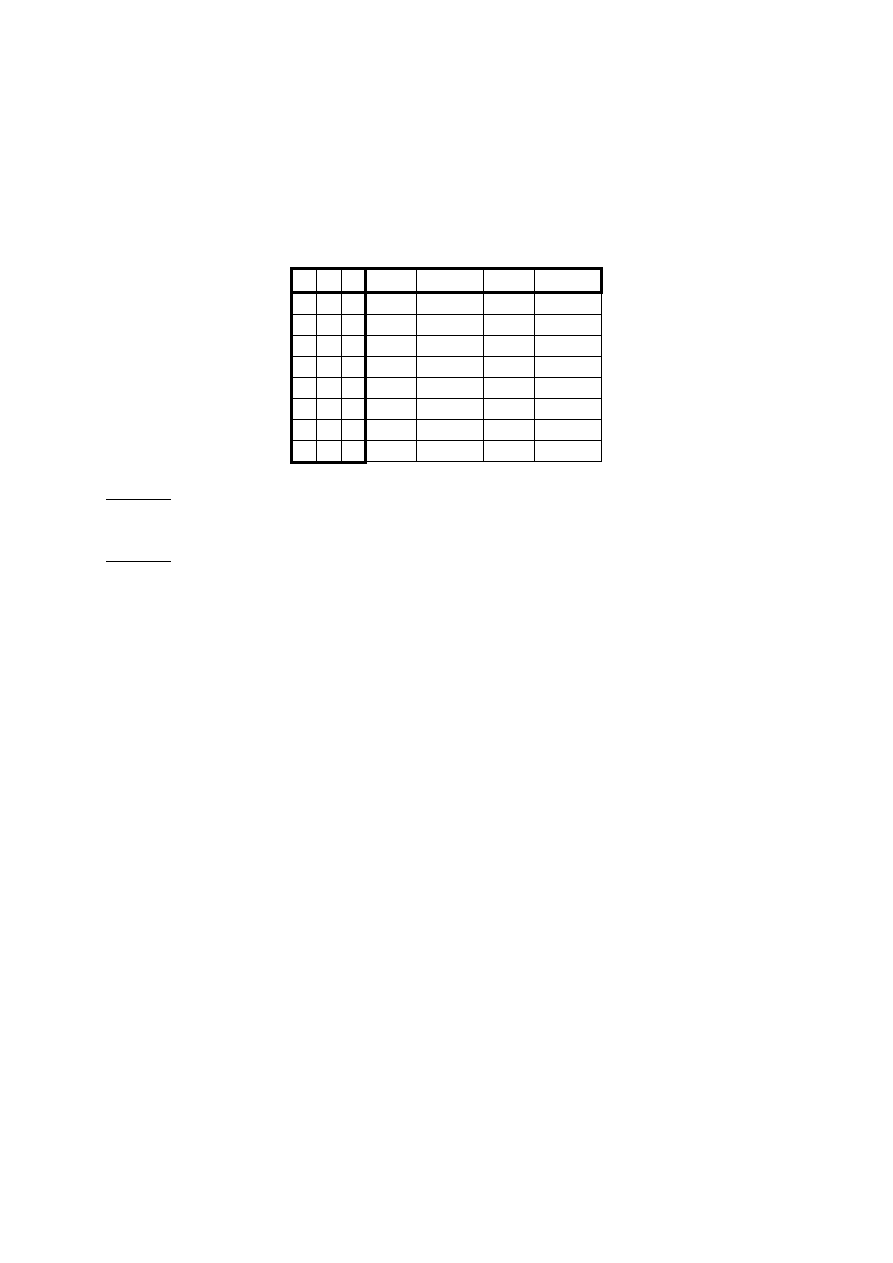
Wykazać, że jest grupą.

Odpowiedź: element neutralny=0 (dwa lewe równania)

elementy przeciwne: a=1 -> a

-1

=1 (dolne prawe równanie),

a=0 -> a

-1

=0 (górne lewe równanie)

łączność:

a b c (a+b) (a+b)+c (b+c) a+(b+c)
0 0 0

0

0

0

0

0 0 1

0

1

1

1

0 1 0

1

1

1

1

0 1 1

1

0

0

0

1 0 0

1

1

0

1

1 0 1

1

0

1

0

1 1 0

0

0

1

0

1 1 1

0

1

0

1

Zadanie 4: Uzasadnić, że zbiór W jest podprzestrzenią liniową przestrzeni liniowej V:

,

Zadanie 5: Zbadać z definicji liniową niezależność układu wektorów:

, ,

w

przestrzeni

.

Jedyne rozwiązanie: