POLITECHNIKA GDAŃSKA

WYDZIAŁ INŻYNIERII LĄDOWEJ I ŚRODOWISKA

KAREDRA MECHANIKI BUDOWLI I MOSTÓW

METODY DOŚWIADCZALNE

W ANALIZIE KONSTRUKCJI

(poprawiona wersja skryptu z 1999 roku)

Jarosław Górski, Tomasz Mikulski

Gdańsk 2007

Drogi

Współpracowniku,

Wykonując przygotowane przez nas doświadczenia i pomiary pamiętaj, że:

„Czwarte prawo termodynamiki” brzmi:

„Żadne urządzenie eksperymentalne nie działa za pierwszym razem, gdy zostaje
zmontowane”,

„Piąte prawo termodynamiki” głosi:
„Żaden eksperyment nie daje nigdy ściśle oczekiwanych wyników”

(T. Kuhn Dwa bieguny. Tradycja i nowatorstwo w badaniach naukowych.
PWN Warszawa 1985).

Pamiętaj również, że:
dokonując pomiaru trzeba wiedzieć nie tylko co mierzyć, ale też w jakim celu!

Jarosław Górski, Tomasz Mikulski

Metody Doświadczalne w Analizie Konstrukcji

2

KILKA UWAG O ĆWICZENIACH

W trakcie zajęć wykonywane są następujące ćwiczenia:
Ćwiczenie

1. Próba statyczna rozciągania metali ..................................................... 4

Ćwiczenie 2.

Próba

statyczna

ściskania metali ....................................................... 9

Ćwiczenie

3. Próba statyczna zginania ................................................................... 12

Ćwiczenie 4.

Próba

udarności ................................................................................. 16

Ćwiczenie 5.

Próba

twardości metali ...................................................................... 20

Ćwiczenie 6.

Pomiar

modułu Younga E oraz współczynnika Poissona

ν .............. 23

Ćwiczenie

7. Twierdzenie Betti-Maxwella i jego wykorzystanie ........................... 25

Ćwiczenie 8.

Badanie

przemieszczeń układów statycznie wyznaczalnych ............ 27

Ćwiczenie 9.

Badanie

przemieszczeń pierścienia kołowego ................................... 29

Ćwiczenie 10. Wyznaczenie

odkształceń w belkach zginanych ............................... 30

Ćwiczenie 11. Wyznaczanie linii wpływu belek ciągłych ........................................ 32
Ćwiczenie 12. Wyznaczenie reakcji podporowej belki ciągłej ................................. 33
Ćwiczenie 13. Wyznaczenie

środka zginania ........................................................... 35

Ćwiczenie 14. Skręcanie swobodne pręta o przekroju pierścieniowym

zamkniętym i otwartym .................................................................... 38

Literatura umożliwiająca prawidłowe wykonanie i zrozumienie ćwiczeń:
[1] A. Chudzikiewicz: „Statyka budowli” cz. 1, cz. 2, PWN, Warszawa 1973.
[2] E. Bielewicz: „Wytrzymałość materiałów”, Gdańsk 2006.
[3] M.

Banasiak: „Ćwiczenia laboratoryjne z wytrzymałości materiałów”, PWN,

Warszawa 1985.

[4] A. Boruszak, R. Sygulski, K. Wrześniowski: „Wytrzymałość materiałów,

doświadczalne metody badań”, PWN Warszawa-Poznań 1984.

[5] D.

Bobrowski, „Probabilistyka w zastosowaniach technicznych”, Wydawnictwo

Naukowo-Techniczne, Warszawa 1986.

Do zajęć można się także przygotować na podstawie innych, dostępnych podręczników
z zakresu statyki budowli i wytrzymałości materiałów. Tematy, z którymi należy się
zapoznać, można z łatwością określić po przeczytaniu instrukcji do poszczególnych
ćwiczeń.
Z każdego ćwiczenia należy wykonać sprawozdanie według szczegółowych uwag
zawartych w instrukcjach. Prosimy o umieszczenie w sprawozdaniu części
zatytułowanej "Uwagi własne". Uważamy ją za bardzo ważny fragment analizy
uzyskanych wyników. Powinna ona zawierać elementy opisane poniżej.
◊

Przeprowadź analizę przyczyn rozbieżności między wynikami uzyskanymi
z doświadczenia a obliczonymi teoretycznie.

◊

Szczegółowo omów błędy pomiaru.

◊

Jeżeli uważasz, że działanie modelu nie jest prawidłowe, to spróbuj określić
dlaczego tak jest i ewentualnie zaproponuj jakie zmiany należy wprowadzić.

◊

Dokonaj krytycznej oceny instrukcji do ćwiczeń.

◊

Jeżeli sposób prowadzenia zajęć ma negatywny wpływ na uzyskiwane przez Ciebie
wyniki, to także napisz to w sprawozdaniu.

Metody Doświadczalne w Analizie Konstrukcji

3

REGULAMIN

LABORATORIUM Z MECHANIKI BUDOWLI

I WYTRZYMAŁOŚCI MATERIAŁÓW

1. Laboratorium obejmuje czternaście ćwiczeń. Liczbę oraz rodzaj ćwiczeń do

samodzielnego wykonania określa prowadzący zajęcia. Każde z ćwiczeń
należy wykonać w trakcie jednej godziny zajęć.

2. Ćwiczenia wykonywane są w podgrupach dwu-, trzy- lub w szczególnym

przypadku czteroosobowych.

3. Obecność jest obowiązkowa na wszystkich zajęciach programowych do

momentu zaliczenia przedmiotu.

4. Przed zajęciami należy zapoznać się z instrukcją do wykonywanego

w danym dniu ćwiczenia oraz powtórzyć materiał teoretyczny wchodzący
w jego zakres. Prowadzący zajęcia ma obowiązek sprawdzić te wiadomości
(ustnie lub pisemne). Osoby nie przygotowane nie będą mogły
przeprowadzić doświadczeń. Będą one mogły ubiegać się o powtórzenie
ćwiczenia w innym terminie.

5. Każda podgrupa jest zobowiązana opracować sprawozdania ze wszystkich

ćwiczeń zgodnie z uwagami zawartymi w instrukcjach.

6. Obrona sprawozdań odbywa się tylko w godzinach przewidzianych

programowo.

7. Zaliczenie laboratorium uzyskuje się na podstawie:

a) obecności na zajęciach (punkt 3),
b) stopnia przygotowania do ćwiczeń (punkt 4),
c) oddanych sprawozdań z ćwiczeń (punkt 5),
d) obrony (ustnej lub pisemnej) sprawozdań (punkt 6).

UWAGA !!!

PODCZAS PRZEPROWADZANIA DOŚWIADCZEŃ

NALEŻY ZWRÓCIĆ UWAGĘ

NA PRZESTRZEGANIE WARUNKÓW BEZPIECZEŃSTWA PRACY,

ORAZ ZACHOWAĆ

JAK NAJDALEJ IDĄCE ŚRODKI OSTROŻNOŚCI,

ABY UCHRONIĆ SIĘ PRZED WYPADKIEM,

KTÓRY MOŻE GROZIĆ ŚMIERCIĄ LUB KALECTWEM !!!

Metody Doświadczalne w Analizie Konstrukcji

4

ĆWICZENIE 1

PRÓBA STATYCZNA ROZCIĄGANIA METALI

Próba statyczna rozciągania (PN-80/H-04310) dzięki posiadanym zaletom jest
podstawową i najbardziej rozpowszechnioną próbą w badaniach własności
wytrzymałościowych i plastycznych materiałów. Za jej pomocą można m.in.
wyznaczyć:
◊

granicę proporcjonalności R

H

,

◊

wyraźną granicę plastyczności R

e

,

◊

górną i dolną granicę plastyczności R

eH

i R

eL

,

◊

wytrzymałość na rozciąganie R

m

,

◊

naprężenie rozrywające R

u

,

◊

wydłużenie względne A

p

,

◊

przewężenie względne Z,

◊

pracę zerwania L

z

.

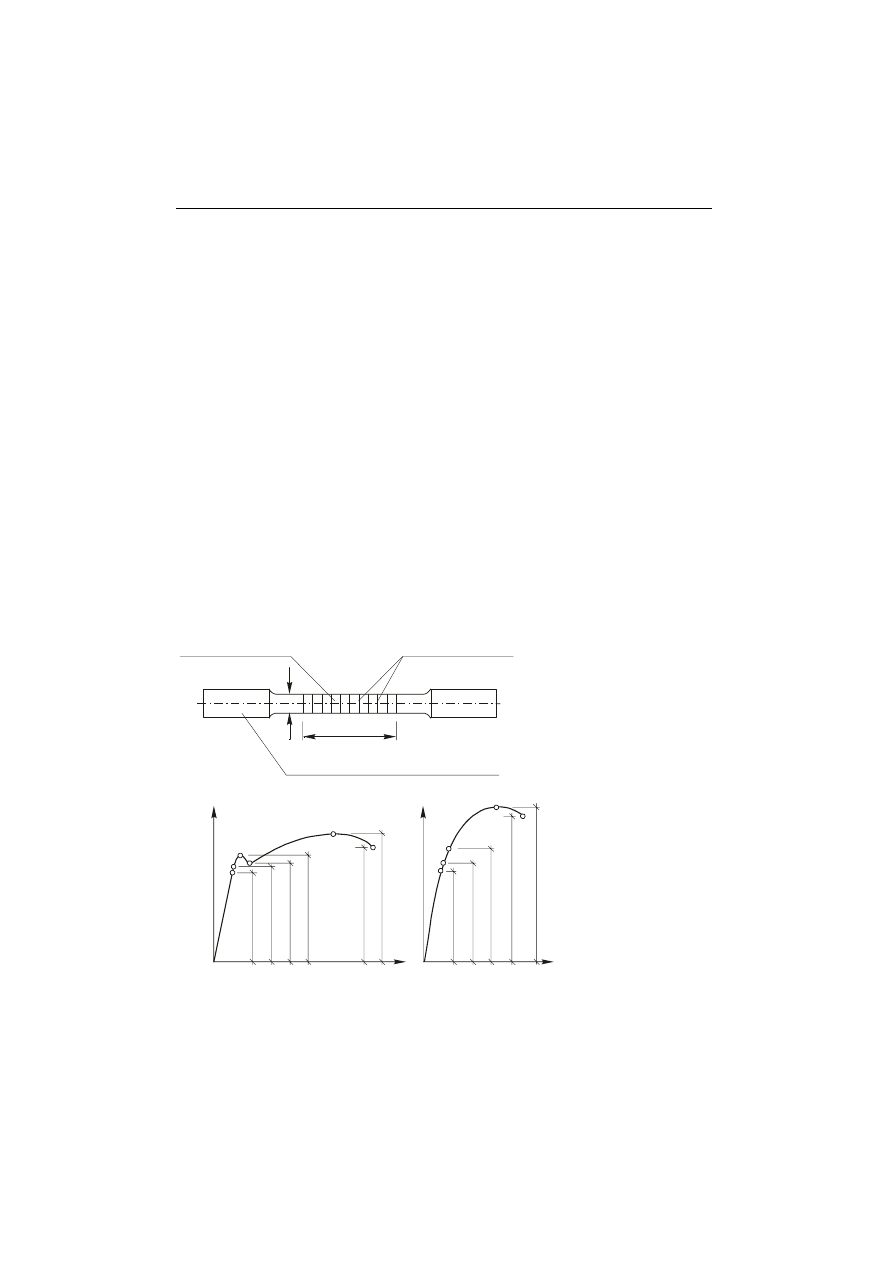
Badanie polega na rozciaganiu specjalnie przygotowanej próbki (rys. 1.1) w maszynie
wytrzymałościowej, umożliwiającej powolny przyrost obciążenia, aż do wartości
powodującej zerwanie próbki. Obciążenie przekazuje się na próbkę w sposób
powodujący jednoosiowy stan naprężenia. Na rys. 1.2 przedstawiono przykładowe
wykresy robocze, sporządzone przez urządzenie samopiszące maszyny
wytrzymałościowej, wyrażające zależności pomiędzy obciążeniem F i wydłużeniem
całkowitym próbki

∆L (F = F(∆L)).

część pomiarowa
o długości L = nd

L

d

część próbki (główka) do zamocowania
w maszynie wytrzymałościowej

kreski ułatwiające
pomiar wydłużenia

o

o

o

o

Rys. 1.1.
Próbka okrągła do próby
rozciągania z główką do
zamocowania w szczękach.

L

o

= 5d

o

– próbka pięciokrotna

L

o

= 10d

o

– próbka dziesięcio-

krotna

Rys. 1.2. Robocze
wykresy rozciągania
dla materiałów:
a) z wyraźną granicą
plastyczności (stal
miękka),
b) bez wyraźnej
granicy plastyczności
(materiał kruchy).

F

F

F

F

F

F

F

F

F

F

F

∆L

a)

b)

∆L

F

F

H

H

eL

eH

u

u

m

m

0,

05

0,

05

0,

2

Stosowanie układu współrzędnych F

−∆L (F = F(∆L)) do opisu próby jest niewygodne

ponieważ porównanie wyników uzyskanych dla dwóch różnych materiałów

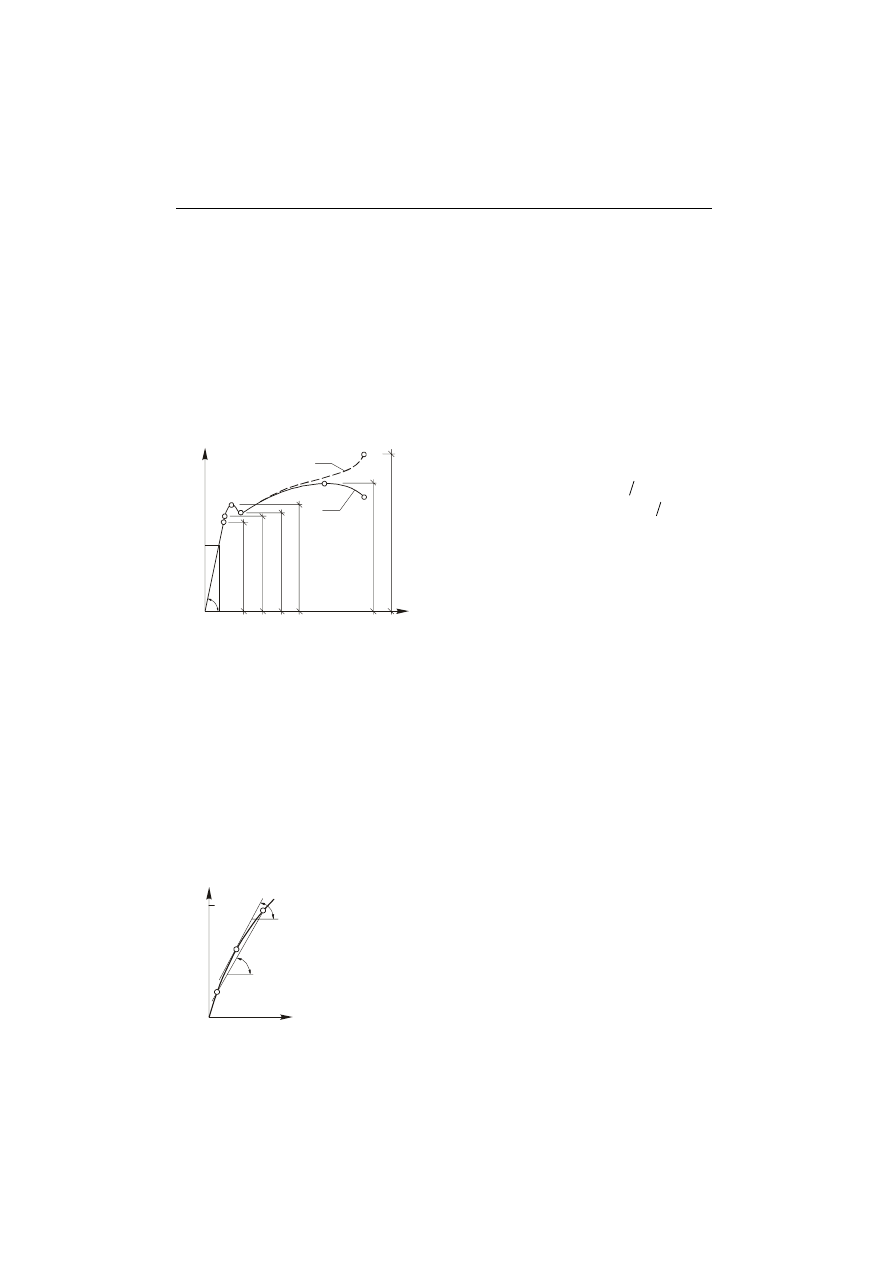
Metody Doświadczalne w Analizie Konstrukcji

5

wymagałoby stosowania próbek o takich samych wymiarach. Aby uniezależnić wyniki
od przekroju próbki stosuje się układ współrzędnych

σ−ε (σ = σ(ε)). Naprężenie

σ = F/S

o

odniesione jest do pola S

o

powierzchni początkowego przekroju próbki,

a odkształcenie

ε = ∆L/L

o

do długości początkowej próbki L

o

. Ponieważ S

o

i L

o

są

wielkościami stałymi zatem wykres rozciągania w układzie

σ−ε można otrzymać

wprost z wykresu maszynowego poprzez zmianę skali rzędnych i odciętych.
Na rys. 1.3, linią ciągłą, przedstawiono umowny wykres rozciągania w układzie

σ−ε dla

stali miękkiej. Linia przerywana przedstawia wykres rzeczywisty w układzie

σ

rz

−ε,

w którym naprężenia

σ

rz

odniesione są do rzeczywistego pola S powierzchni przekroju

próbki zmniejszającego się w trakcie próby. Można uzasadnić, że krzywa ta nie ma
większego znaczenia praktycznego.

Rys. 1.3.

R

R

R

R

R

R

ε

σ

∆ σ

∆ ε

1

2

H

eL

eH

u

m

0,

05

α

Wykresy rozciągania dla stali miękkiej
krzywa 1 - wykres umowny

o

S

F

=

σ

,

krzywa 2 - wykres rzeczywisty

S

F

rz

=

σ

.

Przebieg zmienności zależności

σ do ε

charakteryzuje się występowaniem pewnych
przedziałów, których granice przedstawiono
na rys. 1.3.

Pierwszym charakterystycznym punktem jest granica proporcjonalności (granica
stosowalności prawa Hooke'a) R

H

= F

H

/S

o

. Jest to taka graniczna wartość naprężenia, do

której osiągnięcia przyrostom odkształceń odpowiadają proporcjonalne przyrosty
naprężeń (

∆

σ/∆ε = const.). Oznacza to, że wykres rozciągania do momentu osiągnięcia

granicy proporcjonalności jest linią prostą. Tangens kąta pochylenia tej prostej jest
równoznaczny z modułem odkształcalności podłużnej (modułem sprężystości Younga)
E = tg

α = ∆σ/∆ε [MPa].

W przypadku niektórych metali, na przykład żeliwa i stali sprężynowej, wykres
rozciągania nie ma części prostoliniowej. W takich przypadkach wyznacza się moduł
sprężystości styczny E

t

lub moduł sprężystości sieczny E

s

. Moduł sprężystości styczny E

t

równy jest tangensowi kąta pochylenia stycznej do krzywej rozciągania w dowolnym
punkcie, a moduł sprężystości sieczny E

s

równy jest tangensowi kąta pochylenia siecznej

wykreślonej przez dwa dowolne punkty (rys. 1.4). Moduły te określa się w zakresie
obciążeń odpowiadających naprężeniom wynoszącym 10-90% umownej granicy

sprężystości R

0,05

, która jest kolejną wielkością

charakterystyczną wykresu rozciągania.

ε

σ

α

1

1

2

t

s

2

α

E = tg [MPa]

α

E = tg [MPa]

α

R

0,05

Rys. 1.4.
Definicja stycznego

i siecznego

modułu Younga.

t

E

s

E

Metody Doświadczalne w Analizie Konstrukcji

6

Umowna granica sprężystości R

0,05

= F

0,05

/S

o

, jest to wartość naprężeń, przy których

powstają odkształcenia trwałe nie większe od 0,05%. Oznacza to, że po obciążeniu
i odciążeniu próbki powinno się stwierdzić wydłużenie jej długości początkowej L

o

o 0,05%.
Umowną granicę sprężystości można wyznaczyć na podstawie wykresu umownego

σ−ε

(rys. 1.5). Na osi

ε odkładamy odcinek równy odkształceniu plastycznemu (trwałemu)

ε

p

= 0.05% (odcinek OK). Następnie przez punkt K prowadzimy prostą równoległą do

prostoliniowej części wykresu rozciągania. Prosta ta przecina
wykres rozciągania w punkcie M, którego rzędna jest równa
wartości umownej granicy sprężystości R

0,05

.

ε

σ

R
R

O

K

M

0,05

0,05

H

Rys. 1.5.
Definicja umownej granicy sprężystości

.

05

,

0

R

Po przejściu tej granicy wydłużenia wzrastają szybciej niż przyrost obciążenia, a od
pewnego miejsca, zwanego granicą plastyczności R

e

ich przyrost odbywa się bez

przyrostu siły. Gdy wykres rozciągania zmienia się w sposób przedstawiony na rys. 1.3
można wyróżnić górną i dolną granicę plastyczności R

eH

= F

eH

/S

o

i R

eL

= F

eL

/S

o

.

Dla materiałów, które nie maja wyraźnej granicy plastyczności, przyjmuje się umowną
granicę plastyczności R

0,2

= F

0,2

/S

o

, która oznacza naprężenia wywołujące trwałe

odkształcenie o wartości 0,2% długości początkowej próbki L

o

. Jej wartość można

wyznaczyć w podobny sposób jak umowną granicę sprężystości R

0,05

.

Po zakończeniu plastycznego płynięcia kontynuacja procesu rozciągania możliwa jest po
ponownym wzroście obciążenia. Okres ten nazywamy wzmocnieniem materiału.
Zależność

σ = σ(ε) jest tu krzywoliniowa, przy czym przyrostowi naprężeń towarzyszy

coraz szybszy przyrost odkształceń. Wykres rozciągania osiąga następnie ekstremum,
któremu odpowiada maksymalna wartość siły rozciągającej F

m

określającej

wytrzymałość na rozciąganie R

m

= F

m

/S

o

. Do tego momentu próbka ulega

równomiernemu wydłużeniu na całej długości a zatem i równomiernemu zmniejszaniu
się pola powierzchni przekroju w każdym miejscu próbki. Po przekroczeniu granicy
wytrzymałości na rozciąganie w próbce tworzy się wyraźne przewężenie, tak zwana
szyjka. Siła rozciągająca zmniejsza się, ale naprężenia rzeczywiste w przekroju szyjki
rosną, powodując przy wartości siły F

u

zerwanie próbki. Granicę zerwania określa się

przez naprężenia rozrywające R

u

= F

u

/S

o

. W przypadku materiałów kruchych (np.

żeliwa) granica zerwania pokrywa się z punktem oznaczającym wytrzymałość na
rozciąganie.
Oprócz wskaźników charakteryzujących własności wytrzymałościowe materiału można
wyznaczyć także parametry opisujące własności plastyczne: wydłużenie względne
i przewężenie względne.
Wydłużenie względne A

p

jest to przyrost długości pomiarowej próbki mierzonej po

zerwaniu w odniesieniu do pierwotnej długości pomiarowej próbki, wyrażony w

Metody Doświadczalne w Analizie Konstrukcji

7

procentach A

p

= (L

u

− L

o

)/L

o

× 100%. Litera p jest wskaźnikiem wielokrotności długości

pomiarowej próbki. Na przykład A

5

oznacza wydłużenie próbki pięciokrotnej.

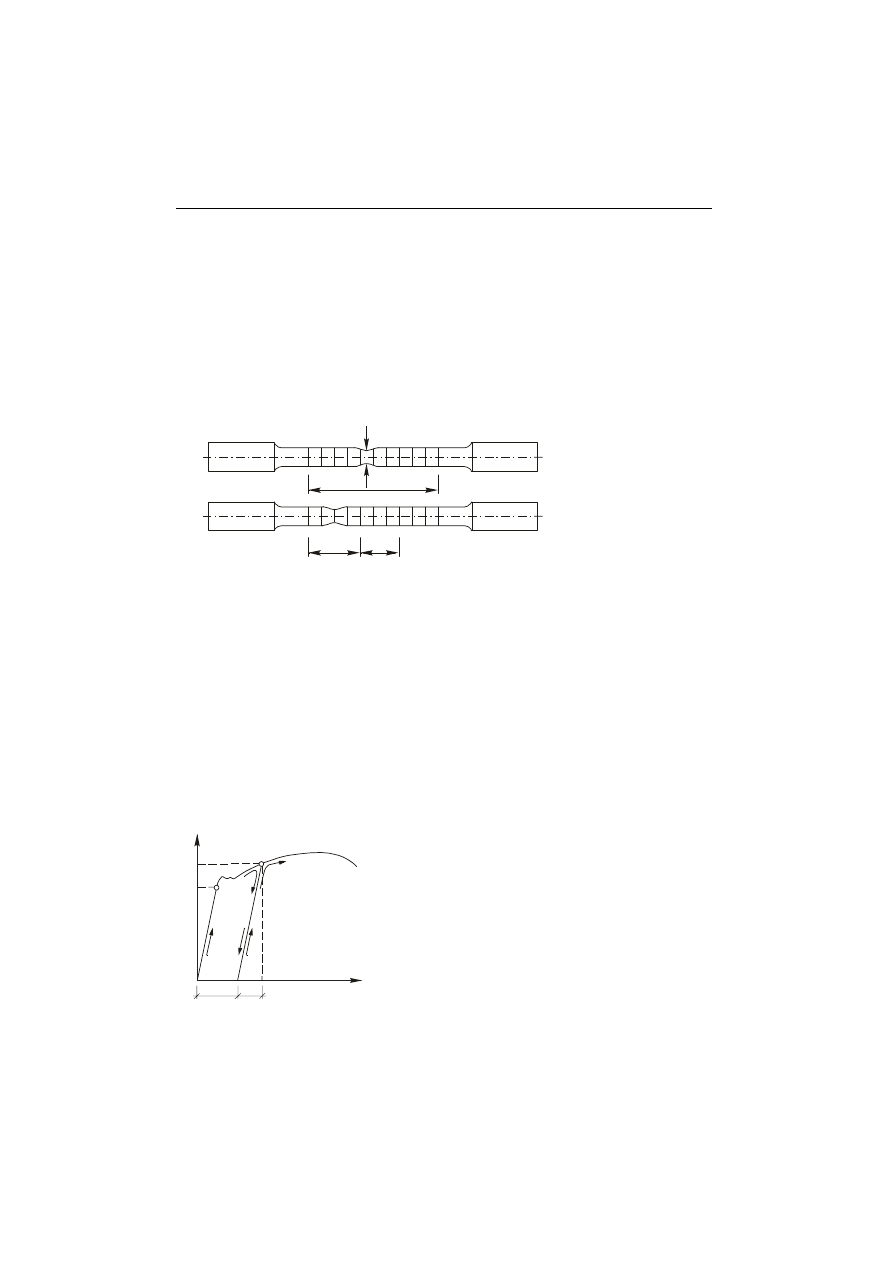
Długość L

u

mierzy się między dwiema skrajnymi rysami na próbce (rys. 1.6.a). Jeżeli

miejsce rozerwania znajduje się poza środkową częścią bazy pomiarowej (to znaczy
poza 1/3 długości pomiarowej próbki), wtedy długość L

u

ustala się w następujący

sposób. W obszarze szyjki przyjmuje się odcinek a, położony symetrycznie względem
miejsca zerwania (rys. 1.6.b). Połowie brakującej jeszcze liczbie działek odpowiada
odcinek b. Przyjmujemy, że gdyby z lewej strony zamiast główki rozciągała się dalej
cylindryczna część próbki, rozkład wydłużeń z obu stron szyjki byłby symetryczny.
Długość L

u

można więc obliczyć jako sumę L

u

= a + 2b.

L

L = a + b

2

a

a)

b)

b

d

u

u

u

Rys. 1.6.
Wyznaczenie długości
pomiarowej próbki po
zerwaniu.

Przewężenie względne Z jest to zmniejszenie powierzchni przekroju poprzecznego
próbki w miejscu zerwania w odniesieniu do jej pierwotnego przekroju
Z = (S

o

− S

u

)/S

o

× 100%.

Omawiając podstawowe zagadnienia związane z próbą rozciągania należy zwrócić
uwagę na pewne towarzyszące jej charakterystyczne zjawiska. Jeżeli na przykład w
procesie rozciągania dojdzie się do pewnego punktu M na wykresie

σ−ε (rys. 1.7),

a następnie rozpocznie się stopniowe odciążenie, to zależność między naprężeniem
i odkształceniem charakteryzuje odcinek prosty MO', równoległy do odcinka OA
wyrażającego prawo Hooke'a przy obciążeniu. Po całkowitym odciążeniu w próbce
pozostanie odkształcenie trwałe, odpowiadające odcinkowi OO'. Jeżeli ponownie
obciąży się próbkę, to do wartości naprężenia, od którego zostało rozpoczęte odciążenie,
zależność pomiędzy naprężeniem i odkształceniem będzie się wyrażać odcinkiem
prostym O'M. Przy dalszym zwiększaniu obciążenia zależność ta będzie przebiegać po
krzywej MN, wzdłuż której przebiegałaby, gdyby nie wystąpiło odciążenie.

ε

σ
σ

ε

ε

M

s

p

O

O’

M’

A

M

N

H

R

Rys. 1.7.
Wykres odciążenia i ponownego obciążenie
rozciąganej próbki.

Metody Doświadczalne w Analizie Konstrukcji

8

Każde odkształcenie

ε po przekroczeniu granicy plastyczności składa się z dwóch

części, sprężystej

ε

s

, która zanika po całkowitym odciążeniu, oraz plastycznej

ε

p

, która

pozostaje po odciążeniu (rys. 1.7). Odkształcenie ma więc charakter sprężysto-
plastyczny. Obszar O'MM' przedstawia energię odwracalnej sprężystej części procesu
odkształcenia, obszar zaś OAMO' energię części nieodwracalnej. Pole zawarte pod
krzywą rozciągania aż do rozerwania się próbki określa tak zwaną pracę zerwania L

z

.

UWAGI O ĆWICZENIU
1. Przed przystąpieniem do próby należy zmierzyć długość pomiarową próbki L

o

,

średnicę d

o

oraz sprawdzić liczbę i prawidłowość wykonania rys na próbce służących

do obliczania wydłużenia.

2. Po zerwaniu próbki należy zmierzyć długość pomiarową próbki po zerwaniu L

u

oraz

najmniejszą średnicę d

u

(w miejscu zerwania).

SPRAWOZDANIE POWINNO ZAWIERAĆ
1. Krótki opis ćwiczenia (cel próby, sposób jej wykonania).
2. Opis próbki.
3. Wykres roboczy i umowny z oznaczeniem charakterystycznych punktów.
4. Obliczenie następujących wielkości (jeżeli można je wyznaczyć na podstawie

wykonanej próby): R

H

, R

e

, R

eH

, R

eL

, R

m

, R

u

, A

p

, Z, L

z

.

5. Dyskusję otrzymanych wyników:

a) omówienie własności wytrzymałościowych i plastycznych badanego metalu,
b) porównanie wyznaczonych wartości z analogicznymi wielkościami dla tych

samych lub podobnych materiałów (np. porównaj dane w tabeli 1.1),

c) uwagi i wnioski.

Tabela

1.1.

Własności niektórych materiałów konstrukcyjnych.

Granica

wytrzymałości

R

m

[

MPa]

Materiał

Moduł

Younga E

10

5

MPa

Współ-

czynnik

Poissona

ν

Granica

plastyczności

R

e

[MPa]

rozciąganie ściskanie

Stal zwykła 2,1

0,33

220

−240 320−380 320−380

Stal o wysokiej wytrzymałości 2,1 0,33 320

−360 520−640 520−640

Stopy aluminium

0,72

0,34

90

−300 90−430 90−430

Drewno (sosna)
równolegle do włókien

0,1

−

−

~55 ~35

Drewno (sosna)
prostopadle do włókien

0,003

−

−

~4 ~5

Beton konstrukcyjny

0,15

−0,40

~0,16

−

0,5

−3 5−50

Cegła

0,02

−0,04

−

−

0,5

−3 5−15

Metody Doświadczalne w Analizie Konstrukcji

9

ĆWICZENIE 2

PRÓBA STATYCZNA ŚCISKANIA METALI

Przed przystąpieniem do czytania opisu ćwiczenia należy zapoznać się z materiałem do
Ćwiczenia 1 (Próba statyczna rozciągania metali).
Celem próby statycznej zwykłej (PN-57/H-04320) jest wyznaczenie:

◊ wyraźnej granicy plastyczności R

ec

,

◊ wytrzymałości na ściskanie R

c

,

◊ skrócenia względnego a

c

.

Należy pamiętać, że wyraźną granicę plastyczności R

ec

określa się jedynie dla

materiałów plastycznych, a wytrzymałość na ściskanie R

c

dla materiałów kruchych, to

znaczy takich, które podczas próby ulegają zniszczeniu (rozkruszeniu).
Celem próby statycznej ścisłej jest wyznaczenie:
◊ modułu sprężystości podłużnej przy ściskaniu E

c

,

◊ umownej granicy sprężystości R

c0,01

,

◊ umownej granicy plastyczności R

c0,2

.

Umowną granicę plastyczności R

c0,2

wyznacza się dla metali plastycznych, które nie

wykazują wyraźnej granicy plastyczności.
Próba ściskania polega na osiowym ściskaniu normowych cylindrycznych próbek
w maszynie wytrzymałościowej. Tak więc z teoretycznego punktu widzenia próba ta jest
prostym odwróceniem próby rozciągania (stan naprężeń przy ściskaniu i rozciąganiu
różnią się tylko znakiem). Istnieją, jednak pewne trudności techniczne
w przeprowadzeniu próby ściskania (w porównaniu z próba rozciągania), a interpretacja
wyników nie jest jednoznaczna.
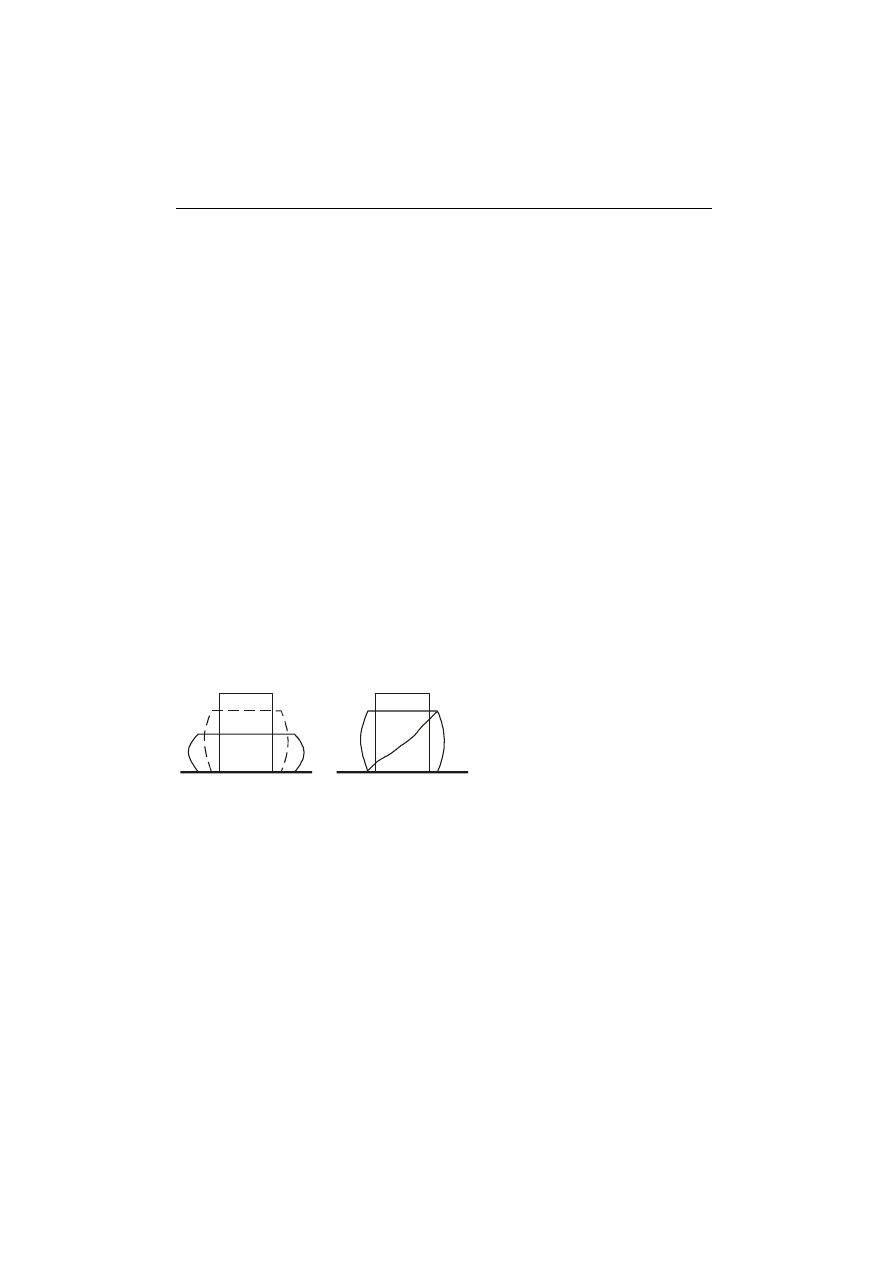
Ściskając próbkę między dwiema płytami prasy można stwierdzić, że zmienia ona swój
kształt na beczkowaty (rys. 2.l).

a)

b)

Rys. 2.l.
Ściskane próbki:
a) ze stali miękkiej,
b) ze stali o wyższej zawartości węgla.

Wynika to stad, że na powierzchni styku z płytami dociskowymi próbka posiada
ograniczoną możliwość zwiększenia wymiarów poprzecznych. Przyczyną tego są
występujące na tych powierzchniach siły tarcia, powodujące powstawanie naprężeń
stycznych, zaburzających przebieg odkształceń w próbce. Wpływ ten jest tak wielki, że
rzeczywisty stan naprężenia nie odpowiada przyjętemu założeniu o równomiernym,
jodnoosiowym rozkładzie naprężeń.
Powyższe przyczyny powodują, że próba ściskania ma dość ograniczone znaczenie
praktyczne, zwłaszcza w zastosowaniu do materiałów sprężysto-plastycznych (miękka
stal, aluminium, miedź), dla których stałe sprężystości oraz granica proporcjonalności,
sprężystości i plastyczności mają w przybliżeniu takie same wartości przy rozciąganiu
jak przy ściskaniu (w obliczeniach dla tych materiałów przyjmuje się jednakową
wytrzymałość na rozciąganie i ściskanie). Natomiast w odniesieniu do materiałów
kruchych (żeliwo, beton), dla których wytrzymałość na ściskanie R

c

jest znacznie

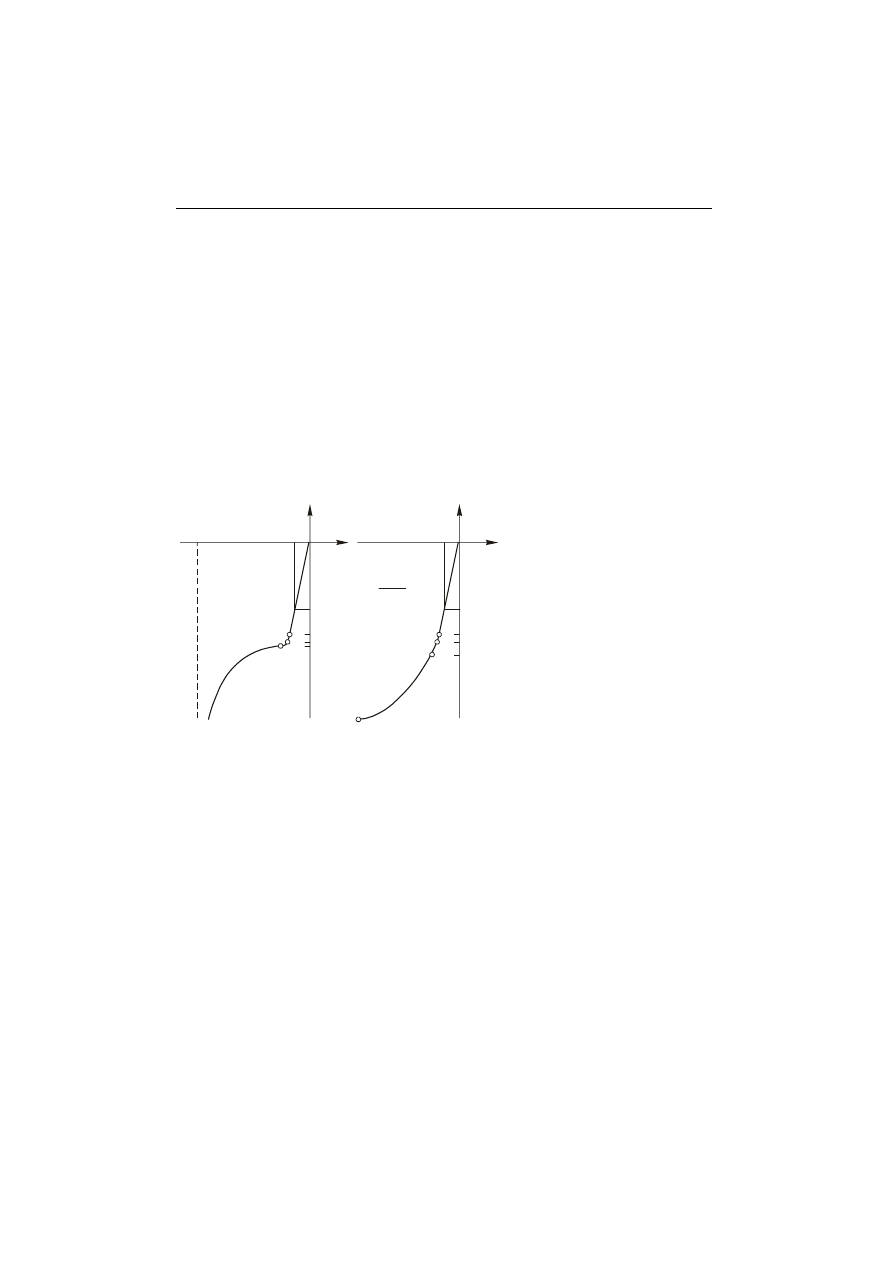
Metody Doświadczalne w Analizie Konstrukcji

10

większa od wytrzymałości na rozciąganie R

m

zachodzi konieczność przeprowadzenia

próby ściskania.
Przygotowane do badań próbki mają kształt walca o zalecanych w normie średnicach d

o

równych 10, 20 lub 30 mm. Wysokość próbki do przeprowadzenia próby zwykłej
wynosi zaledwie 1,5d

o

, gdyż próbka o większej wysokości uległaby wyboczeniu

(bocznemu ugięciu). W przypadku próby ścisłej, w trakcie której wyboczenie nie
wystąpi (obciążenie jest znacznie mniejsze niż w próbie zwykłej), przy określeniu
umownych granic sprężystości i plastyczności stosuje się próbki o wysokości 3d

o

, a przy

określaniu współczynnika sprężystości podłużnej E

c

nawet o wysokości 10d

o

. Z uwagi

na większą wysokość próbek w ich części środkowej wytwarza się jednoosiowy stan
naprężenia, a więc pomierzone wielkości są dokładniejsze.

ŚCISKANIE METALI PLASTYCZNYCH
Na rys. 2.2.a przedstawiono przykładowy umowny wykres ściskania dla metalu
plastycznego.

Rys. 2.2.
Umowny wykres ściskania:
a) metal plastyczny,
b) metal kruchy.

W początkowym okresie
ściskania, skrócenia próbki są
proporcjonalne do naprężeń
i podobnie jak przy rozciąganiu

występuje granica proporcjonalności R

Hc

i umowna granica sprężystości R

c0,01

. Granicę

sprężystości można wyznaczyć w sposób wykreślny omówiony w Ćwiczeniu 1. Po
przekroczeniu granicy sprężystości zaczynają występować niewielkie odkształcenia
trwałe. Przy dalszym wzroście obciążenia osiągana jest granica plastyczności R

ec

, przy

której próbka ulega skróceniu bez wzrostu obciążenia. Okres płynięcia przy ściskaniu
trwa znacznie krócej niż przy rozciąganiu i nie wykazuje górnej i dolnej granicy
plastyczności. Dla materiałów nie mających wyraźnej granicy plastyczności wyznacza
się umowną granicę plastyczności R

c0,2

.

R

a)

b)

R

E =

∆ σ

∆ σ

∆ σ

∆ ε

∆ ε

∆ ε

R

R

R

R

ε

ε

σ

σ

-1,0

Hc

Hc

c

ec

c0,2

c0,01

c0,01

Zwiększenie siły obciążającej po przekroczeniu granicy plastyczności powoduje coraz
silniejsze pęcznienie próbki, objawiające się stałym wzrostem przekroju poprzecznego.
Krzywa wykresu ściskania asymptotycznie dąży do prostej poprowadzonej równolegle
do osi obciążeń, w punkcie odpowiadającym skróceniu równemu początkowej długości
próbki h

o

(rys. 2.2.a).

Mimo spłaszczenia próbki „na plasterek” (rys. 2.1.a) nie widać na niej oznak
zniszczenia. Tylko w niektórych przypadkach (przy niedostatecznej plastyczności) na
powierzchni bocznej próbki pojawiają się drobne rysy. Pęknięcia te nie mogą być
podstawą do oznaczenia wytrzymałości na ściskanie.

Metody Doświadczalne w Analizie Konstrukcji

11

ŚCISKANIE METALI KRUCHYCH
Umowny wykres ściskania dla metalu kruchego przedstawiono na rys.

2.2.b.

Początkowo wykres jest prawie prostoliniowy i lekko odchylony od osi sił. Następnie
coraz bardziej zakrzywia się, urywając się nagle w pewnym punkcie z powodu
zniszczenia próbki.
Punkt ten określa wytrzymałość na ściskanie R

c

. Kształt próbki bezpośrednio przed

zniszczeniem jest lekko beczkowaty (rys. 2.1.b). Świadczy to o istnieniu niewielkich
odkształceń plastycznych. Jednak materiały kruche nie mają wyraźnej granicy
plastyczności. Wyznaczenie umownej granicy sprężystości R

c0,01

i umownej granicy

plastyczności R

c0,2

możliwe jest metodą opisaną w Ćwiczeniu 1. Także moduł

sprężystości podłużnej E

c

oraz skrócenie względne a

c

można obliczyć w sposób

analogiczny jak podobne wielkości w próbie rozciągania metali (Ćwiczenie 1).
Metale kruche doznają podczas ściskania pęknięcia poślizgowego (ścięcia). Pęknięcie
poślizgowe poprzedzone jest odkształceniami trwałymi wywołanymi naprężeniami
stycznymi występującymi w przekrojach nachylonych pod kątem 45

o

do kierunku

naprężeń głównych i zachodzi pod kątem zbliżonym do kąta nachylenia tych
przekrojów.
Należy pamiętać, że wytrzymałość na ściskanie R

c

zależy od wymiarów próbek i dlatego

możliwe jest porównywanie wyników badań otrzymanych na próbkach geometrycznie
podobnych.

UWAGA

PODCZAS PRÓBY ŚCISKANIA METALI KRUCHYCH NALEŻY ZWRÓCIĆ

UWAGĘ NA ZACHOWANIE WARUNKÓW BEZPIECZEŃSTWA PRACY,

ABY UCHRONIĆ SIĘ PRZED SKALECZENIEM OSTRYM ODPRYSKIEM!

UWAGI O ĆWICZENIU
1. Przed przystąpieniem do próby należy dokonać pomiarów próbki.
2. W przypadku próbki z metalu kruchego należy dokonać pomiarów próbki po jej

zniszczeniu.

SPRAWOZDANIE POWINNO ZAWIERAĆ
1. Krótki opis ćwiczenia (cel próby, sposób jej wykonania).
2. Opis próbki.
3. Wykres roboczy i umowny z oznaczeniem charakterystycznych punktów.
4. Obliczenie następujących wielkości (jeżeli można je wyznaczyć na podstawie

wykonanej próby): R

Hc

, R

ec

, R

c0,2

, R

c

, E

c

i A

c

.

5. Dyskusję otrzymanych wyników:

a) omówienie własności wytrzymałościowych i plastycznych badanego metalu,
b) porównanie wyznaczonych wartości z analogicznymi wielkościami dla tych

samych lub zbliżonych materiałów (np. porównaj dane w tabeli 1.1),

c) uwagi i wnioski.

Metody Doświadczalne w Analizie Konstrukcji

12

ĆWICZENIE 3

PRÓBA STATYCZNA ZGINANIA

Przed przystąpieniem do czytania opisu ćwiczenia należy zapoznać się z materiałem do
Ćwiczenia 1 (Próba statyczna rozciągania metali) oraz Ćwiczenia 2 (Próba statyczna
ściskania metali).
Celem ćwiczenia jest wyznaczenie maksymalnego zginającego momentu niszczącego
i porównanie go z momentem granicznym wyznaczonym dla modelu ciała idealnie
sprężysto-plastycznego.
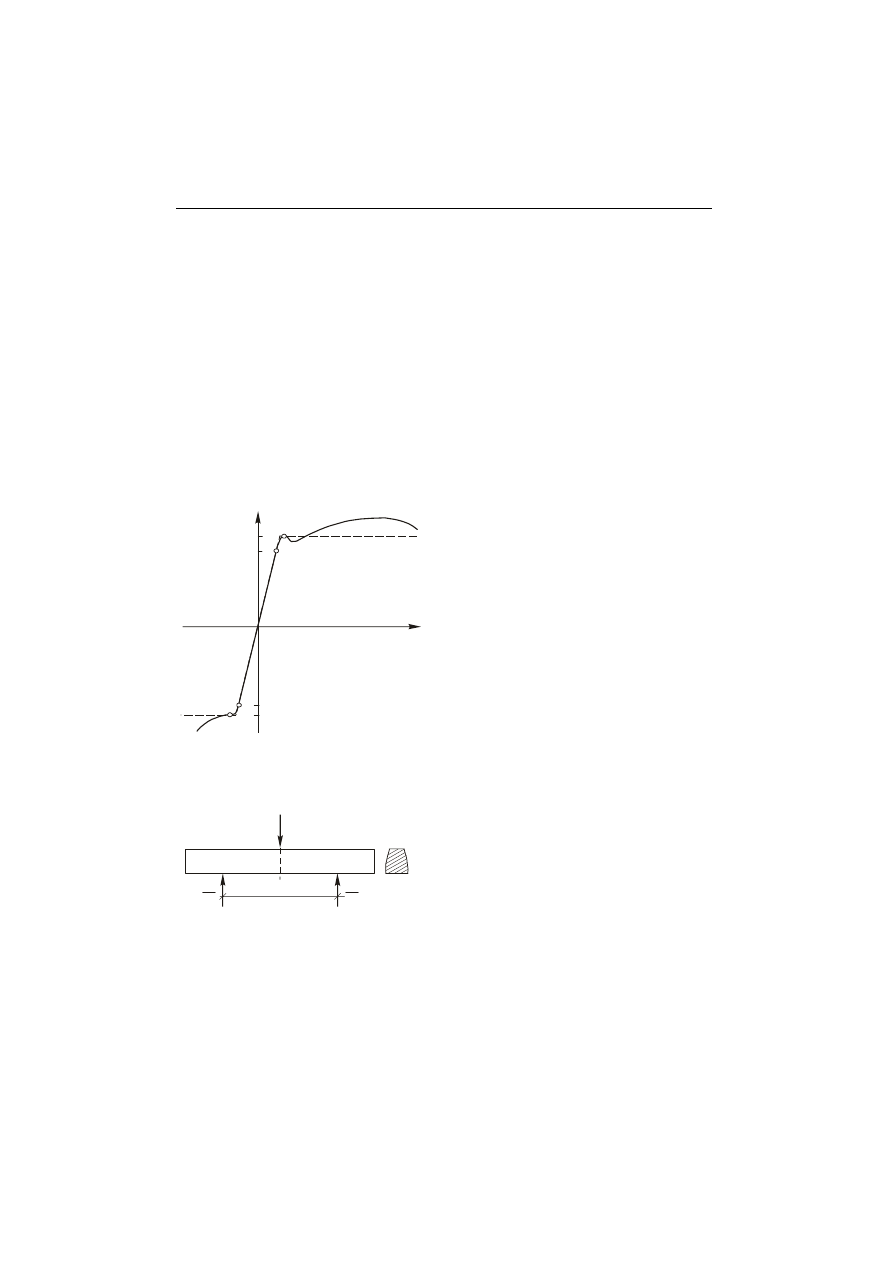
Rozpatrzmy wykres rozciągania i ściskania dla stali konstrukcyjnej (rys.

3.l).

Zakładamy, że materiał zachowuje się, tak samo przy rozciąganiu i ściskaniu. Wykres
rozciągania i ściskania przybliżamy trzema prostymi AB, BC i CD, przyjmując, że
granica proporcjonalności równa jest granicy plastyczności (R

H

≈ R

e

) oraz granica

plastyczności dla rozciągania i ściskania są identyczne (R

e

= R

ec

). Ponadto pomijamy

wzmocnienie materiału. W ten sposób utworzyliśmy model ciała idealnie sprężysto-
plastycznego.

Rys. 3.l
Wykres rozciągania i ściskania dla stali
konstrukcyjnej (linia ciągła) oraz aproksymacja
wykresu do modelu ciała idealnie sprężysto-
plastycznego (linia przerywana).

R

O

A

B

C

D

R

Hc

ec

R

R

ε

σ

H

e

Próbę zginania przeprowadzamy dla belki o schemacie statycznym przedstawionym na
rys. 3.2. Przyjmujemy, że belka wykonana jest z materiału idealnie sprężysto-
plastycznego.

Rys. 3.2.
Schemat obciążenia próbki (belki).

F

F

F

l

α

α − α

α

2

2

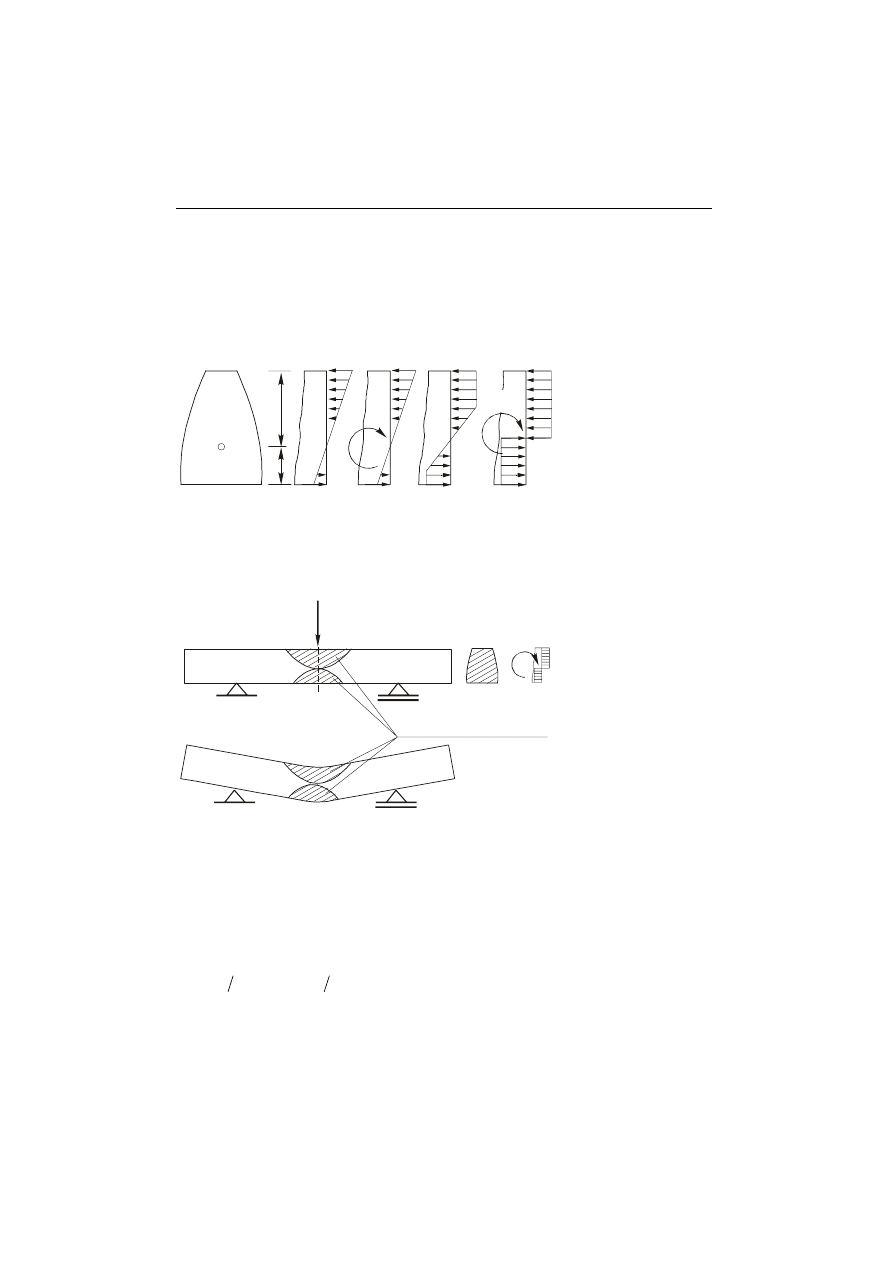
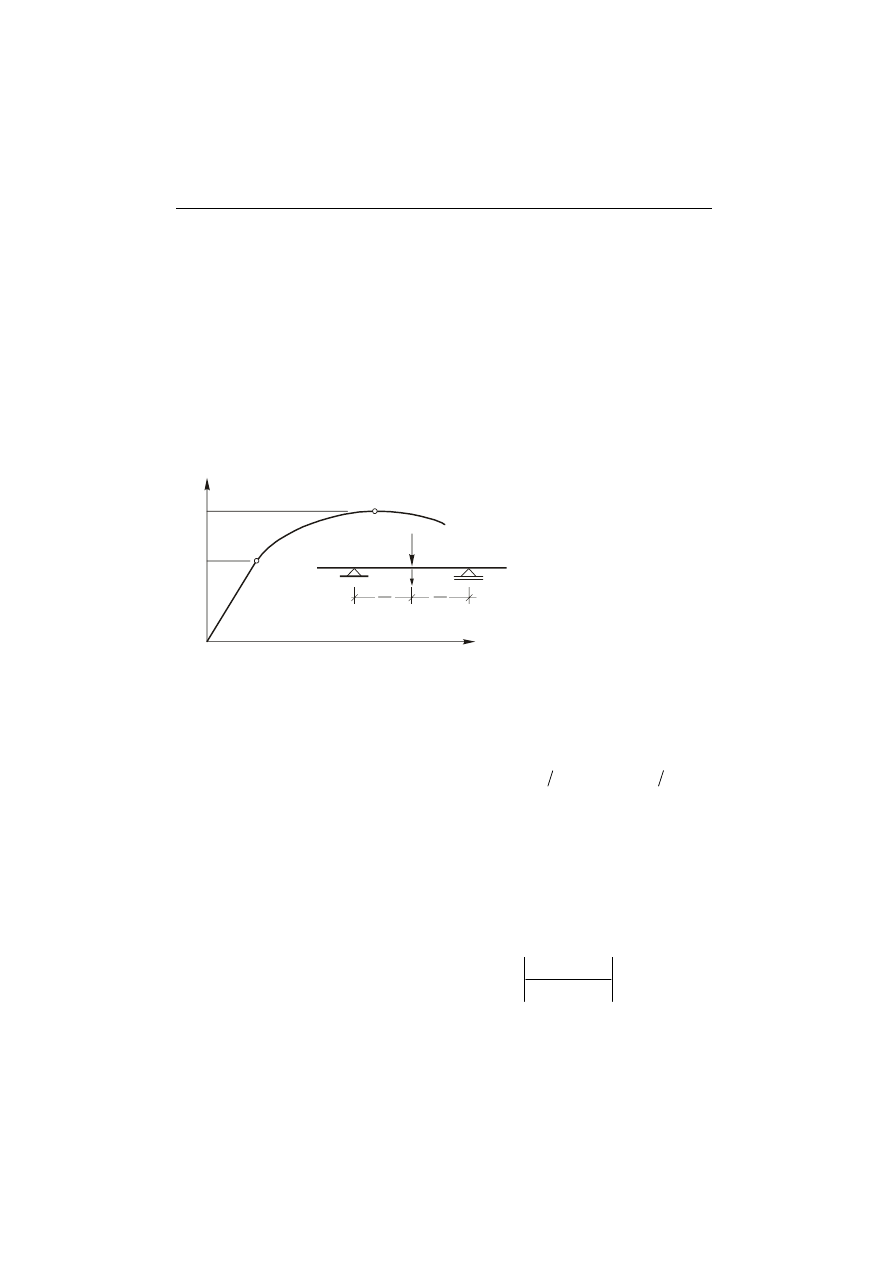
Na rys. 3.3. przedstawiono schemat rozkładów naprężeń normalnych

σ w przekroju

α − α . Rozpatrzmy pracę sił wewnętrznych w tym przekroju.
Wykres naprężeń normalnych dla niewielkiego obciążenia belki przedstawiono na
rys. 3.3.a. Wzrost obciążenia spowoduje uplastycznienie włókien skrajnych przekroju
(rys. 3.3.b). Podczas dalszego obciążenia belki, zgodnie z przyjętym modelem ciała
(rys. 3.1) naprężenia we włóknach skrajnych nie rosną, natomiast granicę plastyczności

Metody Doświadczalne w Analizie Konstrukcji

13

osiągają włókna coraz dalej położone od dołu i od góry belki (rys. 3.3.c). Ponowne
zwiększenie obciążenia doprowadza do całkowitego uplastycznienia wszystkich włókien
(rys. 3.3.d). Według przyjętego modelu ciała wykres naprężeń przedstawiony na
rys. 3.3.d odpowiada powstaniu w tym przekroju przegubu plastycznego (rys. 3.4).
Przegub ten należy rozumieć w ten sposób, że przekroje sąsiadujące z przekrojem
uplastycznionym obracają się względem siebie bez dalszego wzrostu obciążenia.

Rys. 3.3.
Schemat rozkładów
naprężeń normalnych

σ

w

przekroju

α

−

α

:

a) na etapie początkowego

obciążenia belki,

b) przy uplastycznieniu

włókien skrajnych,

e

M

a)

b)

R

R

R

R

R

c)

d)

e

g

e

d

r

r

s

e

e

e

e

e

σ

σ

σ

M

max

c) przy uplastycznieniu warstw wewnętrznych i rozkładzie liniowym w pobliżu warstwy obojętnej,
d) przy pełnym uplastycznieniu w przekroju podczas dalszego obciążenia belki.

R

M

R

e

max

max

Strefy uplastycznienia

- przegub plastyczny

e

F

α

α − α

α

Rys. 3.4
Przegub plastyczny
w belce zginanej

Obliczamy momenty zginające odpowiadające stanom przedstawionym na rys. 3.3.b
i 3.3.d.
W pierwszym przypadku (rys. 3.3.b) maksymalny moment M

e

możemy obliczyć

wykorzystując wzór dla zginania prostego

σ

max

= M

e

/W

sp

, z którego po dokonaniu

podstawienia

σ

max

= R

e

uzyskamy

sp

e

e

W

R

M

⋅

=

. (3.1)

Wskaźnik wytrzymałości W

sp

(górny

lub dolny

) wyznaczymy ze związków

g

sp

W

d

sp

W

g

x

g

sp

e

J

W

=

i

d

x

d

sp

e

J

W

=

, w których J

x

jest momentem bezwładności przekroju

poprzecznego belki, a e

g

i e

d

oznaczają odległość od środka ciężkości przekroju

odpowiednio do górnych i dolnych włókien.

Metody Doświadczalne w Analizie Konstrukcji

14

M

R

R

c

c

y

x

z

A

A

A

max

1

1

2

2

e

e

Rys. 3.5.
Rozkład naprężeń normalnych w przypadku
całkowitego uplastycznienia przekroju

W drugim przypadku (rys.

3.5) w celu wyznaczenia maksymalnego momentu

zginającego M

max

należy obliczyć plastyczny wskaźnik wytrzymałości W

pl

. W pierwszej

kolejności poszukujemy osi obojętnej przekroju. Jej położenie można określić
z warunku:

. (3.2)

0

,

0

=

=

∫

∑

A

x

dA

P

σ

Powyższy związek prowadzi do następującego równania

, (3.3)

0

2

1

=

+

−

A

R

A

R

e

e

z którego wynika, że oś obojętna dzieli przekrój na dwie równe części (A

1

= A

2

= A/2).

Następnie zapisujemy sumę momentów względem osi obojętnej:

. (3.4)

∫

∑

=

=

A

y

dA

z

M

M

σ

max

,

0

Po wykonaniu obliczeń uzyskamy wzór

(

2

1

max

2

c

c

A

R

M

e

+

=

)

, (3.5)

w którym c

1

i c

2

oznaczają odległości środków ciężkości części przekroju poprzecznego

nad i pod osią obojętną. Przyjmując następującą definicję plastycznego wskaźnika
wytrzymałości

(

2

1

2

c

c

A

W

pl

+

=

)

, (3.6)

otrzymamy ostateczną wartość momentu

. (3.7)

pl

e

W

R

M

=

max

Przykładowo dla przekroju prostokątnego o wymiarach b (szerokość przekroju) i h
(wysokość przekroju) wskaźniki wytrzymałości przyjmują wartości:

4

,

6

2

2

bh

W

bh

W

pl

sp

=

=

. (3.8)

Metody Doświadczalne w Analizie Konstrukcji

15

Moment M

max

obliczony przy założeniu całkowitego uplastycznienia przekroju belki

według wzoru (3.7) jest więc 1,5 razy większy niż moment M

e

obliczony za pomocą

wzoru (3.1).


UWAGI O ĆWICZENIU
Przed przystąpieniem do próby należy dokonać pomiarów przekroju poprzecznego
próbki (belki).


SPRAWOZDANIE POWINNO ZAWIERAĆ
1. Krótki opis ćwiczenia.
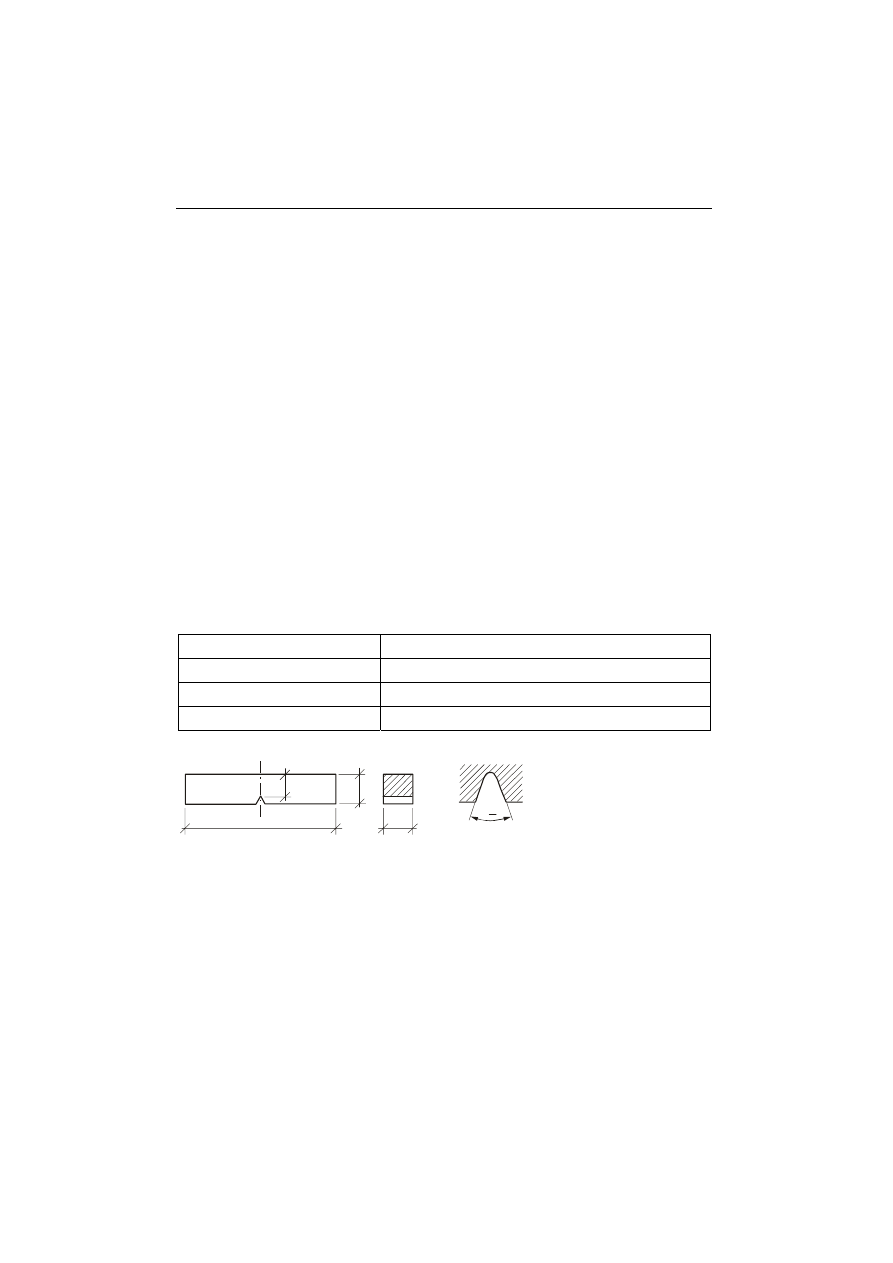
2. Wykres zginania belki uzyskany z maszyny wytrzymałościowej (rys. 3.6).

F

F

F

e

max

F

∆

∆

l

l

2

2

Rys. 3.6
Wykres otrzymany
z maszyny wytrzymałościowej.

3. Odczytane z wykresu wartości sił:
a) F

e

− odpowiadającej załamaniu wykresu, to znaczy uplastycznieniu włókien

skrajnych belki,

b) F

max

− odpowiadającej maksymalnej wartości uzyskanej w trakcie próby.

4. Wykresy momentów zginających oraz obliczenie momentów zginających

i

odpowiadających siłom F

d

e

M

d

M

max

e

i F

max

4

l

F

M

e

d

e

=

,

4

max

max

l

F

M

d

=

(d

−

doświadczalny).

5. Wyprowadzenie wzorów umożliwiających obliczenie wskaźników wytrzymałości

W

sp

i W

pl

dla przekroju belki zastosowanej w doświadczeniu wraz z rysunkami

odpowiadających im naprężeń.

6. Wyliczenie, ze wzoru (3.1), wartości granicy plastyczności R

e

przy założeniu, że

.

d

e

e

M

M

=

7. Wyznaczenie, ze wzoru (3.7), maksymalnej wartości momentu zginającego M

max

dla

ciała idealnie sprężysto-plastycznego.

8. Ocenę poprawności przyjęcia (dla badanego materiału) modelu ciała idealnie

sprężysto-plastycznego (np. wykorzystując wzór

%

100

max

max

max

⋅

−

=

d

d

M

M

M

δ

).

9. Uwagi

własne.

Metody Doświadczalne w Analizie Konstrukcji

16

ĆWICZENIE 4

PRÓBA UDARNOŚCI

Próby udarowe są próbami dynamicznymi, określającymi zdolność materiału do
przenoszenia gwałtownych obciążeń typu uderzeniowego. Charakteryzują one te
własności mechaniczne materiału, których nie można wykryć za pomocą prób
statycznych. Badania udarności mają szczególne znaczenie dla stali ulepszanych
cieplnie, gdyż wraz z korzystnym wzrostom wytrzymałości i twardości zachodzi
szkodliwy wzrost kruchości materiału.
Próbę udarności stosuje się w celu dokonania oceny zachowania się materiału
w warunkach sprzyjających kruchemu pękaniu, stworzonych w próbce obecnością karbu
i dużą szybkością odkształcenia wywołaną działaniem dynamicznym siły oraz
działaniem temperatury.
Celem ćwiczenia jest zapoznanie się z praktycznym sposobem wykonania próby
udarności metali zgodnie z obowiązującą normą (PN-79/H-04370), używanymi do tego
celu próbkami i urządzeniami oraz interpretacją wyników próby.
Wykonanie ćwiczenia polega na udarowym złamaniu kilku metalowych próbek
i zbadaniu wpływu obróbki cieplnej na udarność stali.
Typy próbek stosowanych do próby udarności podano w tabeli 4.1, a wygląd próbki
przedstawiono na rys. 4.1. Próbki powinny być całkowicie obrobione skrawaniem. Karb
wykonuje się za pomocą frezowania lub wiercenia i przecinania. Sposób pobierania
odcinków próbnych i wykonania próbek nie powinien zmieniać własności materiału.

Tabela 4.1.

Charakterystyka próbek do próby udarności.

Typ próbki

Cechy charakterystyczne próbki

Mesnager

karb w kształcie litery U o głębokości 2 mm

ISO-Charpy U

karb w kształcie litery U o głębokości 5 mm

ISO-Charpy V

karb w kształcie litery V o głębokości 2 mm

55 α

α

α − α

45 2

+

o

b

b = 5, 7.5, 5 mm

8

10

Rys. 4.1
Próbka typu ISO - Charpy V

Do prób udarności używa się młotów wahadłowych o stałym zasobie energii lub takich,
których konstrukcja pozwala na zmianę zasobu energii potencjalnej. W laboratoriach
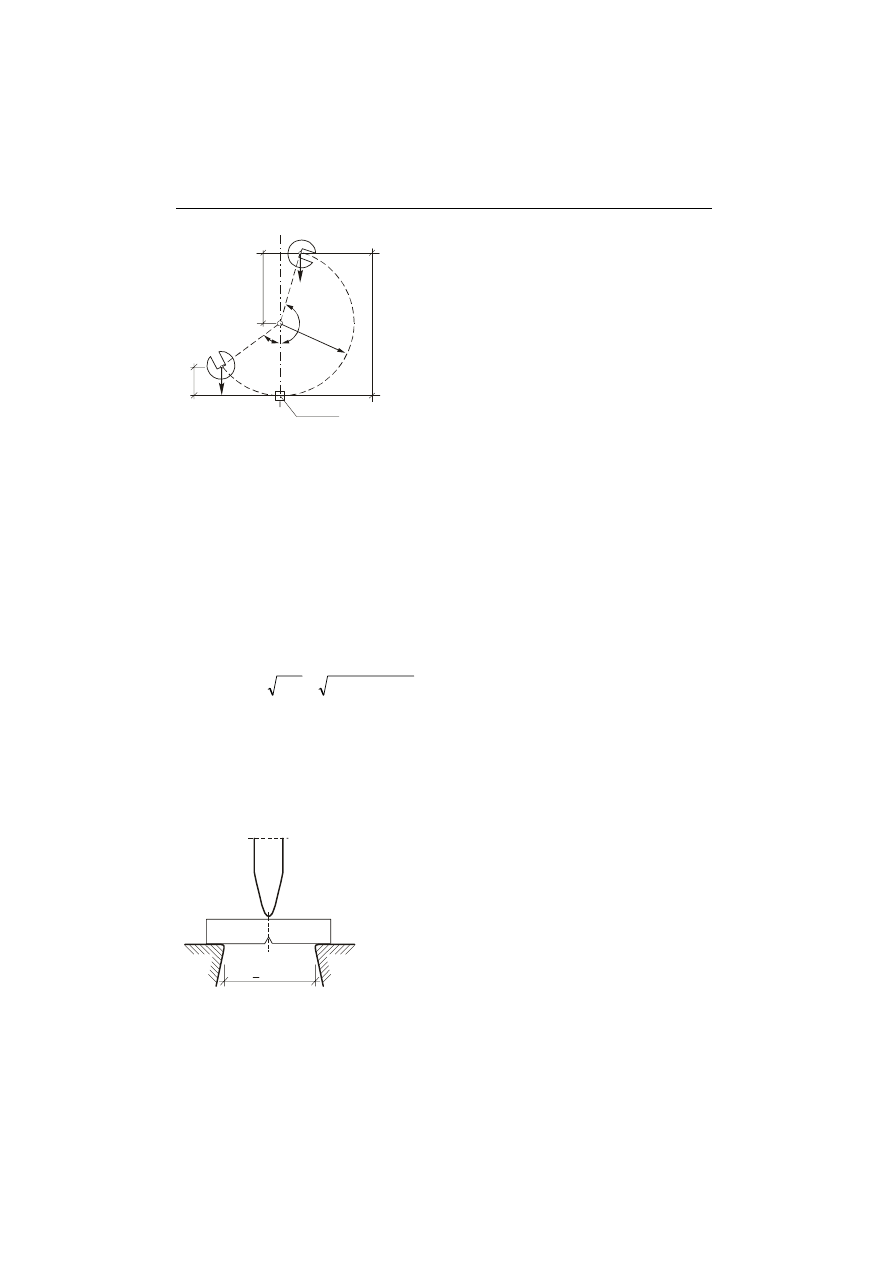
najczęściej stosowany jest młot wahadłowy typu Charpy. Schemat działania młota
i podstawowe wielkości przedstawiono na rys. 4.2. Młot spadając z wysokości h
(położenie 1) do położenia O osiąga w tym punkcie maksymalną prędkość i największą
energię kinetyczną. Po zniszczeniu próbki, pozostała część energii kinetycznej wychyla
młot do położenia 2.

Metody Doświadczalne w Analizie Konstrukcji

17

Rys. 4.2.

G

β

α

R

O

a

h’

h

G

Próbka

2

1

R

R

Schemat działania młota wahadłowego

Energia potencjalna młota w położeniu 1 wynosi

h

G

L

R

=

1

, (4.1)

zaś po złamaniu próbki w położeniu 2

h

G

L

R

′

=

2

, (4.2)

gdzie: G

R

jest ciężarem wahadła młota.

Praca wykonana przez młot na zniszczenie próbki wynosi

(

h

h

G

L

L

L

R

u

)

′

−

=

−

=

2

1

. (4.3)

Z rys. 4.2 wynika, że

(

) (

)

(

)

.

cos

1

,

cos

1

180

cos

β

α

α

−

=

′

−

=

−

+

=

+

=

R

h

R

R

R

a

R

h

(4.4)

Ostatecznie więc wartość wykonanej pracy wyraża się wzorem

(

)

(

)

α

β

cos

cos

−

=

′

−

=

R

G

h

h

G

L

R

R

u

[kGm].

(4.5)

Największa prędkość młota wynosi

(

)

α

cos

1

2

2

−

=

=

gR

gh

v

[m/s],

(4.6)

gdzie: g - przyspieszenie ziemskie [m/s

2

],

R - odległość od osi wahadła młota do środka wahadła [m].

Najczęściej do prób stosowane są młoty o zasobie energii od 15 do 30 kGm. Prędkość
młota w chwili uderzenia powinna zawiera się w granicach od 4,5 do 7 m/s.
Przy przeprowadzeniu próby udarności próbek z karbem (rys. 4.3) należy przestrzegać,
aby:

◊ uderzenie młota było środkowe,

40 0,5 mm

+

◊ oś karbu leżała w płaszczyźnie ruchu młota,

◊ karb był skierowany w kierunku podpór,

◊ próbka przylegała do podpór.

Rys. 4.3.
Sposób podparcia próbki.

Metody Doświadczalne w Analizie Konstrukcji

18

Wykonanie próby udarności polega na złamaniu jednym uderzeniem młota
wahadłowego próbki z karbem, podpartej swobodnie na obu końcach (rys. 4.3)
i pomiarze pracy odpowiadającej energii zużytej na jej złamanie.
Udarnością nazywa się odporność materiału na działanie obciążeń dynamicznych
i oblicza się ją ze wzoru

⎥⎦

⎤

⎢⎣

⎡

=

2

cm

kGm

S

L

K

o

u

, (4.7)

gdzie: L

u

- wartość pracy odpowiadającej energii zużytej na złamanie próbki [kGm],

S

o

- pole powierzchni przekroju poprzecznego próbki w miejscu karbu,

mierzone przed próbą [cm

2

].

Oznaczenie udarności K należy uzupełnić dodatkowym symbolem wskazującym typ
próbki, na której zostało przeprowadzone badanie:
◊ udarność próbek typu Mesnager - oznacza się KM,

◊ udarność próbek typu ISO - Charpy U z karbem w kształcie litery U - oznacza się

KCU,

◊ udarność próbek typu ISO - Charpy V z karbem w kształcie litery V - oznacza się

KV.

W próbach udarności w ogólnym przypadku brak jest zachowania prawa podobieństwa.
Z tego względu wyniki próby mogą być bezpośrednio porównywane ze sobą tylko
wtedy, jeżeli próbki i warunki wykonania próby są takie same. W próbach udarności
rezygnuje się z wyznaczenia naprężeń, określa się natomiast pracę zniszczenia próbki.
Takie podejście podyktowane jest po pierwsze trudnością i małą dokładnością
ewentualnego pomiaru siły, a po drugie tym, że stan naprężenia w próbce obciążonej
statycznie jest zupełnie inny niż przy obciążeniu udarowym. W tym ostatnim przypadku
naprężenia i odkształcenia rozchodzą się z miejsca przyłożenia siły z określoną
prędkością tworząc fale naprężeń i odkształceń. Udarność nie jest więc wskaźnikiem
charakteryzującym własności wytrzymałościowe materiału. Rolę taką może spełniać co
najwyżej w znaczeniu umownym.
Po złamaniu próbki analizie poddaje się również jej przełom. Między wartością pracy
złamania a rodzajem przełomu istnieje pewna zależność dlatego też obserwacje
przełomów uzupełniają wyniki próby i dostarczają szereg dodatkowych informacji.
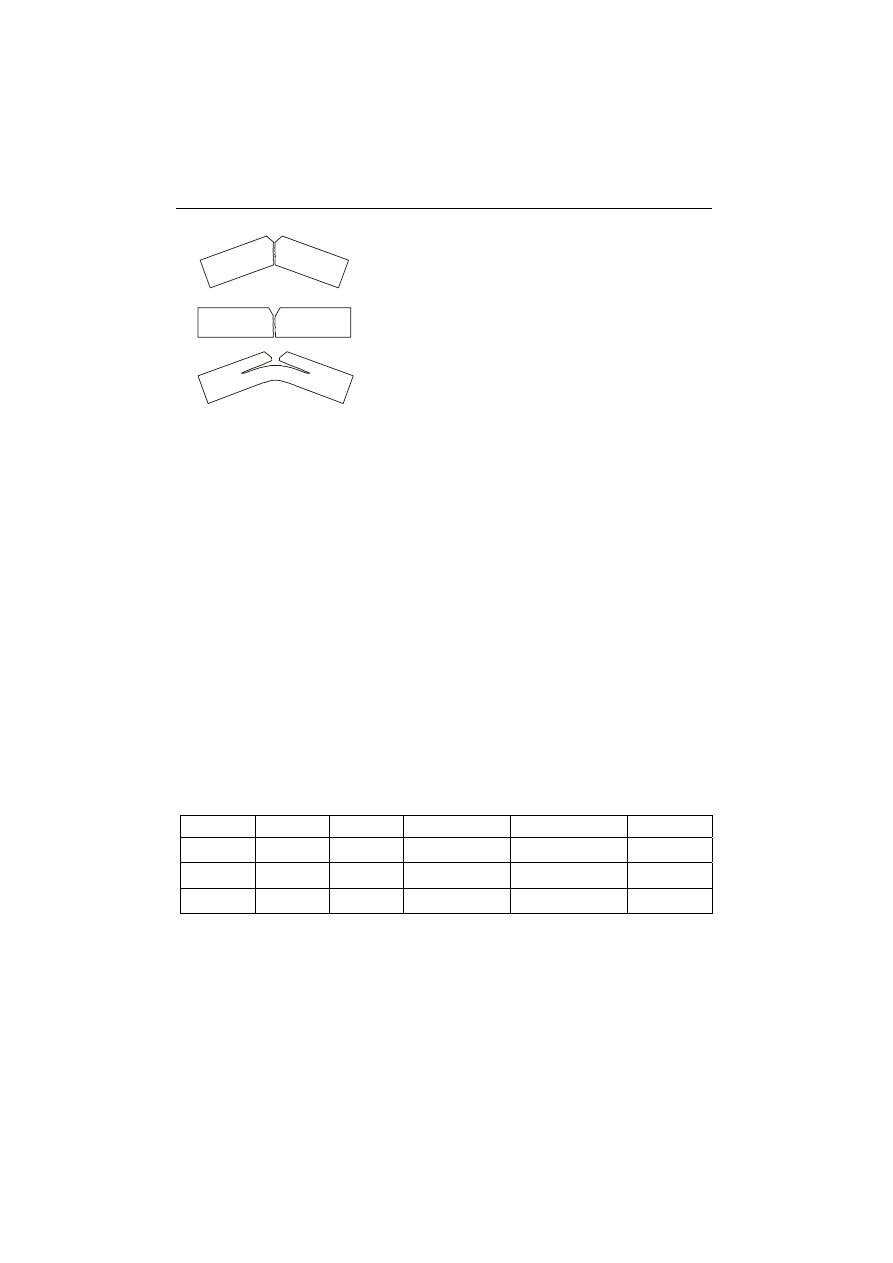
Rozróżnia się trzy charakterystyczne rodzaje przełomów (rys. 4.4):
◊ przełom poślizgowy - próbka została zgięta, pęknięcie nastąpiło po przekroczeniu

granicy plastyczności, to jest przy znacznych odkształceniach trwałych,

◊ przełom kruchy - próbka pękła bez widocznego odkształcenia plastycznego,

◊ przełom z rozwarstwieniem - wskazuje na duży stopień anizotropowości materiału

spowodowany obróbką plastyczną, lub na obecność jednego lub więcej pasm
zanieczyszczeń.

Na rodzaj przełomu wpływają oprócz własności materiału także kształt i wymiary karbu.
Jeżeli przełom na bocznej powierzchni próbki przebiega linią łamaną lub wykazuje
pęknięcia hartownicze, próbę należy uznać za nieważną i powtórzyć ją na próbce
zastępczej.

Metody Doświadczalne w Analizie Konstrukcji

19

Rys. 4.4.

a)

b)

c)

Przełomy próbek:
a) poślizgowy,
b) kruchy,

c) z

rozwarstwieniem.

Jeżeli próbka nie została przełamana, lecz przeszła przez podpory należy zanotować
w protokóle „nie złamana”, a otrzymaną wartość udarności należy ująć w nawiasy.
Jeżeli próbka nie została przełamana z powodu dużej udarności materiału
i niewystarczającej energii uderzenia młota, należy w protokóle umieścić uwagę „nie
złamała się” i pod wartością udarności postawić znak „>”.

UWAGA

OD CHWILI ZACZEPIENIA WAHADŁA (MŁOTA) W GÓRNYM POŁOŻENIU,

AŻ DO CHWILI ZATRZYMANIA MŁOTA PRZY POMOCY HAMULCA

NIE WOLNO NACHYLAĆ SIĘ NAD PRÓBKĄ I NALEŻY ZACHOWAĆ

JAK NAJDALEJ IDĄCE ŚRODKI OSTROŻNOŚCI,

GDYŻ UDERZENIE MŁOTEM GROZI ŚMIERCIĄ LUB KALECTWEM.

SPRAWOZDANIE POWINNO ZAWIERAĆ
1. Krótki opis ćwiczenia (cel próby, sposób jej wykonania).
2. Opis próbki (typ próbki, gatunek stali, obróbka cieplna, wymiary) oraz

charakterystykę młota.

3. Odczyt ze skali młota (zapisać) wartość pracy L

u

oraz obliczenie udarności -

umieścić wyniki w tabeli według poniższego wzoru (tabela 4.2).

Tabela 4.2.

Wzór tabeli pomiarowej.

Nr próbki

Materiał

Typ próbki Pole przekroju

S

o

Praca złamania

L

u

Udarność

K

1

2

3

4. Zrobić szkic próbki po badaniu i zanotować uwagi dotyczące przełomu.
5. Dyskusja otrzymanych wyników.

Metody Doświadczalne w Analizie Konstrukcji

20

ĆWICZENIE 5

PRÓBA TWARDOŚCI METALI

Twardość jest miarą odporności materiału przeciw lokalnym odkształceniom trwałym,
powstałym wskutek wciskania w niego drugiego twardszego ciała, zwanego
wgłębnikiem. Wgłębnikiem jest zazwyczaj kulka stalowa bądź stożek lub ostrosłup
diamentowy.
Metody badania twardości można podzielić na statyczne i dynamiczne. Najbardziej
rozpowszechnione są metody statyczne: Brinnella, Rockwella i Vickersa. W metodach
tych twardość materiału określa się w zależności od wartości siły obciążającej wgłębnik
i wielkości odkształcenia trwałego, wywołanego działaniem tej siły. Wybór metody
zależy od twardości badanego materiału oraz od grubości badanego elementu (próbki)
lub badanej warstwy. Z metod dynamicznych stosowane są: metoda skleroskopowa
Shore'a, polegająca na pomiarze wysokości odbicia opuszczonego ciężarka oraz metoda
porównawcza wykonywana za pomocą młotka Poldi.
Do szerokiego rozpowszechnienia pomiarów twardości przyczyniły się nieskom-
plikowane urządzenia służące do badań (twardościomierze), prostota i szybkość
pomiaru, nieniszczący charakter próby oraz możliwość orientacyjnego określenia, na
podstawie wskaźników twardości, innych własności wytrzymałościowych.
Celem ćwiczenia jest zapoznanie się z pomiarem twardości metali metodą Brinella.
Według normy (PN-78/H-04350) w metodzie Brinella jako wgłębniki używane są kulki
stalowe hartowane o znormalizowanych średnicach 10, 5 i 2,5 mm. Twardość Brinella
HB określa stosunek siły P wciskającej wgłębnik do pola A trwałego odcisku, który
w postaci czaszy kulistej utworzy się na powierzchni materiału (rys. 5.l)

⎥⎦

⎤

⎢⎣

⎡

=

2

mm

kG

A

P

HB

. (5.1)

P

d

h

D

Rys. 5.1.

Pomiar twardości metoda Brinella.

Jest to więc średnia wartość ciśnienia obliczonego
w

sposób umowny, po osiągnięciu którego kulka

przestaje się wgłębiać w materiał. Uwzględniając
zależności geometryczne wzór (5.1) można przedstawić
w postaci

⎥⎦

⎤

⎢⎣

⎡

⎥⎦

⎤

⎢⎣

⎡

−

−

=

2

2

2

2

mm

kG

d

D

D

D

P

HB

π

, (5.2)

gdzie: P - siła obciążająca [kG], D - średnica kulki [mm], d - średnica odcisku [mm].
Jeżeli tą samą kulką wykona się w tym samym materiale szereg odcisków, kolejno
zwiększając siłę P i otrzymując coraz większe odciski, to obliczone każdorazowo liczby
twardości HB nie będą jednakowe lecz będą się zmieniały jak na rys. 5.2. Jako wskaźnik
twardości charakteryzujący materiał przyjmuje się maksymalną wartość HB = HB

max

,

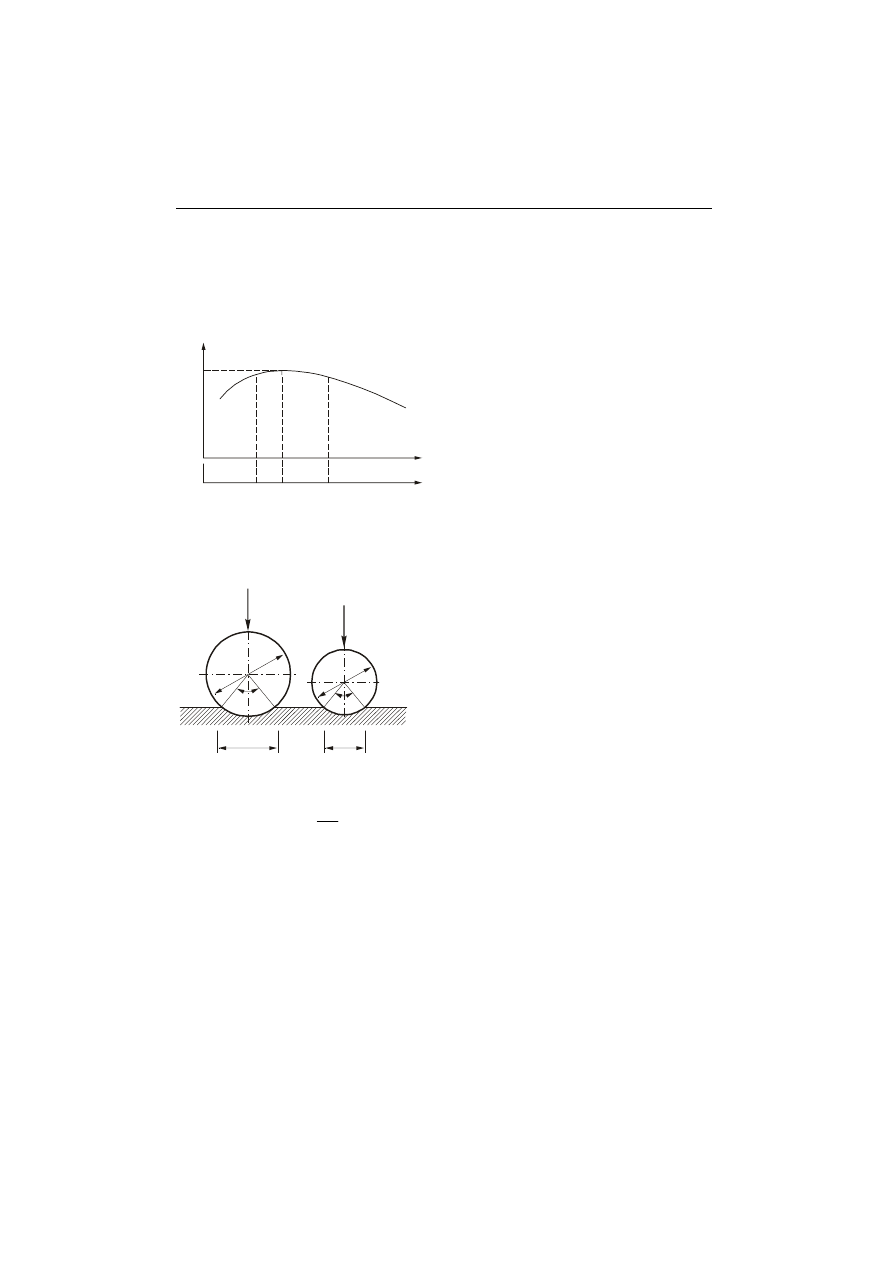
Metody Doświadczalne w Analizie Konstrukcji

21

która wynika z takiego badania. Doświadczenia wykazują, że owo maksimum zachodzi
wtedy, gdy stosunek d/D wynosi w przybliżeniu 0,4. Dopuszczając możliwość odchyłek
liczby twardości od wartości maksymalnej (w granicach błędów pomiarowych),
w normie przyjęto, że średnica odcisków powinna zawierać się w granicach

(5.3)

D

d

D

7

,

0

25

,

0

≤

≤

Rys. 5.2.
Zależność liczby twardości

HB od siły nacisku P

względem rozmiaru odcisku.

W celu uzyskania jednakowych liczb
twardości HB dla tego samego materiału

przy zastosowaniu kulek o różnych średnicach D, należy tak dobrać naciski P dla każdej
kulki, aby wystąpiły jednakowe rozkłady ciśnień na powierzchni odcisku (jednakowe
stany naprężeń w materiale), to znaczy aby zachodziło podobieństwo statyczne prób.
Wówczas odciski będą geometrycznie podobne (rys. 5.3).

HB

P

d/D

0,25 0,4

0,7

HB

max

Rys 5.3.
Odciski kulek o różnych średnicach.

Stwierdzono, że dla danego materiału
otrzymamy tę samą wartość HB, jeżeli
niezależnie od średnicy kulki D, krawędzi
odcisku odpowiada jednakowa wartość kąta
środkowego (kąt wciskania). Powierzchnie

odcisku mają wtedy kształt geometrycznie podobny. Warunkowi temu

ϕ = const

odpowiada spełnienie równości

P

P

ϕ

ϕ

d

d

1

2

1

2

D

D

1

2

2

2

const

kD

P

k

D

P

i

i

=

⇔

=

≡

=

ϕ

(5.4)

Z warunku porównywalności prób (5.4) wynika, że należy tak dobierać wartości nacisku
P dla różnych kulek, aby był zachowany stały współczynnik k (współczynnik
porównywalności). Wartości k dla różnych materiałów należy z kolei dobrać tak, aby
średnica d odcisku spełniała warunek (5.3). Według normy metale techniczne zostały
podzielone na cztery grupy o kolejnych zakresach twardości. Wartości k dla tych grup
podano w tabeli 5.1.
Znormalizowany jest także nominalny czas działania obciążenia, a mianowicie:
◊

10

÷15 s

− stal i żeliwo o HB > 100,

◊

30 s

− materiały o

100

32

≤

≤ HB

,

◊

60 s

− materiały o

HB < 32.

Metody Doświadczalne w Analizie Konstrukcji

22

Tabela 5.1.

Wartości współczynnika k dla różnych materiałów.

Rodzaj materiału

k

Stal, żeliwo lub inne o twardości ponad 100 HB 30
Mosiądz, brąz, duraluminium lub inne o twardości

100

60

≤

≤ HB

10

Miedź, aluminium lub inne o twardości

60

20

≤

≤ HB

5

Stopy łożyskowe lub inne o twardości poniżej 20 HB 2,5

Pole odcisku określa się na podstawie pomiarów średnicy d odcisku, a następnie oblicza
się liczbę twardości z wzoru (5.2) względnie odczytuje się ją ze specjalnych tablic.
Norma określa ponadto w szczegółowych zaleceniach dobór średnicy kulki w zależności
od rozmiarów próbki, minimalne odstępy między sąsiednimi odciskami, dopuszczalną
krzywiznę powierzchni próbki itp.
Między twardością HB w stopniach Brinella a wytrzymałością na rozciąganie R

m

w

kG/mm

2

istnieją pewne zależności. Na podstawie licznych badań ustalono:

◊

dla stali o twardości

175

125

≤

≤ HB

D

R

m

= 0,34 HB,

◊

dla stali o twardości HB > 175

R

m

= 0,36 HB,

◊

dla aluminium (odlewanego)

R

m

= 0,26 HB,

Należy zaznaczyć, że wyznaczone wytrzymałości R

m

mogą być traktowane tylko jako

wielkości orientacyjne.

SPRAWOZDANIE POWINNO ZAWIERAĆ
1. Krótki opis ćwiczenia (cel próby, sposób jej wykonania).
2. Zapisane w tabeli 5.2 dane dotyczące próbki oraz warunków próby.
3. Wyniki pomiarów przekątnych wykonanych odcisków. Średnicę odcisków mierzy

się w dwóch prostopadłych do siebie kierunkach za pomocą specjalnej lupy z
podziałką.

4. Określenie liczby twardości HB za pomocą odpowiednich wzorów - zapisać je

w tabeli 5.2).

5. Dyskusja otrzymanych wyników (miedzy innymi na podstawie zmierzonej

twardości HB należy wyznaczyć orientacyjną wartość R

m

badanych materiałów,

porównać ją z wartością R

m

dla identycznego lub podobnego materiału).

Tabela 5.2.

Wzór tabeli pomiarowej.

Średnica odcisku

Liczba twardości

Materiał

próbki

Średnica

kulki

D

Obcią-

żenie

P

Czas

obciążenia

t

d

1

d

2

d

śr

Zmierzona

średnia

Metody Doświadczalne w Analizie Konstrukcji

23

ĆWICZENIE 6

POMIAR MODUŁU YOUNGA E

ORAZ

WSPÓŁCZYNNIKA POISSONA ν

Próbkę z pleksiglasu należy obciążyć od 0 kG do 200 N przykładając kolejno siły
∆P = 20 N i wykonując dla każdego obciążenia pomiary przyrostu odkształcenia
podłużnego

oraz poprzecznego

(11 pomiarów). Następnie tych samych

pomiarów (

,

) należy dokonać odciążając próbkę od 200 N do 0 kG poprzez

kolejne zdejmowanie sił

∆P = 20 N.

( )

1

x

i

ε

∆

( )

1

y

i

ε

∆

( )

2

x

i

ε

∆

( )

2

y

i

ε

∆

Po założeniu lub zdjęciu kolejnego odważnika pomiary należy wykonywać dopiero po
upływie kilkudziesięciu sekund. Postępując w ten sposób zmniejsza się błędy
wynikające z reologicznych własności pleksiglasu!
W analizie wykorzystujemy przyrosty odkształceń

oraz

obliczone jako

średnie z wartości bezwzględnych uzyskanych w trakcie obciążenia i odciążenia próbki:

( )

śr

x

i

ε

∆

( )

śr

y

i

ε

∆

( )

( )

( )

( )

( )

( )

2

,

2

2

1

2

1

y

i

y

i

śr

y

i

x

i

x

i

śr

x

i

ε

ε

ε

ε

ε

ε

∆

+

∆

=

∆

∆

+

∆

=

∆

. (6.1)

Moduł Younga E oraz współczynnik Poissona

ν należy wyznaczyć analitycznie za

pomocą wzorów podanych niżej.
Wartość modułu Younga obliczoną dla danego przyrostu

określa wzór

( )

śr

x

i

ε

∆

( )

śr

x

i

i

E

ε

σ

∆

∆

=

0

0

(6.2)

w którym przyrost naprężenia

0

σ

∆

jest określony związkiem

A

P

∆

=

∆

0

σ

(A jest

polem przekroju poprzecznego próbki).
Wartość oczekiwana modułu Younga

określa wzór

0

E

∑

=

=

10

1

0

0

10

1

i

i

E

E

. (6.2)

Wariancję modułu Younga

należy wyznaczyć następująco

2

0

E

σ

(

∑

=

−

=

10

1

2

0

0

2

10

1

0

i

i

E

E

E

σ

)

. (6.3)

Ponadto można obliczyć odchylenie standardowe

0

E

σ

2

0

0

E

E

σ

σ

=

. (6.4)

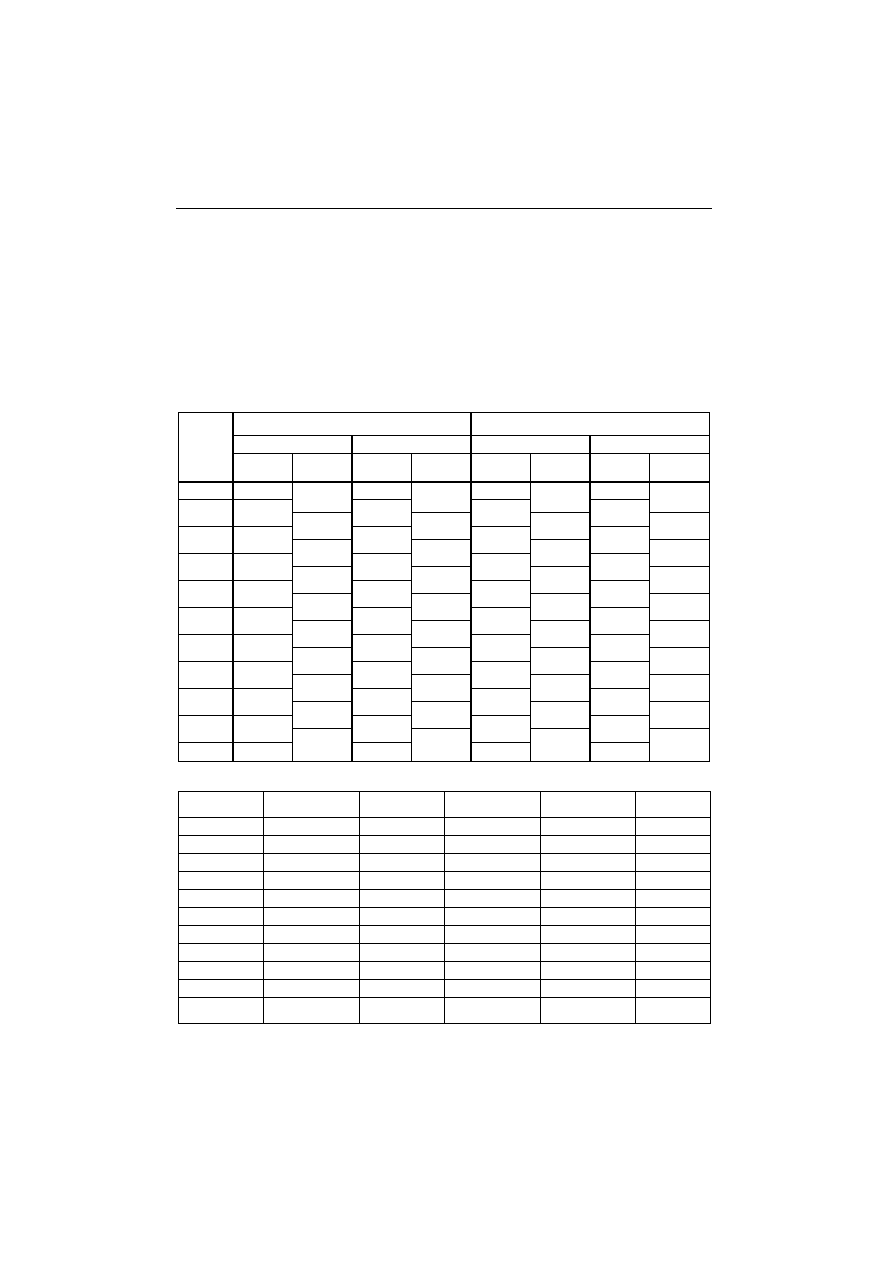
Współczynnik Poissona

ν można wyznaczyć ze wzoru

( )

( )

∑

∑

=

=

∆

=

∆

∆

=

∆

∆

∆

=

10

1

0

10

1

0

0

0

10

1

i

10

1

gdzie

,

i

śr

y

i

y

i

śr

x

i

x

x

y

ε

ε

ε

ε

ε

ε

ν

. (6.7)

Metody Doświadczalne w Analizie Konstrukcji

24

SPRAWOZDANIE POWINNO ZAWIERAĆ
1. Krótki opis doświadczenia.
2. Wyniki pomiarów (tabela 6.1).
3. Wykres

( )

ε

σ

σ

=

.

4. Obliczenia modułu Younga E oraz współczynnika Poissona

ν (tabela 6.2).

5. Histogram rozkładu prawdopodobieństwa modułu Younga E.
6. Uwagi własne, w których m.in. należy dokonać interpretacji uzyskanych wartości

wariancji oraz odchylenia standardowego.

Tabela 6.1.

Wzór tabeli pomiarowej.

Tensometr 1

−

x

ε

∆

Tensometr 2

−

y

ε

∆

Obciążenie Odciążenie Obciążenie Odciążenie

P [N]

Pomiar

( )

1

x

i

ε

∆

Pomiar

( )

2

x

i

ε

∆

Pomiar

( )

1

y

i

ε

∆

Pomiar

( )

2

y

i

ε

∆

0

20

40

60

80

100

120

140

160

180

200

Tabela 6.2.

Wzór tabeli obliczeniowej.

P [N]

( )

śr

x

i

ε

∆

i

E

0

0

0

E

E

i

−

(

)

2

0

0

E

E

i

−

( )

śr

y

i

ε

∆

0

− 20

20

− 40

40

− 60

60

− 80

80

− 100

100

− 120

120

− 140

140

− 160

160

− 180

180

− 200

∑

Metody Doświadczalne w Analizie Konstrukcji

25

ĆWICZENIE 7

TWIERDZENIE BETTI-MAXWELLA

I JEGO WYKORZYSTANIE (cztery doświadczenia)

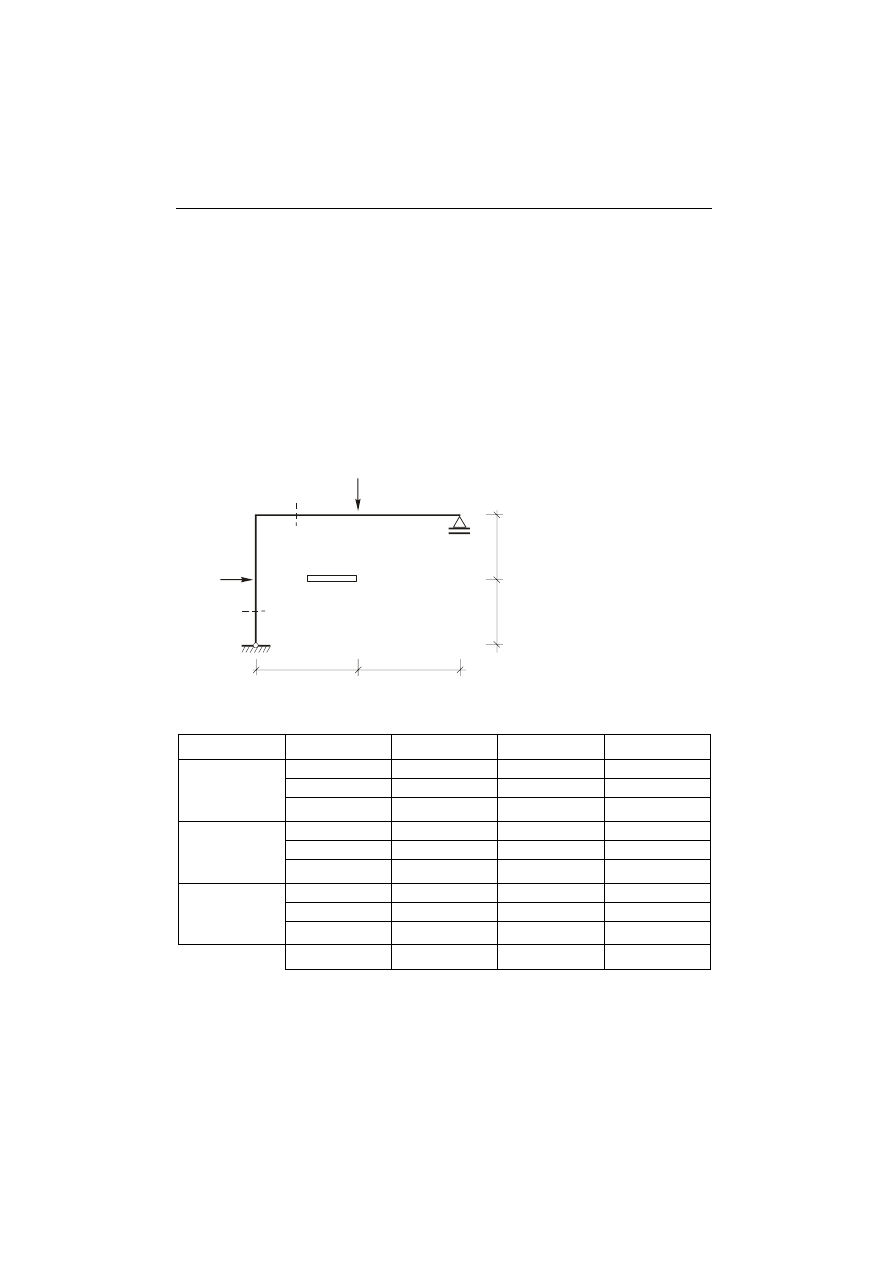
Ćwiczenie wykonuje się dla belki o schemacie statycznym przedstawionym na rys. 7.1.

75

1

2

3

4

5

B

A

6

75

75

75

75

150

75

[mm]

Dane: E = 70 GPa, A = 0,72

×10

−4

m

2

, J = 0,222

×10

−8

m

4

.

Rys. 7.1 Schemat aluminiowej belki o przekroju teowym użytej w doświadczeniu.

DOŚWIADCZENIE 1

POMIAR LINII UGIĘCIA BELKI

1. Dokonać odczytów początkowych (OP) wskazań czujników zegarowych

umieszczonych w punktach od 1 do 6.

2. Belkę obciążyć siłami w punkcie 3 P

3

= 5 kG (49,05 N) oraz w punkcie 6

P

6

= 2 kG (19,6 N).

3. Dokonać odczytów końcowych (OK) wskazań czujników zegarowych.
4. Obliczyć za pomocą wzorów teoretycznych przemieszczenie dwóch dowolnie

wybranych punktów belki.

DOŚWIADCZENIE 2

SPRAWDZENIE TWIERDZENIA O WZAJEMNOŚCI

PRZEMIESZCZEŃ
1. Belkę obciążyć w jednym z punktów i (i = 1, 2, 3, 4, 5) siłą P

i

= 5 kG (49,05 N)

i pomierzyć przemieszczenie w dowolnym punkcie j (j = 1, 2, 3, 4, 5)

−

δ

ij

.

2. Siłę P

j

= 5 kG (49,05 N) ustawić w punkcie j i pomierzyć przemieszczenie

w punkcie i

−

δ

ji

.

UWAGA: nie obciążać belki w punkcie i = 6!
Pomiar wykonać trzy razy i wyliczyć wartości średnie przemieszczeń.
Sprawdzić równość

δ

ij

=

δ

ji

. (7.1)

DOŚWIADCZENIE 3

SPRAWDZENIE TWIERDZENIA BETTI

− MAXWELLA

1. Belkę obciążyć grupą sił I: P

1

= l kG (9,8 N), P

2

= 2 kG (19,6 N), P

3

= 2 kG

(19,6 N) i pomierzyć przemieszczenia w punktach 4, 5, 6 belki.

2. Obciążyć belkę grupą sił II: P

4

= 2 kG (19,6 N), P

5

= 1 kG (9,8 N), P

6

= 1 kG

(9,8 N) i pomierzyć przemieszczenia w punktach 1, 2, 3 belki.

Pomiar wykonać trzy razy.
Sprawdzić równość

, (7.2)

∑

∑

=

=

=

6

1

6

1

i

iII

Ii

j

jI

IIj

P

P

δ

δ

gdzie: P

IIj

(P

Ii

)

− siła z grupy II (I) ustawiona w punkcie j(i),

δ

jI

(

δ

iII

)

− przemieszczenie w punkcie j(i) od grupy sił I (II).

Metody Doświadczalne w Analizie Konstrukcji

26

DOŚWIADCZENIE 4

WYKORZYSTANIE TWIERDZENIA BETTI-MAXWELLA

DO WYZNACZANIA LINII WPŁYWU UGIĘCIA

1. Należy podać rzędne linii wpływu ugięcia dowolnego punktu i (i = 1, 2, 3, 4, 5) od

poruszającej się siły skupionej. W tym celu należy w wybranym punkcie i ustawić
siłę P

i

= 5 kG (49,05 N) i pomierzyć przemieszczenia

δ

ji

punktów j = 1, 2, ... , 6.

UWAGA: nie obciążać belki w punkcie i = 6!
Pomiar powtórzyć trzy razy i wyliczyć wartości średnie przemieszczeń.

2. Na podstawie tych danych wyznaczyć rzędne linii wpływu od poruszającej się siły

skupionej P = 1,0 N. Należy wykonać także obliczenia teoretyczne dwóch
wybranych punktów tej linii.

3. Wykorzystując otrzymane wartości wyliczyć przemieszczenie punktu i dla

obciążenia z Doświadczenia 1. Porównać obie wielkości.

SPRAWOZDANIE POWINNO ZAWIERAĆ
1. Krótki opis poszczególnych doświadczeń.
2. Wyniki pomiarów zapisanych w tabelach według wzoru (tabela 7.1).
3. Rysunki linii ugięcia (Doświadczenie 1) i linii wpływu ugięcia (Doświadczenie 4).
4. Teoretyczne obliczenia linii ugięcia z Doświadczenia 1 i linii wpływu ugięcia z

Doświadczenie 4 (obliczenia należy wykonać dla dwóch wybranych punktów belki).

5. Porównanie wyników doświadczeń z obliczeniami teoretycznymi.
6. Uwagi własne (zgodnie z sugestiami zawartymi we wstępie).

Tabela 7.1.

Wzór tabel pomiarowych.

Nr

punktu

1 2 3 4 5 6

Obciążenie

OP

OK

δ

Metody Doświadczalne w Analizie Konstrukcji

27

ĆWICZENIE 8

BADANIE PRZEMIESZCZEŃ UKŁADÓW

STATYCZNIE WYZNACZALNYCH (dwa doświadczenia)

DOŚWIADCZENIE 1

WYZNACZENIE PRZEMIESZCZEŃ BELKI ZAŁAMANEJ

Wyznaczyć przemieszczenia

δ punktów 1, 2, 3 belki załamanej o schemacie statycznym

podanym na rys. 8.1. W tym celu należy:
1. Przed obciążeniem belki dokonać odczytów początkowych (OP) wskazań czujników

zegarowych umieszczonych w punktach 1, 2, 3.

2. Obciążyć belkę zgodnie ze schematem statycznym i dokonać odczytów końcowych

(OK).

Pomiar należy powtórzyć trzy razy i wyliczyć wartości średnie przemieszczeń.
UWAGA
Wyniki pomiarów są bardzo wrażliwe na wstrząsy!

230,0

230,0

4,6

24,5

wymiary w [mm]

1

2

3

A

B

152,

5

152,

5

P = 1,0 kG

P = 0,5 kG

α

α

α − α

α

α

Rys. 8.1.
Schemat belki załamanej.

Belka wykonana z mosiądzu:
E = 1,25

×10

5

MPa.

Tabela 8.1.

Wzór tabeli pomiarowej

Seria odczytów

Nr punktu

1

2

3

OP

OK

Odczyt I

]

m

[

δ

OP

OK

Odczyt II

]

m

[

δ

OP

OK

Odczyt III

]

m

[

δ

śr

δ

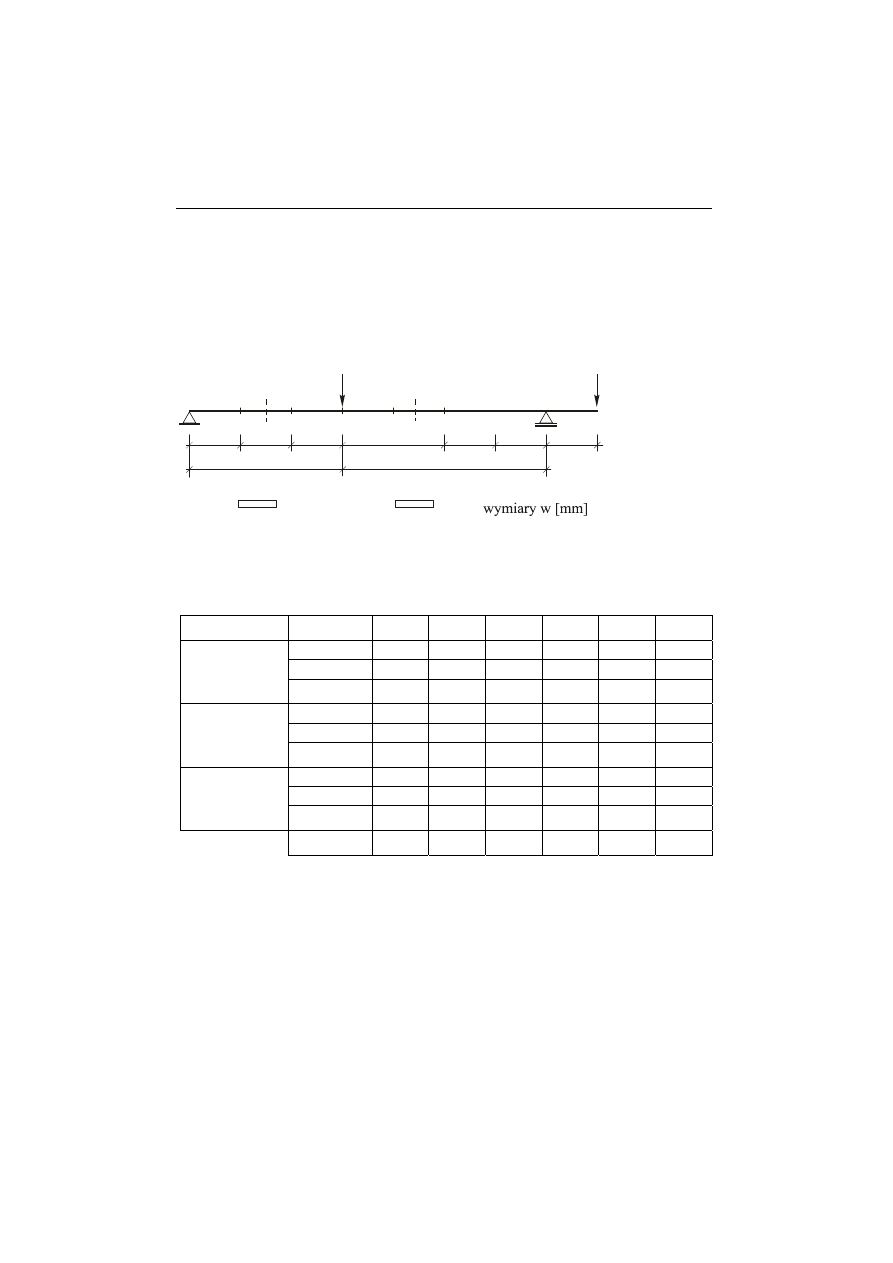
Metody Doświadczalne w Analizie Konstrukcji

28

DOŚWIADCZENIE 2

WYZNACZENIE PRZEMIESZCZEŃ BELKI

O SKOKOWO ZMIENNYM PRZEKROJU

Wyznaczyć rzędne linii ugięcia

δ w punktach 2, 3, 4, 5, 6 belki o schemacie statycznym

podanym na rys.8.2.
Odczyty wskazań czujników zegarowych należy wykonać w identyczny sposób jak
w Doświadczeniu 1.
Pomiar powtórzyć trzy razy i wyliczyć wartości średnie przemieszczeń

δ.

75

8,0

8,0

18,3

10,0

1

2

3

4

5

B

A

6

75

225

300

75

75

75

150

75

F = 5,0 kG

F = 1,0 kG

α

α − α

β − β

β

α

β

Rys.8.2
Schemat belki
wolnopodpartej

Belka wykonana ze stali: E = 210 GPa.


Tabela 8.2.

Wzór tabeli pomiarowej.

Seria

odczytów

Nr

punktu

1 2 3 4 5 6

OP

OK

Odczyt I

]

m

[

δ

OP

OK

Odczyt II

]

m

[

δ

OP

OK

Odczyt III

]

m

[

δ

śr

δ

SPRAWOZDANIE POWINNO ZAWIERAĆ
1. Krótki opis poszczególnych doświadczeń.
2. Wyniki pomiarów wpisane do tabel 8.1, 8.2.
3. Rysunki linii ugięć.
4. Teoretyczne obliczenia przemieszczeń punktów 1, 2, i 3 w doświadczeniu 1 oraz

przemieszczeń dwóch wybranych punktów w doświadczeniu 2.

5. Porównanie wyników doświadczeń z obliczeniami teoretycznymi.
5. Uwagi własne (zgodnie z sugestiami zawartymi we wstępie).

Metody Doświadczalne w Analizie Konstrukcji

29

ĆWICZENIE 9

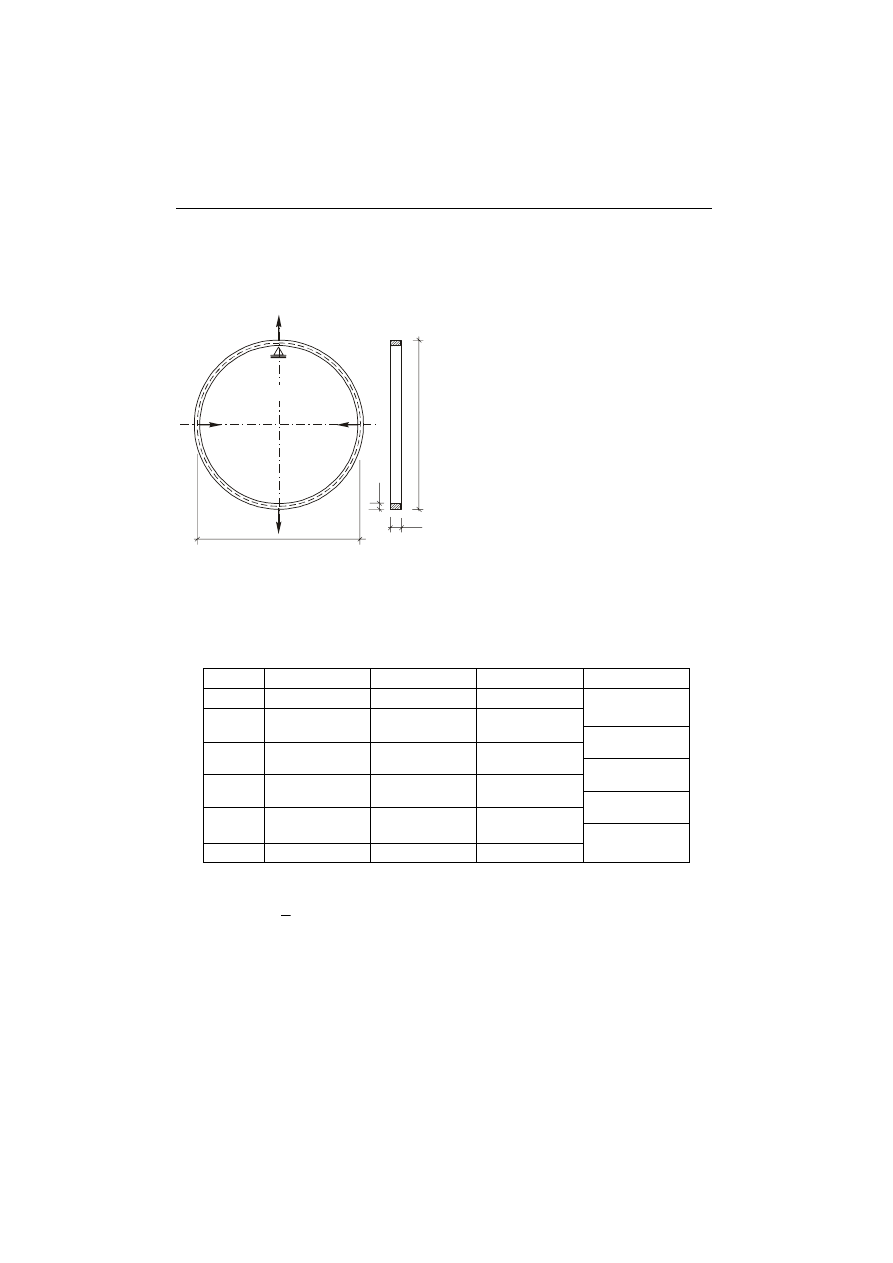
BADANIE PRZEMIESZCZEŃ PIERŚCIENIA KOŁOWEGO

Celem ćwiczenia jest wyznaczenie zmiany długości poziomej

∆ = ∆

1

+

∆

2

średnicy

pierścienia kołowego przedstawionego na rys. 9.1.

153,1

9,8

[mm]

2,

9

156

,0

1

2

R = P

P

∆

∆

2

1

E = 210000 MPa

Rys. 9.1.
Schemat statyczny pierścienia kołowego.

W tym celu należy.
1. Przed obciążeniem pierścienia dokonać
odczytów początkowych wskazań
czujników zegarowych umieszczonych w
punktach 1, 2.
2. Obciążyć pierścień kolejno siłami
P = 2 kG (19,6 N), 4 kG (39,2 N), 6 kG
(58,8 N), 8 kG (78,4 N), 10 kG (98,0 N) za
każdym razem dokonując odczytów
czujników zegarowych.

UWAGA: pierwsze obciążenie siłą 2 kG (19,6 N) uzyskuje się po opuszczeniu szalki
na pierścień.

3. Wyniki pomiarów i obliczeń wpisać do tabeli pomiarowej (tabela 9.1).

Tabela 9.1.

Wzór tabeli pomiarowej.

LP Obciążenie

Czujnik 1

Czujnik 2

Zmiana

∆

1 0

kG

2 2

kG

3

4 kG

4 6

kG

5 8

kG

6 10

kG

Średnią zmianę poziomej średnicy pierścienia należy obliczyć z następującego wzoru

∑

=

∆

=

∆

5

1

5

1

i

i

śr

, (9.1)

SPRAWOZDANIE POWINNO ZAWIERAĆ
1. Krótki opis poszczególnych doświadczeń.
2. Wyniki pomiarów wpisane do tabeli 9.1.
3. Teoretyczne obliczenia zmiany długości poziomej średnicy pierścienia

∆.

4. Uwagi własne (zgodnie z sugestiami zawartymi we wstępie).

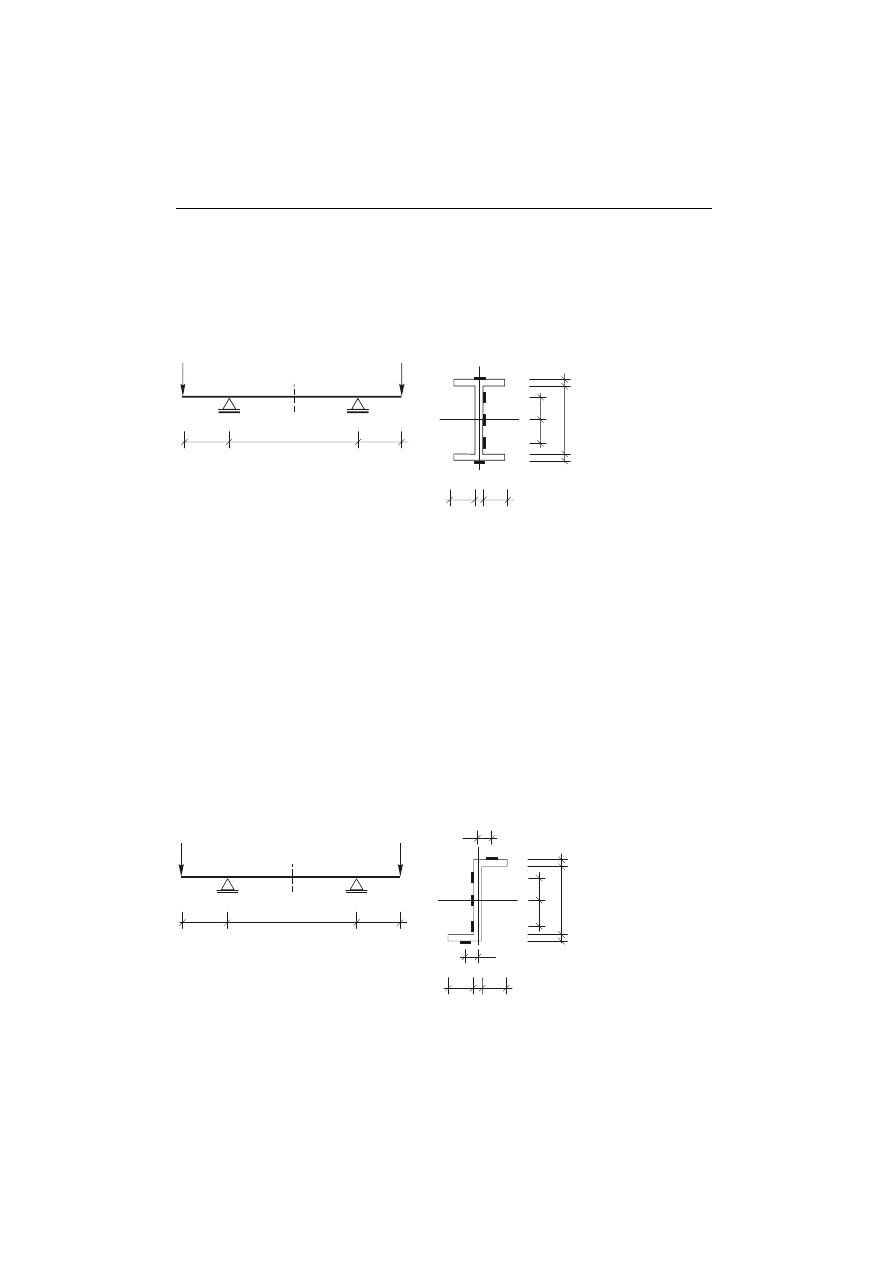
Metody Doświadczalne w Analizie Konstrukcji

30

ĆWICZENIE 10 WYZNCZENIE ODKSZTAŁCEŃ

W BELKACH ZGINANYCH (dwa doświadczenia)

DOŚWIADCZENIE 1

POMIAR ODKSZTAŁCEŃ

W BELCE PODDANEJ ZGINANIU PROSTEMU

W belce o schemacie statycznym przedstawionym na rys. 10.1 pomierzyć odkształcenia
w przekroju

α − α za pomocą tensometrów elektrooporowych.

P = 5 kG

P = 5 kG

T1

T2

T3
T4

T5

x

y

α

α− α

α

150

150

wymiary w [mm]

8

8

32

4

13

13

4

4

Rys. 10.1.
Schemat statyczny
belki

Moduł Younga dla pleksiglasu E = 2900 MPa.

W tym celu należy.
1. Przed obciążeniem belki dokonać odczytów początkowych odkształceń (OP).
2. Obciążyć belkę zgodnie ze schematem statycznym i dokonać odczytów końcowych

odkształceń (OK).

Pomiar powtórzyć trzy razy i wyliczyć wartości średnie odkształceń.
UWAGA
Po przyłożeniu lub zdjęciu obciążenia odczyt należy dokonać dopiero po upływie
kilkudziesięciu sekund. Postępując w ten sposób zmniejsza się błędy wynikające
z reologicznych własności pleksiglasu!


DOŚWIADCZENIE 2

POMIAR ODKSZTAŁCEŃ

W BELCE PODDANEJ ZGINANIU UKOŚNEMU

Doświadczenie 2 należy wykonać analogicznie jak Doświadczenie 1.

P = 2 kG

P = 2 kG

T6

T7

T8
T9

T10

x

y

α

α−α

α

150

150

8

4

4

8

13
13

32

4

4

4

wymiary w [mm]

Rys. 10.2.
Schemat statyczny
belki

Moduł Younga dla pleksiglasu E = 2900 MPa.

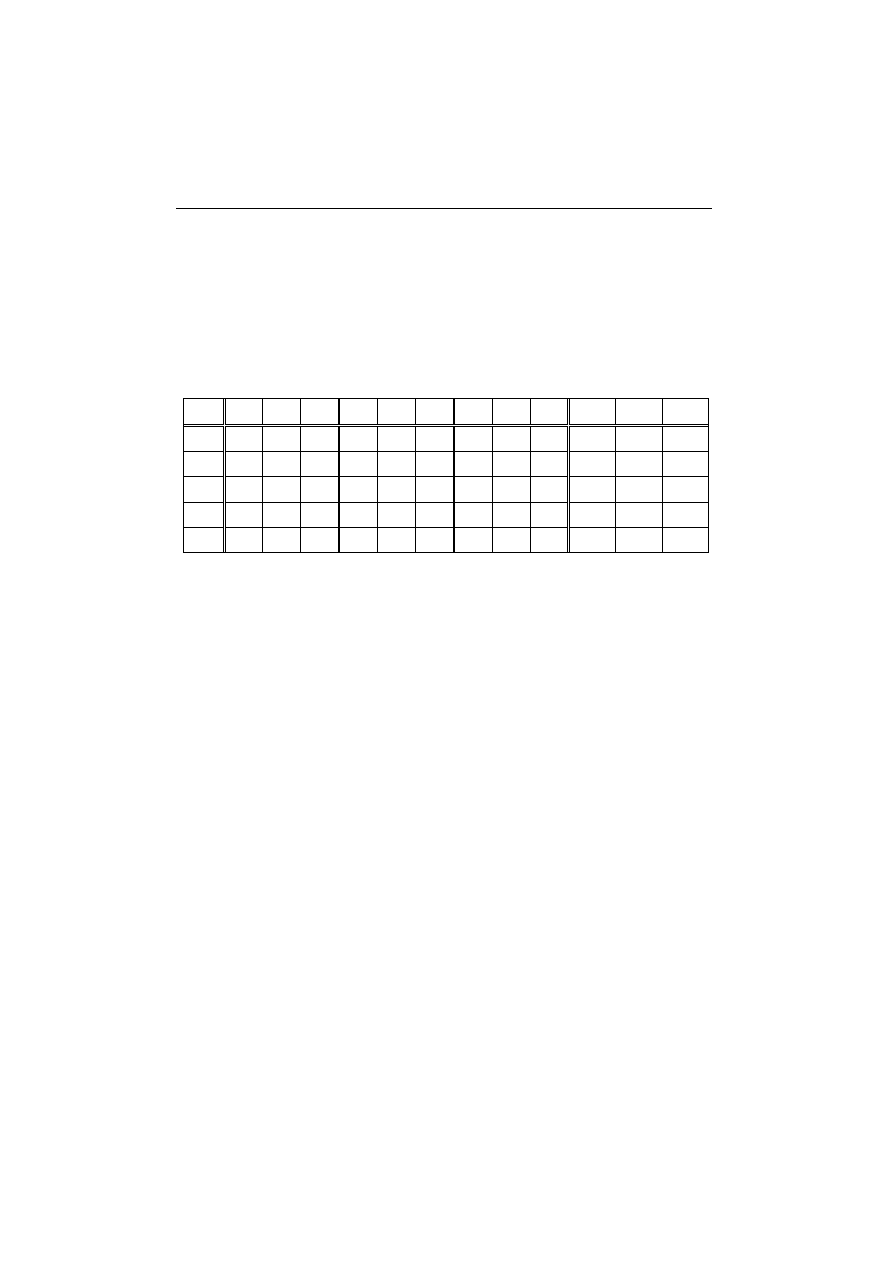
Metody Doświadczalne w Analizie Konstrukcji

31

SPRAWOZDANIE POWINNO ZAWIERAĆ
1. Krótki opis poszczególnych doświadczeń.
2. Wyniki pomiarów wpisane do tabeli 10.1 oraz wykresy pomierzonych odkształceń.
3. Teoretyczne obliczenia wszystkich poszukiwanych odkształceń.
4. Porównanie wyników doświadczeń z obliczeniami teoretycznymi.
5. Uwagi własne (zgodnie z sugestiami zawartymi we wstępie).

Tabela 10.1.

Wzór tabeli pomiarowej.

Punkt OP OK

ε

OP OK

ε

OP OK

ε

ε

śr

ε

obl

Błąd

1

2

3

4

5

Metody Doświadczalne w Analizie Konstrukcji

32

ĆWICZENIE 11 WYZNACZANIE LINII WPŁYWU BELEK CIĄGŁYCH
(trzy

doświadczenia)

Ćwiczenie wykonuje się dla belki o schemacie statycznym przedstawionej na rys. 11.1.

Rys. 11.1

400

1200

D

C

B

A

200

200

400

[mm]

Schemat statyczny belki.

E = 125 GPa,
A = 0,432

⋅10

−4

m

2

J = 0,00117

⋅10

−8

m

4

.

UWAGA przed

rozpoczęciem ćwiczenia należy zaopatrzyć się w papier milimetrowy

(3 kartki formatu A4).

DOŚWIADCZENIE 1

WYZNACZENIE LINII WPŁYWU REAKCJI R

A

1. Umieścić papier milimetrowy między podporami belki ciągłej.
2. Na papierze, za pomocą ołówka odrysować oś belki w jej początkowym położeniu.
3. Obniżyć podporę A o 40 mm.
4. Dokręcić śrubę umieszczoną w punkcie A belki w taki sposób, aby model

odpowiadał przyjętemu schematowi statycznemu (podpora A jest całkowicie
zamocowana).

5. Odrysować odkształconą oś belki.
6. Dokonać pomiarów otrzymanych linii ugięć co 1/5 rozpiętości poszczególnych

przęseł. Na podstawie tych danych obliczyć rzędne linii wpływu reakcji R

A

oraz

wykonać jej rysunek.

DOŚWIADCZENIE 2

WYZNACZENIE LINII WPŁYWU REAKCJI R

B

Doświadczenie 2 należy wykonać w podobny sposób jak Doświadczenie 1.
UWAGA konstrukcja podpory B umożliwia jej opuszczenie o 35 mm.

DOŚWIADCZENIE 3

WYZNACZENIE LINII WPŁYWU

MOMENTU

ZGINAJĄCEGO M

α

1. Przekrój

α − α przemieścić w dół do takiego położenia, aby tangens kąta miedzy

przekrojami poprzecznymi belki po stronie lewej i prawej wynosił tg(

∆

φ

α

) = 0,5

(kąt w przekroju

α − α należy sprawdzić według załączonego szablonu).

2. Odrysować na papierze milimetrowym osie belek przed i po przemieszczeniu oraz

dokonać pomiaru linii ugięcia co 1/5 rozpiętości poszczególnych przęseł.

3. Na podstawie tych danych obliczyć rzędne linii wpływu momentu M

α

i wykonać jej

rysunek.

SPRAWOZDANIE POWINNO ZAWIERAĆ
1. Krótki opis poszczególnych doświadczeń.
2. Rysunki otrzymanych linii wpływu.
3. Analityczne obliczenia jednej wartości rzędnej z każdej linii wpływu i jej

porównanie z wynikami doświadczalnymi.

4. Uwagi własne (zgodnie z sugestiami zawartymi we wstępie).

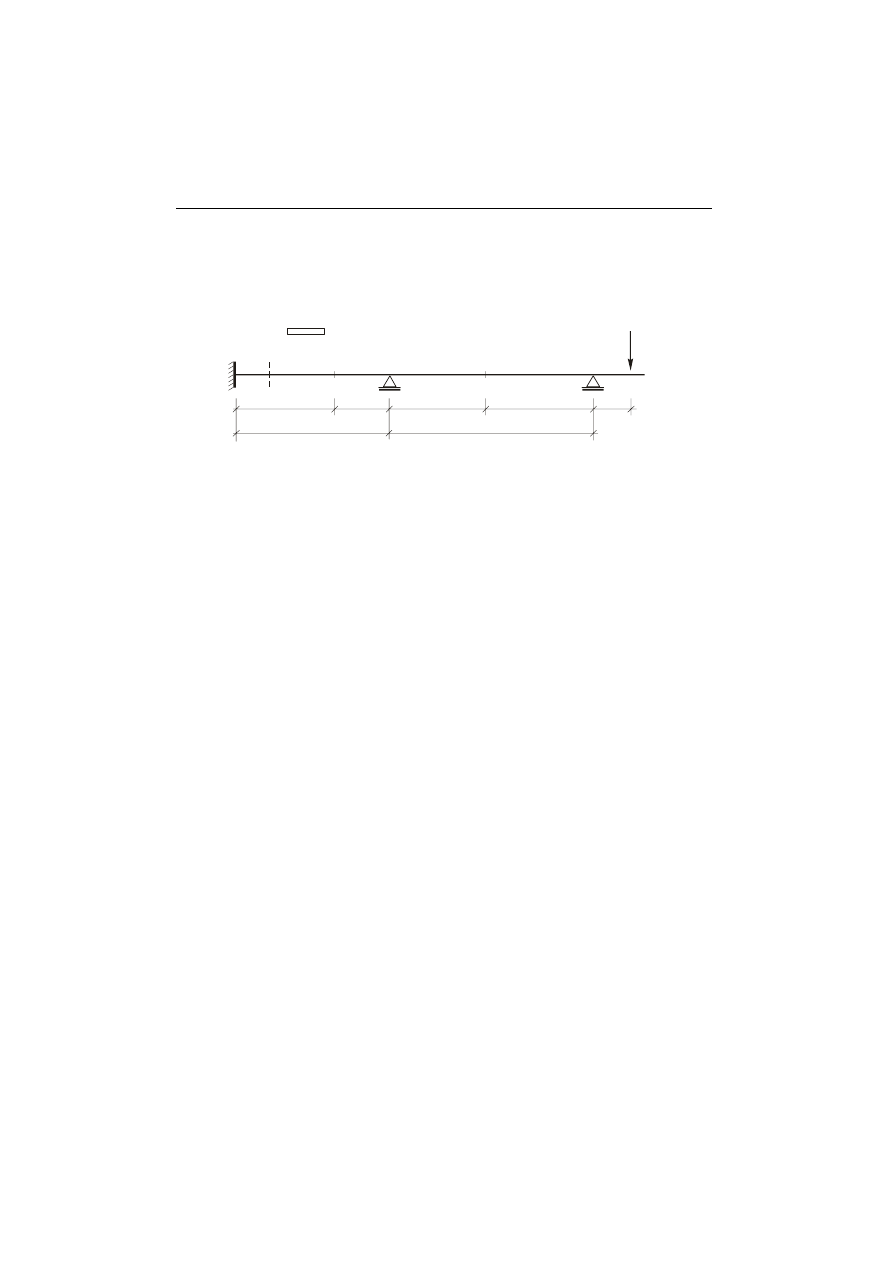
Metody Doświadczalne w Analizie Konstrukcji

33

ĆWICZENIE 12 WYZNACZENIE REAKCJI PODPOROWEJ
BELKI

CIĄGŁEJ (dwa doświadczenia)

Ćwiczenie wykonuje się dla belki o schemacie przedstawionym na rysunku 12.1,

290

4,5

29,0

A

B

C

D

E

440

440

150

225

215

x

[mm]

P = 1,0 kG

α − α

α

α

F

Belka wykonana jest z aluminium: E = 70 GPa.

Rys. 12.1 Schemat belki użytej w doświadczeniu

Konstrukcja belki pozwala na przyjęcie dwóch różnych modeli:
1. belka

ciągła z trzema podporami w punktach: A, C i E,

2. belka

ciągła z dwiema podporami w punktach A i E.

Zmianę schematu statycznego umożliwia ruchoma podpora w punkcie C. Jej
umieszczenie lub usunięcie dokonuje się za pomocą odpowiedniego przemieszczenia
dźwigni.


DOŚWIADCZENIE 1

WYZNACZENIE WARTOŚCI REAKCJI PODPOROWEJ

1. Przyjąć model 1 belki (z podporą w punkcie C).
2. Obciążyć belkę siłą P = 1 kG (9,8 N) w dowolnie wybranym punkcie F (w

odległości x od podpory E) i odczytać wskazania czujnika w punkcie C (odczyt
początkowy).
UWAGA
Rysy określające położenie punktu F zaznaczono w odległości od 17 cm do 25 cm od
podpory E, co 1 cm.

3. Zdjąć obciążenie.
4. Przyjąć model 2 belki (bez podpory w punkcie C) i ponownie przyłożyć siłę

P = 1 kG (9,8 N) w punkcie F. Odczytać wskazania czujnika w punkcie C (odczyt
końcowy).

5. W miejscu podpory C umieścić szalkę i przez dosypywanie śrutu sprowadzić punkt

C do położenia wyjściowego wyznaczonego odczytem początkowym. Ciężar
zawieszony w punkcie C (szalka wraz ze śrutem) umożliwi wyznaczenie wartości
reakcji podporowej R

C

.

6. Dodatkowo, należy obliczyć przemieszczeni punktu C w modelu 2 belki (bez

podpory w punkcie C) i porównać z wynikiem doświadczalnym.

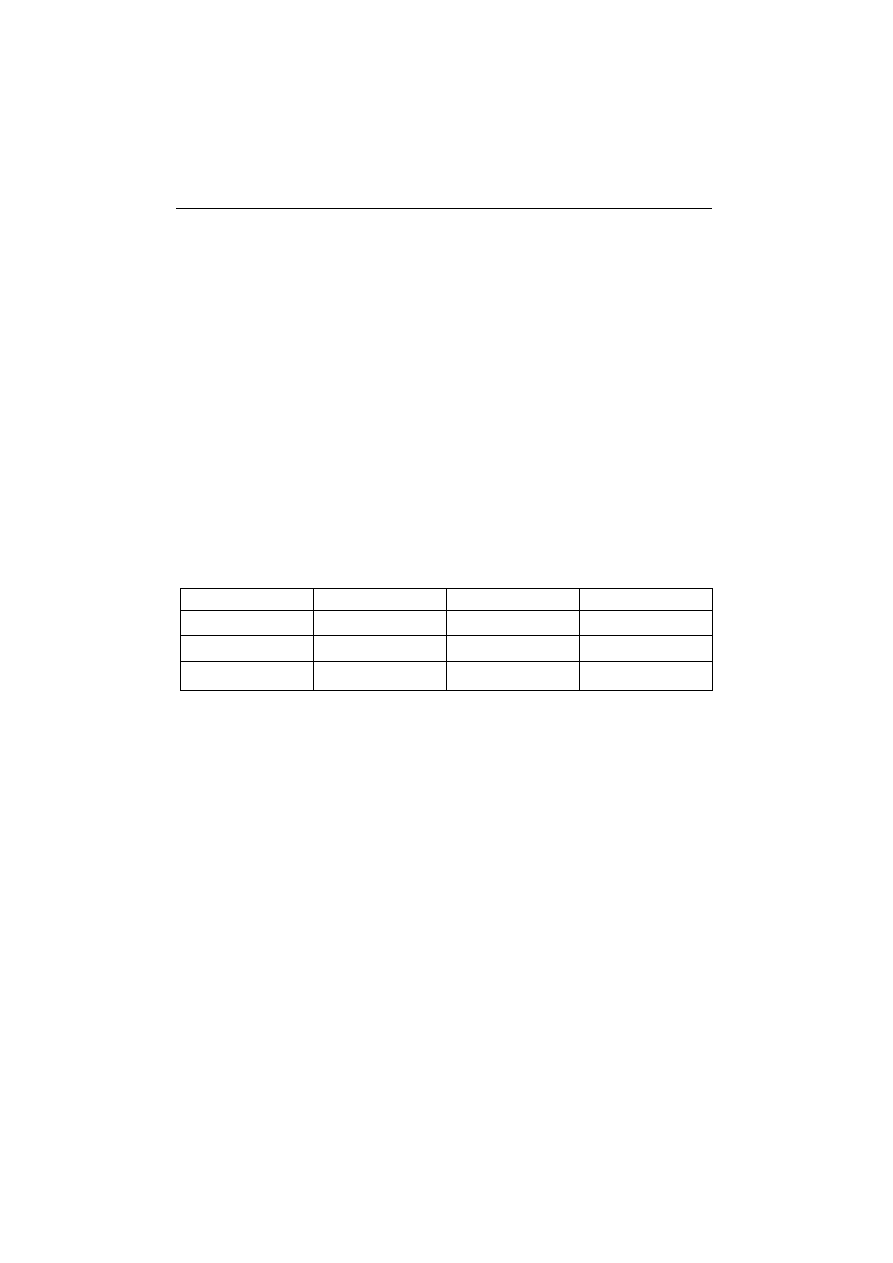
Metody Doświadczalne w Analizie Konstrukcji

34

DOŚWIADCZENIE 2

WYZNACZENIE PRZEMIESZCZEŃ PUNKTÓW B I D

BELKI

CIĄGŁEJ

1. Przyjąć model 1 belki (z podporą w punkcie C).
2. Odczytać wskazania początkowe czujników zegarowych umieszczonych w punktach

B i D (odczyt początkowy). Należy zwrócić uwagę, aby w czasie odczytu belka
w punkcie C opierała się na podporze!

3. Obciążyć belkę w dowolnie wybranym punkcie F (położenie punktu opisuje

współrzędna x – rys. 12.1) i ponownie odczytać wskazania czujników w punktach B
i D (odczyt końcowy).

SPRAWOZDANIE POWINNO ZAWIERAĆ
1. Krótki opis poszczególnych doświadczeń.
2. Wyniki pomiarów wpisane do tabeli 12.1.
3. Teoretyczne obliczenia wartości reakcji R

C

oraz przemieszczeń punktów B, C i D.

4. Rysunek linii ugięcia belki z Doświadczenia nr 2 (na podstawie pomiarów).
5. Porównanie wyników doświadczeń z obliczeniami teoretycznymi.
6. Uwagi własne (zgodnie z sugestiami zawartymi we wstępie).

Tabela 12.1.

Wzór tabeli pomiarowej.

Punkt

B C D

Odczyt początkowy

Odczyt końcowy

]

m

[

δ

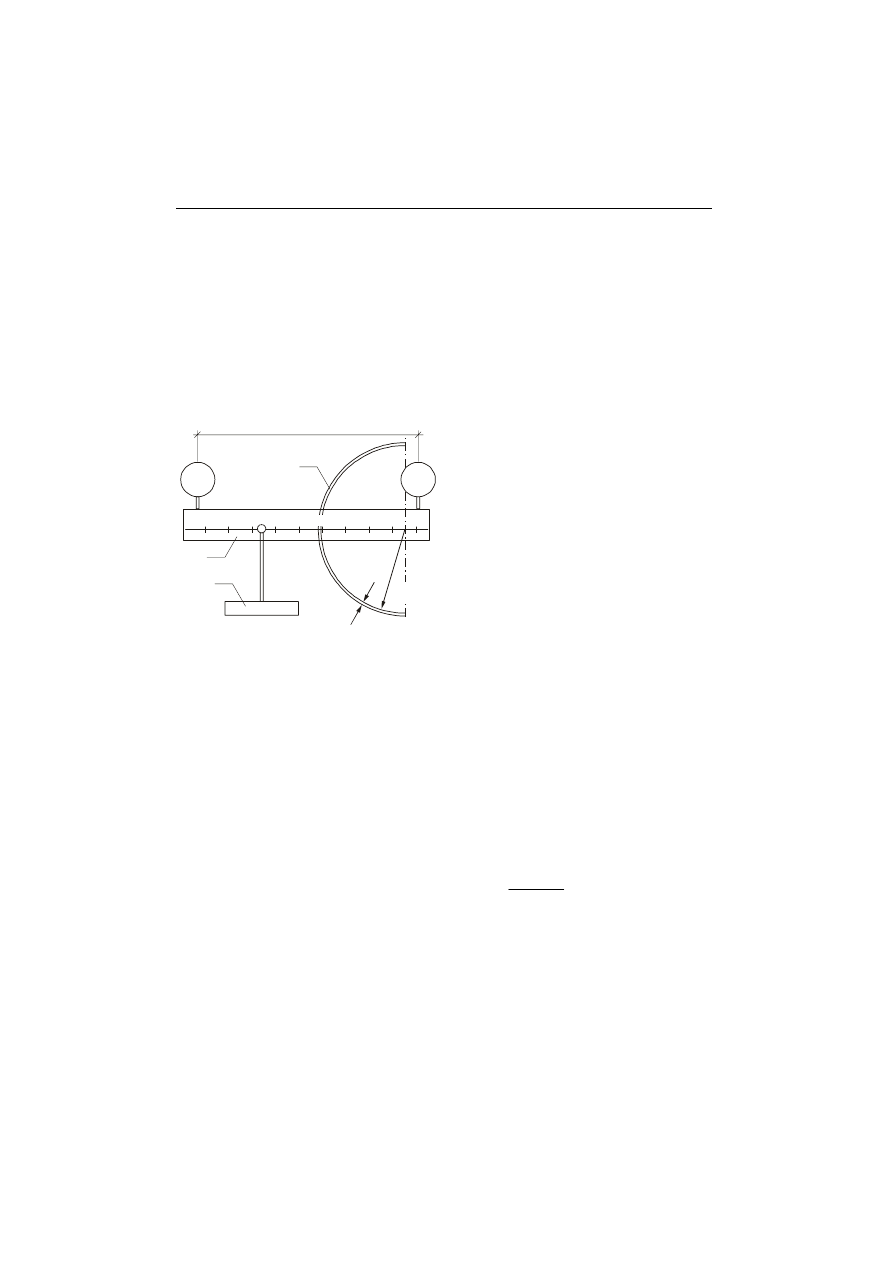
Metody Doświadczalne w Analizie Konstrukcji

35

ĆWICZENIE 13 WYZNACZENIE ŚRODKA ZGINANIA
(dwa

doświadczenia)

Celem ćwiczenia jest wyznaczenie środka zginania (lub ścinania) dwóch
cienkościennych belek wspornikowych.

DOŚWIADCZENIE 1

WYZNACZENIE ŚRODKA ZGINANIA

BELKI O PRZEKROJU RUROWYM

Wymiary przekroju poprzecznego belki oraz położenie przyrządów pomiarowych
przedstawiono na rysunku 13.1.

−4,0

2

4

5

L

a = 20,0

Rys. 13.1

Położenie przyrządów pomiarowych:

1 - belka (1/2 rury),

2 - ruchoma szalka z odważnikami

przymocowana do czoła belki,

3 - miarka przymocowana do czoła

belki umożliwiająca określenie

położenia szalki,

4, 5 - czujniki zegarowe umoż-

liwiające pomiar kąta skręcenia

belki.

P

[cm]

1

3

−3,0 −2,0 −1,0 0,0

2,0 3,0 4,0 5,0

1,0

R = 3,92

δ = 0,27

1. Ustawić szalkę 2 nie obciążoną odważnikami w punkcie zerowym (wg miarki 3).
2. Dokonać odczytów początkowych czujników zegarowych lewego

4

−

i prawego 5

−

.

1

L

f

1

P

f

3. Obciążyć szalkę odważnikami.
4. Przesuwać szalkę w przedziale

±40 mm i notować wskazania czujników

zegarowych f

L

i f

P

co 10 mm.

5. Zdjąć odważniki.
6. Ponownie

ustawić szalkę w punkcie zerowym i dokonać odczytów początkowych

czujników zegarowych

i

.

2

L

f

2

P

f

7. Obliczyć średnie odczyty początkowe

(

)

2

1

0

5

,

0

L

L

L

f

f

f

+

×

=

i

.

(

)

2

1

0

5

,

0

P

P

P

f

f

f

+

×

=

8. Obliczyć ugięcia punktów u

L

i u

P

oraz kąty skręcenia belki

φ :

,

,

0

L

L

L

f

f

u

−

=

0

P

P

P

f

f

u

−

=

(

)

a

u

u

P

L

−

=

φ

.

9. Wyniki

obliczeń umieścić w tabeli 13.1.

10. Narysować wykresy ugięć u

L

i u

P

w funkcji położenia szalki (siły P).

Przykładowy wykres przedstawiono obok na rys. 13.2.

11. Określić położenie e

c

środka zginania z wykresu. Przecięcie się linii ugięcia u

L

i u

P

oznacza, że wskazania obu czujników są jednakowe. Punkt A jest więc

środkiem zginania.

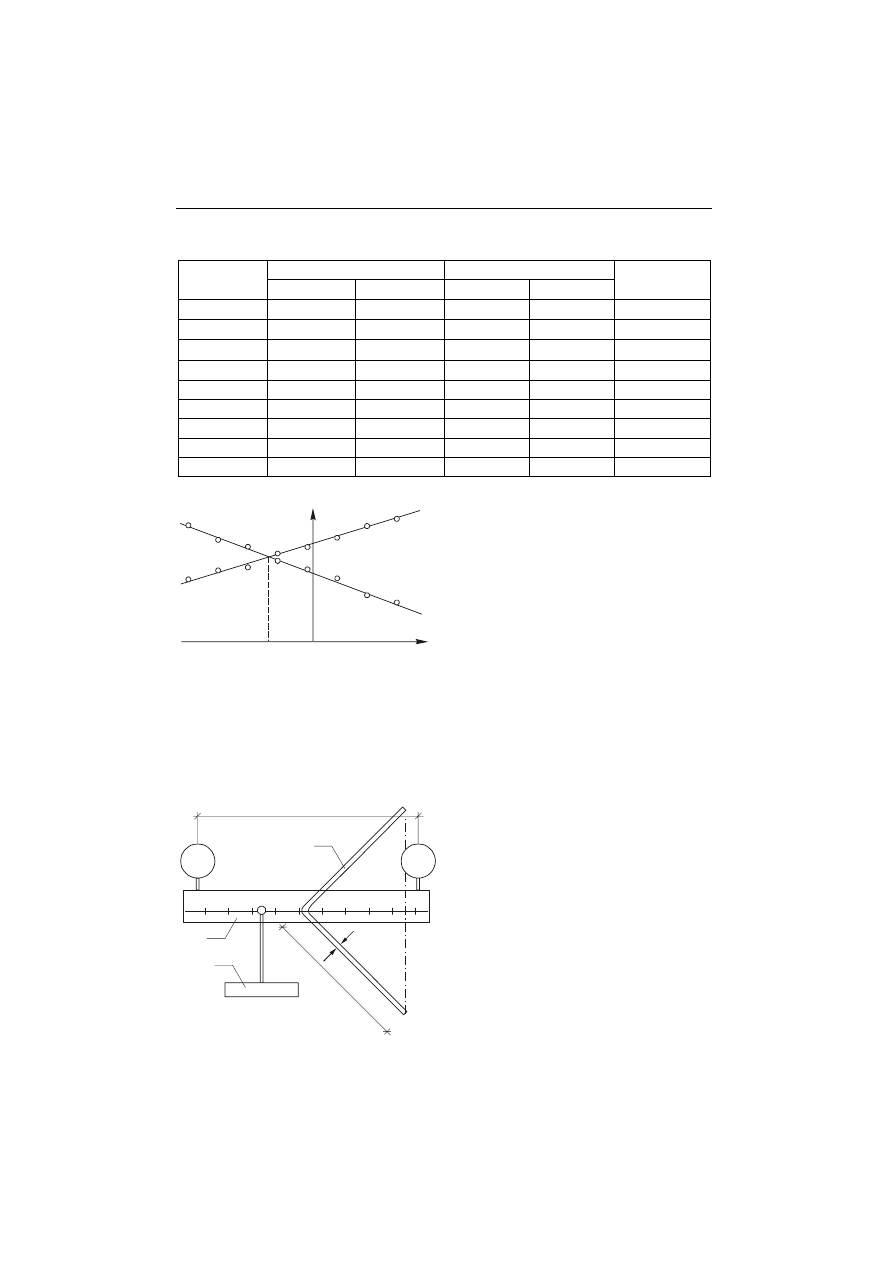
Metody Doświadczalne w Analizie Konstrukcji

36

Tabela 13.1.

Wzór tabeli pomiarowej.

Wskazania czujników

Ugięcie punktów

Położenie siły

[mm]

Lewego

f

L

Prawego

f

P

Lewego

u

L

Prawego

u

P

Kąt skręcenia

φ

−40

−30

−20

−10

0

10

20

30

40

u , u

e

O

x

u

u

A

L

c

L

P

P

Rys. 13.2.
Przykładowy wykres umożliwiający
wyznaczenie położenia środka zginania

DOŚWIADCZENIE 2

WYZNACZENIE ŚRODKA ZGINANIA

BELKI O PRZEKROJU KĄTOWYM

Wymiary przekroju poprzecznego belki oraz położenie przyrządów pomiarowych
przedstawiono na rysunku 13.3.
Doświadczenie 2 należy wykonać w podobny sposób jak Doświadczenie 1.

−4,0

2

4

5

L

a = 20,0

Rys. 13.3

Położenie przyrządów pomiarowych

1 - belka (kątownik),

2 - ruchoma szalka z odważnikami

przymocowana do czoła belki,

3 - miarka przymocowana do czoła

belki umożliwiająca określenie

położenia szalki,

4, 5 - czujniki zegarowe umoż-

liwiające pomiar kąta skręcenia

belki.

P

[cm]

1

3

−3,0 −2,0 −1,0 0,0

2,0 3,0 4,0 5,0

1,0

b =

7,5

δ = 0,35

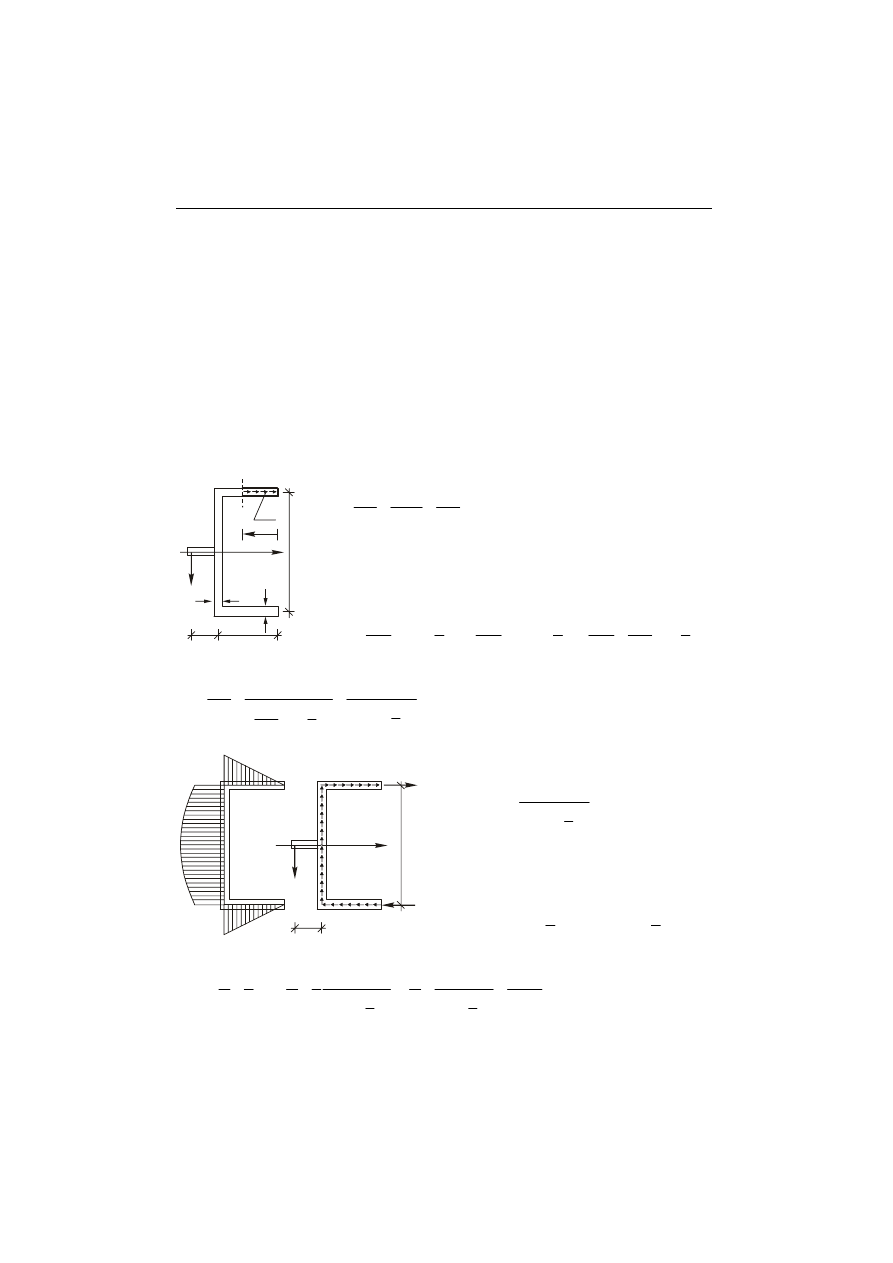
Metody Doświadczalne w Analizie Konstrukcji

37

SPRAWOZDANIE POWINNO ZAWIERAĆ
1. Krótki opis poszczególnych doświadczeń.
2. Wyniki pomiarów.
3. Teoretyczne obliczenia (wraz z wyprowadzeniami wzorów) środków zginania dla

obu przekrojów.

4. Porównanie wyników doświadczeń z obliczeniami teoretycznymi.
5. Obliczenie położenia środka ciężkości przekroju poprzecznego belki.
6. Pomiar kąta skręcenia dla przypadku obciążenia siłą przyłożona w środku ciężkości

przekroju poprzecznego.

7. Uwagi własne.

PRZYKŁAD.
Obliczenie położenia środka zginania dla belki wspornikowej o przekroju ceowym.

Naprężenie ścinające można wyznaczyć z następującego wzoru

h

A

u

B

z

u

P

b

e

δ

δ

α

τ

α

c

z

z

z

z

u

I

Thu

I

Thu

I

TS

2

2

=

=

=

δ

δ

δ

τ

,

gdzie:

I

z

- moment bezwładności przekroju względem osi

z,

S

z

- moment statyczny fragmentu oddzielonego przekrojem

α

−

α

względem osi

z

,

Τ

- siła tnąca w przekroju (T = P).

Ponieważ

h

<<

δ

(przekrój cienkościenny) moment bezwładności

możemy obliczyć następująco

( )

( )

⎟

⎠

⎞

⎜

⎝

⎛ +

=

+

⎟

⎠

⎞

⎜

⎝

⎛

=

+

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

+

=

h

b

h

h

h

b

h

h

b

b

I

z

6

1

2

12

2

2

12

2

12

2

2

3

2

3

2

3

δ

δ

δ

δ

δ

δ

.

Równanie naprężeń tnących w półkach ceownika

u

h

b

h

P

h

b

h

Phu

I

Thu

z

u

⎟

⎠

⎞

⎜

⎝

⎛ +

=

⎟

⎠

⎞

⎜

⎝

⎛ +

=

=

6

1

6

1

2

2

2

2

δ

δ

τ

.

Naprężenia tnące w punkcie A i B:

h

z

B

B

τ

τ

P

O

1

1

T

T

e

c

(

)

(

)

.

6

1

,

0

0

⎟

⎠

⎞

⎜

⎝

⎛ +

=

=

=

=

=

=

h

b

h

Pb

b

u

u

B

A

δ

τ

τ

τ

τ

Przebieg i rozkład naprężeń tnących przedstawiono
na rysunku obok.
Suma momentów wszystkich sił względem punktu
O wyniesie

0

2

2

1

=

−

⋅

=

∑

h

T

e

P

M

c

o

, gdzie

δ

τ

⋅

⋅

=

b

T

D

2

1

1

.

Powyższe równanie pozwala na wyznaczenie środka zginania

h

b

b

h

b

b

P

h

b

h

b

h

Pb

P

h

b

P

h

T

e

D

c

+

=

⎟

⎠

⎞

⎜

⎝

⎛ +

=

⎟

⎠

⎞

⎜

⎝

⎛ +

=

=

=

6

3

6

1

2

6

1

2

1

2

1

2

2

1

δ

δ

δ

τ

.

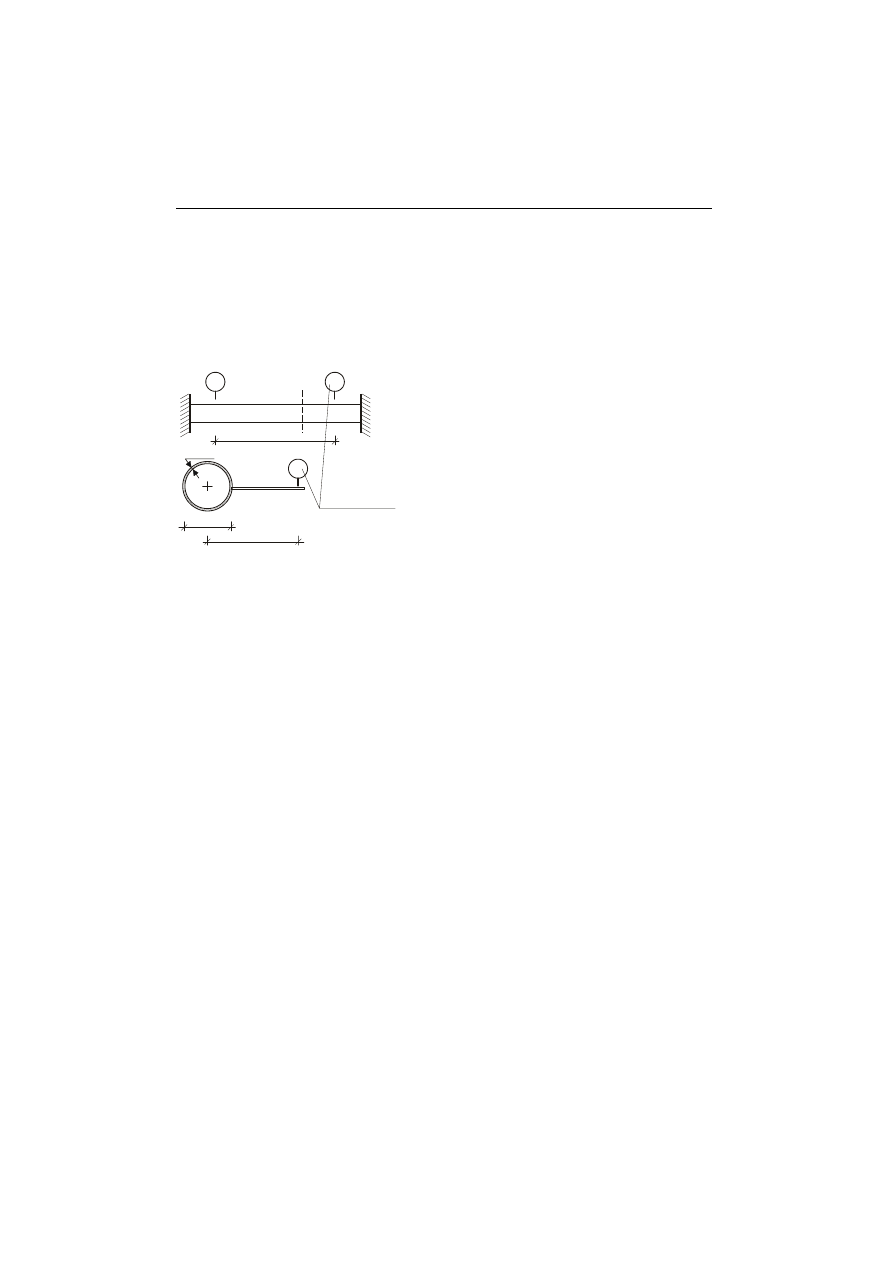
Metody Doświadczalne w Analizie Konstrukcji

38

ĆWICZENIE 14 SKRĘCANIE SWOBODNE PRĘTA

O PRZEKROJU PIERŚCIENIOWYM ZAMKNIĘTYM

I OTWARTYM (dwa doświadczenia)

Celem Ćwiczenia jest porównanie pracy na skręcanie swobodne pręta o przekroju
pierścieniowym zamkniętym i otwartym. Ćwiczenie wykonuje się dla prętów
o schemacie statycznym przedstawionym na rys. 14.1. Belki wykonane są z mosiądzu.

400

d

38,5 mm

D =
d = 1 mm

39 mm

D =

d = 2 mm

Przekrój zamknięty:

Przekrój otwarty:

czujniki

zegarowe

D

[mm]

100

1

2

G = 35000 MPa

α

α − α

α

Rys. 14.1.

Schemat statyczny
skręcanych belek
o przekroju
pierścieniowym

DOŚWIADCZENIE 1

SKRĘCANIE PRĘTA

O PRZEKROJU PIERŚCIENIOWYM ZAMKNIĘTYM

Pręt jest poddany działaniu stałego momentu skręcającego. Stan przemieszczeń pręta
polega na sztywnym obrocie poszczególnych przekrojów. Oznacza to, że przekroje
poprzeczne pręta po skręceniu pozostają nadal płaskie.
1. Obciążyć pręt momentem skręcającym M

0

= P

×r

0

poprzez przyłożenie siły P = 1 kG

na ramieniu początkowym r

0

(odważnik należy przyłożyć na pierwszym nacięciu

dźwigni).

2. Dokonać odczytów początkowych czujników zegarowych.
3. Obciążyć pręt momentem skręcającym M

1

= P

×r

1

poprzez przyłożenie siły P = 1 kG

na dowolnie przyjętym ramieniu r

1

. Określa je jedno z nacięć wykonanych na

dźwigni.

4. Odczytać wskazania czujników zegarowych.
5. Obliczyć kąt skręcenia pręta odpowiadający przyrostowi momentu skręcającego od

M

0

do M

1

.

Pomiary należy powtórzyć trzy razy.
Wykonać obliczenia teoretyczne kąta skręcenia.

DOŚWIADCZENIE 2

SKRĘCANIE PRĘTA

O PRZEKROJU PIERŚCIENIOWYM OTWARTYM

Pręt podobnie jak w Doświadczeniu 1 poddany jest działaniu stałego momentu
skręcającego. Przekroje poprzeczne pręta po odkształceniu nie pozostają płaskie.
Występuje tak zwana deplanacja czyli paczenie się przekrojów. Skręcanie swobodne jest
możliwe dzięki zapewnieniu nieograniczonej deplanacji na końcach pręta.
Doświadczenie 2 należy wykonywać w podobny sposób jak Doświadczenie 1 obciążając
pręt siłą P = 0,l kG.

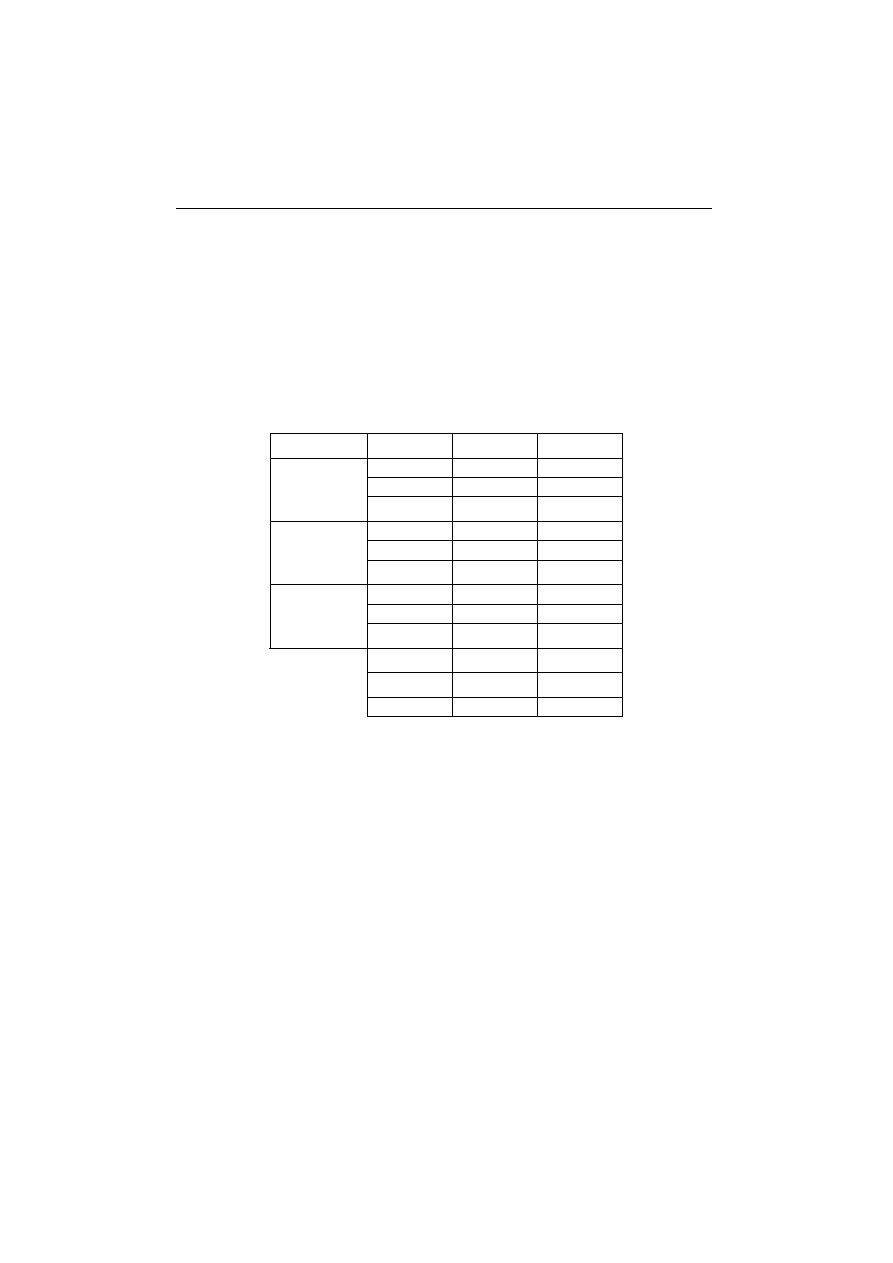
Metody Doświadczalne w Analizie Konstrukcji

39

SPRAWOZDANIE POWINNO ZAWIERAĆ
1. Krótki opis poszczególnych doświadczeń.
2. Wyniki pomiarów wpisane do tabeli 14.1.
3. Obliczenia teoretyczne.
4. Porównanie wyników doświadczeń z obliczeniami teoretycznymi.
5. Wnioski dotyczące pracy na skręcanie prętów o przekroju pierścieniowym otwartym

i zamkniętym.

6. Uwagi własne.

Tabela 14.1.

Wzór tabeli pomiarowej.

Seria odczytów

Nr punktu

1

2

OP

OK

Odczyt I

]

m

[

δ

OP

OK

Odczyt II

]

m

[

δ

OP

OK

Odczyt III

]

m

[

δ

śr

δ

obl

δ

Błąd [%]