Podstawy Analizy

Danych

Opracowanie pytao by

MC_OMEN

1. Przypadek jednej zmiennej losowej: dystrybuanta, gęstośd prawdopodobieostwa, przedział ufności i

poziom ufności.

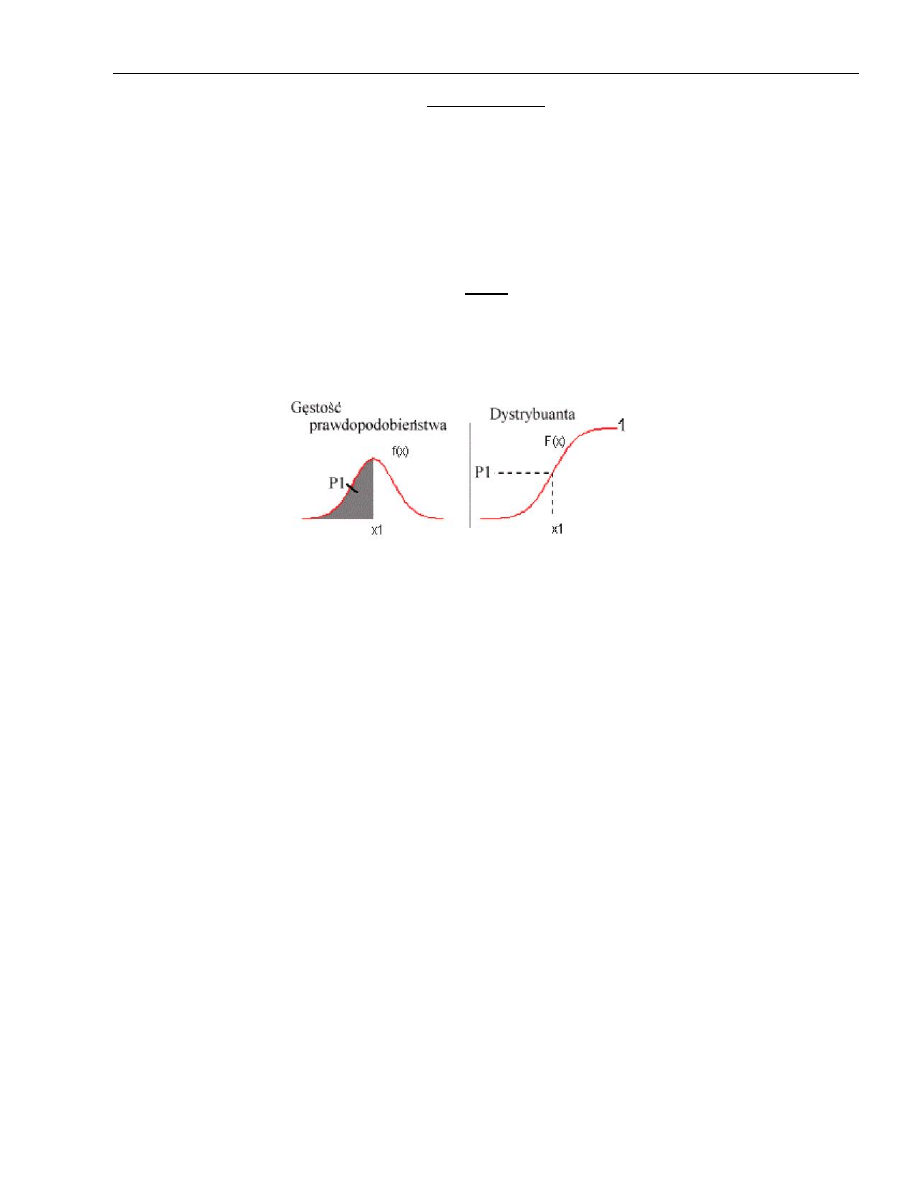
Dystrybuanta oznacza prawdopodobieostwo, że zmienna losowa x jest mniejsza od pewnej liczby rzeczywistej x.

( ) ( )

Dla zmiennych losowych dyskretnych dystrybuanta jest zmienną skokową.

Gęstośd prawdopodobieostwa jest to pierwsza pochodna z dystrybuanty

( )

( )

Funkcja gęstości prawdopodobieostwa to funkcja rzeczywista, która pozwala wyrazid prawdopodobieostwo wystąpienia
dowolnego zdarzenia B za pomocą wartości całki Lebesgue’a z tej funkcji po zbiorze B.

( ) ( ) ∫ ( )

( ) ∫ ( )

∫ ( )

Z gęstością prawdopodobieostwa, z prawdopodobieostwem, wiąże się pojęcie przedziału ufności oraz poziomu ufności.

Wykorzystując znajomośd funkcji gęstości prawdopodobieostwa rozkładu f (x) można obliczyd prawdopodobieostwo α
znalezienia się wyniki w dowolnym przedziale, np. w przedziale od a do b , a mianowicie

( ) ∫ ( )

Przedział ( ) nazywamy przedziałem ufności, a odpowiadające mu prawdopodobieostwo to poziom ufności.
Najczęściej przedział ufności rozmieszcza się symetrycznie wokół wartości średniej.

2. Właściwości rozkładu normalnego ( )

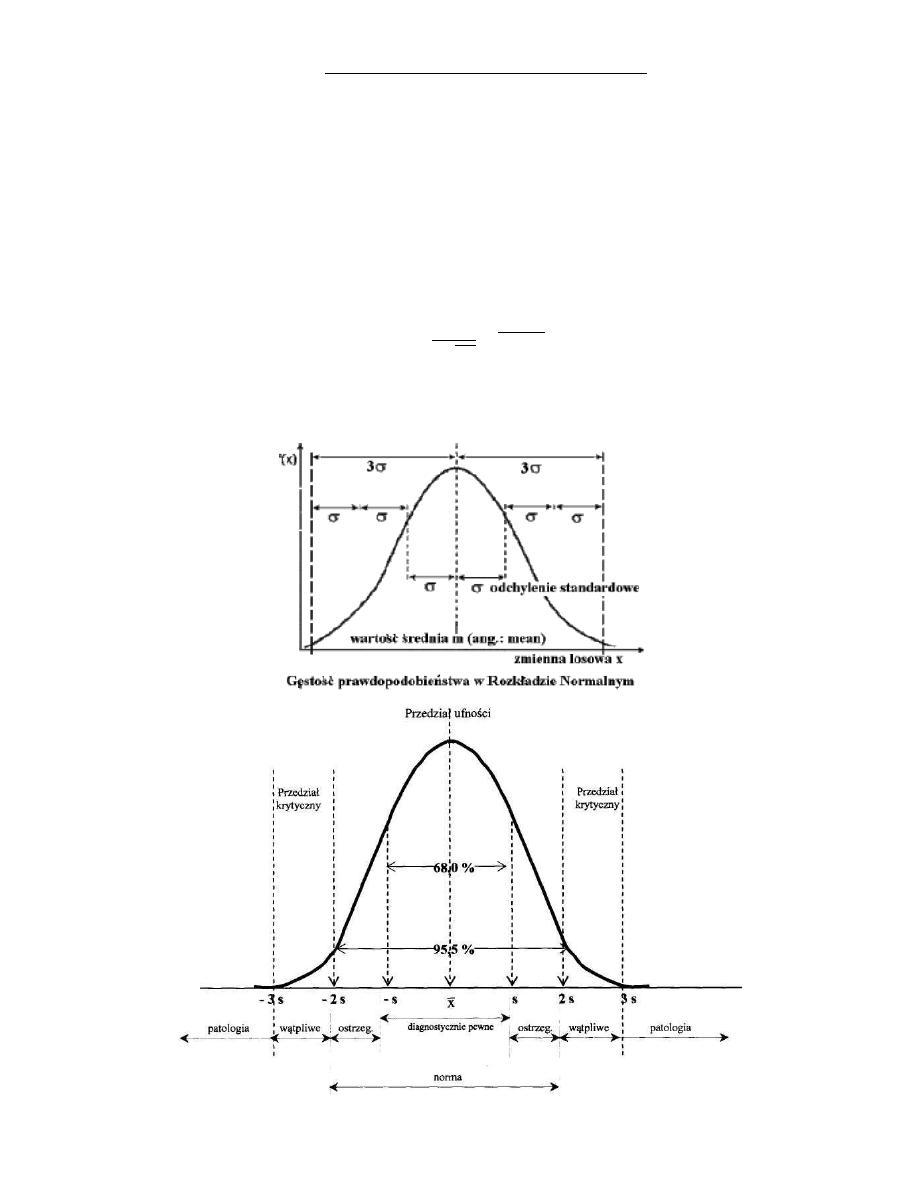
Rozkład normalny jest opisany krzywą Gaussa, a jego skrót to albo ( ) lub ( ),gdzie m to wartośd

średnia zmiennej losowej x (od ang. Mean). Wielkośd to odchylenie standardowe rozkładu. Wartośd średnia i

odchylenie standardowe to parametry rozkładu normalnego.

Krzywa Gaussa (czyli ta którą opisany jest rozkład normalny) ma 2 parametry:

A ogólny zapis funkcji to

( )

√

( )

Wykres i jego właściwości przedstawione są poniżej:

3. Przypadek dwóch zmiennych losowych: dystrybuanta, gęstośd prawdopodobieostwa

Dystrybuanta funkcji dwóch zmiennych losowych mówi prawdopodobieostwie jakie spełniają dwie zmienne losowe ,
które spełniają warunek .

„Duże litery” oznaczają zmienne losowe, z kolei małe po prostu zmienne.

Tak więc z definicji wynika że :

( ) ( )

A to łączy się z pojęciem łącznej gęstości prawdopodobieostwa:

( ) (

) (

) ( )

Które pozwala na wyznaczenie prawdopodobieostwa:

( ) ∫ [∫ ( )

] ∫ [∫ ( )

]

Gdzie „kwadratowe nawiasy” to odpowiednio g(x), h(y)

Gdy zmienne losowe są niezależne to

( ) ( ) ( )

Czyli łączna gęstośd prawdopodobieostwa zmiennych losowych niezależnych jest równa iloczynowi brzegowych gęstości
prawdopodobieostwa.

W przypadku dwóch zmiennych definiujemy także warunkową gęstośd prawdopodobieostwa

( | )

( )

( )

( ) ( )

( )

( )

Czyli wniosek tego jest że wartośd warunkowej gęstości prawdopodobieostwa staje się wartością brzegowa gdy zmienne
są niezależne.

4. Kowariancja i współczynnik korelacji dwóch zmiennych losowych; dla zmiennych losowych. Definicja,

interpretacja

Kowariancja określa stopieo współzależności między zmiennymi losowymi x oraz y. Gdy zmienne losowe są

niezależne, kowariancja jest równa zero.

( ) *( ̂) ( ̂)+

Gdzie funkcja E to wartośd oczekiwana, wygodniejszym wzorem jest :

( ) ( ) ( ) ( )

Co dla jasności sprowadza się do (dla zmiennych dyskretnych):

( )

∑

̂ ̂

Dla dwóch zmiennych losowych definiuje się także współczynnik korelacji ( ).

Jest on różny od zera tylko dla zmiennych losowych zależnych. Dla zmiennych losowych niezależnych zachodzi
( ) .

( )

( )

( ) ( )

Kowariancja i współczynnik korelacji są miarą współzależności zmiennych losowych; dla zmiennych losowych
niezależnych są one równe zero.

5. Centralne twierdzenie graniczne

Załóżmy standardowy rozkład normlany ( taki którego wartośd średnia jest zerowa, a wariancja równa 1):

( )

Funkcja wtedy ma postad :

( )

√

Treśd CTG to:

Suma niezależnych zmiennych losowych, takich że ̂ ( ) oraz ( )

( ), jest także zmienna losową o

wartości ś®edniej wynoszącej ̂ i o wariancji równej

( ).

Praktycznie:

Gdy dodaje się wiele zmiennych niezależnych o jednakowym rozkładzie, to ich suma ma w przybliżeniu (asymptotycznie,
dla ) rozkład normalny.

Twierdzenia te wyjaśniają mechanizm częstego występowania w praktyce rozkładu normalnego. Obserwowane zjawiska
losowe są najczęściej sumą wielu niezależnych przyczyn losowych. Twierdzenie wyjaśnia, dlaczego rozkład normalny jest
tak powszechny (jest taki „normalny”). Na przykład, na błąd pomiaru ma wpływ wiele niezależnych czynników, które
sumują się. Uznajemy, że błąd pomiaru jest zmienną losową o rozkładzie normalnym.

6. Elipsa kowariancji na płaszczyźnie

: równanie elipsy, interpretacja.

Kiedy mówimy o dwóch zmiennych losowych, o ich rozkładzie itp, to rolę przedziału ufności przejmują elipsy

kowariancji. Gdy zmiennych jest więcej, mówimy o elipsoidach wariancji-kowariancji w przestrzeni

wielowymiarowej.

Zakładając

[

]

To równanie elipsy wariancji kowariancji ma postad:

,( ̂)

( ̂)-

Gdzie c to stała.

Po wymnożeniu wektorów i macierzy otrzymujemy równanie algebraiczne (c=1) :

(

)

(

)

Jest to równanie elipsy na płaszczyźnie

, o osiach

i o środku w punkcie o współrzędnych

.

Kąt nachylenia osi elipsy zależy od znaku i wartości współczynnik korelacji ( )

( )

( ) ( )

.

Ważne:

 Korelacja wydłuża i obraca elipsę

 Rozmiar elipsy zależy od wariancji

 Elipsa kowariancji zawiera pełną informację o macierzy kowariancji

 Prawdopodobieostwo zajścia wydarzeo

wewnątrz elipsy kowariancji jest niezależne od samej

elipsy

 Elipsa kowariancji stanowi odpowiednik przedziału ufności dla rozkładu jednowymiarowego

Interpretacja:

Poziome przekroje funkcji gęstości prawdopodobieostwa dla dwuwymiarowego rozkładu Gaussa są elipsami

wzajemnie koncentrycznymi. Dla maksymalnej wartości funkcji elipsa przechodzi przez punkt o współrzędnych

: jest to rzut wierzchołka na płaszczyznę

i ma on współrzędne

.

Pionowe przekroje przechodzące przez wierzchołek to krzywe Gaussa, których szerokości wyznaczane są przez

punkty leżące na elipsie kowariancji i są różne dla różnych przekrojów. Wszystkie linie stałego

prawdopodobieostwa , gdy wykładnik jest przyrównywany do innej stałej c=1, to także elipsy. Leżą one

wewnątrz gdy c>1, lub na zewnątrz gdy c<1, elipsy powstałej dla c=1.

Punkty leżące na elipsie (punkty elipsy e ) są jednakowo prawdopodobne i jest określone przez

prawdopodobieostwo

. Każdy z punktów leżących wewnątrz elipsy jest bardziej prawdopodobny od punktu

leżącego na elipsie, a każdy punkt na elipsie jest bardziej prawdopodobny od punktu leżącego na

zewnątrz elipsy. Jest tak niezależnie od tego jakie są geometryczne odległości tych punktów od środka elipsy.

7. Wykresy punktowe. Zawartośd informacji.

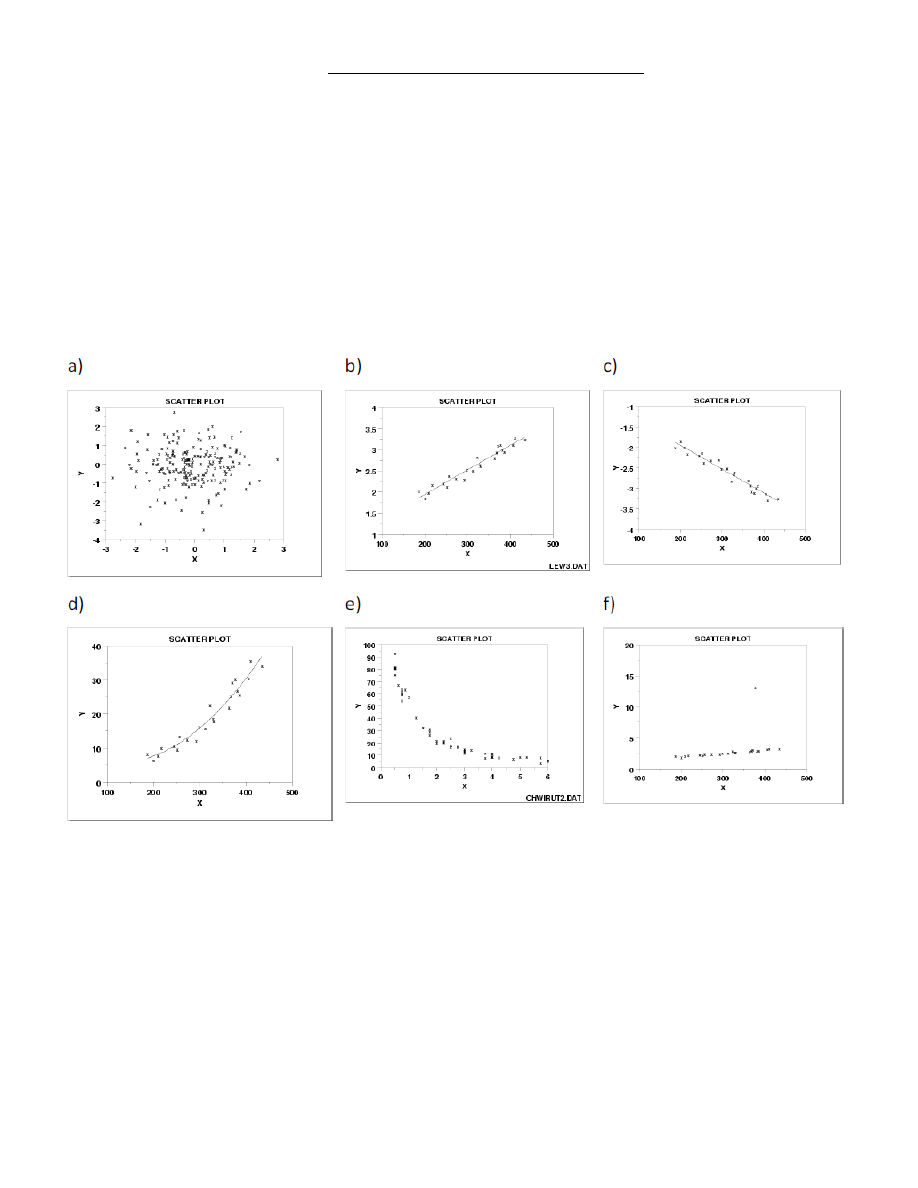
Wykres punktowy pokazuje rodzaj zależności pomiędzy dwoma zmiennymi; zależności te nie są jednakowo

silne w rozważanych przykładach. Analiza wykresu punktowego pozwala znaleźd odpowiedzi, między innymi,

na następujące pytania:

 Czy zmienne są zależne/powiązane?

 Czy zależnośd pomiędzy zmiennymi ma charakter liniowy?

 Czy zależnośd pomiędzy zmiennymi ma charakter nieliniowy?

 Czy występują tzw. outliers czyli odchyłki grube, pomyłki?

Dla przykładu :

Wykres punktowy pokazuje, że zmienne są

a) niezależne,

b) są zależne liniowo, korelacja dodatnia,

c) są zależne liniowo, korelacja ujemna,

d) są zależne w sposób kwadratowy,

e) są zależne w sposób wykładniczy,

f) występuje outlier- jeden z wyników wyraźnie odbiega od ogólnej tendencji zmian i

najprawdopodobniej jest błędnym pomiarem, pomyłką.

8. Ilościowa analiza danych. Estymacja przedziałowa.

W praktyce wartośd poszukiwanej wielkości wyznaczamy na podstawie próby pobranej z populacji generalnej.

Nie jest to zatem wartośd prawdziwa lecz jest tylko jej estymata, estymata z próby. Na przykład, wartośd

średnia obliczona z próby jest traktowana jako estymata wartości rzeczywistej. Jednak wartości średnie

wyznaczane w wyniku pobierania kolejnych prób będą różniły się. Zatem estymata punktowa (jedna wybrana

średnia) jest niedokładnym przybliżeniem wartości średniej.

Estymacja przedziałowa polega na uzupełnieniu informacji o wartości średniej o informację o jej niepewności,

niedokładności. Sprowadza się to do określenia przedziału wokół wartości średniej w którym znajdzie się

wartośd rzeczywista badanej wielkości z określonym prawdopodobieostwem. Rolę taka spełnia przedział

ufności

9. Ilościowa analiza danych. Testowanie hipotez

Testowanie hipotez dotyczy sprawdzania słuszności pewnych stwierdzeo odnoszących się do parametrów

wyznaczonych z próby. Przykładowo, hipoteza może mied jedną z postaci:

 Wartośd średnia z populacji wynosi 7

 Dewiacja standardowa z populacji wynosi 2

 Wartości średnie z dwóch populacji są równe (hipoteza o równości średnich)

 Dewiacje standardowe z dwóch populacji są równe (hipoteza o równości dewiacji standardowych).

Odrzucenie hipotezy oznacza, że hipoteza była fałszywa. Jednak nie odrzucenie hipotezy nie oznacza iż jest ona

prawdziwa a oznacza jedynie, że nie mamy podstaw do jej odrzucenia. Dla przeprowadzenia testu formułuje

się zazwyczaj jedną z dwóch alternatywnych hipotez, są to:

 Hipoteza zerowa

, przykładowo : wartości ś®ednie z dwóch populacji są równe

 Hipoteza alternatywna

: wartości średnie z dwóch populacji nie są równe

Przeprowadzenie statystycznego testu postawionej hipotezy daje odpowiedź w formie: hipoteza jest

przyjęta/odrzucona dla poziomu istotności α .

Poziom istotności to maksymalne ryzyko jakie jesteśmy skłonni zaakceptowad przy odrzuceniu hipotezy gdy

jest ona faktycznie prawdziwa. Poziom istotności α opisuje czułośd testu. Gdy α = 0.05 to oznacza, że dla 5%

przypadków mylimy się odrzucając hipotezę. Gdy wynik testu (wykonują go wyspecjalizowane programy)

mówi: hipoteza przyjęta z poziomem istotności α = 0.01 lub z poziomem α = 0.001 to taki rezultat jest bardzo

wiarygodny. W ostatnim przypadku statystycznie tylko jeden raz na tysiąc mylimy się. Mówimy wówczas o

wysokiej statystycznej istotności.

Ważne jest aby z rozwagą podchodzid do wyników testów statystycznych, gdyż statystyczna istotnośd różnic

pomiędzy badanymi wielkościami i praktyczna istotnośd tych różnic to dwa odrębne problemy. Zdolnośd testu

statystycznego do wykrycia np. różnic wartości średnich, zależy silnie od reprezentatywności próby, od jej

wielkości. Może zdarzyd się, że test odrzuci hipotezę o równości średnich z dwóch procesów a różnica ta z

inżynierskiego punktu widzenia może byd nieistotnie mała. Może byd także odwrotnie: znaczne różnice

średnich (z inżynierskiego punku widzenia), mogą nie zostad rozpoznane przez test statystyczny gdy

pobrano zbyt małą, nie reprezentatywną próbę.

10. Założenia odnośnie stosowalności testu t-Studenta

Aby móc zastosowad test t-Studenta należy sprawdzid, czy spełnione zostały następujące warunki *1, 2,3+:

1. Mała liczba próbek w każdej próbie (n<50).

2. Rozkład wyników zmiennej badanej w każdej grupie jest zbliżony do rozkładu normalnego.

3. Jednorodnośd wariancji - do sprawdzenia tego założenia służy test F, test Levene'a lub test Bartletta.

Jeśli wyżej wymienione testy nie wykazały jednorodności wariancji, do sprawdzenia równości średnich

zamiast t-Testu należy użyd testu Cohrana i Coxa. Warunku jednorodności wariancji nie trzeba

sprawdzad dla zmiennych powiązanych.

4. Reprezentatywnośd każdej próby, czyli próba dobrze reprezentuje analizowaną populację, jej struktura

jest zbliżona do struktury całej populacji.

Zasada randomizacji:

o Należy zapewnid reprezentatywnośd (typowośd) próby. Uzyskujemy to przez losowy wybór

próby (pierwsza zasada randomizacji). Jeśli pierwsza zasada randomizacji nie jest spełniona,

wyciągnięte wnioski mogą dotyczyd tylko badanej grupy a nie populacji (np. tylko wysokich

mężczyzn, tylko z przedziału wiekowego 20-30 lat, itp.). Badania powinny należy przeprowadzid

co najmniej na dwóch grupach aby sprawdzid działanie leku A w porównaniu z lekiem B (lub z

placebo). Decyzja o tym, która osoba otrzymuje lek A lub B lub musi byd podjęta losowo (druga

zasada randomizacji). Jeśli druga zasada randomizacji nie jest spełniona, mogą zostad

wyciągnięte błędne wnioski.

11. Poziomy istotności ex ante oraz ex post w procesie weryfikacji hipotez.

Poziom istotności ex ante, jest to dopuszczalne prawdopodobieostwo odrzucenia hipotezy zerowej

gdy

jest ona prawdziwa.

Poziom istotności ex post jest to poziom istotności dla którego hipoteza zerowa jest prawdziwa.

 Gdy na poziomie istotności to należy odrzucid hipotezę zerową i przyjąd alternatywną.

 Gdy na poziomie istotności to mamy brak podstaw do odrzucenia hipotezy zerowej.

12. Skrzynki z wąsami (Box And Whiskers) – zawartości informacji

Skrzynki z wąsami (Box And Whiskers), pokazują zakresy wybranej zmiennych oraz wartośd średnią oraz

odchylenie standardowe.

Punkt środkowy odpowiada wartości średniej

kwadrat wyznacza zakres

,

natomiast wąsy wyznaczają 95% przedział ufności dla badanych średnich (jest to przedział

).

Hipotezę o równości średnich można odrzucid, gdy wąsy skrzynek na siebie nie zachodzą (tak jak na tym

rysunku).

13. Metoda najmniejszych kwadratów.

Metoda najmniejszych kwadratów została wprowadzona przez Legendre'a i Gaussa. Jej istota jest następująca:

wynik kolejnego pomiaru

można przedstawid jako sumę (nieznanej) wielkości mierzonej

oraz błędu

pomiarowego

Od wielkości

oczekujemy, aby suma kwadratów była jak najmniejsza.

∑

∑(

)

Metoda najmniejszych kwadratów jest najczęściej stosowaną w praktyce metodą statystyczną