Laboratorium Materiałów konstrukcyjnych i Eksploatacyjnych – P.Wr. – WME

1/8

Lepkość, temperatura kroplenia i gęstość

Cel ćwiczenia

Zapoznanie się z metodyką pomiarów i pomiar dla wybranych materiałów lepkości, tempera-
tury kroplenia i gęstości.

Lepkość

Materiały eksploatacyjne zalicza się do substancji, które w systemie technicznym nie tworzą
części, ale są ważne ze względu na jego funkcjonowanie. Pełnią one zwykle następujące role:



Smarów (zmniejszanie tarcia i zużycie: oleje, smary plastyczne, gazy i miękkie materiały

stałe jak np. grafit)



Cieczy roboczych (przenoszenie sygnałów: oleje hydrauliczne, powietrze)



Czynników termodynamicznych (transport energii i masy: woda, powietrze, oleje, freony)



Źródeł energii (paliwa: gazowe, ciekłe i stałe).

Jak widać z powyższego, z małymi wyjątkami, są to substancje zaliczane do płynów (gaz i
ciecz) a ich główną cechą jest łatwość zmiany kształtu, co wynika z faktu, iż w tym stanie brak
jest wiązań utrzymujących molekuły w ustalonej pozycji i związana z tym niemożliwość prze-
noszenia naprężeń stycznych i rozciągających. Dlatego dla tych materiałów moduł Kirchhoffa
G jest równy lub bliski zeru a do opisu własności mechanicznych nie ma zastosowania moduł
Younga E. Jedynie dla gazów stosuje się jeszcze współczynnik ściśliwości



, który jest odwrot-

nością modułu Helmholtza



= 1/K. Zamiast tego definiowane są wielkości opisujące ich wła-

sności reologiczne, do których zalicza lepkość (płyny) i klasy konsystencji (smary). W oparciu o
nie, wiele organizacji ISO, SAE itp. stworzyło normy klasyfikujące te substancje w celu ich
łatwego doboru dla określonego zastosowania.

W związku z powyższym w płynie znajdującym się w bezruchu lub poruszającym się jak

bryła sztywna nie ma naprężeń stycznych a jedynie normalne i to w dodatku tylko ściskające.
Zatem w tensorze naprężenia wszystkie składowe normalne są równe ciśnieniu p wziętym ze
znakiem minus (ze względu na ściskanie)



i

= –p zaś styczne znikają, czyli



ij

= 0. Dzięki temu

stan naprężenia opisuje się skalarem p, a nie tensorem.

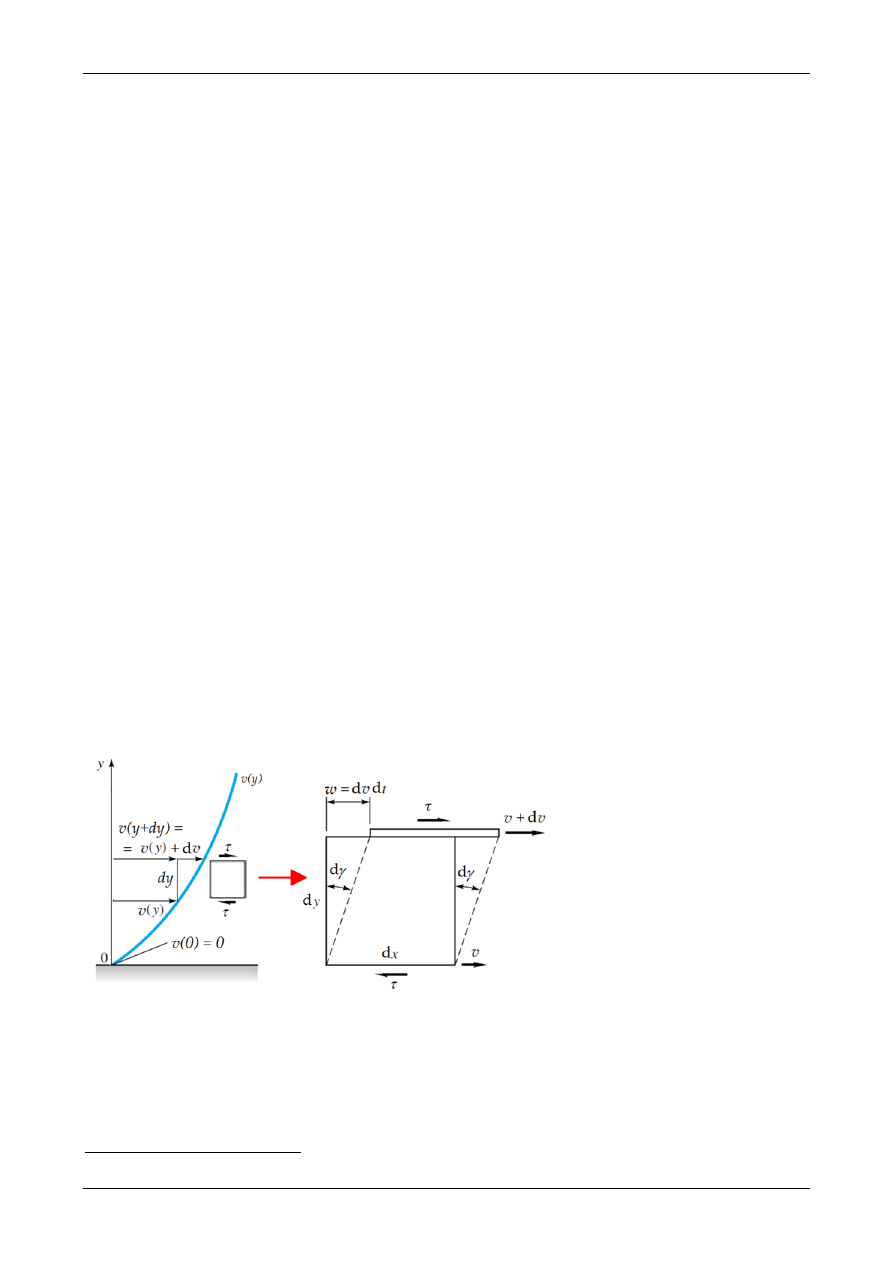
Rys.1. Odkształcenia postaciowe w
płynie wywołane gradientem prędko-
ści v.

Sytuacja zmienia się, gdy wewnątrz płynu ma miejsce względny ruch jednych obszarów w

stosunku do drugich

1

prowadzący do odkształceń postaciowych. W tym stanie powstają nie-

wielkie naprężenia styczne



, które zależą od szybkości odkształcenia postaciowego d𝛾/d𝑡 = 𝛾̇,

czyli 𝜏 = 𝑓(𝛾̇). Naprężenia te znikają, gdy tylko zanika ruch mimo, iż odkształcenie postaciowe

pozostają. Zjawisko takie nazywa się lepkością (viscosity). Na rys.1 pokazano profil prędkości
płynu v poruszającego się równolegle do dna kanału względem odległości od dna y i szkic, wy-
nikających z tego, odkształceń cząstki płynu o wymiarach dy na dx. Jeżeli na wysokości y

1

Czyli niejednorodne pole prędkości v(x,y,z)



const

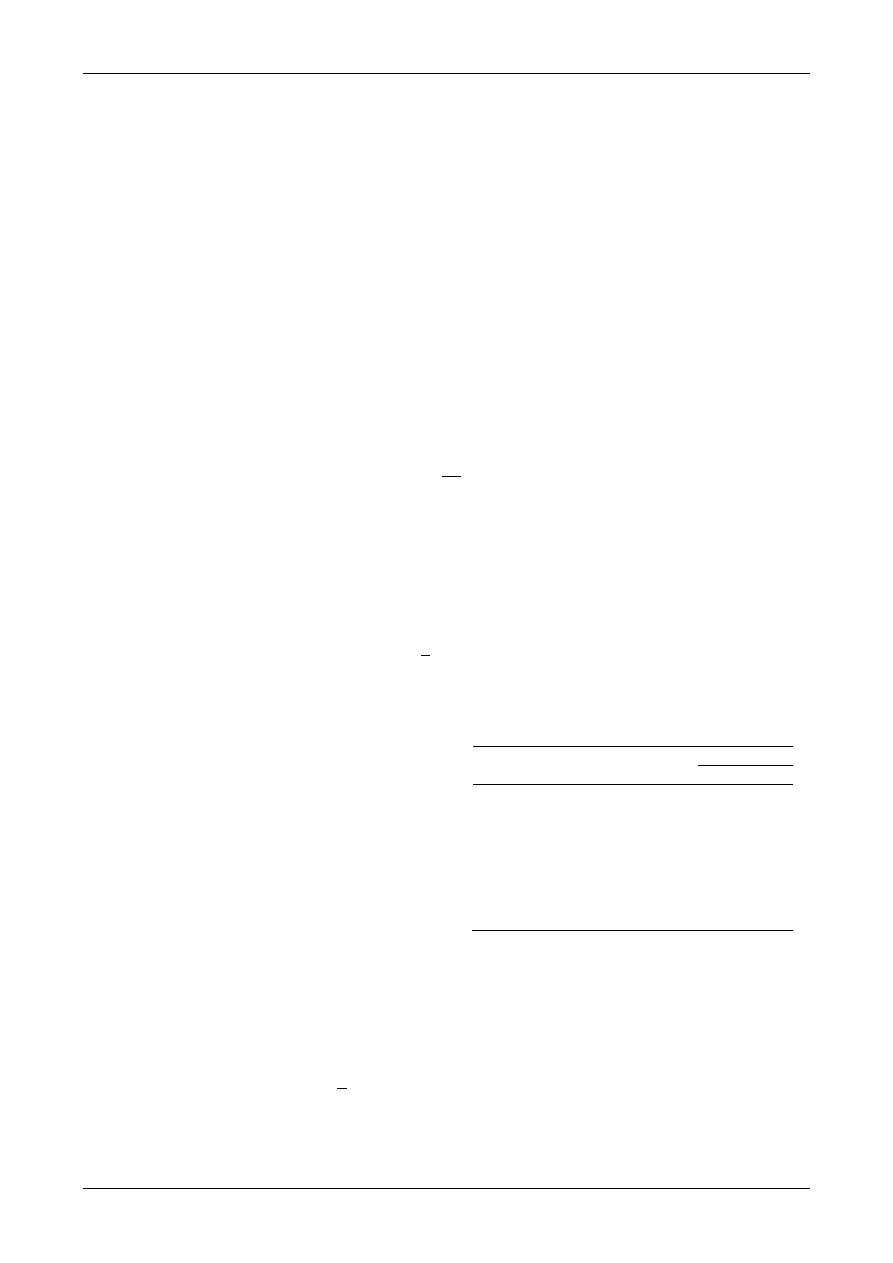
Laboratorium Materiałów konstrukcyjnych i Eksploatacyjnych – P.Wr. – WME

2/8

prędkość płynu wynosi v, to na wysokości y + dy będzie ona większa o wartość dv. Spowoduje
to odkształcenia postaciowe, których miarą jest kąt d



. Z pokazanej na rysunku geometrii od-

kształcenia wynika, że tg d𝑦 ≈ d𝛾 = 𝑤/d𝑦. Biorąc pod uwagę, że odległość w, o jaką przemiesz-
cza się górna powierzchnia cząstki względem dolnej wynosi 𝑤 = d𝑣 ∙ d𝑡, łatwo da się pokazać,

iż szybkość ścinania 𝛾̇ = d𝛾/d𝑡 = d𝑣/d𝑦, czyli że jest ona równa składowej gradientu v w kie-
runku y, czyli kierunku prostopadłym do działania naprężenia stycznego



.

Lepkość jest właściwością płynów i plastycznych ciał stałych charakteryzującą tarcie we-

wnętrzne, czyli ich opór wewnętrzny przeciw płynięciu. Lepkością nie jest opór przeciw płynię-
ciu powstający na granicy płynu i ścianek naczynia. Przyczyną lepkości w cieczy są siły mię-
dzymolekularne, które utrudniają ruch molekuł a co za tym idzie i warstw względem siebie
dając opór przy poślizgu. Im są one większe, tym większe są opory tarcia wewnętrznego cieczy.
Z kolei lepkość gazów jest efektem dyfuzji molekuł między warstwami poruszającymi się
względem siebie z różnymi prędkościami. W wyniku dyfuzji do warstwy wnikają molekuły o
innym pędzie, które przyjmując pęd warstwy oddziaływują na nią z siłą proporcjonalną do
różnicy pędów stwarzającą naprężenia styczne.

Gazy oraz większość płynów jak woda, oleje, alkohole i inne, to płyny newtonowskie, które

charakteryzują się tym, iż



jest proporcjonalne do 𝛾̇. Stała proporcjonalności



między



a 𝛾̇

zwana jest współczynnikiem lepkości dynamicznej, zatem

𝜏 = 𝜂𝛾̇ = 𝜂

d𝑣
d𝑦

(1)

Wzór (1) stanowi treść hydrodynamicznego prawa Newtona. Jednostką lepkości dynamicznej w
SI jest kg/(m



s) = Pa



s. Jednostką z poza układu SI jest puaz (fr. poise) – skrót P. Pomiędzy

jednostkami zachodzi związek 1 Pa



s = 10 P. W praktyce częściej używa się milipaskalosekun-

dy 1

mPa



s = 1 cP. Inną wielkością charakteryzującą tarcie wewnętrzne, którą często używa

się w obliczeniach hydrodynamicznych, jest współczynnik lepkości kinematycznej



(gr. litera

ni) będący stosunkiem lepkości dynamicznej do gęstości płynu



𝜈 =

𝜂
𝜌

(2)

Jego jednostką w SI jest m

2

/s zaś jednostką z poza układu SI jest St (Stokes) = cm

2

/s =

10

-4

m

2

/s. Lepkość kinematyczna jest chętniej

stosowana w przemyśle i, zgodnie z normą ISO
3448, jest podstawą klasyfikacji olejów przemy-
słowych.

Do opisu własności reologicznych stosowane

są też inne wielkości jak płynność



będąca od-

wrotnością współczynnika lepkości dynamicznej



= 1/



oraz dla celów praktycznych, gdy chodzi

tylko o porównanie cieczy, lepkość względna,
która jest stosunkiem lepkości badanej cieczy



x

do lepkości cieczy wzorcowej



w

. Lepkość ta jest

podawana w jednostkach umownych. W kraju
stosuje się stopnie Englera °E, wyrażające sto-
sunek czasu wypływu 200 cm

3

badanej cieczy do czasu wypływu tej samej ilości wody destylo-

wanej w temperaturze 20°C przez kapilarę znormalizowanego aparatu Englera.

Dla płynów newtonowskich lepkość jest funkcją temperatury i ciśnienia. Dla cieczy jej za-

leżność od temperatury wyraża wzór 𝜂 = 𝐴 exp [−𝐸/(𝑘𝑇)], gdzie: A – współczynnik proporcjo-
nalności; k – stała Boltzmanna; T – temperatura bezwzględna i E – energia aktywacji ruchu. Z

kolei dla gazów można wykazać, że 𝜂 = 𝜌𝑙

f

𝑤

s

/3, gdzie: l

f

– średnia droga swobodna (~1/𝑝) a w

s

– średnia prędkość molekuły (~√𝑇). Z powyższego wynika, że lepkość cieczy spada wraz z tem-

peraturą a dla gazów rośnie wraz z nią – rys.

2

. Lepkość gazów jest od 3 do 5 rzędów niższa niż

lepkość cieczy a wody około 100 razy mniejsza niż olejów.

Tabela 1. Lepkość wybranych płynów

Płyn

Lepkość



mPa·s

Woda 20°C

1,0

Oliwa (z oliwek)

84,0

Benzyna

0,7

Olej lniany

44,0

Gliceryna 20°C

1945,0

Aceton

0,3

Olej silnikowy 0W (-30°C)

3250

Olej silnikowy 40 (150°C)

3,7

Laboratorium Materiałów konstrukcyjnych i Eksploatacyjnych – P.Wr. – WME

3/8

Dla olejów przemysłowych, do opisu zależności ich lepkości kinematycznej



od temperatu-

ry, stosuje się wzór empiryczny Walthera

lg lg( 𝜈 + 𝑐) = 𝑚 lg 𝑇 + 𝑘,

(3)

który obowiązuje dla



wyrażonego w mm

2

/s (czyli cSt) i temperaturze T wyrażonej w K. Jego

zgodność z danymi doświadczalnymi jest lepsza w wyższych temperaturach. Stała c = 0,8 (wg
norm europejskich) zaś stałe k i m zależą od rodzaju oleju i wyznacza się je doświadczalnie.

W zastosowaniach technicznych najbardziej pożądaną cechą jest niewrażliwość lepkości na

zmiany temperatury, czyli możliwie małe nachylenie krzywej



(T). Niewrażliwość tą wyraża

podawany w procentach wskaźnik lepkości WL (viscosity index). Wyznaczany jest on przez po-
równanie



badanego oleju i dwóch olei wzorcowych w temperaturze 40°C, tak dobranych by

wszystkie miały w 100°C taką samą



(PN-ISO 2909). Oleje mineralne mają WL w granicach

0% (najgorsze – najwrażliwsze) do 100% (najlepsze – najmniej wrażliwe), zaś WL olei synte-
tycznych może osiągać wartości wyższe niż 160%. Na rys.

2

a lepszy (wyższy) WL posiada olej 3,

natomiast olej 1 ma WL najniższe.

a)

b)

Rys.2. Zależność lep-
kości dynamicznej



od

temperatury (a) cieczy:
1,2,3 – oleje; 4 – woda
×100; 5 – powietrze
×1000; (b) gazy

Dla gazów zależność lepkości od ciśnienia jest niewielka. Dla cieczy w zakresie do

25

MPa jest ona prawie liniowa a dla ciśnień wyższych (rys.3) rośnie wykładniczo



=



o

exp(



p), gdzie:



o

– lepkość przy ciśnieniu normalnym,



– ciśnieniowy współczynnik

lepkości, który spada wraz ze wzrostem temperatury i dla olei mineralnych waha się w grani-
cach od 1,7 do 3,5×10

-3

·bar

-1

.

Rys.3. Zależność lepkości dynamicznej od ciśnienia
dla różnych temperatur dla oleju mineralnego.

Rys.4. Modele cieczy: 1 – binghamowska; 2 –
pseudoplastyczna; 3 –newtonowska; 4 – dylatacyj-
na.

Nie wszystkie ciecze zalicza się do płynów newtonowskich. Istnieją ciecze, dla których za-

leżności 𝜏(𝛾̇) są nieliniowe – rys.4. Dla cieczy newtonowskiej 𝜏(𝛾̇) jest linią prostą 3 przecho-

Laboratorium Materiałów konstrukcyjnych i Eksploatacyjnych – P.Wr. – WME

4/8

dzącą przez punkt (0,0), której nachylenie reprezentuje lepkość



. Ogólnie nachylenie stycznej

do wykresu 𝜏(𝛾̇) jest miarą pozornej lepkości dynamicznej dla określonego 𝛾̇. Cieczą pseudopla-
styczną (krzywa 2) nazywamy ciecz, której lepkość pozorna maleje ze wzrostem prędkości ści-
nania. Są to ciecze o zazwyczaj niesymetrycznej budowie molekuły (np. o wydłużonym kształ-
cie), które w miarę zwiększania prędkości ścinania przyjmują uporządkowane ułożenie, wsku-
tek czego zmniejszają się opory tarcia, a więc i lepkość pozorna. Cieczą dylatacyjną jest ciecz
(krzywa 4), której lepkość pozorna rośnie w miarę wzrostu prędkości ścinania (np. mokry pia-
sek lub inne zawiesiny). Podczas szybkiego ścinania, ciecz spełniająca rolę smaru między
cząstkami zawiesiny, zostaje wyparta i opory ścinania rosną. Cieczą binghamowską jest ciecz
(krzywa 1), która zaczyna płynąć dopiero wówczas, gdy naprężenie styczne



przekroczy pewną

wartość graniczną



o

. Przykładem takiej cieczy mogą być różnego rodzaju pasty, smary pla-

styczne itp., dla których po przekroczeniu



o

struktura wewnętrzna materiału ulega zniszcze-

niu i materiał zachowuje się jak ciecz newtonowska. Te substancje w pewnym zakresie naprę-
żeń zachowują się jak ciała stałe. Ten podział nie jest kompletny, albowiem istnieją też ciecze,
dla których lepkość, nie tylko zależy od 𝛾̇, ale także od czasu jak ciecze tiksotropowe (



spada w

miarę mieszania) lub reopeksyjne (



rośnie w miarę mieszania). Na koniec warto wspomnieć o

niezwykłej właściwości helu, który w temperaturze poniżej 2,17

K wykazuje nadciekłość, czyli

całkowity brak lepkości, co pozwala mu w dowolnym obiegu zamkniętym krążyć bez końca.

Lepkość jest zjawiskiem niekorzystnym albowiem jest przyczyną strat ciśnienia w prze-

wodach oraz powoduje opory ruchu obiektów poruszających się w płynach (łopatki wirników,
statki itp.), co w konsekwencji przekłada się na straty energii. Z drugiej strony, w łożyskach
ślizgowych większa lepkość dynamiczna ułatwia przejście przy niskich prędkościach obroto-
wych i dużych obciążeniach, w stan smarowania hydrodynamicznego, w którym współczynniki
tarcia między współpracującymi częściami osiągają bardzo niskie wartości.

Gęstość

Gęstość (density)



jest jedną z podstawowych cech materii, która określa masę jednostki obję-

tości ciała a zatem formalnie wylicza się ją jako stosunek masy ciała m do jego objętości V

𝜌 =

𝑚

𝑉

(4)

Jednostką gęstości, w układzie SI, jest kg/m

3

a popularną jednostką z poza SI jest t/m

3

, czyli

Mg/m

3

. W mechanice płynów czasami wygodniej jest posługiwać się ciężarem właściwym

𝛾 = 𝜌𝑔 (g – przyśpieszenie ziemskie 9,81 m/s), czyli ciężarem jednostki objętości płynu.

Szczególnym przypadkiem materiałów są materiały porowate (piany stałe). Dla nich, w

skali makro, do objętości materiału wlicza się objętość porów, które są wypełnione gazem,
zwykle powietrzem, stąd gęstość



n

takiego materiału, zwana gęstością pozorną (lub gęstością

usypową dla materiałów sproszkowanych), jest mniejsza od gęstości rzeczywistej substancji



tworzącej dany materiał. Dla tego typu materiałów definiuje się wielkość zwaną porowatością



, która jest stosunkiem objętości porów do pozornej objętości materiału (suma objętości sub-

stancji i porów), a którą można wyliczyć znając gęstość pozorną



n

i gęstość rzeczywistą



sub-

stancji z zależności 𝜙 = 1 − 𝜌

n

/𝜌.

Na gęstość substancji wpływają masa i rozmiary atomów oraz sposób ich upakowania w

przestrzeni, czyli skład pierwiastkowy molekuły i rodzaj sieci krystalicznej. Na przykład gę-
stość dla masywniejszego Ge (M = 72,64

u) wynosząca 5323 kg/m

3

jest mniejsza od lżejszego Fe

(M = 55,8 u), który ma gęstość 7874 kg/m

3

, co jest skutkiem luźniejszego upakowania atomów

Ge w siatce krystalicznej. Gęstość metali jest duża, co wynika z ciasnego ułożenia masywnych
atomów a co jest charakterystyczne dla bezkierunkowego wiązania metalicznego. Mniejsza
gęstość ceramiki jest skutkiem kierunkowości wiązania kowalencyjnego (mniejsze wypełnienie
przestrzeni) oraz mniej masywnych atomów. Z kolei jeszcze niższa gęstość polimerów wynika z
faktu, że tworzą je lekkie składniki materii C, O, H a duże i nieregularne makrocząsteczki nie
dają się ciasno upakować w przestrzeni.

Laboratorium Materiałów konstrukcyjnych i Eksploatacyjnych – P.Wr. – WME

5/8

Gęstość zależy także od stanu skupienia oraz temperatury i ciśnienia. Substancje w stanie

ciekłym posiadają mniejszą gęstość niż w stanie stałym, choć zdarzają się wyjątki jak np. wo-
da, żeliwo, bizmut, gal i german, które w pewnym przedziale temperatur w stanie stałym mają
gęstość niższą niż w ciekłym. Zasadniczo gęstość materiałów spada wraz ze wzrostem tempe-
ratury i rośnie wraz ze wzrostem ciśnienia, przy czym ostatnia zależność jest słaba w przy-
padku ciał stałych i cieczy a mocna dla gazów. Zwykle w tabelach gęstości materiałów podaje
się ich wartości w temperaturze znormalizowanej. Podstawową temperaturą, dla której podaje
się gęstość produktów naftowych jest 15°C a ciał stałych 20°C. Dla gazów gęstości podaje się
dla ciśnienia normalnego 101325 Pa.

Temperatura kroplenia smarów plastycznych

Smar plastyczny jest to substancja o konsystencji od ciekłej do stałej, której podstawowymi
składnikami są faza ciekła (olej) i zagęszczacz (substancja żelująca) tworząca gąbczastą struk-
turę smaru, która nadaje mu pewną sztywność. Niektóre smary plastyczne w swoim składzie
zawierają zdyspergowane substancje stałe. Smary plastyczne zaliczają się do cieczy bingha-
mowskich a niektóre z nich posiadają także własności tiksotropowe. Do oceny jakości smaru
plastycznego bierze się pod uwagę:



lepkość strukturalną (pozorną)



penetrację (określająca klasę konsystencji smaru)



temperaturę kroplenia (drop point)



odporność na utlenianie, wymywanie wodą i obciążenia



właściwości ochronne (przed korozją, przeciwzużyciowe, przeciwzatarciowe)



warunki wydzielania oleju i smaru z łożyska



opór mechaniczny w niskich temperaturach



trwałość w wysokiej temperaturze



kompatybilność z elastomerami uszczelnień

Jednym z podstawowych parametrów dla smarów plastycznych jest temperatura kroplenia,
która jest miarą początku niszczenia (degradacji) gąbczastej struktury zagęszczacza. Zależy
ona od rodzaju zagęszczacza, technologii jego produkcji i sposobu otrzymywania smaru. Do
oznaczenia temperatury kroplenia stosuje się aparat Ubbelhode’a – norma PN-84/C-04139.
Temperatura kroplenia jest to temperatura, w której z naczynia badawczego spada pierwsza
kropla badanego smaru nagrzanego w warunkach opisanych ww. normie. Przyjmuje się, że
temperatura kroplenia smaru powinna być o kilkadziesiąt stopni wyższa niż temperatura, w
której dany smar może pracować. Zwyczajowo przyjmuje się, że temperatura pracy smaru po-
winna być nie wyższa niż 2/3 temperatury kroplenia.

Pomiar lepkości

Lepkość powoduje powstawanie sił przeciwstawiających się przesuwaniu warstw cieczy wzglę-
dem siebie. W przypadku dowolnego ruchu cieczy względem ciała stałego, warstwa cieczy bez-
pośrednio stykająca się z ciałem, dzięki siłom adhezji, przylega do niego i porusza się wraz z
nim. Ten fakt ułatwia określenie profilu prędkości na podstawie znajomości prędkości ciał
względem płynu pod warunkiem, że przepływ będzie laminarny (uwarstwiony). Ruch taki ma
miejsce przy małych liczbach Reynoldsa (Re = vD/











), czyli małych prędkościach v cieczy

względem ciał oraz w przewodach o bardzo małych średnicach D (kapilarach) lub w wąskich
szczelinach. Do pomiaru lepkości stosuje się, między innymi, następujące rodzaje lepkościo-
mierzy (wiskozymetrów).



Przepływowe wykorzystujące przepływ cieczy przez kapilarę (Ostwalda-Pinkiewicza, Vo-

gel-Ossaga i Ubbelohde'a)



Wypływowe oparte na pomiarze czasu wypływu cieczy z naczynia przez otwór (np. kubki

Forda, lepkościomierz Englera, Saybolta, Redwooda)



Rotacyjne wyznaczające opór, spowodowany lepkością dynamiczną, kręcącego się dysku

lub cylindra zanurzonego w cieczy przez pomiar jego momentu lub prędkości obrotowej.

Laboratorium Materiałów konstrukcyjnych i Eksploatacyjnych – P.Wr. – WME

6/8



Lepkościomierze mierzące czas opadania elementu (kulki, tłoka) wiskozymetr Höpplera



Lepkościomierze oscylacyjne wykorzystują fakt, że współczynnik tłumienia drgań zależy

od lepkości – lepkościomierz Stabingera i Stormera



Lepkościomierze bąbelkowe – szybkość wzrostu bąbelka powietrza w cieczy jest odwrotnie

proporcjonalna do lepkości kinematycznej.

W ćwiczeniu zostanie wykorzystany kubek wypływowy Forda (rys.5), który służy do pomiaru
lepkości kinematycznej cieczy w warunkach nielaboratoryjnych. Kształt, pojemność i średnica
otworu w dnie zależy od rodzaju kubka i jest określona przez odpowiednią normę np. FORD,
FRIKMAR, AFNOR, ZAHN, itp.

a)

b)

Rys.5. Pomiar
lepkości kubkiem
Forda: a – schenat
stanowiska; b –
zależność lepkości
kinematycznej od
czasu wypływu.

Pomiaru lepkości dokonuje się przez napełnienie kubka mierzoną cieczą i dopuszczenie do
swobodnego wypływu cieczy przez otwór w dnie kubka. Całkowity czas t opróżniania kubka
jest zależny od lepkości kinematycznej cieczy



, którą można wyznaczyć ze wzoru

𝜈 = 𝑏𝑡 −

𝑎

𝑡

a

b



3 200 0,443



4 200

1,73



5 220

3,28

(5)

gdzie a, b – stałe zależne od rodzaju kubka i średnicy jego otworu



. Tabela obok wzoru podaje

stałe dla kubka Forda, które obowiązują dla lepkości w mm

2

/s oraz czasu wypływu w sekun-

dach. Dla kubków użytych w ćwiczeniu uzyskane wyniki są poprawne, gdy 30 s < t < 100 s.
Jeżeli czas wypływu nie miesi się w tych granicach wówczas pomiar należy wykonać dla kubka
z inną średnicą otworu – mniejszą jeśli t < 30 s i większą gdy t > 100 s. Czas wypływu liczony
jest od chwili, gdy badana ciecz zacznie wypływać z otworu całkowicie wypełnionego kubka, do
chwili, gdy wypływający strumień po raz pierwszy przerwie się w pobliżu otworu.

Wyznaczenie gęstości

Wyznaczanie gęstości ciał polega na zmierzeniu ich objętości V oraz masy m i wykorzystaniu
wzoru (4). O ile wyznaczenie masy nie nastręcza trudności – stosuje się do tego komercyjnie
produkowane wagi o różnej dokładności – to określenie objętości jest zadaniem nieco trudniej-
szym. Objętość, w zależności od stanu skupienia, można wyznaczyć różnymi metodami. W
przypadku cieczy stosuje się do tego celu cylindry miarowe (menzurki) lub zlewki z zaznaczoną
na ściance precyzyjną podziałką objętości. Stosuje się też piknometry, czyli naczynie, które
posiadają jedną konkretną objętość w ściśle określonych temperaturze. Gęstość cieczy można
też wyznaczyć od razu areometrem, w którym wykorzystuje się siłę wyporu, z jaką ciecz działa
na zanurzone w niej ciało stałe. Jest to rodzaj pływaka o podłużnym kształcie z obciążnikiem
na jednym końcu. Głębokość na jaką się on zanurza się w cieczy jest miarą jej gęstości, którą
wprost odczytuje się na umieszczonej na nim skali.

Laboratorium Materiałów konstrukcyjnych i Eksploatacyjnych – P.Wr. – WME

7/8

W przypadku ciał stałych ich objętość można obliczyć na podstawie ich wymiarów charakte-

rystycznych, o ile posiadają one typowe, wykonane z dużą dokładnością kształty. Jeśli obiekt
ma kształt nieregularny, to jego objętość można zmierzyć wkładając go do zlewki wypełnionej
cieczą, tak by ciało zanurzyło się w całości i
na skali objętości odczytać jej przyrost. W
przypadku małych obiektów takie pomiary
nie są dokładne.

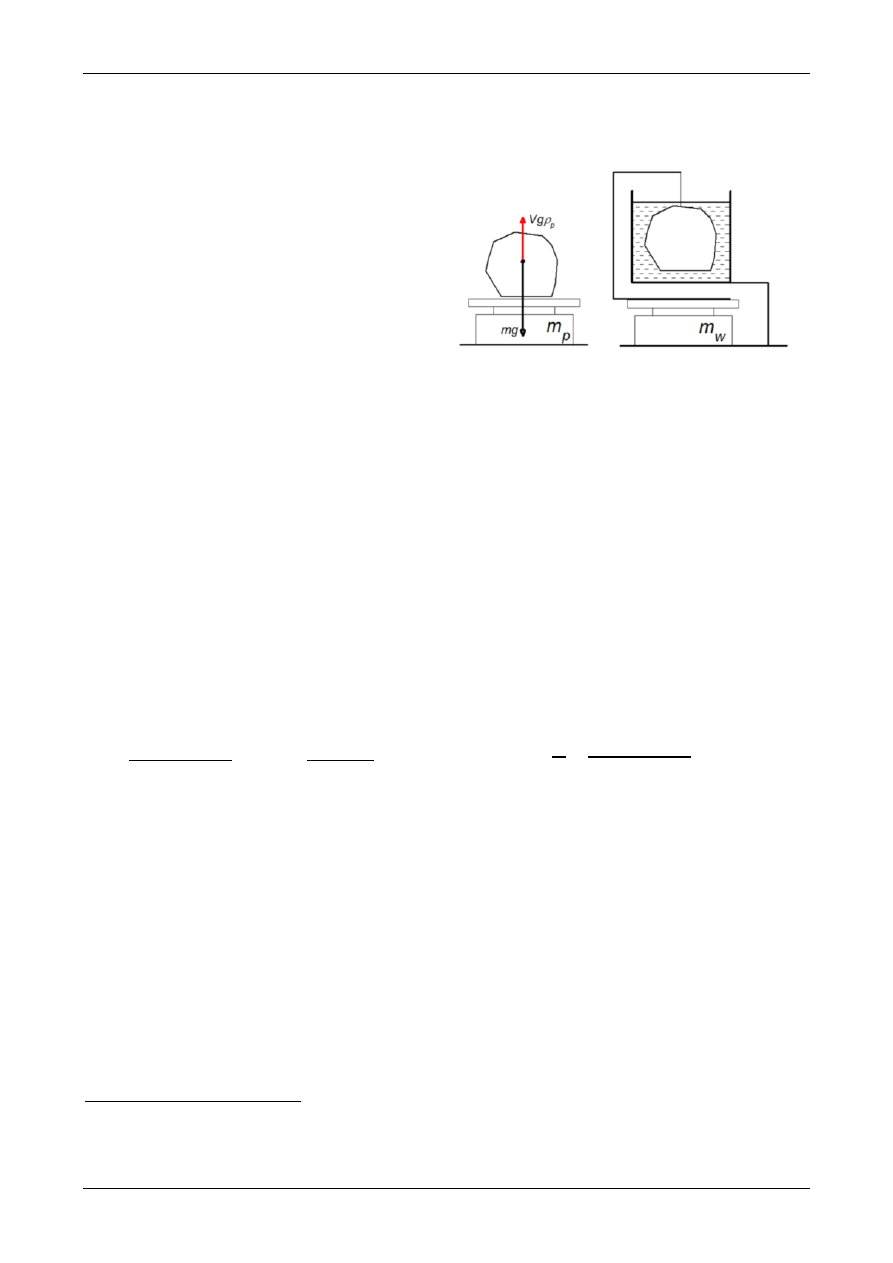
W ćwiczeniu wykorzystuje się metodę po-

legającą na zważeniu ciała w płynach o róż-
nej gęstości a konkretnie w powietrzu i w
wodzie rys.6. Wagi, choć podają, jako wynik
pomiaru masę m obiektu, faktycznie mierzą

jego ciężar, czyli siłę F = mg. Wyrażając się
bardziej precyzyjnie, to mierzony jest nie tyle
ciężar, co siła nacisku F wywierana przez
ciało na szalkę wagi a jako wynik podawana
jest wielkość F/g. Jeśli siła nacisku F wynika tylko z ciężaru ciała, to waga podaje masę obiek-

tu (bo mg /g = m). Jeżeli na obiekt oprócz siły ciężkości działają inne siły, to podawana przez
wagę masa nie odpowiada masie obiektu tylko pewnej pozornej masie m

p

= F/g reprezentują-

cej wypadkową siłę F. Zatem ważąc ciało całkowicie zanurzone w płynie (a takim płynem jest
powietrze) trzeba uwzględnić

2

, skierowaną przeciwnie do ciężaru, siłę wyporu

3

wynoszącą V



p

g

(tu



p

– jest gęstością płynu nie ciała). Siła wypadkowa F, która stanowi nacisk na szalkę wagi,

jest wówczas różnicą ciężaru i siły wyporu i wynosi F = mg –Vg



p

. Z drugiej strony F jest re-

prezentowana przez podawaną przez wagę masę m

p

, czyli F = m

p

g. Łącząc te zależności otrzy-

mujemy po uproszczeniu m

p

= m –V



p

. W tym równaniu niewiadomymi są tylko m i V, bo m

p

jest znane z pomiaru a



p

jest znaną gęstością użytego płynu. Ponieważ są dwie niewiadome,

do uzyskania rozwiązania potrzebne jest drugie podobne równanie, które otrzyma się ważąc
ciało zanurzone w płynie o innej, najlepiej znacznie różniącej się, gęstości. Oznaczmy przez m

p

i m

w

masy podane przez wagę podczas ważenia ciała odpowiednio w powietrzu i w wodzie a

przez



p

i



w

gęstości powietrza i wody. Wówczas rozwiązaniem takiego układu równań będą

wzory na masę m, objętość V ważonego obiektu i gęstość



materiału, z jakiego jest on wyko-

nany w postaci

𝑚 =

𝑚

𝑝

𝜌

𝑤

− 𝑚

𝑤

𝜌

𝑝

𝜌

𝑤

− 𝜌

𝑝

,

𝑉 =

𝑚

𝑝

− 𝑚

𝑤

𝜌

𝑤

− 𝜌

𝑝

zatem

𝜌 =

𝑚

𝑉

=

𝑚

𝑝

𝜌

𝑤

− 𝑚

𝑤

𝜌

𝑝

𝑚

𝑝

− 𝑚

𝑤

(6)

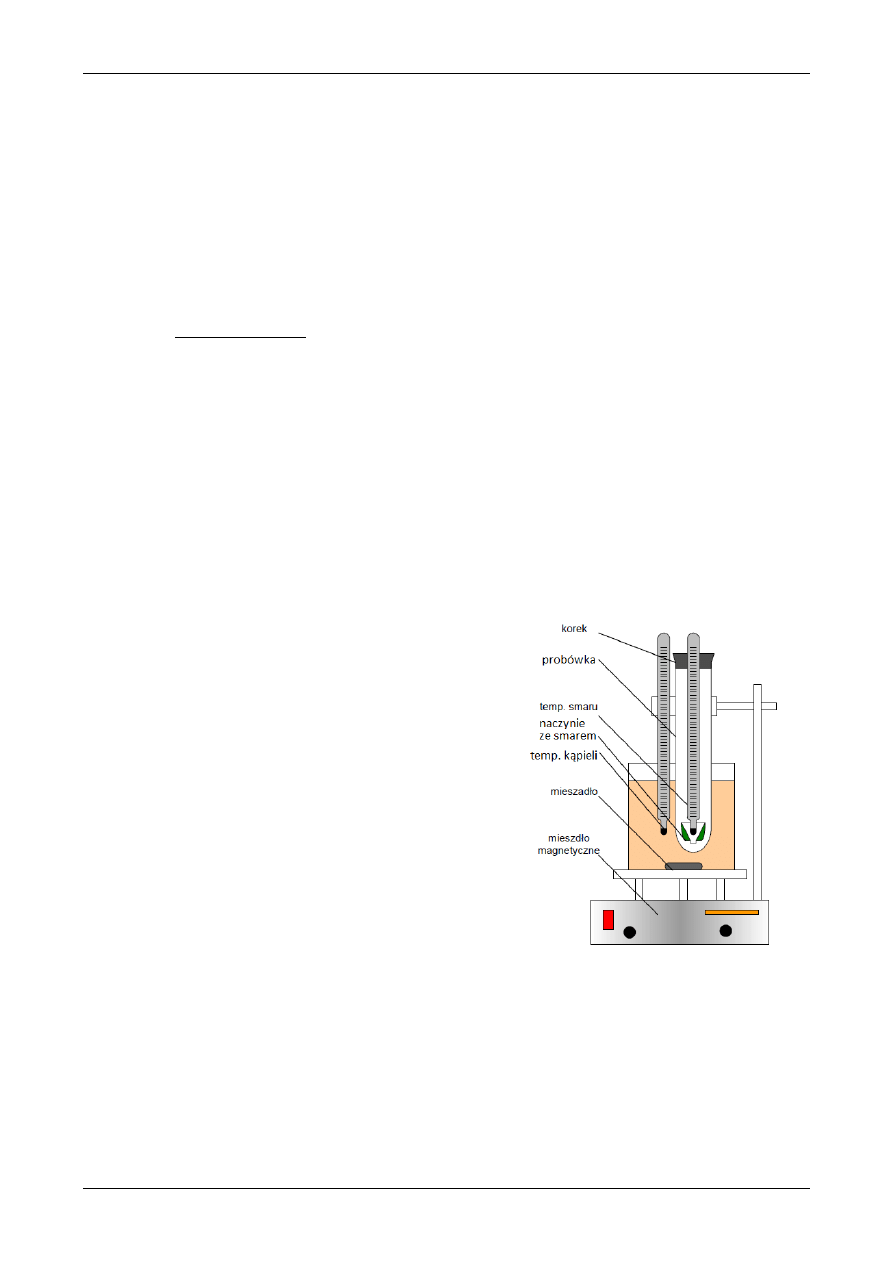
Pomiar temperatury kroplenia

Pomiar temperatury kroplenia dokonuje się na stanowisku pokazanym na rys.7. W celu wy-
znaczenia temperatury kroplenia smaru należy wypełnić naczynie pomiarowe termometru
badawczego smarem, nadmiar smaru należy zebrać łopatką a następnie pręcikiem utworzyć w
smarze lej w kształcie stożka. Potem naczynie należy przymocować do termometru i wprowa-
dzić całość do próbówki zanurzonej w kąpieli wodnej. Po złożeniu całego stanowiska należy
uruchomić mieszadło i podgrzewać cały układ, jednocześnie obserwując wskazania termome-
trów. Po pojawieniu się zalążka kropli należy ją obserwować do momentu oderwania się od
otworu naczynia i w chwili oderwania zarejestrować temperaturę kąpieli wodnej i smaru. Jako
temperaturę kroplenia danego smaru przyjąć średnią arytmetyczną obu tych wartości.

2

Normalnie ważąc obiekty w powietrzu nie uwzględnia się sił wyporu, jako że są one pomijalnie małe. Dla materia-

łów cięższych od wody błąd ten jest mniejszy od 0,12%., np. dla stali wynosi on zaledwie 0,015%.

3

Zgodnie z prawem Archimedesa siła wyporu równa jest ciężarowi wypartej cieczy, czyli iloczynowi objętości zanu-

rzonej części ciała przez ciężar właściwy cieczy.

Rys.6. Zasada pomiaru gęstości

Laboratorium Materiałów konstrukcyjnych i Eksploatacyjnych – P.Wr. – WME

8/8

Przebieg ćwiczenia

Lepkość oleju

1. Zmierz lepkość kinematyczną dostarczonego oleju kubkiem Forda dla różnych tempera-

tur

2. Wyznacz gęstość oleju dla temperatury pokojowej metodą ważenia znanej objętości pły-

nu. Do odmierzenia wybranej objętości oleju użyj zlewki z podziałką objętości.

3. Oblicz lepkości dynamiczne dla temperatury pokojowej
4. Nanieś wynik na wykres
5. Wyznacz stałe do równania Walthera (3) wg wzorów:

𝑚 =

lg lg(𝜈

1

+𝑐)−lg lg(𝜈

2

+𝑐)

lg 𝑇

1

−lg 𝑇

2

𝑘 = lg lg(𝜈

1

+ 𝑐) + 𝑚 lg 𝑇

1

przyjmij

c = 0,8

Wskazówka: W Excelu wykonaj wykres lg lg(



+ 0,8) w funkcji lg(T ) i oblicz współczyn-

niki regresji liniowej

Gęstość ciał stałych

1. Zmierz temperatury otoczenia i wody (jako drugiego płynu).
2. Oblicz gęstości powietrza i wody. Zmierz gęstość wody metodą ważenia znanej objętości

płynu.

3. Wyznacz gęstości trzech próbek wykonanych z różnych materiałów metodą ważenia w

dwóch płynach.

Temperatura kroplenia

Wyznacz temperaturę kroplenia dostarczonego
smaru przy pomocy trzech niezależnych pomiarów.
Wylicz wartość średnią

Rys.7. Schemat stanowiska do pomiaru tem-
peratury kroplenia smaru