10. Kinetyczna teoria gazów.

Wybór i opracowanie zadań od 10.1do 10.6 - Bogusław Kusz.
Więcej zadań z tej tematyki znajdziesz w II części skryptu.


10.1.
Funkcję rozkładu prędkości cząsteczek gazu doskonałego można zapisać w formie:

kT

mV

e

CV

V

f

2

2

2

)

(

−

=

gdzie C jest pewną stałą a m jest masą cząsteczki. Jest to jednocześnie

rozkład prawdopodobieństwa znalezienia w gazie o temperaturze T cząstek o prędkości V.
Wyprowadź wzór oraz oblicz najbardziej prawdopodobną prędkość wodoru i tlenu jeśli
T=300K,

µ

H2

=2g/mol=2·10

-3

kg/mol i

µ

O2

=32g/mol=32·10

-3

kg/mol

, R=8,31 J/(kg mol).

Naszkicuj wykres f(V) obu gazów.

10.2.

Funkcję rozkładu prędkości cząsteczek gazu doskonałego można zapisać w formie:

kT

mV

e

DV

V

f

2

2

2

)

(

−

=

gdzie D jest pewną stałą a m jest masą cząsteczki. Jest to jednocześnie

rozkład prawdopodobieństwa znalezienia w gazie o temperaturze T cząstek o prędkości V.
Wyprowadź wzór oraz oblicz najbardziej prawdopodobną prędkość cząstek azotu gdy
temperatura gazu wynosi T

1

=300K i T

2

=900K

. Naszkicuj wykres f(V) gazu w obu

temperaturach.

µ

N2

=28g/mol=28·10

-3

kg/mol, R=8,31 J/(kg mol).

10.3.

Ocenić ciśnienie i koncentrację powietrza na wysokości: a/ 0m npm, b/ 2499m npm, c/
4807m npm, d/ 8850m npm. Założyć, że przyspieszenie ziemskie i temperatura powietrza nie
zależą od wysokości przy czym g=9.81m/s

2

i t

p

=7

0

C.

10.4.*

Czy na Mount Evereście można zagotować jajko na twardo ? Założenia:
1/ ścinanie białka zachodzi w temperaturze t=60-72

0

C ,

2/ związek temperatury wrzenia wody z ciśnieniem powietrza przy powierzchni wody jest

następujący:

x

x

T

T

p

p

A

1

1

ln

1

0

0

−

=

gdzie: p

0

=9,81·10

4

Pa, T

0

=373K, A=4950 K, a T

x

jest temperaturą wrzenia wody pod

ciśnieniem p

x

, przyspieszenie ziemskie i temperatura powietrza nie zależą od wysokości przy

czym g=9.81m/s

2

i t

p

=7

0

C.

10.5.

Na jakiej wysokości ciśnienie powietrza spada do połowy swej wartości przy powierzchni
morza ? Założyć, że przyspieszenie ziemskie i temperatura powietrza nie zależą od
wysokości. Dane: g=9.81m/s

2

, t

p

=10

0

C, ciśnienie p

0

=1000hPa.

10.6.**

W wirówce o promieniu R=1m obracającej się z prędkością obrotową ω=3000obr/min.
znajdują się pary fluorku uranu UF

3

.Określ jak zmienia się koncentracja tego gazu w

zależności od odległości od osi obrotu. Porównaj koncentracje w przypadku gdy mamy do
czynienia z mieszaniną

235

UF

3

i

238

UF

3

. Założenia:

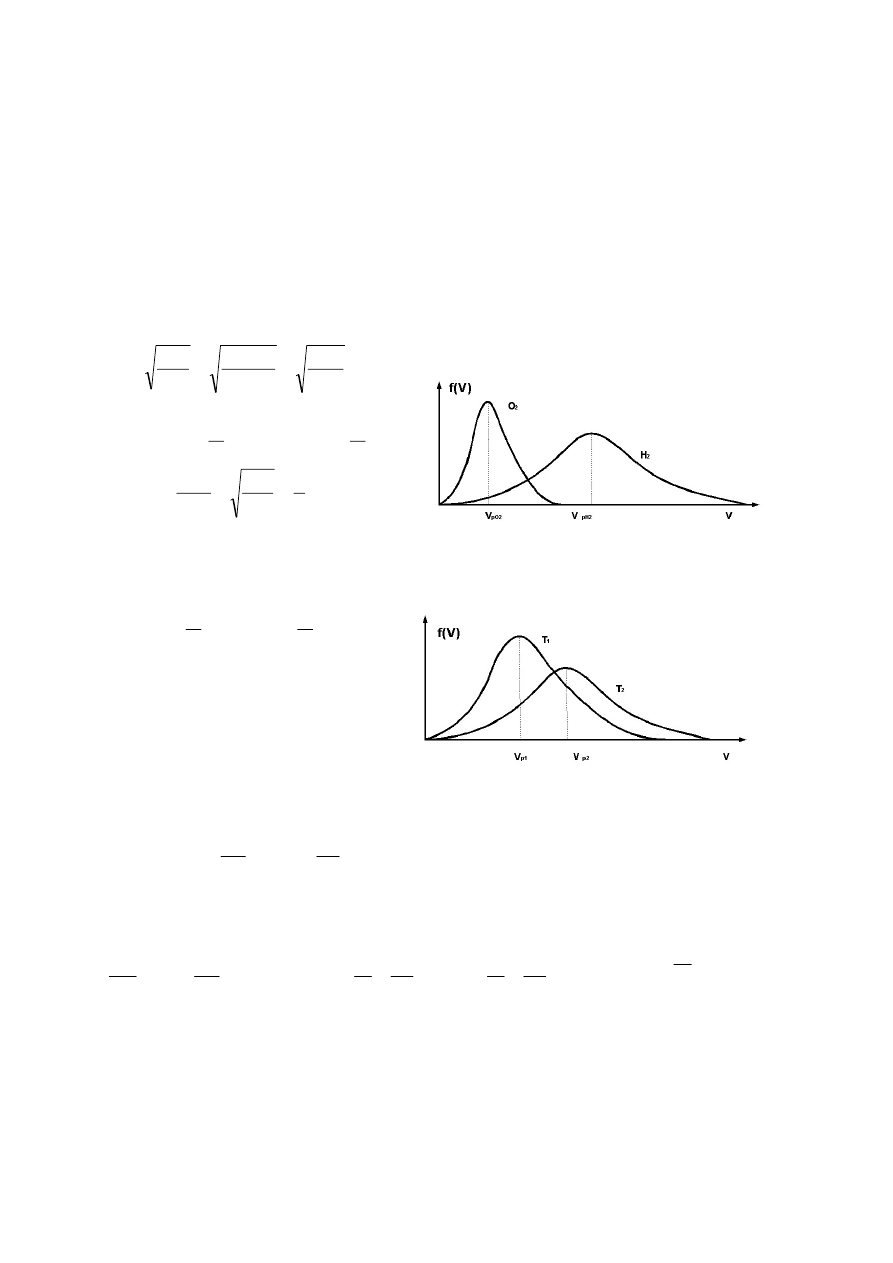
1/ wlot gazu o temperaturze T=400K i ciśnieniu normalnym jest na osi wirówki,
2/ iloraz koncentracji wynosi: η

0

= n

235

/n

238

=0.007 oraz µ

235

=292g/mol, µ

238

=295g/mol,

3/ wirówka jest obracającym się wokół pionowej osi cienkim walcem (wpływ siły ciężkości
można zaniedbać).

10.Rozwiązania:

10.1.R

.

Problem sprowadza się do znalezienia maksimum funkcji f(V) czyli przyrównaniu jej
pochodnej do zera. Taka procedura prowadzi do wyniku:

µ

µ

RT

kT

N

m

kT

V

A

p

2

2

2

=

=

=

.

Dla gazów z zadania:

.

4

1

1579

73

,

394

2

2

2

2

2

2

=

=

=

=

O

H

pH

pO

pH

pO

V

V

oraz

s

m

V

i

s

m

V

µ

µ

10.2.R

.

.

730

422

2

1

s

m

V

s

m

V

pT

pT

=

=

10.3.R.

Przy takich założeniach można zastosować tzw. wzór barometryczny (patrz 10.4.R):

,

)

(

0

0

RT

gh

kT

mgh

e

p

e

p

h

p

µ

−

−

=

=

gdzie: p(h) jest ciśnieniem gazu o temperaturze T na

wysokości h względem poziomu odniesienia na którym panuje ciśnienie p

0

, m- masa

molekuły gazu, µ-masa molowa gazu.
Związek między ciśnieniem i koncentracją η jest następujący:

RT

gh

A

e

czyli

kT

p

V

N

i

kT

p

V

N

Nk

R

N

N

nR

T

pV

µ

η

η

η

η

−

=

=

=

=

=

⇒

=

=

=

0

0

0

.

Dla powietrza możemy przyjąć:

µ

=28,8g, p

0

=1000 hPa.

Wyniki obliczeń:
a/ p(0)=p

0

=1000 hPa, η

0

=2,6 ·10

25

m

-3

,

b/ p(2499m)=0,74p

0

, η(2499m)=0,74η

0

,

c/ p(4807m)=0,55p

0

, η(4807m)=0,55 η

0

,

d/ p(8850m)=0,33p

0

, η(8846m)=0,33 η

0

.

Jak widać z powyższych wyników taternicy na Rysach odczuwają lekki brak powietrza,
alpiniści na Mount Blanc (4807m) muszą głębiej oddychać a himalaiści na Mount Evereście
(8850m) mają bardzo duże problemy z oddychaniem.

10.4.R.

Ciśnienie na Mount Evereście w podanych warunkach wynosi p

x

=0,33p

0

(patrz zadanie 10.3)

więc woda w tym miejscu będzie wrzała w temperaturze

C

K

T

czyli

A

T

p

p

A

T

T

x

x

x

0

0

0

0

72

345

33

.

0

ln

1

ln

1

1

1

=

=

−

=

−

=

.

Wniosek: porównując temperatury krzepnięcia białka i temperaturę wrzenia wody można
sądzić, że na Mont Evereście prawdopodobnie można ugotować jajko na miękko. Ponieważ
przyjęliśmy w naszych obliczeniach parę założeń a temperatury niewiele się różnią więc nie
można wykluczyć, że w pewnych warunkach uda się przygotować jajko na twardo.

10.5.R.

km

g

RT

p

p

g

RT

h

h

77

,

5

2

ln

ln

0

=

=

=

µ

µ

.

10.6.R.
Można znaleźć związek między równaniem Boltzmanna, wzorem barometrycznym i
rozkładem koncentracji gazu w wirówce.

W ogólnym przypadku równanie Boltzmanna jest następujące:

kT

E

E

e

n

n

1

2

1

2

−

−

=

gdzie n

1

i n

2

koncentracje cząstek o energii E

1

i E

2

w temperaturze T.

Także w przypadku gdy cząstkami są cząsteczki powietrza ich koncentracja zależy od ich
całkowitej energii. Na wysokości h cząstki mają energię wyższą o wielkość mgh co wynika ze
stałości siły ciężkości mg. Biorąc to pod uwagę otrzymujemy wzór barometryczny:

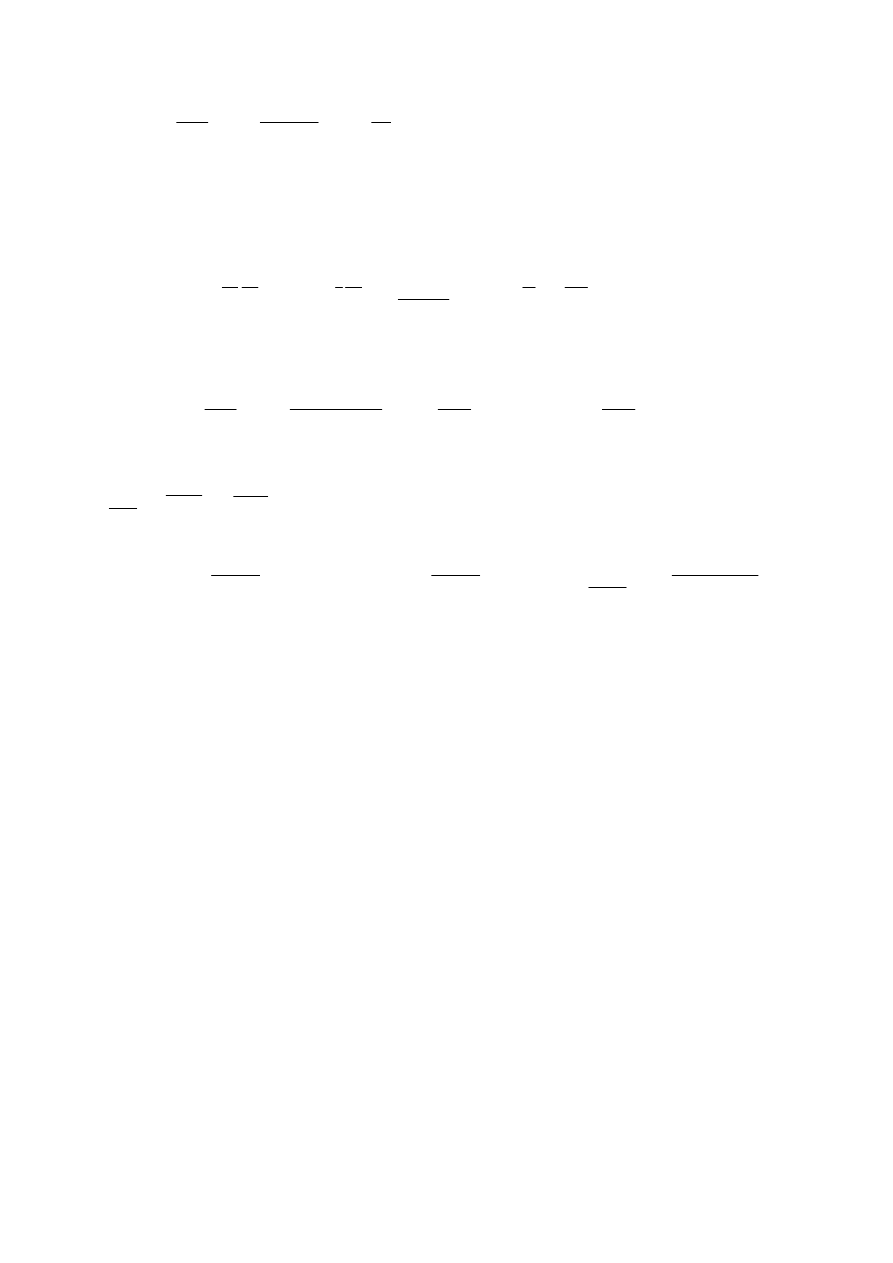
kT

mgh

kT

E

mgh

E

kT

E

E

e

n

e

n

e

n

n

−

−

+

−

−

−

=

=

=

1

1

1

2

0

0

1

2

.

W wirówce obracającej się wokół pionowej osi na stałej wysokości koncentracja cząstek gazu
znajdującego się w bębnie zależy od prędkości obrotowej ω i od odległości od osi obrotu r.
Wynika to z działania siły odśrodkowej F

od

=mω

2

r . Porównując energię potencjalną w polu

siły odśrodkowej cząstek blisko osi E

0

z cząstkami znajdującymi się w odległości r E

r

od osi

stwierdzimy, że :

.

2

)

0

(

)

(

2

2

0

2

0

od

r

r

F

F

gdzie

r

m

dr

r

m

dr

F

E

r

E

−

=

−

=

−

=

=

−

∫

∫

ω

ω

Dlatego podstawiając do równania Boltzmanna

E

1

=E

0

- mω

2

r

2

/2 oraz E

2

= E

0

,

otrzymamy zależność koncentracji cząstek gazu w funkcji odległości od osi obrotu:

.

2

0

2

)

2

/

(

1

0

2

2

2

2

2

2

2

0

0

1

2

kT

r

m

r

kT

r

m

r

kT

r

m

E

E

r

kT

E

E

e

n

n

czyli

e

n

e

n

e

n

n

n

ω

ω

ω

=

=

=

=

=

−

−

−

−

−

−

Przy ścianie bocznej wirówki (r=R

w

) koncentracja drobin

238

UF

3

jest

=

=

=

RT

R

kT

R

m

Rw

w

w

e

e

n

n

2

2

0

2

2

2

2

µω

ω

1,11 razy większa od koncentracji przy osi.

Porównując koncentracje różnych izotopów uranu w tej wirówce mamy:

RT

R

R

R

R

RT

R

R

RT

R

R

w

w

w

e

n

n

czyli

e

n

n

oraz

e

n

n

2

)

(

0

238

235

2

238

0

238

2

235

0

235

2

2

238

235

2

2

238

2

2

235

ω

µ

µ

ω

µ

ω

µ

η

η

−

−

−

=

=

=

=

.

997

,

0

0

⋅

=

η

η

R

Powyższy wynik mówi, że stosunek koncentracji izotopów ulega zmianie w wirówce. Mimo,
że zmiana jest stosunkowo niewielka to układ kaskadowo połączonych wirówek może służyć
do rozdzielenia gazów, których masy niewiele się różnią.