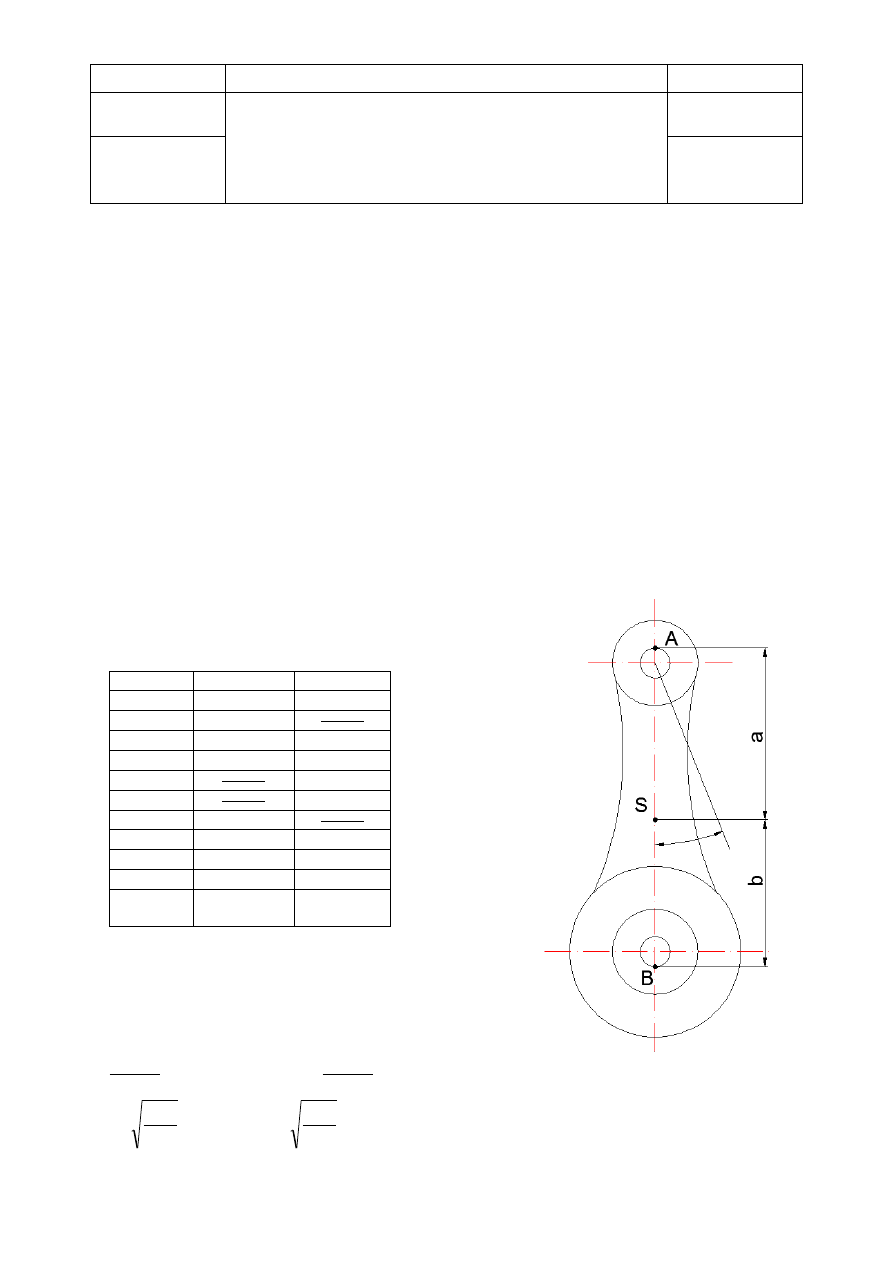
Przedmiot:

Dynamika maszyn - laboratorium

Data:

Temat
ćwiczenia:

Doświadczalne wyznaczanie

momentów bezwładności

części maszyn.

16.10.2013r.

13M3,
zespół I

MiBM
2013/2014

1. Cel ćwiczenia:

Celem ćwiczenia było doświadczalne wyznaczenie masowych momentów

bezwładności trzech różnych elementów konstrukcyjnych. W tym celu
wykorzystaliśmy metody wahadła fizycznego, wahadła torsyjnego i wahadła
płaskiego.

2. Metoda wahadła fizycznego.

Aby wyznaczyć masowy moment bezwładności tego elementu należało wykonać
badania w dwóch różnych położeniach utwierdzając element raz punkcie A, a
następnie w punkcie B. Element został wprowadzany w drgania o niewielkim
wychyleniu z położenia równowagi i dokonywaliśmy pomiarów 20 okresów

dziesięciokrotnie, następnie wyliczaliśmy wartość średnią (po odrzuceniu dwóch
skrajnych wyników traktowanych jako „błędne”) i wyznaczaliśmy średnią wartość
jednego pełnego okresu. Następnie z odpowiednich wzorów wyznaczaliśmy
odległości a i b oraz moment bezwładności względem środka masy.

]

[

161

,

0

]

[

444

,

0

m

l

kg

m





Lp

20 T

A

[s]

20 T

B

[s]

1

15,47

14,59

2

15,52

14,20

3

15,60

14,47

4

15,56

14,50

5

16,30

14,60

6

15,20

14,50

7

15,53

14,83

8

15,45

14,50

9

15,45

14,61

10

15,50

14,60

Wartość

średnia

15,51

14,54

Następnie obliczamy okresy dla jednego pełnego
wychylenia:

]

[

775

,

0

20

0

s

T

T

średnieA

A





,

]

[

727

,

0

20

0

s

T

T

średnieB

B





mga

I

T

A

A



2

0



,

mgb

I

T

B

B



2

0



Przekształcając powyższe wzory na okres drgań wahadła fizycznego otrzymamy:

mga

T

I

A

A



















2

0

2



mgb

T

I

B

B



















2

0

2



Korzystając z twierdzenia Steinera:

2

2

mb

I

ma

I

I

B

A

S









0,161

oraz po wprowadzeniu oznaczeń:

]

[

804

,

0

81

,

9

161

,

0

2

2

0

s

g

l

T













,

b

a

l





Otrzymujemy wzory na odległości a i b

]

[

116

,

0

529

,

0

600

,

0

646

,

0

*

2

529

,

0

646

,

0

*

161

,

0

2

2

0

2

0

2

0

2

0

2

0

m

T

T

T

T

T

l

a

B

A

B



















,

]

[

045

,

0

116

,

0

161

,

0

m

a

l

b











oraz wzór na moment bezwładności względem środka masy:

]

[

001727

,

0

116

,

0

161

,

0

804

,

0

775

,

0

116

,

0

444

,

0

2

2

2

2

0

2

0

m

kg

a

l

T

T

ma

I

A

s











































3. Metoda wahadła torsyjnego:
Element w postaci wirnika silnika elektrycznego został podwieszony na trzech
nierozciągliwych linkach. Następnie zostaje on wprowadzony w wahadłowy ruch
obrotowy. Dokonujemy pomiarów 20 okresów dziesięciokrotnie, następnie

wyliczaliśmy wartość średnią (po odrzuceniu dwóch skrajnych wyników
traktowanych jako „błędne”) i wyznaczaliśmy średnią wartość jednego pełnego
okresu.

Lp

20 T

A

[s]

1

12,72

2

12,86

3

12,9

4

12,78

5

12,82

6

12,89

7

12,86

8

12,95

9

12,72

10

12,8

Wartość

średnia 12,83

φ

z

]

[

6

,

0

kg

m



l = 0,545 [m], r = 0,043 [m]

]

[

641

,

0

20

s

T

T

średnie





Na skutek obrotu elementu o kąt φ jego środek masy podnosi się o odległość:



















2

sin

4

2

2

2



r

l

l

z

lub po rozwinięciu powyższego wyrażenia w szereg Taylora:

2

2

2



l

r

z



Wykorzystując zasadę zachowania energii:

2

2

2

2

1

2

1

2

1











s

s

I

z

m

I

E







E - energia kinetyczna

2

2

2



l

mgr

mgz

U





U - energia potencjalna

Otrzymujemy następujący wzór na okres drgań

2

2

mgr

l

I

T

s





Skąd obliczamy:

2



m

I

s



Gdzie promień bezwładności ρ określony jest związkiem:

]

[

48

,

1

81

,

9

545

,

0

2

2

0

s

g

l

T











]

[

0186

,

0

043

,

0

48

,

1

641

,

0

0

m

r

T

T











Ostatecznie otrzymujemy:

]

[

10

07

,

2

0186

,

0

6

,

0

2

4

2

2

m

kg

m

I

s

















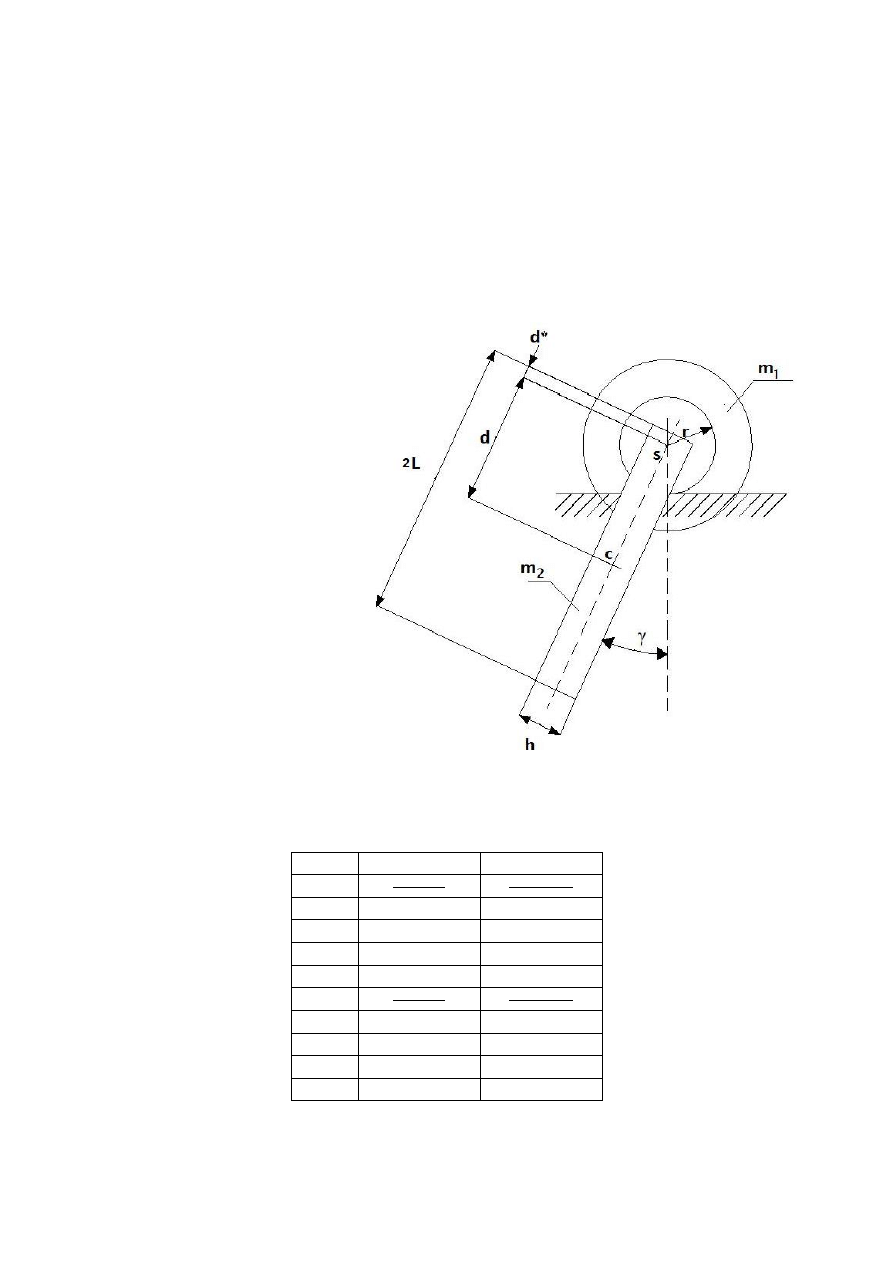
4.Metoda wahadła płaskiego
Moment bezwładności wirnika silnika elektrycznego możemy wyznaczyć za pomocą
metody wahadła płaskiego dołączając element o znanych parametrach dzięki temu
otrzymamy wahadło wykonujące ruch płaski. Wyznaczamy okres drgań T

a

wahadła

metodą doświadczalną mierząc czas 20 wychyleń elementu. Dokonujemy 10
pomiarów i wyznaczamy z nich wartość średnią (po odrzuceniu 2 skrajnych
wyników). Następnie dzięki pozostałym danym możemy wyznaczyć moment
bezwładności dołączonego elementu oraz wirnika.

Dane:
2L=0,40[m]
h=0,05[m]
d*=0,019[m]

d=0,081[m]
r=0,015[m]
m

1

=8,60[kg]

m

2

=3,74[kg]

schemat stanowiska pomiarowego

L.p.

20*T

a

[s]

T

a

[s]

1

19,75

0,9875

2

19,47

0,9735

3

19,47

0,9735

4

19,34

0,9670

5

19,37

0,9685

6

19,19

0,9595

7

19,47

0,9735

8

19,53

0,9765

9

19,40

0,9700

10

19,25

0,9625

T

a

śr.

=0,97[s]

Moment bezwładności dołączonego elementu

J

e

=

1

/

12

.

m

2

(L

2

+h

2

)=1/12*3,74*(0,04+0,0025)

J

e

=0,01325

Moment bezwładności wirnika

J

w

=m

2*

g*d*T

2

/4π

2

– [m

1

r

2

+m

2

(r-d)

2

+J

e

]=

=3,74*9,81*0,081*0,97/4*9,86–[8,60*0,000225+3,74*(0,015-0,081)

2

+0,01325]

J

w

=6,94

5.Wnioski

Podczas zajęć wykonaliśmy trzy bardzo proste metody wyznaczenia momentu
bezwładności elementów. Można powiedzieć że są to właściwie sposoby banalnie

proste, nie wymagające żadnych dodatkowych przyrządów. Dzięki nim możliwe jest
wyważenie różnego rodzaju elementów w sposób bardzo szybki i bezproblemowy
(oczywiście musimy pamiętać o ograniczonej dokładności, zachowaniu możliwości
pewnego błędu).