Punktem wyjściowym do badań niezawodności jest zwykle niezgodność rzeczywistego okresu 
trwałości T obiektu z założonym dla niego czasem oczekiwanej pracy t, przy czym często akcent 
przesuwa się z poznania tego jaką trwałość ma dany obiekt na to, jaki obiekt ma daną trwałość. 
Ogólnie rzecz biorąc mogą zaistnieć trzy przypadki: 
1 Kiedy okres trwałości T jest większy od założonego czasu t

m

 (T > t

m

). 

2.Kiedy okres trwałości T odpowiada dokładnie tej wartości  (T= t

m

). 

3.Kiedy okres trwałości jest mniejszy od założonego czasu T

m

 (T< t

m

). 

Przypadek 3 jest niedopuszczalny. Obiekt pracował krócej niż przewidywano, a więc zawiódł nas. 
Taki przypadek wskazuje na potrzebę dalszej pracy nad udoskonaleniem obiektu lub użytkowaniem 
go w bardziej złagodzonych warunkach obciążeniowych. 
Przypadek 1 jest pożądanym stanem obiektu, chociaż ze względów komercyjnych prowadzi do 
pewnego regresu produkcyjnego (zmniejszenia globalnego zapotrzebowania na dany obiekt). 
Najkorzystniejszym jest przypadek 2. Obiekt był przydatny dokładnie tyle ile miał być, tj. okres 
trwałości T ma wartość optymalną T = T

a

. Z uwagi jednak na nieunikniona losowość warunków pracy, 

celowe jest rozpatrywanie łączne punktu 1. oraz 2., czyli nierówności T> t

m

. 

Chcąc mieć szacunek prawdopodobieństwa czasu „życia" obiektów należy znać przebiegi 

następujących  funkcji,  będących  miarami  niezawodności:  f(t),  F(t),  R(t),  gdzie:  przy  czym:  t  - 
oznacza czas bieżący „życia" obiektów. 

 

Aby więc określić niezawodność obiektu należy: 
1 .Wybrać próbkę losową z pewnej populacji obiektów. 
2.Przeprowadzić badanie trwałości obiektów z tej próbki. 
3.Przeszacować wyniki z próbki na populację. 
4.Wyznaczyć funkcję gęstości prawdopodobieństwa f(T). 
5.Wyznaczyć dystrybuantę trwałości F(T). 
6.Obliczyć niezawodność R(T) badanych obiektów.  

 

Metodyka wyznaczania niezawodności 

Do podstawowych wskaźników niezawodności zalicza się: 



 

Prawdopodobieństwo poprawnego działania obiektu P(t) lub elementu p(t) 



 

Częstość uszkodzeń f(t)  



 

Średnia częstość uszkodzeń (częstość uszkodzeń obiektów nienaprawialnych) f

śr

(t) 



 

Intensywność uszkodzeń obiektów Λ(t) lub elementów λ(t) 



 

Średni czas poprawnego działania do pierwszego uszkodzenia ₸ 



 

Średni czas poprawnego działania pomiędzy kolejnymi uszkodzeniami T

o

  



 

Współczynnik gotowości K

g

  

 

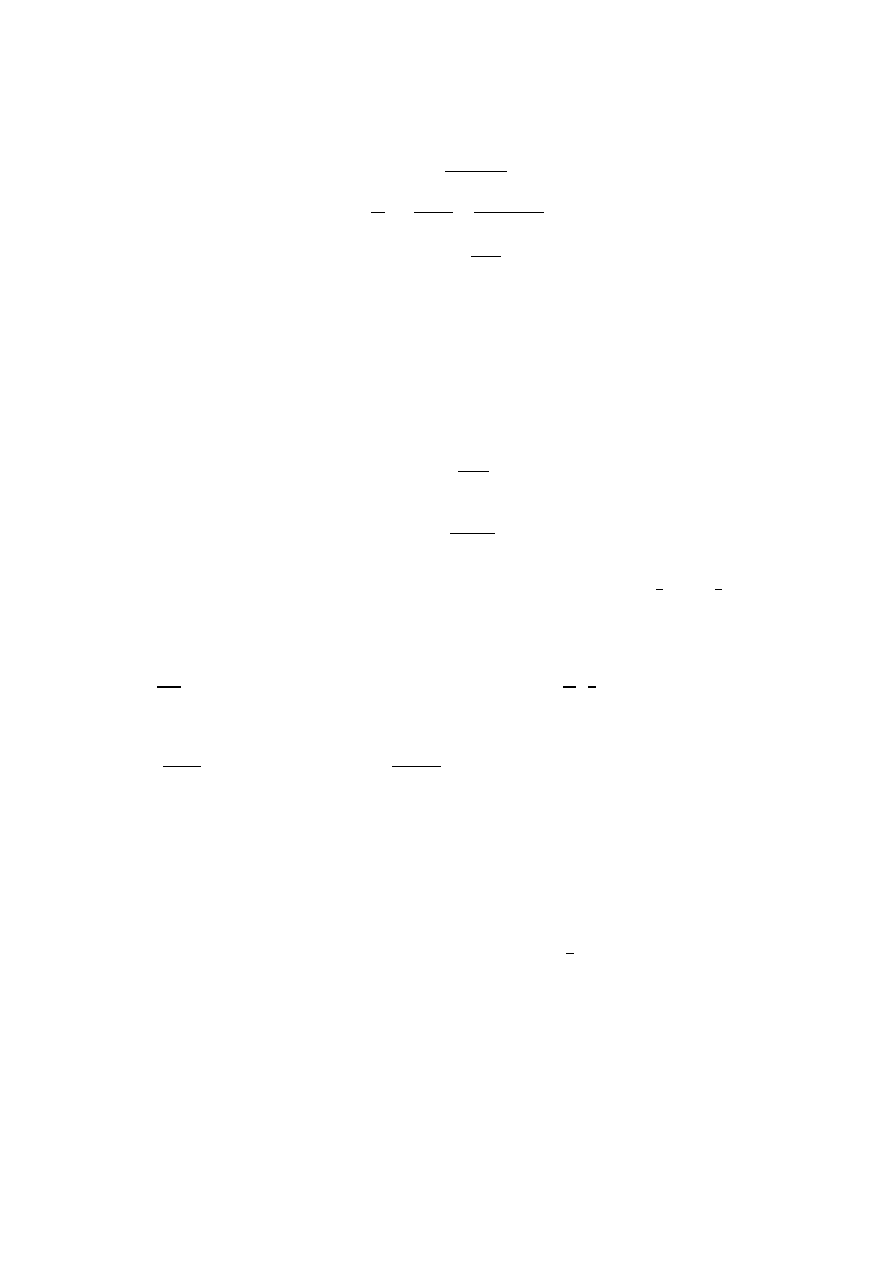
Przydatne wzory: 
Prawdopodobieństwo poprawnego działania obiektu 

 

 

     

        

 

 

   

 

 

 

 

   

   

 

 

   

 

 

 

       

 

 

       

 

 

 

          

    

 

 

W przypadku obiektów o dużej niezawodności dla interesującego nas przedziału czasu (0,t), iloczyn 
Λ*t jest wielkością małą, dużo mniejszą od jedności.  

                 

Niekiedy  zamiast  prawdopodobieństwa  poprawnego  działania  P(t)  jako  wskaźnika  niezawodności 
używa się prawdopodobieństwa uszkodzenia się obiektu Q(t). Zdolność obiektu lub jego uszkodzenie 
się są zdarzeniami wzajemnie wykluczającymi się i tworzą pełny zbiór zdarzeń. W związku z tym na 
podstawie znanych zależności z rachunku prawdopodobieństwa można napisać: 
P(t) + Q(t) = 1a zatem Q(t)=1-P(t). 

      

    

 

 

Do oszacowania częstości uszkodzeń służy estymator o następującej postaci: 

      

     

      

 

gdzie: 

n

t

(Δt) – liczba urządzeń (elementów), które uszkodziły się w przedziale czasu (

   

 
 

       

 
 

    

 
Intensywność uszkodzeń określa się jako tak zwaną gęstość rozkładu prawdopodobieństwa, co wyraża 
się w następujący sposób: 
      

    
    

  

oraz dla zespołów elementów 

     

 

 

 

   

 

   

 

 

 

  

 
 

 (n-liczba zaobserwowanych 

uszkodzeń obiektu w ciągu czasu pracy t

p

.) 

Statystycznym oszacowaniem intensywności uszkodzeń jest poniższy estymator: 
 

 

     

 

 

    

 

  

   

    

przy czym:  

 

  

 

 

 

  

   

 

 

gdzie: 
N

śr

 – średnia ilość poprawnie działających obiektów w przedziale czasu Δt; 

N

i

 – ilość obiektów, które nie uszkodziły się od początku i-tego przedziału czasu. 

N

i+1

 – liczba obiektów poprawnie działających do końca przedziału czasu. 

 
Jeżeli  intensywność  uszkodzeń  jest  stała,  to  średni  czas  poprawnego  działania  do  pierwszego 
uszkodzenia  jest  równy  średniemu  czasowi  poprawnego  działania  obiektu  pomiędzy  kolejnymi 

uszkodzeniami T

o

. W takim przypadku 

        

    

 oraz  

   

 

 

 
 

 

Można  zastosować  do  obliczeń  wzory  przybliżone,  jeżeli  znane  są  prawdopodobieństwa  zdatności 
elementów  obiektu  p

i

(t).  Jeżeli  prawdopodobieństwa  są  wystarczająco  bliskie  jedności,  to 

prawdopodobieństwo zdatności całego obiektu można wyznaczyć za pomocą następującej zależności 
            

 

 

   

 

   

   Jeżeli  dla  wszystkich  elementów  prawdopodobieństwa  niezdatności  q

i

(t)  są  

w przybliżeniu jednakowe, to