Co to jest analiza regresji?
Celem analizy regresji jest badanie związków pomiędzy wieloma
zmiennymi niezależnymi (objaśniającymi) a zmienną zależną (objaśnianą),
która musi mieć charakter liczbowy. W naukach społecznych, przyrodniczych i
ekonomicznych analiza regresji jest szeroko stosowana jako narzędzie badawcze
pozwalające opisać i zrozumieć zjawiska
wielowymiarowe. Należy też
wspomnieć, że w pewnych sytuacjach stworzony model służy do dokonania
prognozy (predykcji) wartości zmiennej zależnej dla nowych obiektów lub
kolejnych okresów czasowych.
W klasycznej analizie regresji wielokrotnej model ma postać:
Y
i
= b
0
+ b
1
X
1
+ ... + b
k
X
k
+ e
i
i pozwala odpowiedzieć na pytanie “jakie wielkości w najlepszy sposób opisują
poziom zmiennej Y”.
Parametr b
0
interpretujemy jako przeciętny (oczekiwany) poziom zmiennej
objaśnianej Y gdy wszystkie zmienne objaśniające przyjmują wartość 0.
Wzrost wartości zmiennej objaśniającej X
i
o jednostkę powoduje zmianę
wartości oczekiwanej zmiennej zależnej o b
i
jednostek, przy założeniu, że
pozostałe zmiennej niezależne zachowują stałe wartości.
Analiza regresji w analizie szeregów czasowych
W przypadku analizy szeregów czasowych, rolę zmiennej objaśniającej
pełni zmienna czasowa (oznaczana czasami symbolem t).
Model trendu liniowego dla szeregu czasowego przyjmuje więc postać:
Y
t
= b
0
+ b
1
t + e
t
Parametr
b
1
interpretować
można
jako
średnioroczny
przyrost
prognozowanej wartości w jednostce czasu.
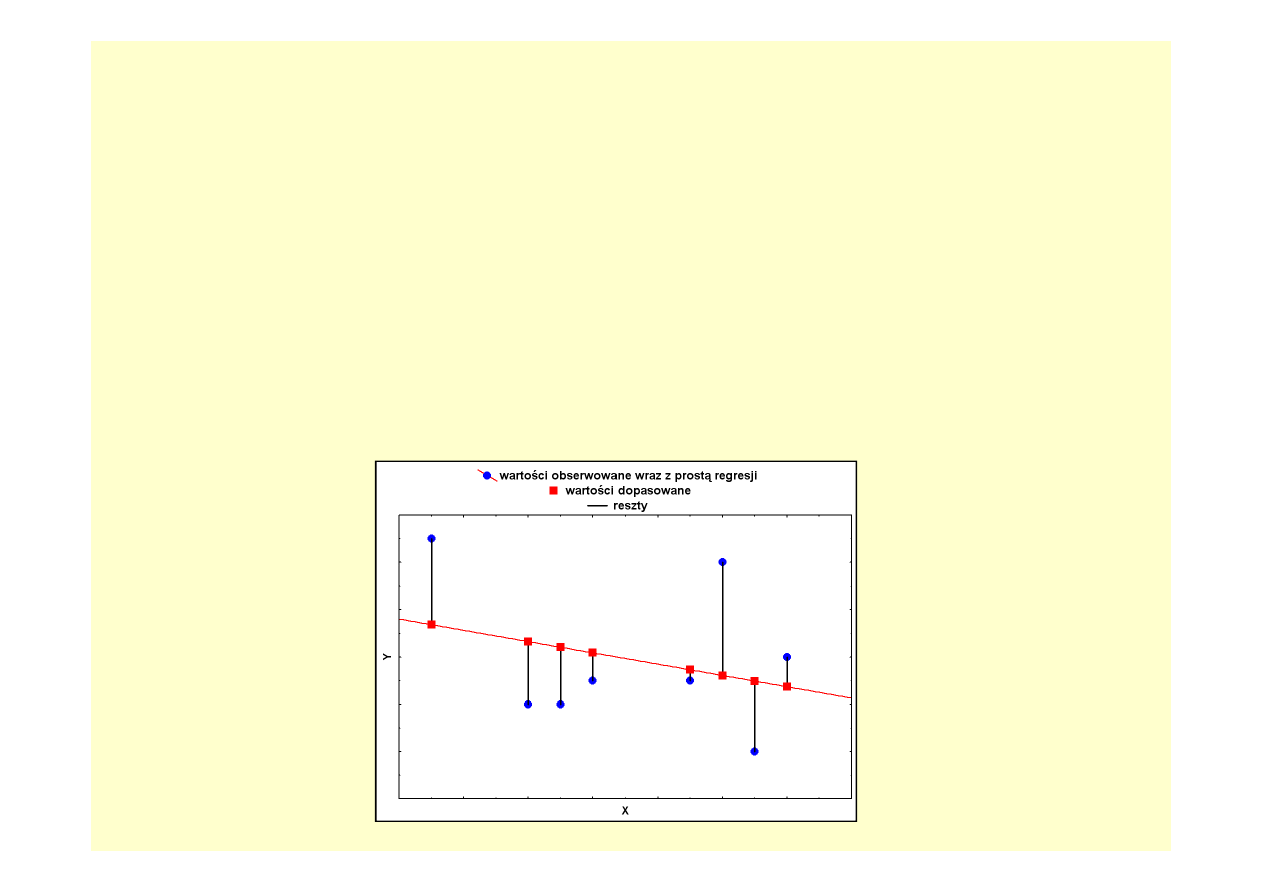
Jak wyznaczany jest model regresji (MNK)?
Wzór m
odelu regresji jest wyznaczany w taki sposób, by zminimalizować
różnicę pomiędzy wartością modelowaną a faktyczną wartością zmiennej
zależnej (Y) dla poszczególnych obiektów (w analizie danych czasowych, dla
poszczególnych okresów czasowych).
W praktyce, najczęściej przedmiotem optymalizacji jest suma kwadratów
odchyleń wartości modelowanych o rzeczywistych pomiarów (tzw. suma
kwadratów reszt). Taka metoda dopasowywania modelu do danych nosi nazwę
METODY NAJMNIEJSZYCH KWADRATÓW (MNK)
.
Sposoby wyznaczania modelu regresji
W programie STATISTICA analiza regresji dostępna jest w module
REGRESJA WIELORAKA
.
Możliwość wyznaczenia wybranych modeli liniowych i nieliniowych
względem jednej zmiennej niezależnej (a więc na przykład dla szeregów
czasowych), udostępniona jest także podczas graficznej analizy danych (za
pomocą
wykresów liniowych
i
wykresów rozrzutu
). Opis możliwości
wykorzystania tych narzędzi do sporządzania prostych prognozo przedstawiono
na poprzednim wykładzie.
Moduł REGRESJA WIELORAKA pozwala na:
• wyznaczenie wzoru modelu regresji;
• ocenę jego dopasowania do danych;
• ocenę istotności poszczególnych zmiennych;
• przeprowadzenia tzw. analizy reszt i określenie wpływu na kształt modelu
ewentualnych obserwacji odstających;
• sporządzenie prognozy punktowej i przedziałowej (z określonym poziomem
ufności).
Czy modele muszą mieć postać liniową?
W programie STATISTICA procedura estymacji i weryfikacji modelu
liniowego dokonywana jest w module
REGRESJA WIELOKROTNA
(warto
wspomnieć, że możliwość oszacowania parametrów modelu regresji i pewnych
podstawowych miar jakości jego dopasowania stwarza także arkusz kalkulacyjny
Excel).
Chociaż natura modelu podlegającego analizie musi być liniowa to za
pomocą formuł arkusza danych bez większych trudności możemy wprowadzać
także
bardziej
skomplikowane
typy
modeli:
np.
model
kwadratowy,
wielomianowy, hiperboliczny (wystarczy w tym celu dodać nową zmienną i
nadać jej wartości według interesującej nas formuły).
Bardziej wyrafinowanym narzędziem służącym do konstruowania modeli
nieliniowych jest moduł
ESTYMACJI NIELINIOWEJ
, który będzie omawiany
na kolejnym wykładzie.
Miary jakości modelu (dopasowania do danych)
Współczynnik determinacji R
2
- parametr ten interpretowany jest zwykle jako
procent zmienności cechy zależnej wyjaśnianej przez model. Tak więc jest to
miernik jakości dopasowania modelu do danych i jako taki może służyć do
porównywania kilku modeli i wyboru najlepszego. Współczynnik determinacji
przyjmuje wartości od 0 do 1 (bywa też wyrażany w procentach), przy czym
oczywiście im jego wartość jest większa tym model lepiej dopasowany.
Współczynnik korelacji wielorakiej (R)
- stopień zależności pomiędzy zmienną
zależną, a wszystkimi cechami niezależnymi uwzględnionymi w modelu jest
określany poprzez wartość R, zwaną współczynnikiem korelacji wielorakiej.
Obliczamy go pierwiastkując współczynnik determinacji, tak więc przyjmuje on
wartości z przedziału [0, 1], przy czym 0 oznacza brak korelacji, zaś wartości 1 to
idealny związek liniowy. W sytuacji, gdy mamy jedną zmienną objaśniającą
dodatkowo możemy ustalić znak współczynnika korelacji, który będzie taki sam
jak znak współczynnika regresji b
1
. Jeśli zmiennych objaśniających jest więcej,
znaku współczynnika korelacji wielorakiej nie da się ustalić, gdyż różne cechy
mogą w różny sposób wpływać na zmienną zależną.
M
a
j-
2
0
0
4
C
ze
-2
0
0
4
L
ip
-2
0
0
4
S
ie
-2
0
0
4
W
rz-
2
0
0
4
P
a
ź-
2
0
0
4
L
is-
2
0
0
4
G
ru
-2
0
0
4
20 000
40 000
60 000
80 000
100 000
120 000
140 000
160 000
180 000
200 000
L
ic
z
b
a
s
a
m
o
c
h
o
d
ó
w
u
ż
y
w
a
n
y
c
h
s
p
ro
w
a
d
z
o
n
y
c
h
z
U
E
Co się dzieje, gdy zwiększamy liczbę zmiennych w modelu?
Współczynnik R
2
rośnie wraz ze zwiększaniem liczby zmiennych w
modelu. Gdybyśmy więc jako jedyne kryterium jakości dopasowania przyjęli
jego wartość, wprowadzimy do modelu wszystkie dostępne cechy objaśniające.
W ten sposób co prawda otrzymalibyśmy model najlepiej dopasowany, lecz jego
złożoność nie pozwoliłaby wyciągnąć sensownych wniosków praktycznych,
ponadto wzajemne oddziaływania licznych zmiennych niezależnych zaburzały by
ich relację z cechą zależną.
W statystyce (i nie tylko) powinna obowiązywać (skądinąd bardzo
sympatyczna zasada KISS): Keep It Sophistically Simple.
Do zaznaczonych na wykresie siedmiu
obserwacji dopasowano dwa modele:
liniowy i wielomian stopnia 5-go.
Bez trudu można zauważyć, że bardziej
złożony model pasuje do danych
niemal idealnie.
Czy jednak prognoza na kolejne
miesiące dokonana na jego podstawie
będzie miała jakąkolwiek wartość?
Istotność statystyczna zmiennych
Prawdopodobieństwo testowe p dla zmiennych występujących w modelu
-
Każde zjawisko da się wyjaśnić jeżeli przyjmiemy odpowiednio dużo zmiennych
objaśniających – taki wniosek można wysnuć na podstawie przykładu
przedstawionego na poprzednim slajdzie. Włączenie do modelu kolejnych potęg
zmiennej czasowej (czyli de facto) wprowadzenie doń kolejnych zmiennych,
spowodowało, iż model był optymalnie dopasowany do danych. Jednakże relacja
ilości danych do liczby zmiennych, nawet intuicyjnie, była zbyt niska.
W praktyce, ocena wzrokowa modelu nie zawsze jest możliwa i nie zawsze
wnioski z niej płynące są jednoznaczne. Aby określić, czy poszczególne zmienne
w modelu regresji opisują jakąś część zmienności cechy zależnej (Y),
przeprowadza się odpowiednie
testy statystyczne
.
W szczególności poddaje się weryfikacji hipotezę, według której wkład danej
zmiennej w wyjaśnianie zmienności cechy Y jest nieistotny.
Wynikiem testu statystycznego jest prawdopodobieństwo testowe p, którego
niskie wartości pozwalają odrzucić „nieciekawą” hipotezę o braku znaczenia
zmiennej objaśniającej w modelu.
Prognozowanie na podstawie modelu regresji
Przewidywanie wartości zmiennej zależnej dla konkretnej jednostki z
rozpatrywanej populacji jest możliwe jedynie wtedy, gdy model jest dobrze
dopasowany, to znaczy wartość współczynnika determinacji daje pożądaną
dokładność prognozy.
Jak zawsze w statystyce prognoza musi być obarczona pewnym błędem.
Miarą jakości prognozy jest tzw. poziom ufności (standardowo przyjmowana
jego wartość to 95%=0,95).
Przedział dla oceny wartości przeciętnych zmiennej zależnej nazywany
jest
przedziałem
ufności
a
dla
konkretnej
jednostki
statystycznej
przedziałem predykcji. Przedział predykcji jest zawsze szerszy od przedziału
ufności.
Przykłady zastosowania modeli regresji
w analizie zjawisk czasowych
Analiza dotyczy danych o liczbie samochodów osobowych, zarejestrowanych
w Polsce w latach 1990-2009. Celem analizy będzie sporządzenie prognozy
tej wielkości na lata 2010-2013.
Do analizy zastosowane zostaną następujące narzędzia statystyczne:
• wykresy liniowe (wraz z wizualizacją wybranych modeli regresji);
• indeksy dynamiki;
• szczegółowa analiza regresji.
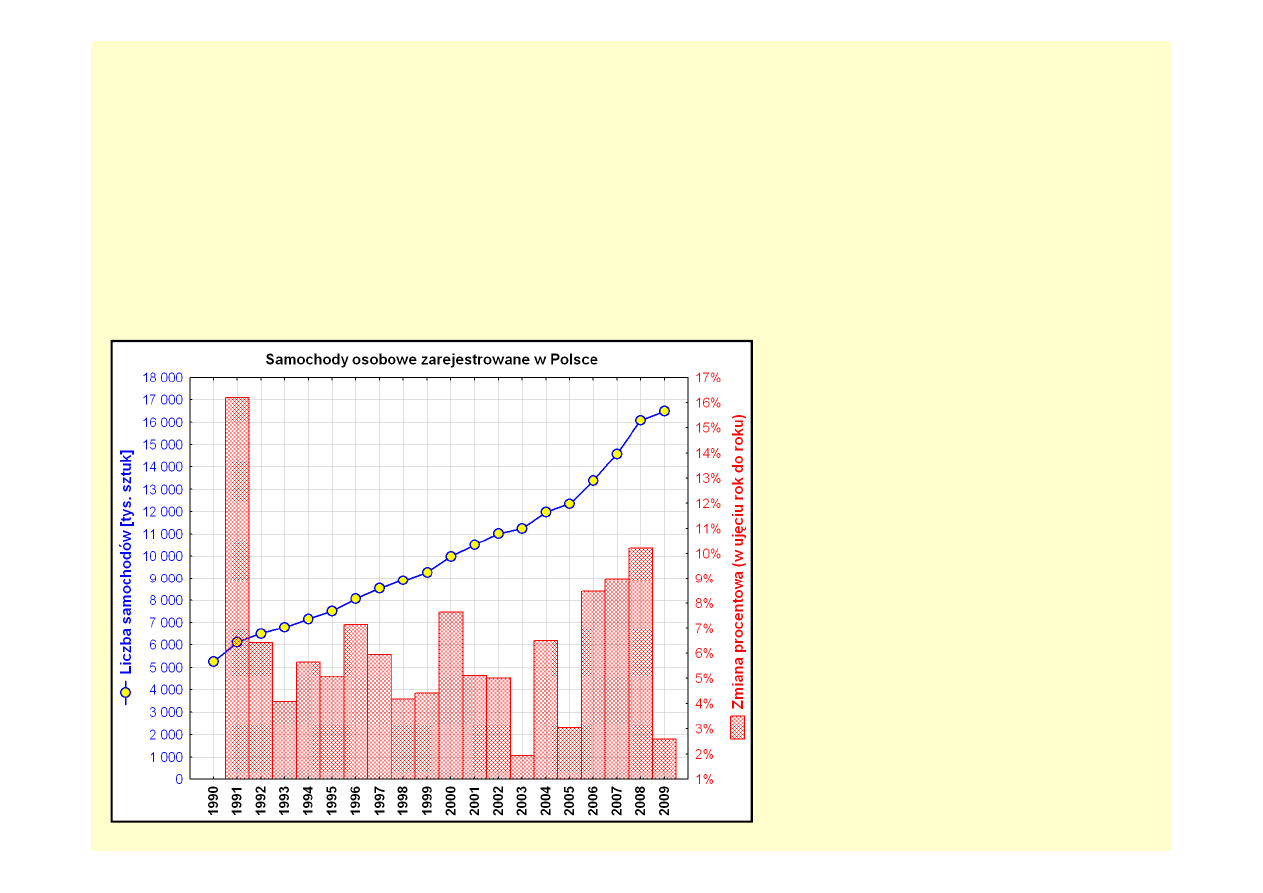
Prezentacja graficzna
Za pomocą wykresu liniowego wraz z nałożonym nań wykresem słupkowym,
przedstawiono informacje o:
• bezwzględnej liczbie samochodów osobowych
• dynamice zmian w ujęciu rok do roku.
Analiza graficzna pozwala wyodrębnić
wyraźny trend wzrostowy. Na tej podstawie
można domniemywać, iż w kolejnym roku
liczba zarejestrowanych samochodów
wzrośnie.
Z drugiej strony, w 2009 roku dynamika
wzrostu liczby samochodów była bardzo
niska, co jednak może być uznane za
pewne losowe odchylenie od wyraźnego
trendu widocznego we wcześniejszych
latach.
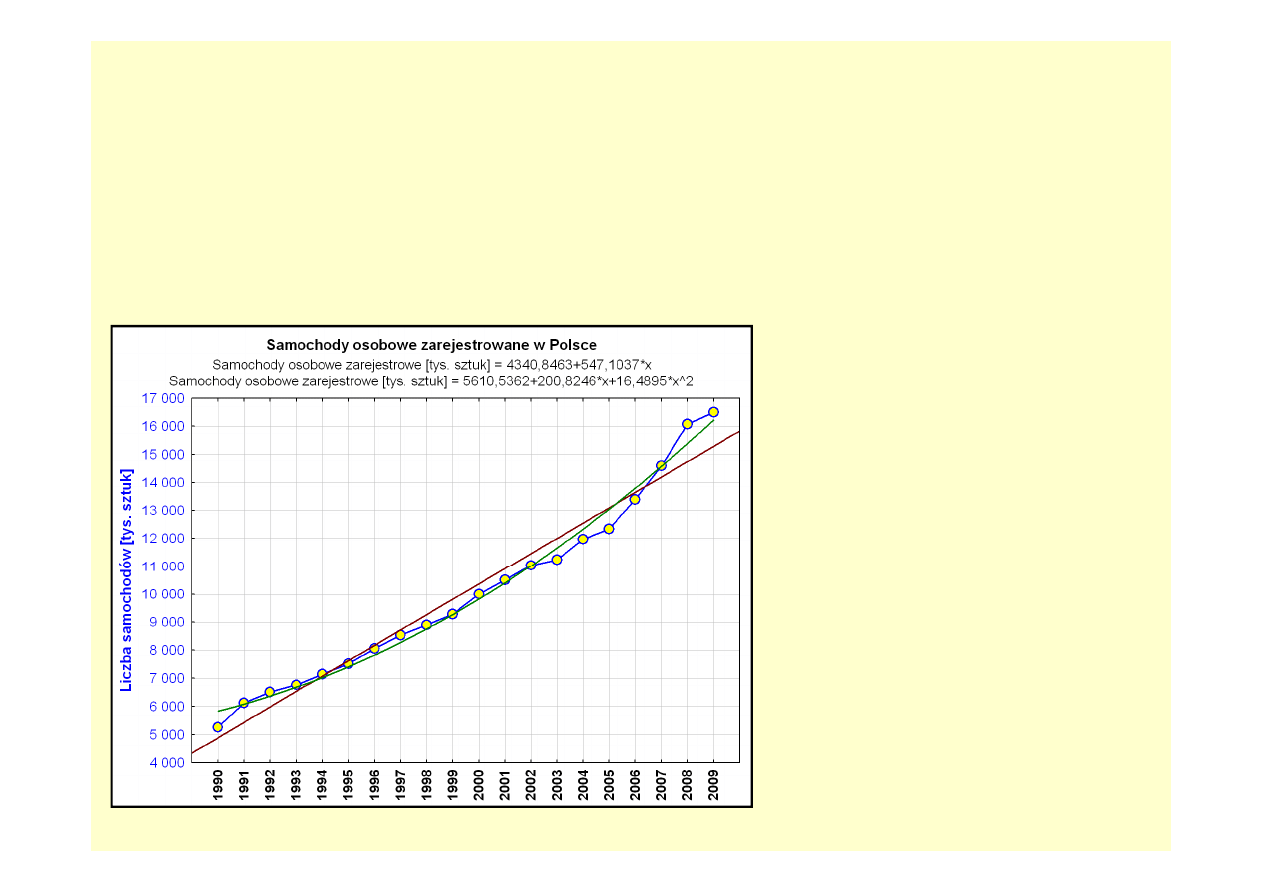
Graficzna wizualizacja wybranych modeli
Wykorzystując
możliwość
dopasowania
pewnych
modeli
trendu
bezpośrednio na wykresie liniowym, sporządzono graficzną prezentację
dopasowania do danych rzeczywistych trendu liniowego i kwadratowego.
Na wykresie uwidoczniono dopasowany do
analizowanego szeregu model liniowy i
model kwadratowy trendu.
Analiza graficzna pozwala stwierdzić, iż
model kwadratowy jest znacznie lepiej
dopasowany do danych, co jest szczególnie
istotne bardzo dobrze odzwierciedla od
zmiany liczby samochodów osobowych w
ostatnich okresach objętych badaniem.
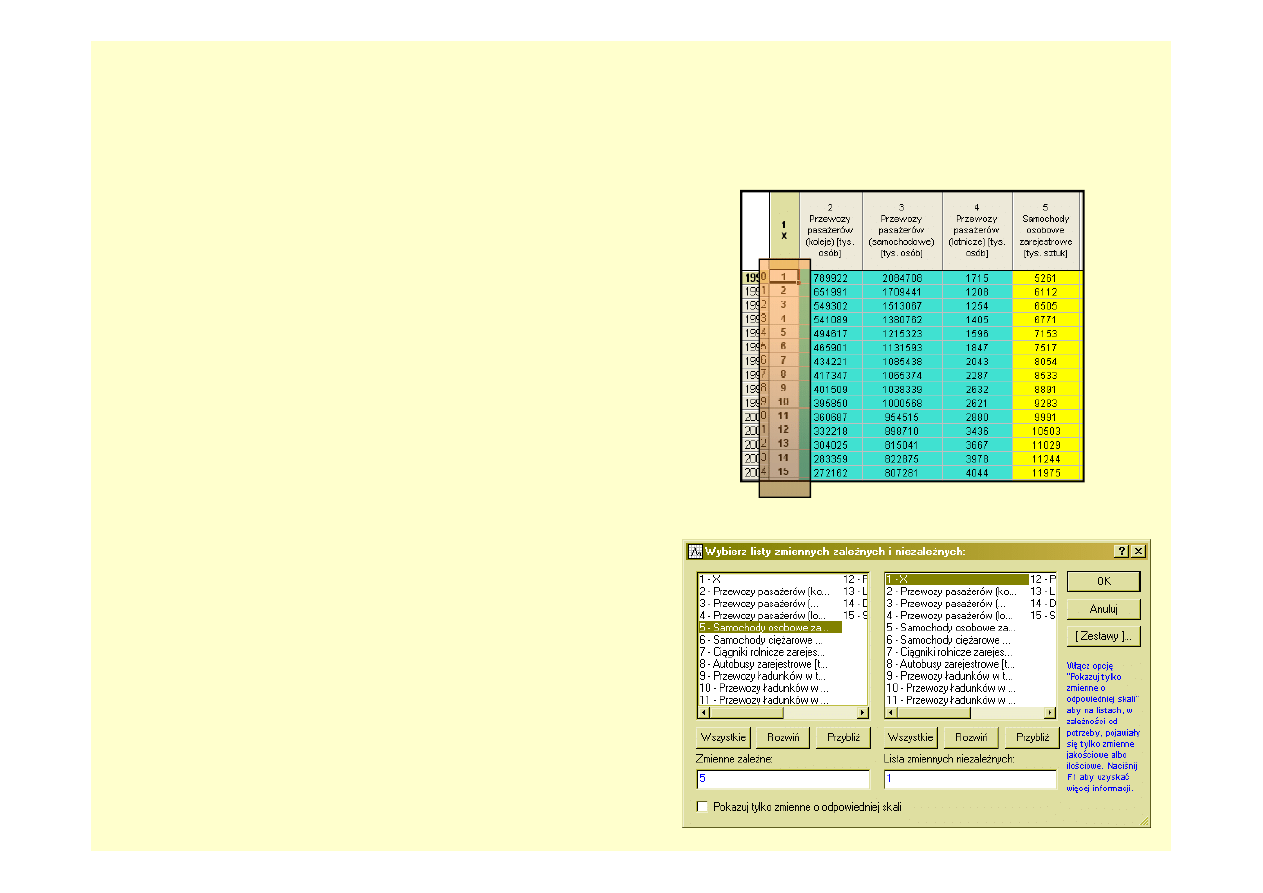
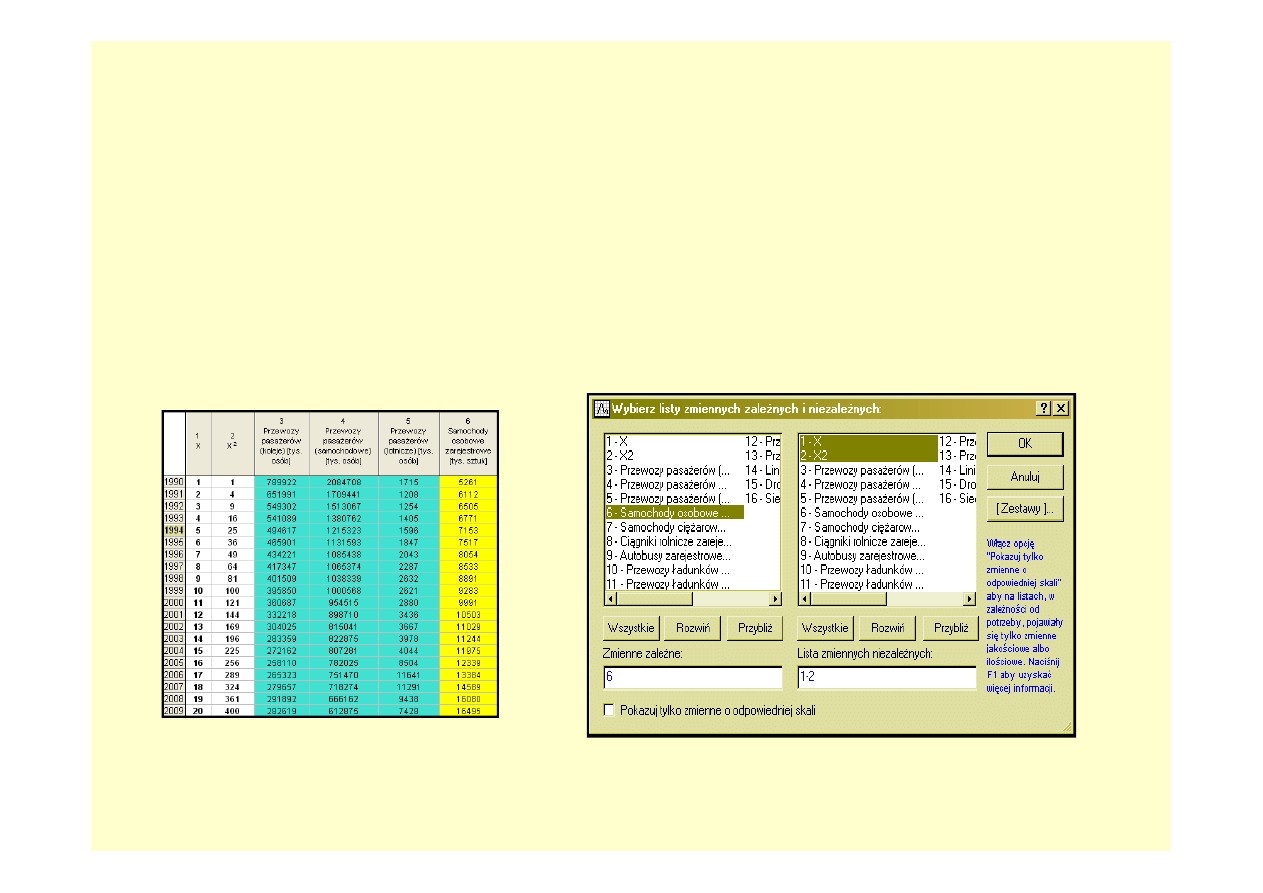
Analiza regresji – przygotowanie danych
i wybór zmiennych
W
module
REGRESJA
WIELORAKA
programu STATISTICA dostępne są liczne
miary dopasowania modelu do danych, oceny
jego
istotności
statystycznej.
Szczegółowa
analiza reszt pozwala na wykrycie obserwacji
odstających
od
modelu,
zaś
narzędzia
predykcji pozwalają na wyznaczenie nie tylko
prognozy punktowej ale także zakresu ufności
dla
prognozy
(tak
zwanej
prognozy
przedziałowej).
Aby
przeprowadzić
analizę
regresji
w
arkuszu danych, musi występować explicite
zmienna zawierająca informacje o numerze
okresu czasowego.
W tym celu w arkuszu dodajemy nową
kolumnę
i
wypełniamy
ją
kolejnymi
wartościami.
Następnie
w
oknie
wyboru
zmiennych wskazujemy zmienną zależną i
niezależną.
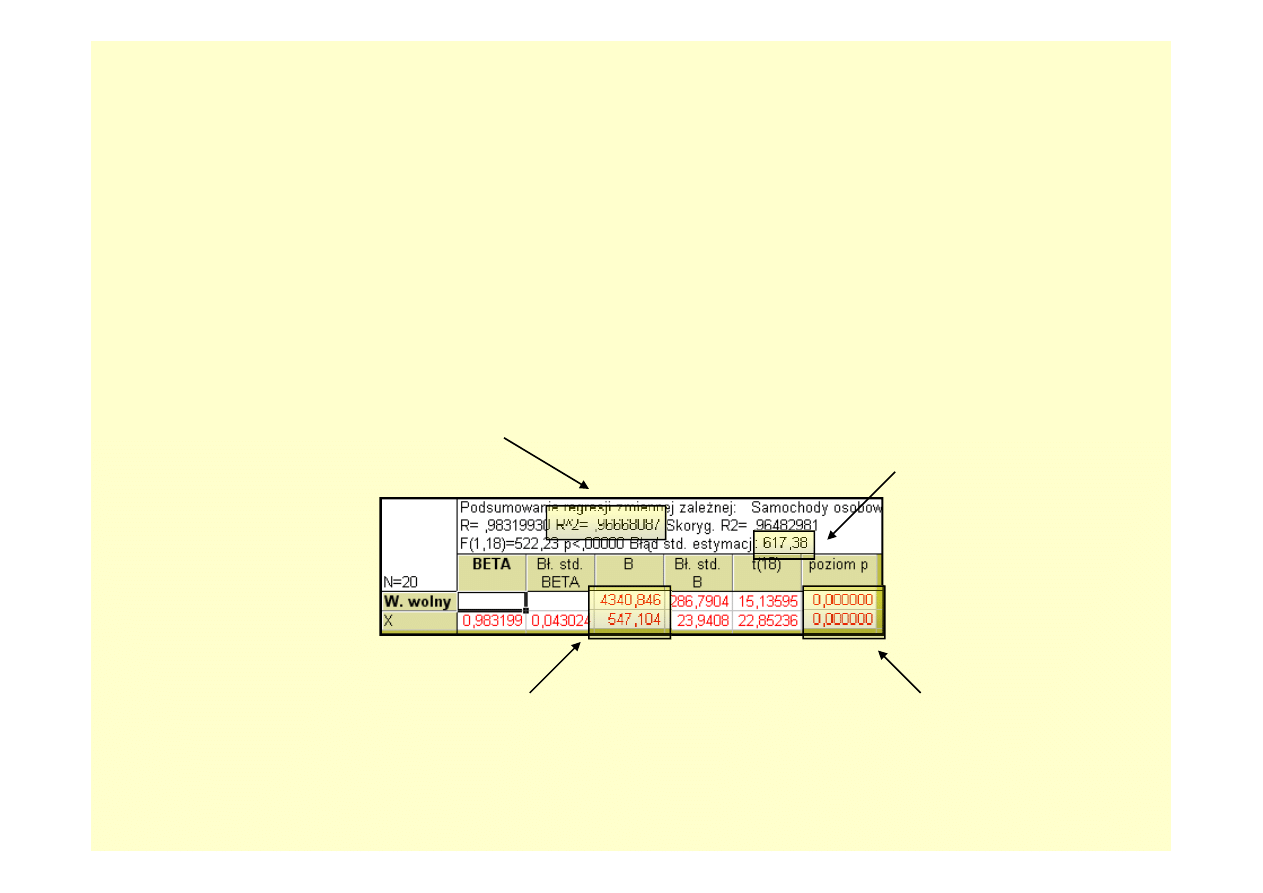
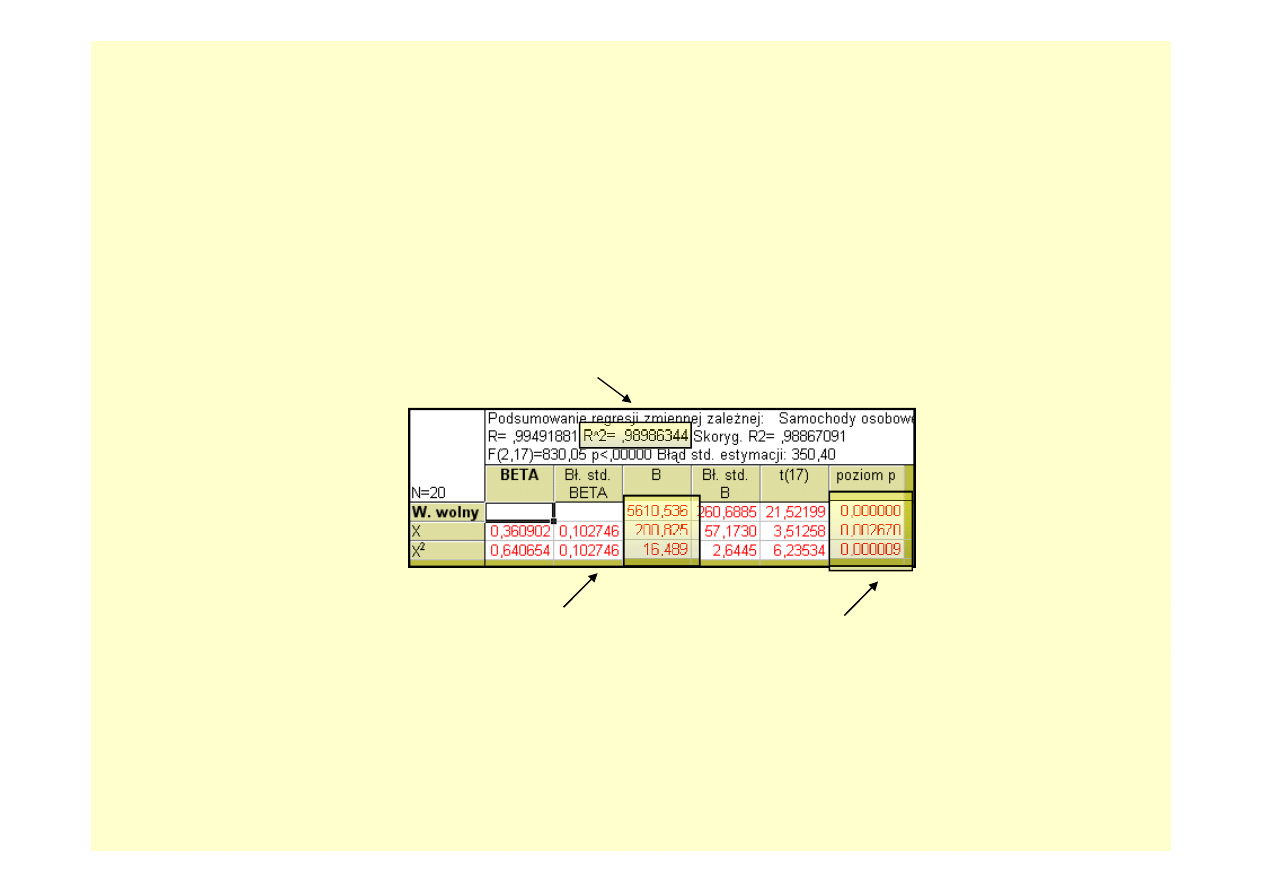
Analiza regresji – kluczowe wyniki
Po przejściu do WYNIKI REGRESJI WIELORAKIEJ w zakładce PODSTAWOWE
znajdujemy PODSUMOWANIE: WYNIKI REGRESJI.
Poniżej wskazano najważniejsze informacje zawarte w tym dość „obfitym” zestawieniu
wyników, które pozwalają na ocenę jakości modelu i decyzję o jego ewentualnym
wykorzystaniu do procesu prognozowania.
Wartość współczynnika determinacji R
2
,
podawana jest zwyczajowo w procentach.
Model liniowy w 96,6% opisuje zmienności
liczby samochodów osobowych w latach
1990-2009, a więc jest znakomicie
dopasowany do danych
Błąd standardowy estymacji pozwala
stwierdzić, iż rzeczywista liczba samochodów
osobowych odstaje zwykle od wartości
prognozowanej o 617 tys. pojazdów
W kolumnie „B” podane są wartości
współczynników modelu, który przyjął
postać: Y = 4340 + 547X
Wartości prawdopodobieństwa
testowego p pozwalają na stwierdzenie,
iż zmienna czasowa jest w statystycznie
istotny sposób powiązana z liczbą
samochodów osobowych
Analiza regresji – prognoza
W zakładce RESZTY, ZAŁOŻENIA, PREDYKCJA znajdują się narzędzia umożliwiające
wyznaczenie punktowej i przedziałowej prognozy zmiennej Y dla zadanych wartości
zmiennej X (w rozważanym przykładzie – liczby samochodów osobowych dla kolejnych
lat.
Aby wyznaczyć prognozę dla roku 2010 sprawdzamy w arkuszu danych jaki numer
miała obserwacja z roku 2009. Na tej podstawie wprowadzamy w pole X wartość 21.
W wynikowej tabeli podawana jest wartość przewidywana analizowanej zmiennej (czyli
prognoza punktowa). W rozważanym przypadku prognoza dla roku 2010 wynosi
15 830 tys.
samochodów osobowych.
W kolejnych dwóch wierszach podany jest przedział, w którym wartość prognozowana winna się
znaleźć z 95% procentową ufnością. Podczas wyznaczania tej wartości uwzględniany jest fakt, iż
model nie opisywał w 100% danych, odchylenia od modelu dla danych historycznych
traktowane są jako wielkości losowe i na tej podstawie szacowany jest błąd prognozy a
następnie prognoza przedziałowa.
Na podstawie przeprowadzonych analiz przypuścić można, iż liczba samochodów będzie
zawarta pomiędzy:
15 227
a
16 432
tys. pojazdów.
Merytoryczna weryfikacja prognozy
Wyznaczona dla roku 2010 wartość prognozowana liczby samochodów osobowych jest
znacząco niższa od poziomu tej cechy dla roku 2009 a nawet 2008. Trudno w tej sytuacji
uznać ją za wiarygodną, gdyż analizowane zjawisko ma tę specyfikę, iż raczej trudno
spodziewać się wystąpienia w jego przebiegu tak wyraźnego spadku.
Powodem uzyskania tak nielogicznego wyniku jest znacząca niezgodność pomiędzy
poziomem badanego zjawiska wynikającym z przyjęcia modelu liniowego a jego
rzeczywistym poziomem w ostatnich latach objętych analizą.
Uzyskaną prognozę należy odrzucić, decyzję o nieuwzględnianiu liniowego modelu
rozwoju badanego zjawiska można było podjąć już na etapie graficznej analizy danych.
Jak widać, nie zawsze model dobrze dopasowany (w sensie istotności statystycznej i
wartości współczynnika determinacji) pozwala na uzyskanie dobrej prognozy.
Model „kwadratowy”
Moduł REGRESJA WIELORAKA umożliwia wprowadzenie do analizy wielu zmiennych
objaśniających. W szczególności, dodając w arkuszu danych odpowiednie kolumny,
możliwe jest zbadanie własności modelu kwadratowego, czy dowolnego wielomianu.
Każdy model postaci:
Y
t
= b
0
+ f
1
(t)b
1
+ … + f
k
(t)·b
k
+ e
t
jest łatwo sprowadzalny do modelu liniowego.
Statystyczna weryfikacja modelu kwadratowego
W
tabeli
PODSUMOWANIE
WYNIKÓW
REGRESJI
znajdujemy
podstawowe
informacje o szacowanym modelu.
Model paraboliczny jest lepiej dopasowany do danych niż model liniowy (R
2
= 99,0%).
Należy jednak pamiętać, iż jest to rzecz oczywista, gdyż model bardziej złożony (a funkcja
kwadratowa „zawiera” w sobie funkcję liniową, zawsze będzie się charakteryzował lepszym
dopasowaniem do danych. Aby znaleźć rozsądny kompromis pomiędzy złożonością modelu i
jego dopasowaniem do danych, należy wziąć pod uwagę istotność zmiennych niezależnych.
Zarówno komponent liniowy jak i kwadratowy w
analizowanym modelu są istotne statystycznie.
Ze statystycznego punktu widzenia, model można
wykorzystać do prognozy.
Parametry modelu nie mają tak łatwej interpretacji
praktycznej, jak w przypadku modelu liniowego.
Prognoza na podstawie modelu kwadratowego
Podstawiają odpowiednie wartości za zmienne X oraz X
2
dokonujemy prognozy liczby
samochodów na rok 2010.
Na podstawie modelu kwadratowego, otrzymujemy
prognozę punktową liczby samochodów osobowych
zarejestrowanych w Polsce w roku 2010 na
poziomie 17099 tys. pojazdów, przy 95% przedziale
ufności na poziomie 17100-17650 tys. pojazdów.
Do
modelu
podstawiamy
numer
odpowiadający kolejnemu rokowi, czyli
wartość 21. Oczywiście za zmienną X
2
podstawiamy 441 (21
2
)
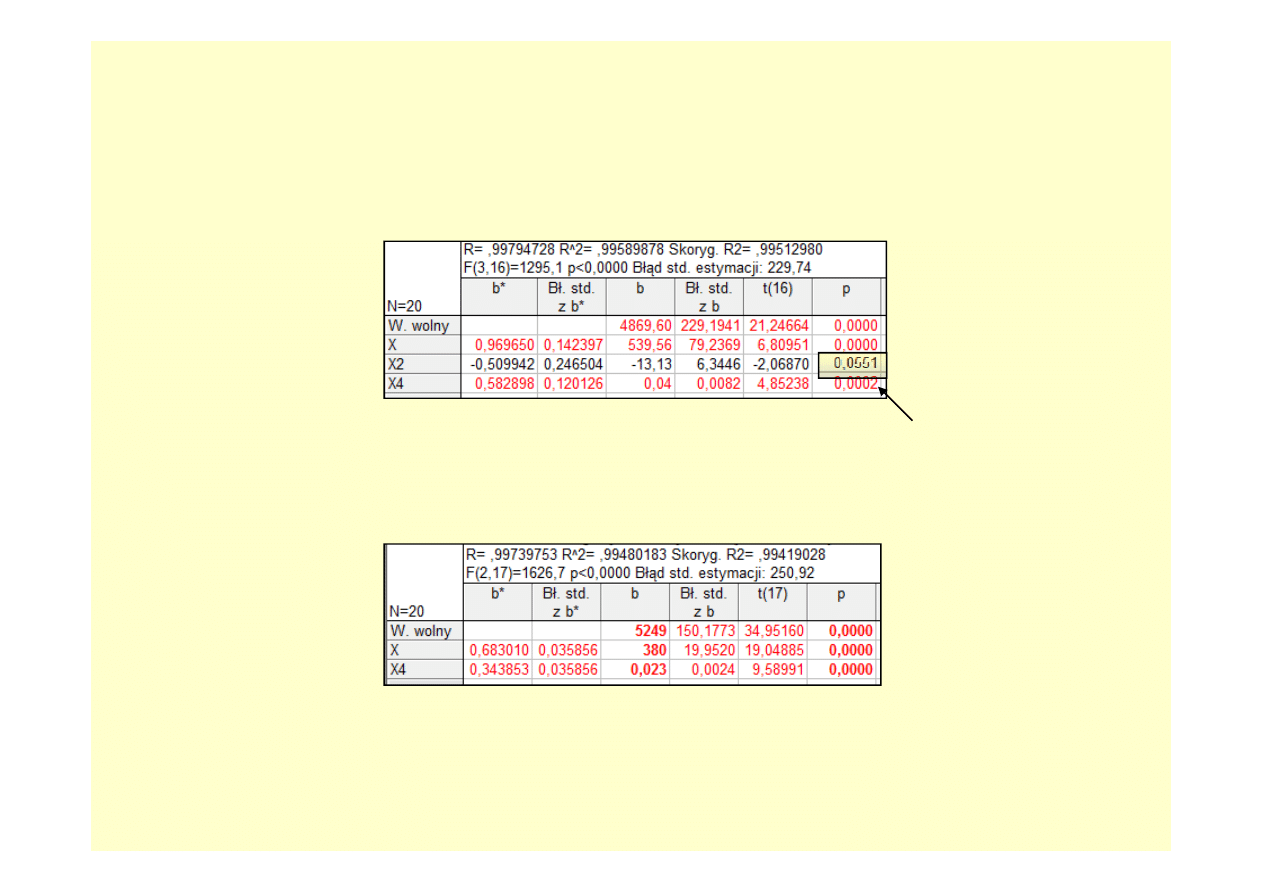
Bardziej skomplikowane modele…
Z technicznego punktu widzenia, nic nie stoi na przeszkodzie, by do modelu wprowadzić
kolejne potęgi zmiennej czasowej. Poniżej zamieszczono przykładowe wyniki dla
modelu, w którym uwzględniono zmienne X, X
2
oraz X
4
.
Zmienna X
2
okazała się być nieistotna statystycznie
po wprowadzeniu do modelu zmiennej X
4
, a więc
należy ją wykluczyć z analizy i ponownie dokonać
obliczeń.
Po wyeliminowaniu zmiennej X
2
pozostałe czynniki
są istotne statystycznie. Jakość dopasowania
modelu jest bardzo wysoka – współczynnik
determinacji wynosi aż 99,5%.
Ponieważ GUS udostępnia już informację o liczbie samochodów zarejestrowanych na
koniec 2010 r. (17 239 tys.) możliwa jest weryfikacja prognoz dla tego okresu.
Poniżej zestawiono błąd procentowy poszczególnych prognoz :
• model liniowy
8,2%
• model kwadratowy
0,8%
• model X i X
4
-3,2%
Jak widać,
zdecydowanie najlepsze przewidywania dał model kwadratowy, którego
prognozę należałoby jedynie nieznacznie zwiększyć w celu otrzymania faktycznie
zaobserwowanej wielkości. Model liniowy dał prognozy zdecydowanie zaniżone (była
już o tym mowa wcześniej), zaś model X i X
4
mimo najlepszego dopasowania do danych,
przeszacowuje liczbę samochodów o 3,2%, co wynika niewątpliwie z matematycznej
własności „szybko rosnącej” funkcji wielomianowej 4. stopnia.
Zestawienie prognoz
Poniżej zestawiono prognozy liczby samochodów osobowych na lata 2010-2013
uzyskane za pomocą modelu liniowego, kwadratowego i zredukowanego wielomianu
stopnia czwartego.
Rok
Model liniowy
Model kwadratowy
Model X i X
4
2010
15 830
17 100
17 783
2011
16 377
18 010
19 094
2012
16 924
18 952
20 541
2013
17 471
19 928
22 137
Uwagi końcowe
Analizując otrzymane wyniki, należy pamiętać, iż zostały one uzyskane jedynie na
podstawie informacji zawartych w wyjściowym szeregu czasowym – nie uwzględniono
żadnych czynników zewnętrznych. Tymczasem prognozując sytuację na rynku
motoryzacyjnym należałoby wziąć pod uwagę jeszcze wiele innych czynników.
Dla przykładu:
• możliwości kredytowe Polaków w kolejnych okresach - w tym kontekście istotne mogą
być też zmiany wynagrodzeń, sytuacja na rynku pracy i działalność banków;
• zmiany demograficzne – spadek liczności populacji i jej starzenie się;
• nasycenie rynku motoryzacyjnego - porównanie wskaźnika liczby samochodów na 1
tys. mieszk. z innymi państwami europejskimi;
• przewidywania odnośnie cen paliw;
• atrakcyjność konkurencyjnych środków transportu (w szczególności transportu
kolejowego).