1

Instytut Inzynierii Ladowej

Zaklad Dynamiki Budowli

Zadanie domowe z

podstaw statyki

AUTOR:

Grzegorz Wojtaczka

Wydzial Budownictwa Ladowego I Wodnego II Rok

ROK AKADEMICKI:

2003/04 r.

DATA WYKONANIA:

28.10.2003r.

TEMAT:

Belka – rozwiazanie analityczne i sporzadzenie wykresów MTN dla

preta glównego

PROWADZACY:

dr inz. Monika Podwórna

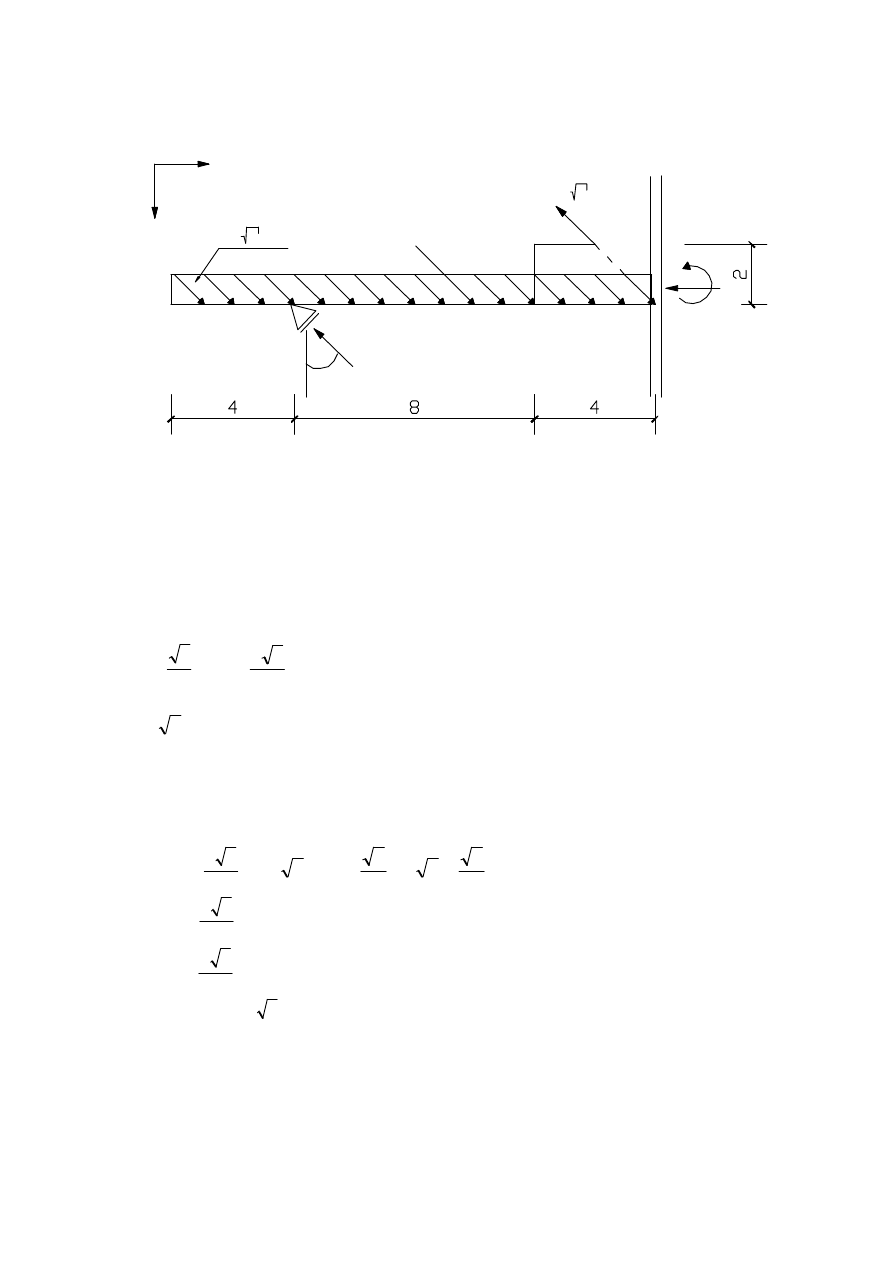
2

q= 2 kN/m

R

B

P = 4 2 kN

1

2

3

4

H

A

M

β

α

α

α

=45°

tg

β

= 1:2

m

X

Y

1.Sprawdzenie statycznej wyznaczalnosci i geometrycznej
niezmiennosci.

Mamy doczynienia z jedna tarcza i trzema podporami nie zbieznymi a wiec zgodnie z
twierdzeniem o dwóch tarczach uklad jest SW i GN

2.Obliczenie reakcji podporowych:

sin

β

=

5

5

i cos

β

5

5

2

Obciazenie równomiernie rozlozone bedziemy równiez zastepowac sila skupiona

Q = 16

2

Sile na wsporniku zredukowano do punktu nr.3. Zgodnie z prawami redukcji w punkcie nr.3
otrzymano sile o wartosci i kierunku dzialania takim samym jak sila na wsporniku oraz
otrzymano moment lewoskretny o wartosci M

P

= 16 kNm

Σ

y = 0 =>

−

R

B

×

cos

β

+ q

×

sin

α

×

16 – P

×

sin

α

= 0

−

5

5

2

R

B

+

2

×

16

×

2

2

−

4

2

×

2

2

=0

−

5

5

2

R

B

+ 16

−

4 =0

5

5

2

R

B

= 12

R

B

= 6 5 [kN] stad R

BY

= 12 [kN]

R

Bx

= 6 [kN]

3

Σ

x = 0 =>

−

R

B

×

sin

β

+ q

×

cos

α

×

16 – P

×

cos

α

−

H

A

= 0

−

R

B

×

5

5

+

2

×

16

×

2

2

– 4

2

×

2

2

−

H

A

= 0

−

6 5

×

5

5

+ 16 – 4

−

H

A

= 0

−

6 + 16 – 4

−

H

A

= 0

H

A

= 6 [kN]

Σ

M

B

= 0 => - M – M

P

+ Q

×

sin

α

×

4 – P

×

sin

α

×

8 = 0 gdzie:

−

M – 16

−

4

2

×

2

2

×

8 + 16

2

×

4

×

2

2

= 0 M

P

=

−

4

×

4 =

−

16[kN]

−

M – 16

−

4

×

8 + 64 = 0 lub

−

M – 16

−

32 + 64 = 0 M

P

=

−

4

×

2

−

4

×

2=

−

16[kN]

M = 16 [kNm]

Sprawdzenie:

Σ

M

3

= 0 =>

−

M – M

P

−

Q

×

sin

α

×

4 + R

B

×

cos

β

×

8 = 0

−

16

−

16

−

16

2

×

2

2

×

4 + 6 5

×

0

8

5

5

2

=

×

−

16

−

16

−

64 +12

×

8 = 0

−

96 + 96 = 0

3. Obliczenie sil przekrojowych

3.1 Momenty zginajace

Punkt 1 => 0 [kNm]
Punkt 2 =>

−

q

×

sin

α

×

4

×

2 =

=

−

2

×

2

2

×

4

×

2 =

−

8 [kNm]

Punkt 3

L

=>

−

q

×

sin

α

×

12

×

6 + R

B

×

cos

β

×

8 =

=

−

2

×

2

2

×

72 + 6 5

×

5

5

2

×

8 =

=

−

72 + 96 = 24 [kNm]

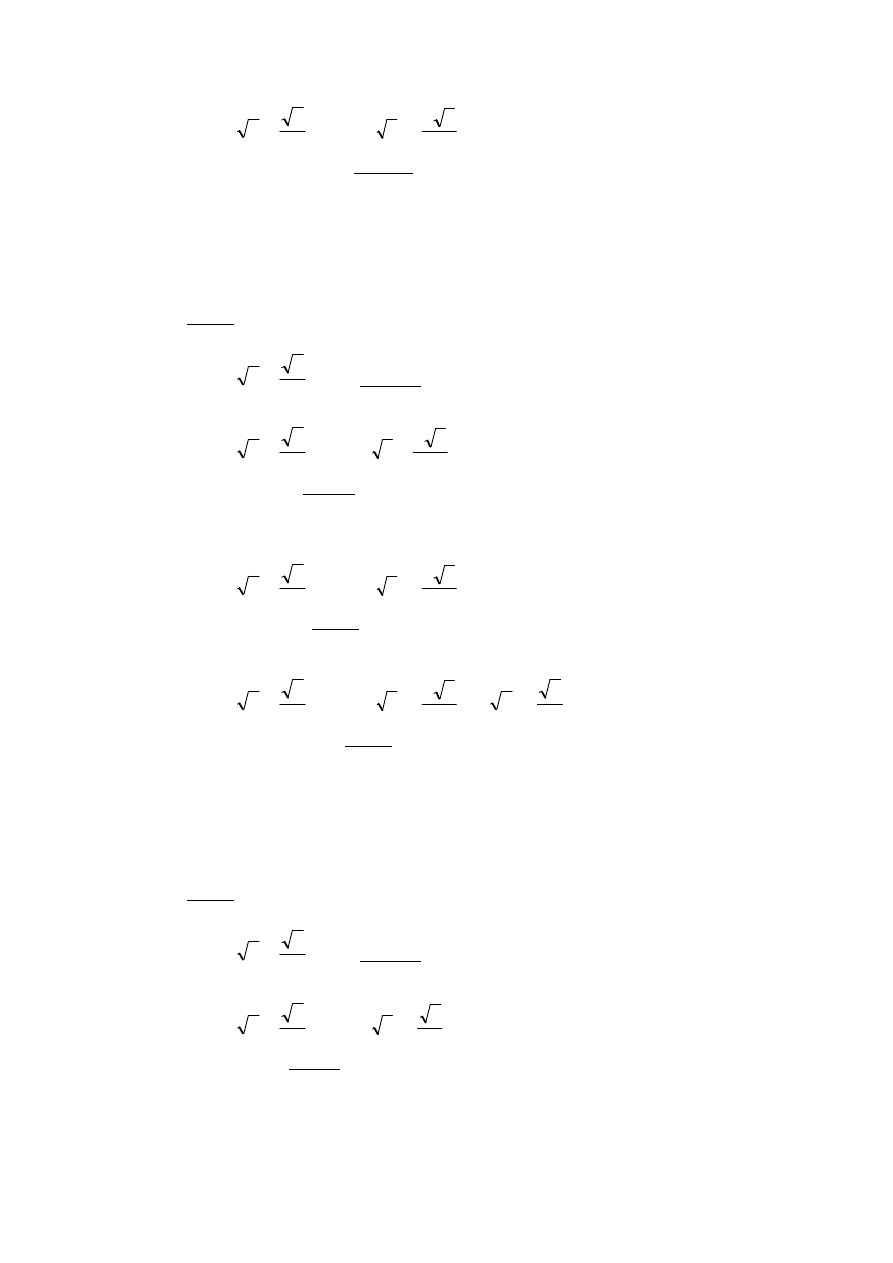
4

Punkt 3

P

=>

−

q

×

sin

α

×

12

×

6 + R

B

×

cos

β

×

8

−

M

P

=

=

−

2

×

2

2

×

72 + 6 5

×

5

5

2

×

8

−

16 =

=

−

72 + 96

−

16 = 8 [kNm]

Punkt 4

P

=> 16 [kN]

3.2 Sily tnace

Punkt 1 => 0 [kN]
Punkt 2

L

=>

−

q

×

sin

α

×

4 =

=

−

2

×

2

2

×

4 =

−

4 [kN]

Punkt 2

P

=>

−

q

×

sin

α

×

4 + R

B

×

cos

β

=

=

−

2

×

2

2

×

4 + 6 5

×

5

5

2

=

=

−

4 + 12 = 8 [kN]

Punkt 3

L

=>

−

q

×

sin

α

×

12 + R

B

×

cos

β

=

=

−

2

×

2

2

×

12 + 6 5

×

5

5

2

=

=

−

12 + 12 = 0 [kN]

Punkt 3

P

=>

−

q

×

sin

α

×

12 + R

B

×

cos

β

+ P

×

sin

α

=

=

−

2

×

2

2

×

12 + 6 5

×

5

5

2

+ 4

2

×

2

2

=

−

12 + 12 + 4 = 4 [kN]

Punkt 4

P

=> 0 [kN]

3.3 Sily osiowe

Punkt 1 => 0 [kN]
Punkt 2

L

=>

−

q

×

cos

α

×

4 =

=

−

2

×

2

2

×

4 =

−

4 [kN]

Punkt 2

P

=>

−

q

×

cos

α

×

4 + R

B

×

sin

β

=

=

−

2

×

2

2

×

4 + 6 5

×

5

5

=

−

4 + 6 = 2 [kN]

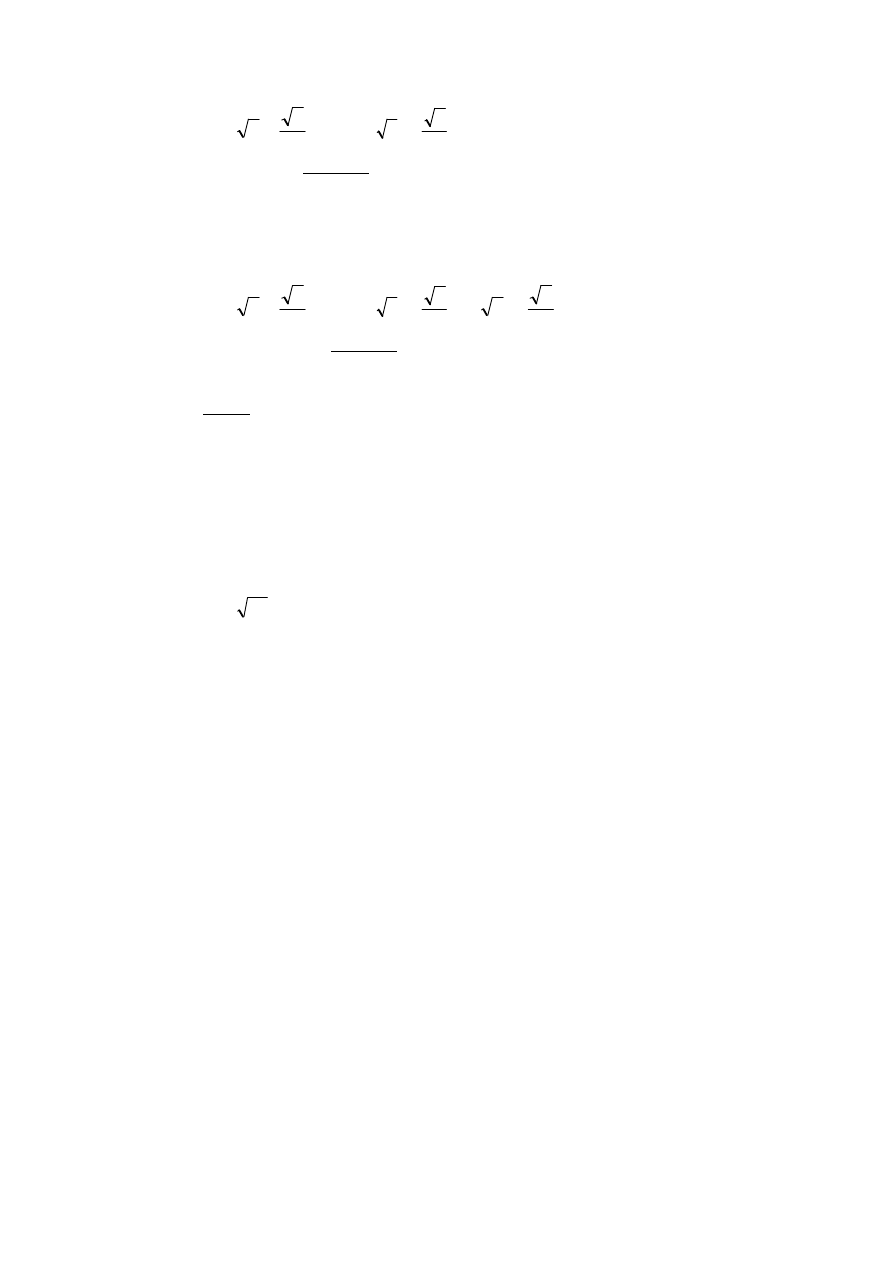
5

Punkt 3

L

=>

−

q

×

cos

α

×

12 + R

B

×

sin

β

=

=

−

2

×

2

2

×

12 + 6 5

×

5

5

=

−

12 + 6 =

−

6 [kN]

Punkt 3

P

=>

−

q

×

cos

α

×

12 + R

B

×

sin

β

+ P

×

cos

α

=

=

−

2

×

2

2

×

12 + 6 5

×

5

5

+ 4

2

×

2

2

=

=

−

12 + 6 + 4 =

−

2 [kN]

Punkt 4

P

=>

−

6 [kN]

4. Wykres sil

Obliczenie miejsca w którym wykres momentów przecina os

−

qsin

α

×

x

×

0,5x + R

B

×

cos

β

×

(x

−

4) =

=

−

0,5x

2

+ 12(x

−

4) =

=

−

0,5x

2

+ 12x

−

48

Otrzymujemy

∆

= 48 = 6,93 a z tego pierwiastki x

1

= 18,93 i x

2

= 5,07 [m]

Pod uwage bierzemy drugi wynik gdyz pierwszy nie spelnia warunku dlugosci naszej belki.

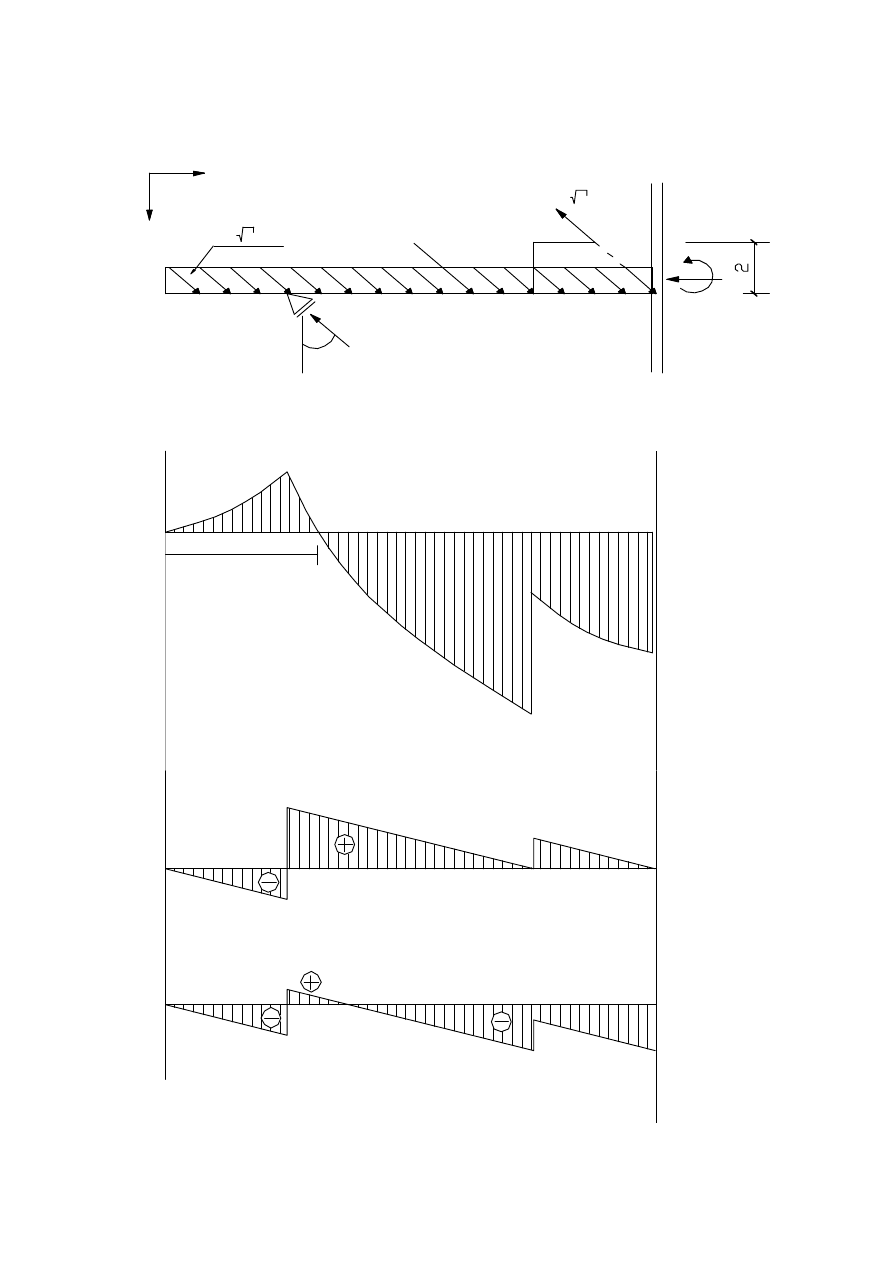
6

q= 2 kN/m

R

B

P = 4 2 k N

1

2

3

4

H

A

M

β

α

α

α

=45°

tg

β

= 1:2

X

Y

8

24

16

8

M

0

[kNm]

5,07[m]

4

8

4

0

T

4

2

6

0

N

6

[kN]

[kN]