Belka prosta

przykład 1 (z objaśnieniami)

Mechanika ogólna

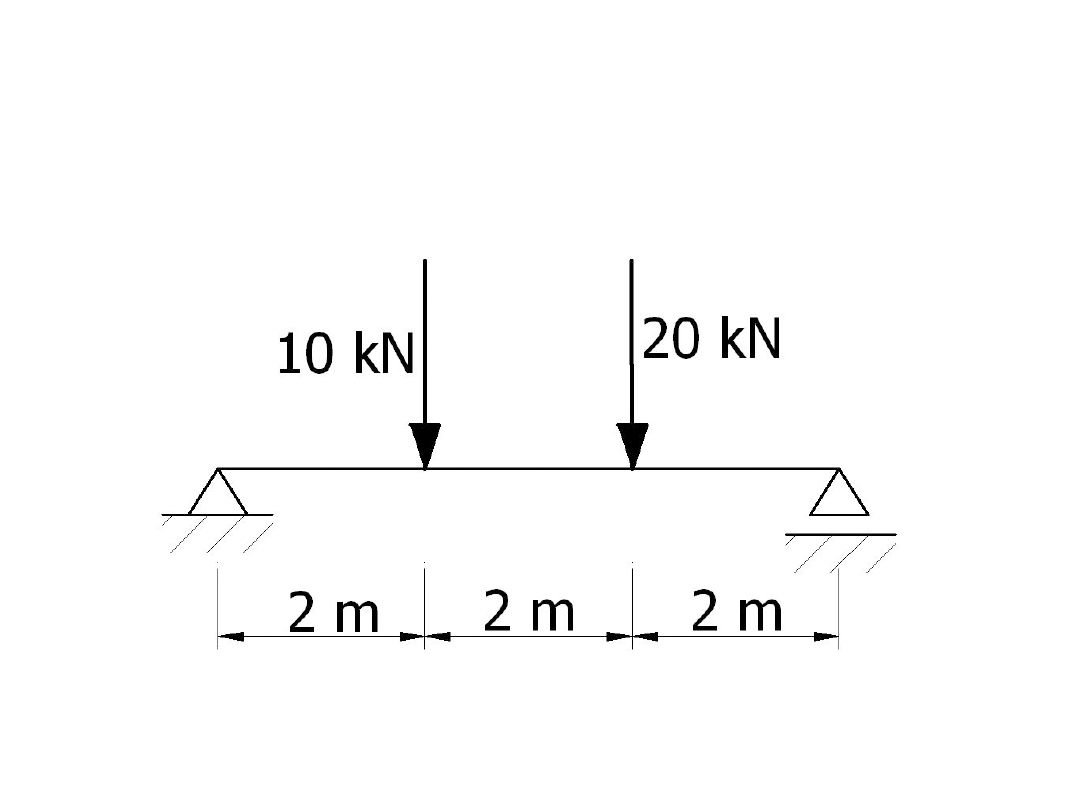
Oto nasza belka

(jak widać całkiem przyjemna)

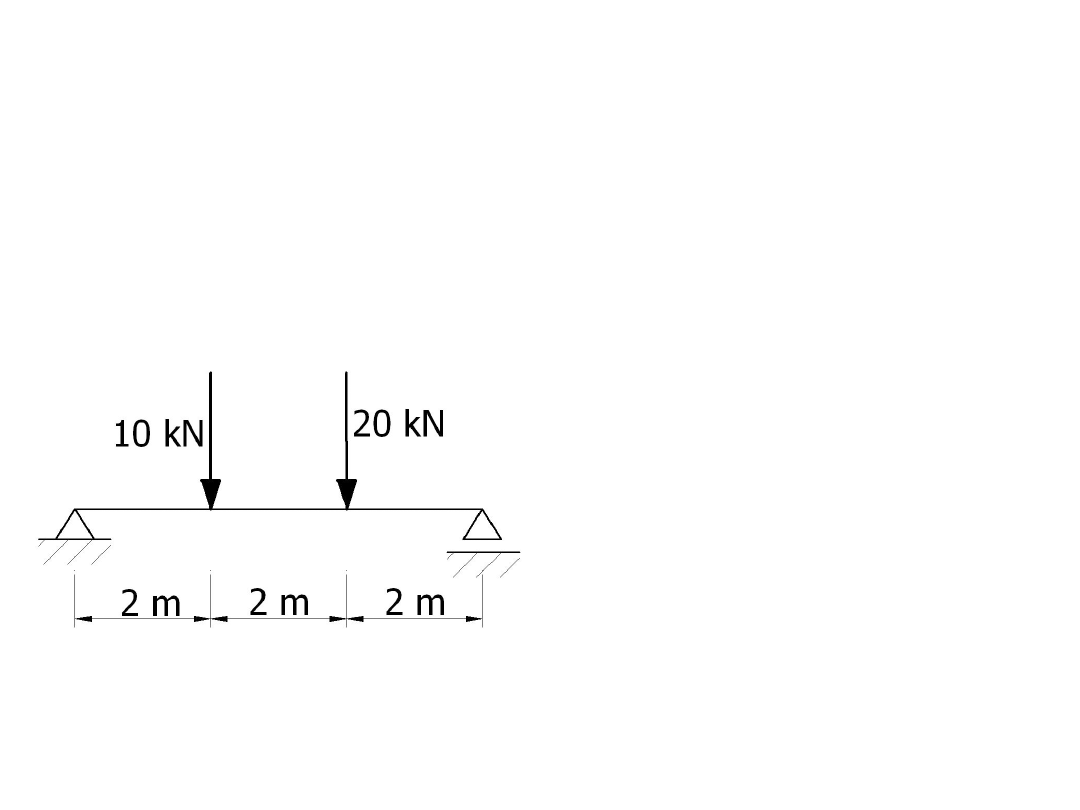
Nasz plan działania

(krok po kroku)

Co robimy?
• 1. Sprawdzamy SW i

GN (statyczną
wyznaczalność i
geometryczną
niezmienność)

• 2. Liczymy reakcje w

podporach

• 3. Rysujemy wykresy

sił przekrojowych –
MTN (momenty, tnące,
normalne – osiowe)

Statyczna wyznaczalość

(inaczej warunek ilościowy)

Sprawdzamy czy układ (w tym padku bardzo prosty) jest SW, tzn czy nie jest
przesztywniony (za dużo więzi) lub czy nie jest mechanizmem (za mało więzi)

• Aby belka była SW

musi spełniać
równanie:

e=3t

Liczba więzi (w
przypadku podpory
przyjmujemy, że to
liczba reakcji w
podporach)

Liczba tarcz – w
przypadku belek prostych
belka jest jedną (całą)
tarczą.

A jak będzie w naszym
przypadku?

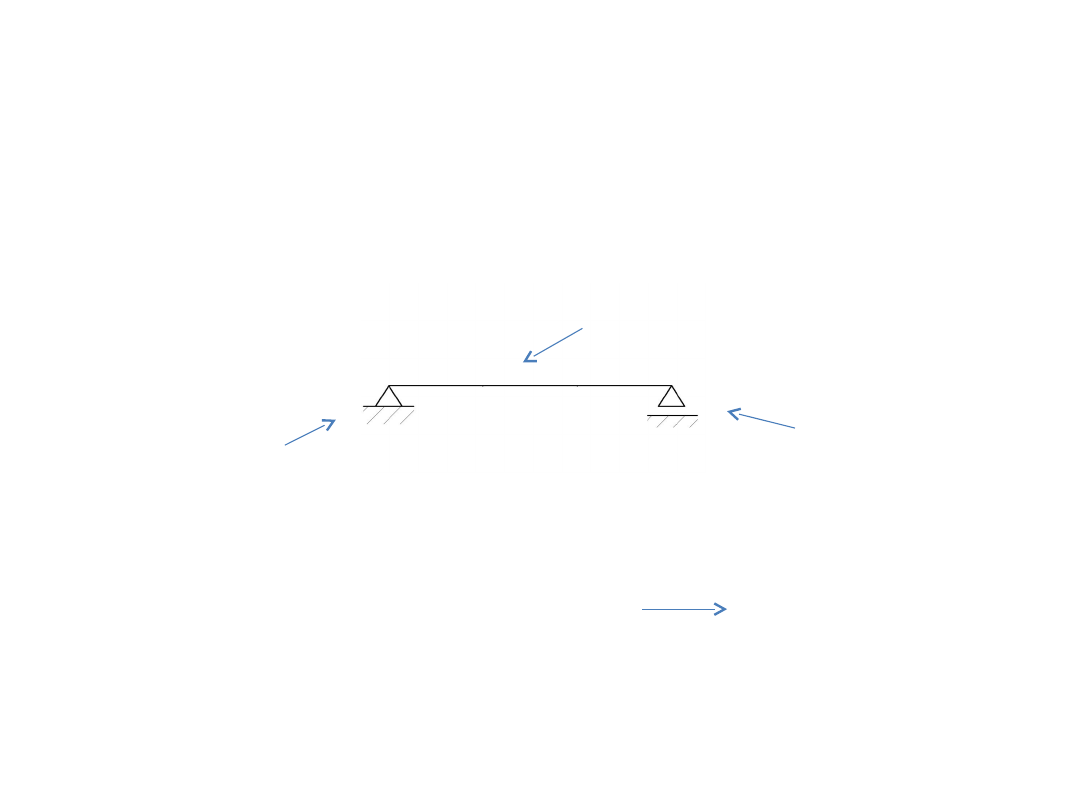
SW – ciąg dalszy

Patrzymy jakie mamy podpory (całe dwie)

Podpora przegubowo
przesuwna
ma

jedną reakcję (więź)

Podpora przegubowo
nieprzesuwna
ma

dwie reakcje (więzi)

(patrz

blog)

Nasza jedna tarcza

Podstawiamy do równania

e=3t

3=3∙1

Widzimy, że równanie jest zachowane, zatem układ

jest SW.

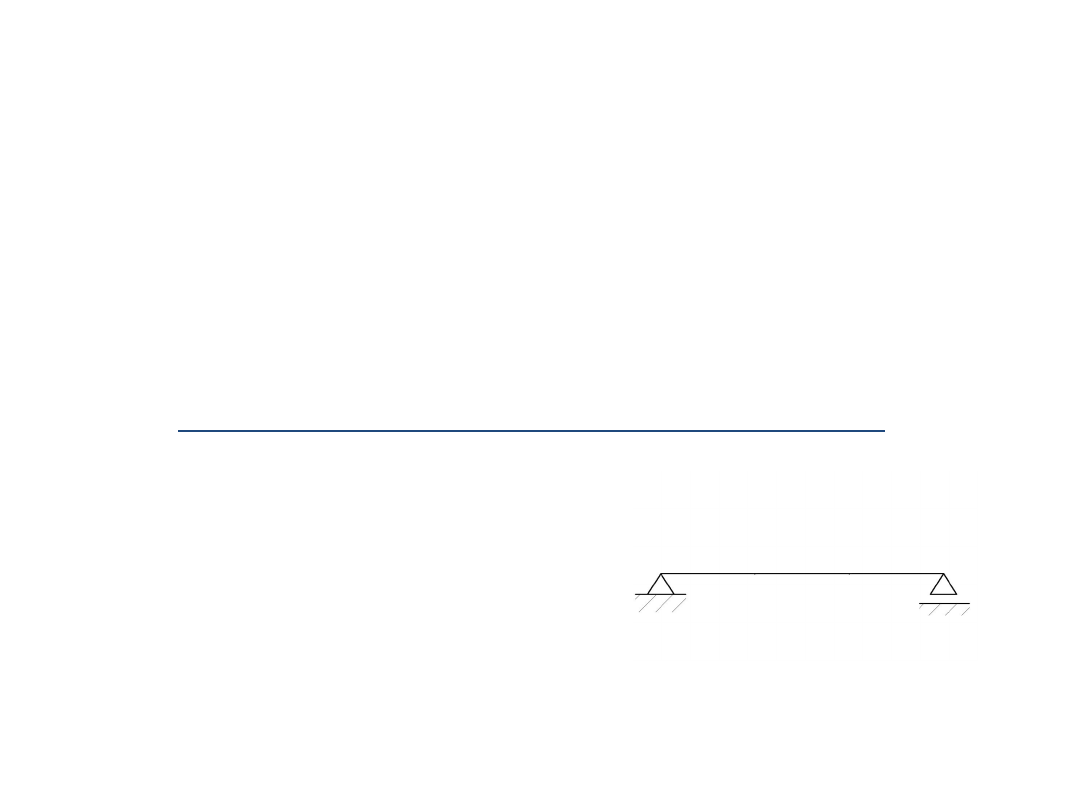
Geometryczna niezmienność

(warunek jakościowy)

Nie będziemy się rozwodzić nad całością zaganienia GN (bo potrzeba by na to całego artykułu), a
skupimy się tylko na naszym przypadku. Sprawdzimy GN, mówiąc łopatologiczne zobaczymy, czy nasza
tarcza jest tak połączona z ostoją, że się nie rusza.

• Wiemy (wiemy?), że jeżeli dwie

tarcze (w tym wypadku nasza
belka i ostoja) są poczłaczone
trzema więziami to możemy je
uznać za jedną tarczę (mówiąc
ogólnie)

• UWAGA! Więzi nie mogą:

– być do siebie równoległe
– schodzić się w jednym punkcie

Korzystamy z twierdzenia o dwóch tarczach (2T)

Jak to sprawdzany?

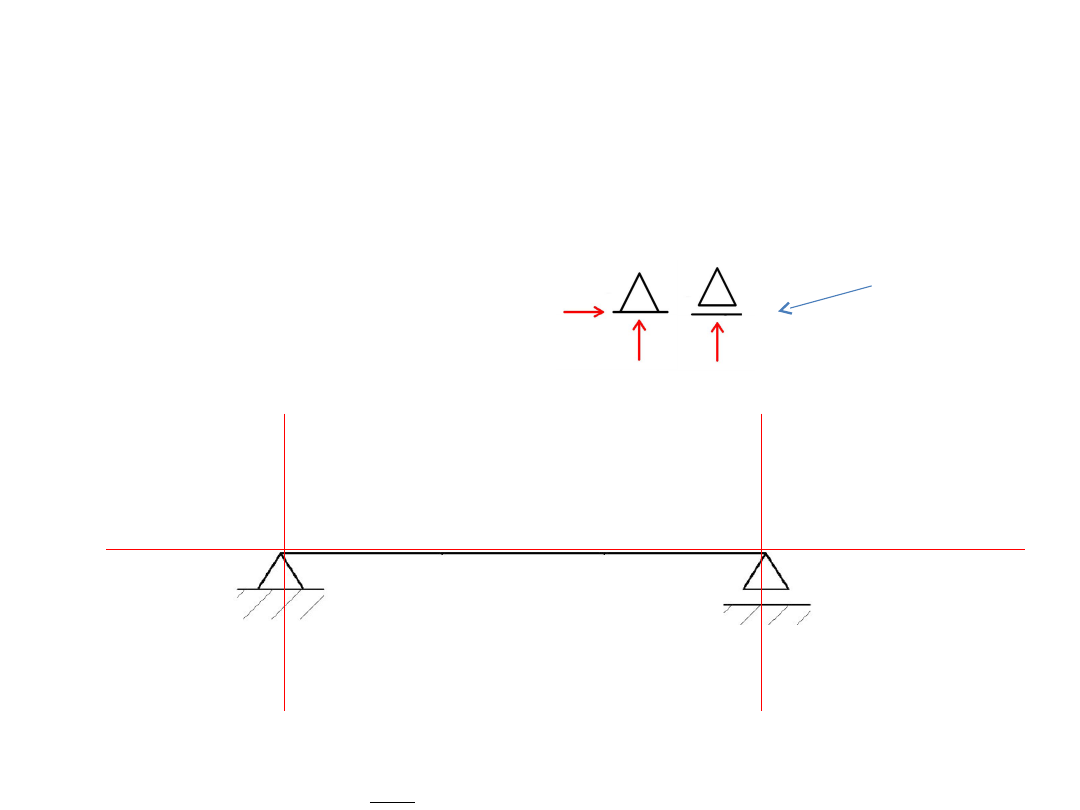
GN – ciąg dalszy

Sposbów na sprawdzenie jest kilka (każdy i tak wypracowóje najwygodnieszy dla
siebie). Moja propozycja to korzystanie (w dalszym ciągu) z reakcji podporwych

.

Nasze
podpory i ich

reakcje

Dalej rysujemy proste

zgodnie z wektorami

reakcji.

Widzimy, że więzi nie są równoległe, ani nie
przecinają się w jednym punkcie, zatem układ
jest GN.

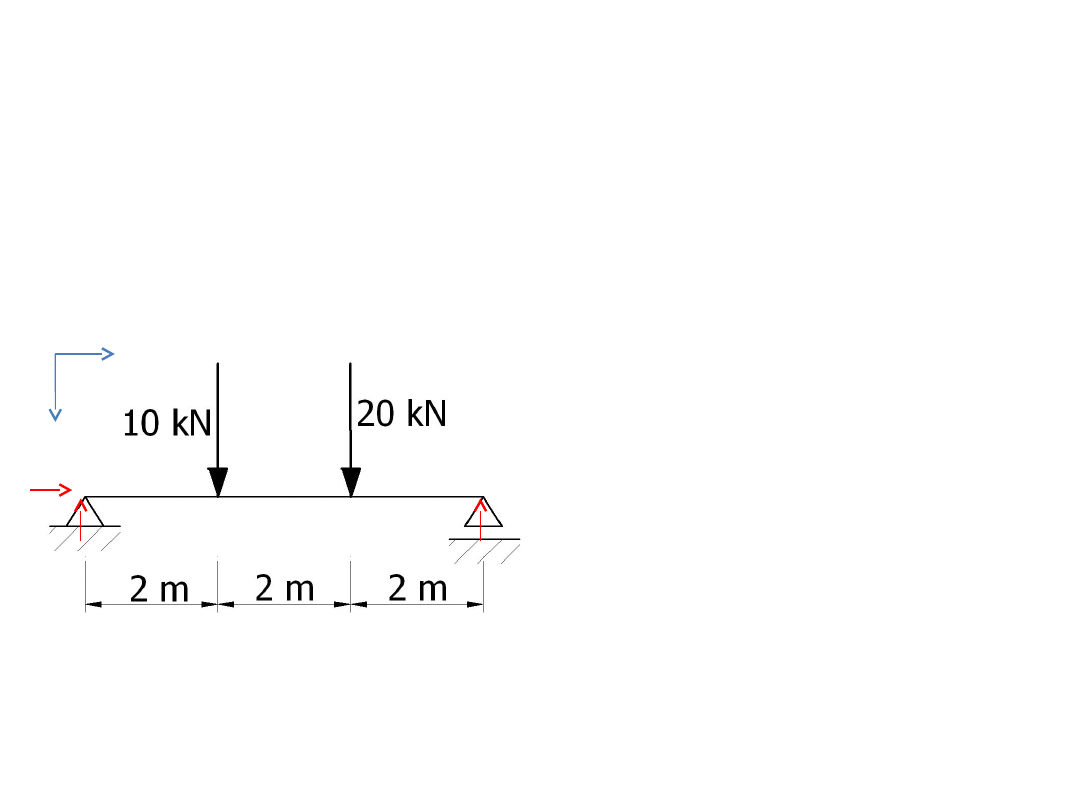
Liczymy reakcje w podporach

(zgodnie z naszym planem działania)

Dla porządku wprowadzamy
oznaczenia (z czasem każdy
będzie oznaczał po swojemu –
gwarantuje)

• A

i

B

punty poporowe – w nich

reakcje poziome oznaczone
jako

H

(horizontal), a pionowe

jako

V

(vertical)

• 1

i

2

punkty charakterystyczne

– przyłożona siła skupiona

• Układ współrzędnych

(kierunek strzałki oznacza +)

• Tak przyjęte osie zwłaszcza z

początku wydają się dziwne,
ale z biegiem czasu zrobią się
wygodne.

Oznaczenia

A

B

V

A

H

A

V

B

1

2

x

y

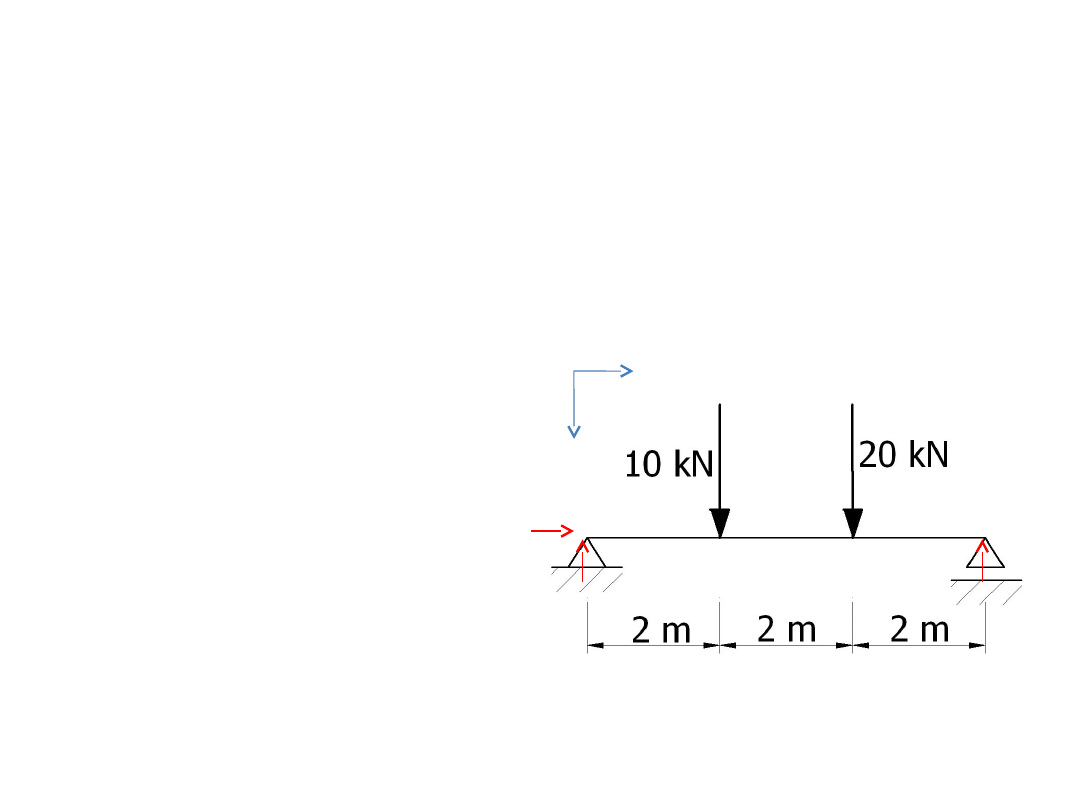
Liczymy reakcje – ciąg dalszy

Mamy oznaczenia to
jedziemy.

• Rzut na oś poziomą

– ∑Px=0 

H

A

+0=0

• Moment w punkcie B

– ∑M

B

=0 

V

A

∙6-10∙4-20∙2=0

– 6

V

A

=80 

V

A

=13,3

• Rzut na oś pionową

– ∑Py=0  -

V

A

+10+20-

V

B

=0

– V

B

=-13,3+30 

V

B

=16,7

• Sprawdzenie – moment w punkcie

1

– ∑M1=0 

V

A

∙2+20∙2-

V

B

∙4=0

– 0=0

UWAGA! Pamiętajmy – belka
prosta oznacza (ZAWSZE) 3
rówania.

Mamy

3 niewiadome i 3

równania

, więc rozwiązanie musi

się znaleźć.

A

B

V

A

H

A

V

B

1

2

x

y

Znaki momentów przy

reakcjach

Pamiętamy! Jak nie to blog :]

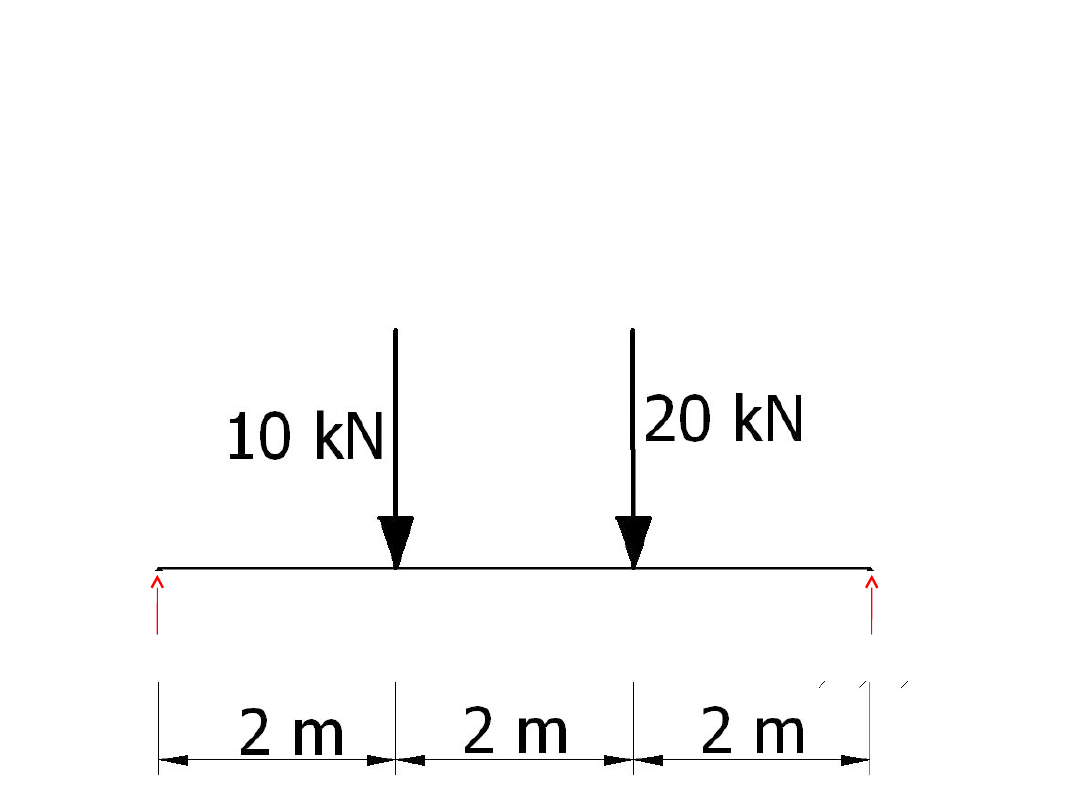
Rysujemy wykres MTN

(punkt 3 planu działania)

Dla wygody robimy tzw.

schemat statytyczny

, czyli nanosimy

na naszą belkę wszsytkie siły jakie na nią działają

13,3

16,7

Reakcja

H

A

wyniosła

zero, dlatego ją
pomijamy

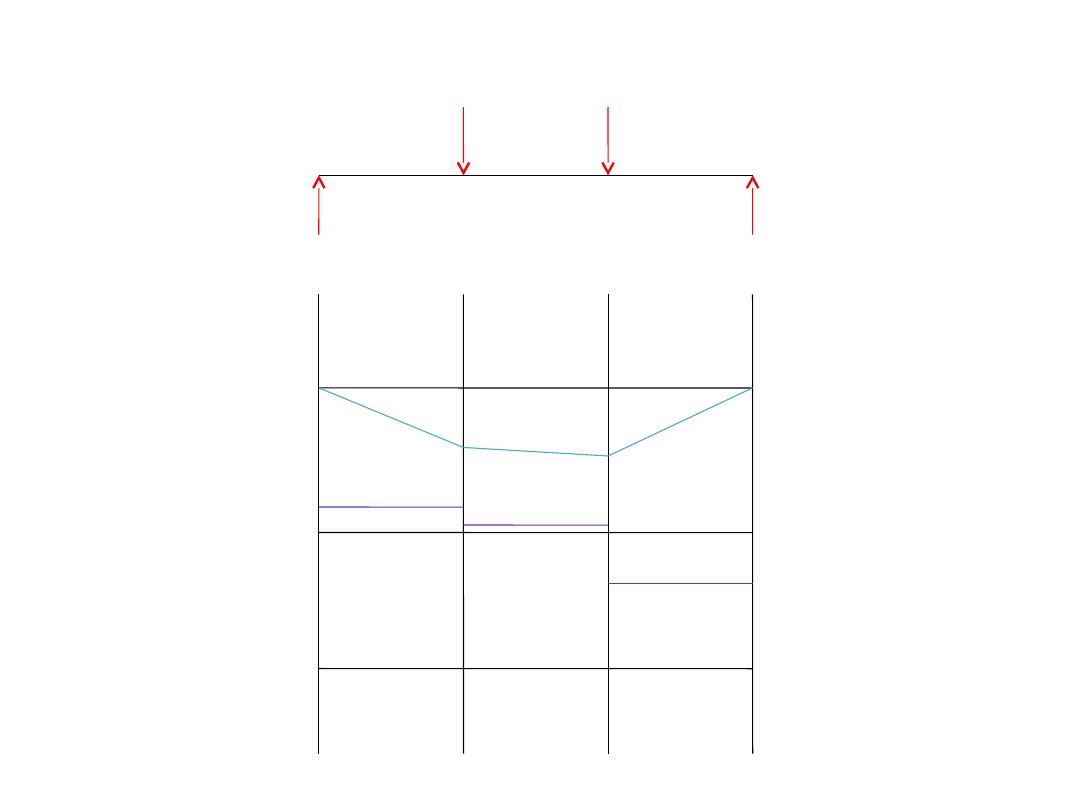
13,3

16,7

20

10

Wykresy

M [kNm]

26,7

33,3

UWAGA!

Na następnych stronach

zasady rysowania

wykresów!

13,3

3,3

16,7

0

N [kN]

T [kN]

+

+

-

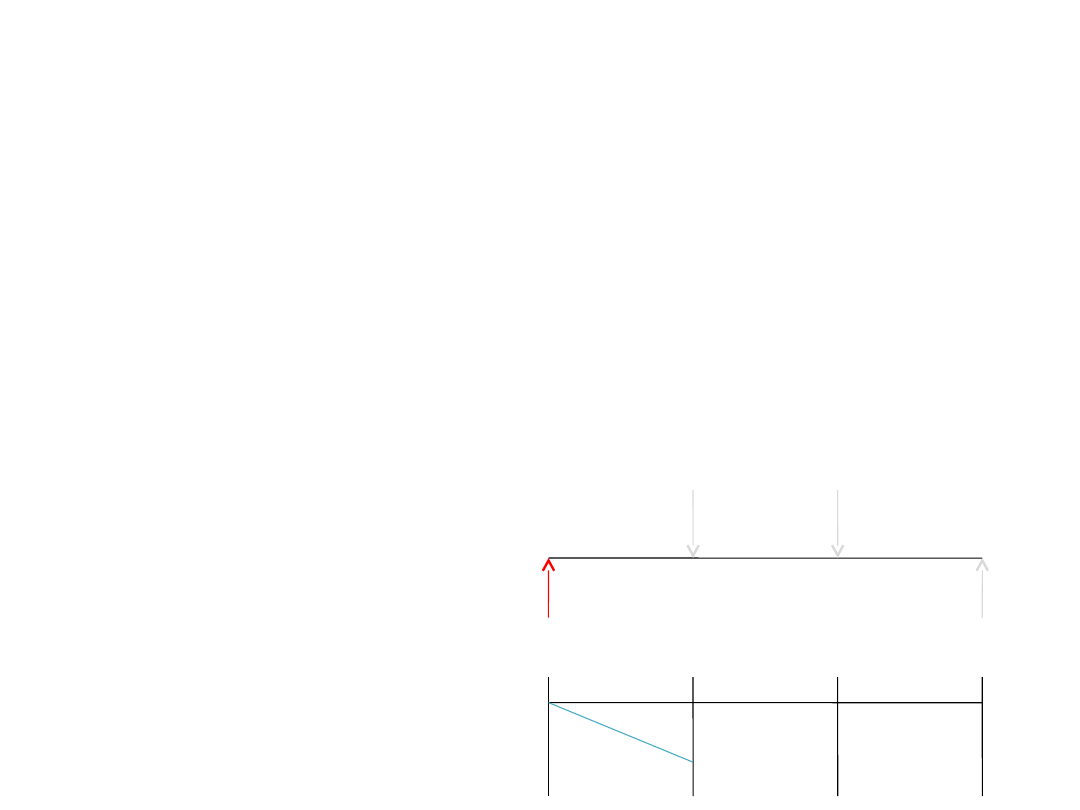
Wykres momentów

UWAGA! Wykres momentu
należy rysować zgodnie z
pewnymi zasadami.

Zwykle przyjmuje się włókna
uprzywilejowane i zwykle na
dole belki.

Proponuję robić to ciut inny
sposób: ZAPAMIĘTAJ –

wykres

momomentu rysujemy po
stronie wółkien rozciganych

(ZAWSZE!).

Rysowanie możemy zacząć od
dowolnej strony – spróbujmy
klasycznie od lewej.

Idąc od lewej będziemy liczyć
wartość momentu w każdym z
punktów, ale tylko z lewej
strony.

13,3

16,7

20

10

4

3

2

1

Jak wyznaczyć ten znak? Po której stronie wykre?

Dla przykładu będziemy wyznaczać momet w punkcie 2.
Pozornie robimy to jak przy reakcjach. Są jednak różnice.

Liczymy od lewej, zatem interesuje nas tylko wszystko na
lewo od punktu 2.

Wyobraź sobie, że nasza belka jest gruba (że nie jest
cienką prostą linią). Dalej co z nią robi nasze

13,3

?

Napiera. I co dalej robi? Rozciąga! I teraz rozciąga górę
czy dół naszej belki?

Jasne, że dół.

Dlatego

wykres

(dla

tego odcinka)

rysyjemy na dole

.

M2 = 13,3 ∙ 2 = 26,7

M [kNm]

26,7

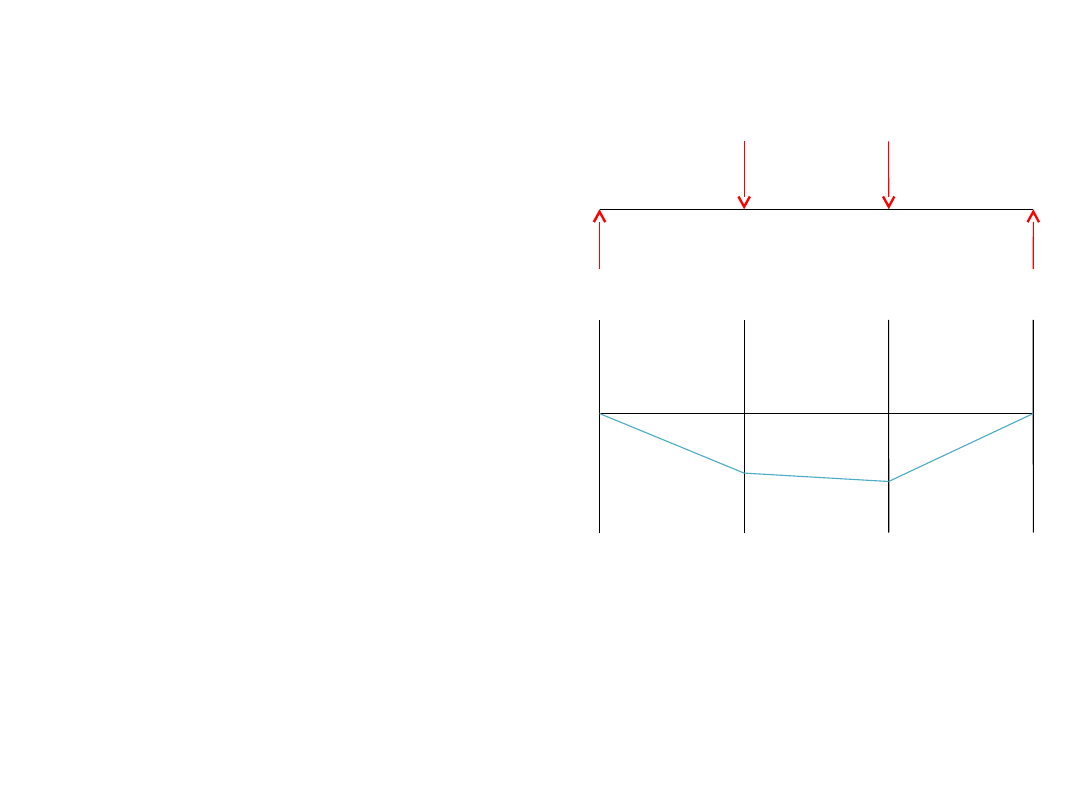
Wykres momentów – ciąg dalszy

∑M

1

=

0

(od lewej nie działa tu żadna siła,

13,3

działa na zerowym

ramieniu)

∑M

2

=

13,3∙2

=

26,7

(interesuje nas tylko to co

na lewo

od punktu 2, mamy tylko siłę

13,3

na ramieniu 2

)

∑M

3

=

13,3∙4 - 10∙2

=

33,3

(j/w; mamy

13,3 na

ramieniu 4

i siłę

10 ma

ramieniu 2

)

∑M

4

=

13,3∙6 - 10∙4 - 20∙2

=

0

(wszystko j/w;

moment

Nam „

spadł” do zera

, co

potierdza że wykres jest

narysowany

prawidłowo)

13,3

16,7

20

10

M [kNm]

26,7

4

3

2

1

33,3

To oczywiście przykład prostej belki, nie ma w niej przyłożonych

momentów, sił na wsporniku, czy obciążenia rozłożonego. Jednak to

podstawy, które trzeba znać

Uwaga! Liczyliśmy nasze momenty od lewes strony. Można przecież również liczyć od
prawe, a wyniki i tak będą identyczne i poprawne. Przykład: ∑M

3

=

16,7

∙ 2

=

33,3

(też

rozciąga włókna dolne)

Drobne nieścisłości wynikają tylko i wyłączne z przyjętych zaokrągleń i są absolutnie
dopuszczalne.

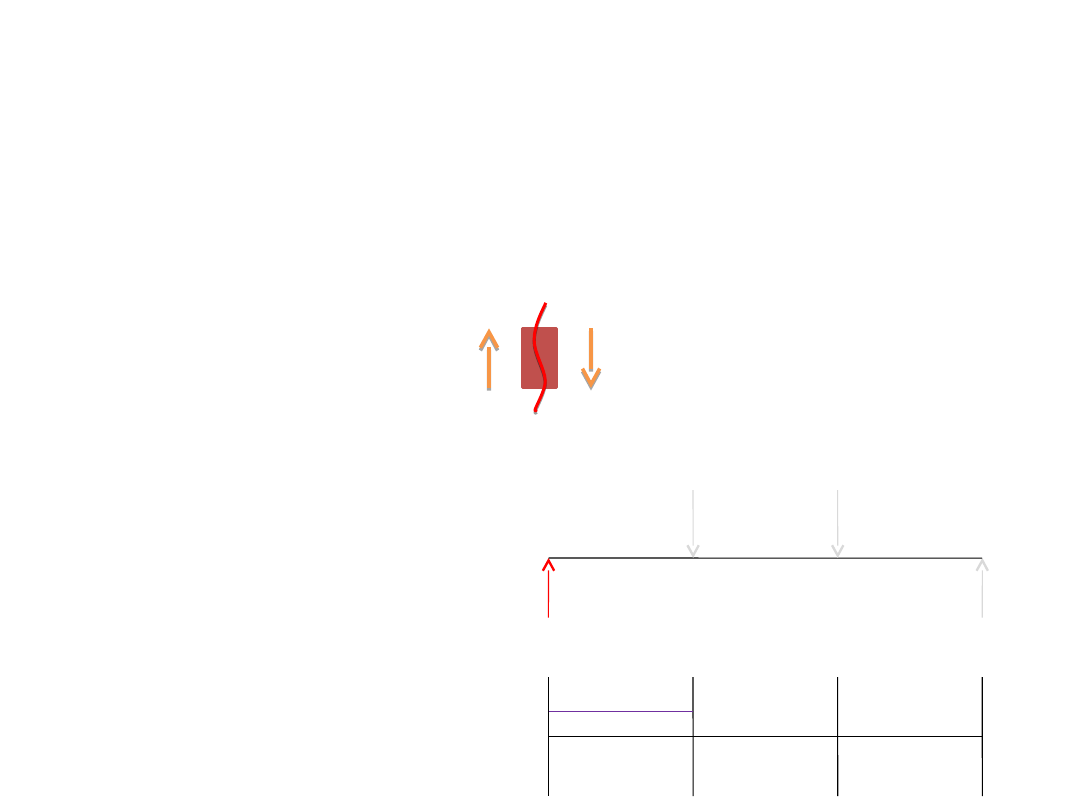
Wykres sił tnących

W siłach tnących należy mocno zwracać uwagę na znak, ponieważ zależnie od strony „z
której idziemy” (od której liczymy) siły tnące inaczej przyjmują wartości.

Oto nasz przekrój:

13,3

16,7

20

10

4

3

2

1

α

α

T

T

Takie zwroty sił oznaczają wartości

dodatnie

(plusy)

+

Oznacza to, że idąc

od lewej

dodatnie są

siły, które skierowane są

do góry

. Idąc

od prawej

dodatnie są te skierowane

w

dół

.

Przykład. Sprawdzamy siły Tnące w

punkcie 1.

∑Px

1

=

+ 13,3

W punkcie 1 zadziała nam tylko

13,3

(od

lewej strony); wektor siły skierowany
jest ku górze, zatem na wykresie
zaznaczamy, na tym odcinku siły
przyjmują

wartości dodatnie

.

13,3

+

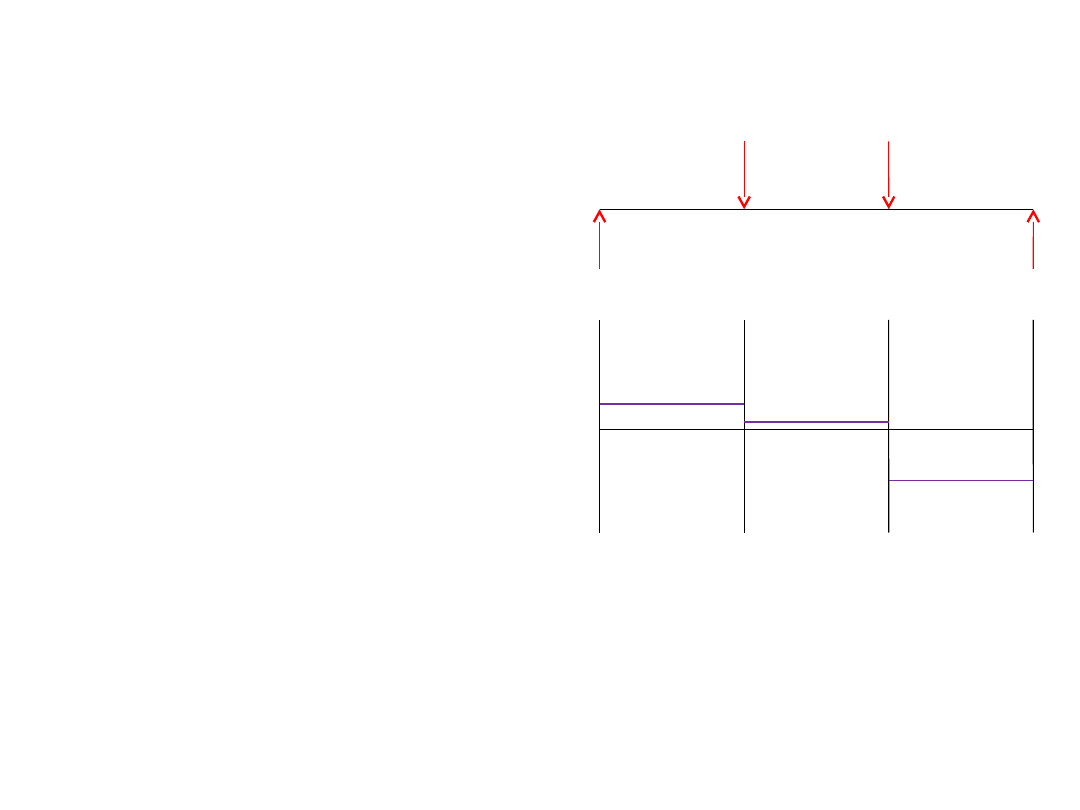
Wykres sił Tnących– ciąg dalszy

∑Px

1

=

13,3

W tym punkcie działa tylko

13,3

∑Px

2

=

13,3 - 10

=

3,3

Interesuje nas tylko to co na lewo od punktu 2,
mamy tylko siłę

13,3

i tak rysujemy wykres – linia

ciągła; dochodzimy do punku 2 i mamy siłę

10

, a

strzałkę w dół, zatem minus. W takim przypadku
mamy do czynienia ze skokiem siły – o jej wartość w
punkcie 2 stąd mamy

3,3.

∑Px

3

=

13,3 – 10 - 20

=

16,7

Sytuacja jak w punkcie 2 (opiszę w inny sposób);
obliczamy wartość sił T nieskończenie blisko punktu
3 (ale nie w samym punkcie) – wynosi

3,3

.

Natomiast już w punkcie 3 mamy siłę na minusie

20.

Zatem ponownie mamy skok siły, tym razem o 20,
co daje nam

16,7

(mówiąc obrazowo z prawej strony

punktu 3).

∑Px

4

=

13,3 - 10 - 20 + 16,7

=

0

13,3

20

10

4

3

2

1

13,3

3,3

16,7

T [kN]

+

+

-

Podobnie jak w 3; tutaj wartość siły maksymalnie blisko punktu 4 jest równa

16,7

; Po dodaniu siły

(

16,7

na plusie, bo strzałka do góry) siły T redukują się do zera. Świadczy to o prawidłowym

wykonaniu wykresu sił T.

16,7

Uwaga! „Strony po których
rysujemy wykres są dowolne (nie jak
w momentach), należy jednak
zaznaczyć po której stronie
zaznaczamy plusy a po której
minusy)

Wykres sił osiowych (normalnych)

W siłach osiowych (inaczej nazywanych normalnymi) mamy do czynienia z podobnym
znakowaniem niezależnie od strony po której mamy przekrój.

Oto nasz przekrój:

α

α

N

N

Takie zwroty sił oznaczają wartości

dodatnie

(plusy)

+

Oznacza to, że siły dziłające

od przekroju

mają wartości

dodatnią

, natomiast

działające w stronę przekroju ujemną

.

W naszym przykładzie siły N mają wartość zero, więc nie mamy czego rysować;
jednak postępujemy z nimi analogicznie jak z siłami T.