
Politechnika Warszawska
Instytut Automatyki i Robotyki
Prof. dr hab. inż. Jan Maciej Kościelny
PODSTAWY AUTOMATYKI
część 5
Charakterystyki częstotliwościowe
2
Charakterystyki częstotliwościowe
0
A
1
(
ω)
t
x
T=2
π/ω
x
y
)]
(
sin[
)
(
sin
)
(
2
1
ω
ϕ
ω
ω
ω
ω
+
=
=
t
A
y
t
A
x
A
2
(
ω)
0
t
y
T=2
π/ω
ϕ(ω)
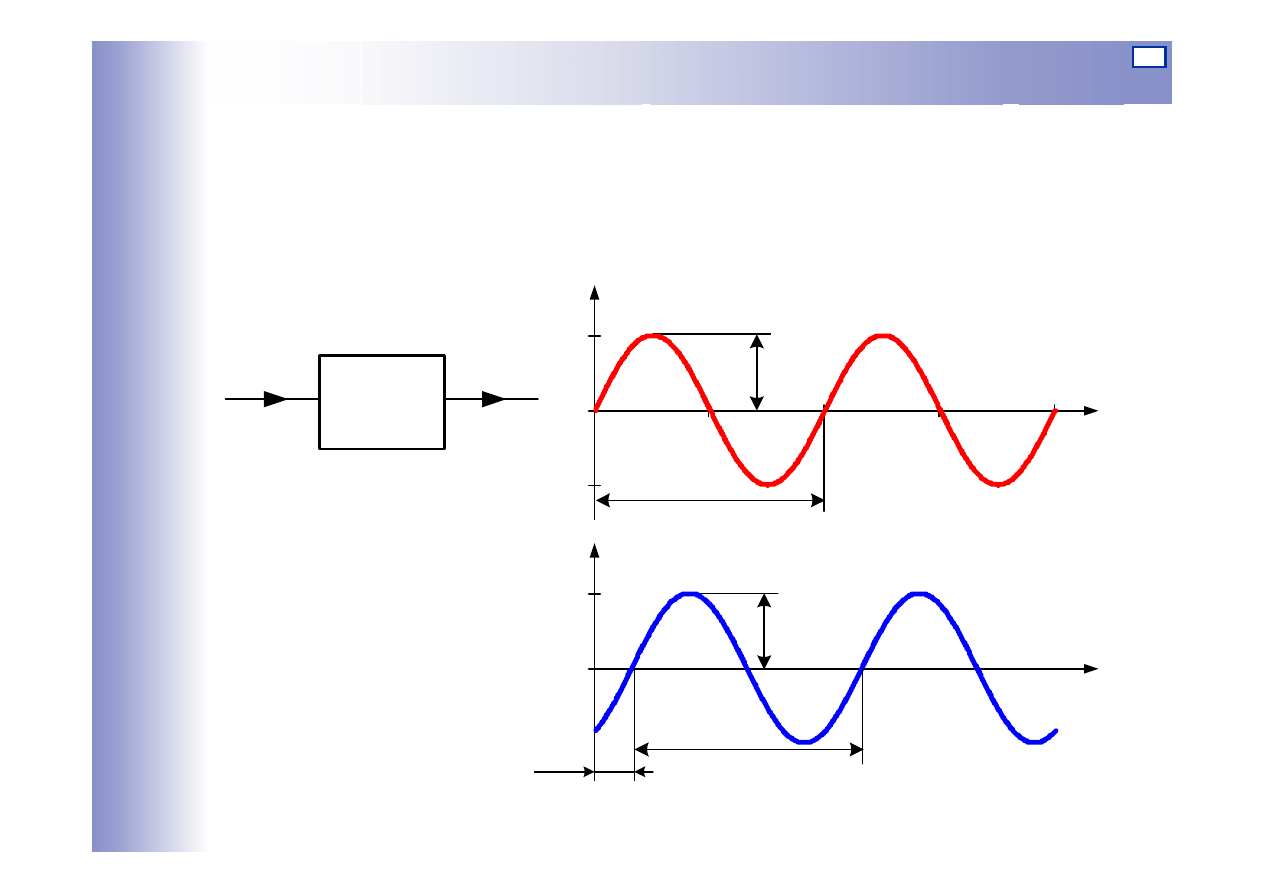
Jeżeli na wejście elementu lub układu liniowego stabilnego wprowadzone zostanie
wymuszenie sinusoidalne o stałej częstotliwości, to na wyjściu, po zaniknięciu
przebiegu przejściowego, ustali się odpowiedź sinusoidalna o tej samej
częstotliwości, ale w ogólnym przypadku, o innej amplitudzie i fazie niż wymuszenie

3
Charakterystyki częstotliwościowe
Charakterystyki częstotliwościowe - określają zachowanie się elementu
lub układu przy wszystkich częstotliwościach wymuszenia
Charakterystyki cz
ę
stotliwo
ś
ciowe -
określają zachowanie się elementu
lub układu przy wszystkich częstotliwościach wymuszenia
Określają w funkcji częstotliwości:
•
stosunek amplitud odpowiedzi do wymuszenia
•
przesunięcie fazowe między odpowiedzią a wymuszeniem
Określają w funkcji częstotliwości:
•
stosunek amplitud odpowiedzi do wymuszenia
•
przesunięcie fazowe między odpowiedzią a wymuszeniem
4
Podstawy teoretyczne
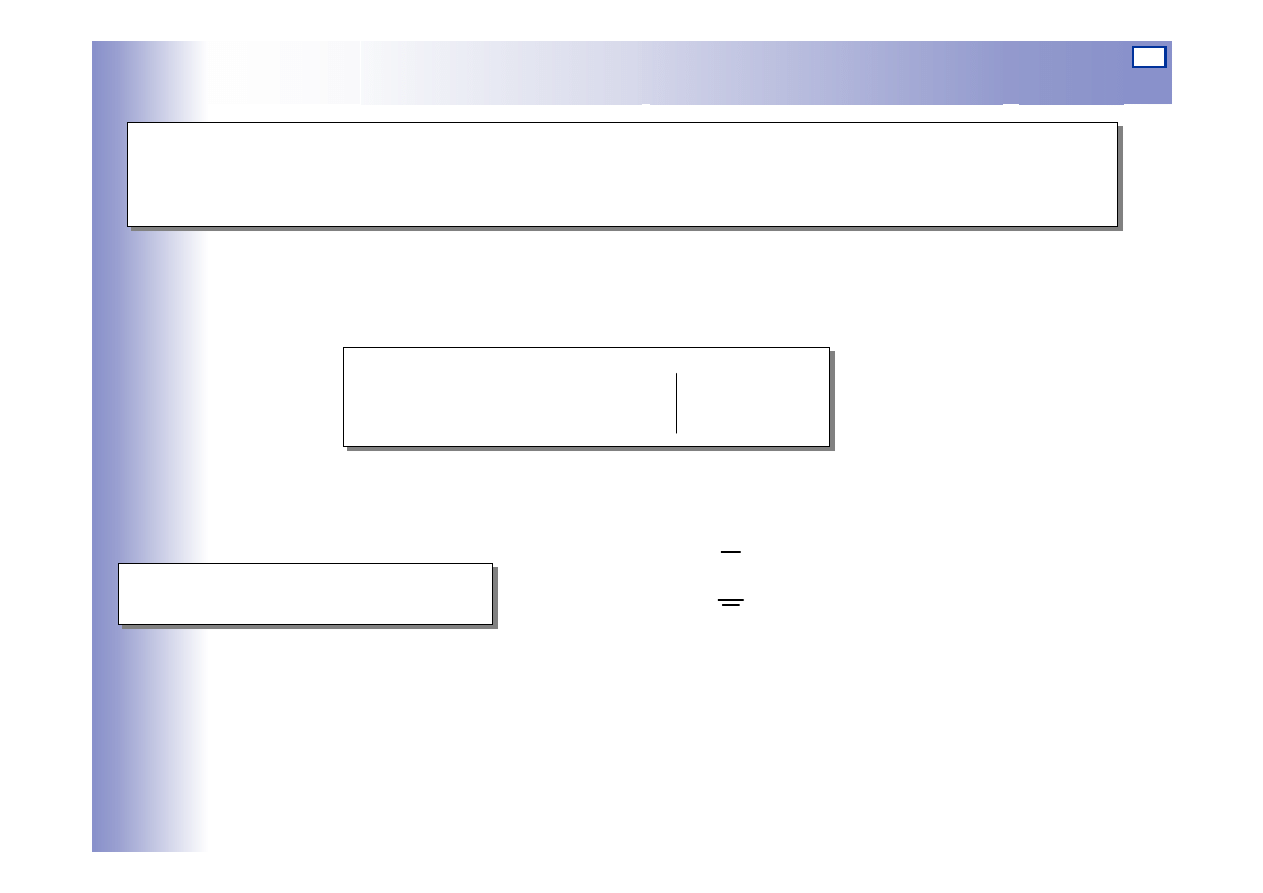
Transmitancja widmowa – szczególny przypadek transmitancji
operatorowej
Transmitancja widmowa – szczególny przypadek transmitancji
operatorowej
Definiowana często jako:
Definiowana często jako:
u
y
j
G
=
)
(
ω
Gdzie: y - wartość zespolona składowej ustalonej odpowiedzi układu
wywołanej wymuszeniem sinusoidalnym
u – wartość zespolona wymuszenia
ω
ω
j
s
s
G
j
G
=
=
)
(
)
(
∫
∞
−
=
0
)
(
)
(
dt
e
t
f
j
F
t
j
ω
ω
przekształcenie Fouriera

5
Podstawy teoretyczne
t
j
e
A
u
ω
ω
)
(
1
_
=
)]
(
[
2
_
)
(
ω
ϕ
ω
ω
+
=
t
j
e
A
y
Podstawiając za: x i y parę odpowiadających sobie funkcji harmonicznych
zapisanych w postaci wykładniczej
Podstawiając za: x i y parę odpowiadających sobie funkcji harmonicznych
zapisanych w postaci wykładniczej
Gdzie: - moduł charakterystyki częstotliwościowej
(stosunek amplitud odpowiedzi do wymuszenia)
)
(
)
(
)
(
1
2
ω
ω
ω
A
A
M
=
]
sin
)[cos
(
)
(
1
1
t
j
t
A
e
A
t
j
ω
ω
ω
ω
ω
+
=
)]}
(
sin[
)]
(
){cos[
(
)
(
2
)]
(
[
2
ω
ϕ
ω
ω
ϕ
ω
ω
ω
ω
ϕ
ω
+
+
+
=
+
t
j
t
A
e
A
t
j
Wejście:
Wyjście:
)
(
1
)
(
2
)
(
)
(
)
(
)
(
ω
ϕ
ω
ω
ϕ
ω
ω
ω
ω
ω
⋅
⋅
⋅
⋅
⋅
⋅
⋅
=
⋅
⋅
⋅
=
j
t
j
j
t
j
e
M
e
A
e
e
A
j
G
6
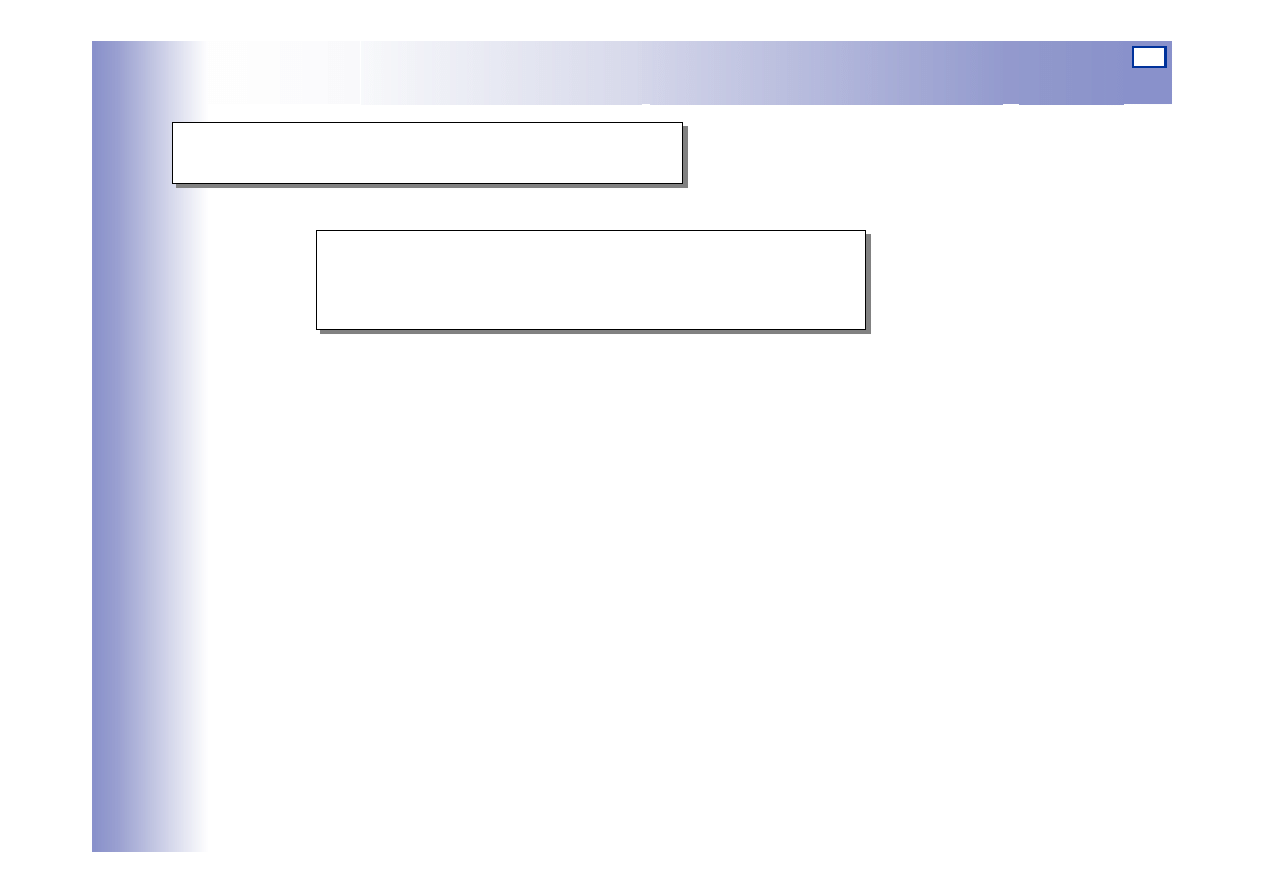
Podstawy teoretyczne
)
(
)
(
)
(
ω
ω
ω
jQ
P
j
G
+
=
G(jω) jest funkcją zespoloną
G(jω) jest funkcj
ą
zespolon
ą
)]
(
Re[
)
(
ω
ω
j
G
P
=
)]
(
Im[
)
(
ω
ω
j
G
Q
=
- część rzeczywista G(j
ω
)
- część
urojona G(j
ω
)
7
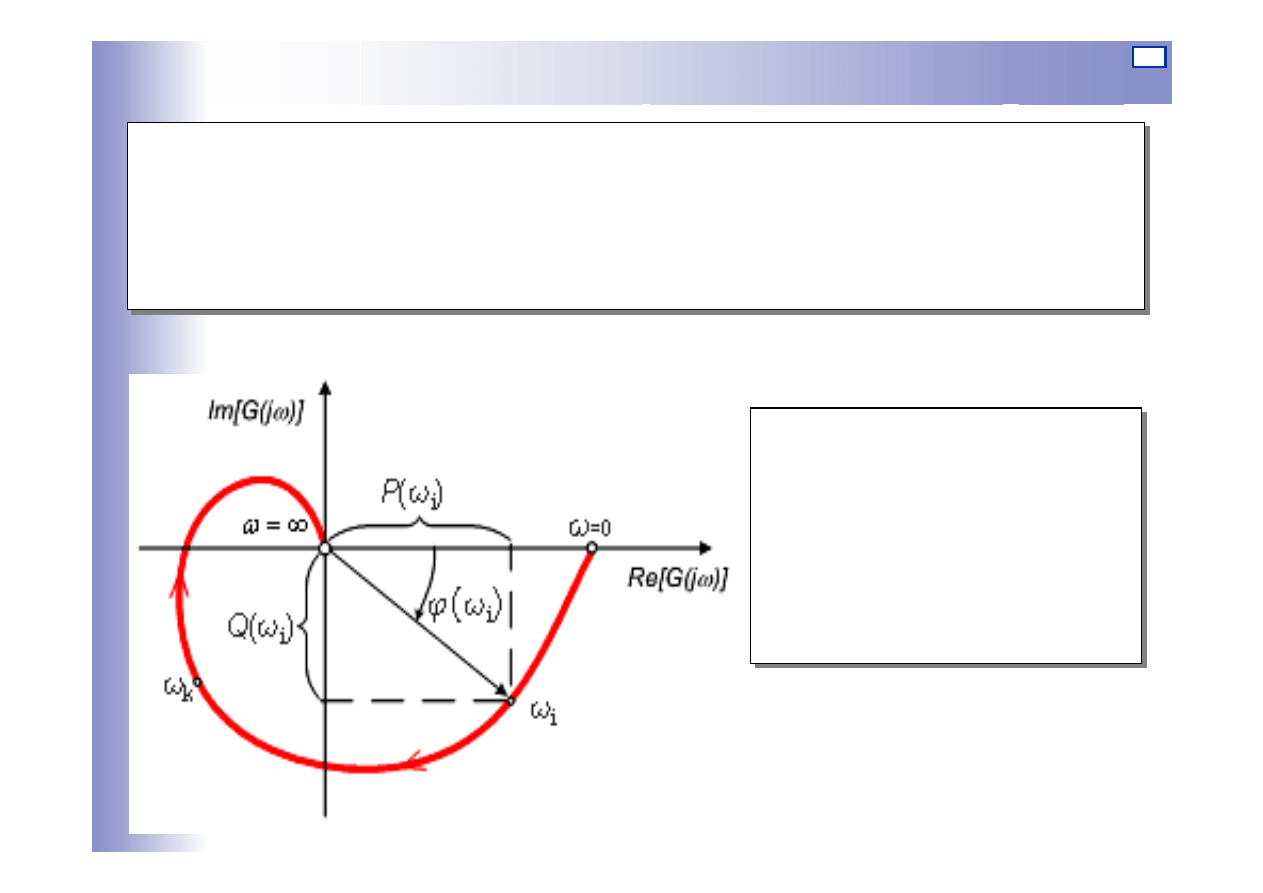
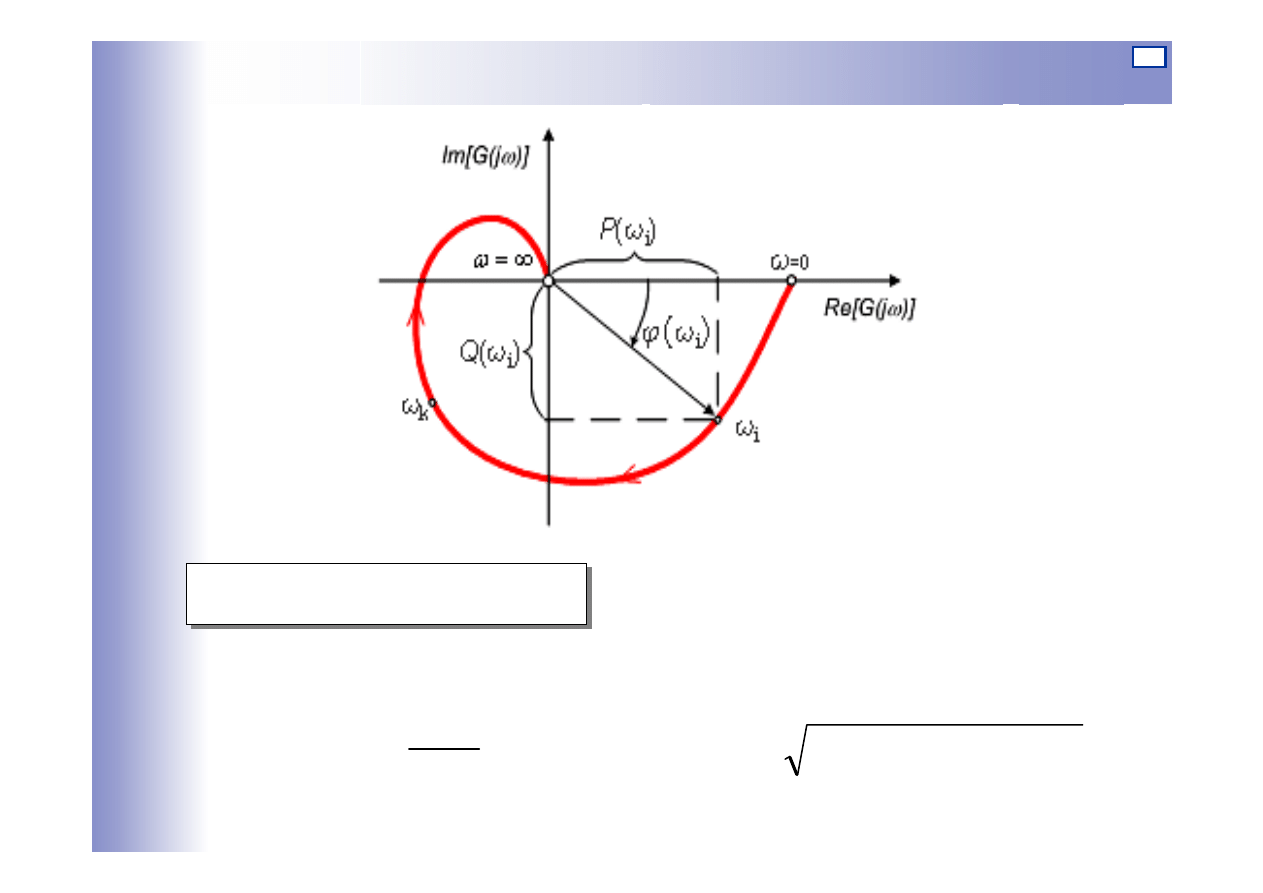
Charakterystyka amplitudowo-fazowa
Charakterystyka amplitudowo-fazowa - wykres końców wektorów,
których:
•
długość reprezentuje stosunek amplitud odpowiedzi do wymuszenia
•
kąt przesunięcie fazowe między odpowiedzią a wymuszeniem
Charakterystyka amplitudowo-fazowa - wykres końców wektorów,
których:
•
długość reprezentuje stosunek amplitud odpowiedzi do wymuszenia
•
kąt przesunięcie fazowe między odpowiedzią a wymuszeniem
Definiowana często jako:
Wykres transmitancji
widmowej G(jω)
Zespolona charakterystyka
częstotliwościowa
Definiowana cz
ę
sto jako:
Wykres transmitancji
widmowej G(jω)
Zespolona charakterystyka
częstotliwościowa
8
Charakterystyka amplitudowo-fazowa
Charakterystyczne związki:
Charakterystyczne związki:
2
2
)]
(
[
)]
(
[
)
(
ω
ω
ω
Q
P
j
M
+
=
)
(
)
(
)
(
ω
ω
ω
ϕ
P
Q
arctg
=
)
(
cos
)
(
)
(
ω
ϕ
ω
ω
M
P
=
)
(
sin
)
(
)
(
ω
ϕ
ω
ω
M
Q
=
9
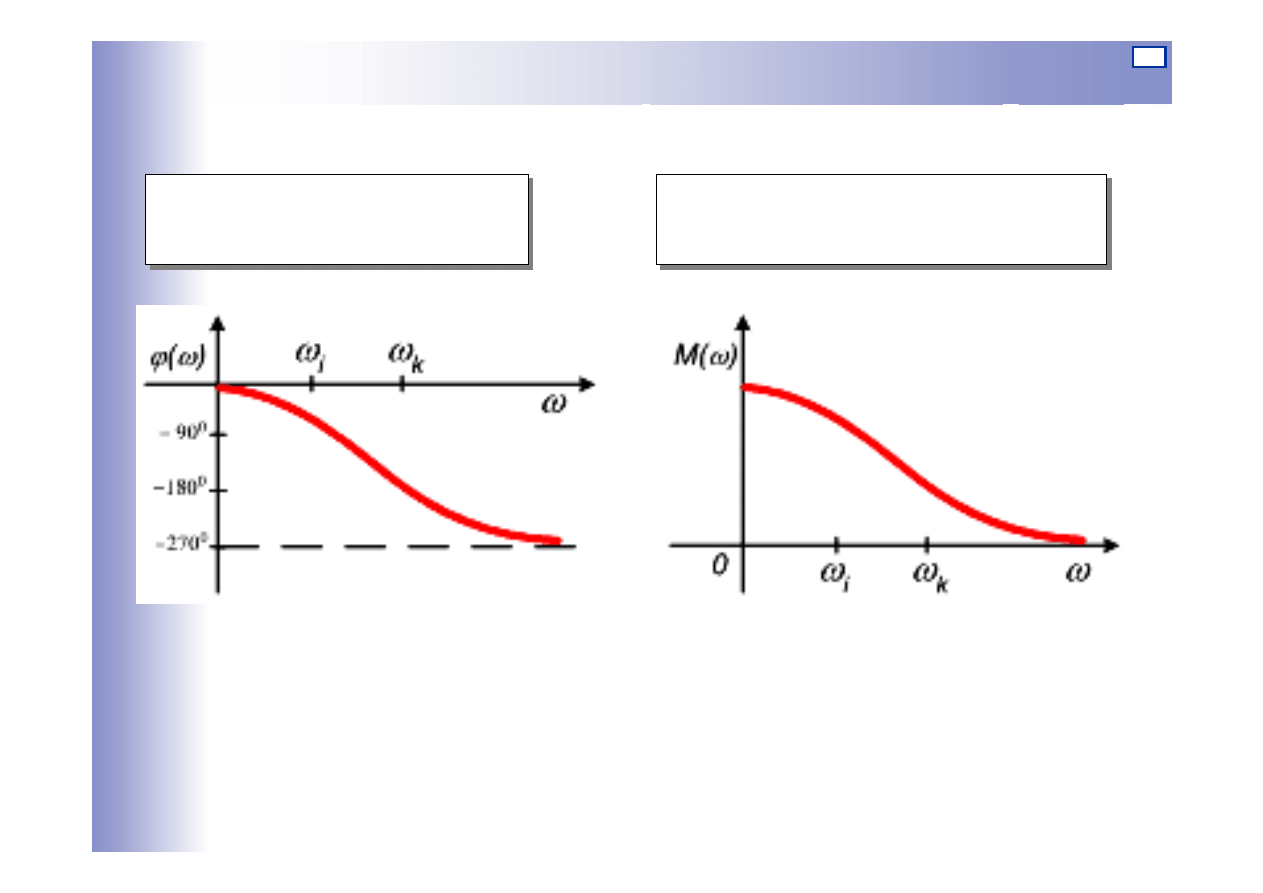
Charakterystyki częstotliwościowe
amplitudowa charakterystyka
częstotliwościowa
amplitudowa charakterystyka
częstotliwościowa
fazowa charakterystyka
częstotliwościowa
fazowa charakterystyka
częstotliwościowa
10
Charakterystyka amplitudowo-fazowa
0,1
1
10
100
0,01
90
0
180
0
-90
0
-180
0
π
-π
π/2
ϕ
(ω)
-π/2
ω
0,1
1
10
100
0,01
20dB
40dB
-20dB
-40dB
100
0,01
10
M(ω)
L(ω)
0,1
ω
Logarytmiczna
charakterystyka amplitudowa
Logarytmiczna
charakterystyka amplitudowa
Logarytmiczna
charakterystyka fazowa
Logarytmiczna
charakterystyka fazowa
)
(
log
20
)
(
ω
ω
M
L
=
)
(
ω
ϕ
11
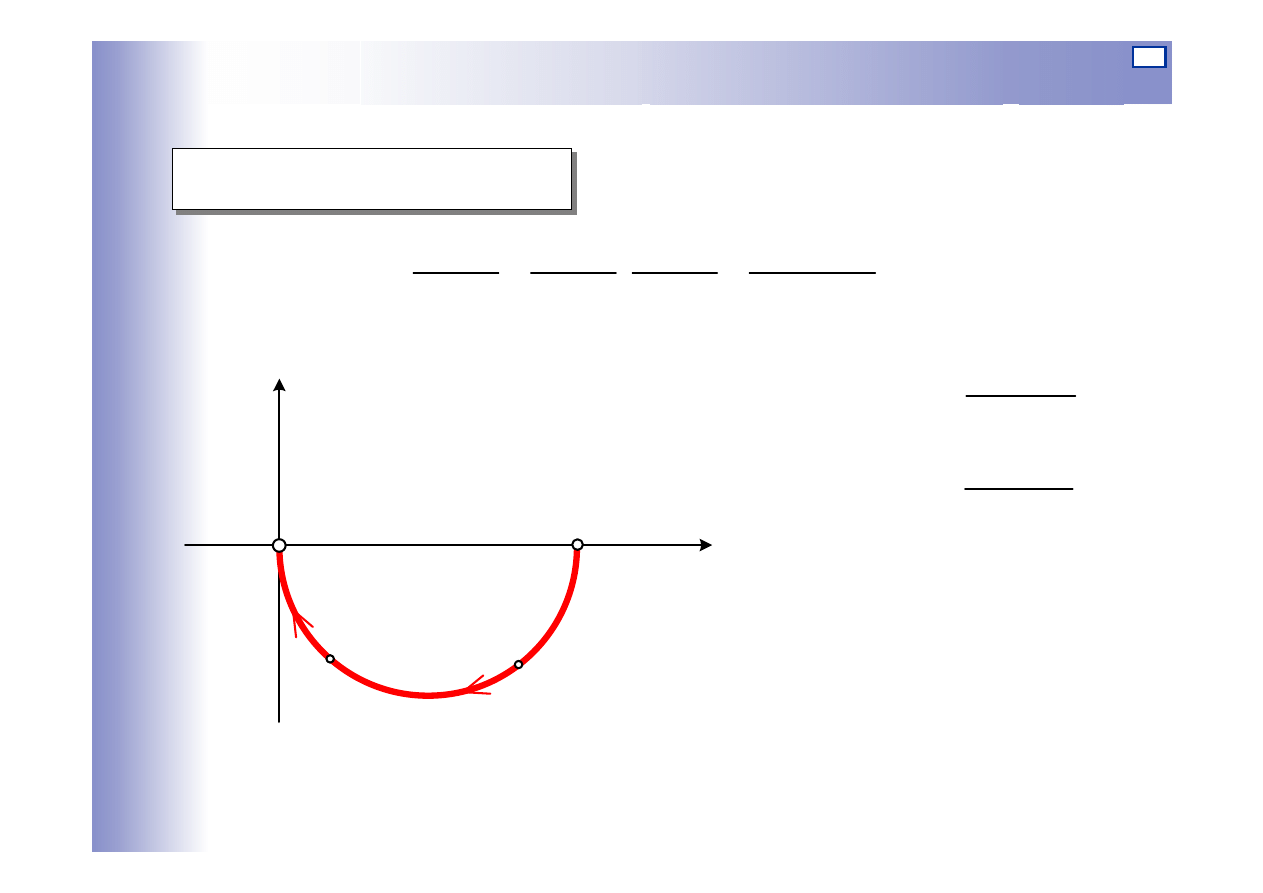
Charakterystyki elementu proporcjonalnego
jQ(
ω
)
P(
ω
)
G( j
ω
)
k
0
)
(
)
(
=
=
ω
ω
Q
k
P
L(
ω
)
dB
ω
20 log k
ω
0
0
ϕ
(
ω
)
12
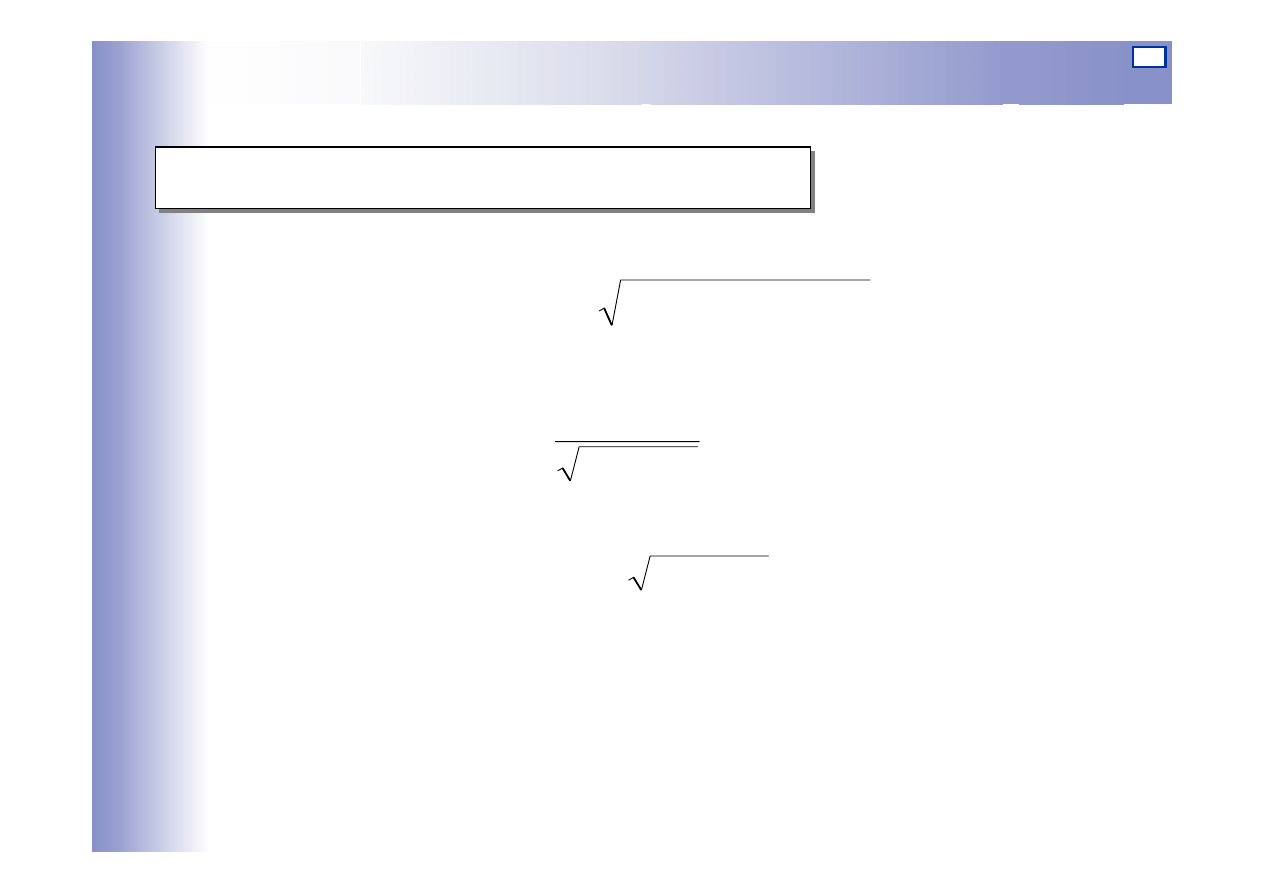
Charakterystyki elementu inercyjnego I rzędu
Transmitancja widmowa:
Transmitancja widmowa:
1
1
1
1
1
)
(
2
2
−
−
+
−
=
−
−
⋅
+
=
+
=
ω
ω
ω
ω
ω
ω
ω
T
kTj
k
Tj
Tj
Tj
k
Tj
k
j
G
Re[G(j
ω
)]
Im[G(j
ω
)]
ω
= 0
ω
i
ω
k
∞
=
ω
k
G(j
ω
)
1
)
(
2
2
+
=
ω
ω
T
k
P
1
)
(
2
2
+
−
=
ω
ω
ω
T
kT
Q
13
Charakterystyki elementu inercyjnego I rzędu
[
] [
]
1
log
20
log
20
)
(
1
log
20
)
(
)
(
)
(
log
20
)
(
log
20
)
(
2
2
2
2
2
2
+
−
=
+
=
+
=
=
ω
ω
ω
ω
ω
ω
ω
ω
T
k
L
T
k
L
Q
P
M
L
c
c
Logarytmiczna charakterystyka amplitudowa:
Logarytmiczna charakterystyka amplitudowa:
14
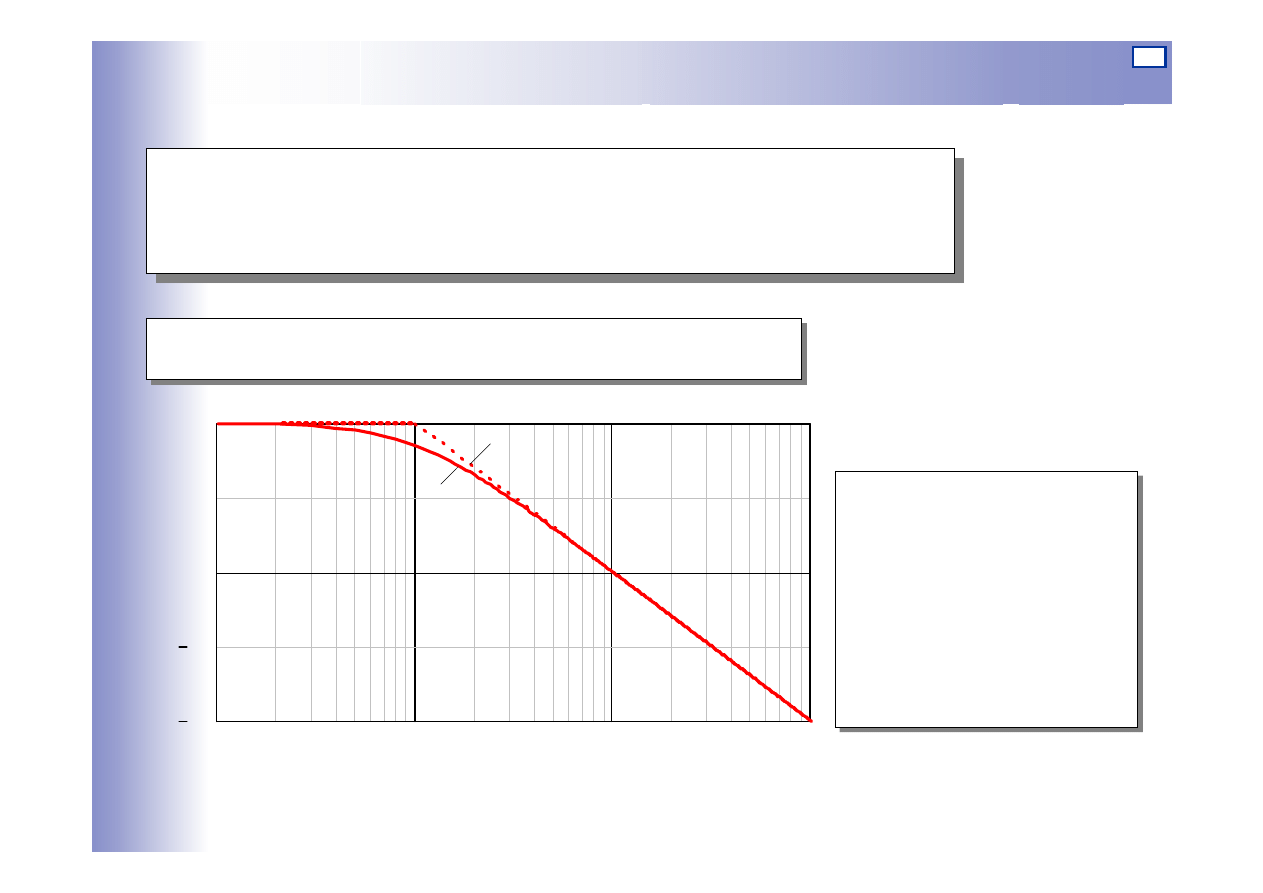
Charakterystyki elementu inercyjnego I rzędu
0.1
1
10
100
20
10
0
10
20
- 20 dB/dek
ω/ω
s
L(
ω)
dB
a
b
Dla:
Dla:
T
/
1
<
ω
k
L
log
20
)
(
=
ω
T
/
1
>
ω
ω
ω
T
k
L
log
20
log
20
)
(
−
=
Dla: k=10
a – charakterystyka
rzeczywista
b – charakterystyka
asymptotyczna
Dla: k=10
a – charakterystyka
rzeczywista
b – charakterystyka
asymptotyczna
Logarytmiczna charakterystyka amplitudowa:
Logarytmiczna charakterystyka amplitudowa:
T
s
/
1
=
ω
15
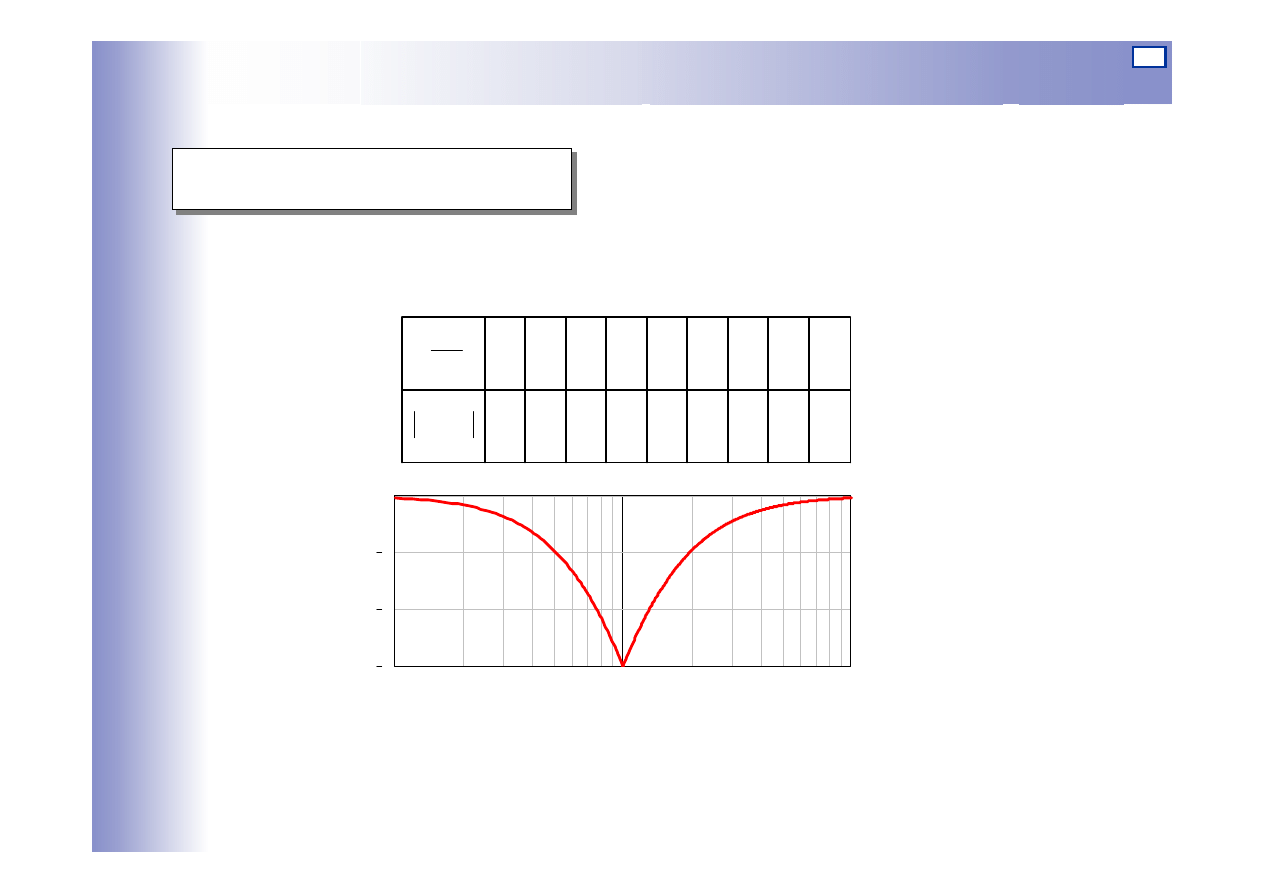
Charakterystyki elementu inercyjnego I rzędu
0,04
0,32
0,65
1,0
3,01
1,0
0,65
0,32
0,04
10,0
4,0
2,5
10
1,0
0,5
0,4
0,25
0,1
Tablica 4.1
ω/ω
s
∆L(ω)
dB
0.1
1
10
3
2
1
0
S
ω
ω
)
(
ω
L
∆
Wykres błędu:
Wykres błędu:
16
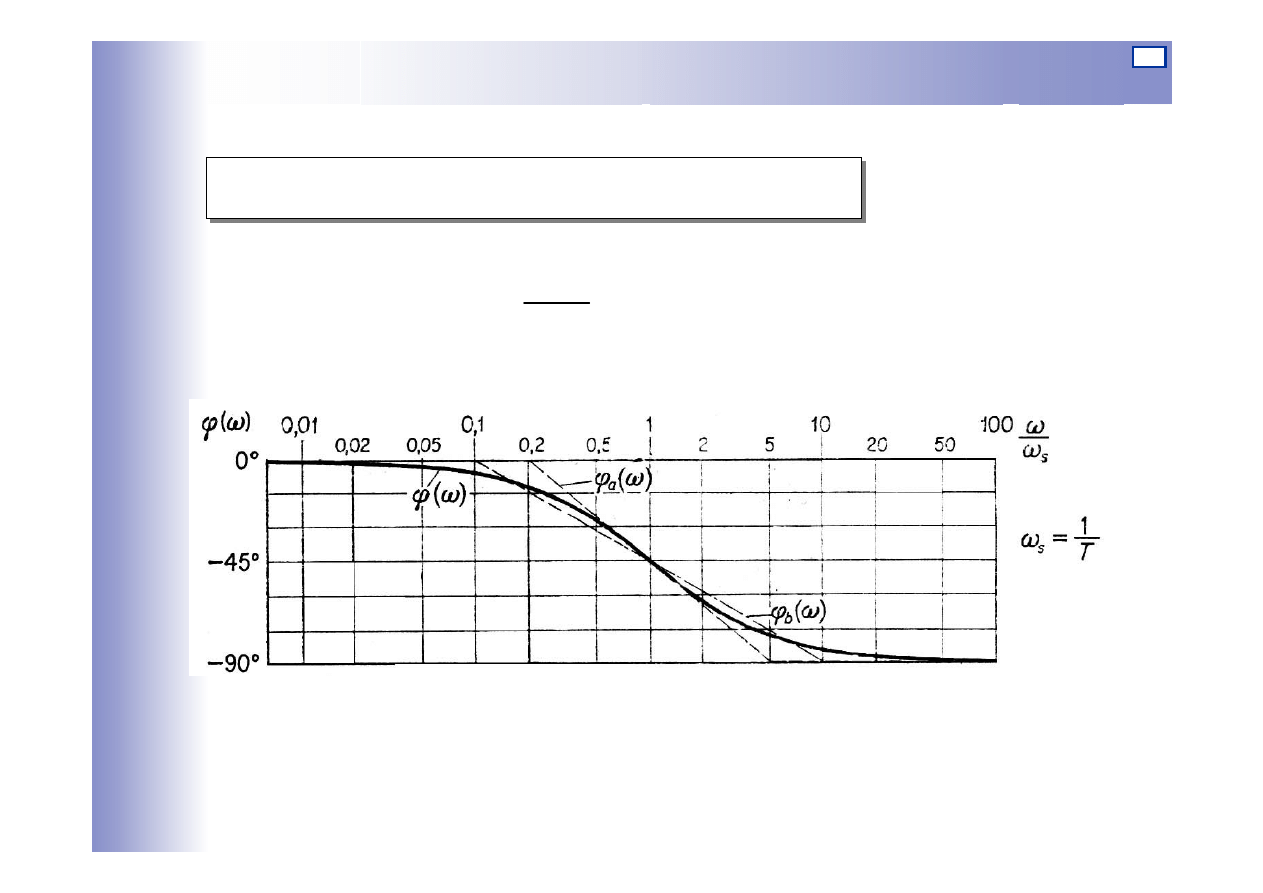
Charakterystyki elementu inercyjnego I rzędu
)
(
)
(
)
(
)
(
)
(
ω
ω
ω
ω
ω
ϕ
T
arctg
T
arctg
P
Q
arctg
−
=
−
=
=
Logarytmiczna charakterystyka fazowa:
Logarytmiczna charakterystyka fazowa:
17
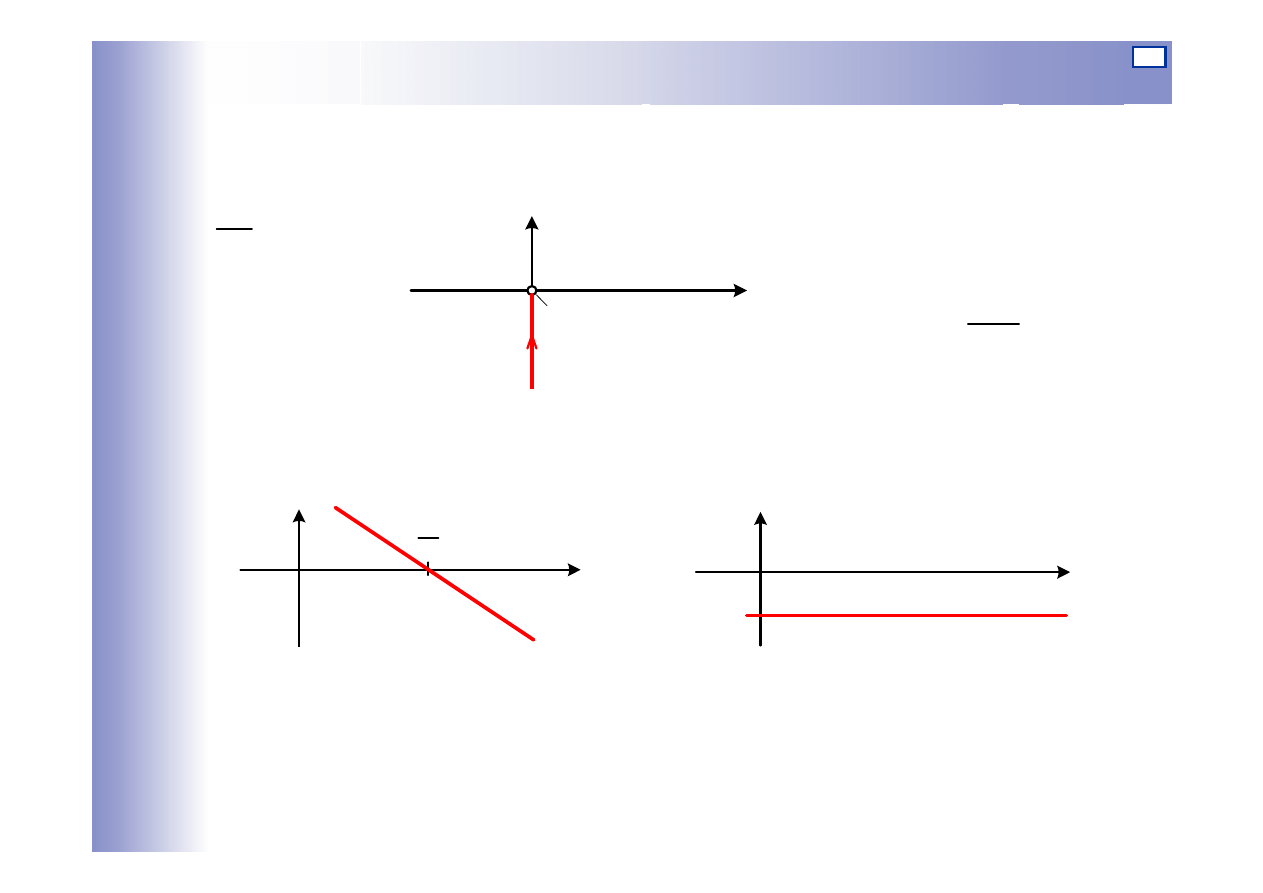
Charakterystyki elementu całkującego
P(
ω
)
jQ(
ω
)
ω
= 0
∞
=
ω
ω
ω
ω
T
Q
P
1
)
(
0
)
(
−
=
=
L(
ω
)
dB
ω
1
T
- 20 dB/dek
ω
ϕ
(
ω
)
−90
0
Ts
1
18
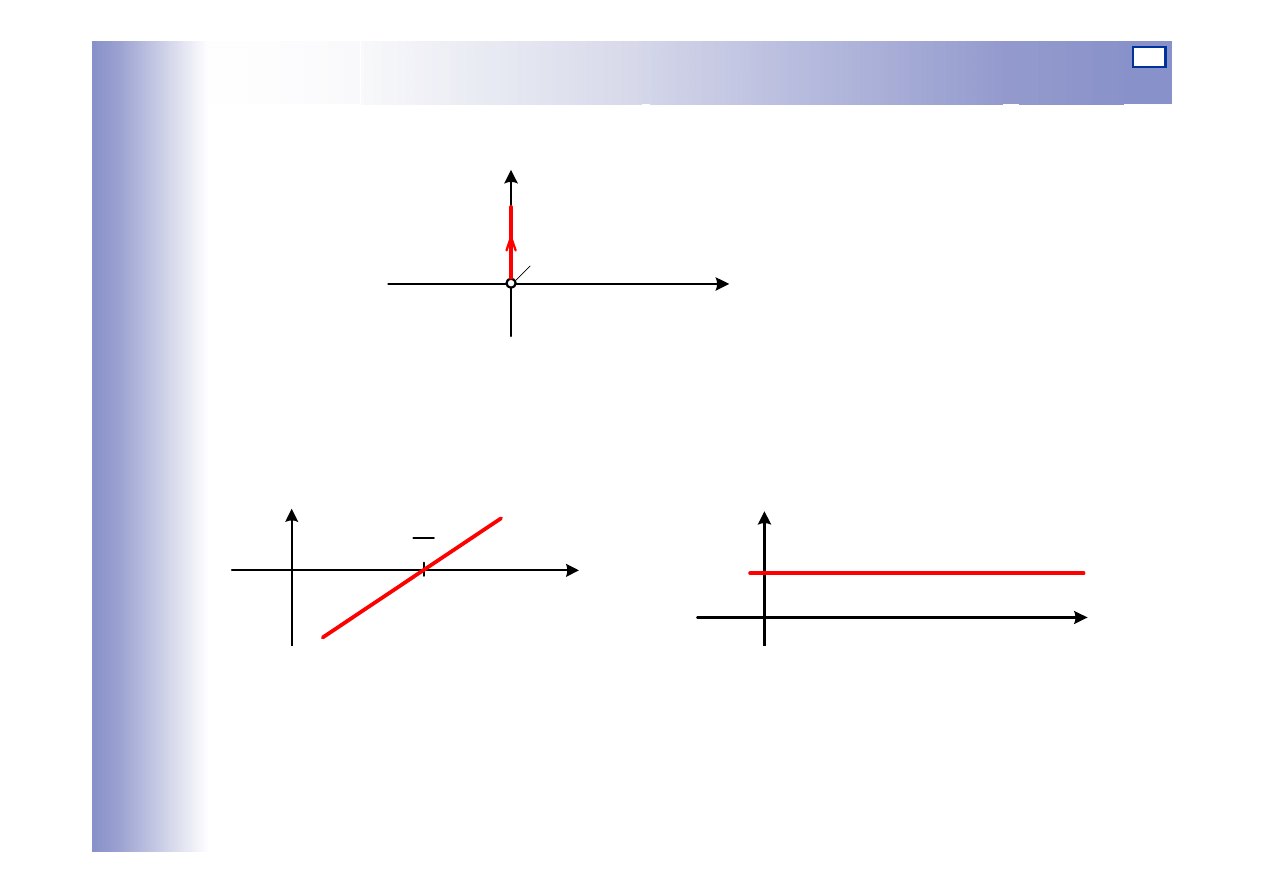
Charakterystyki elementu różniczkującego
P(
ω
)
jQ(
ω
)
ω
= 0
∞
=
ω
ω
ω
ω
T
Q
P
=
=
)
(
0
)
(
L(
ω
)
dB
ω
1
T
+ 20 dB/dek
ω
ϕ
(
ω
)
−90
0
Ts
19
Charakterystyki elementu różniczkującego
Transmitancja widmowa elementu różniczkującego rzeczywistego:
Transmitancja widmowa elementu różniczkującego rzeczywistego:
1
)
(
+
=
ω
ω
ω
Tj
Tj
j
G
1
)
(
2
2
2
2
+
=
ω
ω
ω
T
T
P
1
)
(
2
2
+
=
ω
ω
ω
T
T
Q
Charakterystyka amplitudowo-fazowa:
Charakterystyka amplitudowo-fazowa:
20
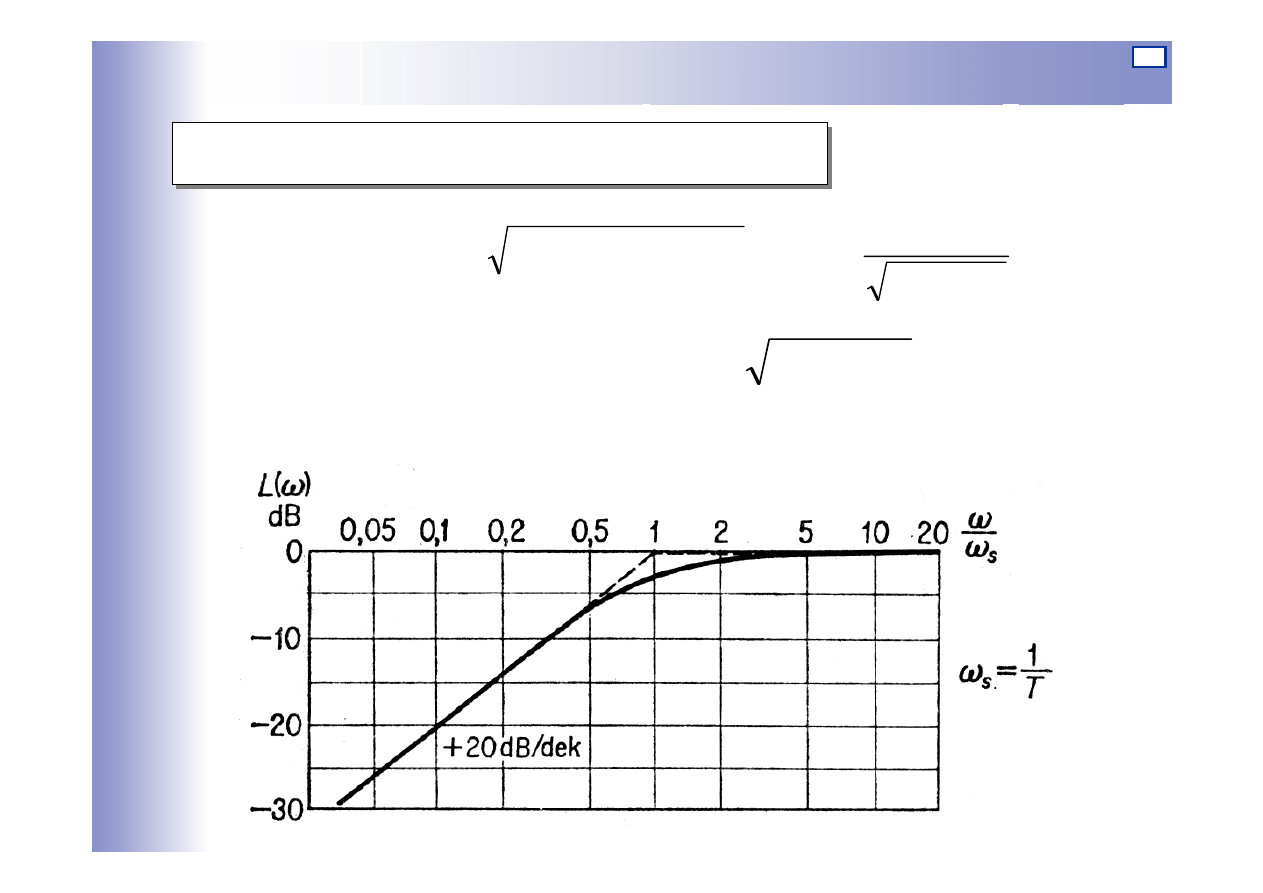
Charakterystyki elementu różniczkującego
[
] [
]
1
log
20
)
(
)
(
log
20
)
(
2
2
2
2
+
=
+
=
ω
ω
ω
ω
ω
T
T
Q
P
L
1
log
20
log
20
)
(
2
2
+
−
=
ω
ω
ω
T
T
L
Logarytmiczna charakterystyka amplitudowa:
Logarytmiczna charakterystyka amplitudowa:
21
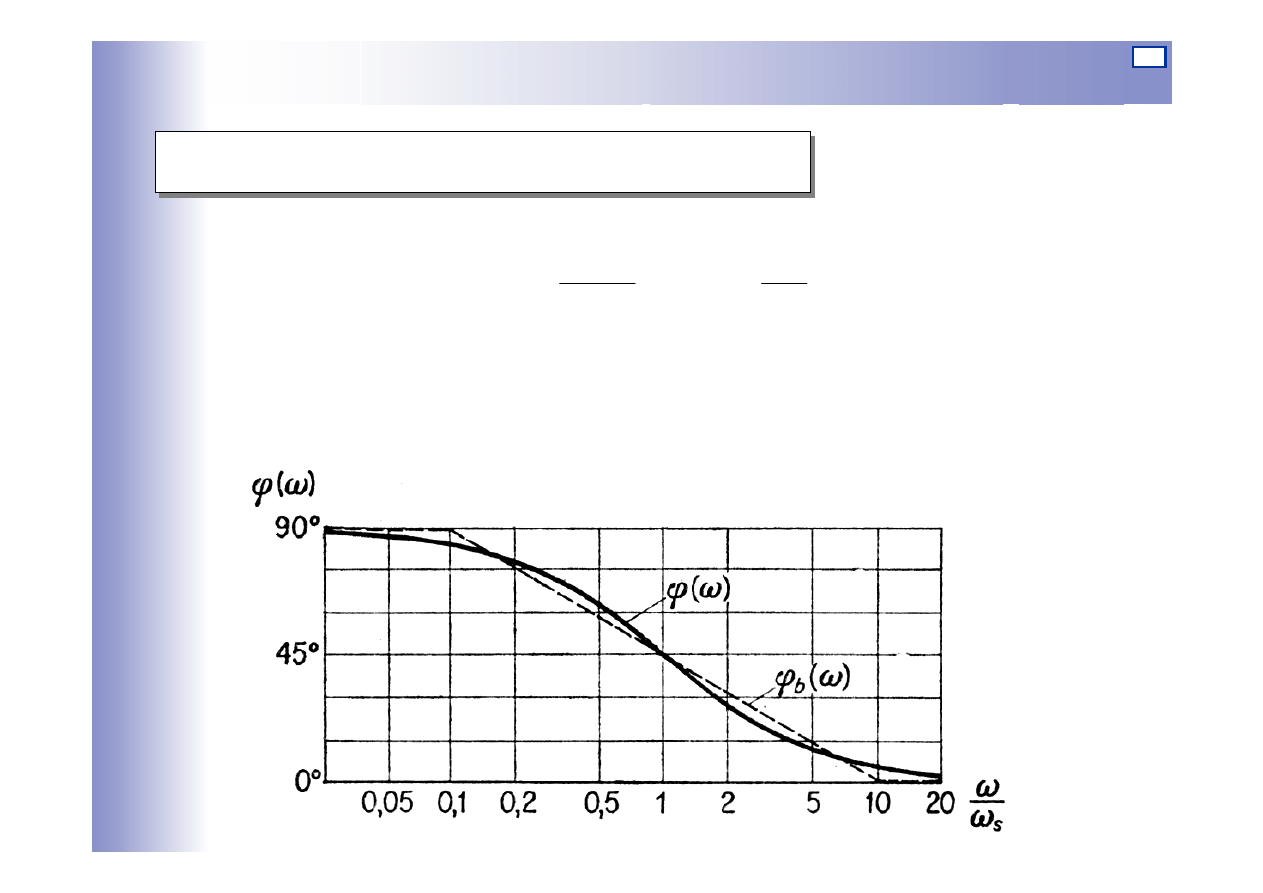
Charakterystyki elementu różniczkującego
)
(
90
)
(
)
1
(
)
(
)
(
)
(
0
ω
ω
ϕ
ω
ω
ω
ω
ϕ
T
arctg
T
arctg
P
Q
arctg
−
=
=
=
c
Logarytmiczna charakterystyka fazowa:
Logarytmiczna charakterystyka fazowa:
22
Charakterystyki elementu oscylacyjnego
Transmitancja widmowa:
Transmitancja widmowa:
( )
( ) ( )
0
2
2
0
2
0
2
0
0
2
2
0
2
2
)
(
ζωω
ω
ω
ω
ω
ω
ζω
ω
ω
ω
⋅
+
−
=
+
+
=
j
k
j
j
k
j
G
Gdzie:
k — współczynnik proporcjonalności
ω
0
— pulsacja oscylacji własnych elementu
ζ — zredukowany (względny) współczynnik tłumienia
Gdzie:
k — współczynnik proporcjonalności
ω
0
— pulsacja oscylacji własnych elementu
ζ — zredukowany (względny) współczynnik tłumienia
2
0
2
2
2
0
2
2
0
2
0
)
2
(
)
(
)
(
)
(
ω
ζω
ω
ω
ω
ω
ω
ω
+
−
−
=
k
P
2
0
2
2
2
0
3
0
)
2
(
)
(
2
)
(
ω
ζω
ω
ω
ω
ζω
ω
+
−
=
k
Q
23
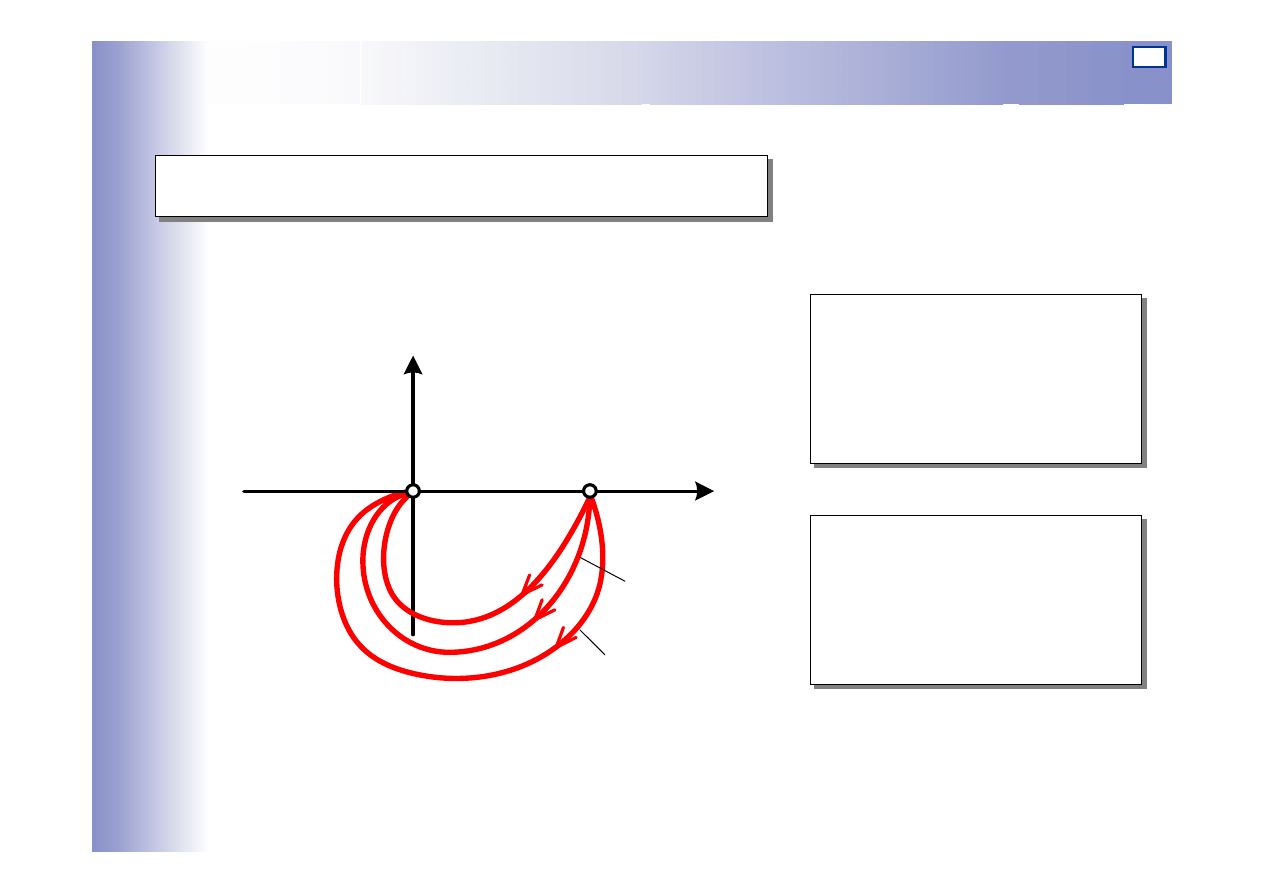
Charakterystyki elementu oscylacyjnego
P(
ω
)
jQ(
ω
)
ω
= 0
ξ
2
ξ
1
ξ
3
∞
=
ω
ξ
3
<ξ
2
<ξ
1
Charakterystyka amplitudowo-fazowa:
Charakterystyka amplitudowo-fazowa:
Dla: ω=0
Dla: ω=0
k
P
=
)
0
(
0
)
0
(
=
Q
Dla: ω=∞
Dla: ω=∞
0
)
(
=
∞
P
0
)
(
=
∞
Q
,

24
Charakterystyki elementu oscylacyjnego
(
) (
)
2
0
2
2
0
2
0
2
2
2
0
2
0
2
2
2
1
log
20
log
20
)
(
)
2
(
)
(
log
20
)
(
)
(
)
(
+
−
−
=
+
−
=
+
=
ω
ω
ζ
ω
ω
ω
ω
ζω
ω
ω
ω
ω
ω
ω
k
L
k
Q
P
L
c
Logarytmiczna charakterystyka amplitudowa:
Logarytmiczna charakterystyka amplitudowa:
25
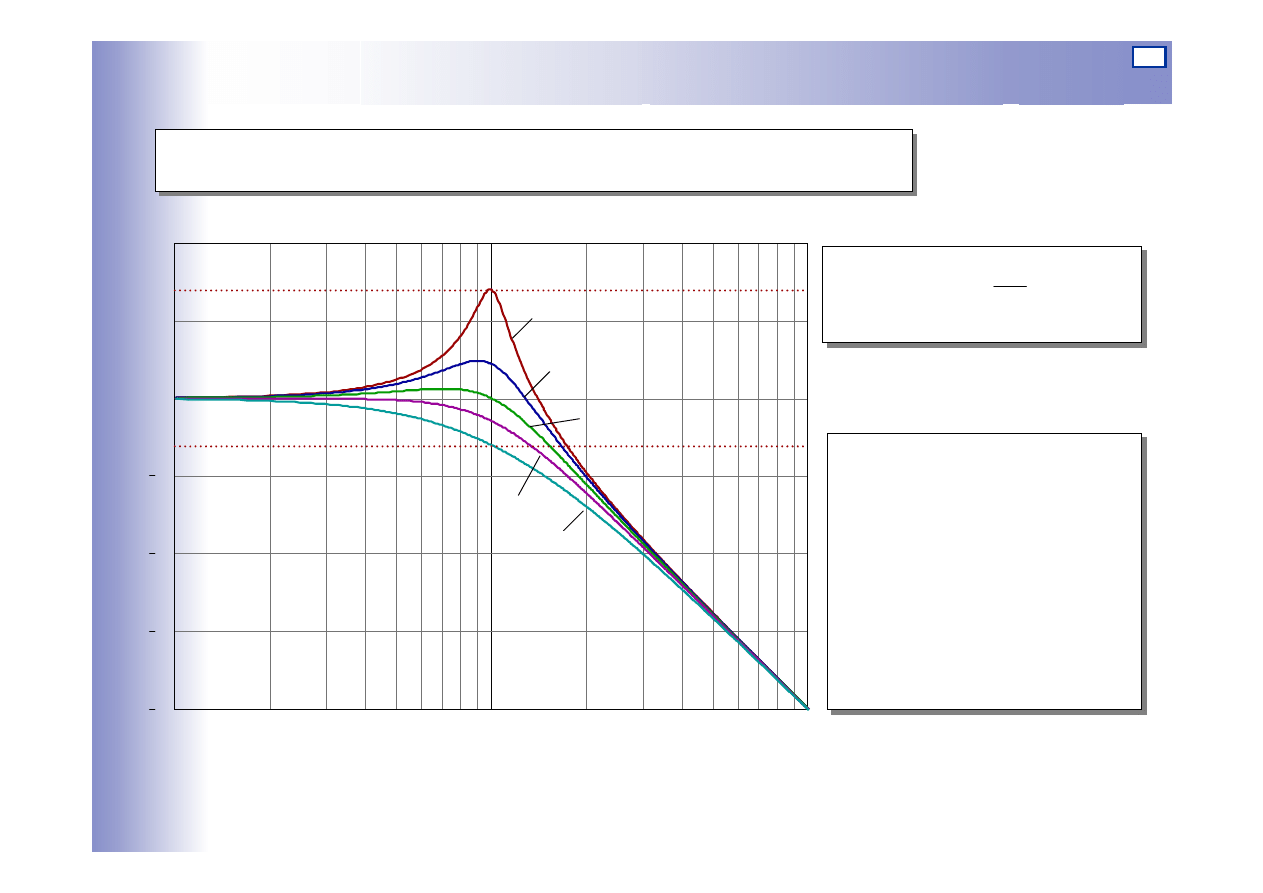
Charakterystyki elementu oscylacyjnego
Dla:
ξ=0
Dla:
ξ=0
∞
=
= )
1
(
0
ω
ω
L
Dla:
ξ=1 – wartość
graniczna,
przebieg
aperiodyczny
(najkrócej
trwający)
Dla:
ξ=1 – wartość
graniczna,
przebieg
aperiodyczny
(najkrócej
trwający)
0.1
1
10
40
30
20
10
0
10
20
6
−
14
L(
ω)
ω/ω
0
ξ
1
= 0.1
ξ
2
= 0.3
ξ
3
= 0.5
ξ
4
= 0.7
ξ
5
= 1
Logarytmiczna charakterystyka amplitudowa dla k=1:
Logarytmiczna charakterystyka amplitudowa dla k=1:
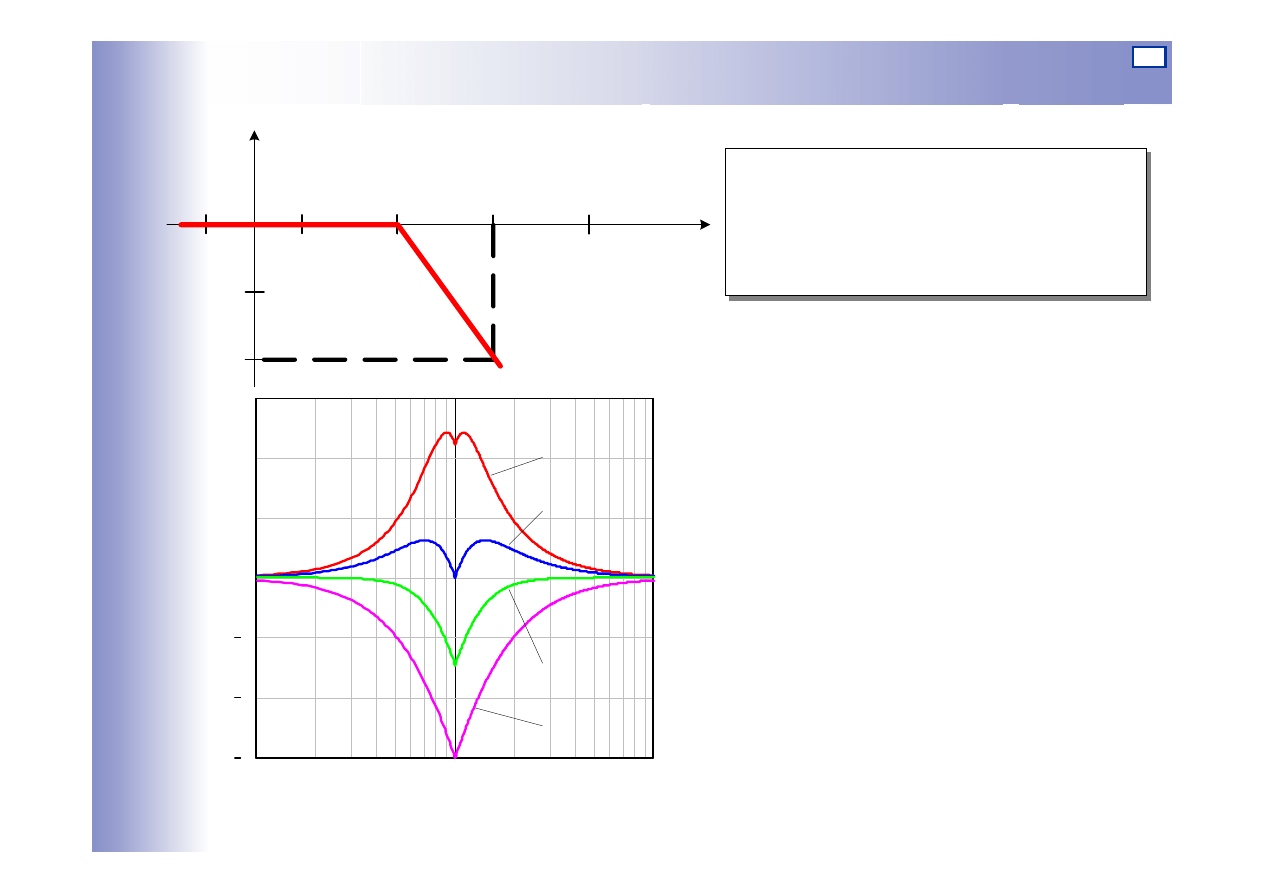
26
Charakterystyki elementu oscylacyjnego
- 40 dB/dek
L(
ω
)
ω/ω
0
0.01 0.1 1 10 100
- 20dB
- 40dB
Asymptotyczna
charakterystyka amplitudowa
dla:
Asymptotyczna
charakterystyka amplitudowa
dla:
1
3
,
0
≤
≤
ξ
0.1
1
10
6
4
2
0
2
4
6
ω/ω
0
∆L(ω)
)
ξ = 0.3
ξ = 0.5
ξ = 0.7
ξ = 1
dB
L
6
)
(
<
∆
ω
27
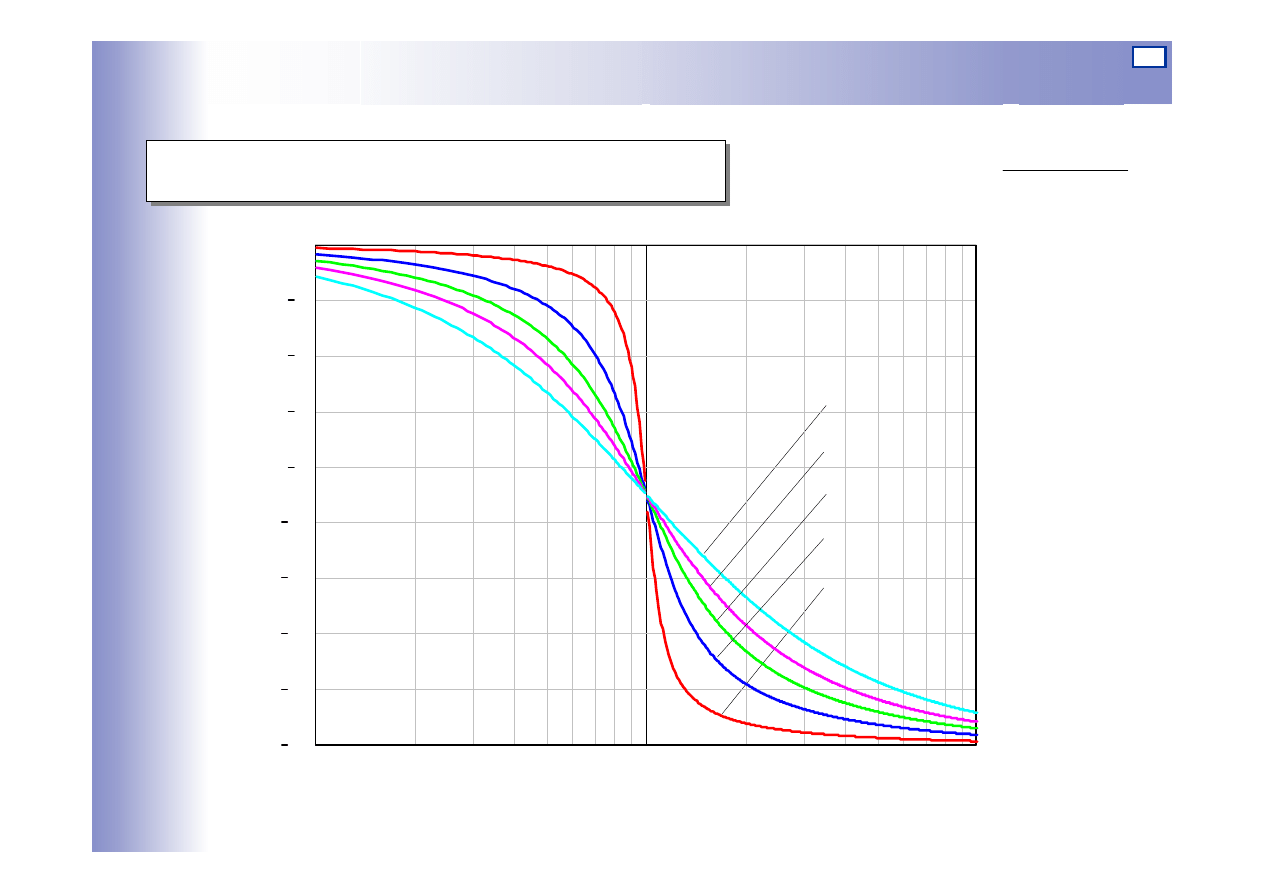
Charakterystyki elementu oscylacyjnego
Logarytmiczna charakterystyka fazowa:
Logarytmiczna charakterystyka fazowa:
ϕ(ω)
[
0
]
ω/ω
0
0.
1
1
1
0
180
160
140
120
100
80
60
40
20
0
ξ
1
= 0.1
ξ
2
= 0.3
ξ
3
= 0.5
ξ
4
= 0.7
ξ
5
= 1
−
−
=
2
2
0
0
2
)
(
ω
ω
ω
ζω
ω
ϕ
arctg
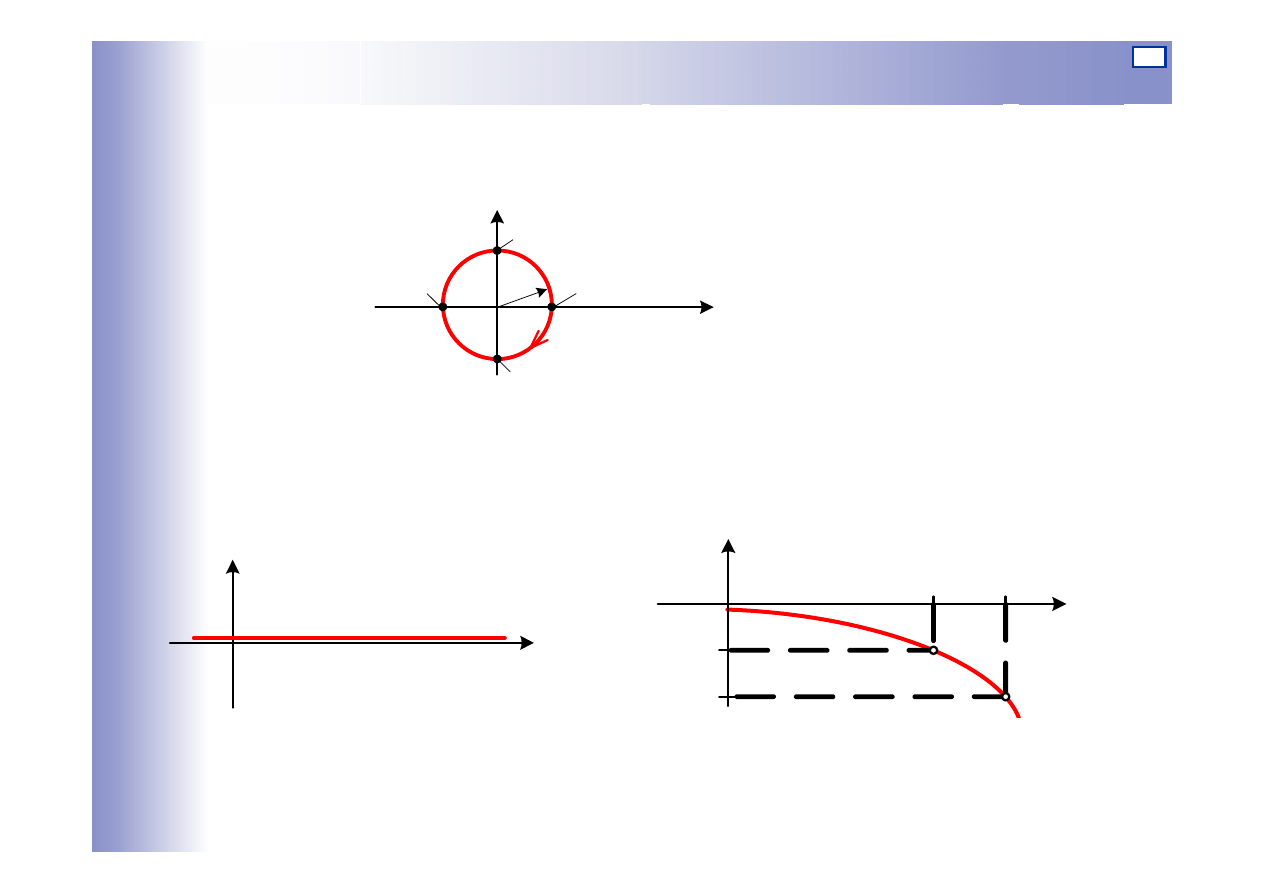
28
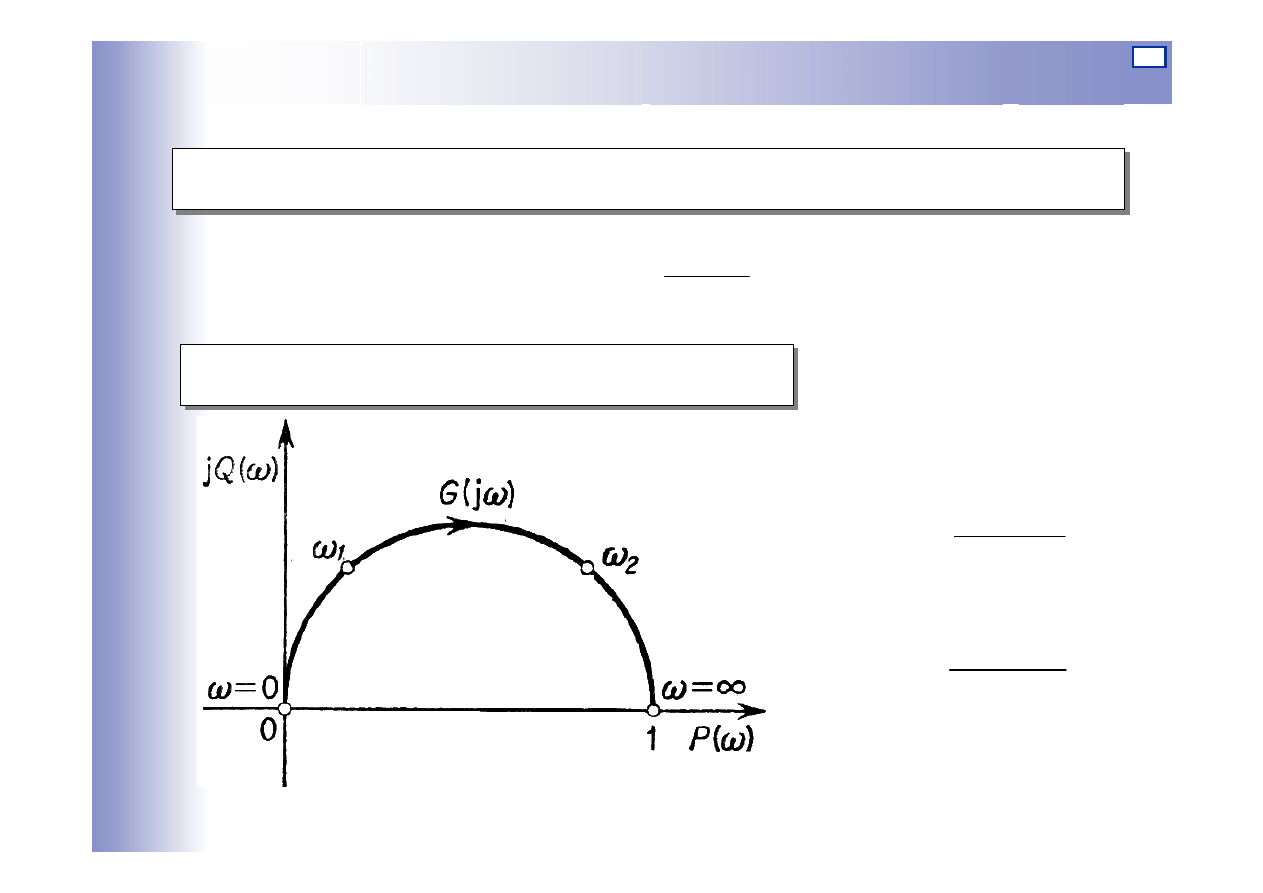
Charakterystyki elementu opóźniającego
L(
ω
)
dB
ω
0 dB
ω
ϕ
(
ω
)
−45
0
−90
0
π/2τ π/τ
P(
ω
)
jQ(
ω
)
ω = 0
ω = 3π/2τ
ω = π/2τ
ω = π/τ
1
ωτ
ω
ωτ
ω
sin
)
(
cos
)
(
−
=
=
Q
P
s
e
τ
−
29
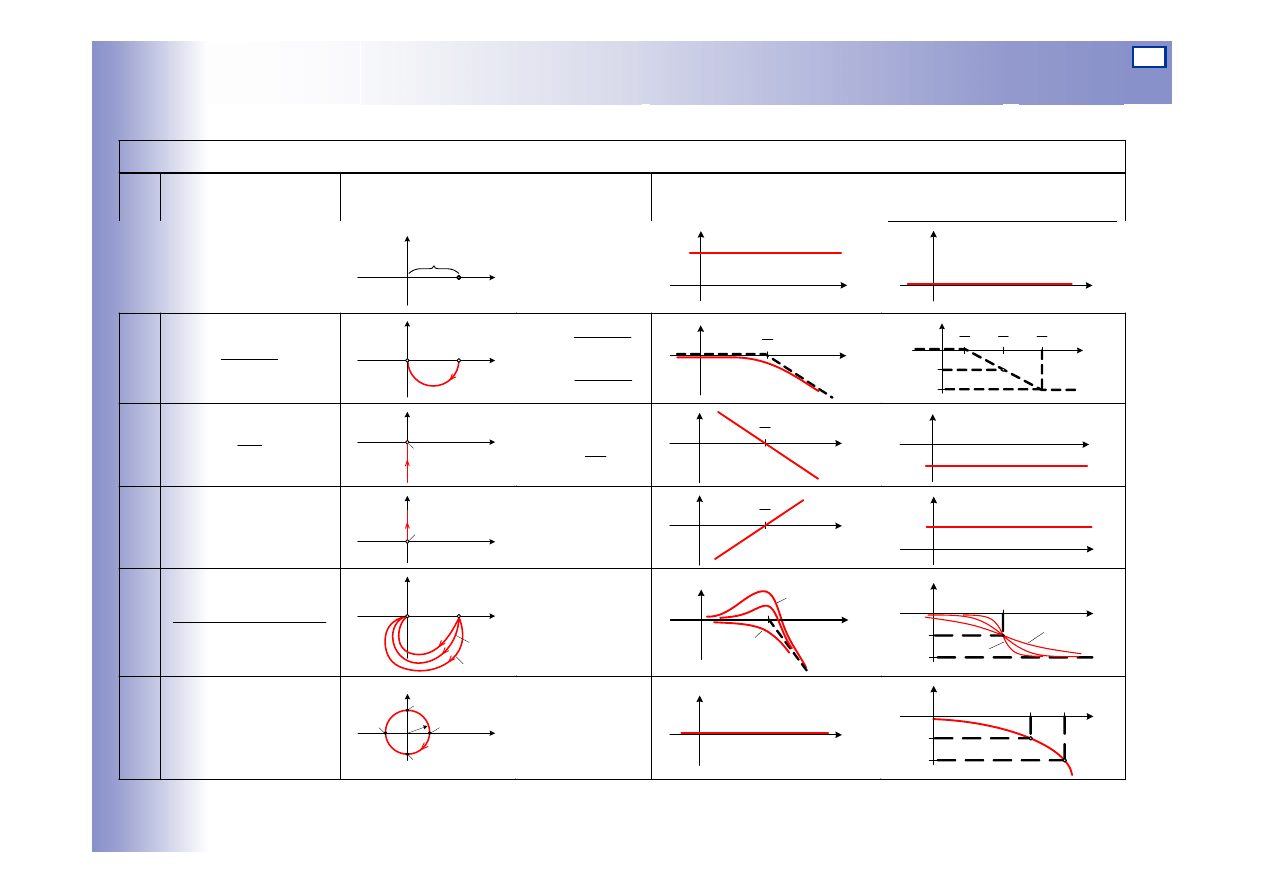
Charakterystyki częstotliwościowe podst. elementów
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE ELEMENTÓW PODSTAWOWYCH
L.p.
Transmitancja
operatorowa
)
(s
G
Wykres charakterystyki amplitudowo-fazowej
)
(
ω
j
G
(transmitancji widmowej)
Wykresy logarytmicznych charakterystyk amplitudowej
)
(
ω
L
i fazowej
)
(
ω
ϕ
1
k
jQ(
ω
)
P(
ω
)
G(j
ω
)
k
0
)
(
)
(
=
=
ω
ω
Q
k
P
L(
ω
)
dB
ω
20 log k
ω
0
0
ϕ
(
ω
)
1
1
+
Ts
P(
ω
)
jQ(
ω
)
G(j
ω
)
∞
=
ω
ω
= 0
1
)
(
1
1
)
(
2
2
2
2
+
−
=
+
=
ω
ω
ω
ω
ω
T
T
Q
T
P
L(
ω
)
dB
ω
1
T
- 20 dB/dek
ω
ϕ
(
ω
)
1
T
10
T
0.1
T
−45
0
−90
0
3
Ts
1
P(
ω
)
jQ(
ω
)
ω
= 0
∞
=
ω
ω
ω
ω
T
Q
P
1
)
(
0
)
(
−
=
=
L(
ω
)
dB
ω
1
T
- 20 dB/dek
ω
ϕ
(
ω
)
−90
0
4
Ts
P(
ω
)
jQ(
ω
)
ω
= 0
∞
=
ω
ω
ω
ω
T
Q
P
=
=
)
(
0
)
(
L(
ω
)
dB
ω
1
T
+ 20 dB/dek
ω
ϕ
(
ω
)
−90
0
5
2
0
0
2
2
0
2
ω
ξω
ω
+
+
s
s
k
P(
ω
)
jQ(
ω
)
ω
= 0
ξ
2
ξ
1
ξ
3
∞
=
ω
1
2
3
ξ
ξ
ξ
<
<
L(
ω
)
dB
ω
0
ξ
3
ξ
1
- 40 dB/dek
ω
ϕ
(
ω
)
−90
0
−180
0
ω
0
ξ
3
ξ
1
6
s
e
τ
−
P(
ω
)
jQ(
ω
)
ω = 0
ω = 3π/2τ
ω = π/2τ
ω = π/τ
1
ωτ
ω
ωτ
ω
sin
)
(
cos
)
(
−
=
=
Q
P
L(
ω
)
dB
ω
0 dB
ω
ϕ
(
ω
)
−45
0
−90
0
π/2τ π/τ
30
Charakterystyki elementów szeregowo połączonych
G
1
(j
ω
)
G
2
(j
ω
)
G
n
(j
ω
)
)
(
)
(
2
2
)
(
1
1
)
(
)
(
)
(
)
(
)
(
)
(
2
1
ω
ϕ
ω
ϕ
ω
ϕ
ω
ω
ω
ω
ω
ω
n
j
n
n
j
j
e
M
j
G
e
M
j
G
e
M
j
G
=
=
=
K
K
K
K
)
(
)]
(
)
(
)
(
[
2
1
)
(
)
(
)
(
)
(
)
(
2
1
ω
ϕ
ω
ϕ
ω
ϕ
ω
ϕ
ω
ω
ω
ω
ω
j
j
n
e
M
e
M
M
M
j
G
n
c
K
K+
+
+
=
31
Charakterystyki elementów szeregowo połączonych
Logarytmiczna charakterystyka amplitudowa:
Logarytmiczna charakterystyka amplitudowa:
)
(
log
20
)
(
log
20
)
(
log
20
)
(
log
20
)
(
2
1
ω
ω
ω
ω
ω
n
M
M
M
M
L
+
+
+
=
=
K
∑
=
=
n
i
i
L
L
1
)
(
)
(
ω
ω
)
(
)
(
)
(
)
(
2
1
ω
ω
ω
ω
n
M
M
M
M
⋅
⋅
⋅
=
K
∑
=
=
n
i
i
1
)
(
)
(
ω
ϕ
ω
ϕ
Logarytmiczna charakterystyka fazowa:
Logarytmiczna charakterystyka fazowa:
32
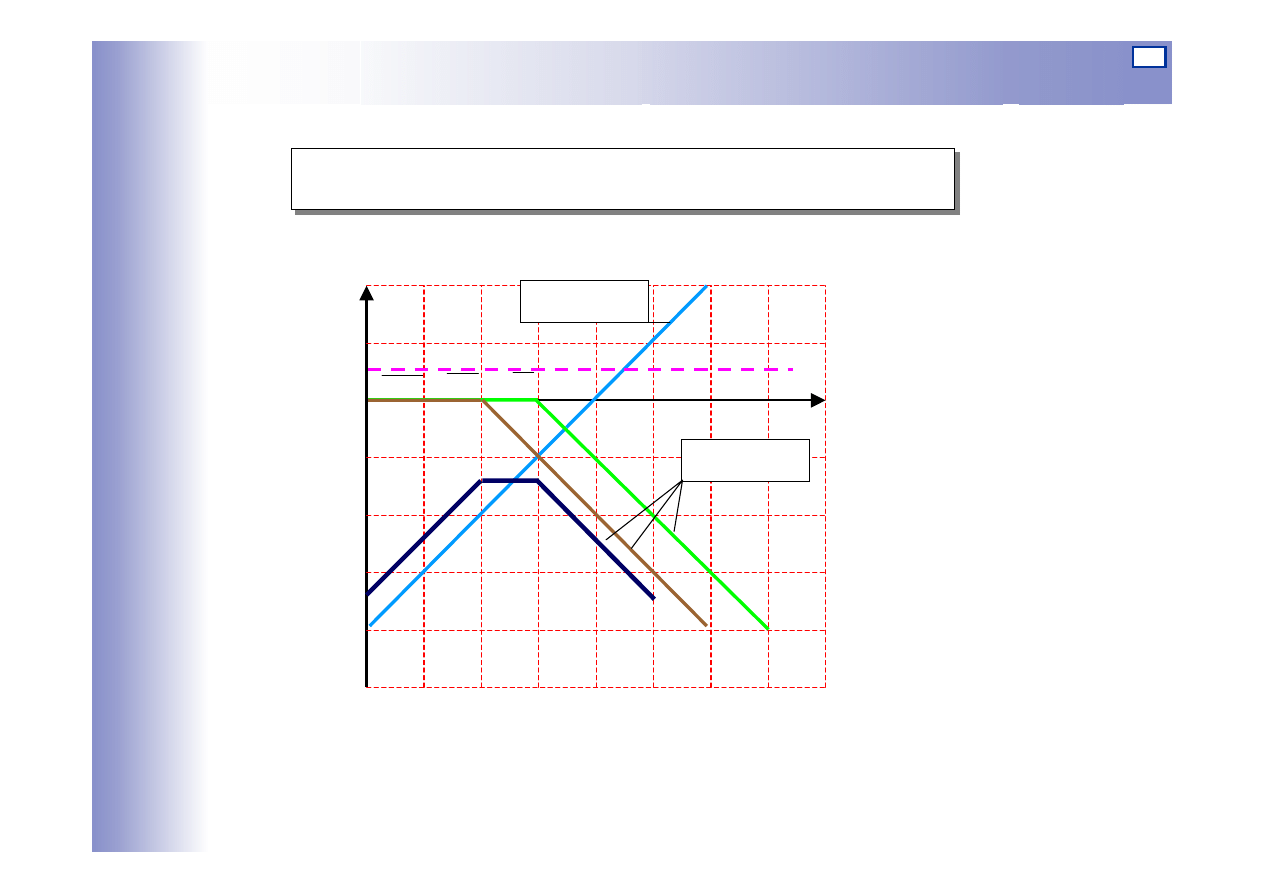
Charakterystyki elementów szeregowo połączonych
Przykład 1:
Przykład 1:
(
) (
)
{ {
3
2
1
3
2
1
c
4
3
3
2
2
1
1
3
2
1
1
1
1
1
)
(
1
1
)
(
+
⋅
+
⋅
⋅
⋅
=
+
⋅
+
⋅
⋅
=
s
T
s
T
s
T
k
s
G
s
T
s
T
s
T
k
s
G
Dla: k=2;
T
1
=1;
T
2
=10;
T
3
=100;
Dla: k=2;
T
1
=1;
T
2
=10;
T
3
=100;
)
(
ω
jQ
)
(
ω
P
33
Charakterystyki elementów szeregowo połączonych
1000
1
100
1
10
1
1
10
100 1000
ω
2
3
4
1
L(ω)
c
Logarytmiczna charakterystyka amplitudowa:
Logarytmiczna charakterystyka amplitudowa:
-20dB/dek
20dB/dek
6dB
-20dB
-40dB
20dB
34
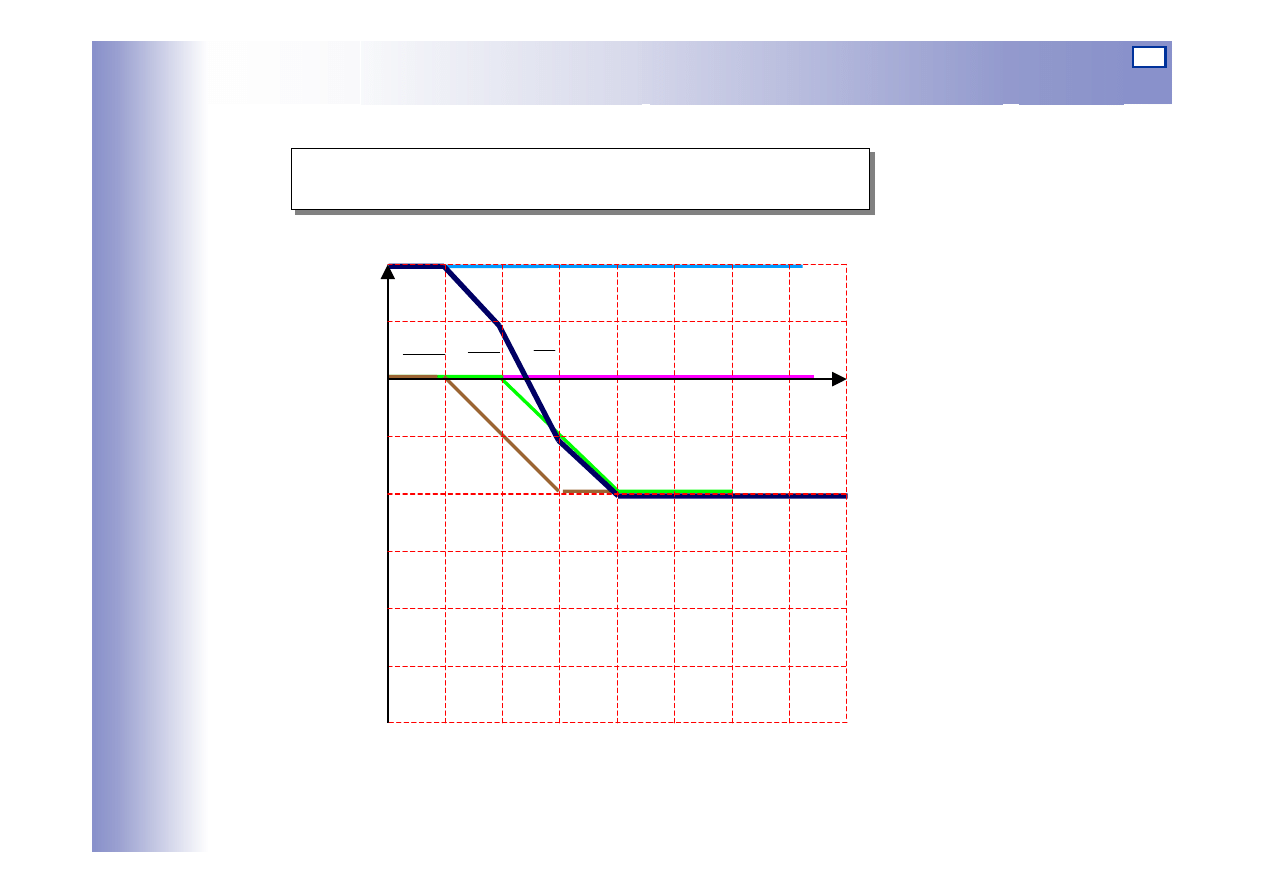
Charakterystyki elementów szeregowo połączonych
Logarytmiczna charakterystyka fazowa:
Logarytmiczna charakterystyka fazowa:
2
3
4
1
c
1000
1
100
1
10
1
1
10
100 1000
ω
ϕ
(ω)
-45
0
-90
0
45
0
-180
0
-270
0
Wyszukiwarka
Podobne podstrony:
PA5 charakterystyki czestotliwosciowe [tryb zgodności]
PA5 charakterystyki czestotliwosciowe
PA5 charakterystyki czestotliwosciowe [tryb zgodności]
Ćw 11 Czwórniki bierne charakterystyki częstotliwościowedocx
Charakterystyki czestotliwosciowe
Charakterystyki czestosciowe
Cw Charakterystyki częstotliwościowe, Semestr III PK, Semestr Zimowy 2012-2013 (III), Automatyka, Au
Miernictwo- Zdejmowanie charakterystyk częstotliwościowych przebiegów odkształconych, ?w._
Badanie częstotliwości i charakterystyk częstotliwościowych
Charakterystyki czestotliwosciowe
Charakterystyki częstotliwościowe podstawowych członów dynamicznych v4
Charakterystyki czestotliwosciowe
Charakterystyki czestotliwo ciowe wybranych elementow liniowych
05 Charakterystyki czestotliwoscio
PROJEKT I?DANIE CZWÓRNIKÓW RC?LEM WYZNACZENIA NAPIĘCIOWEJ CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWEJ
05 Charakterystyki częstotliwościowe
druk, Poziom dźwięku A -poziom ciś akust skorygowanego wg charakterystyki częstotliwościowej A
Cw 4 Czworniki bierne charakterystyki czestotliwoscio
więcej podobnych podstron