LABORATORIUM PODSTAW AUTOMATYKI

MATERIAŁY INFORMACYJNE

do ćwiczenia :

DOBÓR NASTAW REGULATORÓW

R E G U L A T O R Y

Rodzaje regulatorów i ich klasyfikacja

Regulatory można klasyfikować według różnych kryteriów.
Klasyfikacja regulatorów ze względu na :
1. sposób budowy
2. rodzaj nośnika energii użytego do zasilania wzmacniacza regulatora
3. sposób zmiany wielkości nastawiającej (ciągły lub nieciągły)
4. postać transmitancji operatorowej regulatora

Ze względu na sposób budowy regulatory dzielimy na dwie następujące grupy :

1. regulatory nie korzystające z energii pomocniczej (o działaniu bezpośrednim)
2. regulatory z energią pomocniczą (o działaniu pośrednim)

Regulatory z energią pomocniczą dzielimy ze względu na rodzaj nośnika energii , użytego

do zasilania wzmacniacza regulatora , na :

1. regulatory elektryczne
2. regulatory pneumatyczne
3. regulatory hydrauliczne

Ze względu na sposób zmiany wielkości nastawiającej (ciągły lub nieciągły) regulatory z

energią pomocniczą dzielimy na :

1. regulatory o wyjściu ciągłym
2. regulatory impulsowe
3. regulatory dwupołożeniowe

Regulator o wyjściu ciągłym w sposób ciągły oddziaływuje na obiekt za pomocą

wielkości nastawiającej. Regulator impulsowy oddziaływuje na obiekt tylko w pewnych ,
powtarzających się okresowo , chwilach czasowych zwanych chwilami impulsowania. W
regulatorach dwupołożeniowych wielkość nastawiająca może przyjmować tylko dwie różne
wartości (odpowiadające np. włączeniu i wyłączeniu grzejnika w termostacie).

Ze względu na postać transmitancji operatorowej

G

r

(s) =

Y(s)

E(s)

•

Y(s) – transformata wielkości nastawiającej (sterującej) y(t)

•

E(s) – transformata uchybu regulacji e(t)

Do regulatorów liniowych zaliczamy :

1. regulatory proporcjonalne typu P

G

r

(s) = K

p

2. regulatory całkowe I

G

r

(s) =

1

sT

i

3. regulatory proporcjonalno-całkowe określane jako regulatory PI

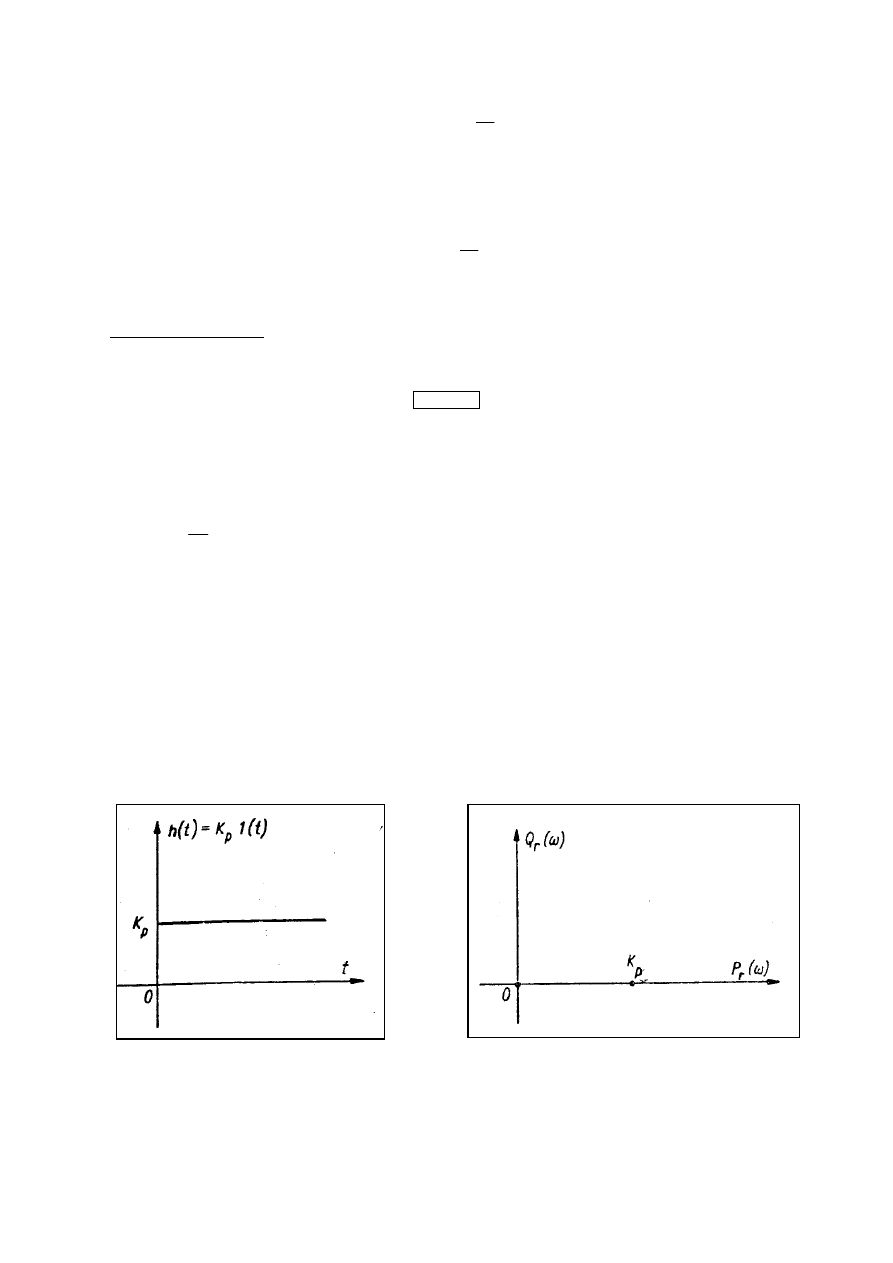
G

r

(s) = K

p

(1+

1

sT

i

)

4. regulatory proporcjonalno-różniczkowe oznaczane PD

G

r

(s) = K

p

(1 + T

d

s)

5. regulatory proporcjonalno-całkowo-różniczkowe PID

G

r

(s) = K

p

(1+

1

sT

i

+ T

d

s)

przy czym : K

p

, T

i

, T

d

są współczynnikami dającymi się nastawiać w danym regulatorze w pewnym

ograniczonym zakresie.

Regulator proporcjonalny

Regulatorem proporcjonalnym nazywamy regulator o transmitancji operatorowej

G

r

(s) = K

p

czyli regulator, dla którego zależność między uchybem regulacji e(t)a zadanym sygnałem
sterującym u(t) ma postać

u(t) = K

p

e(t)

gdzie :

•

K

p

– współczynnik wzmocnienia

•

P =

1

K

p

- stały współczynnik nazywany zwykle zakresem proporcjonalności

Regulator P jest członem bezinercyjnym (proporcjonalnym , wzmacniającym).
Charakterystyka skokowa h(t) regulatora P , określona jako odpowiedź na wymuszenie w
postaci skoku jednostkowego , ma zatem postać

h(t) = K

p

1(t) (2)

Przebieg charakterystyki skokowej regulatora P przedstawia rys. 1
Z zależności (1) mamy :

G

r

(j

ω

) = G

r

(s) s =j

ω

(3)

K

p

= P

r

(

ω

) + jQ

r

(

ω

) (4)

przy czym : P

r

(

ω

) = K

p

, Q

r

(

ω

) = 0

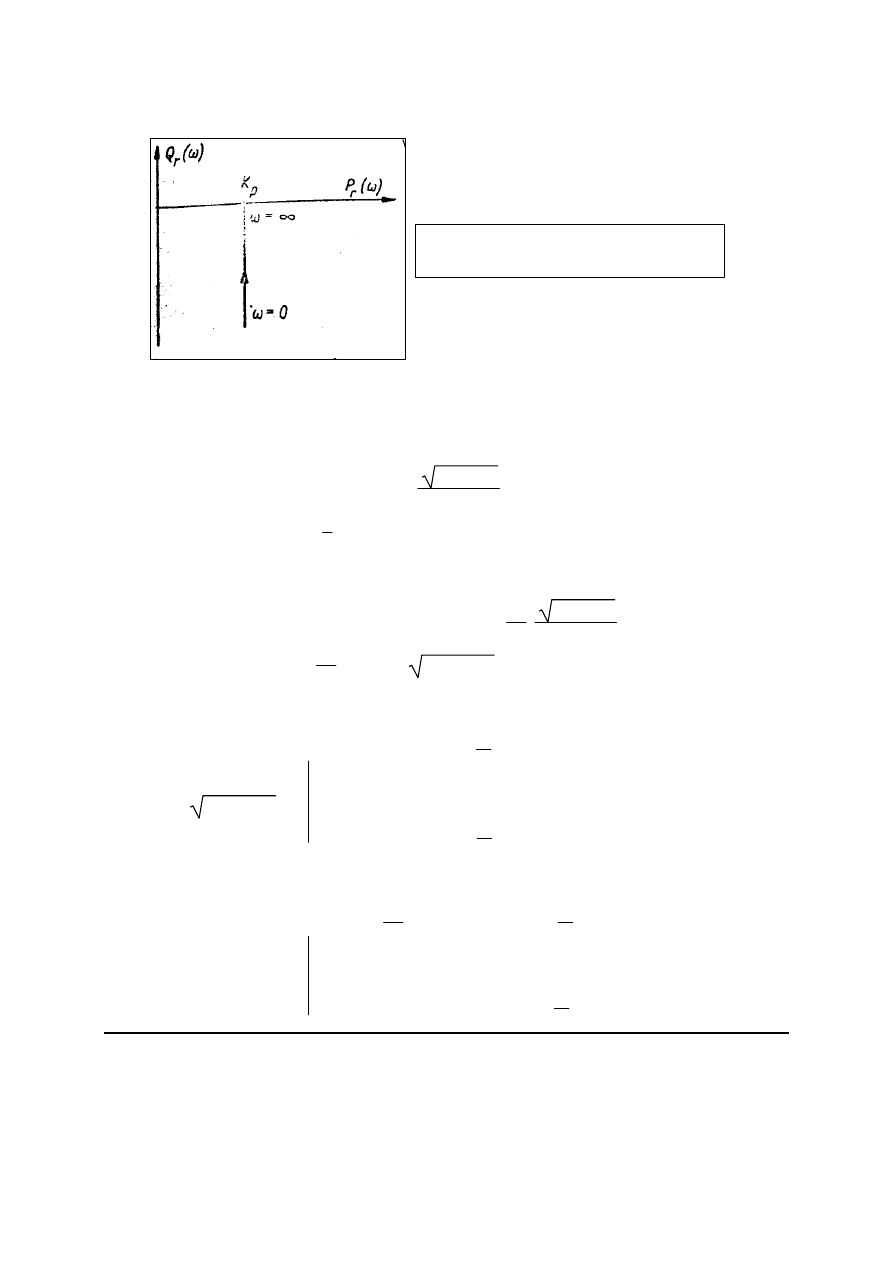
Charakterystyka amplitudowo-fazowa regulatora P ma postać punktu (K

p ,

j0) leżącego

na osi liczb rzeczywistych P

r

(

ω

) – rys 8.2

Rys 1 Charakterystyka skokowa Rys 2 Charakterystyka amplitudowo-fazowa
regulatora P regulatora P

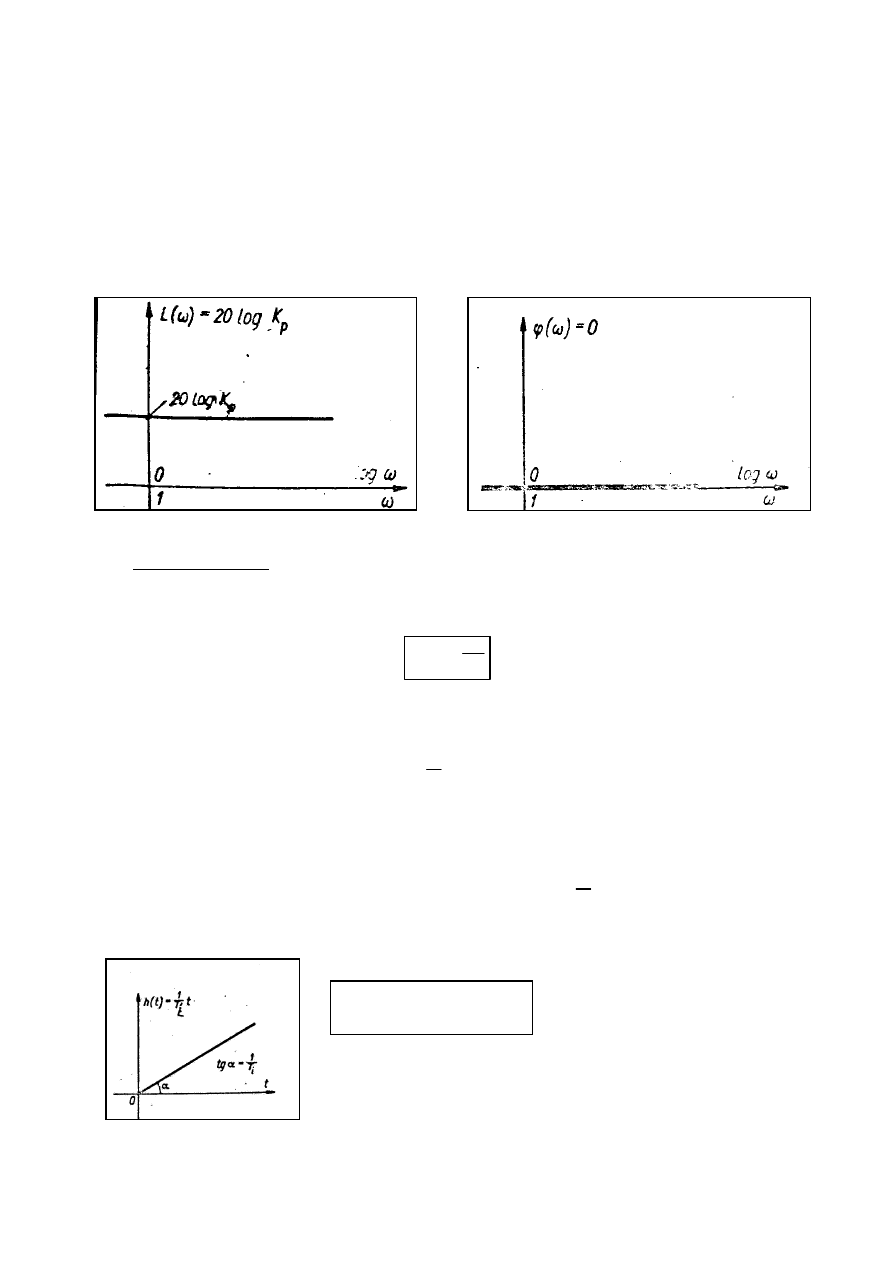
Z zależności (8.4) wynika , że dla regulatora P logarytmiczna charakterystyka

amplitudowa i logarytmiczna charakterystyka fazowa mają postać :

L (

ω

) = 20 log

|

G

r

(j

ω

)

|

= 20 log K

p

ϕ

(

ω

) = 0

Logarytmiczna charakterystyka amplitudowa regulatora p ma zatem postać

równoległej do osi odciętych , a logarytmiczna charakterystyka fazowa pokrywa się z osią
odciętych – rys 3

Rys 8.3 Logarytmiczna charakterystyka amplitudowa i fazowa regulatora P

8.3 Regulator całkowy

Regulatorem całkowym zwanym krótko regulatorem I nazywamy regulator o

transmitancji operatorowej (8)

G

r

(s) =

1

sT

i

czyli regulator , dla którego zależność między uchybem regulacji e(t) a zadanym sygnałęm
sterującym u(t) ma postać (9)

u(t) =

1

T

i

⌡

⌠

0

t

e (

τ

) d

τ

przy czym stały współczynnik Ti nazywa się stałą czasową całkowania.

Regulator I jest idealnym członem całkującym.
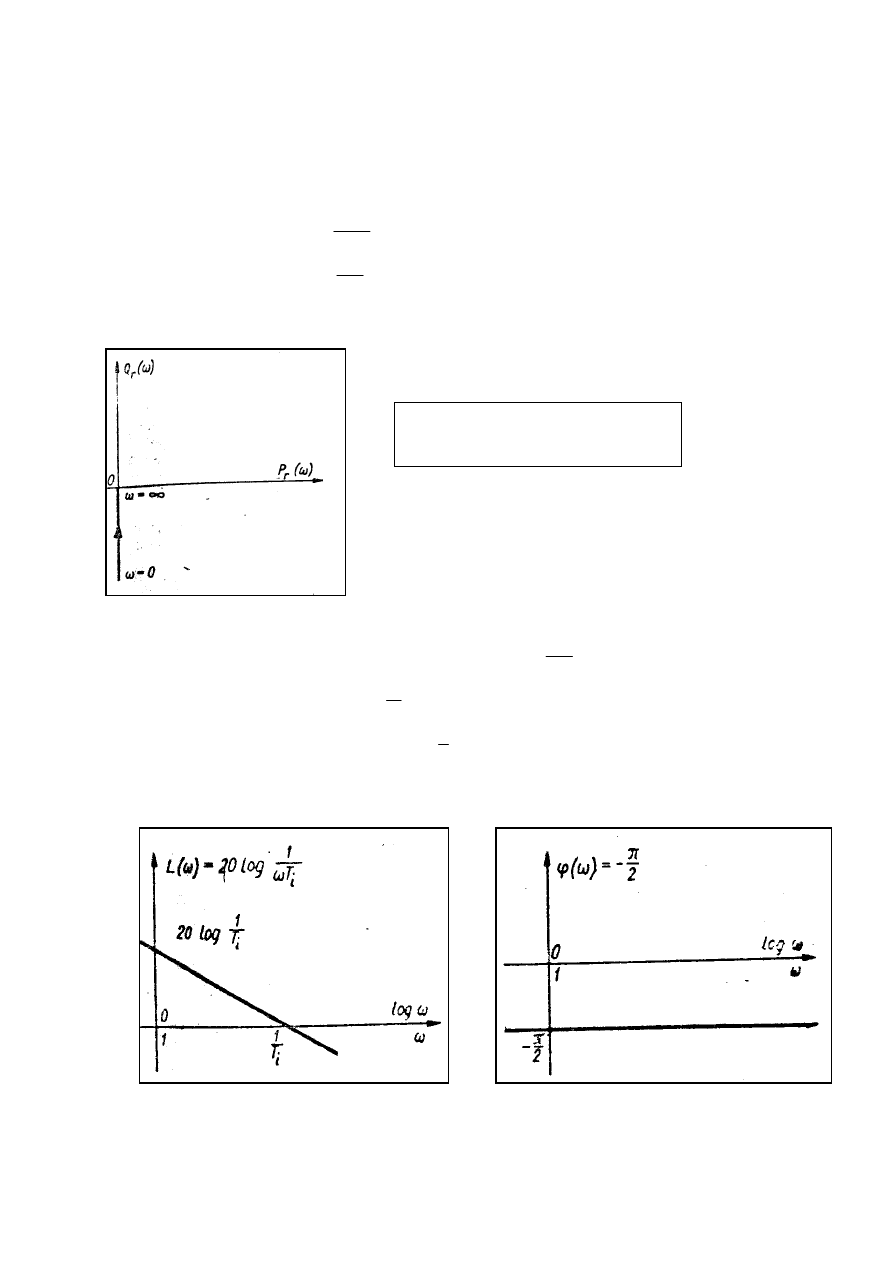
Charakterystyka skokowa h(t) regulatora I , określona jest jako odpowiedź na

wymuszenie w postaci skoku jednostkowego , ma postać), h(t) =

1

T

i

t

Wykres charakterystyki skokowej regulatora I przedstawia - rys 4

Rys 8.4 Charakterystyka
skokowa regulatora I

Wyznaczając transmitancję widmową na podstawie znajomości transmitancji operatorowej
regulatora I otrzymamy

G

r

(j

ω

) = G

r

(s) s =j

ω

Stosując to podstawienie do wzoru (8)

1

T

i

j

ω

= P

r

(

ω

) + jQ

r

(

ω

) (11)

przy czym P

r

(

ω

) = 0 , Q

r

(

ω

) = -

1

T

i

ω

(12)

Charakterystyka amplitudowo-fazowa regulatora I pokrywa się z ujemną półosią liczb
urojonych Q

r

(

ω

) – rys. 5

Z zależności (8.11) wynika , że logarytmiczna charakterystyka amplitudowa i

logarytmiczna charakterystyka fazowa regulatora I mają postać :

L (

ω

) = 20 log

|

G

r

(j

ω

)

|

= 20 log

1

T

i

ω

=

20 log

1

T

i

– 20 log

ω

(13)

ϕ

(

ω

) = -

π

2 (14)

Wykres logarytmicznej charakterystyki amplitudowej i logarytmicznej charakterystyki

fazowej regulatora I przedstawia - rys 8.6.

Rys 6 Logarytmiczna charakterystyka amplitudowa i fazowa regulatora I

Rys. 8.5 Charakterystyka amplitudowo-
fazowa regulatora I

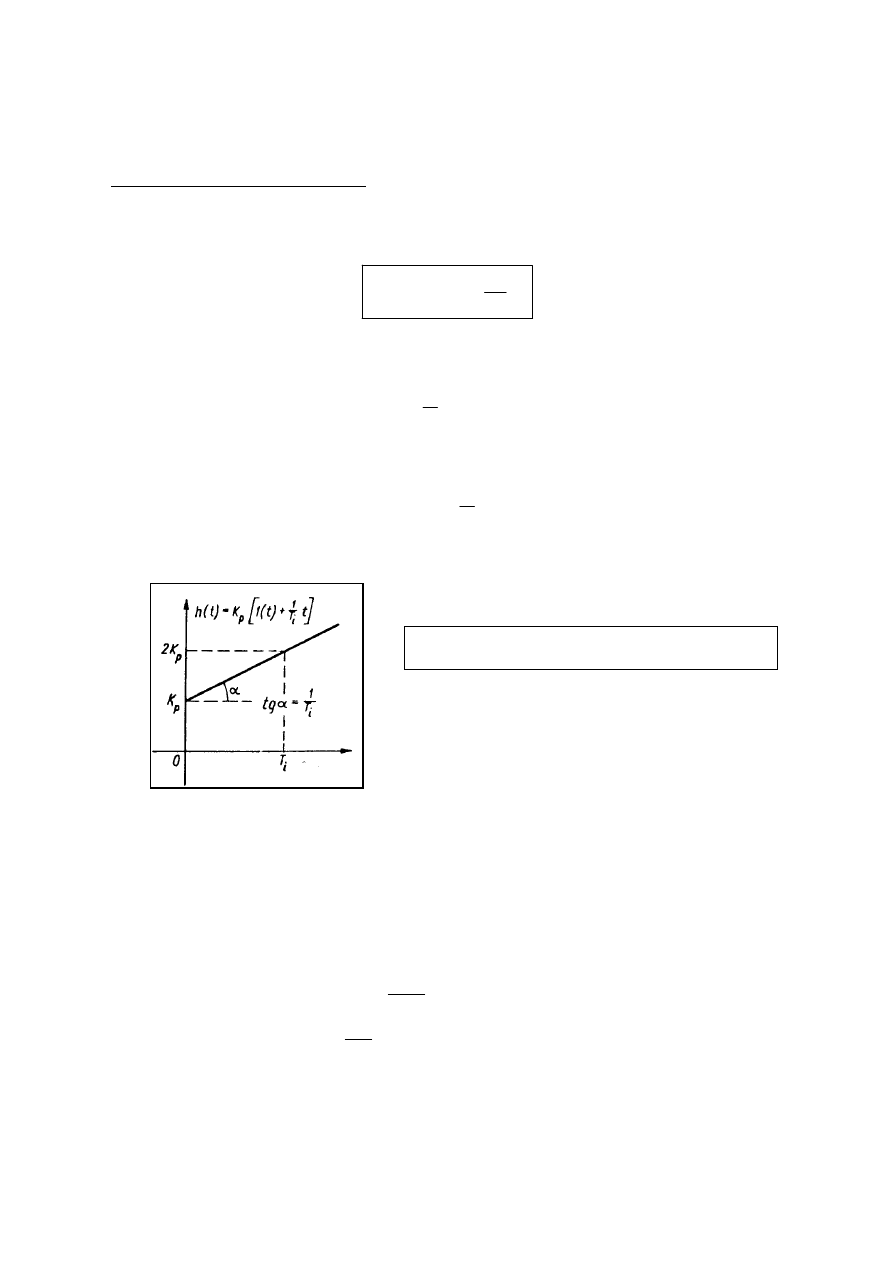
Regulator proporcjonalno–całkowy

Regulatorem proporcjonalno-całkowym zwanym krótko regulatorem PI nazywamy

regulator o transmisji operatorowej (15)

G

r

(s) = K

p

( 1+

1

sT

i

)

czyli regulator , dla którego zależność między uchybem regulacji e(t) a zadanym sygnałem
sterującym u(t) ma postać

u(t) = K

p

[

e(t) +

1

T

i

⌡

⌠

0

t

e (

τ

) d

τ

]

(16)

Charakterystyka skokowa h(t) regulatora PI , określona jako odpowiedź na wymuszenie w
postaci skoku jednostkowego , ma postać

h(t) = K

p

[ 1(t) +

1

T

i

t] (17)

Przebieg charakterystyki skokowej regulatora PI przedstawia – rys 7.

Z zależności (17) wynika , że dla t = T

i

; h(T

i

) = 2 K

p

. Po czasie równym T

i

składowa h(t)

będąca wynikiem działania całkującego regulatora jest równa składowej pochodzącej od
działania proporcjonalnego tego regulatora. Sygnał łączny po czasie T

i

jest więc dwukrotnie

większy niż w chwili t=0 .

Z zależności (15) mamy

G

r

(j

ω

) = G

r

(s) s =j

ω

K

p

(1 +

1

T

i

j

ω

) = P

r

(

ω

) + jQ

r

(

ω

)

przy czym P

r

(

ω

) = K

p

, Q

r

(

ω

) = -

K

p

T

i

ω

Charakterystykę amplitudowo-fazową regulatora PI przedstawia – rys 8.

Rys 8.7 Charakterystyka skokowa regulatora PI

Z zależności (8.18) mamy

G

r

(j

ω

) =

|

G

r

(j

ω

)

|

e

j

ϕ

(

ω

)

=

K

p

1+(T

i

ω

)

2

ω

e

j

ϕ

(

ω

)

(8.20)

przy czym

ϕ

(

ω

) = arctg

ω

T

i

-

π

2 (8.21)

Logarytmiczna charakterystyka amplitudowa regulatora PI będzie miała zatem postać

L (

ω

) = 20 log

|

G

r

(j

ω

)

|

= 20 log

K

p

T

i

1+(T

i

ω

)

2

ω

=

20 log

K

p

T

i

+ 20 log 1 + (T

i

ω

)

2

– 20 log

ω

(8.22)

biorąc pod uwagę , że :



0 dla

ω

<

1

T

i

20 log 1 + (T

i

ω

)

2

=



(8.24)



20 log

ω

T

i

dla

ω

>

1

T

i

z zależności (8.22) otrzymujemy :



20 log

K

p

T

i

– 20 log

ω

dla

ω

<

1

T

i

L(

ω

) =



(8.24)



20 log K

p

dla

ω

>

1

T

i

Doświadczalne metody doboru nastaw regulatorów

Rys 8. Charakterystyka amplitudowo-fazowa
regulatora PI

Dla każdego procesu istnieje możliwość ścisłej analizy teoretycznej układów sterowania, która
pozwala na dowolne wyznaczenie właściwości projektowanego układu, metodyka taka nie jest jednak
przydatna w praktyce, gdyż w tym przypadku przy dobieraniu nastaw regulatorów bardzo rzadko
dysponuje się dokładnymi danymi dotyczącymi obiektu. Zadanie doboru nastaw regulatorów polega
na takim ich ustaleniu, aby otrzymać zadowalające działanie układu sterowania.

E(s)

R(s)

Y(s)

G

R

(s)

Regulator

G(s)

Obiekt

Z(s)

U(s)

Rys. 1. Schemat blokowy układu regulacji

Do wymagań najczęściej stawianych układom regulacji a tym samym regulatorom zaliczamy :

−

wyeliminowanie przeregulowań

%

p

M

= 0...5% oraz osiągnięcie przy zachowaniu tego warunku

najkrótszego z możliwych czasu regulacji t

R

−

najkrótszy z możliwych do osiągnięcia czas regulacji t

R

przy występowaniu przeregulowania do

ograniczonej wartości np.

%

p

M

= 15...25%

−

uzyskanie minimum wybranego wskaźnika całkowego I, np. całki z kwadratu uchybu: I=

dt

t

e

∫

∞

0

2

)

(

min

Dopuszczalne ustalone wartości uchybu regulacji powinny być mniejsze niż

(

)

%

5

...

5

,

0

±

wartości

maksymalnej wielkości regulowanego Y.

Całkowe wskaźniki jakości regulacji

Całkowe wskaźniki jakości umożliwiają prowadzenie na bieżąco obiektywnego pomiaru jakości regulacji.
Ilościowy pomiar jakości jest konieczny w nowoczesnych układach sterowania adaptacyjnego, w układach
automatycznej optymalizacji parametrów układu sterowania i przy projektowaniu układów optymalnych.

Jeśli celem jest poprawa projektu układu lub zaprojektowanie układu sterowania wówczas musi zostać

określone kryterium jakości.

Indeks jakości jest ilościowym wskaźnikiem jakości układu i jest tak dobrany aby uwzględnić ważne
wymagania dotyczące układu.

Układ, określany jest mianem układu sterowania optymalnego wówczas, gdy jego parametry są tak dobrane, aby
indeks osiągał ekstremalną wartość. Indeks jakości aby mógł być użyteczny i łatwy w stosowaniu, musi być
liczbą, która zawsze jest dodatnia lub równa zero.

Ogólna postać całkowego wskaźnika jakości jest następująca

( ) ( ) ( )

(

)

∫

=

T

dt

t

t

y

t

r

t

e

f

I

0

,

,

,

gdzie f jest funkcją uchybu, sterowania, wyjścia i czasu. Można uzyskać numeryczne indeksy oparte na różnych
kombinacjach zmiennych układu i czasu. Dla przykładu, minimalizacja indeksu jakości może być bezpośrednio
odniesiona do minimalizacji zużycia paliwa.

CAŁKA Z KWADRATU UCHYBU

Odpowiednim indeksem jakości jest całka uchybu kwadratowego, ISE (Integral Square Error), który
definiowany jest jako

( )

∫

=

T

dt

t

e

0

2

ISE

(2)

Górna granica T jest czasem skończonym wybranym w sposób arbitralny po to aby całka osiągała wartość
ustaloną. Zazwyczaj jako T wybiera się czas ustalania, t

R

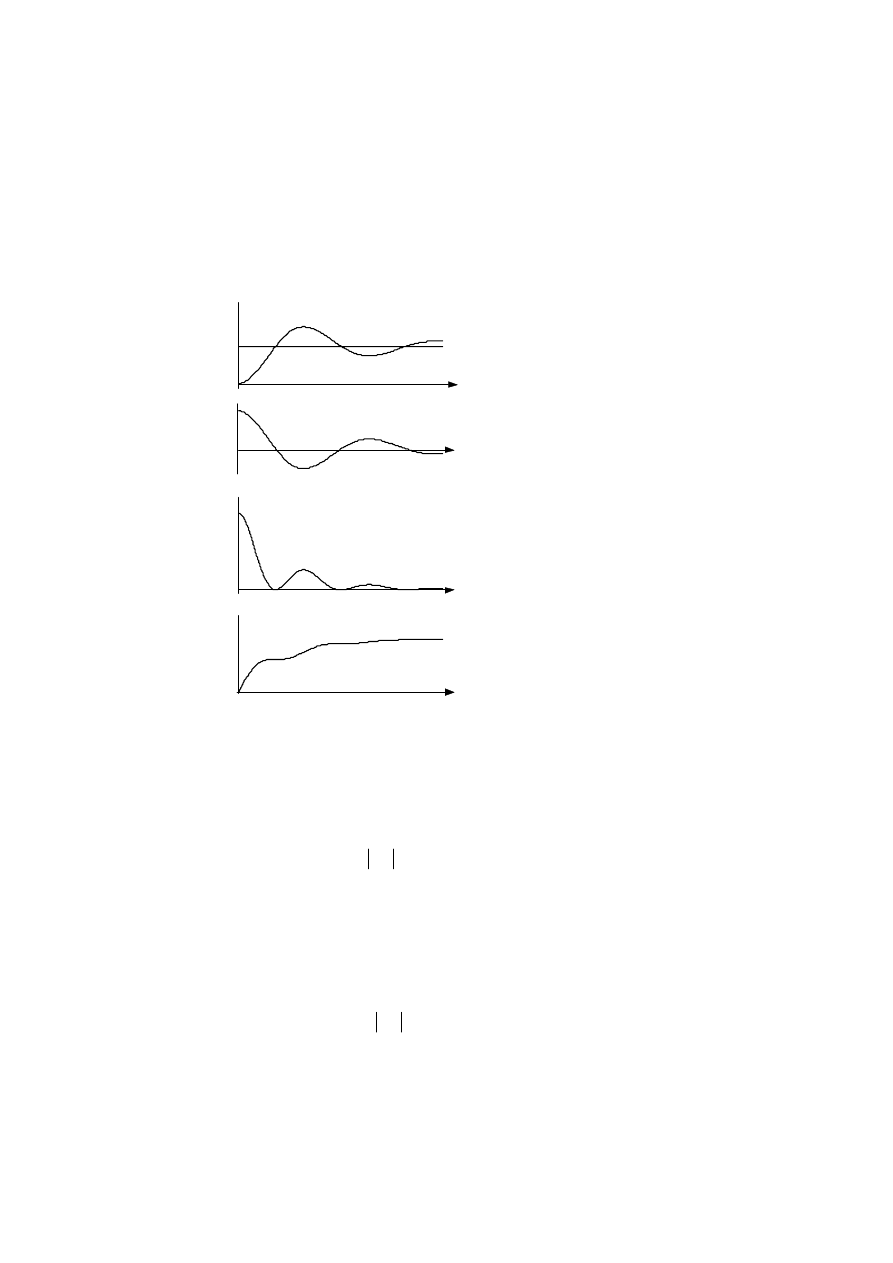
. Odpowiedź skokowa dla określonego układu

sterowania pokazana została na rysunku 1(b), natomiast uchyb na rysunku 1(c). Kwadrat uchybu pokazany
został na rysunku 1(d), a całka uchybu kwadratowego na rysunku 1(e). Minimalna wartość całki pojawia się
wówczas, gdy będzie odpowiednie tłumienie. Indeks jakości opisany równaniem (2) może być łatwo
zastosowany do pomiaru jakości w układach praktycznych. Dlatego też uchyb kwadratowy jest dogodny
matematycznie w celach analitycznych i obliczeniowych.

t

y(t)

e(t)

e

2

(t)

∫

dt

t

e

)

(

2

t

t

t

Rys. 1. Przebiegi wielkości układu regulacji .

CAŁKA Z WARTOŚCI BEZWZGLĘDNEJ UCHYBU

Innym kryterium jakości jest całka z wartości bezwzględnej uchybu, IAE (Integral Absolute Error), który
zapisywany jest następująco:

( )

∫

=

T

dt

t

e

0

IAE

(3)

Ten indeks jest szczególnie użyteczny w symulacjach komputerowych.

CAŁKA Z ILOCZYNU CZASU I WARTOŚCI BEZWZGLĘDNEJ UCHYBU

Aby zmniejszyć udział dużej wartości początkowej uchybu na całkowy wskaźnik jakości i uwidocznić uchyby
pojawiające się w późniejszej odpowiedzi, zaproponowany został następujący indeks

( )

∫

=

T

dt

t

e

t

0

ITAE

(4)

Ten wskaźnik zaprojektowany został jako całka czasu mnożonego przez wartość bezwzględną uchybu, ITAE
(Integral Time Absolute Error). Indeks ITAE jest najbardziej selektywnym z całkowych wskaźników jakości,
gdyż minimalna wartość całki jest łatwo rozpoznawalna gdy zmieniają się parametry układu.

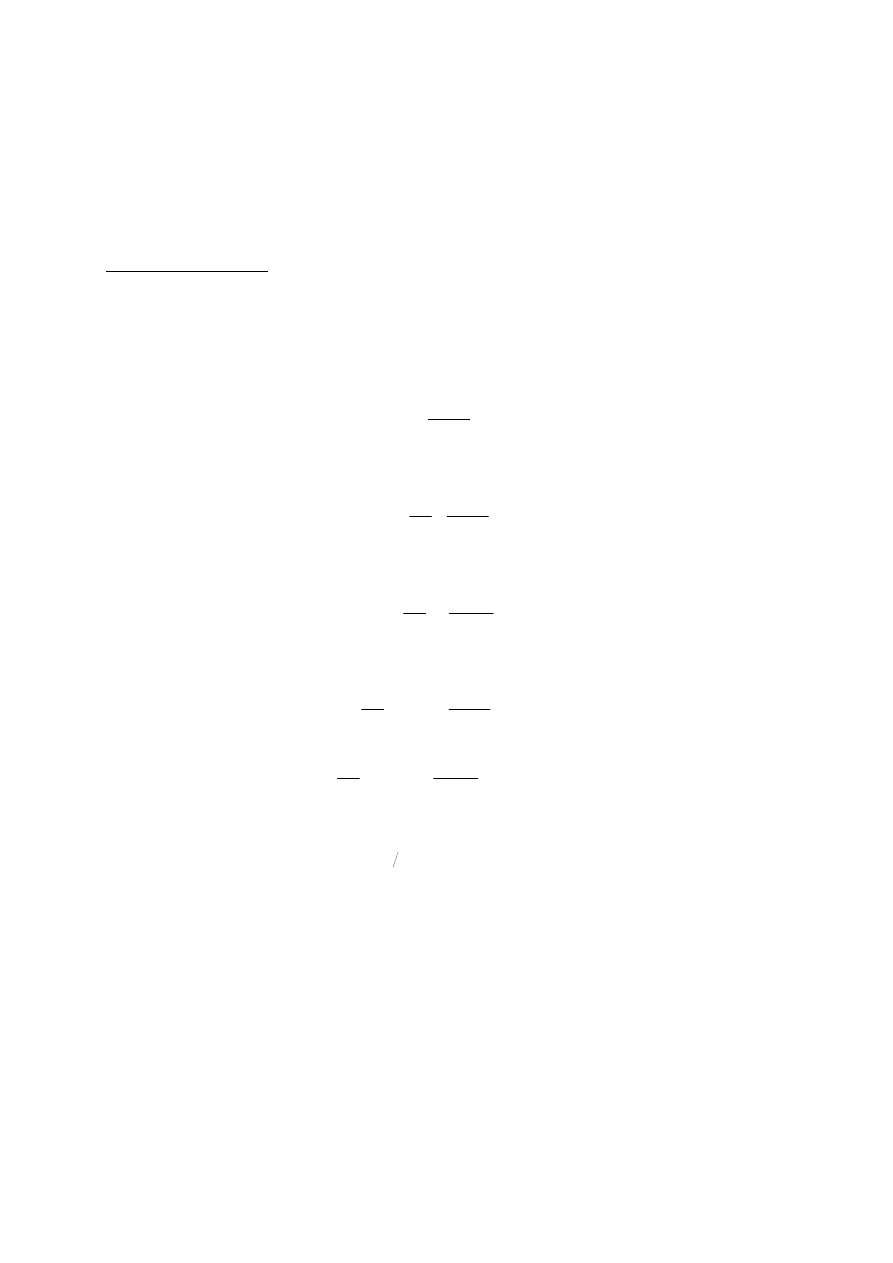
2.4. CAŁKA Z ILOCZYNU CZASU I KWADRATU UCHYBU

Innym podobnym indeksem jest całka z czasu pomnożonego przez kwadrat uchybu, ITSE (Integral Timie Square
Error).

( )

∫

=

T

dt

t

te

0

2

ITSE

Regulatory liniowe

Najczęściej sstosowane są następujące regulatory liniowe:
a)

−

regulator proporcjonalny P

b) regulator proporcjonalno

−

całkujący PI

c) regulator proporcjonalno

−

różniczkujący PD

d) regulator PD z rzeczywistym członem różniczkującym









+

+

=

n

D

P

R

sT

sT

K

s

G

1

1

)

(

e) regulator proporcjonalno

−

całkująco

−

różniczkujący PID

f) regulator PID z rzeczywistym członem różniczkującym









+

+

+

=

n

D

I

P

R

sT

sT

sT

K

s

G

1

1

1

)

(

(6)

Innym rozwiązaniem regulatora PID jest układ szeregowo połączonych bloków PI oraz PD. W tym
przypadku transmitancja regulatora jest następująca









+

+

⋅









+

=

n

D

I

P

r

sT

sT

sT

K

s

G

1

1

1

1

)

(

W innych wykonaniach regulatorów spod działania różniczkującego wyklucza się sygnał wartości
zadanej

z

y

i uzyskuje się nieinteraktywną strukturę regulatora PID

)

(

1

)

(

1

)

(

s

Y

sT

sT

s

E

sT

K

s

U

n

D

I

P

⋅









+

−

⋅









+

=

(8)

Stosowana jest również struktura regulatora o postaci

)

(

)

(

1

1

)

(

1

1

)

(

s

Y

s

Y

sT

sT

s

Y

sT

K

s

U

n

D

z

I

P

⋅

















⋅









+

+

−

⋅









+

=

(9)

gdzie:

P

K

−

współczynnik wzmocnienia regulatora, określany niekiedy przez zakres

proporcjonalności

P

P

K

x

%

100

=

I

T

−

stała czasowa całkowania

D

T

−

stała czasowa różniczkowania

n

T

−

stała czasowa filtru inercyjnego występującego czasami w członach różniczkowania.

Stała ta zawiera się najczęściej w przedziale

(

)

D

n

T

T

25

.

0

05

.

0

÷

≈

Pomiary własności dynamicznych obiektów regulacji przy pomocy charakterystyki
skokowej.

Optymalne nastawy regulatorów mogą być również dobrane na podstawie tabel, wykresów
/nomogramów/ , wzorów empirycznych. Zalecenia te dotyczą obiektów podzielonych na dwie klasy:
obiekty statyczne i obiekty astatyczne, których charakterystyki aproksymuje się następującymi
transmitancjami [1]:

−

obiekty statyczne

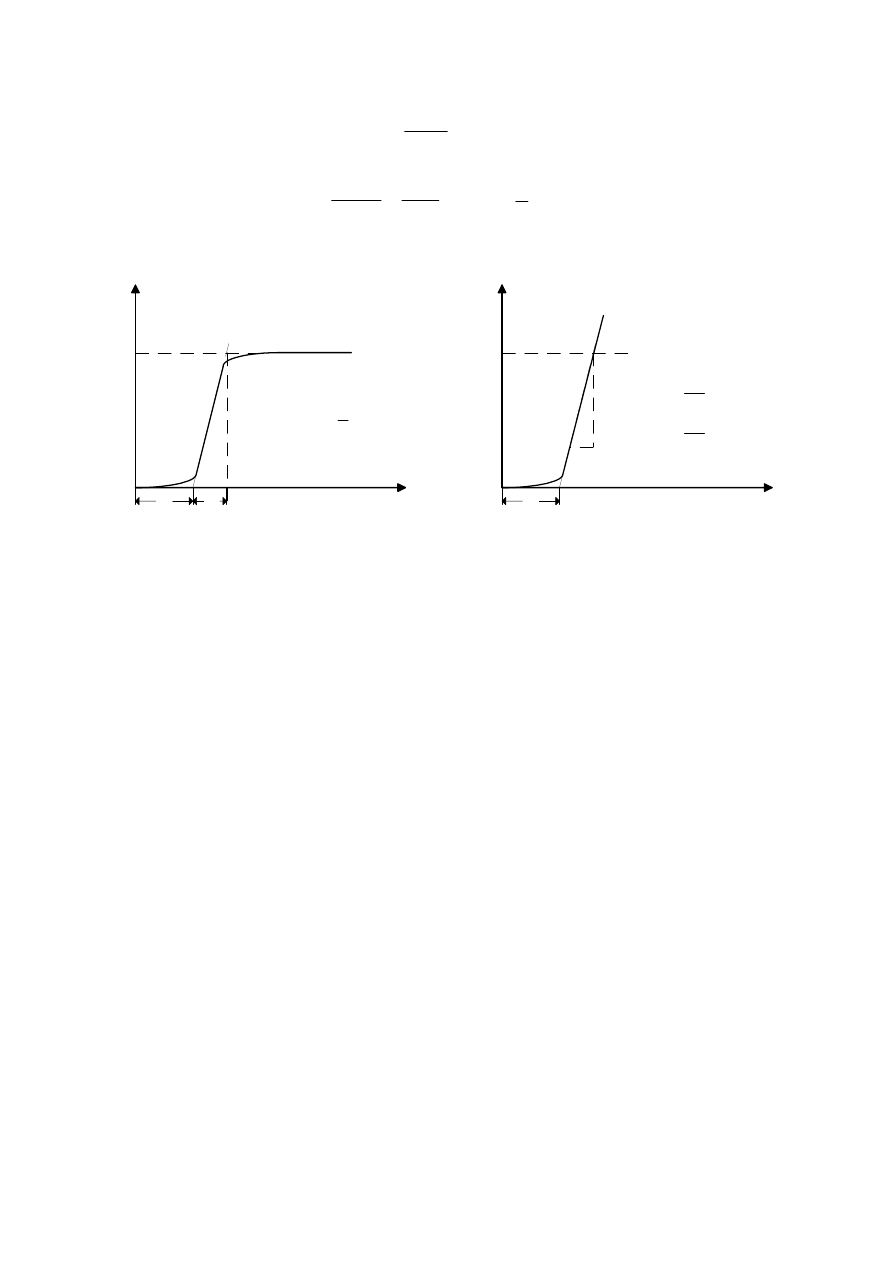
1

)

(

+

=

−

Ts

Ke

s

G

sTo

(10)

−

obiekty astatyczne

Ts

e

s

Ke

s

G

sTo

sTo

−

−

=

=

)

(

;

T

K

1

=

(11)

Sposób wyznaczania parametrów modelu K, T,

o

T

odwzorowującego obiekt na podstawie odpowiedzi

na skok jednostkowy pokazano na rysunku 2.

K

y(t)

t

T

o

T

Nachylenie R=

K

T

u

y(t)

t

T

o

∆

t

∆

y

T =

∆

t

∆

y

u

R =

∆

y

∆

t

(a)

(b)

Rys. 2. Sposób określenia parametrów K, T,

o

T

na podstawie odpowiedzi skokowej (jednostkowej)

procesu. (a) dla obiektu statycznego wieloinercyjnego , (b) dla obiektu astatycznego.

Metody doboru nastaw regulatorów według reguły Zieglera-Nicholsa

Na bazie obserwacji eksperymentalnych strategii strojenia regulatorów PID w procesach
przemysłowych, Ziegler i Nichols zaproponowali dwie metody doboru nastaw. Metody te wymagają
pomiaru odpowiedzi układu i są powszechnie stosowane dla układów statycznych najczęściej
spotykanych w układach sterowania (np. sterowanie poziomem, temperaturą, ciśnieniem, przepływem,
itd.). Metody doboru nastaw opracowane przez Zieglera i Nicholsa opierająca się odpowiedzi
skokowej i możliwe są do zastosowania w tych układach w których odpowiedź skokowa układu
otwartego jest bez przeregulowań tak jak ta pokazana na rysunku 2a. Ziegler i Nichols opracowali
dwie metody strojenia regulatorów dla takich modeli [2].

Metoda bazująca na odpowiedzi skokowej.

Ziegler i Nichols zauważyli, że odpowiedź skokowa większości układów sterowania ma kształt
podobny do tego z rysunku 2a. Krzywa ta może być otrzymana po dokonaniu identyfikacji własności
dynamicznych obiektu.
Krzywa o kształcie S jest charakterystyczna dla układów inercyjnych wyższych rzędów.

Transmitancja (10) aproksymuje układy wyższych rzędów prostym układem pierwszego rzędu z

dodatkowym opóźnieniem T

o

wyrażonym w sekundach. Stałe w równaniu (10) mogą być określone z

odpowiedzi skokowej procesu. Jeśli styczna narysowana jest w punkcie przegięcia krzywej
odpowiedzi, wówczas nachylenie linii jest wyznaczane ze wzoru R=K/T, a przecięcie stycznej z osią
czasu określa czas opóźnienia T

o

.

W pierwszej metodzie wybór parametrów regulatora opiera się na współczynniku zanikania

równym w przybliżeniu 0.25. Oznacza to, że dominująca składowa przejściowa zanika do jednej
czwartej swojej wartości maksymalnej po jednym okresie oscylacji (rys. 3). Takie zanikanie
odpowiada współczynnikowi

ζ

= 0.21 w układzie II rzędu i wartość ta ustalona została na zasadzie

kompromisu pomiędzy szybką odpowiedzią i wystarczającym zapasem stabilności.

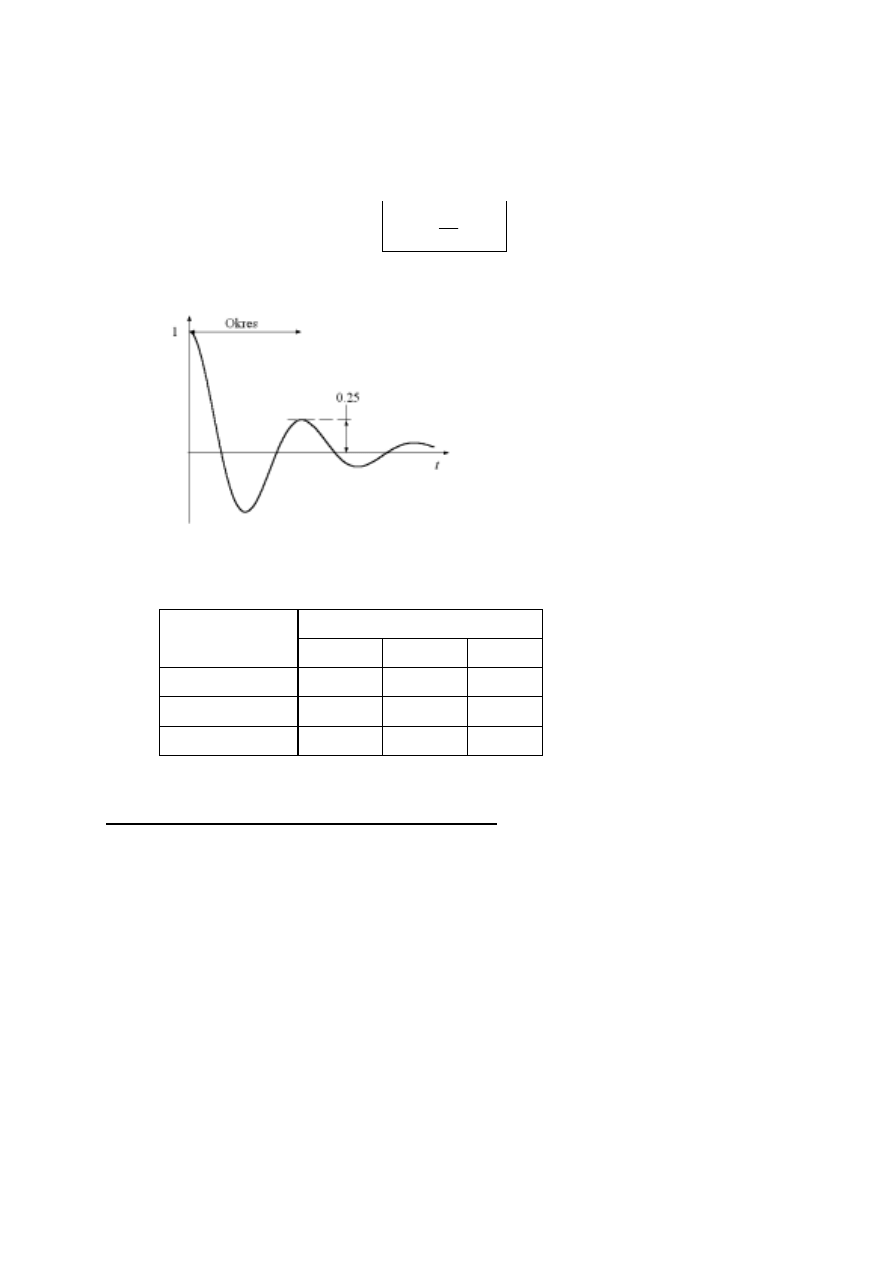
Autorzy symulowali równania dla różnych układów na komputerze analogowym i stroili

parametry regulatorów, aż uzyskali odpowiedzi przejściowe zanikające do 25% poprzedniej wartości
w jednym okresie. Metoda Zieglera-Nicholsa bazująca na odpowiedzi skokowej daje dobre rezultaty
gdy spełniony jest następujący warunek :

6

.

0

15

.

0

<

<

T

T

o

.

Parametry regulatora zaproponowane przez Zieglera i Nicholsa dla typowego regulatora pokazane są
w tabeli 1.

Rys. 3. Kwadratowy współczynnik zanikania

Tabela 1. Strojenie parametrów regulatora metodą odpowiedzi skokowej Zieglera-Nicholsa,

o

RT

a

=

Optymalne wzmocnienia

Typ regulatora

K

p

T

I

T

D

P

1/a

−

−

PI

0.9/a

3T

o

−

PID

1.2/a

2T

o

0.5T

o

Metoda z wyznaczaniem wzmocnienia krytycznego

W drugiej metodzie kryterium strojenia parametrów opiera się na ocenie układu znajdującego się na
granicy stabilności. Ten algorytm strojenia może być stosowany dla układów typu 0 posiadających
rząd > 2. Może być również zastosowana do samonastrajania regulatorów PID. Metoda ta możliwa
jest do zastosowania jeśli możliwe jest znalezienie wzmocnienia przy którym wykres Nyquista
przecina punkt krytyczny lub kiedy linia pierwiastkowa przecina oś liczb urojonych. Wzmocnienie to
może być znalezione eksperymentalnie, wymaga się wówczas zwiększania wzmocnienia w układzie
zamkniętym aż na wyjściu pojawią się oscylacje o stałej amplitudzie. Jest to w niektórych
zastosowaniach praktycznych bardzo niebezpieczna operacja. Zwiększa się wzmocnienie
proporcjonalne aż zauważy się oscylacje o stałej amplitudzie, odpowiada to wzmocnieniu
krytycznemu K

kr

(rys. 4) i oscylacjom o okresie T

osc

(rys. 5). Okres oscylacji powinien być mierzony

kiedy amplituda oscylacji jest dość mała. Dobór nastaw odbywa się według tabeli 2 [2].

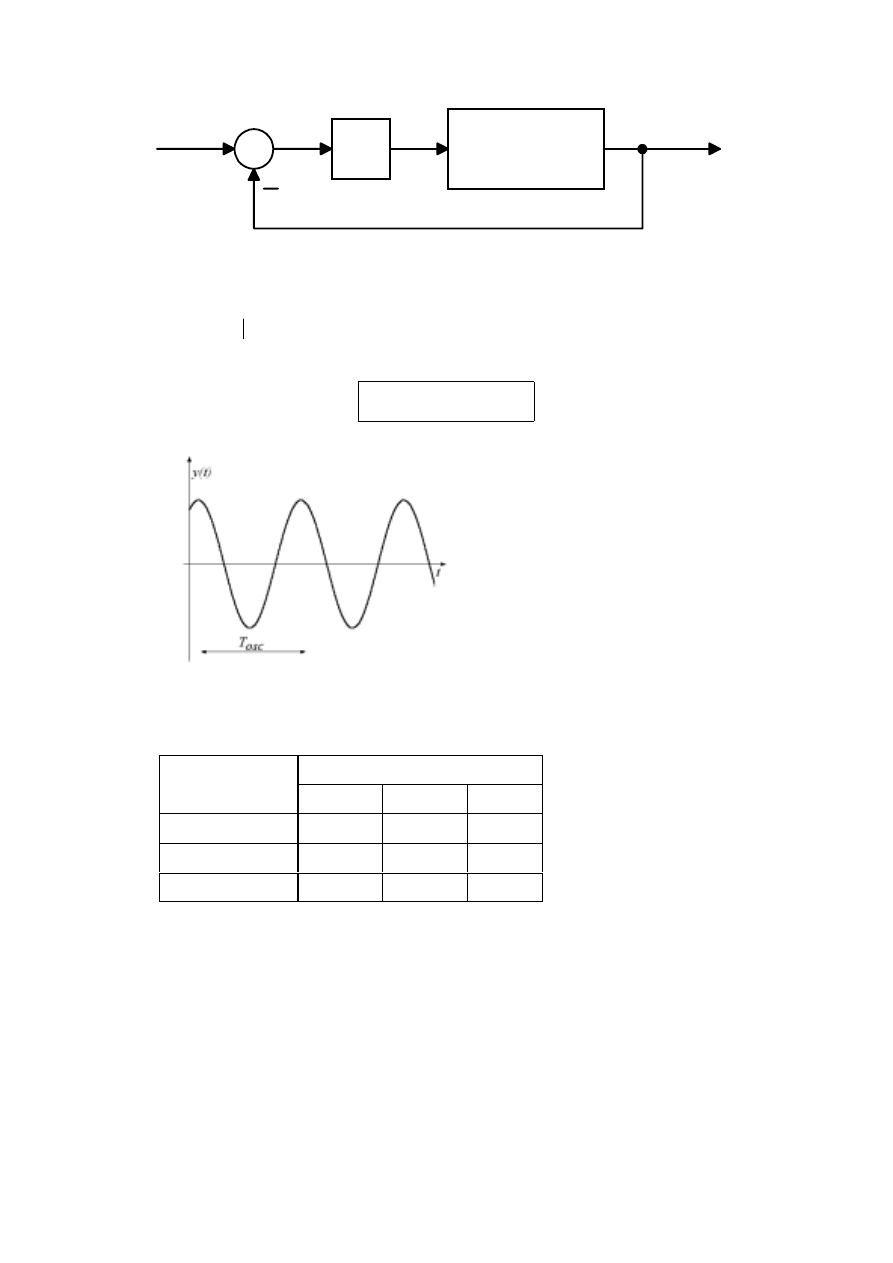
Proces

K

kr

r(t)

e(t)

y(t)

u(t)

Rys. 4. Określenie wzmocnienia krytycznego i okresu oscylacji

Wzmocnienie statyczne dla pętli otwartej układu

( )

0

=

=

s

o

s

GH

K

Metoda strojenia bazująca na wzmocnieniu krytycznym daje dobre rezultaty gdy spełniony jest
warunek:

20

2

<

<

kr

o

K

K

lecz znów odpowiedź układu zamkniętego zawiera oscylacje.

Rys. 5. Układ na granicy stabilności

Tabela 2. Strojenie parametrów regulatora metodą bazującą na granicy stabilności układu

Optymalne wzmocnienia

Typ regulatora

K

P

T

I

T

D

P

0.5K

kr

−

−

PI

0.45K

kr

T

osc

/1.2

−

PID

0.6K

kr

T

osc

/2

T

osc

/8

Metody strojenia Zieglera-Nicholsa dają w rezultacie odpowiedzi w których występują oscylacje i
powinny być jeszcze dostrajane ręcznie.

Inne reguły nastaw regulatorów PID

W tabelach 3 i 4 zebrane zostały zasady doboru nastaw regulatorów dla obiektów statycznych i
astatycznych opisanych transmitancjami (10) oraz (11) według kryteriów: 0% i 20% przeregulowania
oraz minimum całki kwadratu uchybu [3].

Tabela 3. Optymalne nastawy regulatorów w przypadku obiektów statycznych z opóźnieniem (10),

o

RT

a

=

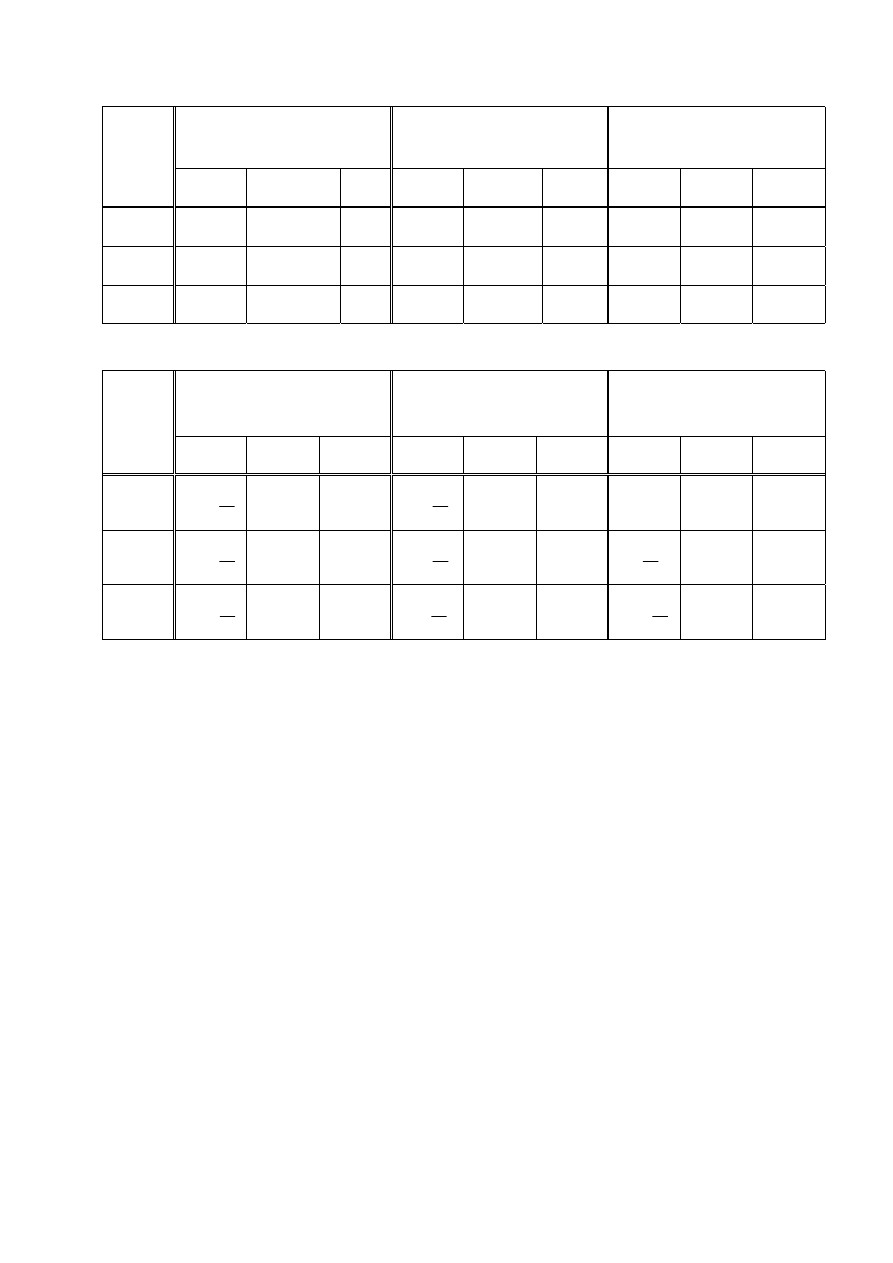
Przeregulowanie

%

0

≈

Minimum czasu regulacji

R

t

Przeregulowanie

%

20

≈

Minimum czasu regulacji

R

t

dt

t

e

∫

∞

0

2

)

(

min

Typ

regulator

a

K

P

T

I

T

D

K

P

T

I

T

D

K

P

T

I

T

D

P

0.3/a

−

−

0.7/a

−

−

−

−

−

PI

0.6/a

0.8T

o

+0.5T

−

0.7/a

T

o

+0.3T

−

1/a

T

o

+0.35T

−

PID

0.95/a

2.4 T

o

0.4 T

o

1.2/a

2.0 T

o

0.4 T

o

1.4/a

1.3 T

o

0.5 T

o

Tabela 4. Optymalne nastawy regulatorów w przypadku obiektów astatycznych z opóźnieniem (11)

Przeregulowanie

%

0

≈

Minimum czasu regulacji

R

t

Przeregulowanie

%

20

≈

Minimum czasu regulacji

R

t

dt

t

e

∫

∞

0

2

)

(

min

Typ

regulator

a

K

P

T

I

T

D

K

P

T

I

T

D

K

P

T

I

T

D

P

o

T

T

⋅

37

.

0

−

−

o

T

T

⋅

7

.

0

−

−

−

−

−

PI

o

T

T

⋅

46

.

0

o

T

⋅

75

.

5

−

o

T

T

⋅

7

.

0

o

T

⋅

3

−

o

T

T

⋅

1

o

T

⋅

3

.

4

−

PID

o

T

T

⋅

65

.

0

o

T

⋅

5

o

T

⋅

23

.

0

o

T

T

⋅

1

.

1

o

T

⋅

2

o

T

⋅

37

.

0

o

T

T

⋅

36

.

1

o

T

⋅

6

.

1

o

T

⋅

5

.

0