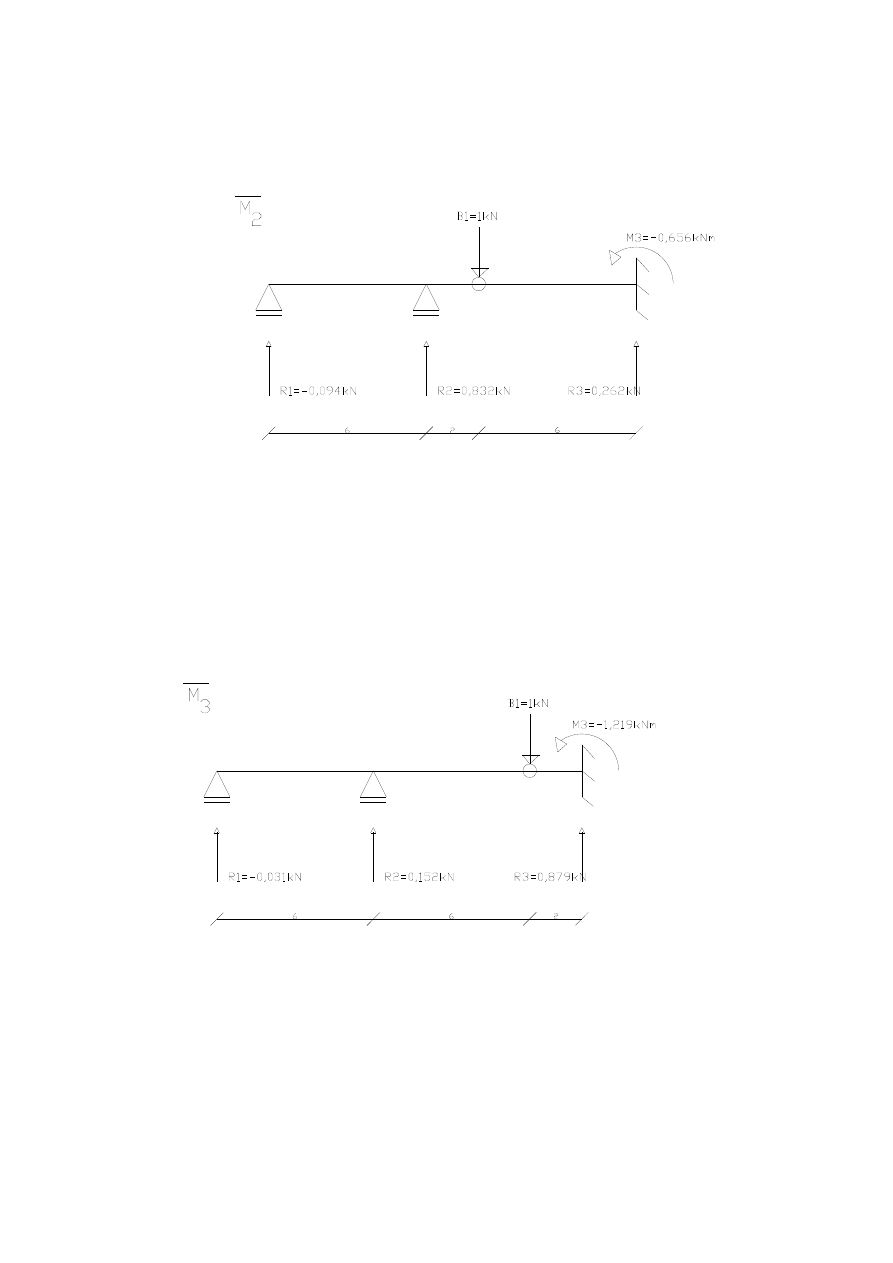
2

x

M

094

,

0

)

6

;

0

(

2

__





992

,

4

738

,

0

)

6

(

832

,

0

094

,

0

)

8

;

6

(

2

__













x

x

x

M

008

,

3

262

,

0

)

8

(

1

992

,

4

738

,

0

)

14

;

8

(

2

__















x

x

x

M

x

M

031

,

0

)

6

;

0

(

3

__





912

,

0

121

,

0

)

6

(

152

,

0

0311

,

0

)

12

;

6

(

3

__













x

x

x

M

088

,

11

879

,

0

)

12

(

1

912

.

0

121

,

0

)

14

;

12

(

3

__















x

x

x

M

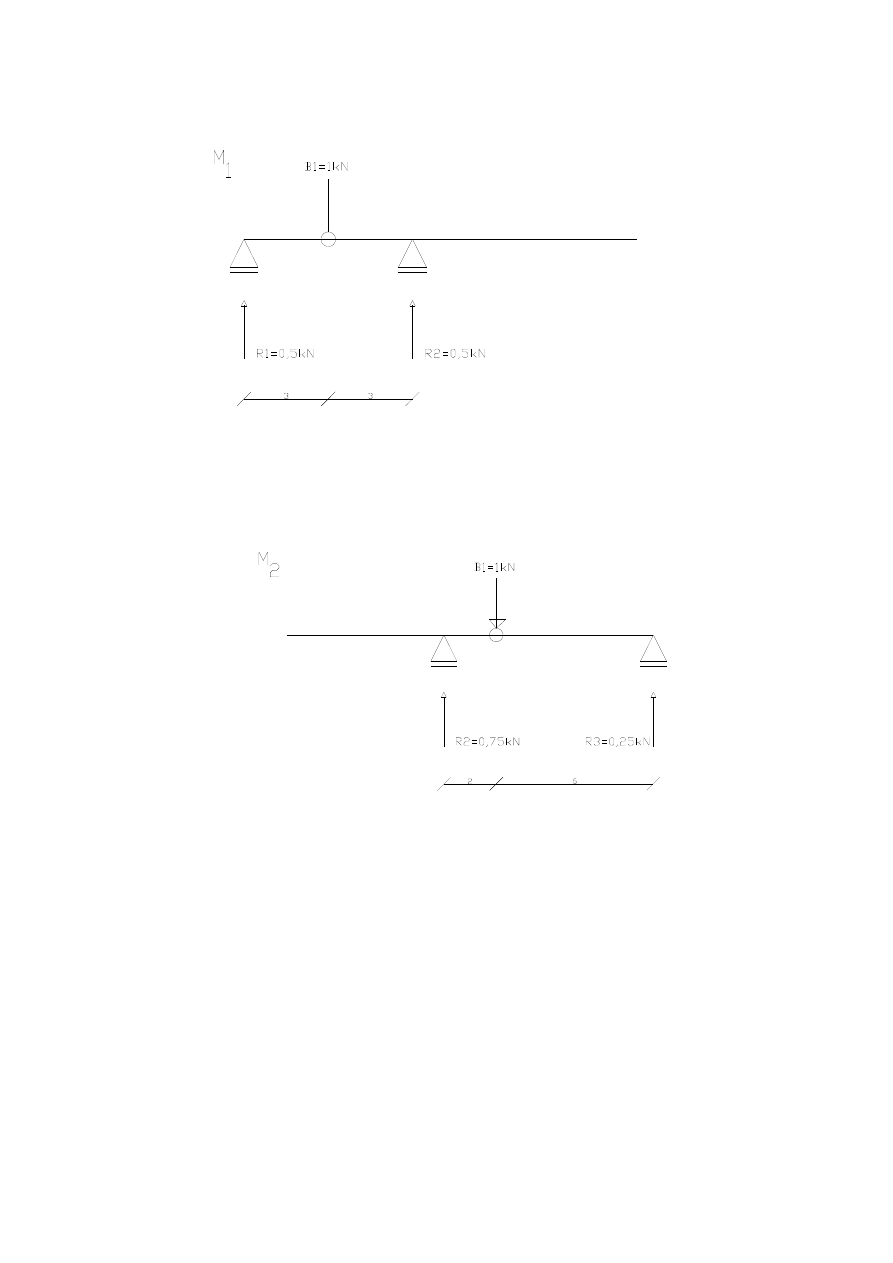
3

x

M

5

,

0

)

3

;

0

(

1



3

5

,

0

)

3

(

1

5

,

0

)

6

;

3

(

1













x

x

x

M

0

)

6

(

5

,

0

3

5

,

0

)

14

;

6

(

1













x

x

M

0

)

6

;

0

(

2



M

5

,

4

75

,

0

)

6

(

75

,

0

)

8

;

6

(

2









x

x

M

5

,

3

25

,

0

)

8

(

1

5

,

4

75

,

0

)

4

1

;

8

(

2















x

x

x

M

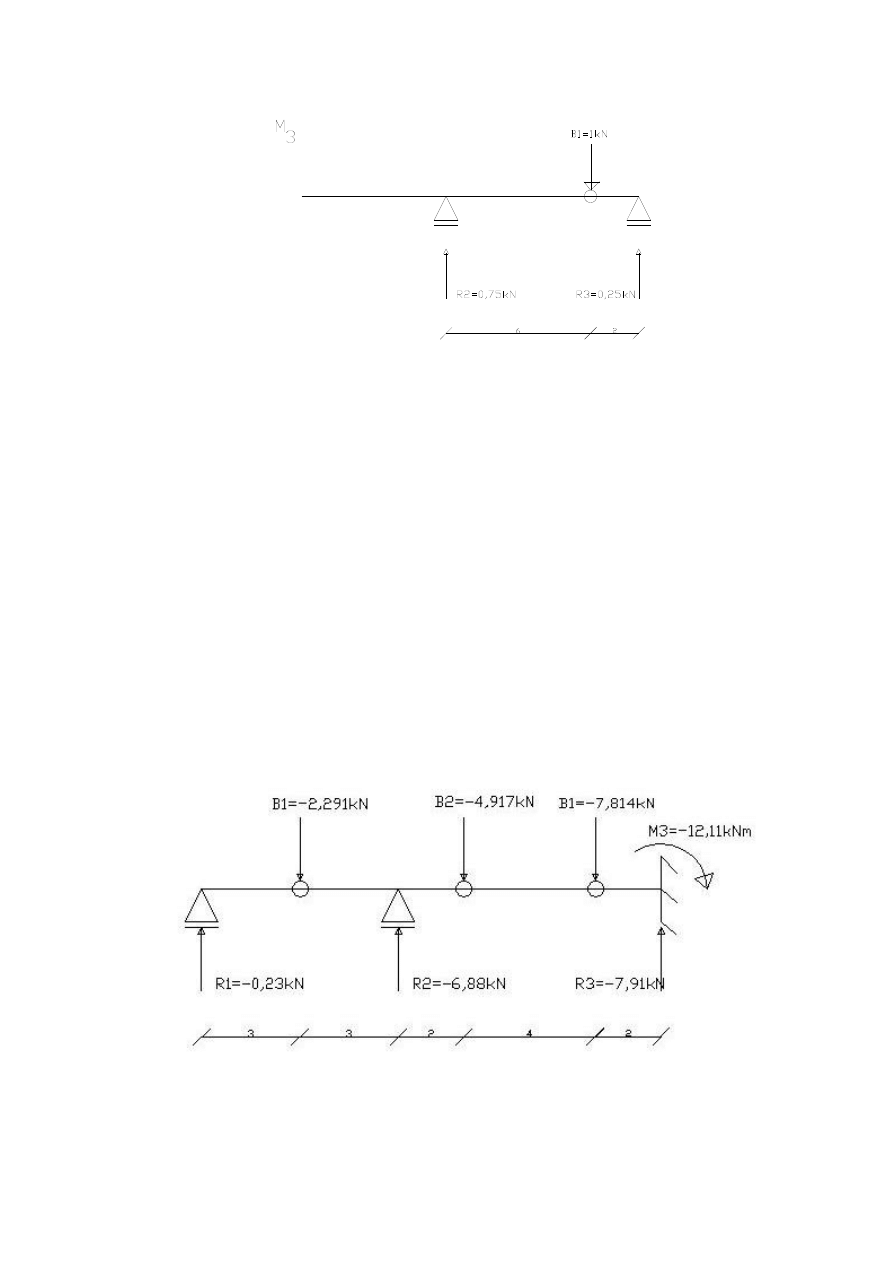
4

0

)

6

;

0

(

3



M

5

,

1

25

,

0

)

6

(

25

,

0

)

2

1

;

6

(

3









x

x

M

5

,

10

75

,

0

)

12

(

1

5

,

1

25

,

0

)

4

1

;

12

(

3















x

x

x

M

OBLICZENIA W MATHEMATICE

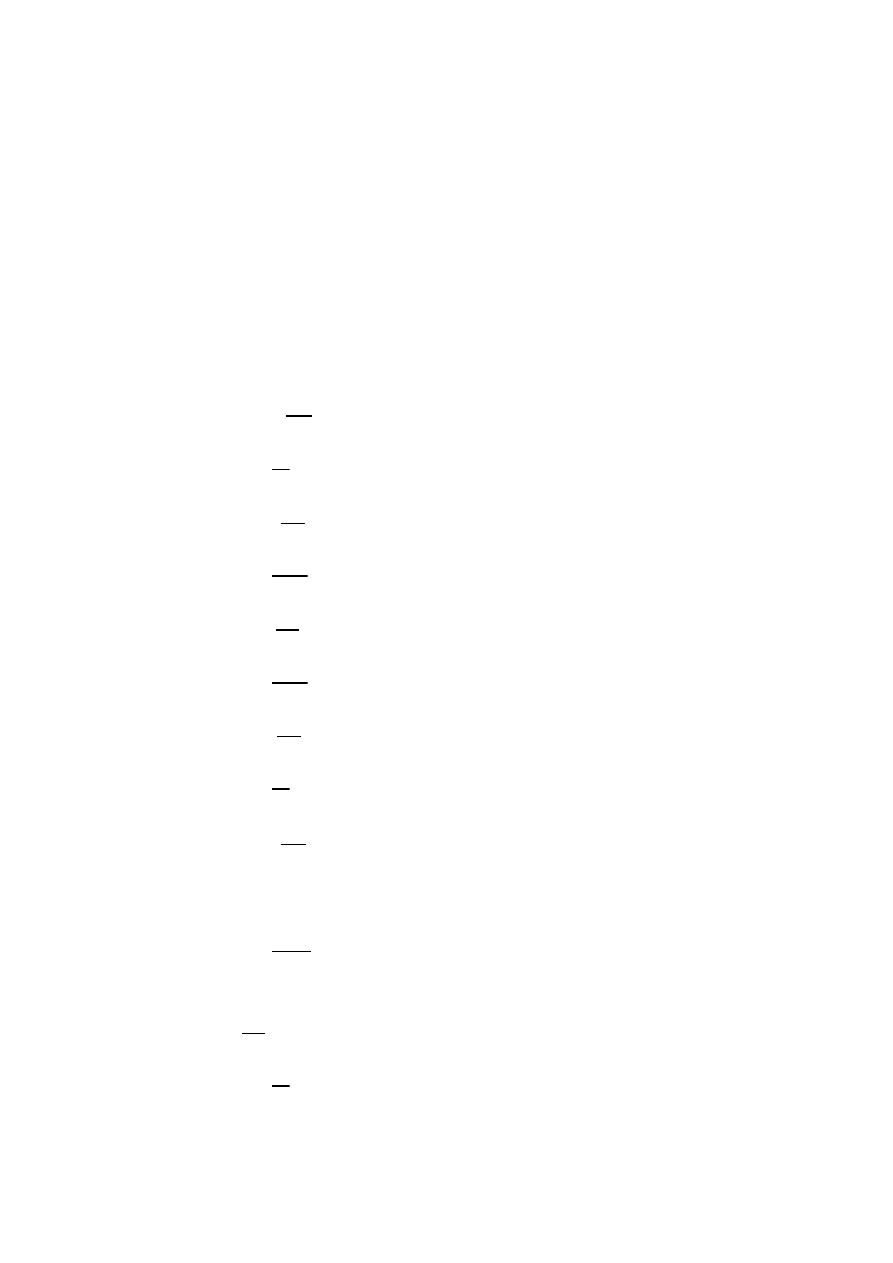
5

K  moduł Younga

K  2  10

11

Pa

J  moment bezwładności dwuteownika 80

J  80.1  10



8

m

4

Masa całej belki wynosi :

m  84kg

Obliczam współczynniki wpływu 

ij



11



1

KJ







0

3

0.406x0.5x x 

3

6

0.594x  3 0.5x 3 x





1

KJ



3.231





12



1

KJ



6

8

0.105x  1.194 0.75x  4.5 x  

8

14

0.25x  3.5 0.105x  1.194 x

1

KJ



1.284





13



1

KJ



6

12

0.25x  1.5 0.105x  1.194 x  

12

14

0.105x 1.194 0.75x  10.5 x

1

KJ



0.444





22



1

KJ



6

8

0.738x  4.992 0.75x  4.5 x  

8

14

0.262x  3.008 0.25x  3.5 x

1

KJ



2.376





23



1

KJ



6

8

0.25x  1.5 0.738x  4.992 x  

8

12

0.262x  3.008 0.25x  1.5 x 



12

14

0.75x  10.5 0.262x  3.008 x

1

KJ



0.946667





33



1

KJ



6

12

0.121x  0.912 0.25x  1.5 x  

12

14

0.75x  10.5 0.879x  11.088 x

1

KJ



1.272



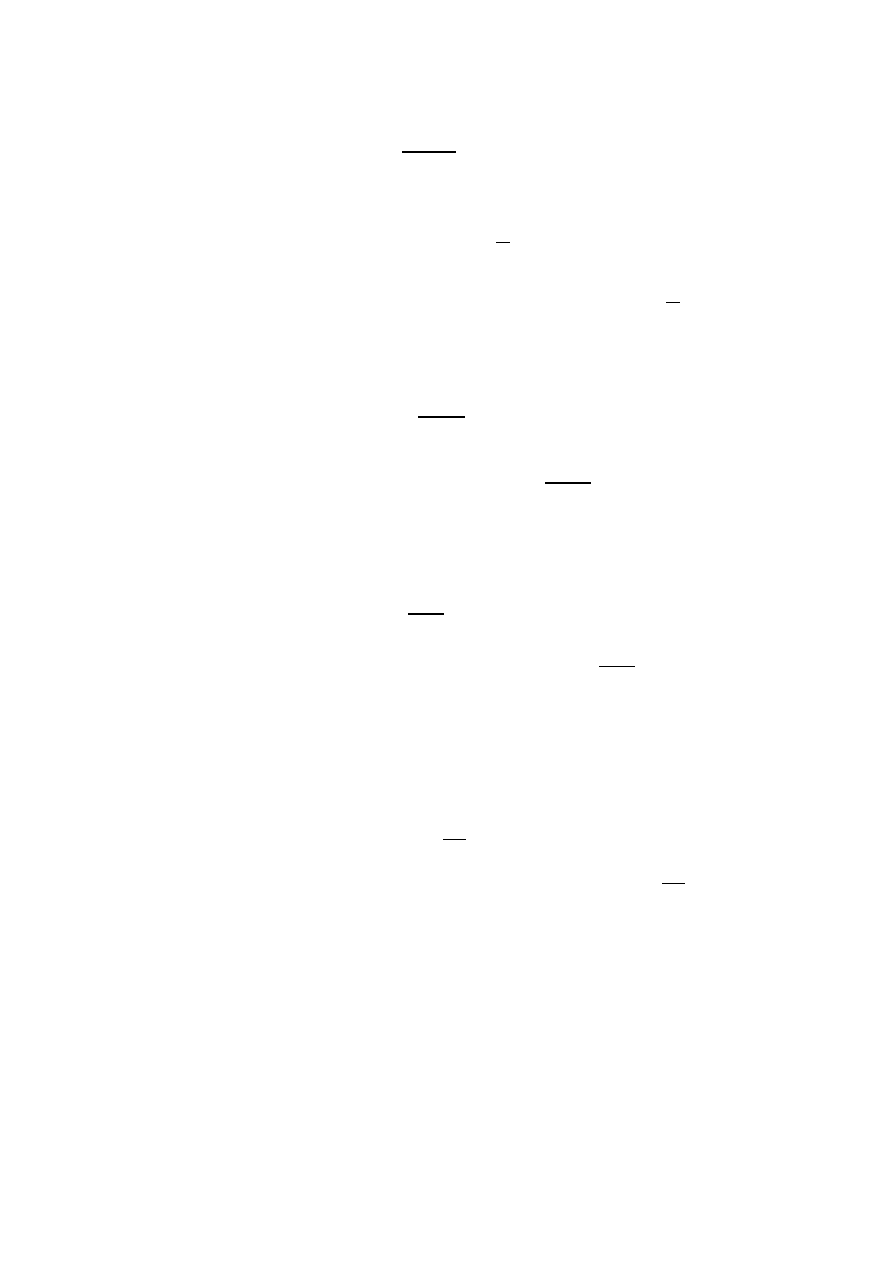
6

Przyjmuję e 

KJ

m

2

Obliczone wartości  jak i wartości mas wstawiam do wyznacznika1

A  3.2309999999999963 

7

3

 e, 1.2840000000000016`, 0.4439999999999866,

1.742999999999994, 2.3759999999999977`

7

2

 e, 0.9466666666666264,

0.4439999999999866, 0.9466666666666264, 1.2720000000000393 

7

2

 e



3.231



7 e

3

,



1.284 ,



0.444



,



1.743 , 2.376



7 e

2

, 0.946667



,



0.444 , 0.946667 , 1.272



7 e

2



MatrixForm[A]













3.231



7 e

3



1.284



0.444



1.743

2.376



7 e

2

0.946667



0.444

0.946667

1.272



7 e

2













Det

m3 















3.2309999999999963` 

7 e

3

1.2840000000000016`

0.4439999999999866`

1.742999999999994`

2.3759999999999977` 

7 e

2

0.9466666666666264

0.4439999999999866`

0.9466666666666264`

1.2720000000000393` 

7 e

2

















4.82657



37.6913 e



69.3718 e

2



343 e

3

12

-----------------

Wyznaczam pierwiastki równania

Solve4.826572672000384` 37.69127651851934` e  69.37175000000026` e

2



343 e

3

12

 0,

e

7

{{e

0.188175},{e0.522981},{e1.71584}}

m=84

84

K  2 10

11

200000000000

J  80.1 10



8

8.01



10



7

Na podstawie wyliczonych e

1

, e

2

, e

3

wyliczam częstości

1,



2,



3

 poszczególnych

mas m

1

, m

2

, m

3



e

3

 0.1881750602863202`

0.188175



3

 

K  J

m  e

3

100.672

e

2

 0.5229813732147199`

0.522981



2

 

K  J

m  e

2

60.3877

e

1

 1.7158435664989693`

1.71584



1

 

K  J

m  e

1

33.339

Wyliczam współczynniki drgań własnych



i



A

2



i

A

1



i



i





A

3



i

A

1



i

----------------------



1

 

Detm2 









3.2309999999999963 

7 e1

3

0.4439999999999866`

1.742999999999994

0.9466666666666264









Detm2 









1.2840000000000016`

0.4439999999999866`

2.3759999999999977` 

7 e1

2

0.9466666666666264









8

-0.53248



1



Detm2 











3.2309999999999963` 

7 e1

3

1.2840000000000016`

1.742999999999994`

2.3759999999999977` 

7 7 e1

2













Detm2 









1.2840000000000016`

0.4439999999999866`

2.3759999999999977` 

7 e1

2

0.9466666666666264









-10.0482



2

 

Detm2 









3.2309999999999963 

7 e2

3

0.4439999999999866`

1.742999999999994

0.9466666666666264









Detm2 









1.2840000000000016`

0.4439999999999866`

2.3759999999999977` 

7 e2

2

0.9466666666666264









1.16058



2



Detm2 











3.2309999999999963` 

7 e2

3

1.2840000000000016`

1.742999999999994`

2.3759999999999977` 

7



e2

2













Detm2 









1.2840000000000016`

0.4439999999999866`

2.3759999999999977` 

7 e2

2

0.9466666666666264









1.17235



3

 

Detm2 









3.2309999999999963 

7 e3

3

0.4439999999999866`

1.742999999999994

0.9466666666666264









Detm2 









1.2840000000000016`

0.4439999999999866`

2.3759999999999977` 

7 e3

2

0.9466666666666264









4.12611



3



Detm2 











3.2309999999999963` 

7 e3

3

1.2840000000000016`

1.742999999999994`

2.3759999999999977` 

7



e3

2













Detm2 









1.2840000000000016`

0.4439999999999866`

2.3759999999999977` 

7 e3

2

0.9466666666666264









-5.64416

y

1

, y

2

, y

3

 przemieszczenia mas

y

1

 A

11

sin

1

t  

1

  A

12

sin

2

t  

2

  A

13

sin

3

t 

3



y

2

 A

21

sin

1

t  

1

  A

22

sin

2

t  

2

  A

23

sin

3

t 

3



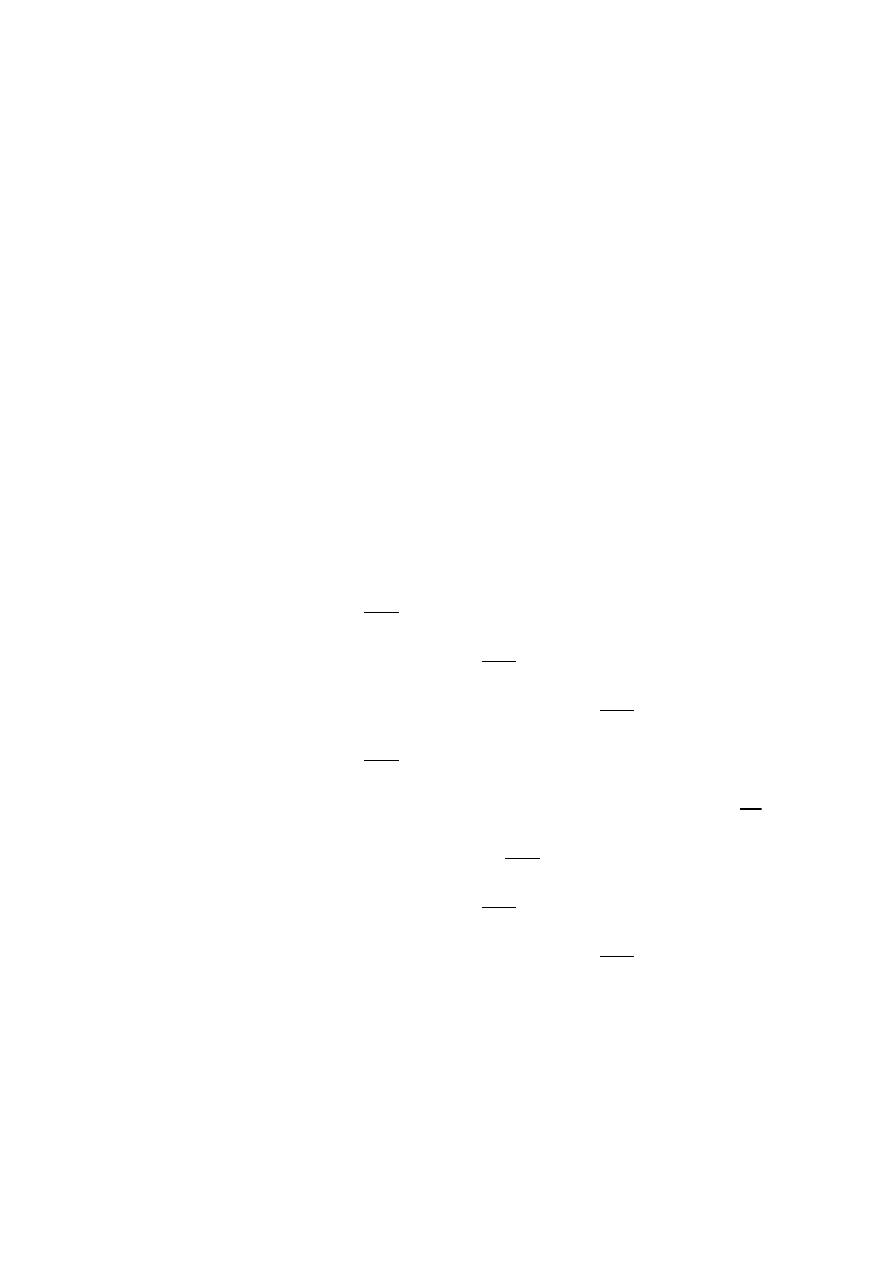
9

y

3

 A

31

sin

1

t  

1

  A

32

sin

2

t  

2

  A

33

sin

3

t 

3



Warunki początkowe :

y

1

0  0 y

2

0  0 y

3

0  0  

1

, 

2

, 

3

 90°

y

1

 0  V

01

y

2

 0  0 y

3

 0  0 V

01

 1m  s

y

1

  A

11



1

cos

1

t  A

12



2

cos

2

t  A

13



3

cos

3

t

y

2

  A

11



1



1

cos

1

t  A

12



2



2

cos

2

t  A

13



3



3

cos

3

t

y

3

  A

11



1



1

cos

1

t  A

12



2



2

cos

2

t  A

13



3



3

cos

3

t

t  0

Wyznaczam amplitudy przemieszczeń A

11

, A

12

, A

13

A

11



1

 A

12



2

 A

13



3

 v

A

11



1



1

 A

12



2



2

 A

13



3



3

 0

A

11



1



1

 A

12



2



2

 A

13



3



3

 0

SolveA

11



1

 A

12



2

 A

13



3

 1, A

11



1



1

 A

12



2



2

 A

13



3



3

 0,

A

11



1



1

 A

12



2



2

 A

13



3



3

 0, A

11

, A

12

, A

13





3.231



7 e

3

,



1.284 ,



0.444



,



1.743 , 2.376



7 e

2

, 0.946667



,



0.444 , 0.946667 , 1.272



7 e

2



11



0.00762174 ,



3.231



7 e

3

,



1.284 ,



0.444



,



1.743 , 2.376



7 e

2

,

0.946667



,



0.444 , 0.946667 , 1.272



7 e

2



12



0.0164303 ,



3.231



7 e

3

,



1.284 ,



0.444



,



1.743 , 2.376



7 e

2

, 0.946667



,



0.444 , 0.946667 , 1.272



7 e

2



13

 

0.00244642



A

11

 0.0076217394872164675`

0.00762174

A

12

 0.016430255580487465`

0.0164303

A

13

 0.0024464160435456227`

-0.00244642

Wyznaczam pozostałe amplitudy przemieszczeń:

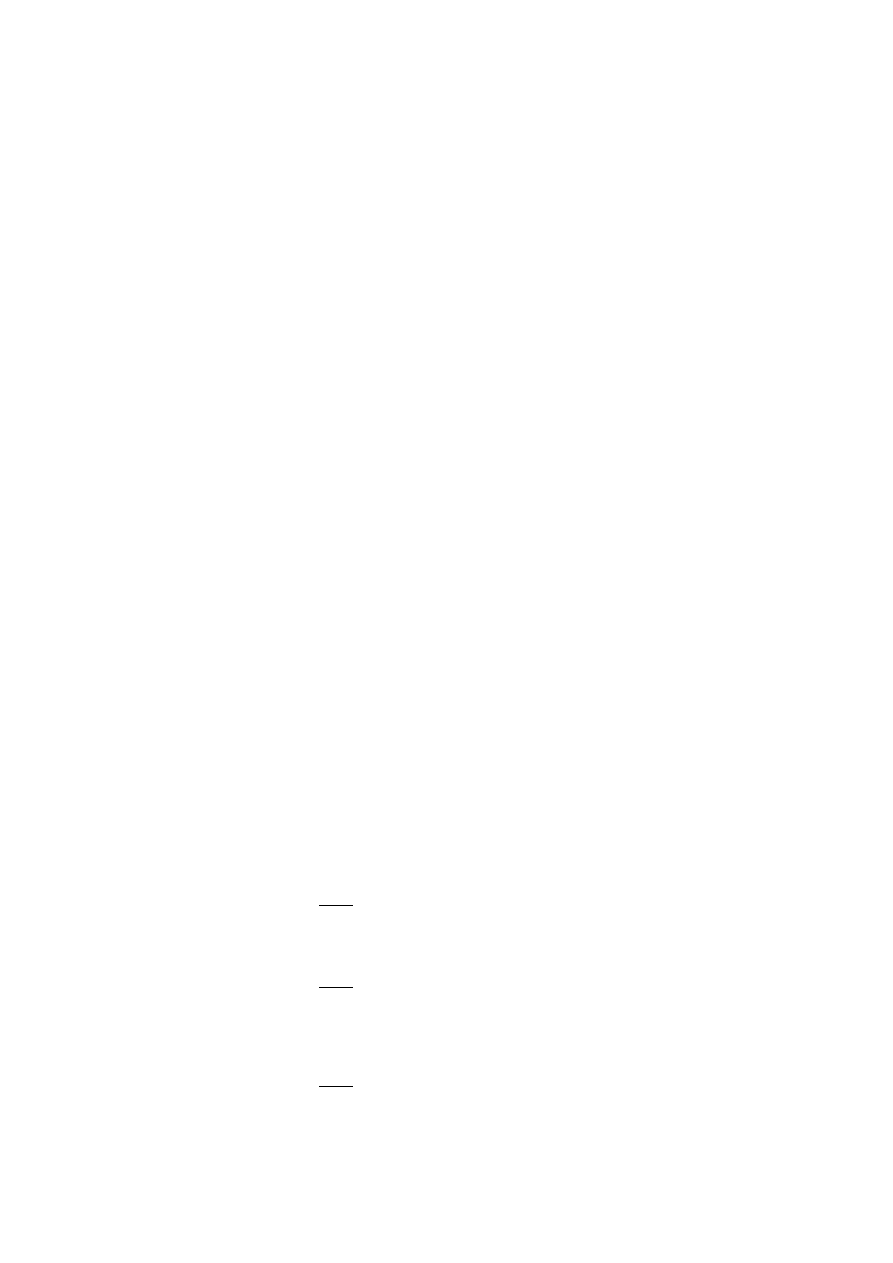
10

A

21

 

1

A

11

-0.00405843

A

22

 

2

A

12

0.0190686

A

23

 

3

A

13

-0.0100942

A

31

 

1

A

11

-0.0765851

A

32

 

2

A

12

0.0192621

A

33

 

3

A

13

0.013808

t    2 

1

0.0471159

Obliczam przemieszczenia mas m

1

, m

2

, m

3



y

1

 A

11

Sin33.33901523315005`` t A

12

Sin60.387701870668515`` t 

A

13

Sin100.67243679608531`` t

0.01486

y

2

 A

21

Sin33.33901523315005`` t A

22

Sin60.387701870668515`` t 

A

23

Sin100.67243679608531`` t

55

0.0116

y

3

 A

31

Sin33.33901523315005`` t A

32

Sin60.387701870668515`` t 

A

33

Sin100.67243679608531` t

-0.0847609
-------------------------------------

Obliczam reakcje w podporach R

1

, R

2

, R

3

, R

4

 jak i siły B

1

, B

2

, B

3

 powodujące

ugięcie



11



1

K J

3.2309999999999963`

0.0000201685



12



1

K J

1.2840000000000016`



8.01498



10



6



13



1

K J

0.4439999999999866`



2.77154



10



6

11



21

 

12



8.01498



10



6



31

 

13



2.77154



10



6



22



1

K J

1.2840000000000016`



8.01498



10



6



23



1

K J

0.9466666666666264`

5.90928



10



6



32

 

23

5.90928



10



6



33



1

K J

1.2720000000000393`

7.94007



10



6

Solvey

1

 

11

B

1

 

21

B

2

 

13

B

3

, y

2

 

21

B

1

 

22

B

2

 

23

B

3

,

y

3

 

31

B

1

 

32

B

2

 

33

B

3

, B

1

, B

2

, B

3





B

1

 

2291.18 , B

2

 

4917.82 , B

3

 

7814.82



B1=-2,291kN B2=-4,917kN B3=-7,814kN