1. Metody numeryczne (analiza numeryczna) – Dział matematyki stosowanej zajmujący się opracowaniem metod

przybliżonego rozwiązywania skomplikowanych zagadnień matematycznych, których rozwiązanie byłoby nadzwyczaj
żmudne lub niemożliwe choćby poprzez konieczność wykonania nieskończenie wielu operacji.

2. Układ równań zawierający n niewiadomych

{

a

11

x

1

a

12

x

2

...a

1n

x

n

=b

1

a

21

x

1

a

22

x

2

...a

2n

x

n

=b

2

..............

a

n1

x

1

a

n2

x

2

...a

nn

x

n

=b

n

3. Macierzowa reprezentacja układu n niewiadomych

A

⋅X=B → X=A

−1

⋅B

, gdzie:

A

=

[

a

11

a

12

...

a

1n

a

21

a

22

...

a

2n

...

...

...

...

a

n1

a

n2

...

a

nn

]

X

=

[

x

1

x

2

...

x

n

]

B

=

[

b

1

b

2

...

b

n

]

A – macierz główna układu
X – wektor wyrazów wolnych
B – wektor wyrazów wolnych

Układ równań posiada jedno rozwiązanie tylko wtedy, gdy jest oznaczony, tzn. macierz główna układu równań A nie jest
osobliwa.
4. Układ równań, w którym tylko główna przekątna macierzy A ma elementy niezerowe

{

a

11

x

1

=b

1

a

22

x

2

=b

2

...

a

nn

x

n

=b

n

Algorytm:

x

i

=

b

i

a

ii

, a

ii

≠0, i=1,2 , ..., n

5. Trójkątny układ równań

{

a

11

x

1

a

12

x

2

...a

1n

x

n

=b

1

a

22

x

2

...a

2n

x

n

=b

2

..............

a

nn

x

n

=b

n

Algorytm:

x

n

=

b

n

a

nn

, x

i

=

b

i

−

∑

s

=i1

n

a

is

x

s

a

ii

, i

=n−1, n−2, ...,1

Przy czym:

a

ii

≠0 , i=1,2 ,... , n

6. Metoda Thomasa dla układów trójprzekątniowych:

[

b

1

c

1

a

2

b

2

c

2

a

3

b

3

c

3

..

..

..

a

n

−1

b

n

−1

c

n

−1

a

n

b

n

]

⋅

[

x

1

x

2

x

3

...

x

n

−1

x

n

]

=

[

d

1

d

2

d

3

...

d

n

−1

d

n

]

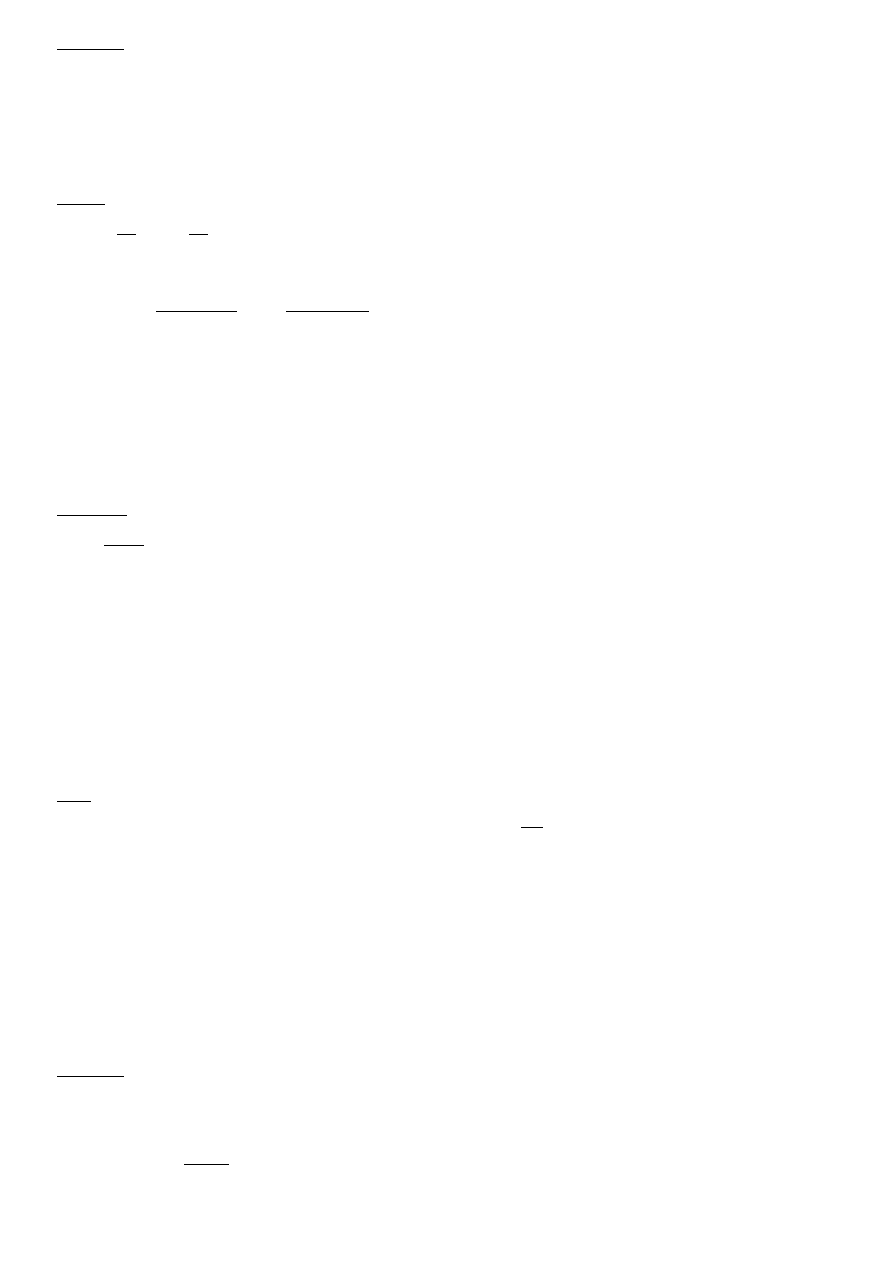
Algorytm:

a

i

x

i

−1

b

i

x

i

c

i

x

i

1

=d

i

, i

=1,2 , ..., n

a

1

=0 , c

n

=0

Wzory:



1

=−

c

1

b

1

,



1

=

d

1

b

1

, x

n

=

n

, x

i

=

i

⋅x

i

1



i

dla :

i

=n−1, n−1, ...,1



i

=−

c

i

a

i



i

−1

b

i

,



i

=

d

i

−a

i



i

−1

a

i



i

−1

b

i

dla :

i

=2,3 , ..., n

7. Metoda Cramera (Wyznacznikowa)

W

=

[

a

11

a

12

...

a

1n

a

21

a

22

...

a

2n

...

...

...

...

a

n1

a

n2

...

a

nn

]

Algorytm

:

x

n

=

[W

n

]

[W ]

,

∣W ∣≠0

b podstawiamy w kolumnę odpowiednią liczonemu x

8. Metoda eliminacji Gaussa: Jest to metoda służąca jedynie do upraszczania układów. Jej celem jest sprowadzenie n

pierwszych kolumn macierzy C do macierzy trójkątnej. Następnie pozostaje już tylko rozwiązanie macierzy trójkątnej.
Macierze A i B zapisujemy to w postaci macierzy C, w której macierz główną uzupełnia się dodatkową kolumną
zawierającą wektor wyrazów wolnych B.

C

=

[

a

11

a

12

... a

1n

b

1

a

21

a

22

... a

2n

b

2

...

...

...

...

...

a

n1

a

n2

... a

nn

b

nn

]

=

[

c

11

c

12

...

c

1n

c

1, n

1

c

21

c

22

...

c

2n

c

2, n

1

...

...

...

...

...

c

n1

c

n2

...

c

nn

c

n ,n

1

]

Kroki

Jeżeli

c

11

≠0

Odejmujemy pierwsze równanie pomnożone przez

c

i1

c

11

od każdego kolejnego i-tego równania, przy

czym:

i

=

2,3

,

...

, n

zaś obliczone współczynniki zapisujemy w miejscu poprzednich. Następnie przeprowadzamy

analogiczne operacje aż do uzyskania macierzy trójkątnej. Po n-1 krokach mamy:

C

n

−1

=

[

c

11

c

12

c

13

...

c

1n

c

1, n

1

0

c

22

1

c

23

1

...

c

2n

1

c

2, n

1

1

0

0

c

33

2

...

c

3n

2

c

3, n

1

2

...

...

...

...

...

...

0

0

0

... c

nn

 n−1

c

n , n

1

c−1

]

Algorytm:

{

s

=1,2, ... , n−1

{

i

=s1, s2,... , n

c

ij

s

=c

ij

s−1

−

c

is

s−1

c

ss

s−1

⋅c

sj

s−1

j

=s1, s2, ..., n1

9. Aproksymacja funkcji jednej zmiennej – Dana jest funkcja jednej zmiennej

y

=f x , x ∈[a , b]

Należy dobrać taką

funkcję

F

x , p

1

, ... , p

k

, x ∈[a , b]

aby możliwie jak najdokładniej odtworzyć przebieg funkcji f(x), czyli

zminimalizować różnice pomiędzy odpowiednimi wartościami w punktach

x

i

, y

i

 , i=1,2, ..., n

Gdzie:

p

1

, ..., p

k

To parametry wzoru empirycznego.

Aproksymacja polega na dobraniu parametrów

p

1

, ... , p

k

wzoru empirycznego w taki sposób aby pełnione było

kryterium minimalizacji odchyłek.
Rodzaje aproksymacji:
Aproksymacja punktowa – funkcja f(x) jest zadana jako zbiór punktów

f

x

1

=y

1

, f

 x

2

=y

2,

... , f

x

n

=y

n

Aproksymacja integralna - funkcja f(x) jest zadana w formie wzoru analitycznego

10.Odchyłka -



i

=F x

i

, p

1

, ... , p

k

−y

i

Kryteria minimalizacji odchyłek:
~wybranych punktów
~średnich
~sumowania bezwzględnych wartości
~najmniejszych kwadratów

11.Metoda najmniejszych kwadratów -

Dobór współczynników funkcji

F

∑

i

=1

n



i

2

=min

Kryterium najmniejszych kwadratów

∑

i

=1

n

[F x

i

, p

1

,... , p

k

−y

i

]

2

=min

Zalety:
~kryterium jest mocne, zawiera kwadraty odchyłek, a więc liczby nieujemne
~Prostota obliczeń minimum funkcji pod warunkiem, że rozpatruje się aproksymację w klasie wielomianów
uogólnionych:

F

x , p

1

, ... , p

k

=p

1



1

x p

2



2

 x...p

k



k

 x

12.Aproksymacja liniowa funkcji jednej zmiennej -

Dany jest zbiór punktów:

x

1

, y

1

, x

2

, y

2

, ..., x

n

, y

n



Funkcja aproksymująca:

y

=p

1

p

2

x

Kryterium najmniejszych kwadratów:

S

 p

1

, p

2

=

∑

i

=1

n

[p

1

p

2

x

i

−y

i

]

2

=min

Warunek konieczny istnienia ekstremum funkcji dwóch zmiennych:

∂S p

1

, p

2



∂ p

1

=2

∑

i

=1

n

[p

1

p

2

x

i

−y

i

]=0

∂S p

1

, p

2



∂ p

2

=2

∑

i

=1

n

[ p

1

p

2

x

i

−y

i

]⋅x

i

=0

Forma 1

∑

i

=1

n

[p

1

p

2

x

i

−y

i

]=0

∑

i

=1

n

[p

1

x

i

p

2

x

i

2

−y

i

x

i

]=0

Forma 2

p

1

n

p

2

∑

i

=1

n

x

i

=

∑

i

=1

n

y

i

p

1

∑

i

=1

n

x

i

p

2

∑

i

=1

n

x

i

2

=

∑

i

=1

n

y

i

x

i

Forma 3

[

n

∑

i

=1

n

x

i

∑

i

=1

n

x

i

∑

i

=1

n

x

i

2

]

⋅

[

p

1

p

2

]

=

[

∑

i

=1

n

y

i

∑

i

=1

n

y

i

x

i

]

X

⋅P=Y ⇒ P=X

−1

⋅Y

Przypadek dla trzech punktów aproksymacji

y

=p

1

p

2

x

p

3

1
x

S

 p

1

, p

2

, p

3

=

∑

i

=1

n

[p

1

p

2

x

i

p

3

1

x

i

−y

i

]

2

=min

∂S p

1

, p

2

, p

3



∂ p

1

=2

∑

i

=1

n

[p

1

p

2

x

i

p

3

1

x

i

−y

i

]=0

∂S p

1

, p

2

, p

3



∂ p

2

=2

∑

i

=1

n

[p

1

p

2

x

i

p

3

1

x

i

−y

i

]⋅x

i

=0

∂S p

1

, p

2

, p

3



∂ p

3

=2

∑

i

=1

n

[ p

1

p

2

x

i

p

3

1
x

−y

i

]⋅

1

x

i

=0

[

n

∑

i

=1

n

x

i

∑

i

=1

n

1

x

i

∑

i

=1

n

x

i

∑

i

=1

n

x

i

2

n

∑

i

=1

n

1

x

i

n

∑

i

=1

n

1

x

i

2

]

⋅

[

p

1

p

2

p

3

]

=

[

∑

i

=1

n

y

1

∑

i

=1

n

x

i

y

i

∑

i

=1

n

1

x

i

y

i

]

X

⋅P=Y⇒ P=X

−1

⋅Y

13.Aproksymacja Funkcji dwóch zmiennych -

Dany jest zbiór punktów

x

1,

y

1,

z

1

 ,x

2,

y

2,

z

2

, ... ,x

n

, y

n

, z

n



Aproksymacją tego zbioru punktów ma być funkcja liniowa, np.:

z=Fx , y , p

1,

p

2,

p

3

=p

1

p

2

x

p

3

y

S

 p

1,

p

2,

p

3

=

∑

i

=1

n

 p

1

p

2

x

i

p

3

y

i

−z

i



2

=min

∂S

∂ p

1

=2

∑

i

=1

n

p

1

p

2

x

i

p

3

y

i

−z

i

=0

∂S

∂ p

1

=2

∑

i

=1

n

p

1

p

2

x

i

p

3

y

i

−z

i

 x

i

=0

∂S

∂ p

1

=2

∑

i

=1

n

p

1

p

2

x

i

p

3

y

i

−z

i

 y

i

=0

[

n

∑

i

=1

n

x

i

∑

i

=1

n

y

i

∑

i

=1

n

x

i

∑

i

=1

n

x

i

2

∑

i

=1

n

x

i

y

i

∑

i

=1

n

y

i

∑

i

=1

n

x

i

y

i

∑

i

=1

n

y

i

2

]

⋅

[

p

1

p

2

p

3

]

=

[

∑

i

=1

n

z

i

∑

i

=1

n

z

i

x

i

∑

i

=1

n

z

i

y

i

]

P

=X

−1

⋅Y

14.Interpolacja – Jej zadaniem jest wyznaczenie przybliżonych wartości funkcji w punktach nie będących węzłami oraz

oszacowanie błędu tych przybliżonych wartości.
Dana jest funkcja

y

=f x , x ∈[x

0

, x

n

]

dla której znamy tablicę jej wartości.

f

 x

0

=y

0

, f

x

1

=y

1

, ..., f

 x

n

=y

n

oraz n+1 węzłów interpolacji:

x

0

, y

0

 ,x

1

, y

1

, ..., x

i

, y

i

, x

n

, y

n



Należy wyznaczyć funkcję W(x) tak aby:

W

 x

0

=y

0

, W

x

1

=y

1

, ..., W

 x

n

=y

n

15.Węzeł interpolacji – Jest to jeden z punktów na bazie których została wyznaczona funkcja interpolująca i którego

wartość musi być dokładnie osiągnięta przez funkcję interpolującą.

16.Funkcja interpolująca – jest to taka funkcja, która w węzłach interpolacji przyjmuje takie same wartości co funkcja

y=f(x)

17.Wielomian uogólniony – Metoda doboru funkcji W(x) w postaci kombinacji liniowej n+1 funkcji bazowych



0

x ,

1

x ,... , 

n

x 

W

 x=

∑

i

=0

n

a

i



i

x = x⋅A

X

=

[



0

 x

0

 

1

 x

0

 ...... 

n

x

0





0

 x

1

 

1

 x

1

 ...... 

n

x

1



......

......

......

......



0

x

n

 

1

x

n

 ...... 

n

 x

n



]

Y

=

[

y

0

y

1

...

y

n

]

I jeżeli macierz X nie jest osobliwa

A

=X

−1

⋅Y

Więc

W

 x=x ⋅X

−1

⋅Y

18.Macierz bazowa -

=[

0

x ,

1

x ,... , 

n

x ]

19.Wektor współczynników -

A

T

=[a

0

, a

1

, ... ,a

n

]

20.Interpolacja wielomianowa (wielomian w postaci naturalnej) – Funkcję bazową przyjmuje się w postaci

jednomianów:



0

x=1, 

1

 x=x , 

2

 x=x

2

, ...,



n

 x=x

n

Warunkiem jest:

{

a

0

a

1

x

0

...a

n

x

0

n

=y

0

a

0

a

1

x

1

...a

n

x

1

n

=y

1

.....................................

a

0

a

1

x

n

...a

n

x

n

n

=y

n

Ponadto kolejne wartości

x

0

, x

1

,... , x

n

muszą się różnić między sobą oraz wyznacznik główny układu musi być różny

od 0

∣X∣=detX=

[

1

x

0

....

x

0

n

1

x

1

....

x

1

n

.... ....

.... ....

1

x

n

....

x

n

n

]

=

∏

i

 j

x

i

−x

j

≠0

Przykład
Wyznaczyć wielomian w postaci naturalnej dla węzłów:

0,6,1,4, 2,12

Więęęęc:

x

=

[

0
1
2

]

y

=

[

6
4

12

]

X

=

[

x

0

0

x

0

1

x

0

2

x

1

0

x

1

1

x

1

2

x

2

0

x

2

1

x

2

2

]

=

[

1

0

0

1

1

1

1

2

4

]

Zaś z ciekawości:

A

=X

−1

⋅Y=

[

6

−7

5

]

W

s =a

0

a

1

s

a

2

s

2

=6−7s5s

2

21.Macierz Lagrange'a – Macierz

X

−1

dla bazy wielomianowej.

22.Interpolacja Lagrange'a -

Funkcja bazowa:

{



0

x = x−x

1

 x−x

2

x−x

3

... x−x

n





1

x = x−x

0

 x−x

2

x−x

3

... x−x

n



.....................................



i

x=x−x

0

 ...x−x

i

−1

 x−x

i

1

 ...x

i

−x

n



.....................................



n

x = x−x

0

x−x

1

x−x

2

... x−x

n

−1



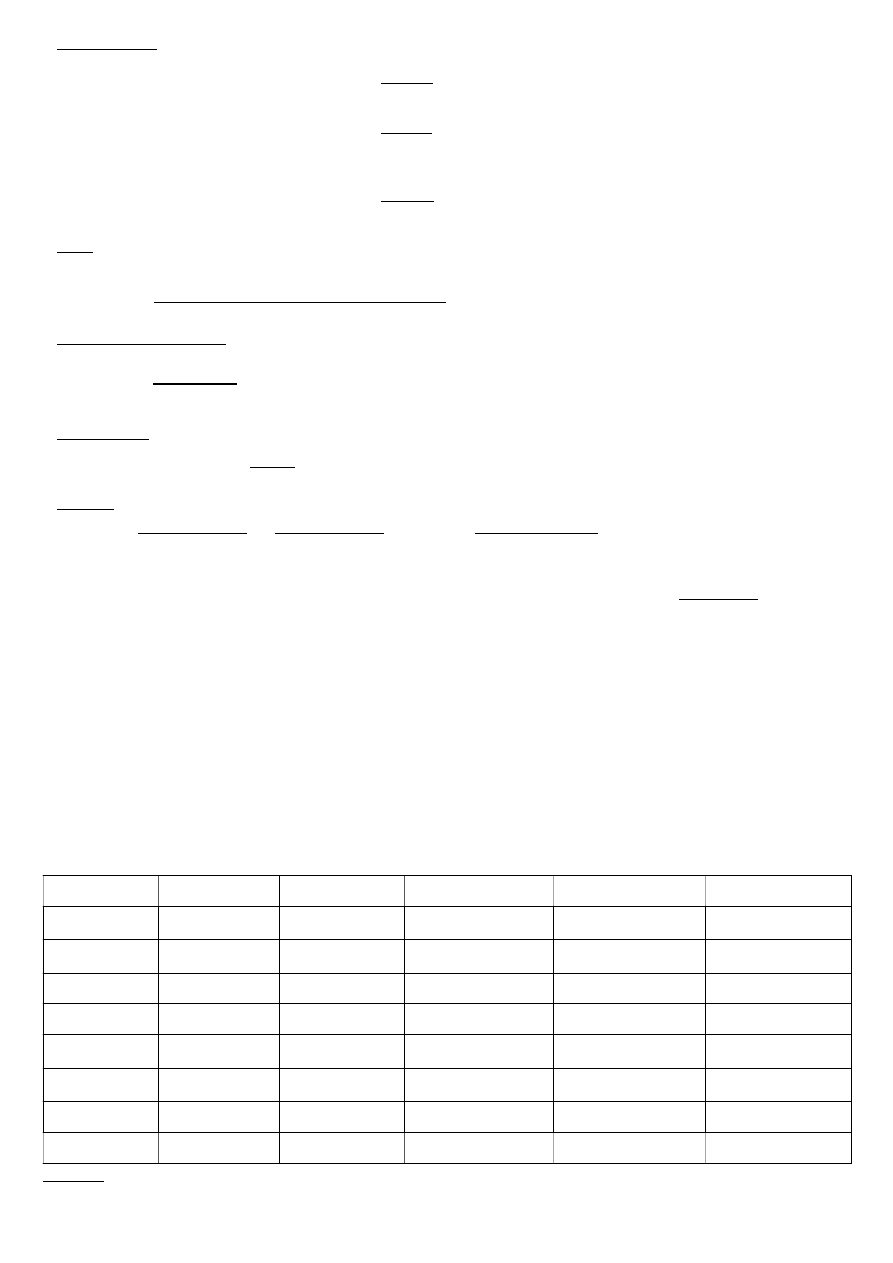
Współczynniki:

X

=

[



0

x

0



0

......

0

0



1

 x

1

 ......

0

......

......

......

......

0

0

......



n

x

n



]

,

{

a

0

=

y

0



0

x

0



a

1

=

y

1



1

x

1



...

a

n

=

y

n



n

 x

n



Toteż

W

 x=a

0



0

x a

1



1

 x...a

n



n

 x

W

 x=

∑

i

=0

n

y

i

x−x

0

 ...x−x

i

−1

 x−x

i

1

 ...x−x

n



x

i

−x

0

 ...x

i

−x

i

−1

 x

i

−x

i

1

...x

i

−x

n



Lub można się wycwanić:

W

 x=

∑

i

=0

n

∏

j

≠i

x−x

j



∏

j

≠i

 x

i

−x

j



, j

=0,1 ,... , n

Dla mathcada:

W

s =

∑

i

=0

n

−1

∏

j

=0

n

−1

if

 j=i,1 ,

s

−x

j

x

i

−x

j



Przykład Zinterpoluj wielomian Lagrange'a dla węzłów

0,4,1,2, 2.5 ,2.75

W

s =4

s−1s−2.5

0−10−2.5

2

s−0s−2.5

1−01−2.5



2.75

s−0s−1

 2.5−02.5−1

W

s =s

2

−3s4

23.Symbol Newtona – Funkcja dwóch argumentów całkowitych nieujemnych o postaci



n
k



=

n !

k !

 n−k !

czytana

jako n po k

24.Różnice skończone– Dla funkcji stabelaryzowanych przy stałym kroku

h

=x

i

1

−x

i

wprowadza się pojęcie różnicy

skończonej rzędu k

 y

i

=y

i

1

−y

i



2

y

i

=[ y

i

]= y

i

1

− y

i

=y

i

2

−2y

i

1

y

i

.....................



k

y

i

=[

k

−1

y

i

]=

k

−1

y

i

1

−

k

−1

y

i

=

=

∑

j

=0

k

−1

j



k

j



y

i

 k− j

Na podstawie wzoru wartości funkcji

y

i

=f x

i



x

i

1

−x

i

=h=const

budujemy tablicę różnic skończonych o

strukturze podobnej do trójkąta Pascala

nr

x

y

 y



2

y



3

y

0

x

0

y

0

 y

0



2

y

0



3

y

0

1

x

1

y

1

 y

1



2

y

1

...

2

x

2

y

2

 y

2

...

...

3

x

3

y

3

...

...

...

...

...

...

...

...



3

y

n

−3

...

...

...

...



2

y

n

−2

...

...

...

 y

n

−1

n

x

n

y

n

Przykład:
Dla podanych więzów zbudować tablicę różnic skończonych

0.2 ,0.259 ,0.4 ,0 .364,0.6 ,0 .448,0.8 ,0 .517,

1,0.577 ,1.2,0 .631

nr

x

y

 y



2

y



3

y



4

y



5

y

0

0.2

0.259

0.105

-0.021

0.006

0

-0.003

1

0.4

0.364

0.084

-0.015

0.006

-0.003

2

0.6

0.448

0.069

-0.009

0.003

3

0.8

0.517

0.06

-0.006

4

1

0.577

0.054

5

1.2

0.631

25.Własności różnic skończonych -

y

=C ⇒ y=0

y

=C⋅f x ⇒C⋅ f x

y

∑

k

f

k

x ⇒ y=C  f

k

 x

y

=x

n

⇒  y=xh

n

−x

n

=nhx

n

−1

...h

n

y

=a

0

a

1

x

...a

n

x

n

⇒  y=b

0

b

1

x

...b

n

−1

x

n

−1

Jeżeli wielomian jest stopnia n, to różnica skończona rzędu n ten funkcji jest stała, a kolejne zerami. Prawdziwe jest
również twierdzenie odwrotne.

26.Interpolacja argumentów równoodległych w przód– Dla zbioru n+1 więzów

x

0

, x

1

=x

0

h , x

2

=x

0

2h ,... , x

n

=x

0

nh

oraz wartości funkcji

f

 x

0

=y

0

, f

x

1

=y

1

, ..., f

 x

n

=y

n

Mamy Wielomian interopolacyjny :

W

 x=a

0

a

1

q

x a

2

q

x q x−1

a

3

q

 xq x −1 q x−2...

a

n

q

x q x−1q  x−2 ...q x −n1

q

 x=

x

−x

0

h

Przy czym:

q

x

0

=0

q

 x

1

=1

...

q

 x

n

=n

Funkcje bazowe:



0

x =1



1

 x=q  x



2

 x=q  xq  x−1



3

 x=q  xq  x−1q  x−2

......



n

 x=q  xq  x−1q x −2... q x −n1

Układ równań do wyznaczenia współczynników:

X

⋅A=Y

X

=

[

1

0

0

0

...

0

1

1

0

0

...

0

1

2

2

0

...

0

1

3

6

6

...

0

...

...

...

...

...

...

1

n

n

n−1 n  n−1 n−2 ... n !

]

A

=

[

a

0

a

1

...
a

n

]

Y

=

[

y

0

y

1

...

y

n

]

A

=X

−1

⋅Y

a

0

=y

0

a

1

= y

0

⇔

y

1

=a

0

a

1

a

2

=



2

y

0

2!

⇔ y

2

=a

0

2a

1

2a

2

a

3

=



3

y

0

3!

⇔ y

3

=a

0

3a

1

6a

2

6a

3

....

a

n

=



n

y

0

n !

⇔ y

n

=a

0

na

1

n n−1 a

2

...n ! a

n

27.Pierwszy wzór interpolacyjny Newtona – interpolacja wprzód

W

 x=y

0

q  y

0



q

 q−1

2 !



2

y

0

...



q

 q−1 q−2... q−n1

n !



n

y

0

W

 x=

∑

i

=0

n

a

i

⋅

i

x=

∑

i

=0

n



i

y

0

i !

⋅

∏

j

=0

i

if

 j=0,1, q− j1

Przykład1: Znajdź wielomian interpolacyjny z dokładnością



3

dla

x

0

=0.4

i wylicz jego wartość w punkcie

x

=0.5

q

=

x

−x

0

h

=

x

−0.4

0.2

=5x−2

W

 x=y

0

q  y

0

q  q−1



2

y

0

2!



q q−1q−2



3

y

0

3!

W

 x=0.125 x

3

−0.0375 x

2

0.9175x0.038

W

 0.5=0.418625

28.Interpolacja argumentów równoodległych w tył - Dla zbioru n+1 więzów

x

0

, x

1

=x

0

−h , x

2

=x

0

−2h ,... , x

n

=x

0

−nh

oraz wartości funkcji

f

x

0

=y

0

, f

x

1

=y

1

,... , f

x

n

=y

n

Mamy Wielomian interopolacyjny :

W

 x=a

0

a

1

q

 xa

2

q

 xq  x1

a

3

q

 xq  x1q x 2...

a

n

q

x q x 1 q x2...q xn−1

q

 x=

x

−x

n

h

q

 x

0

=−n

q

x

1

=−n1

q

 x

2

=−n2

...

q

 x

n

=0

Funkcje bazowe -



0

x =1



1

 x=q  x



2

 x=q  xq  x1



3

 x=q  xq  x1q  x2

......



n

 x=q  xq  x1q x 2... q x n−1

Układ równań do wyznaczenia współczynników:

X

=

[

1

−n −n 1−n  −n 1−n 2−n  ... n !⋅−1

n

...

...

...

...

...

...

1

−3

6

−6

...

0

1

−2

2

0

...

0

1

−1

0

0

...

0

1

0

0

0

...

0

]

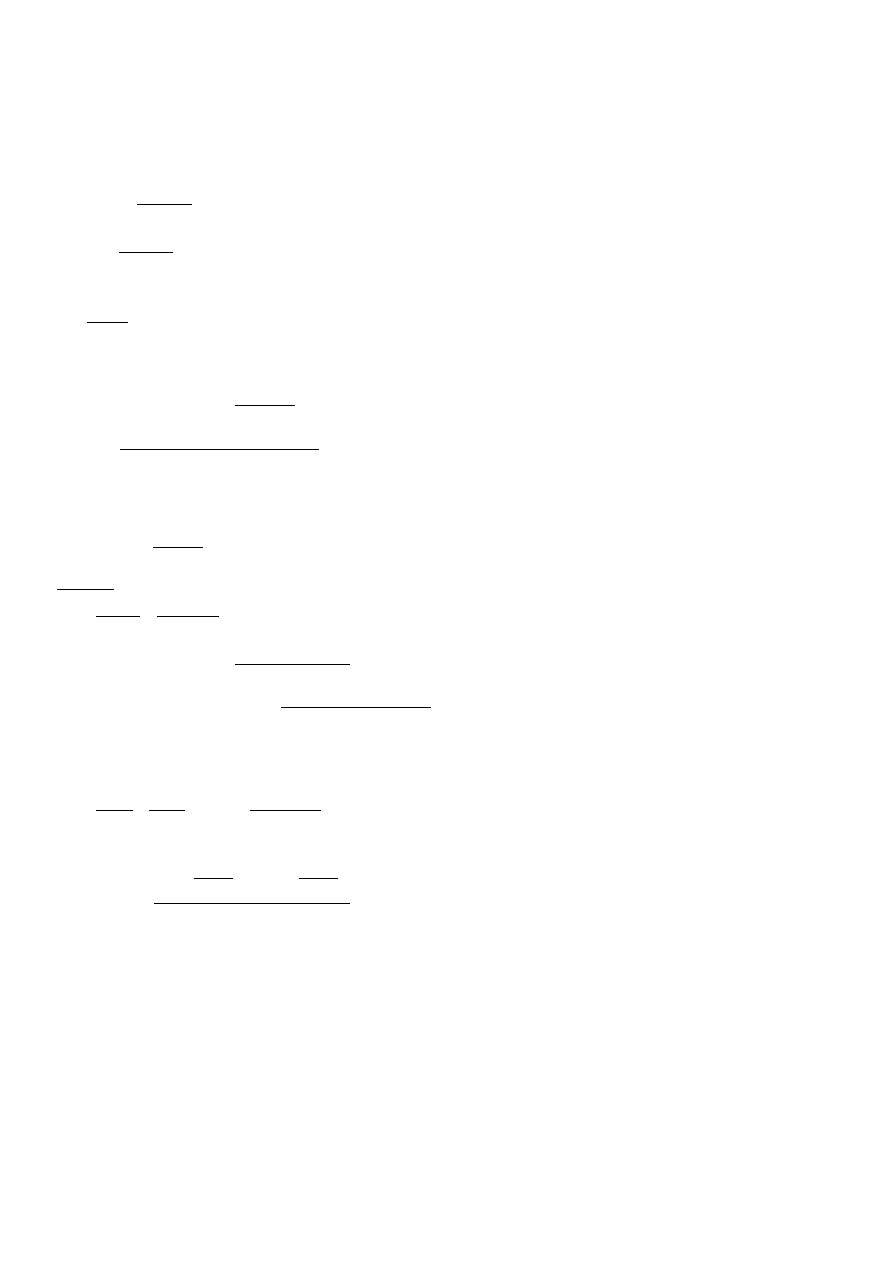
A

=

[

a

0

a

1

...
a

n

]

Y

=

[

y

0

y

1

...

y

n

]

A

=X

−1

⋅Y

a

0

=y

n

a

1

= y

n

−1

⇔ y

n

−1

=a

0

a

1

a

2

=



2

y

n

−2

2 !

⇔ y

n

−2

=a

0

2a

1

2a

2

a

3

=



3

y

n

−3

3!

⇔ y

n

−3

=a

0

3a

1

6a

2

6a

3

....

a

n

=



n

y

0

n !

⇔ y

0

=a

0

na

1

n  n−1 a

2

...n ! a

n

29.Drugi wzór interpolacyjny Newtona – interpolacja wstecz

W

 x=y

n

q  y

n

−1



q

 q1

2 !



2

y

n

−2

...



q

q 1q 2... qn−1

n !



n

y

0

W

x=

∑

i

=0

n

a

i

⋅

i

x

W

 x=

∑

i

=0

n



i

y

n

−i

i !

⋅

∏

j

=0

i

if

 j=0,1 , q j−1

Przykład: Oblicz wartość w punkcie pośrednim tabeli dla

x

=1.1 , x

n

=1.2

q

=

x

−x

n

h

=

1.1

−1.2

0.2

=−0.5

W

 x=y

n

q  y

n

−1



q

q1

2

y

n

−2

2 !

W

1.1=0.631−0.5⋅0.054

−0.5⋅0.5⋅−0.006

2

W

1.1=0.60475

30.Interpolacja Czebyszewa -

Współrzędną

x

∈< a , b >

normalizujemy do

c

∈<−1,1 >

za pomocą wzoru:

x

=

a

b

2



b

−a

2

⋅c ⇒ c=

2x

−a−b

b

−a

Analogicznie postępujemy ze współrzędną y normalizując ją do h .
Następnie tworzymy bazę Czebyszewa z zależności:

T

0

c=1, T

1

c=c , T

j

c=2c⋅T

j

−2

 c−T

j

−1

c

lub:

T

j

c =

c



c

2

−1

j

c−



c

2

−1

j

2

albo jeszcze fajniej:

T

j

c =cos  j⋅arccosc 

Na podstawie tego tworzymy układ równań o postaci T*A=H

[

T

0

c

0

 T

1

 c

0

 .... T

n

c

0



T

0

c

1

 T

1

c

1

 .... T

n

c

1



....

....

....

....

T

0

c

n

 T

1

c

n

 .... T

n

c

n



]

⋅

[

A

0

A

1

....
A

n

]

=

[

h

0

h

1

....

h

n

]

Znormalizowany wielomian interpolujący przybierze postać:

W

 c=

∑

j

=0

n

A

j

⋅T

j

c 

Aby otrzymać rzeczywistą funkcję należy przebudować wielomian W(c) do postaci W(x).

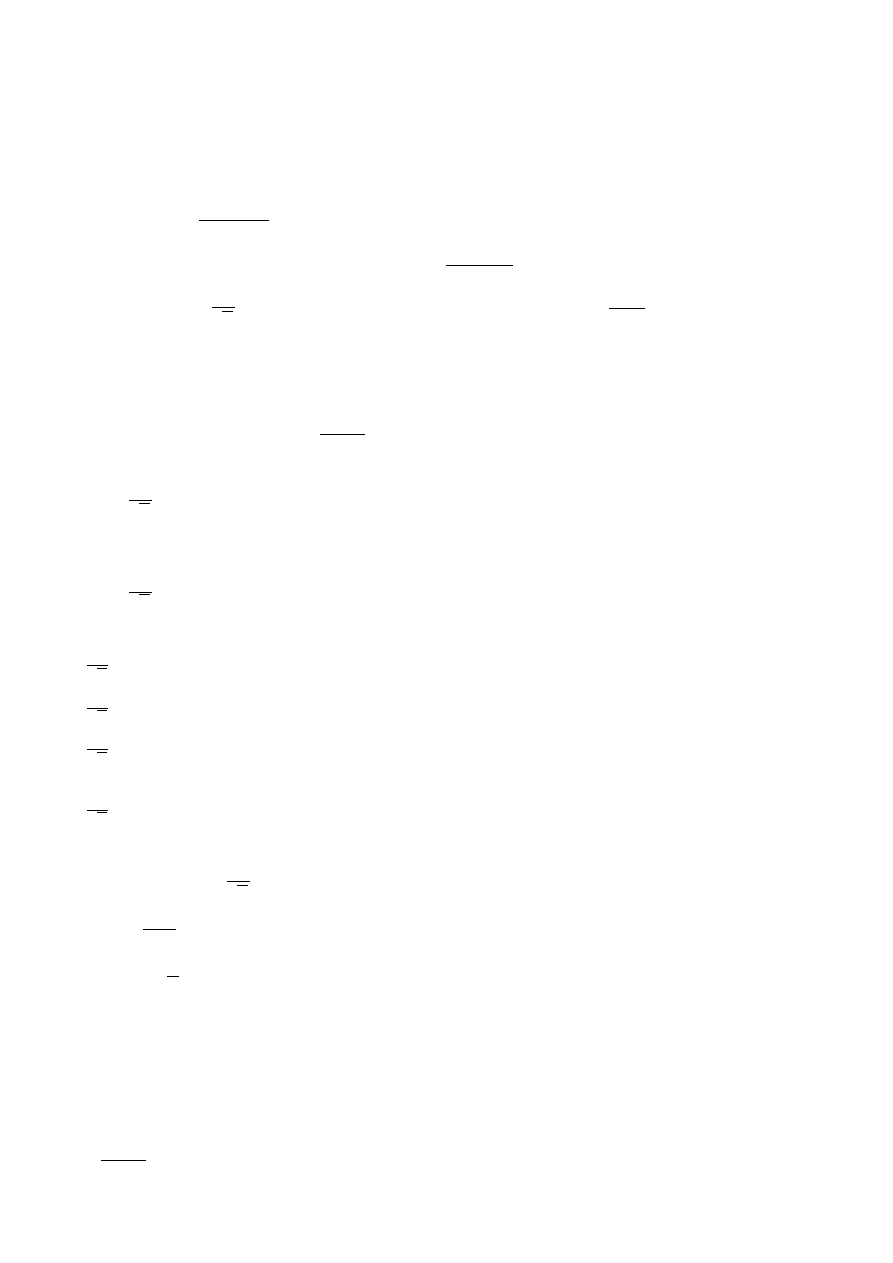
W tym celu modyfikujemy układ równań

[

T

0

c

0

 T

1

 c

0

 .... T

n

c

0



T

0

c

1

 T

1

c

1

 .... T

n

c

1



....

....

....

....

T

0

c

n

 T

1

c

n

 .... T

n

c

n



]

⋅

[

B

0

B

1

....
B

n

]

=

[

y

0

y

1

....

y

n

]

Zaś zaś za c podstawiamy wartość wyrażoną w x
Ostatecznie:

W

 x=

∑

j

=0

n

B

i

⋅T

j



2x

−a−b

b

−a



Ponadto poprzez przyjęcie węzłów z zależności:

x

j

=cos

2j1

2n

2

, j

=0,1 ,... , n

oraz modyfikację pierwszego

punktu bazy

T

0

c=

1



2

upraszcza się wyznaczanie macierzy A i B.

A

B=

2

n

1

T

T

⋅H  Y 

Własność tą wykorzystujemy wpierw określając znormalizowane punkty, następnie przeliczając je na odpowiadające
im współrzędne w przyjętym przedziale, by ostatecznie zmierzyć w nich wartości funkcji.

31.Interpolacja trygonometryczna – Rozważmy funkcję o okresie

2



dla której znamy wartości w

2n

1

węzłach

x

j

∈< 0,2  >

Węzły te określamy z zależności:

x

j

=

2j



2n

1

, j

=0,1 ,... ,2 n

Rozpatrywana funkcja przybierze taką postać:

W

 x=

A

0



2

A

1

sin1x

A

2

cos1x

...

A

2n

−1

sin

 nxA

2n

cos

nx 

lub krócej:

W

 x=

A

0



2



∑

j

=1

n

A

2j

⋅cos j⋅x

∑

j

=1

n

A

2j

−1

⋅sin j⋅x

Współczynniki A wyznaczymy z układu: T*A=Y, gdzie:

T

=

[

1



2

0

1

...

0

1

1



2

sin x

1

cos x

1

...

sin

 n⋅x

1



cos

 n⋅x

1



1



2

sin x

2

cos x

2

...

sin

 n⋅x

2



cos

 n⋅x

2



...

...

...

...

...

...

1



2

sin x

2n

cos x

2n

... sin

n⋅x

2n

 cos n⋅x

2n



]

Lub prościej z trzech równań:

T

0

x =

1



2

T

j

 x=sin



j

1

2

⋅x



dla j

=1,3, ...,2 n−1

T

j

x =cos



j

2

⋅x



dla j

=2,4 , ...,2 n

A

=

[

A

0

A

1

...

A

2n

]

Y

=

[

y

0

y

1

...

y

2n

]

Przy czym należy pamiętać, że również:

A

=

2

2n

1

T

T

⋅Y

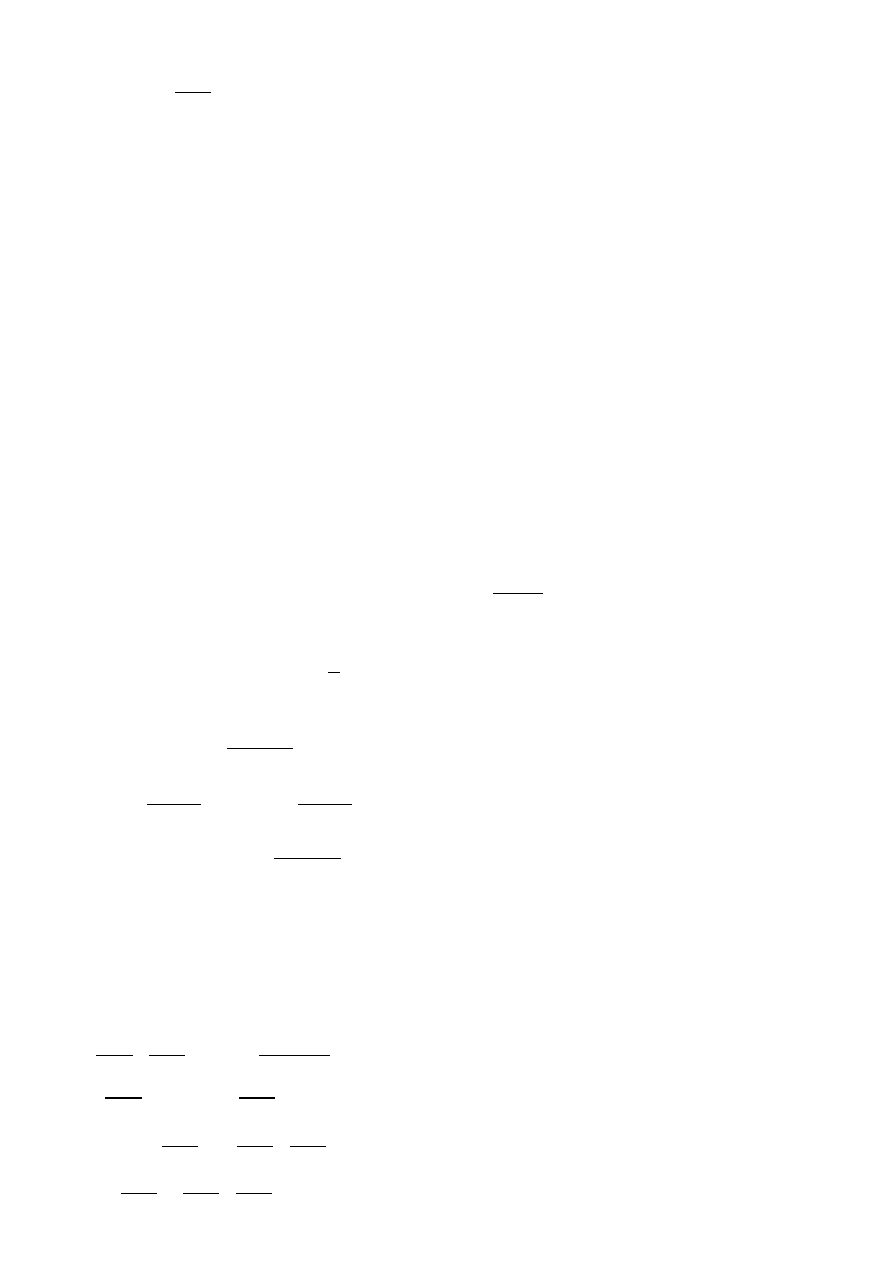
32.Kwadratury interpolacyjne – Mamy funkcję f(x) ciągłą i ograniczoną w przedziale <a,b>. Przedział ten dzielimy na

skończoną liczbę pod-przedziałów, wyróżniając na osi x zbiór punktów o stałym kroku

h

=x

i

1

−x

i

=

b

−a

n

=const

który przybierze postać siatki:

a

=x

0

x

1

x

2

...x

i

x

i

1

...x

n

=b

i=0,1,...,n

Wynika z tego, że:

∫

x

0

=a

x

n

=b

f

x dx=

∑

i

=0

n

−1

∫

x

i

x

i

 1

f

x dx=

∑

i

=0

n

−1



i

Zaś po przybliżeniu wielomianem interpolacyjnym W(x) (np. Newtona 1)



i

=

∫

x

i

x

i

1

f

x dx≈

∫

x

i

x

i

1

W

 x dx

33.Całkowanie metodą prostokątów – Bardzo przyjemne i relaksujące dopóki nie trzeba go robić ręcznie. Przyjmijmy, że

n o wartościach poniżej 1000 dla nas nie istnieje.

W

 x=y

i

, x

∈< x

i

, x

i

1

>



i

=

∫

x

i

x

i

1

y

i

dx

=h

∫

0

1

y

i

dq

=h⋅y

i

Z 'niedomiarem'

∫

a

b

f

 x dx=h

∑

i

=0

n

−1

y

i

=w

Z 'nadmiarem'

∫

a

b

f

 x dx=h

∑

i

=1

n

y

i

=W

Punkty przygotowujemy tak:

x

i

=ah⋅i

y

i

=f x

i



Interesujące wyniki można uzyskać poprzez wyliczenie średniej

W

w

2

Bardzo interesujące.

34.Całkowanie metodą trapezów -

W

 x=y

i

q⋅ y

i

, x

∈< x

i

, x

i

1

>



i

=

∫

x

i

x

i

1

W

x dx=

∫

x

i

x

i

1

y

i

q⋅ y

i

dx

=

1

2

h

y

i

y

i

1



Z 'niedomiarem'

∫

a

b

f

x dx=h

∑

i

=0

n

−1

y

i

y

i

1

2

=

=h

[

∑

i

=1

n

−1

y

i



y

0

y

n

2

]

=h

[

∑

i

=0

n

y

i

−

y

0

y

n

2

]

Z 'nadmiarem'

∫

a

b

f

 x dx=h

∑

i

=1

n

y

i

y

i

−1

2

Tym razem wyliczanie średniej nie da już tak spektakularnych efektów, nie mamy nawet pewności czy rzeczywiście
jedna z funkcji będzie miała wartość mniejszą od rzeczywistej, a druga większą. Nie róbmy więc tego. Liczymy
pierwszym wzorkiem.

35.Kwadratury Gaussa – mamy funkcję f(x) rozpatrywaną i ciągłą w przedziale <a,b>.

Postać całki tej funkcji po danym obszarze normalizujemy

∫

a

b

f

 x dx ⇒

∫

−1

1

F

d 

,gdzie:

x

=

a

b

2



b

−a

2

 ⇒ =

2x

−a −b

b

−a

dx

=

b

−a

2

d

 ⇒ d =

2dx

b

−a

∫

−1

1

F

d =

b

−a

2

∫

−1

1

f



a

b

2



b

−a

2





d



F

=

b

−a

2

⋅f



a

b

2



b

−a

2





Następnie tą znormalizowaną postać przybliżamy wielomianem:

F

=a

0

a

1

a

2



2

...a

2n

−1



2n

−1

∫

−1

1

F

d ≈

∑

i

=1

n

F



i

 w

i

,gdzie:

∈<−1,1 >

odcięte punktów Gaussa

w

i

współczynniki wagowe

n

ilość punktów Gaussa

n



i

w

i

2

-0.57735

0.57735

1
1

3

-0.7746

0

0.7746

0.(5)
0.(8)
0.(5)

36. Całka podwójna po trójkącie (Kubatury Gaussa) – Dana jest funkcja dwóch zmiennych f(x,y) ciągła i ograniczona w

obszarze trójkątnym D wyznaczonym przez nieleżące na jednej prostej wierzchołki trójkąta D:

x

1,

y

1

 ; x

2,

y

2

; x

3,

y

3



Celem jest policzenie wyrażenia

∬

D

f

x , y dxdy

Normalizujemy w tym celu całkę sprowadzając trójkąt D do trójkąta jednostkowego prostokątnego o wierzchołkach

x

1,

y

1

0,0

x

2,

y

2

1,0

x

3,

y

3

0,1

przez podstawienie

x

=x

1

x

2

−x

1

⋅x

3

−x

1

⋅

y

=y

1

 y

2

−y

1

⋅ y

3

−y

1

⋅

Wraz ze zmianą okładu współrzędnych należy funkcję podcałkową wymnożyć przez jakobian przekształcenia

J

=

∣

dx

d



dx

d



dy

d



dy

d



∣

=

∣

x

2

−x

1

x

3

−x

1

y

2

−y

1

y

3

−y

1

∣

∣J∣=2⋅∣D∣

gdzie:

|D| - pole wyjściowego trójkąta D
Postać funkcji podcałkowej

F

,=∣J∣⋅f [ x

1

 x

2

−x

1

x

3

−x

1

 ,

y

1

 y

2

−y

1

  y

3

−y

1

 ]

Postać końcowa

∫

0

1



∫

0

1

−

F

, d ≈

1
2

∑

i

=1

n

F



i

,



i

 w

i



i

,



i

- współrzędne punktów Gaussa

w

i

- wagi punktów Gaussa

n

- liczba punktów Gaussa

Wartości te odczytujemy z tablic:

n



i



i

w

i

1 - liniowa

1/3

1/3

1

3 - kwadratowa

0.5

0

0.5

0.5
0.5

0

1/3
1/3
1/3

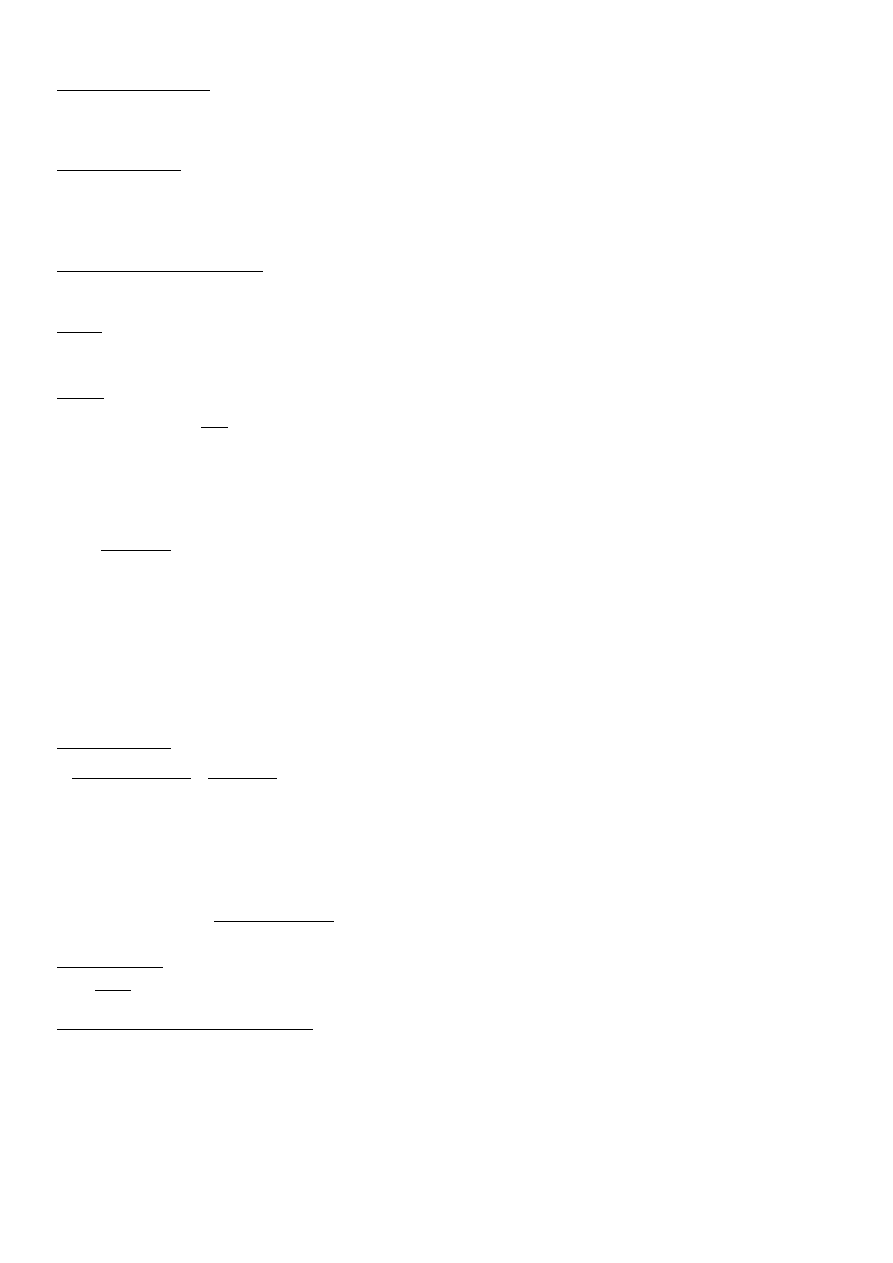
37.Przybliżone metody rozwiązywania równań – Polegają na tworzeniu wzorów rekurencyjnych określających sposób

wyznaczenia kolejnych wyrazów ciągu liczbowego, którego granicą jest szukane rozwiązanie równania F(x)=0.
Podstawowe problemy:
~Lokalizacja pierwiastka (dobór punktu startowego)
~Obliczanie przybliżeń pierwiastków
~Zbieżność procesu iteracyjnego
Popularne metody:
~Bisekcji
~Cięciw
~Stycznych

38.Twierdzenia o lokalizacji pierwiastków:

Pierwsze - Bolzano-Cauchy'ego – Jeżeli funkcja F(x) jest ciągła w przedziale <a,b> i na jego końcach przyjmuje wartości
różnych znaków tzn.

F

a⋅F b0

, to między punktami a i b znajduje się co najmniej jeden pierwiastek równania

F(x)=0.
Drugie – Jeżeli w przedziale <a,b> spełnione są założenia twierdzenia Bolzano-Cauchy'ego i dodatkowo pierwsza
pochodna F(x) jest stałego znaku w tym przedziale (funkcja stale rosnąca lub malejąca) to przedział ten jest
przedziałem izolacji pierwiastków równania F(x)=0, co znaczy, że w tym przedziale jest tylko jeden pierwiastek.

Trzecie – Jeżeli

F

x=a

n

x

n

a

n

−1

x

n

−1

...a

1

x

a

0

, a

n

≠0

to pierwiastki równania F(x)=0 są zawarte w

przedziale

∣x∣1

M

∣a

n

∣

, gdzie

M

=max {∣a

0

∣, ∣a

1

∣,... , ∣a

n

−1

∣}

39.Metoda bisekcji – Niech <a,b> będzie przedziałem izolacji pierwiastków równania F(x)=0. Jako dwa pierwsze wyrazy

ciągu przybliżeń przyjmujemy:

x

1

=a ,

x

2

=b

Kolejne przybliżenia przyjmujemy według wzoru:

x

i

=

x

i

−1

x

k

2

, k

∈< 1,i−2, i2

∣x

i

−x

i

−1

∣≈∣x

i

−x

k

∣, Fx

i

−1

⋅F x

k

0

Metoda jest zbieżna, gdyż przybliżenia znajdują się każdorazowo w przedziałach izolacji.

∣x

i

1

−x

i

∣∣x

i

−x

i

−1

∣

Zaletą jest prostota, wadą wolna zbieżność procesu iteracyjnego.

40.Metoda cięciw – Jeżeli funkcja F(x) jest funkcją klasy

C

2

w przedziale izolacji pierwiastka, to rozwiązanie równania

F(x)=0 przybliżamy ciągiem miejsc zerowych cięciw poprowadzonych między punktami stanowiącymi końce kolejnych
przedziałów izolacji.
Równanie Cięciw

y

−F x

i

−1



F

 x

k

−F x

i

−1



=

x

−x

i

−1

x

k

−x

i

−1

, gdzie

x

k

jest drugim krańcem przedziału izolacji

x

i

−1

, x

k



Pierwszą cięciwę prowadzimy między punktami:

a , F a,  b , F b

Dla

y

=0

x

i

=x

i

−1

−F x

i

−1

⋅

x

k

−x

i

−1

F

x

k

−Fx

i

−1



Punkt kontrolny

z

=

a

b

2

będziemy go używać do sprawdzani wartości

Określanie stałego punktu pęku cięciw

x

∈a , b, F ' x⋅F ' ' x0  x

k

=x

2

=b

x

∈a , b, F ' x⋅F ' 'x 0 x

k

=x

1

=a

Metoda ta jest zawsze zbieżna i to szybciej niż bisekcji.

41.Metoda stycznych Newtona – Przybliżamy F(x)=0 w przedziale izolacji <a,b> wyrazami ciągu utworzonego przez

miejsca zerowe stycznych do funkcji F(x).

Równanie stycznej w punkcie o odcietej

x

i

−1

y

−f x

i

−1

=F 'x

i

−1

⋅ x−x

i

−1



Dla

y=0

x

i

=x

i

−1

−

F

x

i

−1



F '

x

i

−1



, i

1

Wybór pierwszego przybliżenia

x

1

x

∈a , b, F' x⋅F '' x0 x

1

=b

x

∈a , b, F 'x ⋅F ' 'x 0 x

1

=a

Jeżeli druga pochodna nie ma stałego znaku to proces iteracyjny może być rozbieżny.

42.Równania różniczkowe zwyczajne – przybliżone rozwiązywanie

Sposoby rozwiązywania
Szeregi -
~współczynników nieoznaczonych
~kolejnego różniczkowania (metoda jednego punktu)
~kolejnych przybliżeń Picarda
Dyskretne – Rozpatrujemy równanie różniczkowe rzędu pierwszego wraz z warunkiem początkowym

y '

=F x , y , y x

0

=y

0

Zakładamy, że F(x,y) jest ciągła oraz ograniczona w pewnym obszarze płaskim



, w

którym spełnia warunek Cauchy'ego-Lipschitza względem y, tzn. istnieje taka liczba K, że dla wszystkich par punktów

P

1

 x , y

2

 , P

2

x , y

2

, P

1

, P

2

∈

spełniona jest nierówność

∣Fx , y

1

−F x , y

2

∣K y

1

−y

2



~łamanych Eulera
~ulepszenia metody Eulera
~wzory Rungego-Kutty
~metody wielokrokowe

43.Metoda łamanych Eulera – Polega na przybliżonym rozwiązaniu równania

y

x

i

1

=y

i

1

=y

i



∫

x

i

x

i

1

F

[x , y x]dx

Funkcję F(x,y) traktujemy na odcinku

[x

i

, x

i

1

]

jako stałą i równą wartości F w punkcie

x

i

, y

i



∫

x

i

x

i

1

F

[x , y x]dx=h

i

F

x

i

, y

i

, h

i

=x

i

1

−x

i

Ostatecznie otrzymujemy wzór rekurencyjny w postaci:

y

i

1

=y

i

h

i

F

 x

i

, y

i

, h

i

=x

i

1

−x

i

, i

=1,2, ... , n

Pochodna y' została zastąpiona ilorazem różnicowym.

y

i

1

−y

i

h

i

czyli krzywą całkową na odcinku

[x

i

, x

i

1

]

aproksymuje się odcinkiem stycznej do niej,

przechodzącej przez punkt

x

i

, y

i



zwykle przyjmujemy

h

i

=const=h

44.Pierwsze ulepszenie metody łamanych – Styczna do łuku

A

x

i

, y

i

 , Bx

i

1

, y

i

1



w punkcie o odciętej

x

*

= x

i

x

i

1

/2

jest równoległa do cięciwy AB.

Wzory:

x

*

=

1
2

x

i

x

i

1



y

*

=y

i

0.5⋅h⋅F x

i

, y

i



m

*

=F x

*

, y

*



y

i

1

=y

i

h⋅m

*

45.Drugie ulepszenie metody łamanych Eulera-Cauchy'ego – Współczynnik

kierunkowy siecznej AB jest średnią arytmetyczną współczynników
kierunkowych stycznych w punktach A i B.
Wzory:

x

*

=x

i

1

=x

i

h

y

*

=y

i

h⋅F x

i

, y

i



m

*

=F x

*

, y

*



y

i

1

=y

i

0.5⋅h [F x

i

, y

i

m

*

]