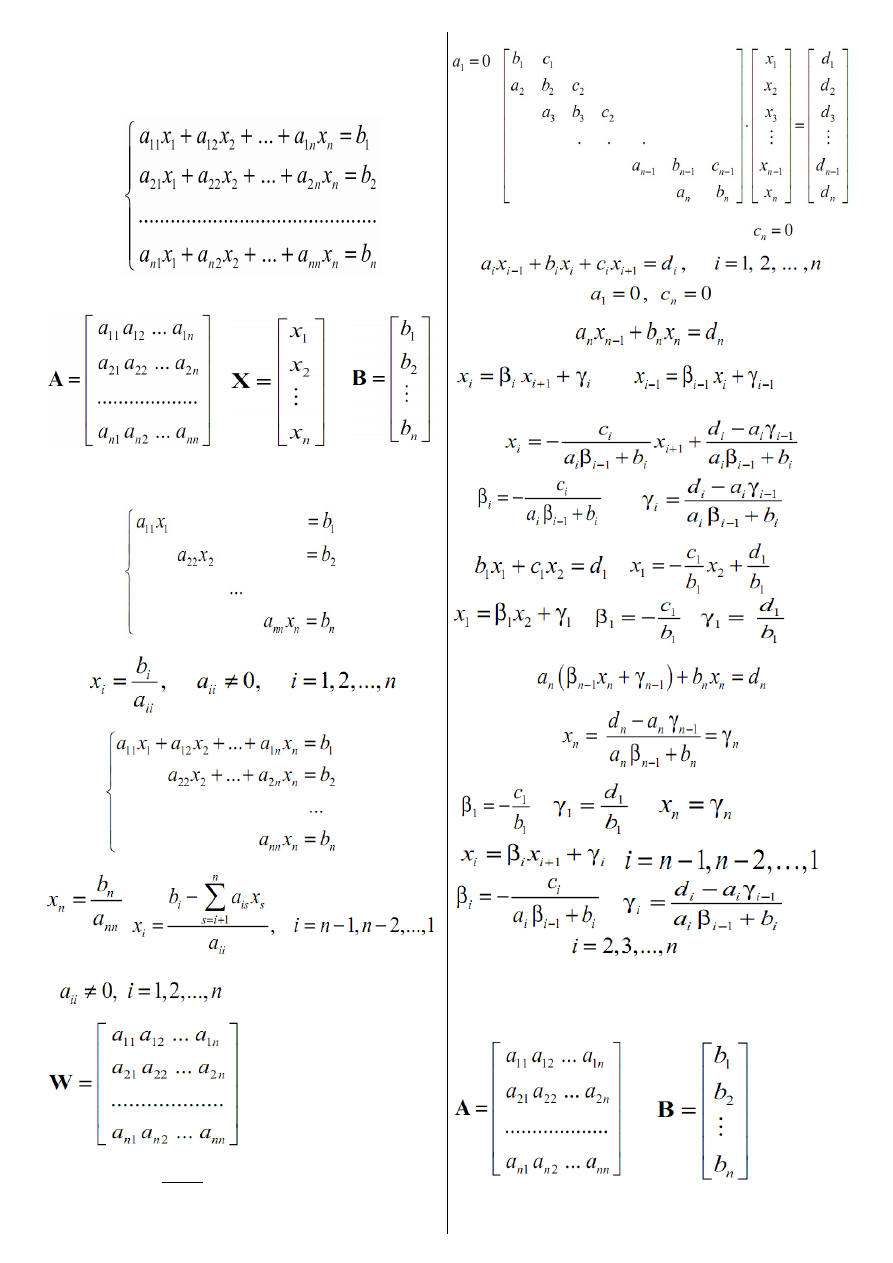
1. Metody numeryczne (analiza numeryczna) – Dział matematyki

stosowanej zajmujący się opracowaniem metod przybliżonego
rozwiązywania skomplikowanych zagadnień matematycznych, których
rozwiązanie byłoby nadzwyczaj żmudne lub niemożliwe choćby poprzez
konieczność wykonania nieskończenie wielu operacji.

2. Układ równań zawierający n niewiadomych

3. Macierzowa reprezentacja układu n niewiadomych

A⋅X=B→ X=A

−

1

⋅

B

, gdzie

Układ równań posiada jedno rozwiązanie tylko wtedy gdy jest oznaczony,
tzn. macierz główna układu równań A nie jest osobliwa.
4. Układ równań, w którym tylko główna przekątna macierzy A ma

elementy niezerowe

Algorytm:

5. Trójkątny układ równań

Algorytm:

Przy czym:

6. Metoda Cramera (Wyznacznikowa)

Algorytm:

xn=

[

Wn]

[

W ]

, |W| != 0

b podstawiamy w kolumnę odpowiednią liczonemu ixowi

7. Metoda Thomasa dla układów trójprzekątniowych:

Algorytm:

Stąd:

Zapisując inaczej:

Po podstawieniu:

Wyznaczamy wartości początkowe:

Łączymy drugi algorytm z czwartym

Stąd:

Ostatecznie: !!!!!!!!!

8. Metoda eliminacji Gaussa: Jest to metoda służąca jedynie do

upraszczania układów. Jej celem jest sprowadzenie n pierwszych
kolumn macierzy C do macierzy trójkątnej. Następnie pozostaje już tylko
rozwiązanie macierzy trójkątnej.
Mamy:

Następnie zapisujemy to w postaci macierzy C, w której macierz główną
uzupełnia się dodatkową kolumną zawierającą wektor wyrazów wolnych
B.

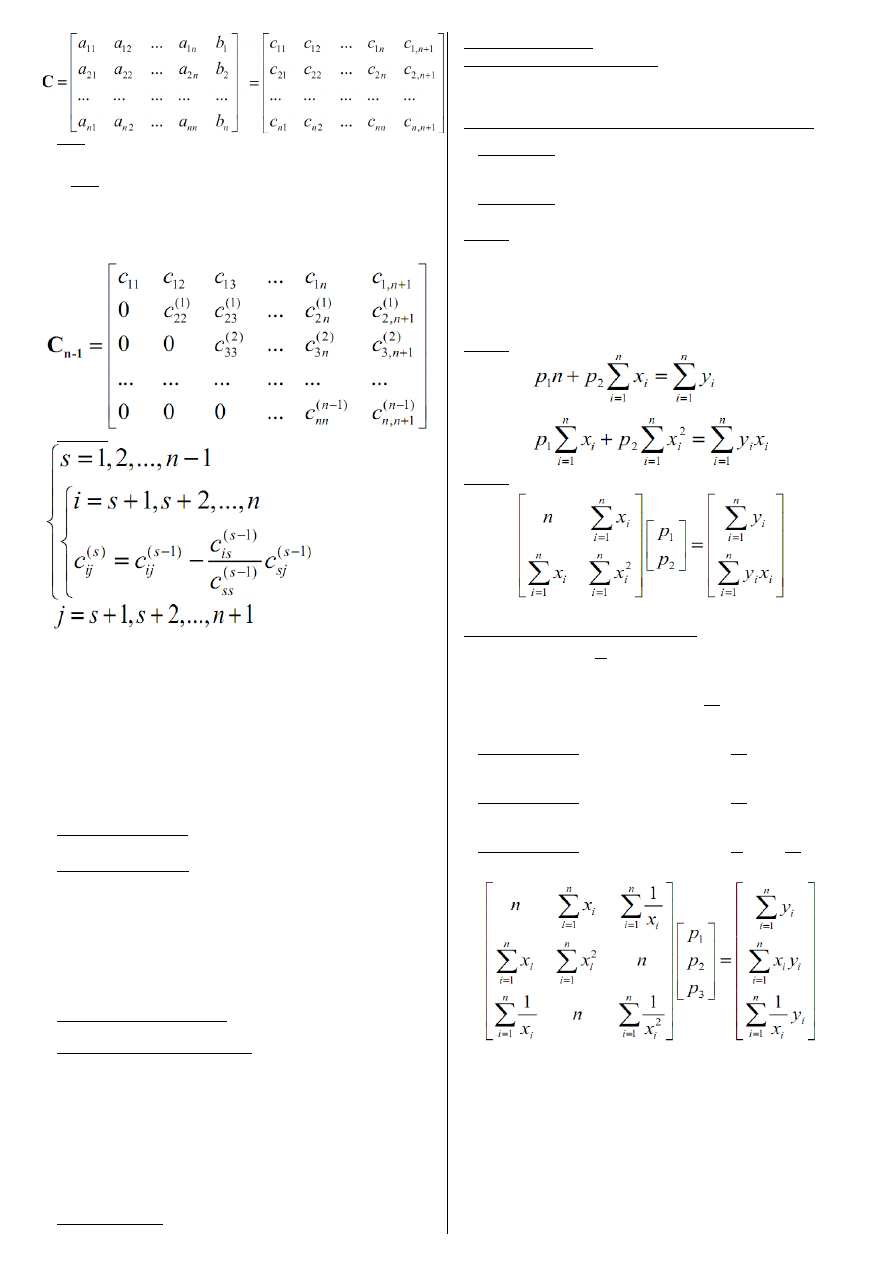
Kroki
Jeżeli

c11≠0

Odejmujemy pierwsze równanie pomnożone przez

ci1

c11

od każdego kolejnego i-tego równania, przy czym:

i=

2,3

,

...

,n

zaś obliczone współczynniki zapisujemy w miejscu

poprzednich. Następnie przeprowadzamy analogiczne operacje aż do
uzyskania macierzy trójkątnej. Po n-1 krokach mamy:

Algorytm:

9. Aproksymacja funkcji jednej zmiennej – Dana jest funkcja jednej

zmiennej

y=f x , x ∈[a , b]

Należy dobrać taką funkcję

F x , p

1

, ... , p

k



, x ∈[a , b]

aby możliwie jak najdokładniej

odtworzyć przebieg funkcji f(x), czyli zminimalizować różnice pomiędzy
odpowiednimi wartościami w punktach



x

i

, y

i



, i=1,2, ..., n

Gdzie:

p

1

, ..., p

k

To parametry wzoru empirycznego.

Aproksymacja polega na dobraniu parametrów

p

1

, ... , p

k

wzoru

empirycznego w taki sposób aby pełnione było kryterium minimalizacji
odchyłek.
Rodzaje aproksymacji:
Aproksymacja punktowa – funkcja f(x) jest zadana jako zbiór punktów

f x

1

=

y

1

, f  x

2

=

y

2,

... , f x

n

=

y

n

Aproksymacja integralna - unkcja f(x) jest zadana w formie wzoru
analitycznego

10.Odchyłka -



i

=

F x

i

, p

1

, ... , p

k

−

y

i

11.Kryteria minimalizacji odchyłek:

~wybranych punktów
~średnich
~sumowania bezwzględnych wartości
~najmniejszych kwadratów

12.Metoda najmniejszych kwadratów -

Dobór współczynników funkcji

F

∑

i=1

n



i

2

=

min

Kryterium najmniejszych kwadratów

∑

i=1

n

[

F x

i

, p

1

,... , p

k

−

y

i

]

2

=

min

Zalety:
~kryterium jest mocne, zawiera kwadraty odchyłek, a więc liczby
nieujemne
~Prostota obliczeń minimum funkcji pod warunkiem, że rozpatruje się
aproksymację w klasie wielomianów uogólnionych:

F x , p

1

, ... , p

k

=

p

1



1



x p

2



2



x...p

k



k



x

13.Aproksymacja liniowa funkcji jednej zmiennej -

Dany zbiór punktów



x

1

, y

1



, x

2

, y

2



, ..., x

n

, y

n



Funkcja aproksymująca

y=p

1



p

2

x

Kryterium najmniejszych kwadratów

S p

1

, p

2

=

∑

i=1

n

[

p

1



p

2

x

i

−

y

i

]

2

=

min

Warunek konieczny istnienia ekstremum funkcji dwóch zmiennych

∂

S p

1

, p

2



∂

p

1

=

2

∑

i=1

n

[

p

1



p

2

x

i

−

y

i

]=

0

∂

S p

1

, p

2



∂

p

2

=

2

∑

i=1

n

[

p

1



p

2

x

i

−

y

i

]⋅

x

i

=

0

Forma 1

∑

i=1

n

[

p

1



p

2

x

i

−

y

i

]=

0

∑

i=1

n

[

p

1

x

i



p

2

x

i

2

−

y

i

x

i

]=

0

Forma 2

Forma 3

X⋅P=Y ⇒ P=X

−

1

⋅

Y

Przypadek dla trzech punktów aproksymacji

y=p

1



p

2

xp

3

1
x

S p

1

, p

2

, p

3

=

∑

i=1

n

[

p

1



p

2

x

i



p

3

1

x

i

−

y

i

]

2

=

min

∂

S p

1

, p

2

, p

3



∂

p

1

=

2

∑

i=1

n

[

p

1



p

2

x

i



p

3

1

x

i

−

y

i

]=

0

∂

S p

1

, p

2

, p

3



∂

p

2

=

2

∑

i=1

n

[

p

1



p

2

x

i



p

3

1

x

i

−

y

i

]⋅

x

i

=

0

∂

S p

1

, p

2

, p

3



∂

p

3

=

2

∑

i=1

n

[

p

1



p

2

x

i



p

3

1
x

−

y

i

]⋅

1

x

i

=

0

X⋅P=Y ⇒ P=X

−

1

⋅

Y