
Rozdział
3
INTERPOLACJA
3.1.
Zagadnienie interpolacji
Niech na przedziale domkniętym [a,b] danych jest n+1 punktów x
0
, x
1
, … , x
n
(rzeczywistych lub zespolonych) nazywanych węzłami interpolacji gdzie x
0
=a oraz
x
n
=b. Ponadto, niech w każdym punkcie (węźle) x
i
znana jest wartość pewnej
funkcji f(x
i
) wraz z jej pochodnymi do k
i
-tej włącznie:
).
(
),
(
),
(
),
(
),
(
),
(
),
(
),
(
),
(
)
(
)
(
1
)
(
)
(
1
1
1
1
0
)
(
)
(
0
0
0
0
1
1
0
0
n
k
k
n
n
n
n
k
k
k
k
x
f
f
x
f
f
x
f
f
x
f
f
x
f
f
x
f
f
x
f
f
x
f
f
x
f
f
n
n
=
′
=
′
=
=
′
=
′
=
=
′
=
′
=
L
M
O
M
M
L
L
(3.1)
Ogólnie, rzędy pochodnej k
i
(
N
∈
≥
i
i
k
k
,
0
) mogą być różne dla poszczególnych
węzłów. W przypadku tym węzły x
i
nazywamy węzłami k
i
+1 krotnymi. Liczba
warunków w (3.1) wynosi zatem:
.
)
1
(
)
1
(
)
1
(
)
1
(
1
0
1
0
∑
=
+
=
+
+
+
+
+
+
=
+
n
i
i
n
k
k
k
k
N
L
(3.2)
Zagadnienie interpolacji można ogólnie sformułować:
Wyznaczyć funkcję Φ(x) nazywaną funkcją interpolującą, która w każdym węźle
interpolacji x
i
przyjmuje wartość funkcji interpolowanej oraz jej pochodne do k
i
-tej
włącznie równe są odpowiednio pochodnym funkcji f(x
i
):
.
)
(
,
)
(
,
)
(
,
)
(
,
)
(
,
)
(
,
)
(
,
)
(
,
)
(
)
(
)
(
)
(
1
1
)
(
1
1
1
1
)
(
0
0
)
(
0
0
0
0
1
1
0
0
n
n
k
n
n
k
n
n
n
n
k
k
k
k
f
x
f
x
f
x
f
x
f
x
f
x
f
x
f
x
f
x
=
′
=
′
=
=
′
=
′
=
=
′
=
′
=
Φ
Φ
Φ
Φ
Φ
Φ
Φ
Φ
Φ
L
M
O
M
M
L
L
(3.3)
Pod pojęciem interpolacji wartości funkcji f(x) w punkcie x zawartym w przedziale
interpolacji [a,b] rozumiemy wyznaczenie jej wartości przybliżonej na podstawie
funkcji interpolującej Φ(x) spełniającej warunki (3.3):

46
Metody numeryczne
).
(
)
(
]
,
[
x
x
f
b
a
x
Φ
≅
∀
∈
(3.4)
Interpolacja zgodnie z (3.4), czyli wyznaczanie przybliżonej wartości funkcji
f(x)
dla argumentu zawartego w przedziale interpolacji, często nazywana jest
interpolacją w wąskim sensie.
Jeśli poszukujemy przybliżenia
f(x) na podstawie funkcji interpolującej
wyznaczonej na przedziale [
a,b] dla argumentu x z poza tego przedziału, wówczas
mówimy o
ekstrapolacji (3.5):
).
(
)
(
]
,
[
x
x
f
b
a
x
Φ
≅
∀
∉
(3.5)
Zagadnienie wyznaczania funkcji interpolującej z warunków (3.3) (układ
N+1
równań algebraicznych w ogólnym przypadku nieliniowych) może nie posiadać
rozwiązań lub może ich posiadać nieskończenie wiele, jeśli za funkcję Φ(
x)
przyjmiemy dowolną funkcje Φ(
x; a
0
,
a
1
, … ,
a
N
), gdzie
a
0
,
a
1
, … ,
a
N
współczynniki wyznaczane na podstawie warunków (3.3) (dla
x=x
0
, … ,
x=x
n
).
Zagadnienie interpolacji jest jednoznaczne, gdy w miejsce dowolnej funkcji Φ(
x)
przyjmujemy wielomian, co najwyżej stopnia
N określonego przez (3.2).
Wielomian taki nazywany jest
wielomianem interpolacyjnym Hermite’a [
xx
]:
).
(
)
(
]
,
[
x
H
x
f
N
b
a
x
≅
∀
∈
(3.6)
W praktyce stosowana jest interpolacja dla węzłów jednakowo krotnych (3.7)
*)
:
.
,
0
1
0
const
k
k
k
k
k
i
n
i
n
=
=
→
=
=
=
∀
∈
K
(3.7)
W szczególności, w najprostszym przypadku interpolacji rozpatrywane są
zagadnienia o węzłach jednokrotnych (
k+1=1). Zagadnienie interpolacji można
wówczas sformułować:
Należy wyznaczyć funkcje Φ(
x), która w węzłach x
i
przyjmuje wartości funkcji
interpolowanej
f(x):
i
i
i
n
i
f
x
f
x
=
=
∀
=
)
(
)
(
,
0
Φ
(3.8)
Interpretując zagadnienie geometrycznie (rys. 3.1) mówimy, że szukamy krzywej
Φ
(
x) przechodzącej przez układ punktów (x
i
,
f
i
) dla
i=0, … ,n.
*)
Węzły jednakowo krotne (k
≥
0) znalazły zastosowanie między innymi w interpolacji tzw.
funkcjami sklejanymi w celu uzyskania gładkich funkcji interpolujących. Zagadnienia
interpolacji funkcjami sklejanymi zostały przedstawione w p. 3..3.

3. Interpolacja
47
Rys. 3.1 Interpretacja geometryczna zagadnienia interpolacji dla krotności k+1=1
Przyjmijmy dalej, że dana jest funkcja Φ(x; a
0
, a
1
, … , a
n
) zależna od n+1
parametrów a
0
, a
1
, … , a
n
. Zadanie interpolacji polega na określeniu parametrów a
i
funkcji Φ tak, aby dla n+1 par (x
i
, f
i
) zachodziło:
i
i
n
i
n
i
j
i
j
i
n
j
i
f
x
f
a
a
x
x
x
=
=
∧
≠
∀
∀
∈
≠
∈
)
(
)
,
,
;
(
0
,
0
,
0
,
K
Φ
(3.9)
Niech dalej będą dane funkcje argumentu x:
Φ
0
(x),
Φ
1
(x), … ,
Φ
n
(x) niezależne od
parametrów a
0
, a
1
, … , a
n
nazywane funkcjami bazowymi.
Jeśli zadanie interpolacji sprowadzimy do wyznaczania funkcji
Φ
liniowo zależnej
od parametrów a
i
:
∑
=
0
=
+
+
+
≡
n
i
i
i
n
n
n
x
a
x
a
x
a
x
a
a
a
x
0
1
1
0
0
),
(
)
(
)
(
)
(
)
,
,
;
(
Φ
Φ
Φ
Φ
Φ
K
K
(3.10)
mówimy o zadaniu interpolacji liniowej.
Jeśli jako funkcje bazowe przyjmiemy
Φ
0
= 1,
Φ
1
= x, …,
Φ
n
= x
n
wówczas mamy
do czynienia z zagadnieniem interpolacji wielomianowej:
*)
.
)
,
,
;
(
0
2
2
1
0
0
∑
=
=
+
+
+
+
≡
n
i
i
i
n
n
n
x
a
x
a
x
a
x
a
a
a
a
x
K
K
Φ
(3.11)
W przypadku, gdy funkcje bazowe zdefiniowane są jako funkcje zmiennej
zespolonej
Φ
0
= e
0ix
= 1,
Φ
1
= e
ix
,
Φ
2
= e
2ix
…,
Φ
n
= x
nix
mówimy o zagadnieniu
interpolacji trygonometrycznej:
**)
*)
Interpolacja wielomianowa była dawniej powszechnie stosowana do interpolacji funkcji
tablicowanych. Innym jej wykorzystaniem jest zastosowanie w całkowaniu i różnicz-
kowaniu numerycznym.
**)
Interpolacja trygonometryczna w szerokim zakresie stosowana jest w analizie Fourier’a
szeregów czasowych serii pomiarowych.

48
Metody numeryczne
.
1
,
)
,
,
;
(
2
0
2
2
1
0
0
−
=
=
+
+
+
+
≡
∑
=
i
e
a
e
a
e
a
e
a
a
a
a
x
n
k
kix
k
nix
n
ix
ix
n
K
K
Φ
(3.12)
W przypadku, gdy funkcje bazowe są również funkcjami parametrów, lub gdy
funkcji interpolacyjnej nie można przedstawić w postaci (3.10), mamy do
czynienia z interpolacją nieliniową. Do często spotykanych w praktyce zagadnień
interpolacji nieliniowej można zaliczyć:
Zadanie
interpolacji funkcjami wymiernymi:
*)
.
)
,
,
,
,
,
,
;
(
0
0
1
0
1
0
1
0
0
∑
∑
=
=
=
+
+
+
+
+
+
≡
m
i
i
i
n
i
i
i
m
m
n
n
m
n
x
b
x
a
x
b
x
b
b
x
a
x
a
a
b
b
b
a
a
x
K
K
K
K
Φ
(3.13)
Interpolacja wymierna znalazła zastosowanie np. w algorytmach przyspieszania
zbieżności [
xx
].
Zadanie
interpolacji wykładniczej:
**)
.
)
,
,
,
,
,
,
;
(
1
1
0
1
0
0
1
0
∑
=
=
+
+
+
≡
n
i
x
b
i
x
b
n
x
b
x
b
n
n
i
n
e
a
e
a
e
a
e
a
b
b
b
a
a
x
K
K
K
Φ
(3.14)
Interpolacja wykładnicza (3.14) znajduje szerokie zastosowanie przy opisie
zjawisk fizycznych i chemicznych a w szczególności w analizie szeregów rozpadu
promieniotwórczego [
xx
].
W dalszej części rozdziału ograniczono się do interpolacji wielomianowej. Inne
przypadki nie omawiane w niniejszym skrypcie, zainteresowany Czytelnik
znajdzie w pracach [
xx, xx, xx
].
3.2.
Interpolacja wielomianowa
Niech dalej jest dany zbiór
Ω
n
zawierający wszystkie rzeczywiste lub
zespolone wielomiany
W
n
(
x) stopnia co najwyżej n:
.
)
(
2
2
1
0
n
n
n
x
a
x
a
x
a
a
x
W
+
+
+
+
=
K
(3.15)
Dla dowolnych
n+1 punktów węzłowych:
*)
W powyższym zagadnieniu występuje n+1 parametrów a
i
oraz m+1 parametrów b
i
.
Wyznaczenie funkcji interpolacyjnej
Φ
wymaga zatem n+m+1 węzłów interpolacji (a
1
=1).
**)
W zagadnieniu interpolacji wykładniczej mamy 2n+2 parametry i liczba węzłów wynosi
2n+2.

3. Interpolacja
49
(
)
,
,
,
0
,
,
,
0
,
j
i
j
i
n
j
i
i
i
x
x
n
i
f
x
≠
=
∀
≠
∈
(3.16)
istnieje dokładnie jeden wielomian
W
n
(
x)
∈
Ω
n
taki że:
.
)
(
,
0
i
i
n
n
i
f
x
W
=
∀
∈
(3.17)
Istnieje kilka sposobów wyznaczania wielomianu interpolacyjnego W
n
(x). W
zależności od stosowanej metody (przyjętych funkcji bazowych
Φ
i
(x), patrz (3.10))
otrzymujemy różne postacie tego samego wielomianu. W dalszej części
ograniczono się do wielomianów interpolacyjnych Lagrange’a i Newton’a.
3.2.1. Wielomian interpolacyjny Lagrange’a
*)
Niech jest dany zbiór n+1 punktów węzłowych (x
i
, f
i
) spełniających warunki
(3.16) czyli:
,
,
0
,
j
i
j
i
n
j
i
x
x
≠
∀
≠
∈
Skonstruujmy za Lagrange’m wielomiany interpolacyjne
Φ
i
(x)
∈
Ω
n
rzędu n
stanowiące funkcje bazowe interpolacji liniowej (3.10) tak, aby wielomian
interpolacyjny posiadał parametry równe wartościom funkcji w węzłach
interpolacyjnych:
∑
=
0
=
+
+
+
≡
n
i
i
i
n
n
n
x
f
x
f
x
f
x
f
x
L
0
1
1
0
),
(
)
(
)
(
)
(
)
(
Φ
Φ
Φ
Φ
K
(3.18)
Z warunku interpolacji wynika ze:
.
)
(
)
(
)
(
)
(
0
0
,
1
i
n
n
i
i
i
i
i
n
i
f
x
f
x
f
x
f
x
L
=
+
+
+
+
=
0
∈
∀
Φ
Φ
Φ
K
K
(3.19)
Czyli wielomiany
Φ
i
(x
j
) muszą spełniać:
.
1
0
)
(
=
≠
=
=
j
i
dla
j
i
dla
x
ij
j
i
δ
Φ
(3.20)
Należy znaleźć wielomian
Φ
i
(x) stopnia n, który w węzłach x
j
(j
≠
i) przyjmuje
wartości równe zero a w węźle x
i
równy jest jeden.
*)
Wielomian ten stanowi między innymi podstawę kwadratur Newton’a Cotes’a
całkowania numerycznego (rozdział 4).

50
Metody numeryczne
Ponieważ węzły spełniają x
k
≠
x
j
dla k
≠
j, wielomian
Φ
i
(x) posiada pierwiastki
jednokrotne równe węzłom x
0
, …, x
i-1
, x
i+1
, …, x
n
.
*)
Zatem jest on iloczynem
jednomianów (rys. 3.2):
),
(
)
)(
(
)
)(
(
)
(
1
1
1
0
n
i
i
i
i
x
x
x
x
x
x
x
x
x
x
K
x
−
−
−
−
−
=
+
−
L
L
Φ
(3.21)
Rys. 3.2 Interpretacja geometryczna funkcji bazowej
Φ
i
(x)
Ponieważ w węźle x
i
zgodnie z warunkiem
Φ
i
(x
i
) = 1 (3.20) stałą K
i
w (3.21)
należy tak wyznaczyć aby zachodziło:
.
1
)
(
)
)(
(
)
)(
(
)
(
1
1
1
0
=
−
−
−
−
−
=
+
−
n
i
i
i
i
i
i
i
i
i
i
x
x
x
x
x
x
x
x
x
x
K
x
L
L
Φ
(3.22)
W konsekwencji mamy:
,
)
(
)
)(
(
)
)(
(
1
1
1
1
0
n
i
i
i
i
i
i
i
i
x
x
x
x
x
x
x
x
x
x
K
−
−
−
−
−
=
+
−
L
L
(3.23)
czyli:
.
)
(
)
(
)
(
)
)(
(
)
(
)
(
)
)(
(
)
(
)
(
0
1
1
0
1
1
0
∏
≠
=
+
−
+
−
−
−
=
−
−
−
−
−
−
−
−
=
n
i
j
j
j
i
j
n
i
i
i
i
i
i
n
i
i
i
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
L
L
L
L
Φ
(3.24)
Podstawiając (3.24) do (3.18) otrzymujemy wzór interpolacyjny Lagrange’a:
.
)
(
)
(
)
(
)
)(
(
)
(
)
(
)
)(
(
)
(
)
(
0
0
1
1
0
1
1
0
0
∑
∏
∑
=
≠
=
+
−
+
−
=
−
−
=
=
−
−
−
−
−
−
−
−
=
n
i
n
i
j
j
j
i
j
i
n
i
i
i
i
i
i
n
i
i
n
i
i
n
x
x
x
x
f
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
f
x
L
L
L
L
L
(3.25)
*)
Równanie
Φ
i
(x)=0 posiada pierwiastki jednokrotne odpowiednio równe: x
0
, …, x
i-1
, x
i+1
,
…, x
n
co wynika z warunku
Φ
i
(x
j
) = 0 dla i
≠
j w (3.20).

3. Interpolacja
51
Zauważyć należy, że dla n+1 z założenia różnych węzłów interpolacyjnych funkcje
bazowe
Φ
i
(x) są wielomianami stopnia n (iloczyn n jednomianów). Wielomian
interpolacyjny Lagrange’a L
n
(x) jest sumą ważoną wartościami funkcji w węzłach
n+1 wielomianów bazowych
Φ
i
(x), czyli jest wielomianem stopnia co najwyżej n
oraz spełnia L
n
(x)
∈
Ω
n
.
Znaleźć wielomian interpolacyjny Lagrange’a, który w węzłach x
0
=-2, x
1
=1, x
2
=2,
x
3
=4 przyjmuje wartości f
0
=3, f
1
=1, f
2
=-3, f
3
=8.
Bazowe wielomiany Lagrange’a wynoszą odpowiednio (3.24):
,
72
)
4
)(
2
)(
1
(
)
4
2
)(
2
2
)(
1
2
(
)
4
)(
2
)(
1
(
)
)(
)(
(
)
)(
)(
(
)
(
3
2
0
1
0
3
2
1
0
−
−
−
−
=
−
−
−
−
−
−
−
−
−
=
−
−
−
−
−
−
=
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Φ
,
9
)
4
)(
2
)(
2
(
)
4
1
)(
2
1
)(
2
1
(
)
4
)(
2
)(
2
(
)
)(
)(
(
)
)(
)(
(
)
(
3
1
2
1
0
1
3
2
0
1
−
−
+
=
−
−
+
−
−
+
=
−
−
−
−
−
−
=
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Φ
,
8
)
4
)(
1
)(
2
(
)
4
2
)(
1
2
)(
2
2
(
)
4
)(
1
)(
2
(
)
)(
)(
(
)
)(
)(
(
)
(
3
2
1
2
0
2
3
2
0
2
−
−
+
−
=
−
−
+
−
−
+
=
−
−
−
−
−
−
=
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Φ
,
36
)
2
)(
1
)(
2
(
)
2
4
)(
1
4
)(
2
4
(
)
2
)(
1
)(
2
(
)
)(
)(
(
)
)(
)(
(
)
(
2
3
1
3
0
3
2
1
0
3
−
−
+
=
−
−
+
−
−
+
=
−
−
−
−
−
−
=
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Φ
Co daje wielomian interpolacyjny (3.25):
.
36
)
2
)(
1
)(
2
(
8
8
)
4
)(
1
)(
2
(
3
9
)
4
)(
2
)(
2
(
1
72
)
4
)(
2
)(
1
(
3
)
(
)
(
)
(
)
(
)
(
3
3
2
2
1
1
0
0
3
−
−
+
+
−
−
+
−
−
−
−
+
+
−
−
−
=
=
+
+
+
=
x
x
x
x
x
x
x
x
x
x
x
x
x
f
x
f
x
f
x
f
x
L
Φ
Φ
Φ
Φ
Po wymnożeniu jednomianów i zgrupowaniu wyrazów podobnych mamy postać (3.11):
.
6
6
25
2
3
3
2
)
4
4
(
9
2
)
8
6
3
(
8
3
)
16
4
4
(
9
1
)
8
14
7
(
24
1
)
(
2
3
2
3
2
3
2
3
2
3
3
+
−
−
=
=
+
−
−
+
+
−
−
+
+
+
−
−
+
−
+
−
−
=
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
L
Dotychczas nie nakładaliśmy żadnych warunków na odległości między węzłami.
Dalej przyjmijmy, że odległości między kolejnymi węzłami są jednakowe (węzły
równoodległe)
*)
:
*)
Węzły równoodległe stosowane są powszechnie w całkowaniu numerycznym. W
przypadku interpolacji rozumianej szeroko, odległości pomiędzy węzłami nie koniecznie
muszą być równoodległe. Istotny jest wybór położenia węzłów tak, aby minimalizować
błędy interpolacji [
xxx
].

52
Metody numeryczne
.
)
(
1
,
1
h
j
i
x
x
const
h
x
x
j
i
i
i
n
i
−
=
−
→
=
=
−
−
=
∀
(3.26)
Wielomiany bazowe Lagrange’a (3.24) przyjmują wówczas postać:
,
)
(
)
(
1
)
(
)
2
(
)
1
(
2
)
0
(
)
(
)
)(
(
)
(
)
(
0
1
1
0
∏
≠
=
+
−
−
−
=
−
−
−
−
−
−
−
−
=
n
i
j
j
j
n
n
i
i
i
j
i
x
x
h
h
n
i
h
h
hh
h
i
x
x
x
x
x
x
x
x
x
L
L
L
L
Φ
(3.27)
a wzór interpolacyjny Lagrange’a (3.25) przechodzi w:
∑
∏
∑
∏
=
≠
=
=
≠
=
−
−
=
−
−
=
n
i
n
i
j
j
j
i
n
n
i
n
i
j
j
j
n
i
n
j
i
x
x
f
h
j
i
x
x
h
f
x
L
0
0
0
0
.
)
(
)
(
1
)
(
)
(
1
)
(
(3.28)
Znaleźć wielomian interpolacyjny Lagrange’a, który w węzłach x
0
=-2, x
1
=0, x
2
=2,
x
3
=4 przyjmuje wartości f
0
=3, f
1
=1, f
2
=-3, f
3
=8.
W rozpatrywanym przykładzie mamy węzły równoodlegle o odległości h=2 oraz n=3.
Bazowe wielomiany Lagrange’a wynoszą odpowiednio (3.27):
,
6
)
4
)(
2
)(
0
(
8
1
)
3
)(
2
)(
1
(
)
4
)(
2
)(
0
(
8
1
)
3
0
)(
2
0
)(
1
0
(
)
)(
)(
(
1
)
(
3
2
1
3
0
−
−
−
−
=
−
−
−
−
−
−
=
−
−
−
−
−
−
=
x
x
x
x
x
x
x
x
x
x
x
x
h
x
Φ
,
2
)
4
)(
2
)(
2
(
8
1
)
2
)(
1
)(
1
(
)
4
)(
2
)(
2
(
8
1
)
3
1
)(
2
1
)(
0
1
(
)
)(
)(
(
1
)
(
3
2
0
3
1
−
−
+
=
−
−
−
−
+
=
−
−
−
−
−
−
=
x
x
x
x
x
x
x
x
x
x
x
x
h
x
Φ
,
2
)
4
)(
1
)(
2
(
8
1
)
1
)(
1
)(
2
(
)
4
)(
1
)(
2
(
8
1
)
3
2
)(
1
2
)(
0
2
(
)
)(
)(
(
1
)
(
3
2
0
3
2
−
−
+
−
=
−
−
−
+
=
−
−
−
−
−
−
=
x
x
x
x
x
x
x
x
x
x
x
x
h
x
Φ
,
6
)
2
)(
1
)(
2
(
8
1
)
1
)(
2
)(
3
(
)
2
)(
1
)(
2
(
8
1
)
2
3
)(
1
3
)(
0
3
(
)
)(
)(
(
1
)
(
2
1
0
3
3
−
−
+
=
−
−
+
=
−
−
−
−
−
−
=
x
x
x
x
x
x
x
x
x
x
x
x
h
x
Φ
Co daje wielomian interpolacyjny (3.25) zgodnie z (3.28):
.
)
2
)(
0
)(
2
(
3
4
)
4
)(
0
)(
2
(
2
3
)
4
)(
2
)(
2
(
2
1
)
4
)(
2
)(
0
(
2
1
8
1
)
(
)
(
)
(
)
(
)
(
3
3
2
2
1
1
0
0
3
−
−
+
+
−
−
+
+
+
−
−
+
+
−
−
−
−
=
=
+
+
+
=
x
x
x
x
x
x
x
x
x
x
x
x
x
f
x
f
x
f
x
f
x
L
Φ
Φ
Φ
Φ
Wyznaczanie wartości wielomianu dla
x
∈
[
a, b] ale nie będącego węzłem (x
≠
x
i
)
wymaga w przypadku postaci (3.25) dużego nakładu obliczeń (liczba mnożeń i
dodawań) co powoduje, że metoda ta jest zbyt kosztowna i o dużej złożoności
obliczeniowej. Innym podejściem jest sprowadzenie wielomianu do postaci (3.15)
(patrz przykład 3.1) co wymaga jednak przekształceń a nie obliczeń.
3. Interpolacja
53
Istnieją jednak algorytmy pozwalające wyznaczać wartości wielomianów inter-
polacyjnych Lagrange’a dla x nie będącego węzłem bez konieczności wyznaczania
samego wielomianu interpolacyjnego.
3.2.2. Algorytm Aitken’a
Przyjmijmy, że dane są wartości interpolowanej funkcji f(x
i
) = f
i
w n + 1
węzłach (dowolnie położonych ale różnych – warunek (3.16)). Należy wyznaczyć
wartość wielomianu interpolacyjnego Lagrange’a stopnia n opartego na punktach
węzłowych (x
0
, f
0
), (x
1
, f
1
), … , (x
n
, f
n
) w punkcie x nie będącym węzłem
*)
.
Zagadnienie podane wyżej można rozwiązać stosując przedstawioną dalej
iteracyjną metodę Aitken’a [
xx
] nazywaną również algorytmem Aitken’a.
Oznaczmy przez W
i,j
(x) wielomian stopnia pierwszego przechodzącego przez
punkty węzłowe (x
i
, f
i
) oraz (x
j
, f
j
). Wielomian ten określony jest przez:
.
)
(
)
(
)
(
)
(
)
(
,
i
j
i
j
j
i
i
j
j
j
i
i
j
i
x
x
x
x
f
x
x
f
x
x
x
x
f
x
x
f
x
W
−
−
−
−
=
−
−
−
=
(3.29)
Podobnie oznaczmy przez W
i,j,k
(x) wielomian stopnia drugiego przechodzącego
przez punkty węzłowe (x
i
, f
i
), (x
j
, f
j
). oraz (x
k
, f
k
):
.
)
)(
(
)
)(
(
)
(
)
(
)
(
)
(
)
(
,
,
,
,
,
,
j
k
j
k
i
k
j
i
j
k
k
k
i
j
j
i
k
j
i
x
x
x
x
x
W
x
x
x
W
x
x
x
x
x
W
x
x
x
W
x
W
−
−
−
−
=
−
−
−
=
(3.30)
Rozszerzając postępowanie (3.29), (3.30), … otrzymamy ogólnie:
.
)
)(
(
)
)(
(
)
(
)
(
)
(
)
(
)
(
)
(
,
1
,
,
1
,
0
,
1
,
,
1
,
0
,
1
,
,
1
,
0
,
1
,
,
1
,
0
,
,
,
1
,
0
k
l
k
l
k
l
k
k
k
l
l
l
k
k
k
k
n
l
k
x
x
x
x
x
W
x
x
x
W
x
x
x
x
x
W
x
x
x
W
x
L
x
W
−
−
−
−
=
=
−
−
−
=
=
−
−
−
−
K
K
K
K
K
(3.31)
W celu wyznaczenia wielomianu interpolacyjnego (dla dowolnej wartości
zmiennej x) czy też obliczenia jego wartości w danym punkcie (ustalonej wartości
zmiennej x) postępowanie sprowadza się do kolejnego tworzenia wielomianów
począwszy od stopnia pierwszego (3.29) aż do stopnia n:
*)
Jak wspomniano wcześniej jeśli x
∈
[a, b] będziemy mówili o interpolacji, w przypadku
przeciwnym, czyli x
∉
[a, b] będziemy mówili o ekstrapolacji.
54
Metody numeryczne
•
dwa węzły
,
)
(
)
(
)
(
)
(
)
(
0
1
0
1
1
0
0
1
1
1
0
0
1
,
0
x
x
x
x
f
x
x
f
x
x
x
x
f
x
x
f
x
W
−
−
−
−
=
−
−
−
=
,
)
(
)
(
)
(
)
(
)
(
0
2
0
2
2
0
0
2
2
2
0
0
2
,
0
x
x
x
x
f
x
x
f
x
x
x
x
f
x
x
f
x
W
−
−
−
−
=
−
−
−
=
M
,
)
(
)
(
)
(
)
(
)
(
0
0
0
0
0
0
,
0
x
x
x
x
f
x
x
f
x
x
x
x
f
x
x
f
x
W
n
n
n
n
n
n
n
−
−
−
−
=
−
−
−
=
•
trzy węzły
,
)
)(
(
)
)(
(
)
(
)
(
)
(
)
(
)
(
1
2
1
2
,
0
2
1
,
0
1
2
2
2
,
0
1
1
,
0
2
,
1
,
0
x
x
x
x
x
W
x
x
x
W
x
x
x
x
x
W
x
x
x
W
x
W
−
−
−
−
=
−
−
−
=
,
)
)(
(
)
)(
(
)
(
)
(
)
(
)
(
)
(
1
3
1
3
,
0
3
1
,
0
1
3
3
3
,
0
1
1
,
0
3
,
1
,
0
x
x
x
x
x
W
x
x
x
W
x
x
x
x
x
W
x
x
x
W
x
W
−
−
−
−
=
−
−
−
=
M
,
)
)(
(
)
)(
(
)
(
)
(
)
(
)
(
)
(
1
1
,
0
1
,
0
1
,
0
1
1
,
0
,
1
,
0
x
x
x
x
x
W
x
x
x
W
x
x
x
x
x
W
x
x
x
W
x
W
n
n
n
n
n
n
n
−
−
−
−
=
−
−
−
=
M
•
n+1 węzłów
.
)
)(
(
)
)(
(
)
(
)
(
)
(
)
(
)
(
1
1
,
2
,
,
1
,
0
1
,
2
,
,
1
,
0
1
,
2
,
,
1
,
0
1
1
,
2
,
,
1
,
0
,
1
,
2
,
,
1
,
0
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
=
=
−
−
−
=
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
x
x
x
x
x
W
x
x
x
W
x
x
x
x
x
W
x
x
x
W
x
W
K
K
K
K
K
Ostatni wielomian (n+1 węzłów dla wartości ogólnej x) jest poszukiwanym
wielomianem interpolacyjnym Lagrange’a. Dla wartości szczególnej x (ustalonej)
jest wartością tego wielomianu w tym punkcie.
3. Interpolacja
55
Kolejne wielomiany obliczane zgodnie z zależnościami podanymi wyżej można
zapisać w tablicy:
Tab. 3.1. Tablica algorytmu Aitken’a.
i
x
i
f
i
k=1
k=2
k=3
k=n
0
x
0
f
0
1
x
1
f
1
W
0,1
(x)
2
x
2
f
2
W
0,2
(x)
W
0,1,2
(x)
3
x
3
f
3
W
0,3
(x)
W
0,1,3
(x)
W
0,1,2,3
(x)
… …
…
…
…
…
…
n
x
n
f
n
W
0,n
(x)
W
0,1,n
(x)
W
0,1,2,n
(x)
…
W
0,1,2,….,n-1,n
(x)
Obliczenia wykonywane w tab. 3.1 wygodne są przy obliczeniach ręcznych.
Ponieważ przy obliczaniu wartości wielomianu Lagrange’a dla określonej wartości
argumentu x wartości wielomianów dla k < n stanowią wielkości przejściowe, nie
ma potrzeby ich pamiętania. W przypadku tym obliczenia automatyczne bardziej
korzystnie jest prowadzić w wektorach. Wartości pośrednie zapisywać w wektorze
wartości funkcji ffff (tab. 3.2):
Tab. 3.2. Zredukowana tablica algorytmu Aitken’a.
x
i
f
i
x
i
f
i
x
0
f
0
x
0
- x
f
0
x
1
f
1
x
1
- x
W
0,1
(x)
x
2
f
2
→
x
2
- x
W
0,1,2
(x)
x
3
f
3
x
3
- x
W
0,1,2,3
(x)
…
…
…
…
x
n
f
n
x
n
- x
W
0,1,2,3,…,n
(x)
Podany niżej algorytm obliczeniowy zapisuje wyniki pośrednie jak w tablicy 3.2.
Algorytm Aitken’a można przedstawić:
input X[0..n], F[0..n], x, n;
{X - tablica zawierająca wartości kolejnych węzłów x
i
}
{F – tablica zawierająca wartości funkcji f
f
w węzłach x
i
}
{x – wartość argumentu x, dla której obliczana jest wartość wielomianu}
{n – rząd wielomianu (n+1 – liczba węzłów interpolacji)}
if x
≠
0.0 then
for i=0 to n do
X[i]
←
X[i]-x;
end do
for i = 0 to n-1 do
for j = i+1 to n do
F[j]
←
(F[j]*X[i]–F[i]*X[j])/(X[j]–X[i]);
end do
end do
output F[n];
56
Metody numeryczne
3.2.3. Algorytm Neville’a
Algorytm Neville’a skonstruowany jest podobnie do algorytmu Aitken’a z tą
różnicą, że kolejne wielomiany przechodzące przez jeden punkt węzłowy więcej
wyznaczane są z wielomianów sąsiednich. Na przykład wielomian drugiego
stopnia przechodzący przez trzy punkty węzłowe (x
i
, f
i
), (x
j
, f
j
) oraz (x
k
, f
k
) w
algorytmie Aitken’a wyznaczamy zgodnie z (3.30):
.
)
)(
(
)
)(
(
)
(
)
(
)
(
)
(
)
(
,
,
,
,
,
,
j
k
j
k
i
k
j
i
j
k
k
k
i
j
j
i
k
j
i
x
x
x
x
x
W
x
x
x
W
x
x
x
x
x
W
x
x
x
W
x
W
−
−
−
−
=
−
−
−
=
W przypadku algorytmu Neville’a mamy natomiast:
.
)
)(
(
)
)(
(
)
(
)
(
)
(
)
(
)
(
,
,
,
,
,
,
i
k
j
k
i
k
j
j
i
k
k
k
j
j
j
i
k
j
i
x
x
x
x
x
W
x
x
x
W
x
x
x
x
x
W
x
x
x
W
x
W
−
−
−
−
=
−
−
−
=
(3.30)
Przyjmijmy jak poprzednio, że dane są wartości interpolowanej funkcji f(x
i
) = f
i
w
n + 1 węzłach dowolnie położonych, ale różnych.
Liczymy kolejno ilorazy dla wielomianów sąsiednich:
•
dwa węzły
,
)
(
)
(
)
(
)
(
)
(
0
1
0
1
1
0
0
1
1
1
0
0
1
,
0
x
x
x
x
f
x
x
f
x
x
x
x
f
x
x
f
x
W
−
−
−
−
=
−
−
−
=
,
)
(
)
(
)
(
)
(
)
(
1
2
1
2
2
1
1
2
2
2
1
1
2
,
1
x
x
x
x
f
x
x
f
x
x
x
x
f
x
x
f
x
W
−
−
−
−
=
−
−
−
=
M
,
)
(
)
(
)
(
)
(
)
(
1
1
1
1
1
1
,
1
−
−
−
−
−
−
−
−
−
−
−
=
−
−
−
=
n
n
n
n
n
n
n
n
n
n
n
n
n
n
x
x
x
x
f
x
x
f
x
x
x
x
f
x
x
f
x
W
•
trzy węzły
,
)
)(
(
)
)(
(
)
(
)
(
)
(
)
(
)
(
0
2
1
2
,
1
2
1
,
0
0
2
2
2
,
1
1
1
,
0
2
,
1
,
0
x
x
x
x
x
W
x
x
x
W
x
x
x
x
x
W
x
x
x
W
x
W
−
−
−
−
=
−
−
−
=
3. Interpolacja
57
,
)
)(
(
)
)(
(
)
(
)
(
)
(
)
(
)
(
1
3
2
3
,
2
3
2
,
1
1
3
3
3
,
2
2
2
,
1
3
,
2
,
1
x
x
x
x
x
W
x
x
x
W
x
x
x
x
x
W
x
x
x
W
x
W
−
−
−
−
=
−
−
−
=
M
,
)
)(
(
)
)(
(
)
(
)
(
)
(
)
(
)
(
2
1
,
1
1
,
2
2
,
1
1
1
,
2
,
1
,
2
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
=
=
−
−
−
=
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
x
x
x
x
x
W
x
x
x
W
x
x
x
x
x
W
x
x
x
W
x
W
M
•
n+1 węzłów
.
)
)(
(
)
)(
(
)
(
)
(
)
(
)
(
)
(
0
1
,
1
,
,
1
1
,
2
,
,
1
,
0
1
,
1
,
,
1
1
1
,
2
,
,
1
,
0
,
1
,
2
,
,
1
,
0
x
x
x
x
x
W
x
x
x
W
x
x
x
x
x
W
x
x
x
W
x
W
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
−
−
−
−
=
=
−
−
−
=
−
−
−
−
−
−
−
−
−
−
−
K
K
K
K
K
Ostatni wielomian (
n+1 węzłów dla wartości ogólnej x) jest poszukiwanym
wielomianem interpolacyjnym Lagrange’a jak w przypadku algorytmu Aitken’a.
Podobnie dla wartości szczególnej
x jest wartością wielomianu w punkcie x.
W tab. 3.3 podano kolejne obliczenia ilorazów w algorytmie Neville’a podobnie do
ilorazów metody Aitken’a w tab. 3.1.
Tab. 3.3. Tablica algorytmu Neville’a
.
i
x
i
f
i
k=1
k=2
k=3
k=n
0
x
0
f
0
W
0,1
(x)
1
x
1
f
1
W
0,1,2
(x)
W
1,2
(x)
W
0,1,2,3
(x)
2
x
2
f
2
W
1,2,3
(x)
W
2,3
(x)
W
1,2,3,4
(x)
3
x
3
f
3
W
2,3,4
(x)
W
3,4
(x)
W
2,3,4,5
(x)
…
…
…
…
…
…
…
W
0,1,2,….,n-1,n
(x)
…
…
…
…
…
W
n-4,n-3
(x)
W
n-5,n-4,n-3,n-2
(x)
n-3
x
n-3
f
n-3
W
n-4,n-3,n-2
(x)
W
n-3,n-2
(x)
W
n-4,n-3,n-2,n-1
(x)

58
Metody numeryczne
n-2
x
n-2
f
n-2
W
n-3,n-2,n-1
(x)
W
n-2,n-1,
(x)
W
n-3,n-2,n-1,n
(x)
n-1
x
n-1
f
n-1
W
n-2,n-1,n
(x)
W
n-1,n
(x)
n
x
n
f
n
W obliczeniach maszynowych podobnie jak wcześniej, wyniki pośrednie
zapamiętywane są w wektorze wartości funkcji w węzłach interpolacyjnych.
Tab. 3.4. Zredukowana tablica algorytmu Neville’a.
x
i
f
i
x
i
f
i
x
0
f
0
x
0
-x
f
0
W
0,1
(x)
x
1
f
1
x
1
-x
W
0,1,2
(x)
W
0,1,2,3
(x)
x
2
f
2
x
2
-x
W
0,1,2,3,4
(x)
W
0,1,2,3,4,5
(x)
…
…
…
…
→
W
0,1,2,….,n-1,n
(x)
…
…
…
…
W
n-4,n-3,n-2,n-1,n
(x)
x
n-2
f
n-2
x
n-2
-x
W
n-3,n-2,n-1,n
(x)
W
n-3,n-2,n-1,n
(x)
x
n-1
f
n-1
x
n-1
-x
W
n-2,n-1,n
(x)
W
n-1,n
(x)
x
n
f
n
x
n
-x
f
n
3.2.4. Wielomian interpolacyjny Newton’a
Przedstawione w punktach 3.2.2. oraz 3.2.3. algorytmy Aitken’a i Neville’a są
przydatne w przypadku kiedy wymagane jest obliczenie wartości tego samego
wielomianu w jednym punkcie x. W przypadku potrzeby obliczania wartości
wielomianu w wielu punktach lub konieczności określenia samego wielomianu,
algorytmy te są mało przydatne [
xxx
]. Bardziej użyteczny zarówno do
wielokrotnego wyznaczania wartości wielomianu jak i samego wielomianu jest
algorytm Newton’a.
Niech jak poprzednio jest dany zbiór n+1 punktów węzłowych (x
i
, f
i
)
spełniających warunki (3.16) czyli:
,
,
0
,
j
i
j
i
n
j
i
x
x
≠
∀
≠
∈
W przypadku wielomianu interpolacyjnego Lagrange’a funkcje bazowe
Φ
i
(x)
powstawały zgodnie z warunkiem (3.20) jako wielomiany stopnia n.
W podejściu Newton’a jako funkcje bazowe
Φ
i
(x) przyjęto wielomiany stopnia i:

3. Interpolacja
59
).
)(
(
)
(
)
(
)
)(
(
1
)
(
),
)(
(
)
(
)
)(
(
1
)
(
),
)(
(
)
)(
(
1
)
(
),
)(
(
)
(
1
)
(
,
1
)
(
1
1
1
1
1
0
1
1
1
1
0
1
1
1
0
2
0
0
0
1
0
−
−
−
−
−
−
−
−
=
−
−
−
−
≡
−
=
−
−
−
≡
−
=
−
−
≡
−
=
−
≡
≡
n
n
n
i
n
i
i
i
i
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Φ
Φ
Φ
Φ
Φ
Φ
Φ
Φ
Φ
L
L
M
L
M
(3.31)
Jak łatwo zauważyć, każdy następny wielomian jest iloczynem wielomianu
poprzedniego i odpowiedniego jednomianu określonego przez odpowiedni węzeł
interpolacyjny. Funkcje bazowe (3.31) można zapisać przy pomocy zależności
rekurencyjnej:
).
)(
(
)
(
,
1
)
(
1
1
,
1
0
−
−
=
−
≡
≡
∀
i
i
i
n
i
x
x
x
x
x
Φ
Φ
Φ
(3.32)
Zgodnie z (3.10) (interpolacja liniowa) jest:
).
(
)
)(
)(
(
)
(
)
)(
(
)
(
)
(
)
(
1
2
1
0
0
1
1
0
0
1
0
−
=
−
−
−
−
−
+
+
+
−
−
−
+
+
−
+
=
=
∑
n
n
n
i
i
i
i
i
n
x
x
x
x
x
x
x
x
a
x
x
x
x
x
x
a
x
x
a
a
x
a
x
N
L
L
L
L
Φ
(3.32)
Należy wyznaczyć wartości współczynników
a
i
tak, aby wielomian
N
n
(
x) w (3.32)
spełniał warunki interpolacji z węzłami jednokrotnymi (3.8):
.
)
(
)
(
0
,
0
i
n
i
i
i
i
i
n
n
i
f
x
a
x
N
=
=
∑
∀
=
∈
Φ
(3.33)
Zapiszmy wielomian N
n
(x) w postaci:
)
(
)
(
)
(
)
)(
)(
(
)
(
)
(
)
)(
)(
(
)
(
)
)(
)(
(
)
)(
)(
(
)
)(
(
)
(
)
(
1
1
2
1
0
1
2
1
0
1
1
2
1
0
2
1
0
3
1
0
2
0
1
0
−
−
−
+
−
−
−
−
−
−
−
+
+
+
+
−
−
−
−
−
+
+
−
−
−
−
+
+
+
+
−
−
−
+
+
−
−
+
+
−
+
+
=
n
k
k
n
k
k
k
k
k
n
x
x
x
x
x
x
x
x
x
x
x
x
a
x
x
x
x
x
x
x
x
x
x
a
x
x
x
x
x
x
x
x
a
x
x
x
x
x
x
a
x
x
x
x
a
x
x
a
a
x
N
L
L
L
L
L
L

60
Metody numeryczne
Zauważmy, że podstawiając za x wartość węzła x
k
wszystkie wielomiany bazowe
od
Φ
k+1
(x
k
) do
Φ
n
(x
k
) równe są zero (zawierają czynnik (x
k
– x
k
)=0).
Zatem podstawiając kolejno węzły mamy:
dla x = x
0
:
,
)
(
0
0
0
0
0
f
a
f
a
x
N
n
=
→
=
=
dla x = x
1
:
,
)
(
)
(
)
(
0
1
0
1
1
1
0
1
1
0
1
0
1
1
0
1
x
x
f
f
a
f
x
x
a
f
f
x
x
a
a
x
N
n
−
−
=
→
=
−
+
→
=
−
+
=
dla x = x
2
:
0
2
0
1
0
1
1
2
1
2
2
2
1
2
0
2
2
0
2
0
1
0
1
0
2
1
2
2
0
2
1
0
2
)
)(
(
)
(
)
(
)
(
)
(
x
x
x
x
f
f
x
x
f
f
a
f
x
x
x
x
a
x
x
x
x
f
f
f
f
x
x
a
x
x
a
a
x
N
n
−
−
−
−
−
−
=
→
→
=
−
−
+
−
−
−
+
→
→
=
−
+
−
+
=
Postępując dalej dla kolejnych węzłów i podstawiając wcześniej wyznaczone
wartości współczynników a
i
, otrzymamy wszystkie współczynniki wielomianu
Newton’a. Podane wyżej postępowanie stosowane w praktyce sprowadza się do
rekurencyjnego obliczania odpowiednich ilorazów różnicowych.
*)
Niech jest danych n + 1 punktów interpolacyjnych (x
0
, f
0
), … , (x
n
, f
n
). Dla węzłów
oczywiście jest x
i
≠
x
j
dla każdego i
≠
j.
Różnice (np. dla węzłów) definiowane są przez:
.
1
1
,
0
i
i
i
n
i
x
x
x
−
=
+
−
∈
∀
∆
(3.34)
Ilorazami różnicowymi pierwszego rzędu nazywamy:
.
,
,
1
1
,
1
1
2
1
2
2
,
1
0
1
0
1
1
,
0
−
−
−
−
−
=
−
−
=
−
−
=
n
n
n
n
n
n
x
x
f
f
f
x
x
f
f
f
x
x
f
f
f
L
(3.35)
*)
Przedstawiając dalej ilorazy różnicowe mówi się o tzw. różnicach progresywnych.
Należy zaznaczyć, że w praktyce obliczeniowej występują również tzw. różnice wsteczne i
centralne[
xxx
]. Ze względu na zakres materiału, w tym rozdziale ograniczono się tylko do
różnic progresywnych. O różnicach wstecznych jak i centralnych wspomina się w rozdziale
dotyczącym różniczkowania numerycznego (rozdz. 5).
3. Interpolacja
61
Tworząc dalej ilorazy z ilorazów różnicowych pierwszego rzędu powstają ilorazy
różnicowe drugiego rzędu:
.
,
,
2
2
,
1
1
,
,
1
,
2
1
3
2
,
1
3
,
2
3
,
2
,
1
0
2
1
,
0
2
,
1
2
,
1
,
0
−
−
−
−
−
−
−
−
=
−
−
=
−
−
=
n
n
n
n
n
n
n
n
n
x
x
f
f
f
x
x
f
f
f
x
x
f
f
f
L
(3.36)
Ogólnie iloraz różnicowy k-tego rzędu tworzony jest z ilorazów (k-1)-go rzędu na
podstawie wzoru rekurencyjnego:
.
1
,
,
2
,
1
,
,
,
2
,
1
,
,
2
,
1
,
i
k
i
k
i
i
i
i
k
i
i
i
k
i
i
i
i
x
x
f
f
f
−
−
=
+
−
+
+
+
+
+
+
+
+
+
K
K
K
(3.37)
Z ilorazów różnicowych (3.35) – (3.37) zazwyczaj budowana jest tablica.
Tab. 3.5. Ilorazy różnicowe dla n+1 punktów interpolacyjnych.
x
i
f
i
rząd k=1
rząd k=2
rząd k=3
…
rząd k=n
x
0
f
0
f
0,1
x
1
f
1
f
0,1,2
f
1,2
f
0,1,2,3
x
2
f
2
f
1,2,3
f
2,3
f
1,2,3,4
…
…
…
…
…
…
f
0,1,2,….,n-1,n
…
…
…
f
n-3,n-2
f
n-4,n-3,n-2,n-1
x
n-2
f
n-2
f
n-3,n-2,n-1
f
n-2,n-1,
f
n-3,n-2,n-1,n
x
n-1
f
n-1
f
n-2,n-1,n
f
n-1,n
x
n
f
n
Jeśli porównamy kolejne wyznaczanie wartości współczynników a
0
, a
1
, … , a
n
na
podstawie wartości wielomianu N
n
(x) w kolejnych węzłach zauważymy, że są one
równe pierwszym ilorazom różnicowym:
0
0
f
a
=
(3.38)

62
Metody numeryczne
,
0
1
0
1
1
,
0
1
x
x
f
f
f
a
−
−
=
=
(3.39)
0
2
1
,
0
2
,
1
2
,
1
,
0
2
x
x
f
f
f
a
−
−
=
=
(3.40)
aż do ostatniego:
0
1
,...,
1
,
0
,...,
2
,
1
,
1
,...,
2
,
1
,
0
x
x
f
f
f
a
n
n
n
n
n
n
−
−
=
=
−
−
(3.41)
Tłustym drukiem w tab. 3.5 zaznaczone zostały ilorazy (3.38) – (3.41) stanowiące
współczynniki
a
0
,
a
1
, … ,
a
n
wielomianu interpolacyjnego Newton’a.
Funkcja w węzłach x
0
=0, x
1
=1, x
2
=2, x
3
=3, x
5
=4, x
6
=5 przyjmuje wartości f
0
=-1, f
1
=0,
f
2
=7, f
3
=26, x
4
=63, x
5
=124. Wyznaczyć wielomian interpolacyjny Newton’a.
Budując tablicę ilorazów różnicowych (tab. 3.5) zgodnie z(3.35) – (3.37) otrzymamy:
x
i
f
i
k=1
k=2
k=3
k=4
k=5
0
-1
1
1
0
6
7
6
2
7
12
0
19
6
0
3
26
18
0
37
6
4
63
24
61
5
124
Zatem jest a
0
=-1, a
1
=1, a
2
=6, a
3
=6, a
4
=0 oraz a
5
=0. Ponieważ ilorazy różnicowe rzędu k=4
oraz k=5 równe są zero poszukiwany wielomian jest rzędu n=3.
Zgodnie z (3.32) jest:
N(x) = -1+
+ 1(x-0)+
+ 6(x-0)(x-1)+
+ 6(x-0)(x-1)(x-2)+
+ 0(x-0)(x-1)(x-2)(x-3)+
+ 0(x-0)(x-1)(x-2)(x-3)(x-4),
czyli
N(x) = -1+
+ 1(x-0)+
+ 6(x-0)(x-1)+
+ 6(x-0)(x-1)(x-2).
Co po wymnożeniu i redukcji wyrazów podobnych daje wielomian N
3
(x) = 6x
3
-12x
2
+7x-1.
3. Interpolacja
63
3.2.5. Zbie
ż
no
ść
interpolacji wielomianowej
Rozwiązanie zagadnienia interpolacji (3.3) przy zastosowaniu wielomianów
posiada jednoznaczne rozwiązanie bez względu na stosowaną metodę wyznaczania
wielomianu. Mając dane wartości funkcji f(x) w n+1 różnych punktach (węzłach)
poszukiwany był wielomian W
n
(x) rzędu co najwyżej n taki że W
n
(x
i
) = f(x
i
) = f
i
.
Wielomian ten w węzłach interpolacyjnych przyjmuje wartości równe wartości
interpolowanej funkcji natomiast w przedziałach pomiędzy kolejnymi węzłami
wartości wielomianu stanowią jedynie przybliżenie. Można zatem postawić
pytanie, czy przybliżenie poprawi się jeśli zwiększymy liczbę węzłów
interpolacyjnych, czyli zwiększymy rząd wielomianu interpolacyjnego.
Rozpatrzmy problem interpolacji wielomianowej z węzłami równoodległy-
mi.
*)
Niech interpolowana będzie f(x) =
x
w przedziale [-1, 1]. Wyznaczmy wielomia-
ny rzędów odpowiednio n=2 oraz n=4.
Dla n=2, x
0
= -1, h =1
→
W
2
(x) = x
2
.
Dla n=4, x
0
= -1, h =1/2
→
2
4
4
3
7
3
4
)
(
x
x
x
W
+
−
=
.
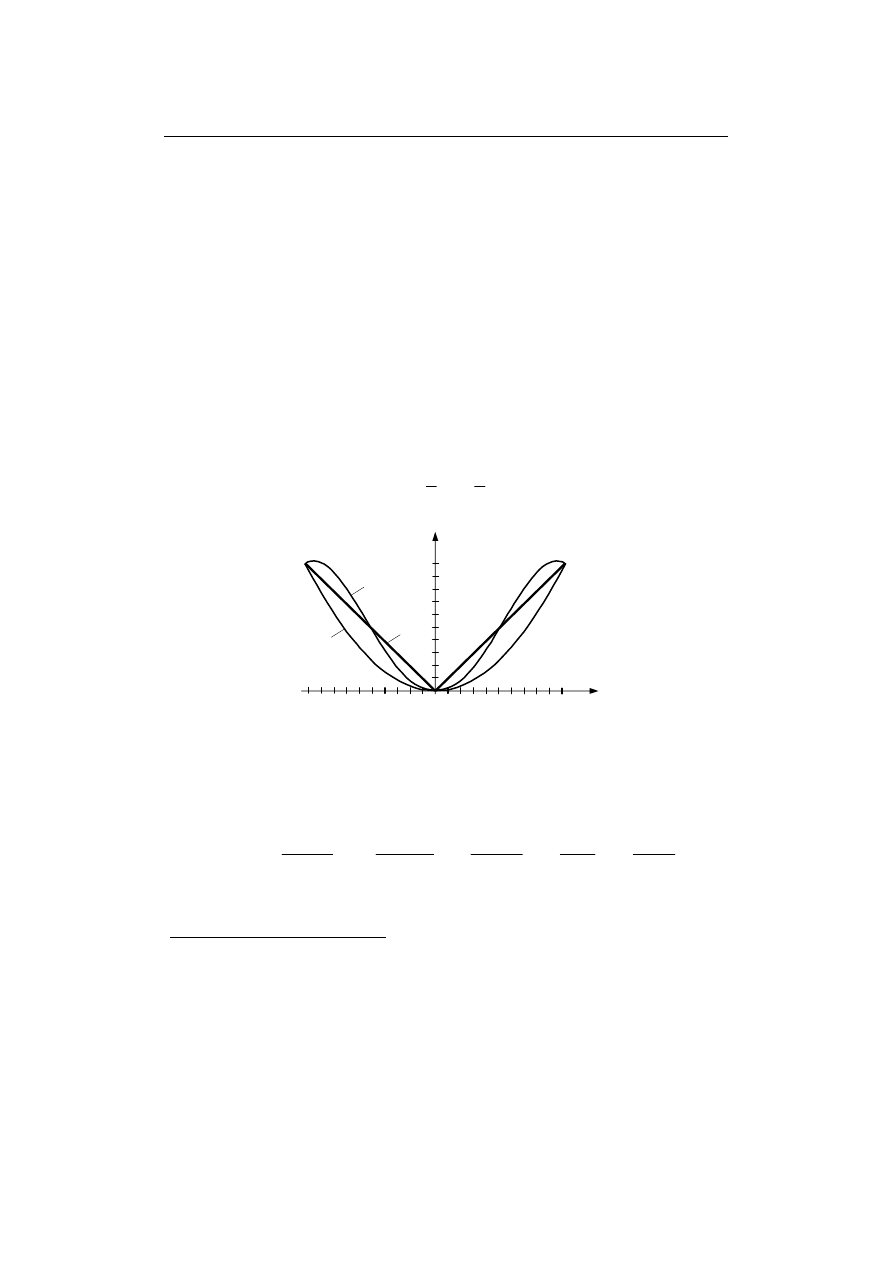
Rys. 3.3 Interpolacja f(x) =
x
w przedziale [-1, 1 wielomianami
W
2
(x) oraz W
4
(x)
Z rys. 3.3 można by wnioskować, że zagęszczenie węzłów powinno poprawić
dokładność przybliżenia. Dokonajmy zatem interpolacji wielomianem rzędu 10.
Dla n=10, x
0
= -1, h =1/5 jest:
x
x
x
x
x
x
W
1792
11527
162
6835
1728
221875
6048
1015625
5184
390625
)
(
4
6
8
10
10
+
+
+
−
−
=
.
*)
Interpolacja z węzłami równoodległymi jest wygodna w obliczeniach i znajduje
zastosowanie w wielu praktycznych algorytmach. Należy jednak pamiętać o ograniczeniach
wynikających ze
zbieżności jednostajnej (max
W
n
(x)-f(x)
).
-1,0 -0,8 -0,6 -0,4 -0,2 0
0,2 0,4 0,6 0,8 1,0
x
y
1,0
0,8
0,6
0,4
0,2
f(x)=|x|
W
4
(x)
W
2
(x)
64
Metody numeryczne
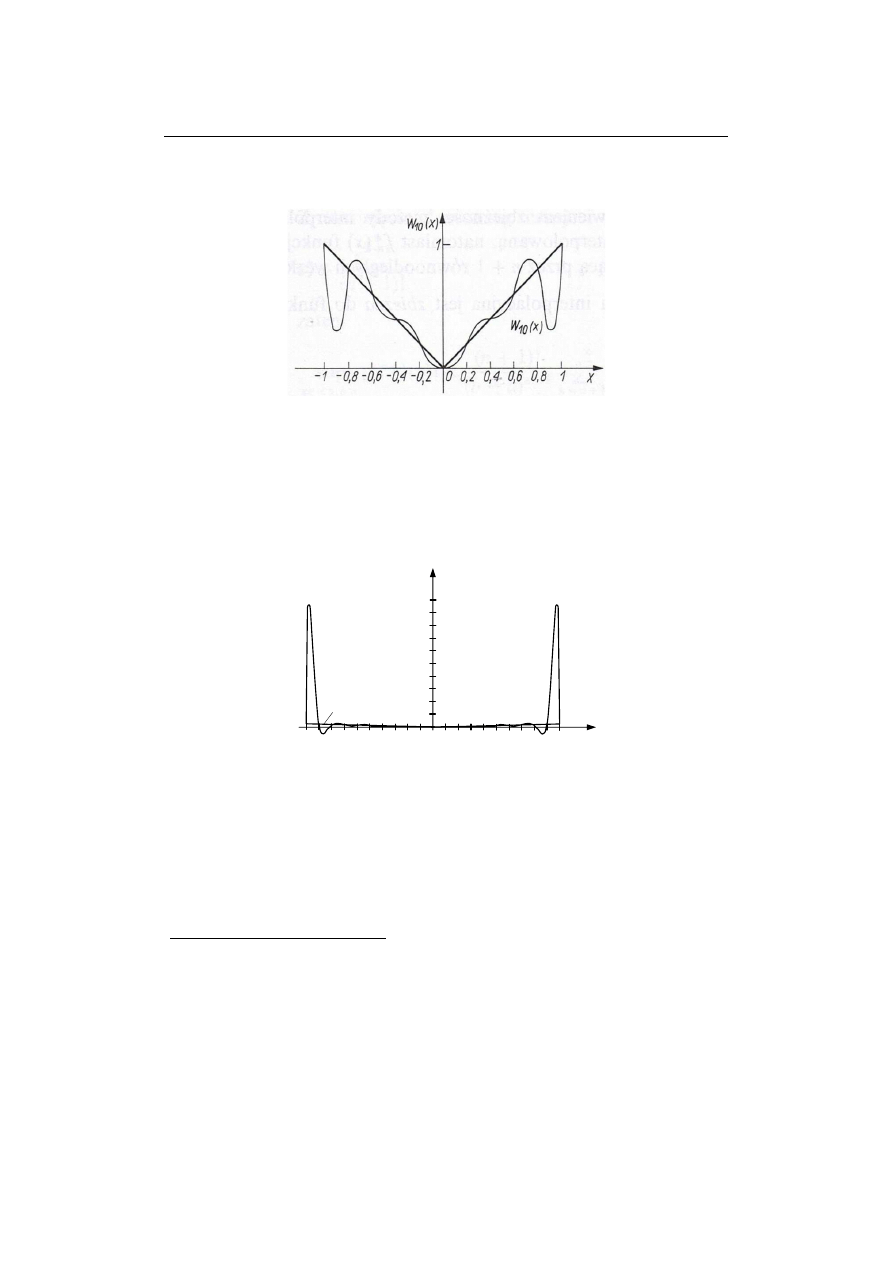
Graficzne przedstawienie tego wielomianu w porównaniu z interpolowaną funkcja
podano na rys. 3.4.
Rys. 3.4 Interpolacja f(x) =
x
w przedziale [-1, 1] wielomianami
W
10
(x)
Jak można zauważyć, zagęszczenie węzłów pogorszyło dokładność przybliżenia na
końcach przedziału. Jedynie w otoczeniu środka nastąpiła poprawa.
Dalsze zagęszczanie jeszcze bardziej pogarsza przybliżenie. Na rys. 3.5 przedsta-
wiona jest interpolacja wielomianem rzędu 20. Zauważyć należy, ze skale na osi
argumentów i wartości funkcji mają się jak 1/100!
Rys. 3.5 Interpolacja f(x) =
x
w przedziale [-1, 1 wielomianem
W
20
(x)
Jak można zauważyć, na krańcach przedziału wartości wielomianu są ponad 100
razy większe niż wartości funkcji, co nie zachodziło przy wielomianach niższych
rzędów. Ze wzrostem rzędu wielomianu różnice te rosną i są szczególnie istotne na
końcach przedziału.
*)
W środku przedziału interpolacji ze wzrostem rzędu wielomianu obserwuje się
natomiast wzrost dokładności przybliżenia.
*)
Taki zachowanie się wielomianów przy stosowaniu węzłów równoodległych jest
zjawiskiem typowym zwłaszcza dla wielomianów wyższych rzędów. Efekt ten nazywany
jest zjawiskiem Runge’go.
40
80
-1,0 -0,8
-
0,6
0,2
0,6
0,8
1,0
-0,4
0
f(x)=|x|
W
20
(x)
y
x
-
0,2
0,4
10
0
60
20
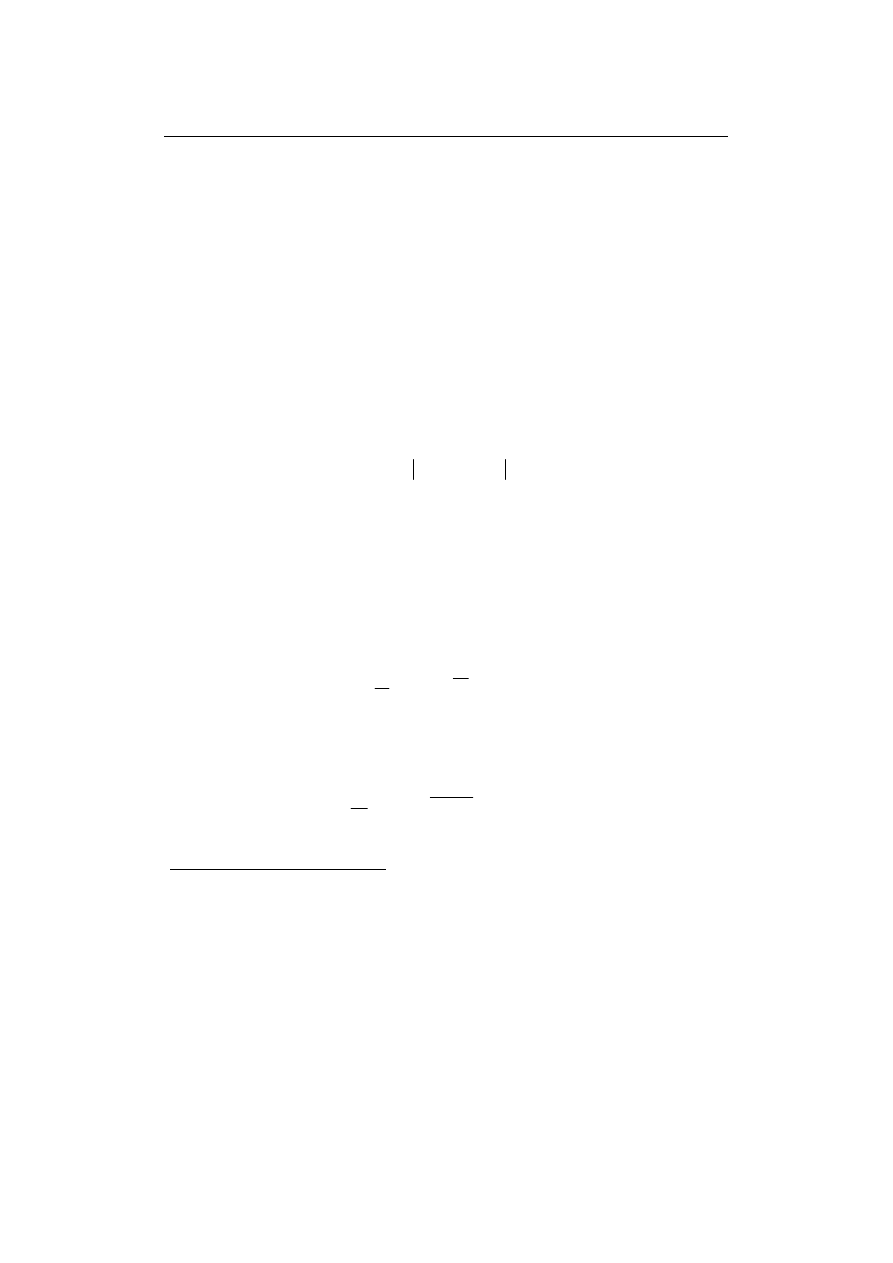
3. Interpolacja
65
Cecha ta jest bardzo istotna w zastosowaniu praktycznym interpolacji
wielomianowej z węzłami równoodległymi. Jeśli funkcja określona jest w postaci
stablicowanej i występuje konieczność zagęszczenia siatki, wówczas stosować
można z powodzeniem interpolację wielomianami wyższych rzędów z węzłami
równoodległymi. Pamiętać jednak należy aby węzły interpolacyjne wybierać tak,
aby wartość argumentu dla którego obliczana będzie wartość wielomianu
znajdowała się w otoczeniu środka przedziału interpolacji.
W przypadku, kiedy zależy nam na dobrym przybliżeniu w całym przedziale
interpolacji podejście takie nie daje zadawalających rezultatów. W przypadkach
takich stosować należy inne funkcje bazowe interpolacji
*)
, interpolacja
wielomianami niższych rzędów w mniejszych podprzedziałach przedziału
interpolacji
**)
czy też zastosowanie węzłów nie równoodległych.
W przypadku ostatnim bardzo istotne a wręcz zasadnicze znaczenie dla
dokładności interpolacji ma położenie węzłów. Położenie węzłów powinno
zapewniać zbieżność jednostajną, tzn.:
{
}
)
(
)
(
max
min
]
,
[
0
x
W
x
f
n
x
x
x
n
−
∈
,
(3.42)
czyli minimalizować maksymalne odchylenie w całym przedziale interpolacji.
Problem ten był badany miedzy innymi przez Czebyszewa. Efektem tych prac są
tzw.
węzły Czebyszewa których położenie zapewnia prawie optymalne wartości
(3.42) dla danego rzędu wielomianu
n.
Rozpatrzmy dla porównania interpolacje z
węzłami równoodległymi i węzłami
Czebyszewa dla funkcji f(x) = 1/(1+25x
2
) i
n=10 w przedziale [-1, 1] (rys.3.6)
***)
.
Dla
n+1 węzłów rownoodległych mamy
****)
n
i
x
i
n
i
2
1
,
1
+
−
=
∀
=
.
(3.43)
Natomiast położenie węzłów Czebyszewa określone jest (dla przedziału
znormalizowanego [-1, 1]) przez [
xxx
]:
+
+
=
∀
=
π
2
2
1
2
cos
,
0
n
i
x
i
n
i
.
(3.44)
*)
Np. interpolacja funkcjami wymiernymi. Należy jednak liczyć się z dużym wzrostem
złożoności obliczeniowej. Algorytmy interpolacji wymiernej można znaleźć np. w [
xxx
].
**)
Podejście takie stosowane jest np. w przypadku złożonych kwadratur całkowania
numerycznego (rozdz. 4) czy też w interpolacji funkcjami sklejanymi (podrozdział 3.3).
***)
Każdy ograniczony przedział interpolacji można poprzez podstawienie sprowadzić do
przedziału znormalizowanego [-1, 1].
****)
Sprawdzenie położenia węzłów pozostawia się jako ćwiczenie Czytelnikowi.
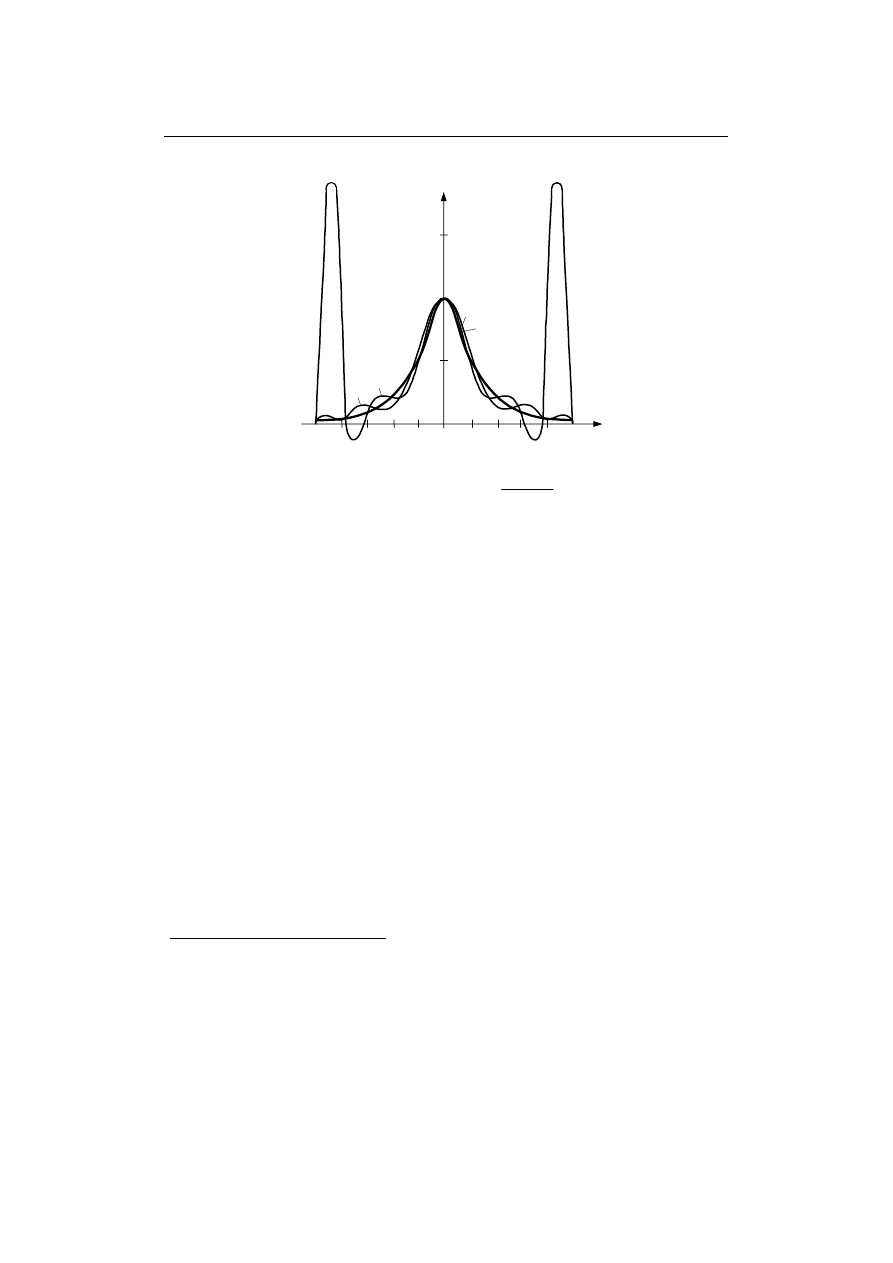
66
Metody numeryczne
Rys. 3.6 Porównanie interpolacji funkcji
2
25
1
1
)
(
x
x
f
+
=
wielomianem W
10
(x)
I – węzły równoodległe
II – węzły Czebyszewa
Analizując rys. 3.6 można zauważyć, że na końcach przedziału następuje
zagęszczenie węzłów w przypadku węzłów Czebyszewa z jednoczesnym
rozsunięciem w otoczeniu środka. Poprawa zbieżności na końcach pogorszyła
jednak dokładność w otoczeniu środka w porównaniu z węzłami równoodległymi.
Można zatem wnioskować, że jeśli zależy nam na dobrej interpolacji
wielomianowej w całym przedziale, to bardziej przydatne jest stosowanie węzłów
Czebyszewa. Jeśli natomiast wymagana jest większa dokładność w otoczeniu
ś
rodka przedziału, to lepsze rezultaty daje nam interpolacja z węzłami
równoodległymi
*)
.
3.3.
Interpolacja funkcjami sklejanymi
W punkcie 3.2.5 rozpatrywano problem zbieżności interpolacji wielomia-
nowej z uwzględnieniem położenia węzłów oraz rzędu wielomianu. Jak
wspomniano, uzyskanie najlepszej zbieżności jednostajnej (minimum normy
maksymalnej (3.42)) jest trudne, a węzły Czebyszewa są rozwiązaniem nie w pełni
optymalnym. Problem jeszcze bardziej będzie się komplikował jeśli przedział
interpolacji będzie bardzo szeroki a funkcja posiada różnorodny przebieg.
*)
Wybór węzłów, rzędu wielomianu czy algorytmu uwarunkowany jest rozwiązywanym
zagadnieniem i należy do rozwiązującego dany problem. Powinien on zapewniać najlepsze
warunki dla rozwiązania danego zagadnienia praktycznego.
y
x
0
1
-1
0,5
1,0
1,5
II
I
I
II
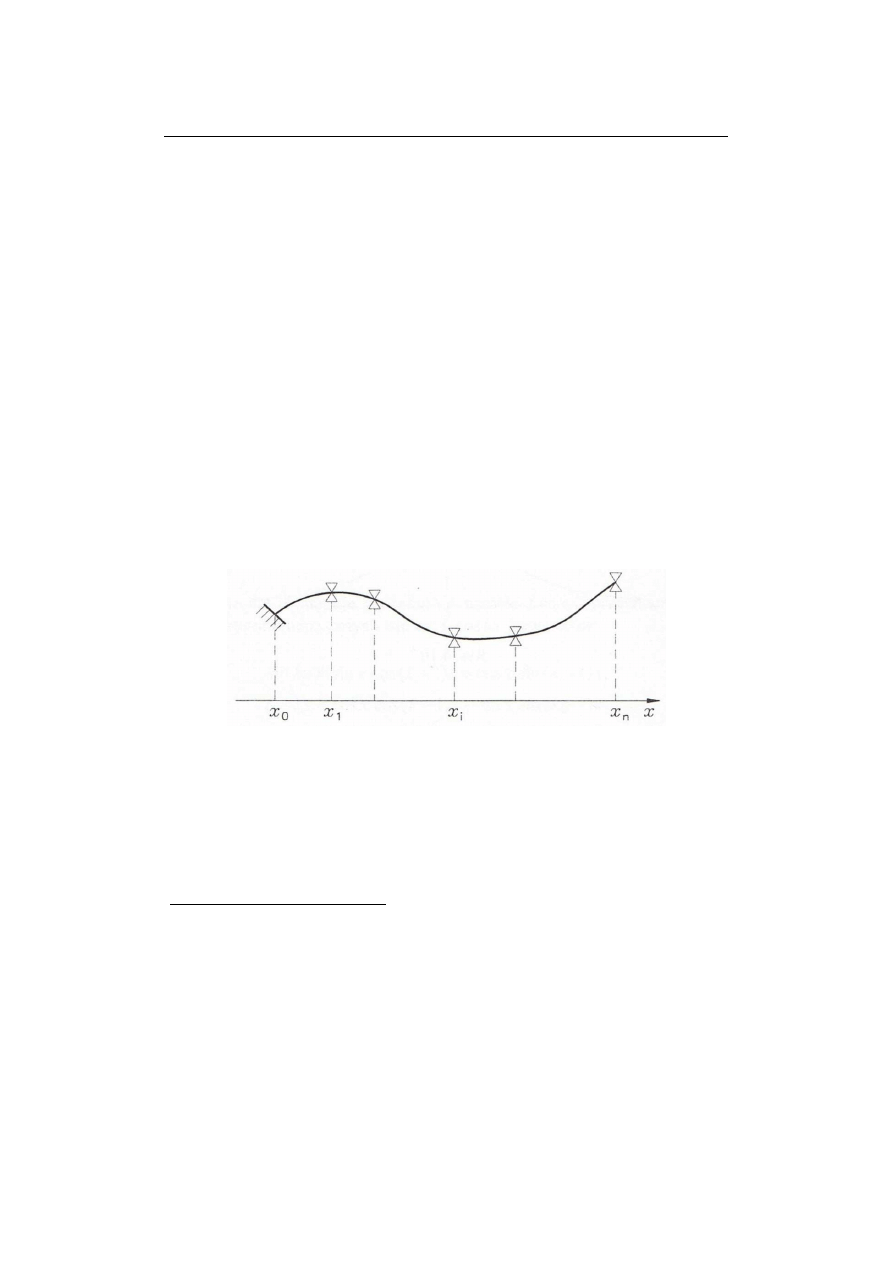
3. Interpolacja
67
3.3.1. Poj
ę
cia podstawowe funkcji sklejanych
Wspomniane trudności prowokowały do poszukiwania innych sposobów
przybliżania funkcji. Jeśli uwzględnimy, że w przypadku wielomianów niskiego
rzędu dokładność w całym szerokim przedziale nie jest zbyt zadawalająca a
wielomiany rzędów wysokich dają efekt Runge’go, naturalnym wydaje się
kompromis. Zamiast jednego wielomianu wysokiego stopnia przybliżającego
funkcje w całym przedziale interpolacji [a, b] zastosować wiele wielomianów
niskiego stopnia, z których każdy przybliża funkcje w innym odpowiednio wąskim
podprzedziale [x
i
, x
i+1
] dla i=0,...,n-1 przedziału interpolacji [a, b]
*)
.
Aby uzyskać przybliżenie funkcji z wymaganą gładkością w całym przedziale
konieczne jest uwzględnienie odpowiednich warunków na sklejenie kolejnych
wielomianów pomiędzy kolejnymi podprzedziałami [x
i
, x
i+1
]. W konsekwencji
otrzymamy gładkie przedziałami wielomianowe funkcje będące zbiorem
wielomianów tego samego odpowiednio niskiego rzędu. W literaturze najczęściej
spotyka się określenie funkcje sklejane (w przypadku wielomianów – wielomia-
nowe funkcje sklejane) czy też spline-funkcje
**)
Określenie spline pochodzi z języka angielskiego i oznacza liniał giętki (giętka)
stosowany do kreślenia i trasowania gładkich linii krzywych przechodzących przez
określone punkty na powierzchni. Giętke można zatem traktować jako swoisty
interpolator fizyczny funkcjami sklejanymi (rys. 3.7) [
xxx
].
Rys. 3.7 Interpolowanie krzywej o danych węzłach za pomocą giętki
Niech są dane węzły x
i
oraz odpowiadające im wartości funkcji f
i
= f(x
i
) określające
punkty interpolacji {x
i
, f
i
} dla i=0,...,n. Niech giętka zostanie przytwierdzona do
punktu {x
0
, f
0
} a następnie ustawiona i podparta w kolejnych punktach {x
i
, f
i
} jak
pokazano na rys. 3.7. W efekcie uzyskano krzywą gładką przechodzącą przez
wszystkie punkty interpolacji.
*)
W dalszej części omawiana jest interpolacja wielomianowymi funkcjami sklejanymi.
Pamiętać jednak należy, że można również stosować inne funkcje bazowe (nie tylko
wielomiany).W skrypcie ograniczono się do wielomianów ze względu na objętość skryptu i
jego zakres.
**)
Można również spotkać określenia s-funkcje, funkcje gięte czy spline’y.

68
Metody numeryczne
Pisząc równanie na równowagę giętki między punktami oraz po dokonaniu
koniecznych do rozwiązania uproszczeń otrzymuje się równanie wielomianowej
funkcji sklejanej trzeciego stopnia [
xxx
]
*)
będące jednocześnie pierwszym
opublikowanym równaniem funkcji sklejanej
**)
.
W przypadku interpolacyjnych wielomianów Lagrange’a, zwiększając liczbę
węzłów zwiększaliśmy rząd wielomianu i wzrastały problemy związane ze
zjawiskiem Runge’go czyli związane ze zbieżnością. Natomiast w przypadku
funkcji sklejanych wzrost liczby węzłów zwiększa liczbę składowych
wielomianów nie zwiększając ich rzędu. W efekcie otrzymujemy funkcje sklejane
coraz lepiej przybliżające interpolowaną funkcje. Ponadto, jak podano w [
xxx
],
optymalne w sensie różnych kryteriów rozwiązania wielu zagadnień fizycznych
wyznaczane są przez funkcje sklejane.
Dla ogólnej interpolacji wielomianowej niech będzie dana siatka (zbiór n+1
węzłów interpolacji) o własności:
b
x
x
x
x
x
a
n
n
n
=
<
<
<
<
<
=
−
1
2
1
0
:
L
∆
.
(3.45)
Ponadto niech
Ω
m
oznacza zbiór wszystkich wielomianów stopnia co najwyżej m
(m
≥
0) a C
(p)
= C
(p)
[a, b] (p
≥
0), zbiór funkcji posiadających ciągle pochodne na
przedziale [a, b] do rzędu p włącznie.
Wielomianową funkcją sklejaną stopnia m z defektem k (1
≤
k
≤
m) dla siatki
(3.45) nazywamy funkcje [P9]
( )
(
)
n
k
m
x
S
x
S
∆
,
,
=
,
(3.46)
spełniającą warunki:
( )
[
]
1
1
,
0
,
+
−
=
∈
∀
i
i
m
i
n
i
x
x
na
x
S
Ω
,
(3.47)
( )
[ ]
b
a
C
x
S
k
m
,
)
(
−
∈
.
(3.48)
Punkty {x
i
} siatki (3.45) nazywamy węzłami funkcji sklejanej, a funkcja S(x) może
mieć nieciągłą pochodną rzędu m–k+1.
***)
Funkcja sklejana stopnia zerowego (warunek (3.48) w tym przypadku nie ma
ż
adnego znaczenia) jest przedziałami stała Przykład takiej funkcji przedstawia rys.
3.8. Funkcja ta definiowana jest jako lewostronnie ciągła w węzłach siatki
∆
n
.
*)
Więcej na temat równania giętki oraz wyprowadzenia można znaleźć w cytowanej
literaturze.
**)
Pierwsza funkcji sklejana została opublikowana przez I.J. Schoenberga w 1946 roku.
***)
Często wygodnie jest wykorzystywać funkcje sklejane mające różną gładkość w
różnych węzłach siatki
∆
n
. Mają one zastosowanie przy przybliżaniu takich funkcji, których
gładkość jest różna w różnych częściach przedziału [a, b].
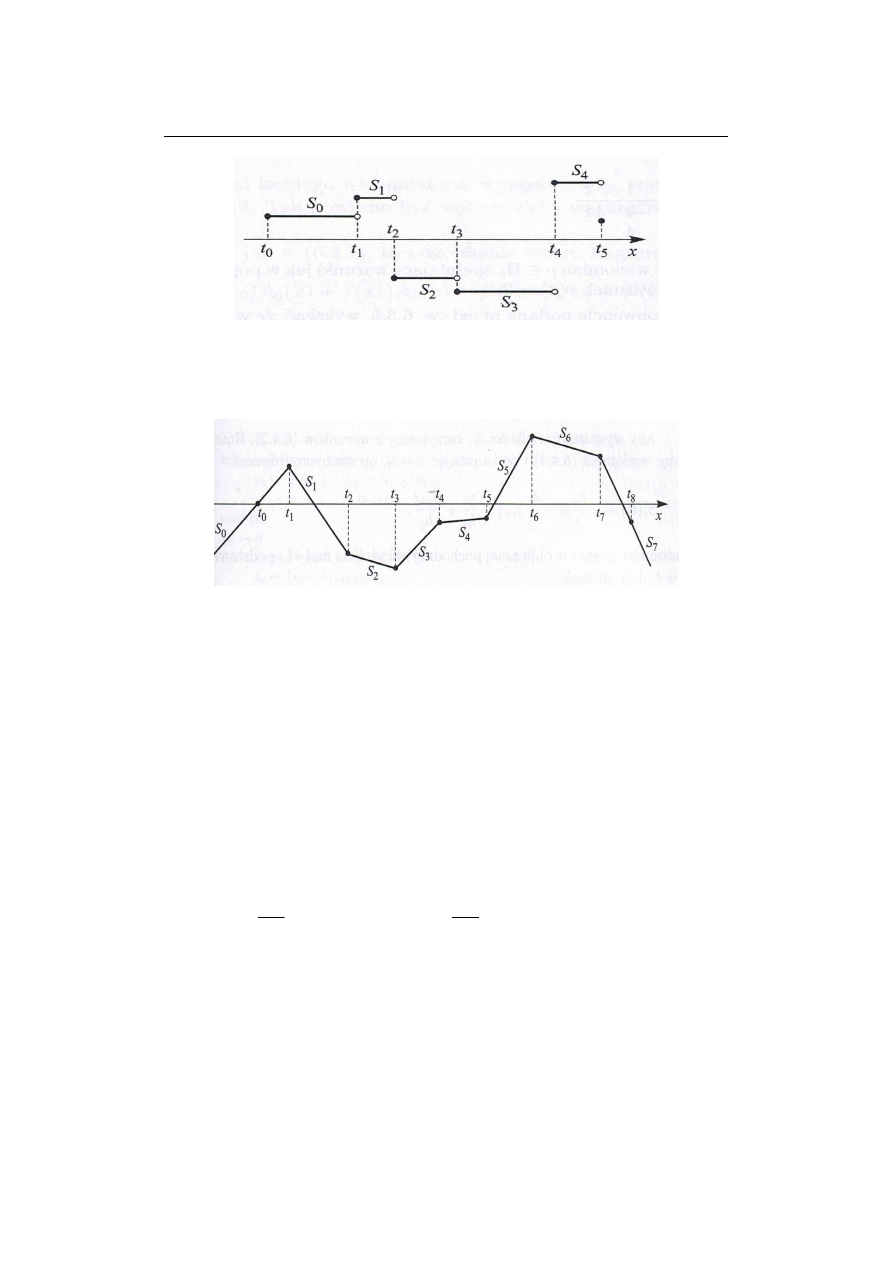
3. Interpolacja
69
Rys. 3.8 Wielomianowa funkcja sklejana stopnia zerowego (m=0)
Przykład funkcji sklejanej stopnia pierwszego (funkcja łamana odcinkami liniowa,
ciągła na [a, b]) z defektem k równym jeden (p=m–k=0) przedstawiono na rys. 3.9.
Rys. 3.9 Wielomianowa funkcja sklejana stopnia pierwszego (m=1)
W powyższym przykładzie warunek (3.48) przechodzi w
( )
[ ]
( )
[ ]
b
a
C
x
S
b
a
C
x
S
k
m
,
,
)
0
(
)
(
∈
→
∈
−
czyli żądanie ciągłości funkcji w poszczególnych węzłach. Warunek ten wiąże
współczynniki wielomianów w sąsiadujących podprzedziałach interpolacji.
Powyższe odpowiada spełnieniu warunków na sklejenie w kolejnych węzłach
x
1
,...,x
n-1
:
(
) (
)
( )
( )
i
i
i
i
i
i
x
S
x
S
x
S
x
S
=
⇒
+
=
−
−
1
0
0
.
W przypadku funkcji sklejanych klasy S(x)
∈
C
(p)
[a, b], czyli ciągłych do p-tej
pochodnej włącznie warunek (3.48) przechodzi w:
– ciągłość funkcji
(
) (
)
( )
( )
i
i
i
i
n
i
i
i
n
i
x
S
x
S
x
S
x
S
=
⇒
−
=
+
−
−
=
−
=
∀
∀
1
1
,
1
1
,
1
0
0
,
(3.49)
– ciągłość pierwszej pochodnej

70
Metody numeryczne
(
)
(
)
( )
( )
i
i
i
i
n
i
i
i
n
i
x
S
x
S
x
S
x
S
′
=
′
⇒
−
′
=
+
′
−
−
=
−
=
∀
∀
1
1
,
1
1
,
1
0
0
,
(3.50)
– ciągłość drugiej pochodnej
(
)
(
)
( )
( )
i
i
i
i
n
i
i
i
n
i
x
S
x
S
x
S
x
S
′′
=
′′
⇒
−
′′
=
+
′′
−
−
=
−
=
∀
∀
1
1
,
1
1
,
1
0
0
,
(3.51)
– i dalej aż do warunku ciągłość
p-tej pochodnej
(
)
(
)
( )
( )
i
p
i
i
p
i
n
i
i
p
i
p
n
i
x
S
x
S
x
S
x
S
)
(
)
(
1
1
,
1
)
(
)
(
1
,
1
0
0
=
⇒
−
=
+
−
−
=
−
=
∀
∀
.
(3.52)
Warto zauważyć, że jeśli rozpatrujemy wielomianowe funkcje sklejane stopnia n,
to wszystkie jej pochodne do p-tej włącznie (p=n–1) są również funkcjami
wielomianami o malejącym stopniu. Funkcja sklejana p–tej pochodnej jest
wielomianową funkcją sklejaną pierwszego stopnia (rys.3.9).
W rozpatrywanym w następnym punkcie przypadku wielomianowej funkcji
sklejanej trzeciego stopnia, istotne są warunki sklejenia (3.49) – (3.51).
*)
3.3.2. Wielomianowe funkcje sklejane trzeciego stopnia
Rozpatrzmy dalej zagadnienie interpolacji wielomianową funkcją sklejaną
stopnia trzeciego.
**)
Dla (3.46) – (3.48) mamy:
– wielomianowa funkcja sklejana trzeciego stopnia z defektem jeden
( )
(
)
n
x
S
x
S
∆
,
1
,
3
=
,
– poszczególne wielomiany S
i
(x) w podprzedziałach [x
i
, x
i+1
] są stopnia najwyżej
trzeciego
( )
[
]
1
3
1
,
0
,
+
−
=
∈
∀
i
i
i
n
i
x
x
na
x
S
Ω
,
– funkcja interpolująca w przedziale [a, b] jest ciągła wraz z pierwszą i drugą
pochodną
( )
[ ]
b
a
C
x
S
,
)
2
(
∈
.
Niech w i-tym podprzedziale [x
i
, x
i+1
] funkcja S(x) określona jest przez:
*)
Jeśli interpolujemy wielomianową funkcją sklejaną stopnia m, wówczas ciągłość
pochodnych jest zachowana do p=m–1.
**)
Wielomiany trzeciego stopnia mają bardzo szerokie zastosowanie w praktyce. Wynika to
głównie z niskiego stopnia wielomianu (brak zjawiska Runge’go), wystarczająca zbieżność
oraz prostota algorytmów obliczeniowych.
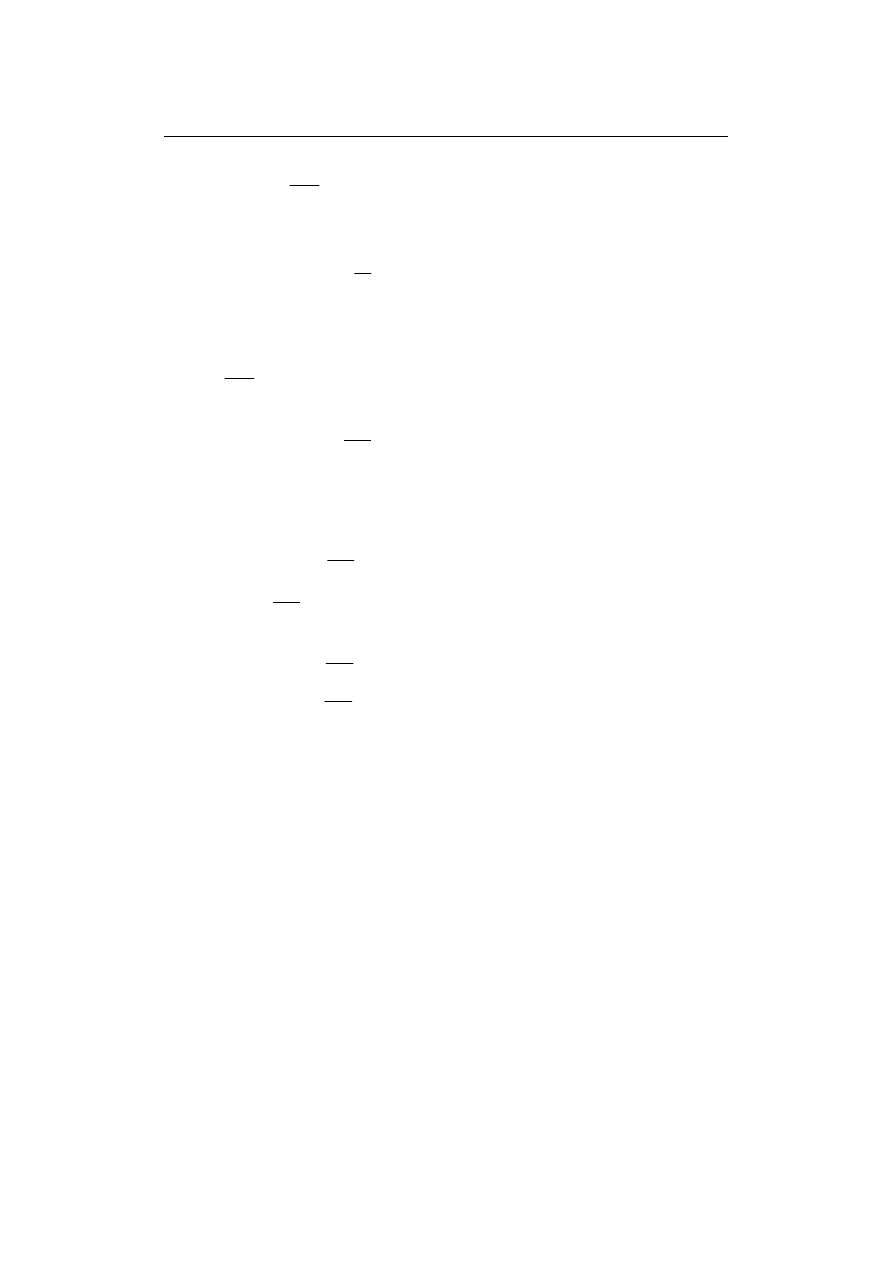
3. Interpolacja
71
( )
( )
.
2
3
1
,
0
i
i
i
i
i
n
i
d
x
c
x
b
x
a
x
S
x
S
+
+
+
=
=
∀
−
∈
(3.53)
Funkcja
S(x) jest sklejaną funkcją interpolacyjną trzeciego stopnia funkcji f(x)jeśli:
( ) ( )
,
,
0
i
i
i
n
i
f
x
f
x
S
=
=
∀
∈
(3.54)
co w połączeniu z (3.53) i warunkiem na ciągłość funkcji (3.49) daje
( )
( )
=
+
+
+
=
=
=
+
+
+
=
=
+
+
+
+
+
+
−
∈
∀
1
1
2
1
3
1
1
1
2
3
1
,
0
)
(
)
(
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
n
i
f
d
x
c
x
b
x
a
x
S
x
S
f
d
x
c
x
b
x
a
x
S
x
S
,
(3.55)
oraz
( )
( )
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
n
i
d
x
c
x
b
x
a
d
x
c
x
b
x
a
x
S
x
S
+
+
+
=
+
+
+
⇒
⇒
=
−
−
−
−
−
−
∈
∀
2
3
1
1
2
1
3
1
1
1
,
1
.
(3.56)
Dalej z warunku na ciągłość pierwszej i drugiej pochodnej (3.50) i (3.51) jest:
( )
( )
,
2
3
2
3
)
(
2
1
1
2
1
1
,
1
1
1
,
1
i
i
i
i
i
i
i
i
i
i
n
i
i
i
i
i
i
n
i
c
x
b
x
a
c
x
b
x
a
x
S
x
S
x
S
+
+
=
+
+
⇒
′
=
′
=
′
−
−
−
−
∈
−
−
∈
∀
∀
(3.57)
oraz
( )
( )
.
2
6
2
6
)
(
1
1
1
,
1
1
1
,
1
i
i
i
i
i
i
n
i
i
i
i
i
i
n
i
b
x
a
b
x
a
x
S
x
S
x
S
+
=
+
⇒
′′
=
′′
=
′′
−
−
−
∈
−
−
∈
∀
∀
(3.58)
Zauważmy, że mając n podprzedziałów w których funkcja interpolująca w danym
podprzedziale jest wielomianem trzeciego stopnia otrzymujemy 4n współczynniki
wielomianów (a
i
, b
i
, c
i
, d
i
dla i=0, ..., n–1). Z warunków (3.55) otrzymujemy 2n
równań liniowych a z (3.57) i (3.58) po n–1 równań również liniowych. W
konsekwencji uzyskujemy 4n–2 równania liniowe z 4n zmiennymi. Aby układ był
jednoznacznie określony konieczne jest jego uzupełnienie dwoma dodatkowymi
warunkami. Wybór warunków dodatkowych zależy od własności interpolowanej
funkcji oraz od wiedzy o tej funkcji.
Najczęściej rozpatrywane są warunki dodatkowe:
(
)
( )
(
)
( )
2
1
1
0
0
0
0
,
0
α
α
=
′
=
−
′
=
′
=
+
′
−
n
n
n
x
S
x
S
x
S
x
S
.
(3.59)
lub
(
)
( )
(
)
( )
2
1
1
0
0
0
0
,
0
β
β
=
′′
=
−
′′
=
′′
=
+
′′
−
n
n
n
x
S
x
S
x
S
x
S
,
(3.60)
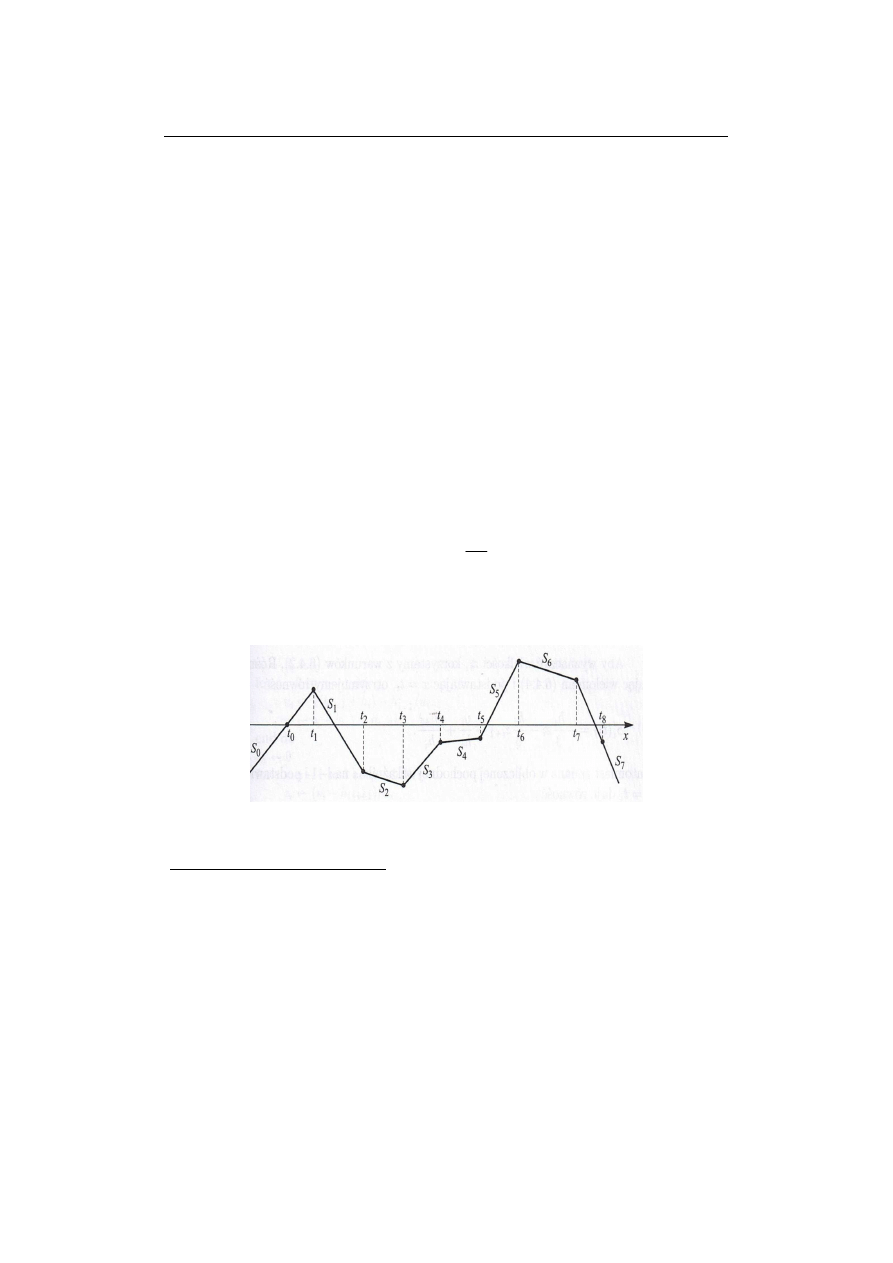
72
Metody numeryczne
gdzie
α
1
,
α
2
,
β
1
,
β
2
ustalone liczby rzeczywiste.
W przypadku gdy interpolowana funkcja jest funkcją okresową o okresie b–a (x
n
–
x
o
) wówczas żądamy aby funkcję sklejaną rozszerzyć na ]-
∞
,
∞
[ i jednocześnie
funkcja ta będzie różniczkowalna w sposób ciągły.
W tym przypadku należy spełnić warunki:
(
)
(
)
( )
( )
n
n
n
x
S
x
S
x
S
x
S
1
0
0
0
0
0
−
′
=
′
⇒
−
′
=
+
′
,
(3.61)
oraz
(
)
(
)
( )
( )
n
n
n
x
S
x
S
x
S
x
S
1
0
0
0
0
0
−
′′
=
′′
⇒
−
′′
=
+
′′
.
(3.62)
Tworząc równania z warunków (3.55) oraz (3.57) i (3.58) i uzupełniając o (3.59)
albo (3.60) albo (3.61) i (3.62) otrzymamy układ 4n równań liniowych z 4n
niewiadomymi.
W
wyniku
jego
rozwiązania
otrzymujemy
parametry
poszczególnych wielomianów interpolujących S
i
(x) (a
i
, b
i
, c
i
, d
i
dla i=0, ..., n–1)
wielomianowej funkcji sklejanej trzeciego stopnia S(x) na przedziale [a, b].
*)
Rozpatrzmy teraz stosowany algorytm dla ogólnego przypadku w którym
siatka (3.45) zawiera węzły dowolnie odległe.
Oznaczmy wartości drugich pochodnych w poszczególnych węzłach:
**)
( )
n
i
M
x
S
i
i
,
0
,
=
=
′′
.
(3.62)
Z własności wielomianów trzeciego stopnia wynika, że druga pochodna określona
jest wielomianem stopnia pierwszego (patrz (3.58)), a z warunku na ciągłość jest
linią łamaną.
Rys. 3.10. Zależność
( )
[
]
i
i
x
x
x
S
,
e
al
podprzedzi
na
1
−
′′
*)
Podane podejście do rozwiązania problemu wyznaczania wielomianowej funkcji
sklejanej ma na celu jedynie ogólne zobrazowanie metody. W praktyce algorytm
konstruowany jest tak, aby wykorzystać powiązania wynikające z warunków ciągłości.
Pozwala to na zmniejszenie wymiaru układu równań. Podejście takie omawiane jest w
dalszej części tego podrozdziału jak i w podrozdziale 3.3.3.
**)
Wartości te nie są znane. Stanowić będą dalej poszukiwane rozwiązanie! Wszystkie
parametry wyznaczanej funkcji sklejanej będą zależne od tych wartości.

3. Interpolacja
73
Napiszmy równanie pierwszego stopnia (druga pochodna wielomianu trzeciego
stopnia) przechodzące przez punkty węzłowe (x
i-1
,M
1-1
) oraz (x
i
,M
1
)
( )
]
[
i
i
i
i
i
i
i
i
i
i
i
x
x
x
x
x
h
h
x
x
M
h
x
x
M
x
S
,
,
,
1
1
1
1
−
−
−
−
∈
−
=
−
+
−
=
′′
.
(3.63)
Całkując obustronnie równanie (3.63) otrzymamy równanie dla pierwszej
pochodnej
( )
(
)
(
)
]
[
i
i
i
i
i
i
i
i
i
x
x
x
A
h
x
x
M
h
x
x
M
x
S
,
,
2
2
1
2
1
2
1
−
−
−
∈
+
−
+
−
−
=
′
.
(3.64)
Całkując ponownie obustronnie (3.64) otrzymujemy funkcje sklejaną
( )
(
)
(
)
(
)
]
[
i
i
i
i
i
i
i
i
i
i
i
x
x
x
B
x
x
A
h
x
x
M
h
x
x
M
x
S
,
,
6
6
1
1
3
1
3
1
−
−
−
−
∈
+
−
+
−
+
−
−
=
, (3.65)
gdzie A
j
i B
j
są stałymi całkowania (3.63) oraz (3.64).
W celu wyznaczenia stałych A
j
i B
j
na (3.64) i (3.65) nałóżmy warunki interpolacji
(3.55) i (3.57).
( )
( )
=
+
+
=
=
+
=
−
−
−
.
6
,
6
2
1
2
1
1
i
i
i
i
i
i
i
i
i
i
i
i
f
B
h
A
h
M
x
S
f
B
h
M
x
S
(3.66)
Z (3.66) wyznaczmy stale A
j
i B
j
(
)
−
−
−
=
−
−
=
−
=
−
−
−
−
.
6
6
1
,
6
1
2
1
2
2
1
1
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
M
M
h
h
f
f
h
M
B
f
h
A
h
M
f
B
(3.67)
Wartości pierwszej pochodnej w węzłach
(
)
( )
(
)
( )
−
+
−
−
=
′
=
+
′
−
=
+
=
′
=
−
′
+
+
+
+
+
−
−
−
,
6
3
0
,
3
6
0
1
1
1
1
1
1
1
1
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
h
f
f
M
h
M
h
x
S
x
S
h
f
f
M
h
M
h
x
S
x
S
(3.67)
muszą spełniać warunek ciągłości
(
) (
)
( )
( )
.
1
,
1
,
0
0
1
−
=
′
=
′
⇒
+
′
=
−
′
−
n
i
x
S
x
S
x
S
x
S
i
i
i
i
i
i
,
(3.68)
74
Metody numeryczne
czyli zachodzi
( )
( )
.
6
3
6
1
1
1
1
1
1
1
1
1
,
1
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
n
i
h
f
f
h
f
f
M
h
M
h
h
M
h
x
S
x
S
−
+
+
+
+
+
−
−
−
=
−
−
−
=
+
+
+
⇒
⇒
′
=
′
∀
(3.69)
Dokonując podstawienia dla
1
,
1
−
=
n
i
:
,
1
1
+
+
+
=
i
i
i
i
h
h
h
λ
i
i
λ
µ
−
=
1
,
−
−
−
+
=
−
+
+
+
i
i
i
i
i
i
i
i
i
h
f
f
h
f
f
h
h
1
1
1
1
6
δ
.
warunki (3.69) przyjmują prostą postać
*)
( )
( )
i
i
i
i
i
i
i
i
i
i
n
i
M
M
M
x
S
x
S
δ
λ
µ
=
+
+
⇒
′
=
′
+
−
−
−
=
∀
1
1
1
1
,
1
2
.
(3.70)
Powyższa zależność opisuje
n-1 równań. Liczba poszukiwanych zmiennych
rozwiązania wynosi
n+1, zatem mamy dwa stopnie swobody. Do pełnego
sformułowania zadania dodajmy dwa dodatkowe warunki zależne od
rozwiązywanego problemu (3.59) albo (3.60) lub (3.61) i (3.62).
Dla warunku (3.59) czyli
(
)
( )
(
)
( )
2
1
1
0
0
0
0
,
0
α
α
=
′
=
−
′
=
′
=
+
′
−
n
n
n
x
S
x
S
x
S
x
S
mamy
n
n
n
M
M
M
M
δ
δ
=
+
=
+
−
2
,
2
1
0
1
0
(3.71)
gdzie:
−
−
=
1
1
0
1
1
0
6
α
δ
h
f
f
h
,
−
−
=
−
n
n
n
n
n
h
f
f
h
1
2
6
α
δ
.
Dla warunku (3.60)
(
)
( )
(
)
( )
2
1
1
0
0
0
0
,
0
β
β
=
′′
=
−
′′
=
′′
=
+
′′
−
n
n
n
x
S
x
S
x
S
x
S
jest
*)
Warto zwrócić uwagę na fakt, że w każdym równaniu występują tylko trzy niewiadome
(M
i-1
, M
i
, M
i+1
oraz kolejne równania różnią się tylko jedną zmienną!

3. Interpolacja
75
2
1
0
,
β
β
=
=
n
M
M
.
(3.72)
Natomiast z warunków dla funkcji okresowej (3.61) i (3.62)
(
)
(
)
( )
( )
n
n
n
x
S
x
S
x
S
x
S
1
0
0
0
0
0
−
′
=
′
⇒
−
′
=
+
′
(
)
(
)
( )
( )
n
n
n
x
S
x
S
x
S
x
S
1
0
0
0
0
0
−
′′
=
′′
⇒
−
′′
=
+
′′
mamy
n
n
n
n
n
n
M
M
M
M
M
δ
µ
λ
=
+
+
=
−
1
1
0
,
(3.73)
gdzie:
,
1
1
n
n
h
h
h
+
=
λ
n
n
λ
µ
−
=
1
,
−
−
−
+
=
−
n
n
n
n
n
h
f
f
h
f
f
h
h
1
1
0
1
1
6
δ
.
W wyniku otrzymujemy układ stworzony z (3.70) (
n-1 równań) i uzupełniony
przez (3.71) lub (3.72) lub (3.73) dający
n+1 równań z n+1 parametrami.
*)
Dla warunków dodatkowych (3.71) czyli (3.59) otrzymujemy:
=
×
−
−
−
−
n
n
n
n
n
n
M
M
M
M
M
δ
δ
δ
δ
δ
λ
µ
µ
λ
µ
1
2
1
0
1
2
1
0
1
1
2
1
1
2
1
0
0
0
0
2
0
0
0
0
0
0
2
0
0
0
0
2
0
0
0
0
1
2
M
M
L
L
M
M
M
O
M
M
M
L
L
L
.
(3.74)
Otrzymany układ równań charakteryzuje się specyficzną strukturą macierzy, tzw.
macierz trójdiagonalna. Nadto istotne jest, że wszystkie współczynniki
µ
i
oraz
λ
i
są
mniejsze od jeden, zatem macierz ta jest diagonalnie dominująca.
**)
Zaznaczyć należy, że dla układów równań z macierzami trójdiagonalnymi
diagonalnie dominującymi opracowano specjalne efektywne algorytmy ich
rozwiązywania. Zagadnienia te przedstawiono w rozdz. 6 i 7 przy omawianiu
metod rozwiązywania układów równań liniowych.
*)
Zauważmy, że poszukując wartości współczynników wielomianów trzeciego stopnia w
postaci jawnej (3.53) mieliśmy 4n równania o 4n poszukiwanych parametrach. Przy
omawianym podejściu zredukowano zagadnienie do n+1 równań z n+1 parametrami!
**)
Macierzą diagonalnie dominującą nazywamy macierz w której moduły elementów na
przekątnej są większe od sumy modułów pozostałych elementów w tym samym wierszu.

76
Metody numeryczne
Na zakończenie rozpatrzy problem interpolacji wielomianową funkcją
sklejaną trzeciego stopnia przy węzłach równoodległych.
Przy węzłach równoodległych węzły siatki (3.45) na przedziale [a, b] określone są
przez długość kroku
n
a
b
h
n
i
ih
x
x
a
x
i
−
=
=
+
=
=
,
,
1
dla
,
0
0
.
(3.75)
Ponieważ na mocy (3.75)mamy
const
h
h
i
n
i
=
=
∀
∈
,
1
,
(3.76)
zatem
2
1
1
,
1
=
=
∀
−
∈
i
i
n
i
λ
µ
.
(3.77)
Układ (3.74) przechodzi w
=
×
−
−
n
n
n
n
M
M
M
M
M
δ
δ
δ
δ
δ
1
2
1
0
1
2
1
0
2
1
0
0
0
0
2
1
2
2
1
0
0
0
0
0
0
2
2
1
0
0
0
0
2
1
2
2
1
0
0
0
0
1
2
M
M
L
L
M
M
M
O
M
M
M
L
L
L
.
(3.78)
Rozwiązując powyższy układ równań liniowych otrzymujemy wartości drugich
pochodnych w węzłach siatki. Podstawiając uzyskane wartości do (3.67)
otrzymujemy wartości stałych całkowania i w efekcie wszystkie parametry
interpolacji wielomianową funkcją sklejaną trzeciego stopnia (3.65) oraz
pochodnej (3.64).
3.3.3. B-funkcje sklejane trzeciego stopnia
Innym bardzo praktycznym podejściem do interpolacji wielomianową funkcją
sklejaną jest zastosowanie funkcji bazowych o ograniczonych nośnikach.
*)
Ze względu na kształt funkcji (przypominający dzwon), funkcje te nazywane są
funkcjami dzwonowymi (ang. bell) lub też B-funkcjami.
Znormalizowaną B-funkcje sklejaną stopnia m rozpiętą na węzłach:
x
i
, x
i+1
, ... ,x
i+m+1
określa się przez [
xxx
]:
*)
Inaczej, funkcji określonych na całej osi liczbowej ale jedynie w skończonym przedziale
różnych od zera.

3. Interpolacja
77
( )
[
]
[
]
∉
∈
=
+
+
=
∀
1
1
0
,
0
,
0
,
1
i
i
i
i
i
n
i
x
x
x
dla
x
x
x
dla
x
B
(3.79)
oraz zależność rekurencyjną:
( )
( )
( )
0
,
1
1
1
1
1
1
,
0
>
−
−
+
−
−
=
+
−
+
+
+
+
+
−
+
=
∀
m
x
B
x
x
x
x
x
B
x
x
x
x
x
B
i
m
i
m
i
m
i
i
m
i
m
i
i
i
m
n
i
.
(3.80)
Z (3.80) wynika pochodna
B-funkcji:
( )
( )
( )
x
B
x
x
m
x
B
x
x
m
dx
x
dB
i
m
i
m
i
i
m
i
m
i
i
m
n
i
1
1
1
1
1
,
0
+
−
+
+
+
−
+
=
−
−
−
=
∀
.
(3.81)
Z (3.79), (3.80) oraz (3.81) wynika, że funkcje
( )
x
B
i
m
są na siatce
n
∆
wielomianowymi funkcjami sklejanymi stopnia m z defektem jeden.
*)
Funkcje (3.80) są liniowo niezależne i mogą stanowić bazę dla wielomianowych
funkcji sklejanych stopnia m z defektem jeden po uzupełnieniu siatki
b
x
x
x
x
x
a
n
n
n
=
<
<
<
<
<
=
−
1
2
1
0
:
L
∆
dodatkowymi punktami:
.
,
1
0
1
m
n
n
n
m
x
x
x
b
x
a
x
x
+
+
−
−
<
<
<
=
=
<
<
<
L
L
.
(3.82)
Każdą wielomianową funkcje sklejana stopnia m z defektem jeden można
jednoznacznie określić przez:
)
(
)
(
1
x
B
x
S
i
m
n
m
i
i
m
∑
−
−
=
=
γ
,
(3.83)
gdzie jest:
.
1
)
(
1
=
∑
−
−
=
x
B
n
m
i
i
m
(3.84)
Funkcje pierwszego stopnia otrzymamy z (3.79) oraz zależności rekurencyjnej
(3.80):
*)
Tak samo jak w przypadku funkcji sklejanych opisanych w p. 3.3.2.
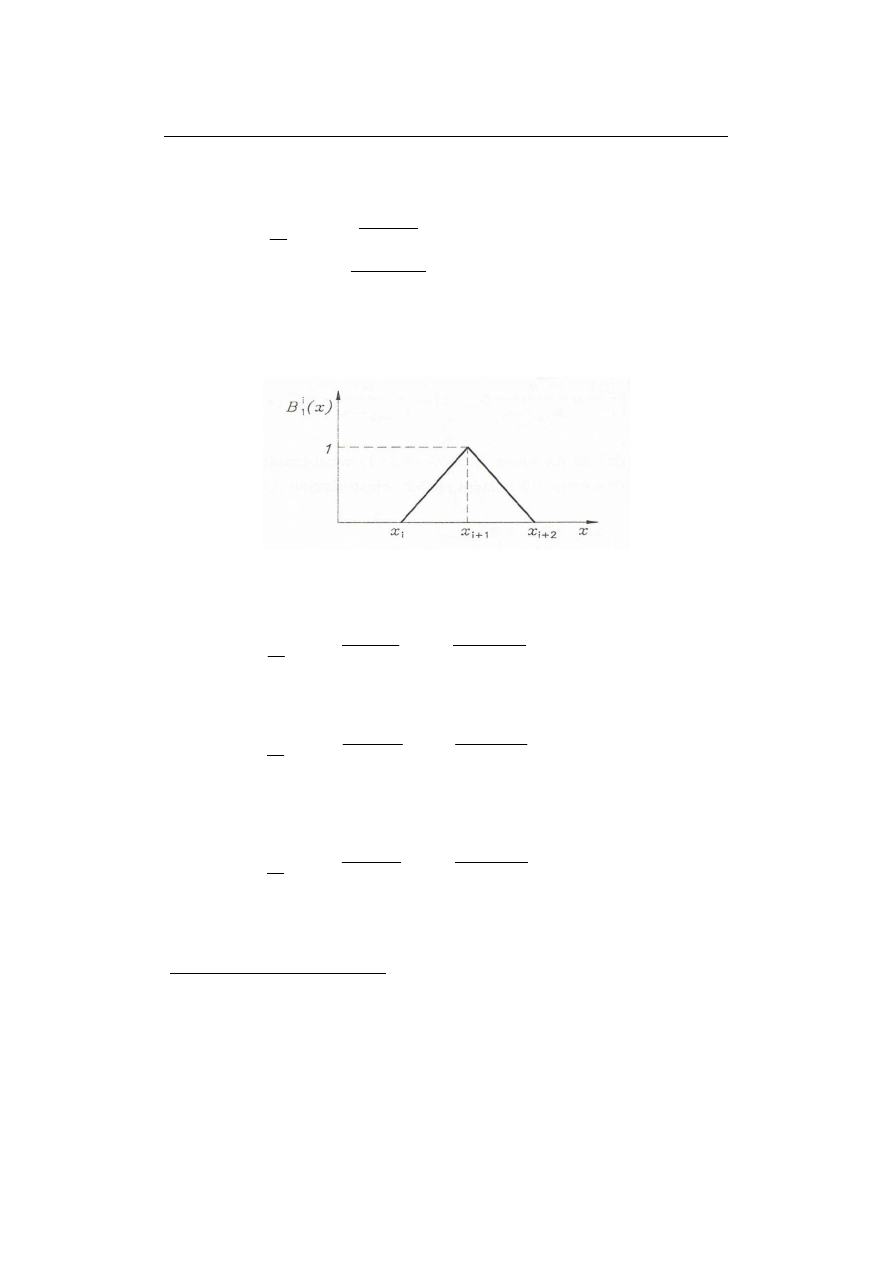
78
Metody numeryczne
]
[
≤
≤
−
−
≤
≤
−
−
∉
=
+
+
+
+
+
+
+
+
=
∀
2
1
1
2
2
1
1
2
1
,
0
,
0
)
(
i
i
i
i
i
i
i
i
i
i
i
i
i
n
i
x
x
x
dla
x
x
x
x
x
x
x
dla
x
x
x
x
x
x
x
dla
x
B
.
(3.85)
Przebieg funkcji
)
(
1
x
B
i
określoną dla przedziału [
x
i
,
x
i+1
] przedstawiono na rys.
3.11. Funkcja ta jest kawałkami liniowa i sama w sobie jest funkcją sklejaną
pierwszego stopnia.
*)
Rys. 3.11. Zależność
( )
[
]
2
1
,
ale
podprzedzi
na
+
i
i
i
x
x
x
B
Dokonując podstawienia (3.79) do zależności rekurencyjnej (3.80) mamy:
( )
( )
x
B
x
x
x
x
x
B
x
x
x
x
x
B
i
i
i
i
i
i
i
i
i
n
i
1
0
1
2
2
0
1
1
,
0
)
(
+
+
+
+
+
=
−
−
−
−
−
=
∀
.
(3.86)
Dalej podstawiając (3.86) do (3.80) jest:
( )
( )
x
B
x
x
x
x
x
B
x
x
x
x
x
B
i
i
i
i
i
i
i
i
i
n
i
1
1
1
3
3
1
2
2
,
0
)
(
+
+
+
+
+
=
−
−
−
−
−
=
∀
.
(3.87)
Dokonując kolejnego podstawienia do rekurencji otrzymujemy B-sklejaną funkcje
trzeciego stopnia:
( )
( )
x
B
x
x
x
x
x
B
x
x
x
x
x
B
i
i
i
i
i
i
i
i
i
n
i
1
2
1
4
4
2
3
3
,
0
)
(
+
+
+
+
+
=
−
−
−
−
−
=
∀
.
(3.88)
Zależność ta po podstawieniach i przekształceniach przyjmuje postać:
*)
Ze względu na kształt (rys. 3.11) często nazywane są funkcjami daszkowymi.

3. Interpolacja
79
]
[
≤
≤
−
−
≤
≤
−
−
+
+
−
−
≤
≤
−
−
+
−
−
≤
≤
−
−
∉
=
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
=
∀
4
3
3
4
3
2
2
3
2
3
3
2
1
1
2
1
1
2
2
1
1
4
3
,
0
2
,
0
)
(
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
n
i
x
x
x
dla
x
x
x
x
C
x
x
x
dla
x
x
x
x
C
x
x
x
x
B
x
x
x
dla
x
x
x
x
B
x
x
x
x
A
x
x
x
dla
x
x
x
x
x
x
x
dla
x
B
(3.89)
gdzie:
(
)
(
)
)
(
2
3
2
i
i
i
i
i
i
x
x
x
x
x
x
A
−
−
−
=
+
+
,
(
)(
)
(
)
(
)(
)
(
)
)
(
)
(
1
3
1
4
4
1
1
3
3
3
+
+
+
+
+
+
+
+
+
+
−
−
−
−
+
−
−
−
−
=
i
i
i
i
i
i
i
i
i
i
i
i
i
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
B
,
(
)
(
)
)
(
2
4
1
4
2
4
+
+
+
+
+
−
−
−
=
i
i
i
i
i
i
x
x
x
x
x
x
C
.
W praktycznych zastosowaniach najczęściej przyjmowane są węzły równoodległe.
Przyjmując odległość pomiędzy kolejnymi węzłami
h=x
i+1
-
x
i
=const oraz
przyjmując jako węzeł środkowy
x
i+2
=0 mamy (rys. 3.12):
*)
(
)
(
)
≥
≤
≤
−
≤
≤
+
−
≤
≤
−
+
−
−
−
≤
≤
−
+
−
≤
=
h
x
dla
h
x
h
dla
x
h
h
x
dla
h
hx
x
x
h
dla
h
hx
x
h
x
h
dla
h
x
h
x
dla
h
x
B
2
0
2
2
0
4
6
3
0
4
6
3
2
2
2
0
1
)
(
3
3
2
3
3
2
3
3
3
(3.90)
*)
Ponieważ dalej rozpatrywana jest B-funkcja sklejana trzeciego stopnia pomijany jest
indeks 3 (
( ) ( )
x
B
x
B
≡
3
).
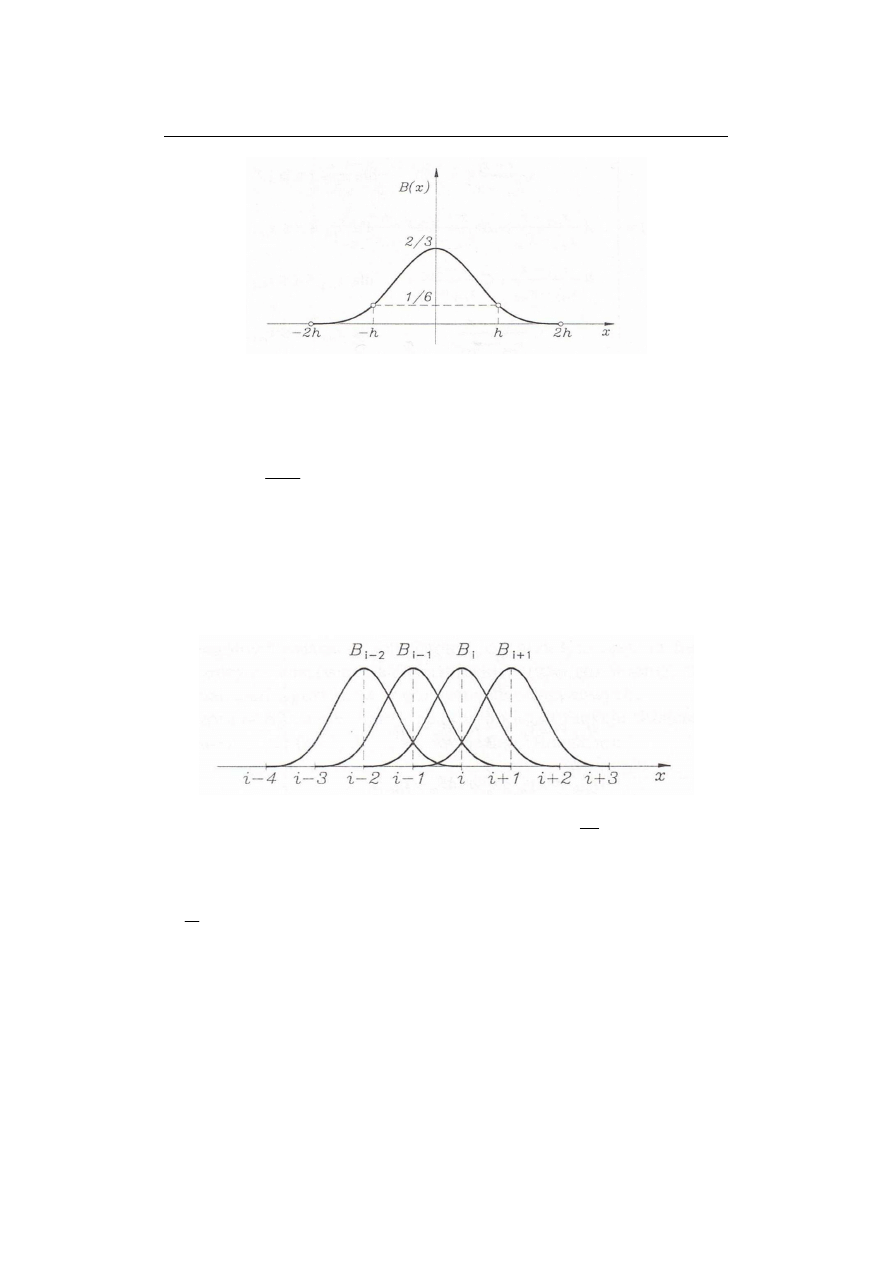
80
Metody numeryczne
Rys. 3.12. Zależność
( )
[
]
h
h
x
B
2
,
2
ale
podprzedzi
na
−
Mając określoną funkcje trzeciego stopnia w postaci (3.90), wszystkie funkcje
( )
x
B
i
określamy przez (rys. 3.13):
( ) (
) (
)
]
[
∞
∞
−
∈
−
=
−
=
∀
+
−
=
,
,
1
,
1
x
ih
x
B
x
x
B
x
B
i
i
n
i
,
(3.91)
co definiuje bazę w przestrzeni wielomianowych funkcji sklejanych trzeciego
stopnia.
Funkcje sklejaną (3.83) stosując funkcje bazowe (3.91) można przedstawić:
)
(
)
(
)
(
1
1
3
x
B
x
S
x
S
i
n
i
i
∑
+
−
=
=
=
γ
,
(3.92)
Rys. 3.13. Funkcje bazowe w otoczeniu węzła x
i
Uwzględniając, że w każdym podprzedziale [
x
i-1
,
x
i
] dla
n
i
,
1
=
nie znikają tylko
cztery składniki sumy, (3.92) przechodzi w (patrz rys. 3.13):
)
(
)
(
)
(
)
(
)
(
)
(
1
1
1
1
2
2
1
2
,
1
x
B
x
B
x
B
x
B
x
B
x
S
i
i
i
i
i
i
i
i
j
i
i
j
j
n
i
+
+
−
−
−
−
+
−
=
=
+
+
+
=
=
∑
∀
γ
γ
γ
γ
γ
.
(3.93
)

3. Interpolacja
81
Z powyższej postaci uwzględniając (3.91) i (3.90) mamy w poszczególnych
węzłach siatki:
( ) (
)
1
1
,
0
4
6
1
+
−
=
+
+
=
∀
i
i
i
i
n
i
x
S
γ
γ
γ
,
(3.94)
( )
(
)
1
1
,
0
2
1
−
+
=
−
=
′
∀
i
i
i
n
i
h
x
S
γ
γ
,
(3.95)
( )
(
)
1
1
2
,
0
2
1
+
−
=
+
−
=
′′
∀
i
i
i
i
n
i
h
x
S
γ
γ
γ
(3.96)
oraz
(
)
(
)
1
1
2
3
,
0
3
3
1
0
+
−
−
=
+
−
+
−
=
−
′′′
∀
i
i
i
i
i
n
i
h
x
S
γ
γ
γ
γ
.
(3.97)
Podstawiając do równania (3.94) warunek interpolacji otrzymamy układ
n+1
równań z
n+3 niewiadomymi:
( )
(
)
i
i
i
i
i
i
n
i
f
f
x
S
=
+
+
⇒
=
+
−
=
∀
1
1
,
0
4
6
1
γ
γ
γ
.
(3.98)
Do pełnego sformułowania zadania dodajmy jak w poprzednio omawianym
podejściu (punkt 3.3.2) dwa dodatkowe warunki zależne od rozwiązywanego
problemu (3.59) albo (3.60) lub (3.61) i (3.62).
Dla warunku (3.59) czyli
(
)
( )
(
)
( )
2
1
1
0
0
0
0
,
0
α
α
=
′
=
−
′
=
′
=
+
′
−
n
n
n
x
S
x
S
x
S
x
S
mamy:
( )
( )
=
+
−
⇒
=
′
=
+
−
⇒
=
′
+
−
−
.
3
,
3
2
1
1
2
1
1
1
1
0
α
γ
γ
α
α
γ
γ
α
h
x
S
h
x
S
n
n
n
(3.99)
Z warunków (3.99) otrzymujemy:
−
=
⇒
=
+
−
−
=
⇒
=
+
−
−
+
+
−
−
−
.
3
3
,
3
3
2
1
1
2
1
1
1
1
1
1
1
1
α
γ
γ
α
γ
γ
α
γ
γ
α
γ
γ
h
h
h
h
n
n
n
n
(3.100)
Redukując z warunków interpolacji (3.98)
γ
-1
oraz
γ
n+1
zgodnie z (3.100) mamy:
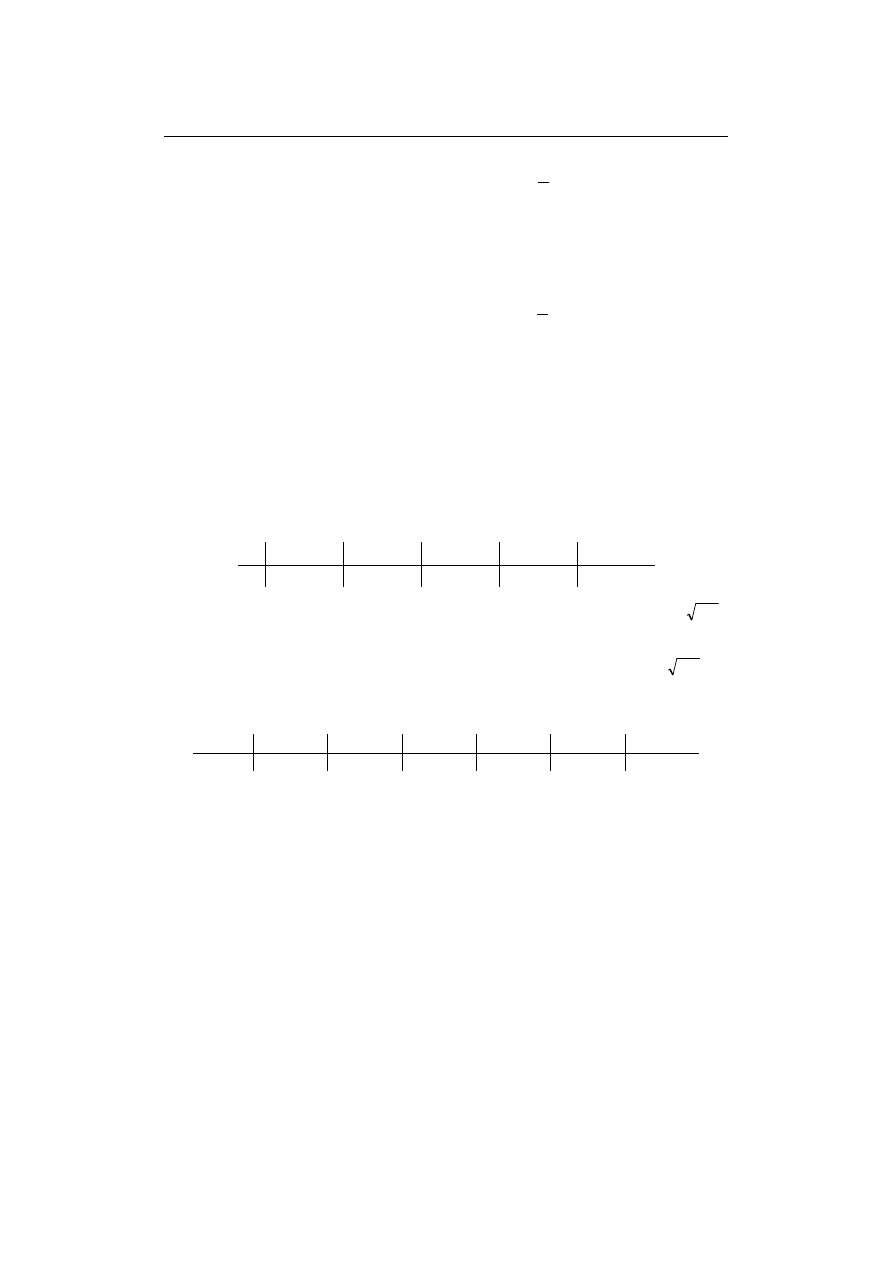
82
Metody numeryczne
+
+
=
×
−
−
2
1
2
1
1
0
1
2
1
0
3
3
4
2
0
0
0
0
1
4
1
0
0
0
0
0
0
4
1
0
0
0
0
1
4
1
0
0
0
0
2
4
α
α
γ
γ
γ
γ
γ
h
f
f
f
f
h
f
n
n
n
n
M
M
L
L
M
M
M
O
M
M
M
L
L
L
(3.101)
Jak łatwo zauważyć, macierz układu równań (3.101) jest macierzą trójdiagonalną
diagonalnie dominującą tak jak we wcześniej (punkt 3.3.2) omawianym podejściu.
Na uwagę zasługuje fakt, że w celu obliczenia wartości wielomianu w dowolnym
punkcie przedziału interpolacji wystarcza znajomość współczynników
γ
i
oraz
wystarczy wyznaczyć wartość co najwyżej czterech funkcji
B
i
(
x) (wielomiany
trzeciego stopnia), ponieważ wartości pozostałych równe są zero.
Zadania
3.1.
Wyznaczyć wielomian interpolacyjny Lagrange’a dla funkcji określonej wartościami:
x
i
0
2
3
5
6
f
f
1
3
2
5
6
3.2.
Dysponując węzłami interpolacji x
0
=100, x
1
=121 oraz x
2
=144 obliczyć wartość
117
za pomocą wzoru interpolacyjnego Lagrange’a
Dysponując węzłami interpolacji x
0
=100, x
1
=121 oraz x
2
=144 obliczyć wartość
117
za
pomocą wzoru interpolacyjnego Lagrange’a.
3.3.
Dana jest tablica wartości funkcji sin(x) dla x
∈
[20
°
,45
°
] z krokiem 5
°
:
x
i
20
°
25
°
30
°
35
°
40
°
45
°
sin(x
i
)
0,342020
0,422618
0,5
0,573576
0,642788
0,766044
Algorytmem Aitken’a obliczyć wartości sin(x) dla x
∈
[30
°
,35
°
] z krokiem = 1
°
.
3.4.
Dla tablicy z zadania 3.3 ekstrapolować wartości sin(x) dla x
∈
[15
°
,20
°
] z krokiem
równym 1
°
.Do obliczeń zastosować algorytm Neville’a.
Zbadać dokładność ekstrapolacji w zależności od odległości wartości x od przedziału
interpolacji.
3.5.
Dane są wektory X[0...n] oraz F[0...n] zawierające węzły i wartości funkcji w
węzłach. Napisać program realizujący obliczanie wartości wielomianu Lagrange’a wg
algorytmu Neville’a:
input X[0...n], F[0...n], x, n;
{X - tablica zawierająca wartości kolejnych węzłów x
i
}

3. Interpolacja
83
{F – tablica zawierająca wartości funkcji f
f
w węzłach x
i
}
{x – wartość argumentu x, dla której obliczana jest wartość wielomianu}
{n – rząd wielomianu (n+1 – liczba węzłów interpolacji)}
????????
????????
output Fx;
gdzie Fx jest poszukiwaną wartością wielomianu interpolacyjnego.
3.6.
Dana jest tablica wartości funkcji f(x)=e
x
:
x
i
3,50
°
3,55
3.60
°
3,65
°
3,70
°
3,75
°
3,80
°
exp(x
i
)
33,115
34,813
36,598
38,475
40,447
42,521
44,701
Wyznaczyć wielomian interpolacyjny Lagrange’a interpolujący funkcję e
x
w podanym
w tablicy przedziale zmienności x.
3.7.
Dla tablicy z zadania 3.6 wyznaczyć wielomiany interpolacyjne Newtona dla
przypadków z siedmioma i czterema węzłami interpolacyjnymi. Porównać dokładność
interpolacji w obu przypadkach.
Uwaga. W przypadku interpolacji z czterema węzłami odrzucić punkty interpolacyjne
oznaczone w tablicy kursywą.
3.8.
Dana jest tablica wartości pewnej funkcji:
x
i
-3
°
-2
-1
°
0
°
1
°
2
°
3
°
f
i
-22
-3
4
5
6
13
32
Wyznaczyć wielomian interpolacyjny Newtona interpolujący funkcję w podanym w
tablicy przedziale zmienności x.
3.9.
Dla danych z tabeli z zadania 3.7 wyznaczyć wielomian interpolacyjny Newton’a dla
funkcji odwrotnej.
*)
Wyznaczyć wartość funkcji odwrotnej dla argumentu równego -1, 0 oraz 1.
3.10.
Dla tablicy z zadania 3.7 obliczyć interpolowane wartości funkcji odwrotnej w
punktach -1, 0 oraz 1 za pomocą algorytmu Aitken’a oraz Neville’a.
3.11.
Dane są wektory X[0...n] oraz F[0...n] zawierające węzły i wartości funkcji w
węzłach. Napisać program realizujący obliczanie współczynników wielomianu
interpolacyjnego Newton’a dla funkcji f(x).
input X[0...n], F[0...n], n;
{X - tablica zawierająca wartości kolejnych węzłów x
i
}
{F – tablica zawierająca wartości funkcji f
f
w węzłach x
i
}
{n – rząd wielomianu (n+1 – liczba węzłów interpolacji)}
????????
????????
output a
n
, a
n-1
, ... , a
1
, a
0
;
gdzie a
n
, a
n-1
, ... , a
1
, a
0
poszukiwane współczynniki wielomianu Newton’a.
*)
Dla funkcji odwrotnej (interpolacja odwrotna) węzłami są wartości funkcji f
i
.

84
Metody numeryczne
3.12.
Dane są wektory X[0...n] oraz F[0...n] zawierające węzły i wartości funkcji w
węzłach. Napisać program realizujący obliczanie współczynników wielomianu
interpolacyjnego Newton’a dla funkcji odwrotnej f
--1
.
input X[0...n], F[0...n], n;
{X - tablica zawierająca wartości kolejnych węzłów x
i
}
{F – tablica zawierająca wartości funkcji f
f
w węzłach x
i
}
{n – rząd wielomianu (n+1 – liczba węzłów interpolacji)}
????????
????????
output b
n
, b
n-1
, ... , b
1
, b
0
;
gdzie b
n
, b
n-1
, ... , b
1
, b
0
poszukiwane współczynniki wielomianu Newton’a dla
interpolacji odwrotnej f
-1
.
3.13.
Rozwiązywane jest zagadnienie interpolacji funkcjami sklejanymi (wielomiany
trzeciego stopnia). Zbudować układ równań dla rozwiązania zagadnienia przy
warunku uzupełniającym
(3.60)
(dane wartości drugich pochodnych na końcach przedziału
interpolacji):
(
)
( )
(
)
( )
2
1
1
0
0
0
0
,
0
β
β
=
′′
=
−
′′
=
′′
=
+
′′
−
n
n
n
x
S
x
S
x
S
x
S
.
3.14.
Zagadnienie interpolacji rozwiązywane jest poprzez zastosowanie B-funkcji
sklejanych trzeciego stopnia. Zbudować układ równań dla rozwiązania zagadnienia
przy warunku uzupełniającym (3.60) (analogicznie do zadania 3.13).
3.15.
Zbudować układ równań dla problemu interpolacji z zadania 3.13 przy warunku
dodatkowym na okresowość funkcji (3.61) i (3.62):
(
)
(
)
( )
( )
n
n
n
x
S
x
S
x
S
x
S
1
0
0
0
0
0
−
′
=
′
⇒
−
′
=
+
′
,
(
)
(
)
( )
( )
n
n
n
x
S
x
S
x
S
x
S
1
0
0
0
0
0
−
′′
=
′′
⇒
−
′′
=
+
′′
.
3.16.
Zbudować układ równań dla problemu interpolacji B-funkcamii sklejanymi trzeciego
stopnia dla (3.61) i (3.62) jak w zadaniu 3.15.
Wyszukiwarka
Podobne podstrony:
MN rozdz 2 id 286501 Nieznany
7 ROZDZ 9 id 45559 Nieznany (2)
MN wyklad id 304106 Nieznany
7 ROZDZ 9 id 45559 Nieznany (2)
MN I id 304086 Nieznany
MN id 304064 Nieznany
Antysemityzm w MN id 66622 Nieznany
8 ROZDZ 10 id 47210 Nieznany (2)
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
więcej podobnych podstron