.

1

Modelowanie Procesów Dyskretnych

SKRYPT

Lech Jamroż, Jerzy Raszka

Wydział Fizyki, Matematyki i Informatyki

Politechniki Krakowskiej

Kraków 2011

Materiały dydaktyczne zostały przygotowane w ramach Projektu

„Politechnika XXI wieku - Program rozwojowy Politechniki Krakowskiej – najwyższej

jakości dydaktyka dla przyszłych polskich inżynierów”

współfinansowanego ze środków Unii Europejskiej w ramach Europejskiego Funduszu

Społecznego. Umowa o dofinansowanie nr UDA-POKL.04.01.01-00-029/10-00

Niniejsza publikacja jest rozpowszechniana bezpłatnie

1. ZAGADNIENIE SZEREGOWANIA ZADAŃ........................................................... 4

1.1. Wprowadzenie ....................................................................................................... 4

1.2. Struktury systemów wykonawczych ........................................................................ 6

1.3. Czasowe parametry zadań ................................................................................... 10

1.4. Kryteria optymalizacji ......................................................................................... 12

1.5. Specyfikacja problemów szeregowania................................................................. 14

1.6. Algorytmy szeregowania ...................................................................................... 16

1.7. Szeregowanie zadań z dodatkowymi zasobami...................................................... 27

1.8. Szeregowanie zadań cyklicznych .......................................................................... 31

2. METODY OPTYMALIZACJI DYSKRETNEJ ...................................................... 36

2.1. Metoda podziału i ograniczeń .............................................................................. 38

2.2. Algorytm zachłanny ............................................................................................. 43

2.3. Algorytmy metaheurystyczne................................................................................ 47

3. MODELE SIECIOWE PROCESÓW DYSKRETNYCH ........................................ 54

3.1. Wprowadzenie ..................................................................................................... 54

3.2 Podstawowe pojęcia i definicje ............................................................................. 55

3.3. Sieci znakowane .................................................................................................. 57

3.4. Własności dynamiczne sieci ................................................................................. 58

3.5 Czasowe sieci Petriego ......................................................................................... 61

3.6. Przykłady sieciowego modelowania procesów dyskretnych.................................. 62

3.7. Konstrukcja drzew i grafów pokrycia znakowań .................................................. 68

3.8 Oprogramowanie narzędziowe ND. ..................................................................... 72

3.9. Edytor i symulator PIPE ..................................................................................... 78

4. JĘZYKI SYMULACYJNE SYSTEMÓW DYSKRETNYCH ............................. 83

4.1 Zastosowanie........................................................................................................ 83

4.2 Język GPSS .......................................................................................................... 85

4.3 Przykłady do ćwiczeń i tematy zadań................................................................... 103

4.4 Obsługa pakietu GPSS World ............................................................................ 106

4.5 Inne wersje pakietów GPSS ............................................................................... 112

.

3

5. PROGRAMOWANIE SYSTEMÓW DYSKRETNYCH ....................................... 115

5.1 Wprowadzenie.................................................................................................... 115

5.2 Proces projektowania symulacji.......................................................................... 116

5.3. Elementy modelu symulacyjnego....................................................................... 120

5.4 Metody symulacji dyskretnej ............................................................................... 122

5.5. Sterowanie i monitoring procesów dyskretno-ciągłych ....................................... 133

5.6 Systemy SCADA/HMI ......................................................................................... 144

.

4

1. ZAGADNIENIE SZEREGOWANIA ZADAŃ

1.1. Wprowadzenie

Dziedzinę wiedzy zajmującą się szeregowaniem zadań nazywamy teorią

szeregowania (scheduling theory, sequencing theory).
Ogólne zagadnienia szeregowania zadań, nazywane również zagadnieniami
kolejnościowymi lub sekwencyjnymi można umiejscowić w obszarze badań
operacyjnych, programowania dyskretnego lub optymalizacji kombinatorycznej.
Zagadnienia szeregowania modelują funkcjonowanie rzeczywistych systemów.
Przykładem takich systemów są systemy komputerowe ogólnego przeznaczenia,
systemy uwarunkowane czasowo RTS (Real Time Systems), Elastyczne systemy
produkcyjne FMS (Flexible Manufacturing Systems), Systemy wytwarzania na
czas JIT (Just-in-Time).

Zdecydowana większość stawianych zagadnień praktycznych, charakteryzuje

się NP-trudnością odpowiednich problemów optymalizacyjnych. Implikuje ona
wykładniczy czas obliczeń algorytmów komputerowych wyznaczających
optymalne rozwiązanie, co podważa zasadność ich stosowania.
Zagadnienie rozdziału zasobów systemowych, w szczególności szeregowanie
zadań, pojawia się niemal w sposób oczywisty przy ustalania wszelkich
harmonogramów. W ogólności, wyróżnione są dwa podejścia do jego
rozwiązywania:

1.

dynamiczne szeregowanie (dynamic scheduling, on-line scheduling),

2.

statyczne szeregowanie (static scheduling, off-line scheduling).

W zależności od typu systemu, poszczególne strategie szeregowania są
implementowane na różne sposoby.

Szeregowanie dynamiczne odbywa się w trakcie pracy systemu. Na podstawie

aktualnego stanu systemu podejmowane są decyzje, które zadanie będą
wykonywane następnie. Podstawową cechą szeregowania dynamicznego jest
nieznajomość, na etapie projektowania systemu, kolejności wykonywania zadań
(kolejność ta zależy od kolejności zdarzeń zachodzących w otoczeniu systemu). W
pewnych okolicznościach cecha ta może być zaletą, jednakże w systemach
krytycznych MCS (Mission Critical Systems) ze względu na bezpieczeństwo jest
ona wadą. Trudno jest także realnie oszacować czas odpowiedzi (response time)
dla obsługi konkretnego zdarzenia.
W przypadku szeregowania dynamicznego wymagane jest zastosowanie prostych
algorytmów np. EDD (Earliest Due Date), gdyż w przeciwnym razie czas
przeznaczony na budowaniu uszeregowania może być zbyt długi, co z kolei
doprowadziłoby do naruszenia linii krytycznej konkretnego zadania. Szeregowanie
dynamiczne składa się z tylko etapu wykonawczego (run-time).

.

5

Alternatywą dla szeregowania dynamicznego jest statyczne szeregowanie.

Wymagana jest znajomość czasów ich wykonywania, albo też okresów
powtarzania na etapie kompilacji oprogramowania (przed uruchomieniem systemu).
Szeregowanie statyczne składa się z dwóch etapów: przygotowawczego (pre-run
time) oraz wykonawczego (run-time). Podstawową zaletą szeregowania
statycznego w stosunku do dynamicznego jest większa skuteczność wynikająca z
przeniesienia większości obliczeń do etapu przygotowawczego. Analiza i
uruchamianie systemu ze statycznym szeregowaniem jest znacznie prostsze. W
systemach krytycznych, ze względu na bezpieczeństwo należy wyłącznie stosować
szeregowanie statyczne, gdyż tylko wówczas mamy pewność, że wszystkie
ograniczenia czasowe zostaną spełnione. Przykładem statycznego szeregowania są
algorytmy RMS (Rate Monotonic Scheduling), DMPO (Deadline Monotonic
Priority Ordering) oraz CES (Cyclic Executive Scheduling).
Przyjmijmy następujące oznaczenia:

1. Zadania (jobs, tasks),

Z={Z

1

, Z

2

, ..., Z

n

}

2. Procesory, maszyny (processors, machines),

P={P

1

, P

2

, ..., P

m

}

3. Zasoby (resources),

R={R

1

, R

2

, ..., R

s

}.

Przykładowe interpretacje zadania:

-

program komputerowy, proces obliczeniowy (w systemie komputerowym),

-

proces obróbki detalu (w przemyśle maszynowym),

-

proces montażu (w przemyśle samochodowym),

-

zlecenie inwestycyjne (w budownictwie),

-

prace naukowe (w projekcie badawczym).

Zasobami mogą być: procesory, maszyny, stanowiska montażu, personel, surowce
energetyczne, kapitał itp. Zarówno zadania jak i zasoby posiadają swoje cechy
charakterystyczne np. termin gotowości do wykonania, żądany termin zakończenia,
przerywalność wykonywania itp. W przypadku zasobów mogą to być następujące
kategorie:

-

odnawialne (procesor, maszyna, robot),

-

nieodnawialne (surowce, materiały podlegające zużyciu),

-

podwójnie ograniczone (energia, kapitał).

Zasoby odnawialne charakteryzuje ograniczona dostępność, nieodnawialne –
ograniczenie globalnej ilości, zaś podwójnie ograniczone oba rodzaje ograniczeń.

.

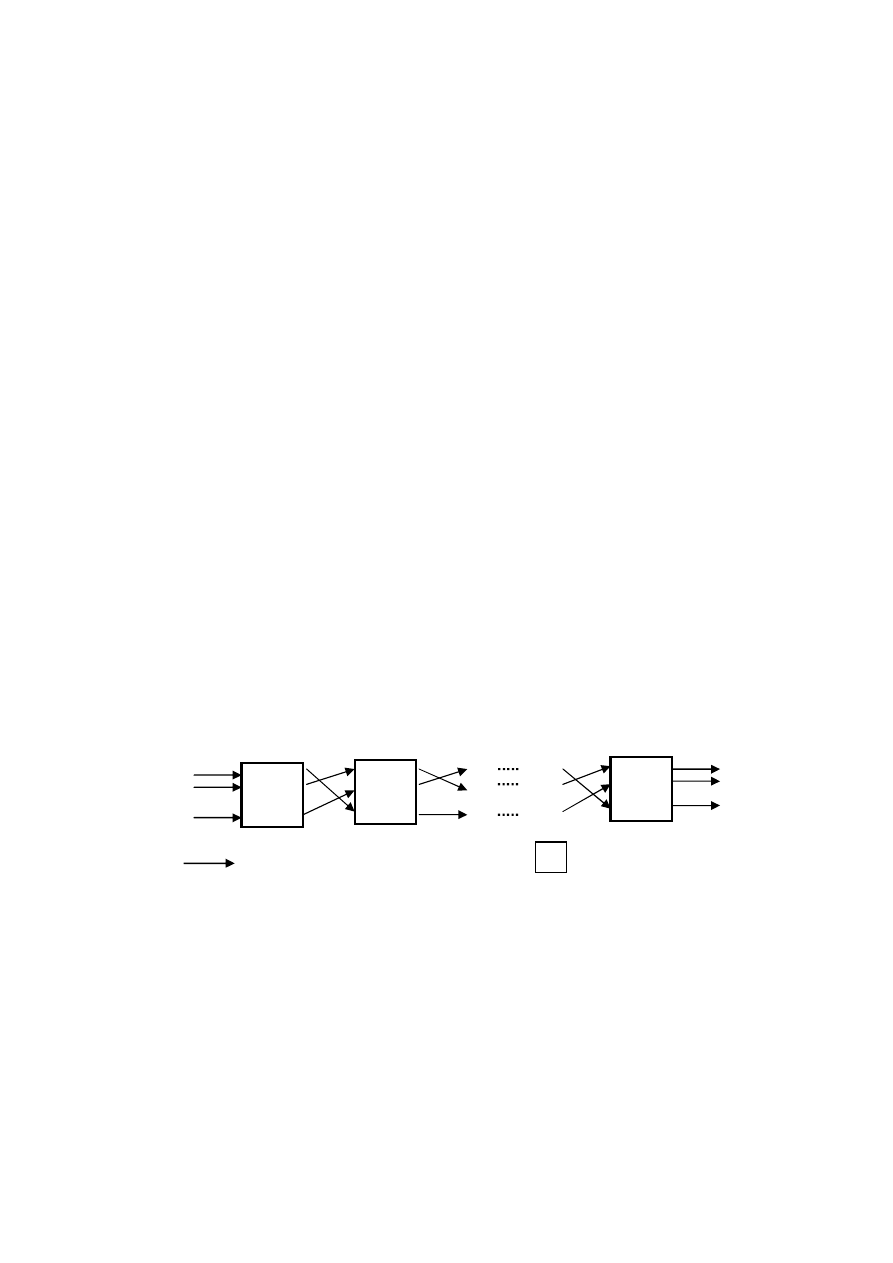
6

1.2. Struktury systemów wykonawczych

Rozważane są przepływowe systemy obsługi zadań. Systemy przepływowe są

jednymi z prostszych i często analizowanych modeli systemów, w szczególności
produkcyjnych (przemysłowych). Mają bardzo dobre aplikacje praktyczne,
głównie

w

procesach

chemicznych,

niektórych

procesach

przemysłu

elektronicznego czy samochodowego.
Tworzą podstawy do analizy bardziej złożonych struktur szeregowo-równoległych
(potokowe linie automatyczne), dominujących we współczesnych systemach
wytwarzania. Traktowane są także, jako wskaźniki praktycznych możliwości
rozwiązywania trudnych numerycznie problemów, przy użyciu narzędzi i metod
teorii szeregowania zadań.
Do podstawowych systemów obsługi zadań należą:

1.

Przepływowy F (Flow-shop system).

2.

Permutacyjny przepływowy PF (Permutation flow-shop system).

3.

Otwarty O (Open-shop system).

4.

Gniazdowy J (Job-shop system).

1.2.1. System przepływowy

W przepływowym systemie obsługi wszystkie zadania (sekwencja operacji,

potoki operacji) posiadają jednakową marszrutę technologiczną, wykonywane są
na wszystkich maszynach (procesorach, stanowiskach), a każda z maszyn wymaga
określenia odpowiedniej kolejności wprowadzania zadań.

1

2

m

Przepływ zadań

Maszyna (procesor)

.

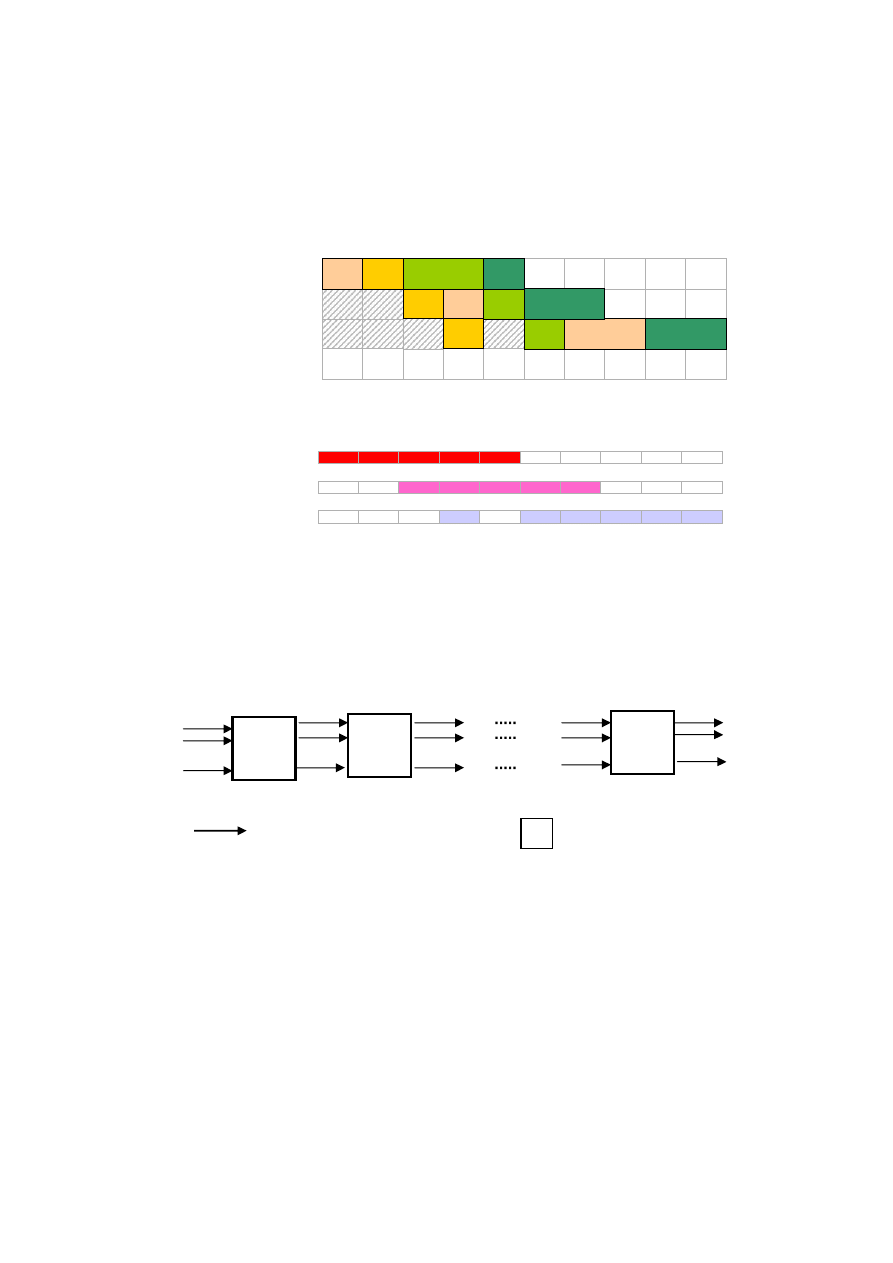
7

1.2.2. Permutacyjny system przepływowy

W permutacyjnym systemie przepływowym obsługi zadań złożenia są takie

same jak dla systemu typu F z dodatkowym wymaganiem, aby kolejność
(permutacja) wykonywania zadań była taka sama, zgodna z kolejnością
wprowadzania zadań do systemu.

Ciągłość pracy P

1

P

3

1

2

3

4

5

6

7

8

9

10

P

2

P

1

Z

1

Z

1

Z

1

Z

3

Z

2

Z

3

Z

2

Z

4

Z

4

Z

4

Z

2

Z

3

Rys. 1.1. Przykładowy diagram Gantta uszeregowania dla systemu F

Ciągłość pracy P

2

Ciągłość pracy P

3

1

2

m

Przepływ zadań

Maszyna (procesor)

.

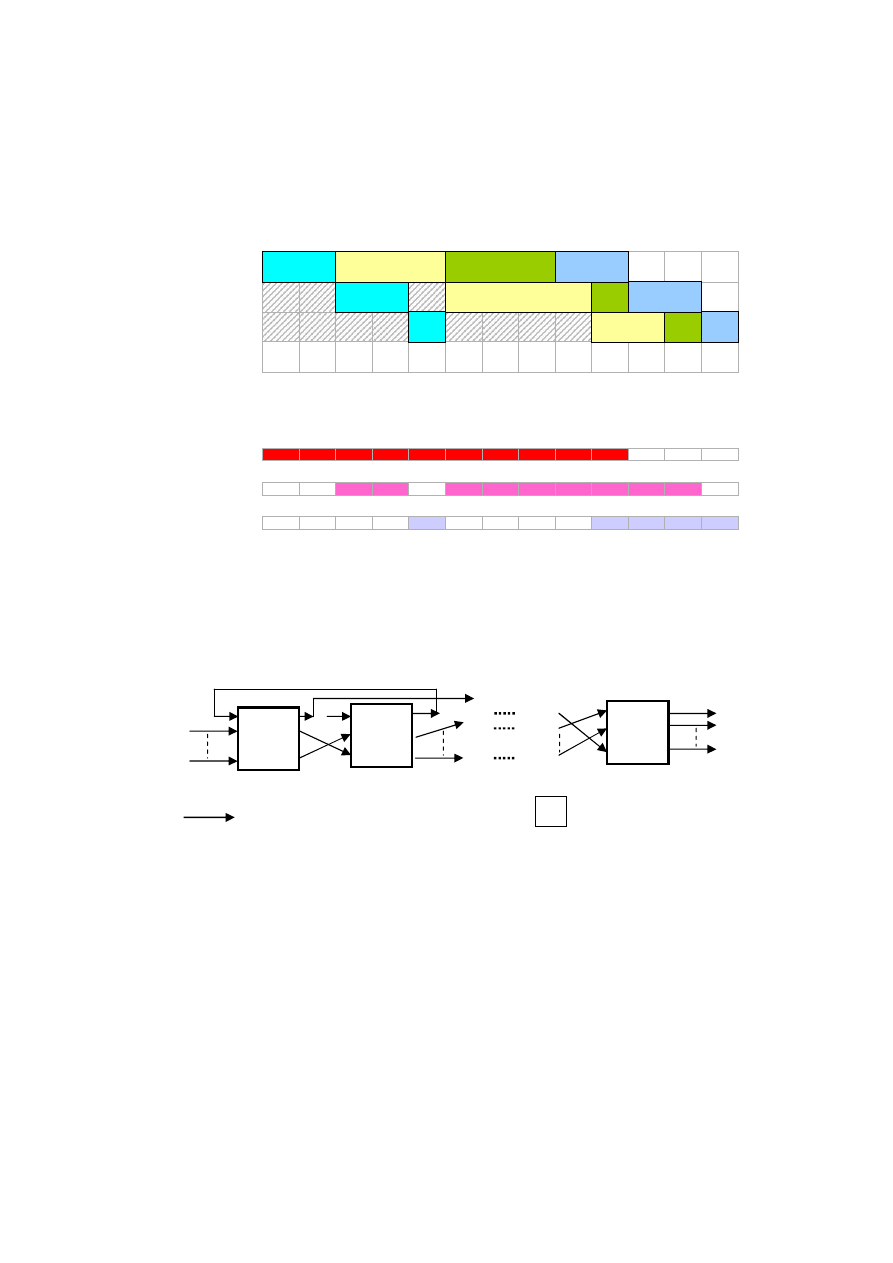
8

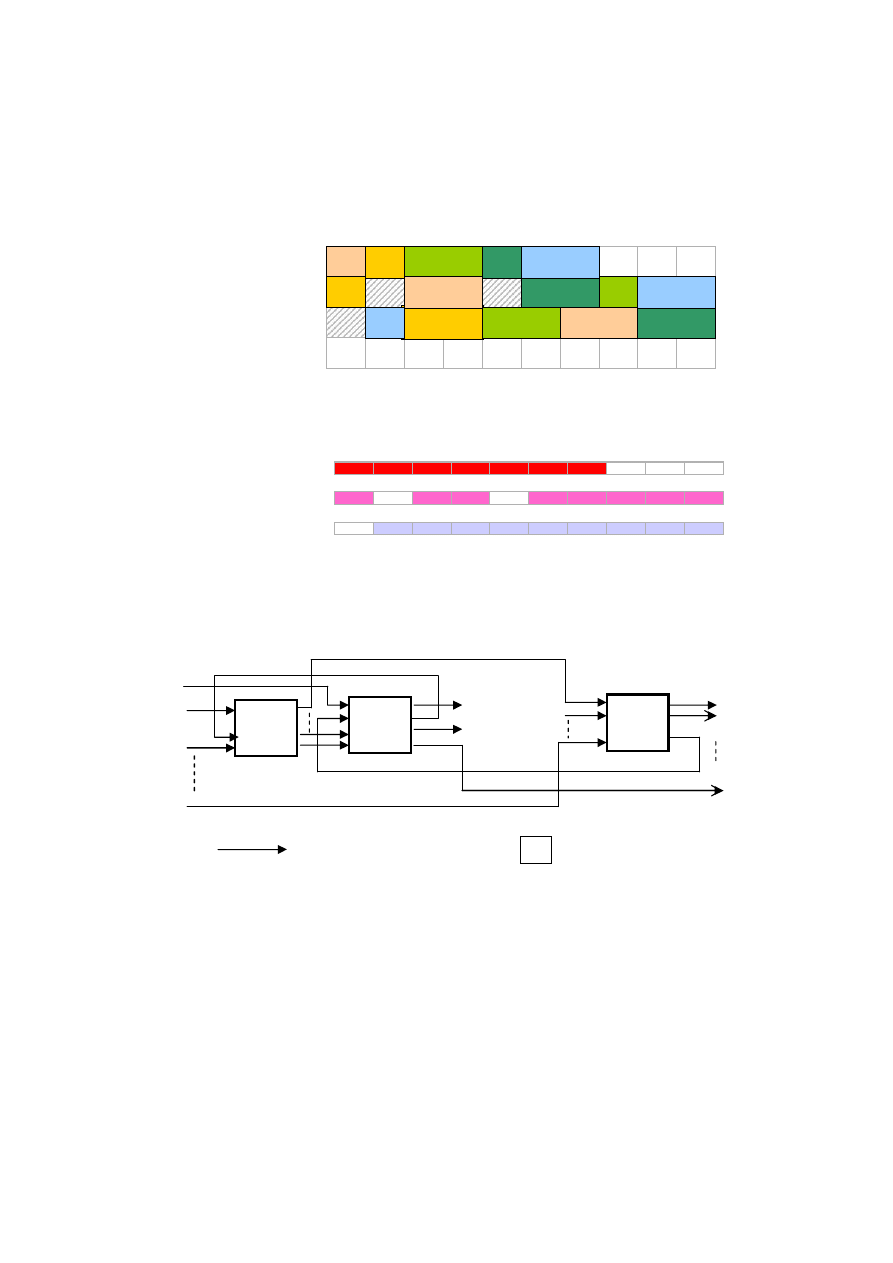
1.2.3. System przepływowy otwarty

W systemie obsługi otwartym, każde zadanie wykonane jest na wszystkich

maszynach, lecz kolejność wykonywania operacji w obrębie zadań może być
dowolna, nie jest ustalona.

Rys. 1.2. Przykładowy diagram Gantta uszeregowania dla systemu PF

P

3

1

2

3

4

5

6

7

8

9

1
0

1
1

1
2

P

2

P

1

Z

2

Z

2

Z

2

Z

3

Z

Z

1

Z

3

Z

3

1
3

Z

4

Z

4

Z

1

Z

4

Ciągłość pracy

P

Ciągłość pracy

P

Ciągłość pracy

P

Przepływ zadań

Maszyna (procesor)

m

1

2

.

9

1.2.4. System gniazdowy

W systemie gniazdowym założenia dla F i FP nie są zachowane. Zadania mogą
posiadać różne (co do liczby jak i kolejności) marszruty technologiczne.

Ciągłość pracy P

1

Ciągłość pracy P

2

Ciągłość pracy P

3

P

3

1

2

3

4

5

6

7

8

9

1
0

P

2

P

1

Z

1

Z

3

Z

2

Z

4

Z

4

Z

4

Z

2

Z

3

Z

2

Z

1

Z

3

Z

1

Z

5

Z

5

Z

5

Rys. 1.3. Przykładowy diagram Gantta uszeregowania dla

systemu otwartego

Maszyna (procesor)

Przepływ zadań

1

2

m

.

10

1.3. Czasowe parametry zadań

Do najważniejszych czasowych (timingowych) parametrów zadań należą:

r

i

(release time, arrival time) – najwcześniejszy możliwy termin rozpoczęcia

wykonywania zadania, termin uwolnienia jest chwilą, gdy zadanie dołącza do
kolejki zadań gotowych do wykonania. Czas, w którym zadanie uzyskuje
uprawnienia do wykonania. Zdanie może być wykonane w każdej chwili po
uwolnieniu, jeśli tylko spełnione będą specyficzne warunki zewnętrzne, (np.
obecność danych wejściowych, dostępność zasobu itp.).

p

i

(execution time, processing time, computation time) - czas wykonania,

maksymalny czas trwania wykonania zadania, czas trwania obliczeń.

s

i

(start time, inception) - rzeczywisty (aktualny) moment rozpoczęcia

wykonywania zadania. Chwila, w której zadanie rozpoczyna wykonywanie.

c

i

(completion time, finishing time) – rzeczywisty (aktualny) termin zakończenia

wykonywania zadania. Chwila, w której zadanie kończy wykonywanie.

d

i

(deadline, due date) - żądany termin zakończenia wykonywania zadania, termin

ostateczny, maksymalny dopuszczalny czas odpowiedzi. Opcjonalny parametr.
Występuje w dwóch wariantach. Może oznaczać czas, od którego nalicza się
spóźnienie (due date), lub termin, którego przekroczyć nie wolno (deadline).
Parametr ten może być zastąpiony przez okno czasowe [d

j

, D

j

].

L

i

= c

i

– d

i

- nieterminowość (Lateness), opóźnienie w wykonywaniu zadania.

Ciągłość pracy P

1

Ciągłość pracy P

2

Ciągłość pracy P

3

P

3

1

2

3

4

5

6

7

8

9

10

P

2

P

1

Z

3

Z

4

Z

3

Z

6

Z

4

Z

2

Z

5

Z

6

Z

5

Z

3

Z

2

Rys. 1.4. Przykładowy diagram Gantta uszeregowania dla systemu

gniazdowego

.

11

T

i

= max[0, c

i

– d

i

] – spóźnienie (Tardiness) w wykonywaniu zadania.

U

i

= w(C

i

> d

i

) - znacznik spóźnienia (0/1 Nie/Tak).

E

i

= max[0, r

i

– s

i

] - przyspieszenie w wykonywaniu zadania (Earliness).

V

i

- priorytet zadania (ważność zadania).

F

i

= (c

i

– r

i

) - czas reakcji, czas odpowiedzi zadania (response time), czas od chwili

uwolnienia zadania do chwili zakończenia jego wykonania.

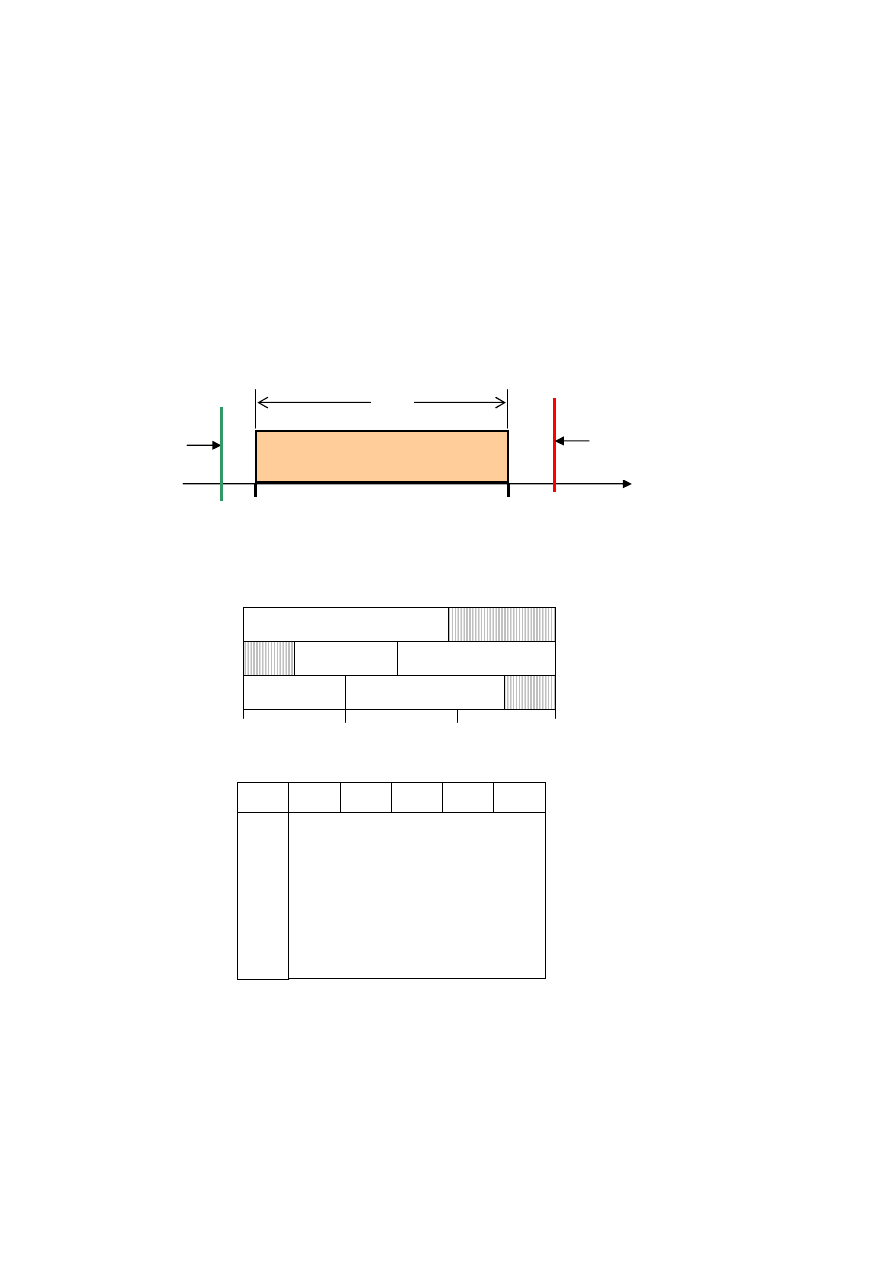
Rys. 1.4. Interpretacja parametrów timimingowych zadania

Z

i

t

s

i

c

i

d

i

r

i

p

i

Z

3

Z

5

Z

1

Z

2

Z

4

P

1

P

2

P

3

0

2

4

6

d

i

5

3

2

7

4

r

i

0

1

0

2

1

s

i

0

1

0

3

2

c

i

4

3

2

6

5

L

i

-1

0

0

-1

1

T

i

0

0

0

0

1

Z

1

Z

2

Z

3

Z

4

Z

5

.

12

W zbiorze zadań można wprowadzić ograniczenia kolejnościowe w postaci
dowolnej relacji częściowego porządku. Wówczas Z

i

 Z

j

oznacza, że zadanie Z

j

może być wykonywane dopiero po zakończeniu zadania Z

i

. Jeżeli ograniczenia te

nie występują, mówimy o zadaniach niezależnych (domyślnie).
Dla zadań niepodzielnych przerwy w ich wykonywaniu są niedopuszczalne.
Zadania podzielne mogą być wywłaszczane i wznawiane ponownie.
Uszeregowaniem nazywamy przyporządkowanie w czasie maszyn i dodatkowych
zasobów do zadań, dla którego spełnione są następujące warunki:

-

w każdej chwili każdy maszyna wykonuje co najwyżej jedno zadanie,

-

zadanie wykonywane jest w przedziale czasowym [r

j

, ),

-

dla każdych dwóch zadań Z

i

, Z

k

Z takich, że Z

i

 Z

k

, wykonywanie

zadania Z

k

rozpoczyna się po zakończeniu zadania Z

i

,

-

w przypadku zadań niepodzielnych żadne zadanie nie jest przerywane, dla
zadań podzielnych liczba przerw w wykonywaniu każdego zadania jest
skończona,

-

wszystkie zadania zostaną wykonane.

Zarządzanie (sterowanie) wykonywaniem zadań ma na celu efektywne
wykorzystanie dostępne zasoby.

1.4. Kryteria optymalizacji

Wyróżniamy dwie kategorie kryteriów optymalizacji: czasowe oraz kosztowe.

I. Przykładowe kryteria czasowe:

1. Długość uszeregowania (czas wykonania zbioru zadań) (maximum completion

time, makespan)

gdzie c

i

jest momentem zakończenia wykonywania zdania Z

i

w danym

uszeregowaniu. N – zbiór liczb naturalnych.

2. Suma terminów zakończenia zadań.

3. Średni czas przepływu zdań.

gdzie F

i

= c

i

– r

i

jest łącznym czasem wykonywania i oczekiwania na obsługę

zadania Z

i

.

C

max

= max

i=1,...,n

{c

i

}

(1.0)

C = 

i=1,...,n

c

i

,

(1.1)

F = 1/n 

i=1,...,n

F

i

(1.2)

.

13

4. Maksymalne opóźnienie zadania.

5.

Maksymalne spóźnienie.

6.

Całkowite spóźnienie.

7. Ważone spóźnienie (wprowadzenie wag dla zadań).



8.

Liczba spóźnionych zadań.

II. Kryteria kosztowe.

fi(t), gi(t) – niemalejące funkcje względem swoich argumentów.

L

max

= m a x

i=1,...,n

{L

i

}

(1.3)

T

max

=max

i=1,...,n

{T

i

}

(1.4)

T = 

j=1,...,n

T

j

(1.5)

wT = 

j=1,...,n

w

j

T

j

(1.6)

U= 

j=1,...,n

U

j

(1.7)

H

max

= max[m a x

[f(T

j

)], m a x [g(E

j

)]]

(1.8)

 h = 1/n 

j=1,...,n

[ f(T

j

) + g(E

j

)]

(1.9)

.

14

1.5. Specyfikacja problemów szeregowania

Problematyka szeregowania zadań i rozdziału zasobów systemowych doczekała

się standardu specyfikacji. Standardem tym jest trójpolowa notacja Grahama:



Interpretacja parametrów.
1. Parametr  = 

1



2

opisuje typ systemu i środowisko wykonawcze.

Parametr 

1

:

a)

Gdy 

1

{ PF, F, O, J }:



1

= F – system przepływowy,



1

= PF – system przepływowy permutacyjny,



1

= O – system otwarty,



1

= J – system gniazdowy (ogólny).

Parametr 

2

oznacza liczbę maszyn. Gdy 

2

= , to liczbę maszyn dowolna,

jest zmienną w problemie, (oczywiście 

1

=  wtedy i tylko wtedy, gdy 

2

= 1).

2.

Parametr  charakteryzuje zadania, dodatkowe zasoby i ograniczenia.

{, prm} określa dopuszczalność przerywania wykonywania zadań,

-  =  - zadania niepodzielne (nonpreemptive),
-  = prm – zadania podzielne (preemptive),
- {



, prec, tree, chain, seq-par} - określa wymaganą kolejność

wykonywania zadań precedence) oznacza odpowiednio: brak ograniczeń
kolejnościowych (zadania niezależne), dowolny graf, drzewo, łańcuch,
graf szeregowo-równoległy.

{r

i

, } określa chwile dostępności zadań.

-  =  - chwile dostępności są równe tj. r

i

= 0, i=1, 2, ..., n.

-  = r

i

– chwile dostępności dowolne,

{p

i

= 1, p

d

 p

i

 p

g

, } - określa czasy wykonywania zadań.

- p

i

= 1 – czasy wykonywania zadań (operacji) są równe,.

- p

d

 p

i

 p

g

– czasy wykonywania zadań (operacji) są ograniczone od

dołu i od góry,

-  - czasy wykonywania zadań są dowolne.

no-idle - maszyny muszą pracować w sposób ciągły,

no-wait – oznacza, że czas rozpoczęcia operacji następnych (w sensie

porządku technologicznego) jest równy czasowi zakończenia operacji
poprzednich.

.

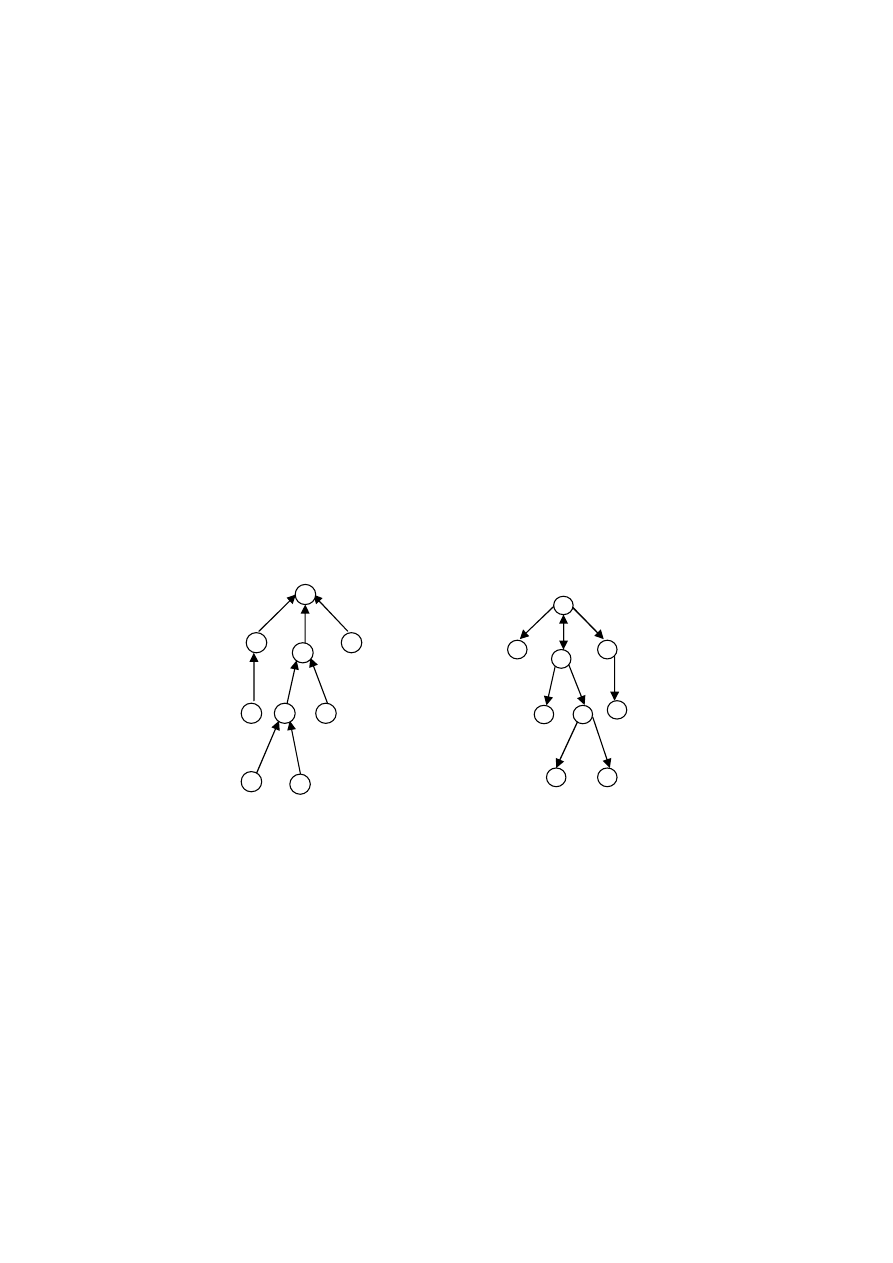
15

{, res   } opisuje ograniczenia i żądania zasobowe: (discretely-

additional resources).

-

 - brak dodatkowych zasobów,

-

 = res    - istnieją dodatkowe zasoby:

    {, k} – oznaczają odpowiednio: liczbę rodzajów dodatkowych

zasobów, ograniczenia zasobowe, żądania zasobowe zadań.

   = k – oznaczają odpowiednio: k rodzajów dodatkowych zasobów, k
jednostek każdego rodzaju, żądania zasobowe każdego zadania nie
przekraczają k jednostek każdego zasobu.
   =  - liczba rodzajów dodatkowych zasobów, ograniczenia oraz
żądania zasobowe są dowolne.

Domyślnie, jeżeli pole  jest puste, przyjmujemy, że: zadania są niepodzielne,
niezależne, r

j

= 0, czasy wykonania i ewentualne wymagane terminy zakończenia

d

j

są dowolne.

Interpretacja 3 (precedence) - szczególne postaci relacji zależności
kolejnościowych.

Przykłady specyfikacji wybranych problemów szeregowania w notacji
trójpolowej:

F2 C

max

P  r

j

, p

j

=1L

max

1  prm, prec L

max

P res 11, r

j

, p

j

=1C

max

in–tree

out–tree

.

16

1.6. Algorytmy szeregowania

1.6.1. Permutacyjny system przepływowy

Specyfikacja zagadnienia szeregowania n zadań w dwumaszynowym

systemie permutacyjnym przepływowym w zapisie notacji trójpolowej ma
postać: PF2C

max

. Kryterium optymalizacji jest czasem zakończenia

wykonania wszystkich zadań C

max

.

Założenia:

- każda maszyna wykonuje jednocześnie co najwyżej jedno zadanie,
- w każdej chwili zadanie może być obsługiwane przez co najwyżej jedną

maszynę,

- każde zadanie wykonuje się nieprzerwanie w pewnym domkniętym

przedziale czasowym,

- przydział każdego zadania jest dosunięty w harmonogramie maksymalnie w

lewo,

- optymalność uszeregowania wyprowadzamy jako wniosek z nieprzerwanej

pracy maszyny P

1

w horyzoncie szeregowania.

Algorytm Johnsona.

Algorytm Johnsona wyznacza optymalne uszeregowanie. Rząd złożoności

algorytmu O(n logn). Idea algorytmu:

1. Utworzyć dwa rozłączne podzbiory zadań: A={Z

i

: p

i1

 p

i2

, i=1,2,...,n} oraz

B={Z

i

: p

i1

> p

i2

, i=1,2,...,n}. Zadania ze zbioru A uszeregowane wg

niemalejących wartości p

i1

tworzą permutację 

A

. Analogicznie, zadania ze

zbioru B uszeregowane wg nierosnących wartości p

i2

tworzą permutację 

B

.

2.

Permutacja * będąca konkatenacją <

A



B

> jest optymalnym

uszeregowaniem zadań.

3.

Wyznaczyć C

max

(*) = c

*(n),2

Interpretacja algorytmu.

p

ik

Z

1

Z

2

Z

3

Z

4

Z

5

P

1

3

3

1

5

2

P

2

4

1

1

3

3

C

max

(*) = m i n

 

C

max

()

(1.10)

.

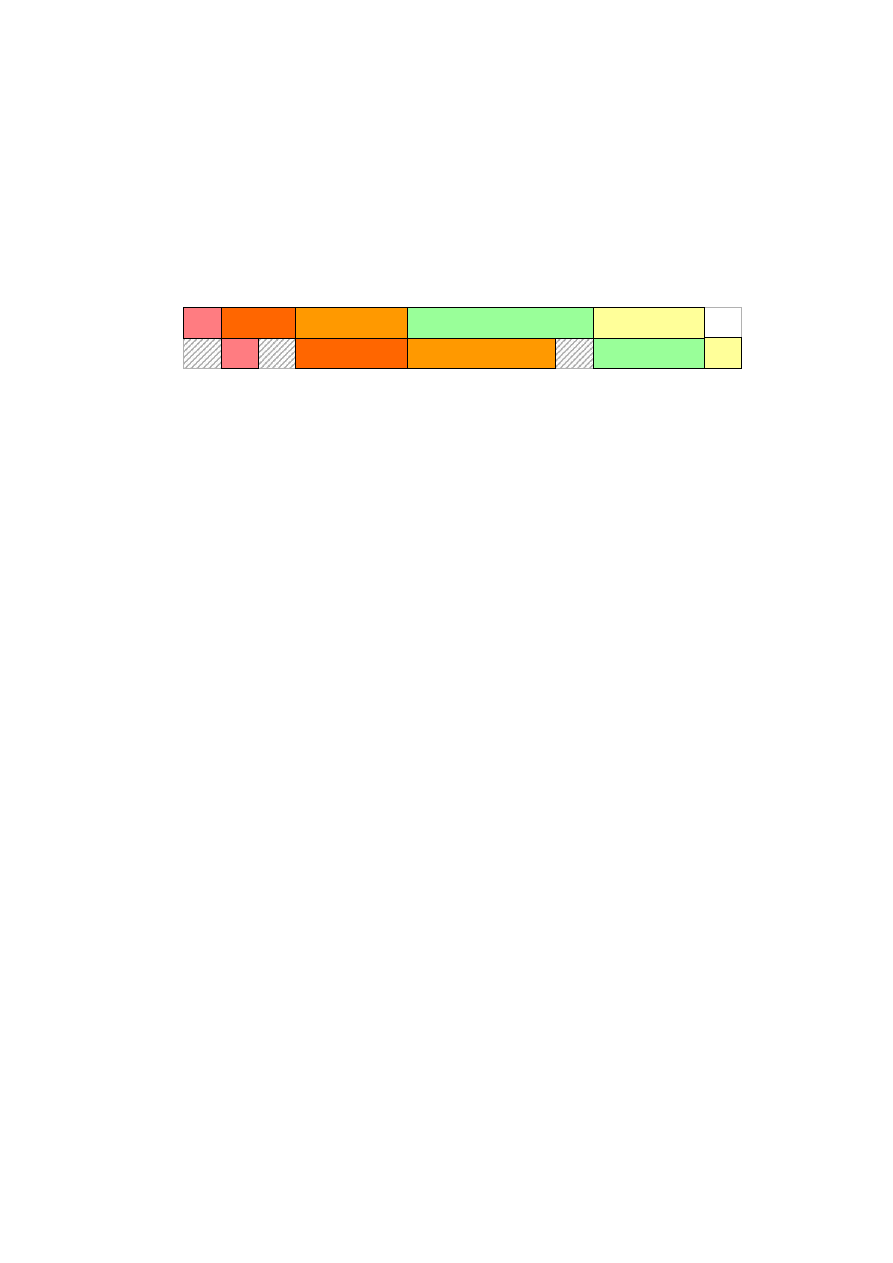
17

P

2

1

2

3

4

5

6

7

8

9

1
0

1
1

1
2

1
3

1
4

1
5

P

1

Z

3

Z

3

Z

5

Z

5

Z

1

Z

1

Z

4

Z

4

Z

2

Z

2

Rys. 1.7. Diagram Gantta uszeregowania.

Optymalne uszeregowanie zadań:

< Z

3

Z

5

Z

1

Z

4

Z

2

>

Wartość funkcji kryterialnej C

max

= c

*(n),2

=

15.

Istnieje optymalna kolejność  wykonywania zadań dla zagadnienia: PF2 | | C

max

taka, że dla każdej pary i oraz k, (1  i < k  n) spełniony jest warunek Johnsona:



Jeżeli założymy, że optymalną permutacją jest  = (1, 2, …, n) oraz, że k=i+1, to
warunek Johnsona przyjmie postać:



Rozszerzenie algorytmu Johnsona

na przypadek trzech maszyn.

Istnieje optymalna kolejność wykonywania zadań dla problemu:

PF3|P

2

, no-bottl.|C

max

z czasami p

i1

, p

i2

, p

i3

wykonywania zadań Z

i

Z, taka jak optymalna kolejność dla

problemu PF2C

max

z czasami p

'

i1

= p

i1

+ p

i2

, p

'

i2

= p

i2

+ p

i3

przy założeniu, że:

W takim przypadku, czas wykonywania zadań na drugiej maszynie nie odgrywa
roli, a optymalne uszeregowanie można otrzymać stosując algorytm Johnsona dla
problemu pomocniczego. Warunek pierwszy reprezentuje dominację P

1

nad P

2

,

zaś

drugi dominację P

3

nad P

2

.

Problem pomocniczy dostarcza tylko permutacji , zaś odpowiednie terminy
zakończenia wykonywania zadań dla problemu: PF3|P

2

, no-bottl.|C

max

należy

wyznaczyć posługując się danymi p

ij

, przy czym dla maszyn P

1

, P

3

należy

skorzystać z rekurencyjnej zależności:

c

(i),j

= max { c

(i-1),j

, c

(i),j-1

} + p

(i),j

t 0

1

2

3

4

5

6

7

8

9 10 11 12

13 14 15

P

2

P

1

Z

3

Z

3

Z

5

Z

5

Z

1

Z

1

Z

4

Z

4

Z

2

Z

2

Rys. 1.7. Diagram Gantta uszeregowania.

min ( p

(i),1

, p

(k),2

)  min ( p

(k),1

, p

(i),2

)

min ( p

(i),1

, p

(i+1),2

)  min (p

(i+1),1

, p

(i),2

)

min {p

i1

}  max {p

i2

}

i i

lub

min {p

i3

}  max {p

i2

}

i i

.

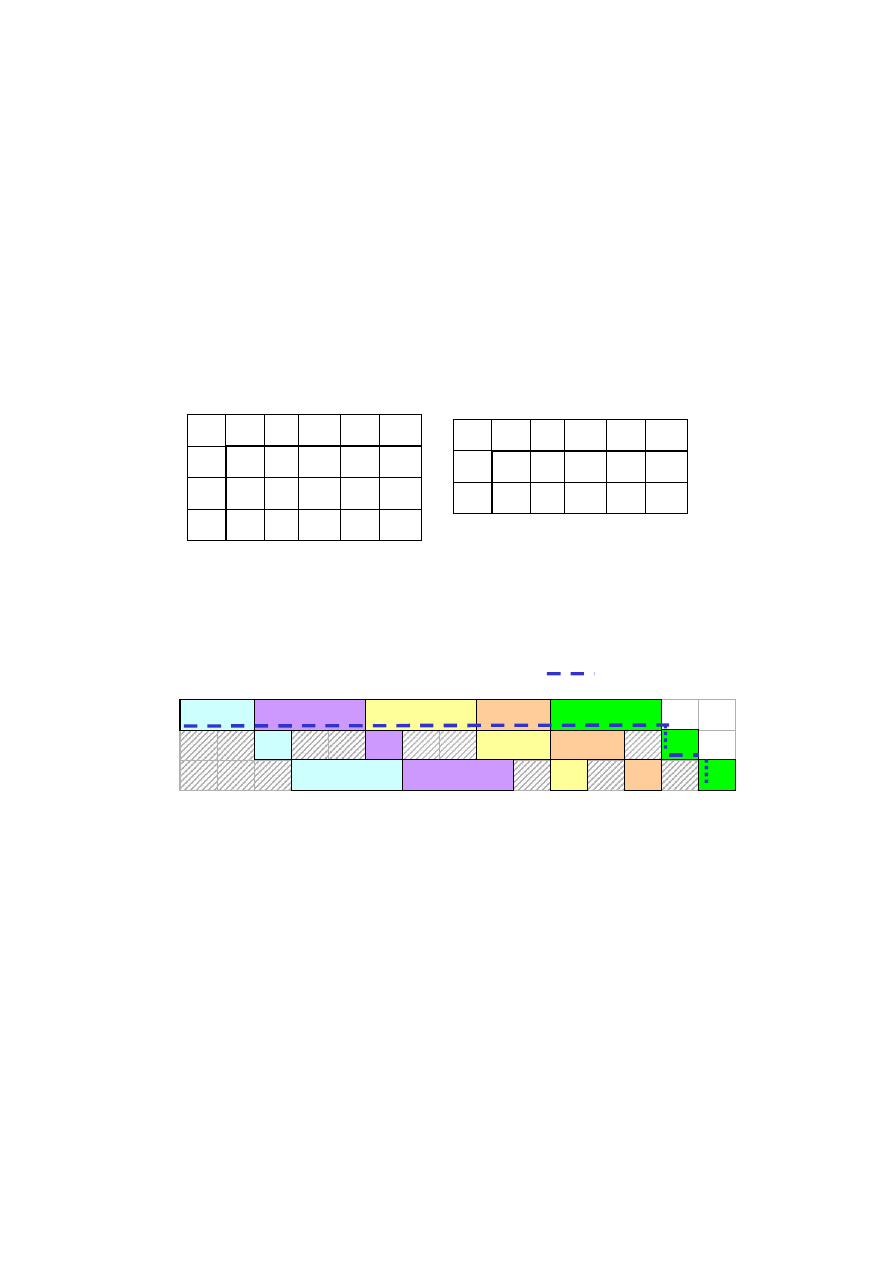
18

zaś dla maszyny P

2

z zależności:

c

(i),j

= c

(i),j-1

+ p

(i),j

Dla przypadku dominacji P

1

nad P

2

spełniony jest warunek:

min {p

i1

}  max {p

i2

}

i i

(

P

2

zdominowany przez P

1

)

p

ik

Z

1

Z

2

Z

3

Z

4

Z

5

P

1

3

3

2

2

3

P

2

1

2

2

1

1

P

3

3

1

1

3

1

p

’

ik

Z

1

Z

2

Z

3

Z

4

Z

5

P

1

4

5

4

3

4

P

2

4

3

3

4

2



A

: < Z

4

, Z

1

>



B

: < Z

2

, Z

3

, Z

5

>

Optymalne uszeregowanie zadań: < Z

4

Z

1

Z

2

Z

3

Z

5

>

P

3

P

2

P

1

Z

4

Z

4

Z

1

Z

2

Z

1

Z

2

Z

3

Z

3

Z

5

Z

5

Z

4

Z

1

Z

2

Z

3

Z

5

Ścieżka krytyczna

Rys. 1.8. Diagram Gantta uszeregowania. Wartość funkcji kryterialnej C

max

(*)

= c

*(n),3

= 15

t 0

1

2

3

4

5

6

7

8

9 10 11 12

13 14 15

.

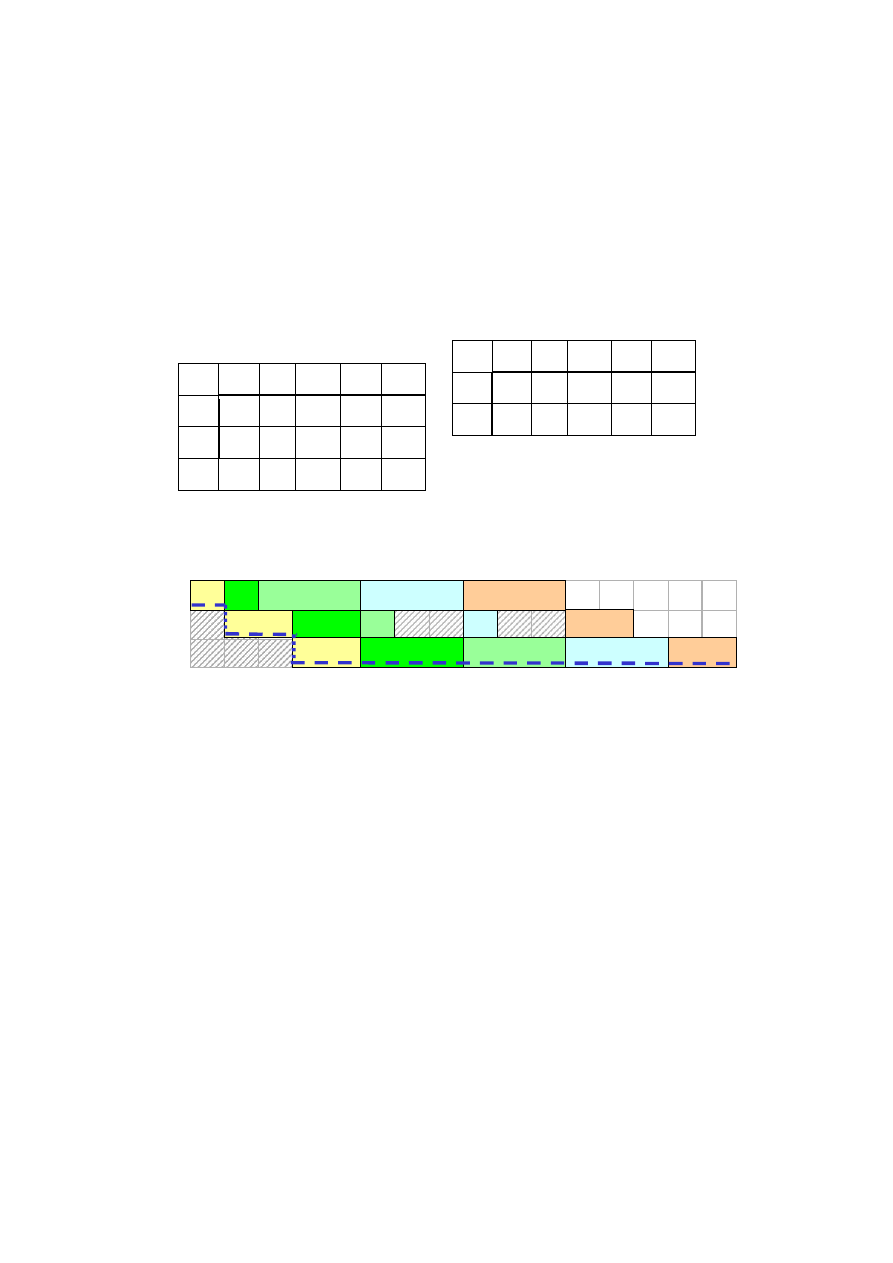
19

W przypadku dominacji P

3

nad P

2

spełniony jest warunek:

1.6.2. Jednomaszynowe problemy szeregowania

Stopień złożoności problemów szeregowania zależy od liczby maszyn,

struktury zadań oraz od charakteru i liczby dodatkowych ograniczeń. Z tego punktu
widzenia, problemy jedno-maszynowe zalicza się do najprostszych, pomimo iż
wiele z nich należy już do klasy problemów NP-trudnych

.

Zasadność badań problemów jednomaszynowych można uzasadnić kilkoma

względami:

-

problemy te są przydatne jako problemy pomocnicze przy rozwiązywaniu
bardziej złożonych zagadnień szeregowania,

-

wykazane dla nich własności szczególne mogą być przeniesione przez
analogię na bardziej złożone zagadnienia,

-

stanowią podstawę metodologii rozwiązywania wielu problemów NP-
trudnych.

P

3

p

ik

Z

1

Z

2

Z

3

Z

4

Z

5

P

1

3

1

3

3

1

P

2

1

2

2

1

2

3

2

2

3

3

(

P

2

zdominowany przez P

3

)

p

’

ik

Z

1

Z

2

Z

3

Z

4

Z

5

P

1

4

3

5

4

3

P

2

4

4

4

4

5



A

: < Z

2

, Z

5

, Z

1

, Z

4

>



B

: < Z

3

>

Optymalne uszeregowanie zadań: < Z

2

Z

5

Z

1

Z

4

Z

3

>

min {p

i3

}  max {p

i2

}

(1.11)

i i

Diagram Gantta uszeregowania:

P

3

P

2

P

1

Z

2

Z

2

Z

1

Z

4

Z

5

Z

4

Z

3

Z

3

Z

2

Z

5

Z

1

Z

5

Z

1

Z

4

Z

3

Rys. 1.9. Wartość funkcji kryterialnej C

max

(*) = c

*(n),3

= 16

t 0

1

2

3

4

5

6

7

8

9 10 11 12 13 14 15 16

.

20

Rozważane zostaną jednomaszynowe problemy z kryteriami optymalizacji C

max

,

oraz L

max

. Zbiór indeksów zadań oznaczmy przez N = {l, 2, ... , n}. Każde

zadanie ma ustalony, znany czas wykonywania p

i

>0, iN. Rozwiązaniem

problemu jest harmonogram wykonania zadań, reprezentowany przez wektory
terminów ich rozpoczęcia s = (s

1

... , s

n

) oraz zakończenia c=(c

1

, ... , c

n

).

W praktyce rozwiązanie jest charakteryzowane przez jeden z tych wektorów,

ponieważ istnieje wzajemnie jednoznaczna zależność c

i

= s

i

+ p

i

.

Jeśli funkcja celu jest regularna, np. C

max

, L

max

, to harmonogram optymalny

jest dosunięty w lewo na osi czasu, co oznacza, że zadania rozpoczynają się
w najwcześniejszym dopuszczalnym momencie. Rozwiązania optymalnego
poszukuje się tylko w zbiorze takich harmonogramów.
W przypadku jednej maszyny, każdy taki harmonogram może być
jednoznacznie reprezentowany kolejnością wykonywania zadań, ta zaś z
kolei jest reprezentowana permutacją  = ((1), (2), …, (n)) na zbiorze N.
Dla danej permutacji , terminy zakończenia wykonywania określone są
wzorem rekurencyjnym



gdzie: (0) = 0, c

0

= 0.

Dla kryterium C

max()

=c

(n)

każda permutacja jest optymalna, bowiem wartość

sumy (1.13) nie zależy od permutacji .

1. Zagadnienie: 1r

j

C

max

Rozważane jest zagadnienie uwzględniające terminy gotowości zadań r

j

, dla

których zachodzi r

j

s

j

, i=1,2,..,n. Zagadnienie to opisywane jest symbolem

klasyfikacyjnym 1r

j

C

max

, rozwiązywane jest przez wielomianowy algorytm

o złożoności O( n log n). W celu wyznaczenia rozwiązania generujemy permutację
, odpowiadającą uporządkowaniu zadań według niemalejących wartości r

j

, a

następnie wyznaczamy odpowiednie terminy zakończenia wykonywania zadań,
wykorzystując wzór rekurencyjny:

c

(j)

= max{r

(j)

, c

(j-1)

} +p

(j)

, j = l, ... , n,

(1.14)

wówczas wartość funkcji kryterialnej wynosi C

rnax

()=c

(n)

.

c

(i)

= c

(i-1)

+ p

(i)

i=1,2,...,n

(1.12)

c

(j)

= 

j

i=1

p

(i)

j=1,…, n

(1.13)

.

21

Rozwinięcie wzoru rekurencyjnego (1.14) prowadzi do wyrażenia na terminy c

j

c

(j)

= max

1ij

(r

(i)

+ 

j

k=i

p

(k)

),

j=1,2,…,n

(1.15)

implikującego wzór określający C

max

() postaci:

C

max

() = max

1in

(r

(i)

+ 

j

k=i

p

(k)

),

j=1,2,…,n

(1.16)

Innym praktycznym uogólnieniem problemu jest wprowadzenie czasów q

j

,

mających sens niekrytycznych czynności zakończeniowych (wymagających tylko
upływu czasu, lecz nie angażujących maszyny), wykonywanych po zasadniczej
obsłudze zadania na maszynie.

2. Zagadnienie: 1q

j

C

max

Problem 1q

j

C

max

, jest symetryczny do problemu 1r

j

C

max

. Symetria ta

oznacza, że podstawiając r

j

= q

j

, optymalne wartości funkcji kryterialnej obu

problemów są sobie równe, zaś permutacje optymalne są wzajemnie odwrotne.
Rozwiązanie problemu 1q

j

C

max

można wyznaczyć poprzez zastosowanie

własności wynikającej z symetrii. Istnieje rozwiązanie optymalne, w którym
zadania są wykonywane w kolejności nierosnących wartości q

j

.

Generujemy zatem permutację  odpowiadającą uporządkowaniu zadań według
nierosnących wartości q

j

(złożoność obliczeniowa O(n log n)), wyznaczamy

terminy ich zakończenia ze wzoru (1.12), następnie obliczamy wartość funkcji celu
z zależności:

C

max

() = max

1in

(c

(i)

+ q

(i)

)

(1.17)

Wykorzystując zależność

(1.13)

otrzymujemy:

C

max

() = max

1in

(

i

k=1

p

(k)

+ q

(i)

)

(1.18)

3. Zagadnienie: 1L

max

Istnieje rozwiązanie optymalne problemu szeregowania 1L

max

, w którym

zadania są wykonywane w kolejności niemalejących wartości żądanego terminu
zakończenia d

j

.

Generowana jest permutacja  odpowiadającą uporządkowaniu zadań według
niemalejących wartości d

j

, a następnie wyznaczane są odpowiednie terminy

rozpoczęcia i zakończenia wykonywania zadań ze wzoru (1.12). Wartość funkcji
celu obliczamy z zależności:

.

22

L

max

()=max

jN

L

j

=max

jN

(c

j

- d

j

)= max

1jn

(

j

i=1

p

(i)

+d

(j)

) (1.19)

Złożoność obliczeniowa algorytmu O(nlgn).

1.6.3. Zadania podzielne

Dążenie do konstruowania algorytmów szeregowania o jak najmniejszej

złożoności obliczeniowej jest szczególnie istotne w przypadku systemów
komputerowych, gdyż algorytmy te często wchodzą w skład procedury
szeregującej systemu operacyjnego. W związku z tym stosuje się algorytmy,
których funkcja złożoności obliczeniowej jest ograniczona od góry przez
wielomian od rozmiaru rozwiązywanego zagadnienia.

1. Zagadnienie: P| prm |C

max

Z punktu widzenia rozważanego kryterium C

max

możliwość przerywania

wykonywania zadań jest korzystna. W tym przypadku czas wykonania zadań nie
może być mniejszy niż większa z dwóch wartości: najdłuższy z czasów
wykonywania poszczególnych zadań i średni czas wykonywania wszystkich zadań
przez maszyny. Powyższy algorytm zawsze dostarcza uszeregowania, a jego
optymalność wynika z faktu, że długość tego uszeregowania jest zawsze określona
wzorem C*

max

a zatem jest minimalna.

Algorytm McNaughtona R.

1.

Wyznaczyć wartość:
C*

max

= max {max

i=1,...,n

{ p

i

}, 

i=1,..n

p

i

/ m}, Rozpocząć wykonywanie

dowolnego zadania na dowolnym procesorze w chwili t = 0.

2.

Wybrać dowolne nieuszeregowane jeszcze zadanie i rozpocząć jego
wykonywanie na tej samej maszynie w chwili zakończenia wykonywania
poprzedniego zadania. Powtarzać ten krok do chwili, gdy wszystkie
zadania zostaną uszeregowane lub t = C*

max

.

3.

Część zadania pozostającą do wykonania po osiągnięciu t = C*

max

przydzielić do innej wolnej maszyny, rozpoczynając jej wykonanie od
chwili t=0. Wykonać krok 2.

Złożoność algorytmu jest O(n), ponieważ każde zadanie jest rozpatrywane tylko
raz, natomiast czas z tym związany jest stały i niezależny od zadań.

.

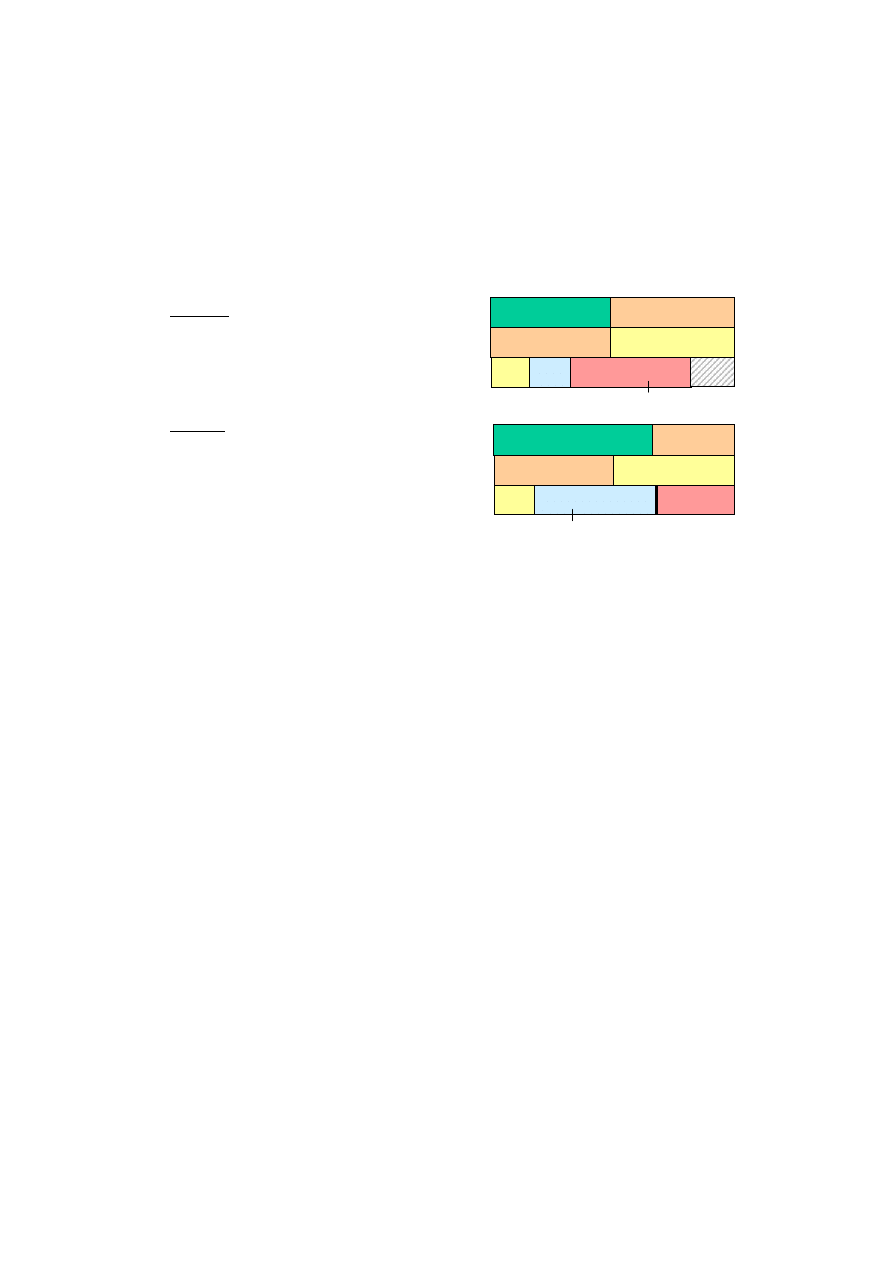
23

Przykład.
n=5, m=3,

Wersja1.

{p

j

}={3, 6, 4, 1, 3}



i=1,...,5

p

i

=17, max {p

i

} =6,

C

max

*=max{17/3, 6}=6

Wersja2.

{p

j

}={4, 5, 4, 3, 2}



i=1,...,5

p

i

=18, max {p

i

} =5,

C

max

*=max{18/3, 5}=6

W przypadku zadań niepodzielnych problem minimalizacji długości
uszeregowania jest NP-zupełny.

2.

Zagadnienie: P| p

i

=1, in–tree|C

max

Ze specyfikacji zagadnienia wynika założenie o jednostkowych czasach

wykonania zadań, a ponadto zbiór zadań tworzy digraf typu drzewo. Poziom
zadania określa się jako liczba węzłów na drodze od węzła reprezentującego
zadanie do korzenia drzewa. Zadanie jest gotowe do wykonania jeżeli wcześniej
wykonane zostały wszystkie zadania poprzedzające.
Algorytm polega na szeregowaniu listowym, według nierosnącego poziomu zadań
z uwzględnieniem ograniczeń kolejnościowych.

Algorytm szeregowania listowego.

1. Określić poziomy zadań.
2. Jeśli liczba zadań bez poprzedników jest mniejsza lub równa m, to

przydzielić tym zadaniom maszyny, wykonać p.3. W przeciwnym
przypadku wybrać spośród nich m zadań o najwyższych poziomach i
przydzielić im maszyny.

3. Usunąć wybrane zadania z grafu. Powtarzać p. 2 dopóki wszystkie zadania

nie zostaną wykonane.

Złożoność obliczeniowa algorytmu O(n).

2

6

4

0

P

1

P

2

Z

5

Z

3

P

3

Z

3

Z

4

Z

2

Z

1

Z

2

2

6

4

0

P

1

P

2

Z

4

Z

3

P

3

Z

3

Z

2

Z

1

Z

2

Z

5

.

24

Przykład: n=11, m=2

Złożoność algorytmu wynika z liczby łuków w digrafie typu in-tree.

1.6.4. Minimalizacja opóźnienia

Kryterium L

max

jest uogólnieniem kryterium C

max

, zagadnienia NP–trudne dla

C

max

pozostaną też NP–trudne w przypadku L

max

. Intuicyjnie, szeregując zadania z

różnymi wymaganymi terminami zakończenia deadline spóźnimy się „najmniej”
zaczynając zawsze od „najpilniejszego” zadania. Reguła EDD bazuje na
uszeregowaniu zadań w kolejności niemalejących wymaganych terminów
zakończenia.

1. Zagadnienie: 1|r

j

, prm, prec|L

max

Dla zadań podzielnych, szeregowanych na jednym procesorze można podać

algorytm wielomianowy optymalny dla dowolnych ograniczeń kolejnościowych i
różnych momentów uwolnienia zadań. Polega on na określeniu wartości
zmodyfikowanych terminów zakończenia i szeregowaniu zadań w kolejności
niemalejących ich wartości.

1

2

3

4

Z

1

Z

2

Z

3

Z

4

Z

5

Z

6

Z

7

Z

8

Z

10

Z

11

Z

9

2

6

4

0

P

2

Z

2

Z

4

Z

6

Z

8

Z

10

P

1

Z

1

Z

3

Z

5

Z

7

Z

9

Z

11

.

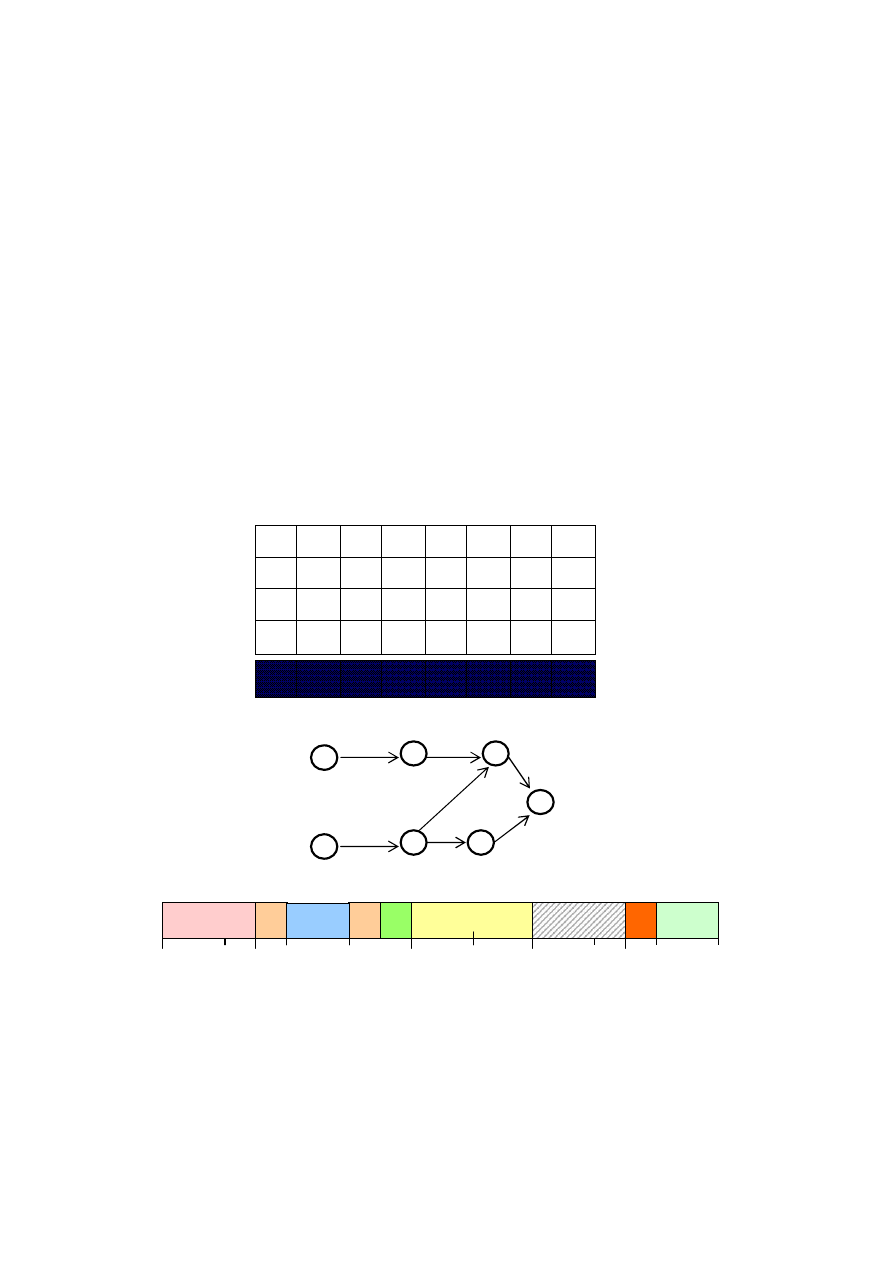
25

Algorytm Liu C.L.

1. Określić dla każdego zadania Z

j

(j=1,2,…,n) zmodyfikowane terminy

zakończenia:

d

j

*

=min{d

j

, min{d

i

:Z

j

 Z

i

}}

2. Przydzielić procesor dostępnemu zadaniu Z

j

, które ma najmniejszą wartość

d

j

*

. Zadanie wykonywane jest tak długo, dopóki nie zakończy się, albo nie

będzie dostępne zadanie Z

k

, dla którego d

k

*

< d

j

*

, wtedy wykonywanie

zadanie Z

j

będzie przerwane.

3. Powtarzać p. 2 dopóty, dopóki wszystkie zadania nie zostaną wykonane.

Złożoność obliczeniowa algorytmu O(n

2

).

Z

1

Z

2

Z

3

Z

4

Z

5

Z

6

Z

7

p

j

3

2

2

1

4

1

2

r

j

0

4

2

5

6

15

15

d

j

4

6

8

15

10

20

25

Z

7

Z

6

Z

5

Z

1

Z

3

Z

2

Z

4

2

6

4

0

Z

1

Z

3

Z

5

Z

4

Z

3

Z

2

8

10

12

Z

6

Z

7

14

18

16

1.10. Uszeregowanie optymalne L

*

max

= 2

d

j

*

4

6

8

10

10

20

25

.

26

Złożoność obliczeniowa algorytmu.

Graf o n wierzchołkach zawiera co najwyżej n(n-1)/2 łuków, wyznaczenie d

*

j

,

j=1, 2, ..., n, może być przeprowadzona w O(n

2

) krokach.

Rozpatrzmy punkty 2 i 3 oraz niekorzystny przypadek zadań niezależnych.
Uszeregowanie zadań dostępnych w chwili t=0 według rosnących wartości
zmodyfikowanych terminów zakończenia wykonywania ma złożoność równą
O(n log n). W chwili przybycia nowego zadania średnia liczba obsługiwanych i
oczekujących (łącznie) zadań wynosi bn, gdzie 0  b  1. Umieszczenie nowego
zadania w odpowiednim miejscu ciągu zadań, uszeregowanych zgodnie z
rosnącymi zmodyfikowanymi terminami zakończenia wykonywania, wymaga co
najwyżej O(n) kroków. Ponieważ przybyć może co najwyżej n zadań, zatem
złożoność obliczeniowa punktów 2 i 3 wynosi O(n

2

). Rząd złożoności algorytmu

jest również O(n

2

).

Możliwość przerywania zadań w przypadku problemu 1| prm, prec |L

max

nie

wpływa na wartość opóźnienia L

max.

. Wystarczy wykazać, że jeśli istnieje

uszeregowanie optymalne dla zadań podzielnych, to istnieje także uszeregowanie
dla zadań niepodzielnych o nie większej wartości L

max

. Implikacja odwrotna jest

słuszna, gdyż każde uszeregowanie dla zadań niepodzielnych jest jednocześnie
uszeregowaniem dla zadań podzielnych

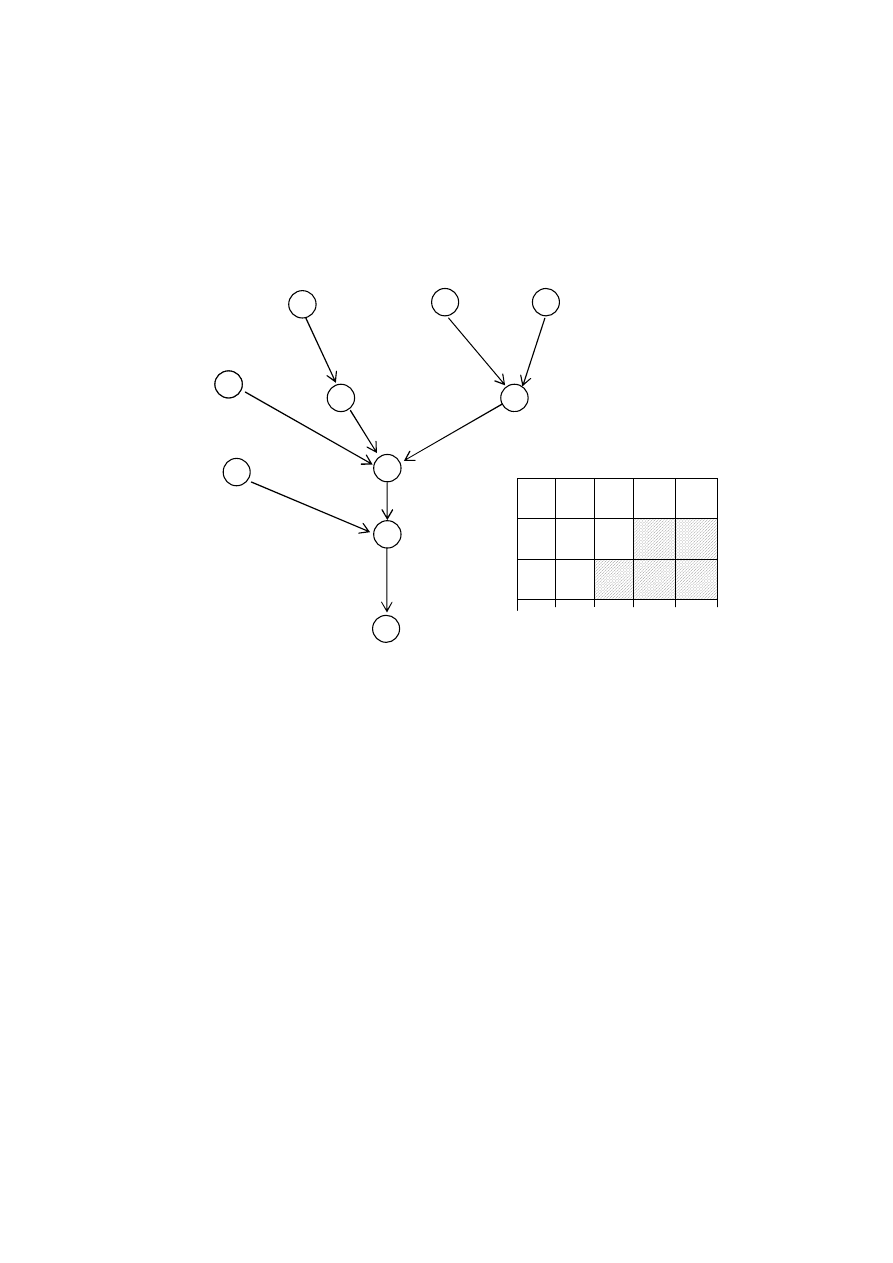
2. Zagadnienie: P|p

j

=1, in–tree|L

max

Algorytm Bruckera P.,

Oznaczmy przez next(j) - bezpośredni następnik zadania Z

j

.

1. Podstawić d

root

*=1 – d

root

2.

Dla zadania Z

j

, j=2,3,..,n wyznaczyć zmodyfikowane terminy zakończenia:

d

j

* = max{1+ d

next(k)

*, 1– d

j

}

3. Uszeregować zadania w kolejności nie rosnących wartości ich zmody-

fikowanych terminów zakończenia, zgodnie z ograniczeniami kolejnoś-
ciowymi.

.

27

Złożoność obliczeniowa algorytmu O(n log n).

1.7. Szeregowanie zadań z dodatkowymi zasobami

Oznaczmy przez R zbiór dodatkowych zasobów (discretely-divisible resources):

R={R

1

, R

2

, ..., R

s

}.

W ogólności, zadanie Z

j

Z jest scharakteryzowane przez wektor żądań zasobo-

wych

R(Z

j

) = [R

1

(Z

j

), R

2

(Z

j

), ..., R

s

(Z

j

)]

gdzie: 0  R

v

(Z

j

)  |R

v

|, v=1, 2, ..,s, oznacza liczbę jednostek zasobu R

v

potrzebną do wykonania zadania Z

j

.

Dla każdego 0  t,



j

R

k

(Z

j

)  |R

v

|,

k=1, 2, ...,s, Z

j

A(t),

gdzie: A(t) - zbiór zdań wykonywanych w chwili t.

(-4

*

, 5)

(-1

*

, 2)

(-1

*

, 3)

(-2

*

, 3)

(0

*

, 4)

Z

1

Z

2

Z

3

Z

5

Z

6

Z

7

Z

8

Z

10

Z

9

Z

4

(-6

*

, 7)

(-5

*

, 6)

(0

*

, 2)

(0

*

, 2)

(-1

*

, 4)

(d

j

*

, d

j

)

L

*

max

= 0

2

4

0

P

2

P

3

Z

3

Z

2

Z

6

Z

5

Z

7

Z

9

Z

1

P

1

Z

4

Z

8

Z

10

5

2

.

28

Pole  w notacji trójpolowej  specyfikuje zadania i dodatkowe
zasoby jest postaci:

res   

    { , k} - oznaczają odpowiednio: liczbę rodzajów dodatkowych zasobów,
ograniczenia zasobowe, żądania zasobowe zadań.

   = k - oznaczają odpowiednio: k rodzajów dodatkowych zasobów, k jednostek

każdego rodzaju, żądania zasobowe każdego zadania nie przekraczają k
jednostek każdego zasobu.

   =  - liczba rodzajów dodatkowych zasobów, ograniczenia oraz żądania

zasobowe są dowolne.

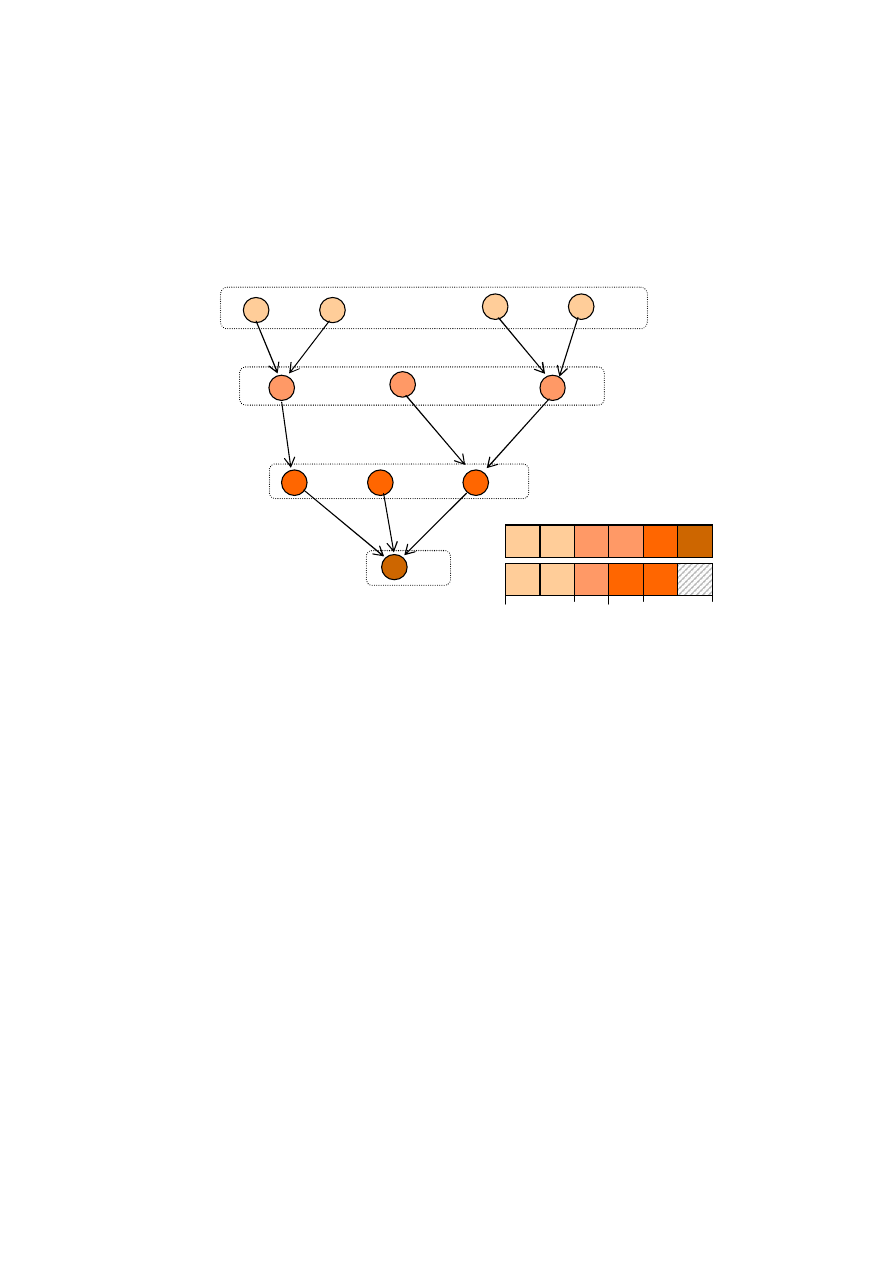
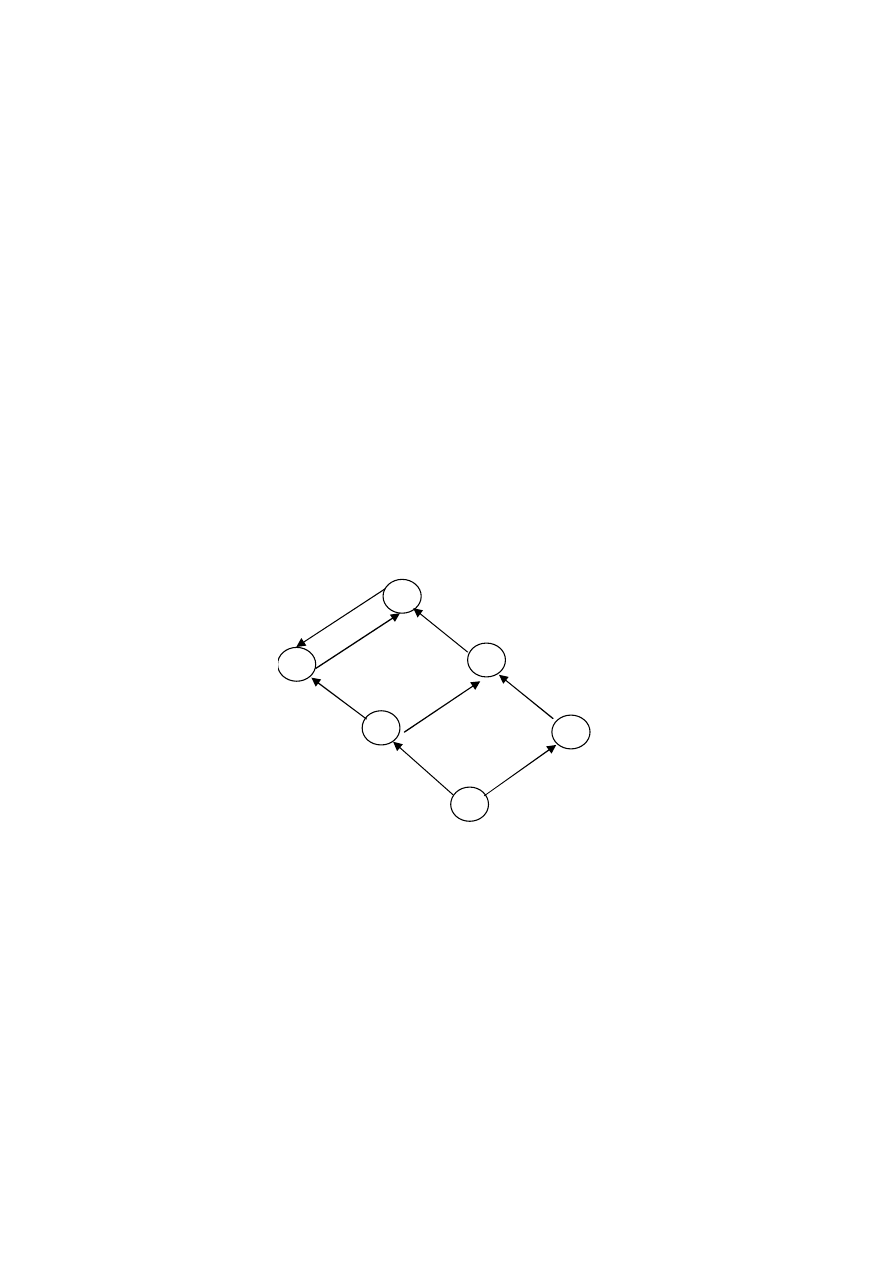
Poniższy diagram jest schematem uogólnień pomiędzy problemami

szeregowania z ograniczonymi zasobami

Wierzchołki grafu reprezentują problemy szeregowania różniące się jedynie

liczbą rodzajów dodatkowych zasobów, ograniczeniami lub żądaniami
zasobowymi zadań. Łuki wskazują kierunek uogólnienia problemów.
Udowodnienie NP-zupełności wybranego problemu implikuje NP-zupełność tych
problemów, do których prowadzi skierowana ścieżka od danego problemu NP-

res ...

res 1..

res 1.1

res 111

res .11

res ..1

Rys. 1.11. Wielomianowa transformowalność pomiędzy problemami

szeregowania z ograniczeniami zasobowymi.

.

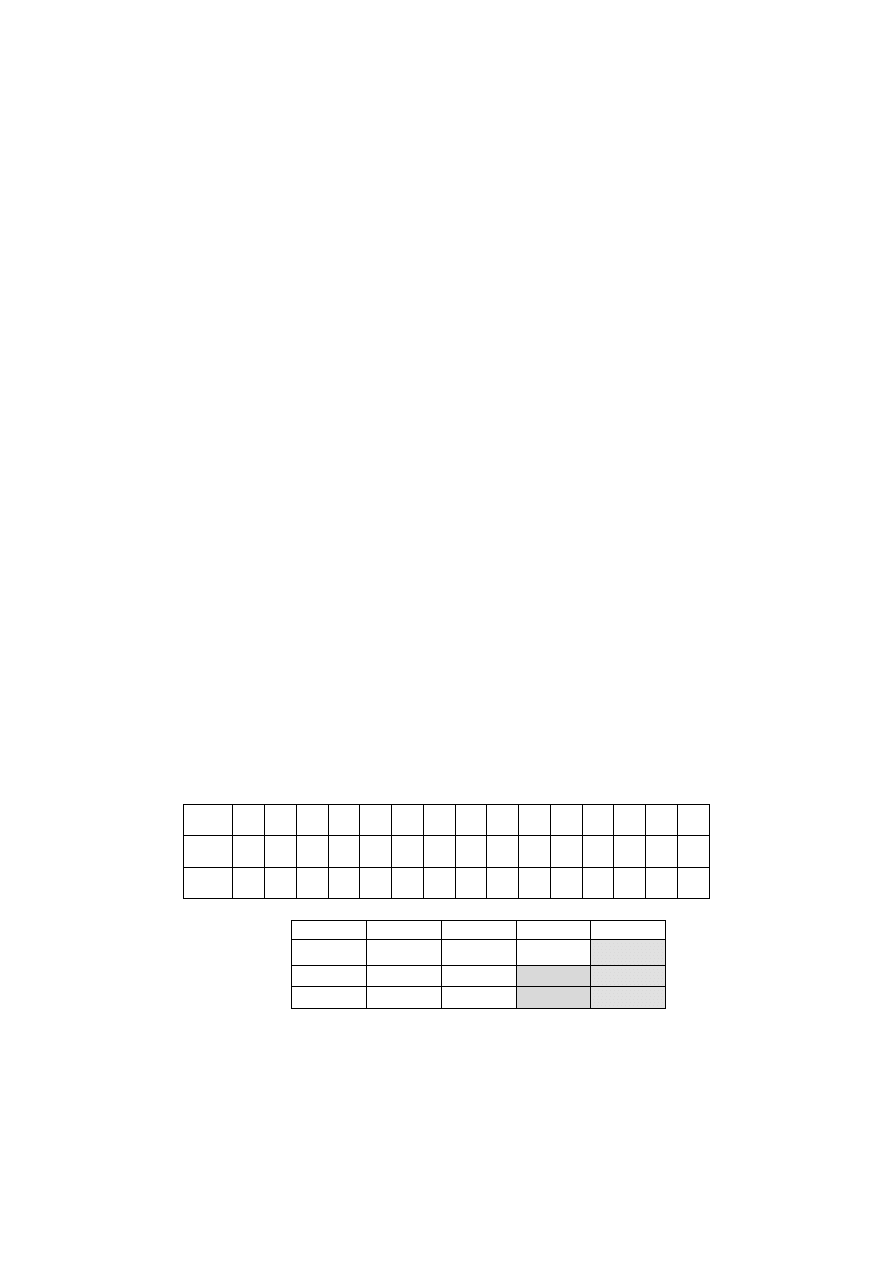
29

zupełnego. Podobnie jeśli dany problem należy do klasy P, to wszystkie problemy
leżące na ścieżkach prowadzących do niego także należą do klasy P.
Wykazanie np NP-zupełności problemu scharakteryzowanego żądaniami
zasobowymi res111, implikuje NP-zupełność wszystkich pozostałych problemów o
identycznych parametrach i jakichkolwiek założeniach dotyczących dodatkowych
zasobów.

1.7.1. Minimalizacja długości uszeregowania.

Specyfikacja rozwiązywanego problemu: Pr

j

, p

j

=1, res11C

max

Algorytm (złożoność obliczeniowa O(n)).

1.

t=0, k=0.

2. Przydzielić w chwili t do wolnej maszyny dostępne zadanie Z

j

, dla którego

R

1

(Z

j

)=1, podstawić k=k+1.

Powtarzać ten punkt dopóty, dopóki albo k=|R

1

|, albo nie będzie zadania o

powyższych własnościach.

3. Przydzielić do pozostałych wolnych maszyn w chwili t, dostępne zadania,

dla których R

1

(Z

i

)=0. Podstawić t=t+1 oraz k=0 i powtórzyć p.2 jeśli są

jeszcze nie przydzielone zadania.

Optymalność algorytmu wynika z faktu, że w każdej chwili zapewnia on

maksymalne wykorzystanie maszyn i dodatkowego zasobu, minimalizując długość
uszeregowania a tym samym średni czas przepływu przez system zadań.
Algorytm sprawdza każde zadanie jednokrotnie. Ponieważ czas związany z takim
sprawdzeniem jest stały O(1), niezależnie od zadania, więc złożoność algorytmu
jest T(n)=n O(1) = O(n).

Z

1

2

3

4

5

6

7

8

9 10 11 12 13 14 15

R

1

(Z

i

)

1

0

0

1

1

1

0

0

0

1

1

0

1

0

1

r

i

3

2

0

1

0

2

2

1

0

0

1

2

0

1

4

P

1

Z

5

Z

13

Z

11

Z

1

Z

15

P

2

Z

10

Z

4

Z

6

Z

12

P

3

Z

3

Z

8

Z

2

P

4

Z

9

Z

14

Z

7

Rys. 1.12. Uszeregowanie wg. algorytmu dla |R

v

| = 2

0 1 2 3 4 5

.

30

Szeregowanie zadań podzielnych z ograniczonymi zasobami. Specyfikacja
rozwiązywanego problemu: Pprm, res11C

max

.

Algorytm (złożoność obliczeniowa O(n)).

1. Wyznaczyć minimalną długość uszeregowania

C*

max

= max { max

j

{p

j

}, 

j=1,n

t

j

/m, 

ZjZR

p

j

/|R

1

|}

(ZR - zbiór zadań, dla których R

1

(Z

j

) = 1, m-liczba procesorów).

Podstawić t = 0.

2. Jeżeli są nie przydzielone zadania należące do zbioru ZR, rozpatrzyć dowolne

z nich, (założymy Z

j

)

, w przeciwnym przypadku wykonaj p. 3.

Jeśli t+p

j

 C*

max

, przydzielić Z

j

do pierwszego wolnego procesora w

przedziale czasu [t, t+p

j

], podstawić t = t + p

j

.

W przeciwnym przypadku przydzielić Z

j

do tego procesora w przedziale

[t, C*

max

] i do następnego wolnego procesora w przedziale [0, p

j

– (C*

max

– t)]

oraz podstaw t = p

j

– (C*

max

- t). Powtórz p. 2.

3. Jeżeli są jeszcze nieprzydzielone zadania, przydzielić je w ten sam sposób jak

zadania ze zbioru ZR w p. 2. W przeciwnym przypadku STOP.

Wartość C*

max

jest minimalną długością uszeregowania, nie może być krótsze niż

maksymalna spośród trzech wartości:

1.

najdłuższego czasu wykonywania zadania,

2.

wartości średniej czasu wykonywania zadania przez jedną maszynę,

3. czasu wykonywania zadań o żądaniu zasobowym równym jednej jednostce

zasobu przypadającego na jednostkę tego zasobu.
Szeregując zadania według powyższego algorytmu nie przekroczymy wartości
C

*

max

. Analizując złożoność obliczeniową powyższego algorytmu należy

zauważyć, że każde zadanie rozpatrywane jest jednokrotnie a ponieważ liczba
kroków związana z tym jest stała zatem złożoność algorytmu jest T(n)=O(n).

.

31

1.8. Szeregowanie zadań cyklicznych

W celu uporządkowania zbioru współbieżnych zadań cyklicznych nadaje się im

priorytety. Strategia doboru priorytetów oraz zasada posługiwania się nimi
określona jest algorytmem szeregowania. Ze względu na przyczynę podejmowania
decyzji szeregujących wyróżniamy:

- szeregowanie wymuszane czasem (clock driven scheduling),
-

szeregowanie wymuszane zdarzeniami (event driven scheduling).

W szeregowaniu wymuszanego czasem decyzje szeregujące podejmowane są w
specyficznych, często ustalonych z góry chwilach czasu. Gdy parametry zadań są
znane apriori, plan szeregowania można ułożyć w postaci tabeli (szeregowanie
cykliczne).

W przypadku szeregowania wymuszanego zdarzeniami decyzje podejmowane

są gdy zachodzą określone zdarzenia np.: zadanie staje się gotowe do wykonania,
procesor jest zwalniany przez bieżące zadanie lub zmienia się priorytet zadania.
Procedura szeregująca może być uaktywniona gdy wystąpiło przerwanie sprzętowe
lub wewnętrzne (wyjątek), albo też proces bieżący wykonał wywołanie systemowe.

Algorytmy szeregowania zadań cyklicznych, w szczególności dotyczących

systemów czasu rzeczywistego (real time systems) opierają się na podstawowym
modelu zadnia, w którym czas dyskretny biegnie od chwili początkowej t=0.
Zadanie (task) Z

i

=(p

i

, T

i

, d

i

) jest charakteryzowane przez następujące parametry:

p

i

- czas wykonania zadania (processing time),

T

i

- okres (period) występowania zadania,

d

i

- względne ograniczenie czasowe zadania (relative deadline), odniesione do

chwili wystąpienia żądania wykonania zadania.
Względne ograniczenie czasowe zadania oznacza limit czasu, przed upływem
którego procesor powinien zakończyć jego wykonanie. Zwykle takie ograniczenie
czasowe jest mniejsze lub równe okresowi występowania zadania. Okres
występowania zadania T

i

, czas jego wykonania p

i

oraz ograniczenie czasowe d

i

powinny spełniać warunek:

i

i

i

T

d

p





.

.

32

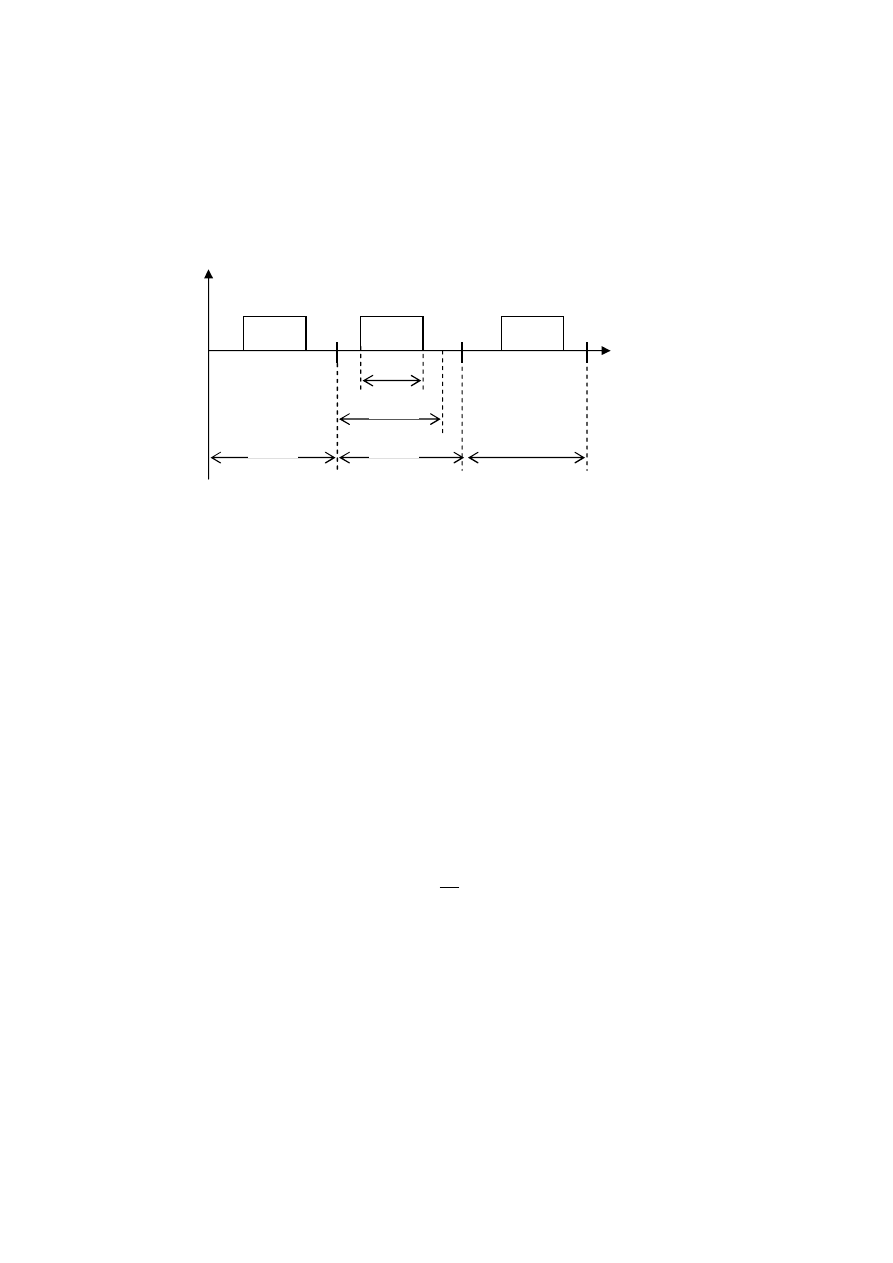
Parametry czasowe zadania cyklicznego przedstawia poniższy rysunek.

Własności zadań cyklicznych:
-

wszystkie zadania są cykliczne ze znanym okresem T

i

pomiędzy kolejnymi

wystąpieniami,

-

wszystkie instancje zadania mają niezmienny czas wykonania p

i

,

-

zadania są od siebie niezależne, dopuszcza się ich wywłaszczanie,

-

zadania wykonywane są cyklicznie z założoną częstotliwością określoną na
podstawie wymagań danej aplikacji (np. wolna, szybka pętla obliczeń).

Implementacją zadania jest sekwencyjny program uruchamiany w
dyskretnych chwilach t

i

takich, że t

i+1

=t

i

+T

i

. Instancje (kolejne wystąpienia)

zadania periodycznego są regularnie aktywowane ze stałą częstotliwością i
mają ten sam najdłuższy czas wykonywania WCET (Worst Case Execution
Time). Wszystkie instancje zadania mają tą samą wartość względnego
ostatecznego terminu zakończenia. Współczynnik wykorzystania procesora
definiowany jest następująco:







n

i

i

i

T

p

U

1

(1.20)

Współczynnik ten opisuje obciążenie procesora podczas wykonywania zbioru
zadań cyklicznych.
Dla różnych algorytmów szeregowania i różnych zbiorów zadań współczynnik U
może przyjmować różne graniczne wartości, dla których dany zbiór zadań jest
szeregowalny tzn. może wykonać wszystkie swoje obliczenia w zadanych
ograniczeniach czasowych.

t

p

i

Z

i

Z

i

Z

i

d

i

T

i

T

i

T

i

Rys. 1. 13. Parametry czasowe zadania cyklicznego

.

33

Celem algorytmu szeregowania zadań cyklicznych jest takie ustalenie kolejności
ich wykonywania, aby żadne zadanie nie przekroczyło swojego żądanego terminu
zakończenia. Jeżeli istnieje taka kolejność mówimy, że zbiór zadań jest
szeregowalny. Ewentualne włączanie nowego zadania do systemu odbywa się
według ściśle określonej procedury (mode change protocol). Zadania sporadyczne
są uwzględniane poprzez traktowanie ich jako zadania cykliczne, o okresie
równym minimalnemu czasowi pomiędzy kolejnymi wystąpieniami tego typu
zadań.

Wiele aplikacji w szczególności aplikacji czasu rzeczywistego składa się ze

zbioru zadań wykonywanych cyklicznie (odczyt danych sensorycznych, pętle
sterowania, monitorowanie). Często stosowaną metodą szeregowania takich zadań
jest przydzielanie priorytetu, wówczas w danej chwili jest uruchamiane zadanie o
najwyższym priorytecie. Podstawowe algorytmy priorytetowe do szeregowania
zadań cyklicznych:
1. RMS (Rate Monotonic Scheduling) – algorytm monotoniczny w częstotliwości.
2. EDD (Earliest Due Date) – pierwszy z najmniejszą wartością względnego

ograniczenia czasowego („najwcześniejsza linia krytyczna najpierw”).

3. CE (Cyclic Executive) - wykonywanie cykliczne.

1.8.1. Algorytmy priorytetowe

I. Algorytm RMS.

Algorytm RMS jest algorytmem statycznym. Działanie algorytmu oparte jest na

systemie priorytetów przydzielanych do poszczególnych zadań w ten sposób, że im
krótszy okres, tym wyższy priorytet. Stosowanie tej zasady wynika z faktu, że
zadania występujące częściej zazwyczaj są ważniejsze od zadań występujących
rzadziej.
System niezależnych, wywłaszczanych zadań cyklicznych ze względnymi
ograniczeniami czasowymi równymi ich okresom tj. d

i

= T

i

, może mieć poprawny

harmonogram na jednym procesorze utworzony przez algorytm RMS, jeśli
współczynnik wykorzystania procesora spełnia warunek konieczny:

1

1







n

i

i

i

T

p

(1.21)

Powyższy warunek na szeregowalność zadań wynika z faktu, że łączny stopień

wykorzystania czasu pracy procesora przez wszystkie zadania nie może być
większy niż 100%. Warunek wystarczający pozwalający na weryfikację spełnienia
warunków czasowych i gwarantujący, że n zadań zostanie wykonanych przed

.

34

upływem ich ograniczenia czasowego został podany przez Liu i Laylanda i wyraża
się wzorem:

)

1

2

(

/

1

1











n

n

i

i

i

gr

n

T

p

U

(1.22)

Dla dużych wartości n , U

gr

= ln2  0.69 co oznacza, że każdy zbiór zadań,

dla którego współczynnik wykorzystania procesora jest 0.69 zawsze będzie
szeregowalny. Jeśli dla danego zbioru zadań współczynnik wykorzystania
procesora U mieści się w przedziale U

gr

 U 1 to zbiór ten może nie być

szeregowalny. Wówczas dla rozstrzygnięcia należy rozważyć przypadek najgorszy
(worst case), dla którego wszystkie zadania podlegające szeregowaniu wchodzą
jednocześnie w stan gotowości. Jeżeli każde z rozważanych zadań zostanie
zakończone przed upływem swego ograniczenia czasowego, to dany zbiór zadań
jest szeregowalny.

Algorytm RMS, spośród priorytetowych algorytmów statycznych, wyznacza

uszeregowanie optymalne, w tym sensie że jeżeli nie są utrzymywane ograniczenia
czasowe, to żaden inny algorytm z tej klasy również ich nie dotrzymuje.

II. Algorytm EDD.

Systemy, w których podczas pracy priorytet przydzielany zadaniu, może zostać

zmieniony nazywamy systemami z dynamicznym przydziałem priorytetu.
Przykładem

dynamicznego

przydziału

priorytetu

jest

algorytm

EDD

wykorzystujący zasadę zgodnie, z którą najwyższy priorytet przydzielany jest
zadaniu, któremu najwcześniej kończy się ograniczenie czasowe. Algorytm EDD
jest ogólnym algorytmem szeregującym zbiory zadań w oparciu o jeden procesor,
przy czym żądany termin wykonania każdego z zadań jest równy jego okresowi,
ponadto zadania są niewywłaszczalne.

Podstawą działania algorytmu EDD jest regularne aktualizowanie żądanych

terminów zakończenia zadań. Czynność ta wykonywana jest po wystąpieniu
każdego przerwania obsługiwanego przez moduł szeregujący tj. przerwania
zegarowego, pojawienia się nowego zadania czy też zakończenia wykonywania
aktualnego.

Zaletą metody dynamicznego przydziału priorytetu EDD, w porównaniu do

metod statycznego przydziału priorytetu RMS, jest lepsze wykorzystanie procesora.
Jej wadą jest większe obciążenie procesora czynnościami szeregowania podczas
pracy. Pojawiające się w systemie nieokresowe zadania traktowane są przez
algorytm analogicznie do zadań okresowych. Jedyną różnicą jest brak cyklicznego
ich wykonywania.

.

35

II. Algorytm CE.

Zastosowanie wykonywania cyklicznego CE to jedno z pierwszych i

popularnych podejść do szeregowania zadań cyklicznych. Procedura szeregująca
wywoływana jest w cyklu minimalnym (minor cycle). Cyklem głównym jest
najmniejsza wspólna wielokrotność z cykli poszczególnych zadań (T

1

, T

2

, ..., T

n

).

Plan szeregowania sporządzany jest dla cyklu głównego, w którym wszystkie
zadania przyporządkowane do procesora powinny zostać wykonane tak, aby
ograniczenia czasowe zadań nie zostały przekroczone.

Główny cykl określa maksymalny cykl w systemie.

Przyjmuję się, że względny

termin d

i

jest równy okresowi T

i

.

Cechami charakterystycznymi algorytmu CE są determinizm i brak wywłaszczeń.
Opracowanie tabeli wykonywania cyklicznego jest w ogólności trudne trudna
aktualizacja, powstaje problem z włączeniem zadań o długim okresie a także z
włączeniem zadań sporadycznych.

Z

i

T

i

p

i

Z

1

25

10

Z

2

25

8

Z

3

50

6

Z

4

50

4

Z

5

100

2

// Ustawić przerwania na 25 jedn.

DO {

wait_for_interrupt;
procedure Z

1

; procedure Z

2

;

procedure Z

3

;

wait_for_interrupt;
procedure Z

1

; procedure Z

2

;

procedure Z

4

; procedure Z

5

;

wait_for_interrupt;
procedure Z

1

; procedure Z

2

;

procedure Z

3

;

wait_for_interrupt;
procedure Z

1

; procedure Z

2

;

procedure Z

4

;

}

WHILE (1);

.

36

2. METODY OPTYMALIZACJI DYSKRETNEJ

Problemy szeregowania zadań najczęściej formułowane są w terminach

optymalizacji dyskretnej, w której zmienne decyzyjne przyjmują wartości,
całkowitoliczbowe lub binarne. Problemy te należą do klasy problemów
wyjątkowo trudnych z obliczeniowego punktu widzenia. Głównymi powodami
tych trudności jest częsty brak analitycznych własności oraz wieloekstremalność ze
znaczną liczbą ekstremów lokalnych. Istnienie wielu ekstremów, kłopotliwe już dla
przypadku optymalizacji ciągłej, nabiera dla problemów dyskretnych szczególnego
znaczenia. Bezpośrednią konsekwencją NP-trudności jest to, że czas obliczeń
odpowiedniego algorytmu komputerowego jest funkcją wykładniczą od rozmiaru
rozwiązywanego problemu.

W celu uniknięcia kłopotów, próbuje się zamiast rozwiązywać problem

dokładnie, wyznaczać jego rozwiązanie przybliżone. Z tego też powodu, dziedzina
deterministycznego szeregowania zadań charakteryzuje się znaczną rozmaitością
zarówno modeli jak i metod rozwiązywania, zwykle dedykowanych dla wąskich
klas zagadnień. Ograniczenie ogólności modeli ma na celu wykrycie tych
szczególnych własności problemu, których umiejętne wykorzystanie w algorytmie
zdecydowanie poprawia jego cechy numeryczne, takie jak czas obliczeń, czy
zbieżność do rozwiązania optymalnego. Często dla tego samego problemu NP-
trudnego występuje wiele różnych algorytmów o istotnie różnych cechach
numerycznych. Znajomość dziedziny zastosowań oraz metod rozwiązywania,
pozwala na właściwy dobór dla każdego nowo postawionego problemu
odpowiedniego algorytmu.

Rozważany problem optymalizacji dyskretnej zapisujemy jako zadanie

minimalizacji:

gdzie: K() - funkcja celu (kryterium optymalizacji),  - dyskretny zbiór
rozwiązań dopuszczalnych, określonych przez zestaw warunków ograniczających.

Tak zdefiniowane problemy, w kontekście szeregowania są od wielu lat

przedmiotem intensywnych badań. W związku z tym istnieje duża ilość
różnorodnych podejść do rozwiązywania takich zagadnień.

Najogólniej, metody optymalizacji dyskretnej można podzielić na dokładne i

przybliżone. Do metod dokładnych można zaliczyć metody oparte na schemacie
podziału i ograniczeń (B&B), metody subgradientowe, metody programowania
całkowitoliczbowego czy też pewne algorytmy dedykowane do poszczególnych
zagadnień.

K*=

def

K(

*

) = min



K()

(2.1)

.

37

Współczesne wymagania dotyczące optymalizacji dyskretnej wymuszają

osiąganie rozwiązań bardzo szybko. Z tego względu trudna do zastosowania staje
się kosztowna metoda bezpośredniego przeglądu całej przestrzeni rozwiązań
dopuszczalnych. W takiej sytuacji pojawia się konieczność wypracowania zupełnie
nowych podejść do optymalizacji i sięgnięcie po prostsze, gorsze jakościowo , ale
za to szybsze metody przybliżone. Słuszność takiego przejścia jest tym bardziej
uzasadniona, że przy pomocy takich metod, wiele problemów uznawanych
dotychczas za trudne z obliczeniowego punktu widzenia, doczekało opracowania
szybkich technik rozwiązywania.
Metody przybliżone wyznaczają pewne rozwiązanie 

A

 takie, że:

Metody przybliżone są z reguły problemowo zorientowane. Podstawową ich cechą,
odróżniającą je od metod dokładnych, jest najczęściej brak formalnych dowodów
na ich zbieżność do rozwiązania optymalnego.

Z drugiej strony, rozwiązania znajdowane przez algorytmy przybliżone nie

tylko okazują się dobre w sensie oceny ich optymalności, ale także uzyskiwane są
w zdecydowanie krótszym czasie. Kolejną cechą algorytmów przybliżonych są
parametry sterujące. O ile w algorytmach dokładnych nie mają wpływu na
końcowe rozwiązanie, o tyle w przypadku technik heurystycznych ich znaczenie
jest duże. Wśród algorytmów przybliżonych wyróżnia się kilka klas, które
wzajemnie się przenikają. Najczęściej wyróżnia się algorytmy konstrukcyjne oraz
algorytmy typu ”popraw rozwiązanie”. Pierwsze z nich są metodami szybkimi,
łatwo implementowanymi, jednak generują rozwiązania obarczone względnie
dużym błędem przybliżenia. Do drugiej grupy należą algorytmy, które są
wolniejsze wymagają rozwiązania początkowego poprawianego następnie krokowo,
ale dostarczają rozwiązań o bardzo dobrej jakości. Algorytmy konstrukcyjne służą
do generowania rozwiązań początkowych dla metod bardziej ogólnych. Ważną
grupę metod stanowią algorytmy metaheurystyczne.
Optymalizacja dyskretna ma znaczenie w rozwiązywaniu praktycznych zagadnień
takich jak:

•

Szeregowanie zadań (Sequencing , Scheduling Problem)

•

Zagadnienie komiwojażera (Traveling Salesman Problem)

•

Problem osiągalności w grafie (Reachability problem)

•

Zagadnienie przepływu (Max-flow Problem)

•

Problem plecakowy (Knapsack Problem)

•

Problem przydziału (Assignment problem )

Zagadnienia te mają charakter kombinatoryczny i należą do optymalizacji
dyskretnej.

K(



A

)  K(

*

)

(2.2)

.

38

2.1. Metoda podziału i ograniczeń

Metoda podziału i ograniczeń B&B (Branch and Bound method) należy do

podstawowych metod wyznaczania optymalnych rozwiązań dla dyskretnych
problemów optymalizacyjnych. Dekompozycja zbioru rozwiązań dokonywana jest
tak długo aż dalszy podział jest niemożliwy, czego rezultatem jest drzewo podziału
(branching tree). W węzłach drzewa znajdują się częściowe rozwiązania,
natomiast w liściach odnajdziemy potencjalne rozwiązanie optymalne. Istotą
algorytmu B&B jest znalezienie dokładnego optymalnego rozwiązania bez
konieczności przeglądania całego drzewa rozwiązań cząstkowych.

Ogólna idea metody podziału i ograniczeń polega na uporządkowanym

przeszukiwaniu skończonego zbioru rozwiązań. Przegląd zupełny (pełny przegląd)
zbioru rozwiązań zastępujemy przeglądem ukierunkowanym. Pozwala to ocenić
pośrednio pewne podzbiory rozwiązań i ewentualnie je odrzucić lub czasowo
pominąć, bez utraty rozwiązania optymalnego, co znacznie przyspiesza uzyskanie
rozwiązania. Zbiór wszystkich rozwiązań dzieli się (branch), sukcesywnie na
coraz mniejsze podzbiory, a dla każdego podzbioru oblicza się dolną granicę ( w
przypadku minimalizacji) LB (Lower Bound) wartości funkcji celu.

Algorytm podziału i ograniczeń w każdym węźle drzewa podziału wylicza

wartość LB, które pozwala stwierdzić, czy węzeł ten jest „potencjalnie obiecujący”
do dalszego uwzględniania. Wartość ta jest granicą wartości rozwiązania, jakie
można uzyskać dzięki rozwinięciu tego węzła. Jeżeli wartość ta nie jest lepsza niż
wartość dotychczas znalezionego rozwiązania, węzeł jest oznaczany jako
„nieobiecujący”, w przeciwnym razie potencjalnie zawiera rozwiązanie optymalne.
Po każdym podziale, podzbiory, dla których dolne ograniczenie jest większe od
wartości funkcji celu dla najlepszego, znanego dotychczas rozwiązania są
eliminowane z dalszego podziału. Dzięki temu unika się bezpośredniego
sprawdzania rozwiązań należących do eliminowanych podzbiorów. Podział
postępuje do chwili znalezienia rozwiązania dopuszczalnego, dla którego wartość
funkcji celu jest nie większa niż najmniejsze dolne ograniczenie wszystkich
niepodzielonych podzbiorów. W najgorszym razie trzeba sprawdzić wszystkie
rozwiązania, co przesądza o wykładniczej złożoności obliczeniowej metody
podziału i ograniczeń (worst-case complexity). Na ogół liczba rozwiązań
sprawdzanych przed znalezieniem rozwiązania optymalnego jest znacznie mniejsza,
co świadczy o efektywności metody.

Schemat B&B określa tylko ogólne podejście, oparte na dekompozycji i

„inteligentnym” przeszukiwaniu zbioru rozwiązań dopuszczalnych problemu
optymalizacyjnego. Istnieje wiele algorytmów opartych na tym schemacie. Jego
zastosowanie jest uzasadnione tylko wtedy gdy rozwiązywany problem jest NP-
zupełny.

.

39

2.1.1. Ogólny schemat B&B

Metoda wyznacza rozwiązanie globalnie optymalne * takie, że

Dla dowolnego zadania optymalizacji zachodzi

gdzie 

j

, jS jest rozbiciem zbioru  na podzbiory parami rozłączne i

wyczerpujące tzn.

Zatem rozwiązanie problemu można otrzymać rozwiązując wpierw zbiór
podproblemów postaci:

dla jS, a następnie stosując zależność (2.4).
Pełny zbiór podproblemów jest scharakteryzowany poprzez:

•

funkcję kryterialną (funkcję celu) K()

•

rozbicie P = {

j

: jS}.

Odpowiednie podproblemy mogą być rozwiązywane szeregowo (system
jednoprocesorowy) lub równolegle (system wieloprocesorowy).
Dekompozycja problemu jest uzasadniona jeśli uzyskanie rozwiązania dla
problemu (2.7) jest istotnie łatwiejsze niż dla problemu (2.1).
Problem (2.7) dla wybranego ustalonego jS można rozwiązać stosując przegląd
niejawny (implicite search) oraz rekaksację ograniczeń lub funkcji kryterium.

2.1.2. Metoda relaksacji

1.

Relaksacja ograniczeń.

Relaksacja ograniczeń to usunięcie lub złagodzenie części (lub całości)

ograniczeń wyznaczających zbiór rozwiązań dopuszczalnych 

j

. Zachodzi bowiem



j



j

R

, gdzie 

j

R

jest zbiorem rozwiązań dopuszczalnych problemu, w stosunku

do którego zastosowano relaksację. Spełniona jest również zależność:

K(

*

) = m i n



K()

(2.3)

m i n



K() = min {m i n

1

K(),..., m i n

s

K()}}

(2.4)

j

i

S

j

i

i

j













,

,

0

(2.5)











j

S

j

(2.6)

m i n

j

K()

(2.7)

m i n

j

K()  m i n

j

R

K() = K(

* R

) =

def

LB(

j

)

(2.8)

.

40

Jeżeli dla wyznaczonego rozwiązania optymalnego *

R

problemu zrelaksowanego

zachodzi *

R



j

, to otrzymane rozwiązanie jest również rozwiązaniem

optymalnym problemu postaci (2.7). W przeciwnym przypadku K(*

R

) stanowi

dolne ograniczenie LB(

j

) wartości funkcji kryterialnej dla wszystkich rozwiązań

problemu (2.7).

2. Relaksacja funkcji kryterium.

Relaksacja funkcji kryterium to zastąpienie funkcji K() funkcją K’() taką, że

K’()  K() dla wszystkich .
W ten sposób zachodzi:

Jeżeli dla wyznaczonego rozwiązania optymalnego ` problemu zrelaksowanego
m i n

j

K`() zachodzi K(`) = K`(`) to otrzymane rozwiązanie ’ jest także

rozwiązaniem optymalnym problemu bez relaksacji. W przeciwnym przypadku
wielkość K(

*R

) stanowi dolne ograniczenie LB’(

j

) wartości funkcji kryterialnej

dla wszystkich rozwiązań problemu (2.7).
Postać relaksacji jest w zasadzie dowolna, chociaż zakłada się domyślnie, że
rozwiązanie problemu zrelaksowanego powinno być istotnie łatwiejsze niż
problemu (2.7), np. problem zrelaksowany należy do P-klasy.
W praktyce relaksacja jest silnie specyficzna dla każdego rozważanego problemu.
Pośrednio rozwiązany został również problem (2.7) dla którego stwierdzono
zachodzenie warunku

gdzie: UB (Upper Bound) jest pewnym górnym ograniczeniem wartości funkcji
celu dla wszystkich rozwiązań problemu (2.1).
Problem taki faktycznie nie jest rozwiązywany lecz eliminowany z rozwiązań
bowiem nie zawiera rozwiązania o wartości funkcji celu mniejszej niż podana
wartość progowa UB. Dla szeregu problemów szczególnych możliwe jest
uzyskanie specyficznych reguł eliminacji, które mimo iż nie zawsze są
przedstawiane w formie warunku (2.10) mogą być do niego sprowadzone.
Problem (2.7) odpowiadający wybranemu 

j

jest usuwany ze zbioru , zaś na

jego miejsce dodawane są podproblemy otrzymane przez podział 

j

na pewną

liczbę podproblemów potomnych, skojarzonych ze zbiorem rozwiązań Y

k

,

k=1,2,..,r, takimi, że Y

k

, k=1,2,..,r jest podziałem zbioru 

j

.

Proces ten wygodnie jest przedstawić w postaci drzewa rozwiązań, w którym
każdemu węzłowi drzewa odpowiada pewien zbiór 

j

, zaś krawędziom drzewa

para podzbiorów (

i

, 

j

,) taka, że 

j

został otrzymany poprzez podział 

i

.

Korzeniowi drzewa odpowiada zbiór .

m i n

j

K()  m i n

j

K’() = K

’

(

’

) =

def

LB`(

j

)

(2.9)

LB(

j

)  UB

(2.10)

.

41

Jeżeli jest zbiorem skończonym, algorytm zatrzyma się po skończonej

liczbie kroków. Każdy algorytm B&B wymaga precyzyjnego określenia
następujących elementów:

•

Reguła wyboru, określająca kolejność rozwiązywania podproblemów.

•

Przyjęta relaksacja dostarczająca dolne ograniczenie.

•

Reguły eliminacji stosowane.

•

Zasada podziału.

•

Technika dostarczająca górne ograniczenie funkcji celu.

Algorytm B&B jest tym lepszy im więcej podproblemów ze zbioru  jest
eliminowanych. Skuteczność eliminacji zależy od wielu współdziałających
czynników:

•

sposobu relaksacji,

•

dokładności dolnego / górnego ograniczenia wartości funkcji celu,

•

reguły podziału,

•

reguły wyboru.

Rozwiązanie można otrzymywać przyjmując różne strategie wyboru kolejnych
węzłów, z których kontynuowany jest proces podziału. Istnieją dwie podstawowe
strategie wyboru węzła do podziału:

1.

Podział z węzła o minimalnym dolnym ograniczeniu ( strategia wszerz,
breadth-first).

2.

Podział z kolejnego otrzymanego węzła (strategia głąb, depth-first-search).

Podział według strategii 1 wymaga, przechowywania w pamięci stanów wszystkich
węzłów, z których wybierany jest jeden do dalszego podziału.
Podział wg strategii 2, prowadzony jest wzdłuż wybranej gałęzi drzewa, aż do
chwili otrzymania pojedynczego elementu podzbioru, który niekoniecznie jest
elementem ekstremalnym. W przypadku strategii w głąb, droga w drzewie podziału
jest wyznaczana dopóty, dopóki jej ostatni element nie zostanie określony jako
węzeł końcowy. Poszukiwanie jest zawsze prowadzone od ostatnio sprawdzanego
węzła, którego nie wszystkie gałęzie były jeszcze rozwijane. Główną operacją
strategii w głąb jest ekspansja węzłów (tzn. generowanie wszystkich jej
potomków). Strategia w głąb może być nieskuteczna, gdy zostanie zastosowana dla
grafów o dużej głębokości. Z tego powodu jest ona zazwyczaj uzupełniana
mechanizmem kontroli ograniczenia głębokości. W strategii w głąb stosunkowo
łatwo można oszacować wymagania pamięciowe, (w pamięci przechowywane są
tylko węzły z aktualnie badanej ścieżki).

W przypadku strategii wszerz, rozważa się kolejne poziomy grafu o jednakowej

głębokości. Główną operacją strategii wszerz jest ekspansja węzłów. Strategia ta
daje gwarancję, że dla lokalnie skończonych grafów (tj. takich, w których każdy
węzeł ma skończoną liczbę potomków) osiągnie się węzeł celu.

.

42

Wadą strategii wszerz jest to, że w pamięci są przechowywane wszystkie węzły o
danej głębokości przed wygenerowaniem jakiegokolwiek węzła o głębokości o
jeden większej. W każdym kroku następują powroty do węzłów wygenerowanych i
przechowywanych w pamięci w krokach wcześniejszych.

2.1..3. Specjalizowane warianty B&B

Schematy B&B dedykowane konkretnym zastosowaniom są zwykle bardziej

efektywne, dzięki wykorzystaniu szczególnych własności problemu do poprawy
własności eliminacyjnych schematu. Postacie tych własności zależą od
konkretnego problemu.

Rozważmy problem 1r

j

, q

j

C

max

. W celu wyznaczenia dolnego ograniczenia

dla IN wprowadźmy następujące pojęcia:

r(I)=min

iI

r

i

p(I) =

iI

p

i

q(I)=min

iI

q

i

h(I) = r(I)+ p(I)+ q(I)

1. Dolne ograniczenie skojarzone ze zbiorem zadań.

Najprostsze dolne ograniczenie jest skojarzone z zadaniami i określone

wzorem

Złożoność obliczeniowa wyznaczenia tej wartości jest liniowa O(n).

2. Dolne ograniczenie wyznaczane poprzez relaksację ograniczenia r

j

< S

j

do

ograniczenia słabszego r(N) < S

j

.

Prowadzi to do problemu szeregowania postaci:

1r

j

=r(N), q

j

C

max

który posiada algorytm wielomianowy o złożoności O(nlog n).
Niech C

max

*q

będzie optymalną wartością funkcji celu problemu 1q

j

C

max

,

wówczas wartość dolnego ograniczenia wyniesie:

3. Dolne ograniczenie

wyznaczane

poprzez relaksację funkcji celu max

jN

(C

j

+q

j

)

do słabszej postaci:

max

jN

(C

j

+q(N)) = max

jN

C

j

+ q(N)

LB

0

= max

1jn

(r

j

+ p

j

+ q

j

)

(2.11)

LB

1r

= r(N) + C

max

*q

(2.12)

.

43

Prowadzi to do problemu szeregowania postaci:

1r

j

, q

j

=q(N)C

max

o wielomianowej złożoności obliczeniowej O(nlogn). Niech C

max

*r

będzie

optymalną wartością funkcji celu problemu 1r

j

C

max

, wówczas odpowiednia

wartość dolnego ograniczenia może być wyznaczona z zależności:

Efektywność algorytm B&B zależy od reguły podziału, reguły wyboru kolejnego
węzła do podziału oraz funkcji dolnego (górnego) ograniczenia.
Funkcja

dolnego

ograniczenia

przyporządkowuje

każdemu

rozwiązaniu

częściowemu liczbę rzeczywistą reprezentującą dolne ograniczenie funkcji celu.
Przy wyborze LB konieczny jest kompromis między dokładnością a czasem
wyznaczenia. Górne ograniczenie funkcji celu, jest to jej wartość dla pewnego
rozwiązania kompletnego znanego przed rozpoczęciem działania algorytmu, może
być też wyznaczona heurystycznie i aktualizowana w razie znalezienia rozwiązania
lepszego.

2.2. Algorytm zachłanny

Rozwiązywanie problemów z wykorzystaniem algorytmów zachłannych

(greedy algorithms) polega na podejmowaniu sekwencji wyłącznie na podstawie
informacji lokalnych. Wybierana jest lokalnie optymalna możliwość zakładając, że
doprowadzi ona do globalnie optymalnego rozwiązania.
Algorytmy zachłanne nie zawsze prowadzą do optymalnych rozwiązań, choć dla
wielu problemów takie rozwiązania są wystarczające. W przypadku „podejścia
zachłannego” nie występuje etap dzielenia na mniejsze realizacje tak jak np. w
programowaniu dynamicznym. Problem rozwiązywany jest poprzez realizację
ciągu kroków. Ich popularność wynika z prostoty. W podejściu tym założono
istnienie heurystyki podejmowania decyzji, która daje w każdym kroku najlepszy
ruch, najlepszy "zysk". Stąd pochodzi też nazwa zachłanne podejście.

Etapy podejścia zachłannego:

1. Procedura wyboru (Selection procedure).

2. Sprawdzenie wykonalności (Feasibility check).

3. Sprawdzenie rozwiązania (Solution check).

LB

1q

= C

max

*r

+ q(N)

(2.13)

.

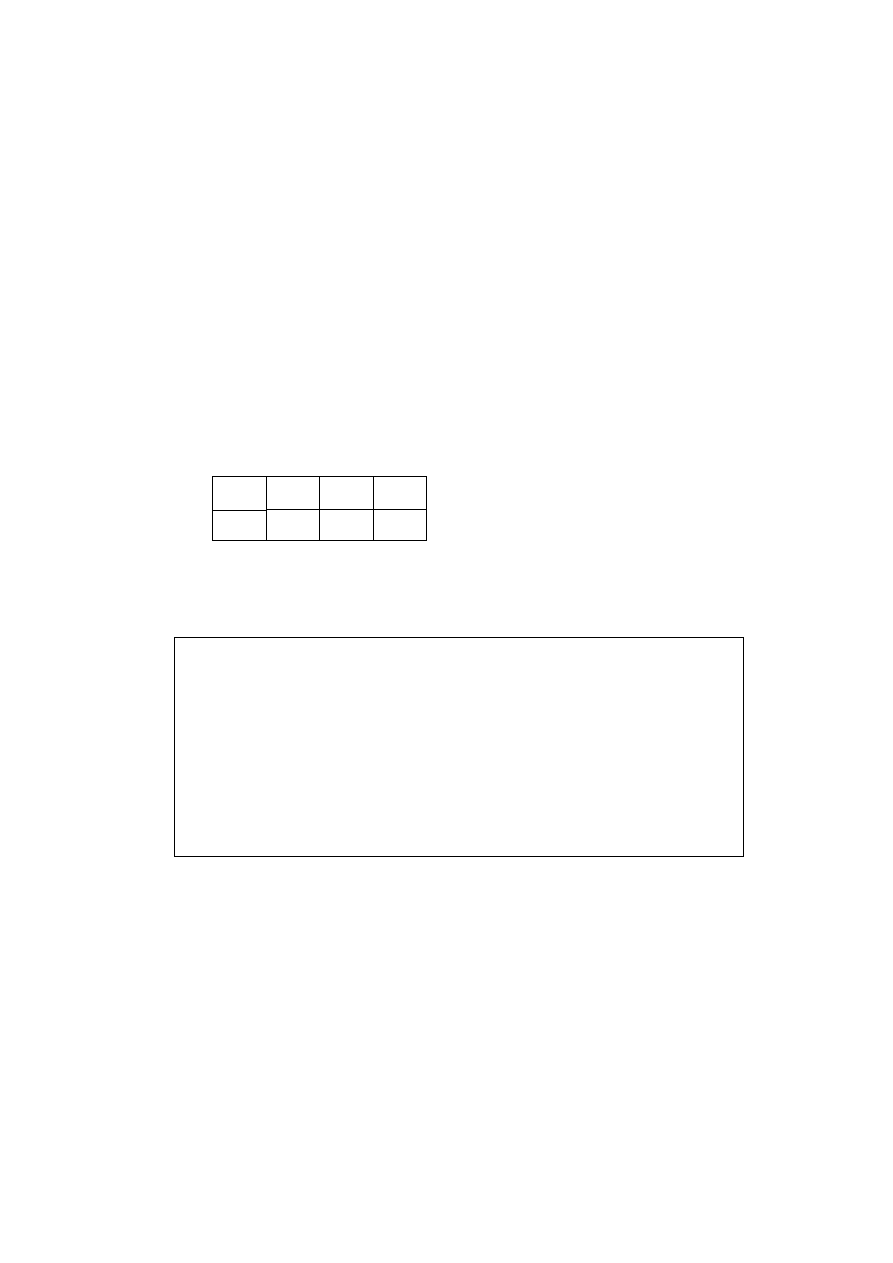
44

2.2.1. Minimalizacja czasu pobytu w systemie.

Rozwiązywany jest problem minimalizacji całkowitego czasu pobytu w

systemie (time in the system) za pomocą algorytmu zachłannego. Rozwiązanie tego
problemu polega na uwzględnieniu wszystkich możliwych uszeregowań zadań i
wybraniu optymalnego, dla którego czas oczekiwania i wykonania zadań jest
minimalny.
Algorytm zostanie przedstawiony na przykładzie szeregowania operacji dostępu do
dysku przez użytkowników w celu zminimalizowania całkowitego czasu, jaki
spędzają na oczekiwaniu i obsłudze. Załóżmy, że mamy do czynienia z trzema
zadaniami o określonych czasach obsługi:

Faktyczne jednostki czasu nie mają znaczenia dla istoty problemu. Jeżeli
uszeregujemy je w porządku [Z

1

, Z

2

, Z

3

], czas spędzony w systemie dla trzech

zadań będzie przedstawiał się następująco:

Ta sama metoda obliczeniowa daje następującą listę wszystkich możliwych usze-
regowań i całkowitego czasu w systemie:

Zadanie

Czas w systemie

Z

1

5 (czas obsługi)

Z

2

5 (oczekiwanie na Z

1

) + 10 (czas obsługi)

Z

3

5 (oczekiwanie na Z

1

) + 10 (czas obsługi Z

2

) + 4 (czas obsługi)

Całkowity czas w systemie dla tego uszeregowania wynosi:

5 + (5+10) +(5+10+4)=39

Z

i

Z

1

Z

2

Z

3

p

i

5

10

4

.

45

Optymalne uszeregowanie wystąpiło, kiedy zadanie o najkrótszym czasie obsługi
(zadanie Z

3

o czasie obsługi 4) zostało ustawione jako pierwsze, po nim zostało

ustawione zadanie o drugim co do długości czasie obsługi (zadanie Z

l

, o czasie

obsługi 5) i w końcu zadanie o najdłuższym czasie obsługi (zadanie Z

2

, o czasie

obsługi 10).
Intuicyjnie możemy stwierdzić, że takie uszeregowanie jest optymalne, gdyż po-
woduje wykonanie zadań najkrótszych najwcześniej.
Pseudokod algorytmu zachłannego dla takiego podejścia ma następującą postać:

Podstawowym działaniem algorytmu jest sortowanie zadań według czasu
obsługi. Jego złożoność czasową jest rzędu: O(n lg n).
Wykazać można, że uszeregowanie minimalizujące całkowity czas w

systemie, to takie, które szereguje zadania w porządku niemalejącym według czasu
obsługi.
Dla l  in-l niech p

i

będzie czasem obsługi i-tego zadania, występującego w

pewnym szeregowaniu optymalnym (takim, które minimalizuje całkowity czas w
systemie).

Uszeregowanie Całkowity czas w systemie

[Z

1

, Z

2

, Z

3

]

5+(5+10)+(5+10+4) = 39

[Z

1

, Z

3

, Z

2

]

5+(5+4)+(5+4+10) = 33

[Z

2

, Z

1

, Z

3

]

10+(10+5)+(10+5+4) = 44

[Z

2

, Z

3

, Z

1

]

10+(10+4)+(10+4+5) = 43

[Z

3

, Z

1

, Z

2

]

4+(4+5)+(4+5+ 10) = 32

[Z

3

, Z

2

, Z1]

4+(4+10)+(4+10+5) = 37

Uszeregowanie [Z

3

, Z

1

, Z

2

] optymalne przy czasie całkowitym wynoszącym 32.

Algorytm greedy
{
Posortować zadania według czasu obsługi w porządku niemalejącym;

WHILE (realizacja nie ukończona) {

Uszereguj kolejne zadanie; //Procedura wyboru i sprawdzenie

wykonywalności;

IF (zadania wyczerpane)

Realizacja ukończona; // Sprawdzenie rozwiązania;

}

}

.

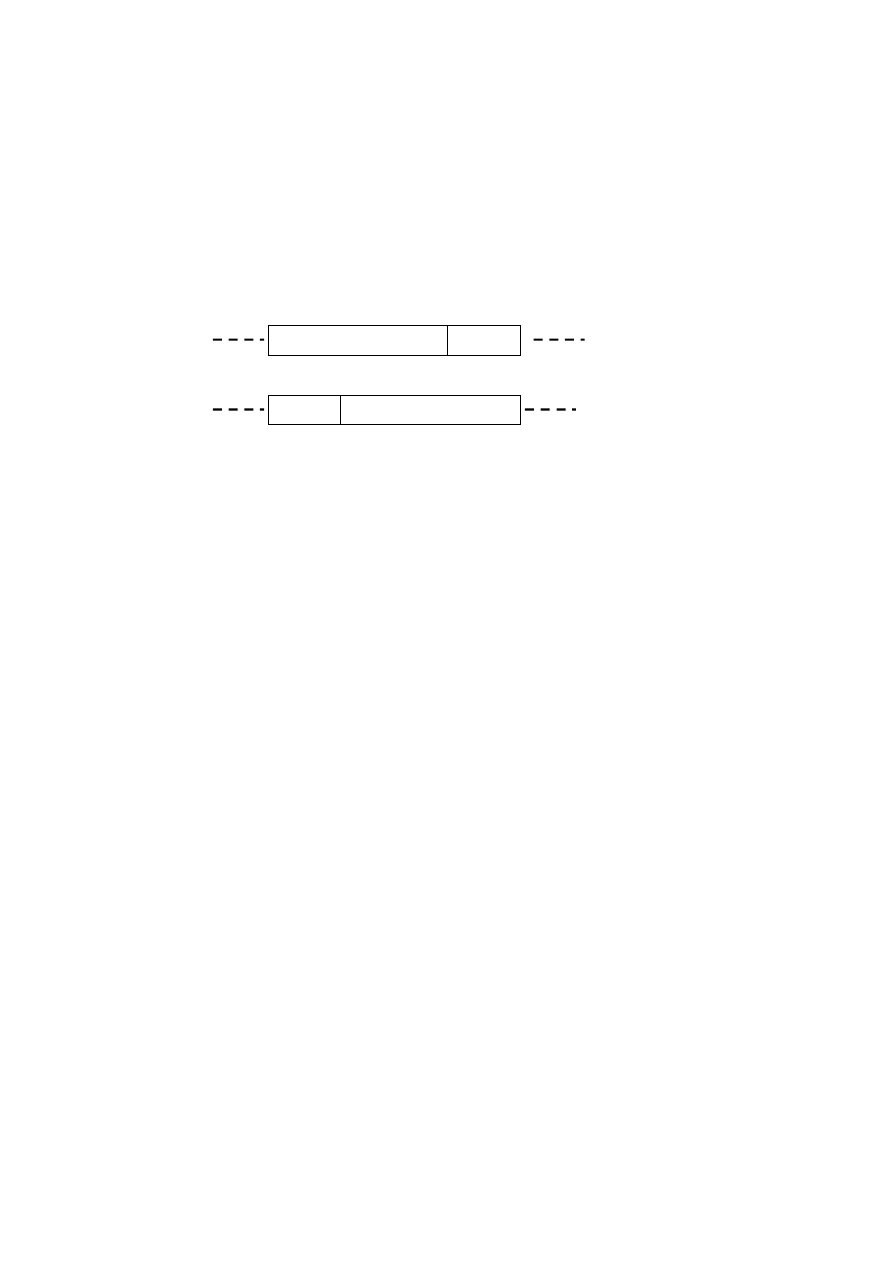
46

Jeżeli zadania nie są uszeregowane w porządku niemalejącym, to dla przynajmniej
jednego i, gdy l  in-l,

p

i

> p

i+1

Jak zmienia się czas pobytu zadań przy zmianie uszeregowania zamieniając
miejscami zadanie i-te oraz (i+ l)-te. Czas pobytu zadania (i+1)-szego zmniejszy
się o p

i

, a czas pobytu i-ego zadania zwiększy się o p

i+1

w stosunku do

poprzedniego uszeregowania.
Takie lokalne przestawienie zadań nie wpływa na czas pobytu pozostałych zadań.
Stąd, jeżeli T jest całkowitym czasem pobytu zadań w systemie, związanym z
poprzednim uszeregowaniem, oraz T' jest całkowitym czasem pobytu zadań w
systemie, związanym ze zmienionym uszeregowaniem, to:

T' = T + p

i+1

-

p

i

Ze względu na fakt p

i

> p

i+1

T' <T

co jest sprzeczne ze stwierdzeniem o optymalności pierwotnego uszeregowania.

p

i

p

i+1

T – czas pobytu zadań

p

i+1

p

i

T’ – czas pobytu zadań

.

47

2.3. Algorytmy metaheurystyczne

Pod pojęciem „Mataheurystyki” rozumiemy grupę algorytmów heurystycznych

ogólnego przeznaczenia. Wśród algorytmów heurystycznych, wiele jest silnie
związanych z rozwiązywanym problemem. Są to tzw. algorytmy "szyte" i
specjalnie przeznaczone dla pewnego problemu.
Z drugiej strony można wyróżnić grupę algorytmów heurystycznych ogólnego
przeznaczenia tzw. metaheurystyk. Określenie metaheurystyka ma dwojakie
znaczenie jako:

-

szkielet

(schemat)

nakładany

na

heurystyki

specyficzne

dla

rozwiązywanego problemu,

-

metoda ogólnego przeznaczenia, niespecyficzna dla żadnego szczególnego
problemu.

Metaheurystykami nazywa się więc zasady generowania reguł dla konkretnych
algorytmów heurystycznych. W ramach jednej metaheurystyki można zatem
zaproponować przynajmniej kilka algorytmów heurystycznych, będących
wariantami pewnego ogólnego podejścia. Znanymi metaheurystykami są:

1. Metoda symulowanego wyżarzania (simulated annealing).
2. Metoda przeszukiwania z zabronieniami (tabu search).
3. Metoda genetyczna (genetic search).

Wszystkie metaheurystyki są metodami lokalnego poszukiwania rozwiązania a
jako miarę oceny wykorzystują funkcję celu. Potrzeba znalezienia efektywnych
rozwiązań dla praktycznych problemów NP-zupełnych sprawiła, że rozpoczęto
poszukiwania alternatywnych metod rozwiązań

.

Źródłem inspiracji stała się natura.

Metaheurystyki wzorują się na fizyce, biologii i naukach społecznych.
Metaheurystyki uzyskuje się poprzez:

-

określenie specjalnego mechanizmu współpracy-współzawodnictwa,

-

użycie pewnej liczby powtarzalnych prób,

-

samo-modyfikację reprezentantów problemu (chromosomy).

Metaheurystyki są niedeterministycznymi metodami, które przenoszą model
zjawisk istniejących w naturze na grunt konkretnego problemu.
Działanie algorytmów metaheurystycznych nawiązuje do takich mechanizmów
występujących w przyrodzie, jak osiąganie przez ciało stałe minimalnej energii w
procesie schładzania (symulowana relaksacja), naturalna selekcja z zakazem cykli
(przeszukiwanie tabu) czy też naturalne selekcje genetyczne (algorytm genetyczny).

Do skonstruowania rozwiązań problemów optymalizacji metaheurystyki nie

potrzebują kodować złożonych procedur algorytmicznych, potrzebują jedynie
określenia parametrów problemu i funkcji celu oraz odwzorowania tych danych na
wewnętrzny schemat metaheurystyki.

.

48

2.3.1 Algorytm symulowanego wyżarzania

Algorytm Symulowanego wyżarzania jest oparty na analogii zaczerpniętej z

termodynamiki i nawiązuje do wyżarzania ciał stałych. Charakterystyczną cechą
tego procesu jest stopniowe obniżanie temperatury. W procesie wyżarzania nowe
stany ciała stałego osiągane są przez elementarne zmiany stanu bieżącego, tzn.
przez małe przemieszczenia cząstek w losowo wybranej części ciała. Jeśli
wynikiem tej zmiany jest niższa energia ciała stałego (E<0) to proces jest
kontynuowany od nowego stanu. W przeciwnym wypadku (E0) nowy stan
przyjmowany jest z prawdopodobieństwem exp(-E/k

B

T), gdzie k

B

jest stałą

Boltzmanna, a T temperaturą.

W przypadku optymalizacji kombinatorycznej rozwiązanie  pełni rolę stanu, a

funkcja celu K() odpowiada energii..
Procedurę

symulowanej

relaksacji

charakteryzują

ponadto:

temperatura

początkowa (T

0

) liczba ruchów na każdym poziomie temperatury (L), warunek

stopu, oraz sposób zmiany wartości temperatury.
Algorytm symulowanego wyżarzania może być zapisany w następujący sposób:

Algorytm SA
{

initialize:



0

, T

0

, L;

k=0;
= 

0

;

WHILE (!war_stop){

FOR(i=1; i

L; i=i+1){

GENERATE(

`N



);

IF( K(`)K())

=`;

ELSE{

= K(`)-K();

IF(exp(-/T

k

)) > rand[0,1))

=`;

}

}

k=k+1;

CALCULATE (T

k

);

}
}

.

49

Dla efektywności algorytmu ważny jest sposób wyznaczenia sąsiedztwa
określonego rozwiązana.
Konieczne jest określenie sposobu zmian parametrów: liczby iteracji wewnętrznej
oraz temperatury chłodzenia. Sposób ten określany jest jako schemat chłodzenia
(coolin schedule). Powszechnie stosowane jest chłodzenie wg. schematu
logarytmicznego lub geometrycznego. Jeżeli studzenie jest zbyt szybkie, algorytm
szybko kończy swoje działanie w lokalnym ekstremum słabej jakości.

Jeżeli studzenie jest zbyt powolne, czas przebiegu algorytmu staje się

nieakceptowanie długi z kolei pozwala na swobodną eksplorację sąsiedztwa
otrzymanego rozwiązania.

23.2. Przeszukiwanie TABU

Metoda poszukiwania TABU (TS, Tab-Search) oparta jest na metodzie

iteracyjnego polepszenia funkcji kryterialnej (iterative improvement). Metoda
określa tylko ogólne ramy postępowania i dlatego zbudowanie algorytmu
bazującego na jej podstawie dla danego problemu optymalizacyjnego, wymaga
podania szeregu niezbędnych elementów, takich jak.: ruch, sąsiedztwo, pamięć
krótkoterminowa, pamięć długoterminowa, poziom aspiracji, definicja zabronienia,
oraz związana z nią metoda dywersyfikacji poszukiwań, strategia przeglądania
sąsiedztwa, sposób znajdowania najlepszego ruchu.

Technika TABU powiela naturalny proces poszukiwania rozwiązania

problemów wykonywanych przez człowieka. Podstawowa wersja TS rozpoczyna
działanie od pewnego rozwiązania początkowego 

0

, zazwyczaj uzyskiwanego

algorytmem konstrukcyjnym. Niektóre bardziej zaawansowane wersje tego
algorytmu mogą zaczynać optymalizację od rozwiązania niedopuszczalnego.
Elementarny krok tej metody wykonuje, dla danego rozwiązania 

k

,

przeszukiwanie całego sąsiedztwa N(

k

) rozwiązania 

k

. Sąsiedztwo N(

k

) jest

definiowane poprzez ruchy, które można wykonać z 

k

. Ruch jest elementarną

zmianą w bieżącym rozwiązaniu taką, która transformuje je w inne, nie tracąc
dopuszczalności.

Celem procesu poszukiwania w danej iteracji jest znalezienie w N(

k

)

rozwiązania 

k +1

z najmniejszą wartością funkcji celu K(). Następnie, niezależnie

od relacji między wartością K(

k +1

) a K(

k

), algorytm przechodzi do rozwiązania



k +1

przeszukując jego sąsiedztwo. Po wykonaniu ruchu, proces poszukiwania jest

powtarzany od znalezionego rozwiązania, wyznaczając tym samym trajektorię
poszukiwań x

0

, x

1

,... . Metoda TS zwraca jako wynik najlepsze rozwiązanie z tej

trajektorii. Konsekwencją przyjętej strategii poszukiwań jest możliwość łatwego
wpadnięcia w cykl, rozumiany jako cykliczne generowanie pewnego ciągu
rozwiązań. W celu zabezpieczenia się przed tą cechą, wprowadza się tak zwaną
listę Tabu, T ruchów zabronionych, zwaną też pamięcią krótkoterminową (Short
Term Memory). Przechowuje ona przez ograniczony czas najświeższe rozwiązania

.

50

z trajektorii poszukiwań, wybrane atrybuty tych rozwiązań, przejścia prowadzące
do tych rozwiązań, traktując je jako formę zabronienia dla ruchów wykonywanych
w następnych iteracjach.

Wykonanie ruchu, którego atrybuty znajdujące się na liście T jest zabronione,

czyli odpowiednie rozwiązanie musi zostać pominięte w dalszych iteracjach.
Najprostszą realizacją listy Tabu jest pamięć cykliczna typu FIFO. Wybór
elementów przechowywanych na liście T zależy od specyfiki rozwiązywanego
problemu.
Lista Tabu – wygodna implementacyjnie - posiada jednak pewną wadę.
Zabraniając wykonania więcej niż maxt ruchów może nie dopuszczać do
wykonania takich, które zmniejszają funkcję celu nie powodując cykli. W celu
uniknięcia tej sytuacji, wprowadza się tak zwaną funkcję aspiracji ruchu, oraz
poziom aspiracji do zabronienia. Jeżeli dany ruch jest zabroniony, ale jego funkcja
aspiracji jest mniejsza niż aktualny poziom aspiracji do zabronienia, to ruch ten,
zwany zabronionym – perspektywicznym, traktuje się jako niezabroniony. Funkcja
aspiracji w najogólniejszej postaci może zależeć tylko od aktualnego rozwiązania


i

, ruchu oraz aktualnie najmniejszej znalezionej wartości funkcji celu K(*). W

prostych implementacjach przyjmuje się poziom aspiracji równy K(*), istnieją
jednak takie realizacje algorytmu TS, w których poziom ten zależy również od
całego procesu poszukiwań.

Niektóre, bardziej zaawansowane wersje metody Tabu Search uwzględniają

dodatkowy mechanizm dywersyfikacji i intensyfikacji procesu poszukiwań. W
przypadku wykonania pewnej liczby iteracji bez poprawy globalnego kryterium,
proces poszukiwań powraca do rozwiązania, które jako ostatnie poprawiało tą
wartość, i następnie poszukiwania są kontynuowane po innej trajektorii. Omawiana
metoda dywersyfikacji wykorzystuje strukturę Pamięci Długoterminowej.
Poszukiwanie zatrzymuje się, jeśli została wykonana pewna liczba iteracji bez
poprawy wartości funkcji celu, wykonano założoną z góry całkowitą ilość iteracji
lub

znaleziono

satysfakcjonujące

rozwiązanie.

Znalezienie

rozwiązania

optymalnego zapewnia własność styczności (Connectivity Property). Własność ta
określa warunki, przy których dla dowolnego rozwiązania początkowego 

k0

,

istnieje skończona trajektoria poszukiwań 

0

, 

1

,..., 

r

taka, że 

k+1

 N(

k

),

zbieżna do rozwiązania optymalnego 

r

= *.

Procedurę przeszukiwania TABU charakteryzują ponadto: liczba sąsiadów V
generowanych w sąsiedztwie N(

k

), oraz warunek stopu. Procedurę

przeszukiwania tabu można zapisać następująco:

.

51

Zasadniczym warunkiem efektywnego działania algorytmów metaheurystycznych,
symulowanego wyżarzania i przeszukiwania TABU jest dobre zdefiniowanie
sąsiedztwa,

2.3.3. Algorytm genetyczny

Algorytm genetyczny (GA, Genetic Algorithms) jest przykładem algorytmów

ewolucyjnych

(EA,

Evolutionary

Algorithms)

rozwiązujących

problemy

optymalizacji w sposób naśladujący pewne procesy zachodzące w przyrodzie:
doboru naturalnego oraz dziedziczenia.
Algorytm działa nie na pojedynczych rozwiązaniach, lecz na populacji rozwiązań.
Każde rozwiązanie jest zakodowane w tak zwany chromosom, i przedstawia
jednego osobnika populacji. Sposób kodowania zależy od rozważanego problemu.

Pierwsze pokolenie w EA zadane jest odgórnie lub tworzy się je losowo. Do

każdego z następnych pokoleń, w kolejnych iteracjach, wybiera się pewną liczbę
osobników najlepiej przystosowanych, według tak zwanej funkcji przystosowania.
Osobniki te są kojarzone następnie w pary, po czym następuje wymiana „materiału
genetycznego” osobników rodzicielskich przy pomocy operatora krzyżowania
(cross- over). W wyniku pojedynczego zadziałania tego operatora powstają dwa
nowe rozwiązania, odpowiadające genotypowi potomków.

W takiej symulacji procesu ewolucji, istnieje odpowiednik zjawiska mutacji.

Zazwyczaj zachodzi ona losowo, z niewielkim prawdopodobieństwem. W
optymalizacji dyskretnej odpowiada ona za dywersyfikację poszukiwań
rozwiązania optymalnego. Po krzyżowaniu i mutacji grupa powstałych rozwiązań
tworzy nową populację. Warunkiem zakończenia algorytmu jest przekroczenie
pewnej ilości iteracji lub osiągnięcie założonego stopnia przystosowania.

Algorytm TS
{

INITIALIZE:



0

, 

best

T;

= 

0

;

WHILE (!war_stop){

GENERATE(

VN();

SELECT (`)

//najlepsza wartość funkcji K w zbiorze V}

UPDATE (T)

//Uaktualnij listę TABU}

IF( K(`)K(

best

)) {



best

=`;

}
=`;

}
}

.

52

Cecha związana z pojedynczym elementem rozwiązania nazywana jest „genem”.
Ponadto z każdym chromosomem związana jest pewna wartość zwana
dopasowaniem, której odpowiada wartość funkcji kryterialnej.

W Algorytmach Genetycznych wymagane jest co najmniej określenie sposobu

kodowania atrybutów w chromosomach, postać funkcji przystosowania, metoda
wyboru puli rodzicielskiej, operatory krzyżowania, schemat mutacji. W przypadku
optymalizacji

kombinatorycznej

oraz

prostego

algorytmu

genetycznego,

najczęściej pojawiające się w kontekście szeregowania zadań operatory
krzyżowania to: PMX (Partial – Mapped Crossover), OX (Ordered Crossover)
oraz CX (Cyclic Crossover). Operator mutacji zastępowany jest między innymi
przez:

-

Inwersję, polegającą na wycięciu losowego fragmentu permutacji i
wstawieniu go w to samo miejsce, ale w odwrotnej kolejności,

-

Wstawienie, polegające na wylosowaniu liczby z przedziału [1... n] i
wstawieniu jej w losowe miejsce permutacji,

-

Przemieszczanie, polegające na wycięciu losowego fragmentu permutacji
i wstawieniu go w innym, losowym miejscu,

-

Wzajemną wymianę, polegającą na wylosowaniu dwóch elementów w
permutacji i zamianie ich miejscami.

Algorytm genetyczny może być zapisany w następujący sposób:













Algorytm genetyczny rozpoczyna działanie od utworzenia populacji N

rozwiązań. Rozmiar populacji pozostaje stały przez cały czas działania algorytmu.
Generacja n+1 tworzona jest z n-tej generacji (n). Z generacji (n) na podstawie
dopasowania wybierane są najlepsze osobniki. Następnie dokonywane są na nich
operacje krzyżowania, czego rezultatem jest powstanie potomstwa, które zastąpi
słabszych osobników w bieżącej populacji.

Algorytm GA
{

INITIALIZE:

(1);

FOR (k=2; k

L k=k+1){

SELECT ;

//Wybrać dobrych osobników

CROSSOVER ;

MUTATION ;

REPLACE ;

//Zastąpić słabszych osobników

}
}

.

53

Literatura (do rozdz. 1, 2).

1.

Audsley N. C., Deadline Monotonic Scheduling, YCS 146, Department of
Computer Science, Uniwersity of York, 1990.

2.

Buhr R., Bailey D., An Introduction to Real-Time Systems. Prentice Hall, 1999.

3.

Cormen T., Leiserson C., Rivest R..: Wprowadzenie do algorytmów. WNT,
2001.

4.

Gaj P., Kwiecień A [red]., Systemy informatyczne z ograniczeniami
czasowymi. Wydawnictwo Komunikacji i Łączności, Warszawa 2006, 115-
126.

5.

Grabowski J., Nowicki E., Smutnicki Cz., Metoda blokowa w zagadnieniach
szeregowania zadań. Akademicka Oficyna Wydawnicza Exit, Warszawa
2003.

6.

Liu J., Real Time Systems. Prentice Hall, 2000.

7.

Nowicki E., Metoda TABU w problemach szeregowania zadań produkcyjnych.
Oficyna Wydawnicza Politechniki Wrocławskiej, Wrocław 1999.

8.

Sacha K., Systemy czasu rzeczywistego, Oficyna Wydawnicza Politechniki
Warszawskiej, Warszawa 2006.

9.

Smutnicki Cz., Algorytmy Szeregowania. Akademicka Oficyna Wydawnicza
Exit, Warszawa 2002.

10.

Szmuc T., Specyfikacja i projektowanie oprogramowania systemów
czasu rzeczywistego. Uczelniane Wydawnictwo Naukowo-Dydaktyczne,
AGH, Kraków 2000.

11.

Ułasiewicz J., Systemy czasu rzeczywistego. Wydawnictwo BTC,
Warszawa 2007.

.

54

3. MODELE SIECIOWE PROCESÓW DYSKRETNYCH

3.1. Wprowadzenie

Sieci Petriego (Petri nets) są narzędziem do modelowania, stosowanym w wielu

różnych dziedzinach nauki, w szczególności informatyki, automatyki i robotyki.
Charakteryzuje je intuicyjny graficzny język modelowania, wspierany przez
zaawansowane metody formalnej analizy ich własności.

Naturalnym zjawiskiem w sieciach Petriego jest współbieżność wykonywanych

akcji, dlatego też są one najczęściej postrzegane jako narzędzie do modelowania
dyskretnych procesów współbieżnych.
Sieci, których definicję rozbudowano o parametr czasu, mogą być stosowane do
modelowania systemów czasu rzeczywistego.
Typowe zastosowania sieci Petriego to:

1

Modelowanie obliczeń współbieżnych.

2.

Modelowananie procesów technologicznych i przemysłowych.

Sieci Petriego zostały zdefiniowane przez Carla Petriego, w jego pracy

doktorskiej na Politechnice Darmstadt. Teoria sieci Petriego rozwija się od lat 60-
tych, zapoczątkowana opublikowaniem pracy:

Petri C.A.: Kommunikation mit Automaten. University of Bonn 1962.

Petri C.A.:Communication with Automata. Technical report New York 1965.
W wyniku ponad czterdziestoletniego rozwoju tej teorii powstało wiele różnych
klas sieci i rozszerzonych zakresów zastosowań. W zależności od potrzeb definicję
sieci zmieniano i dostosowywano do rozwiązywanych problemów. Dzięki
różnorodności znanych obecnie klas sieci można stosunkowo łatwo dobrać klasę
najwłaściwszą dla danej dziedziny zastosowań. Różnorodność ta jednak utrudnia
opracowanie jednolitych metod analizy różnych klas sieci.

Sieć Petriego jest przedstawiana jako graf dwudzielny. Może ona mieć strukturą

hierarchiczną, znacznie ułatwiającą modelowanie złożonych systemów.
Możliwa jest symulacja pracy sieci (najczęściej wspomagana przez odpowiednie
narzędzia komputerowe), dzięki której model taki staje się wirtualnym prototypem
projektowanego systemu.

Oprócz reprezentacji graficznej i możliwości symulacji pracy, na uwagę

zasługuje rozbudowana teoria. Różnorodność klas sieci powoduje, że metody ich
analizy znacznie się różnią. Dla sieci o najprostszej strukturze istnieje najszerszy
wachlarz tych metod i są one stosunkowo łatwe w użyciu. W przypadku sieci
bardziej rozbudowanych, możliwości formalnej analizy są zazwyczaj uboższe lub
trudniejsze do zastosowania.

.

55

Sieci Petriego są podstawowym językiem modelowania współbieżności i

synchronizacji dyskretnych procesów. Modelowanie z zastosowaniem sieci
Petriego pozwala na przedstawienie aspektów systemu, powiązanych ze
współbieżnością działania, współdzieleniem zasobów, komunikacją między
procesami oraz synchronizacją przebiegających procesów.
Sieci mają szczególne zastosowania w:

•

Projektowaniu i specyfikacji systemów procesów dyskretnych, systemów
czasu rzeczywistego, systemów wbudowanych.

•

Analizie poprawności oprogramowania (weryfikacja, walidacja).

•

Ocenie wydajności i niezawodności systemów procesów dyskretnych.

W celu oceny wydajności systemów, sieci Petriego są wzbogacane o czynnik czasu.
W swojej pierwotnej formie sieci miały ograniczone możliwości.

Różnorodność istniejących klas sieci Petriego, a także narzędzi programowych

spowodowała, że nie istnieje jednolita notacja ich opisu. Notacje graficzne sieci
różnią się w zależności od wybranego oprogramowania, ale różnice te nie są zbyt
zasadnicze. Sytuacja wygląda inaczej, w przypadku formalnego opisu sieci, gdyż
nawet w obrębie jednej klasy stosuje się różne notacje.

3.2 Podstawowe pojęcia i definicje

Jedną z zasadniczych cech sieci Petriego jest ich stosunkowo prosta i intuicyjna

reprezentacja graficzna, wspólna dla wszystkich klas sieci. Sieci Petriego są
przedstawiane w postaci grafów skierowanych, zawierających dwa rodzaje węzłów
(grafy dwudzielne) nazywanych miejscami i przejściami. Tych dwóch rodzajów
węzłów używa się odpowiednio do reprezentowania stanów i aktywności
modelowanego systemu.

De

f

inicj

a

3.1

.

Grafem skierowan

y

m (g

r

afem)

n

azywa

m

y

up

o

r

zą

dk

owa

n

ą

t

ró

jk

ę

po

s

t

ac

i (

G

=

(V

,

A

, 

)

, p

rzy czy

m:

V je

s

t

z

bi

o

r

e

m

wę

z

ł

ów g

r

a

fu

.

A jest z

bi

o

r

e

m

łukó

w

(k

r

aw

ę

d

z

i

)

gr

a

f

u

,

t

ak

im

że V

A = .



: A  VV

j

e

st

f

u

n

k

c

ją

z

ac

z

ep

i

en

i

a

,

któ

ra

ka

ż

d

e

mu łuk

owi

pr

zy

pi

s

u

je

up

o

r

zą

dk

owa

n

ą

p

arę węzłów

.

Definicja 3

.

2

.

Graf

s

kiero

wa

n

y

(

G

=

(V

,

A,



)

,

naz

yw

am

y g

r

afe

m

et

y

ki

etow

an

y

m nad

z

bior

e

m

e

t

y

ki

et L (label)

,

j

eże

li łu

k

i

g

r

af

u G

ma

j

ą

pr

zy

p

isa

n

e ety

ki

e

t

y ze z

b

ior

u L.

De

fi

nicj

a

3.3.

Graf skierowany

G

=

(V

,

A

,

)

nazywamy grafem dwudzielnym, jeżeli zbiór

V

.

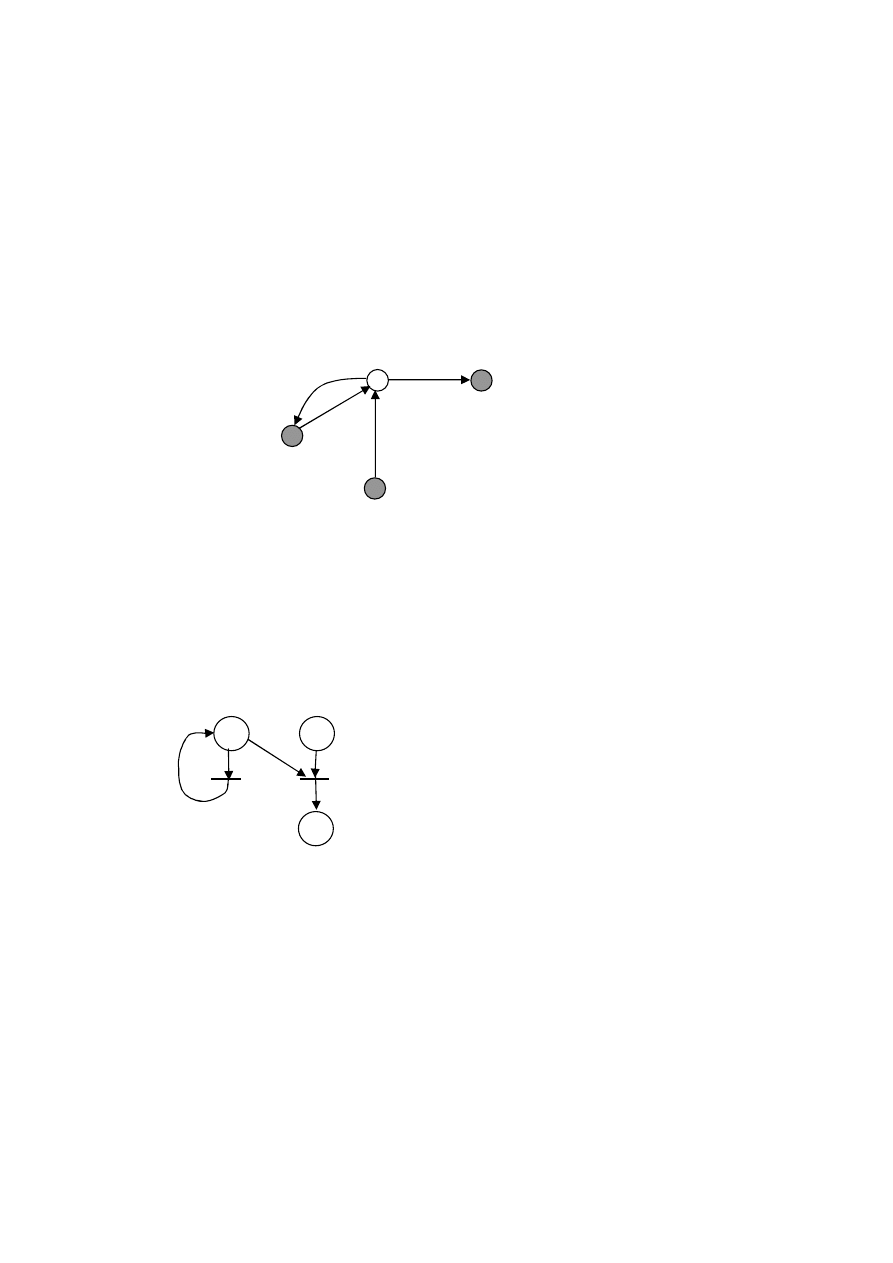
56

jest sumą dwóch rozłącznych zbiorów

V

1

,

V

2

i dowolny łuk grafu G łączy

węzły należące do rożnych zbiorów, tzn.

Węzły różnych typów oznaczono odmiennymi kolorami.

Łuki

w gra

f

ie

s

iec

i

mogą łączyć

t

y

l

ko węz

ł

y

r

óż

n

yc

h t

ypów

. Z

e wzglę

du n

a c

h

a

-

ra

kt

e

r t

yc

h poł

ą

c

ze

ń d

e

finiu

je się s

i

e

ci o ro

z

m

a

it

y

ch

w

ł

a

s

n

oś

c

iac

h

s

tru

k

tu

ra

ln

yc

h

,

m

.

in.

:

s

i

ec

i

czys

t

e

,

siec

i pr

os

t

e, s

i

ec

i

swo

b

o

dn

ego wy

b

o

ru

,

grafy

s

y

n

c

h

ro

n

izacj

i

,

m

aszy

n

y s

t

a

no

we

it

d

.

[4]

,

[5

]

.

Sieci Petriego są przedstawiane jako grafy dwudzielne, w których własności

dynamiczne są modelowane poprzez przepływ tzw. znaczników (markers).

Definicja 3.4.

Sieć Petri (PN) jest uporządkowaną czwórką PN= (P,T,F,W),

gdzie:
P=(p

1

,p

2

,...,p

n

) – zbiór (skończony) miejsc (places), P0,

T=(t

1

,t

2

,...,t

m

) - zbiór (skończony) przejść (transitions), T0,

F  ( PxT)  (TxP) - zbiór łuków,
W: FN\{0} – funkcja krotności (waga) łuku, N-zbiór liczb naturalnych.

3.2. Konwencja graficzna dla sieci Petriego

p

3

t

1

t

2

p

2

p

1

P = (p

1

, p

2

)

T = (t

1

, t

2

)

F = {(p

1

, t

1

), (p

1

, t

2

), (p

2

, t

2

), (t

1

,

p

1

), (t

2

,

p

3

)}

W  1

a

A:

(a)



(

V

1

V

2

)



(

V

2

V

1

)

3.1. Graf dwudzielny

3

5

1

2

x

1

x

2

x

4

x

3

.

57

Powyższa definicja opisuje sieć Petriego jako graf dwudzielny, w którym
wyróżnia się dwa rozłączne podzbiory wierzchołków: zbiór miejsc i zbiór
przejść. W reprezentacji graficznej, miejsca przedstawiane są w postaci
kółek, natomiast przejścia w postaci kresek. Łukami mogą łączyć się
wyłącznie elementy należące do różnych podzbiorów. Łuki mogą być
wielokrotne. Jeżeli krotność łuku fF spełnia zależność W(f)>1, to łuk
obciążony jest liczbą W(f). Jeśli W(f)=1, to symbol 1 jest pomijany.

Powyższa definicja sieci pozwala scharakteryzować strukturę sieci, ale nie daje
możliwości opisu jej zachowania. Aby można było w pełni modelować systemy
współbieżne musimy rozszerzyć tę definicję o znakowanie, które reprezentuje stan
modelowanego systemu i ulega zmianie w trakcie symulacji pracy sieci.

3.3. Sieci znakowane

W celu modelowania systemów współbieżnych, należy rozszerzyć te definicję o

znakowanie, które reprezentuje stan modelowanego systemu i ulega zmianie w
trakcie symulacji pracy sieci. Znakowanie sieci umożliwia opis własności
dynamicznych, które są modelowane przez przepływ znaczników powodowany
drożnością, wzbudzeniem (firing) przejść sieci.

Definicja 3.5.
Znakowanie PN jest funkcją M: PN. Wartość M(p

i

) wyraża liczbę znaczników w

miejscu p

i

. Liczba znaczników jest oznaczana na przez liczbę kropek.

Definicja 3.6.
Znakowana sieć Petriego MPN (Marked Petri Net) jest parą:

MPN =(PN, M

0

)

gdzie: M

0

– jest znakowaniem początkowym (initial marking) sieci

M

0

: P  N funkcja znakowania początkowego.

Zbiory Int(t) ={pP: <p, t>F} oraz Out(t) ={pP: <t, p>F} jest zbiorem miejsc
wejściowych oraz wyjściowych przejścia t.
W podobny sposób są zdefiniowane zbiory Int(p), Out(p) przejść wejściowych
(wyjściowych) miejsca p.
Dowolne miejsce p nazywa się miejscem wejściowym dla przejścia t, jeśli istnieje
łuk łączący, skierowany od tego miejsca do przejścia t. Wykonanie dowolnego
przejścia (palenia się tranzycji) w sieci polega na pobraniu znaczników z miejsc
wejściowych danego przejścia i wstawienia znaczników do miejsc wyjściowych.
Ilość znaczników pobieranych jest określona przez wagi przypisane do
odpowiednich łuków.

.

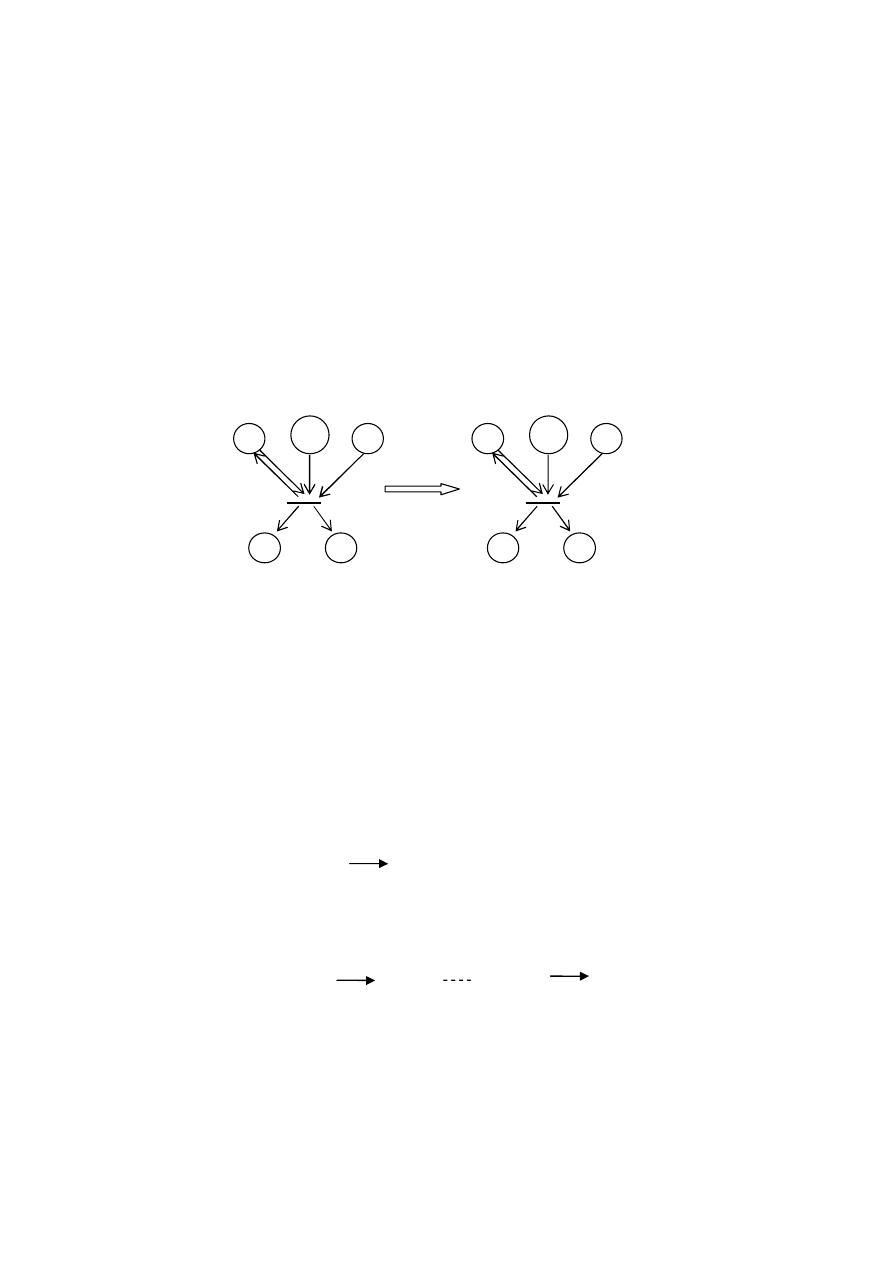
58

Definicja 3.7.
Przejście t

j

jest przygotowane do wzbudzenia (firing), jeśli w każdym miejscu

poprzedzającym znajduje się co najmniej W(<p

i

, tj>) znaczników. Jeśli przejście

jest przygotowane do wzbudzenia, to może nastąpić jego wzbudzenie. Gdy
przejście t

j

jest wzbudzone, wówczas W(<p

i

, t

j

>) znaczników jest usuwanych z

każdego miejsca p

i

 Int(t) oraz W(<t

j

, p

k

>) znaczników jest dodawanych do

każdego miejsca p

k

 Out(t).

3.4. Własności dynamiczne sieci

Analiza zachowania sieci jest związana z badaniem własności kolejnych jej

stanów, w tym przypadku znakowań osiągalnych z znakowania początkowego.
Problem osiągalności określonego znakowania (stanu) jest więc podstawowym
przy analizie sieci.
Jeżeli w wyniku wzbudzenia przejścia t

i

następuje zmiana znakowania z M

i

na M

i+1

to stosujemy oznaczenie

Sekwencją wzbudzenia nazywamy taką sekwencję przejść  = t

i1

, ..., t

is

, dla której

istnieją znakowania M

p

, M

p+1

, ..., M

p+s

spełniające warunek:

W danym przypadku stosujemy oznaczenie

Rys 3.3. Realizacja przejścia (firing of transition)

2

2

t

1

p

1



p

2



p

3



p

4

p

5



M

i

M

i+1

[t

i

]

[t

i1

]

M

p

M

p+1

,

[t

is

]

M

p+s-1

M

p+s

2

2

t

1

p

1



p

2



p

3

p

4



p

5



.

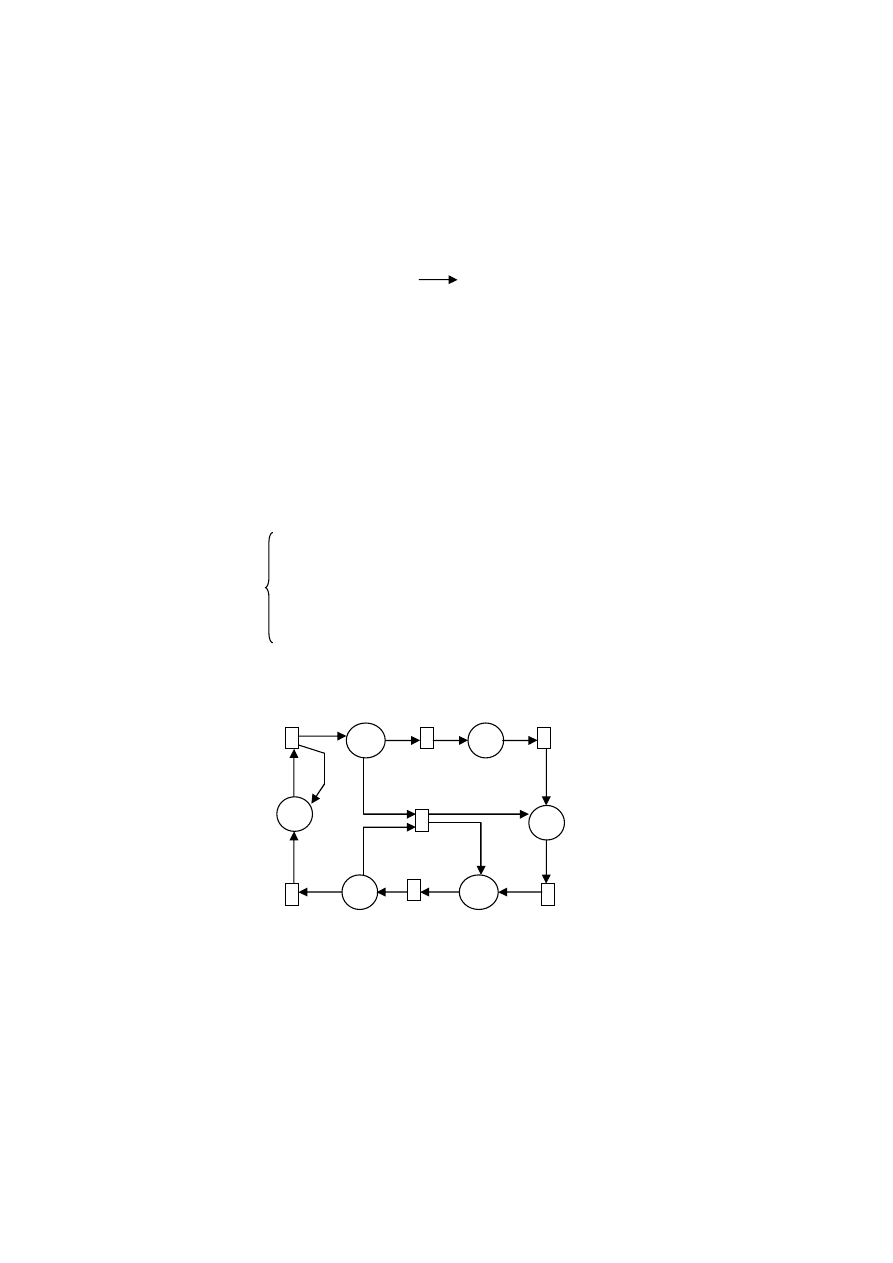
59

Znakowanie M

p+s

nazywamy znakowaniem osiągalnym ze znakowania M

p

.

Możliwość

przesyłania

większej

liczby

znaczników

przy

wzbudzeniu

pojedynczego przejścia ma wpływ na aktywność danego przejścia oraz zmianę
poszczególnych znakowań sieci.

Definicja 3.8.
Przejście tT jest aktywne przy znakowaniu M (jest M-aktywne), jeżeli każde z
jego miejsc wejściowych zawiera co najmniej tyle znaczników, ile wynosi waga
łuku prowadzącego od tego miejsca do przejścia t.
Jeżeli przejście t jest M-aktywne, to nowe znakowanie M' uzyskane w wyniku
wykonania przejścia t jest określone w sposób następujący:

Rozważmy przykład sieci przedstawionej na rys. 3.4. Przy znakowaniu
początkowym:

M

p

M

p+s

[]

M(p) – W(p,t)

gdy pIn(t) – Out(t)

M(p) + W(t,p)

gdy pOut(t) – In(t)

M`(p) =

M(p) - W(p,t) + W(t,p) gdy pIn(t)  Out(t)

M(p)

w pozostałych przypadkach

2

3

2

p

6

t

4

p

5

t

5

t

6

p

1

p

4

t

3

p

3

t

2

p

2

Rys. 3.4. Sieć znakowana

t

1





t

7







.

60

M

0

= (1, 2, 0, 1, 2, 1) aktywne są przejścia t

1

, t

2

, t

4

, t

6

i t

7

.

wykonanie każdego z tych przejść prowadzi odpowiednio do znakowań:

M

1

= (1, 3, 0, 1, 2, 1),

M

2

= (1, 1, 1, 1, 2, 1),

M

4

= (1, 2, 0, 0, 3, 1),

M

6

= (3, 2, 0, 1, 2, 0),

M

7

= (1, 1, 0, 3, 3, 0).

Przejścia t

3

i t

5

nie są aktywne, ponieważ odpowiednio miejsce p

3

jest puste, a

miejsce p

5

zawiera zbyt mało znaczników.

Definicja 3.9.
Znakowana sieć MPN jest żywą (liveness), jeśli dla każdego znakowania M
osiągalnego ze znakowania początkowego M

0

i dla każdego przejścia tT, istnieje

sekwencja palenia umożliwiająca palenie przejścia t.

Zagadnienie żywotności jest niezwykle istotne w analizie własności systemów
współbieżnych. Klasycznie żywotność jest kojarzona z ciągłością działania, np.
system czasu rzeczywistego powinien być zawsze gotowy do obsługi zdarzeń
zachodzących w jego otoczeniu.

Definicja 3.10.

Znakowana sieć MPN jest k- ograniczona (k-bounded), jeśli przy dowolnym
osiągalnym znakowaniu, w każdym miejscu ilość znaczników nie
przekracza liczby k.

Definicja 3.11.
Znakowana sieć MPN jest bezpieczna (safed), jeśli jest 1-ograniczona.

Ograniczoność sieci wiążę się z pojęciem bezpieczeństwa systemów. Definicja

bezpieczeństwa oznacza niemożliwość wystąpienia niepożądanych stanów podczas
działania systemu. W przypadku sieci Petriego niepożądane stany dotyczą
najczęściej nieograniczonego wzrostu liczby znaczników w pewnych miejscach
sieci. Własność bezpieczeństwa jest charakterystyczna dla pewnej klasy sieci
zwanych sieciami warunkowo-zdarzeniowymi C/E (Condition-Event). Wystąpienie
znaczników we wszystkich miejscach wejściowych odpowiada spełnieniu
wszystkich warunków wystąpienia zdarzenia. Fakt zaistnienia zdarzenia jest
opisywany przez wykonanie przejścia. W takim przypadku dla każdego miejsca
możliwe są tylko dwa oznakowania: brak znacznika (niespełnienie warunku) i
wystąpienie pojedynczego znacznika – spełnienie warunku.

.

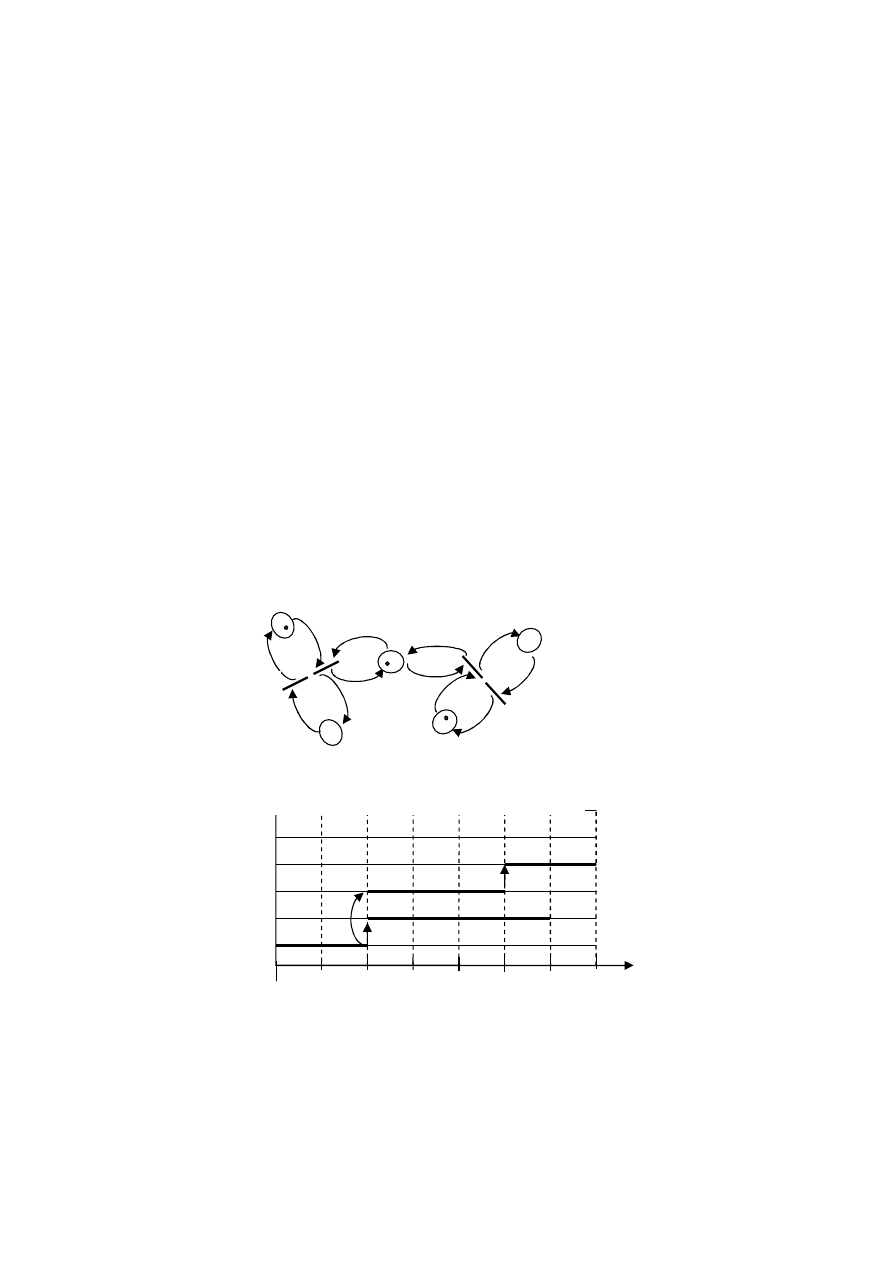
61

3.5 Czasowe sieci Petriego

Definicja 3.12.
Czasowa znakowana sieć Petrego TMPN (Timed Marked Petri Net) jest parą
TMPN=(MPN,),
gdzie: : TR

+

, (R

+

- jest zbiorem nieujemnych liczb wymiernych).

W chwili początkowej =0, znakowanie sieci TMPN jest znakowaniem
początkowym M

0

.

Dodanie parametru czasu do definicji sieci Petriego umożliwia ocenę wydajności
systemów. Istnieją dwa sposoby przypisania czasu elementom sieci Petriego do
przejść (tranzycji) lub miejsc.

W literaturze dominuje przypisanie czasu przejściom. Gdy przejście t

i

jest

przygotowane do wzbudzenia, wówczas może nastąpić jego wzbudzenie. Faza
palenia przejścia t

i

trwa przez czas (t

i

).

1

3.6. Czasowy diagram palenia tranzycji

2

3

4

5

6

7

t

1

t

2

t

3

t

4

t

5

t

6

p

2

p

3

t

1

t

2

p

5

t

4

t

3

p

4

3.5. Czasowa sieć Petriego.

t

1

=2;

t

2

=4;

t

4

=2;

t

3

=3;

.

62

3.6. Przykłady sieciowego modelowania procesów dyskretnych

Sieci Petriego są uniwersalnym modelem szerokiej klasy procesów dyskretnych,

wobec tego miejsca i przejścia mogą być różnie interpretowane, w zależności od
modelowanego systemu. Najczęściej spotykane interpretacje:

Miejsca wejściowe

Przejścia

Miejsca wyjściowe

Prewarunki

Zdarzenie

Postwarunki

Zasoby żądane

Operacja lub zadanie

Zasoby zwalniane

Dane wejściowe

Wykonanie obliczeń (akcji)

Wyniki

Warunki

Klauzula logiki

Konkluzje

Sygnały wejściowe

Przetwarzanie

Sygnały wyjściowe

Wymienione reprezentacje charakteryzują się różnym stopniem abstrakcji, co

może decydować o różnych wymaganiach względem własności sieci. Przykładowo
przy rozważaniu systemu rozdziału zasobów, znaczniki mogą reprezentować
jednostki zasobu określonego typu i w związku z tym będą interpretowane jako
elementy, których ogólna ilość jest stała.
Z kolei w sieciach warunkowo-zdarzeniowe prewarunek poprzedza zdarzenie i jest
przesłanką wystąpienia zdarzenia. Wystąpienie zdarzenia kończy obowiązywanie
prewarunku i zaczyna obowiązywać postwarunek.

Przykład 1.
Model automatu w postaci sieci Petriego, akceptującego monety 5 i 10 zł. i
sprzedającego dwa rodzaje produktów w cenie po 15 i 20 zł.

Sygnały wejściowe z otoczenia są specyfikowane poprzez strzałki swobodne do

odpowiednich przejść. Etykiety tych strzałek oznaczają rodzaj monety wrzucanej w
odpowiednich stanach do otworu automatu. Napisy przy miejscach wskazują kwotę
przyjętą przez automat.
Automat początkowo znajduje się w stanie

Wait

, później w zależności od

wrzucanej monety przechodzi do stanu 5 lub 10. Czynności te są kontynuowane aż
do osiągnięcia żądanej kwoty. Wprowadzono dodatkową parę sygnałów
wejściowych, która jest używana do akceptacji kupna

OK

lub odrzucenia

NOK

i

zwrotu pieniędzy.

.

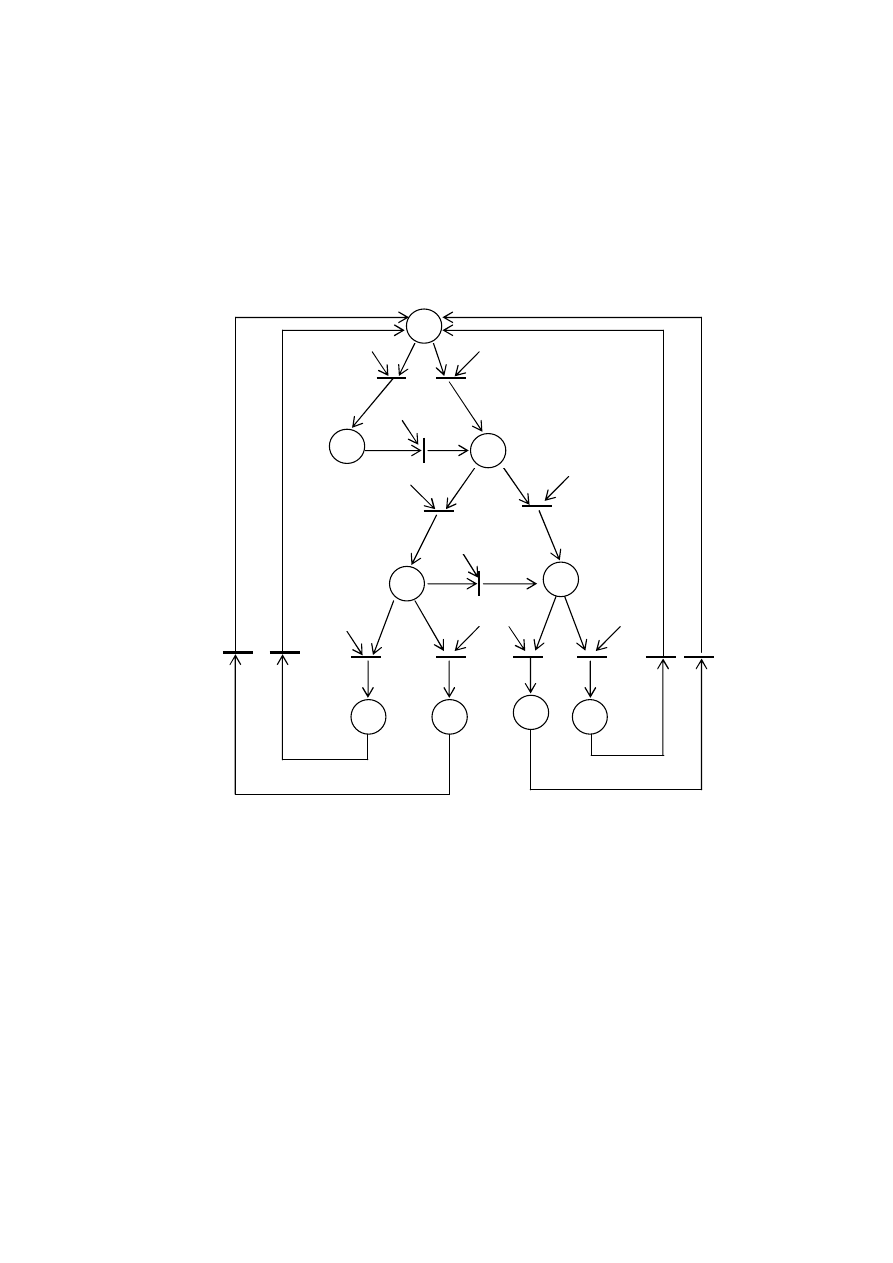
63

Przykład 2.
Model sieciowy dwóch procesów współbieżnych.

Po wykonaniu przejścia t

0

, tranzycja Begin inicjuje dwa procesy współbieżne

przez umieszczenie znaczników w miejscach p

1

i p

2

. W takiej sytuacji tranzycje t

1

oraz t

2

są wzbudzone niezależnie.

Rys. 3.7. Model automatu sprzedającego z mozliwością zwrotu pieniędzy

get

get

get_20

NOK

OK

10

5

10

5

Wait

5

10

5

5

15

20



OK

get_15

.

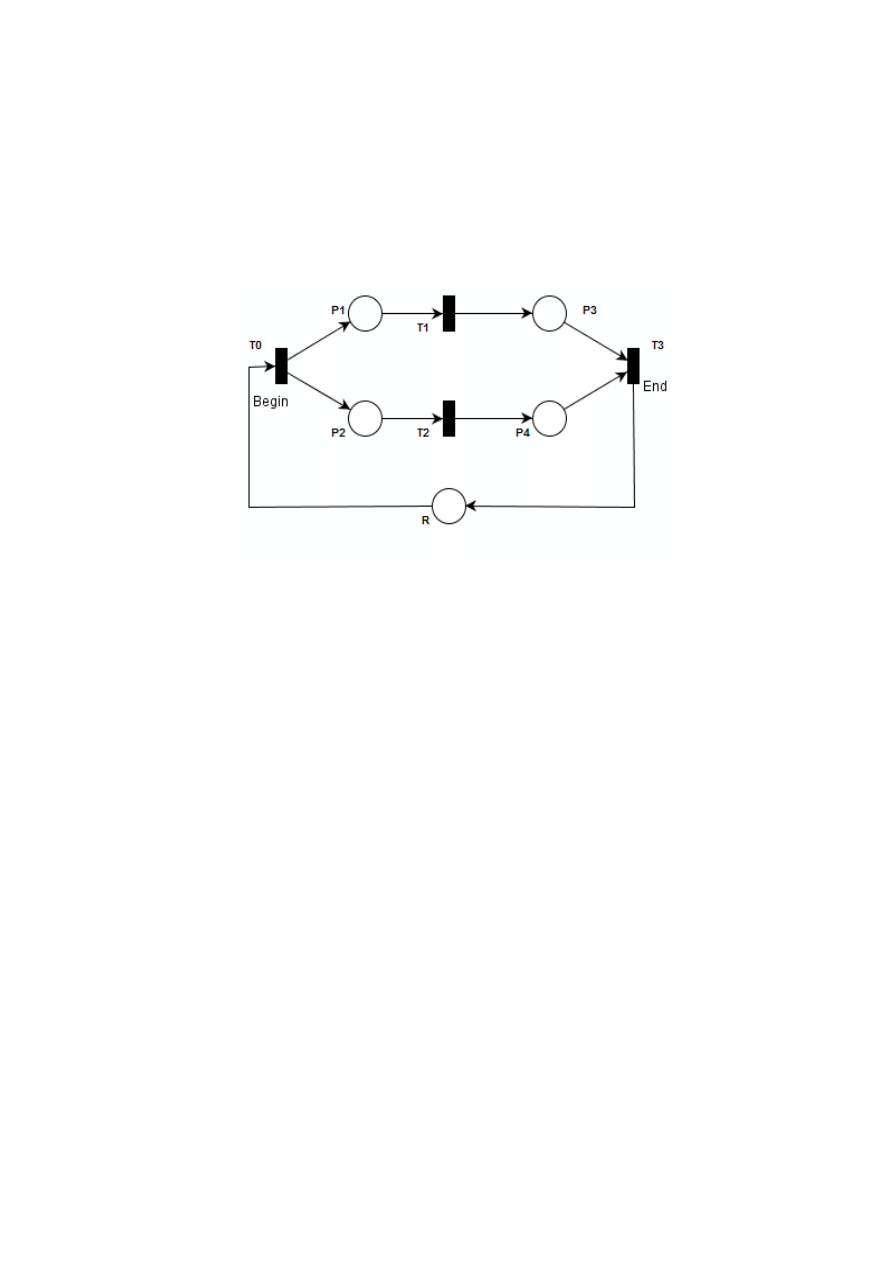
64

Zakończenie współbieżnych procesów jest synchronizowane przez tranzycję
t

3

(End), gdyż do wzbudzenia tegj tranzycji konieczne jest zakończenie

dwóch procesów sekwencyjnych (znaczniki w miejscach p

3

i p

4

).

Przykład 3.
Model sieciowy dwóch procesów współbieżnych, wymieniających komunikaty z
zastosowaniem protokołu z potwierdzeniem.

Własność ograniczoności sieci nie dopuszcza do nieograniczonego wzrostu ilości
znaczników w dowolnym miejscu sieci. Jest to istotne wymaganie, w
szczególności uniemożliwiające nieskończone wykonywanie wyłącznie pewnych
fragmentów sieci.

Rys. 3.8. Model procesów współbieżnych

.

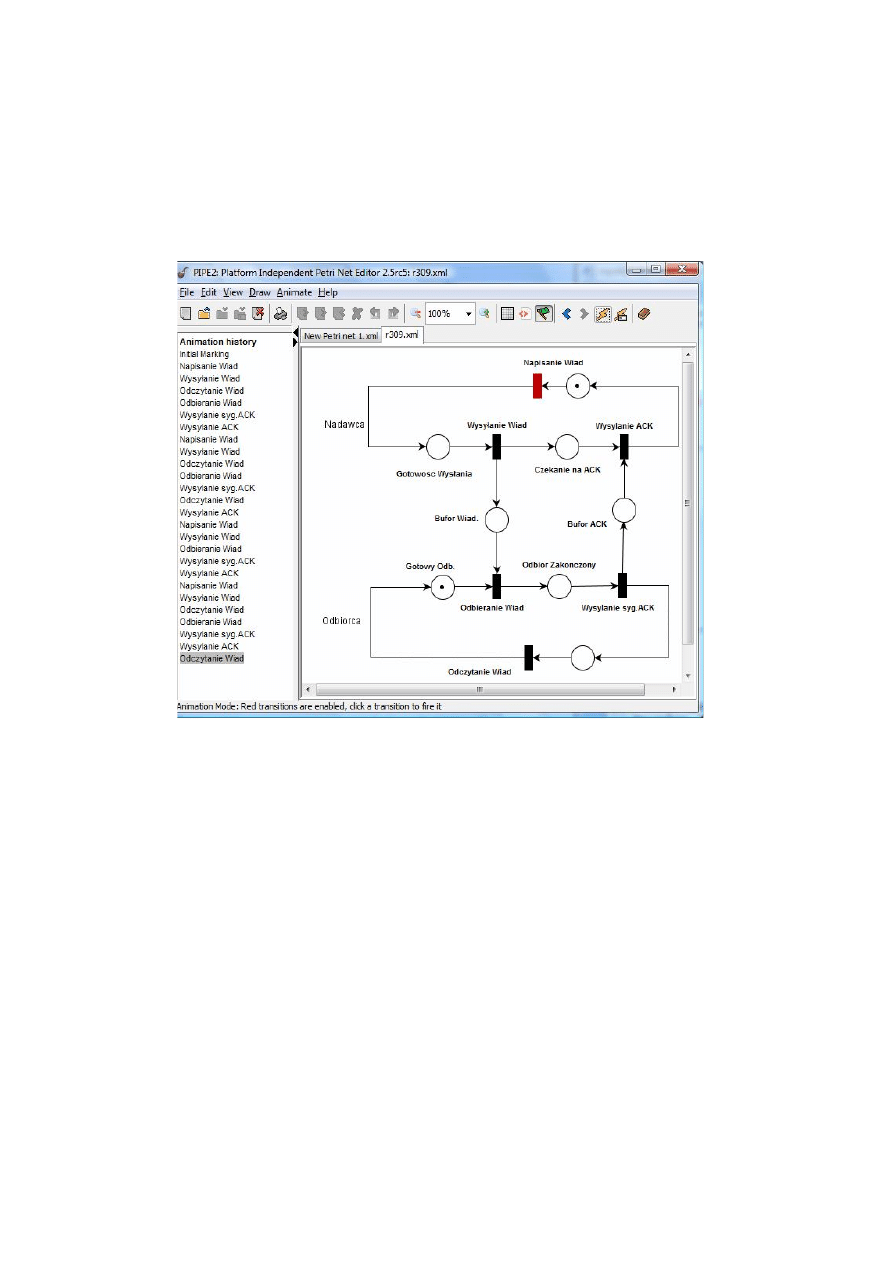
65

3.9. Model protokołu z potwierdzeniem

.

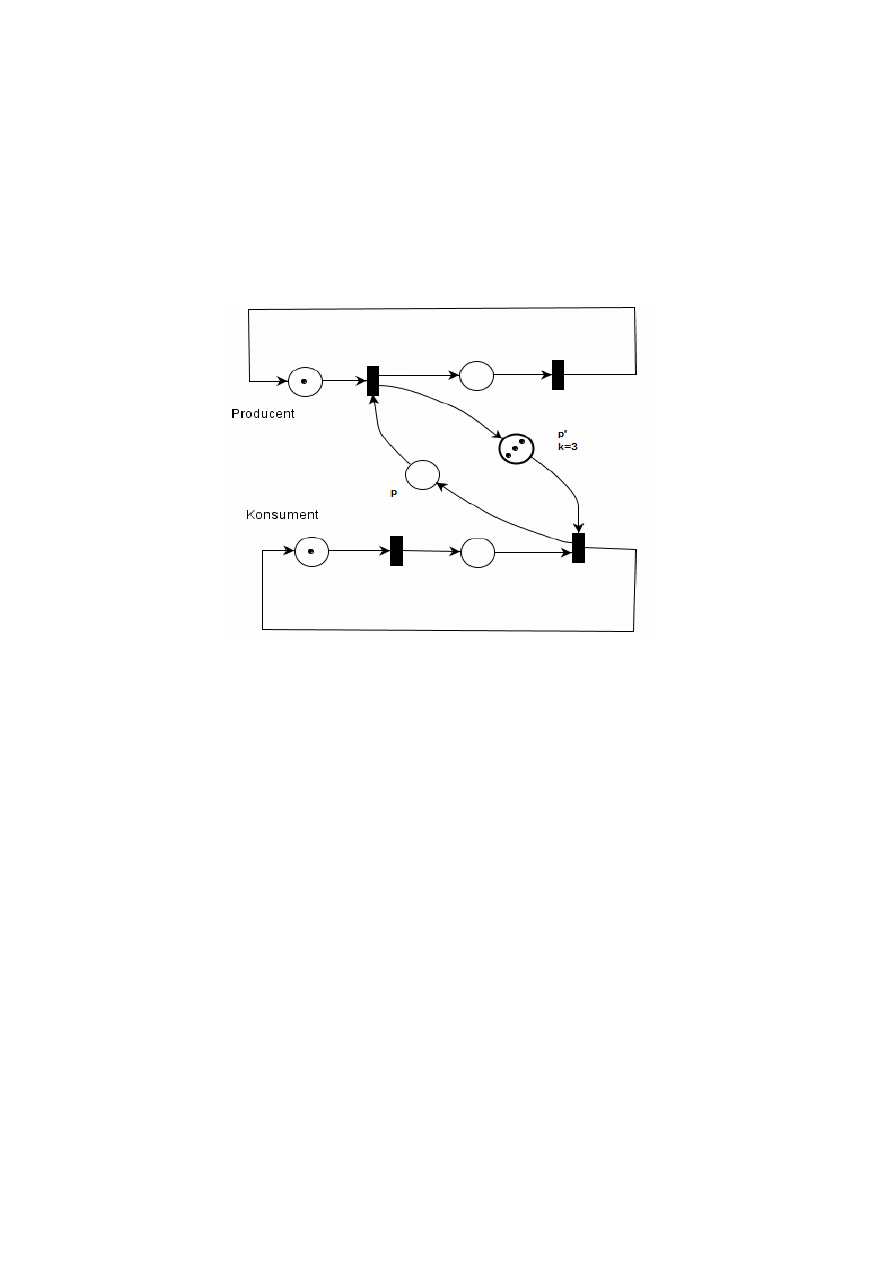
66

Przykład 4.
Model sieciowy producent-konsument.

Proces producenta może wykonywać się ściśle określoną liczbę razy i przesyłać
znaczniki do miejsca p. Dodatkowe miejsce p

’

z k znacznikami (przy znakowaniu

początkowym M

0

) powoduje ograniczenie ilości znaczników zawartych w miejscu

p. Dla każdego oznakowania M

s

osiągalnego z M

0

jest spełniona zależność:

M

s

(p) + M

s

(p

’

) = k

Ilość znaczników w sieci nie przekracza wartości k. Taki sposób poprawiania
struktury powinien być zastosowany w kontekście wszystkich miejsc, w których
może wystąpić nieograniczony wzrost ilości znaczników.

Rys. 3.10. Procesy komunikujące się poprzez k-ograniczony bufor

.

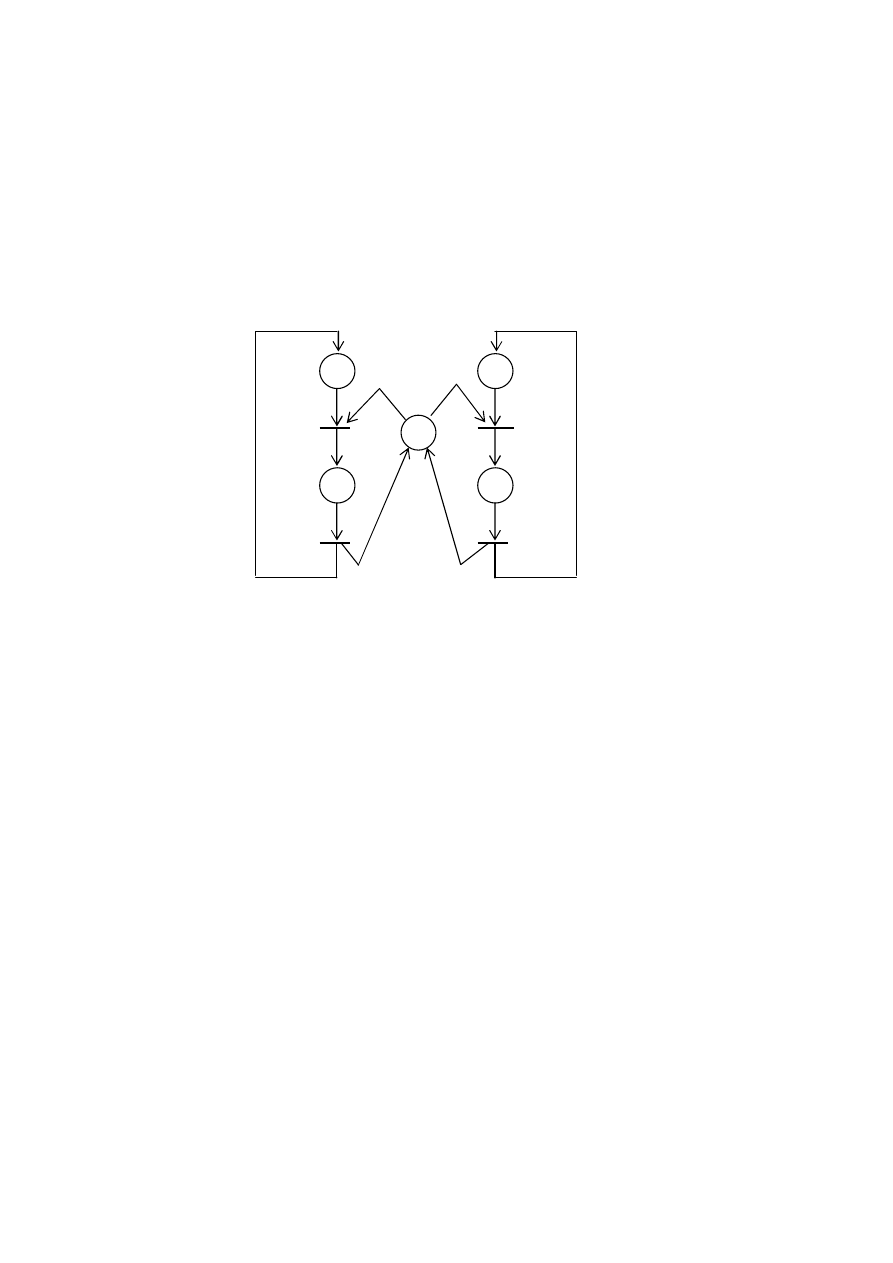
67

Przykład 5.
Model synchronizacji procesów.

Miejsce p

0

w powyższej sieci pełni funkcje synchronizujące, nie dopuszczając, aby

dwa procesy znalazły się w stanie M

s

takim, że M

s

(p

2

) = M

s

(p

4

) = 1, co modeluje

wzajemne wykluczanie dostępu do obszaru krytycznego. W dowolnym stanie M

s

spełniony jest bowiem warunek M

s

(p

2

) + M

s

(p

4

)  1.



p

1

Rys 3.11 Synchronizowany dostęp do obszaru krytycznego

p

0

p

3

t

2

t

1

p

2

p

4



t

4

t

3



.

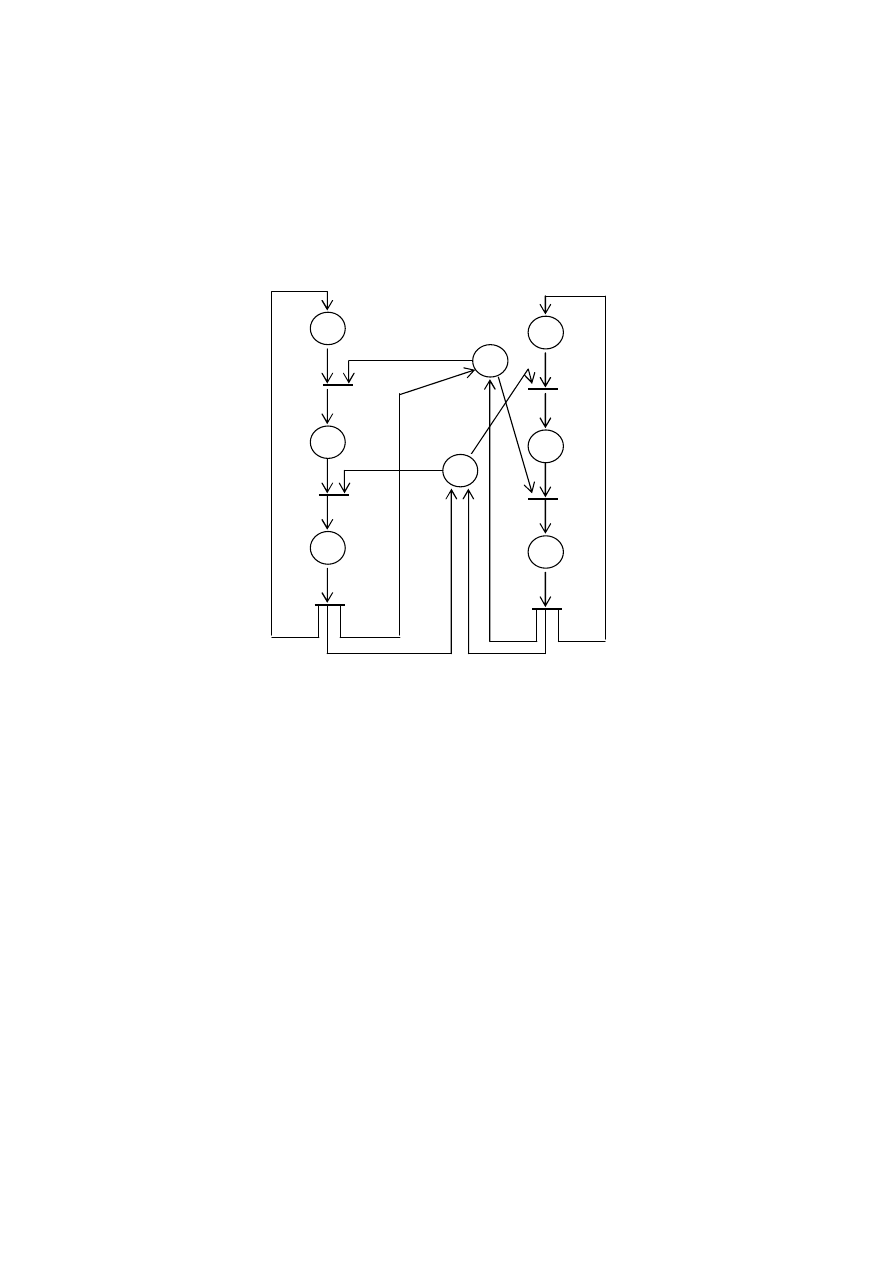
68

W sieci na powyższym rysunku może wystąpić stan zakleszczenia (brak

żywotności). Stan taki jest określony jako M(p

2

)= M(p

5

)=1 oraz M(p

i

)=0 dla

pozostałych miejsc p

i

. Stan ten jest osiągany przez wykonanie przejść t

1

oraz t

4

w

dowolnej kolejności.
Z drugiej strony, sieć może wykonywać się nieograniczenie, jeśli tylko w każdym
procesie będziemy wykonywać dwa kolejne przejścia <t

1

, t

2

> albo <t

4

, t

5

>

. Tego

typu sekwencje wykonania będą nieskończone.

3.7. Konstrukcja drzew i grafów pokrycia znakowań

Definicja 3.13.
Znakowanie M sieci MPN nazywamy pokrywalnym, jeżeli istnieje znakowanie
M`R(M

0

), takie że dla każdego miejsca pP jest spełniony warunek M`(p) M(p).

Konstrukcja drzewa pokrycia (coverability tree) znakowań polega na

utworzeniu drzewa pokrywającego wszystkie znakowania osiągalne ze stanu
początkowego. Wykonanie dowolnej sieci jest w ogólności (i najczęściej)

q

p



p

3

p

2

p

1

Rys 3.12 Sieć z możliwością zakleszczenia



t

3

t

2

t

1



p

6

p

5

p

4



t

5

t

4

t

6

.

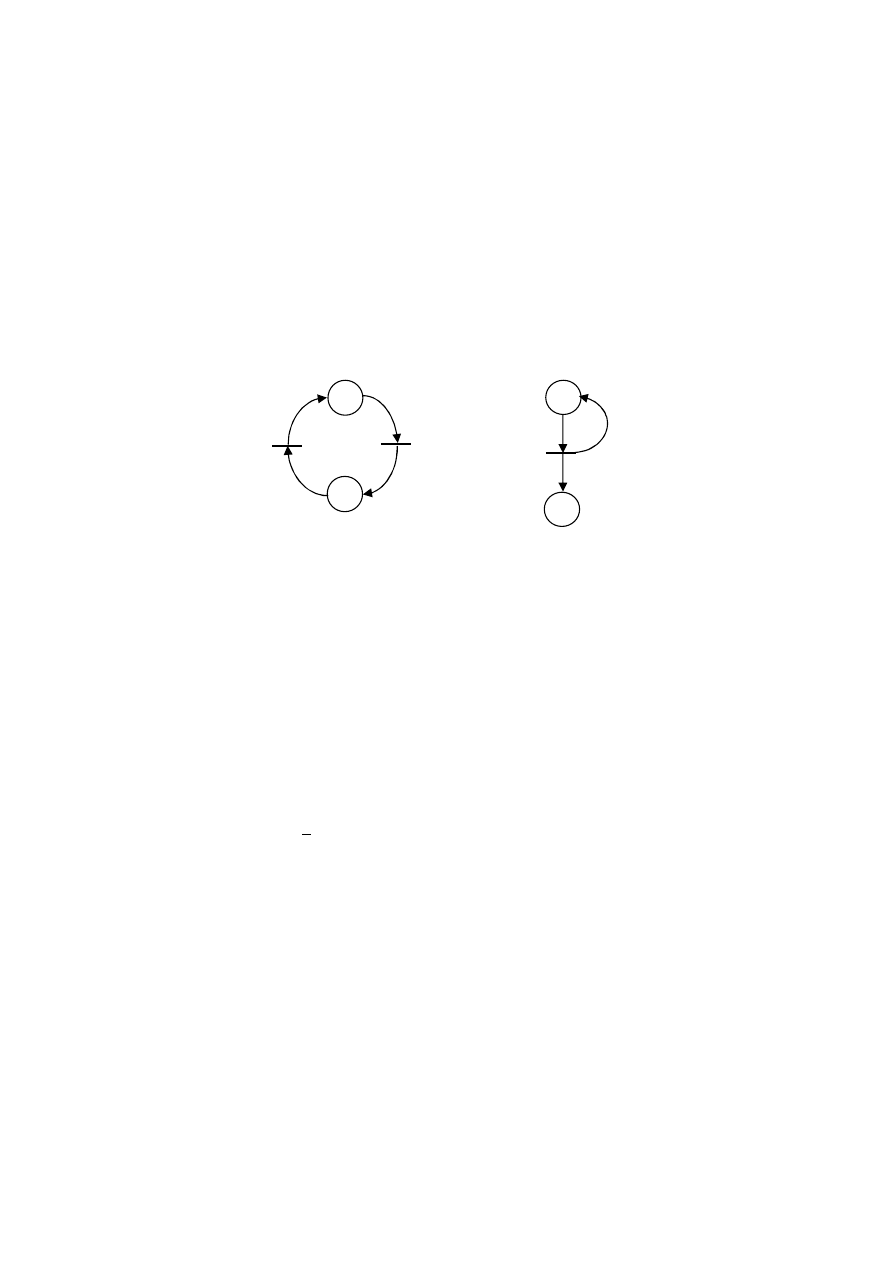
69

reprezentowane przez nieskończone sekwencje realizacji odpowiednich przejść
sieci. Konstrukcja drzewa o skończonej ilości wierzchołków wymagać więc będzie
wprowadzenia pewnych uproszczeń. W ogólnym przypadku możemy mówić o
dwóch przyczynach powodujących generację nieskończonych sekwencji stanów
osiągalnych: powtarzające się sekwencje wykonań pewnych przejść oraz
nieograniczony wzrost ilości znaczników w pewnych miejscach.

W przypadku a) mamy do czynienia z nieskończoną sekwencją wykonań:

Wykonanie drugiej sieci b) polega na generacji kolejnych znakowań w myśl
sekwencji:

W przypadku powtarzających się sekwencji możemy zakończyć generację w
momencie osiągnięcia stanu powtórzonego <1, >. Wprowadza się symbol
nieskończoności  taki, że dla dowolnej skończonej liczby całkowitej n spełnione są
zależności >n, +n=. Kolejne stany będą pochłaniane przez oznakowanie
<1, >. Drzewo pokrycia będzie budowane z wykorzystaniem powyższych dwóch
mechanizmów. Algorytm konstrukcji drzewa będzie posługiwać się następującą
klasyfikacją węzłów drzewa:
- węzły nowe, czyli takie które nie były jeszcze przetwarzane,
- węzły powtórzone, które pojawiły się już na danej ścieżce budowania drzewa,
- węzły końcowe, dla których nie ma znakowania następnego.
Znakowanie początkowe M

0

stanowi korzeń drzewa i zarazem węzeł nowy.

Algorytm działa tak długo, dopóki istnieją węzły nowe.

t

1

t

2

t

2

p

1

p

2



a)

p

2

p

1



t

1

b)

Rys. 3.13. Źródła generacji nieskończonej sekwencji znakowań

<

1, 0>



<0, 1>



<1, 0>



<0, 1>

 . . .

t

1

t

2

t

1

t

2

. . .

<1, i >  <1, i+1 > . . .

t

1

.

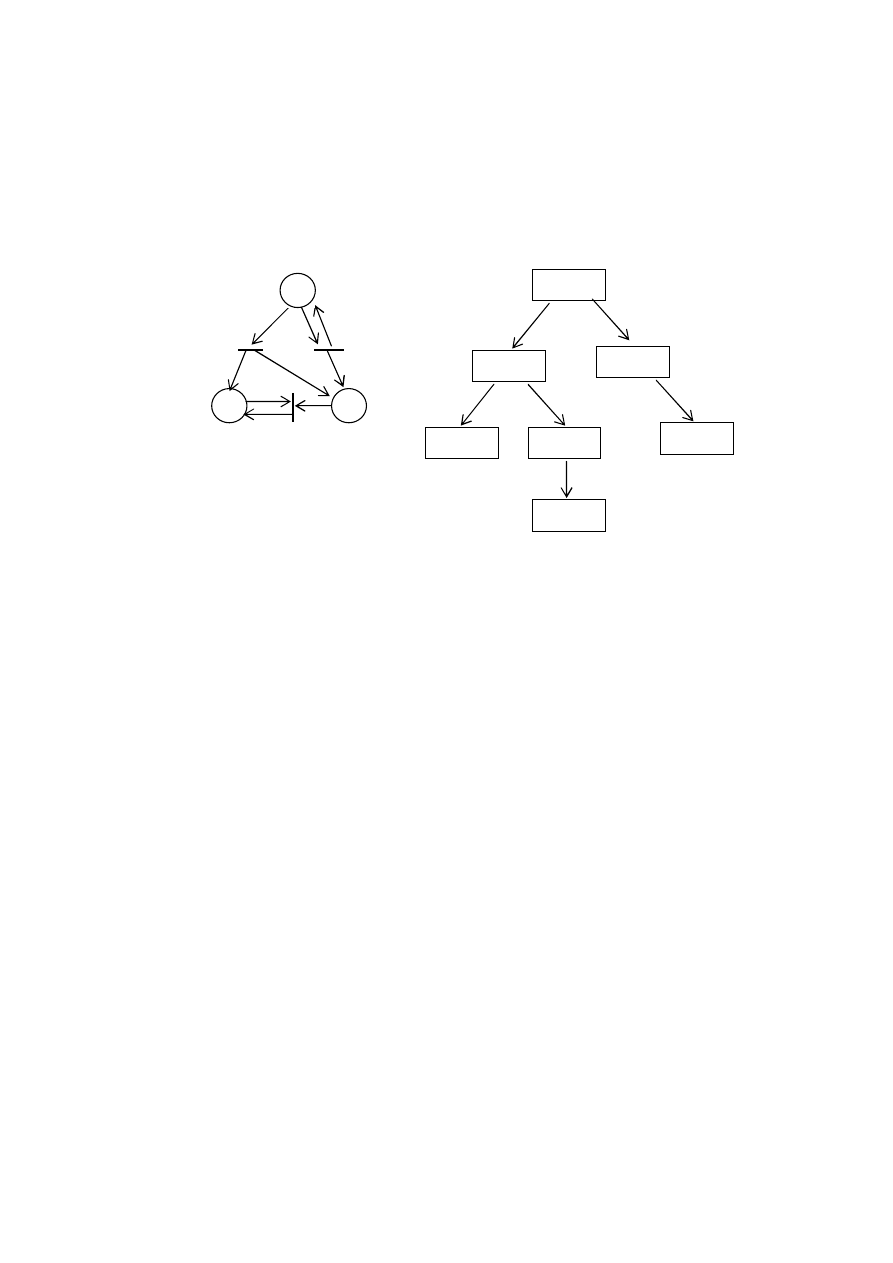
70

Na powyższym rysunku, wprowadzenie symbolu  jest realizowane już przy
pierwszym wykonaniu przejścia t

1

. Wykonanie przejścia t

1

powoduje zmianę stanu,

czyli wzrost ilości znaczników w miejscu p

2

przy niezmienionych wartościach w

miejscach pozostałych. Tym samym spełnione są warunki wstawienia symbolu 
na pozycję odpowiadające miejscu p

2

.

Drzewo pokrycia znakowań składa się ze skończonej ilości węzłów, co

umożliwia badanie własności dynamicznych, w szczególności można podać
następujące:
 Sieć PN jest ograniczona, gdy symbol  nie występuje w drzewie pokrycia.

Wówczas drzewo stanów osiągalnych jest skończone.

 Sieć PN jest bezpieczna, gdy w węzłach drzewa występują znakowania

składające się wyłącznie z zer i jedynek,

 Przejście t jest martwe, jeśli w drzewie pokrycia nie występuje łuk etykietowany

przez t.

 Znakowanie M

i

jest osiągalne ze znakowania początkowego M

0

, jeśli w drzewie

pokrycia istnieje węzeł M

i

oraz ścieżka prowadząca z M

0

do M

i

.

Wyżej wymienione własności mogą być analizowane przez przeglądanie drzewa
pokrycia. Dynamiczne własności sieci Petriego mogą być również opisywane przez
równania macierzowe.

t

3

t

3

t

1

t

2

t

2

t

1

1,0,0

1,,0

0,1,1

1,,0

0,,1

0,0,1

0,,1

p

3

p

2

p

1



t

1

t

2

t

3

3.14. Konstrukcja drzewa pokrycia dla sieci Petriego

.

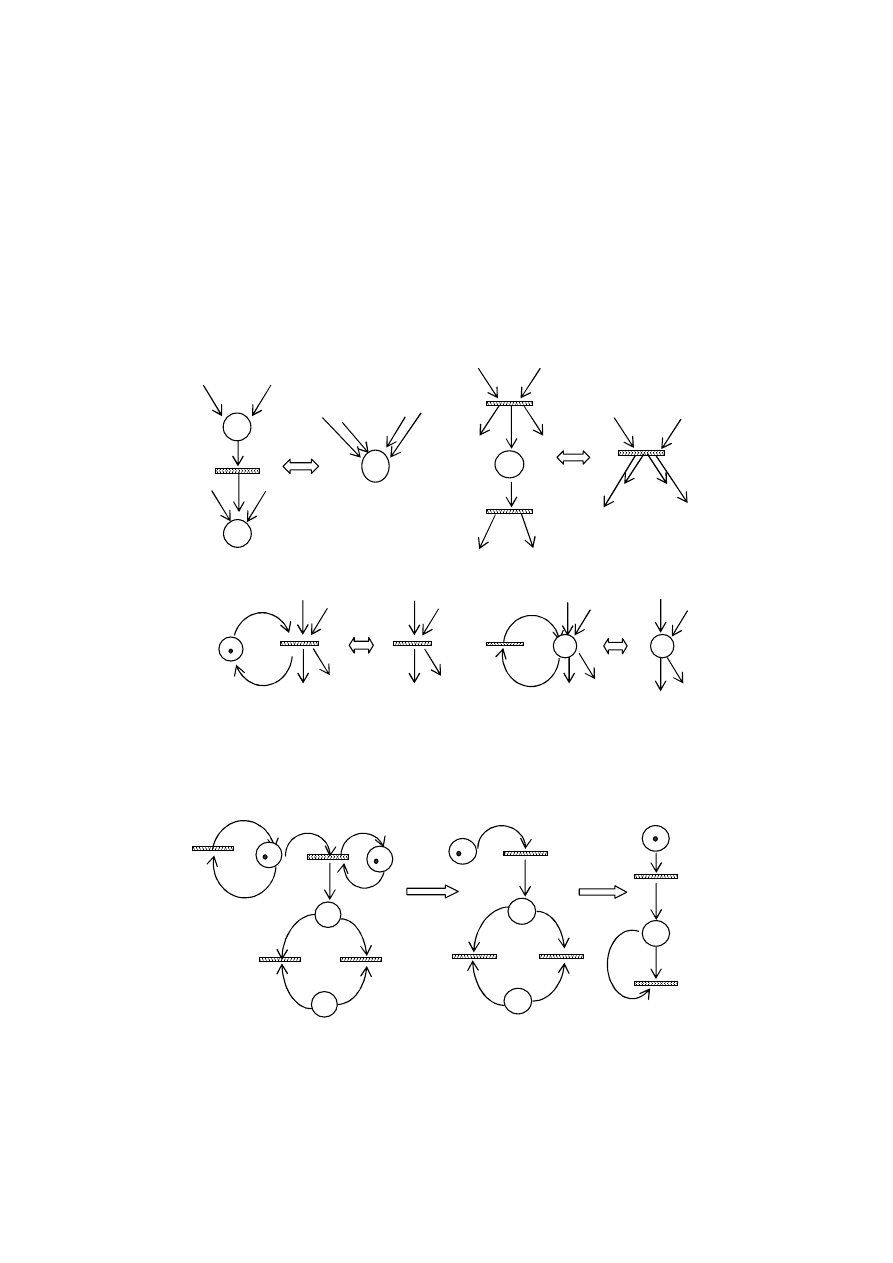
71

Podstawowe redukcje sieci zachowujące własność: żywotności, ograniczoności i
bezpieczeństwa. Oznacza to, że jeśli sieć przed transformacją miała, którąkolwiek
z tych własności, to sieć uzyskana w wyniku zastosowania transformacji
zachowuje również odpowiednie własności.

t

2

t

1

t

2

p

1

p

2

t

4

p

4

t

3

p

3

t

1

t

2

t

2

p

1

p

2

t

4

p

3

t

2

p

1

t

4

p

3

Łączenie sekwencji miejsc

Eliminacja pętli miejsca

Eliminacja pętli przejścia

Łączenie sekwencji przejść

3.15. Różne przypadki eliminacji

.

72

3.8 Oprogramowanie narzędziowe ND.

Program ND (Net Draw) jest jednym z narzędzi pakietu TINA (Timed

Integrated Net Analyzer). Przeznaczony jest do edycji i symulacji sieci Petriego
zarówno deterministycznej jak i stochastycznej. Edytor pozwala na graficzną i
tekstową prezentację sieci, natomiast symulator umożliwia realizację trybu pracy
krokowej oraz automatycznej symulacji. Dodatkowo program zapewnia analizę
wybranych właściwości sieci [1] [2][3].
Dane wejściowe programu są zapisane w pliku tekstowym z rozszerzeniem, które
kojarzy go z wybranym modelem sieci i sposobem prezentacji (widokiem).

model / widok

graficzny

tekstowy

Sieć Petriego

*.ndr

*.net

Graf automatu

*.adr

*.aut

I. Tryb edycji.

Edytor uruchamia się poleceniem nd.exe.

1. Skrócony zapis działania klawiszem myszy.

LK - lewy klik,

PK - prawy klik,
SK - środkowy klik

.

Rys. 3.17. Ekran główny programy ND

.

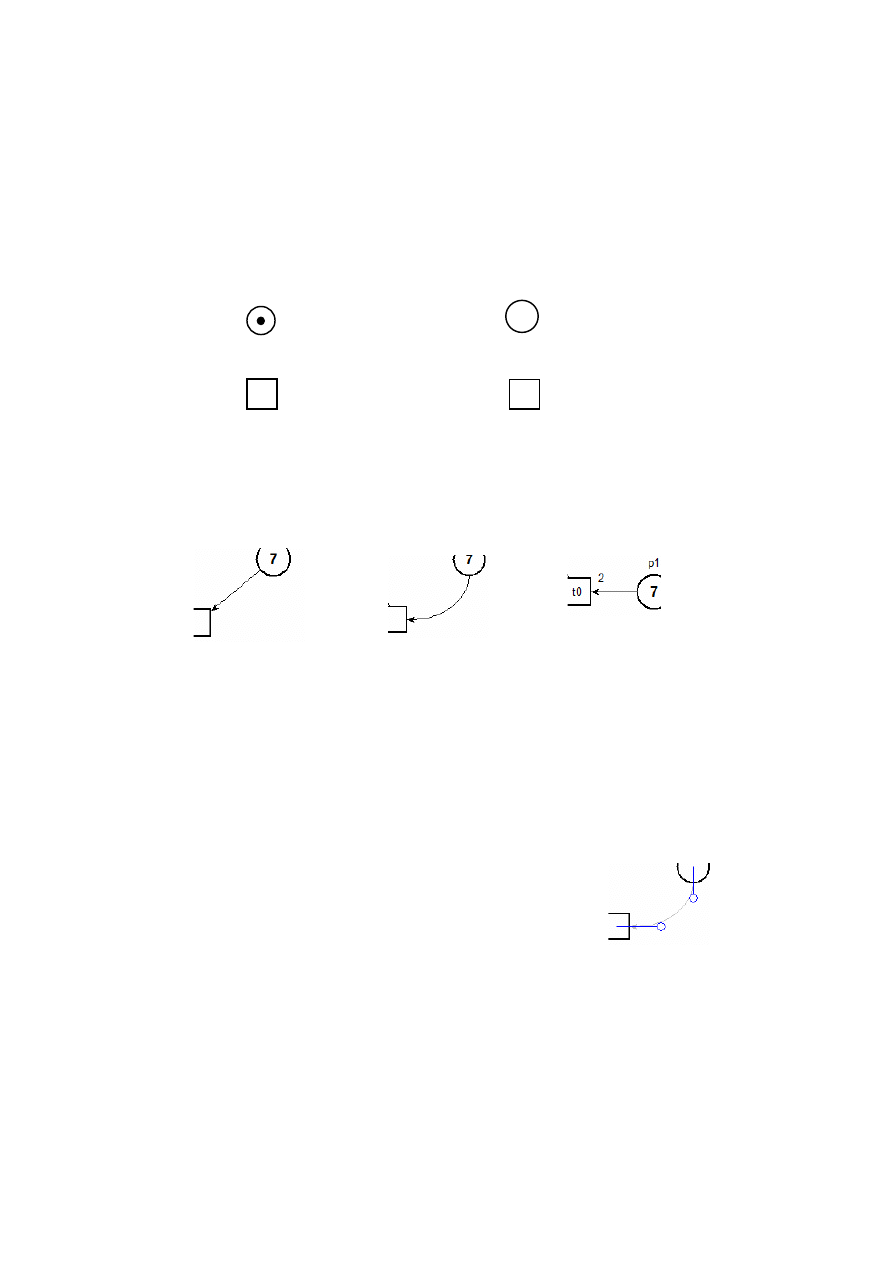
73

2. Elementy sieci.

Węzły:

Krawędzie:
prostoliniowa

krzywoliniowa krawędź z wagą (waga>1)

3. Modyfikacja elementów graficznych.

Położenie węzłów i opisów: LK, przesunięcie.

Usuwanie węzła i krawędzi: LK, [Delete] lub

LK, [Ctrl+X] lub

LK, PK, LK na wybór Cut.

Kopiowanie i wstawienie:

LK, [Ctlr+C] [Ctlr +V].

Edycja krawędzi:

LK, przesunięcie znaczników

promienia krzywizny
(edges rays).

p0

- miejsce (place)

p

0

= 1

t0

- tranzycja t

0

(transition)

dla TPN

0 

< 

praktycznie 0 

0

< 

7

p1

p

1

= 7

t1

- tranzycja t

1

(transition)

dla TPN

4 

1

< 

[4 -7]

.

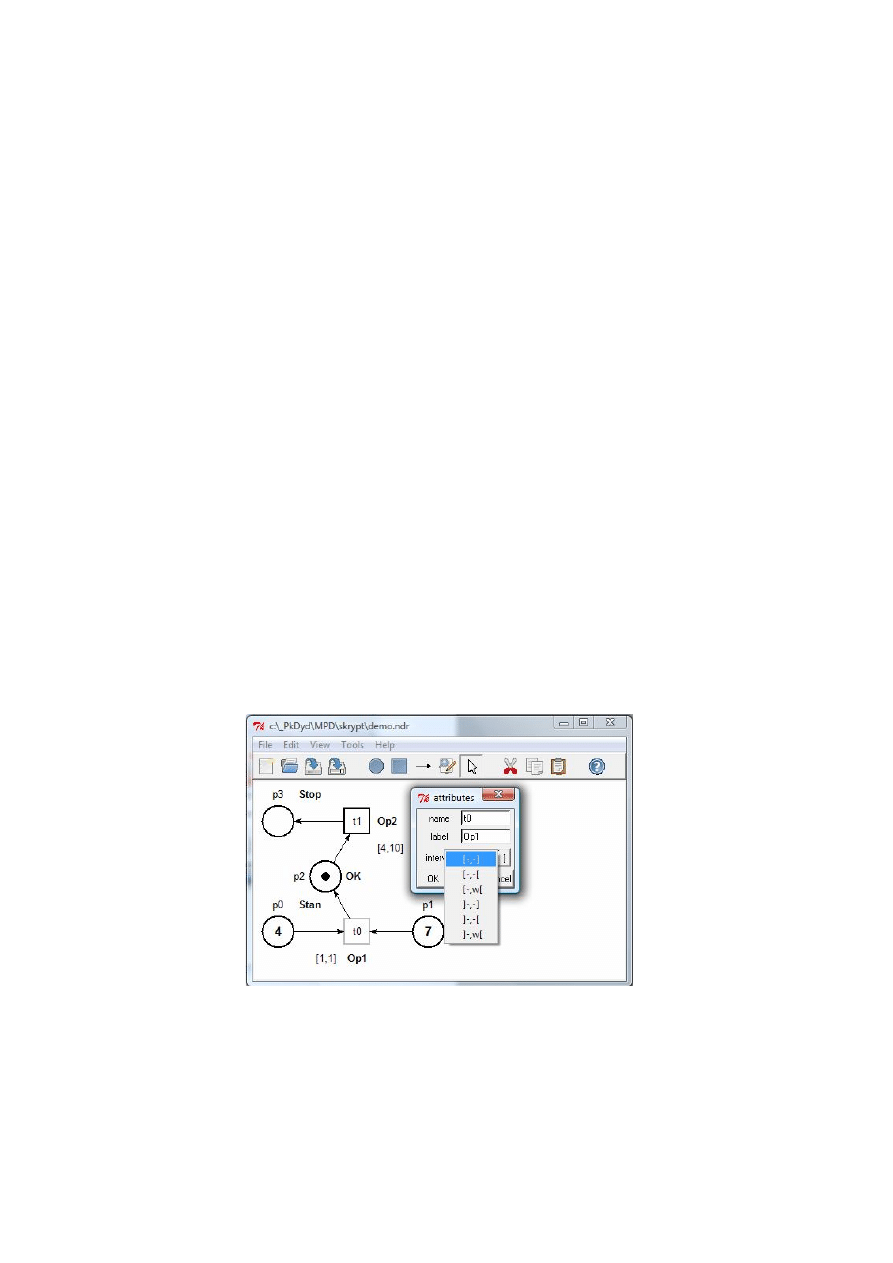
74

4. Ustawienie ogólnego sposobu aktualizowania krawędzi poprzez menu:

View /

redraw edges



auto

- zachowuje bieżący tryb,



straight

- tryb prostoliniowy,



keep rays

- tryb krzywoliniowy z zachowaniem kierunków

5. Operacje grupujące.

N

a grupie elementów można wykonać wszystkie w/w operacje (z

wyłączeniem edycji

krzywizn

y

krawędzi

).

Grupowanie elementów – LK, zaznaczenie prostokątnej ramki.

Dodawanie do grupy i usuwanie z grupy - [Ctlr]+LK na wybranym elemencie.

6. Dodawanie nowych elementów.

Wprowadzanie nowych elementów realizowane jest poprzez kliknięcie

na

wybranej pozycji środkowym klawiszem myszy [SK] odpowiednio dla:

miejsca

- SK,

tranzycji - [Ctlr]+SK,

krawędzi - naciśnięcie środkowym klawiszem myszy na wybranym węźle

początkowym, oraz przesunięcie i puszczenie klawisza na węźle
końcowym.

Rys 3.19. Przykład edycji czasu tranzycji t0

.

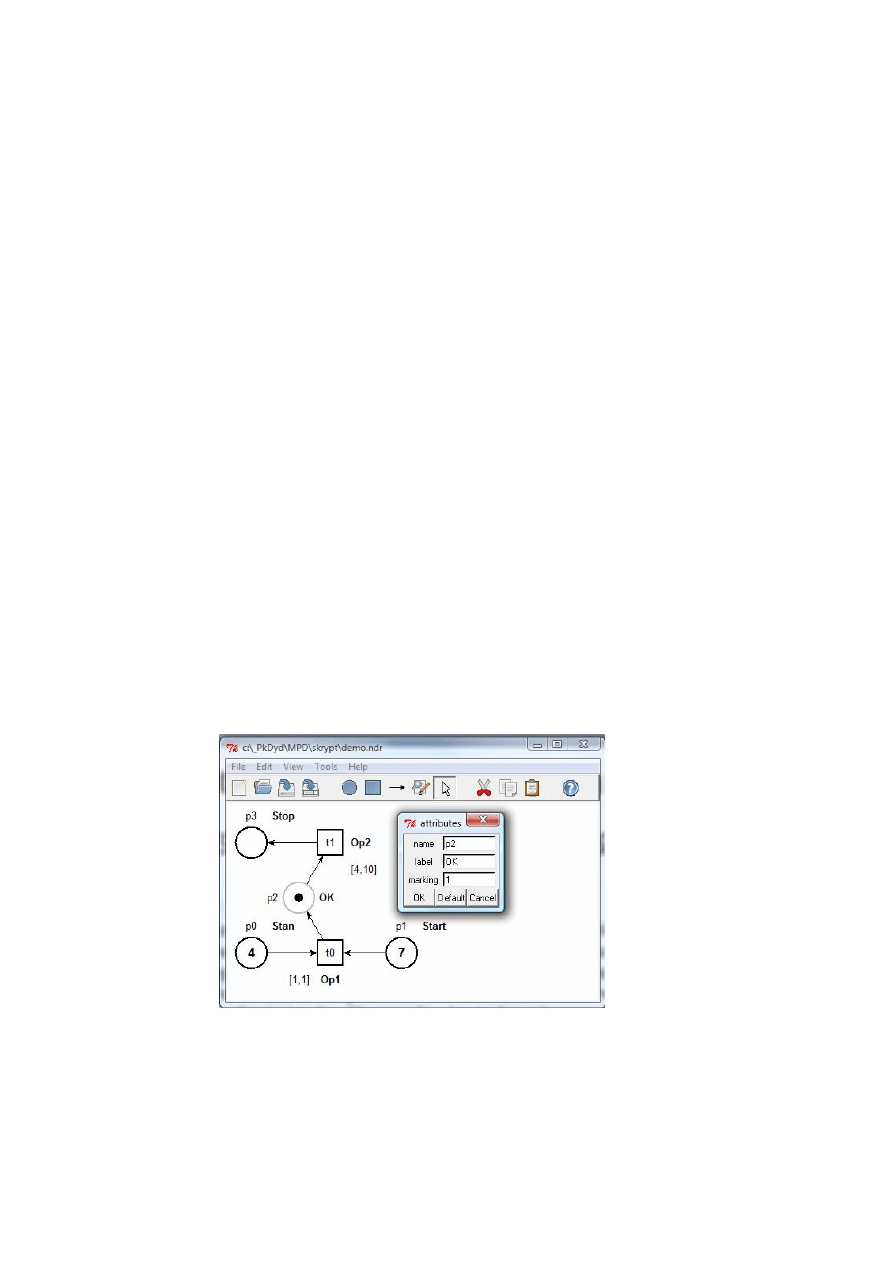
75

7. Modyfikacja parametrów.

Parametry (attributes) elementów sieci można modyfikować w odpowiednim
oknie dialogowym, otwieranym poprzez kliknięcie prawym klawiszem myszy
[PK] na wybranym elemencie.

Waga (weight)

- [PK] na krawędzi.

Identyfikator (name) - obligatoryjny i nadawany automatycznie (możliwy do

edycji) unikalny ciąg znaków alfanumerycznych (uży-
wany w raportach wynikowych).

Etykieta (label)

- opcjonalny unikalny ciąg znaków alfanumerycznych

Czas (interval)

- czas palenia się tranzycji 

i

 R

+

dla sieci czasowych

(deterministycznych) należy ustawić na jednakowej
wartości zakresu losowania wybierając pierwszy na liście
przypadek oznaczony symbolem [-

, -].

Program ND pozwala na symulację również czasowych sieci stochastycznych dla
wielu różnych specyficznych sposobów generowania czasu palenia się tranzycji
(Rys 3.19).

Rys 3.20. Przykład edycji argumentów miejsca p2

.

76

Uwagi ogólne:

-

edycja położenia węzła modyfikuje także przyległe krawędzie,

-

liczba znaczników jest dodatnią liczbą całkowitą domyślnie równa zero,

-

wagi krawędzi domyślnie ustawione są na wartość równą 1,

-

położenie parametrów można zmienić w zakresie 8 ustalonych pozycji
wokół symbolu graficznego (dla tranzycji także wnętrze symbolu),

-

identyfikatory węzłów p

i,

t

j

są automatycznie numerowane od zera, ale

można je zmieniać z zachowaniem unikalności,

-

w edycji graficznej ważne jest dokonywanie właściwego, wyboru elementu
np. krawędzi lub bliskiej okolicy a nie opisu np. tranzycji.

II. Tryb symulacji.

Przebieg symulacji można śledzić, zapisywać i odtwarzać zarówno w trybie

ręcznym jak i automatycznym przechodząc wzajemnie z jednego trybu do
drugiego w trakcie symulacji.

1.

Z trybu edycji przechodzi się do trybu symulacji przez menu:

Tools  stepper simulator
a wraca automatycznie przez:
- zamknięcie okna symulacji:

[Alt+F4 ],

[ Ctrl+q ] lub

menu:

File

 return to edytor [Ctrl+q]

2. W automatycznym trybie symulacji można wprowadzić opóźnienie zwalniające

szybkość jej wizualizacji przez zaznaczenie w menu :

Mode

 firing duration (ms).

na poziome 0, 1, 10, 1000

3. Aktywacja zapisu do pliku namefile.scn przez zaznaczenie w menu:

Mode  record history

4. Odtworzenie zapisanej symulacji w menu:

File

 open history

wybór

pliku

namefile.scn

5. Symulacja może być przeprowadzona w trybie sieci czasowej (TPN)

Mode

 timed

lub zwykłej (PN)

.

77

Mode

 untimed

6. Inicjalizacja trybu automatycznej symulacji:

- uruchomienie: przycisk [Rand],

- zatrzymanie:

przycisk [Stop].

7. Nawigacja:

- przejście na początek [|<] zapisanej historii stanów,

- na koniec [|>] zapisanej historii stanów,

- przejście do poprzedniego [<] następnego [>] stanu,

- wybrane np. istotne stany można zapamiętać, wybierając przycisk [ M]

- zapamiętane stany można

odtworzyć wybierając przyciskiem

[>>] następny zapamiętany stan

lub przyciskiem [<<] poprzedni zapamiętany stan.

6. Ręczne sterowanie symulacją.

Jeżeli w trybie zwykłym jest co najmniej jedna przygotowana do przejścia
tranzycja (oznaczona czerwonym tłem ( np: t0 na Rys 3.21):

- nacisnąć lewy klawisz na aktywnej tranzycji (przygotowanej do przejścia)

wprowadzając chwilowy stan przejściowy, zachodzi zmiana (zmniejszenie)
stanu markowania w miejscach wejściowych aktywnej tranzycji i oznaczenie
jej czerwoną ramką z białym tłem,

- po zwolnieniu klawisza występuje zmiana markowania na wyjściu

oznaczająca osiągnięcie nowego stanu markowania.

W trybie czasowej sieci Petriego dodatkowo występuje ręczne sterowanie
czasem symulacji. Jeżeli nie ma przygotowanej do przejścia tranzycji a
występują tranzycje oznaczone szarym tłem to można przesunąć znacznik czasu
(delay) w sposób skokowy 1 lub ciągły do chwili uaktywnienia co najmniej
jednej tranzycji. Czas do momentu uaktywnienia się tranzycji (zmiany stanu)
jest na bieżąco wizualizowany.

.

78

3.9. Edytor i symulator PIPE

Opisany w poprzednim podrozdziale program ND z pakietu TINA posiada

ciekawe rozwiązania w zakresie śledzenia symulacji szczególnie dla
stochastycznych sieci Petriego, ale ma także wiele ograniczeń np: brak możliwości
ograniczenia ilości znaczników (pojemności miejsc), symulacji sieci kolorowanych
oraz graficznej reprezentacji wyników z analizy sieci.

Drugą propozycją w zakresie symulacji sieci Petriego jest program PIPE

(Platform Independent Petri net Editor), posiadający bardziej rozbudowaną
funkcjonalność. Program PIPE2 jest niezależnym od platformy narzędziem do
tworzenia i analizy sieci Petriego. Ponadto:

- należy do otwartego oprogramowania (open source),
- posiada przyjazny w użyciu interfejs np.: skalowalną grafikę,
- zawiera wiele modułów do analiz: metody inwariantów, symulacji, przestrzeni

stanów, klasyfikacji, porównań, macierzy incydencji i wektora markowania

- umożliwia generowanie grafu osiągalności (3.23)
-

symulacji sieci kolorowanych

- eksportowanie sieci Petriego w formacie graficznym.

Podstawowy ekran programu w trybie animacji przedstawia rysunek 3.22




















a wyniki analiz tej siec przedstawione są w kolejnych w tabelach.

Rys 3.22 Ekran programu pipe w trybie animacji (bieżącej symulacji)

.

79

1. Zbior stabilnych stanów markowania:

Set of Tangible States

P0

P1

P2

P3

P4

P5

P6

P7

M0

0

0

1

0

0

1

0

3

M1

0

0

1

1

0

0

0

3

M2

0

0

1

0

0

1

1

2

M3

0

0

1

0

0

1

2

1

M4

0

0

1

0

0

1

3

0

M5

1

0

0

0

0

1

3

0

2. Średnia liczba i rozkład gęstości znaczników:

Average Number
of Tokens on a
Place

Token Probability Density

Place

Number
of
Tokens

µ=0

µ=1

µ=2

µ=3

P0

0,1667

P0

0,8333

0,1667

0

0

P1

0

P1

1

0

0

0

P2

0,8333

P2

0,1667

0,8333

0

0

P3

0,1667

P3

0,8333

0,1667

0

0

P4

0

P4

1

0

0

0

P5

0,8333

P5

0,1667

0,8333

0

0

P6

1,5

P6

0,3333

0,1667

0,1667

0,3333

P7

1,5

P7

0,3333

0,1667

0,1667

0,3333

3. Czas trwania i rozkład stabilnych stanów oraz przepustowość czasowa tranzycji

Sojourn times
for tangible
states

Steady State
Distribution of
Tangible States

Throughput of Timed
Transitions

Mark Value

Marking Value

Trans

Throughput

M0

0,5

M0

0,1667

T4

0,8333

M1

1

M1

0,1667

T5

0,8333

M2

0,5

M2

0,1667

M3

0,5

M3

0,1667

M4

0,5

M4

0,1667

M5

1

M5

0,1667

.

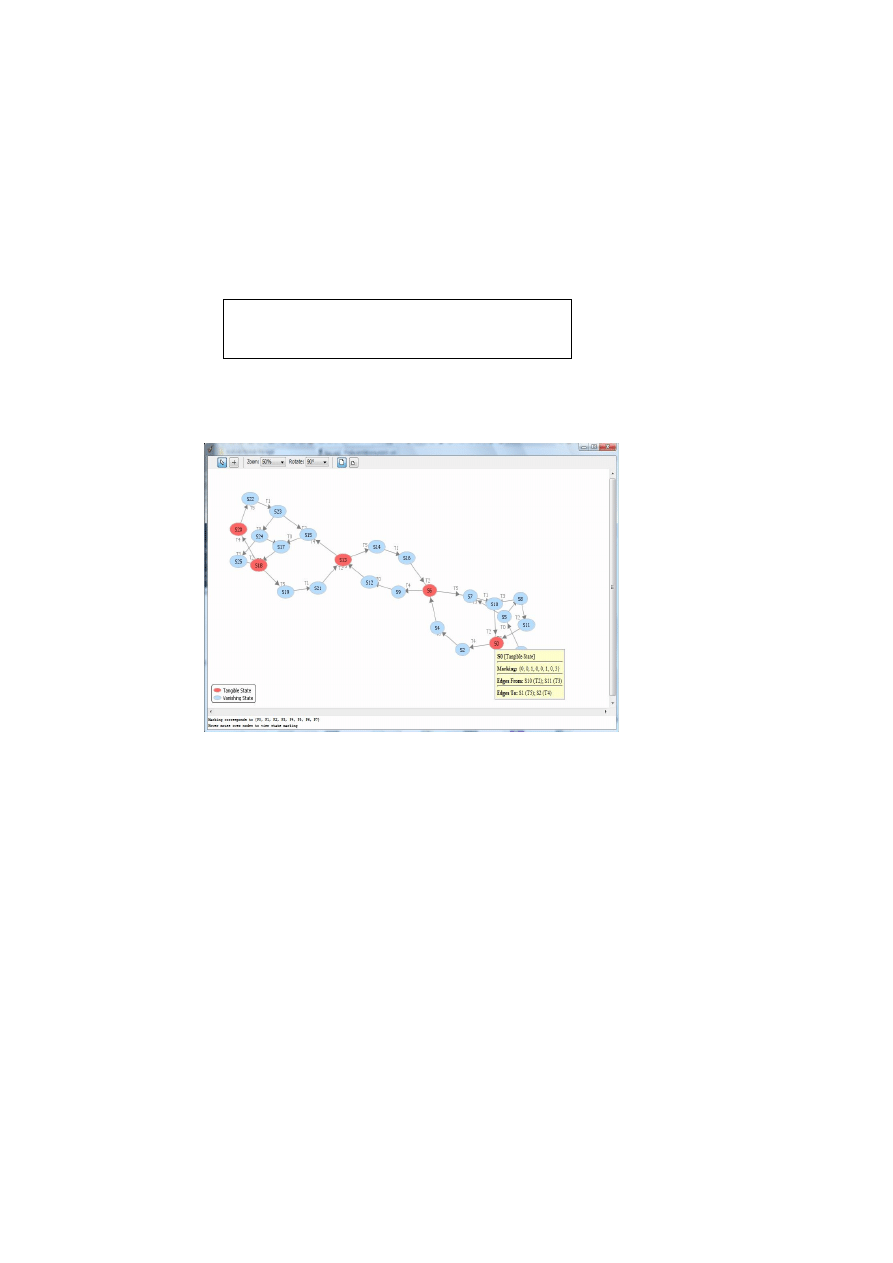
80

4. Ogólne parametry czasowe symulacji

State space exploration took 0,304s
Solving the steady state distribution took 0,116s
Total time was 0,504s

Wszystkie wyniki można zapisać w formacie html a analizę sieciową
można rozszerzyć na sieć kolorowaną. Rys 3.24

Rys 3.23. Przykładowy graf osiągalności wygenerowany

.

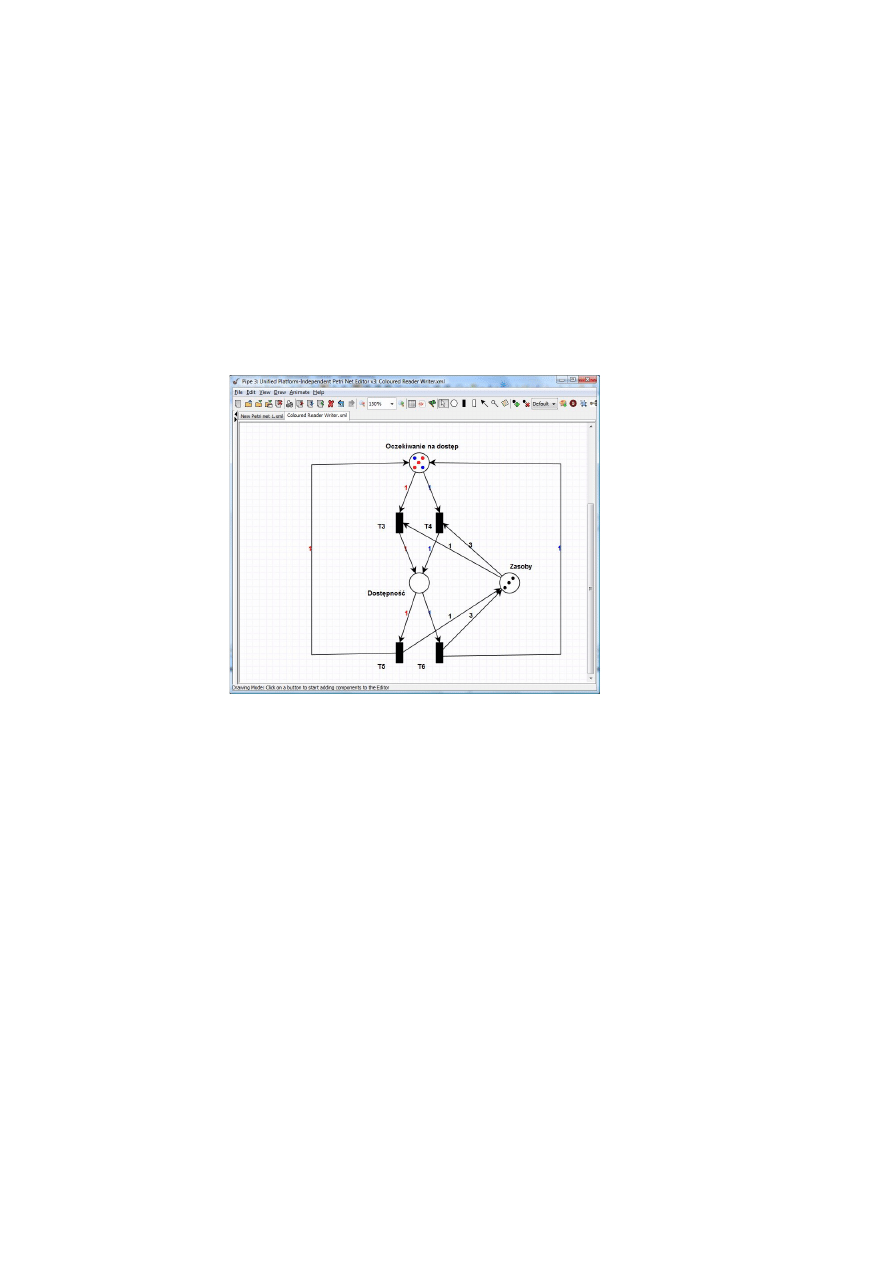
81

Literatura do rozdz. 3.

1.

Berthomieu B., Vernadat F., The tool TINA. Construction of Abstract State
Spaces for Petri Nets and Time Petri Nets. International Journal of Production
Research, Vol. 42, No 14, July 2004.

2.

Berthomieu B., Diaz M., Modeling and verification of time dependent systems
using time Petri nets. IEEE Transactions on Software Engineering, 17(3),
1991.

3.

Berthomieu B., Vernadat F., State class constructions for branching analysis
of Time Petri nets. Springer Verlag, LNCS, 2003.

Rys 3.24. Kolorowana Sieć Petriego

.

82

4.

Mur

a

t

a

T.,

P

e

tri N

e

t

s

:

pr

ope

rtie

s

, a

n

a

l

y

s

i

s

a

nd a

p

p

li

cat

i

o

n

s

.

Pr

oceed

in

g

s

of t

he

I

EEE

,

1

9

89

,

v

o

l

.

77

.

5.

R

eisig

W

: Sieci

P

e

triego.

WN

T 1

988

6.

Ross K., Wright C., Matematyka dyskretna. PWN 1996.

7.

Szpyrka M.,Sieci Petriego w modelowaniu i analizie systemów współbieżnych.
WNT, 2008.

8.

Wilson R.,Wprowadzenie do teorii grafów. PWN 1998.

Strona internetowa.

http://pipe2.sourceforge.net/

-

Platform Independent Petri net Editor 2

.

83

4. JĘZYKI SYMULACYJNE SYSTEMÓW

DYSKRETNYCH

4.1 Zastosowanie

Symulacja dyskretna często dotyczy systemów z kolejkowaniem zadań, takich

jak np. kasy w supermarketach czy linie produkcyjne w fabrykach. Symulacja
umożliwia natychmiastowe sprawdzanie nowych konstrukcji maszyn, automatów i
robotów w warunkach ich pracy, łącznie z ich programami sterującymi (tzw.
wirtualne uruchomienie produkcji). Dzięki takiej symulacji możemy dowolnie
testować kolejne zmiany w systemie np nowe wymiary elementów, parametry czy
procedury pracy i do tego nie zakłócając produkcji rzeczywistych urządzeń. Nowy
program sterujący zostaje przesłany do sterownika rzeczywistego urządzenia
dopiero po jego gruntownym przetestowaniu. Przy dziesiątkach tysięcy różnych
parametrów manualne poszukiwanie właściwej konfiguracji systemu może zająć
dużo czasu

Zakres zastosowań jest bardzo szeroki i obejmuje np: ogólną produkcję i

specjalizowane linie produkcyjne, automatykę i robotykę, logistykę, magazyny, w
tym transport surowców, produktów i towarów, transmisję danych systemach
informatycznych, obsługę stanowisk np: szpitale, banki i urzędy oraz inne punkty
usługowe a także złożoną siec linii komunikacyjnych.

Poprzez wczesne testowanie nowych rozwiązań można zaoszczędzić czas i

pieniądze uzyskując odpowiedź na wiele istotnych pytań: co produkować, gdzie i
kiedy, jak minimalizować koszty prowadzenia działalności z zachowaniem
odpowiedniej jakości i odpowiedniego stopnia zadowolenia klientów lub w jaki
sposób określić najlepsze rozplanowanie środków transportu i personelu, czy
można to samo wykonać np z mniejszą liczbą maszyn?.

Symulacja pozwala na przetestowanie nowych rozwiązań dotyczących

ulepszenia programów sterujących i optymalizujących tj. zmniejszających ilość
przestojów oraz zwiększających wydajność systemów produkcyjnych, magazynu
czy całego systemu logistycznego. Z punktu widzenia optymalizacji opisana
problematyka często sprowadza się do likwidacji tzw. wąskich gardeł oraz
właściwego rozwiązania ogólnie pojętego problemu obsługi kolejek zadań.

Przykładem może być obsługa kolejki w aplikacji służącej do komunikacji w

firmie, której zadaniem jest usprawnienie telefonicznej obsługi klientów
(http://www.ipfon.pl/callcenter.htm)). Taka usługa pozwala między innymi na tym
że wielu pracowników - w tym także rozproszonych po całym świecie - może

.

84

obsługiwać jedną wspólną linię telefoniczną. Istotne jest w tym przypadku
zapewnienie inteligentnego kształtowania obciążenia konsultantów przejawiające
się między innymi w tym, że klienci nigdy nie usłyszą sygnału zajętości a w
zamian za to zostaną wprowadzeni do kolejki i poinformowani o ilości osób
oczekujących na połączenie z konsultantem (agentem) wraz szacowanym czasem
oczekiwania na to połączenie a okres oczekiwania zostanie umilony odsłuchaniem
muzyki. Z drugiej strony konsultant odbierający połączenia może być infor-
mowany o tym, że aktualne połączenie pochodzi z kolejki wraz z podanym czasem
oczekiwania klienta a ponadto może na bieżąco w przeglądarce internetowej
śledzić stan kolejki i decydować o skróceniu czasu rozmowy lub przełączeniu
klienta na innego konsultanta (specjalisty).

Inny przykład kolejkowania dotyczy aplikacji realizującej kopiowanie plików z

serwerów hostujących w warunkach pozwalających na efektywniejsze wyko-
rzystanie internetu przy ograniczonej szybkości transmisji, minimalizacji kosztów i
czasu. Oczywiście ustawianie w kolejce plików oczekujących na skopiowanie nie
przyśpieszy prędkości, która nadal zależeć będzie od lokalnego dostawcy internetu
ale jednak można oszacować koszty związane z płatnym kontem, ograniczeniem
prędkości, czasem oczekiwania na przyjęcie kolejnego zlecenia i maksymalną
ilością plików ustawionych przez administratora strony dla darmowych kont a
także własnych strat czasu związanych z oczekiwaniem na kolejne pliki i
zatrzymaniem obsługi.

Omawiane przykłady możliwe do symulacji dotyczą ogólnej problematyki

problemów decyzyjnych i szeregowania zadań. Przykładem może być kolejne
opracowanie (http://www.jstor.org/pss/2629693), którego celem jest określenie i
ocena poziomu wykorzystania w szpitalu sal operacyjnych i zaplecza (gabinetów
lekarskich, sal operacyjnych, laboratoriów, pomieszczeń zabiegowych) a także sal
chorych pod różnymi względami mającymi na celu dobro pacjenta. Kryteria oceny
biorą pod uwagę ograniczenia, dotyczące konkretnego szpitala, z którego uzyskano
dane empiryczne, jednak model i podejście zostały zaprojektowane z myślą o
ogólnych zastosowaniach. Model został zaprogramowany w GPSS, w badaniach
symulacyjnych przyjęto losowe wartości parametrów modelu ograniczone otrzy-
manymi z pomiarów zakresami i kryteria optymalizacji, pochodzące z aktywnej
działalności szpitala "w świecie rzeczywistym". Uzyskane wyniki zostały
zastosowane i potwierdziły, że efektywność wykorzystania zasobów może być
uzyskana przy jednoczesnym spełnieniu ograniczeń podyktowanych normalną
działalnością szpitala i koniecznością obniżenia kosztów.

W momencie, podejmowania decyzji, bardzo często nie wiemy, czy ta decyzja

jest optymalna. Dopiero po pewnym czasie, czyli po uzyskaniu większej ilości
informacji, dowiadujemy się o trafności naszego wyboru. Celem może być taka
strategia decydowania aby zminimalizować straty w pesymistycznym przebiegu
przyszłych wydarzeń.

.

85

Tematyka problemów decyzyjnych jest ściśle powiązana ze sferami technologii

informatycznych, ekonomii i zarządzania, dotyczy zagadnień związanych z
pozyskiwaniem danych i ich obiektywną analizą, która pozwala na podejmowanie
optymalnych decyzji.

W sferze technologii informatycznych przykładem jest problem kolejkowania

zadań w maszynie wieloprocesorowej. System w momencie uzyskania nowego
zadania do zrealizowania, musi przydzielić mu procesor, który będzie go w stanie
efektywnie zrealizować. Problem polega na tym, że podjęta decyzja może być
nieoptymalna w stosunku do danych nadchodzących w przyszłości, których nie
znamy. W takiej sytuacji, standardowe rozwiązania są nieadekwatne. Potrzebne
jest stworzenie mechanizmów, które dawałyby natychmiastową odpowiedź, nawet
przy niepełnej informacji i minimalizowałyby one straty spowodowane przyszłym,
niekorzystnym scenariuszem wydarzeń. Celem w tym przypadku byłaby minima-
lizacja ilości potrzebnych procesorów oraz optymalizacja czasu i efektywności
systemu. Przykładem z zakresu ekonomii i zarządzania może być problem
zarządzania przepływem produktów w firmie, dopasowania produkcji do potrzeb
rynku, zarządzanie transportem, środkami produkcji, czy też zasobami ludzkimi.
Nieznajomość przyszłych potrzeb rynku, pociąga za sobą brak wiedzy, otym jak
powinniśmy modyfikować ofertę, a tym samym utratę sprawności i zwiększenie
kosztów w takich czynnościach wewnątrz firmy jak przepływ pracowników,
danych, półproduktów i środków produkcji.

Poza tym utrudnia planowanie w doszkalaniu pracowników i zakupu nowych

urządzeń. Problemy te na ogół są rozwiązywane przez ludzi opierających się na
doświadczeniu i intuicji. To niestety z powodu braku wsparcia oprogramowaniem
opartym na solidnych podstawach teoretycznych prowadzi do utraty optymalności
stosowanych dotychczasowych rozwiązań.

Opracowanie odpowiedniego programu z wykorzystaniem języka symulacyj-

nego może posłużyć w realizacji praktycznych celów. Bazując na nich zaistnieje
możliwość tworzenia oprogramowania wspomagającego mechanizmy decydowa-
nia w firmach i innych organizacjach. Poza tym będą przydatne w komputerowych
systemach wieloprocesorowych usprawniając i zmniejszając koszty działania
systemu.

4.2 Język GPSS

4.2.1 Wprowadzenie

GPSS (ang. General Purpose Simulation Software - pierwotnie Gordon's

Programmable Simulation System) jest językiem programowania stosowanym do
symulacji komputerowej procesów w szczególności procesów dyskretnych. Język
został stworzony w latach 60-tych przez Geoffreya Gordona. Pierwotna nazwa

.

86

została zmieniona, gdy zdecydowano się wydać język jako produkt komercyjny.
Aktualnie są dostępne pełne funkcjonalnie darmowe wersje edukacyjne jedynie o
ograniczonej pojemności modelu. Język w jego obecnym kształcie jest wynikiem
ponad kilkudziesięciu lat ewolucji. Podczas gdy GPSS ma swoje korzenie w
początkach systemów typu mainframe, to jego podstawowe idee okazały się
odpowiednie do wykorzystania we współczesnych problemach z wykorzystaniem
nowoczesnych środowisk informatycznych. Popularność GPSS wynika w części, z
dużej mocy wyrażania rzeczywistości (język, reguły składni i semantyki);. Aby
osiągnąć podobny cel krótki i łatwy do zrozumienia model GPSS, wymagałby
wielu stron kodowania w języku algorytmicznym (C, Pascal, Fortran). Użytkownik
pakietu symulacyjnego GPSS może skoncentrować się na istotnych zagadnieniach
dotyczących modelu ponieważ elementy samego języka zbierają statystyki,
generują tabele wyników i wykonują wiele żmudnych i złożonych zadań.

Język posiada wiele realizacji (GPSS/PC, GPSS/W, GPSS/H), pomiędzy

którymi występują nieznaczne różnice – jednak podstawowe zasady są wspólne

Symulacja z zastosowaniem języka GPSS, opiera się na metodzie interakcji

procesów, w którym połączono zalety metody planowania z metodą przeglądu i
wyboru zdarzeń zapewniając efektywne obliczenia zarówno dla dużej ilości zadań i
zdarzeń (patrz rozdz. 5). Ogólnie symulacja polega na grupowaniu działań w
procesy wykonywane na pojedynczych dynamicznych obiektach (transakcjach),
które po wprowadzane do systemu, są przekazywane przez kolejne bloki z
rejestrowaniem ich stanu od chwili pojawienia się w systemie aż do chwili zaniku.

Na wstępie omówione zostaną ogólne własności języka i przedstawione

niektóre podstawowe pojęcia, umożliwiające wstępne zrozumienie szerokiego
zakresu zastosowań, mocy i łatwości obsługi tego języka w symulacji.

GPSS dostarcza zestaw abstrakcyjnych elementów różnych typów i zestaw

operacji, określanych jako bloki, które wykonują określone czynności dla tych
elementów. Transakcja jest takim elementem, który przechodzi przez ciąg bloków,
które zostały wprowadzone do modelu badanego systemu. Stan elementu modelu
określa szczegóły sposobu działania bloku danego typu. Na przykład blok, który
daje możliwość pewnej transakcji na przejęcie kontroli nad wybranym sprzętem
nie pozwoli tego dokonać, jeżeli ten sprzęt jest już w stanie maksymalnej zajętości.

GPSS udostępnia wiele różnych rodzajów obiektów. Obiekt reprezentujący

wyposażenie lub urządzenie (ang. facilities np: maszyna, procesor, pojazd), może
być w danej chwili używane (zajęte) przez co najwyżej jedną transakcję. Z kolei
obiekt cechujący się pewną ograniczoną pojemnością może reprezentować
magazyn (ang. storage) ale także np: pamięć, ładowność pojazdu czyli obiekty,
których pojemność określona jest wymaganiami projektowanego systemu.
Wreszcie, przełącznik logiczny jest prostym elementem (on/off), który może być
ustawiany i testowany w celu dokonania zmiany ścieżki przepływu transakcji
poprzez bloki modelu.

.

87

Należy podkreślić, że wszystkie omówione obiekty są abstrakcyjne. W

symulacji konkretnego modelu np. funkcjonowania fabryki, transakcje mogą
stanowić montowane jednostki, urządzenia mogą reprezentować spawającego
robota a przełączniki logiczne mogą być wykorzystane do symulacji awarii
maszyny lub do jej sterowania .

W przypadku modelowania sieci szybkiej komunikacji, transakcjami mogą być

przesyłane wiadomości, urządzeniami linie przesyłowe a z kolei magazyny
stanowić bufory pamięci. Niezależnie od zastosowań, obiekty GPSS stanowią
naturalne równolegle działające modele elementów i procesów badanego lub
projektowanego systemu e świecie rzeczywistym.

W trakcie przemieszczania się transakcji poprzez bloki, realizacja określonych

działań na obiektach, jest zapamiętywana w postaci wielu rodzajów statystyk
dostępnych w trakcie symulacji jak i włączanych automatycznie do generowanego
raportu w chwili zakończenia symulacji (np: średnia ilościowa, średni czas
obecności, wartość maksymalna itp). Dodatkowe wyniki i raporty są tworzone
przez procesy kolejkowe, które generują odpowiednie raporty statystyczne, takie
jak: maksymalna i średnia długość kolejki, średnie opóźnienie, odsetek transakcji,
które zostały opóźnione lub natychmiast obsłużone. Wyniki są gromadzone w
postaci wartości próbek w tabeli częstotliwości wystąpień (histogramie).

GPSS zapewnia zasadniczy mechanizm kontroli, który jest przezroczysty dla

użytkownika, ale gwarantuje, że współzawodnictwo pomiędzy transakcjami (na
przykład za korzystanie z obiektu) jest arbitralnie rozstrzygane i w ten sposób
transakcje są przenoszone przez bloki modelu w sposób uporządkowany i
efektywny. Ten mechanizm kontroli jest zarządzany także przez zegar GPSS’a,
który stanowi podstawę czasu symulacji modelu

Zegar GPSS’a jest także abstrakcyjny, mierząc czas w umownych jednostkach

zegarowych, interpretowanych odpowiednio przez projektanta. W modelu
procesów produkcyjnych jednostka zegarowa może odpowiadać sekundzie lub
minucie, podczas gdy w sieci komunikacyjnej bardziej odpowiednia może być
wyższa rozdzielczość np. rzędu milisekund. Z kolei w systemie logistycznego
zaopatrzenia będzie wymagana bardzo niska rozdzielczość rzędu godziny lub doby.

Zdefiniowane funkcje wspomagają realizacje różnych relacji w obliczeniach

numerycznych. Mogą one być wykorzystywane do generowania zmiennych
losowych z teoretycznych lub empirycznych rozkładów prawdopodobieństwa.
Zmienne losowe można wykorzystać do zmiany zachowania transakcji w
zależności od zachowania się całego systemu, wybranych obiektów lub atrybutów
transakcji.

Wartości zmienne są używane do wykonywania obliczeń arytmetycznych we

wszystkich implementacjach GPSS, przy czym charakteryzują się one
zróżnicowaną elastycznością w różnych w wersjach języka GPSS. GPSS/W,
GPSS/VX i GPSS/C pozwala na używanie wyrażeń arytmetycznych wszędzie tam,
gdzie jest dozwolone używanie wartości stałych.

.

88

Niektóre przypadki modelowanych sytuacji mogą skorzystać z koncepcji

zawartych w grupach jednostek jednakowego typu a innych sytuacjach korzystne
będzie użycie bloków operujących na pojedynczych elementach.

Transakcja ma własny zestaw atrybutów numerycznych oraz prywatną nazwę

parametru, którą można wykorzystać do przechowywania różnych informacji
wymaganych przez użytkownika, takich jak numer identyfikacyjny części, rozmiar
lub waga przedmiotu reprezentowanego przez transakcję.

Szeroki zestaw standardowych atrybutów numerycznych (SNA) zapewnia

wygodny dostępu do zapisu składników modelu, które mogą być używane
wszędzie tam gdzie jest dopuszczone użycie wartości numerycznych. Przykładowo
jeżeli zmienna Q$OBS reprezentuje długość kolejki to może być użyta w prostej
sytuacji podjęcia decyzji o wyborze kolejki w bloku testującym

TEST L Q$OBS, FN$DOP, WYJSCIE

Przykładowe parametry bloku TEST pozwalają transakcji na przejście jeśli

aktualna długość kolejki o nazwie OBS jest mniejsza niż wartość zwracana przez
funkcję DOP lub w przeciwnym wypadku przekierowuje ją do bloku WYJSCIE. Z
kolei funkcja DOP może zwrócić wartość zmiennej losowej o dowolnym
rozkładzie prawdopodobieństwa, wartość zmiennej z pory dnia czasu
symulacyjnego lub wartość zależną od aktualnego parametru innych urządzeń np
pojemności (reprezentowanej przez parametr transakcji). Pierwszy znak wraz ze
znakiem dolara oznacza odniesienie się do predefiniowanych nazw systemowych.

Oprogramowanie symulacyjne GPSS zapewnia możliwość interaktywnego

śledzenia, które pozwala na ustawienie pułapki w modelu oraz obserwację
parametrów obiektów modelu podczas krokowego przebiegu symulacji. Każda
kolejna

wersja

pakietu

symulacyjnego

opartego

na

języku

GPSS,

wprowadza dodatkowe innowacyjne narzędzia przeznaczone do debugowania w
sposób coraz bardziej efektywny. Uwarunkowane pułapki i animowane prezentacje
pozwalają na optymalizację procesu projektowania a dla gotowego modelu skrócić
rzeczywisty czas obliczeń przebiegu symulacji.

Wstępny prosty przykład pozwoli na zapoznanie się z elementarnymi zasadami

programowania i podstawowymi blokami języka GPSS World. Program modeluje
obsługę sprzedaży biletów dla klientów oczekujących w indywidualnych kolejkach
do trzech kas. Założono że obiekty reprezentują kasjerów biletowych obsługu-
jących transakcje klientów.
Przykład nr 1

01 SIMULATE
02 TSObs EQ U 30 ; czasu sredni obsługi
03 DTWej FUNCTION RN1,C3 ;funkcja ciagła rozkład równo -
04 0,4/.5,2/1,1 ; mierny wart. 3 odcinki liniowe
05 GENERATE 10,FN$DTWej
06 QUEUE Kolejka
07 SEIZE Kasa

.

89

08 DEPART Kolejka
09 ADVANCE UNIFORM(2,TSObs-2,TSObs+2)
10. RELEASE Kasa
11. TERMINATE 1
12. START 100

W kolejnych wierszach modelu o numerach:
0

1.

SIMULATE

jest opcjonalną instrukcją oznaczającą początek symulacji,

02.

EQU

określa parametr TSObs - wartość średnią czasu obsługi w kasie biletowej,

03,04. linie definiujące funkcję, która generuje przekształcenie ciągłej zmiennej

losowej z przedziału [0, 1) z pierwszego strumienia (

RN1

), do zależności wg

wartości zadanych punktów (z interpolacją wartości pośrednich),

05. klienci przybywają średnio co 10 jednostek czasu z odchyleniem określonym

przez funkcje w liniach 03 i 04,

06. ustawienie się klienta na końcu kolejki,
07. kiedy kasa jest dostępna

następuje jej zajęcie oraz

0

8. opuszczenie kolejki, z zapisem czasu w statystykach kolejki,

09. zachodzi opóźnienie średnio o TSObs jednostek z odchyleniem o 2 jednostki

w obu kierunkach, związane z czasem obsługi klienta w kasie.

10. zwolnienie kasy i z umożliwieniem zajęcia jej przez kolejnego klienta.
11. zakończenie jednego cyklu obsługi klienta.
12. uruchomienie symulacji dla 100 klientów do momentu aż wszyscy zostaną

usunięci z procesu osiągając kolejno blok

TERMINATE 1

.

W linii 09 okres czasu w którym kasa jest zajęta jest losowo wybrany z

jednakowym prawdopodobieństwem (wg rozkładu równomiernego) z przedziału
od 28 do 32 jednostek a liczba określająca aktualny czas opóźnienia jest pobierana
z drugiego strumienia liczb losowych, a więc w stosunku do czasów wejścia,
czasy opóźnień są statystycznie niezależne.

Standardowy raport zawiera nagłówek, listę nazw stałych przypisanymi wartoś-

ciami i zmiennych z identyfikatorami numerycznymi oraz szereg danych statys-
tycznych z przebiegu symulacji np: ENTRY COUNT – liczba wejść do każdego
bloku, nazwa kolejki (QUEUE) i maksymalna jej długość.

GPSS World Simulation Report - s0bilet

Saturday, October 15, 2010 01:19:58

START TIME END TIME BLOCKS FACILITIES STORAGES
0.000 2998.582 7 1 0

NAME VALUE
DTWEJ 10001.000
KASA 10003.000
KOLEJKA 10002.000

.

90

TSOBS 30.000

LABEL LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY
1 GENERATE 136 0 0
2 QUEUE 136 35 0
3 SEIZE 101 1 0
4 DEPART 100 0 0
5 ADVANCE 100 0 0
6 RELEASE 100 0 0
7 TERMINATE 100 0 0

FACILITY ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY
KASA 101 0.997 29.589 1 101 0 0 0 35

QUEUE MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY
KOLEJKA 36 36 136 1 18.097 399.009 401.965 0

W modelu może być wiele równolegle przebiegających procesów w odrębnych

segmentach, ale pomiędzy nimi mogą występować wzajemne interakcje a o tym
który proces decyduje o zakończeniu symulacji określa sposób usuwania transakcji
w bloku

TERMINATE.

Ponadto w przypadku konieczności wyboru decyzji o

pierwszeństwie wykonania operacji można określić jej priorytet. Omówione
problemy wyjaśnia prosty przykład:
Przykład nr 2;

; proces 1 który decyduje o zakonczeniu symulacji
; gdy inny nie zmienia swojego licznika
01 GENERATE 10,0 ; priorytet domyslny 0
02 TERMINATE 1 ; zmienia licznik tranzycji

; proces 2
03 GENERATE 20,0,,,-1 ; priorytet -1 i 49 transakcji

; lub tymczasowo w komentarzu

04 ; GENERATE 20,0,,,1 ; priorytet 1 to 50 transakcji
05 TERMINATE

; nie zmienia licznika tranzycji

06 START 100

; zakonczenie po 1000 jedn. czasu

4.2.2 Opis podstawowych elementów języka GPSS ver World

Pełny opis języka zawiera ponad kilkadziesiąt instrukcji, z których większość

ma od 2 do 7 parametrów. Jest to wiedza, która może być wykorzystana tylko po
jej bardzo dobrym opanowaniu i będzie użyteczna w przypadku modelowania
złożonych i skomplikowanych procesów - wymaga sporego niekiedy długotrwa-
łego procesu szkolenia i praktycznego doświadczenia. Poniżej przedstawione
zostały tylko najbardziej podstawowe i najczęściej używane elementy języka oraz
ogólne zasady jego używania, których zastosowanie będzie wystarczające do
rozwiązania załączonych zadań. Pełny opis parametrów wraz z przykładami
załączono w pkt 6. Z kolei kompletny opis języka, można znaleźć w bogatej
dokumentacji dołączonej do pakietu GPSS World.

.

91

Obiekty blokowe

W GPSS obiekt blokowy (ang. Block entity) jest podstawowym elementem

strukturalnym programu symulacyjnego. Określenie to jest związane z
możliwością przedstawienia programu symulacyjnego w postaci schematu
blokowego (patrz rozdz. 4.5). Bloki są identyfikowane poprzez nazwy, które
sugerują ich zastosowanie i wykonywanie pewnych akcji np: generowanie, zajęcie
lub zakończenie (zwykle napisane są dużymi literami odpowiednio GENERATE,
SEIZE, TERMINATE). Każdy z bloków ma listę argumentów oddzielonych
przecinkami. Kolejność pozycji argumentów określa zwykły porządek
alfabetyczny ich nazw oznaczonych dużymi literami alfabetu. Bloki mogą mieć
unikalne etykiety, których nazwa sugeruje wykorzystanie bloku w procesie
rzeczywistym. Blok ma następującą składnię.

etykieta

TYPBLOKU A, B, C, ...

; komentarz po średniku

Argumenty, które mogą być pominięte przyjmują domyślne wartości ale ich

pozycje muszą być zaznaczone przez przecinki z wyjątkiem pomijania kolejno
operatorów od końca np w przykładzie nr 2 linia 03. Gdy wszystkie argumenty
końcowe są puste mogą być pominięte wraz z przecinkami.

Systemowe atrybuty numeryczne (SNA)

Systemowe atrybuty numeryczne (SNA - System Numerical Attribute) są

predefiniowanymi zmiennymi stanu symulacji, które są dostępne do wykorzystania
podczas symulacji. Udostępniają one wartości numeryczne lub łańcuchowe i mogą
być stosowane w instrukcjach i wyrażeniach GPSS. Są one ściśle związane z
obiektami i ich znaczenie najlepiej rozpatrywać z podmiotami, które je opisują.

Transakcje (ang. Transaction)

Transakcja jest w GPSS obiektem dynamicznym ze ściśle określonym zbiorem

atrybutów, które są określane także mianem parametrów (ang. parameters)
Transakcje są tworzone albo pojedynczo lub w zestawach w bloku GENERATE a
następnie mogą w symulacji przechodzić przez kolejne bloki niekiedy wraz z
innymi obiektami GPSS. Pojedyncza transakcja może się składać się z wielu
poszczególnych obiektów np: wiele produktów transportowanych przez pojazd.

Sposobem na identyfikację transakcji w systemie (procesie) rzeczywistym i tym

samym konieczność wprowadzenie jej do modelu GPSS jest jej słowny sposób
opisu. Najczęstsze takie opisy zawierają użycie wyrażeń takich jak "wejście do
czegoś”, przejście przez coś, jest zawarte w czymś, nabycie czegoś itp”., w których
tych pojawia się czasownik. Ten czasownik często może reprezentować typ bloku
jak np w określeniu, „Transakcja zajęła urządzenie” (ang. Transaction SEIZE’s
Facility), która bezpośrednio reprezentuje operację na typie bloku SEIZE. Każda
transakcja w modelu może zawierać dokładnie jeden blok, ale większość bloków

.

92

może zawierać wiele transakcji. Każda transakcja wchodzi jeden blok, potem
następny, i tak dalej, aż do jej usunięcia (ang. TERMINATE) lub zakończenia
symulacji. Transakcje czasami są w stanie oczekiwania przed blokiem, aż
odpowiednie korzystne warunki zostaną spełnione uprawniające na wejście do
niego. Bloki zapisane w kolejnych liniach programu GPSS przepuszczają kolejne
transakcje, pod warunkiem, że nie natrafią na blok TRANSFER, który może ją
przesłać do innego bloku nie będącego w aktualnej sekwencji .

GENERATE - blok tworzący transakcje, które będą się pojawiały w symulacji w
określonym odstępie czasowym, ilości i priorytecie.
GENERATE A,B,C,D,E

A – czas pomiędzy dwoma kolejnymi transakcjami (odstęp), (A=0)
B – rozrzut, odchylenie, (tolerancja) dla A który jest wartością średnią rozkładu

równomiernego, (B=0)

C – opóźnienie dla pierwszej transakcji, D – maksymalna liczba ograniczająca

liczbę wprowadzonych transakcji, (D = )

E – priorytet transakcji (E = 0 do 9)
Przykłady
GENERATE 50

;transakcja jest generowana co 50 jednostek

GENERATE 20, 2.5 ; losowy o rozkładzie równomiernym odstęp czasu w

; przedziale [17.5, 22.5]

GENERATE (Exponential(1,20,2)); losowy o rozkładzie ekspotencjalnym odstęp

;czasu pomiędzy generowanymi transakcjami

GENERATE , , , 1

;wygenerowanie pojedynczej transakcji

ASSIGN – blok przypisujący lub modyfikujący wartość parametru transakcji, -
jeżeli parametr nie istnieje to jest on tworzony:
ASSIGN A, B, C

A - numer parametru lub nazwa aktywnej transakcji opcjonalnie zakończona

znakiem + lub -, znak +/- oznacza, że wartość argumentu B należy
odpowiednio dodać do / odjąć od oryginalnej wartości parametru A.

B - wymagany argument (nazwa, numer, string, wyrażenie w nawiasach lub SNA)
C - opcjonalna nazwa funkcji, której wartość będzie mnożona przez par. B

Przykłady

ASSIGN Ilość+, 1

; inkrementacja licznika Ilość o 1

ASSIGN P1, 10

; pierwszemu parametru transakcji przypisano wartosc 10

Stanowisko obsługi jednokanałowej - FACILITY

Stanowisko obsługi jest obiektem, posiadającym kilka cech, z których

najważniejszym jest własność zajętości. Stanowisko jest tworzone automatycznie
gdy pierwsza transakcja osiągnęła blok, który korzysta z tego stanowiska.
Stanowiska nie muszą być deklarowane i definiowane przez instrukcje sterujące.

.

93

GPSS posiada kilka bloków, które używają i wykonują pewne akcje dotyczące
stanowisk:

SEIZE A

- zajęcie stanowiska A;

RELEASE A

- zwolnienie stanowiska jednokanałowego A.

A - nazwa/numer stanowiska,urządzenia lub wyposażenia)

Przykłady:

SEIZE Kasa

; ustawienie się przy okienku o nazwie Kasa

RELEASE Kasa

; odejście od okienka o nazwie Kasa

FAVAIL A

Blok, który sprawia, że wskazane jednokanałowe A jest dostęne

Przykład:

FAVAIL Kasa1 ;

Ustawienie dostępności do stanowiska Kasa1.

FUNAVAIL (Facility Unavailable). jednokanałowe będzie niedostępne i określa
los tak zatrzymanych transakcji.

FUNAVAIL A,B,C,D,E,F,G,H - zablokowanie stanowiska jednokanałowego
A – nazwa urządzania, stanowiska jednokanałowego
B – tryb traktowania transakcji: usunięcie (RE), kontynuacja (CO),
C – nr bloku dla przerwanej transakcji,
D – nr parametru przechowującego czas pobytu (gdy RE),
E – tryb traktowania dla wywłaszczonych transakcji (RE, CO),
F – nr bloku dla wywłaszczonej transakcji,
G – tryb traktowania dla transakcji opóźnionej,
H – numer bloku dla transakcji opóźnionej

Przykłady:

A B C D E F G H

FUNAVAIL Kasa1, RE, Kasa2, 30, RE, Rez, CO

Ustawienie niedostępności do stanowiska Kasa1.
C = Kasa2 - transakcja z Kasa1 jest przesyłana do bloku Kasa2,
D = 30 – parametr który przechowuje czas pobytu transakcji,
F = Rez - transakcje wywłaszczone wcześniej są przesyłane do bloku Rez
FUNAVAIL Kasa ; ustanowienie niedostępności stanowiska Kasa
Standardowe Atrybuty Numeryczne (SNA) – dla stanowiska jednokanałowego

FNrObiektu – Zwraca stan zajętości stanowiska
FNrObiektu zwraca wartość 1 gdy stanowisko jest aktualnie zajęte
oraz wartość 0 w przeciwnym wypadku
NrObiektu - symbol oznaczajacy liczbę/ nazwę obiektu.

Stanowisko wielokanałowe (grupa urządzeń) - STORAGE

Stanowisko wielokanałowe jest złożone z wielu nierozróżnialnych i

równouprawnionych jednostek pozwalających na obsługę wielu transakcji,
Stanowisko musi być jawnie zadeklarowane z podaniem rozmiaru przez instrukcję:
Nazwa STORAGE A

Nazwa - obowiązkowa etykieta reprezentująca identyfikator stanowiska

.

94

A – wymagany rozmiar (pojemność, ilość stanowisk, liczba jednostek składo-

wania itp., dostępnych dla transakcji).

Bloki GPSS, które mogą obsługiwać stanowiska wielokanałowe:
ENTER A,B uwarunkowane wejście i zajęcie stanowiska wielokanałowego

A - nazwa (identyfikator) stanowiska wielokanałowego
B - zajęcie B jednostek (domyślnie 1) ;
warunki : wolne B jednostek i dostępność stanowiska A

LEAVE A,B - zwolnienie stanowiska wielokanałowego

A - nazwa (identyfikator) stanowiska wielokanałowego
B - zwolnienie B jednostek (domyślnie B=1) ;

SUNAVAIL A - blokuje stanowisko wielokanałowe (jest niedostępne)

A - nazwa (identyfikator) stanowiska wielokanałowego

SAVAIL A - odblokowanie stanowisko wielokanałowego ( jest udostępnione)

A - nazwa (identyfikator) stanowiska wielokanałowego

Ogólnie bloki ENTER i LEAVE maja po dwa argumenty, z których pierwszy

jest wymagany i wskazuje stanowisko wielokanałowe, które jest odpowiednio
zajmowane i zwalniane, natomiast drugi to liczba zajmowanych i zwalnianych
przez transakcję kanałów. Jeżeli tylko jeden kanał ma być zajęty lub zwolniony to
drugi argument można pominąć.

Bloki SAVAIL i SUNAVAIL wymagają tylko jednego argumentu, który repre-

zentuje blokowane i udostępniane stanowisko wielokanałowe. Gdy transakcja
pojawi się na wejściu do stanowiska wielokanałowego wykorzystuje (zajmuje)
jeden lub więcej kanałów określonych przez argument B. Transakcja może mieć
zakazane wejście do bloku ENTER jeśli on nie spełnia warunków na jej obsługę,
jest zatrzymywana i oczekuje do czasu aż inne transakcje zwolnią kanały przez
wejście do bloku LEAVE.

Praktycznie bloki ENTER i LEAVE są używane do aktualizacji statystyk

związanych z obsługą stanowisk wielokanałowych, Szereg zmiennych SNA służy
do ich zapamiętania np są to:
RNrObiektu – Pozostała do wykorzystania (Rest) przez transakcje ilość kanałów

na stanowisku wielokanałowym NrObiektu

SNrObiektu – Użyta (zmagazynowana – Store) aktualnie ilość kanałów przez

transakcje na stanowisku wielokanałowym NrObiektu.

SANrObiektu – Średnia użyta (zmagazynowana – Store Average) aktualnie ilość

kanałów przez transakcje na stanowisku wielokanałowym NrObiektu.

SCNrObiektu - Ilość użytych kanałów (Store Count) na stanowisku

wielokanałowym NrObiektu

SENrObiektu - Sprawdza niedostępność stanowiska (Store Empty) przyjmując

wartość równą 1 jeśli stanowisko wielokanałowe NrObiektu jest całkowicie
niewykorzystane a wartość 0 w przeciwnym przypadku.

SFNrObiekt - Sprawdza dostępność stanowiska (Store Full) przyjmując wartość

równą 1 jeśli stanowisko wielokanałowe NrObiektu

.

95

jest całkowicie wykorzystane (pełne) a wartość 0 w przeciwnym przypadku

SRNrObiekt – Stopień wykorzystania (ang. Utilization) stanowiska
wielokanałowego NrObiekt określający stosunek średniego czasu w którym
stanowisko było zajęte do całkowitego czasu symulacji wyrażona w postaci
ułamka tysięcznego

SMNrObiekt - Maksymalna ilość kanałów używana na stanowisku

wielokanałowym NrObiektu

• STNrObiektu - Średni czas zajętości dla pojedynczego kanału używanego na

stanowisku wielokanałowym NrObiektu

SVNrObiekt - Sprawdza dostępność stanowiska (Store Full) przyjmując wartość

równą 1 jeśli stanowisko wielokanałowe NrObiektu

jest dostępne a wartość 0 w przeciwnym przypadku

Kolejki i bloki kolejek

Kolejki są używane głównie do zbierania danych statystycznych, takich jak

aktualna długość, ilość wejść, średni czas pobytu i inne. Śledzą one także
transakcje, które są zablokowane przed wejściem na zajęte stanowisko
jednokanałowe i pełne stanowisko wielokanałowe. Analogicznie jak stanowisko
jednokanałowe kolejka jest tworzona gdy pierwszy obiekt transakcji osiągnie blok,
który używa kolejki.
Bloki obsługujące obiekty w kolejce:
QUEUE blok w którym zachodzi wzrost zawartości obiektów w kolejce.
DEPART w którym zachodzi zmniejszenie zawartości obiektów w kolejce.
Bloki te mają dwa argumenty:
A - nazwę lub numer z kolejki
B - opcjonalna liczba podmiotów (domyślnie 1) wchodzących lub

wychodzących z kolejki.

Bloki z obsługą kolejki są ściśle jest związane z blokami obsługi stanowisk i ich
operacje są naprzemienne tj. SEIZE lub ENTER pomiędzy QUEUE i DEPART a
następnie RELEASE lub LEAVE. W przykładzie 1 obsługi w kasie biletowej
osoba w kolejce (linia 08) opuszcza ją dopiero po pomyślnym podejściu do kasy
(linia 07) .

Z obsługą kolejek związanych jest szereg zmiennych SNA które są używane do
generowania danych statystycznych Przykładowo są to:

QNrObiektu - aktualna długość kolejki NrObiektu określona przez licznik ilości

transakcji

QANrObiektu - średnia ważona w czasie długość
QC NrObiektu - Suma wszystkich wejść do kolejki NrObiektu.
QMNrObiektu - Maksymalna długość kolejki NrObiektu

.

96

QTNrObiektu - Średni czas pobytu transakcji w kolejce NrObiektu z

uwzględnieniem wszystkich transakcji.

QTABLE - dane statystyczne gromadzone w postaci rozkładów częstotliwości za
pomocą instrukcji sterującej QTABLE powalającej na ich inicjalizację
Nazwa QTABLE A, B, C, D

A - nazwa bloku kolejki
B - górna granica zapisu pierwszego zakresu częstotliwości.
C - rozmiar zakresu częstotliwości.
D – ilość zakresów częstotliwości.

ADVANCE
Blok ADVANCE jest jedynym blokiem, który jest ściśle związany z postępem
czasu. Gdy transakcja dochodzi do bloku ADVANCE jest ona opóźniana o
określoną ilość czasu symulacyjnego o a następnie przechodzi do następnego bloku.
Składnia bloku jest następująca:
ADVANCE A, B

A - wymagany średni przyrost czasu.
B - opcjonalnie rozrzut, odchylenie, (tolerancja) dla A który jest wart średnią
rozkładu równomiernego, (B=0)

Przyrost czasu można obliczyć na kilka sposobów. Jeśli jest tylko argument A to
określa on deterministyczny przyrost czasu. Jeśli są oba argumenty A i B a B nie
jest funkcja to przyrost czasu jest liczbę losową między A - B i A + B włącznie.
Jeśli B jest funkcją to jej wartość po pomnożeniu przez argument A określa
przyrost czasu, który może być zależny od innych zmiennych w symulacji.

FUNCTION
Funkcje GPSS funkcji są używane do określenia wartości na podstawie innych
argumentów np liczb losowych, a także właściwie każda wartość SNA może być
używana jako argument. Funkcja jest określona przez linię nagłówka z poleceniem
FUNCTION z parametrami i ewentualnym komentarzem oraz w kolejno
następujących po sobie liniach specyfikację danych w postaci pary wartości x, f(x)
oddzielonych znakiem / .
Nazwa FUNCTION A, B

; komentarz

x1,y1 / x2,y2 ...

... xn,yn

A – argument (zmienna niezależny)
B – jest konkatenacją typu funkcji oraz liczby par, która pojawią się w specyfikacji
danych będących liczbami stałymi, nazwami lub zmiennymi SNA.
Istnieje 5 różnych typów argumentów funkcji, z których najczęściej ma
zastosowanie: Typ C - funkcja jest ciągła z interpolowanymi liniowo wartościami

.

97

pośrednimi. Jeśli argument zawarty jest w określonym segmencie linii, jest
wykonywana interpolacja liniowa. Na przykład dla funkcji
Output FUNCTION V$Input,C5
1.1,10.1/20.5,98.7/33.3,889.2
93.5,2003/200.4,8743
jeśli V$Input wynosi 25, to FN$Output zwraca wynik obliczenia:

98,7 + (889.2-98.7) * (25-20.5) / (33.3-20.5).

Typ D - dyskretne wartości funkcji - każda wartość argumentu lub gęstości
prawdopodobieństwa ma przypisaną osobną wartość.

Sterowanie kolejnością przepływu transakcji.
TRANSFER
Blok TRANSFER umożliwia przeskok transakcji do innego bloku nie będącego w
sekwencji. Może on być: bezwarunkowy, warunkowy lub probabilistyczny.
TRANSFER A, B, C
Ogólnie tryb działania pracy dotyczący transferu określa parametr A a B i C to
numery bloków lub ich lokalizacje.
Tryb bezwarunkowy : Parametr A – jest pusty a aktywna transakcja zawsze
przechodzi do bloku B - transakcja nigdy uzyskuje odmowy wejścia do bloku
TRANSFER ale jeśli dostaje odmowę wejścia do bloku docelowego B to pozostaje
w bloku TRANSFER.
Tryb losowy: Parametr A określa prawdopodobieństwo (0–1) przy którym aktywna
transakcja przechodzi do bloku określonego argumentem C oraz z prawdopodo-
bieństwem 1–A do bloku określonego przez operand B. Jeśli parametr B jest pusty
to transakcja przechodzi do następnego bloku sekwencyjnego (NSB) - jest to
najczęstsze zastosowanie bloku TRANSFER.
Tryb warunkowy: Gdy parametr A jest równy BOTH to blok określony przez
parametr B jest testowany i gdy są warunki na przyjęcie aktualnej transakcji to
następuje jej przejście do tego bloku W przeciwnym wypadku testowany jest blok
C i on przejmuje transakcję. Kiedy żaden ze wskazanych bloków nie może przejąć
transakcji, czeka ona w bloku TRANSFER na spełnieni któregokolwiek warunku
Poniżej opis indywidualny parametrów:

A – brak parametru oznacza przejście bezwarunkowe do etykiety w parametrze B

albo słowo BOTH (przejście warunkowe) albo wartość prawdopodobieństwa
przejścia np wartość p,

B – etykieta przejścia bezwarunkowego albo pierwsza etykieta dla przejścia

warunkowego albo etykieta przejścia o prawdopodobieństwie 1-p dla transakcji,

C – druga etykieta przejścia (przejście warunkowe)

albo etykieta przejścia o prawdopodobieństwie p

Przykłady
TRANSFER , Wyjscie ; przejście bezwarunkowe do bloku z etykietą Wyjscie
TRANSFER BOTH, S1,S2 ;przejście warunkowe – w pierwszej kolejności

.

98

do bloku z etykietą S1, a gdy jest niemożliwe do bloku z etykietą S2

TRANSFER .35, S1, S2 ; przejście losowe z prawdopodobieństwem 0.65
do bloku z etykietą S1 i z prawdopodobieństwem 0.35 do bloku z etykietą S2
TEST
Blok TEST porównuje wartości, zwykle zmienne SNA i steruje przejściem
transakcji na podstawie wyników porównania z użyciem zwykłych operatorów
relacyjnych. Jest to kolejny sposób, aby umożliwić niesekwencyjne działania
symulacji. Składnia bloku testującego ma postać:
TEST O A, B, C - sterowanie przejściem transakcji z badaniem warunku;

O – operator warunkowy, typ relacji (G, GE, E, NE, LE, L),

Oznaczenia:
G – większe; GE – większe lub równe; E – równe; NE – nierówne;
LE – mniejsze lub równe; L – mniejsze

A – pierwszy argument relacji (nazwa/numer obiektu, wartość wyrażenia),
B – drugi argument relacji (nazwa/numer obiektu, wartość wyrażenia),
C - etykieta (numer) bloku dla przypadku False.

Przykłady:
TEST LE Q$S1,4,KONIEC

;zajęcie stan. S1, gdy kolejka przed nim jest nie

większa od 4; w przeciwnym przyp. przejście do bloku z etykietą KONIEC
TEST E Steruj, 3, Transport

; gdy kod sterowania Steruj jest równy 3 to

transakcja przechodzi dalej, jeżeli nie, to idzie do bloku Transport

GATE
Blok GATE podobnie jak TEST steruje przejściem transakcji ale na podstawie
stanu urządzeń jest to następny sposób, na niesekwencyjne działanie symulacji.
Składnia bloku testującego ma postać:
GATE O A,B Sterowanie przepuszczeniem transakcji z badaniem warunku;
O – operator warunkowy, kodowanie stanu urządzenia
(FNV, FV, I, LS, LR, M, NI, NM, NU, SE, SF, SNE, SNF, SNV, SV, U),
A – nazwa lub numer obiektu testowanego,
B – etykieta (numer) bloku dla przypadku nieprawdy . Oznaczenia:
Stanowisko Facility:
FNV/FV– (nie)dostępne; NI/I – (nie)jest w przerwaniu; NU/U – (nie)jest w użyciu
Przełącznik Logic switch: LS / LR – ustawienie/ zerowanie
Blok MATCH: NM /M– (nie) posiada powiązaną(ej) transakcję(i)
Stanowisko Storage: SE/SF –jest puste/pełne; SNE/SNF – nie jest puste/pełne ;

SNV/ SV –(nie)jest dostępne; (nie to samo co pełne/puste);

Przykłady
GATE SNF Susz ;Zajęcie stanowiska Susz, gdy jest ono puste (Storage Not Full)
GATE NU Kasa1,Kasa2 ; Przejście do Kasa1, gdy jest wolna (NotUsed) , a w
przeciwnym przypadku przejście do stanowiska Kasa2

.

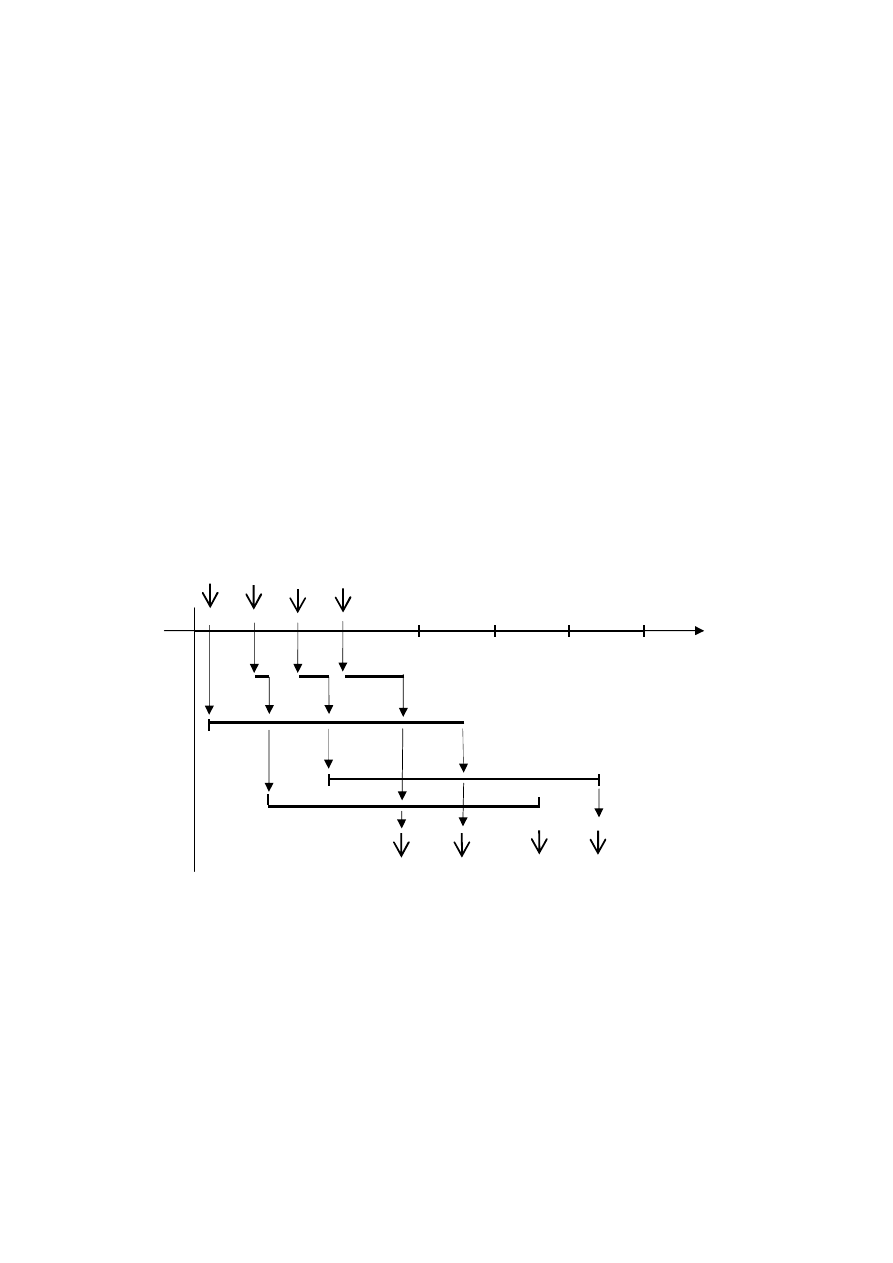
99

4.2.3 Przykłady programów

Przykład 3.
Przykład przedstawia podstawową obsługę bloków jedno i wielokanałowych.
Części z magazynu wejściowego są składowane kolejno na transporterze co 9 min.
skąd po przeniesieniu przez robota poddawane są obróbce mechanicznej przez
okres 12 min. Następnie robot jest zwalniany poprzez pozostawienie części do
pomalowania i wysuszenia na wolnym stanowisku w suszarce na okres 27 min. W
celu zwiększenia przepustowości suszarka może pomieścić równocześnie 2 części.
Gotowe części po wysuszeniu są wyprowadzane na transporter do magazynu
wyrobów gotowych. Należy napisać program modelu systemu w języku GPSS
zakładając pomijalny czas pracy robota oraz przeprowadzić symulację procesu dla
4 identycznych części (zadań) rozpoczynając proces w pierwszej minucie.

Rozwiązanie
Listing programu - przykład 3

z1

z2

z3

z4

Kolejka
transporter

z1

z2

z3

z4

1

13

25

40

z1

z2

z4

Obróbka mechaniczna
1 obrabiarka

52

13

25

40

52

67

79

z1

z2

z3

z4

0

z1

z2

z3

z3

1

10

19

28

45

75

60

90

malowanie i
suszenie
2 stanowiska

Otoczenie
magazyn
produktów

Otoczenie systemu
magazyn części

z4

czas

?

.

100

; Produkcja (kolejka, stanowiska jedno i wielokanałowe)
Susz STORAGE

2

;

2 stanowiska do suszenia

GENERATE

9,,1,4

;

co 9 min, od 1 min, 4 zadania

QUEUE

Transp

;

zajęcie miejsca na transporterze

SEIZE

Obrab

;

zajęcie obrabiarki

DEPART

Transp

; zwolnienie miejsca na transporterze

ADVANCE

12

;

obróbka w czasie 12 min.

ENTER

Susz

; z

ajęcie suszarki

RELEASE

Obrab

; z

wolnienie obrabiarki

ADVANCE

27

; m

alowanie i suszenie (27 min.)

LEAVE

Susz

; z

wolnienie suszarki

TERMINATE 1

; zakończenie zadania

START

4

;

uruchomienie symulacji dla 4 zadań

Standardowy Raport z symulacji

GPSS World Simulation Report – Prod3.12.1 Tue, Oct 18, 2010 00:18:21

START TIME END TIME BLOCKS FACILITIES STORAGES
0.000 79.000 10 1 1

NAME VALUE
OBRAB 10002.000
SUSZ 10000.000
TRANSP 10001.000

LABEL LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY

1 GENERATE

4

0

0

2 QUEUE

4

0

0

3 SEIZE

4

0

0

4 DEPART

4

0

0

5 ADVANCE

4

0

0

6 ENTER

4

0

0

7 RELEASE

4

0

0

8 ADVANCE

4

0

0

9 LEAVE 4

0

0

10 TERMINATE

4

0

0

FACILITY ENTR UTIL. AVE. T.AVAIL. OWNER PEND INTER RETRY DELAY
OBRAB 4 0.646 12.750 1 0 0 0 0 0

QUEUE MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY
TRANSP 1 0 4 1 0.266 5.250 7.000 0

STORAGE CAP. REM. MIN. MAX. ENTRIES AVL. AVE.C. UTIL. RETRY DELAY
SUSZ 2 2 0 2 4 1 1.367 0.684 0 0

Na Rys 4.1 przedstawiono graficzne wyniki symulacji przykładu 3.

.

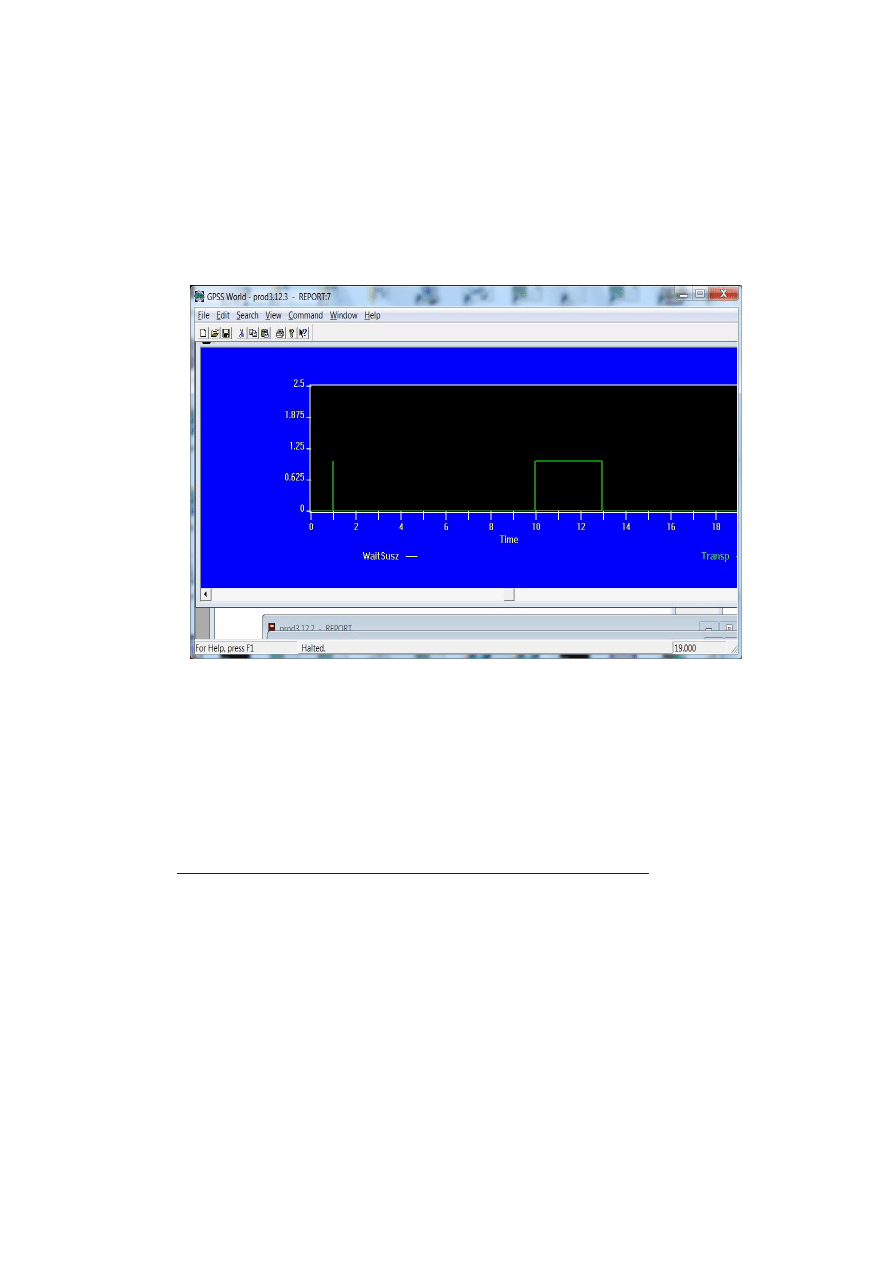
101

Następny przykład (Rys 4,1) jest tylko fragmentem schematu blokowego GPSS
(niedostępnym ze względu na prawa autorskie) ale przekonuje o aktualności
problematyki i stosowanych narzędziach symulacyjnych. Rozwiązany problem
dotyczy budowy modelu złożonego procesu logistycznego - organizacji transportu
i produkcji z Dalekim Wschodem w tzw. łańcuchu dostaw. Pozostałe szczegóły są
dostępne w artykule
"

http://www.elogmar-m.org/misc/simulationELogisticsSupplyChain.doc

"

Pozostałe przykłady objaśniające inne bloki a w szczególności dotyczące bloków
sterujących są zawarte i dostępne w plikach źródłowych na serwerze w katalogu do
ćwiczeń oraz opisane w rozdz. 4.3. Ponadto należy skorzystać z dostępnego na
serwerze szczegółowego podręcznika i pomocy do wersji GPSS World.

Rys 4.1 Wyniki symulacji - zajętość transport w przykładzie 3

.

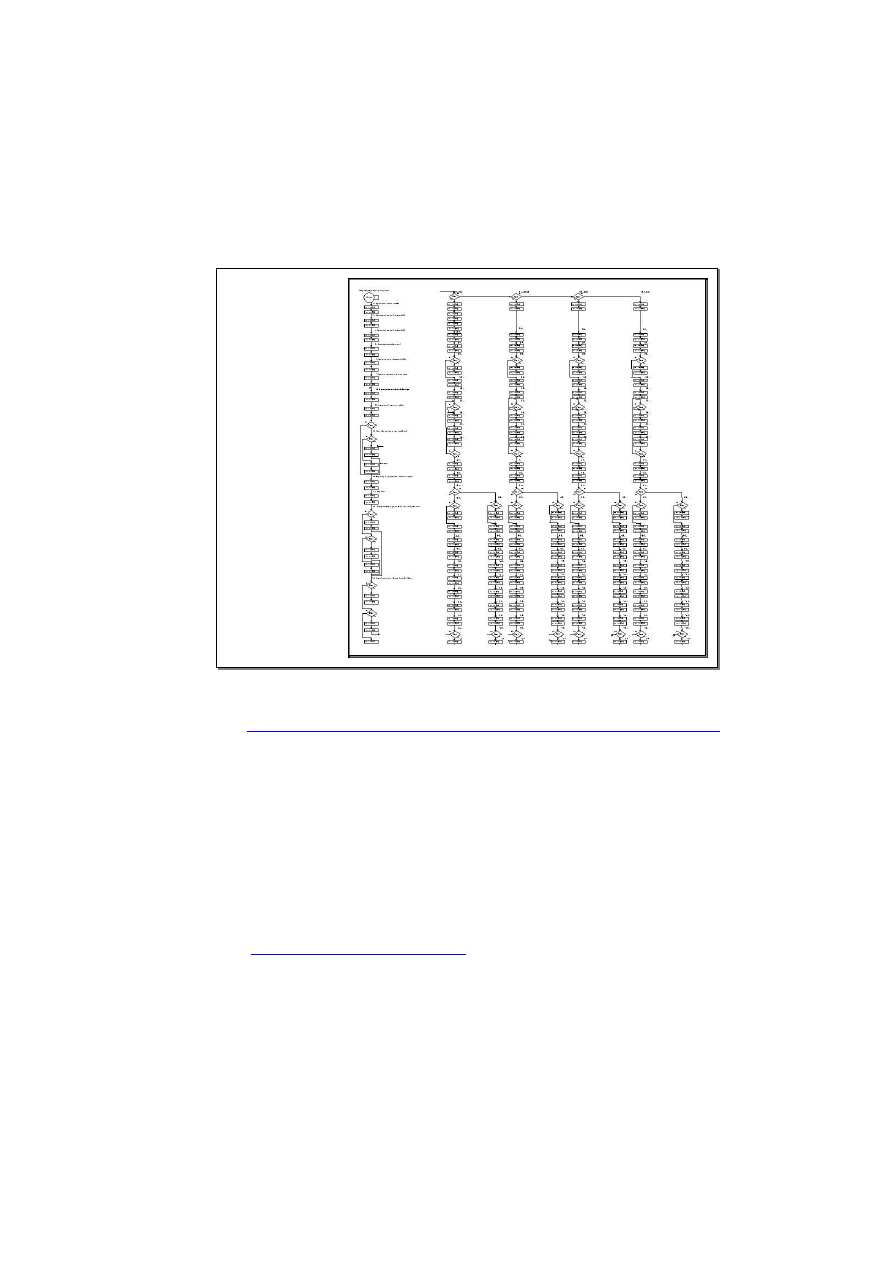
102

Złożoność języka GPSS, konieczność pamiętania składni kilkudziesięciu bloków, z
których większość posiada wiele parametrów, powoduje że język ten traci na
popularności. Z drugiej jednak strony konieczność symulacji procesów
dyskretnych a szczególności procesów obsługi masowej jest coraz powszechniejsza.
Obserwuje się zatem pojawianie się na rynku coraz większej ilości aplikacji o
bardziej przyjaznej obsłudze, korzystającej z graficznego środowiska 3D
prowadzonej z powodzeniem przez osoby nie pracujące bezpośrednio w branży IT
(np. Flexim

http://www.flexsim.com/flexsim

),.

Extract from

a Time- and

Cost-based

GPSS

Model of an

Intermodal

Supply Chain

from the

Far-East to

NW-Europe

Extract from

a Time- and

Cost-based

GPSS

Model of an

Intermodal

Supply Chain

from the

Far-East to

NW-Europe

Rys. 4.2 Model blokowy w języku GPSS złożonego problemu logistycznego

źródło:

http://www.elogmar-m.org/misc/simulationELogisticsSupplyChain.doc

"

.

103

4.3 Przykłady do ćwiczeń i tematy zadań

Zadania powinny być wykonywane kolejno a wyniki zapisywane w plikach
źródłowych z numerami zadań w postaci zadnr.gps i w raportach zadnr.gpr

1. Obsługa stanowiska jednokanałowego z zadaną ilością zakończonych zadań
Problem: Ile wynosi czas obsługi i maksymalna długość kolejki w myjni
samochodowej dla 100 klientów napływających w sposób równomierny w
przedziale od 2 do 12 minut. Czas mycia samochodu (z manewrowaniem) wynosi
3 - 9 min. Rozwiązanie - Przykład programu w pliku Myjnia01

Zad 1.0 Napisz program symulujący pracę drukarki dla 20 plików jako urządzenia

jednokanałowego pobierającego pliki do drukowania z kolejki FIFO na
serwerze wydruku. Kolejka ma nieograniczoną pojemność, wydruki nadchodzą
w przedziale czasu od 5 do 10 min, a czas wydruku wynosi od 10 do 20 min

2. Obsługa z zadanym czasem stanowiska jednokanałowego

Zad 2.0 Napisz program symulujący 10 godz. pracę obsługi drukarki ( w tym

20+60+20 min przerw) jako urządzenia jednokanałowego pobierającego pliki
do drukowania z kolejki FIFO zorganizowanej na serwerze wydruku. Kolejka
ma nieograniczoną pojemność, wydruki nadchodzą w przedziale czasu od 5 do
10 min, a czas wydruku wynosi od 10 do 20 min
Wskazówka - zastosować bloki z przykładu Myjnia01
Zdefiniować proces symulacji czasu złożony z jednego zadania o odpowiednim
czasie trwania i priorytecie 5

Zad 2.1 Modyfikacja Zad 2.0 - Zmiana ( uproszczenie ) generacji czasu symulacji

- uprościć usuwając blok opóźniający, pozostawić pozostałe parametry bez
zmian

Zad 2.2 Modyfikacja Zad 2.1 - Zwiększenie dokładności pomiaru czasu - zmiana

jednostki czasu na 0.1 min

Zad 2.3 Modyfikacja Zad 2.2 - Dwukrotne zwolnienie (w stosunku do zad 2.2)

zmniejszenie ilości nadchodzących zadań w jednostce czasu,

Zad 2.4 Modyfikacja. Zad 2.3 Dwukrotne przyspieszenie (w stosunku do zad 2.2)

zwiększenie częstości (ilości jw. porównać wyniki )

.

104

3. Obsługa stanowiska wielokanałowego (o identycznych parametrach )
Przykład obsługi myjni na jednym z wielu identycznych stanowisk Myjnia03)

Zad 3.0 Modyfikacja Zad 2.4 symulacja 8 godz. pracy urządzeń wielokanałowych

zespołu 3 drukarek DRUK Symulacja wydruku zadań na jednej pierwszej
wolnej drukarce wybranej z zespołu 3 identycznych drukarek

Wskazówka - zastos: STORAGE, ENTER, LEAVE (patrz Myjnia03.gps)
Zad 3.1 Modyfikacja Zad 3.0 - uszkodzenie (brak) jednej drukarki w zespole
Zad 3.2 Modyfikacja Zad 3.0 - uszkodzenie (brak) dwóch drukarek (porównać

wynik z Zad 2 o tych samych parametrach )

Zad 3.3 Modyfikacja Zad 3.0 - wszystkie drukarki po pierwszym wydruku

zatrzymują się

Zad 3.4 Modyfikacja Zad 3.0 - wprowadzenie nowego procesu obsługi dla zadań

uprzywilejowanych

Zadania uprzywilejowane do wydruku nadchodzą rzadziej, ale mają dłuższy czas

wydruku np co 10 min oraz mają najwyższy priorytet (uwaga szef profesor
może wyrzucić z roboty !!! )

4. Obsługa 2 stanowisk jednokanałowych z określeniem warunków wyboru
Przykład Myjnia04.gpr (myjnia ręczna i automatyczna) zastosowanie bloku
TRANSFER do zmiany kolejności przemieszczania się zadań - mycie na dwóch
stanowiskach do których są indywidualne kolejki, wybór kolejki stanowiska
przypadkowy z określonym prawdopodobieństwem - samochody nie mogą
zmieniać stanowiska po wybraniu kolejki (Przykład)
Zad 4.0 Wprowadzenie dwóch drukarek DR1 i DR2 wraz z indywidualnymi

serwerami. Wybór sprzętu dla nadchodzących zadań jest uwarunkowany
jednakowym prawdopodobieństwem dla jednakowych drukarek jak w Zad 2.0)

Zad 4.1 Modyfikacja (4.0) poprzez zmianę prawdopodobieństwa i czasu obsługi.

Dobrać prawdopodobieństwo dla przypadku gdy drukarka DR1 przyspieszyła
dwukrotnie wydruk

Zad 4.2 Modyfikacja (4.0) poprzez usuniecie warunku prawdopodobieństwa i

czasu obsługi drukarki

Zad 4.3 Modyfikacja (4.0) z jednym serwerem wydruku wprowadzić wybór

bezwarunkowy ( warunek BOTH A, B określa wybór A a gdy zajęte B )

5. Obsługa 2 stanowisk jednokanałowych z określeniem warunków wyboru
dobranym wg aktualnego stanu obsługi (parametrów)
Przykład Myjnia05 (myjnia ręczna i automatyczna) zastosowanie bloku TEST
Zad 5.0 Obsługa sterowania zadaniami na 2-ch stanowiskach jednokanałowych

.

105

6. Porównanie obsługi zadań wg zasady FIFO i SPT
Symulacja pracy narzędziowni

Pewien pracownik pracuje w narzędziowni. Jego zadaniem jest sprawdzenie,

konserwacja i przyjmowanie/wydawanie narzędzi, stosowanych przez mechaników
naprawiających maszyny. Narzędzia te są zbyt kosztowne i jest ich równocześnie
zbyt wiele, by każdy mechanik posiadał je w swoim podręcznym wyposażeniu
naprawczym. Czas pomiędzy dwoma kolejnymi zapotrzebowaniami na wydanie
tych narzędzi oraz czas potrzebny na przygotowanie i wydanie potrzebnego
narzędzia

(czas

obsługi

mechanika)

zależą

od

mechanika. Rozkłady

prawdopodobieństw i ich parametry dla czasów pomiędzy zapotrzebowaniami oraz
obsługi dwóch typów mechanika są następujące:
Zad 6.0 Pracownik narzędziowni stosuje regulamin obsługi FCFS (pierwszy

przyszedł, pierwszy obsłużony: First Come, First Served). Jednakże jest także
propozycja zastosowania SPT (najkrótszy czas obsługi: Shortest Processing
Time), ponieważ prawdopodobne jest zmniejszenie wtedy średniej liczby
mechaników oczekujących na obsługę przez pracownika narzędziowni. Może to
wtedy spowodować oszczędności, ponieważ: (1) zmniejszony zostanie czas
oczekiwania w narzędziowni, (2) zmniejszony zostanie czas naprawy psujących
się maszyn. Zbuduj model 8-godzinnego dnia pracy narzędziowni dla dwóch
wariantów regulaminu obsługi mechaników. Czy regulamin SPT spowoduje
zmniejszenie liczby mechaników oczekujących na obsługę?.

Wskazówka: Wykorzystać priorytety obsługi zadań

.

106

4.4 Obsługa pakietu GPSS World

Zapoznanie się z obsługą pakietu symulacyjnego GPSS World Student
przeprowadzone będzie na przykładzie programu prod3.gps omówionego w
rozdz. 4.2.2.

1. W katalogu

path

/

cw4/GPSS/

uruchomić GPSSws.exe

2. Otworzyć plik prod3.gps w katalogu

path

/

cw4/

File -> Open

3. Zapoznać się z treścią programu w oknie edytora

4. Uruchomić symulacje (Rys 4.3)

Command -> Create Simulation

Rys. 4.3 Okno główne

.

107

W wyniku przeprowadzonej pomyślnie symulacji uzyskano dodatkowe okna
standardowy raport (REPORT) oraz w oknie JOURNAL tzw. dziennika ślad
symulacji przedstawiający w czasie rzeczywistym komunikaty o wybranych
zdarzeniach i ich parametrach.
Zawartość okien można zapisać, wydrukować i wykorzystać w szczegółowej
analizie procesu
- w dzienniku można zapisać wyniki śledzenia TRACE / UNTRACE).
- wyniki śledzenia obserwujemy także na bieżąco w trybie pracy krokowej

5. Symulacja krokowa.
Eliminujemy automatyczny START wprowadzając

komentarz w ostatniej linii .

; START

Następnie kompilujmy

Command -> Create Simulation

Powtarzamy wielokrotnie

Command -> Step 1

Wyniki obserwujemy (Rys 4.4)

w oknie dziennika

lub w oknie obiektów blokowych (BLOCK ENTITIES )

Rys 4.4 Podstawowe okna po uruchomeniu przykładu

.

108

Okno z obiektami blokowymi włączamy jednorazowo przez

Command -> Window ->

Simulation Window -> Block Window

W bieżącym oknie bloku pracę krokowa można kontynuować

przy pomocy ikony STEP

6. Generowanie wykresów

Wykresy przedstawione będą w szerszym horyzoncie czasowym
W tym celu :

Usuń ograniczenie na ilość zadań - pozostaw GENERATE 9
Zapisz program pod nowa nazwą

Prod30

Otwórz okno wykresu

Simulation Window -> Plot Window

Rys 4.4 Komunikaty w trybie pracy krokowej i w blokach obiektów

.

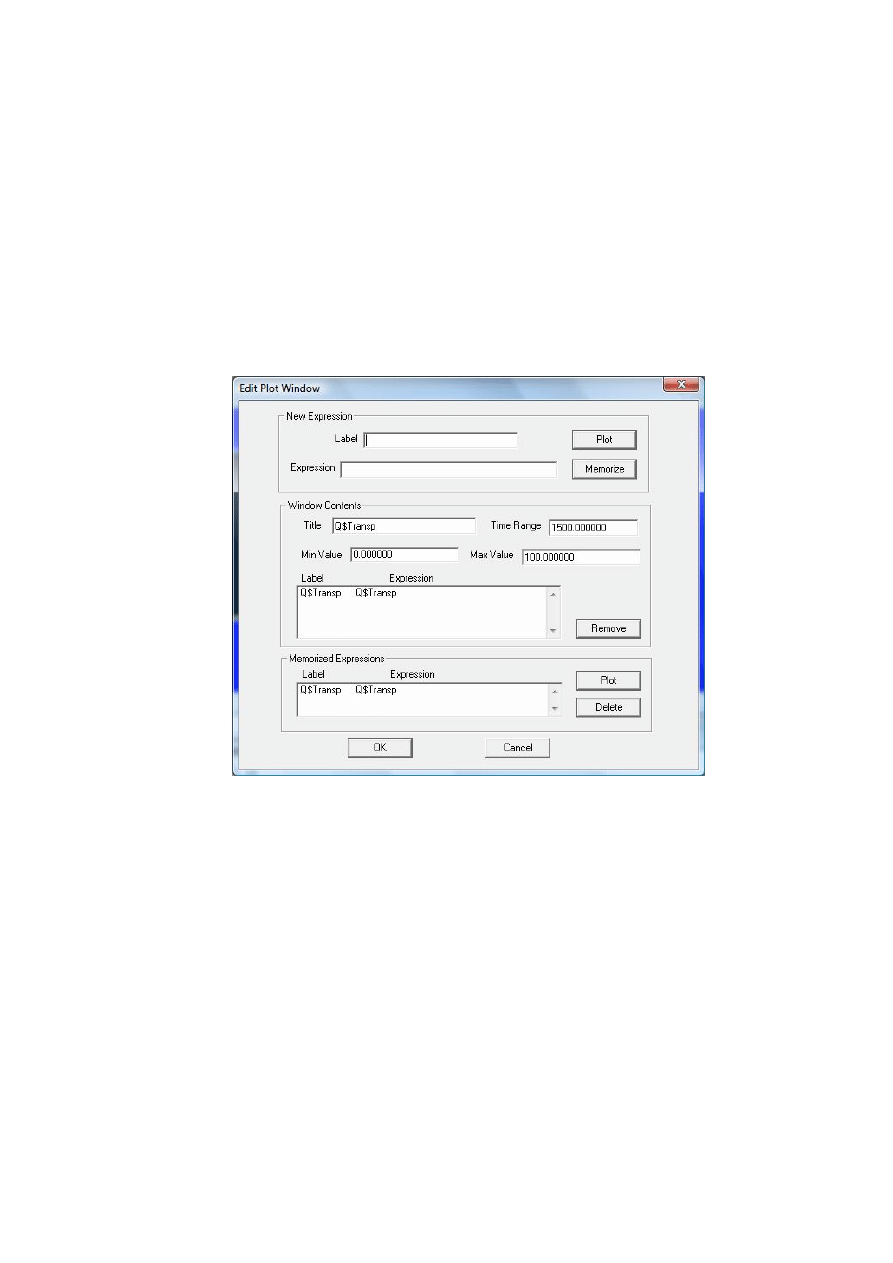
109

Wprowadź (Rys 4.5 ) etykietę wykresu , wyrażenie i tytuł okna
(w uproszczeniu wspólną nazwę) oznaczająca długość kolejki Q$Transp

Zakres czasu

t

max

= 1500 min domyślnie od t

min

= 0

Zakres osi pionowej

[0, 100]

Uruchom

START 100

Wynik na Rys 4.6

Rys 4.5 Edycja parametrów wykresu

.

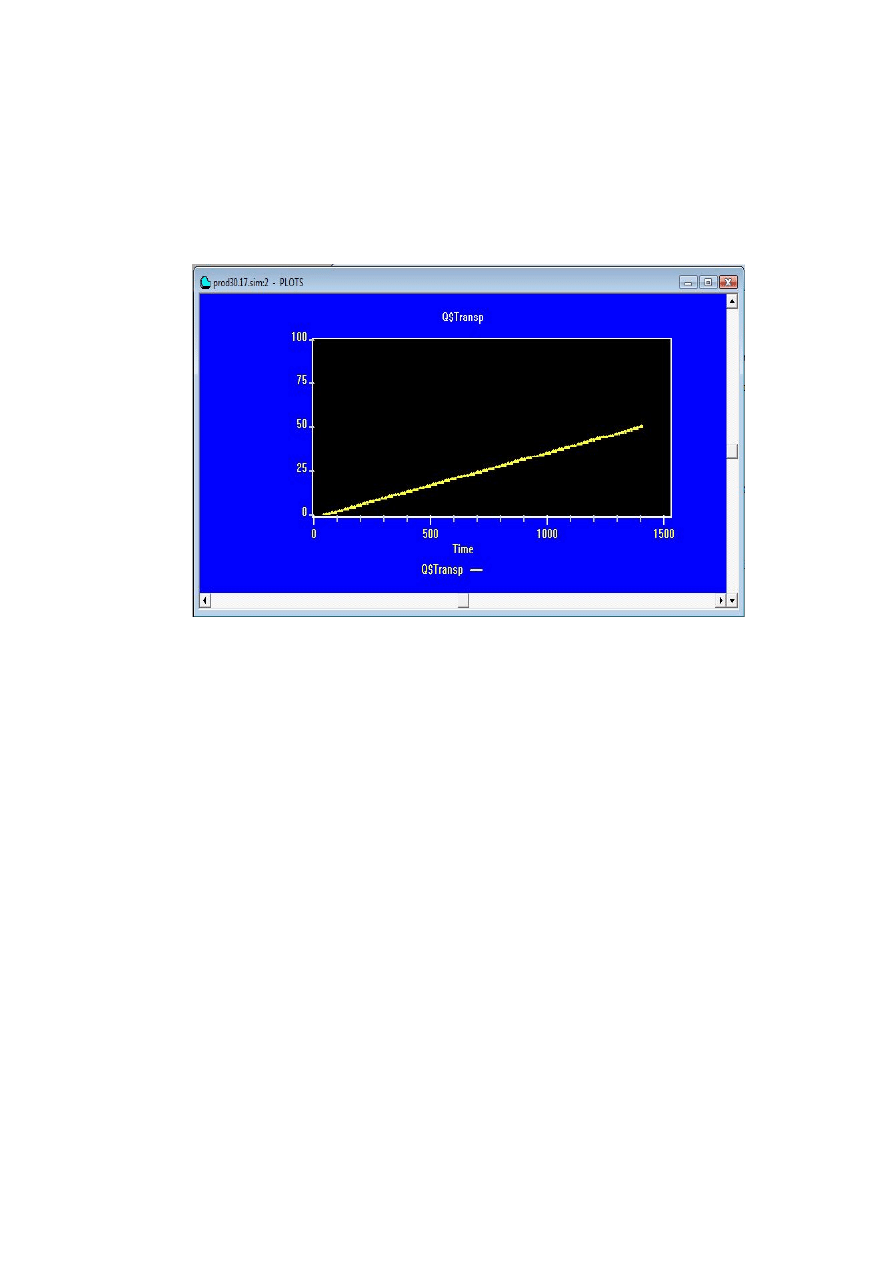
110

7. Skalowanie

Szczegóły wykresu (Rys 4.8) zobaczymy po zmianie skali
Parametry wykresu można zmodyfikować (Rys 4.7) przez

Edit -> Plot Window

Wprowadzamy

Zakres czasu

t

max

= 200 min ,

Zakres osi pionowej

[0, 20]

Rys 4.6 Wynik symulacji w oknie wykresu – długość kolejki

.

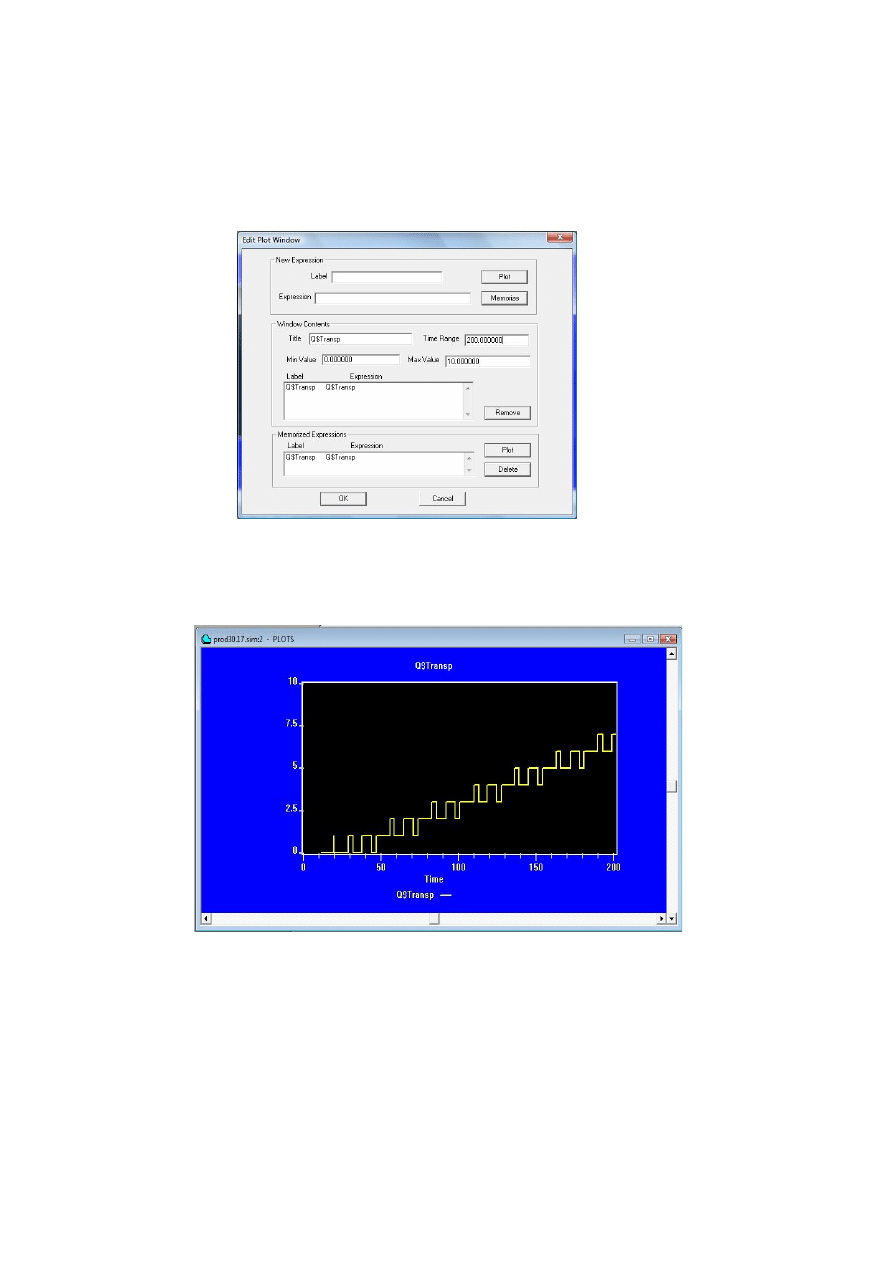
111

Rys 4.8 Wynik symulacji w oknie wykresu – wg nowej skali

Rys 4.7 Modyfikacja parametrów wykresu

.

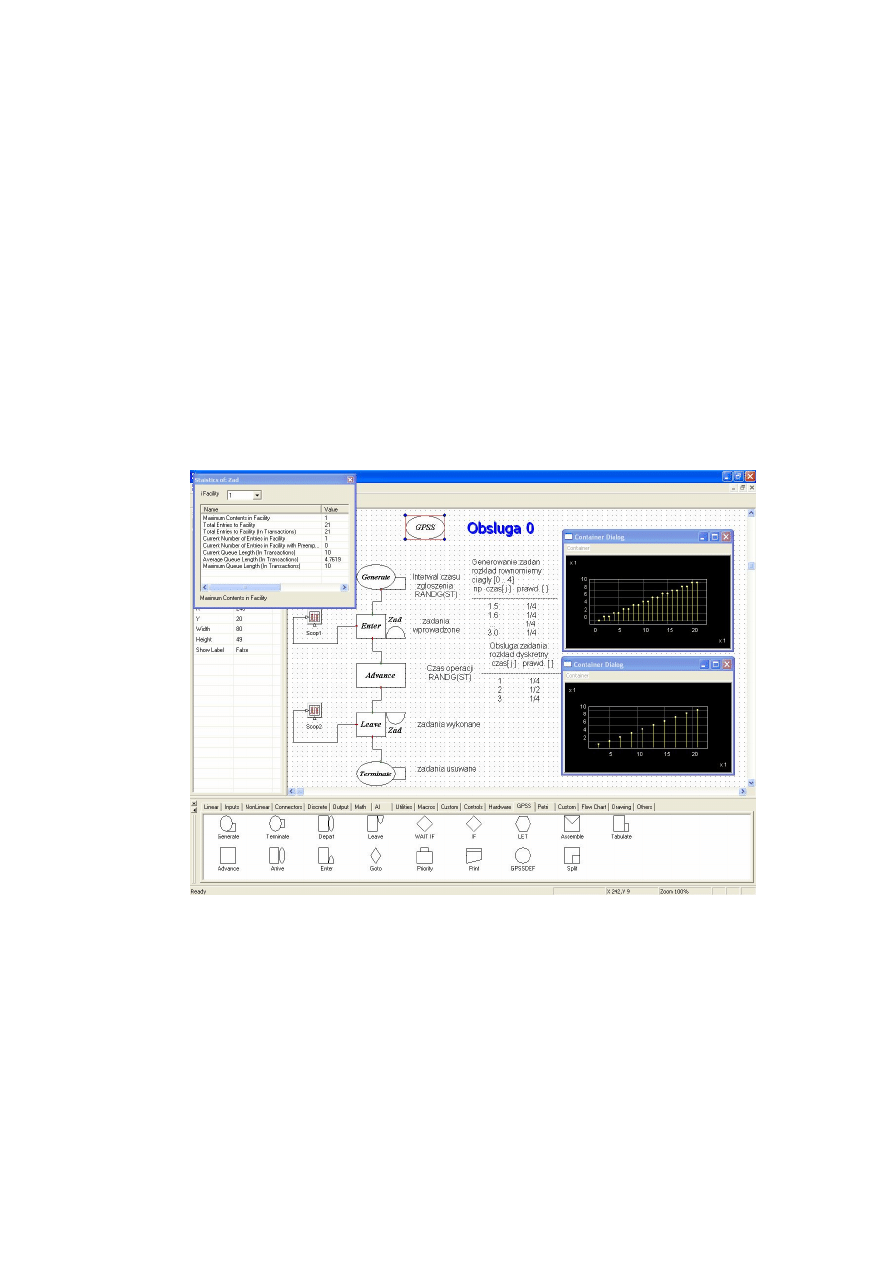
112

4.5 Inne wersje pakietów GPSS

GPSS jako język wszedł do niektórych pakietów symulacyjnych także dla układów
ciągłych . Przykładem może być implementacja w pakiecie SIMULA ( Rys 4.9,
4.10) gdzie wprowadzono graficzną realizację programu przy pomocy symboli
blokowych.

W wersji internetowej WebGPSS budowę programu można też zrealizować
przy pomocy elementów schematu blokowego (Rys 4.12) - przykład takiej
realizacji przedstawia Rys 4.13.

Rys. 4.9 SIMULA Okna: schematu blokowego, symboli bloków i ich parametrów oraz

wyników wykreślnych i raportu statystycznego

.

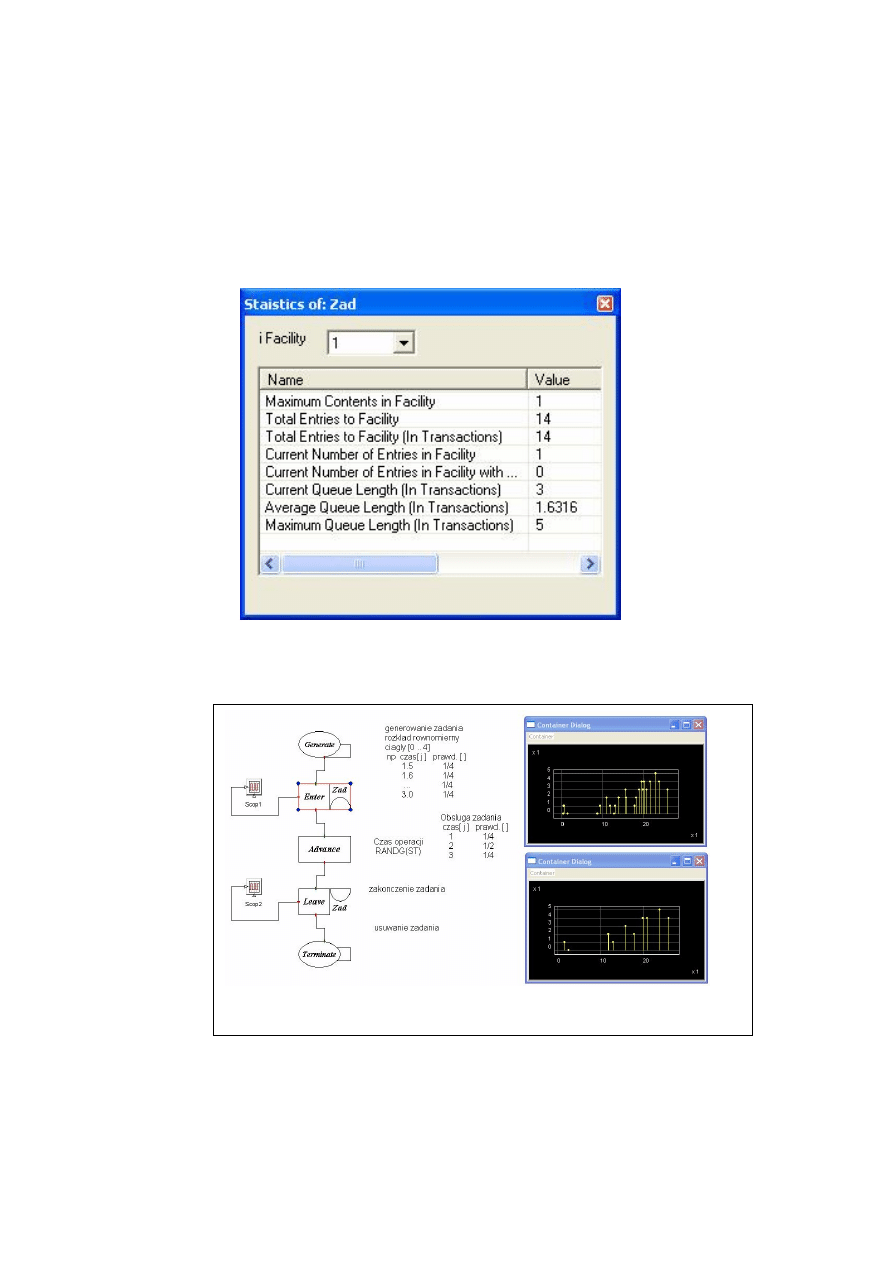
113

Rys. 4.11 SIMULA - Okna symulacji

Rys. 4.10 SIMULA Okno raportu statystycznego

.

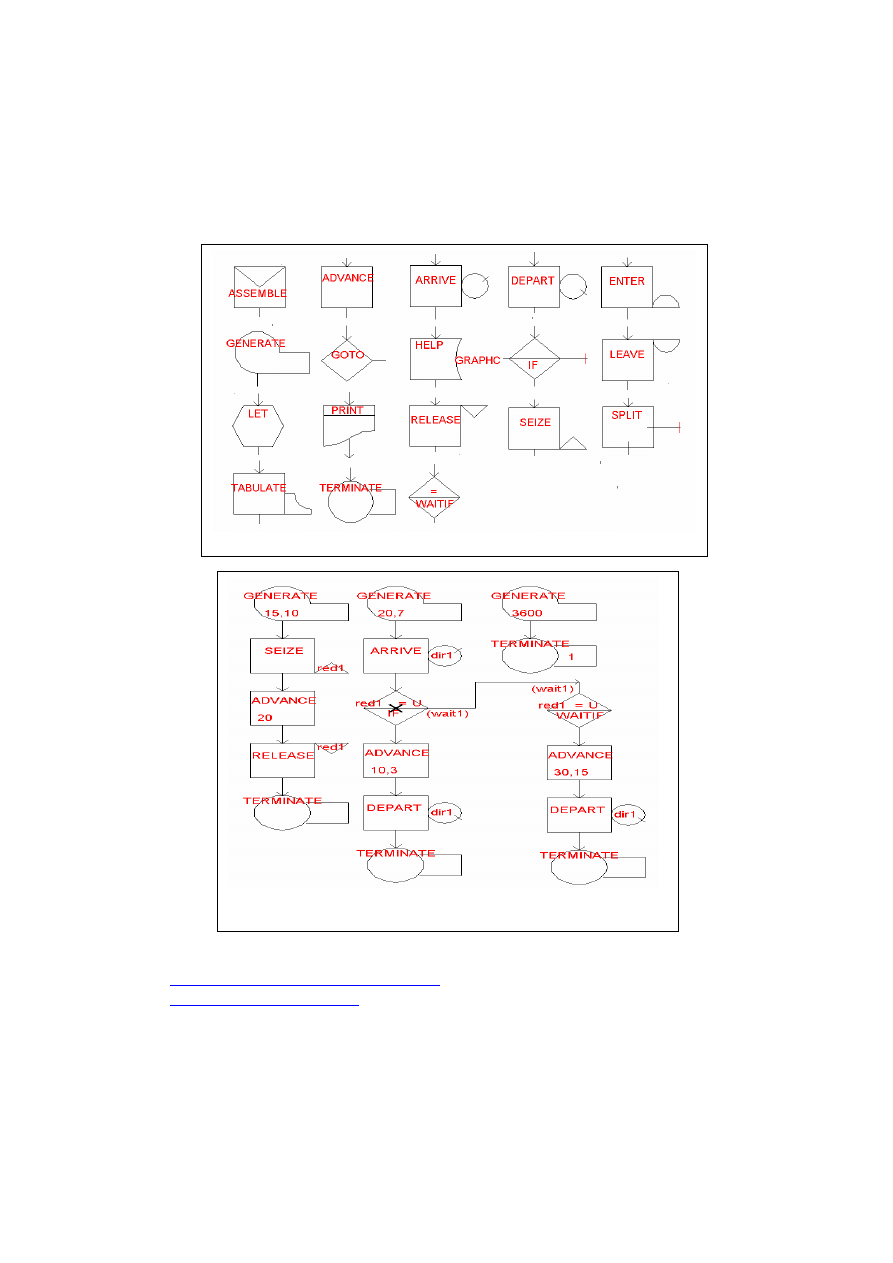
114

Literatura do rozdz. 4

http://www.minutemansoftware.com/

http://www.webgpss.com/

Rys 4.12 Symbole schematu blokowego GPSS Web

Rys. 4.13 Przykład schematu blokowego modelu procesów

.

115

5. PROGRAMOWANIE SYSTEMÓW DYSKRETNYCH

5.1 Wprowadzenie

Programowanie systemów dyskretnych, w głównej mierze opiera się na

tworzeniu oprogramowania do symulacji komputerowej dyskretnych procesów
zachodzących w modelach systemów rzeczywistych. Symulacja komputerowa jest
metodą,

która

w

pewnym

zakresie

używając

odpowiednich

modeli

matematycznych pozwala na odtwarzanie zjawisk zachodzących w świecie
rzeczywistym (niekiedy uzyskujemy jedynie ocenę niektórych parametrów i
właściwości symulowanego systemu rzeczywistego). Istotne jest w tym przypadku
modelowanie przy użyciu programów komputerowych i praktyczna realizacja
symulacji z wykorzystaniem sprzętu komputerowego. Symulacja umożliwia
uzyskanie informacji o procesach, dla których bezpośrednia obserwacja jest
niemożliwa lub zbyt kosztowna.

Symulacja procesów dyskretnych - dotyczy procesów, których stan zmienia się

tylko w dyskretnych punktach czasu i zależy od zmian stanów systemu.

Do istotnych zalet symulacji komputerowych należy możliwość przetestowania

procesu w sposób oszczędny i bezpieczny, z jednej strony unikając błędów i
kosztów związanych z testami i poprawkami dla układu rzeczywistego a z drugiej
także wczesnego wykrywania błędów i świadomego symulowania sytuacji
awaryjnych. Modelowanie czasu w systemie pozwala na jego skalowanie i w
efekcie skrócenie czasu przeprowadzenia wielu badań symulacyjnych i w ten
sposób znalezienia najlepszych rozwiązań możliwych do zastosowania w
rzeczywistości. Z symulacji może skorzystać zarówno projektant jak i przyszły
użytkownik, którzy wspólnie korzystając z wielu środków wizualizacyjnych, mogą
poznać ograniczenia, lepiej zrozumieć proces i wspólnie skonsultować najlepsze
rozwiązania.

Symulacja jest tylko pewnym przybliżeniem rzeczywistości i stąd wynikają

także jej wady oraz ograniczenia w uzyskaniu zadawalających rezultatów.
Konieczne jest w tym przypadku duże doświadczenie projektanta, ażeby
adekwatnie do założonego celu symulacji uwzględnić w modelu wszystkie jego
aspekty. W przypadku złożonych problemów symulacyjnych istotne mogą być
także koszty samego oprogramowania symulacyjnego, przeprowadzanie testów,
generowanie wyników symulacyjnych a także konieczność zaangażowania w
projekcie grona specjalistów w celu interpretacji złożonych wyników.
Z reguły koszty symulacji są pomijalne i warto ją przeprowadzić, ale należy jednak
przeanalizować jej zastosowanie biorąc pod uwagę prognozowanie kosztów.

.

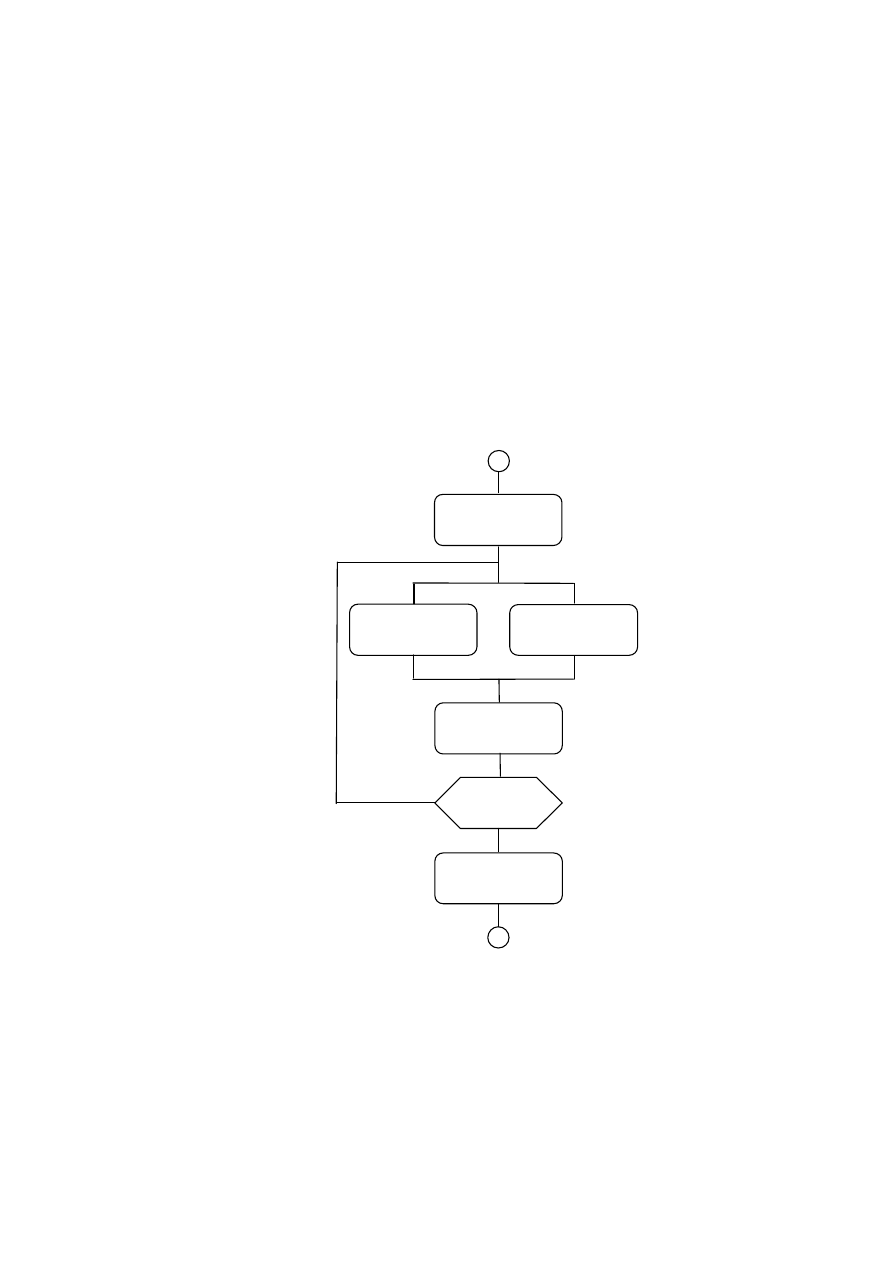
116

5.2 Proces projektowania symulacji

W rozdziale tym przedstawiony zostanie ogólny plan etapów symulacji,

opracowany na podstawie [Branks, Carson, Nelson and Nicol „Discrete Event
System Simulation”] i omówiony pod kątem symulacji jako pewnego
przedsięwzięcia projektowego. Rysunek 5.1 przedstawia ogólną postać takiego
przedsięwzięcia, złożonego z szeregu etapów.

1. Problem, Cel

i Harmonogram

2. Model

Abstrakcyjny

3. Zbior

Danych

4. Model

Symulacyjny

5.Weryfika-

cja Modelu

6. Badania

Symulacyjne

Rys 5.1 Plan etapów projektu symulacji

.

117

Etap 1: Sformułowanie problemu. Cel i harmonogram.

Symulowana rzeczywistość i występujące zjawiska powinny być dobrze
sprecyzowane. Programista lub analityk w przypadku wieloosobowego
zespołu projektowego sporządza specyfikację wymagań. Na tym etapie
powinien być jasno sformułowany cel symulacji. Są to istotne założenia, które
powinny być w postaci dokumentu uzgodnione z ewentualnym klientem lub
zespołem kontrolno-nadzorczym. Istotne jest też na tym etapie określenie i
uzgodnienie ogólnego harmonogramu, przydziału zasobów i oszacowanie
kosztów.

Etap 2: Model Abstrakcyjny.

Zbudowanie modelu w którym rzeczywistość zostaje zastąpiona przez
abstrakcyjne modele matematyczne. Formalizm reguł matematycznych
wspomaga dalsze zrozumienie procesu i uściśla wstępne założenia. Na tym
etapie wymagane są niekiedy konsultacje specjalistyczne z zakresu dziedziny
symulowanej rzeczywistości.

Etap 3: Zbiór Danych.

Zebranie danych wejściowych jest konieczne do skonkretyzowania badanego
procesu i do weryfikacji adekwatności przyjętego modelu abstrakcyjnego. Na
tym etapie powinien być opracowywany plan testów jakości. Z uwagi na
efektywność czasową etap te można wykonać równolegle w stosunku do 2-go
etapu.

Etap 4: Model symulacyjny.

Zaprogramowanie symulacji jest najważniejszym etapem, w którym następuje
zastosowanie narzędzi symulacyjnych, języków oraz procedur bibliotecznych
do realizacji programu modelu, jego wstępne uruchomienie i przetestowanie.
Na tym etapie wymagana jest przede wszystkim specjalistyczna wiedza
programisty.

Etap 5: Weryfikacja modelu.

Weryfikacja modelu pozwala na wychwycenie błędów projektowania, które
wymuszają konieczność powrotu do wcześniejszego etapu. Zasadniczą
poprawność modelu należy zweryfikować wg opracowanych na etapie 3 testów
jakości.

Etap 6: Badana symulacyjne.

Przeprowadzenie badań symulacyjnych jest zasadniczym celem projektu. Na
tym etapie należy zadbać o dobrą dokumentację, która będzie pomocna nie

.

118

tylko w realizacji praktycznej rzeczywistego układu ale także stanowiła istotny
element w realizacji przyszłych projektów.

Omówiony proces projektowania jest tylko pewnym szablonem i powinien być
skonkretyzowany w zależności od szczególnych okoliczności projektu.
Zasadniczym kryterium są tutaj nie tylko cele projektowania, ale także
wykorzystywane środki programistyczne. Zawężając problematykę do zakresu
symulacji komputerowej należy sprecyzować podstawowy cel projektu, a przede
wszystkim wykorzystywane narzędzia programistyczne.

Cel projektu może być:

C1: Ogólny - narzędzia, pakiet symulacyjny z ewentualnym uszczegółowieniem

na system dyskretny, ciągły i współbieżny.

C2: Szczegółowy – aplikacja dla ściśle sprecyzowanego zagadnienia lub ich

pewnej klasy wynikającej z założonego obszaru zastosowań branżowych.

W zakresie środków programistycznych można zastosować:

P1: Pakiet symulacyjny - gotowe dostępne na rynku narzędzie oparte często na

określonym języku symulacyjnym wyższego poziomu dopasowane do
bardziej lub mniej ogólnych zastosowań i o zróżnicowanej funkcjonalności.

P2. Język programowania poziomu niższego (proceduralny lub obiektowy)

wraz pakietem wspomagającym projektowanie aplikacji i niekiedy
wyposażony w dodatkowe biblioteki pozwalające na realizacje wybranych
podproblemów symulacyjnych.

Biorąc pod uwagę w/w wymienione podziały najbardziej złożonym projektem

jest kombinacja (C1, P2) wymagająca bardzo dobrego przygotowania teore-
tycznego w aspekcie teorii systemów, a także praktycznego w zakresie
wykorzystania narzędzi informatycznych. Decyzja o zastosowaniu tej kombinacji
ma też sens w przypadku przewidywanego wielokrotnego profesjonalnego
wykorzystania. Często zaczątkiem tego rozwiązania może być wieloletnia praktyka
w realizacji pozostałych kombinacji (C2, P1) i (C2, P2) oraz (C2, P2). Z uwagi na
szeroką dostępność pakietów, rozwiązanie (C2, P1) jest stosowane dosyć często,
chociaż wymaga ono niekiedy dość dużego wstępnego nakładu pracy.
Atrakcyjność tego rozwiązania polega też na mniejszym zaangażowaniu w zakresie
wiedzy IT.

Złożone i poważniejsze problemy powinny też być rozwiązywane na bardziej

szczegółowym poziomie weryfikacji, w którym symulacja jest pewnym istotnym
etapem, ale nie zasadniczym celem. Taki model przedstawia sieć działań na Rys
5.2, w którym dodatkowo należy zweryfikować prawidłowy wybór koncepcji
rozwiązania i określenie modelu analitycznego, a także ocenić wyniki badań
symulacyjnych, które potwierdzą decyzję o wdrożeniu realizacji układu fizycznego.

.

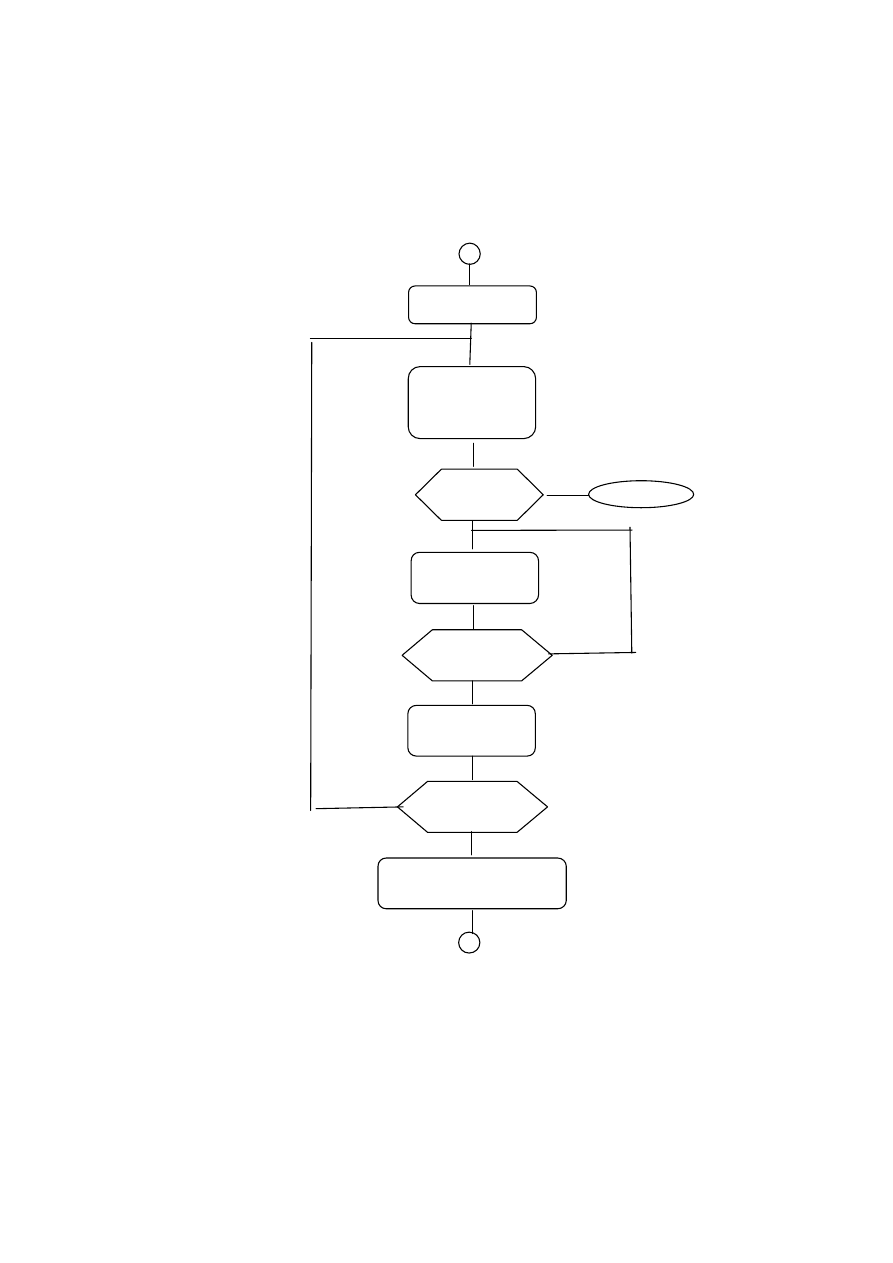
119

1 Problem / Cel

2. Model

Koncepcyjny

Analityczny

4. Program

Symulacyjny

5.Weryfikacja

Programu

6. Badania

Symulacyjne

Rys 5.2 Plan etapów złozonego projektu z zastosoaniem

symulacji komputerowej

3.Weryfika-

cja Modelu

7.Weryfikacja

Badań

Przerwanie

8 Budowa. Wdrożenie

układu rzeczywistego

Symulacyjne

NO

OK

OK

OK

NO

NO

.

120

Często na podstawie wyników symulacji określa się kryteria jakości i w tym

przypadku symulacja może być elementem automatycznie działającego programu
optymalizacyjnego – poszukującego najlepszych rozwiązań. Przykład tak
postawionego problemu ilustruje rys 5.6

5.3. Elementy modelu symulacyjnego

Zawężając rozważania do zakresu metod symulacji dyskretnej należy wyróżnić

wiele elementów, ale do podstawowych należą: zdarzenia, działania i procesy. Są
one

składnikami

każdego

schematu

organizującego

przebieg

obliczeń

symulacyjnych, chociaż w szczegółowych opisach pakietów i algorytmów
symulacyjnych mogą być używane inne równoważne i dodatkowe określenia np:
obiekty i ich atrybuty, uwarunkowane zgłoszenia, transakcje, operacje, czynności,
stany itp.

Podane elementy wynikają także z podstawowej definicji symulacji procesu

dyskretnego podanej przez R. E. Shanon’a i zmodyfikowanej przez J. B. Evans’a:

Obiekty opisane atrybutami po spełnieniu określonych warunków kreują w

ramach działań sekwencje zdarzeń zmieniających stan systemu.

Rozpoczynając budowę modelu należy jednoznacznie opisać problem, który

będzie rozwiązany metodami symulacyjnymi. Istotna w opisie jest identyfikacja
zdarzeń i działań, które występując zmieniają stan obiektów. Mimo, że zdarzenie
jest „nieuchwytną migawką” tzn. nie jest związane z upływem czasu to jednak jest
ono bardzo często od niego uzależnione, występując w określonej chwili
(wymuszone czasem zdarzenie synchroniczne) lub uwarunkowane wystąpieniem
innych zdarzeń. Czasami wiele zdarzeń może wystąpić w tej samej chwili czasu,
ale w sekwencji przyczynowo-skutkowej, lub co gorsza w nieokreślonej i wtedy
możemy wybrnąć z kłopotu przez dostęp do priorytetu, który jednak podniesie nam
złożoność modelu. Z uwagi na istotną rolę zdarzeń wymagamy w opisie słownym
nawet pewnej nadmiarowości, w rodzaju „początek czegoś” i koniec „czegoś”
gdzie to „coś” jest logicznie związane z określonym działaniem.

Reasumując, zdarzenie w określonym chwilowym czasie wiąże się ze zmianą

stanu obiektów reprezentowanych w systemie poprzez zmianę ich atrybutów, ale
także poprzez wprowadzanie nowych i usuwanie istniejących obiektów.

Z kolei działanie, przyjmując odpowiednią szczegółowość modelu może się

składać z jednej lub wielu niepodzielnych operacji, które mogą wpływać na zmianę
stanu systemu. Czasami działania określane są też mianem czynności.

Ciąg uporządkowanych w czasie zdarzeń związanych z każdym pojedynczym

obiektem jest określony mianem procesu, który przebiega od chwili wejścia
obiektu do systemu aż do chwili jego wyjścia. W ten sposób też działania na
obiektach określone są poprzez chronologiczne zdarzenia wchodzące w skład
procesu. Zdarzenia mogą zachodzić w sposób:

.

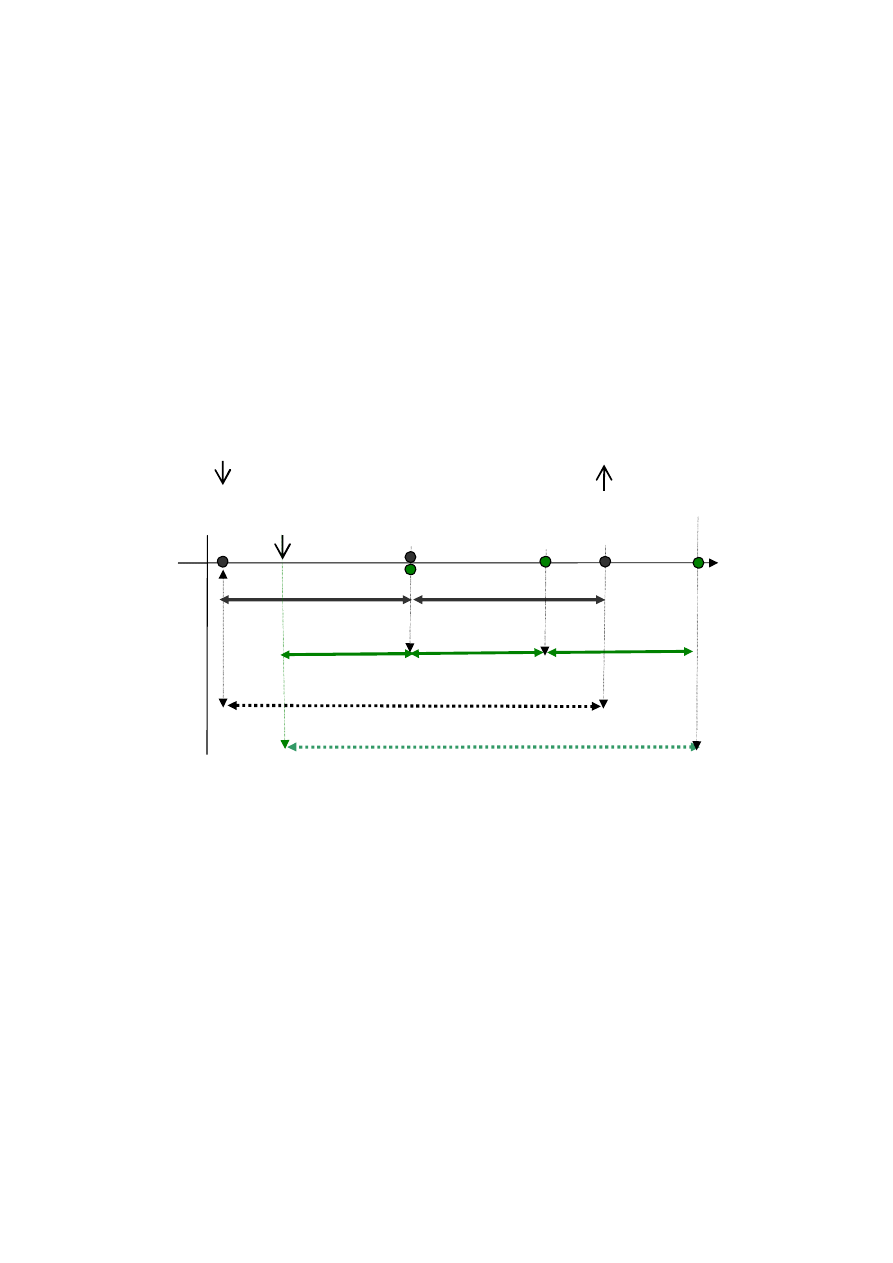
121

- bezwarunkowy, który jest bezpośrednio zależny od czasu,
- warunkowy, który jest pośrednio zależny od czasu poprzez zmiany stanu

systemu, uzależnione z kolei od innych związanych z czasem zdarzeń.

Omówione pojęcia ilustruje Rys. 5.3, przedstawiający historię zdarzeń związaną z
powtarzającym się prostym procesem produkcyjnym.

Często używanymi pojęciami w opisywaniu procesów dyskretnych jest pojęcie

transakcji, które przyjęło się z angielskiego odpowiednika transaction spotykanego
w dokumentacji pakietów symulacyjnych. Transakcje opisują przemieszczanie się
obiektu oraz zmiany jego stanu.
Budując model symulacyjny systemu dyskretnego należy w nim wyróżnić
następujące elementy:

- zegar systemowy - rejestruje czas modelowanego systemu rzeczywistego,
- kalendarz systemowy - sterowany zegarem systemowym, jest to zbiór

informacji o zdarzeniach (typ zdarzeń i parametry zdarzeń),

Działanie

Obróbka e1

0

Zdarzenie
Poczatek
obróbki e1

Zdarzenie
Nadejscie
e2

Działanie

Czekanie e2

Zdarzenie
Poczatek
obróbki e2

Zdarzenie
Nadejscie
e1

Działanie

Obróbka e2

Działanie

Malowanie
e1

Zdarzenie
Koniec
obróbki e1

Działanie

Malowanie e2

Proces

Produkcja e1

Zdarzenie
Koniec
malowanie e1

Zdarzenie
Koniec
malowania e2

Proces

Produkcja e2

czas

Rys 5.3. Ilustracja pojęć Zdarzenie, Działanie i Proces

.

122

- transakcje, obiekty mobilne pojawiające się w systemie jako zdarzenia,

(zgłoszenia), które posiadają argumenty przemieszczają się, zmieniają zasoby
systemu (obiekty stacjonarne) i tym samym mają wpływ na zmianę stanu
systemu,

- zasoby mogą być pojedyncze lub złożone, w odróżnieniu do pozostałych

obiektów są obiektami statycznymi systemu, określane są jako jednokanałowe
i wielokanałowe stanowiska obsługi.

5.4 Metody symulacji dyskretnej

Omawiając w sposób bardziej ścisły metody symulacji dyskretnej należy także

omówić szczególne przypadki symulacji, dla których jest ona przeprowadzana w
warunkach zależnych od zewnętrznych sygnałów (czynników). Można zapewnić
możliwość interakcji użytkownika z programem symulacyjnym w trakcie
prowadzenia obliczeń w tym śledzenia realizacji symulacji z otrzymywaniem
bieżących wyników oraz wprowadzania zmian do modelu w trakcie działania
programu symulacyjnego. Istotna jest możliwość zawieszenia wykonywanej
symulacji np: w celu przejęcia sterowania procesem, zmiany parametrów a nawet
struktury modelu. W tak prowadzonej symulacji często jednak trzeba zapewnić
odpowiednią szybkość przeprowadzanych obliczeń dostosowaną do operatora,
która nie może być zbyt duża ze względu na ograniczoną jego szybkość reakcji
oraz także zbyt małą biorąc pod uwagę sensowny czas symulacji. Bardzo ważne
jest rozróżnienie pojęcia czasu symulowanego i czasu rzeczywistego obliczeń
symulacyjnych. W przypadku, gdy te czasy pokrywają się można przyjąć, że mamy
do czynienia z tzw. symulacją w czasie rzeczywistym w przeciwnym przypadku
zapewniając stały współczynnik proporcjonalności łatwo określamy symulację z
uwzględnieniem skali czasu.

Biorąc pod uwagę rzeczywiste uwarunkowania czasowe i dodatkowo

połączenie ze wspomnianą wcześniej symulacją interaktywną uzyskuje się
symulator o specyficznych zastosowaniach uwzględniający także procesy ciągłe np.
w celach treningowych lub edukacyjnych. Systemy symulacyjne o takim
charakterze są częściowo omówione w rozdz. 5.5.

W kolejnych rozdziałach omówione będą dwie podstawowe metody symulacji

dyskretnej ze szczególnym uwzględnieniem zastosowanej algorytmizacji.

5.4.1. Metoda planowania zdarzeń.

Metoda planowania zdarzeń (event oriented discrete simulation) oparta jest na

kalendarzu zdarzeń, specjalnej struktury będącej zbiorem opisanych zdarzeń.
Zastosowany kalendarz zdarzeń definiuje kolejność zdarzeń bezwarunkowych

.

123

wraz ze szczegółową specyfikacją czynności, które powinny być zrealizowane po
tym zdarzeniu. Jest to zbiór zawierający dane o typie, atrybutach i czasie
wystąpienia zdarzenia zorganizowany w postaci listy lub kopca. Aktualny czas
wyznacza zawsze pierwsze zdarzenie na liście a uporządkowanie (planowanie)
ustala się na podstawie atrybutów czasów pozostałych zdarzeń. W szczególności
należy:

- zapewnić ogólne sterowanie przebiegiem symulacji w oparciu o dynamiczny

kalendarz zdarzeń,

- zapamiętać w kalendarza tylko zdarzenia bezpośrednio zależne od czasu

(bezwarunkowe),

- zaplanować kolejne zdarzenia bezwarunkowe dla działań, które zostały

określone dla wcześniejszego zdarzenia,

- wprowadzić działania związane z zaistnieniem zdarzenia warunkowego do

czynności dotyczących zdarzeń bezwarunkowych, które będą rozpatrywane
tylko przy okazji działań bezwarunkowych.

Wprowadzanie zdarzeń w systemie ma charakter planowania czasów oraz typów i
parametrów zdarzeń bezwarunkowych, które będą zachodzić w systemie.
Wystąpienie zdarzenia bezwarunkowego w symulacji dyskretnej wg metody
planowania zdarzeń, pociąga za sobą wykonanie sekwencji czynności związanych
z wystąpieniem tego zdarzenia, w tym dotyczących zdarzeń warunkowych.

Przykładowo po zakończeniu obróbki należy zwolnić obrabiarkę, sprawdzić

kolejkę następnych zgłoszonych części do obróbki, a następnie zgodnie z
regulaminem kolejki wprowadzić do obróbki kolejną część. Charakterystyczne w
tej metodzie jest planowanie sposobu generowania następstwa zdarzeń
bezwarunkowych.

Rysunek 5.4 przedstawia szkic algorytmu symulacyjnego omawianej metody

planowania zdarzeń. Algorytm rozpoczyna się ustaleniem stanu początkowego i
parametrami modelu symulacyjnego a także przyjęciem wartości czasu
symulacyjnego, odpowiadającej wartości początkowej czasu rozpoczęcia
pierwszego zdarzenia występującego w kalendarzu. Kolejno należy wykonać
działania związane z obsługą tego zdarzenia. Jest to najbardziej złożona część
algorytmu, ponieważ wśród wykonywanych czynności może zachodzić zdarzenie
bezwarunkowe, czynności zdarzeń warunkowych oraz zaplanowanie poprzez wpis
do kalendarza następnych zdarzeń. W kolejnym etapie należy zaprogramować
usunięcie zrealizowanego zadania z kalendarza i zaktualizować czas symulacji
zgodnie z wystąpieniem następnego zdarzenia bezwarunkowego. Omówione etapy
algorytmu będą cyklicznie powtórzone z badaniem warunku zakończenia symulacji.

.

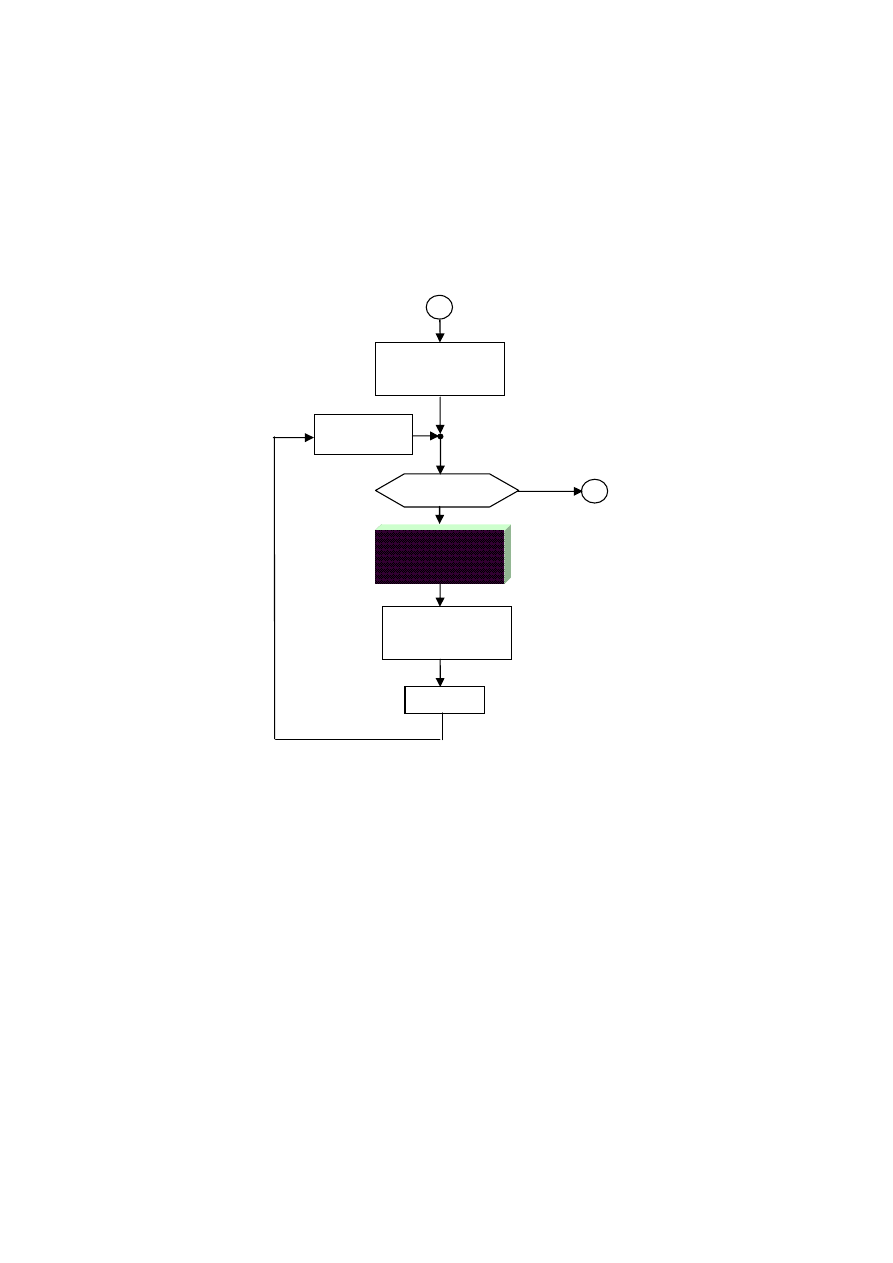
124

Warunki

początkowe

Czy Koniec ?

t

P

= t

N

Usunięcie 1-go

Zdarzenia

T

N

Aktualizacja

czasu

Rys. 5.4 Algorytm planowania zdarzeń.

Działanie 1-go

Zdarzenia

Analizę szczegółowa algorytmu przeprowadzimy na prostym modelu obróbki

na wielu identycznych obrabiarkach. Założymy, że bezwarunkowo następuje
pojawienie się części do obróbki oraz biorąc pod uwagę zadany czas obróbki także
bezwarunkowe jest zdarzenie dotyczące zakończenia obróbki. Natomiast zdarzenie
dotyczące rozpoczęcia obróbki, jest zdarzeniem warunkowym, ponieważ ta
czynność zależy od istnienia, co najmniej jednej wolnej obrabiarki i części do
obróbki.
Zgodnie z ogólnym schematem symulacyjnym Rys 5.4 w pętli głównej istotne jest
określenie opisujące jedynie procedurę związaną z obsługą pierwszego zadania na
liście zadań czasowych bezwarunkowych natomiast złożoność symulacji kryje się
w wykonaniu procedur opisujących realizację tych zadań i ich planowaniu z
uwzględnieniem zadań warunkowych.

.

125

Procedury te dotyczą:
- nadejścia części do obróbki: zaplanowanie przyjęcia następnej części,

sprawdzenie dostępności obrabiarki i odpowiednio zajęcie jej i zaplanowanie
zakończenia obróbki lub w przeciwnym wypadku wstawienie na końcu kolejki.

- zakończenia obróbki: jeżeli jest w kolejce część do obróbki to należy ją usunąć z

kolejki i zaplanować zakończenie jej obróbki a w przeciwnym wypadku
obrabiarka powinna być zwolniona.

Reasumując metoda opiera się na szeregowaniu zdarzeń czasowych i realizacji

zdarzeń warunkowych w ramach procedur czasowych. W złożonych problemach w
porządkowaniu zdarzeń oprócz omówionego typowego wstawiania nowych zadań
oraz ich usuwania mogą również zachodzić zdarzenia związane z odwołaniem
zdarzeń lub ich realokacją związaną ze zmianą czasu ich wystąpienia.

Ponadto powiększeniu może ulec także ilością zdarzeń i wtedy istotne może być

zastosowanie odpowiednich struktur danych i algorytmów które zapewnią
optymalna złożoność obliczeniową w realizacji opisanych operacji.

5.4.2. Metoda przeglądania działań.

Algorytm metody przeglądu i wyboru działań (activity scanning approach)

polega na wyborze działań, które z nich z chwilą zajścia określonego zdarzenia
powinny być rozpoczęte, a które zakończone. Wyboru dokonuje się przeglądając
wszystkie zadania zależne od czasu jak i od stanu systemu i wybór działań polega
na rozpatrywaniu wszystkich działań systemu celem określenia, które z nich z
chwilą zajścia określonego zdarzenia powinny być rozpoczęte, a które zakończone.
Atrybuty czasowe obiektów mogą określać chwilę symulowanego czasu (charakter
bezwzględny) lub czas pozostający do pojawienia się zdarzenia (charakter
względny). Wynikają stąd dwa przypadki algorytmu aktualizacji czasu, które
przebiegają następująco:
I. Czas względny

1. wybieranie najmniejszego dodatniego atrybutu czasu t

min

2. zmniejszenie wszystkich atrybutów czasy o t

min

3. dodanie t

min

do czasu systemowego.

II Czas bezwzględny

1. wybieranie najmniejszego dodatniego atrybutu czasu t

min

większego od

czasu systemowego,

2. przyjęcie t

min

jako czas systemowy

Oznacza to:

-

wprowadzenie do kalendarza zdarzeń bezwarunkowych, bezpośrednio
zależnych od czasu oraz zdarzeń warunkowych,

.

126

-

rozpatrywanie czynności związanych ze zdarzeniami warunkowymi
niezależnie od wystąpienia zdarzeń bezwarunkowych,

-

sterowanie przebiegiem symulacji w oparciu o listę warunków, jakie
powinny być spełnione by zaszło w systemie określone zdarzenie.

Wprowadzanie zdarzeń w systemie odbywa się poprzez cykliczne sprawdzanie
listy warunków, które powinny być spełniane przy zachodzeniu zdarzeń.

Algorytm przebiegu symulacji modelu zbudowanego w oparciu o metodę

przeglądu i wyboru działań przedstawia rysunek 5.4. Po ustaleniu warunków
początkowych systemu (stan początkowy systemu, parametry systemu) należy
wykonać badanie listy warunków wystąpienia zdarzeń dla chwili czasu systemu, w
której zajdzie najbliższe zdarzenie (t

min

). Jeżeli dla określonego zdarzenia spełnione

są warunki jego zajścia, to oznacza to, że doszło do zajścia tego zdarzenia (zmiany
stanu systemu) i należy wtedy przesunąć czas systemu do chwili t

min

wystąpienia

tego zdarzenia i wykonać procedurę czynności związanych z tym zdarzeniem
(obsługi zdarzenia). Powyższe czynności ulegają powtórzeniu z badaniem warunku
zakończenia obliczeń symulacyjnych.

Rozpatrzmy przykładową symulację wielokanałowego, otwartego systemu

obsługi. Konstrukcja modelu symulacyjnego opisującego ten system przy
zastosowaniu metody przeglądu i wyboru działań oparta jest na analizie warunków
zajścia wszystkich zdarzeń systemu, bezwarunkowych i warunkowych. Algorytm
symulacji funkcjonowania tego systemu obsługi jest następujący:

1.

Ustalenie warunków początkowych.

2.

Sprawdzenie, czy spełniony jest jakikolwiek warunek końca symulacji i
gdy jest spełniony, to zakończenie obliczeń symulacyjnych, w przeciwnym
przypadku przejdź do kroku 3.

3.

Skasuj flagę zmiany stanu (będzie ustawiana w chwili zmiany stanu)

4.

Sprawdzenie dla wszystkich zdarzeń warunków ich zajścia i jeżeli warunek
ten jest spełniony, to wykonanie czynności obsługi tego zdarzenia i
ustawienie flagi zmiany stanu.

5.

Jeżeli flaga zmiany stanu jest ustawiona to powrót do pkt 3

6.

Zwiększenie czasu systemowego i przejście do kroku 2.

Inny przypadek zastosowania algorytmu przeglądu przedstawiono na Rys 5.6,.

Jest to specjalistyczny algorytm programu realizujący symulację sieci Petriego
wraz optymalizacją i z generacją wykresów Gantta Rys 5.7.

.

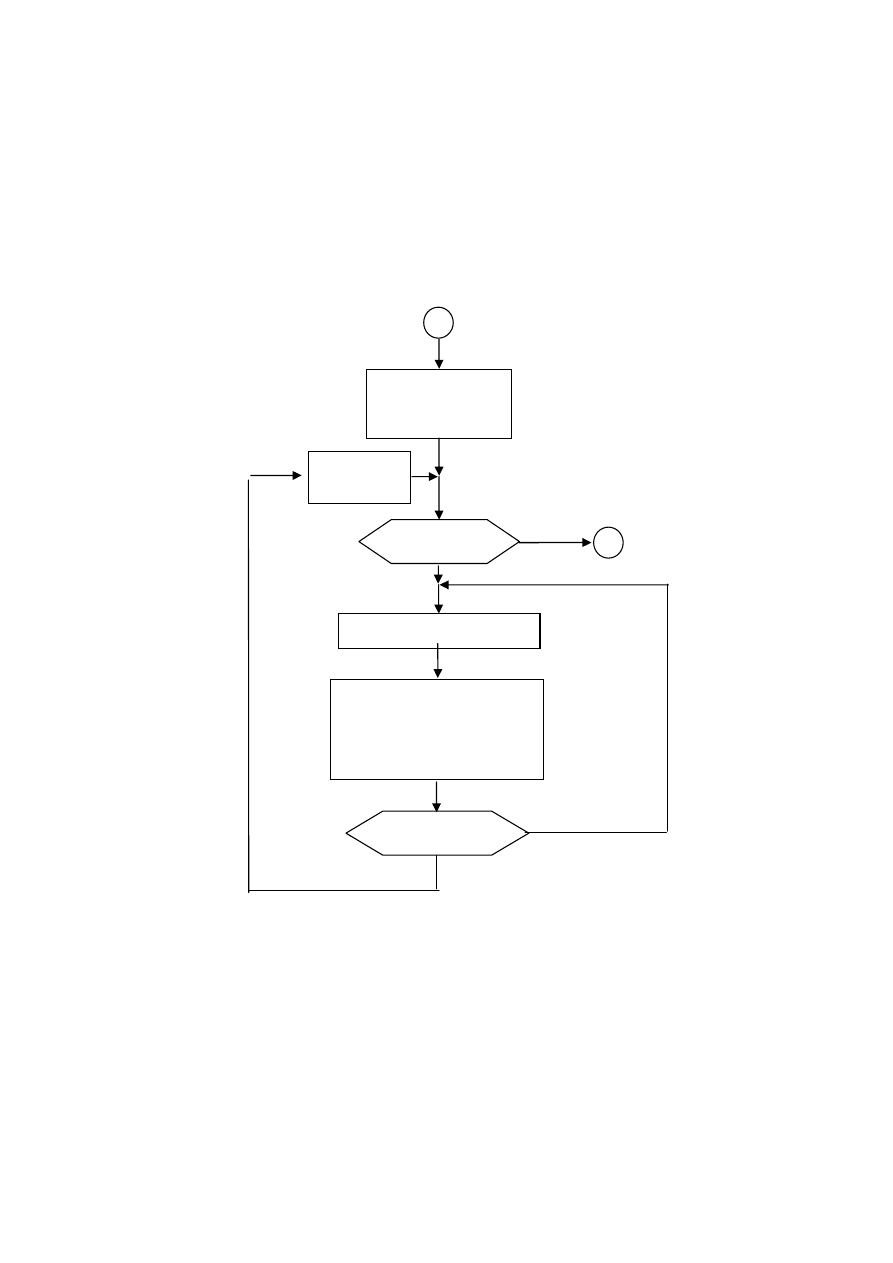
127

Warunki

początkowe

Czy Koniec ?

T

N

aktualizacja

czasu

Rys. 5.5. Algorytm przebiegu symulacji dyskretnej

w metodzie przeglądu działań.

Obsługa zdarzeń

Warunki zajścia zdarzeń

z ustawieniem flagi

zmianu stanu

flaga zmiany ?

skasuj flage zmiany stanu

T

.

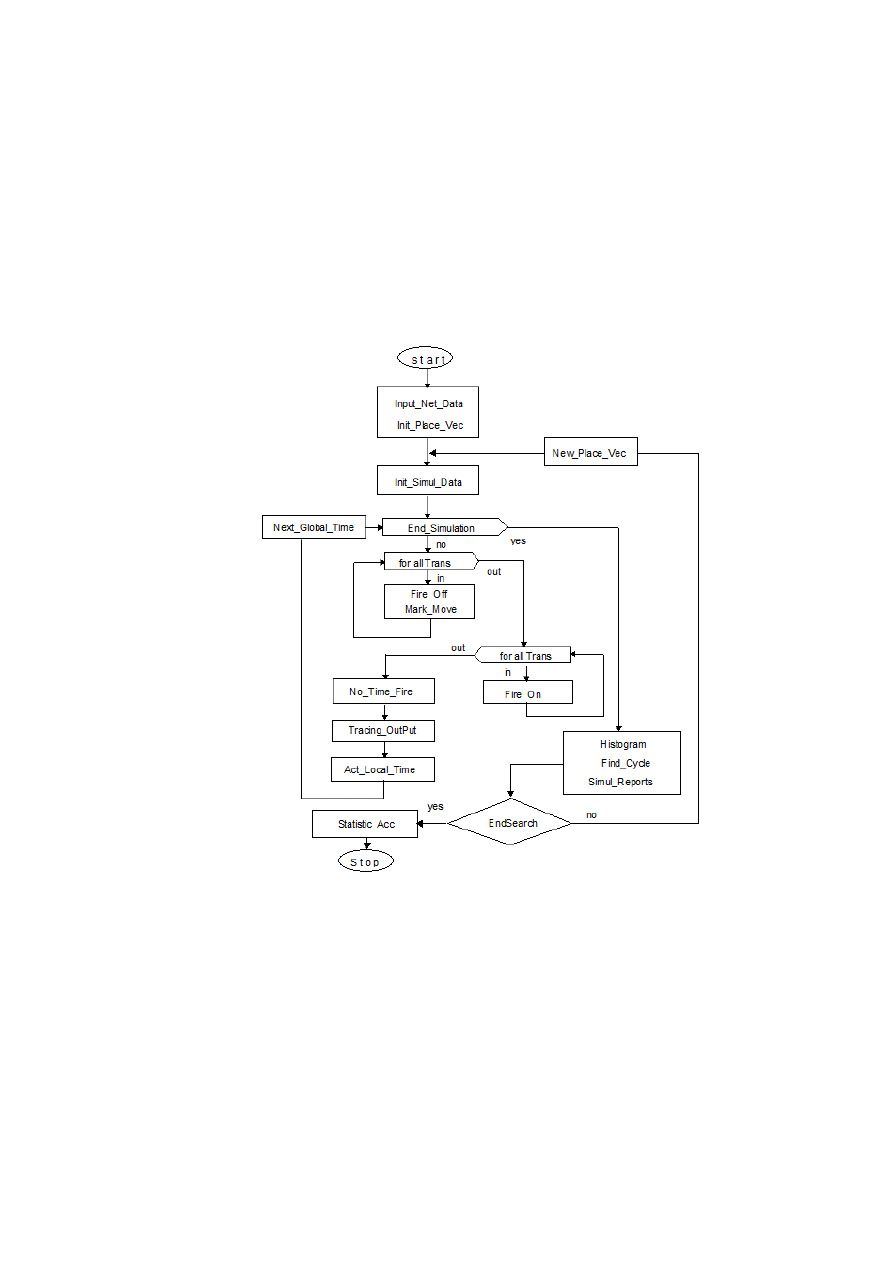
128

Rys 5.6 Algorytm symulatora sieci Petriego

.

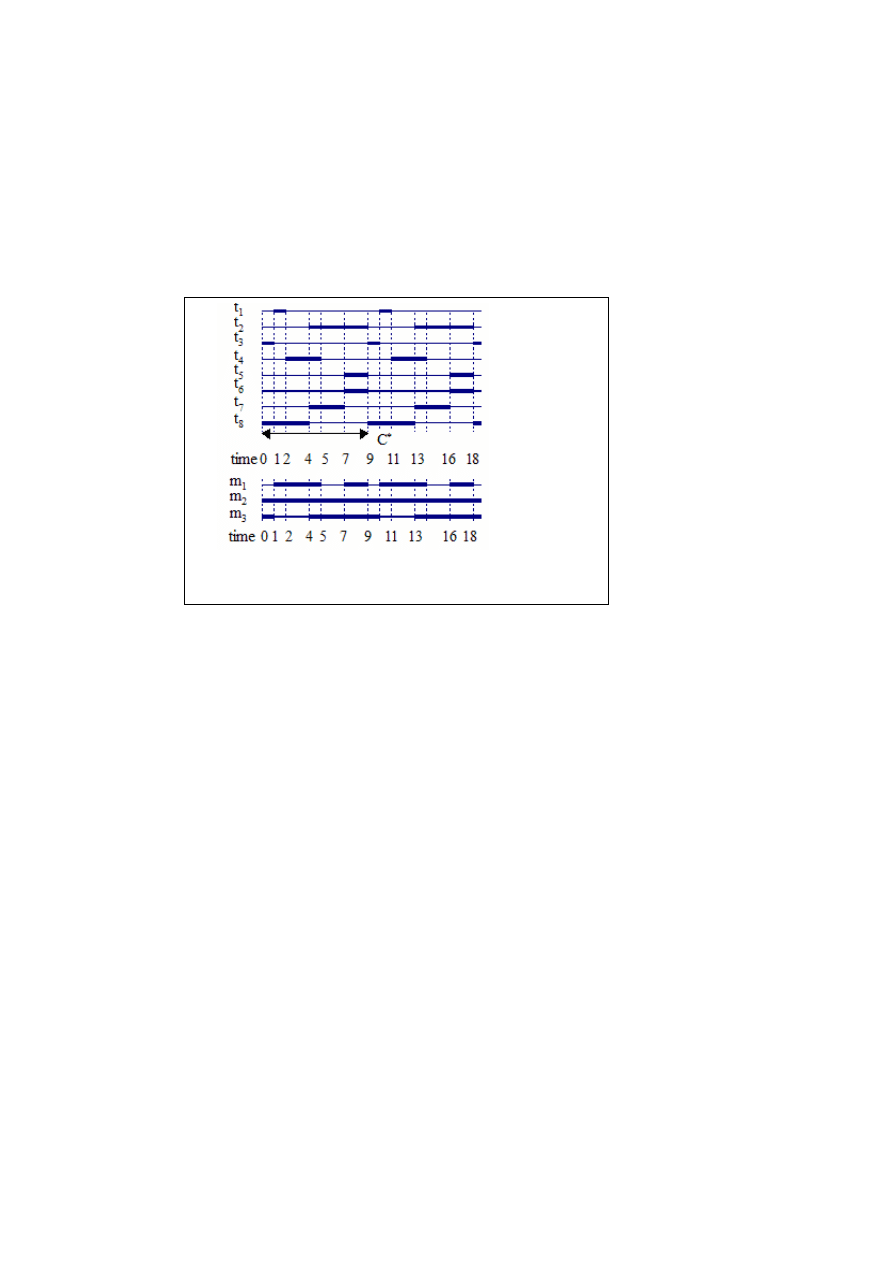
129

Opis podstawowych procedur algorytmu z rys 5.

 Input_Net_Data - dane wejściowe struktura i stałe parametry sieci,
 Init_Place_Vec - dane inicjujące wartości znakowania początkowego,
 Init_Simul_Data - warunki początkowe symulacji (np globalny czas),
 End_Simulation - warunki zakończenia symulacji (odtwarzanie stanów),
 Fire_Off

- zakończenie wzbudzenia tranzycji,

 Mark_Move

- określenie nowego znakowania osiągalnego,

 Freon

- uwarunkowane wzbudzenie tranzycji,

 No_Time_Fire

- zmiana stanu dla tranzycji o zerowym czasie wzbudzenia,

 Tracing_Output - zapamiętanie bieżącego stanu z ewentualną wizualizacją,
 Next_Global_Time - obliczenie następnej chwili zmiany znakowania,
 Act_Local_Times - obliczenie i aktualizacja lokalnych czasów (zegarów)
 Histogram

- histogramowa analiza wyników symulacji,

 Find_Cycle

- określenie czasu cyklu pracy systemu,

 Simul_Reports

- obliczenie i zapamiętanie wskaźników jakości,



EndSearch

- warunki zakończenia przeglądu,

 Statistic_Acc

- obróbka statystyczna dopuszczalnych rozwiązań

Rys 5.7 Przykładowe wyniki z symulatora sieci Petriego

.

130

5.4.3. Przegląd innych metod.

W rozdziale zostały przedstawione jedynie wybrane podstawowe algorytmy

symulacji dyskretnej. Wraz z rozwojem zarówno ogólnych pakietów
symulacyjnych a także specjalistycznych pojawiają się także nowe metody
symulacji. Budowane są także biblioteki procedur, które można wykorzystać w
modelowaniu wykorzystując ogólno dostępne języki programowania. Bardzo
często nowe metody powstają na bazie innych metod i są one oparte na opisanych
metodach łącząc zalety metody planowania i przeglądu. Do takich metod należy
metoda ABC łącząca omówione metody. Z metody planowania przyjęty jest czas
pierwszego zdarzenia (Advance of simulation time), wybór jego obsługi (Bounded
event) i usuniecie z kolejki. Z kolei metoda przeglądu wprowadza uwzględnienie
zdarzeń warunkowych (Conditional events) ich wybór i wykonanie. włączając w
algorytm kontrolę flagi zmiany stanu. Powstają także pewne modyfikacje gdzie
przykładem może być metoda przeglądu i wyboru działań, która z kolei w
połączeniu z metodą planowania określana jest jako metoda interakcji procesów
(process interaction approach). W tych rozwiązaniach stosuje się metody
aktywowania, zawieszania i opóźniania procesów.

W efektywnym projektowaniu programu w szczególności dla złożonych

problemów, konieczny jest podział funkcjonalny i strukturalny. Taki podział
pozwala też na implementacje gotowych do wykorzystania uniwersalnych bibliotek
procedur W związku z tym przedstawiona zostanie koncepcja tzw. podejścia
trójwarstwowego [Fishman, George S „Concepts and methods in discrete event
digital simulation”] Zakłada ona występowanie trzech warstw
- poziom koordynatora (Executive), który przejmuje rolę zarządzającą przebiegi

symulacji (aktualizacja czasu sterowanie wykonywaniem procedur i
zakończeniem symulacji.

- poziom procedur (Operations) zasadnicze funkcje programu, które mogą być

zgrupowane jako moduły i przyporządkowane do danych obiektów, mogą też
być różnymi blokami procedur, które są wykonane przez obiekty.

- poziom pomocniczy (Detailed routines) będący zbiorem procedur wspomagają-

cych warstwę procedur (np. generatory liczb losowych, generatory statystyk i
ich wykresów, procedury kontroli błędów itp.)

Wyróżnione są cztery typy koordynatorów:
- Zdarzeniowy (Event)
- Działaniowy (Activity)
- Procesowy (Process)
- Podejście trójfazowe (The three-phase approach)

Szczegółowy opis można znaleźć w literaturze [Micheal Pidd "Computer

Simulation in Management Science] i na stronach internetowych.

.

131

W opisach bardzo często zachodzi duże podobieństwo, które trudno ściśle

sprecyzować w przypadku ich ogólnego charakteru. Stąd często różnicy de facto
nie ma a wynika jedynie z zastosowanego nazewnictwa. W związku z powstaniem
nowych języków lub raczej rozbudowy ich dotychczasowych wersji np przez
wprowadzenie elementów programowania obiektowego powstają nowe metody
symulacyjne, które bazując na podstawowych algorytmach wykorzystują elementy
programowania obiektowego. W wyniku takich działań powstaje szereg bibliotek
dla różnych języków np dla języka Java.

Wśród programistów zajmujących się budowaniem modeli symulacyjnych

pewną popularność uzyskał oparty na Javie obiektowy Framework Desmo-J

http://desmoj.sourceforge.net/home.html

http://asiwww.informatik.unihamburg.de/themen/sim/forschung/Simulation/Desmo-J/

Skrót „DESMO-J" pochodzi od słów "Discrete Event Simulation and MOdelling in
Java" i sama już nazwa wskazuje na dwie istotne właściwości:
Desmo-J wspiera paradygmat symulacji dyskretnych zdarzeń spełniając

wszystkie wymagania symulacji zdarzeń występujących w dyskretnych
punktach czasu.

Desmo-J jest zaimplementowana w powszechnie uzywanym przez programistów
języku Java.

Framework DESMO-J posiada wiele cech, które znacznie ułatwiają projektowanie
symulacji w postaci:

- zestawu komponentów takich jak: kolejki, generatory liczb pseudolosowych i

kolekcje danych określające zachowanie modeli, bytów, wydarzeń czy
procesów i abstrakcyjne klasy, które zmuszają programistę do projektowania
zgodnie z przyjętymi zasadami.

- infrastrukturę symulacji tzn.: środowisko planowania, listę wydarzeń i zegar

czasu symulacji

- automatyczne generatory raportów z przebiegu symulacji na podstawie

informacji pobieranej z każdego symulowanego obiektu

DESMO-J jest zbudowana z wielu pakietów:

.

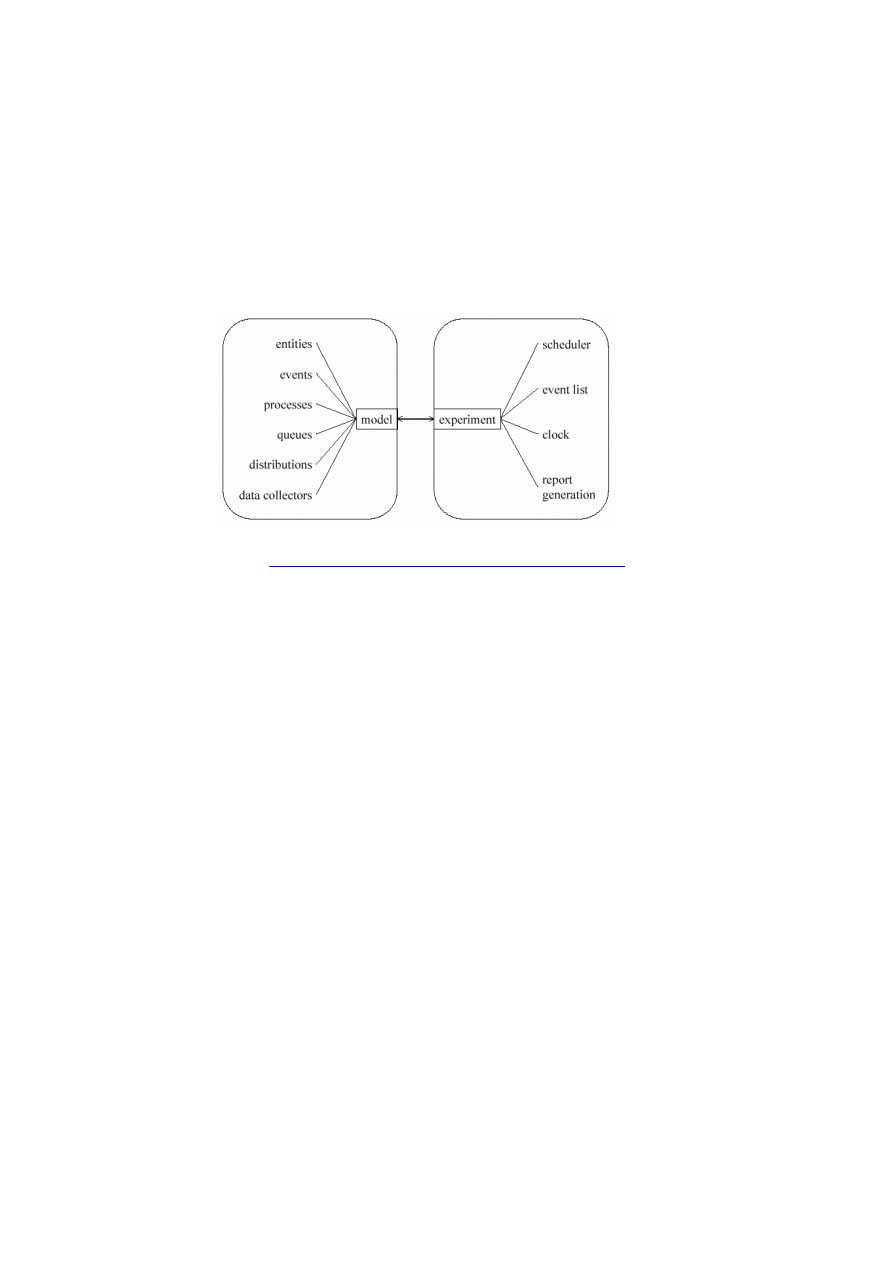
132

 desmoj.core.simulator - zawiera klasy rdzenia, wykorzystywane

do zbudowania modelu i rozpoczęcia eksperymentu

 desmoj.core.dist – jest źródłem metod generujących liczby

pseudolosowe

 desmoj.core.exception zawiera klasy dla wewnętrznego

obsługiwania wyjątków i może bezpiecznie zostać zignorowany przez
programistów.

 desmoj.core.report - automatyczne generowanie raportów w wielu

formatach, najczęściej w formacie XML.

 desmoj.core.statistic – wspiera opracowanie wyników

statycznych generowanych po zakończonej symulacji – obejmują funkcje:
max, min, średnia, odchylenie standardowe, histogram, suma.

 desmoj.core.advancedModellingFeatures – posiada

mechanizmy zapewniające zaawansowaną na poziomie abstrakcyjnym
synchronizację przebiegu symulacji.

 desmoj.extension.

zawiera składniki,ułatwiające budowanie

modelu w domenach aplikacji np logistyka i produkcja.

 desmoj.extension experimentation - podstawowy graficzny

interfejs użytkownika ułatwiający prowadzenie eksperymentu i prezentacje
wyników w technologich 2d i 3d

źródłó

http://desmoj.sourceforge.net/basic_features.html

.

133

5.5. Sterowanie i monitoring procesów dyskretno-ciągłych

5.5.1.Założenia projektowe.

Systemy monitoringu i sterowanie procesami technologicznymi z obsługą
przerwań czasowych i sprzętowych z reguły posiadają następujący zakres
funkcjonalności,
1.

Odbiór danych sygnałów ciągłych i dyskretnych: analogowe, impulsowe,
binarne i stany obiektów.

2.

Wysyłanie danych lokalnych i retransmisja odebranych do stacji nadrzędnych.

3.

Rejestracja danych z obiektów technologicznych w tablicach systemowych.

4.

Wizualizacja znakowa pomiarów i stanu obiektów na ekranach synoptycznych
a także z uwzględnieniem animacji graficznej stanu i pomiarów dla
wybranych procesów.

5.

Rejestrowanie i archiwizacja stanów awaryjnych.

6.

Sygnalizacja wizualna i dźwiękowa zdarzeń i sytuacji awaryjnych.

7.

Obsługa na ekranie zestawu o zaistniałych zdarzeniach i sytuacjach
awaryjnych i z podaniem aktualnego ich statusu.

8.

Raportowanie danych w zadanym zakresie czasu i poziomie dyskretyzacji i
wyników zagregowanych w określonych przedziałach czasowych.

9.

Monitorowanie stanu transmisji w sieciowej strukturze sterowników.

10. Wysyłanie i odbiór poczty komputerowej.
11. Przygotowanie danych (kompresja) dla tablicy synoptycznej).
12. Zestawienie komend i poleceń sterujących, pomoc.
13. Obsługa menu systemowego (GUI) użytkownika.
14. Obsługa konserwatorska i testująca stany pracy sytemu.

Zakres zadań i wyposażenie na poziomach hierarchicznego rozproszonego systemu
(Rys.5.8)

1. Poziom Centralny(CentrCtr) - konsola operatorska, synoptyka graficzna,

raporty, archiwizacja, badanie trendów, transmisja globalna, retransmisja.

2. Regionalny (RegCtr) - konsola operatorska, ekran tryb graficzny, agregacja

danych, raporty, archiwizacja, transmisja, obsługa tablicy synoptycznej.

3. Lokalny (LocCtr) - konsola operatorska, ekran tekstowo-semigraficzny,

transmisja globalna, agregacja, skalowanie, obsługa komend sterowania
zdalnego.

4. Obiektowy (ObjCtr) - brak stałej konsoli, obsługa mikroprocesorowa: odczyt z

układów AKP, obsługa sterownia, algorytmy regulacji bezpośredniej,
transmisja lokalna

.

.

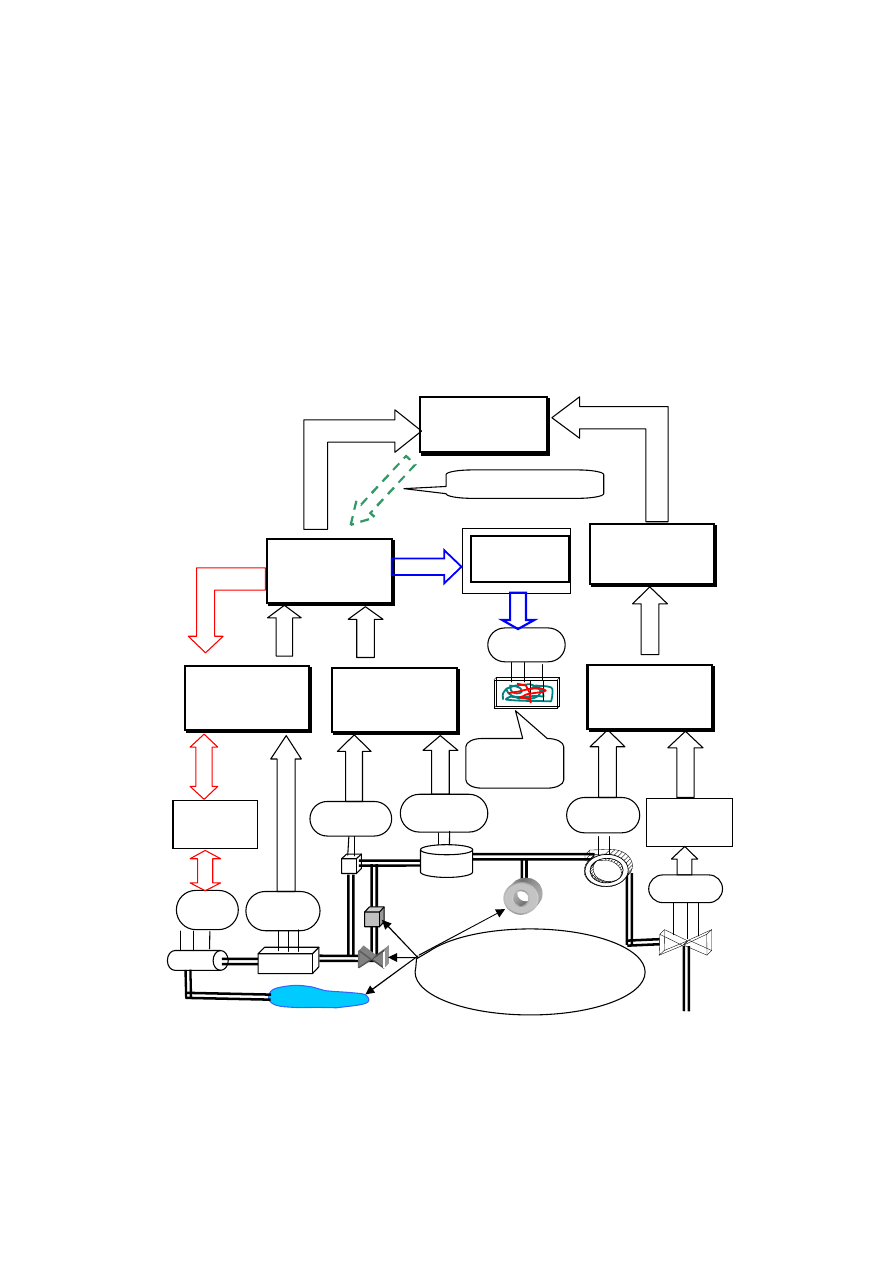
134

5. Obiekty (Obj n) Automatyki Kontrolno Pomiarowej (AKP): układy pomiarowe,

czujniki, przetworniki A/C i C/A, liczniki, rejestry, inne układy i bramki
logiczne, specjalizowane układy mikroprocesorowe.

6. Obiekty Procesu Technologicznego - (urządzenia i media technologiczne)

napędy maszyn roboczych, materiały, surowce, układy: transportowe, zasilające,
kontrolujące i sterujące.

CentrCtr

Adr 000

ObjCtr

Adr 111

RegCtr

Adr 100

RegCtr

Adr 200

LocCtr

Adr 110

LocCtr

Adr 120

LocCtr

Adr 210

ObjCtr

Adr TSN

TSN

Obj A

TSN

Obj B

Obj C

Obj F

Obj E

Obj D

obiekty poza sytemowe,
tylko wizualizacja brak
pomiarów i sterowania.

retransmisja

ObjCtrAd

r

211

tablica
synoptyczn
a

Rys. 5.8. Wyposażenie poziomów hierarchicznego systemu

.

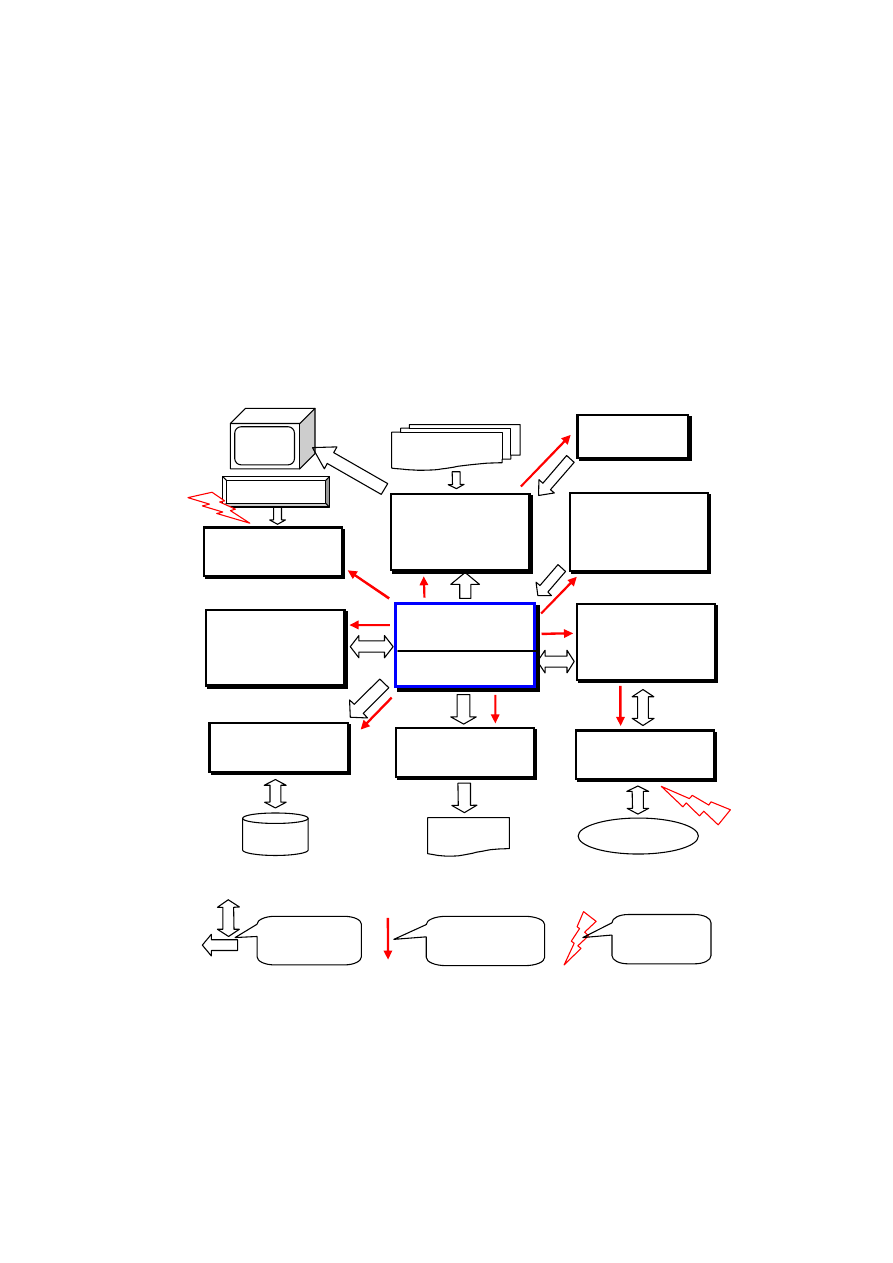
135

Realizacja tak złożonych zadań wymaga ścisłej klasyfikacji wszystkich
projektowanych funkcji i zgrupowania ich w funkcjonalnych modułach. Na
rysunku (Rys 5.9) przedstawiono pewien przykładowy ogólny podział na takie
moduły. Z założonej funkcjonalności wynika także, opracowanie odpowiednich
struktur danych i związków zachodzących między nimi, które zapewnią efektywny
do nich dostęp i ich obsługę. Rozwiązanie tego problemu będzie przedmiotem
ćwiczeń.

Prog. Główny

stzuw

110

Dane Systemu

Obsł. Konsoli

console

Obsługa

Ekranów

display

Obsługa

Transmisji

obstra

Transmisja

transm

Archiwizacja

archiv

Obsł. przerw.

czasowych

timedate

Inicjalizacja

Konfiguracja

conf

110

Raporty

reports

Disk

Printer

Sieć

monitor

Keybord

obiekty ekran

synopt

ekr

110

??

strumienie

danych

wywoływanie

funkcji

obsługa
przerwań

Rys. 5.9. Schemat związków międzymodułowych

.

136

5.5.2. Przykłady aplikacji monitoringu procesów technologicznych.

Ćwiczenia
Przedstawione w pkt. 5.5.1 założenia doczekały się praktycznej realizacji, w
postaci dwóch aplikacji. Ze względu na ich historyczny charakter (lata 1989-92 i
1994-97) posiadają one dość rygorystyczne ograniczenia w zakresie interakcji z
użytkownikiem wynikające z limitowanego w tamtych czasach dostępu do
wielkości i jakości sprzętu a także oprogramowania. Warto jednak poznać te
rozwiązania ponieważ one dalej obowiązują tylko, że są ukryte w złożonych
procedurach i dostępne na najniższym poziomie w profesjonalnych rozwiązaniach.
Uwaga:

path/

oznacza indywidualną ścieżkę do przekopiowanych z serwera

materiałów do ćwiczeń

A. Uruchomienie aplikacji RPW (Rys 5.10)
1. Zmień rozdzielczość ekranu na 800x600 i włącz autoukrywanie paska zadań w

menu Start

2. W katalogu path

/

cw5/RPW uruchomić s.bat

3. Przejść na ekrany ZUW, KP3, Nastawn, wykonać sterowanie wybraną zasuwą.
4. Prześledzić opis stanu obiektów i pomiarów na ekranie Legenda, wysłać pocztę

i zakończyć program

Rys. 5.10. Ekran główny RPW

.

137

.

138

Rys. 5.11. Ekran KP4 – sterowanie zasuwą

Rys. 5.12. Ekran ZUW

.

139

B. Aplikacji konsolowa na platformie systemu Win XP – Rys. 5.13
1. W katalogu

path

/

cw5/zuw/ uruchomić s.bat.

2. Przejść klawiszami strzałek na ekran Zbiorniki RII )

3. Włączyć CapsLock (symulacja awarii transmisji) i po pewnym czasie

wyłączyć (ok ½ minuty) zaobserwować i zinterpretować efekt migotania
danych na ekranach.

4. Przejść na ekran Awarie (Rys 5.14) – wykonać strzałkami przewijanie ekranu.
5. Podjąć próbę odbioru poczty (menu główne) – obsłużyć komunikat.
6. Napisać i wysłać pocztę ( menu główne – nadrzędne)

Rys 1.2

Rys. 5.14. Ekran awarii

Rys. 5.13. Ekran Zbiorniki

.

140

C. Opracowanie algorytmu programu testującego przerwanie i projektu
podstawowej obsługi.

Na tym etapie zostanie uruchomiony i przetestowany przykład programu

będący niewielkim ale podstawowym fragmentem z zaprezentowanych w punktach
A i B złożonych funkcjonalnie aplikacji. Fragment ten dotyczy między innymi
dyskretnego synchronicznego w czasie procesu wyświetlania danych pomiarowych
na ekranie. Należy podkreślić że większość zdarzeń w omawianych systemach jest
czasowo uwarunkowana (np: animacje, dźwięki, synchroniczna transmisja,
timeout’y określające czasy reakcji użytkownika na wybrane zdarzenia itp.).
Ponadto istotnym założeniem jest bezpośrednie wykorzystanie obsługi przerwania
czasowego sterowanego impulsami zegara czasu rzeczywistego pozwalające na
bardzo szybką i niezawodną obsługę zdarzeń. Szybkość i niezawodność obsługi
jest często bardzo istotnym warunkiem realizacji sterowania procesami
szybkozmiennymi i ważnymi z punktu widzenia bezpiecznego ich przebiegu.
Zadanie dotyczy uruchomienia aplikacji konsolowej.

1. W katalogu path

/

cw6/

uruchomic ztint1.exe. (zad. time interrupt)

2. Zaobserwować na ekranie (Rys 5.15) zmiany czasu, animację mijających

sekund oraz wydruk wartości z 1 sekundowym time'outem.

3. W katalogu path

/

cw6/

uruchomić ztint2.exe.

4. Wykonać polecenia z klawiatury: wpisz tekst i steruj strzałkami.
5. Uruchomić jeszcze np 2 razy aplikacje ztint1.exe i zaobserwować

równoległą realizację wszystkich procesów obliczeniowych (obserwowana
współbieżność była prawidłowo zrealizowana dopiero od wersji. Windows
NT )

6. Wybrać wersję kompilatora TC2 lub MC4, wchodząc do odpowiedniego

katalogu i zapoznać się z funkcjami obsługi przerwania czasowego testując
wskazany program źródłowy:. zmodyfikować wydruk, wygenerować sygnał
dźwiękowy.

a) wer. TC2. plik

path

/

cw

6/tc2/c

tintc.c

:zapoznać się z funkcjami

w programie oraz edytorem tc, kompilacją i wykonaniem Ctrl+F9

b) wer. MC4 plik

path

/

cw

6/ctint

.c

: zapoznać się z funkcjami w

programie z edytorem - mec , kompilacją - ct, linkowaniem - lkt i
wykonaniem ctint

7. Opracować algorytm obsługi wydruku i następnie pozostałych operacji

odwołując się do obsługi przerwań z zegara i z klawiatury i wzorując się na
działaniu ztint1.exe, Na podstawie opracowanego algorytmu napisać
program zad5.c. Uwaga w zadaniu wykorzystać wstępnie przygotowany
program z procedurami obsługi przerwań plik ctintc.c

.

141

8. Opracować własny projekt programu modelującego układ rzeczywisty.

Wzorując się na działaniu ztint2.exe, rozszerzyć obsługę zdarzeń i
procesów dyskretnych wzbogacając program o własne pomysły. Opracować i
załączyć do projektu strukturę danych, przeprowadzić symulację testującą

Rys. 5.15. Ekrany dla programów zad1mtime i zad2mtime

.

142

program żródłowy ctintc.c

/**************************************************************************
* *
* PROGRAM CTINTC.C *
* *
* Test procedur zarzadzajacych obsluga przerwania czasowego *
* *
**************************************************************************/

#define MAIN
#include <conio.h>

/* int getch(void); int kbhit(void); */

#include <stdio.h>

/* sprintf(tekst,wzorzec, par,...), puts(tekst),

int cprintf(*char),int putch(int),int ungetch(int);*/

#include <dos.h>

/* getvect(INT), setvect(INT, Funkcja ) */

#include <time.h>

/* time_t czas; time( &czas );

tt = *localtime( &czas ); struct tm tt; */

#define INT 0x1C

/* numer dla przerwania czasowego 18 razy na sek */

/* Prototypy funkcji wlasnych modulu */

void Intr_Init( void );
void interrupt far Intr_Obsluga( void );
void Intr_Close( void );

static void (interrupt far * intr_old )();

/* poprzednie przerwanie */

/*-----------------------------------------------------------------------
| PROCEDURA Intr_Init
| CEL: Procedura inicjalizuje obsługę - przerwania czasowego kod 1C.
| PARAMETRY: brak.
| ODWOLANIA:
| -----------------------------------------------------------------------*/

void Intr_Init( void ) {
intr_old = getvect( INT );

/*zapamietaj aktualna obsługe*/

setvect( INT, Intr_Obsluga);

/* ustaw nową obsługę */

}

/*--------------------------------------------------------------------------
| PROCEDURA Intr_Close
| CEL: Procedura odtwarza obsługę przerwania czasowego
| PARAMETRY: brak.
| ODWOLANIA:
-------------------------------------------------------------------------*/

void Intr_Close( void ) {
setvect(INT, intr_old);

/*odtworzenie obsługi przerwania*/

}

/*--------------------------------------------------------------------------
| PROCEDURA Intr_Obsluga( void ){
| CEL: Procedura obsługiwana przez przerwanie czasowe
| PARAMETRY: brak.
| ODWOLANIA:
-------------------------------------------------------------------------*/

.

143

void interrupt far Intr_Obsluga( void ){

/* ????????????
tutaj napisz kod funkcji zgodny z
opracowanym na ćwiczeniach algorytmem symulacji . */

};

/*--------------------------------------------------------------------------
| PROCEDURA MAIN
| CEL: Koordynuje i obsługuje podstawowe zadania systemu ...
| PARAMETRY: brak.
| ODWOLANIA:
-------------------------------------------------------------------------*/

int main()
{

// PROGRAM testujacy

int i=15000;

char buf1[80];
clrscr();

// MS4 system("cls");

Intr_Init();
gotoxy(40,10);

// MS4 _settextposition(10,40);

sprintf(buf1,"%10d",i);
cprintf(buf1);

// MS4 _outtext(buf1)

Intr_Close();
gotoxy(25,20);
getch();
return 0;
}

.

144

5.6 Systemy SCADA/HMI

Systemy pozyskiwania danych procesowych z graficzną wizualizacją

SCADA/HMI (Supervisory Control And Data Acquisition/Human Machine
Interface).

I. Uruchomienie przykładowego projektu (Rys 5.16).

1. Wykonać kopię katalogu cw7 w

"C:\Documents and Settings\

swoj_login

”

2. Otworzyć okno poleceń (konsolę) w katalogu

"C:\Documents and Settings\

swoj_login

\cw7

”

3. Uruchomić log

swoj_login

(mapowanie katalogu na dysk K:)

4. Uruchomić programy do komunikacji DDE, np Excel Zeszyt1.xls

Histdata,

tymczasowo zatrzymać aktualizację łącza, ustawić dla

uwikłanych formuł:

Narzędzia/Opcje/Przeliczanie – Iteracje = Tak ,
Maksymalna liczba iteracji = 1

5. Uruchomić w trybie wykonywalnym (Viewer - runtime) intouch

wskazać K:\newapp\example i kliknąć prawą ikonę,
zignorować brak klucza i potwierdzić wybór okno2

dokończyć aktualizację łącza DDE np.Excel Zeszyt1.xls

6. Uruchomić w trybie projektowania okien (Window Maker)

intouch

wybrać projekt K:\newapp\example\

i kliknąć lewą ikonę) a następnie zignorować brak klucza i potwierdzić
wybór okno2

II. Wizualizacja i sterowanie w przykładowym modelu układu.

7. Obsłużyć kolejno:

- przycisk lub przełącznik lub tekst [Wyłączony/Załączony] lub Ctrl+Shift+S,
- zaobserwować linię czasu na wykresie,
- zmienić Ciśnienie i Force
- zaobserwować pojawianie się i odwoływanie alarmów i oraz zmiany na

wykresie,

- nacisnąć przycisk, moto 10[On/Off],
- zaobserwować wyniki na przyrządzie wskazówkowym oraz w opisach

tekstowych nacisnąć przycisk Otwórz Okno o1,

- zmodyfikować okres trendu historycznego zmienić parametr i zamknąć okno
8. Powrót na ekran projektowania i przegląd elementów modelu układu.

.

145

9. Słownik zmiennych systemowych (ze znakiem $) oraz użytkownika menu

Special/ Tagname Dictionary/ Select.

10. Skrypty i właściwości wyzwalające zdarzenia wg pkt 7 ( Double Click)
- ogólne aplikacji - menu Special/ Scripts/ Application Scripts/ On Startup
- obiektów – np podwójne kliknięcie przycisku moto / Action / On Key Down
- tekst Zal/Wył., obsługa okna Sterowanie Message i przycisków On /Off i

klawisza Ctrl+Shift+S

- tekst Alarm, obsługa kolorów i migotania Sterowanie Message
- Force, realizacja Next Links dla opcji

User Inputs = Analog Text Color = Analog zaobserwować zmianę kolorów

11. Realizacja pozostałych elementów - kliknij na wykres oraz wybrane obiekty
- zinterpretuj parametry modelu układu

12. Realizacja połączenia DDE np. Intouch => Excel

Zeszyt1.A4 = VIEW|TAGNAME ! t0

Zeszyt1.A1 = VIEW | TAGNAME ! Cisnienie

Zeszyt1.B1= 25 los()=> Zakłocenie Cisnienia(ZmDDE)

5.16a Przykładowe okno aplikacji

.

146

5.16b Przykładowa konfiguracja kanału DDE obiekt

5.16 c Przykładowa konfiguracja kanału DDE system

.

147

Realizacja prostego projektu - na dowolnie wybrany temat


Opracowanie projektu prostej aplikacji - wizualizacja i sterowanie wybranym
układem z wykorzystać połączenie dwukierunkowego DDE
- wykorzystać narzędzia (Rys 5.17) do zamodelowania ekranów synoptycznych
własnego projektu)

Przykładowy ekran projektu przedstawia Rys 5.18

5.16 d. Przykładowa konfiguracja kanału DDE system cd

Real-Time
Trend

Button

Wizard

Rys 5.17 Narzędzia do projektowania okien

.

148

Intouch ver 10.0

Aktualnie firma Wonderware udostępnia wersję Demo w wersji 10.0,

której wybrane ekrany Rys 19, … Rys 21- przedstawiają aplikację w stanie
edycji modelu a Rys 22. w stanie symulacji Na ćwiczeniach należy
zapoznać się z rozszerzona funkcjonalnością tej wersji.

Rys 5.18 Przykładowy ekran projektu

.

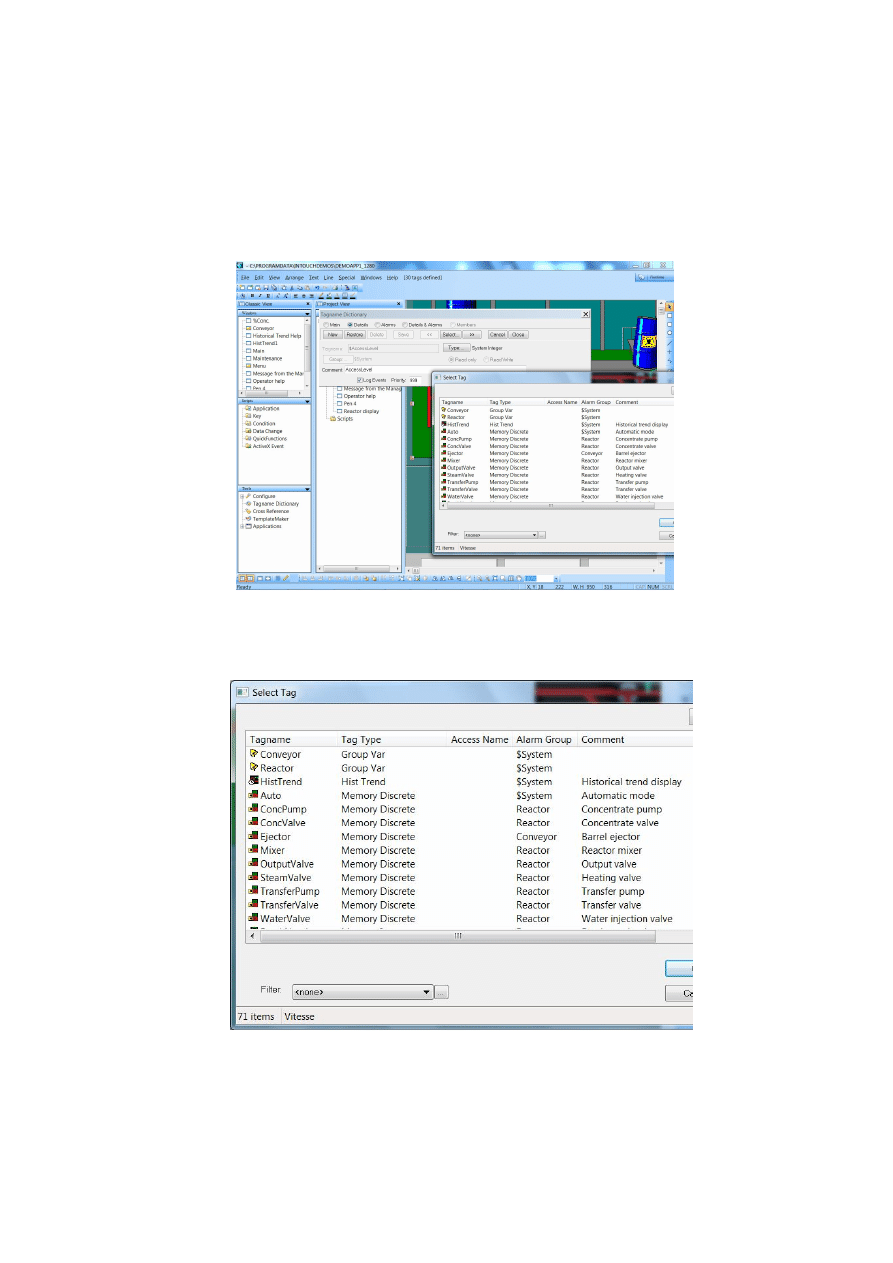
149

Rys 5.20 Lista zmiennych systemowych i procesowych

Rys 5.19 Edycja zmiennych - Windows/Tagname Directory/Select Tag

.

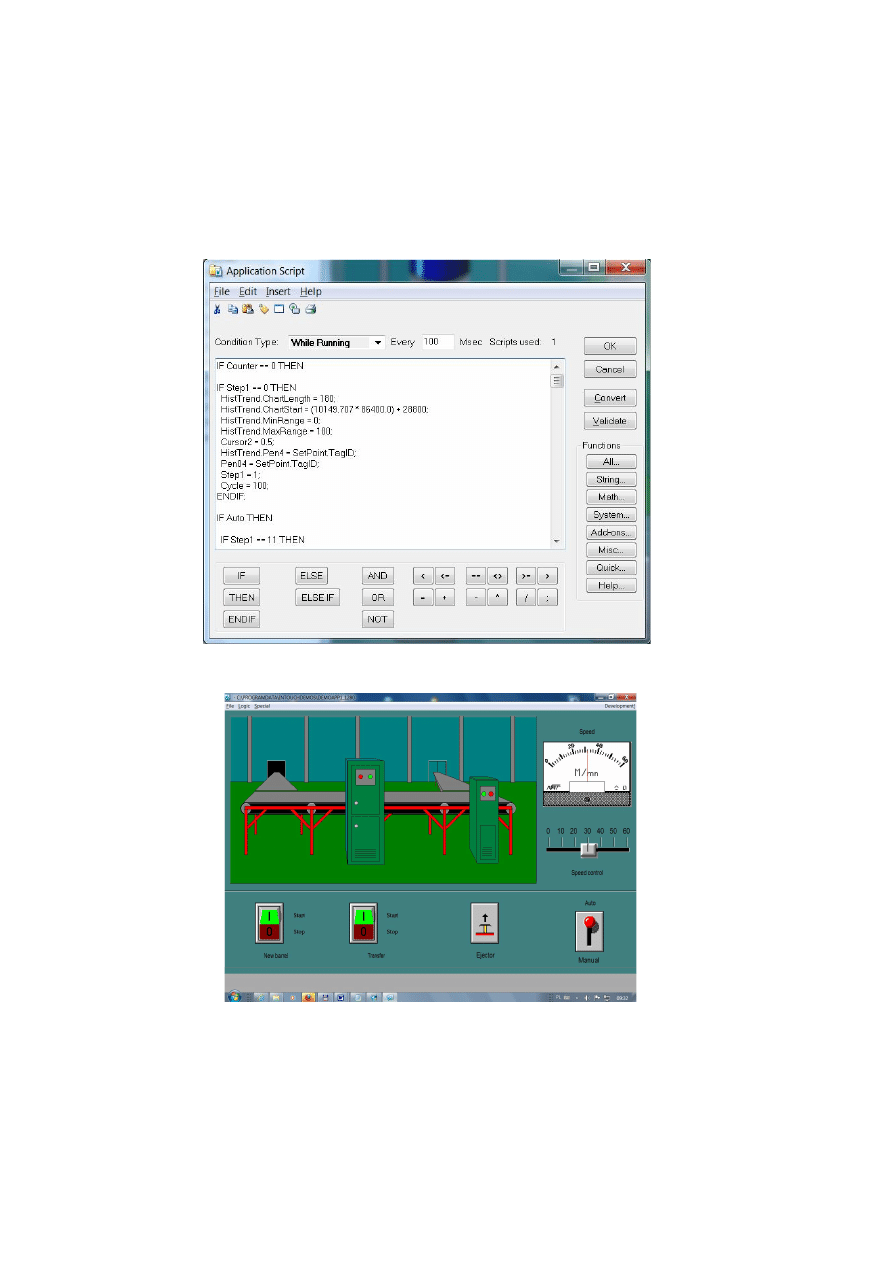
150

Rys. 5.21. Program skryptu

.

Rys 3.22 Ekran symulacji procesu

.

151

Literatura (do rozdz. 5.).

1. Kondratowicz L., Modelowanie symulacyjne systemów. WN-T, 1978.

2. Perkowski P.: Technika symulacji cyfrowej, WN-T, Warszawa 1980.

3. Tyszer J., Symulacja cyfrowa, WN-T, Warszawa 1990.

4. Winiecki W., Jacek Nowak J., Stanik S., Graficzne zintegrowane środowiska

programowe do projektowania komputerowych systemów pomiarowo-
kontrolnych. Wydawnictwo MIKOM, 2001.

Strony internetowe.

1.

http://warp.cpsc.ucalgary.ca/

2.

http://www.dcs.ed.ac.uk/home/hase/simjava/

3.

http://jist.ece.cornell.edu/jist-user/

4.

http://asi-www.informatik.uni-

hamburg.de/themen/sim/forschung/Simulation/Desmo-J/

5.

www.astor.com.pl/www/Produkty_i_technologie/

6.

http://www.wonderware.com.pl/www/index.php/wizualizacja-hmi/wonderware-
intouch.html