UKSW ALGEBRA LINIOWA
Informatyka 2015/2016 Kazimierz Jezuita

1

Kolokwium 1 - zakres, typowy zestaw zadań

Zadanie 1.

1.1. Iloczyn kartezjański, relacje.

Zbadać właściwości następujących relacji

R

w zbiorze





2

,

1

,

0



A

:

A

A

R

n

m







)

,

(

jeśli

a)

m

mn



, b)

A

n

m





, c)

 

1

,

max n

m



, d)

2

2

2





n

m

, e)

n

m



1.2. Relacja, częściowy porządek.

Niech





4

,

3

,

2

,

1



B

. Wykazać, że relacja w zbiorze

B

B



określona następująco:

)

,

(

~

)

,

(

l

k

n

m

jeśli

k

m



i

l

n



, jest relacją porządku? Podać przykład najdłuższego,

uporządkowanego ciągu elementów zbioru

B

B



.

1.3. Relacja równoważności, klasy równoważności.

Wykazać, że relacja w

R

R



taka, że



 



2

2

1

1

,

~

,

y

x

y

x

jeśli

1

2

2

1

y

x

y

x







jest relacją

równoważności. Opisać klasy równoważności.

1.4. Relacja, wykres funkcji.

Czy relacja

Z

N

R





,





2

2

:

)

,

(

y

x

y

x

R





może być wykresem funkcji

Z

N

f



:

?

1.5. Funkcja, injekcja, surjekcja, obraz zbioru, przeciwobraz zbioru.

Czy funkcja

Z

Z

Z

f









:

,

1

)

,

(







n

m

n

m

f

jest: a) injekcją? b) surjekcją?

Znaleźć

})

1

{

(



A

f

oraz

})

0

({

1



f

i

})

3

({

1



f

.

Zadanie 2.

2.1. Współrzędne wektora w bazie.

Czy układ trzech wektorów z przestrzeni

jest liniowo zależny? Wybrać spośród tych wektorów takie, które utworzą bazę.
Wyznaczyć współrzędne wektora

w tej bazie. W trakcie rozwiązywania zadania

wektor

pojawił się w trzech różnych postaciach. Podać te postaci.

2.2. Baza w przestrzeni liniowej

Czy wielomiany:

,

,

tworzą bazę w przestrzeni

]

[

2



R

?

Wyznaczyć współrzędne wektora

w tej

bazie.

2.3. Podprzestrzeń liniowa.

Wykazać, że następujące zbiory wektorów w przestrzeni liniowej tworzą podprzestrzenie
liniowe w przestrzeni

. Wyznaczyć bazy i wymiary tych podprzestrzeni:

a) pierwsza i ostatnia współrzędne są sobie równe,
b) parzyste współrzędne są sobie równe,
c) nieparzyste współrzędne są sobie równe.

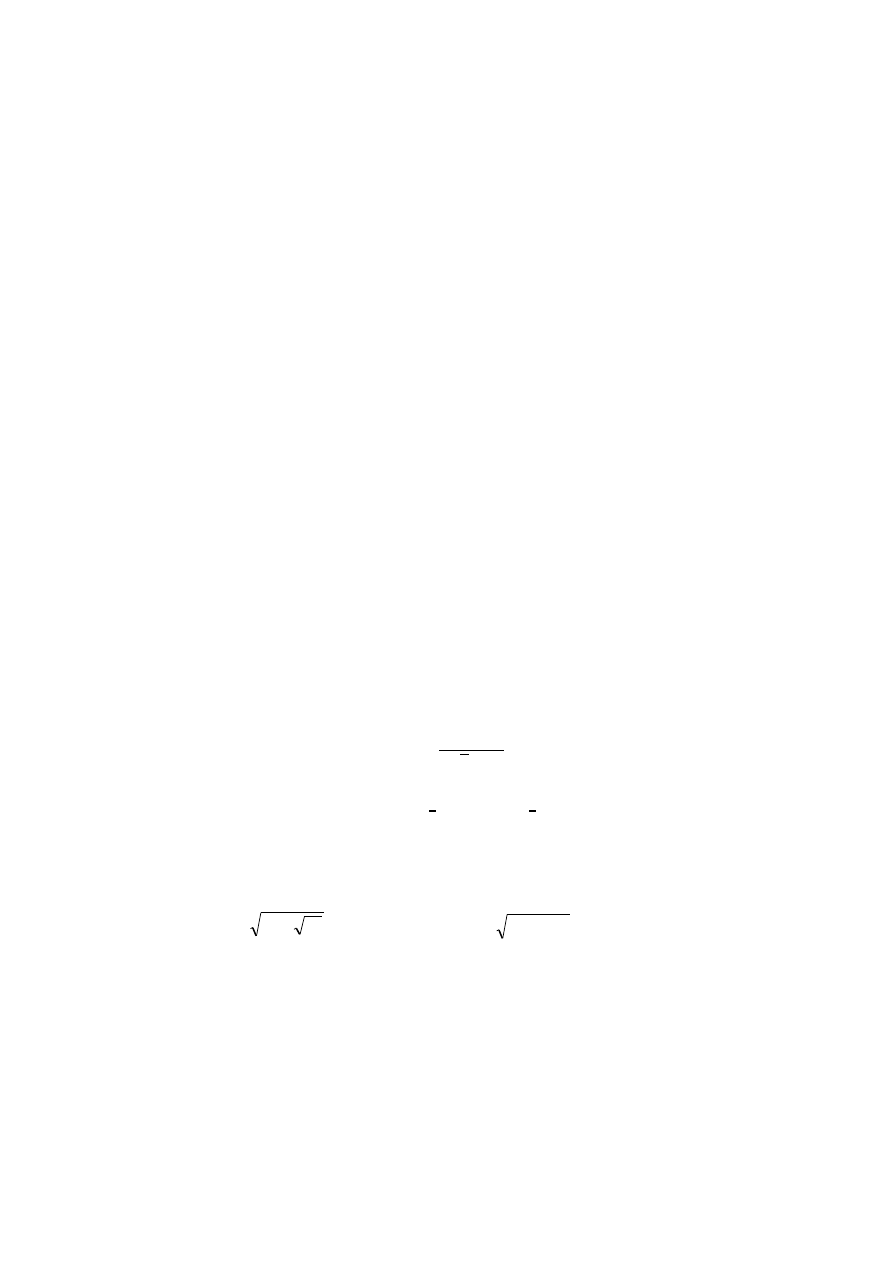
UKSW ALGEBRA LINIOWA
Informatyka 2015/2016 Kazimierz Jezuita

2

Zadanie 3.

3.1. Przekształcenie liniowe,

macierz przekształcenia

Które z poniższych odwzorowań są przekształceniami liniowymi?

a)

R

R

f



2

:

,





2

1

2

1

3

2

)

,

(

x

x

x

x

f





b)

R

R

f



2

:

,





2

2

1

2

1

2

3

)

,

(

x

x

x

x

f





c)

2

:

R

R

f



,

)

2

,

(

)

(

2

x

x

x

f



d)

2

3

:

R

R

f



,

)

2

,

3

(

)

(

x

x

x

f





.

W przypadku przekształcenia liniowego wyznaczyć macierz przekształcenia liniowego w bazach
standardowych.

3.2. Przekształcenie liniowe, macierz przekształcenia

Macierz przekształcenia liniowego

]

[

:

2

2





R

R

f

w bazach:

)

0

,

1

(

1



e

,

)

1

,

0

(

2



e

oraz

2

1

)

(

'

x

x

e



,

x

x

e



)

(

'

2

,

1

)

(

'

3



x

e

, ma postać

Znaleźć wielomian będący obrazem wektora

.

Zadanie 4.

4.1. Liczba zespolona. Postać algebraiczna i trygonometryczna. Płaszczyzna zespolona.

Znaleźć część rzeczywistą i urojoną liczby zespolonej z postaci:

Obliczyć moduł liczby zespolonej z .

Czy liczba z należy do zbioru

?

4.2. Pierwiastki z liczby zespolonej. Płaszczyzna zespolona.

Obliczyć i narysować na płaszczyźnie zespolonej pierwiastki:

a)

4

12

2 i



b)

4

)

4

5

(

i



4.3. Pierwiastki z liczby zespolonej. Płaszczyzna zespolona. Odległość punktów.

Jednym z wierzchołków kwadratu jest punkt

i

z





4

1

. Wyznaczyć pozostałe wierzchołki

kwadratu oraz długość jego boku, jeśli środkiem tego kwadratu jest

a)

i

z





3

0

b)

0

0



z