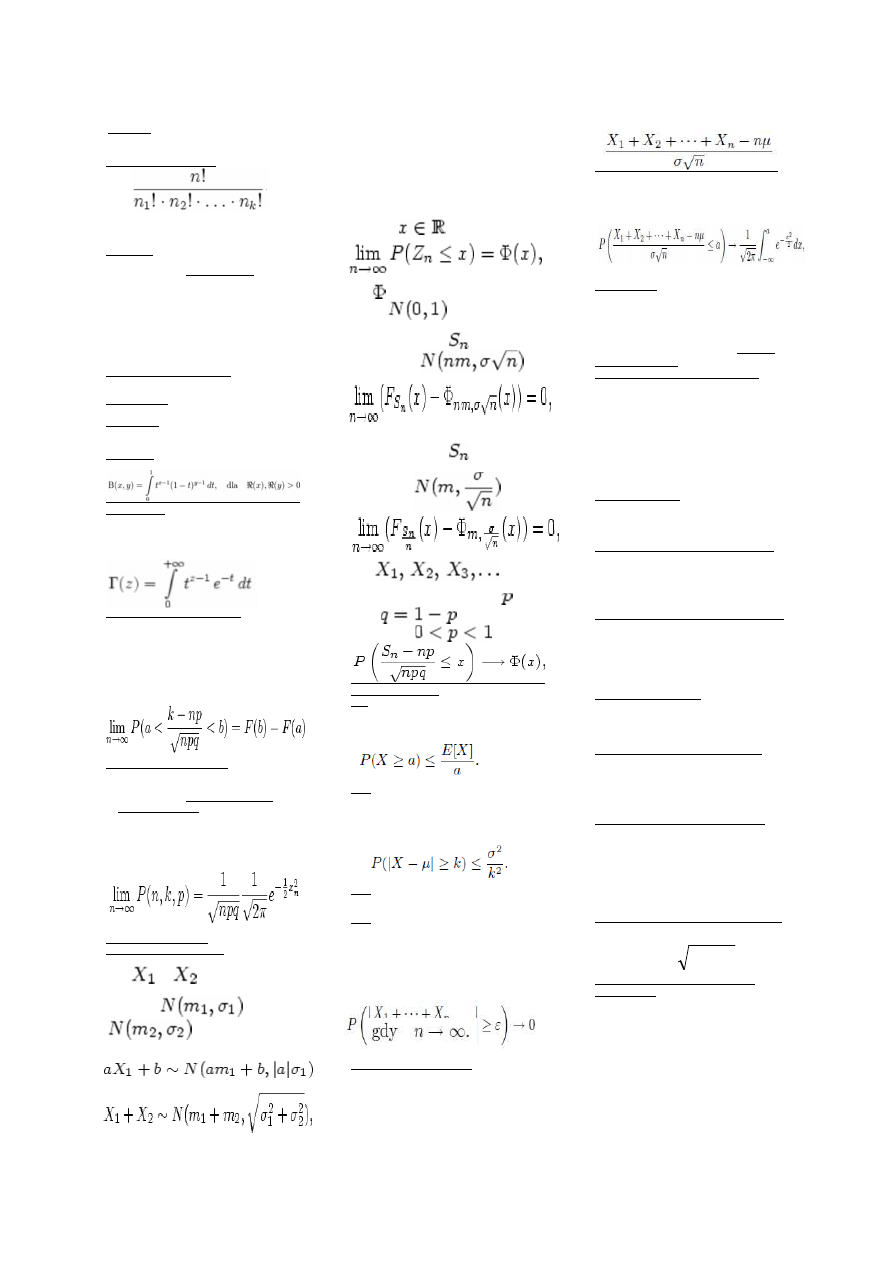
Permutacja:
wzajemnie jednoznaczne przekształcenie pewnego
zbioru na siebie.
Permutacja z powtórzeniami:

Permutacje bez powtórz:

!

Kombinacje:

!

!

!

Rozmieszczeniem n elementów po k elementów
nazywamy zbiór składający się z k elementów
wybranych spośród n elementów i rozmieszczonych
w określonym porządku.

A

( − )( − ) …( − − )

Rozmieszczenia z powtórzeniami:

Zmienna losowa – funkcja przypisująca zdarzeniom
elementarnym liczby.
Dystrybuanta – funkcja rzeczywista jednoznacznie
wyznaczająca rozkład prawdopodobieństwa ,a więc
zawierająca wszystkie informacje o tym rozkładzie
Funkcja beta (Całka Eulera pierwszego rodzaju) —
jedna z funkcji specjalnych zdefiniowana jako

Funkcja gamma (zwana też gammą Eulera) — jedna
z funkcji specjalnych, która rozszerza pojęcie silni na
zbiór liczb rzeczywistych i zespolonych. Gdy część
rzeczywista liczby zespolonej z jest dodatnia, to
całka (całka Eulera):

Twierdzenie INTEGRALNE Laplace’a:
Jeżeli:
k - liczba sukcesów w schemacie Bernoulliego
p - prawdopodobieństwo sukcesu w schemacie
Bernoulliego
q - prawdopodobieństwo porażki w schemacie
Bernoulliego
n - liczba prób
to:

Twierdzenie LOKALNE Laplace’a:

Jeżeli:
k - liczba sukcesów w schemacie Bernoulliego
p - prawdopodobieństwo sukcesu w schemacie
Bernoulliego
q - prawdopodobieństwo porażki w schemacie
Bernoulliego
n - liczba prób
To:

Twierdzenie o rach. Prawd:
Twierdzenia o rachunku prawd.
TW.1

Niech

oraz

będą niezależnymi

zmiennymi losowymi o rozkładach normalnych,

odpowiednio

oraz

Wtedy:

oraz:

T

WIERDZENIE

[L

INDEBERGA

-L

EVY

'

EGO

]

Dla każdego

zachodzi równość:

gdzie

jest dystrybuantą

rozkładu

.

T

WIERDZENIE GRANICZNE DLA SUM

:

Rozkład zmiennej losowej

jest asymptotycznie

równy rozkładowi

.

Inaczej:

T

WIERDZENIE GRANICZNE DLA ŚREDNICH

:

Rozkład zmiennej losowej

jest asymptotycznie

równy rozkładowi.

Inaczej:

T

WIERDZENIE

[

DE

M

OIVRE

'

A

-L

APLACE

'

A

]

Niech

będzie

ciągiem niezależnych prób Bernoulliego, z takim

samym prawdopodobieństwem sukcesu

i

porażki

w każdej próbie (

). Wtedy:

Twierdzenia Graniczne!
TW1
(Nierówność Markowa)
Jeżeli X jest zmienna, losowa, o wartościach
nieujemnych wtedy dla dowolnego a > 0

TW.2
(Nierówność Czebyszewa)
Jeżeli X jest zmienna, losowa, o skończonej wartości

oczekiwanej ¹ i wariancji ¾2, wtedy dla dowolnego

k >

0:

TW.3

Jeżeli V ar[X] = 0, to P(X = E[X]) = 1.

TW.4

Twierdzenie (Słabe prawo wielkich liczb)

Niech X1;X2; : : : ; będzie ciągiem niezależnych
zmiennych losowych o tym samym rozkładzie
prawdopodobieństwa, o skończonej wartości
oczekiwanej E[Xi]. Wtedy :

TW.5 (Centralne Tw. Graniczne):
Niech X1;X2… będzie cięgiem niezależnych
zmiennych losowych o tym samym rozkładzie i
skończonej wartości

oczekiwanej E[Xi] oraz skończonej wariancji V
ar[Xi] . Wtedy rozkład zmiennej losowej:

dąży do rozkładu normalnego standaryzowanego

gdy

n→∞

Zmienną losową można traktować jako pewną

funkcję określoną na przestrzeni próby związanej z

eksperymentem. Przyporządkowanie

prawdopodobieństw różnym możliwym wartością

zmiennej losowej, czyli „probabilistyczne prawo

rządzące zmienną losową „ nazywamy rozkładem

prawdopodobieństwa zmiennej losowej.

Zmienna losowa jest skokowa ( dyskretna ), gdy

może przyjmować wartości ze zbioru najwyżej

przeliczalnego.

0

)

(

≥

X

P

dla wszystkich wartości x

∑

=

wszystkiex

X

P

1

)

(

Zmienna losowa ciągła może przyjmować wartości

z dowolnego przedziału liczbowego. Możliwe

wartości takiej zmiennej tworzą zbiór

nieprzeliczalnie nieskończony.

Skumulowaną funkcją rozkładu ( dystrybuantą )

skokowej zmiennej losowej X jest funkcja

Oczekiwana wartość skokowej zmiennej losowej X
jest równa sumie wszystkich możliwych wartości tej
zmiennej mnożonych przez ich
prawdopodobieństwa

Wariancja zmiennej losowej jest to oczekiwana
wartość kwadratu odchylenia tej zmiennej od jej
średniej . Pojęcie to jest podobne do pojęcia
wariancji w zbiorze wyników obserwacji ( w próbie
lub populacji ) .
Wariancją skokowej zmiennej losowej X jest

:

Wartość oczekiwana zmiennej losowej ciągłej

wyraża się następującym wzorem :

∫

+∞

∞

−

=

=

dx

x

xf

x

E

)

(

)

(

µ

Odchylenie standardowe zmiennej losowej ciągłej

dane jest wzorem :

Przedział ufności dla wariancji i odchylenia

standardowego:

Przedział ufności dla wariancji

2

δ

w populacji

generalnej można wyznaczyć , gdy cecha X

charakteryzująca zbiorowość ma rozkład

)

,

(

δ

µ

N

, przy czym parametry

δ

µ

,

są

nieznane. Na podstawie próby losowej pochodzącej

z tej populacji budujemy przedział ufności dla

nieznanej wariancji

2

δ

, przyjmując

współczynnik

ufności

1-

α

.

Estymatorem parametru

2

δ

jest

∑

≤

=

≤

=

x

i

i

P

x

X

P

x

F

)

(

)

(

∑

=

=

wszystkiex

x

xP

X

E

)

(

)

(

µ

( )

)

(

]

)

[(

)

(

2

2

2

x

P

x

X

E

X

V

wszystkiex

∑

−

=

−

=

=

µ

µ

δ

)

(

)

(

2

x

D

x

D

=

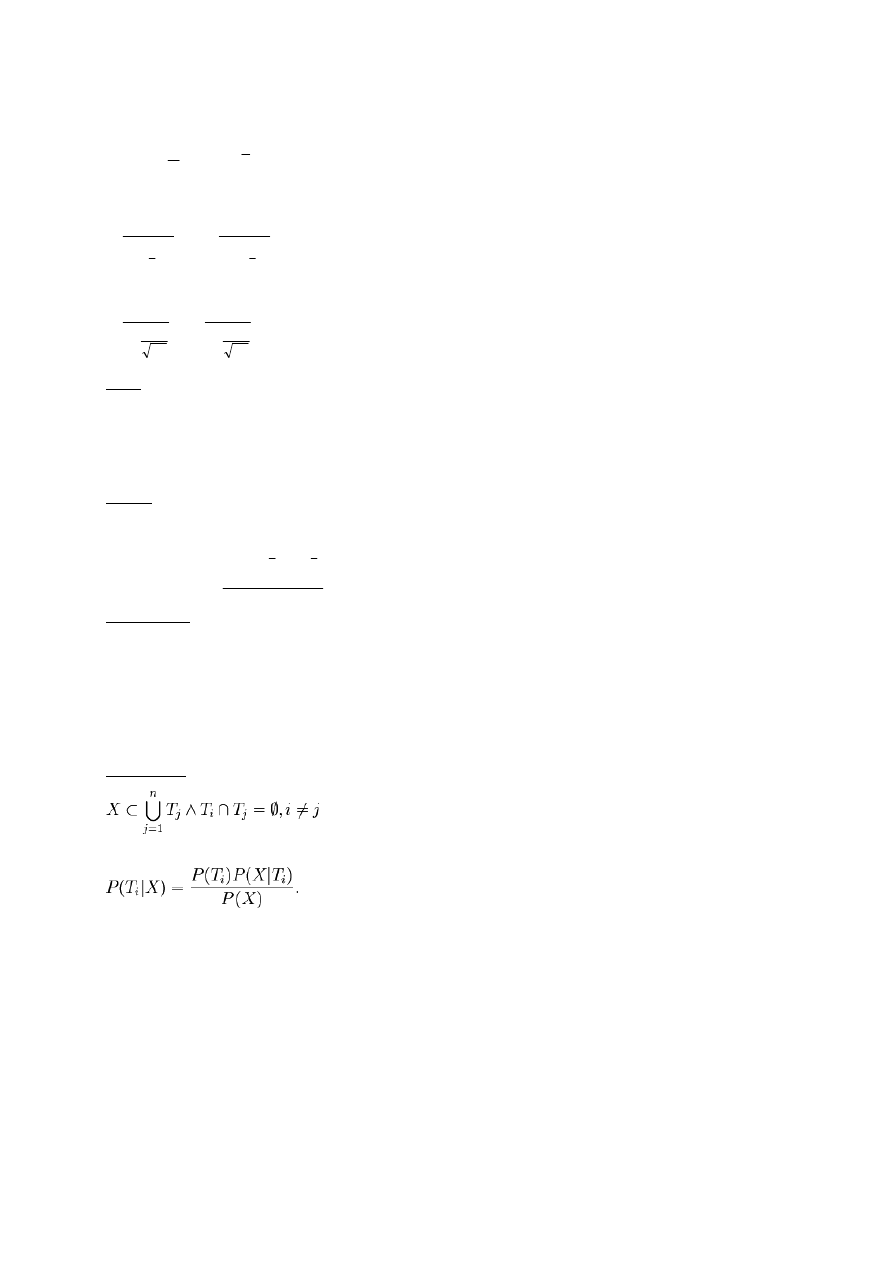
wariancja z próby

2

s

określona wzorem

Przedział ufności dla wariancji

2

δ

określony jest

wzorem :

α

χ

δ

χ

α

α

−

=

−

<

<

−

−

1

}

ˆ

)

1

(

ˆ

)

1

(

{

2

2

1

2

2

2

2

2

S

n

S

n

P

Przedział ufności dla odchylenia standardowego

można wyrazić wzorem :

α

δ

α

α

−

≈

−

<

<

+

1

}

2

1

2

1

{

n

u

s

n

u

s

P

Korelacja

jest to współzależność , czyli wzajemne

oddziaływanie lub współwystępowanie dwóch

zjawisk lub cech tej samej zbiorowości .

Celem analizy współzależności jest stwierdzenie ,

czy między badanymi zmiennymi zachodzą jakieś

zależności , jaka jest ich siła , kształt i kierunek.

Współzależność między zmiennymi może być,

funkcyjna lub stochastyczna.

Kowariancja

jest średnią arytmetyczną iloczynem odchyleń

wartości zmiennych X i Y ich średnich , co zapiszemy

dla danych w szeregach :

Schemat Bernoulliego nazywamy ciąg
doświadczeń niezależnych, w których dane
doświadczenie powtarzamy n-razy (n-liczba
skończona) i w którym prawdopodobieństwo
zdarzenia A (zdarzenie A-wynik doświadczenia) jest
stałe, nie zależy od wyników poprzednich.

P

n

(k) = (

n

k

) · p

k

·q

n-k

gdzie:
- zajście zdarzenia A nazywamy sukcesem i
oznaczamy p
- zajście zdarzenia A’ nazywamy porażką i
oznaczamy q, q = 1 – p

Twierdzenie Bayesa:
Niech :

Wtedy:

n

y

y

x

x

yx

xy

n

i

i

i

∑

=

−

−

=

=

1

)

)(

(

)

cov(

)

cov(

∑

=

−

=

n

i

i

x

x

n

s

1

2

2

)

(

1