1

Politechnika Krakowska im. Tadeusza Kościuszki Katedra Automatyki

i Technik Informacyjnych (E-3)

Automatyka

Laboratorium

– Układ regulacji ciągłej. Badanie regulatorów –

1. Cel ćwiczenia

Zapoznanie się z budową regulatorów, działaniem zamkniętego układu sterowania w

aspekcie doboru nastaw regulatorów. Problem doboru nastaw można sprowadzić do określenia
wartości współczynników

, ,

, które są w oczywisty sposób związane ze strukturą regulatorów.

2. Regulatory ciągłe liniowe

Zadaniem regulatora w ukłądzie regulacji automatycznej jest wytworzenie sygnału

sterującego ( ), który oddziałuje na przebieg procesu. Sygnał ( ) jest sygnałem wyjściowym
regulatora, natomiast sygnałem wejściowym regulatora w układzie regulacji jest sygnał uchybu
regulacji ( ). Sposób przetworzenia uchybu na sygnał sterujący nazywa się prawem regulacji.

Regulatorami ciągłymi (o działaniu ciągłym lub analogowym) nazywamy regulatory, w których sygnał
wyjściowy zależy w sposób ciągły od sygnału wejściowego. Regulatory liniowe są opisywane
równaniami różniczkowymi liniowymi. Wśród regulatorów ciągłych liniowych wyróżnia się
następujące typy: P, I, PI, PD i PID.

2.1. Regulator proporcjonalny (P)

Realizuje prawo regulacji:

( ) =

( ).

(1)

Jego transmitancja dana jest wzorem:

( ) = .

(2)

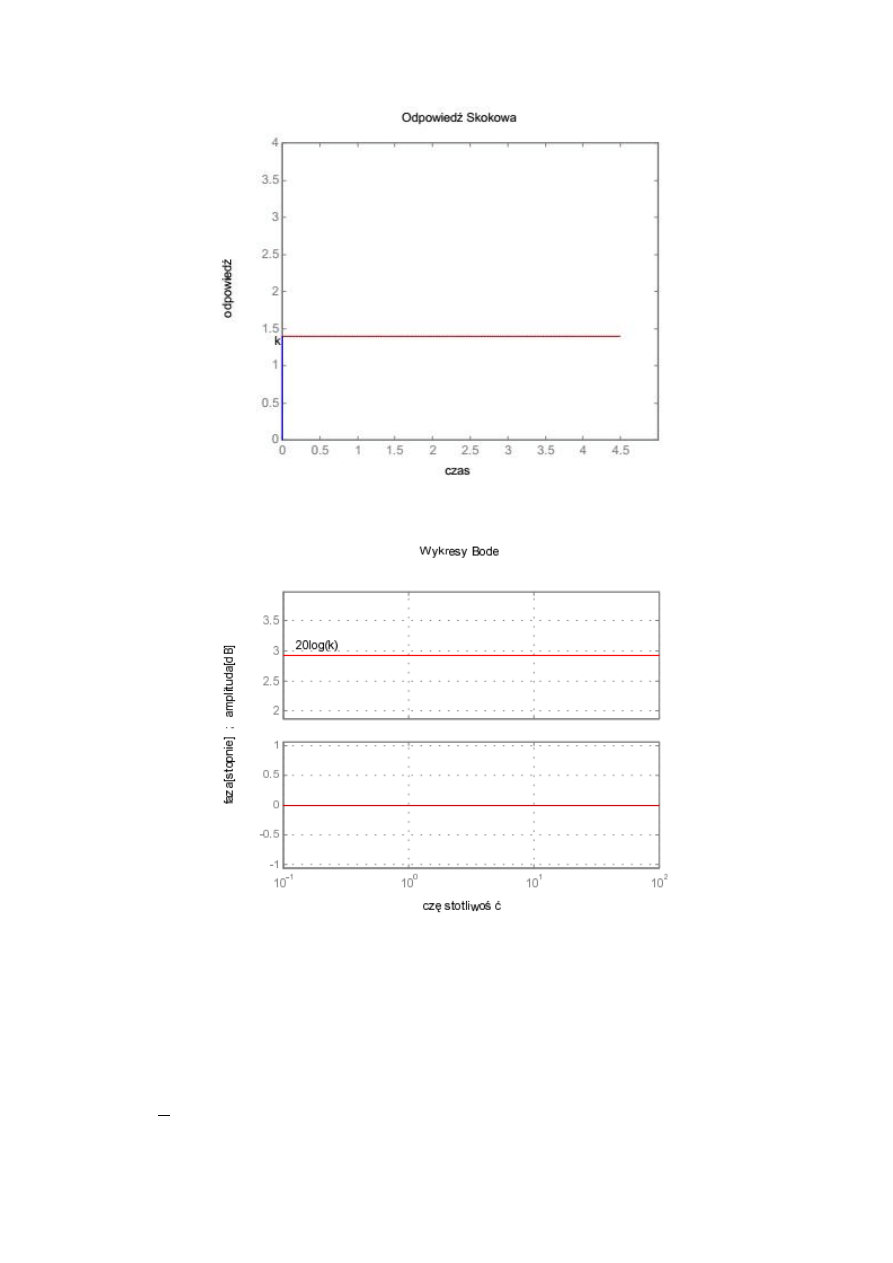
Poniżej, na rys. 1, przedstawiono odpowiedź skokową regulatora dla = 1.4, a na rys. 2 pokazano
jego logarytmiczne charakterystyki częstotliwościowe.

2

Rys. 1. Charakterystyka skokowa regulatora P.

Rys. 2. Charakterystyki częstotliwościowe regulatora P.

2.2. Regulator całkujący (I)

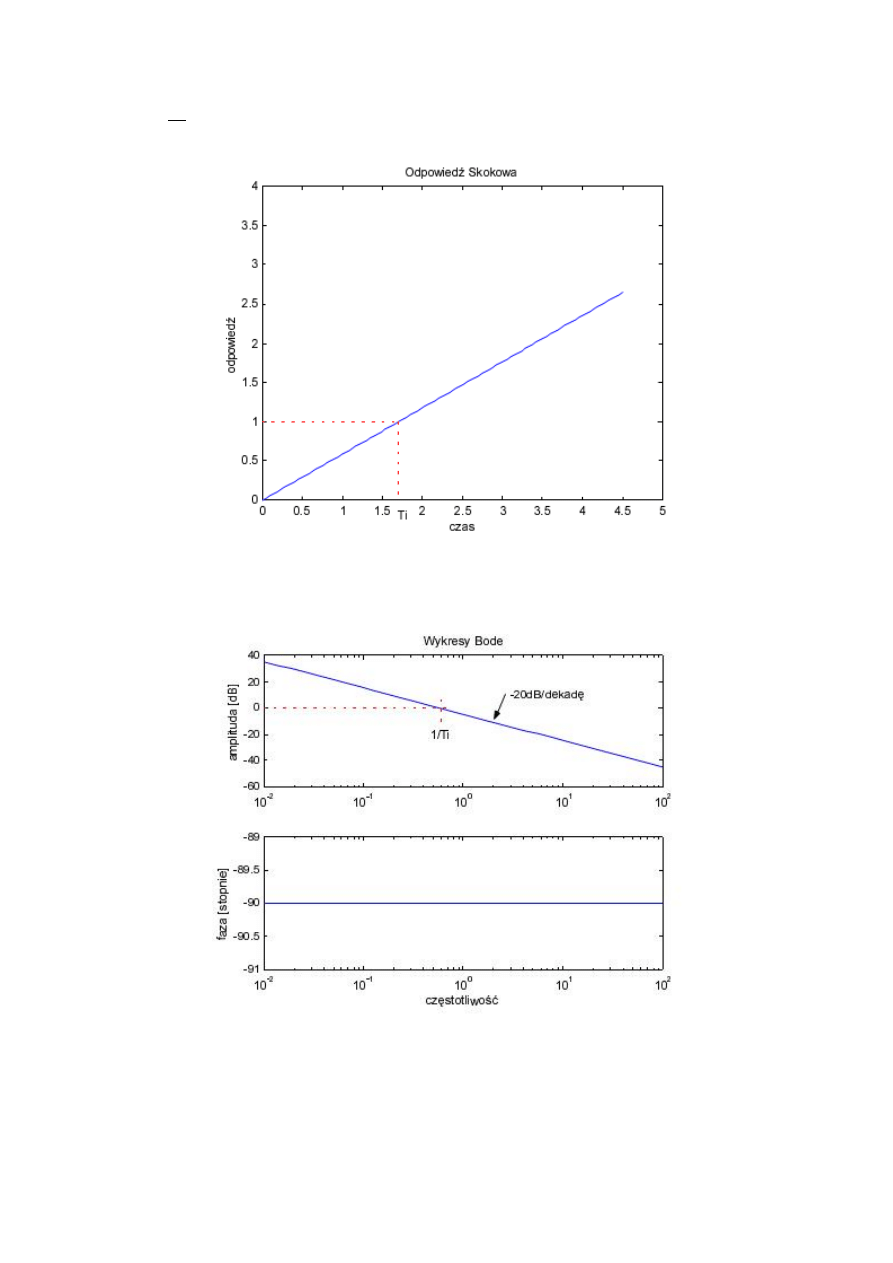
Prawo regulacji regulatora opisuje równanie (3), a transmitancję – wzór (4). Jego odpowiedź skokową
i charakterystyki czestotliwościowe dla

= 1.7 przedstawiono na rys. 3 i 4.

( ) =

∫ ( )

,

∗ ̇ ( ) = ( ),

(3)

3

( ) =

.

(4)

Rys. 3. Charakterystyka skokowa regulatora I.

Rys. 4. Charakterystyki częstotliwościowe regulatora I.

4

2.3. Regulator proporcjonalno-całkujący (PI)

Prawo regulacji regulatora opisuje równanie (5), a transmitancję – wzór (6).

( ) =

( ) +

∫ ( )

,

(5)

( ) =

1 +

.

(6)

Parametr nosi nazwę czasu zdwojenia lub czasu izodromu. Jest to czas, po którym wartość
odpowiedzi egulatora na wymuszenie skokowe podwoi się w stosunku do wartości w chwili
początkowej (0 +), czyli czas, po którym wartość odpowiedzi części całkującej i proporcjonalnej
zrównają się.

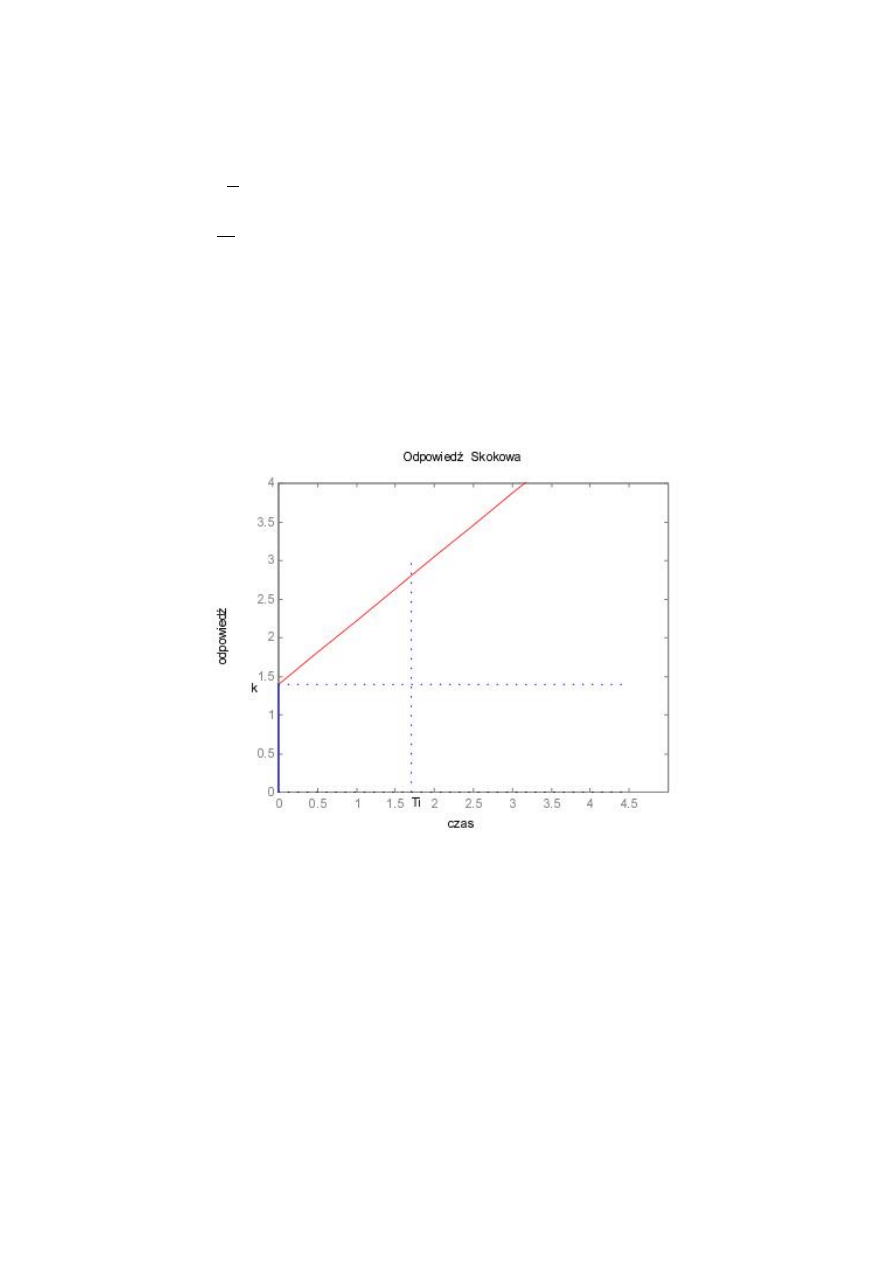
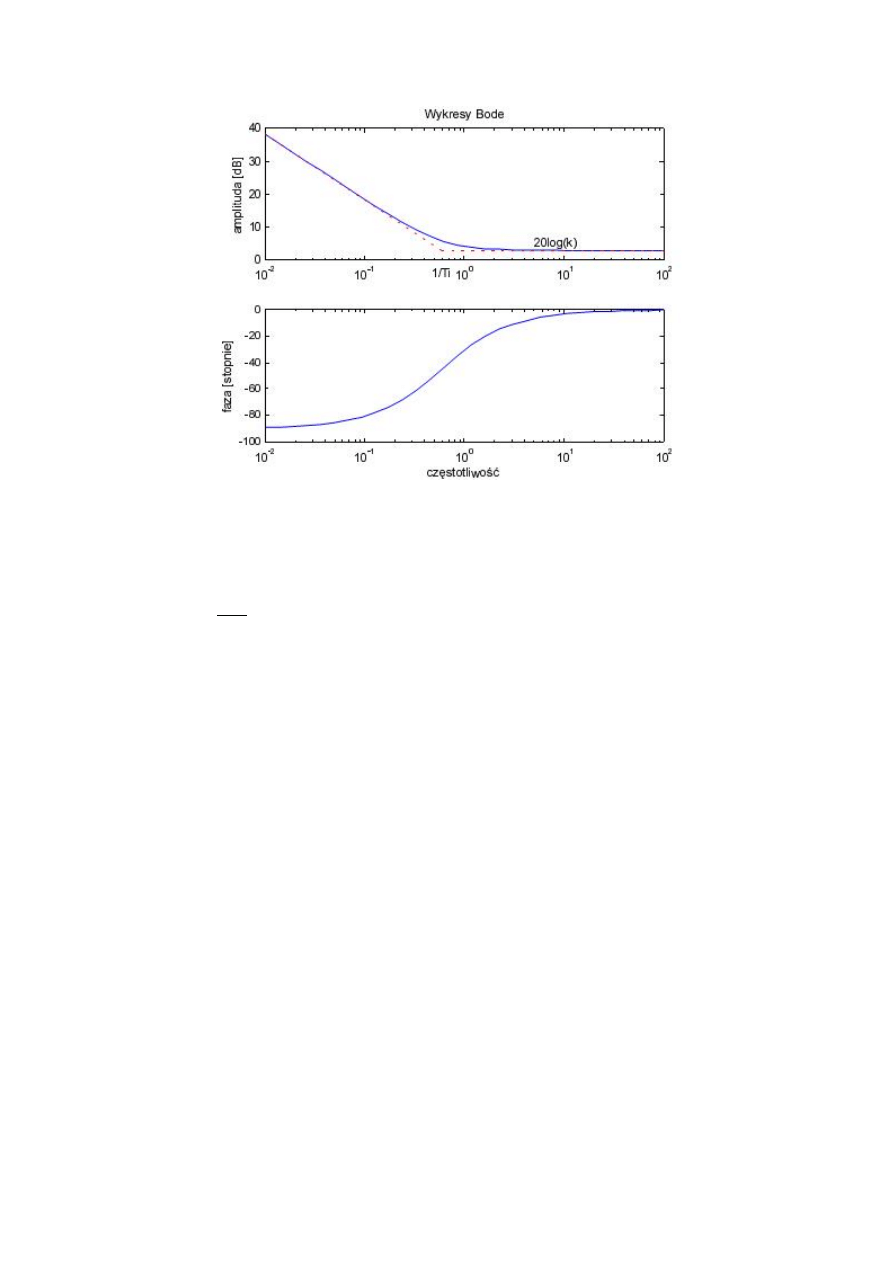
Na rys. 5 i 6 przedstawione są charakterystyka skokowa i charakterystyki częstotliwościowe
regulatora dla = 1.4,

= 1.7.

Rys. 5. Charakterystyka skokowa regulatora PI.

5

Rys. 6. Charakterystyki częstotliwościowe regulatora PI.

2.4. Regulator proporcjonalno-różniczkujący (rzeczywisty) (PD)

Transmitancja regulatora zapisana jest wzorem (7).

( ) =

1 +

.

(7)

Uwaga: Regulator nosi nazwę rzeczywistego ze względu na tzw. Rzeczywistę różniczkowanie
(z inercją). Im mniejsze , tym bardziej działąnie regulatora zbliża się do działania tzw. regulatora
idealnego.

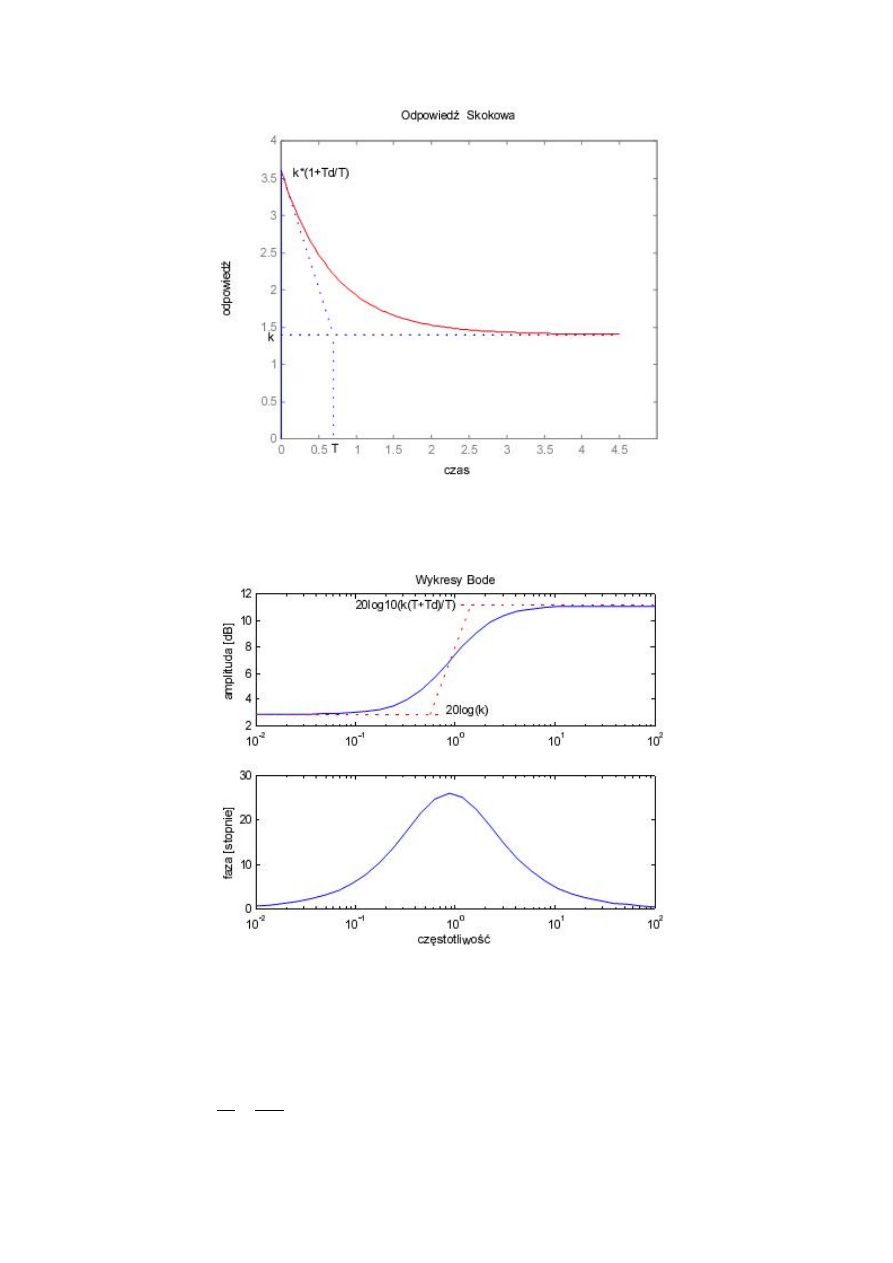
Na rys. 7 i 8 przedstawione są charakterystyka skokowa i charakterystyki częstotliwościowe
regulatora dla = 1.4,

= 1.1,

= 0.7.

6

Rys. 7. Charakterystyka skokowa regulatora PD.

Rys. 8. Charakterystyki częstotliwościowe regulatora PD.

2.5. Regulator

proporcjonalno-całkująco-różniczkujący

(rzeczywisty)

(PID)

Transmitancja regulatora zapisana jest wzorem (8).

( ) =

1 +

+

.

(8)

7

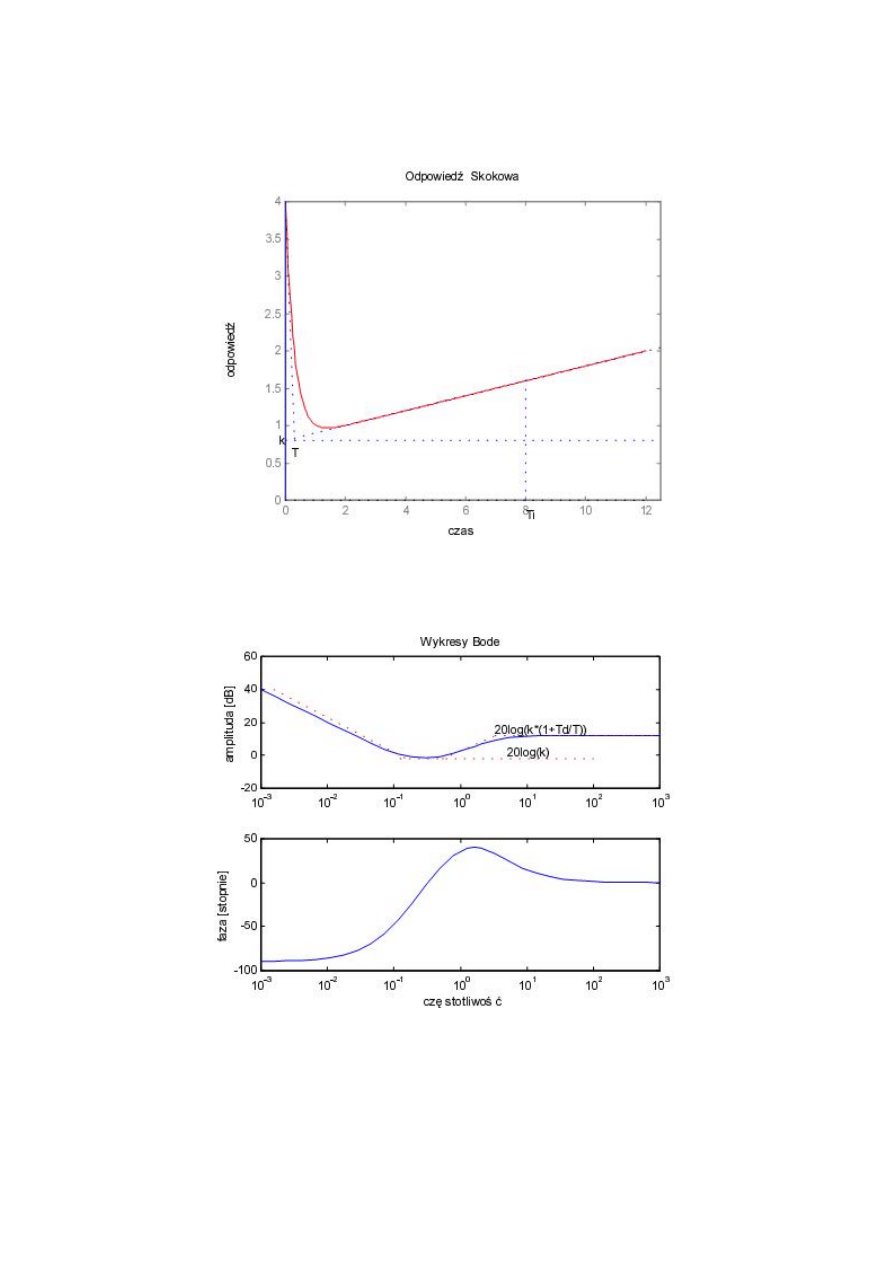
Na rys. 9 i 10 przedstawione są charakterystyka skokowa i charakterystyki częstotliwościowe
regulatora dla = 0.8,

= 8,

= 1.2,

= 0.3.

Rys. 9. Charakterystyka skokowa regulatora PID.

Rys. 10. Charakterystyki częstotliwościowe regulatora PID.

8

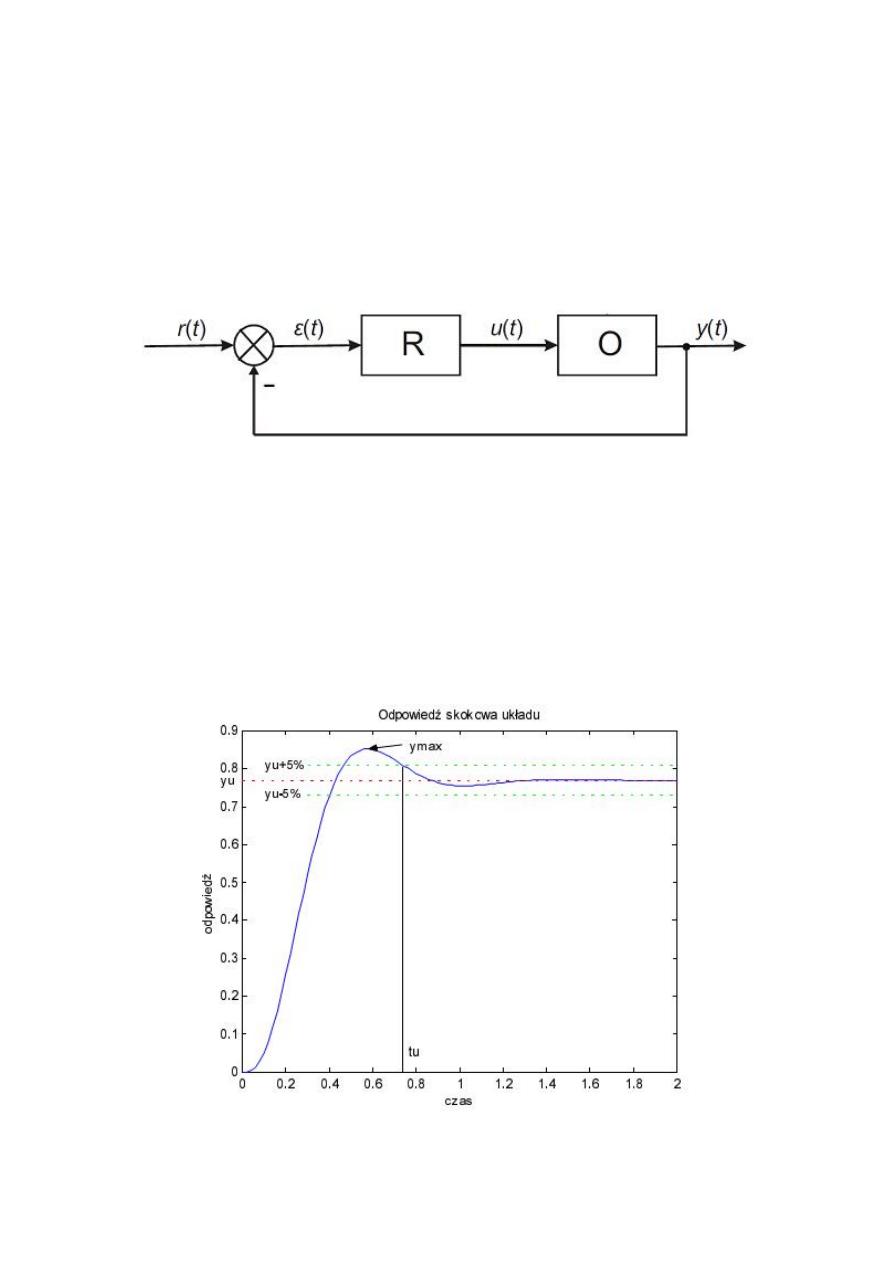
3. Układ regulacji ciągłej

Schemat układu regulacji ciągłej przedstawiony jest na rys. 11. Regulator oznaczono literą , a obiekt
(proces) regulowany – literą . W układzie zaznaczono następujące sygnały:

( ) – sygnał wielkości zadanej,
( ) – sygnał uchybu (błędu) regulacji,

( ) – sygnał sterujący,
( ) – sygnał odpowiedzi układu.

Rys. 11. Schemat układu regulacji.

Jest to klasyczny układ sterowania o szeregowym połączeniu obiekt – regulator w torze głównym
systemu. Układ o takiej strukturze zapewnia stabilne sterowanie obiektem pod warunkiem
poprawnego dobrania typu i współczynników wzmocnienia regulatora.

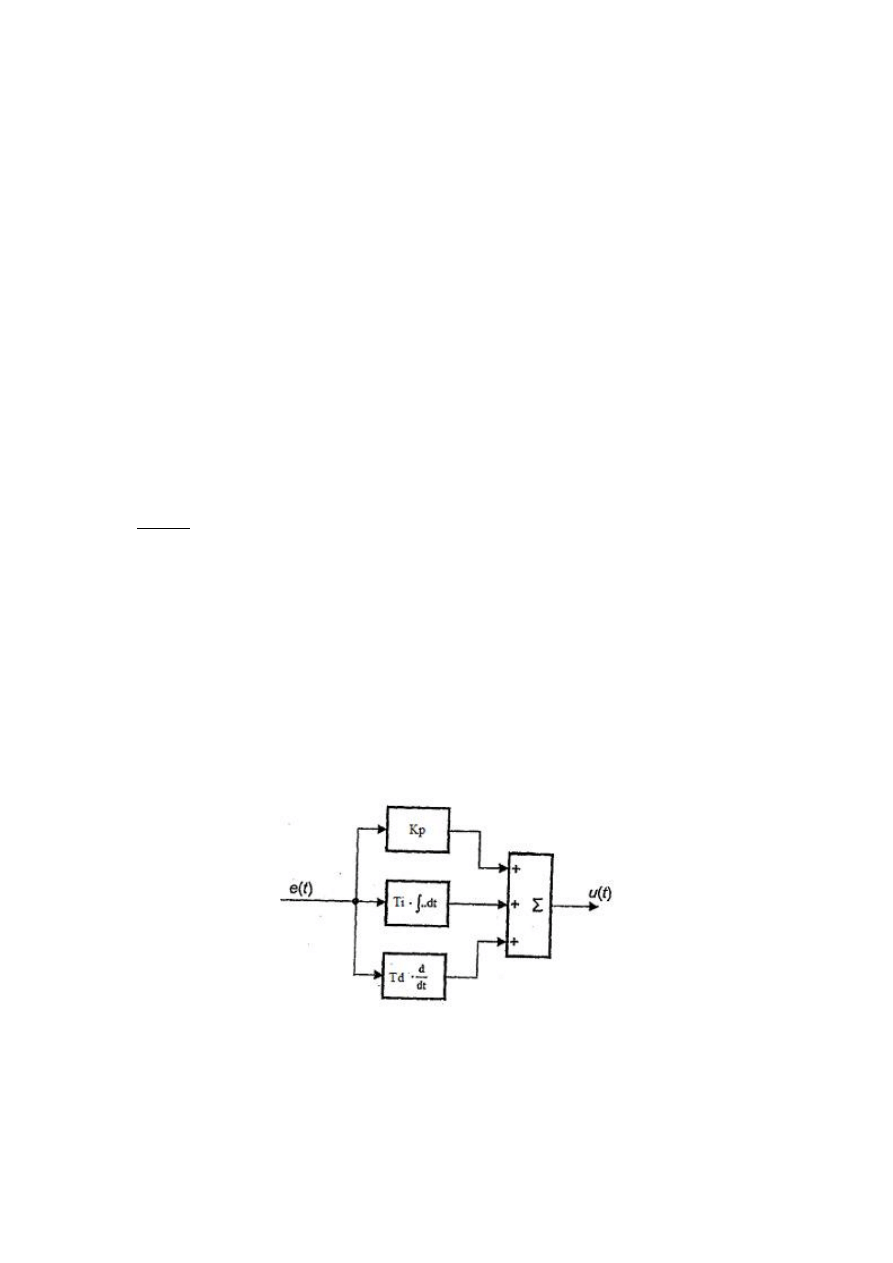
Jednym ze sposobów oceny działania układów sterowania jest porównanie ich zachowania się
(odpowiedzi) na wymuszenie skokowe. Do tej oceny mogą służyć takie parametry odpowiedzi układu
jak: czas regulacji, wartość ustalona, przeregulowanie, czas maksymalnego piku, uchyb ustalony,
uchyb przejściowy, czas narastania odpowiedzi (rys. 12).

Rys. 12. Odpowiedź skokowa układu regulacji przy zmianie sygnału zadanego.

9

1. Uchyb ( ) jest to różnica między wartością sygnału zadanego a wartością odpowiedzi układu.

Formalnie uchyb rozkłada się na uchyb przejściowy (dynamiczny) i uchyb ustalony (statyczny)

( =

+

).

2. Uchyb ustalony to różnica między sygnałem zadanym a odpowiedzią układu w stanie ustalonym.
3. Uchyb przejściowy to różnica między sygnałem zadanym a odpowiedzią układu w stanie

nieustalonym (przejściowym).

4. Czas regulacji (czas ustalania się odpowiedzi) jest to czas mierzony od chwili zadziałania

wymuszenia na układ (zmiany sygnału zadanego lub zakłócenia) do chwili, gdy bezwzględna
wartość uchybu przejściowego zmaleje trwale poniżej % jego maksymalnej bezwzględnej
wartości. Najczęściej przyjmuje się równe 2% lub 5%. Gdy wymuszeniem jest sygnał zadany,
czas regulacji wyznacza się również w sposób równoważny jako czas od zmiany sygnału
zadanego do chwili, gdy odpowiedź układu nie różnie się od wartości ustalonej w sposób trwały
o więcej niż (odpowiedź wchodzi trwale w „korytarz” ± wokół wartości ustalonej.

5. Przeregulowanie jest to bezwzględna wartość stosunku uchybów

do

, gdzie

jest

największą wartością uchybu przejściowego, a największą wartością uchybu przejściowego
o znaku przeciwnym niż . Przeregulowanie podawane jest często w procentach. W przypadku,
gdy wymuszeniem jest sygnał zadany, przeregulowanie można wyznaczyć ze wzoru (9).

=

∗ 100%

(9)

Ze względu na pewną ilość wymienionych wyżej parametrów odpowiedzi skokowej układu, od decyzji
projektanta systemu będzie zależało, który przebieg wielkości regulowanej uzna on za najlepszy.
Na potrzeby ćwiczenia zakłada się, że najlepszym przebiegiem będzie taki, którego czas regulacji oraz
przeregulowanie są najkorzystniejsze.

4. Układ sterowania silnika obcowzbudnego prądu stałego z regulatorem

PID

Testowany układ będzie zawierał:

1. regulator PID, którego strukturę przybliża schemat blokowy z rys. 13.

Rys. 13. Schemat blokowy regulatora.

Zawiera on współczynniki wzmocnień części regulatora

(proporcjonalnej), (całkującej) oraz

(różniczkującej).

10

2. Silnik jako obiekt regulacji

Przykładowym obiektem będzie silnik obcowzbudny prądu stałego o następujących danych
znamionowych i stałych:

= 22

,

= 440 ,

= 56.2 ,

= 120

,

= 2.62

∗

,

= 2.62

,

= 0.465 Ω,

= 0.015 ,

= 2.7

∗

,

= 1500

,

= 157

Założono stały strumień wzbudzenia. Obecność w modelu znamionowych wartości napięcia i prądu
magnesującego jest wyrażona poprze wartości stałych: elektrycznej

oraz mechanicznej

.

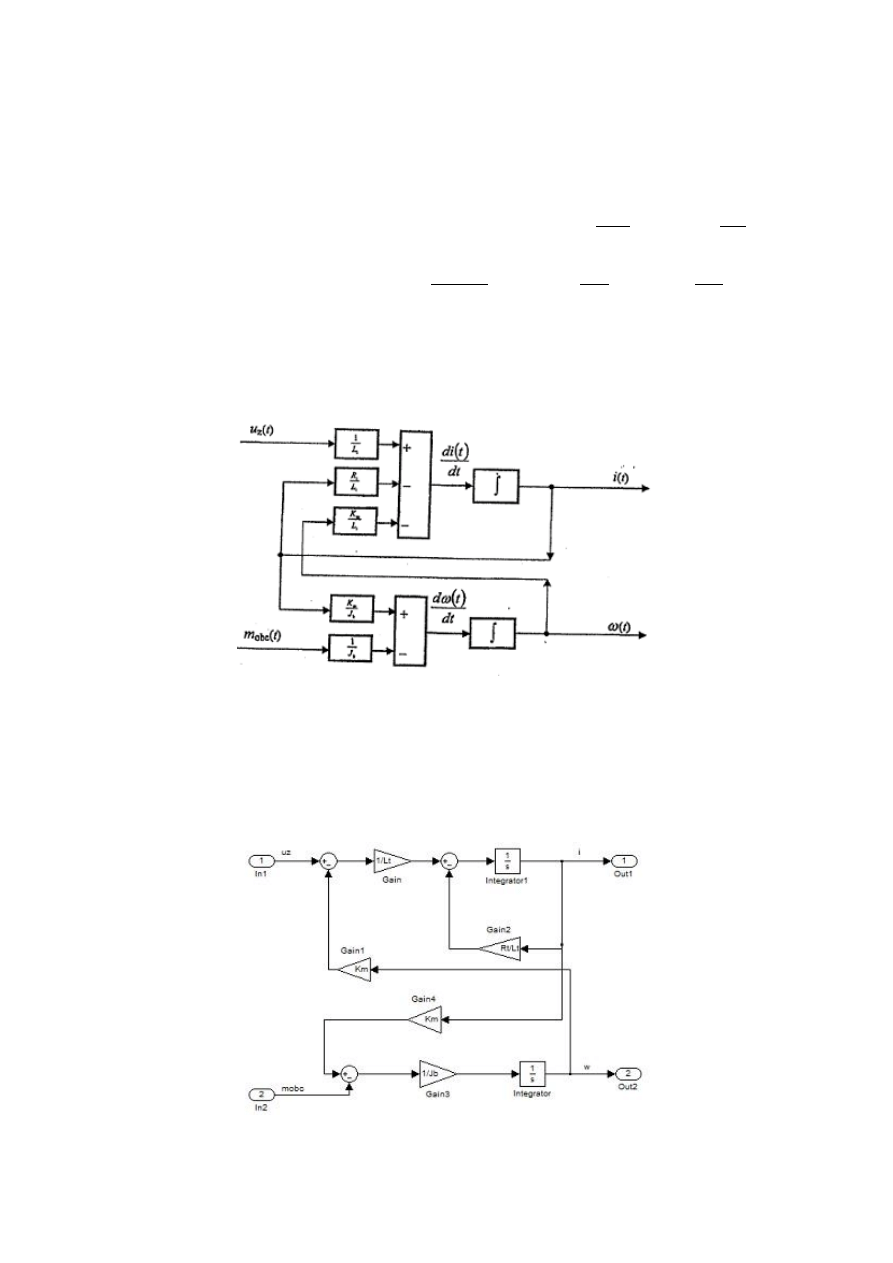
Schemat blokowy silnika przedstawia się następująco:

Rys. 14. Schemat blokowy silnika.

4.1. „Silnik – solo” – wymuszenie skokowe

Badanie dynamiki samego silnika, jako obiektu regulacji, można prowadzić za pomocą przytoczonego
poniżej programu, który korzysta ze schematu blokowego silnika zapisanego w pliku o nazwie
mg.mdl (rys. 15).

Rys. 15. Schemat blokowy silnika zapisany w pliku mg.mdl.

11

Powyższy schemat realizuje program Matlaba o nazwie silnik_solo.m:

%Obiekt regulacji-silnik

clear

clc

Rt = 0.465;
Lt = 0.015;
Km = 2.62;
Jb = 2.7;
ster = [0.0, 1.0, 0.0

%pierwsza kolumna - czas

0.5, 1.0, 0.0

%druga kolumna - zasilanie

1.0, 1.0, 0.0

%trzecia kolumna - obciążenie

1.5, 1.0, 0.0
2.0, 1.0, 0.0
2.5, 1.0, 0.0
3.0, 1.0, 0.0
3.5, 1.0, 0.0];
[t,x,y]=sim(

'mg'

, 1.5, [], ster);

%zainicjowanie symulacji

plot(ster(:,1), ster(:,2),

'.-'

, t, y);

grid
axis([0, 1.5, -0.2, 1.8]);
title(

'Przebiegi w silniku - wymuszenie skokowe'

)

xlabel(

'czas [s]'

)

ylabel(

'prad obroty obciazenie'

)

X=[0.60, 0.60, 0.30];

%opis wykresów

Y=[1.05, 0.45, 0.70]

text(X(1), Y(1),

'wymuszenie skokowe'

)

text(X(2), Y(2),

'predkosc silnika'

)

text(X(3), Y(3),

'prad silnika'

)

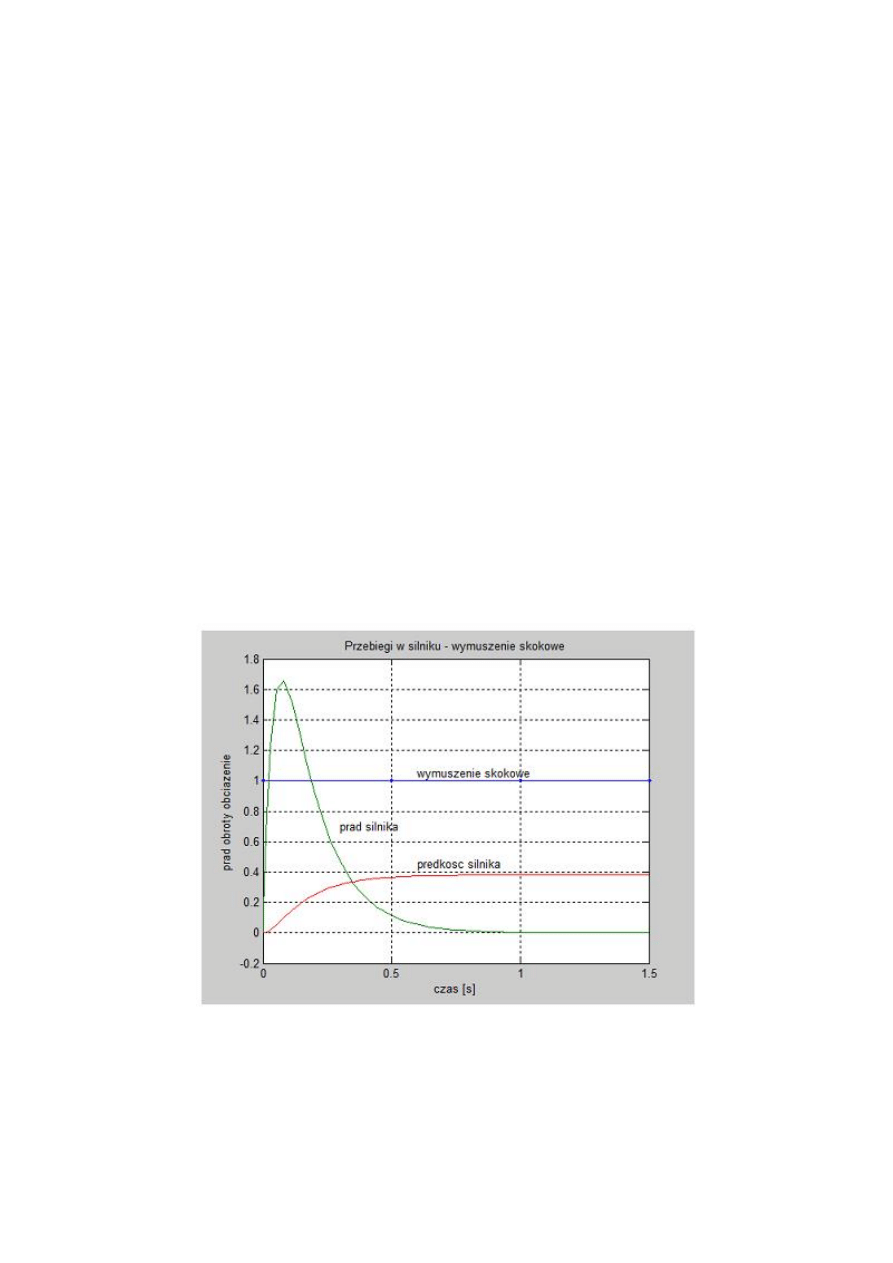
Rys. 16. Przebiegi napięcia zasilającego, prądu silnika, prędkości silnika w układzie otwartym –

wymuszenie skokowe.

W zapisanym powyżej programie zrealizowano nie tylko samą symulację, ale również opisy
uzyskanych wykresów.

12

Należy zauważyć, że wymuszenia, czyli sygnały sterujące, związane z portami wejściowymi 1 i 2,
zapisane zostały w programie w formie macierzy „ster”. Macierz ta jest jednym z argumentów
głównej procedury symulacyjnej „sim”. Dzięki takiej formie zapisu wymuszenia, zachodzi możliwość
łatwej programowej realizacji różnych prostych sygnałów zadających. W omawianym przykładzie
w macierzy „ster” zapisano, że

= 1 oraz

= 0. W wyniku wykonania programu powstały

wykresy na rys. 16.

4.2. Silnik w UAR (układzie automatycznej regulacji) z regulatorem PID

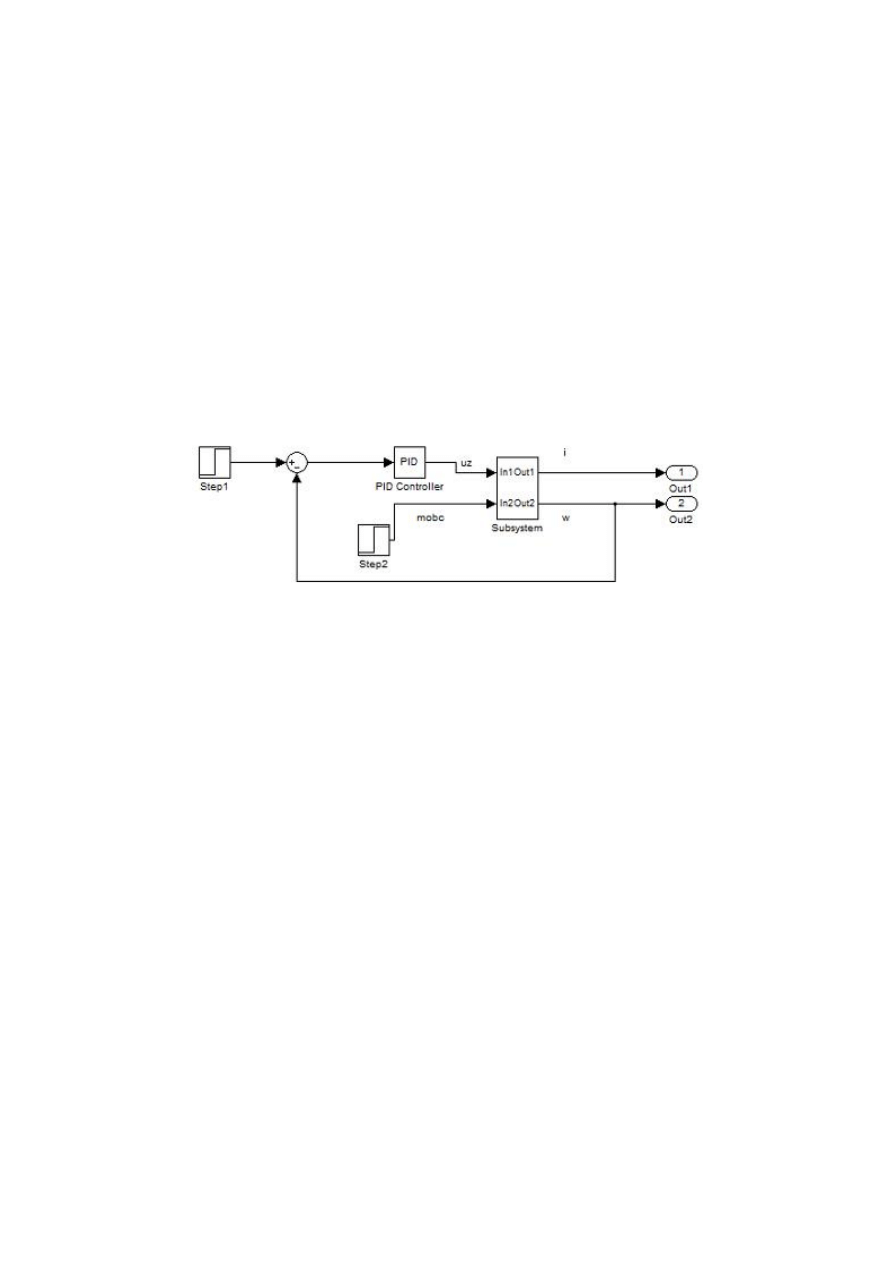
Rys. 17. przedstawia, wykonany w oknie edycyjnym Simulinka, schemat blokowy zamkniętego układu
sterowania prędkością silnika. Schemat ten, został zapisany pod nazwą uar.mdl. Aby schemat był
bardziej czytelny, obiekt regulacji – silnik z pliku mg.mdl, umieszczono w bloku „subsystem”. Wyjścia
tego bloku stanowią: prąd (

1) oraz prędkość obrotowa wału silnika (

2). Ustawiona wartość

1:

= 0.001.

Rys. 17. Schemat blokowy zamkniętego układu sterowania prędkością silnika.

Jako regulator zastosowano, dostępny w bibliotekach Simulink, blok regulatora PID Controller,
w którego okienku dialogowym wpisano symbole współczynników

, ,

.

W układzie na rys. 17 występują dwa bloki generujące sygnał wejściowy.

1 wytwarza skok

jednostkowy, który jest sygnałem sterującym w UAR prędkości. Blok

2 przewidziany został

do generacji sygnału symulującego mechaniczne obciążenie silnika, jednak zgodnie z uczynionym
na wstępie założeniem, wszystkie badania symulacyjne zostaną przeprowadzone w warunkach
idealnego biegu jałowego. Oznacza to, że sygnał wejściowy bloku

2 będzie równy zero. Warto

zapamiętać, że zachodzi tu jednak możliwość łatwego rozszerzenia programu badań symulacyjnych o
przypadki uwzględniające niezerową wartość

.

5. Przebieg ćwiczenia

Należy zbudować opisane regulatory (proporcjonalny, całkujący, proporcjonalno-całkujący,

proporcjonalno-różniczkujący, proporcjonalno-całkujaco,różniczkujący), przy użyciu bloków podanych
przez prowadzącego, w programie Simulink, a otrzymane wyniki symulacji. Następnym krokiem
będzie przeprowadzenie symulacji działania zamkniętego układu regulacji prędkości silnika
w zależności od zastosowanego regulatora i wartości jego współczynników.

5.1. Regulator P

Najprostszym przypadkiem jest układ UAR z regulatorem proporcjonalnym (P). Program uarP.m
demonstruje działanie takiego układu dla trzech arbitralnie wybranych wartości współczynnika

.

13

%Badanie UAR z regulatorem P

clear

clf

;

Rt = 0.465;

Lt = 0.015;

Km = 2.62;

Jb = 2.7;

Ti = 0;

Td = 0;

hold

on

;

for

Kp = [2,5,20];

%przyjęte na próbę trzy wartości współczynnika Kp

[t,x,y] = sim(

'uar'

,1);

plot (t,y(:,2));

end

axis ([0,1,0,1.5]);

title(

'UAR predkosci - regulator P'

);

xlabel (

't[s]'

)

ylabel(

'predkosc obrotowa'

)

grid

X=[0.52, 0.52, 0.52];

Y=[0.46,0.7, 0.93];

text(X(1),Y(1),

'k=2'

)

text(X(2),Y(2),

'k=5'

)

text(X(3),Y(3),

'k=20'

)

hold

off

Proszę uruchomić program uarP.m i dokonać analizy otrzymanego wykresu, na którym pokazano trzy
przebiegi prędkości silnika. Należy zwrócić uwagę na dość znaczną różnicę pomiędzy wartością
zadaną (skok jednostkowy), a prędkością rzeczywistą silnika. Proszę również wskazać zależność
pomiędzy trzema rozpatrywanymi wartościami

, a zmniejszaniem tej różnicy bądź też

wystąpieniem przeregulowania prędkości (ogólny wpływ współczynnika na prędkość obrotową).

5.2. Regulator PI

Dalsze badania symulacyjne doryczą UAR prędkości silnika z regulatorem proporcjonlano-całkującym
(PI).

%Badanie UAR z regulatorem PI

clear

clf

;

Rt = 0.465;

Lt = 0.015;

Km = 2.62;

Jb = 2.7;

Kp = ???;

Td = 0;

hold

on

;

for

Ti = [5,40,100];

%przyjęte na próbę trzy wartości współczynnika Ti

[t,x,y] = sim(

'uar'

,10);

plot (t,y(:,2));

end

axis ([0,1,0,1.5]);

title(

'UAR predkosci - regulator PI'

);

xlabel (

't[s]'

)

ylabel(

'predkosc obrotowa'

)

grid

14

X=[0.52, 0.38, 0.23];

Y=[0.80,1.05, 1.4];

text(X(1),Y(1),

'Ti=5'

)

text(X(2),Y(2),

'Ti=40'

)

text(X(3),Y(3),

'Ti=100'

)

hold

off

Proszę uruchomić powyższy program uarPI.m i w miejsce

zaznaczone na żółto, wpisać wartość

współczynnika wzmocnienia wyselekcjonowaną w zadaniu z regulatorem P. Dalsze obliczenia
prowadzone są dla trzech, również arbitralnie wybranych, wartości współczynnika dla części
całkującej regulatora .

Należy ponownie przeanalizować otrzymane przebiegi prędkości silnika, zaznaczając na wstępie
co dało dołączenie do regulatora części całkującej. Po dokonaniu oceny uzyskanych przebiegów,
należy wybrać najkorzystniejszy (uzasadniając odpowiedź warto wziąć pod uwagę sposób ustalania
się prędkości).

5.3. Regulator PID

Do tej pory, posługując się metodą symulacji komputerowej, określone zostały takie wartości
współczynników

i , które zapewniają pożądany kształt przebiegu prędkości silnika prądu stałego.

Wprowadzamy do istniejącego regulatora PI część różniczkującą, czyli konstruujemy regulator PID.
Program do obliczeń i symulacji UAR z regulatorem PID przedstawiono poniżej. Działając zgodnie
z zastosowanym już wcześniej schematem, należy uruchomić plik uarPID.m, wpisać w miejsce
znaków zapytania ustalone wartości

i , a następnie przeprowadzić badania dla trzech, próbnie

dobranych, wartości współczynnika wzmocnienia

części różniczkującej regulatora.

%Badanie UAR z regulatorem PID

clear

clf

;

Rt = 0.465;

Lt = 0.015;

Km = 2.62;

Jb = 2.7;

Kp = ???;

Ti = ???;

hold

on

for

Td = [0.01, 1, 3];

%przyjęte na próbę trzy wartości współczynnika Td

[t,x,y] = sim(

'uar'

,1);

plot (t,y(:,2));

end

axis ([0,1,0,1.5]);

title(

'UAR predkosci - regulator PID'

);

xlabel (

't[s]'

)

ylabel(

'predkosc obrotowa'

)

grid

X=[0.07, 0.21, 0.35];

Y=[0.8,0.8, 0.8];

text(X(1),Y(1),

'Td=0.01'

)

text(X(2),Y(2),

'Td=1'

)

text(X(3),Y(3),

'Td=3'

)

hold

off

15

Po dokonaniu oceny otrzymanych wykresów, należy wybrać najkorzystniejszy przebieg prędkości
(odpowiedź proszę uzasadnić).

5.4. Zadanie regulacji prędkości obrotowej silnika

Powracając do UAR z regulatorem PID, którego parametry zostały już ręcznie dobrane, raz jeszcze
przytoczony zostanie przebieg prędkości oraz nie zaprezentowany poprzednio przebieg prądu.

W tym celu proszę otworzyć program uarPID2.m i jeszcze raz uzupełnić, otrzymane w wyniku
poprzednich zadań, wartości

, i

.

%Badanie UAR z regulatorem PID

clear

clf

;

Rt = 0.465;

Lt = 0.015;

Km = 2.62;

Jb = 2.7;

Kp = ???;

Ti = ???;

Td = ???;

hold

on

[t,x,y]=sim(

'uar'

,1);

plot(t,y(:,1),t,y(:,2)*10);

title(

'silnik w UAR prędkości'

);

xlabel (

't[s]'

)

ylabel(

'predkosc prad'

)

text(0.42,10.4,

'predkosc*10'

)

text(0.42, 0.7,

'prad'

)

grid

hold

off

Proszę spróbować osiągnąć kompromis pomiędzy szybkością narastania prędkości obrotowej,
a skokiem prądu rozruchowego. Otrzymane wyniki proszę skomentować.
Również można przeprowadzić dobór nastaw regulatora PID przy użyciu metody Zieglera-Nicholsa.

5.5. Sprawozdanie

Sprawozdanie z ćwiczenia ma zawierać:

1) Wstęp teoretyczny (maksymalnie 2 strony A4).
2) Schematy blokowe regulatorów wykonane w Simulinku oraz ich charakterystyki skokowe.
3) Wpływ współczynników regulatorów na czas regulacji i przeregulowanie (np. „dla wartości …

czas regulacji jest większy/mniejszy niż w przypadku …”, itp.).

4) Wyniki osiągnięte w zadaniu regulacji prędkości obrotowej silnika. Krótki opis sposobu

doboru nastaw.

5) Wnioski i obserwacje nasuwające się po przeprowadzonych badaniach.