Nazwisko: Łotysz Maciej Informatyka gr.25

Sprawozdanie z laboratorium z fizyki

Temat: 222. Pomiar czasu zderzenia kul, sprawdzenie wzoru Hertza.

Data: Ocena: Podpis: Zespół: 6

1. Część teoretyczna.

Rozróżniamy 2 skrajne rodzaje zderzeń ciał: idealnie sprężyste oraz idealnie niesprężyste. W
praktyce idealne zderzenia nie występują; badane zjawiska łączą w sobie cechy zdarzeń
sprężystych i niesprężystych.
Gdy 2 ciała zderzają się ze sobą, odkształcają się w miejscu zetknięcia. Przez bardzo krótką chwilę
ciała zwykle poruszają się razem. Wywierają one na siebie nawzajem krótko trwające impulsy, po
czym rozłączają się i biegną dalej ze zmienionymi prędkościami. Jeżeli są to ciała sprężyste, tak
jak badane kule, to powracają do poprzedniego kształtu. Zderzenie jest doskonale sprężyste, jeżeli
suma energii kinetycznych po zderzeniu równa się sumie energii kinetycznych przed zderzeniem.
Jeżeli normalna do płaszczyzny, zwana linią zderzenia, przechodzi przez środkui mas obu ciał,
to zderzenie nazywa się cenralnym lub środkowym. Zderzenie kul jednorodnych, badane w tym
ćwiczeniu, jest zawsze centralne. Jeżeli środki obu kul poruszają się po tej samej prostej, to linia
zderzenia z nią się schodzi. Takie zderzenie nazywamy prostym lub czołowym. W przeciwnym
razie nazywa się ukośnym. Po zderzeniu czołowym środki obu kul biegną w dalszym ciągu po tej
samej prostej co przed zderzeniem.
Rozpatrzmy zderzenie czołowe 2 doskonale sprężystych kul, o masach m oraz M, których
środki poruszają się po linii prostej. Kula o masie m ma prędkość v, kula o masie M - prędkość V. Na
układ kul nie działają żadne siły zewnętrzne. Stosujemy tu więc zasadę zachowania pędu i energii.
Pędy obu kul:
przed zderzeniem: p1=m*v1, P1=M*V1.
po zderzeniu : p2=m*v2, P2=M*V2

Energie kinetyczne przed zderzeniem:

m v1

2

⋅

2

p1

2

2 m

⋅

:=

M V1

2

⋅

2

P1

2

2 M

⋅

:=

Energie kinetyczne po zderzeniu:

m v2

2

⋅

2

p2

2

2 m

⋅

:=

M V2

2

⋅

2

P2

2

2 M

⋅

:=

Stosując zasadę zachowania energii i pędu, możemy przekształcić te równania, aż do
otrzymanie wzoru na prędkości kul po zderzeniu:

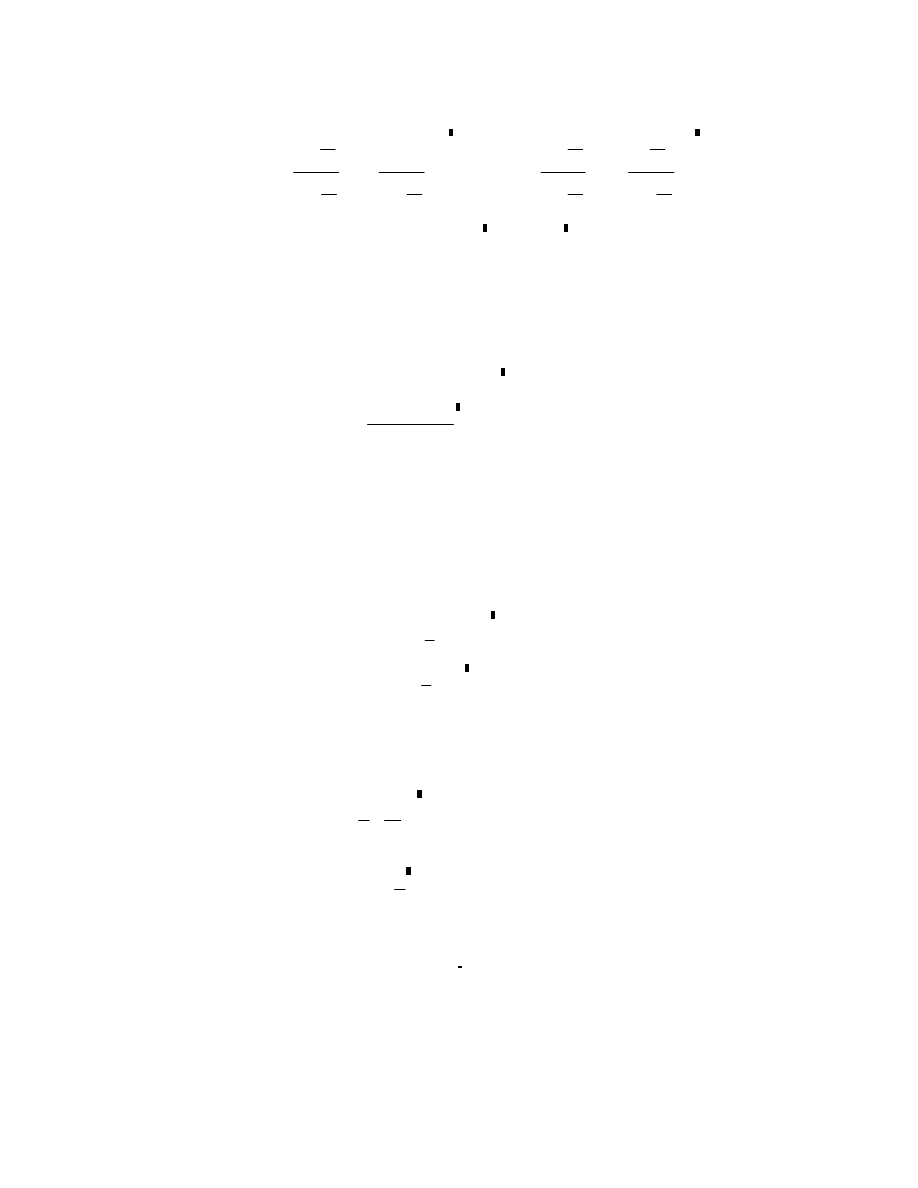
v2

1

m

M

−

1

m

M

+

−

v1

⋅

2

1

m

M

+

V1

⋅

+

:=

V2

1

m

M

−

1

m

M

−

V1

⋅

2

m

M

⋅

1

m

M

+

v1

⋅

+

:=

Jeśli masy obu kul są równe, to:

v2

V1

:=

V2

v1

:=

Przypadek zderzenia doskonale niesprężystego.
Jeśli obie kule są doskonale niesprężyste, np. z ołowiu lub miękkiej gliny, to nie odbijają się
wcale. Rozpatrując zderzenia niesprężyste, należy stosować tylko zasadę zachowania pędu
(energia mechaniczna poruszających się kul zużyta zostaje na pracę odkształceń
sprężystych i nie jest zachowywana). Zgodnie z zasadą zachowania pędu musi być więc
spełnione równanie:

m v1

⋅

M V1

⋅

+

m v

⋅

M v

⋅

+

:=

v - prędkość kul po zderzeniu

Stąd prędkość:

v

m v1

⋅

M V1

⋅

+

m

M

+

:=

Doświadczenie.

Rozmiary geometryczne kuli opisuje promień R, a bezwładność - masa M. Własności
sprężyste są określone przez: moduł Younga E oraz wsp. Poissona .Rozpatrzmy
przypadek, że jedna z kul spoczywa, a druga zbliża się do niej ze stałą prędkością, w
układzie środka masy obu kul. Energia kinetyczna tych kul wynosi :

σ

E

k

2

1

2

⋅

M

⋅

v

1

( )

2

⋅

:=

M - masa zredukowana obu kul
v - prędkość względna

E

k

1

2

μ

⋅ v

2

⋅

:=

Podczas zderzenia dochodzi do odkształceń sprężystych. Niech parametr h określa
względne zbliżenie środków kul w procesie zderzenia. Zmienia się on od 0 do pewnej wartości
maksymalnej h0 i z powrotem. Energia kinetyczna jest proporcjonalna do kwadratu szybkości
zmian parametru h:

E

k

μ

2

dh

dt









2

⋅

:=

zaś energia potencjalna:

E

p

k h

5

2

⋅

:=

k - stały współczynnik

Stosując zasadę zachowania energii, można napisać:

(*)

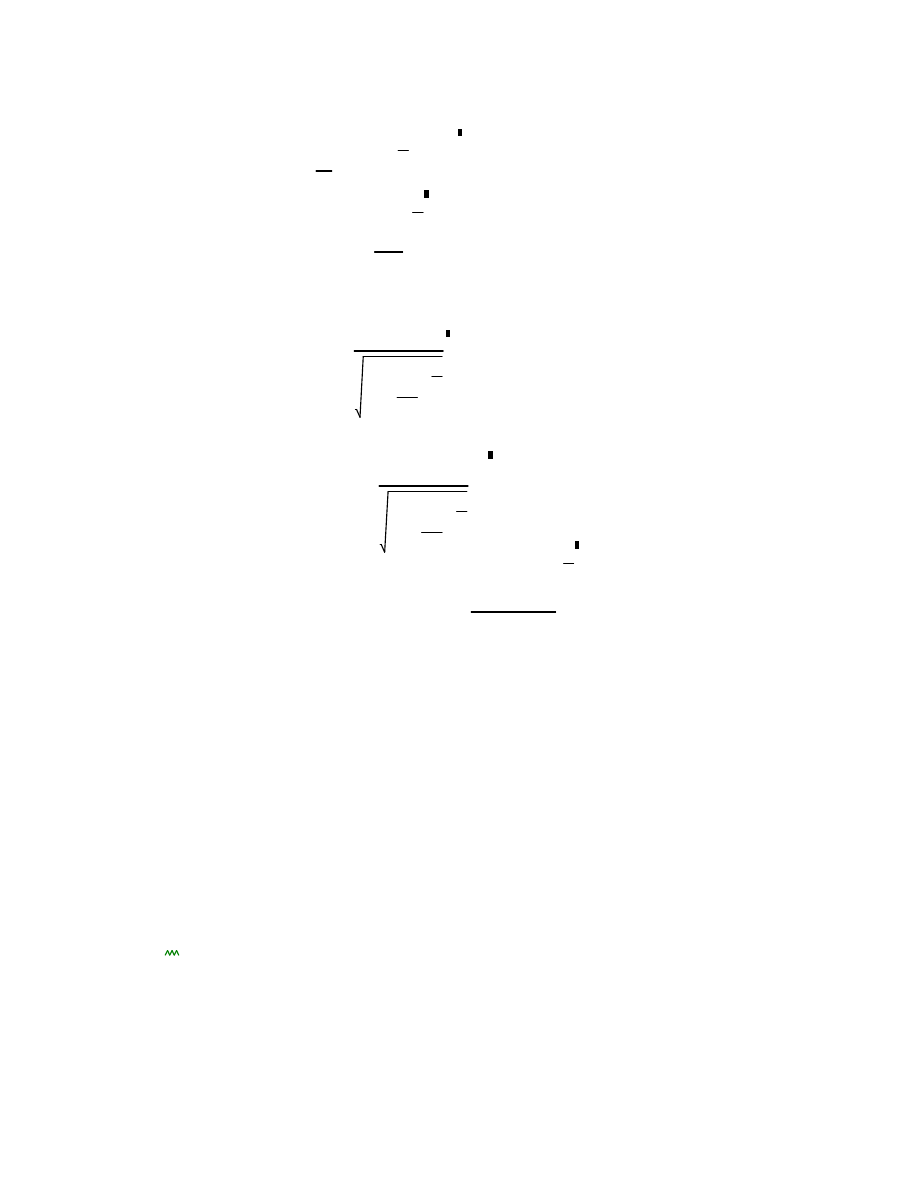
μ

dh

dt









2

⋅

2 k

⋅ h

5

2

⋅

+

μ v

2

⋅

:=

Stąd wzór na h0:

h

0

μ v

2

⋅

2 k

⋅













2

5

:=

Z równania (*) wyznaczamy dt:

dt

dh

v

2

2 k

⋅

μ

h

5

2

⋅

−

:=

Stąd

t

2

0

h

0

h

1

v

2

2 k

⋅

μ

h

5

2

⋅

−

⌠











⌡

d

⋅

:=

Po obliczeniu całki
otrzymujemy:

t

3.291

M

2

1

σ

2

−

(

)

2

⋅

E

2

R

⋅ v

⋅

















1

5

⋅

:=

(wzór Hertza)

Opis czynności w doświadczeniu.

1. Sprawdzić poziome ustawienie przyrządu pomiarowego.
2. Wkręcić pierwszą parę kul na trzpienie.
3. Zmierzyć długość nici, na której zawieszone są kule.
4. Oczyścić kule denaturarem.
5. Włączyć przyrząd.
6. Ustawić żądany kąt wychylenia kuli.
7. Ustawić kulę przy elektromagnesie.
8. Wcisnąć klawisz "nyck" . Uwolniona kula uderzy w kulę spoczywającą. Odczytać czas
zderzenia (mikros.) i wpisać do tabelki.
9. Wyzerować mikrosekundomierz. Dla każdego kąta powtórzyć pomiar ośmiokrotnie.
10. Wykonać opmiary dla 6-ciu kątów.

g

9.81

:=

l

0

0.47

:=

k

0 1

,

5

..

:=

n

0 1

,

7

..

:=

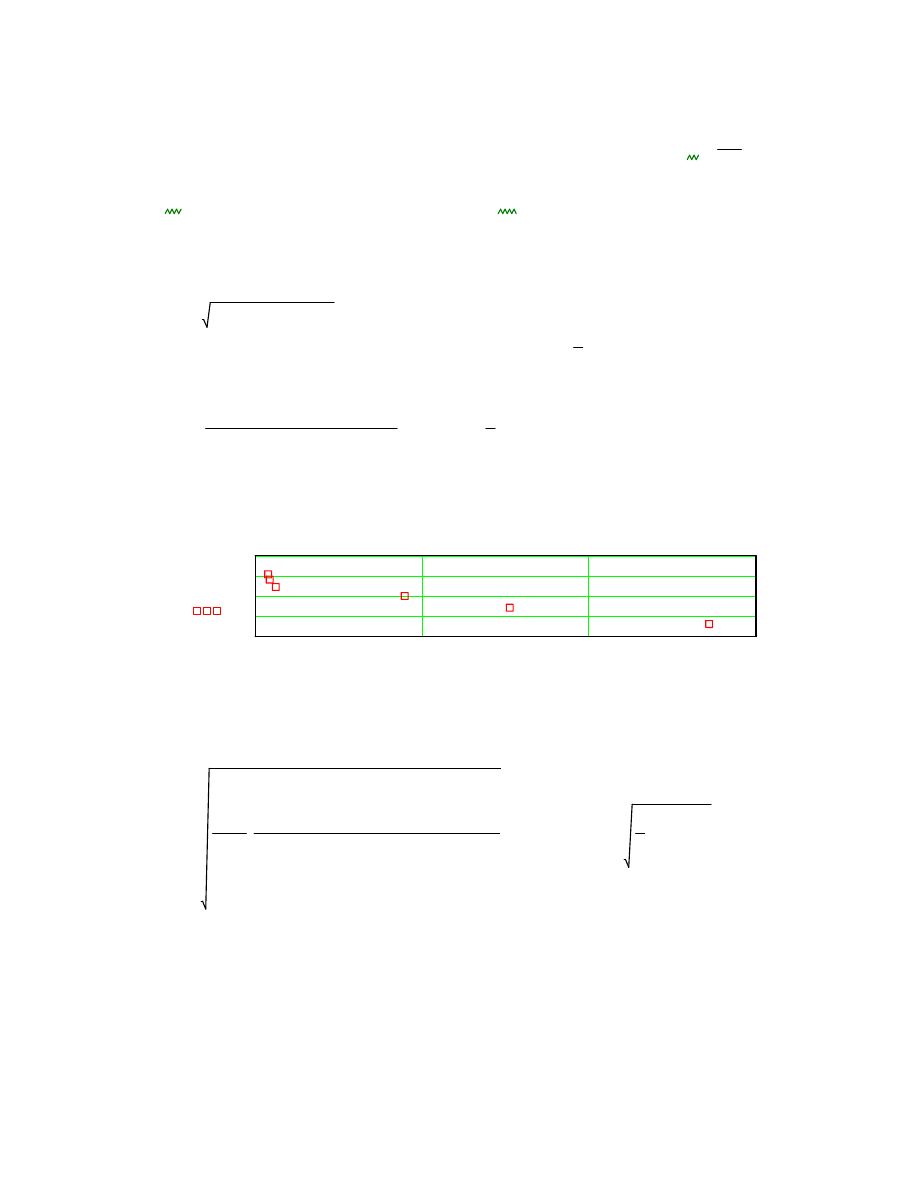
s

π

180

:=

T

182

161

145

118

118

137

191

167

154

153

143

145

166

156

157

150

129

139

184

145

134

137

140

133

175

146

135

144

151

134

185

168

150

137

116

133

171

159

154

126

149

124

167

159

155

131

146

146

































10

3

−

⋅

:=

Φ

3

4.5

6

7.5

9

10.25

































s

⋅

:=

v

k

2 g

⋅ l

0

⋅

1

cos

Φ

k

( )

−

(

)

⋅

:=

τ

k

1

8

0

7

i

T

k i

,

∑

=

⋅

:=

τ

0.178

0.158

0.148

0.137

0.137

0.136

































=

a

6

0

5

i

v

i

τ

i

⋅

( )

∑

=

⋅

0

5

i

v

i

∑

=

0

5

i

τ

i

∑

=

⋅

−

6

0

5

i

v

i

( )

2

∑

=

⋅

0

5

i

v

i

∑

=

















2

−

:=

b

1

6

0

5

i

τ

i

∑

=

a

0

5

i

v

i

∑

=

⋅

−

















⋅

:=

a

0.148

−

=

b

0.186

=

2

−

1.9

−

1.8

−

1.7

−

2.5

−

2

−

1.5

−

1

−

0.5

−

Zaleznosc

czas

p

re

d

k

o

sc

ln v

k

( )

ln

τ

k

( )

Niepewność związana z pomiarem dla współczynników a i b:

S

a

6

6

2

−

0

5

i

τ

i

( )

2

∑

=

a

0

5

i

τ

i

v

i

⋅

( )

∑

=

⋅

b

0

5

i

τ

i

∑

=

⋅

−

















−

6

0

5

i

v

i

( )

2

∑

=

⋅

0

5

i

v

i

∑

=

















2

−

⋅

:=

S

b

S

a

1

6

0

5

i

v

i

( )

2

∑

=

⋅

⋅

:=

S

a

1.257

=

S

b

0.337

=

Współczynnik korelacji pomiędzy v i

τ:

r

6

0

5

i

v

i

τ

i

⋅

( )

∑

=

⋅

0

5

i

v

i

∑

=

0

5

i

τ

i

∑

=

⋅

−

6

0

5

i

v

i

( )

2

∑

=

⋅

0

5

i

v

i

∑

=

















2

−













6

0

5

i

τ

i

( )

2

∑

=

⋅

0

5

i

τ

i

∑

=

















2

−













⋅

:=

r

0.92

=